Устройство и принцип действия морских бесплатформенных инерциальных систем наиболее подробно описаны в книге О.Н. Анучин, Г.И. Емельянцев, под общей редакцией члена-корреспондента РАН В.Г. Пешехонова «Интегрированные системы ориентации и навигации для морских подвижных объектов» (С-Петербург, 1999 г., 357 с.) (Работа 1).
В этом источнике дается ссылка на работу М.Б. Мафтера «Выбор алгоритма бескарданного лазерного гирогоризонткомпаса» (Работа 2), где подробно описан алгоритм БИНС, использующей в качестве инерциальных датчиков лазерные гироскопы - датчики угловой скорости (ДУС) и маятниковые акселерометры, вырабатывающие приращения абсолютного угла поворота ΔQ и кажущейся скорости ΔV за цикл съема информации - Τ в проекциях на оси БИНС: ΔQ (ΔQ1, ΔQ2, ΔQ3), ΔV=(ΔV1, ΔV2, ΔV3)
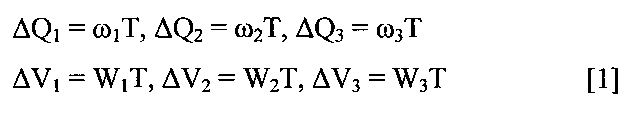
где ω1, ω2, ω3, W1, W2, W3 - проекции на оси БИНС абсолютной угловой скорости (ω) и кажущегося ускорения (W) БИНС.
Для морского объекта, у которого расстояние R (Χ, Υ, Ζ) между центром БИНС (т. О) и центром качания (т. А) (см. рис.1) является постоянной величиной, выражение для измеряемого акселерометрами кажущегося ускорения W в условиях качки со скоростью ω, может быть получено на основе известного выражения для производной вектора во вращающейся системе координат

где V - абсолютная скорость т. О,
 - локальная производная - относительная скорость т. О,
- локальная производная - относительная скорость т. О,
g - вектор ускорения силы тяготения,
ω′ - угловое ускорение качки.
Проекции на оси 1, 2, 3 БИНС тангенциальной ω′R и нормальной ω2R составляющих кажущегося ускорения, порождаемых угловой скоростью качки, могут быть найдены с помощью векторных произведений

С использованием полученных соотношений проекции кажущегося ускорения на оси БИНС, измеряемые триадой акселерометров в условиях качки с угловой скоростью ω и угловым ускорением ω′, будут иметь вид

где g1, g2, g3 - проекции ускорения силы тяготения на оси БИНС.
Приведенный в указанной работе (см. Работа 2) алгоритм морской БИНС осуществляет следующие вычисления:
- вычисляет параметры ориентации осей БИНС относительно аналитического опорного трехгранника (матрицу направляющих косинусов Μ или кватернион λ) путем интегрирования кинематического уравнения Пуассона

где Ω - вектор угловой скорости коррекции аналитического трехгранника, ω=ΔQ/T - абсолютная угловая скорость БИНС,
- перепроектирует сигналы триады акселерометров W=ΔV/T на горизонтальную плоскость аналитического трехгранника с использованием полученных выше параметров ориентации
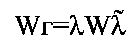
где  - сопряженный кватернион, WГ (WГ1, WГ2, WГ3) - кажущееся ускорение БИНС в проекциях на оси аналитического трехгранника,
- сопряженный кватернион, WГ (WГ1, WГ2, WГ3) - кажущееся ускорение БИНС в проекциях на оси аналитического трехгранника,
- формирует угловую скорость коррекции «Ω» по информации о проекциях на горизонтальную плоскость аналитического трехгранника сигналов триады акселерометров WГ1, WГ2
Ω=f(WГ).
Составляющие сигналов акселерометров, порождаемые силой тяготения, при перепроектировании на горизонтальную плоскость аналитического т-ка не равны нулю, если оси аналитического и географического трехгранников не совпадают.
Скорость коррекции Ω изменяет кватернион λ до тех пор, пока горизонтальные составляющие ускорений не станут равны нулю, т.е. когда горизонтальные оси аналитического и географического трехгранников будут коллинеарны. В рабочем режиме скорость коррекции Ω формируется в соответствии с известными (cм. Работы 1, 2) алгоритмами шулеровской интегральной коррекции или корректируемого гирогоризонткомпаса.
В режиме выставки используются известные алгоритмы пропорциональной или интегральной коррекции, которые в общем случае имеют вид

Примечание: при К2=0 - пропорциональная коррекция.
В начале выставки, когда требуется отработать большие рассогласования в ориентации аналитического и географического трехгранников, используется пропорциональная коррекция, при которой ошибки угловой ориентации пропорциональны дрейфам угловых скоростей, измеренных ДУС.
На втором этапе используется интегральная коррекция, при которой ошибки угловой ориентации пропорциональны производным дрейфов.
Основная ошибка угловой ориентации аналитического трехгранника по отношению к географическому в обоих режимах выставки связана с периодическими возмущениями составляющих сигналов акселерометров, порождаемых качкой. Например, теоретическое моделирование уравнений БИНС в режиме начальной выставки показывает, что при постоянной времени режима интегральной коррекции 100 с и действии линейных ускорений качки с амплитудой 1 м/с2 периодические возмущения горизонтальных составляющих угловых скоростей коррекции аналитического трехгранника Ωе, Ωn составят 0.1-0.5 град/ч.
При определении курсового угла К и широты φ методом гирошироткомпаса, используемым в современных БИНС
К=arctg (Ωe/Ωn)

где U - угловая скорость Земли.
Указанные периодические возмущения сигналов Ωe, Ωn вызовут ошибки ΔΚ, Δφ на уровне нескольких градусов. Для современных БИНС ошибки начальной выставки по курсу и широте не должны превышать единиц угловых минут.
Для уменьшения периодических ошибок начальной выставки в существующих морских БИНС осуществляют фильтрацию периодических составляющих ускорений путем увеличения постоянной времени τ переходных процессов за счет уменьшения величины коэффициентов Κ1 и К2 так, чтобы τ>>Тк (период качки).
Например, в первой отечественной морской БИНС КАМА-НС-В τ=5-10 минут и время готовности составляет 15-30 минут.
Дальнейшее уменьшение периодических погрешностей начальной выставки требует увеличения τ, а следовательно, и увеличения времени готовности.
Таким образом, указанный в работе (Работа 2) способ выставки морской БИНС или морского гирогоризонткомпаса содержит следующие операции:
- вычисление параметров ориентации БИНС относительно аналитического трехгранника (матрицы направляющих косинусов или кватерниона) путем интегрирования кинематического уравнения Пуассона по информации ДУС и угловой скорости коррекции;
- перепроектирование сигналов триады акселерометров на горизонтальную плоскость аналитического трехгранника с использование полученных параметров ориентации;
- формировании угловой скорости коррекции по информации о проекциях на горизонтальную плоскость аналитического трехгранника сигналов триады акселерометров с использованием алгоритмов пропорциональной или интегральной коррекции.
Недостатком указанного способа в условиях воздействия линейных ускорений качки являются большие погрешности начальной выставки (в частности, по курсу и широте), которые могут быть уменьшены лишь за счет увеличения постоянной времени переходных процессов путем снижения величины коэффициентов коррекции, что приводит к увеличению времени готовности.
Указанный недостаток устраняется, если в способ-прототип вводятся следующие операции:
- вычисление угловых скоростей и ускорений в проекциях на собственные оси БИНС по сигналам ДУС
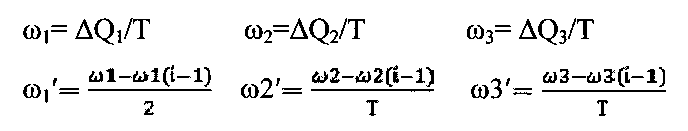
где i - номер цикла съема информации ДУС;
- формирование поправок к сигналам триады акселерометров по информации о вычисленных угловых скоростях ω1, ω2, ω3 и ускорениях ω1′, ω2′, ω3′ и расстоянии R (Χ, Υ, Ζ) между центром БИНС и центром качания корабля в соответствии с формулами
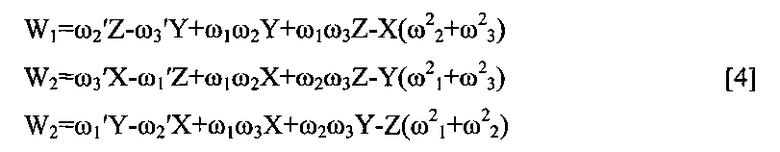
- перед перепроектированием производят вычитание из сигналов триады акселерометров указанных поправок.
Эффективность предлагаемого способа подтверждается следующими теоретическими расчетами и практическими испытаниями первой отечественной морской БИНС КАМА-НС-В.
При формировании поправок в соответствии с формулами [4], в которых информация об угловых скоростях, ускорениях и расстоянии от центра качания не имеет погрешностей, в сигналах триады акселерометров, как видно из формул [3], не будет составляющих, порождаемых качкой.
Остаточные периодические составляющие сигналов акселерометров будут порождаться погрешностями формирования поправок, которые в свою очередь определяются ошибками сигналов ДУС и неточностью измерения положения центра качания корабля.
Максимальное расстояние между центром БИНС и центром качания может составлять 100 м, а изменение положения центра качания не превышает 1-10 метров, что приводит к относительной ошибке формирования поправок на уровне 0,01-0,1.
Ошибка измерения сигналов ДУС прежде всего определяется погрешностью масштабного коэффициента, величина которой для современных лазерных и волоконно-оптических датчиков не превышает 5*10-5.
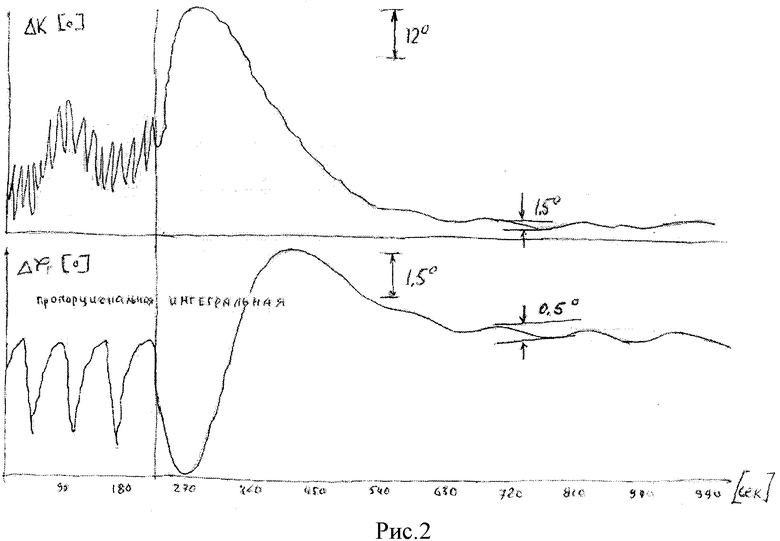
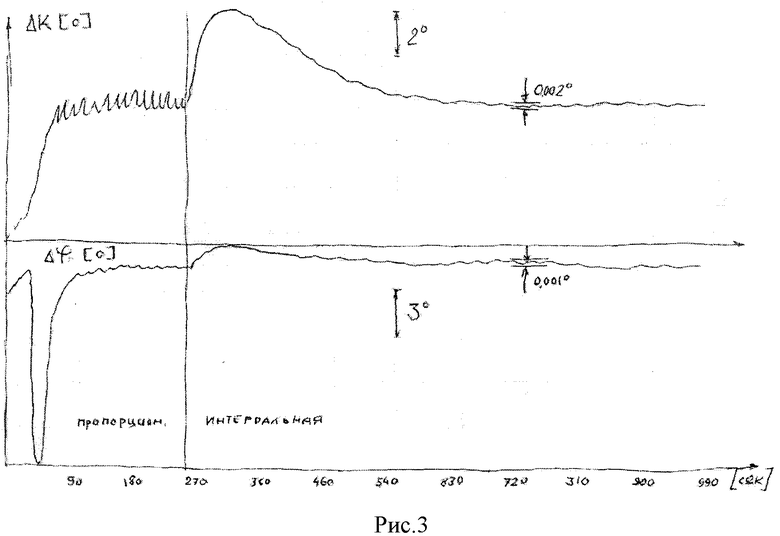
Таким образом, погрешность формирования поправок определяется только изменением положения центра качания и не превышает 0,1 (10%). Этот факт подтверждается теоретическим моделированием уравнений БИНС на компьютере и экспериментальными испытаниями БИНС КАМА-НС-В на качающемся стенде. На рис.2 и 3 представлены результаты теоретического моделирования уравнений, реализующих предлагаемый способ выставки БИНС в условиях воздействия ускорений качки с амплитудой 1 м/с2 и периодом 60 с: графики погрешности курсового угла ΔΚ и широты Δφ, определенных методом гирошироткомпаса при постоянной времени режимов пропорциональной коррекции 30 с и интегральной коррекции 100 с. Представленные на рис.2 графики погрешностей обычного способа выставки имеют амплитуду ΔΚ=1,5°, Δφ=0,5°, а на рис.3 при использовании предлагаемого способа амплитуды значительно меньше - ΔΚ=0,002°, Δφ=0,001°.
Таким образом, теоретическое исследование предлагаемого способа подтверждает существенное (на несколько порядков) снижение периодических погрешностей, порождаемых линейными ускорениями качки, без увеличения постоянной времени режимов приведения, а следовательно, и времени готовности БИНС.
На рис.4 и 5 представлены результаты экспериментальных испытаний на качающимся стенде «СКОРСБИ» серийной БИНС КАМА-НС-В при воздействии ускорений качки с амплитудой 0,6 м/с2 и периодом 10-20 с: графики погрешностей курсового угла ΔΚ и широты Δφ, определенных методом гирошироткомпаса, при постоянной времени режимов пропорциональной коррекции -30 с и интегральной коррекции -100 с; при этом погрешность определения расстояния от центра качания стенда Rz=1,8 м не превышала 6 см, то есть составляла 3%.
Представленные на рис.4 графики с обычным способом выставки имеют амплитуды ΔΚ=2′, Δφ=3′, а на рис.5 - с применением предлагаемого способа - амплитуды ΔΚ=0,015′, Δφ=0,01′.
Таким образом, экспериментальная проверка предлагаемого способа также подтверждает его эффективность.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИНТЕГРИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ СИСТЕМА НАВИГАЦИИ СРЕДНЕЙ ТОЧНОСТИ ДЛЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2013 |
|
RU2539140C1 |
| БЕСПЛАТФОРМЕННАЯ ИНТЕГРИРОВАННАЯ НАВИГАЦИОННАЯ СИСТЕМА СРЕДНЕЙ ТОЧНОСТИ ДЛЯ МОБИЛЬНОГО НАЗЕМНОГО ОБЪЕКТА | 2013 |
|
RU2539131C1 |
| СПОСОБ ОЦЕНКИ ОШИБОК И КОНТРОЛЯ ДАТЧИКОВ ПЕРВИЧНОЙ ИНФОРМАЦИИ В СОСТАВЕ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ В НАЗЕМНЫХ УСЛОВИЯХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2537513C2 |
| ИНТЕГРИРОВАННЫЙ КОМПЛЕКС ДЛЯ НАВИГАЦИИ И УПРАВЛЕНИЯ МОРСКИХ СУДОВ | 1997 |
|
RU2117253C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ УПРАВЛЯЕМЫХ ПОДВИЖНЫХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2241959C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2634071C1 |
| Способ определения ориентации объекта в бесплатформенной инерциальной навигационной системе | 2022 |
|
RU2794283C1 |
| Адаптивный корректор углов ориентации для БИНС | 2020 |
|
RU2749152C1 |
| Способ определения углов ориентации ЛА на вертикальных траекториях полета | 2017 |
|
RU2671291C1 |
| Судовой электронный кренодифферентометр | 2023 |
|
RU2817308C1 |


Изобретение относится к области навигационного приборостроения и может найти применение в системах морской навигации. Технический результат - повышение быстродействия. Для этого выставку морской бесплатформенной инерциальной навигационной системы (БИНС), обеспечивающей уменьшение погрешностей начальной выставки в условиях качки без увеличения времени готовности, осуществляют за счет использования поправок к сигналам акселерометров, формируемых по информации об угловых скоростях, угловых ускорениях и расстоянии между центром БИНС и центром качания корабля. 5 ил.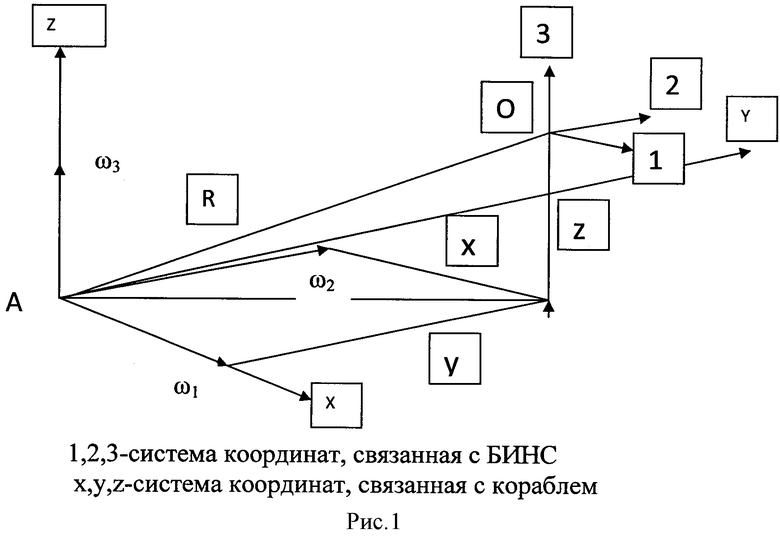
Способ выставки морской бесплатформенной инерциальной навигационной системы (БИНС), включающий вычисление параметров ориентации БИНС относительно аналитического трехгранника путем интегрирования кинематического уравнения Пуассона по информации датчиков угловой скорости (ДУС) и угловой скорости коррекции; перепроектирование сигналов триады акселерометров на горизонтальную плоскость аналитического трехгранника с использованием полученных параметров ориентации; формирование угловой скорости коррекции по информации о проекциях на горизонтальную плоскость аналитического трехгранника сигналов триады акселерометров с использованием алгоритмов пропорциональной или интегральной коррекции, отличающийся тем, что с целью уменьшения погрешностей начальной выставки в условиях качки дополнительно вычисляются по сигналам ДУС угловые скорости и угловые ускорения, формируются поправки по информации об угловых скоростях, угловых ускорениях и о расстоянии между центром БИНС и центром качания корабля по соответствующим формулам и перед проектированием производится вычитание из триады акселерометров указанных поправок.
Авторы
Даты
2016-01-20—Публикация
2014-09-09—Подача