Изобретение относится к области обработки данных в бесплатформенных инерциальных навигационных системах (БИНС), работающих в автономном режиме.
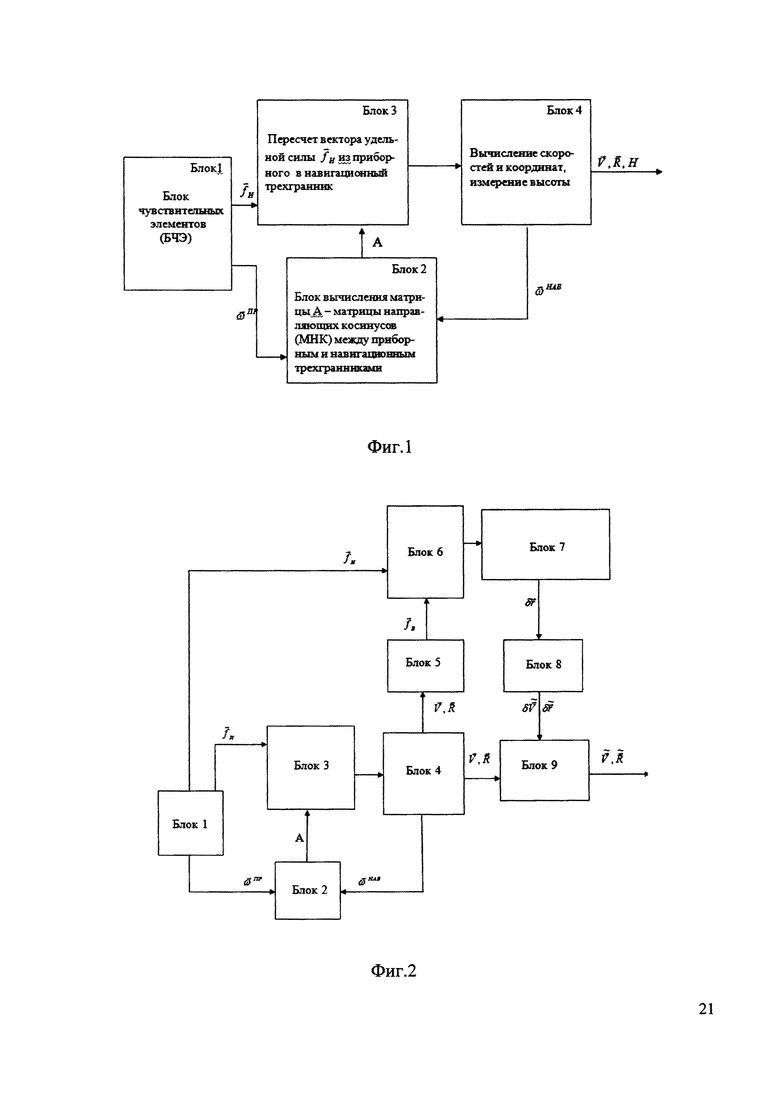
Из уровня техники известен выбранный в качестве прототипа способ определения навигационных параметров бесплатформенной инерциальной навигационной системой (Патент RU 2348903 C1, МПК: G01C 21/10, опубл. 10.03.2009) (фиг. 1), основанный на использовании сигналов блока акселерометров и гироскопических датчиков угловых скоростей путем расчета матрицы направляющих косинусов между связанной и навигационной системами координат, пересчета показаний акселерометров из связанной в навигационную систему координат и их интегрирования для расчета текущих скоростей и координат. Этот способ основан также на вычислении совокупности матриц, связывающих приборный и навигационный трехгранники. Вычисления осуществляются по одним и тем же показаниям блока чувствительных элементов (БЧЭ). Для каждой из полученных матриц вычисляются навигационные параметры. При этом каждая из матриц имеет индивидуальный закон управления и обусловливает индивидуальный частотный спектр погрешностей навигационных параметров. Выходной сигнал БИНС формируется с помощью т.н. мастер-фильтра, формирующего оптимальную комбинацию навигационных решений в зависимости от параметров движения носителя (сильный маневр, слабое маневрирование и крейсерское движение без маневрирования).
Таким образом, сущность известного способа состоит в управлении собственной частотой БИНС в зависимости от динамики движения объекта с оценкой некоторых составляющих погрешностей датчиков первичной информации и компенсацией ошибок БИНС.
Основным недостатком прототипа является то, что при совершении маневров известный способ предполагает включение традиционного режима работы БИНС. В этом случае ошибки системы зависят от точности работы БЧЭ и практически не корректируются внутренними связями, что может затруднить использование прототипа на маневренных носителях.
Техническим результатом предложенного способа является существенное повышение точности автономного счисления навигационных параметров (координат, линейных скоростей, высоты).
Технический результат достигается тем, что известный способ определения навигационных параметров бесплатформенной инерциальной навигационной системой основан на использовании сигналов акселерометров и датчиков угловых скоростей и включает измерение на борту движущегося объекта с помощью акселерометров вектора удельной внешней силы в проекциях на оси приборного трехгранника, расчет матрицы направляющих косинусов между приборным и навигационным трехгранниками, пересчет вектора удельной внешней силы в проекции на оси навигационного трехгранника и интегрирование этих показаний для расчета текущих скоростей и координат в виде вектора относительной линейной скорости в осях навигационного трехгранника и вектора положения, при этом при вычислении матрицы направляющих косинусов используется абсолютная угловая скорость приборного трехгранника, измеряемая датчиками угловых скоростей, и абсолютная угловая скорость навигационного трехгранника, вычисляемая как функция от рассчитанных текущих скоростей и координат. При этом согласно изобретению на основании входных параметров текущих скоростей и координат производится вычисление в проекциях на оси навигационного трехгранника вектора удельной внешней силы, соответствующего измеренному с помощью акселерометров, после чего вектор удельной внешней силы, измеренный в проекциях на оси приборного трехгранника, сравнивается с соответствующим ему вектором удельной внешней силы, вычисленным в проекциях на оси навигационного трехгранника, в результате чего вычисляется соответствующая разности измеренного и вычисленного векторов погрешность компенсации вектора удельной силы тяжести и, следовательно, возможность компенсации динамических погрешностей инерциальных координат и ошибок измерения высоты.
Технический результат достигается также тем, что бесплатформенная инерциальная навигационная система, осуществляющая предложенный способ определения навигационных параметров, включает блок чувствительных элементов, соединенный своим первым выходом с первым входом блока вычисления матрицы направляющих косинусов A, а вторым выходом с первым входом блока пересчета вектора удельной внешней силы в проекции на оси навигационного трехгранника, соединенного вторым входом с выходом блока вычисления матрицы направляющих косинусов A, а выходом с блоком вычисления скоростей, координат и измерения высоты, который соединен своим первым выходом со вторым входом блока вычисления матрицы направляющих косинусов A. При этом согласно изобретению блок вычисления скоростей и координат соединен первым выходом со входом блока вычисления вектора удельной внешней силы, пересчитанного в осях навигационного трехгранника, и соединенного выходом с первым входом блока сравнения измеренного в проекциях на оси приборного трехгранника и вычисленного векторов удельной внешней силы, при этом блок сравнения соединен вторым входом с третьим выходом блока чувствительных элементов, а выходом со входом блока вычисления поправок к координатам и высоте, который соединен выходом со входом блока фильтрации поправок, соединенного выходом с первым входом блока уточнения навигационных параметров, причем последний вторым входом соединен с третьим выходом блока вычисления скоростей и координат.
Сущность предложенного способа состоит в следующем.
Пусть в приборной системе координат измеряется некоторый физический вектор 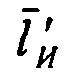 , такой что
, такой что

где 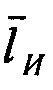 - идеальный измеряемый вектор;
- идеальный измеряемый вектор;
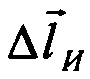 - вектор погрешности измерений.
- вектор погрешности измерений.
Предположим также, что в результате использования известной математической модели можно вычислить в навигационной системе координат вектор 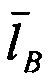 , соответствующий измеренному
, соответствующий измеренному

где 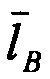 - идеальный вычисленный вектор;
- идеальный вычисленный вектор;
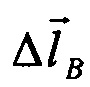 - погрешность определения вычисленного вектора.
- погрешность определения вычисленного вектора.
Требуется найти способ, в результате использования которого можно определить погрешность вычисленного и измеренного вектора. Для этого сравним квадраты модулей измеренного и вычисленного вектора
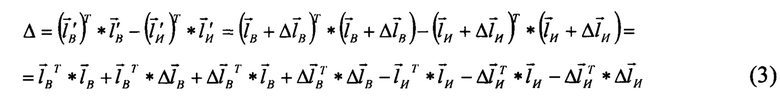
Модули идеальных векторов равны, т.е.
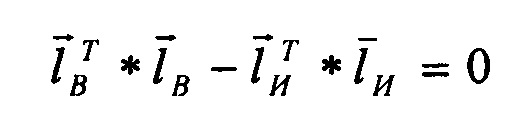 , тогда
, тогда
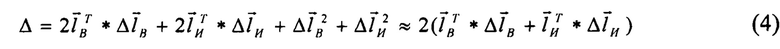
Из последнего соотношения следует общий вывод: в первом приближении разница модулей есть удвоенное скалярное произведение идеального вектора и вектора погрешностей его определения. Значит для существования решения рассматриваемой задачи (4) указанные векторы не должны быть ортогональны.
Рассмотрим бесплатформенную навигационную систему (БИНС). В процессе работы БИНС производится измерение вектора удельной силы 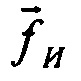 с помощью акселерометров в приборной системе координат и расчет этого вектора в горизонтальном географическом навигационном трехграннике с помощью следующих уравнений:
с помощью акселерометров в приборной системе координат и расчет этого вектора в горизонтальном географическом навигационном трехграннике с помощью следующих уравнений:

где g - удельная сила тяжести;
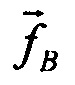 - вычисленный в осях горизонтального географического навигационного трехгранника вектор удельной внешней силы;
- вычисленный в осях горизонтального географического навигационного трехгранника вектор удельной внешней силы;
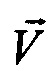 - вектор относительной линейной скорости в осях горизонтального географического навигационного трехгранника;
- вектор относительной линейной скорости в осях горизонтального географического навигационного трехгранника;
 - кососимметрическая матрица, соответствующая относительной угловой скорости,
- кососимметрическая матрица, соответствующая относительной угловой скорости,
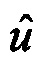 - кососимметрическая матрица, соответствующая абсолютной угловой скорости Земли.
- кососимметрическая матрица, соответствующая абсолютной угловой скорости Земли.
В инерциальном пространстве система (5) и погрешность определения удельной внешней силы примет вид
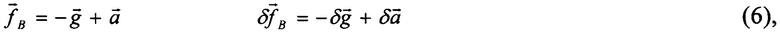
где 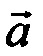 - вектор абсолютного ускорения;
- вектор абсолютного ускорения;
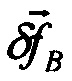 - погрешность вычисленного вектора,
- погрешность вычисленного вектора,
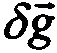 ;
; 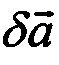 - погрешность компенсации вектора удельной силы тяжести и погрешность вычисления ускорения соответственно.
- погрешность компенсации вектора удельной силы тяжести и погрешность вычисления ускорения соответственно.
Пусть погрешность измерения высоты равна нулю.
В результате анализа (5) и (6) следует, что в инерциальном пространстве погрешность определения удельной силы 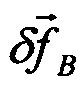 есть ошибка первого дифференциала от абсолютной линейной скорости (вектор погрешности акселерометров)
есть ошибка первого дифференциала от абсолютной линейной скорости (вектор погрешности акселерометров) 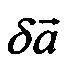 плюс ошибка аналитического учета вектора силы тяжести
плюс ошибка аналитического учета вектора силы тяжести 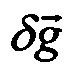 . В свою очередь, погрешность аналитического учета вектора удельной силы тяжести является функцией от горизонтальной составляющей динамической абсолютной ошибки местоположения и частоты Шулера ω0
. В свою очередь, погрешность аналитического учета вектора удельной силы тяжести является функцией от горизонтальной составляющей динамической абсолютной ошибки местоположения и частоты Шулера ω0

где 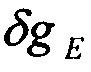 ,
, 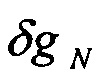 - горизонтальные составляющие вектора
- горизонтальные составляющие вектора 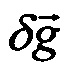 ;
;
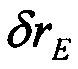 ,
, 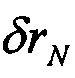 - динамические составляющие горизонтальной абсолютной ошибки местоположения.
- динамические составляющие горизонтальной абсолютной ошибки местоположения.
Для определения упрощенных аналитических соотношений, выражающих условия успешной реализации изобретения в БИНС, допустим, что объект движется на постоянной высоте и вертикальный канал системы корректируется от идеального высотомера.
Математическая модель погрешности вычисленного вектора в географическом горизонтальном трехграннике при корректируемом вертикальном канале БИНС
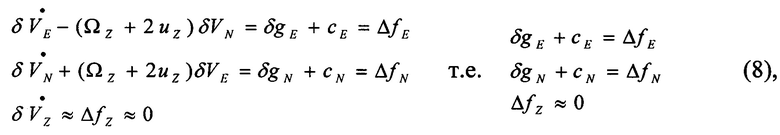
где 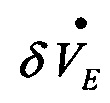 ,
, 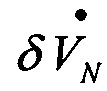 ,
, 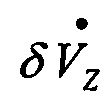 - первый дифференциал от составляющих вектора погрешности БИНС по скорости;
- первый дифференциал от составляющих вектора погрешности БИНС по скорости;
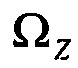 - вертикальная составляющая вектора относительной угловой скорости;
- вертикальная составляющая вектора относительной угловой скорости;
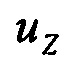 - вертикальная составляющая вектора угловой скорости Земли;
- вертикальная составляющая вектора угловой скорости Земли;
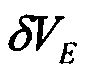 ,
, 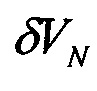 - горизонтальные составляющие вектора погрешности БИНС по скорости;
- горизонтальные составляющие вектора погрешности БИНС по скорости;
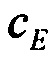 ,
, 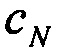 - горизонтальные составляющие вектора погрешностей акселерометров;
- горизонтальные составляющие вектора погрешностей акселерометров;
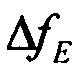 ,
, 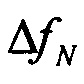 ,
, 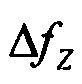 - составляющие погрешностей вычисления вектора удельной силы;
- составляющие погрешностей вычисления вектора удельной силы;
С учетом (6) и (8) равенство (4) для рассматриваемого случая примет следующий вид:
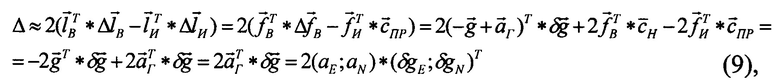
где 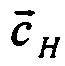 ;
; 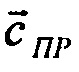 - инструментальные погрешности акселерометров в навигационных и приборных осях соответственно;
- инструментальные погрешности акселерометров в навигационных и приборных осях соответственно;
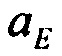 ;
; 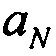 - горизонтальные составляющие вектора ускорения.
- горизонтальные составляющие вектора ускорения.
Из последнего выражения следует:
- поскольку вектор 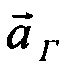 не ортогонален вектору
не ортогонален вектору 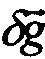 (как следует из (7)), выполняется условие (4);
(как следует из (7)), выполняется условие (4);
- при выполнении следующих условий движения объекта

Можно составить и решить систему линейно независимых уравнений относительно 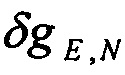 . Здесь индексы «(1)», «(2)» обозначают номера замеров
. Здесь индексы «(1)», «(2)» обозначают номера замеров 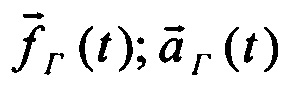 . Отсюда следует, что при непрерывном изменении вектора горизонтального ускорения
. Отсюда следует, что при непрерывном изменении вектора горизонтального ускорения 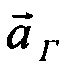 относительно навигационного трехгранника и при коррекции от идеального высотомера задача автономного повышения точности БИНС имеет решение.
относительно навигационного трехгранника и при коррекции от идеального высотомера задача автономного повышения точности БИНС имеет решение.
Для повышения надежности определения высоты с помощью высотомера бывает весьма полезно проводить параметральный контроль работы этого датчика. Для этого контроля весьма желательно иметь дополнительную информацию о высоте или о погрешностях определения высоты. Однако в этом случае рассматриваемая задача усложняется и приводит к системе уже не второго, а третьего порядка.
С целью получения общих условий движения объекта, обусловливающего существование решения поставленной задачи (автономного увеличения точности определения трехмерного вектора навигационных погрешностей БИНС), допустим, что высота объекта измеряется высотомером. Погрешность высотомера - ΔH. Поведение навигационных параметров подчиняется системе (5). Третье уравнение системы (8) примет вид
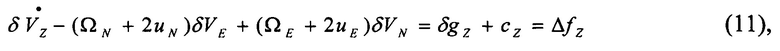
где 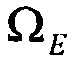 ,
, 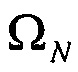 - восточная и северная составляющая вектора относительной угловой скорости;
- восточная и северная составляющая вектора относительной угловой скорости;
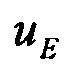
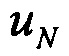 - восточная и северная составляющая вектора угловой скорости Земли;
- восточная и северная составляющая вектора угловой скорости Земли;
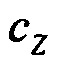 - вертикальная составляющая вектора инструментальных погрешностей акселерометров;
- вертикальная составляющая вектора инструментальных погрешностей акселерометров;
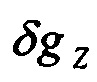 - погрешность аналитического учета вертикальной составляющей вектора
- погрешность аналитического учета вертикальной составляющей вектора 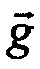 .
.
Указанная погрешность является функцией инструментальной ошибки высотомера и равна

Как было отмечено выше (см. (4)), в основе процедуры получения уточняющих параметров лежит сравнение соответствующих измеренного физического вектора удельной силы 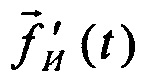 в проекциях на оси приборного трехгранника и этого же, но вычисленного вектора в проекциях на оси второй, сопровождающей навигационной системы координат
в проекциях на оси приборного трехгранника и этого же, но вычисленного вектора в проекциях на оси второй, сопровождающей навигационной системы координат 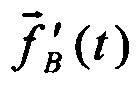 . В результате сравнения квадратов модулей, аналогично (6), можно получить выражение для разности
. В результате сравнения квадратов модулей, аналогично (6), можно получить выражение для разности
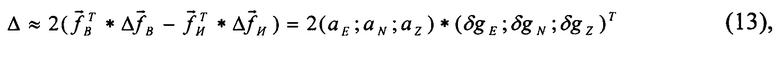
где 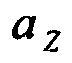 - вертикальная составляющая ускорения.
- вертикальная составляющая ускорения.
Из (9) и (11) следует, что разность Δ не является функцией 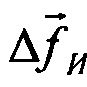 . Динамическая ошибка вектора погрешностей положения БИНС
. Динамическая ошибка вектора погрешностей положения БИНС 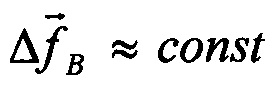 .
.
Допустим, что 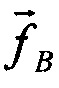 меняет свою ориентацию в пространстве навигационной системы координат БИНС. Последовательно измеряя
меняет свою ориентацию в пространстве навигационной системы координат БИНС. Последовательно измеряя 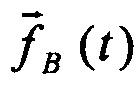 , можно составить систему линейных алгебраических уравнений относительно
, можно составить систему линейных алгебраических уравнений относительно 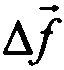 . (Далее для упрощения обозначений индекс «в» опускается).
. (Далее для упрощения обозначений индекс «в» опускается).
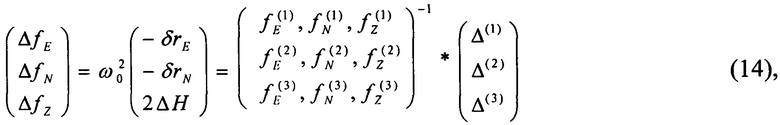
где индексы «(1)», «(2)», «(3)» обозначают номера замеров 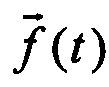 .
.
Пусть приращение вектора между вторым и первым замером 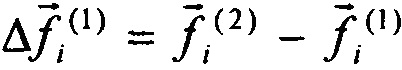 ;
;
приращение вектора между третьим и вторым замером 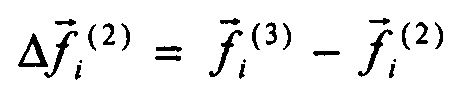 ;
;
приращение между третьим и первым замером 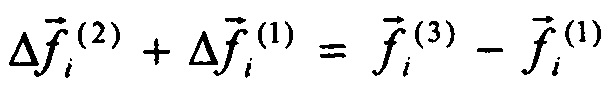 .
.
Обычно выполняются следующие соотношения: 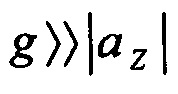 - в режиме крейсерского полета или
- в режиме крейсерского полета или 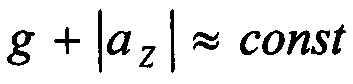 - при взлете или посадке. Поэтому можно принять, что
- при взлете или посадке. Поэтому можно принять, что 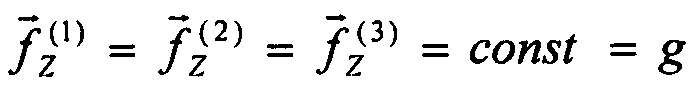 . Тогда определитель матрицы (14) будет описываться следующими соотношениями:
. Тогда определитель матрицы (14) будет описываться следующими соотношениями:
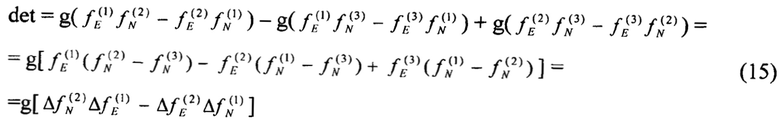
Из (15) следует, что для хорошей обусловленности системы приращение вектора должно меняться от измерения к измерению. Это достигается, например, при изменении ориентации вектора по гармоническому закону при развороте носителя. При этом, чем больше скорость разворота, тем больше обусловленность матрицы (14).
Далее возможна оценка наблюдаемых элементов вектора состояния погрешностей системы.
Допустим, что вектор 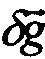 получен с использованием предлагаемого способа и, следовательно, известен в проекциях на оси навигационного сопровождающего трехгранника, например географического:
получен с использованием предлагаемого способа и, следовательно, известен в проекциях на оси навигационного сопровождающего трехгранника, например географического: 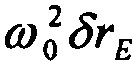 ;
; 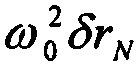 ; 0. Покажем наличие внутренних информационных связей, а значит и возможность косвенного определения наблюдаемых элементов погрешности БИНС
; 0. Покажем наличие внутренних информационных связей, а значит и возможность косвенного определения наблюдаемых элементов погрешности БИНС 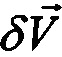 ,
, 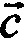 ,
, 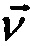 по информации о
по информации о 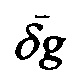 . Здесь
. Здесь 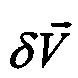 - вектор погрешности БИНС по скорости,
- вектор погрешности БИНС по скорости, 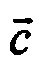 - вектор погрешности акселерометров,
- вектор погрешности акселерометров, 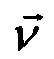 - вектор погрешности ДУС - датчиков абсолютной угловой скорости БИНС. Для этого необходимо рассмотреть математическую модель погрешностей системы.
- вектор погрешности ДУС - датчиков абсолютной угловой скорости БИНС. Для этого необходимо рассмотреть математическую модель погрешностей системы.
Искомые уравнения погрешностей представим упрощенно, но без потери иллюстративных свойств примера. Для этого введем свободный в азимуте трехгранник: ω3=0. Тогда упрощенная математическая модель примет вид

где 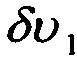 ;
; 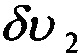 - динамические составляющие абсолютной линейной скорости движения центра масс объекта;
- динамические составляющие абсолютной линейной скорости движения центра масс объекта;
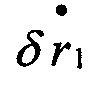 ;
; 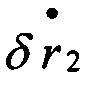 - первый дифференциал от горизонтальных составляющих вектора позиционных погрешностей БИНС;
- первый дифференциал от горизонтальных составляющих вектора позиционных погрешностей БИНС;
R - вектор положения;
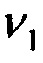 ;
; 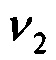 - горизонтальные составляющие вектора погрешностей ДУС;
- горизонтальные составляющие вектора погрешностей ДУС;
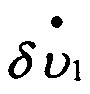 ;
; 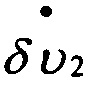 - горизонтальные составляющие вектора абсолютной линейной скорости;
- горизонтальные составляющие вектора абсолютной линейной скорости;
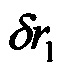 ;
; 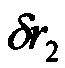 - горизонтальные составляющие вектора позиционных погрешностей;
- горизонтальные составляющие вектора позиционных погрешностей;
c1; c2 - горизонтальные составляющие вектора погрешностей акселерометров.
При этом

Выберем систему уравнений, соответствующих одному каналу измерений, например «1»

Пусть объект движется прямолинейно и равномерно, тогда можно допустить, что c1 = const, ν2 = const.
Рассмотрим первое уравнение:
δr1 - известно (по условию задачи), следовательно, 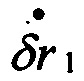 - можно вычислить; отсюда следует, что δυ1 оценивается с точностью до величины Rν2
- можно вычислить; отсюда следует, что δυ1 оценивается с точностью до величины Rν2
Из первого уравнения следует также

где 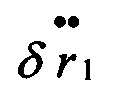 - второй дифференциал от первой составляющей вектора позиционных погрешностей.
- второй дифференциал от первой составляющей вектора позиционных погрешностей.
Значит 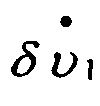 можно вычислить. Тогда из второго уравнения следует
можно вычислить. Тогда из второго уравнения следует

Отсюда следует, что поддается оценке погрешность акселерометра c1, погрешность по скорости оценивается с точностью до гироскопической скорости Rν2.
Пусть движение объекта обусловливает изменение навигационно-пилотажных параметров, пусть также в приборной системе координат 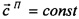 ,
, 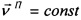 . Уравнения для канала «1» примут вид
. Уравнения для канала «1» примут вид
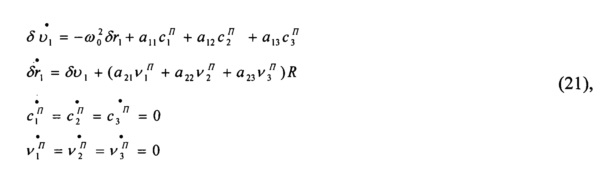
где αij - элемент матрицы A, связывающей приборный и навигационный трехгранники;
δυ1; δυ2 - динамические составляющие абсолютной линейной скорости движения центра масс объекта;
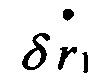 ;
; 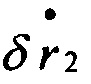 - первый дифференциал от горизонтальных составляющих вектора позиционных погрешностей БИНС;
- первый дифференциал от горизонтальных составляющих вектора позиционных погрешностей БИНС;
R - вектор положения;
ν1; ν2 - горизонтальные составляющие вектора погрешностей ДУС;
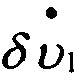 ;
; 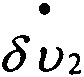 - первый дифференциал от горизонтальных составляющих вектора абсолютной линейной скорости;
- первый дифференциал от горизонтальных составляющих вектора абсолютной линейной скорости;
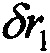 ;
; 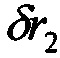 - горизонтальные составляющие вектора позиционных погрешностей;
- горизонтальные составляющие вектора позиционных погрешностей;
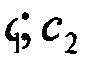 - горизонтальные составляющие вектора погрешностей акселерометров;
- горизонтальные составляющие вектора погрешностей акселерометров;
c3 - вертикальная составляющая вектора инструментальных погрешностей акселерометров;
ν3 - вертикальная составляющая вектора инструментальных погрешностей ДУСов.
Из последнего уравнения следует система
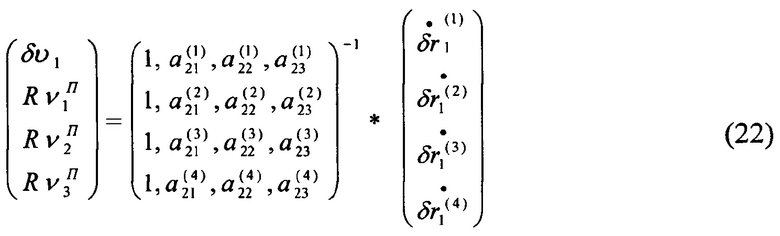
Здесь 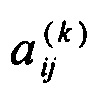 -
-  измерение соответствующего элемента матрицы A, связывающей приборный и навигационный трехгранники.
измерение соответствующего элемента матрицы A, связывающей приборный и навигационный трехгранники.
Решая эту систему можно определить собственные уходы гироскопов и погрешности БИНС по скорости. Определив  , построим систему уравнений относительно
, построим систему уравнений относительно 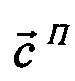
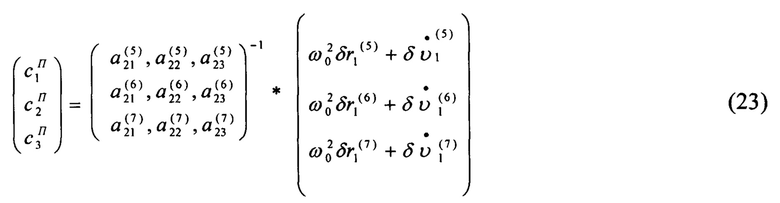
Очевидно, что для решения приведенных систем необходима их хорошая обусловленность. В частности, условие решения аналогичной системы приведено в выражении (14).
Полученные уравнения можно решить, например, методом наименьших квадратов или используя процедуру оптимальной фильтрации и т.д.
Сущность изобретения поясняется фиг. 2, на которой приведена блок-схема БИНС, реализующая предлагаемый способ и состоящая из следующих функциональных элементов:
1 - блок чувствительных элементов (БЧЭ);
2 - блок вычисления матрицы A направляющих косинусов;
3 - блок пересчета вектора удельной внешней силы в проекции на оси навигационного трехгранника;
4 - блок вычисления скоростей, координат и измерения высоты;
5 - блок вычисления вектора удельной внешней силы;
6 - блок сравнения измеренного в проекциях на оси приборного трехгранника и вычисленного векторов удельной внешней силы;
7 - блок вычисления поправок к координатам и высоте;
8 - блок фильтрации поправок;
9 - блок уточнения навигационных параметров.
В соответствии с фиг. 2 Блок 1 содержит измерители удельной силы и абсолютной угловой скорости в проекциях на оси приборной системы координат (акселерометры, ДУСы). Блок 2 реализует процедуру определения матрицы направляющих косинусов A (МНК), связывающей навигационный и приборный трехгранники (в соответствии с известными методами решения матричного уравнения Пуассона с использованием, например, вектора ускорений и (или) угловых скоростей). С помощью этой матрицы производится пересчет вектора удельной силы 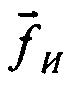 , (измеряемого акселерометрами) на оси навигационного трехгранника для дальнейшего расчета навигационных параметров в Блоке 3. Процедура определения матрицы A выполняется с использованием абсолютной угловой скорости приборного трехгранника
, (измеряемого акселерометрами) на оси навигационного трехгранника для дальнейшего расчета навигационных параметров в Блоке 3. Процедура определения матрицы A выполняется с использованием абсолютной угловой скорости приборного трехгранника 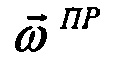 , измеряемой ДУСами (Блок 1). Матрица A вычисляется также с использованием абсолютной угловой скорости навигационного трехгранника
, измеряемой ДУСами (Блок 1). Матрица A вычисляется также с использованием абсолютной угловой скорости навигационного трехгранника 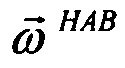 , вычисляемой в Блоке 4 как функция от навигационных параметров. Информация об измеренном векторе
, вычисляемой в Блоке 4 как функция от навигационных параметров. Информация об измеренном векторе 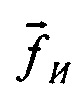 в Блок 3 поступает из Блока 1. Блок 4 реализует уравнения движения материальной точки в поле сил тяготения под действием силы
в Блок 3 поступает из Блока 1. Блок 4 реализует уравнения движения материальной точки в поле сил тяготения под действием силы 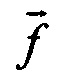 (алгоритм вычисления навигационных параметров движения объекта). В результате получается вычисленный вектор относительной скорости
(алгоритм вычисления навигационных параметров движения объекта). В результате получается вычисленный вектор относительной скорости 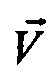 и вектор положения
и вектор положения 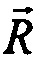 .
.
В Блоках 5, 6 и 7 получается основная информация для определения искомых навигационных параметров БИНС.
В основе процедуры получения параметров лежит сравнение соответствующих измеренных физических векторов удельной силы 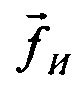 в проекциях на оси приборного трехгранника и этих же векторов
в проекциях на оси приборного трехгранника и этих же векторов 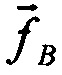 , вычисленных в Блоке 5 с использованием математической модели (5) в проекциях на оси второй, сопровождающей системы координат. Вычисление вектора удельной силы
, вычисленных в Блоке 5 с использованием математической модели (5) в проекциях на оси второй, сопровождающей системы координат. Вычисление вектора удельной силы 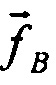 производится с использованием выходной информации Блока 4. Относительная скорость и вектор положения
производится с использованием выходной информации Блока 4. Относительная скорость и вектор положения 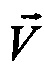 ,
, 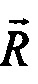 используются для вычисления параметров, входящих в (5). В Блоке 6 в соответствии с (13) сравниваются квадраты модулей, т.е.
используются для вычисления параметров, входящих в (5). В Блоке 6 в соответствии с (13) сравниваются квадраты модулей, т.е.

где 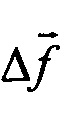 - вектор погрешности
- вектор погрешности 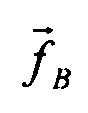 , подчиняющийся соотношению (11).
, подчиняющийся соотношению (11).
Это инструментальные погрешности акселерометров и ошибка компенсации вектора 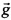 , возникающая из-за наличия динамической составляющей погрешности вектора положения БИНС.
, возникающая из-за наличия динамической составляющей погрешности вектора положения БИНС.
В результате последовательного измерения трех векторов 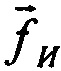 и решения системы (14) в Блоке 7 получается информация о
и решения системы (14) в Блоке 7 получается информация о 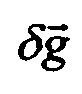 , а значит о погрешности БИНС
, а значит о погрешности БИНС 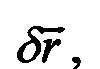 включая, в том числе, поправку к инструментальным погрешностям высотомера. При этом необходимо движение объекта, обусловливающее существование решения системы (14), т.е. выполнение условия (15).
включая, в том числе, поправку к инструментальным погрешностям высотомера. При этом необходимо движение объекта, обусловливающее существование решения системы (14), т.е. выполнение условия (15).
В Блоке 8 известными методами отфильтровывается шум, возникающий при решении системы (14) из-за ее плохой обусловленности. Производится также восстановление наблюдаемой составляющей вектора состояния погрешностей БИНС такие, например, как погрешность определения относительной скорости, отклонение от вертикали и т.д. Например, с помощью наблюдающего устройства Льюинбергера или фильтра Калмана.
В Блоке 9 происходит определение выходных навигационных параметров. Для этого из Блока 4 получаются инерциальные навигационные параметры и формируется выход с учетом информации Блока 8, т.е.

где 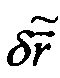 ,
, 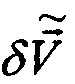 - оценки погрешностей БИНС;
- оценки погрешностей БИНС;

где 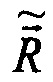 ,
, 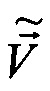 - выходные навигационные параметры.
- выходные навигационные параметры.
Таким образом, предложенный способ определения навигационных параметров БИНС в отличие от прототипа основан на совершенно другой идеологии использования дополнительной информации о динамике движения носителя, а именно на сравнении векторов, измеряемых с помощью акселерометров и вычисляемых как функция от текущих навигационных параметров. В результате синтеза и решения специальной системы линейных алгебраических уравнений производится увеличение точности компенсации удельной силы тяжести. Определение выходных навигационных параметров производится за счет обеспечения возможности демпфирования Шулеровских колебаний динамической составляющей погрешностей БИНС по положению, оценки наблюдаемых составляющих погрешностей системы без использования какой-либо дополнительной измеряемой информации не инерциальной природы.
При этом, как следует из системы (10), предложенный способ увеличивает свою эффективность при увеличении скорости изменения навигационных параметров. В то время, как прототип - напротив, при спокойном крейсерском полете с увеличением собственной частоты БИНС. Это обстоятельство позволяет предполагать увеличение общей эффективности при совместном использовании обоих подходов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ОБЪЕКТА И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2017 |
|
RU2661446C1 |
| СПОСОБ КОМПЛЕКСИРОВАНИЯ БЕСПЛАТФОРМЕННЫХ ИНЕРЦИАЛЬНЫХ НАВИГАЦИОННЫХ СИСТЕМ | 2016 |
|
RU2634082C1 |
| НАВИГАЦИОННО-ПИЛОТАЖНЫЙ КОМПЛЕКС | 2016 |
|
RU2634083C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩИХ ПОПРАВОК В БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЕ | 2017 |
|
RU2654964C1 |
| КОМБИНИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ АСТРОИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2017 |
|
RU2654965C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА, КОРРЕКТИРУЕМАЯ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668659C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБОК БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668658C1 |
| Способ определения ориентации объекта в бесплатформенной инерциальной навигационной системе | 2022 |
|
RU2794283C1 |
| СПОСОБ ПОСТРОЕНИЯ АСТРОИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2016 |
|
RU2641515C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ УПРАВЛЯЕМЫХ ПОДВИЖНЫХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2241959C1 |
Изобретение относится к области обработки данных в бесплатформенных навигационных системах (БИНС), работающих в автономном режиме. Способ определения навигационных параметров бесплатформенной инерциальной навигационной системой, основанный на использовании сигналов акселерометров и датчиков угловых скоростей, включает измерение на борту движущегося объекта с помощью акселерометров вектора удельной внешней силы в проекциях на оси приборного трехгранника, расчет матрицы направляющих косинусов между приборным и навигационным трехгранниками, пересчет вектора удельной внешней силы в проекции на оси навигационного трехгранника и интегрирование этих показаний для расчета текущих скоростей и координат в виде вектора относительной линейной скорости в осях навигационного трехгранника и вектора положения, при этом при вычислении матрицы направляющих косинусов используется абсолютная угловая скорость приборного трехгранника, измеряемая датчиками угловых скоростей, и абсолютная угловая скорость навигационного трехгранника, вычисляемая как функция от рассчитанных текущих скоростей и координат. При этом на основании входных параметров текущих скоростей и координат производится вычисление в проекциях на оси навигационного трехгранника вектора удельной внешней силы, соответствующего измеренному с помощью акселерометров, после чего вектор удельной внешней силы, измеренный в проекциях на оси приборного трехгранника, сравнивается с соответствующим ему вектором удельной внешней силы, вычисленным в проекциях на оси навигационного трехгранника, в результате чего вычисляется соответствующая разности измеренного и вычисленного векторов погрешность компенсации вектора удельной силы тяжести и, следовательно, возможность компенсации динамических погрешностей инерциальных координат и ошибок измерения высоты. Техническим результатом предложенного способа является существенное повышение точности автономного счисления навигационных параметров (координат, линейных скоростей, высоты). 2 н.п. ф-лы, 2 ил.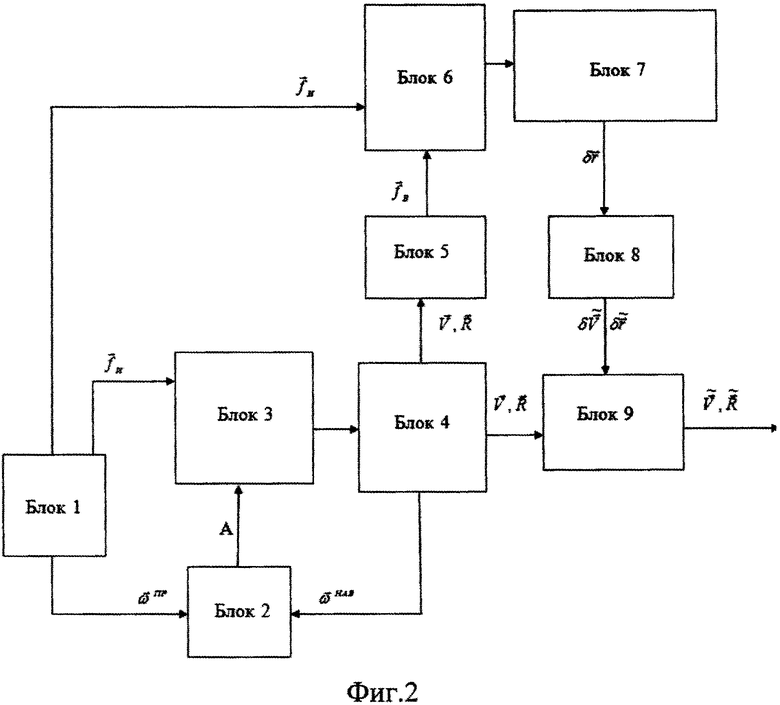
1. Способ определения навигационных параметров бесплатформенной инерциальной навигационной системой, основанный на использовании сигналов акселерометров и датчиков угловых скоростей, включающий измерение на борту движущегося объекта с помощью акселерометров вектора удельной внешней силы в проекциях на оси приборного трехгранника, расчет матрицы направляющих косинусов между приборным и навигационным трехгранниками, пересчет вектора удельной внешней силы в проекции на оси навигационного трехгранника и интегрирование этих показаний для расчета текущих скоростей и координат в виде вектора относительной линейной скорости в осях навигационного трехгранника и вектора положения, при этом при вычислении матрицы направляющих косинусов используется абсолютная угловая скорость приборного трехгранника, измеряемая датчиками угловых скоростей, и абсолютная угловая скорость навигационного трехгранника, вычисляемая как функция от рассчитанных текущих скоростей и координат, отличающийся тем, что на основании входных параметров текущих скоростей и координат производится вычисление в проекциях на оси навигационного трехгранника вектора удельной внешней силы, соответствующего измеренному с помощью акселерометров, после чего вектор удельной внешней силы, измеренный в проекциях на оси приборного трехгранника, сравнивается с соответствующим ему вектором удельной внешней силы, вычисленным в проекциях на оси навигационного трехгранника, в результате чего вычисляется соответствующая разности измеренного и вычисленного векторов погрешность компенсации вектора удельной силы тяжести и, следовательно, возможность компенсации динамических погрешностей инерциальных координат и ошибок измерения высоты.
2. Бесплатформенная инерциальная навигационная система, включающая блок чувствительных элементов, соединенный своим первым выходом с первым входом блока вычисления матрицы направляющих косинусов, а вторым выходом с первым входом блока пересчета вектора удельной внешней силы в проекции на оси навигационного трехгранника, соединенного вторым входом с выходом блока вычисления матрицы направляющих косинусов, а выходом с блоком вычисления скоростей, координат и измерения высоты, который соединен своим первым выходом со вторым входом блока вычисления матрицы направляющих косинусов, отличающаяся тем, что блок вычисления скоростей и координат соединен первым выходом со входом блока вычисления вектора удельной внешней силы, пересчитанного в осях навигационного трехгранника, и соединенного выходом с первым входом блока сравнения измеренного в проекциях на оси приборного трехгранника и вычисленного векторов удельной внешней силы, при этом блок сравнения соединен вторым входом с третьим выходом блока чувствительных элементов, а выходом со входом блока вычисления поправок к координатам и высоте, который соединен выходом со входом блока фильтрации поправок, соединенного выходом с первым входом блока уточнения навигационных параметров, причем последний вторым входом соединен с третьим выходом блока вычисления скоростей и координат.
| СПОСОБ ВЫРАБОТКИ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И ВЕРТИКАЛИ МЕСТА (ВАРИАНТЫ) | 2005 |
|
RU2272995C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНЫХ ОБЪЕКТОВ И КОМПЛЕКСИРОВАННАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2395061C1 |
| US 20140229109 A1, 14.08.2014 | |||
| СПОСОБ ОЦЕНКИ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ДАТЧИКОВ УГЛОВОЙ СКОРОСТИ | 2013 |
|
RU2526508C1 |
Авторы
Даты
2017-10-23—Публикация
2016-11-08—Подача