Изобретение относится к области радиолокации и может быть использовано в комплексах, определяющих параметры движения контролируемых объектов многошкальным методом, а также в системах, использующих сигналы спутниковых радионавигационных систем для разрешения неоднозначности измерений нетрадиционными методами конструктивной теории конечных полей.
Традиционный подход с разрешением неоднозначности измерений связан с необходимостью получения затрубленных оценок возможных значений дальности. Он может быть обеспечен при реализации многошкального метода измерений ([1], Теоретические основы радиолокации /Под ред. В.Е. Дулевича/. - М: «Советское радио», 1978 г., с. 217-220). Суть многошкального метода применительно к фазометрическим системам измерений состоит в создании множества излучаемых масштабных частот: ωмГ, …, ωмПрi, …, ωмТ, где ωмГ - грубая масштабная частота, ωмПрi - i-тая промежуточная масштабная частота и ωмТ - точная масштабная частота.
При радиолокации модулирующие колебания каждой масштабной частоты выделяют из излучаемого и принимаемого сигналов. Разность фаз между этими колебаниями связана со временем запаздывания т равенством:

где R - наклонная дальность до контролируемого объекта,
с - скорость света (распространения радиоволн).
Из формулы (1) следует, что
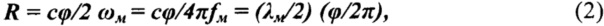
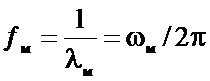
Разность фаз ϕ может быть однозначно измерена в интервале (0, 2π). При этом максимальная дальность, в пределах которой возможно однозначное измерение, определяется соотношением

Поэтому при радиолокационных измерениях для обеспечения требуемой точности параметров движений контролируемого объекта применяют несколько масштабных волн λм1, λм2, …, λмn и соответствующих им частот излучения ƒм1, ƒм2, …, ƒмn. В известном способе многошкальных измерений ([1]) наименьшая из масштабных частот определяет самую грубую шкалу измерений дальности и выбирается из условия однозначности измерений:

Например, для обеспечения однозначных измерений, например, в пределах от 0 до 100 км масштабная частота ƒм не должна превышать значения 1,5 кГц.
Следующая, более высокая масштабная частота ƒм2 определяет вторую более точную шкалу дальности. Она выбирается таким образом, чтобы интервал однозначного измерения по второй шкале превышал удвоенное значение максимальной ошибки измерений по первой шкале. Только при этом условии, которое называется условием согласования смежных шкал, при традиционном подходе можно избежать грубых ошибок измерений, кратных интервалу однозначности по более точной шкале. В соответствии с данным правилом выбирается следующая масштабная частота ƒм3 по отношению к предыдущей масштабной частоте ƒм2. В результате этого число шкал измерений может быть очень большим, особенно в тех случаях, когда Rmax известно не точно. Такой случай имеет место при радиотехнических измерениях в дальнем космосе.
Таким образом, в известном способе [1] устранение неоднозначности производят последовательно: вначале определяют значение результата измерений в грубой шкале, а затем полученные данные уточняют на основе определения разности фаз, полученных по промежуточным масштабным частотам ƒм2, ƒм3, …, ƒм(n-1) и точной масштабной частоте ƒмn. Однако последовательная процедура раскрытия неоднозначности в ряде случаев не удовлетворяет предъявляемым требованиям по оперативности.
Кроме того, в практике радиотехнических измерений достаточно часто условие согласования смежных шкал не выполняется из-за того, что истинные значения максимальной ошибки измерений по предыдущим шкалам могут превышать расчетные их значения, которые были использованы при выборе последующих шкал измерений, и тогда получают аномальные измерения.
На устранение основного недостатка способа [1], связанного с новыми операциями раскрытия неоднозначности, ориентировано изобретение «Способ определения дальности до объекта с источником излучения с разными частотами» ([2], Патент RU 2469349 С1, заявка №2011122988/07, МПК G01S 13/84 (2006/01), опубл. 10.12.2012, бюл. №34. 10 с), заключающийся в одновременном приеме не менее двух сигналов с разными частотами и последующем измерении фаз принятых сигналов относительно фаз сигналов опорного генератора, отличающийся тем, что осуществляют преобразование измеренного значения фазы каждого сигнала в цифровое значение временного интервала между сигналом опорного генератора и принятым сигналом, а расстояние вычисляют по формуле:
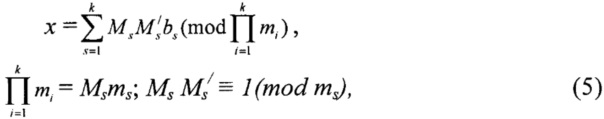
где х - восстановленное значение расстояния с раскрытием неоднозначности;
bs - образы-остатки (интерпретируемые как значения, пропорциональные измеренным значениям фаз, например, как значения остатков, соответствующих измеренному значению фазы, умноженному на соответствующую длину волны λs);
ms - модули сравнения, под которыми понимают длины волн принимаемых сигналов λs;
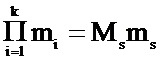
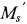 - мультипликативно-обратный элемент, при котором выполняется следующее сравнение:
- мультипликативно-обратный элемент, при котором выполняется следующее сравнение: 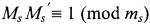 .
.
Основной недостаток изобретения-прототипа [2] связан с ограничениями, которые накладывает формула (5) классической математической теории конечных полей Э. Галуа, известная как китайская теорема об остатках ([3], Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях / Под ред. В.Ф. Шангина - М.: Радио и связь, 1999. - 328 (Китайская теорема об остатках, стр. 311, 312)). Китайская теорема об остатках ориентирована на использование только целочисленных значений образов-остатков bs и предполагает подбор или вычисление на основе алгоритма Евклида «мультипликативно-обратных элементов» 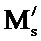
Кроме того, существуют и другие недостатки, которые могут быть наиболее просто пояснены на иллюстративном примере (фиг. 1). Математическое описание задачи, сформулированной в терминах теории конечных полей, может быть представлено как применение при измерениях длины комнаты двух модулей сравнения m1=27 и m2=29. В этом случае алгоритм китайской теоремы об остатках имеет следующий вид:
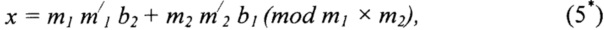
где m/1 и m/2 - мультипликативно-обратные элементы:
(m1m/1≡1 (mod m2)) и (m2m/2≡1 (mod m1)),
b1 и b2 - полученные образы-остатки в интерпретации, используемой при описании формулы изобретения способа-прототипа [2].
Мультипликативно-обратные элементы m/1 и m/2 определяют на основе соотношений:
27×74=378≡1 (mod 29); 29×14=406≡1 (mod 27).
Для задачи, приведенной на фиг. 1, они равны: m/1=14 и m/2=14.
В результате алгоритм решения задачи на основе китайской теоремы об остатках имеет следующий вид:
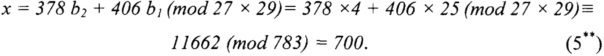
Поскольку остатки были представлены в см, то и измеряемая длина комнаты составляет 700 см.
Таким образом, классический алгоритм решения подобных задач не в полной мере соответствует потребностям практического применения. Его недостатки заключены в следующем: 1) он сложен; 2) мультипликативная структура построения формулы (5) и ее частного варианта (5*) приводит к необходимости, сначала, умножения данных измерений на большие числа (применительно к рассмотренной задаче результаты измерений умножают на числа 378 и 406, а затем нормируют полученный результат вычислений путем сравнения по укрупненному модулю, равному произведению значений исходных модулей; 3) результаты измерений фаз должны быть представлены только целочисленными значениями.
Данных недостатков лишен алгоритм (6), основанный на конструктивной теореме об остатках ([4], Кукушкин С.С. Теория конечных полей и информатика. Т.1., М: Минобороны России, 2003. - 278 с, стр. 38-43). Его использование составляет основу формулировки отличительных признаков предлагаемого изобретения.
Предлагаемый способ заключается в одновременном приеме не менее двух сигналов с разными частотами и последующем измерении фаз принятых сигналов относительно фаз сигналов опорного генератора, при котором осуществляют преобразование измеренного значения фазы каждого сигнала в цифровое значение временного интервала между сигналом опорного генератора и принятым сигналом. Он отличается тем, что дальность вычисляют с использованием следующей адаптивной формулы:
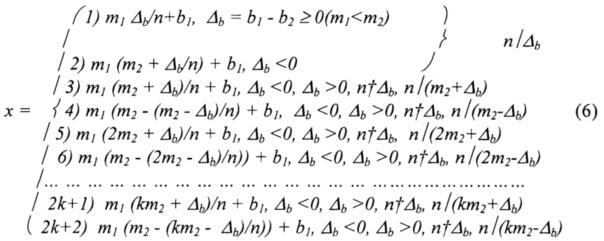
число звеньев k которой на единицу больше значения абсолютной разности между модулями сравнений k=n+1,
где n=|m1-m2| - абсолютная разность между модулями сравнения, а обозначения 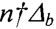 , с одной стороны, и n/Δb, n/(km2+Δb), n/(km2-Δb) (k=0, 1, …), с другой стороны, означают, что Δb не делится на n без остатка, в первом случае, и Δb, (km2+Δb), (k2+Δb) делятся на n без остатка, во втором случае;
, с одной стороны, и n/Δb, n/(km2+Δb), n/(km2-Δb) (k=0, 1, …), с другой стороны, означают, что Δb не делится на n без остатка, в первом случае, и Δb, (km2+Δb), (k2+Δb) делятся на n без остатка, во втором случае;
ms - модули сравнения, под которыми понимают длины волн принимаемых сигналов λs, s=1, 2;
bs - образы-остатки, интерпретируемые как значения, пропорциональные измеренным значениям фаз;
Δb=(b1-b2) - разность образов-остатков bs, которую интерпретируют как разность фаз между сигналом опорного генератора и принятым сигналом Δϕ=(ϕ1-ϕ2).
Технический эффект от предлагаемого способа заключается в следующем:
- он расширяет возможности существующей практики измерений фаз ϕs многошкальным методом при излучении двух и более частот за счет того, что позволяет восстановить для раскрытия неопределенности измерений значения псевдодальности Rs, являющиеся результатом определения разности фаз Δϕ=ϕi-ϕj, на основе вычислений с использованием предлагаемой адаптивной формулы без использования специальных технических приемов в виде смешения сигналов с частотами λi и λj в смесителе с последующим определением разности фаз разностного сигнала;
- позволяет контролировать достоверность восстанавливаемых результатов измерений, в том числе и псевдодальностей;
- нет прежних жестких ограничений, которые предъявляются к выбору модулей сравнения ms (длинам радиоволн λs в предлагаемой в описании математической интерпретации проблемы разрешения неоднозначности радиотехнических измерений).
Так, например, при использовании алгоритма китайской теоремы об остатках, составляющего основу способа-прототипа модули сравнения mi должны быть взаимно простыми - это означает, что их наибольшим общим делителем (НОД) должна быть 1: (m1, m2)=1, а в новом способе НОД (m1, m2)=р, где р - это не только единица (р=1), но и любое простое число р (р=2, 3, 5, 7, 11, 13, …). Снятие этого ограничения расширяет возможности использования предлагаемой математической модели (6), обеспечивая более полный учет уже принятых практических решений.
Известное соотношение, связывающее дальность до объекта с измеренной фазой несущей, представляют в следующем виде [1]:

где Rs - дальность,
λs - длина волны несущей,
ϕs - измеренное значение фазы,
ls - неизвестное число целых длин волн, укладывающихся в дальности до объекта.
Известное решение задачи разрешения неоднозначности измерений связано с необходимостью получения затрубленных оценок возможных значений дальности. Она может быть обеспечена при реализации многошкального метода измерений [1], суть которого заключается в том, что создают множество излучаемых масштабных частот: ωмГ, …, ωмПрi, …, ωмТ, где ωмГ - грубая масштабная частота, ωмПрi - i-тая промежуточная масштабная частота и ωмТ - точная масштабная частота.
В известном способе многошкальных измерений [1] наименьшая из масштабных частот определяет самую грубую шкалу измерений дальности и выбирается из условия однозначности измерений:

Следующая, более высокая масштабная частота ƒм2 определяет вторую более точную шкалу дальности. Она выбирается таким образом, чтобы интервал однозначного измерения по второй шкале превышал удвоенное значение максимальной ошибки измерений по первой шкале. Только при этом условии, которое называется условием согласования смежных шкал, можно избежать грубых ошибок измерений, кратных интервалу однозначности по более точной шкале. В соответствии с данным правилом выбирается следующая масштабная частота ƒм3 по отношению к предыдущей масштабной частоте ƒм2. В результате этого число шкал измерений может быть очень большим, особенно в тех случаях, когда Rmax известно не точно.
В известном способе [1] устранение неоднозначности производится последовательно: вначале определяется значение результата измерений в грубой шкале, а затем полученные данные уточняются на основе определения разности фаз, полученных по промежуточным масштабным частотам ƒм2, ƒм3, …, ƒм(n-1) и точной масштабной частоте ƒмn.
Предлагаемая математическая модель задачи раскрытия неопределенности при измерениях дальности может быть вначале представлена следующей системой уравнений:

где λs - длина s- той масштабной волны при многошкальных измерениях;
ls - целое число длин волн λs, которое укладывается в измеренной дальности и которое неизвестно при измерениях;
ϕs - измеренное значение фазы принятого сигнала по отношению к начальной фазе: 1) опорного генератора, засинхронизированного с сигналом передающей стороны при использовании первого метода или 2) излученного сигнала при применении второго метода (при этом подстрочный символ s=1, 2, 3, … указывает на то, что выражение (1) является системой уравнений).
Основой формулы (9) является основная теорема арифметики, представленная в виде соотношения:

где ms - делитель (модуль сравнения);
ls - неполное частное, которое опускается при переходе к сравнению: х≡bs (mod ms);
bs - остаток от деления.
Э. Галуа предложена следующая «сжатая» математическая модель основной теоремы арифметики (10).

Она предполагает замену равенств («=») символами «тождественно равно» («≡»), а «сжатой» она является из-за исключения неполных частных ls.
При этом возможность восстановления неполных частных ls. В классической теории конечных полей Э. Галуа была сформулирована, как требование взаимной простоты модулей сравнения ms, где s=1, 2, …, i, …, j, …μ. (записывают его так: (mi, mj)=1).
В изобретении-прототипе [2] и в рассматриваемой заявке предлагается замена существующей физико-математической модели радиотехнических измерений псевдодальностей (9) с использованием фазового метода на предлагаемую физико-математическую модель:

Она совпадает по форме со «сжатой» математической моделью основной теоремы арифметики (11).
Ее основу составляет математическая теория конечных полей, поскольку никакая другая математическая теория не предназначена для работы с образами-остатками. При этом принципиальное различие между техническими решениями, предлагаемыми в патенте-прототипе [2] и в предлагаемой заявке заключается в вычислительных операциях: в патенте-прототипе [2] предполагается использовать для вычислений китайскую теорему об остатках, а в рассматриваемом предложении - «адаптивную формулу».
В предлагаемом способе для раскрытия неоднозначности применяют адаптивную формулу, предполагающую сокращение числа звеньев вычислений k, которые необходимо использовать для восстановления данных в традиционном виде до значения k=n+1, где n=|m1-m2|. В соответствующем классическом алгоритме китайской теоремы об остатках (5*) сложность вычислений не зависит от абсолютной разности (n) между выбранными модулями. В случае использования предлагаемой адаптивной формулы (6) эта зависимость присутствует: следовательно, соответствующим выбором значений масштабных частот λs может быть уменьшена сложность технических решений, используемых для разрешения неоднозначности измерений.
Например, если n=1, то необходимо использовать только два первых звена формулы (k=2) в аналитическом описании (6):
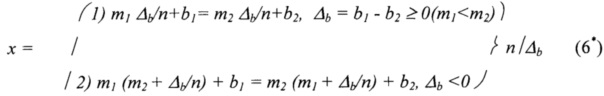
Если n=|m1-m2|=|27-29|=2, как это имеет место в рассмотренной задаче (фиг. 1), то число звеньев k алгоритма равно 3:
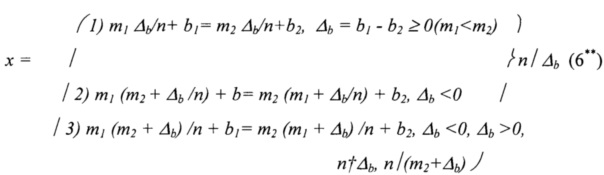
Данное свойство зависимости числа звеньев k вычислительной формулы и обеспечения ее симметричности относительно индексов модулей сравнения i и j (mi, mj) и их образов-остатков (bi, bj) позволяет сформулировать следующий зависимый пункт формулы изобретения.
Способ по п. 1, заключающийся в том, что число звеньев k=n+1 адаптивной формулы задают соответствующим выбором модулей сравнения (ms), под которыми понимают длины волн принимаемых сигналов (λs), s=1,2, при этом для повышения оперативности решения задачи раскрытия неоднозначности измерений и минимизации времени обработки модули сравнения выбирают так, чтобы минимизировать их абсолютную разность n=|mi-mj|, при этом модули сравнения имеют общий делитель в виде числа р ((mi, mj)=р), где р - единица или простое число, восстановление псевдодальностей, под которыми понимают результаты последовательного приближения к истинному значению дальности, обеспечивают методом последовательного укрупнения модуля сравнения на основе решений систем попарных сравнений, обеспечивают контроль достоверности получения значений псевдодальностей на основе равенств, которые получают с использованием адаптивной формулы при замене в ней индексов модулей и остатков, условно равных 1 (i=1) на индексы модулей и остатков, условно равных 2 (j=2):
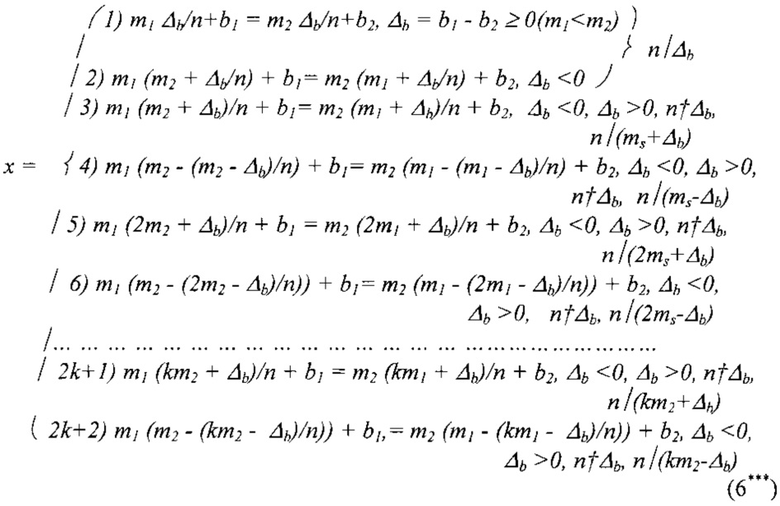
Алгоритм решения задачи, приведенной на фиг. 1. Сначала определяют исходные данные: n=|β1-β2|=|27-29|=2, где β1 и β2 - длины ботинков, интепретируемые в математической постановке задачи, приведенной на фиг. 1, как модули сравнения m1 и m2, и Δb=b1-b2=25-4=21>0 - разности результатов измерений остатков, когда целые длины ботинков не помещаются в измеряемой длине комнаты. Из полученных исходных данных следует, что выполняется делимость вида n|(m1+Δ), а это означает, что необходимо воспользоваться 3-им звеном формулы (k=3) (6**). Отметим, что в соответствии с принятой в приведенном примере интерпретацией модули mi - это длина ботинка βi.
Следовательно,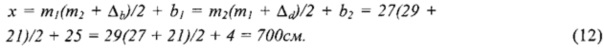
В результате применения нового алгоритма получили тот же результат, что и при использовании классического алгоритма китайской теоремы об остатках, составляющего основу способа-прототипа.
Преимущества:
- конструктивная теорема об остатках, помимо прочего, ориентирована на измерение разности фаз, которое реализовано в технических приложениях - этому соответствует разность: Δb=(b1-b2) - в математической интерпретации конструктивной теории измерений;
- обеспечивается минимально возможная сложность вычислений и восстановления результатов измерений, которая достигается за счет соответствующего выбора масштабных частот λi (модулей сравнения mi при используемой математической интерпретации задачи измерений);
- модули сравнения могут и не удовлетворять требованию взаимной простоты: (m1, m2)=(β1, β2)=(λ1, λ2)=1 (требованию наличия только одного общего делителя при числовом представлении их значений, равного 1), в предлагаемом способе предполагается, что общим множителем может быть и число р, равное не только 1, но и соответствующее любому простому числу. В этом случае определяемые исходные данные, необходимые для вычислений с использованием предлагаемой адаптивной формулы (6) - это n*=|pm1-pm2|=pn и Δb*=pb1-pb2=pΔb. Тогда деление Δb|n в формуле (6) конструктивной теоремы об остатках эквивалентно делению: Δb*|n*, так как р сокращается при делении. Следовательно, обеспечивается достоверное восстановление и при выборе масштабных частот λs, номиналы которых являются целыми числами, которые являются не только взаимно простыми, но и имеют общий делитель, равный простому числу.
Достоинство предлагаемого способа также заключается в снятии ограничений на представление данных измерений (образов-остатков bi) только целыми числами. При использовании предлагаемого алгоритма они могут быть и дробными.
Еще одно преимущество нового способа заключается в том, что при восстановлении данных измерений из остатков используются два симметричных алгоритма, например, х=m1(m2+Δb)/2+b1=m2(m1+Δd)/2+b2 (формулы 6*, 6** и 6***), так как математическая запись идентична относительно модулей сравнения и получаемых остатков. При этом равенство полученных значений свидетельствует о достоверности восстановления результата измерений. Этого эффекта также нет при использовании способа-прототипа [2].
Отмеченные преимущества позволяют определить технический эффект, достигаемый при использовании предлагаемого изобретения:
1) расширенная область применения предлагаемого технического решения, обеспечиваемая, в том числе, и за счет возможность приспособления к существующей практике выбора масштабных частот λi;
2) упрощение технической реализации и повышения оперативности выполнения операций по разрешению неоднозначности измерений.
Для сравнения преимуществ предлагаемого изобретения по отношению к патенту-прототипу [2] воспользуемся примером их использования для СРНС ГЛОНАСС, использующей радиоволны λ1, λ2, λ3, равные следующим значениям: 19 см, 24 см и 25 см.
Математическая постановка задачи измерений дальности на основе радиоволн λ1, λ2, λ3 с использованием теории конечных полей заключается в том, чтобы найти х, удовлетворяющее системе сравнений:

при следующих значениях модулей сравнения m1=19, m2=24, m3=25 и образах-остатках b1=9, b2=16, b3=0, которые соответствуют измеренным значениям фаз ϕ1, ϕ2 и ϕ3, по каждой из перечисленных радиоволн λ1, λ2 и λ3.
В предполагаемом изобретении предлагаемое техническое решение заключается в том, чтобы, например, заменить систему сравнений (13) на две системы сравнений следующего вида:


где xd(1) и xd(2) - псевдодальности.
Если воспользоваться алгоритмом китайской теоремы об остатках (5*), то решение первой системы сравнений (14) при b1=9 и b2=16 будет иметь вид:
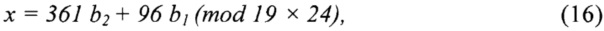
так как мультипликативно-обратные элементы m/1=19 и m/2=4:
(19×19≡1 (mod 24)) и (24×4≡1 (mod 19)).
После подстановки численных значений b1=9 и b2=16 получим:
х=361 b2+96 b1 (mod 19×24)=5776+864+6640=256 (mod 456).
Для решения той же системы (14) при использовании предлагаемого способа определим исходные данные: Δb=b1-b2=9-16=-7; n=|m1-m2|=|19-24|=5. Найдем условие делимости - их два: 1) при k=6 → n|(2mi-Δb) и 2) при k=7 → n|(3mi+Δb). Проверяем: 1) для первого случая для k=6 формула (6***) определяет следующий тип делимости без остатка n|(2mi-Δb), что соответствует получению для m2=24 следующего числового результата: 2mi-Δb=(2×24-(-7))=55, а 55 делится на n=5 без остатка, следовательно, k=6 удовлетворяет требуемому условию делимости; 2) для второго случая делимости n|(3mi+Δb) получим (3×24+7)=65, при этом также выполняется делимость на n=5 без остатка: 65:5=13.
Для проверки заявленного свойства симметричности адаптивной формулы используем m1=19 для проверки выполнения свойств делимости. Для первого случая (k=6 → n|(2mi-Δb)) получим: (2×19-(-7))=45, и делимость на n=5 без остатка также выполняется. Для второго случая делимости n|(3mi+Δb) получим (3×19+(-7)=50, полученный результат также делится на 5 без остатка: 50:5=10.
Следовательно, алгоритм восстановления при использовании конструктивной теоремы об остатках может иметь следующий вид (звено 6 (k=6) формулы (6***)):
xd(1)=m1(m2-(2m2-Δb))/n+b1=19(24-(48+7)/5)+9=19×13+9=24(19-(38+7)/5)+16=24×10+16=256.
Полученный результат совпадает с ранее найденным на основе алгоритма китайской теоремы об остатках.
С целью контроля достоверности полученного результата может быть использовано и 7 звено (k=7) формулы (6***)):
xd(1)=m1(3m2+Δ)/n+b1=m2(3m1+Δ)/n+62=19×13+9=24×10+16=256.
Таким образом, использование различных звеньев k адаптивной формулы, при которых также получают совпадающие результаты, является дополнительным подтверждением достоверности восстановленного значения псевдодальности xd(1), полученной по укрупненному модулю сравнения, равному М12=m1×m2=19×24=456.
Для решения системы (15) на основе предлагаемого способа определим исходные данные: Δ=b1-b2=9-0=9; n=|m1-m2|=|19-25|=6. Условие делимости имеет вид, соответствующий звену k=7: n|(3mi+Δ). Проверяем (3×19+9)=57+9=66, а число 66 делится на 6 без остатка 66:6=11, следовательно, требование делимости выполнено. Аналогично, (3×25+9)=75+9=84 и 84 также делится на 6 без остатка: 84:6=14.
Таким образом, алгоритм восстановления при использовании конструктивной теоремы об остатках будет иметь вид, определяемый звеном (k=7) формулы (6***):
xd(2)=m1(3m2+Δ)/n+b1=m2(3m1+Δ)/n+b2=19×14+9=25×11+0=275.
При этом укрупненный модуль сравнения будет равен: М23=m2×m3=19×24=456.
В результате первого этапа вычислений с использованием адаптивной формулы новая укрупненная система сравнений будет иметь вид:

В численном виде система сравнений (17) имеет вид:
х≡256 (mod 456),
х≡275 (mod 475).
Для ее решения определим исходные данные: Δb=256-275=-19 и n=|m1-m2|=|456-475|=19. Выполняется условие делимости: n|Δb при Δb<0. Следовательно, в соответствии с условиями делимости необходимо воспользоваться вычислительным звеном 2 (k=2) формулы (6***):
х=m1(m2+Δb/n)+b1=m2(m1+Δb/n)+b2=456(475-1)+256=475(456-1)+275=216400 см.
Так как модули сравнения (длины радиоволн) были представлены в см, то и полученный результат определения дальности также измеряется в см.
Дополнительный контроль достоверности полученного результата может быть получен на основе решения следующей системы сравнений:

После подстановки численных значений система сравнений будет иметь следующий вид:
xd(3)≡16 (mod 24),
xd(3)≡0 (mod 25).
Определим исходные данные: Δb=16-0=16 и n=|m1-m2|=|24-25|=1. Следовательно, необходимо для восстановления воспользоваться звеном 1 формулы (6***):
х=m1Δb/n+b1=m2Δb/n+b2=24×16+16=25×16+0=400.
Определим число периодов результата, который может быть получен при смешении двух близких частот λ2=24 см и λ3=25 см в воображаемом смесителе частот, присутствие которого является обязательным при реализации традиционного подхода к получению разностных частот: l24×25=216400:400=541. Если l24×25 целое число, то это является еще одним подтверждением достоверности определения значения дальности.
Однако применение технической операции смешения принятых радиочастот, которая используется в существующей практике, приведет к внесению дополнительных погрешностей в результаты измерений. Применение вычислительной формулы погрешностей не вносит, если не переполняется используемая для вычислений разрядная сетка и нет округлений полученных данных. Представление данных образами-остатками составляет основу новых технологий распараллеленных вычислений, известных под названием «вычисления в системе остаточных классов (СОК)» [5].
Технический эффект от использования предлагаемого способа и способа-прототипа, таким образом, заключается в том, сигналы более грубой масштабной частоты ƒмi могут не передаваться, а восстанавливаться на основе комбинаций других более точных частот, например, ƒм(i+1) и ƒм(i+2) (8). При этом комбинирование более точных масштабных частот, например, ƒм(i+1) и ƒм(i+2), позволяет восстановить с меньшей погрешностью результаты измерений по воображаемой более грубой масштабной частоте ƒмi.
Технический эффект также заключен в том, чтобы, с одной стороны, уменьшить число масштабных частот, которое требуется для решения задачи раскрытия неоднозначности известным способом [1], а с другой, повысить точностные характеристики системы измерений за счет использования не одной, а нескольких точных масштабных частот.
Источники информации
1. Теоретические основы радиолокации /Под ред. В.Е. Дулевича/. - М: «Советское радио», 1978 г., с. 217-220.
2. Патент RU 2469349 С1, заявка №2011122988/07, МПК G01S 13/84 (2006/01), опубл. 10.12.2012, бюл. №34. 10 с.
3. Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях / Под ред. В.Ф. Шангина - М.: Радио и связь, 1999. - 328 (Китайская теорема об остатках, стр. 311, 312).
4. Кукушкин С.С. Теория конечных полей и информатика. Т.1., М: Минобороны России, 2003. - 278 с, стр. 38-43.
5. Торгашев В.А. Система остаточных классов и надежность ЦВМ. М.: Сов. радио, 1973. - 120 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ОБЪЕКТА С ИСТОЧНИКОМ ИЗЛУЧЕНИЯ СИГНАЛОВ С РАЗНЫМИ ЧАСТОТАМИ | 2011 |
|
RU2469349C1 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2586605C2 |
| СПОСОБ ЭКОНОМНОГО ПРЕДСТАВЛЕНИЯ И ПЕРЕДАЧИ БИПОЛЯРНЫХ ДАННЫХ И СИГНАЛОВ | 2017 |
|
RU2649291C1 |
| СПОСОБ ПЕРЕДАЧИ ТЕЛЕМЕТРИЧЕСКОЙ ИНФОРМАЦИИ | 2020 |
|
RU2757306C1 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ | 2022 |
|
RU2801462C1 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО СЖАТИЯ ДАННЫХ ДЛЯ ПЕРЕДАЧИ И ХРАНЕНИЯ ИНФОРМАЦИИ | 2021 |
|
RU2840261C2 |
| СПОСОБ ПЕЛЕНГАЦИИ ИЗЛУЧАЮЩЕГО ОБЪЕКТА В ФАЗОВЫХ МНОГОШКАЛЬНЫХ УГЛОМЕРНЫХ СИСТЕМАХ | 2022 |
|
RU2786495C1 |
| СПОСОБ ОПЕРАТИВНО-ТЕХНИЧЕСКОЙ ОХРАНЫ РУБЕЖЕЙ ОБЪЕКТОВ И ГРАНИЦ | 2017 |
|
RU2674809C9 |
| СПОСОБ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ АДАПТИВНОЙ НЕЛИНЕЙНОЙ ФИЛЬТРАЦИИ ДАННЫХ ИЗМЕРЕНИЙ | 2017 |
|
RU2672392C1 |
| СПОСОБ ПЕРЕДАЧИ ТЕЛЕМЕТРИЧЕСКОЙ ИНФОРМАЦИИ | 2020 |
|
RU2739335C1 |

Изобретение относится к области радиолокации и может быть использовано в комплексах, определяющих параметры движения контролируемых объектов многошкальным методом, а также в системах, использующих сигналы спутниковых радионавигационных систем для разрешения неоднозначности измерений нетрадиционными методами конструктивной теории конечных полей. Достигаемый технический результат - раскрытие неоднозначности измерений дальности в фазометрических радиотехнических системах. Указанный результат достигается тем, что способ определения дальности до объекта с источником излучения сигналов с разными частотами, заключается в одновременном приеме не менее двух сигналов с разными частотами и последующем измерении фаз принятых сигналов относительно фаз сигналов опорного генератора, при этом осуществляют преобразование измеренного значения фазы каждого сигнала в цифровое значение временного интервала между сигналом опорного генератора и принятым сигналом, затем вычисляют дальность с использованием соответствующей адаптивной формулы. 1 ил.
Способ определения дальности до объекта с источником излучения сигналов с разными частотами, заключающийся в одновременном приеме не менее двух сигналов с разными частотами и последующем измерении фаз принятых сигналов относительно фаз сигналов опорного генератора, осуществляют преобразование измеренного значения фазы каждого сигнала в цифровое значение временного интервала между сигналом опорного генератора и принятым сигналом, отличающийся тем, что дальность вычисляют с использованием следующей адаптивной формулы:
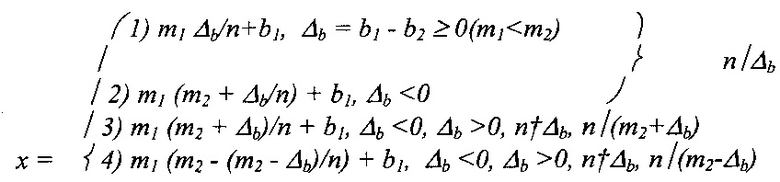
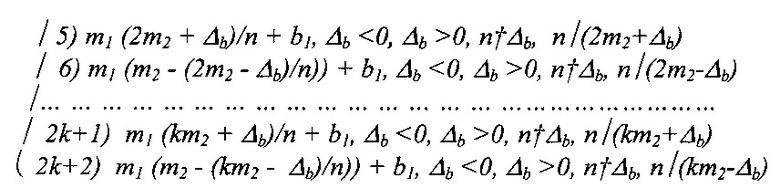
число звеньев k которой на единицу больше значения абсолютной разности между модулями сравнений k=n+1,
где n=⎜m1-m2⎜ - абсолютная разность между модулями сравнения, а обозначения 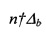 , с одной стороны, и n/Δb, n/(km2+Δb), n/(km2-Δb) (k=0, 1, …), с другой стороны, означают, что Δb не делится на n без остатка, в первом случае, и Δb, (km2+Δb), (km2+Δb) делятся на n без остатка, во втором случае;
, с одной стороны, и n/Δb, n/(km2+Δb), n/(km2-Δb) (k=0, 1, …), с другой стороны, означают, что Δb не делится на n без остатка, в первом случае, и Δb, (km2+Δb), (km2+Δb) делятся на n без остатка, во втором случае;
ms - модули сравнения, под которыми понимают длины волн принимаемых сигналов λs, s=1, 2;
bs - образы-остатки, интерпретируемые как значения, пропорциональные измеренным значениям фаз;
Δb=(b1-b2) - разность образов-остатков bs, которую интерпретируют как разность фаз между сигналом опорного генератора и принятым сигналом Δϕ=(ϕ1-ϕ2).
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ОБЪЕКТА С ИСТОЧНИКОМ ИЗЛУЧЕНИЯ СИГНАЛОВ С РАЗНЫМИ ЧАСТОТАМИ | 2011 |
|
RU2469349C1 |
| СПОСОБ ИЗМЕРЕНИЯ ДАЛЬНОСТИ И СКОРОСТИ ИМПУЛЬСНО-ДОПЛЕРОВСКОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИЕЙ | 2001 |
|
RU2206102C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕЛИ В ТРЕХПОЗИЦИОННОЙ ДАЛЬНОМЕРНОЙ РАДИОЛООКАЦИОННОЙ СИСТЕМЕ | 2012 |
|
RU2515571C1 |
| US 7265710 B2, 04.09.2007 | |||
| Устройство для определения сорта хлопка-сырца | 1978 |
|
SU676649A1 |
| US 7280069 B2, 09.10.2007 | |||
| US 8723720 B2, 13.05.2014. | |||
Авторы
Даты
2017-01-10—Публикация
2014-12-31—Подача