Изобретение относится к технологии изготовления кулачков с наружными и внутренними контурами двухволновых одноволновых приборных, силовых с высокой крутильной жесткостью негерметичных и герметичных редукторов и копиров, эллиптических и выполненных по эпитрохоиде, и кулачков с эллиптическими наружными сопряженными цилиндрическими и конической поверхностями герметичных редукторов с внутренним генератором волн и эллиптических кулачков-эталонов, изготовляемых из материалов с эффектом памяти и формы.
Уровень техники
Широко известная в специальной литературе работа Е.Г. Гинзбург «Волновые зубчатые передачи», изд-во «Машиностроение», 1969, приводит способ профилирования внутреннего кольца генератора посредством восьми опорных точек на призме, получаемых их пригонкой по размерам по формулам, обеспечивающим параметры деформации кольца, и является аналогом.
Данный способ получения генераторов волн малопроизводителен, опорные фиксирующие точки сминаются при сборке/разборке и нагрузке, деформация кольца не выдерживается по размерам и не обеспечивает необходимую конфигурацию кольца под нагрузкой и нецелесообразен для специализированного производства волновых редукторов, так как контактирование по поверхностям не ощущается.
Некоторые инновационные решения в производстве кулачков генераторов можно отметить в работе «Планетарные передачи. Справочник. / Под ред. В.Н. Кудрявцева, Ю.Н. Кирдяшева / Л.: Машиностроение, 1977, 536 с. [1], в схеме образования профиля кулачка обкаткой круглым эксцентричным инструментом - круглым чашечным резцом на зубодолбежном станке.
Однако схема непригодна для обработки сложных сопряженных цилиндрических и конической поверхности на кулачке. Например, образующей по АС СССР №781430, ОИПОТЗ, БИ №43, 80, решающему актуальную задачу по волновым герметичным передачам. Схема сопряжена с проблемой получения заготовок с малыми припусками на обработку, поверхность требует шлифования, малопроизводительна, организация рабочего места и настройки технологического оборудования сложные.
В [1] схема обработки профиля кулачка на круглошлифовальном станке раскрывает способ точения (шлифования) с планетарным движением заготовки обрабатываемого кулачка. Для реализации способа необходим планетарный редуктор, трудоемкость изготовления которого составляет 100…115 нормочасов, подготовительный процесс и процесс обработки трудоемкие, требуется высококвалифицированный персонал, производительность труда низкая, способ травмоопасен. Оба способа в [1] являются аналогами предлагаемому способу.
Прототипом предлагаемого способа является работа в журнале «Вестник машиностроения», 1980, №2, «Обработка кулачков генераторов волн волновых передач на фрезерном станке с ЧПУ», инж. В.А. Абрамов, к.т.н. И.С. Кузьмин.
Способ является высокопроизводительным, технологичным, универсальным.
Оси симметрии эллиптического кулачка различных модификаций и копиров приняты за координатные оси фрезерного станка, в качестве базового агрегата используются стол станка с Т-образными пазами и станочное приспособление в виде диска ДСП-Ш-09 (85×65×15), например.
Оправка прижимается к заготовке кулачка и к диску. На оправку посредством служебного отверстия установки кулачка на вал генератора, заготовка устанавливается на оправку, установленную в посадочное отверстие диска.
Приспособление в сборе с заготовкой устанавливается на столе станка и крепится прижимными планками.
Математическая проработка контура в статье отсутствует, т.к. позаимствованные расчетные формулы были призваны для демонстрации самого способа как доминирующего, а размеры профиля кулачка, приведенные в учебном пособии Д.В. Чернилевский, Б.Б. Панич «Курсовое проектирование одноступенчатых редукторов», Москва, «Высшая школа», 1975 [2], по конструктивным соображениям, использованы как демонстрационные.
Сущностью и основной задачей изобретения является получение аналитической формы образующей контура кулачка и копиров для обработки кулачков с сопряженными эллиптическими цилиндрическими и конической поверхностями, сформированной двумя парами сопряженных дуг окружностей. Одна пара дуг является дугами окружностей радиуса, равного (см. И.И. Привалов. Аналитическая геометрия, М., 1957 [3]) фокальному параметру эллипса р=r=b2/a для вершин эллипса K, L (И.Н. Бронштейн и К.А. Семендяев. Справочник по математике для инженеров и учащихся втузов, Гос. изд. технико-теоретической литературы, М., 1953 [4]; Справочник машиностроителя в 6 Т. Под ред. Н.С. Ачеркана, М., 1960 [5], с. 244; Г. Корн и Т. Корн, Справочник по математике для научных работников и инженеров, Изд-во «Наука», Главная редакция физико-математической литературы, М., 1973 [6]). В источнике [4] формула для радиуса R=a2/b; приведенная также и в источнике [5], причем без доказательств в обоих источниках: как далеко кривизна радиусов R и r распространяется, и достигает ли она до точек А, Д, Д1, A1 (α как утверждал великий Морис Дрюон: «Уверенность без доказательств никогда не бывает полной») и распространяется ли до точек А, Д пересечения фокальных параметров с эллипсом, точек, принадлежащих одновременно описанной окружности треугольника ABD и эллипса кулачка и на каких участках действует R. Поэтому следует придерживаться теоремы:
а) около любого треугольника можно описать окружность или через три точки можно провести окружность и притом только одну (см. Геометрия для общеобразовательных организаций. М., Просвещение. 2015, 383 с.) [7];
б) радиус описанной окружности равен отношению произведения длин трех сторон треугольника к его учетверенной площади.
В случае б) это правило выглядит так:
r=DL2*DD1/4SΔDLD1; и R=AB2*AD/4SΔABD;
Из приведенного Решения Задачи, см. с 480 «Элементарная математика» В.В. Зайцев, В.В. Рыков, М.И. Сканави, Издательство «Наука», М. 1976 [8], по определению радиуса описанной окружности R равнобедренного треугольника ABC с боковой стороной m=AB (см. фиг. 1), основанием его n=AD
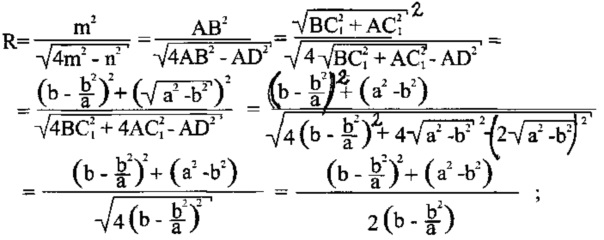
Приведенное решение задачи по определению радиуса описанной окружности «r» для равнобедренного треугольника DD1L в [8] с боковой стороной m1=LD1 (см. фиг. 1), основанием его n1=DD1 имеет вид
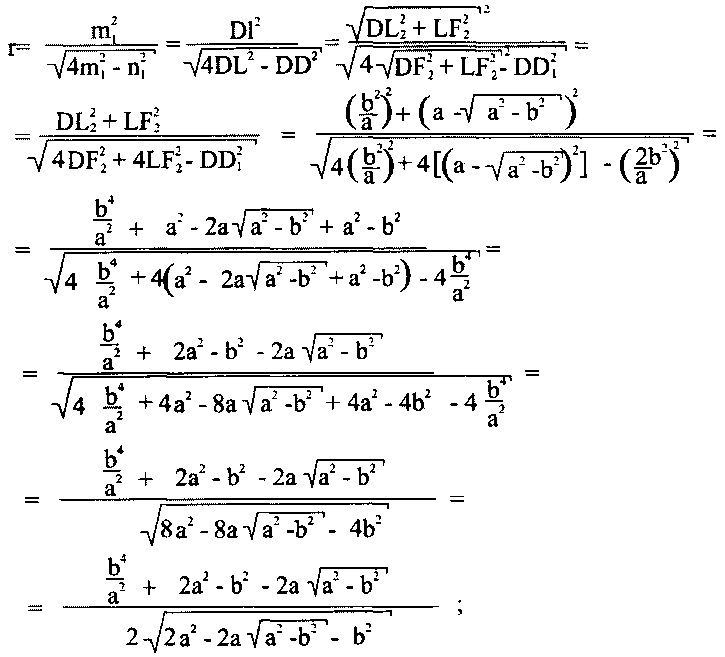
Существует много источников определения r и R (у каждого источника свои r и R - Ф.Л. Литвинов, В.И. Анурьев, Г. Корн, Т. Корн, Ю.Н. Березовский и др., В.Н. Кудрявцев и др.), но годятся они только для расчетов сфер крыш сараев в Ленинградской области.
Детали с формами любой сложности и с точностью до 0,01 мм выполняет посредством электроэрозионной обработки Производственно-внедренческий центр «Лазеры и Технологии» (info@pvlt.ru).
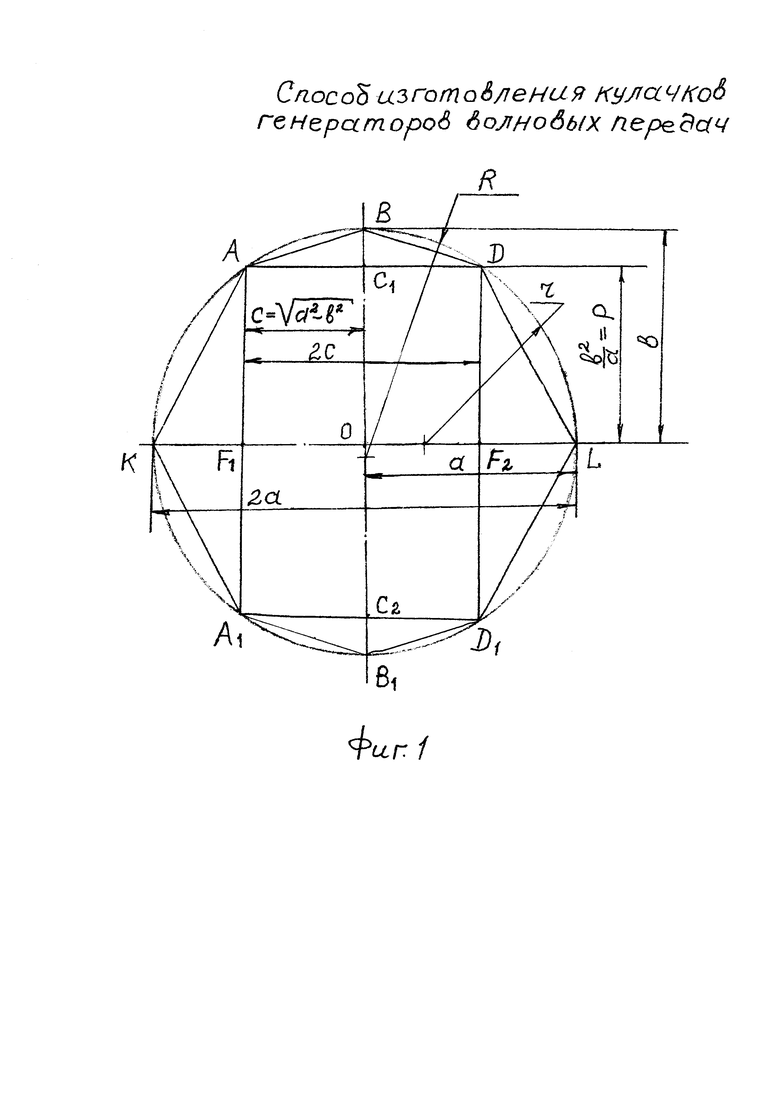
На фиг. 1 изображена расчетная схема контура эллиптического кулачка волновых передач, где a - большая полуось эллипса (длина) кулачка; b - малая полуось эллипса (длинна) кулачка; p - фокальный параметр эллипса кулачка; 2c - фокусное расстояние; F1, F2 - фокусы эллипса; K, L, B, B1 - вершины; O - центр; r=p=b2/a, r - радиус описанной окружности ΔDD1L и ΔAA1K; R - радиус описанной окружности ΔABD и ΔA1B1D1.
Высокотехнологичность технического эффекта достигается за счет оперативного ввода конструкторских и технологических данных о кулачке как изделии в оперативную систему создания программ обработки кулачка путем простого ввода параметров в программу непосредственно с чертежа.
Получение профиля эллиптического кулачка при обработке достигается заданием длин большой полуоси «a» и малой полуоси эллипса кулачка «b», обработку контура осуществляют по заданным двум парам дуг окружностей, одной пары дуг окружности с центрами, расположенными на большой оси 2a по обе стороны от центра эллипса на расстоянии 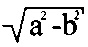
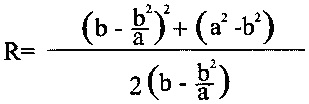 или
или 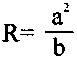 и
и 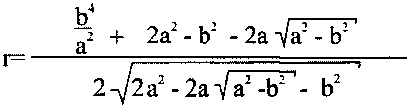
Радиусами «r», равными фокальному параметру р=r=b2/2, проведенному через фокусы параллельной малой оси 2b эллипса до пересечения с эллипсом, при этом профильные поверхности кулачка, образованные радиусами «r», сопрягают с профильными поверхностями кулачка, образованными по радиусам R, описываемыми из центров кривизны, располагаемых на малой оси 2b эллиптического контура кулачка и составляют пары радиусов R и r.
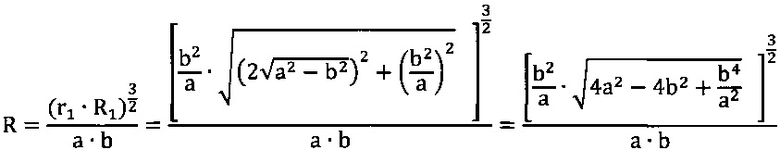
и  из [4, стр. 239] следует, что радиус кривизны равен радиусу дуги окружности,
из [4, стр. 239] следует, что радиус кривизны равен радиусу дуги окружности,
где r1 и R1 - фокальные радиус-векторы
или 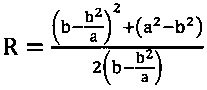 и
и 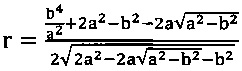
Инвариантность величин r1 и R1 при различных вариантах аналитических геометрических преобразований сохраняется и проверяется по соотношению
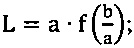 [5, с. 107]
[5, с. 107] 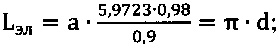
где d - диаметр отверстия измерительного гибкого калибра.
Задан равнобедренный треугольник ABD в прямоугольной системе координат XOY, вокруг треугольника ABD описана окружность с центром на оси «Y», то есть X=0, а радиус R окружности равен ординате. Найти величину ординаты центра окружности, координаты вершин треугольника ABD.
Вершина 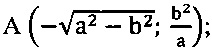
вершина B (0; b)
вершина 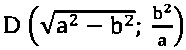
Уравнение описанной окружности имеет вид (x-a1)2+(y-b1)2=R2,
где a1 и b1 в уравнении - координаты центра окружности и R - радиус окружности,
x, y - текущие координаты окружности.
Подставляя эти координаты вершин равнобедренного треугольника в уравнение описанной окружности, получаем систему уравнений с одним неизвестным b=R. Аналогичное решение следует и для равнобедренных треугольников DLD1 и AKA1.
При вычислении R=и в пару с ним можно включить, например, 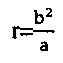 или r, определенное относительно оси абсцисс X, или составить пару радиусов
или r, определенное относительно оси абсцисс X, или составить пару радиусов
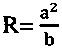 и
и 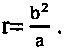
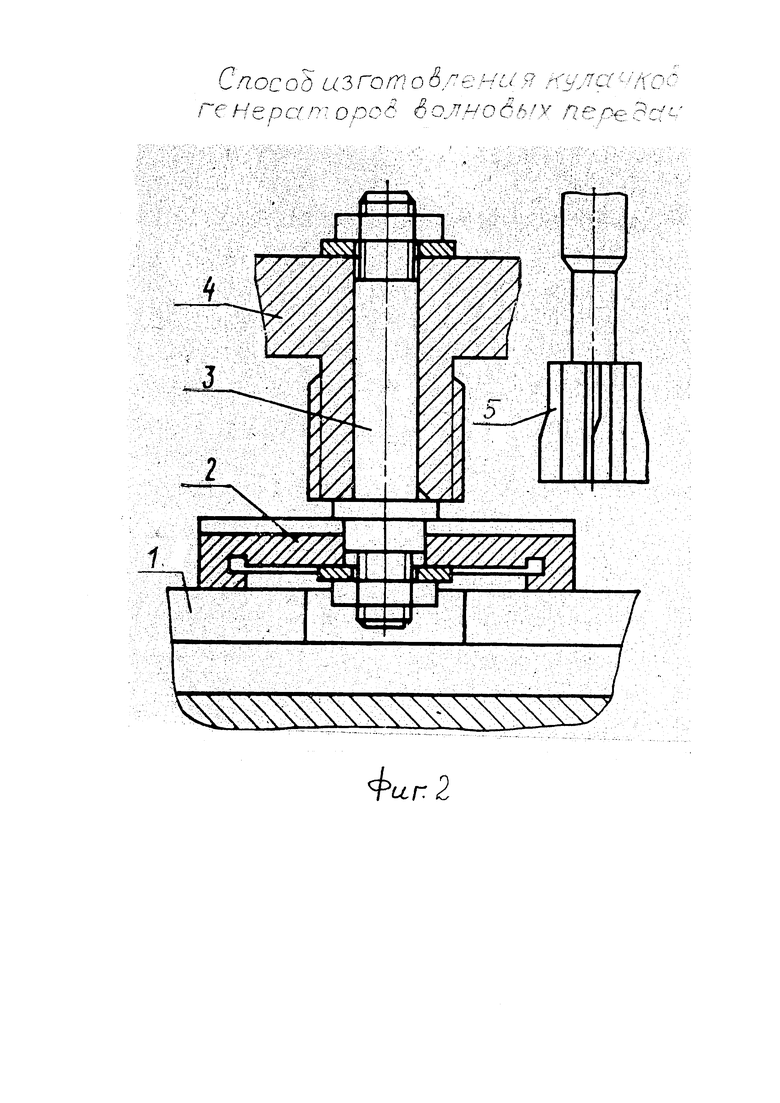
На фиг. 2 изображено базирование (согласование систем СПИД и ЧПУ) и установка эллиптического кулачка 4 с эллиптическими сопряженными наружными цилиндрическими поверхностями конической поверхностью на столе фрезерного станка, в сборе, обрабатываемых фрезой 5 за один установ.
Способ является высокопроизводительным, технологичным, универсальным, может быть осуществлен фрезой, кругом, электродом и проволокой электроэрозионным методом.
Оси симметрии эллиптического кулачка различных модификаций и копиров принимаются за координатные оси фрезерного станка с ЧПУ, в качестве базового агрегата используются стол 1 станка с Т-образными пазами и станочное приспособление в виде, например, диска ДСП-Ш-09 (85×65×15), 2.
Оправка 3 прижимается к заготовке кулачка 4 и к диску 2. На оправку 3 посредством служебного отверстия установки кулачка 4 на вал генератора заготовка устанавливается на оправку 3, установленную в посадочное отверстие диска 2.
Приспособление в сборе с заготовкой устанавливается на столе 1 станка и крепится прижимными планками.
Фокусное расстояние 2С при а=50 мм и b=49 мм равно 20 мм и составляет 20% от 2а и тем не менее при малом размере (b-b2/a) и большом R спрямление ∪AB не допускается, т.к. возникнут вибрации и гибкий подшипник выйдет из строя.
Целесообразно кулачок выполнять из БрБ2 ГОСТ 15835-70 или на стальные кулачки нанести покрытие из дисульфида молибдена.
Изобретение относится к области машиностроения, а более конкретно волновым передачам. Способ изготовления кулачков генераторов волновой передачи, в котором контур кулачка выполняют заданием двух пар дуг окружностей. Одна парой дуг окружностей с центрами, расположенными на большой оси эллипса на расстоянии 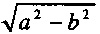 радиусами «r», где r=b2/а. Эти дуги сопрягают дугами окружностей цилиндров радиусов R кулачка другой пары, описываемыми из центров располагаемых на малой оси эллиптического контура кулачка радиусами
радиусами «r», где r=b2/а. Эти дуги сопрягают дугами окружностей цилиндров радиусов R кулачка другой пары, описываемыми из центров располагаемых на малой оси эллиптического контура кулачка радиусами 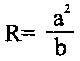 , где «b» - длина малой полуоси эллипса кулачка, а «а» - длина большой полуоси эллипса кулачка. Достигается повышение технологичности изготовления. 2 ил.
, где «b» - длина малой полуоси эллипса кулачка, а «а» - длина большой полуоси эллипса кулачка. Достигается повышение технологичности изготовления. 2 ил.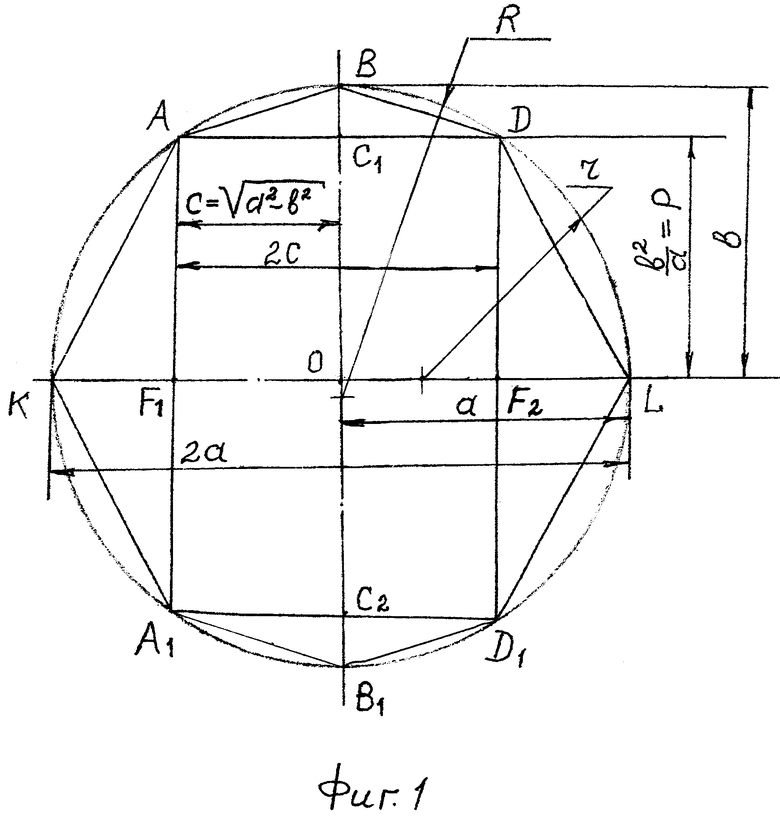
Способ изготовления кулачков генераторов волновой передачи наружных и внутренних контуров, заданных длинами большой полуоси «а» и малой полуоси «b» эллипсов, включающий базирование, закрепление установленных в приспособлении заготовок на столе универсального фрезерного станка или фрезерного станка с числовым программным управлением, написание управляющей программы движения центра фрезы шлифовального круга, электрода, проволоки машинным или ручным способом, отличающийся тем, что контур кулачка выполняют режущим инструментом или электроэрозионной обработкой и осуществляют их заданием двух пар дуг окружностей, одной пары дуг окружностей с центрами, расположенными на большой оси 2а по обе стороны от вершин эллипса радиусами «r», равными фокальному параметру p=r=b2/а,
при этом дуги окружностей цилиндров радиусов «r» сопрягают с дугами окружностей цилиндров радиусов R кулачка другой пары, описываемыми из центров кривизны, располагаемых на малой оси 2b эллиптического контура кулачка радиусами
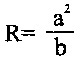
где «b» - длина малой полуоси эллипса кулачка;
«а» - длина большой полуоси эллипса кулачка.
| Способ базирования и закрепления заготовки на столе металлорежущего станка | 1987 |
|
SU1565618A1 |
| Кулачок генератора принудительной деформации волновой передачи | 1973 |
|
SU659812A1 |
| KR 2012046703 A, 10.05.2012 | |||
| Кулачковый механизм | 1973 |
|
SU508624A1 |
| Кулачковый механизм и способ изготовления кулачка | 1984 |
|
SU1231307A1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТЕКУЧЕЙ СРЕДЫ ВО ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ КРЫЛА И УСТАНОВКА ДЛЯ ОСУЩЕСТВЛЕНИЯ ЭТОГО СПОСОБА | 1996 |
|
RU2157919C2 |
| CN 201787028 U, 06.04.2011. | |||
Авторы
Даты
2017-05-03—Публикация
2015-07-31—Подача