Изобретение относится к вычислительной и измерительной технике и может быть использовано в информационно-измерительных системах и приборах с цифровой обработкой информации.
Известен способ аналого-цифрового преобразования, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой, варьируя величину, воспроизводимую мерой, с помощью АЦП с линейной шкалой квантования [П.П. Орнатский. Автоматические измерения и приборы. Киев.: Вища школа, 1980. 560 с].
Недостатком этого способа является то, что при линейной измерительной шкале относительная погрешность квантования изменяется обратно пропорционально измеряемой величине. Большая неравномерность изменения относительной погрешности квантования линейной шкалы ограничивает диапазон измерения.
Известен способ аналого-цифрового преобразования [патент СССР №1336240, Н03М 1/48 Способ аналого-цифрового преобразования / О.А. Цыбульский. Заявл. 26.08.85. Опубл. 07.09.87. Бюл. 33], в котором на измерительном входе АЦП формируют сигнал в виде первой линейной комбинации измеряемого и опорных сигналов, на опорном входе АЦП формируют сигнал в виде второй линейной комбинации измеряемого и опорных сигналов, сравнивают с помощью АЦП с линейной шкалой квантования сигналы на измерительном и опорном входах и рассчитывают результат измерения по формуле
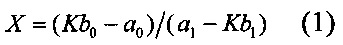
где a0, a1, b0, b1 - постоянные масштабные коэффициенты;
X - измеряемая величина; К - выходной код.
Для получения шкалы, обеспечивающей наибольший диапазон измерений при заданной максимально допустимой погрешности квантования, должно быть выполнено условие равенства граничных относительных погрешностей квантования
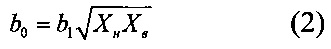
где Хн и Хв соответственно нижняя и верхняя границы диапазона измерения.
Соотношение (2) оптимально, когда предельная относительная погрешность измерения постоянна вдоль диапазона. Но в реальных приборах предельная относительная погрешность измерения изменяется неравномерно по диапазону. Соответственно, граничные погрешности требуемой шкалы квантования могут значительно отличаться.
Данный способ ограничивает возможность согласования полосы погрешности квантования с полосой предельной погрешности прибора, что приводит к уменьшению динамического диапазона измерения.
Задачей предлагаемого технического решения является расширение динамического диапазона измерения.
Для этого в способе аналого-цифрового преобразования, включающем подачу преобразуемого сигнала на первый вход первого и второго сумматоров и подачу опорных сигналов а0 и b0 на вторые входы сумматоров, подают сигнал с выхода первого сумматора, равный (X+a0), на измерительный вход блока сравнения и формирования выходного кода, а сигнал с выхода второго сумматора, равный (b1X+b0), подают на опорный вход блока сравнения и формирования выходного кода, осуществляют в блоке сравнения и формирования выходного кода регулирование сигнала (b1X+b0) до момента его равенства с сигналом (X+a0), а измеренное значение X рассчитывают по формуле
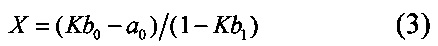
где: -a0, b0, b1, - постоянные масштабные коэффициенты;
X - измеряемая величина;
К - выходной код блока сравнения и формирования выходного кода.
Выполнение условия (2) обеспечивает равенство граничных относительных погрешностей шкалы квантования в уравнении измерения (3). Реальная же полоса предельной относительной погрешности широкодиапазонных приборов имеет, как правило, неравные граничные погрешности. Поэтому выполнение условия (2) приведет к ограничению диапазона измерения при неравных граничных погрешностях диапазона измерения.
Как известно, наиболее общим законом, нормирующим полосу предельной абсолютной погрешности широкодиапазонного измерительного прибора, является трехчленная формула [Цыбульский О.А. Критерий для обобщенной оценки широкодиапазонного прибора по точности и диапазону измерений // Измерительная техника. - 2014. - №5. - С. 5-7].
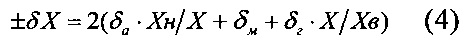
где X, Хн, Хв - соответственно текущее значение измеряемой величины, нижняя и верхняя границы диапазона измерения;
δм - мультипликативная составляющая относительной погрешности.
δа=Δа/Хн - составляющая относительной погрешности, определяемая аддитивной погрешностью измерения;
δг=Δг/Хв - составляющая относительной погрешности, определяемая погрешностью нелинейности (гиперболической) Δг при Х=Хв.
Несоответствие закона изменения предельной погрешности измерения (4) и полосы погрешности квантования с равными граничными погрешностями приводит к ограничению диапазона измерения.
Чтобы исключить этот недостаток, необходимо, чтобы полоса погрешности квантования имела тот же закон изменения по диапазону, что и полоса предельной погрешности (4). Если задать погрешность квантования не меньше суммы прочих погрешностей (например, δХк=0,5δХ), то можно полагать, что ни один квант такого прибора не будет избыточным. Если полоса предельной относительной погрешности прибора нормирована выражением (4), то полоса погрешности квантования такого прибора должна соответствовать выражению
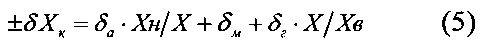
В этом случае АЦП будет иметь минимально необходимое число квантов, обеспечивающее требуемую полосу погрешности квантования (5).
В работе [Цыбульский О.А. Критерий для обобщенной оценки широкодиапазонного прибора по точности и диапазону измерений // Измерительная техника. - 2014. - №5. - С. 5-7] решалась задача определения уравнения измерения широкодиапазонного прибора, погрешность квантования которого изменяется вдоль диапазона по тому же закону, что и полоса предельной погрешности прибора. Это условие без избыточного квантования.
Для решения этой задачи применен метод трансформации шкалы аналого-цифрового преобразователя. Согласно этому методу, для того чтобы аналого-цифровой преобразователь, у которого цена деления ΔК выходного кода К изменяется по закону ΔК=ψ(К), имел шкалу измеряемой величины Х, цена деления которой изменяется по закону ΔХ=ϕ(Х), уравнение измерения должно иметь вид
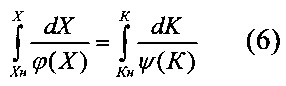
где Хн и Кн - соответственно, нижние граничные значения измеряемой величины X и выходного кода К.
Для полосы квантования (5) цена деления ΔX изменяется по закону

Для выходного кода линейного АЦП цена деления ΔК постоянна
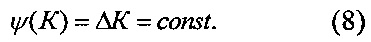
Подставляя выражения (8) и (7) в (6), получим, что для того, чтобы полоса погрешности погрешности квантования X изменялась по тому же закону, что и предельная погрешность (4), необходимо, чтобы уравнение измерения имело дробно-линейный вид (3).
При этом, если выполняется неравенство
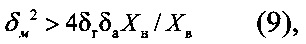
то выходной код К АЦП должен иметь цену деления, изменяющуюся по экспоненциальному закону.
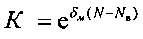 - выходной код экспоненциальной шкалы. N=1, 2 … Nв
- выходной код экспоненциальной шкалы. N=1, 2 … Nв
В частном случае, при условии
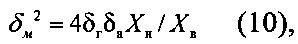
выходной код К АЦП должен иметь цену деления ΔК постоянную по диапазону, где 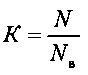 - выходной код с линейной аддитивной шкалой квантования, N=0, 1, 2 … Nв.
- выходной код с линейной аддитивной шкалой квантования, N=0, 1, 2 … Nв.
В реальных приборах полоса предельной погрешности, как правило, соответствует условию (9). В то время как выполнение условия (10) соответствует всем полосам квантования, получаемым на базе шкалы с постоянной ценой деления, т.е. на базе линейных АЦП. При условии (10) полоса погрешности квантования прибора с уравнением измерения (3) и с АЦП с постоянной ценой деления АДГ имеет вид
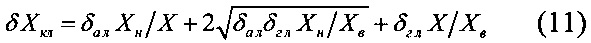
δХкл - полоса погрешности квантования прибора с уравнением измерения (3) и АЦП с постоянной ценой деления ΔК;
Хн, Хв - соответственно нижняя и верхняя границы диапазона измерения.
δал и δгл - аддитивная и гиперболическая составляющие полосы погрешности квантования при применении АЦП с линейной шкалой К.
Применение экспоненциального АЦП в уравнении измерения (3) является оптимальным для построения требуемой полосы погрешности квантования с использованием наименьшего количества квантов. Однако АЦП с экспоненциальной шкалой квантования существенно уступают по своим технико-экономическим характеристикам АЦП с линейной шкалой. Учитывая одинаковость уравнения измерения (3) для обоих условий (9) и (10), а также близость выражений (5) и (11) для погрешности квантования, целесообразно аппроксимировать полосу погрешности квантования (5) полосой (11), заменив в уравнении (3) АЦП с экспоненциальной шкалой К на АЦП с линейной шкалой К.
Подставив (8) и (7), при условии (10), в уравнение (6), получим после преобразований дробно-линейное уравнение измерения, в котором применяется АЦП с линейной шкалой К.
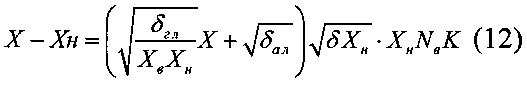
где 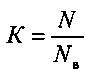 выходной код с линейной аддитивной шкалой квантования, N=0, 1, 2 … Nв;
выходной код с линейной аддитивной шкалой квантования, N=0, 1, 2 … Nв;
Значения аддитивной и гиперболической составляющих для полосы (11) определяем приравняв в граничных точках диапазона измерения δХн и δXв погрешности квантования (5) и (11).
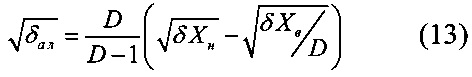

где: 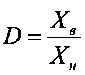 - динамический (относительный) диапазон измерений,
- динамический (относительный) диапазон измерений,
δХн, δХв - соответственно относительные погрешности в нижней и верхней границах диапазона измерения.
Представим выражение (3) в виде уравнения измерения
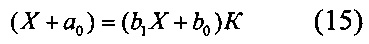
Сопоставляя коэффициенты (15) с соответствующими коэффициентами (12), получим соотношения
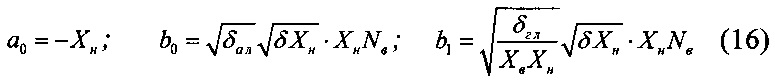
Уравнение (12) соответствует общему виду дробно-линейного уравнения измерения (15) и реализует полосу погрешности квантования (11), аппроксимирующую полосу погрешности квантования (5). А выражение для погрешности квантования (11) соответствует общему выражению для погрешности квантования [2].
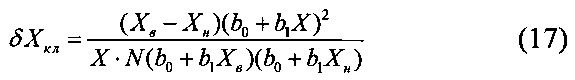
В отличие от общих выражений (15) и (17) коэффициенты уравнений (11) и (12) однозначно связаны со всеми параметрами, определяющими вид и значение шкалы квантования.
Из (15) и (17) следует, что отличие характеристики преобразования и характеристики квантования дробно-линейного АЦ преобразования от соответствующих характеристик линейного АЦ преобразования определяется неравенством нулю коэффициента b1≠0. При дробно-линейном АЦ преобразовании равномерная полоса абсолютной погрешности квантования линейного АЦП трансформируется при b1≠0 в параболу, параметры которой определяются отношением коэффициентов 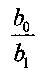 и границами диапазона измерения.
и границами диапазона измерения.
Запишем отношение коэффициентов 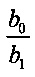 в уравнении (12)
в уравнении (12)
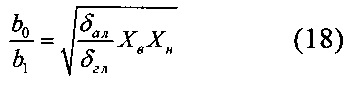
В частном случае, при условии равенства граничных относительных погрешностей квантования, из (18) следует выражение (2).
Для определения динамического диапазона измерения АЦП с уравнением измерения (12) воспользуемся выражением, связывающим между собой относительные погрешности квантования в нижней границе диапазона измерения δXн и верхней границе диапазона измерения δXв с динамическим диапазоном 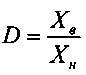 и числом квантов Nв АЦП с линейной шкалой К [Патент СССР №1336240, Н03М 1/48 Способ аналого-цифрового преобразования / О.А. Цыбульский. Заявл. 26.08.85 Опубл. 07.09.87. Бюл. 33].
и числом квантов Nв АЦП с линейной шкалой К [Патент СССР №1336240, Н03М 1/48 Способ аналого-цифрового преобразования / О.А. Цыбульский. Заявл. 26.08.85 Опубл. 07.09.87. Бюл. 33].
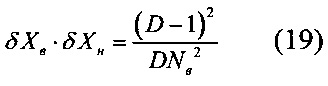
Выразив из (19) значение диапазона измерения, получим
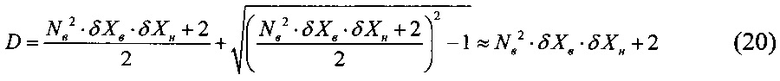
Выражение (20) позволяет сравнивать динамические диапазоны дробно-линейных АЦП при различных значениях граничных относительных погрешностях квантования. Например, если при Nв=4096 относительная погрешность квантования в нижней границе диапазона должна быть δХв=0,02, в верхней границе диапазона должна быть δХв=0,005, то из (20) получим D=40962⋅0,02⋅0,005+2=1679.
Если же применять, как в прототипе, условие (2), то при равных граничных погрешностях квантования δХв=δХв=0,005 результирующий динамический диапазон будет в 4 раза меньше, чем в предыдущем примере D=40962⋅0,0052+2=421.
Зададим в уравнении (12) значения нижней границы диапазона измерения Хн=0,002 и верхней границы Хв=0,002⋅1679=3,358. Количество квантов шкалы Nв=4096. Подставляя значения граничных погрешностей δХн=0,02; δХв=0,005 в (13), (14), рассчитаем значения аддитивной и гиперболической составляющих в уравнении измерения (12). В результате получим уравнение дробно-линейного АЦП с динамическим диапазоном измерения 1:1679 на основе 12-разрядного линейного АЦП.
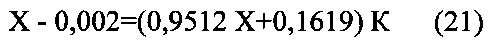
где К изменяется от 0 до 1.
В приведенном примере полоса погрешности квантования АЦП с уравнением измерения (21) стыкуется с оптимальной полосой квантования (7) по двум граничным точкам в соответствии с условием (18). В результате достигается расширение динамического диапазона измерения в 4 раза по сравнению с диапазоном прототипа при выполнении условия (2), когда стыковка осуществляется по минимальной из граничных погрешностей.
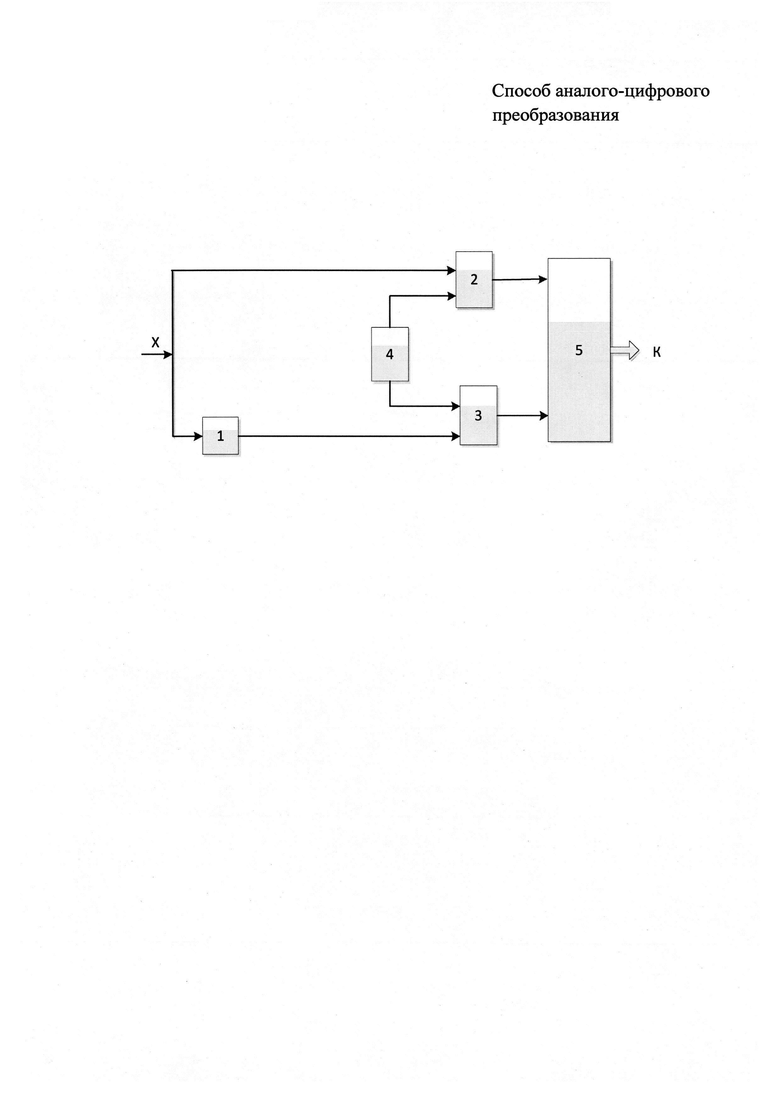
На прилагаемом рисунке представлена функциональная схема устройства, реализующая способ аналого-цифрового преобразования, позволяющий расширить динамический диапазон измерения применяемого АЦП с линейной шкалой квантования.
Устройство содержит масштабирующий преобразователь 1, первый и второй блоки сумматора, соответственно 2 и 3, блок опорных сигналов 4, блок сравнения и формирования выходного кода 5.
Преобразуемый сигнал X поступает на первый вход сумматора 2 и на масштабирующий преобразователь 1, который формирует масштабируемый сигнал с коэффициентом b1, поступающий на первый вход сумматора 3. С блока опорных сигналов на вторые входы сумматоров 2 и 3 поступают соответственно первый а0 и второй b0 опорные сигналы. Сигнал с выхода первого сумматора 2, равный (Х+а0), поступает на измерительный вход блока сравнения и формирования выходного кода 5. Сигнал с выхода второго сумматора 3, равный (b1X+b0), поступает на опорный вход блока сравнения и формирования выходного кода 5. Затем блок сравнения и формирования выходного кода 5 осуществляет регулирование сигнала (b1X+b0) до момента его равенства с сигналом(Х+а0), т.е.
(X+a0)=(b1X+b0)К
Результат сравнения - код К, совместно с величинами a0, b0, b1,, значения которых предварительно занесены в память блока 5, используются для расчета измеряемой величины. В качестве блока сравнения и формирования выходного кода может быть использован микроконтроллер с встроенным линейным АЦП.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ аналого-цифрового преобразования | 1985 |
|
SU1336240A1 |
| Система измерения расхода газа | 2019 |
|
RU2709439C1 |
| Способ измерения вещественной и мнимой составляющих переменного напряжения | 2021 |
|
RU2780348C1 |
| Аналого-цифровое множительное устройство | 1983 |
|
SU1163335A1 |
| Цифровой измеритель действующего значения сигнала | 2018 |
|
RU2685062C1 |
| СПОСОБ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2009 |
|
RU2444125C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПЕРЕХОДНОГО ПРОЦЕССА | 2001 |
|
RU2187822C1 |
| Устройство аналого-цифрового преобразования | 1986 |
|
SU1325697A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИНТЕГРАЛЬНОЙ И ДИФФЕРЕНЦИАЛЬНОЙ НЕЛИНЕЙНОСТЕЙ АЦП И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2024 |
|
RU2828783C1 |
| Цифровой измеритель параметров случайных процессов с распределением Накагами | 2020 |
|
RU2742695C1 |
Изобретение относится к вычислительной и измерительной технике и может быть использовано в информационно-измерительных системах и приборах с цифровой обработкой информации. Технический результат заключается в расширении динамического диапазона измерения. Технический результат достигается за счет способа аналого-цифрового преобразования, который включает подачу преобразуемого сигнала на первый вход первого и второго сумматоров и подачу опорных сигналов а0 и b0 на вторые входы сумматоров, при этом подают сигнал с выхода первого сумматора, равный (X+a0), на измерительный вход блока сравнения и формирования выходного кода, а сигнал с выхода второго сумматора, равный (b1X+b0), подают на опорный вход блока сравнения и формирования выходного кода, осуществляют в блоке сравнения и формирования выходного кода регулирование сигнала (b1X+b0) до момента его равенства с сигналом (X+a0). 1 ил.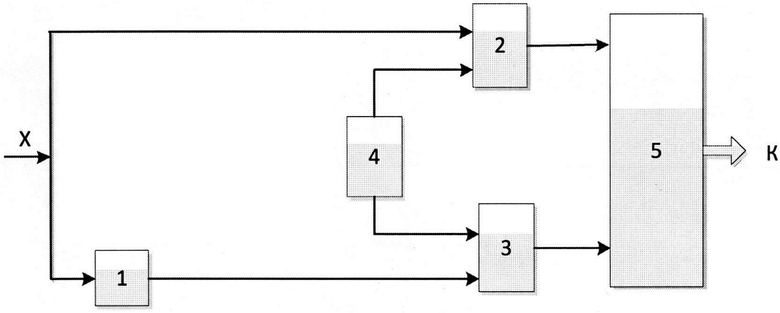
Способ аналого-цифрового преобразования, включающий подачу преобразуемого сигнала на первый вход первого и второго сумматоров и подачу опорных сигналов а0 и b0 на вторые входы сумматоров, подают сигнал с выхода первого сумматора, равный (Х+а0), на измерительный вход блока сравнения и формирования выходного кода, а сигнал с выхода второго сумматора, равный (b1X+b0), подают на опорный вход блока сравнения и формирования выходного кода, осуществляют в блоке сравнения и формирования выходного кода регулирование сигнала (b1X+b0) до момента его равенства с сигналом (Х+а0), а измеренное значение X рассчитывают по формуле
X=(Kb0-a0)/(1-Kb1),
причем коэффициенты a0, b0, b1, рассчитывают по формулам
a0=-Xн; 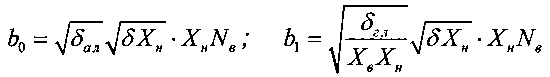
где: - Хн, Хв - соответственно нижняя и верхняя границы диапазона измерения;
Nв - число квантов;
δXн, - относительная погрешность в нижней границе диапазона измерения;
δал и δгл - аддитивная и гиперболическая составляющие полосы погрешности квантования.
| АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2546621C1 |
| ПАРАЛЛЕЛЬНЫЙ АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ ДИНАМИЧЕСКОГО ТИПА (ВАРИАНТЫ) | 2008 |
|
RU2389133C1 |
| Способ приготовления одно-металлического фосфата марганца | 1939 |
|
SU58825A2 |
| Машина для одновременного печатания и тиснения | 1925 |
|
SU4190A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| СПОСОБ ИДЕНТИФИКАЦИИ МИКРООРГАНИЗМОВ ИЗ ТЕСТИРУЕМОГО ОБРАЗЦА ГЕМОКУЛЬТУРЫ | 2009 |
|
RU2541775C2 |
Авторы
Даты
2017-05-11—Публикация
2016-02-25—Подача