Предлагаемое изобретение относится к компонентам твердотельных механических гироскопов, конкретно, к подшипникам подвеса вращающегося ротора. Предложенное техническое решение (TP) касается сферического подшипника качения (СФК) для предложенного абсолютного гироскопического датчика угловых положений (1, 2) объектов с шестью степенями свободы и может быть использовано в обозначенных датчиках для повышения точности и снижения ухода оси вращения ротора гироскопа.
Широко известны подшипники качения (ПК) с одной степенью свободы вращательного движения (3, 4). Известные ПК содержат два кольца, наружное и внутреннее, с дорожками качения, комплект тел качения и сепаратор, служащий для удержания тел качения на фиксированных расстояниях друг от друга.
Известные ПК имеют ряд преимуществ по сравнению с подшипниками скольжения. Основное состоит в том, что коэффициент трения качения Мк значительно меньше коэффициента трения скольжения Мс (5). ПК имеют низкий нагрев, малый пусковой момент, позволяют достигать больших скоростей вращения, что имеет особенно важное значение для механических гироскопов. Недостатком является всего одна степень свободы вращательного движения. Поэтому при использовании в кардановых подвесах гироскопов известных ПК на больших углах отклонения оси в карданах возбуждаются колебательные моменты, которые снижают устойчивость вращательного движения ротора, повышают склонность к нутационным колебаниям ротора, вызывают повышение ухода его оси вращения. (Эти недостатки и противоречия снимаются в предложенном СПК).
Известны СПК с бочкообразными телами качения (3, 4). Они допускают отклонения оси вращения по второй и третьей координатам, но диапазон возможных отклонений весьма мал и не обеспечивает полной свободы движений.
Основываясь на изложенном выше, видно, что известные ПК и СПК имеют сходство с предложенным TP только по технической сущности использования тел и соответственно трения качения. Однако назначение и достигаемые результаты другие. Поэтому в качестве аналогов и прототипа условно выбираем известные ПК и СФК, так как по определению аналог и прототип это "близкий и наиболее близкий объект того же назначения, что и заявляемый, сходный с ним технической сущностью и результатом, достигаемым при его использовании" (6).
Целями изобретения являются расширение диапазона вращательного движения СПК до неограниченного по всем трем степеням свободы и обеспечение полной симметрии технических характеристик при любой ориентации оси вращения.
Указанная цель в СПК, содержащем две поверхности качения, внешнюю и внутреннюю, комплект тел качения, сепаратор для удержания тел качения на фиксированных друг от друга расстояниях, достигается тем, что внешняя поверхность качения выполняется сопряженной с внутренней поверхностью сферы статора, а внутренняя - сопряженной с внешней поверхностью ротора гироскопа, а сепаратор выполняется в виде механически соединенных между собой двух тонкостенных сфер из немагнитного материала, на которых на равных расстояниях друг от друга по дугам больших окружностей в вершинах равных между собой по площади граней-симплексов в форме треугольников Эйлера расположены гнезда с шариками из немагнитного или диамагнитного материала.
В современном уровне развития теории и практики гироскопии, а также известных конструкций ПК и СПК неизвестны СПК для механических твердотельных гироскопов, которые обеспечивали бы неограниченный диапазон вращательного движения по всем трем степеням свободы, а также полную симметрию технических характеристик при любой заданной ориентации оси вращения в пространстве. Также не известна в уровне техники предложенная конструкция со сферическими дорожками качения и сферическим сепаратором, что говорит о соответствии предложенного TP критериям новизны и изобретательского уровня, тем более, что полученные полезные технические свойства СПК напрямую связаны с неизвестным ранее полным сферическим выполнением всех его компонентов. Если говорить о промышленной применимости, то известны материалы с необходимыми свойствами для изготовления предложенного СПК. Единственная трудность состоит в том, что предстоит освоить новые технологии изготовления сферических компонентов конструкции СПК, прецизионные как по точности размеров, так и форме всех его компонентов. Также потребуется освоить точное деление поверхности сепаратора в сферических координатах, чтобы обеспечить равные между собой по площади сферические треугольники с фиксацией шариков в вершинах этих треугольников на равных друг от друга расстояниях с целью равномерного распределения нагрузки на шарики и сферические поверхности качения. Трудности такого рода всегда возникают при освоении технологий новой техники, и они преодолимы, если перефразирую Ленина "работать, работать и работать", а не делать прибыль на основе продажи природных ресурсов и присвоения в свой карман результатов деятельности предыдущих поколений.
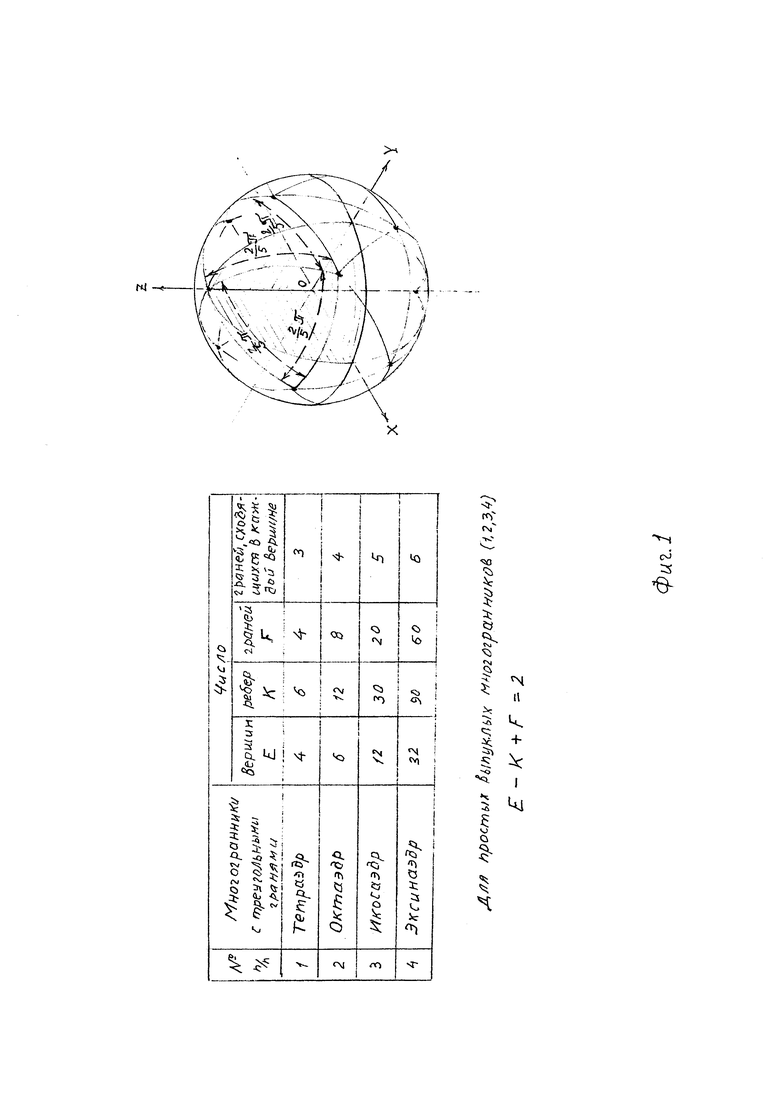
Теперь перейдем к теоретическому обоснованию устройства сепаратора и решению геометрической топологической задачи правильного деления сферы. Известно, что сфера имеет высшую группу симметрии (символ ∞/∞ m), то есть, бесконечное количество осей бесконечного порядка, бесконечное количество плоскостей (для шара) и окружностей (для сферы), и центр симметрии, и ее можно получить вращением бесчисленным количеством способов. Топологически сферу можно получить центральным проецированием на нее граней вписанных выпуклых правильных многоугольников (см. 7, 8, 9, 10). Основываясь на методах геометрии и ее раздела топологии, а также подраздела топологии теории неподвижных точек, теории групп и некоторых соображений комбинаторики, произведем триангуляцию сферы с разбиением ее на отдельные выпуклые грани-симплексы, правильно примыкающие друг к другу. Для решения поставленной задачи более всего подходит ее разбиение на сферические треугольники, стороны которых являются дугами больших окружностей (треугольники Эйлера).
На Фиг. 1 справа изображен такой способ триангуляции сферы, полученный центральным проецированием на нее граней вписанного икосаэдра. При выборе икосаэдра мы получаем 12 точек, вершин равносторонних треугольников Эйлера, в каждой из которых сходятся 5 граней, а всего граней 20, ребер 30 (см. таблицу простых выпуклых многогранников слева, Фиг. 1). Координаты всех 12 точек полученной правильной точечной системы находятся на равных друг от друга расстояниях, и их легко определить в сферической системе координат, так как экваториальные ϕ и азимутальные θ между любыми из них равны 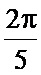
Таким образом, при использовании для отображения сфер икосаэдра мы можем изготовить сепаратор с 12-тью гнездами для шариков, равномерно распределенными по сфере. Двенадцати точек качения вполне достаточно для датчиков ориентации для 6-ти степенных объектов-аппаратов кратковременного одноразового действия (зенитные, крылатые, противотанковые ракеты и управляемые снаряды, ракеты воздушного боя). Если же СПК будет предназначен для датчиков угловых положений аппаратов многократного использования (например, космических и атмосферных летательных аппаратов), тогда нужно будет обеспечить большой ресурс работы. Для этого потребуется увеличить количество узлов качения, чтобы снизить нагрузку на поверхности качения и уменьшить износ гнезд и шариков. Однако простых выпуклых правильных многогранников с треугольными гранями существует всего три (см. пп. 1, 2, 3 в таблице Фиг. 1).
Для решения этой задачи разработан вариант триангуляции на основе использования простого выпуклого полуправильного (т.е. гранями которого служат не равносторонние, а равнобедренные треугольники) многогранника эксинаэдра (см. п. 4 в таблице Фиг. 1). Такой вариант дает 32 точки качения с незначительным неравенством расстояний друг от друга. Но этот незначительный недостаток будет компенсироваться почти трехкратным снижением нагрузки на сферические поверхности качения, шарики и гнезда сепаратора за счет увеличения точек качения. Расчет координат точек качения для этого варианта остается моим "ноу-хау". Несмотря на то, что эксинаэдр полуправильный многоугольник, он так же как и известные правильные тетраэдр, октаэдр и икосаэдр может быть превращен в сферу при помощи непрерывной деформации, что делает его также пригодным для триангуляции.
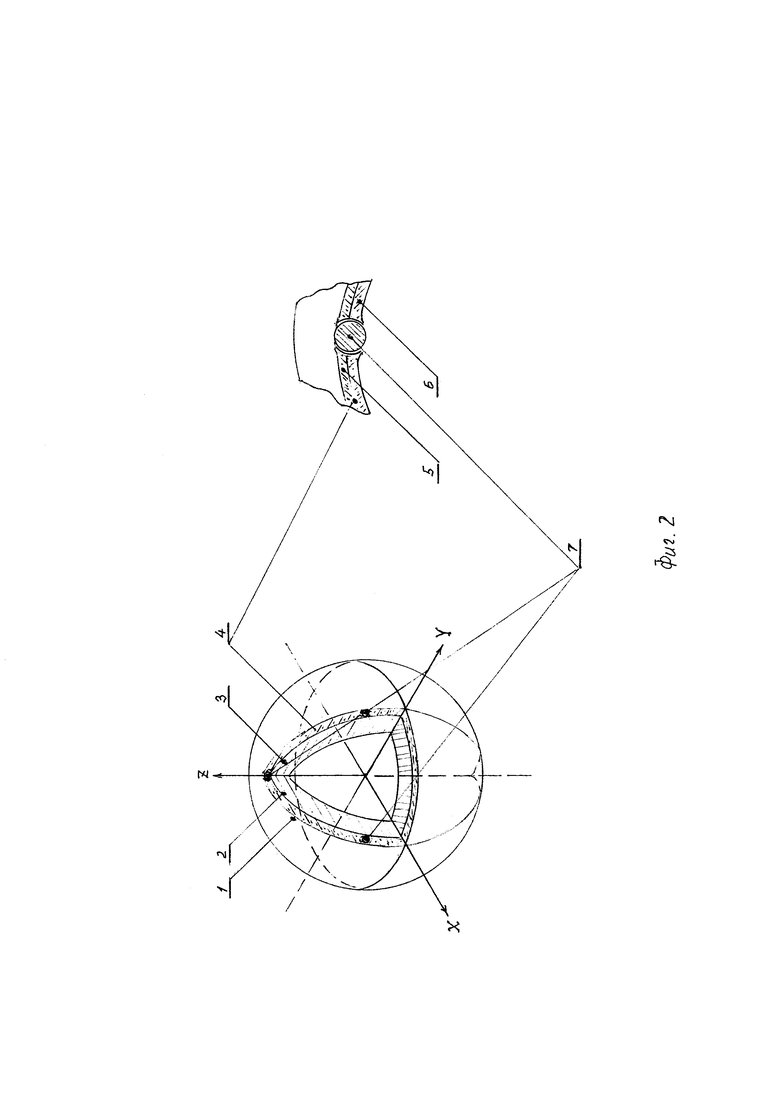
На Фиг. 2 слева изображен эскиз предложенного СПК, а справа - эскиз гнезда качения. СПК на Фиг. 2 содержит вогнутую сферическую поверхность 1 качения, сопряженную со статором гироскопа, выпуклую сферическую поверхность 2 качения, сопряженную с ротором-магнитом 3 гироскопа, сепаратор 4, расположенный между этими сферическими наружной и внутренней поверхностями СПК. Сепаратор 4 состоит из двух скрепленных между собой тонкостенных сфер 5, 6, удерживающих и фиксирующих шарики 7 в своих гнездах.
Полость между статором и ротором-магнитом гироскопа заполняют смазкой. Для СПК с высокой скоростью вращения предпочтительнее вариант, когда в эту полость подается под некоторым давлением масло с оптимальной температурой для снижения потерь на нагрев. Так как ротор гироскопа намагничен, сепаратор должен быть выполнен из немагнитного материала (например, армированный пластик), а шарики - из немагнитного или диамагнитного. Это необходимо, чтобы исключить деформацию тороидальной конфигурации вращающегося магнитного поля ротора, что могло бы привести к снижению точности воспроизведения синусно-косинусной формы измерительных сигналов датчика и соответственно точности определения углов ориентации объекта.
В материалах авторских заявок (1, 2) приведены примеры исполнения датчика угловых положений 6-ти степенных объектов с использованием подшипника скольжения ротора гироскопа относительно статора, так как к тому времени еще не была отработана конструкция предлагаемого СПК. Применение СПК в обозначенных датчиках позволит резко снизить уход оси вращения ротора гироскопа, увеличить время выбега и повысить точность определения угловых положений. Для изготовления предложенных СПК и датчиков потребуется освоение прецизионных трехмерных технологий, но эта задача в наш век 3-д принтеров решаема. Если конечно к принятию решений будут привлечены технические специалисты, а не так называемые менеджеры и финансовые специалисты по учету и хранению денег, что характерно для либерального режима современной РФ. Такие приоритеты привели к тому, что в отличие от СССР, который был на первом месте по количеству регистрируемых изобретений, сегодня РФ не входит даже в первую десятку стран лидеров по количеству регистрируемых патентов на изобретения (см. данные ВОИС), зато стоит на первом месте по количеству миллиардеров. Но среди них что-то не обнаруживается ни одного изобретателя.
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. 3аявка на изобретение "Гироскопический датчик угловых положений объекта с 6-ю степенями свободы", №2016110019.
2. 3аявка на изобретение "Способ автономного определения угловых положений объекта с 6-ю степенями свободы пространственного движения", №2016110020.
3. Нарышкин В.Н., "Подшипники качения", М., Маш-е, 1983.
4. Черменский О.Н., Федотов Н.Н, "Подшипники качения", М., Маш-е, 2003.
5. Кухлинг X, "Справочник по физике", М., Мир, Киев, 1985, стр. 74.
6. Прахов Б.Г. "Изобретательство и патентоведение", Высш. шк, Киев, 1987, стр. 9, 127.
7. Стинрод Н, Чинн У, "Первые понятия топологии", М., Мир, 1967.
8. Болтянский В.Г., Ефремович В.А. "Наглядная топология", М., Наука, 1982.
9. Гильберт Д, Кон-Фоссен С. "Наглядная геометрия", М., Наука, Физматгиз, 1981.
10. Виленкин Н.Я, "Метод последовательных приближений", М., Наука, 1968.
Изобретение относится к новому типу сферического подшипника качения, предназначенного для подвеса ротора-магнита абсолютного датчика угловых положений объектов с шестью степенями свободы пространственного движения. Сферический подшипник качения содержит внешнюю обойму, сопряженную со статором гироскопа и его внешней вогнутой сферической поверхностью (1) качения, сопряженную с ротором-магнитом (3) и его выпуклой сферической поверхностью (2) качения внутреннюю обойму, между которыми расположен сепаратор (4), выполненный в форме двух скрепленных между собой тонкостенных сфер (5, 6) из немагнитного материала, на которых на равных друг от друга расстояниях по дугам больших окружностей в вершинах равных между собой по площади граней-симплексов в форме треугольников Эйлера расположены гнезда с шариками (7) качения, выполненными из немагнитного или диамагнитного материала. Технический результат: расширение до неограниченных диапазонов вращательных движений по всем трем степеням свободы и обеспечение полной симметрии технических характеристик при любой ориентации оси вращения в пространстве. 2 ил.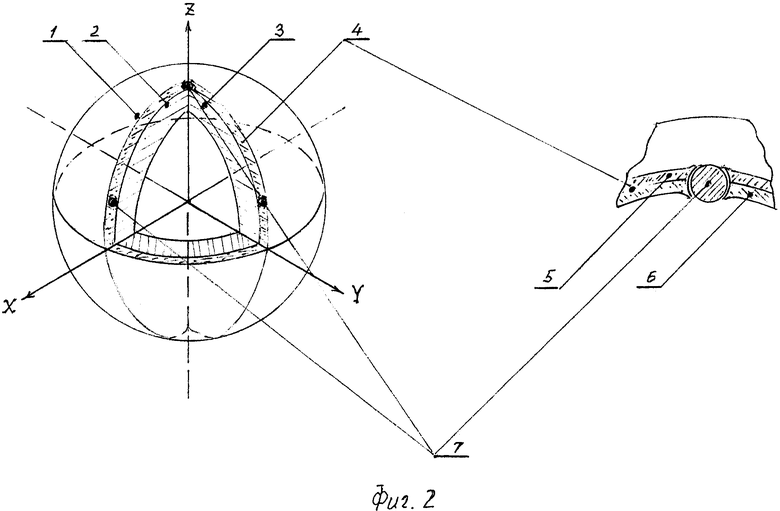
Сферический подшипник качения, содержащий внешнюю и внутреннюю обойму с поверхностями качения, комплект тел качения, сепаратор для удержания тел качения, отличающийся тем, что внешняя обойма сопряжена со статором гироскопа, на внутренней поверхности которого расположена вогнутая сферическая поверхность качения, внутренняя обойма сопряжена с ротором-магнитом гироскопа, на внешней поверхности которого расположена выпуклая сферическая поверхность качения, а сепаратор выполнен в форме двух скрепленных между собой тонкостенных сфер из немагнитного материала, на которых на равных друг от друга расстояниях по дугам больших окружностей в вершинах равных между собой по площади граней-симплексов в форме треугольников Эйлера расположены гнезда с шариками качения из немагнитного или диамагнитного материала.
| СФЕРИЧЕСКИЙ ПОДШИПНИК | 2014 |
|
RU2563295C1 |
| ПОДШИПНИК СФЕРИЧЕСКИЙ ДВУХРЯДНЫЙ | 2014 |
|
RU2563298C1 |
| ДВУХРЯДНЫЙ СФЕРИЧЕСКИЙ ШАРИКОПОДШИПНИК И СНАБЖЕННЫЙ ИМ НАВЕСНОЙ ПРИБОРНЫЙ КОНТЕЙНЕР (ВАРИАНТЫ) | 2005 |
|
RU2286485C1 |
| СФЕРИЧЕСКИЙ ШАРИКОПОДШИПНИК И СНАБЖЕННЫЙ ИМ НАВЕСНОЙ ПРИБОРНЫЙ КОНТЕЙНЕР | 2004 |
|
RU2268410C1 |
| JP 2011179624 A, 15.09.2011. | |||
Авторы
Даты
2017-08-01—Публикация
2016-07-19—Подача