Предлагаемое изобретение относится к области техники первичного измерительного преобразования физических величин в электрические сигналы и касается способа определения угловых положений объекта с 6-ю степенями свободы пространственного движения. Предлагаемое техническое решение (TP) может быть использовано в системах управления и стабилизации угловых положений летательных аппаратов (ЛА) любого типа и назначения, в системах ручного и автоматического пилотирования ЛА, в системах самонаведения управляемых ракет, снарядов и других носителей с 6-ю степенями свободы, использующих трехмерные методы слежения, самонаведения и навигации.
Широко известны способы измерительного преобразования углов и угловых перемещений с одной степенью свободы (1, 2, 3), основанные на физическом явлении электромагнитной индукции, открытом Фарадеем и уточненном Максвеллом. Известный способ используется в синусно-косинусных и линейных вращающихся трансформаторов (СКВТ, ЛВТ). При повороте ротора с двумя перпендикулярными обмотками, которые запитываются переменным током, магнитный поток в зазоре между статором и ротором изменяется пропорционально синусу и косинусу угла поворота, и в обмотках СКВТ индуцируются квадратурные сигналы.
Известный способ позволяет реализовать абсолютный датчик угла различных классов точности, но только с одной степенью свободы, что снижает информативность преобразования. Известный способ имеет и другие недостатки: необходимость механического контакта с управляемым или контролируемым объектом, наличие обратной реакции на объект, аналоговая форма представления информации, наличие скоростной погрешности и т.д.
Известны ферродинамический, электродинамический и индуктивный способы преобразования углов с двумя степенями свободы (4). Они основаны на использовании физического явления электромагнитного взаимодействия неподвижных и подвижных элементов.
Известные способы имеют низкую точность и малоинформативны, и их область применения ограничена объектами с двумя степенями свободы.
Известны более точные фотоэлектрические способы преобразования углов с одной степенью свободы (5), в том числе моего авторства (6), но их информативность ограничена одной степенью свободы.
Известны более информативные фотоэлектрические способы преобразования углов по двум координатам моего авторства (7), но их информативность ограничена для объектов с двумя степенями свободы.
Известен абсолютно информативный способ для вращающихся управляемых и контролируемых объектов с одной степенью свободы (8) моего авторства, с параллельным одновременным формированием функциональных синусно-косинусных зависимостей, а также производных и первообразных функций, но его область применения ограничена объектами с одной степенью свободы.
Более близкими по технической сущности, но также ограниченными одной степенью свободы, являются способы измерительного преобразования на основе использования двухстепенных гироскопов Фуко первого рода (гирокомпас) и второго рода (9), (в сочетании с гировертикалью измеряет географическую широту). Но эти способы также малоинформативны.
Более близкими по назначению и достигаемым результатам (но не по технической сущности) являются известные способы измерительного преобразования по всем трем координатам на основе использования трех двух и/или трехстепенных гироскопов (10). Эти близкие известные способы высокоинформативны, но обусловливают повышенную сложность конструктивного исполнения в виде гирорам и целых систем, большие массогабариты и стоимость, так как по каждой координате требуется отдельный чувствительный гироскоп.
Наконец, известны комбинированные инерциально-спутниковые системы определения более чем одного параметра ориентации шестистепенных объектов, но они относятся к другой области техники радиоизмерений углов с амплитудной и фазовой модуляцией пространственно-временных радиосигналов сверхвысоких частот 1200-1800 ГГц и здесь не рассматриваются.
Таким образом, все известные способы преобразования угловых положений 6-степенных объектов по трем координатам используют 3 датчика, по одному по каждой координате, соответственно, имеют сложные принципы функционировния, сложные алгоритмы определения угловых положений (будет показано ниже).
Наиболее близким по технической сущности к предлагаемому является TP способа определения координат воздушных целей, реализованное в оптико-электронном следящем гирокоординаторе (ОЭСК) оптических головок самонаведения (ОГС) вращающихся зенитных управляемых ракет (ВЗУР) комплексов ПЗРК "Стрела", "Игла", "Верба" (РФ), "Stinger POST", "Stinger RST" (США), "Мистраль" (Франция) (11).
Наиболее близкий способ основан на формировании информативного гармонического сигнала частоты вращения трехстепенного астатического гироскопа с радиально намагниченным ротором-магнитом в виде кольца, внутри которого и снаружи расположены сферические соленоиды путем индуцирования эдс в обмотке внутреннего соленоида, механически закрепленного на объекте, электическом арретировании ротора и наведении его оси с помощью совмещенной с ним оптической системы на объект внешнего пространства (воздушная цель), разарретировании ротора, выделении координат объекта по курсу и тангажу и коррекции ориентации оси ротора ОЭСК пропусканием тока через витки наружного соленоида. Обмотка внутреннего соленоида является датчиком по двум угловым координатам, а внешний соленоид является исполнительным элементом задания ориентации ротора вдоль продольной оси ракеты (в режиме электрического арретирования) и коррекции его ориентации посредством управления прецессионным движением (в режиме слежения за целью). Оба соленоида и втулка, на которую крепится кардановый подвес, установлены на вращающемся вместе с ракетой основании.
Наиболее близкий способ обеспечивает точное определение двух координат объекта, используя только один гироскоп, то есть является двумерной системой (по третьей координате, крену, ракета стабилизируется вращением). Таким образом, наиболее близкий способ не позволяет определить все три угла ориентации, имеет неполную информативность определения угловых положений и, соответственно, ограниченную область применения.
Целями изобретения являются повышение информативности способа до абсолютной за счет автономного, независимого от внешних сигналов, определения всех трех угловых положений с использованием только одного гироскопического датчика, а также расширение областей применения для объектов с неограниченными углами рассогласования.
Указанная цель в способе определения ориентации объекта, основанном на формировании информативного гармонического сигнала индуцированием эдс частоты вращения гироскопа, в обмотке сферического соленоида, механически закрепленного на объекте, путем разгона и вращения вокруг него радиально намагниченного ротора-магнита, электрическом арретировании ротора, наведении его оси вращения на объект внешнего пространства для задания начального отсчета координат, разарретировании ротора, отслеживании объекта внешнего пространства и демодуляции информативного сигнала с выделением двух координат по курсу и тангажу, достигается тем, что формируют одновременно три синусно-косинусных попарно биортогональных сигнала путем вращения внутри или снаружи сферы, механически связанной с объектом, с тремя расположенными на ней взаимно перпендикулярными соленоидами, полого полного или неполного (если он подвешен на внутреннем кардановом подвесе) шара, намагниченного перпендикулярно его оси вращения, и представляющего систему координат внешнего пространства, а угловые положения объекта определяют одновременной параллельной амплитудно-фазовой демодуляцией трех пар полученных биортогональных сигналов по трем каналам по заданным алгоритмам.
Таким образом, введение указанной неизвестной ранее совокупности операций одновременного формирования трех попарно биортогональных синусно-косинусных сигналов индуцированием эдс с помощью вращения внутри или вне сферы с тремя расположенными на ней взаимно перпендикулярными соленоидами, механически закрепленной и связанной с объектом, полого ротора-магнита, намагниченного перпендикулярно оси вращения и представляющего систему координат внешнего пространства, обеспечивает внесение в эти сигналы пространственной модуляцией их амплитуд и фаз информационных признаков и параметров трех угловых положений. Эта совокупность, как и ее связь с обозначенными полезными результатами неизвестны как в наиболее близких TP, так и в современном уровне науки и техники гироскопических датчиков, измеряющих одновременно три угловых положения 6-степенных объектов. Это говорит о соответствии критериям новизны и изобретательского уровня предложенного способа.
Прежде чем переходить к рассмотрению примера для осуществления способа, вниманию экспертизы предлагаются теоретические основы способа в геометрическом и аналитическом представлении.
Из различных разделов математики, а также теории и практики пилотирования, навигации известно много систем отсчета координат, как связанных с объектом, так и представляющих внешнее пространство. Системы координат для отсчета внешнего пространства разделяются на инерциальные (звездные), псевдоинерциальные и неинерциальные. Из геометрии известны левая и правая прямоугольные (декартовы) системы координат, полярная, цилиндрическая, сферическая, тороидальная и другие системы отсчета пространства. Из теории и практики систем пилотирования и навигации известны сферическая гелиоцентрическая, географическая, экваториальная, ортодромическая и другие, например комбинированные горизонтально-ортодромическая, свободная в азимуте горизонтальная и т.д.
Рассмотрим сочетание декартовой и сферической систем координат. Здесь возможны 4 комбинации: 1 - внешнее пространство и объект представляют в декартовой системе; 2 - с объектом связывают декартову систему координат, а внешнее пространство представляют сферической; 3 - с объектом связывают сферическую, а с внешним пространством декартову систему; 4 - с объектом связывают сферическую, а внешнее пространство представляют также сферической системой координат.
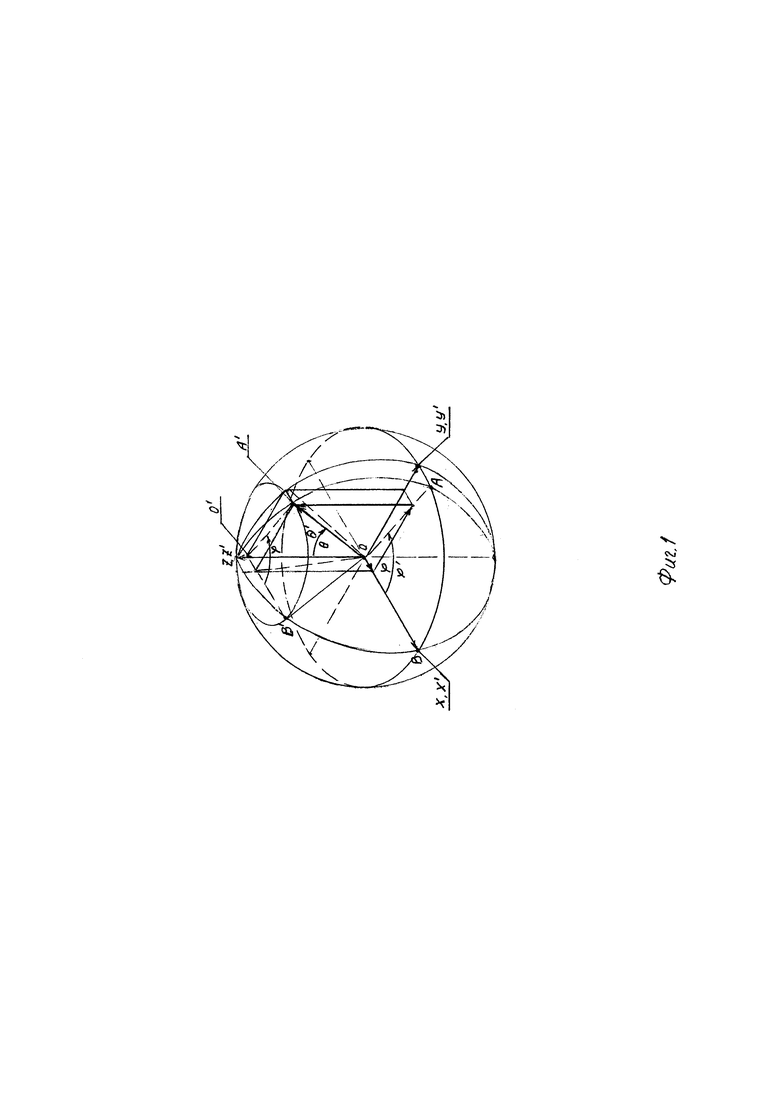
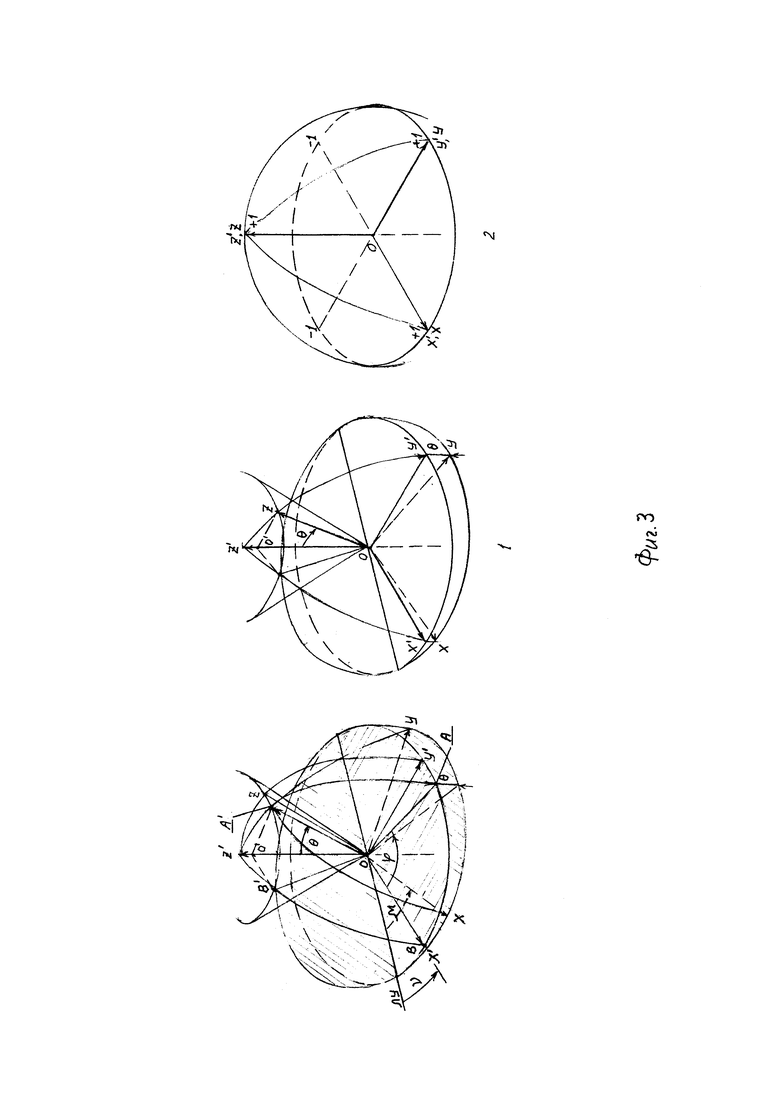
Для упрощения алгоритмов обработки сигналов мной применен следующий математический прием (см. Фиг. 1). Сферическая система упрощается, если координату радиуса приравниваем единице, назовем ее единичной сферической. Декартову систему нормируем, ограничивая ее сферой единичного радиуса. На Фиг. 1 представлена такая комбинация, где показаны правая декартова система координат OX'Y'Z', совмещенная с единичной сферической, представляющие пространство, и связанная с объектом OXYZ ортонормированная декартова система. Показана точка А с произвольно выбранными координатами. В единичной сферической системе ее координаты определяются полуосью ОХ' начального отсчета, азимутальным (широта) и зенитным (долгота) углами ϕ и θ. На Фиг. 1 также показаны первая координатная поверхность, сфера единичного радиуса ρ=1=const; вторая - полуплоскость ОʺZ'А', проходящая через точку А', уравнение которой будет ϕ,ϕ'=const; и третья, конус, определяемый θ, θ=const.
Также на Фиг. 1 показаны связанная с объектом ортонормированная декартова система координат ОXYZ, совмещенная с единичной сферической в виде основной полярной плоскости OXY, полуосью ОХ начального отсчета, причем азимутальные и зенитные углы ϕ, ϕ' и θ, θ' совпадают, так как все системы имеют общее начало и оси их совмещены. Применение такой комбинации ортонормированной декартовой и единичной сферической позволяет упростить известные формулы перехода, и они приобретают вид: х=cos θ cos ϕ; у=cos θ sin ϕ; z=sin θ; θ=arctg z, так как 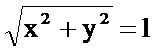
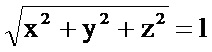
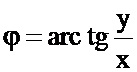
Добавлю, что такой выбор координат для определения Эйлеровых углов обусловлен следующими соображениями. В природе все тела находятся в движении, отличном от прямолинейного поступательного, поэтому для внешнего пространства используется соответствующая его топологии сферическая система. Кроме того, шар и ограничивающая его сфера имеют самую высшую группу симметрии ∞/∞ m. Это означает, что у шара бесконечное количество осей симметрии бесконечного порядка, а также бесконечное количество плоскостей симметрии. Но все известные в настоящее время летательные аппараты имеют асимметрию формы по одной и более координатам (аппараты в виде шара или плоского эллипсоида пока не созданы). Кроме того, исторически сложилась связанная с объектом система координат с осями курса, крена и тангажа, поэтому для объекта более приемлема декартова система координат (кроме вращающихся ракет и снарядов).
Теперь проведем сравнительный анализ алгоритмов совмещения декартовых систем координат и сферических, имеющих общее начало координат, и угловые положения, как известно, однозначно определяемые Эйлеровыми углами ν, μ, θ. Л. Эйлер для доказательства этого математического факта использовал понятие "линии узлов" (далее ЛУ), как развитие такого базового понятия "узел", введенного К. Гауссом и уточненного А. Пуанкаре. В своем доказательстве Эйлер использовал только одну ЛУ, как прямую пересечения координатных плоскостей (ребро двугранного угла) OXY и O'X'Y', хотя при расхождении угловых положений 2-х систем координат образуются три ЛУ. Поэтому его алгоритм последовательный и весьма сложный (см., например, 12, стр. 643).
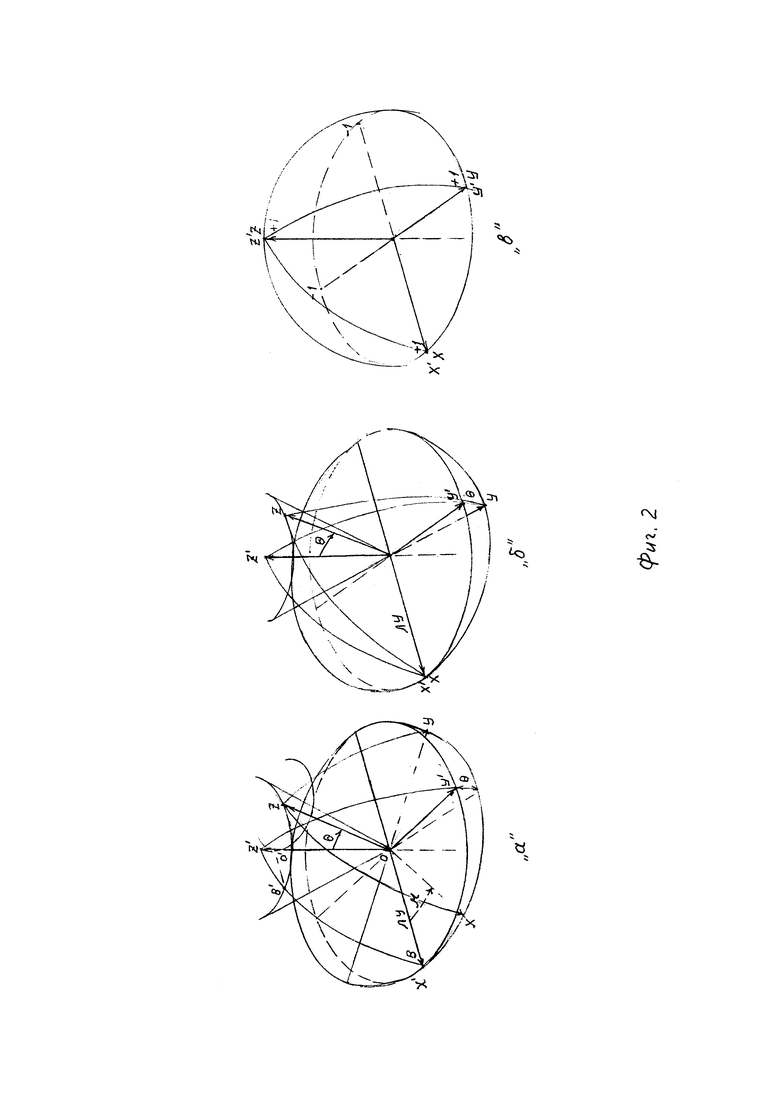
На Фиг. 2 изображен этот алгоритм в геометрическом представлении в виде последовательных поворотов "а", "б" и "в" (исходное положение совмещенных систем координат смотреть на Фиг. 3 слева): а - поворачиваем на угол ν в плоскости OXY в направлении кратчайшего поворота оси ОХ к оси OY, после чего получаем совмещение оси ОХ и ЛУ; б - поворачиваем на угол μ от ЛУ в плоскости O'X'Y' в направлении кратчайшего поворота О'Х' к O'Y'; в - совмещаем оси OZ и O'Z' по кратчайшему пути на угол θ. К тому добавим, что ЛУ выбираем из двух ее лучей таким образом, чтобы три луча ЛУ, OZ и O'Z' образовали правую тройку.
Теперь сравниваем совмещение единичных сферических координат (второе и третье изображение на Фиг. 3 слева направо под номерами 1, 2.) 1 - поворачиваем на угол ϕ (долгота) в базовой экваториальной плоскости OXY; 2 - затем поворачиваем на угол θ (широта) в азимутальной плоскости.
Таким образом, совмещение единичных сферических систем дает несомненные преимущества упрощения алгоритма и, соответственно, уменьшение затрат обработки сигналов для демодуляции и выделения информативных признаков и параметров угловых положений, а также упрощает формулы перехода из сферической системы координат в декартову (показано ниже, л. 4).
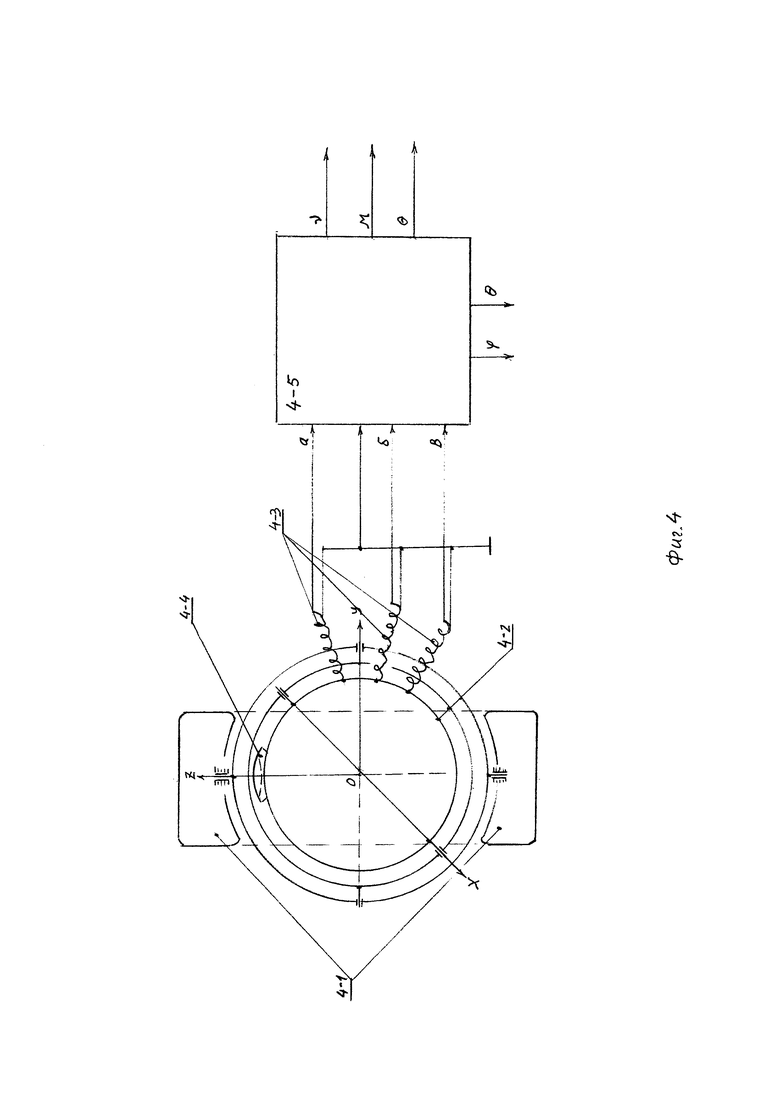
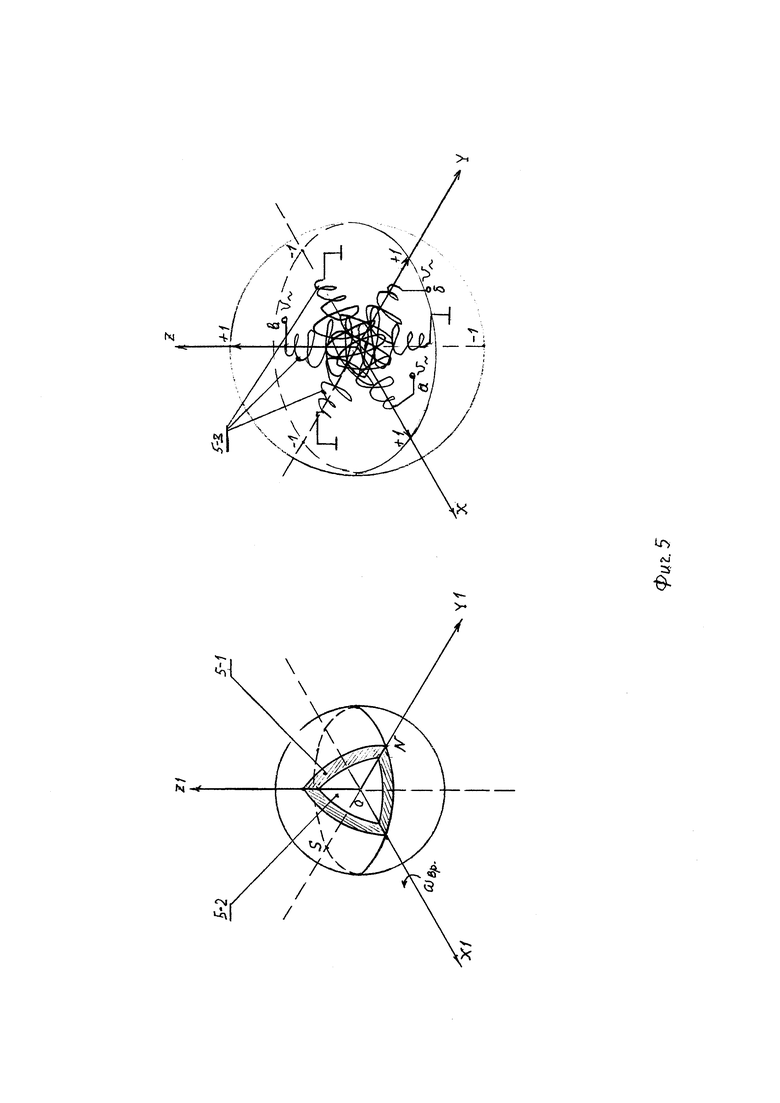
На Фиг. 4 представлена блок-схема примера реализации способа; на Фиг. 5 - эскиз ротора гироскопа (слева) и эскиз сферического статора (справа), с расположенными на нем тремя взаимно перпендикулярными соленоидами; на Фиг. 6 - электрическая схема статора и временные диаграммы индуцированных при вращении ротора синусно-косинусных сигналов в диапазоне поворота объекта от 0 до 2π; на Фиг. 7 представлен в разрезе шаровый ротор-магнит. Устройство, представленное на Фиг. 4, содержит разгонное устройство 4-1, снабженное системой электрического арретирования и при необходимости системой стабилизации частоты вращения ротора, наружный кольцевой кардановый подвес 4-2 сферы с соленоидами, гибкие кабели 4-3 и блок 5 (вычислитель) определения угловых положений объекта.
Шаровый ротор-магнит, представленный на Фиг. 5 слева, выполнен в форме полого шара 5-1, намагниченного перпендикулярно оси вращения, и имеет внутреннюю полость 5-2, которая частично заполняется жидкостью для демпфирования ударных и вибрационных воздействий. Справа на Фиг. 5 изображен статор, выполненный в форме сферы из немагнитного материала с расположенными на нем взаимно перпендикулярно тремя сферическими соленоидами 5-3. Также на Фиг. 5 изображены оси OX1, OY1, OZ1 декартовой системы координат внешнего пространства, совмещенной с единичной сферической, и оси ОХ, OY, OZ связанной с объектом декартовой системы, также совмещенной с единичной сферической.
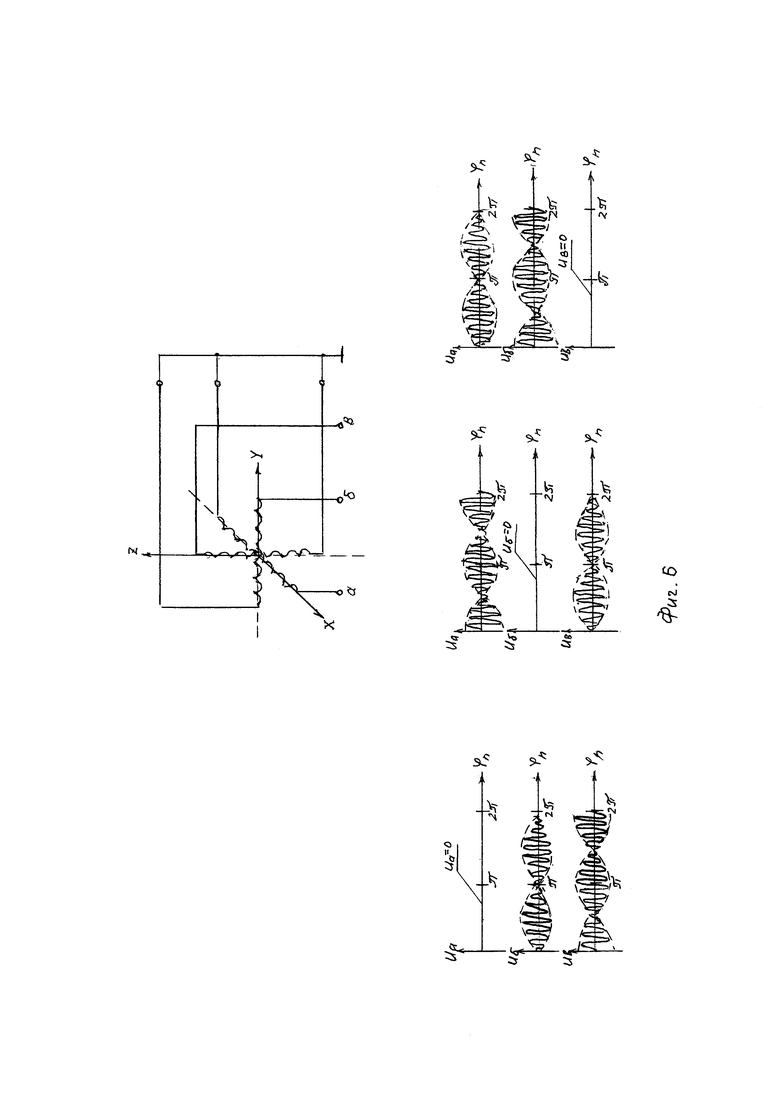
Электрическая схема, представленная на Фиг. 6, состоит из трех попарно биортогональных обмоток соленоидов, на которых при вращении ротора-магнита индуцируются эдс а, б, в. Временные диаграммы синусно-косинусных сигналов а, б, в показаны ниже при повороте объекта с закрепленной на нем сферой в трех плоскостях в диапазоне от 0 до 2π.
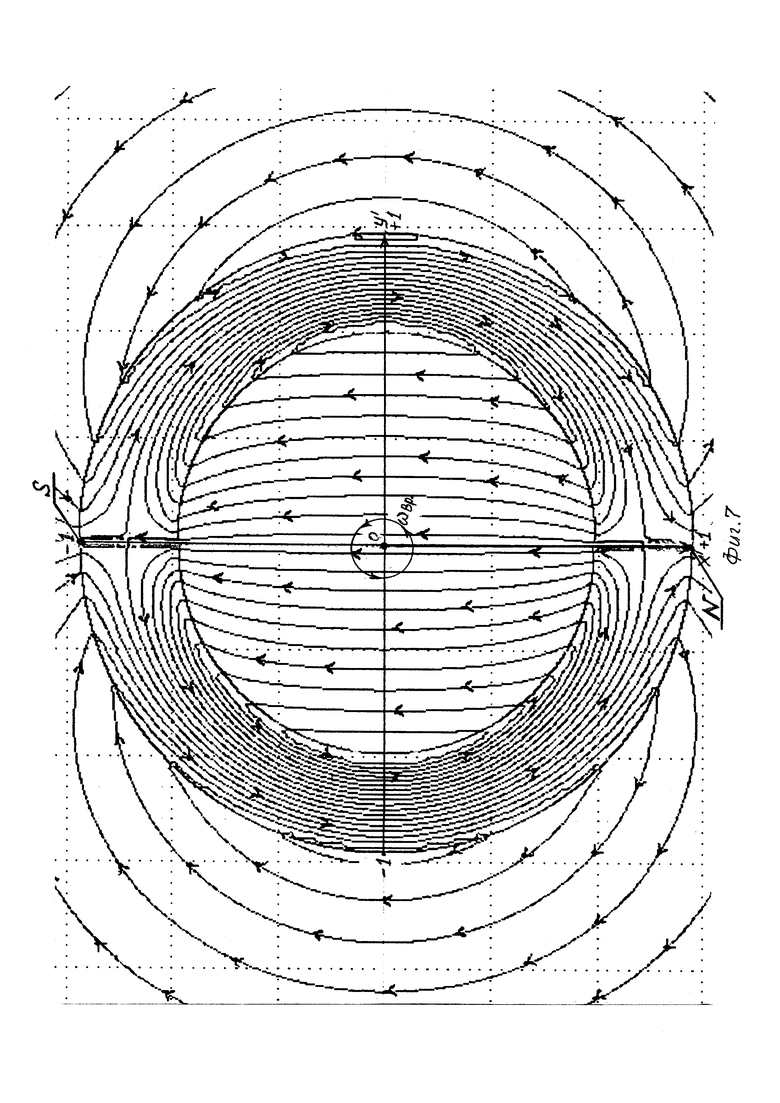
На Фиг. 7 показан в разрезе ротор-магнит и силовые линии его вихревого магнитного поля (расчет произведен на компьютере с помощью специальной программы), здесь также показаны северный N и южный S полюса.
Устройство для реализации предложенного способа (как один из вариантов), изображенное на Фиг. 4 - Фиг. 7, работает следующим образом.
На втулках осей карданового подвеса 4-2 установлены фиксирующие винты (чтобы не загружать эскиз вспомогательными элементами, на эскизе они не показаны). Вначале включают разгонное устройство 4-1, а затем переводят его в режим стабилизации частоты вращения ротора и режим электрического арретирования. Затем ослабляют винты фиксаторов карданового подвеса и производят установку начального отсчета координат, нацеливая гироскоп на объект внешнего пространства (например, на Полярную звезду, если используется инерциальная система координат), используя для этого оптическое или другое прицельное устройство 4-4. Затем винты фиксаторов стопорят. Если устройство используют в одноразовом объекте кратковременного действия, например зенитной ракете ближнего боя, используется неинерциальная система координат, и "привязка" начального отсчета произойдет без фиксации - расфиксации карданового подвеса, когда головка самонаведения захватит цель в поле зрения и будет ее отслеживать. В этом случае можно обойтись и без системы стабилизации частоты вращения ротора, так как его уходом в режиме кратковременного функционирования объекта можно будет пренебречь.
Если же устройство используется в режиме долговременного функционирования, то должна быть предусмотрена система периодической коррекции ориентации оси ротора или простейшая система слежения за звездой. Все эти варианты устройства для реализации в первичных материалах заявки не рассматриваются, тем более, объем притязаний данной заявки ограничивается только способом. Что касается алгоритмов работы вычислителя угловых положений 4-5, то он будет зависеть от выбранной комбинации систем координат. Привожу один из возможных алгоритмов (остальные остаются моим "ноу-хау").
Демодуляцию полученных на выходах обмоток сферических соленоидов попарно биортогональных синусно-косинусных сигналов а, б, в с параллельным выделением всех трех параметров ориентации объекта можно обеспечить так. На пиковых (амплитудных) детекторах выделяют напряжения амплитуд сигналов а, б, в, а затем вычисляют арктангенсы их отношений
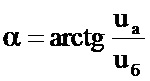
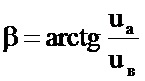
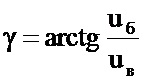
Далее вычисляют косинусы направляющих углов, и по известным формулам (см. 13, стр. 198) или с помощью матрицы перехода (см. там же) определяют угловые положения объекта. Можно применить и более простые алгоритмы, сначала переводя декартову систему координат, связанную с объектом, в единичную сферическую, и вычислить экваториальный и азимутальные углы рассогласования между единичными сферическими системами координат, представляющими как объект, так и внешнее пространство. Это значительно упрощает алгоритм и снижает объем вычислительных операций, так как таким образом трехмерная задача сводится к двумерной.
В настоящее время известны магнитные и немагнитные материалы с необходимыми для реализации способа свойствами. Намотка прецизионных сферических соленоидов освоена на ОАО, ЛОМО, Спб для ОЭСК оптических головок самонаведения ПЗРК "Стрела", "Игла" и "Верба". Разгонное устройство, снабженное системой электрического арретирования, давно известно с времен разработок "Стрелы", оно описано в документации на стендовую аппаратуру КПАСМ (гриф секретности с этой аппаратуры снят). Предстоит освоить только технологию изготовления сферического ротора. Следует отметить, что балансировки роторов не потребуется, так как при неполной заливке внутренней полости жидкой средой будут не только демпфироваться внешние механические воздействия, но также ротор будет самобалансироваться за счет влияния центробежных сил на жидкость. Таким образом, предложенный способ соответствует критерию промышленной применимости. При реализации способа возможны варианты исполнения устройства как с внешним кардановым подвесом, так и с внутренним. В последнем случае мы ограничиваем допустимые углы рассогласования и получим их меньше 360°, но при этом чувствительные обмотки датчика будут экранироваться ротором, что резко уменьшит помехи от обмоток разгонного устройства. При использовании внешнего кардана может потребоваться введение обмоток компенсации этих помех.
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Д.Э. Брускин и др. "Электрические машины", Т. 2, М., Высш. шк., 1986, стр. 32-40.
2. М.В. Баканов и др. "Информационные микромашины следящих и счетно-решающих устройств", М., Сов. радио, 1977.
3. Э.И. Осиновский и др. "Высокоточные преобразователи угловых перемещений", М., Энергоатомиздат, 1986.
4. Е.М. Карпов, "Измерительные преобразователи с двумя степенями свободы", М., Энергия, 1972.
5. Л.Н. Преснухин, "Фотоэлектрические преобразователи информации", М., Маш-е, 1980.
6. СССР, А.с. 297567 (гриф "с").
7. ССР, А.с. 1810857, 1777090.
8. РФ, Патент 2549115.
9. М.А. Павловский, "Теория гироскопов", Высш. шк., 1986, стр. 79, 84, 85.
10. Д.С. Пельпор, "Гироскопические системы", М., Высш. шк., 1986, стр. 363; В.Я. Распопов, "Технические системы для измерения угловых координат", Авиакосмическое приборостроение, 2004, №3, стр. 6-10; Патент РФ 2014563.
11. В.В. Козелкин, И.Ф. Усольцев, "Основы инфракрасной техники", М., Маш-е, 1986, стр. 204; Техническое описание изделия 9Э410, ОГС "Игла" и комплекса ПЗРК 9К38М, Оборонгиз, 1980 (гриф секретности снят).
12. Математический энциклопедический словарь, М., Сов. энциклопедия, 1988, стр. 643.
13. И.Н. Бронштейн, К.А. Семендяев, "Справочник по математике", Наука, Физматгиз, 1986, стр. 198.
Пп. 1-10 аналоги, П. 11 - прототип.
Использование: для преобразования угловых положений. Сущность заключается в том, что способ автономного определения положения объекта основан на формировании информативного гармонического сигнала частоты вращения гироскопа с радиально намагниченным ротором–магнитом путем индуцирования эдс в обмотке сферического соленоида, механически закрепленного на объекте, электрическом арретировании ротора гироскопа, наведении его оси вращения на объект внешнего пространства и установке начального отсчета координат, разарретировании и выделении из информативного сигнала параметров по двум координатам, курса и тангажа, при этом формируют одновременно три попарно биортогональных между собой синусно-косинусных сигнала индуцированием эдс частоты вращения ротора, выполненного в форме полого полного или неполного шара, намагниченного перпендикулярно его оси вращения и помещенного внутри или снаружи сферы из немагнитного материала, на которой взаимно пространственно перпендикулярно расположены три сферических соленоида, а параметры трех угловых положений объекта, представленного связанной с ним системой координат в виде трех попарно биортогональных между собой синусно-косинусных сигналов, относительно внешнего инерциального, псевдоинерциального или неинерциального пространства, представленного вращающимся шаровым ротором-магнитом, определяют одновременной демодуляцией по трем каналам амплитуд и фаз трех пар обозначенных синусно-косинусных сигналов по заданным алгоритмам. Технический результат: обеспечение возможности повышения информативности измерительного преобразования, расширения областей применения для 6-степенных объектов с неограниченными углами рассогласования и упрощения алгоритмов обработки информативных сигналов. 7 ил.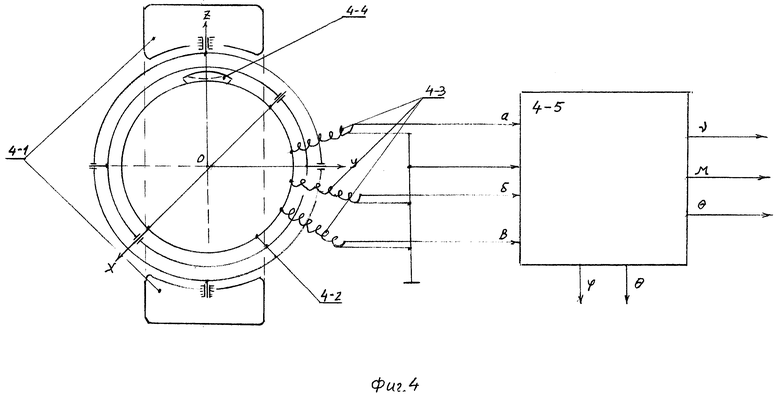
Способ автономного определения угловых положений объекта с шестью степенями свободы пространственного движения, основанный на формировании информативного гармонического сигнала частоты вращения гироскопа с радиально намагниченным ротором-магнитом путем индуцирования эдс в обмотке сферического соленоида, механически закрепленного на объекте, электрическом арретировании ротора гироскопа, наведении его оси вращения на объект внешнего пространства и установке начального отсчета координат, разарретировании и выделении из информативного сигнала параметров по двум координатам, курса и тангажа, отличающийся тем, что формируют одновременно три попарно биортогональных между собой синусно-косинусных сигнала индуцированием эдс частоты вращения ротора, выполненного в форме полого полного или неполного шара, намагниченного перпендикулярно его оси вращения и помещенного внутри или снаружи сферы из немагнитного материала, на которой взаимно пространственно перпендикулярно расположены три сферических соленоида, а параметры трех угловых положений объекта, представленного связанной с ним системой координат в виде трех попарно биортогональных между собой синусно-косинусных сигналов, относительно внешнего инерциального, псевдоинерциального или неинерциального пространства, представленного вращающимся шаровым ротором-магнитом, определяют одновременной демодуляцией по трем каналам амплитуд и фаз трех пар обозначенных синусно-косинусных сигналов по заданным алгоритмам.
| БЕСКОНТАКТНЫЙ ДАТЧИК УГЛОВОГО ПОЛОЖЕНИЯ ВАЛА | 2005 |
|
RU2378613C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ВЕКТОРА КИНЕТИЧЕСКОГО МОМЕНТА НЕКОНТАКТНОГО ГИРОСКОПА | 1993 |
|
RU2065134C1 |
| RU 94005696 A1, 10.06.1996 | |||
| Механизм для получения дифференциального ряда чисел оборотов шпинделя металлорежущих станков | 1947 |
|
SU70553A1 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ПРИ ПОДДЕРЖАНИИ ЗАДАННОЙ ОРИЕНТАЦИИ С ПОМОЩЬЮ РЕАКТИВНЫХ МАХОВИКОВ | 2004 |
|
RU2281233C2 |
Авторы
Даты
2017-08-31—Публикация
2016-03-17—Подача