Настоящее изобретение относится к области вычислительной техники и дискретной автоматики и может быть использовано при построении подсистем управления с повышенным уровнем безопасности за счет динамического контроля каждого такта выдачи команд управления сложными техническими системами или технологическими процессами.
Контроль автоматов управления может производиться в двух режимах при проверке:
- правильности реакции на изменение входных условий по тестам до начала работы автомата [1-3];
- правильности выдачи команд управления в процессе работы автомата (динамический контроль) [4-6].
В настоящей заявке на изобретение предлагается способ динамического контроля.
Известны несколько способов динамического контроля автоматов управления, из которых наиболее распространенными являются два:
1. Различные варианты дублирования основной комбинационной схемы, реализующей функции переходов от настоящего a(t) к последующему состоянию a(t+1) автомата со сравнением результата основной и дублирующей схем [4-6];
2. Использование специальных кодов (коды Хэмминга, коды с фиксированным числом единиц, код Бергера, и др. [1-5]).
Простым и эффективным (из класса кодов с фиксированным числом единиц) является способ на основе двоичного геометрического кода [7].
Вышеназванные способы применялись для контроля автоматов Мили и Мура, в которых код нового состояния a(t+1)-y1y2…ym вычисляется по коду предыдущего состояния a(t)-x1x2…xm и полной конкатенации логических условий α0α1α2…αq [8-11].
Известны автоматы нового типа [11-13], в которых код a(t+1) вычисляется по формуле:
a(t+1)=F1(αjx1x2…xm), j=F3(y1y2…ym), A(t+1)=F2(y1, y2, …, yn)
Далее при описании используются следующие сокращения:
ОУ - операционное устройство (объект управления), М - мультиплексор, DC - дешифратор, Сч (или Ст) - счетчик, Рг - регистр памяти, СЛ - схема сложения по mod2, CP - схема сравнения, ПР - схема принятия решений, БС - блок синхронизации, Fi комбинационные схемы (I=1, 2, …5), ГСА - граф-схема алгоритма управления, ПЗУ - постоянное запоминающее устройство с электрическим или ультрафиолетовым стиранием информации, УА - управляющий автомат (автомат управления), СУА - самоконтролируемый управляющий автомат, ПЛМ - программируемая логическая матрица, ПЛИС - программируемая логическая интегральная схема, mod2 - операция сложения по модулю два. Для сокращения в тексте УА называется просто автоматом.
В автоматах нового типа вводится мультиплексор для выбора на каждом такте работы единственного αj из всего множества входных логических условий (переменных) α0α1α2…αq. по коду состояния a(t). Такое решение обеспечивает снижение затрат оборудования для реализации основной комбинационной схемы F1 в Q=V/W=2q-1 раз. Здесь V=m2m+q - объем ПЗУ комбинационной схемы переходов автомата Мура; W=m2m+1 - объем этой же схемы в автоматах нового типа при реализации УА для одного и того же алгоритма управления сложной технической системой. Несмотря на снижение объема основной комбинационной схемы F1 и наличие оборудования на реализацию мультиплексора (М), комбинационной схемы F2, а также схемы F3 для вычисления адреса αj∈{α} по коду a(t+1) даже для УА средней сложности (m=5, q=12) требуются специальные меры для обеспечения контроля правильности функционирования.
Известны несколько способов контроля и конструкции самоконтролируемых автоматов, например, представленные в патентах: №63588 БИ №15, 2007; №2475816 БИ №5, 2013; №2502121 БИ №17, 2013. Недостатком этих решений является отсутствие динамического контроля работы автомата.
Наиболее близким к предлагаемому изобретению является способ, используемый в управляющем автомате (по патенту №2475816 G06F 9/00 (2006.01). Обеспечение контроля в прототипе потребовало удвоения затрат на основную схему формирования кодов переходов F1. Способ контроля, использованный в прототипе, сводится к следующему:
1. Кроме основной схемы F1 вводится дублирующая схема в виде двух полусхем с половинной разрядностью.
2. Код состояния a(t) разделяется пополам.
3. К каждой половинной части добавляются два дополнительных разряда:
- один - это αj, которое выбирается по коду a(t+1);
- второй разряд доопределяется так, чтобы по группе младших разрядов кодов a(t) с учетом двух дополнительных разрядов можно было правильно определить соответствующие младшие разряды выходного кода состояния a(t+1). Точно также доопределяются и старшие разряды состояния a(t).
Прототип содержит основную F1 и дублирующую схему в виде двух полусхем (F11, F12), причем в дублирующей схеме итоговый код a(t+1) вычисляется по частям кода a(t) разрядностью m/2+2 для каждой полусхемы.
Недостатками прототипа являются относительно большие затраты оборудования на реализацию схем F11, F12, сложность реализации блоков контроля и принятия решений, а также сложность процедуры вычисления выходного кода.
С целью устранения недостатков предлагается новый способ контроля.
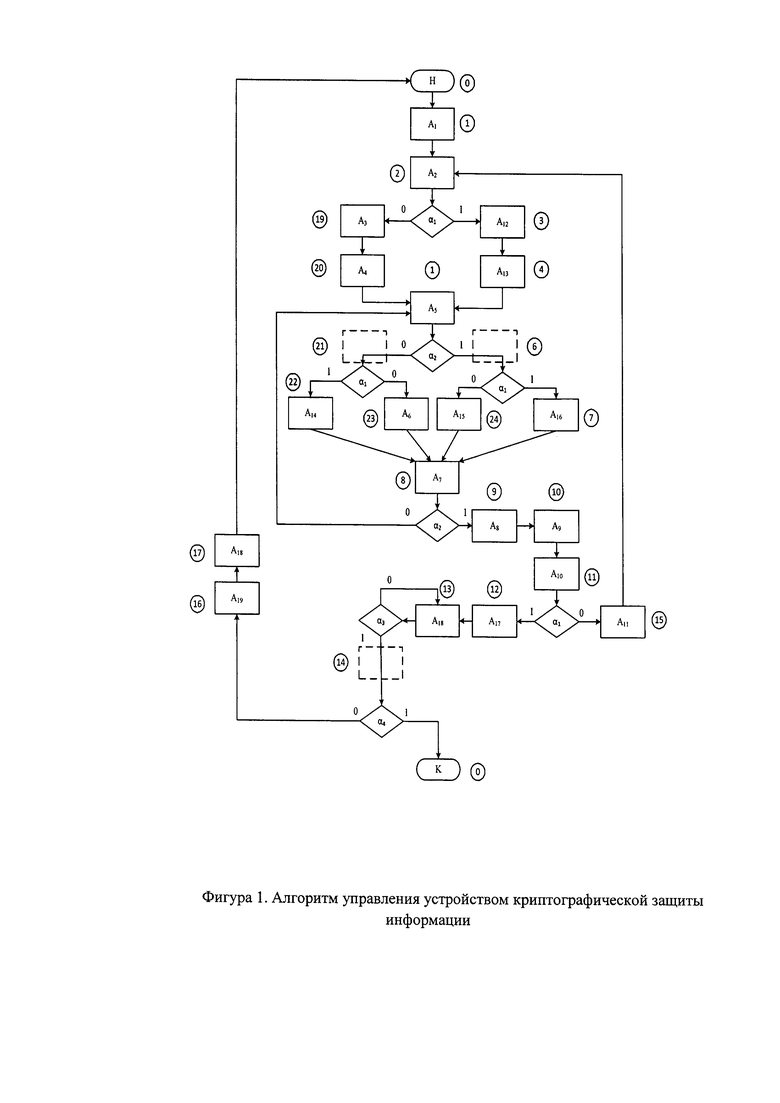
Существо способа поясним на основе граф-схемы алгоритма (ГСА), как наиболее распространенной и самой наглядной из известных операторных схем алгоритмов [13]. Например, на фиг. 1 представлен алгоритм управления устройством криптографической защиты информации [19]. Преобразования ГСА, не нарушающие ни причинно-следственный порядок операторов действия A1A2…Ak, ни их логической взаимосвязи в соответствии со всем комплексом (множеством {α}) входных логических условий α0α1…αq, сводятся к следующему:
1) если в ГСА имеется непосредственный переход по нулевому или единичному выходу некоторого αi к другому αj без промежуточного оператора действия A1∈{А}, то между αi и αj вставляется пустой оператор Ар, не производящий действий из множества {А} операторов, заданных изначально.
2) пустой оператор Ар ставится также перед любым логическим условием α1∈{α}, если к нему передается управление от нескольких других операторов. Эти преобразования ГСА использовались ранее в патенте автора [12] и в прототипе [14] для снижения затрат оборудования в Q раз по сравнению с классическим автоматом Мура. Преобразования по пункту 1 и 2 позволяют использовать структурную организацию автомата по патенту [12] для организации в нем режима динамического контроля, которые также использовались автором в патенте [14].
В отличие от ранее использованного способа, кроме пунктов 1, 2, вводятся следующие дополнительные модификации ГСА и графа переходов автомата:
3) За счет введения пустых операторов ГСА приводится к такому виду, в котором к любому оператору {А} управление передается только от одного или двух (не более) операторов.
4) В ГСА выделяется непрерывный (самый длинный) путь от начальной вершины к конечной, в котором все Ai∈{А} нумеруются по порядку по мере следования и им присваиваются коды из таблиц Грея (табл. 1 Коды Грея). Выделяются также последовательности операторов с числом операторов действия не менее трех, которые называются условно длинными путями.
5) Если переход на непрерывном пути от Ai к Aj осуществляется по условию  то
то  заменяется на
заменяется на 
6) Все остальные операторы вне отмеченных длинных путей также нумеруются после операторов Aj∈{А} отмеченных длинных путей.
7) По ГСА определяется граф переходов автомата, в котором каждому оператору Ai∈{А} сопоставляется вершина графа, соответствующая состоянию автомата.
8) Анализируется граф переходов и при наличии петель (переход к тому же самому состоянию ai∈{а}) вводится «пустое» состояние перед состоянием с петлей.
9) Все состояния на непрерывном (длинном пути) в графе переходов последовательно кодируются кодом Грея (табл. 1).
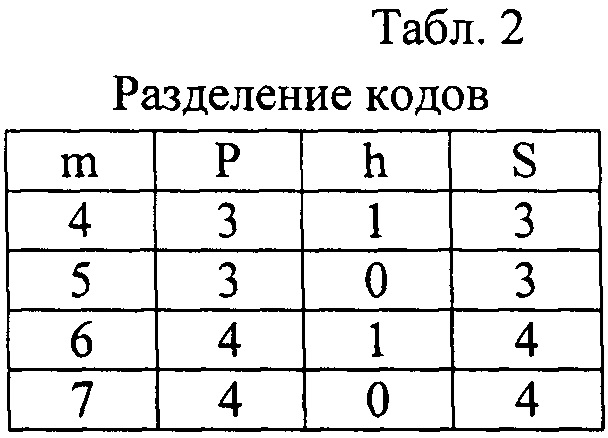
10) Для двух соседних состояний ai(t) и aj(t+1) вне длинного пути выбираются такие коды из таблицы кодов Грея, чтобы в р младших разрядах коды состояний ai(t) и aj(t+1) при сложении по mod2 давали в сумме одну единицу (не ноль и не две единицы). Т.е. ai(t) ⊕ aj(t+1)=1. Разделение на младших x1…xp и старших xp+1…xm производится либо точно по m/2, если m четно, но возможно и с перекрытием в h разрядов, если m не четное (табл. 2).
11) Если же такое условие невыполнимо при существующих номерах состояний по пунктам 4-6, то между ai(t) и ai+1(t+1) вставляется пустая вершина с таким номером, чтобы в коде Грея выполнялись условия:
ai(t) ⊕ai+1(t+1)=1 ai+1(t+1) ⊕ai+2(t+2)=1, где ai+1(t+1) - номер вставляемой вершины.
12) Число путей с последовательно изменяемыми номерами (условно длинные пути) может быть несколько. Поэтому несколько участков графа переходов модифицируются по правилам 4-11.
13) Для двух любых ai(t) и aj(t+1) вне длинного пути возможны две ситуации:
а) ai(t) ⊕ aj(t+1)=1 для полных кодов x1x2…xm и y1y2…ym;
б) только для р младших разрядов кодов a(t) и a(t+1) выполняется условие x1x2…xp ⊕ y1y2…yp=1.
14) Со старшими (S) разрядами кодов ai(t) и aj(t+1), относящихся к пункту 13б, производятся следующие преобразования:
- составляется таблица соответствия xmxm-1…xp→ymym-1…yp. Количество старших разрядов S не обязательно равно (m-р), т.к. для нечетных значений m «пограничные» разряды могут входить как в группу младших, так и в группу старших разрядов. Выбор значений m, Р, S, h поясняется табл. 2. Распределение младших (Р) и старших (S) разрядов при разных (m) приведено в табл. 2, где h - количество перекрываемых разрядов.
- к коду xmxm-1…xp дописывается один разряд справа (х0), т.е. разряд, предшествующий коду xmxm-1…xp. Тогда получим код  с неопределенным значением разряда
с неопределенным значением разряда  :
:
- к коду ymym-1…yp добавляется последующий старший разряд слева ym+1. Тогда получим код 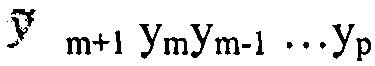 с неопределенным значением разряда
с неопределенным значением разряда 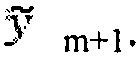
15) Доопределяется значение х0 и ym+1 в каждой строке таблицы соответствия 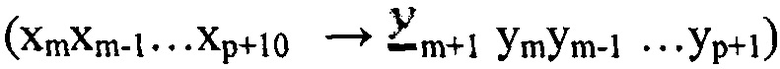 так, чтобы сумма их кодов по mod 2 тоже давала «1», т.е. xmxm-1…xrx0 ⊕ ym+1ymym+1…yp=1.
так, чтобы сумма их кодов по mod 2 тоже давала «1», т.е. xmxm-1…xrx0 ⊕ ym+1ymym+1…yp=1.
16) После всех приведенных изменений ГСА и графа переходов как по известным (1, 2) пунктам, так и по новым (3-15) производится проверка правильности формирования выходного кода ymym-1…y1 по коду xmxm-1…x1 и значению αj∈{α}.
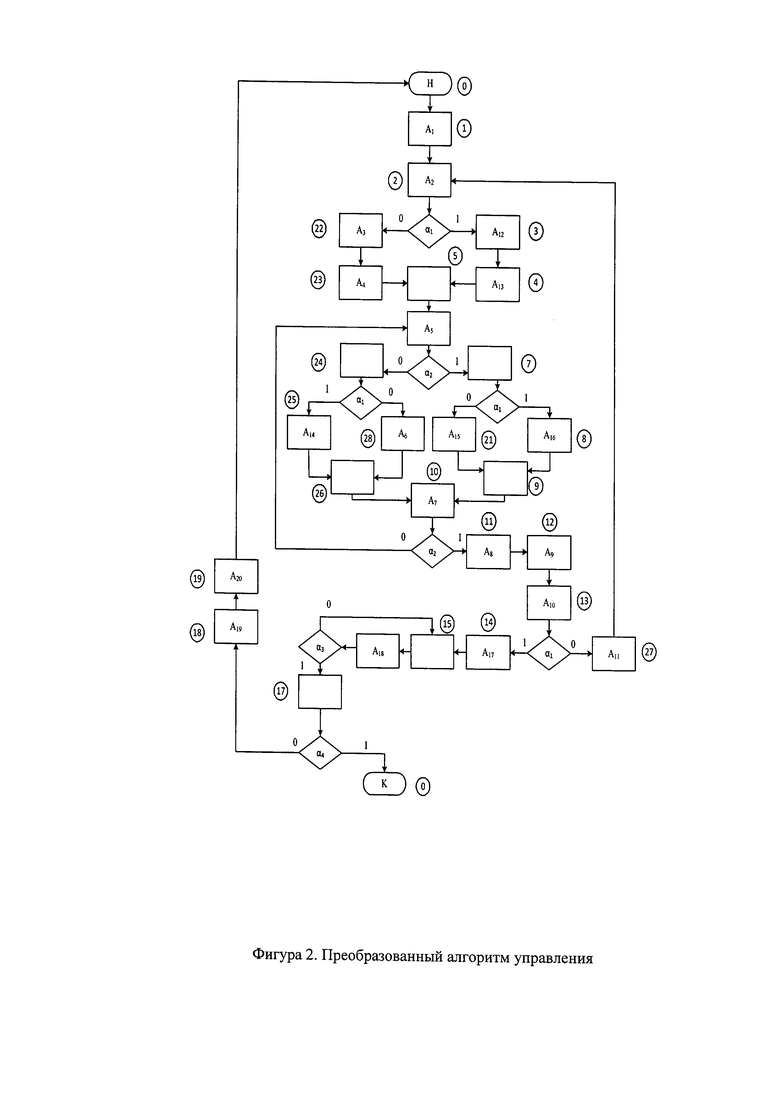
Рассмотрим реализацию предложенного способа контроля на основе ГСА (фиг. 1) из патента [19]. Модифицированная ГСА по предложенному способу представлена на фиг. 2, а граф переходов на фиг. 3. После соответствующих замен номеров состояний получен граф, фиг. 4. На графе переходов, фиг. 4, рядом с некоторыми вершинами указаны их коды в трех младших разрядах (р=3), причем коды этих трех разрядов совпадают с другими кодами: 2 - 13, 5 - 10, 6 - 9, 7 - 8. Различие полных кодов состояний определится значением старших разрядов. Специфика данной ГСА в том, что имеется возврат по  к тому же состоянию. Следовательно, в графе переходов возникла необходимость введения пустой вершины 15 для устранения петли. Кроме того, произведена замена α4 на
к тому же состоянию. Следовательно, в графе переходов возникла необходимость введения пустой вершины 15 для устранения петли. Кроме того, произведена замена α4 на  Для соблюдения условий получения сумм по модулю два для младших разрядов вне длинного пути ряду вершин присвоены другие номера (фиг. 3 и 4). По предложенному способу номера вершин выбраны по таблице кодов Грея (табл. 1). Переходы вне счетчика выбраны таким образом, чтобы при суммировании по mod2 трех (или четырех) разрядов кодов a(t) и a(t+1) в результате был получен код с одной единицей в одном из трех (четырех) разрядов суммы. В табл. 3 представлены переходы вне счетчика.
Для соблюдения условий получения сумм по модулю два для младших разрядов вне длинного пути ряду вершин присвоены другие номера (фиг. 3 и 4). По предложенному способу номера вершин выбраны по таблице кодов Грея (табл. 1). Переходы вне счетчика выбраны таким образом, чтобы при суммировании по mod2 трех (или четырех) разрядов кодов a(t) и a(t+1) в результате был получен код с одной единицей в одном из трех (четырех) разрядов суммы. В табл. 3 представлены переходы вне счетчика.
По фиг. 4 вводится признак (γ) как необходимость (+1) к содержимому счетчика.
В табл. 4 номера логических условий представлены через соответствие номерам состояний.
Предлагаемый способ эффективен для любых значений m. При m≥7 значение р=4, поэтому для старших разрядов (S) потребуется два дополнительных разряда ym+1, ym+2. Однако варианты с m≥7 практически очень редко используются. Для m≥7 чаще всего СУА разделяются на 2 или 3 автомата (декомпозируются), для каждого из которых m≤6 [9].
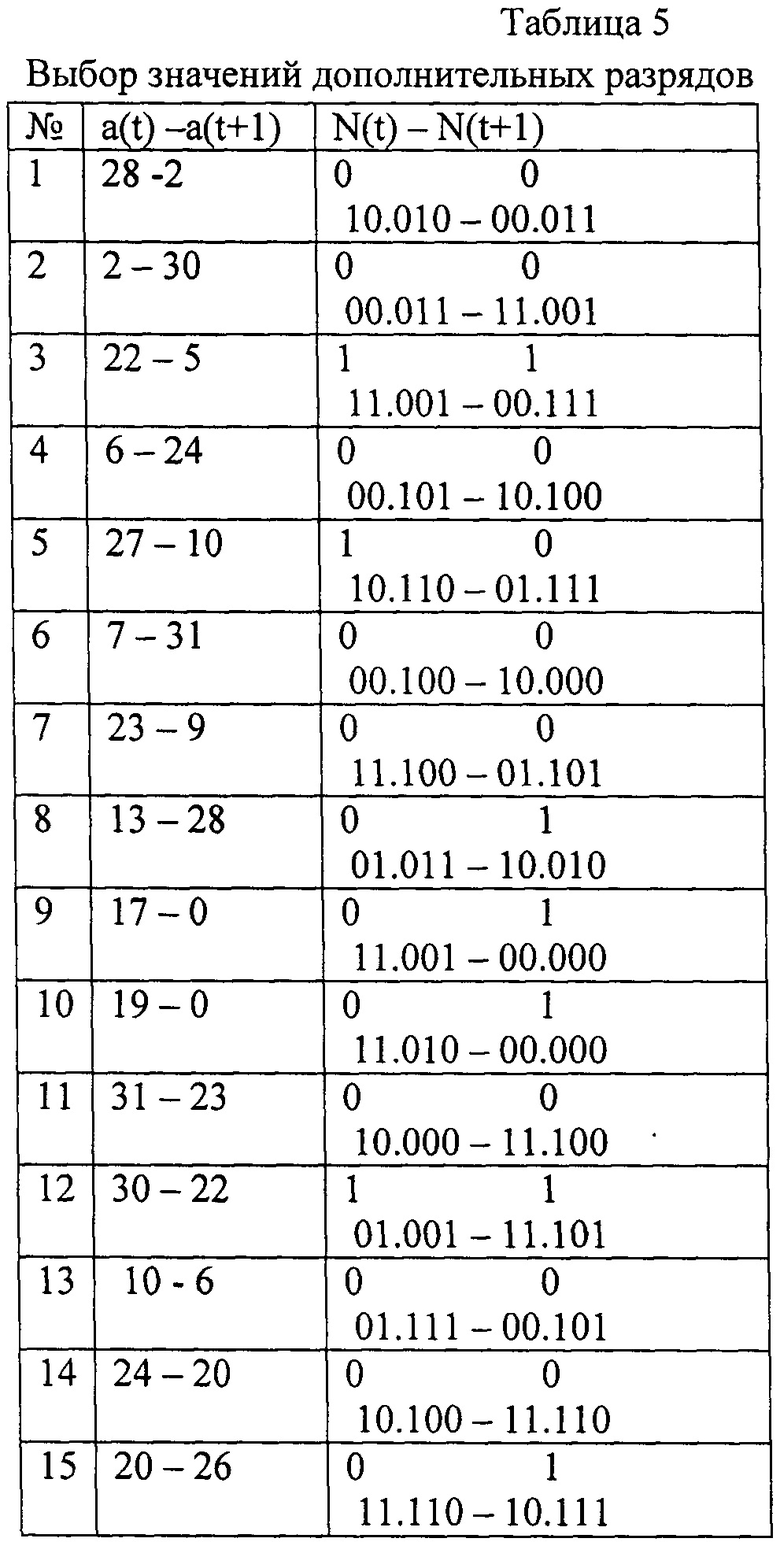
Выпишем из табл. 3 переходы a(t)→a(t+1) и соответствующие им коды N(t)→N(t+1). При р=3 определим значения двух разрядов:
- в N(t) разряда х0,
- для двух старших разрядов N(t+1) доопределяется значение ym+1. В табл. 5 значения этих доопределяемых разрядов в соответствующих строках указаны выше записи самих кодов N(t) и N(t+1).
Анализ полученных полных кодов (с учетом значений х0 и ym+1) дает возможность убедиться в том, что условие равенства сумм по mod2 как для группы старших, так и для группы младших разрядов выполняется, т.е. предлагаемый способ контроля действительно эффективен.
Новый способ по сравнению с известными способами динамического контроля позволяет построить самоконтролируемый автомат с минимальными затратами оборудования на осуществление контроля и принятия решений.
Как в способе прототипа, так и в предлагаемом способе контроля, используется процедура разделения разрядов кодов a(t) и a(t+1) пополам. В прототипе, как к младшим, так и к старшим разрядам добавляется по два дополнительных разряда для вычисления параллельного кода y1y2…ym специальными комбинационными схемами разрядностью m/2+2. Кроме того, используется вариант реализации автомата с дублированием схемы F1(4), но при другом дублирующем способе вычисления кода y1y2…ym, чем в классических схемах с дублированием.
Предлагаемый способ контроля является новым, т.к. он не известен в других изобретениях, патентах и технической литературе.
Предлагаемый самоконтролируемый автомат, реализованный по предложенному способу динамического контроля по снижению затрат оборудования и быстродействию, превосходит прототип, а следовательно, при той же степени самоконтролируемости способен обеспечить более надежную работу в экстремальных условиях.



Литература
1. Щербаков Н.С. Достоверность работы цифровых устройств, М.: Машиностроение, 1989. - 224 с.
2. Согомонян Е.С., Слабаков Е.В. Самопроверяемые устройства и отказоустойчивые системы. М.: Радио и связь, 1989. - 208 с.
3. Проектирование тестируемых и самотестируемых матричных БИС / в кн. Файзураева Е.Н., Шатурина И.И., Карамзинского А.П. и др. Быстродействующие матричные БИС и СБИС. М.: Радио и связь, 1989. - С. 250-254.
4. Сапожников В.В., Сапожников Вл.В. Основы технической диагностики. М.: Маршрут. 2004. - 318 с.
5. Труды по теории синтеза и диагноза конечных автоматов и релейных устройств / под ред. В.В. Сапожникова и Вл.В. Сапожникова. СПб.: Элмор, 2009. - 894 с.
6. Сапожников В.В., Сапожников Вл.В. Гессель М. Самодвойственные дискретные устройства. СПб.: Энергоатом издат, 2001. - 331 с.
7. Мухопад А.Ю., Бадмаева Т.С., Мухопад Ю.Ф. Самоконтролируемый автомат управления // Патент РФ №63588. 2007. БИ №15, G11C 11/00 (2006.01).
8. Карпов Ю.Г. Теория автоматов. - СПб.: Питер, 2003. - 208 с.
9. Горшков А.П. Синтез диагностируемых схем вычислительной техники. - М.: Наука, 1987. - 288 с.
10. Barry Wilkinson. The essence of digital design. Prentice Hall, Europe, 1998. - 318 р. - перевод Барри Уилкинсон. Основы проектирования цифровых схем. - М.: Издательский дом «Вильямс». Киев. 2004. - 320 с.
11. Мухопад Ю.Ф. Микроэлектронные системы управления. - Братск: БрГУ, 2009. - 285 с.
12. Мухопад А.Ю., Мухопад Ю.Ф. Микропрограммный автомат // Патент на полезную модель №82888. 2009. - БИ №13.
13. Мухопад Ю.Ф. Теория дискретных устройств. - Иркутск: ИрГУПС, 2010. - 172 с.
14. Мухопад А.Ю., Мухопад Ю.Ф. Структурная организация самоконтролируемых автоматов для систем реального времени // Проблемы информатики. Новосибирск: СО РАН, 2013. - №1. - С. 4-15.
15. Мухопад А.Ю., Мухопад Ю.Ф. Управляющий автомат // Патент РФ №2475816 БИ №5, 20013. RU 2475816 С1 МПК G06F 9/00 (2006.01).
16. Муттер В.М., Петров Г.А., Маринкин В.И., Степанов B.C. Микропроцессорные кодеры и декодеры. - М.: Радио и связь, 1991. - 184 с. Прямые методы декодирования кода Рида-Соломона. С. 41-45.
17. Угрюмов Е.П. Цифровая схемотехника. - СПб.: БХВ - Петербург, 2010. - 760 с.
18. Соловьев В.В., Климович А. Логическое проектирование цифровых систем на основе ПЛИС. М.: Горячая линия. - Телеком, 2008, - 374 с.
19. Мухопад А.Ю., Мухопад Ю.Ф. Устройство криптографической защиты информации Патент РФ №2475838. 2013. БИ №5 от 07 ноября 2011 г., RU 2475838 С1 МПК G06F 21/00 2013.01) H04L 9/00 (2006.01).
20. Амосов В.В. Схемотехника и средства проектирования цифровых устройств. - СПб: БХВ - Петербург, 2007. - 542 с.
21. Мухопад А.Ю., Мухопад Ю.Ф. Самоконтролируемый автомат. Патент на изобретение №2502121 Российская Федерация МПК(51) G06F 9/22, G06F 11/00; - №2011148883/08; заявл. 30.11.2011; опубл. 20.12.2013, Бюл. №35. - RU 2502121 С2.
| название | год | авторы | номер документа |
|---|---|---|---|
| САМОКОНТРОЛИРУЕМЫЙ АВТОМАТ | 2011 |
|
RU2502121C2 |
| Самоконтролируемый автомат | 2020 |
|
RU2775173C1 |
| МИКРОПРОГРАММНЫЙ АВТОМАТ | 2013 |
|
RU2527190C1 |
| УПРАВЛЯЮЩИЙ АВТОМАТ С КОНТРОЛЕМ СОСТОЯНИЙ | 2022 |
|
RU2793301C1 |
| УПРАВЛЯЮЩИЙ АВТОМАТ | 2011 |
|
RU2475816C1 |
| УСТРОЙСТВО КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2011 |
|
RU2475838C1 |
| ИЗМЕРИТЕЛЬНОЕ УСТРОЙСТВО ИНФОРМАЦИОННО- ЛОГИЧЕСКОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО УЧЕТА ОБЪЕМОВ И КОЛИЧЕСТВА ЛЕСОМАТЕРИАЛОВ | 1971 |
|
SU301525A1 |
| Устройство для контроля хода микропрограмм | 1988 |
|
SU1661772A1 |
| Устройство для возведения в квадрат | 1985 |
|
SU1280616A1 |
| Устройство для контроля кода программ | 1988 |
|
SU1564632A1 |

Изобретение относится к области вычислительной техники и дискретной автоматике. Технический результат – упрощение реализации блоков контроля и управления. Для этого предложен способ динамического контроля автоматов управления, заключающийся в том, что алгоритм управления и граф переходов автомата приводятся к контролепригодному виду путем введением пустых операторов без нарушения причинно-следственных и логических связей операторов действия, позволяющих производить сравнение предыдущего и последующего состояний кодов автоматов при специальном выборе из таблиц значения их номеров по кодам Грея с добавлением по одному разряду в старшие половины кодов и последующем доопределении дополнительных разрядов предыдущего и последующего кода состояний с целью получения сумм по модулю два равных «1» при безошибочном функционировании. 4 ил., 5 табл.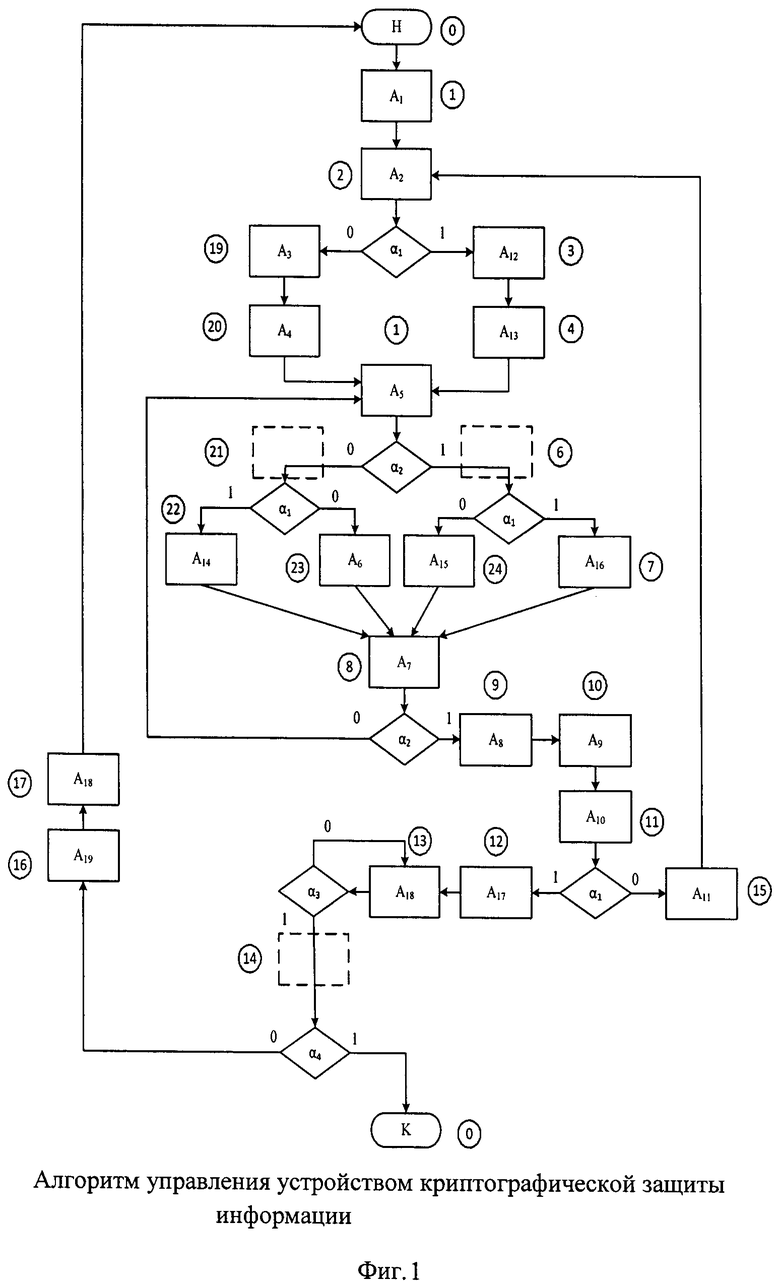
Способ динамического контроля автоматов, использующий модификацию операторной схемы алгоритма путем введения пустых операторов перед логическим условием, если к нему осуществляется переход от двух и более операторов, а также путем введения пустого оператора между двумя логическими условиями, не разделенными оператором действия, отличающийся тем, что в операторной схеме алгоритма вводятся пустые операторы таким образом, чтобы к любому оператору передавалось управление не более чем от двух других операторов, а в графе переходов автомата ликвидируются петли за счет введения пустой вершины перед состоянием с петлей; для самого длинного пути вершины кодируются кодом Грея, а для соседних с вершинами длинного пути, но не относящихся к вершинам длинного пути, выбирается код для Р младших разрядов, обеспечивающий одну «1» в сумме по mod2 для кодов Грея предыдущей и последующей вершины; если условие не выполнимо, то между этими вершинами вводится промежуточная пустая вершина, код Грея которой обеспечивает выполнение условий как с предыдущей, так и с последующей вершиной для Р младших разрядов, причем для старших S разрядов вершин, не относящихся к самому длинному пути, до младшего разряда приписывается дополнительный разряд к коду предыдущего состояния и дополнительный разряд после старшего разряда кода последующего состояния, значение которых доопределяется соответственно равным «0» или «1» так, чтобы сумма по mod2 кодов старших разрядов предыдущей и последующей вершины была равна «1»; при этом динамический контроль правильности функционирования осуществляется по результатам сравнения суммы по модулю кодов половинной разрядности разным частям младших и старших разрядов предыдущих и последующих состояний автомата управления, причем принятие решений об исправности осуществляется по правилам:
- если предыдущее и последующее состояния относятся к непрерывному пути, то сумма по mod2 равна «1», либо для младшей, либо для старшей группы разрядов;
- иначе в обеих группах (младших и старших разрядов) сумма по mod2 равна «1».
| УПРАВЛЯЮЩИЙ АВТОМАТ | 2011 |
|
RU2475816C1 |
| МИКРОПРОГРАММНЫЙ АВТОМАТ | 2013 |
|
RU2527190C1 |
| САМОКОНТРОЛИРУЕМЫЙ АВТОМАТ | 2011 |
|
RU2502121C2 |
| US 7716542 B2, 11.05.2010. | |||
Авторы
Даты
2018-04-18—Публикация
2015-11-30—Подача