Изобретение относится к области микромеханики и измерительной технике, в частности к микромеханическим резонаторам.
Клеевые соединения микромеханических элементов с основанием при корпусировании таких микромеханических изделий как гироскопы, акселерометры, резонаторы существенно влияют на точность этих изделий, особенно при их работе в широком диапазоне температур.
Так в работе [1] показано (см. рис. 2), что температурные изменения масштабного коэффициента существенно зависят от марки клея, который используется для крепления чувствительного элемента (ЧЭ) микромеханического гироскопа (ММГ).
В работах [2, 3, 4] исследовано влияние разных типов клеев для крепления ЧЭ на механические напряжения и смещения кристалла при термоциклах, а также влияние клея на такие параметры составных частей ММГ, как резонансная частота автоколебаний и добротность.
В работах [3, 4] при анализе такого влияния используется модель Кельвина-Фойгта, состоящая из параллельно соединенных пружины (с коэффициентом жесткости k) и демпфера (с коэффициентом демпфирования С). Такая модель описывает поведение полимеров при их анализе в частотной и временной областях [5 (с. 224), 6].
При экспериментальных исследованиях свойств полимеров применяют приборы, построенные на использовании метода вдавливания тел определенной формы, т.е. индентеры (Indenter) [7-9].
Современные индентеры имеют разрешающую способность по перемещению на уровне 10 мкм и создаваемому усилию на уровне 10 нН. Некоторые типы индентеров могут работать как в статическом режиме, так и в режиме колебаний. При этом в обоих случаях измеряются усилия, действующие на вдавливаемое в исследуемый материал тело, и смещения этого тела. Однако частота таких колебаний, как правило, не превышает 100 Гц, что не позволяет получить адекватные параметры модели на рабочих частотах современных ММГ и микромеханических резонаторов, которые выше 10 кГц. Кроме того, конструкция интендеров затрудняет проведение испытаний при изменении температуры окружающей среды в широком диапазоне температур.
Наиболее близким к предложенному способу определения коэффициентов модели Кельвина-Фойгта является способ, описанный в работе [10], заключающийся в измерении изменений резонансной частоты (ƒр) и добротности (Q) микромеханического резонатора при его механическом контакте с исследуемым материалом.
Микромеханический резонатор представляет собой консоль, возбуждение которого производится с помощью пьезоэлектрического привода. В отличие от описанных выше индентеров в способе-прототипе измеряют не усилия, действующие на вдавливаемое в исследуемый материал тело, и смещения этого тела, а изменения ƒр и Q микромеханического резонатора при его механическом контакте с исследуемым материалом.
Последовательность действий при измерении ƒр и Q заключается в измерении спектра колебаний резонатора в двух случаях: в отсутствии контакта резонатора с исследуемым материалом и при его контакте с ним, с последующим определением изменений ƒр и Q.
Полученные разности значений этих величин характеризуют качественно исследуемые материалы.
К недостаткам описанного в работе [10] способа прототипа могут быть отнесено следующее:
- в нем отсутствует процедура определения коэффициентов модели Кельвина-Фойгта,
- определение параметров материала проводится не в реальном времени, а после обработки результатов измерения, полученных с помощью достаточно громоздкого оборудования, которое не допускает работу в широком диапазоне температур (например, от -60 до +85°С), соответствующем требованиям к рабочему диапазону температур современных ММГ и резонаторов,
- отсутствует возможность измерения свойств материалов при изменении температуры окружающей среды в широком диапазоне.
Задачей изобретения является повышение точности определения коэффициентов модели Кельвина-Фойгта, возможность определения их изменений во времени и от температуры окружающей среды за счет использования внутренних сигналов микромеханического резонатора, в котором реализован режим автогенератора со стабилизацией амплитуды колебаний.
Преимуществом предлагаемого способа (по сравнению с аналогами и прототипом) является то, что для проведения измерений не требуется сложная дополнительная аппаратура, измерения параметров могут проводиться в условиях, близких условиям, в которых используется исследуемый материал.
Поставленная задача решается тем, что для определения коэффициентов модели Кельвина-Фойгта для клеевого соединения микромеханического резонатора с основанием измеряют резонансную частоту и добротность микромеханического резонатора по крайней мере два раза, причем первый раз их измеряют после изготовления микромеханического резонатора в составе пластины кремния, а второй - после соединения микромеханического резонатора с основанием, при этом коэффициенты определяют по построенным зависимостям максимального значения модуля передаточной функции микромеханического резонатора, рассчитанного для разных значений коэффициентов модели Кельвина-Фойгта, и частоты, соответствующей этим максимальным значениям.
Кроме того, поставленная цель достигается тем, в случае, когда микромеханический резонатор содержит контур возбуждения колебаний со схемой автоматического регулирования усиления для стабилизации амплитуды колебаний, что измеряют выходной сигнал схемы автоматического регулирования усиления Uвых, а добротность определяют как величину, пропорциональную величине (Uвых)-1.
Описания микромеханических резонаторов, которые могут быть использованы для определения коэффициентов модели Кельвина-Фойгта, описаны в литературе [3, 11, 12].
Для решения поставленной задачи могут использоваться одномассовые резонаторы с линейными [11, с. 25] и круговыми [12, фиг. 26] перемещениями подвижной массы, или двухмассовые резонаторы в случае синфазных колебаний этих масс [3, фиг. 5].
На фиг. 1 приведена фотография микромеханического резонатора.
На фиг. 1 приняты следующие обозначения:
1 - микромеханический элемент (ММЭ в дальнейшем),
2 - специализированная интегральная схема (в дальнейшем СИС),
3 - корпус, к которому с помощью специального клея 4 (на фиг. 1 не показано), находящегося между одной из поверхностей микромеханического элемента и корпусом, закреплен микромеханический элемент 1;
4 - клеевое соединение (на фиг. 1 не показан, находится между нижней поверхностью микромеханического элемента и корпусом).
На фиг. 2 представлена блок-схема ММЭ, который с помощью клея закреплен в неподвижном корпусе.
На фиг. 2 приняты следующие обозначения:
5 - подвижная масса ММЭ (далее ПМ 5);
6 - основание ММЭ;
7 - неподвижный корпус;
8 - элементы ограничения перемещения подвижных частей в одном направлении;
9 - пружина, характеризующая жесткость подвеса ПМ 5 к основанию 6;
10 - демпфер, характеризующий потери энергии при движении ПМ 5;
11 - пружина, характеризующая жесткость клеевого соединения 4 основания 6 с корпусом 7;
12 - демпфер, характеризующий потери энергии при движении основания 6 относительно корпуса 7.
На фиг. 3 приведены графики амплитудно-частотных характеристик для случаев идеального и реального клеевого соединения ММЭ 1 и корпуса 3.
ММЭ 1 и СИС 2 (см. фиг. 1) электрически связаны между собой. Вместе они образуют микромеханический резонатор.
ММЭ1 включает в себя механический подвес ПМ 5 к основанию 6, выполняемый, например, в виде торсионов и систему электродов (подвижных, связанных с ПМ 5, и неподвижных, связанных с корпусом 3) для измерения перемещения ПМ 5 и управления ее положением. Более подробно варианты конструкции ММЭ 1 достаточно подробно описаны как в цитируемой литературе, так и в ряде книг учебного характера.
При подаче электрического напряжения на СИС 2 подвешенная к основанию 6 ПМ 5 начинает колебаться за счет формируемых с помощью электродов ММЭ 1 сил.
На фиг. 2 показана межэлектродная сила F, которая действует ПМ 5 массой m1 и корпусом 6 массой m2.
Под действием этой силы, в случае, если корпус 6 неподвижен, колеблется только ПМ 5, и добротность подвеса ПМ 5 будет определяться только потерями энергии в ММЭ 1. Если же из-за конечной жесткости клеевого соединения корпус 6 может двигаться, действие силы F вызовет также и перемещения корпуса 6, при котором из-за потерь энергии в клеевом соединении эквивалентная добротность подвеса оказывается ниже.
Передаточная функция резонатора в случае, когда корпус 6 неподвижен имеет вид [14]:
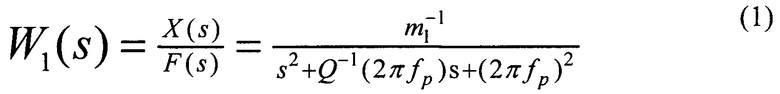
При этом (в обозначениях фиг. 2):


Измерение ƒр и Q, и, соответственно, определение коэффициентов c1, k1 является стандартной операцией при контроле параметров ЧЭ на кремниевой пластине до ее разрезания. На этой пластине все ММЭ связаны между собой и таким образом, можно считать, что они жестко закреплены.
При типичных значениях k1=100 Н/м, Q=100000, амплитуде колебаний ПМ 5, равной 10 мкм, из (1)-(3) получим оценку для F=10 нН.
То есть резонатор можно рассматривать как индентер, формирующий силу на уровне 10 нН.
Выполняется эта операция на проб-станций, которая может снабжаться термокамерой, что позволяет измерять зависимости c1, k1 от температуры и использовать эти значения при нахождении зависимостей коэффициентов c2, k2 от температуры.
Передаточная функция электромеханической системы на фиг. 2 в случае реального клеевого соединения имеет более сложный вид.
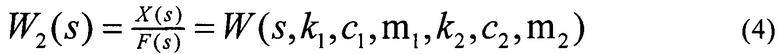
При некоторых допущениях она имеет вид:
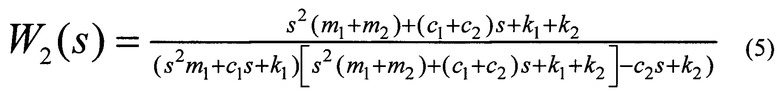
Однако, поскольку величины k1, c1 могут быть определены на стадии контроля ММЭ на пластине, а величины m1, m2 определяются конструкцией резонатора, задача определения коэффициентов k2, c2 упрощается.
Она сводится к определению коэффициентов k2, c2 по результатам экспериментального измерения изменений ƒр и Q после крепления ММЭ к корпусу с помощью клеевого соединения.
Это явление иллюстрируется графиками амплитудно-частотных характеристик для случаев идеального и реального клеевого соединения ММЭ 1 и корпуса 3 [3].
Влияние клеевого соединения 4 на добротность и резонансную частоту резонатора зафиксировано во многих исследованиях.
Например, для двух типов клеев установлены разные зависимости этих величин от температуры в работе [4], где для объяснения этой зависимости используется модель Кельвина-Фойгта.
Могут быть использованы различные методы измерения добротности и резонансной частоты резонатора.
Так резонансная частота может быть измерена стандартными частотомерами.
Отдельные СИС позволяют получать данные о частоте колебаний ПМ 5 через их SPI интерфейс.
Методы измерения добротности подвеса ПМ также описаны в литературе [11, 12].
Структура СИС, которая позволяет в реальном времени определять добротность в работающем по прямому назначению резонаторе описана в [13].
Отметим, что в системе возбуждения колебаний, содержащей схему автоматической регулировки усиления (АРУ), динамический диапазон задаваемых амплитуд превышает 40 дБ. Это позволяет варьировать задаваемые резонатором силы с шагом 0,1 нН, т.е. микромеханический резонатор может рассматриваться как индентер с более высокой (на 2 порядка) разрешающей способностью по формируемой силе по сравнению с описанными выше аналогами.
Преимущество определения добротности по выходному сигналу схемы АРУ (Uвых) заключается в том, что измерение проводится в реальном времени без изменения режима работы резонатора [12].
Таким образом, в литературе достаточно подробно описаны способы измерения величин ƒр и Q.
Для того чтобы определить значения коэффициентов k2, c2 при фиксированных значениях величин k1, с1, m1, m2, предлагается следующая процедура.
1. Для разных значений k2, c2 путем численного расчета определяется максимальное значение модуля W2(s), т.е. max⎟W2(s)⎢ для случая, когда s=j(2πƒ), ƒ - переменная, и значение ƒmax, при котором достигается максимальное значение ⎟W2(s)⎢.
2. Выполняется построение функций ƒmax и max⎟W2(s)⎢ от двух переменных k2, c2.
3. На построенных функциях отмечаются экспериментально полученные значения ƒр и Q.
4. По пересечению проекции сечений функций ƒmax и max⎟W2(s)⎢ от k2, c2 с помощью полученных значений ƒр и Q определяют коэффициенты модели Кельвина-Фойгта.
Отметим, что описанная процедура может быть выполнена в виде программы для автоматического вычисления коэффициентов модели Кельвина-Фойгта.
Таким образом, предложенный способ определения коэффициентов модели Кельвина-Фойгта для клеевого соединения с помощью микромеханического резонатора обеспечивает получение результатов при типовых воздействиях на клеевое соединение, которое имеет место на практике как по уровню воздействия, так и по частотному диапазону, а также при изменениях температуры окружающей среды.
Технический эффект от использования изобретения заключается в повышении точности определения коэффициентов модели Кельвина-Фойгта для клеевых соединений, возможности получения зависимостей этих коэффициентов от температуры и их изменений во времени.
Литература
1. A. Filipe et al., Impact of die-attach materials on MEMS Gyro performance, International Symposium on Inertial Sensors and Systems (ISISS), 2014.
2. S. Walwadkar et al., Effect of Die-Attach Adhesives on the Stress Evolution in MEMS Packaging, IEEE Transactions on Components and Packaging Technologies V. 29, №4, Dec. 2006.
3. Alexander A Trusov, A substrate energy dissipation mechanism in in-phase and anti-phase micromachined z-axis vibratory gyroscopes, J. Micromech. Microeng. 18 (2008), pp 1-10.
4. Z. Hou et al., Effect of die attachment on key dynamical parameters of micromachined gyroscopes, Microsyst Technol (2012) 18:507-513.
5. Перепечко И.И. Введение в физику полимеров, М., изд. "Химия", 1978 г., 312 с.
6. Wikipedia, статья "Вязкоупругость", https://ru.wikipedia.org.
7. Agilent_G300_Nano_Indenter_Data_Sheet, www.kprime.net.
8. Патент WO №2014202551, Measuring head for nanoindentation instrument and measuring method.
9. Патент США №7568381. Apparatus and method for surface property measurement with in-process compensation for instrument frame distortion.
10. H.S. Wasisto et al. Microtactile cantilever resonators for characterizing surface deposits, Procedia Engineering 120 (2015) 861-864.
11. J. Yan et al., Research of Resonant Frequency and Quality Factor Test Methods for High Vacuum Sealed Microgyroscope Based on LabVIEW Procedia Engineering 15 (2011) 2566-2570.
12. Патент РФ №2564699. Способ измерения добротности резонансного контура и устройство для его реализации.
13. Nekrasov Ya.A., Moiseev N.V., Liukshonkov R.G., Belogurov A.A. Compensation of MEMS Gyroscope Drift Based on Amplitude Primary Oscillation Measurement, Inertial Sensors and Systems - Symposium Gyro Technology, 2013, pp. 1-1 - 1-9.
14. C. Acar, A. Shkel MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness Springer Publishing Company 2008.
| название | год | авторы | номер документа |
|---|---|---|---|
| МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП | 2004 |
|
RU2279634C2 |
| СПОСОБ ПОДСТРОЙКИ РЕЗОНАНСНОЙ ЧАСТОТЫ ПОДВЕСА ПОДВИЖНОЙ МАССЫ МИКРОМЕХАНИЧЕСКОГО ГИРОСКОПА ПО ОСИ ВТОРИЧНЫХ КОЛЕБАНИЙ И МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП | 2007 |
|
RU2347191C1 |
| МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП (ВАРИАНТЫ) И СПОСОБЫ ЕГО НАСТРОЙКИ, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ АМПЛИТУДНО-МОДУЛИРОВАННОГО КВАДРАТУРНОГО ТЕСТОВОГО ВОЗДЕЙСТВИЯ | 2008 |
|
RU2388999C1 |
| МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП | 2010 |
|
RU2447403C1 |
| МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП ВИБРАЦИОННОГО ТИПА | 2008 |
|
RU2370733C1 |
| Устройство измерения зазора в микромеханическом гироскопе RR-типа | 2016 |
|
RU2649226C1 |
| ЭЛЕКТРОДНАЯ СТРУКТУРА ДЛЯ МИКРОМЕХАНИЧЕСКОГО ГИРОСКОПА И МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП НА ЕЕ ОСНОВЕ | 2006 |
|
RU2320962C1 |
| Микромеханический гироскоп | 2019 |
|
RU2714870C1 |
| МИКРОМЕХАНИЧЕСКИЙ ГИРОСКОП | 2006 |
|
RU2319929C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ГРЕБЕНЧАТЫМ ДВИГАТЕЛЕМ МИКРОМЕХАНИЧЕСКОГО ДАТЧИКА | 2005 |
|
RU2282150C1 |
Настоящее изобретение относится к области микромеханики и измерительной технике, в частности к микромеханическим резонаторам. Способ определения коэффициентов модели Кельвина-Фойгта для клеевого соединения микромеханического резонатора с основанием, заключающийся в измерении резонансной частоты и добротности микромеханического резонатора. При этом резонансную частоту и добротность микромеханического резонатора измеряют по крайней мере два раза, причем первый раз их измеряют после изготовления микромеханического резонатора в составе пластины кремния, а второй - после соединения микромеханического резонатора с основанием, при этом коэффициенты определяют по построенным зависимостям максимального значения модуля передаточной функции микромеханического резонатора, рассчитанного для разных значений коэффициентов модели Кельвина-Фойгта, и частоты, соответствующей этим максимальным значениям. Технический результат - повышение точности определения коэффициентов модели Кельвина-Фойгта. 1 з.п. ф-лы, 3 ил.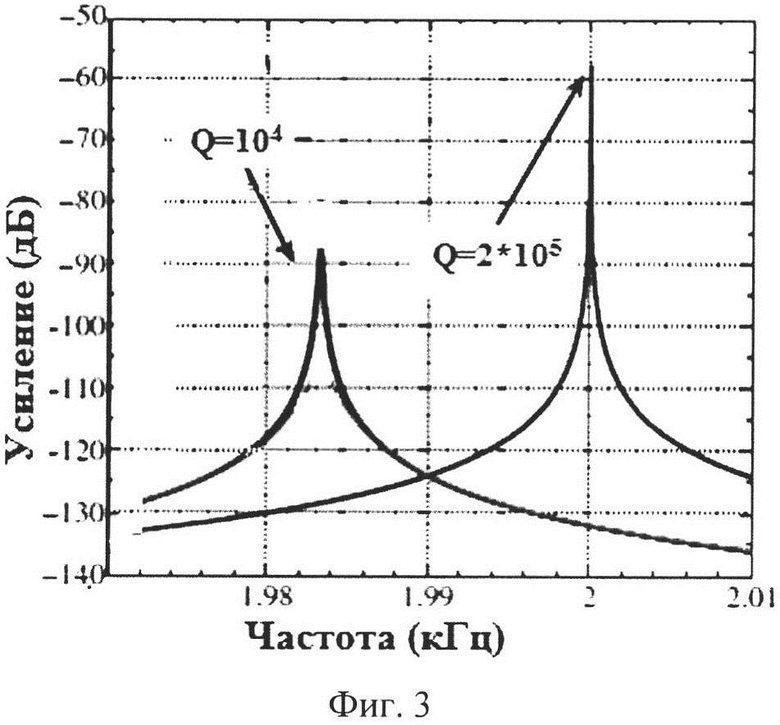
1. Способ определения коэффициентов модели Кельвина-Фойгта для клеевого соединения микромеханического резонатора с основанием, заключающийся в измерении резонансной частоты и добротности микромеханического резонатора, отличающийся тем, что резонансную частоту и добротность микромеханического резонатора измеряют по крайней мере два раза, причем первый раз их измеряют после изготовления микромеханического резонатора в составе пластины кремния, а второй - после соединения микромеханического резонатора с основанием, при этом коэффициенты определяют по построенным зависимостям максимального значения модуля передаточной функции микромеханического резонатора, рассчитанного для разных значений коэффициентов модели Кельвина-Фойгта, и частоты, соответствующей этим максимальным значениям.
2. Способ по п. 1, отличающийся тем, что микромеханический резонатор содержит контур возбуждения колебаний со схемой автоматического регулирования усиления для стабилизации амплитуды колебаний, при этом измеряют выходной сигнал схемы автоматического регулирования усиления Uвых, а добротность определяют как величину, пропорциональную (Uвых)-1.
| Alexander A Trusov, A substrate energy dissipation mechanism in in-phase and anti-phase micromachined z-axis vibratory gyroscopes // J | |||
| Micromech | |||
| Microeng | |||
| Способ использования делительного аппарата ровничных (чесальных) машин, предназначенных для мериносовой шерсти, с целью переработки на них грубых шерстей | 1921 |
|
SU18A1 |
| Z | |||
| Hou et al, Effect of die attachment on key dynamical parameters of micromachined gyroscopes // Microsyst Technol (2012) 18:507-513 | |||
| СПОСОБ ИЗМЕРЕНИЯ ДОБРОТНОСТИ РЕЗОНАНСНОГО КОНТУРА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2013 |
|
RU2564699C2 |
| US 20140001984 A1, 02.01.2014 | |||
| US 6845669 B2, 25.01.2005. | |||
Авторы
Даты
2018-04-28—Публикация
2017-02-27—Подача