Изобретение относится к области корректируемых инерциальных навигационных систем и может быть использовано при разработке комплексированных навигационных систем, в которых основная навигационная информация, поставляемая бесплатформенными инерциальными навигационными системами (БИНС), корректируется по позиционной и скоростной информации, поставляемой спутниковой навигационной системой (СНС), и угловой (астро) информации, поставляемой астросистемой.
Далее при описании предлагаемого способа в тексте используются следующие обозначения:
- векторы и матрицы обозначаются жирным шрифтом;
- надстрочный индекс "'" обозначает операцию дифференцирования;
- надстрочный индекс "т" обозначает операцию транспонирования;
- надстрочный индекс "-1" обозначает операцию обращения матрицы;
- надстрочный индекс "^", стоящий после матрицы, обозначает кососимметрическую матрицу.
При описании способа используются следующие ортогональные системы координат (трехгранники):
- трехгранник Oh1h2h3, лежащий в плоскости Гринвичского меридиана, ось Oh3 направлена на Северный полюс;
- идеальный (сопровождающий) трехгранник Mx1x2x3 с началом в точке М, связанной с объектом, ось х3 совпадает с местной вертикалью;
- модельный трехгранник Му1у2у3, реализуемый бортовой ЦВМ;
- приборный трехгранник Mz1z2z3, связанный со строительными осями системы (блока чувствительных элементов).
Взаимная ориентация трехгранников Mx1x2x3 и My1y2y3 определяется вектором α малых углов поворота.
Взаимная ориентация трехгранников Mz1z2z3 и My1y2y3 задается матрицей ориентации А.
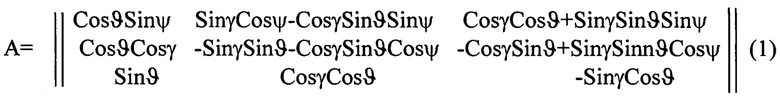
где ϑ, γ, ψ - углы крена, тангажа и гироскопического курса соответственно.
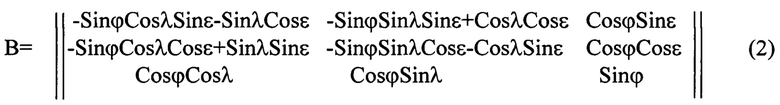
где ϕ, λ, ε - географические координаты и курсовой угол.
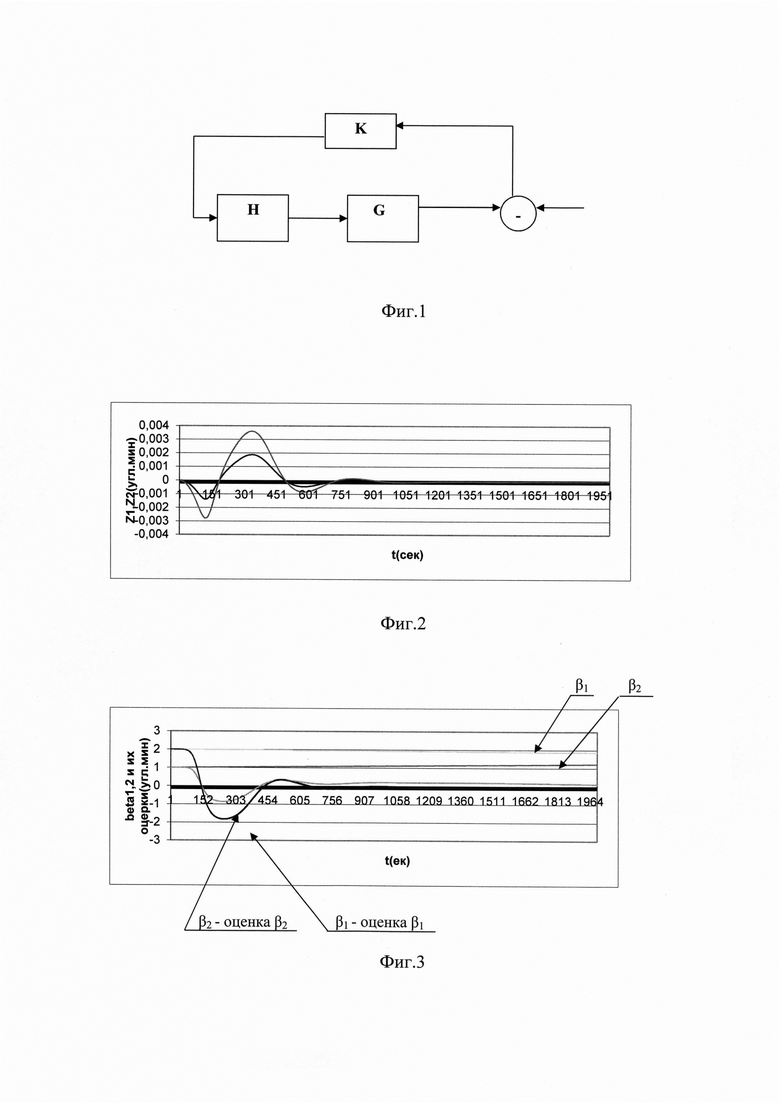
Стандартная схема, по которой строится способ определения корректирующих поправок в БИНС, представлена на Фиг. 1, где
G - импульсная переходная функция объекта регулирования;
Н - матрица связи вектора корректируемых параметров системы х и вектора измерения z;
K - коэффициент усиления сигнала.
На один вход разностной блок-схемы подается сигнал Нх, а на другой - измерение z. Полученная разность (невязка) z-Hx подается на вход блока обратной связи с коэффициентом усиления К, выход которого подключен к входу блока G. Математическая запись системы, представленной на Фиг. 1, имеет вид:

Примером такого способа определения корректирующих поправок БИНС по внешней позиционной и скоростной информации, поставляемой доплеровским измерителем скорости и угла сноса (ДИСС), является известный способ, реализованный в серийных астроинерциальных системах Л-14МА [1] и Л41 [2], входящих в состав навигационных комплексов ВП-021 и Н-202.
В известном способе определения корректирующих поправок в БИНС используется астроинерциальная информация с астроинерциальной навигационной системы, а также позиционная и скоростная информация с ДИСС. Для получения корректирующих поправок из каталога визируемых звезд последовательно выбираются две звезды, доступные визированию в данный момент времени в данной точке местоположения объекта, проводится их последовательное визирование с определением разностей между их расчетными и фактическими углами (угловых поправок), пересчет полученных угловых поправок в вектор кинематических ошибок корректируемой системы, и по скорости изменения этого вектора на базе кинематических уравнений ошибок системы определяются такие инструментальные ошибки корректируемой системы, как нескомпенсированные дрейфы гироскопов. Внешняя скоростная информация используется для определения ошибок построения вертикали на базе динамической группы уравнений ошибок системы, при этом ошибки местоположения объекта определяются как алгебраическая сумма определенных ошибок построения вертикали и кинематических ошибок системы.
В известной системе при построении фильтра ставилась задача оценки ошибок построения вертикали, скоростных ошибок и линейной комбинации кинематических ошибок системы, инструментальных ошибок (нескомпенсированные дрейфы и ошибки акселерометров) и ошибок измерения, вызванных ошибками взаимной привязки осей корректируемой системы и антенн ДИСС. Базовой при построении фильтра скоростной коррекции (импульсная переходная функция G) была принята динамическая группа уравнений ошибок системы (6)-(11), приведенная ниже.
Асимптотически устойчивый фильтр шестого порядка, реализованный в системе Л-14МА, обеспечивал готовность оценок ошибок построения вертикали и скоростной ошибки за время, превосходящее 30 минут, а фильтр того же порядка, реализованный в системе Л41 с использованием метода калмановской фильтрации (метод корня), обеспечивал готовность оценок ошибок построения вертикали и скоростной ошибки за 12 минут времени. Однако ошибки внешней скоростной информации, вызванные ошибками взаимной привязки осей корректируемой системы и антенн ДИСС, приводят к дополнительным ошибкам корректируемых параметров инерциальной системы.
Задачей изобретения является разработка способа определения корректирующих поправок в БИНС, свободного от указанных недостатков путем использования позиционной и скоростной информации, поставляемой СНС, и астроинформации, поставляемой средствами астросистемы, а также существенно повышающего надежность проведения коррекции.
Поставленная задача решается способом определения корректирующих поправок в бесплатформенной инерциальной навигационной системе, в котором для коррекции бесплатформенной инерциальной навигационной системы используется астроинерциальная информация с астроинерциальной навигационной системы, а также позиционная и скоростная информация со спутниковой навигационной системы, при этом в процессе формирования астроинформации выбирается из каталога визируемых звезд звезда, доступная визированию в данный момент времени в данной точке местоположения объекта, ее визирование с определением двух угловых поправок посредством вычисления разности между расчетным и фактическим углами визирования звезды по азимуту и разности между расчетным и фактическим углами ее визирования по высоте; по полученной позиционной и скоростной информации на базе динамической группы уравнений ошибок корректируемой системы вычисляются ее позиционная ошибка, скоростная ошибка и ошибка построения вертикали, по совокупности ошибок определяются горизонтальные проекции вектора кинематических ошибок системы на плоскость местного горизонта, как результат визирования гипотетической звезды, находящейся в зените, затем по полученной в виде угловых поправок астроинерциальной информации и горизонтальных проекций вектора кинематических ошибок вычисляется его вертикальная проекция, производится пересчет горизонтальных и вертикальной проекций в вектор кинематических ошибок, после чего по его скорости определяются такие инструментальные ошибки, как некомпенсированные дрейфы гироскопов.
При построении способа учитывается то обстоятельство, что в совокупности определяемых ошибок системы такие ошибки, как ошибка α построения вертикали и ошибки γ определения местоположения, являются двухкомпонентными векторами, определяемыми в проекциях на оси сопровождающего трехгранника (местного горизонта), а кинематические ошибки β и инструментальные ошибки системы ν, ε (некомпенсированные дрейфы и ошибки акселерометров) являются трехкомпонентными векторами, при этом инструментальные ошибки ν, ε, которые рассматриваются как систематические ошибки, определены в проекциях на оси приборного трехгранника, ориентированного в БИНС относительно сопровождающего трехгранника, как было сказано выше, произвольным образом. Взаимная ориентация этих трехгранников определяется матрицей ориентации (1).
Учет этих особенностей при построении способа идентификации ошибок БИНС привел к построению трехступенчатого алгоритма, на первой ступени которого, представляющей двухканальную систему, определяются такие ошибки системы, как ошибка определения координат γ, скоростная ошибка Δω, ошибка построения вертикали α. Полученные оценки ошибок БИНС используются как новый вектор измерения, поступающий на вход алгоритма второй ступени, решающей задачу определения третьей компоненты β3 вектора β кинематических ошибок, при этом, как будет показано ниже, для определения третьей компоненты β3 вектора β достаточно визирования одной звезды, что существенно повышает надежность формирования оценок ошибок корректируемой системы; на третьей ступени, представляющей собой трехканальную систему, определяются такие инструментальные ошибки, как нескомпенсированные дрейфы системы ν.
В качестве базовых при построении алгоритма оценки ошибок БИНС используются уравнения, описывающие поведение динамических и кинематических ошибок в проекциях на оси сопровождающего трехгранника классической платформенной системы [1], [2], в которых учтены особенности построения БИНС.






где
Δω1 Δω2 - скоростные ошибки системы;
α1, α2 - ошибки построения вертикали;
β - вектор кинематических ошибок системы;
δε1, δε2, δω - проекции векторов инструментальных ошибок ε, ν (ошибок акселерометров, некомпенсированных дрейфов системы соответственно) на оси сопровождающего трехгранника, определяемые как:


где
ε, ν - систематические составляющие векторов инструментальных ошибок системы (ошибок акселерометров, некомпенсированных дрейфов системы соответственно), определенные в проекциях на оси приборного трехгранника как:


А - матрица ориентации, определяемая по (1);
ω - кососимметрическая матрица, соответствующая вектору абсолютных угловых скоростей вращения сопровождающего трехгранника;
ω1=V2/R+ub13,
ω2=-V1/R+ub23,
где
b13, b23 - элементы матрицы направляющих косинусов В, определяемые по (2);
V1, V2 - линейные скорости движения объекта;
R - радиус Земли;
u=15 град/ч - скорость вращения Земли.
Прежде чем приступать к изложению предложенного способа, проведем стандартную процедуру выделения наблюдаемого подпространства.
Задача построения наблюдаемого подпространства и определения меры наблюдаемости достаточно подробно и исчерпывающе изложена в [5].
Необходимым и достаточным условием наблюдаемости линейной динамической системы (6)-(9) является максимальный ранг матрицы наблюдаемости, равный размерности системы: 
где
A=E+Gdt;
Е - единичная матрица;
dt - шаг интегрирования.
В основе процедуры построения наблюдаемого подпространства лежит преобразование:

где
Т - невырожденная матрица, структура которой может быть представлена в виде:

приводящее систему к каноническому виду, в котором импульсная переходная функция будет иметь вид:

с матрицей связи вектора измерения z с вектором х оцениваемых параметров системы:

или блочный вид:

где
& - элементы матрицы, отличные от нуля;
* - элементы матрицы, которые могут отличаться от нуля.
Процедура заключается в определении элементов xi вектора х наблюдаемых параметров.
Обозначим:




где Δω1, Δω2, γ1, γ2 определяются как:




ϕснс, λснс - географические широта и долгота, поставляемые СНС;
ϕ, λ - географические широта и долгота, поставляемые инерциальной системой;
γ1, γ2, Δϕ, Δλ - элементы вектора измерения z, формируемого по внешней позиционной и скоростной информации, т.е. наблюдаемыми величинами.
Подставляя х1, х2, х5, х6 в (20), (21), получаем:








где




Здесь при дифференцировании х2, х3, х6, х7 сделаны допущения о равенстве нулю производных членов δε1/ω02+ω1δω3/ω02, δε2/ω02+ω2δω3/ω02, ub13β3+δω1, ub13β3+δω2, поскольку эти производные представляют величины второго порядка малости.
В результате проделанных преобразований получили автономную систему, в новых переменных xi, i=1, 2, …, 8:

переходная матрица которой имеет форму жордановой матрицы:

вида (19) с матрицей связи:

вида (10), т.е. наблюдаемую систему.
Сделанные выше допущения о малости переменных δε1/ω02+ω1δω3/ω02, δε2/ω02+ω2δω3/ω02, ub13β3+δω1, ub13β3+δω2 позволили построить относительно простую наблюдаемую систему четвертого порядка по каждому каналу.
Построенная система в новых (наблюдаемых) переменных xi представляет первую ступень предложенного способа. Выходом этой ступени являются оценки β1, β2 горизонтальных каналов системы, определяемые по (9) по x1, x3, x4, x7, полученные на выходе первой ступени, а также переменные х3, х7, являющиеся (как это следует из (36), (37)) оценками ошибок построения вертикали. Эти переменные используются в качестве исходных параметров второй ступени для получения оценки β3 корректируемой БИНС.
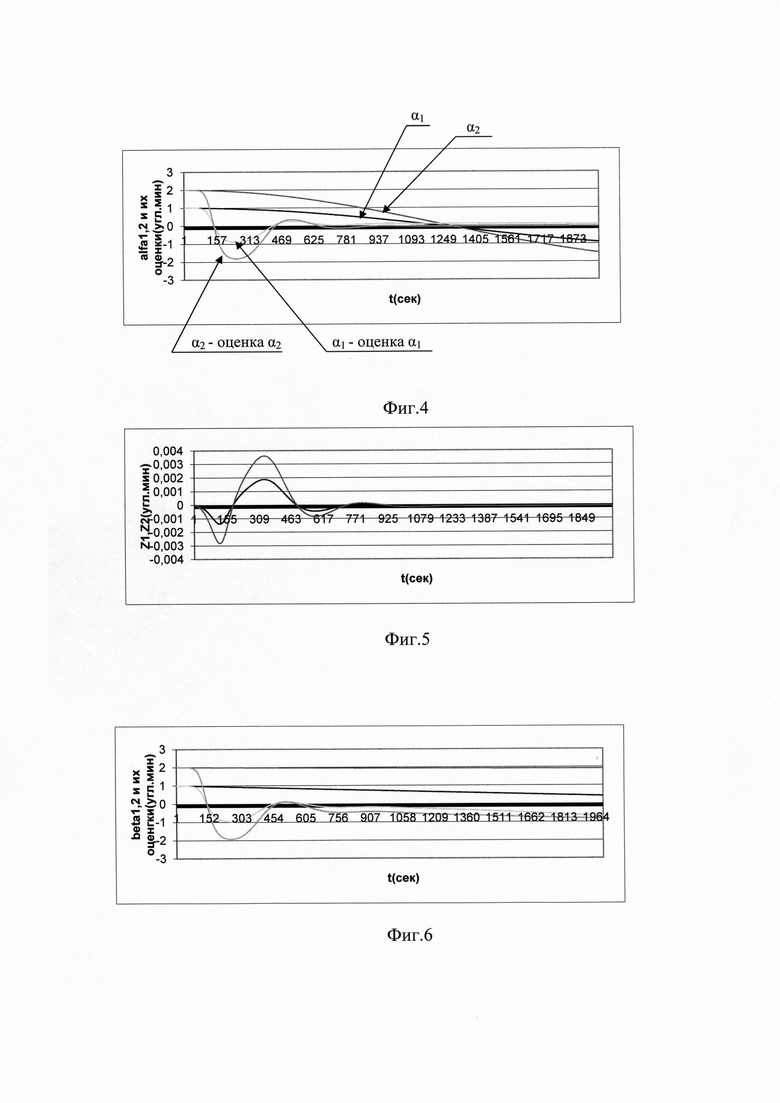
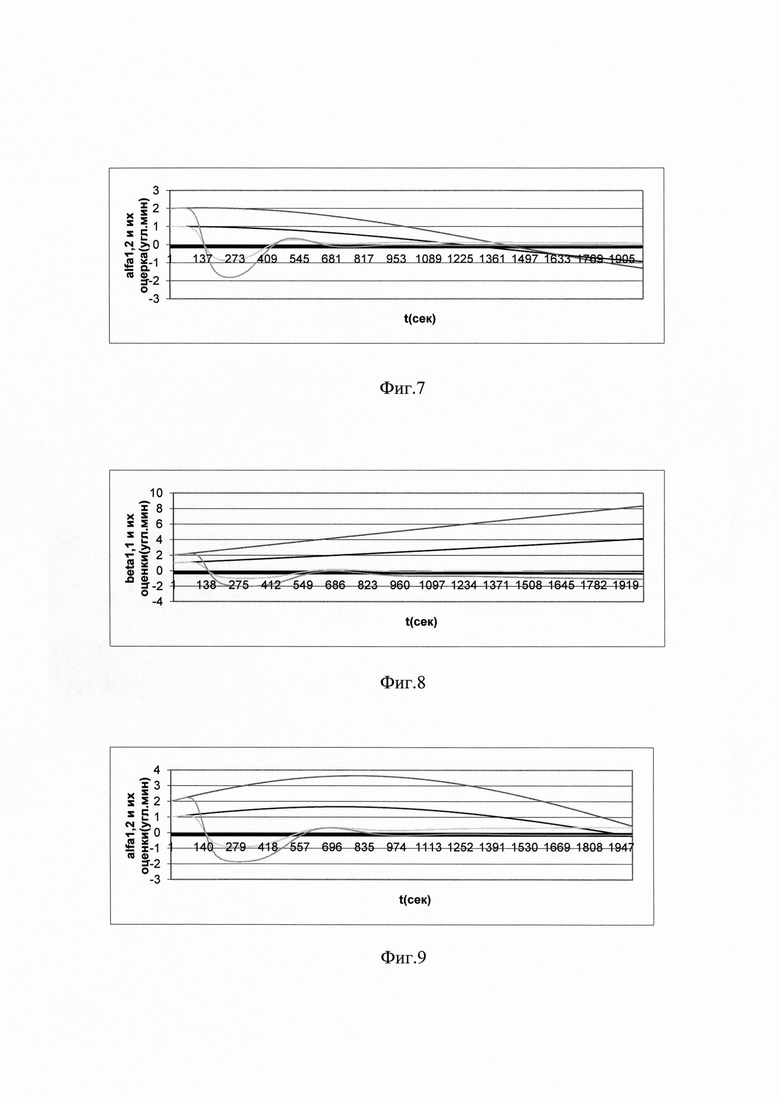
На графиках Фиг. 2 представлены измерения Z1, Z2, полученные при работе первой ступени. Асимптотическая сходимость этих переменных к нулю свидетельствует об устойчивости и наблюдаемости полученной системы. На графиках Фиг. 3 представлены оцениваемые параметры β1 β2 и разницы между этими параметрами и их оценками, определяющими точность оцениваемых параметров. На графиках Фиг. 4 представлены оцениваемые параметры α1 α2 и разницы между этими параметрами и их оценками. На графиках Фиг. 5-7 представлены измерения, параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 2-4, при ошибке β3=10 угл. мин. На графиках Фиг. 8, 9 представлены параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 2-4, при инструментальных ошибках системы δω1=0.1 угл. мин/мин и δω2=0.2 угл. мин/мин. На графиках Фиг. 10, 11 представлены параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 2-4, при центрированной позиционной случайной ошибке, равномерно распределенной в диапазоне ±0.5 угл. мин, и при нулевых инструментальных и курсовой ошибках системы. Графики Фиг. 5-11 показывают влияние таких ошибок системы, как курсовая ошибка, нескомпенсированные дрейфы по горизонтальным осям и случайная ошибка измерения позиции, на точность определяемых выходных параметров системы при сделанных выше допущениях.
Выбор коэффициентов усиления в цепи обратной связи схемы Фиг. 1 может производиться любым из известных способов и не входит в рассмотрение данной заявки. В частности, для определения коэффициентов усиления может применяться асимптотически устойчивый способ, по которому коэффициенты усиления выбираются из условия равенства корней рассматриваемой системы, обеспечивающих ее сходимость с заданным коэффициентом затухания 0<λ<1; при определении коэффициентов усиления может быть использован критерий Гаусса:

где
Z - вектор измерений;
Н - матрица связи вектора измерений с вектором χ оцениваемых параметров;
D - матрица весовых коэффициентов;
т - операция транспонирования,
и построенный на базе этого критерия Гаусса фильтр Калмана; определенную привлекательность представляет критерий оптимальности, предложенный в свое время Чебышевым, минимизирующий кусочно-линейную форму:

где m - число измерений.
Привлекательность использования критерия (48) заключается в том, что в отличие от критерия (47) определяется не доверительный, а гарантированный интервал, за рамки которого не выходит ошибка оценки, полученной в данной конкретной реализации, - метод, получивший название метода гарантированной оценки.
При использовании угловой (астро) информации связь между угловыми поправками и кинематическими ошибками инерциальной навигационной системы определяется линейным соотношением

или в скалярной форме:

где
z - вектор угловых поправок (вектор измерения);
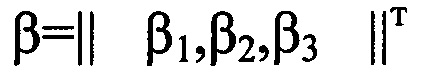 - вектор кинематических ошибок системы, подлежащих определению;
- вектор кинематических ошибок системы, подлежащих определению;
Н - матрица связи, структура которой определяется схемой подвеса телеблока и кинематикой отработки его углов наведения;
h1, h2, h3 - элементы матрицы Н.
Поскольку при визировании одной звезды получаем два измерения (две угловые поправки), для решения уравнения (45) требуется проведение измерений, получаемых при визировании как минимум двух звезд.
Базовыми при построении алгоритма оценки ошибок БИНС по результатам астроизмерений являются кинематические уравнения ошибок системы (8). Не нарушая общности изложения, рассмотрим схему азимутально-высотного подвеса телеблока, в котором углы наведения телеблока отрабатываются разворотом кардана телеблока на азимутальный угол А против часов в плоскости местного горизонта и угол В, отсчитываемый от плоскости местного горизонта в ортогональной плоскости. Тогда в уравнении (45) структура матрицы Н в (46) определится как:
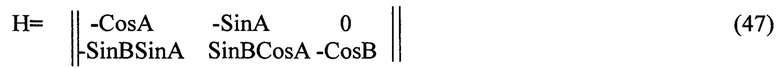
Для однозначного определения трехкомпонентного вектора β необходимо, как было сказано, визирование как минимум двух звезд. Тогда матрица связи Н будет иметь вид:
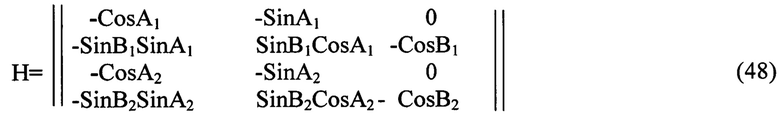
где подстрочными индексами 1, 2 обозначены номера визируемых звезд.
Необходимым и достаточным условием невырожденности системы (45) с матрицей связи (48) является синус угла между визируемыми звездами, т.е. синус этого угла является мерой наблюдаемости системы.
Отметим, что система (48), определяющая связь вектора измерения Z с вектором определяемых параметров β, является избыточной, поскольку содержит четыре уравнения для определения трех неизвестных βi.
В настоящей заявке рассматривается задача построения наблюдаемого подпространства для достаточно узкого класса систем вида

где
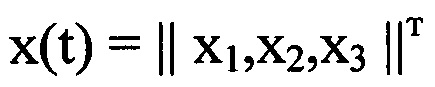 - трехкомпонентный вектор;
- трехкомпонентный вектор;
Ω^ - кососимметрическая матрица, соответствующая вектору Ω угловых скоростей трехгранника (предполагается, что G'=Ω'=0, либо частотные характеристики этих параметров настолько ниже частотных характеристик строящихся алгоритмов, что позволяют сделать такое допущение без ухудшения качества работы этих алгоритмов).
Не составляет труда убедиться, что тип уравнений (4)-(11), с которыми предстоит работать в дальнейшем, соответствует (49). Кроме того, как было сказано выше, перепроектирование векторов из системы координат, связанной с сопровождающим трехгранником, в систему координат, связанную с приборным трехгранником, и обратно осуществляется перемножением исходного вектора на матрицу ориентации А, либо на Ат, представляющую ни что иное как ортонормированную матрицу направляющих косинусов.


Дифференциируя (50), (51) с учетом уравнения Пуассона

получаем:

Уравнение (53) получено транспонированием уравнения (52) Пуассона с учетом свойства кососимметрических матриц (Ω^)т=-Ω^.

Прежде чем строить наблюдаемое подпространство второй ступени, докажем одно утверждение.
Лемма 1
Для кососимметрической матрицы Ω^

справедливо:

где

(56), (57) доказывается непосредственно перемножением матриц
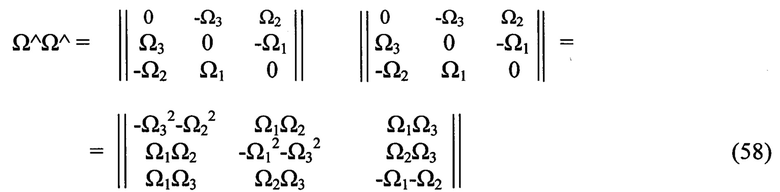
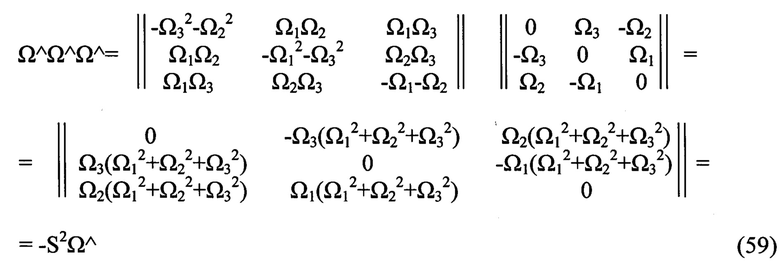
Непосредственно из Леммы 1 следует Теорема 1.
Теорема 1
Для систем вида (50) с f(t)=Const имеет место тождество:

Утверждение доказывается непосредственным дифференцированием x(t). С учетом уравнения Пуассона:


Обозначив, как и выше, Ω12+Ω22+Ω33=S2, получим (60).
Теорема 2
Для алгебраических соотношений вида:



где А - ортонормированная матрица, образуемая разворотом исходной системы координат (трехгранника) на три угла Эйлера (примером такой матрицы является матрица (1)), справедливо:


Доказательство
Дифференцируя (63), (64), из уравнений Пуассона получаем:


откуда, проведя два шага дифференцирования, получаем (66), (67), где вектор  представляет проекции вектора инструментальных ошибок системы ν на оси сопровождающего трехгранника
представляет проекции вектора инструментальных ошибок системы ν на оси сопровождающего трехгранника

Обозначим вектор  через у. Тогда:
через у. Тогда:

и в соответствии с Теоремой 1, последовательно дифференцируя у, получаем:

Применим полученные результаты (Теорема 1) для построения наблюдаемого подпространства второй ступени.
Будем решать задачу определения векторов β и ν в проекциях на оси сопровождающего трехгранника, где в качестве базовых берутся кинематические уравнения (8) ошибок системы, записанные в проекциях на оси сопровождающего трехгранника.
Для построения наблюдаемого подпространства второй ступени введем переменные:


i=l, 2, 3
В новых переменных (8) запишется:



Тогда из (48) по измерениям z однозначно определяется вектор xi, i=1, 2, 3 (при условии, что матрица Н имеет максимальный ранг; условия, обеспечивающие максимальный ранг матрицы Н оговорены выше), а система (8) в новых переменных (75)-(77) с измерением z запишется:


где


Структура (81) совпадает с (63).Тогда, последовательно дифференцируя и вводя новые переменные, в соответствии с Теоремой 1 получаем:




где

где ωi, i=1, 2, 3 - скорости вращения матрицы ориентации А (скорости изменения углов курса, крена и тангажа).
Тогда уравнение кинематических ошибок системы в матричном виде запишется:

где переходная матрица имеет блочный вид (каждый блок имеет размер 3×3)
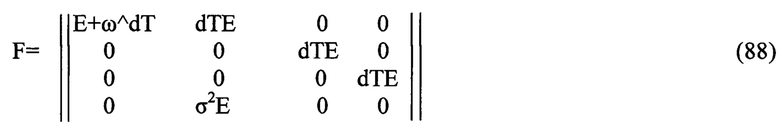
где
Е - единичная матрица размера 3×3;
dT - шаг интегрирования;
σ2 - определяется по (86).
Использование фильтра (80)-(88) для определения ошибок β, ν системы по результатам астроизмерений является стандартной процедурой, используемой для коррекции БИНС по результатам астроизмерений. Использование скоростной и позиционной информации, поставляемой СНС, существенно упрощает способ коррекции БИНС, повышая надежность его работы.
Прежде всего отметим, что поскольку выходными параметрами рассмотренной выше первой ступени являются элементы β1, β2 вектора β кинематических ошибок системы, то результат работы первой ступени можно рассматривать как результат визирования гипотетической звезды, находящейся в зените. Тогда, принимая это во внимание для определения всех трех компонент вектора β при наличии внешней позиционной и скоростной информации, достаточно визирования одной звезды, что существенно облегчит получение необходимых для коррекции системы астропоправок. При этом матрица связи Н будет иметь вид:

где азимутальный угол А в первых двух строках матрицы Н может быть определен как:

Процедура определения третьей компоненты β3 может быть еще более упрощена, если формировать вектор измерения, получаемый при визировании второй (реальной) звезды, как алгебраическую сумму угловой поправки, получаемой в результате визирования выбранной звезды, и оценок β1, β2 вектора β, получаемых на выходе первой ступени, использующей позиционную и скоростную информацию, как это было показано выше. Так, из четвертой строки (89) получаем:
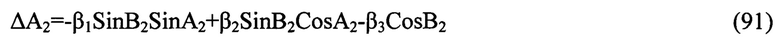
откуда, сформировав вектор измерения
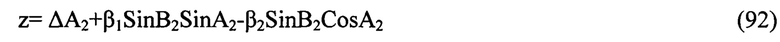
где β1, β2 - выходные параметры первой ступени, получаем:

где
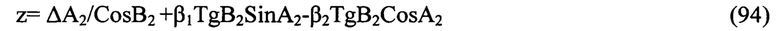
В результате проделанных выкладок построили вторую ступень в виде линейного уравнения (93) первого порядка, выходом которого является оценка третьей компоненты β3 вектора кинематических ошибок системы β.
Выходом двух ступеней построенного метода определения вектора β кинематических ошибок системы является оценка этого вектора.
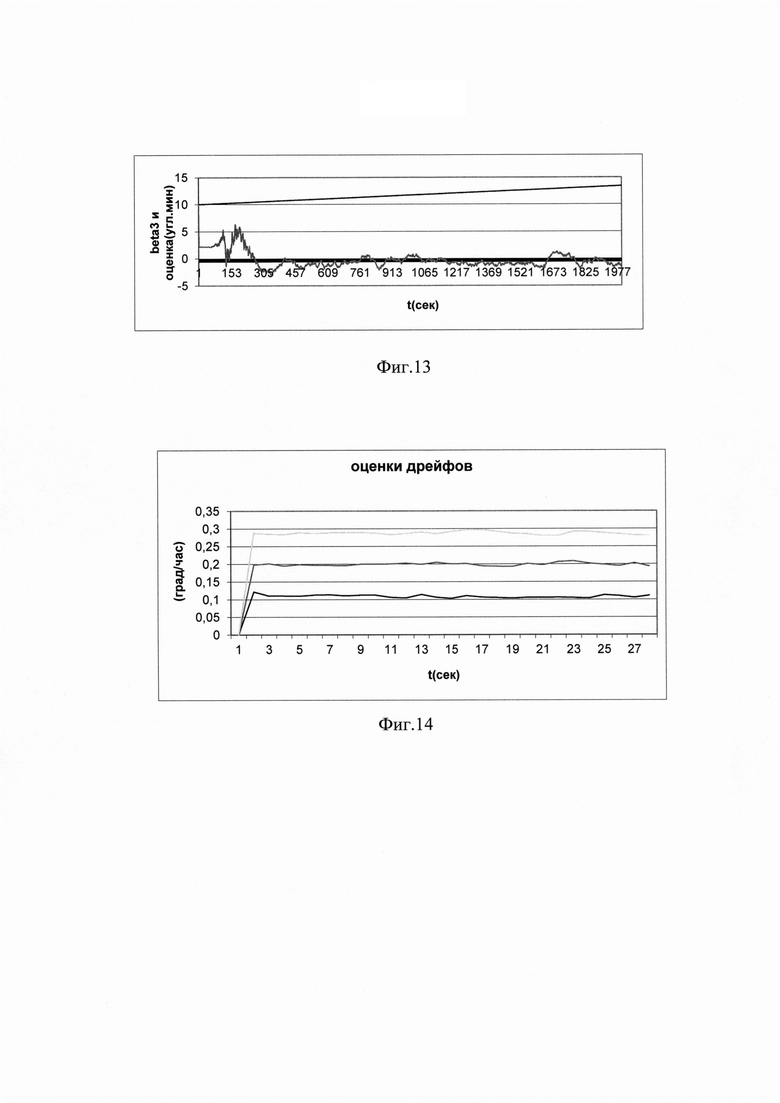
На графиках Фиг. 12 представлены кинематическая ошибка системы β3 и разность между этой ошибкой и ее оценкой, полученной по (93), (94) при наличии азимутального дрейфа ν3=0.1 град/ч и при нулевых ошибках измерения, характеризующая точность получаемой по этому способу оценки. Большая ошибка получаемой оценки на первых 500 секундах вызвана переходным процессом при получении оценок β1, β2 на первой ступени. В установившемся состоянии ошибка оценки не превышает 0.8 угл. мин. На графиках Фиг. 13 представлены аналогичные результаты при наличии центрированной случайной позиционной ошибки измерения, распределенной по равномерному закону в диапазоне 0.1 угл. мин.
Для получения оценки вектора v инструментальных ошибок системы построим третью ступень, используя в качестве измерения выходные параметры βi, i=1, 2, 3, получаемые на выходе первой и второй ступеней. В этом случае, строя наблюдаемое подпространство из (8), как и выше, получаем:

где


Последовательно дифференцируя и вводя новые переменные, в соответствии с Теоремой 1 получаем:




где

ωi, i=1, 2, 3 - скорости вращения матрицы ориентации А (скорости изменения углов курса, крена и тангажа).
Сформировав измерение как:

получаем:

где

откуда, применяя Теорему 1, получаем в векторной форме:

где матрица F имеет блочный вид F=E+GdT,

где
Е - единичная матрица размера 3×3;
σ2 - определяется по (103).
На графиках Фиг. 14 показаны оценки дрейфов ν1=0.1 град/ч, ν2=0.2 град/ч, ν3=0.3 град/ч при наличии случайной центрированной ошибки измерения, равномерно распределенной в диапазоне 0.01 угл. мин.
В результате проделанных операций построен относительно простой способ использования позиционной и скоростной информации, поставляемой СНС, и астроинформации, представляющий трехступенчатую схему обработки информации, на первой ступени которой используется позиционная и скоростная информация для определения таких ошибок БИНС, как скоростная и позиционная ошибки и ошибки построения вертикали. По совокупности полученных на выходе первой ступени оценок позиционных ошибок и ошибок построения вертикали определяются горизонтальные проекции β1, β2 вектора β кинематических ошибок системы, что позволило на второй ступени, в которой для коррекции системы используется астроинформация, использовать только одну звезду в качестве астроориентира, что существенно облегчило условие проведения астрорежима, а также повысило точность за счет улучшения частотных характеристик способа обработки информации (за счет исключения времени, затрачиваемого на переброс визирной оси телеблока с линии визирования одной звезды на линию визирования другой при визировании двух звезд). И, наконец, на третьей ступени по информации, получаемой с выхода второй ступени, определяются такие инструментальные ошибки системы как нескомпенсированные дрейфы.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОМБИНИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ АСТРОИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2017 |
|
RU2654965C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА, КОРРЕКТИРУЕМАЯ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668659C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБОК БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668658C1 |
| Астроинерциальная навигационная система с коррекцией по гравитационному полю Земли | 2023 |
|
RU2820600C1 |
| СПОСОБ ПОСТРОЕНИЯ АСТРОИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2016 |
|
RU2641515C2 |
| СПОСОБ АСТРОКОРРЕКЦИИ | 2016 |
|
RU2641619C1 |
| СИСТЕМА АСТРОИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2016 |
|
RU2639583C1 |
| СПОСОБ КОМПЛЕКСИРОВАНИЯ БЕСПЛАТФОРМЕННЫХ ИНЕРЦИАЛЬНЫХ НАВИГАЦИОННЫХ СИСТЕМ | 2016 |
|
RU2634082C1 |
| НАВИГАЦИОННО-ПИЛОТАЖНЫЙ КОМПЛЕКС | 2016 |
|
RU2634083C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2634071C1 |

Изобретение относится к области корректируемых инерциальных навигационных систем и может быть использовано при разработке комплексированных навигационных систем. Способ определения корректирующих поправок в бесплатформенной инерциальной навигационной системе, где для коррекции бесплатформенной инерциальной навигационной системы используется астроинерциальная информация с астроинерциальной навигационной системы, а также позиционная и скоростная информация со спутниковой навигационной системы. При этом в процессе формирования астроинформации выбирается из каталога визируемых звезд звезда, доступная визированию в данный момент времени в данной точке местоположения объекта, ее визирование с определением двух угловых поправок посредством вычисления разности между расчетным и фактическим углами визирования звезды по азимуту и разности между расчетным и фактическим углами ее визирования по высоте. По полученной позиционной и скоростной информации на базе динамической группы уравнений ошибок корректируемой системы вычисляются ее позиционная ошибка, скоростная ошибка и ошибка построения вертикали, по совокупности ошибок определяются горизонтальные проекции вектора кинематических ошибок системы на плоскость местного горизонта, затем по полученной в виде угловых поправок астроинерциальной информации и горизонтальных проекций вектора кинематических ошибок вычисляется его вертикальная проекция, производится пересчет горизонтальных и вертикальной проекций в вектор кинематических ошибок, после чего по его скорости определяются такие инструментальные ошибки, как нескомпенсированные дрейфы гироскопов. Техническим результатом изобретения является разработка способа определения корректирующих поправок в БИНС, свободного от указанных недостатков путем использования позиционной и скоростной информации, поставляемой СНС, и астроинформации, поставляемой средствами астросистемы, а также существенно повышающего надежность проведения коррекции. 14 ил.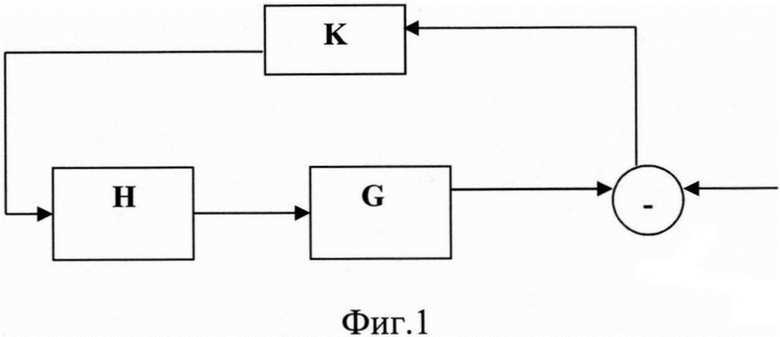
Способ определения корректирующих поправок в бесплатформенной инерциальной навигационной системе, в котором для коррекции бесплатформенной инерциальной навигационной системы используется астроинерциальная информация с астроинерциальной навигационной системы, а также позиционная и скоростная информация со спутниковой навигационной системы, при этом в процессе формирования астроинформации выбирается из каталога визируемых звезд звезда, доступная визированию в данный момент времени в данной точке местоположения объекта, ее визирование с определением двух угловых поправок посредством вычисления разности между расчетным и фактическим углами визирования звезды по азимуту и разности между расчетным и фактическим углами ее визирования по высоте; по полученной позиционной и скоростной информации на базе динамической группы уравнений ошибок корректируемой системы вычисляются ее позиционная ошибка, скоростная ошибка и ошибка построения вертикали, по совокупности ошибок определяются горизонтальные проекции вектора кинематических ошибок системы на плоскость местного горизонта как результат визирования гипотетической звезды, находящейся в зените, затем по полученной в виде угловых поправок астроинерциальной информации и горизонтальных проекций вектора кинематических ошибок вычисляется его вертикальная проекция, производится пересчет горизонтальных и вертикальной проекций в вектор кинематических ошибок, после чего по его скорости определяются такие инструментальные ошибки, как нескомпенсированные дрейфы гироскопов.
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
| Способ определения и компенсации девиации магнитометрических датчиков и устройство для его осуществления | 2015 |
|
RU2607305C1 |
| СПОСОБ КОРРЕКЦИИ ДРЕЙФА МИКРОМЕХАНИЧЕСКОГО ГИРОСКОПА, ИСПОЛЬЗУЕМОГО В СИСТЕМЕ ДОПОЛНЕННОЙ РЕАЛЬНОСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ | 2013 |
|
RU2527132C1 |
| СПОСОБ АСТРОВИЗИРОВАНИЯ | 2015 |
|
RU2586443C1 |
| СПОСОБ ПОВЫШЕНИЯ ОСТРОТЫ ЗРЕНИЯ ПРИ СМЕШАННОМ АСТИГМАТИЗМЕ | 1993 |
|
RU2112472C1 |
Авторы
Даты
2018-05-23—Публикация
2017-06-27—Подача