Изобретение относится к навигационно-пилотажным комплексам, объединяющим несколько инерциальных навигационных систем (ИНС) для формирования обобщенной выходной информации о местонахождении объекта, его ориентации в пространстве и его скоростях, а также использующих внешнюю информацию для коррекции систем, входящих в состав комплекса.
Из уровня техники известен навигационно-пилотажный комплекс ВП-021 (см. Фиг. 1), включающий три бесплатформенные инерциальные навигационные системы (БИНС) и блок обработки их выходной информации, связанный входами с выходами БИНС.
В известном навигационно-пилотажном комплексе комплексирование инерциальных навигационных систем осуществляется посредством выбора выходной информации инерциальных навигационных систем (ИНС) по мажоритарному признаку, т.е. наиболее достоверной информацией, поступающей в комплекс от различных систем, считается та информация, которая имеет наименьшее расхождение, в частности, выбирается та система, для коррекции которой используется внешняя информация, обеспечивающая повышение точности выходных параметров системы. Другие системы, входящие в состав навигационного комплекса, выполняют функции не более как резервного канала, обеспечивающие повышение надежности всего комплекса.
Технической задачей предлагаемого навигационно-пилотажного комплекса является повышение точности выходной информации комплекса и глубины контроля систем, входящих в состав комплекса.
Указанная техническая задача решается посредством навигационно-пилотажного комплекса, в состав которого входят по меньшей мере две бесплатформенные навигационные системы и связанный с ними блок обработки первичной информации, при этом в состав комплекса дополнительно входят блок решения навигационных уравнений и блок контроля, первым входом подключенный к выходу блока решения навигационных уравнений, а вторым и третьим входами подключенный к первым выходам бесплатформенных навигационных систем, при этом блок обработки первичной информации включает последовательно соединенные по направлению сигнала блок вычисления переменных bi(k, r), входами подключенный к вторым выходам бесплатформенных навигационных систем, блок вычисления измерений zi, блок вычисления невязок δi, блок фильтрации невязок δi и блок вычисления матрицы ориентации, выходом подключенный к первому входу блока решения навигационных уравнений, а также последовательно соединенные по направлению сигнала блок вычисления переменных γi, входами подключенный к третьим выходам бесплатформенных навигационных систем, блок фильтрации γi и блок вычисления матрицы направляющих косинусов, выходом подключенный к второму входу блока решения навигационных уравнений.
Специфика решения задачи навигации с использованием БИНС заключается в отсутствии сигналов управления датчиками моментов (ДМ) системы. Поэтому для повышения точности выходной информации комплекса и повышения глубины контроля систем, входящих в состав комплекса, комплексирование нескольких БИНС предлагается выполнять путем предварительной обработки первичной информации, поступающей с систем - матрица ориентации и ускорения в осях акселерометров блока чувствительных элементов (БЧЭ) - с последующим решением навигационных уравнений на основе обработанной первичной информации, получаемой от систем, входящих в состав комплекса, с последующим контролем поступающей от систем в комплекс информации, что повышает глубину контроля систем, входящих в состав комплекса (см. Фиг. 2). Рассмотрим задачу комплексной обработки первичной информации, поступающей с нескольких БИНС (поз. 1, 2) в виде матрицы ориентации и ускорений (или приращений линейных скоростей), поступающих с выходов первых интеграторов систем. Взаимная ориентация блока чувствительных элементов (БЧЭ) БИНС при решении задачи может быть произвольной и определяться в режиме начальной выставки систем как:

i=1, 2,…, N,
j=1, 3, …, N,
j≠i,
где
Ai0, Aj0 - начальное значение матриц ориентации Ai, Aj;
N - общее число БИНС, входящих в комплекс.
Здесь и далее по тексту векторы и матрицы обозначаются жирным шрифтом, операции транспонирования обозначаются надстрочным индексом “т”, операции обращения матриц обозначаются надстрочным индексом “-1”.
При решении задачи в самом общем случае в качестве исходной информации используется N матриц ориентации Ai, 1=1, 2, …, N, или эквивалентных им углов курса, крена и тангажа.
Определим матрицу ориентации  , связанную с Ai соотношениями:
, связанную с Ai соотношениями:

где
δ^i - кососимметрическая матрица, соответствующая вектору
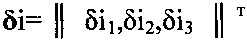 малых углов поворота;
малых углов поворота;
E - единичная матрица.
Взаимная ориентация матриц Ai, Aj определяется как:

откуда с учетом
А-1=Aт - для ортогональных матриц,
(δ^)т=-δ^ - для кососимметрических матриц,
Умножая (3) на 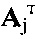 справа, получаем:
справа, получаем:

Обозначим:

Тогда:

ij=1, 2, …, N
i≠j
(6) не дает однозначного решения. Для подтверждения этого утверждения рассмотрим частный случай N=3.
Имеем:



Умножив (9) на Cij справа и сложив с (8), получаем:

Подставляя (9) в (10), получаем:

В (11) имеем неопределенность вида 0/0, т.е. система (11) не имеет единственного решения. В общем случае при N>3 любая тройка из N выбранных уравнений будет линейно зависимой, т.е. ранг этой системы не будет максимальным.
Геометрическая интерпретация полученного результата совершенно прозрачна. Полученная по (11) точка является точкой пересечения трехмерных сферических поверхностей радиуса δi в 3N-мерном пространстве, где δi - длина вектора δi, с центрами, определяемыми матрицами Ai. Такая точка может быть определена произвольным заданием вектора δj; все остальные векторы δi, i=1, 2, …, N, i≠j определяются решением уравнений (11).
Для получения однозначного решения введем критерий Гаусса:

Приравнивая к нулю первые частные производные J по δi, получаем:

Суммируя (11) по i=1, 2, …, N, i≠j получаем:

или с учетом (13):

Приравнивая верхние недиагональные элементы в (15), получаем уравнения в скалярном виде:
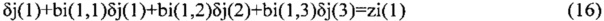
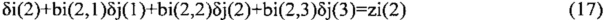
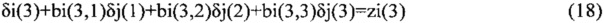
где
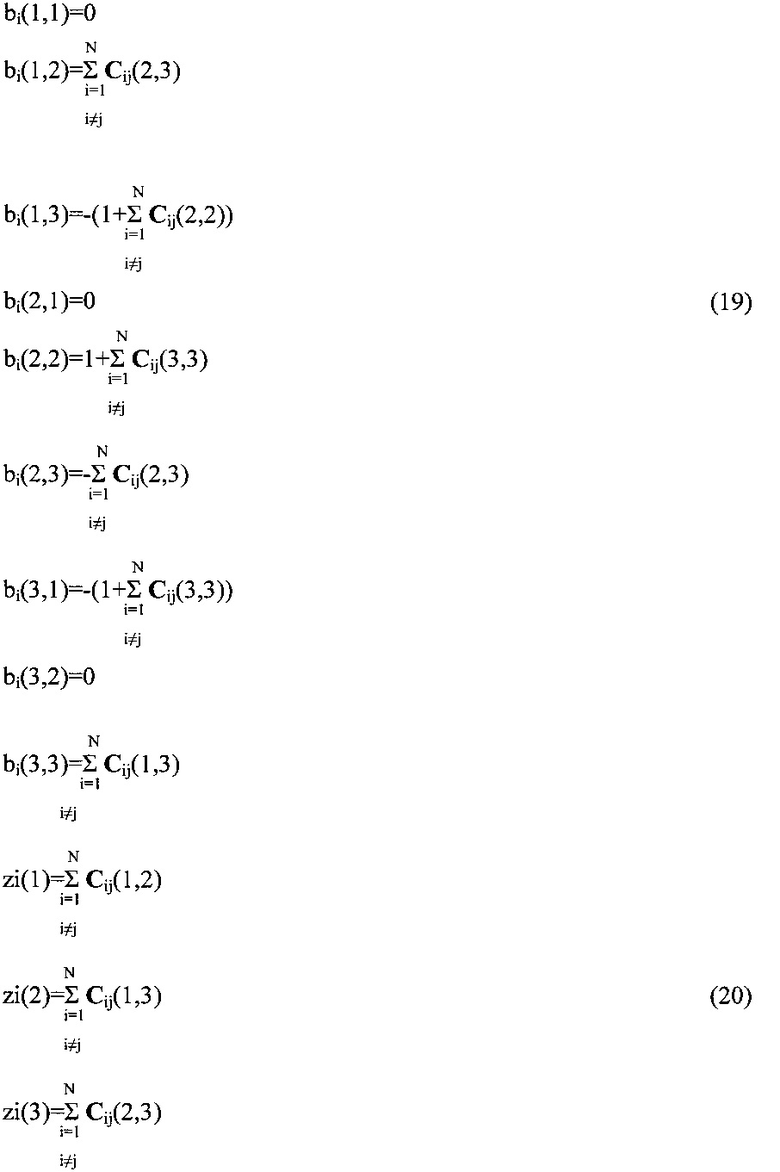
(в скобках стоят номера элементов матриц Cij, Bi и векторов δi, zi), или в векторной форме:

где элементы матрицы В и вектора z определяются по (19) и (20).
Искомый вектор δi определяется как:

Искомая матрица 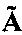 определяется как:
определяется как:

где Aj - матрица ориентации j-го БИНС.
Следует отметить, что матрицы 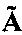 , определяемые как
, определяемые как  и
и 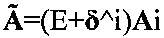 (равно как и матрицы δ^i, δ^j), не являются тождественными и отличаются в общем случае начальной матрицей Aij0 взаимной ориентации, что может оказаться важным в ряде приложений.
(равно как и матрицы δ^i, δ^j), не являются тождественными и отличаются в общем случае начальной матрицей Aij0 взаимной ориентации, что может оказаться важным в ряде приложений.
Отметим специфику применения критерия (12) при построении алгоритма. Стандартно критерий Гаусса применяется для получения решения переопределенной системы (метод наименьших квадратов).
В рассматриваемом алгоритме критерий (12) введен для получения однозначного решения системы 3N уравнений с 3N неизвестными. Вообще говоря, можно получить переопределенную систему, написав N уравнений (11) с i=1, 2, …, N. Однако такой подход не даст желаемого результата ввиду полной тождественности написанных уравнений. Действительно, рассмотрим систему:



Подставляя (26) в (25):

и умножая справа на Cki, получаем с учетом CkiCkj=Cjj:

тождественное (24).
Задача определения 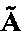 решалась выше с использованием критерия Гаусса (12). Задача может решаться с использованием критерия Чебышева:
решалась выше с использованием критерия Гаусса (12). Задача может решаться с использованием критерия Чебышева:

В рассматриваемом случае решение задачи с критерием (29) сводится к решению системы 3N уравнений с 2N неизвестными, а критерий (29) сводится к:

или эквивалентному ему:

Геометрически решение 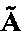 как точка в 3N-мерном пространстве, равноудаленная от трехмерных гиперплоскостей (22). Такой точкой является центр гиперсферы, вписанной в замкнутый симплекс-многогранник, образованный системой 3-мерных гиперплоскостей (22) в 3N-мерном пространстве, а условие (31) трансформируется в условие:
как точка в 3N-мерном пространстве, равноудаленная от трехмерных гиперплоскостей (22). Такой точкой является центр гиперсферы, вписанной в замкнутый симплекс-многогранник, образованный системой 3-мерных гиперплоскостей (22) в 3N-мерном пространстве, а условие (31) трансформируется в условие:

для всех i,j=1, 2, …, N, эквивалентное (29).
Умножая (32) на 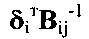 слева, получаем параметрическую систему алгебраических уравнений:
слева, получаем параметрическую систему алгебраических уравнений:

решая которую, получим результат δi, эквивалентный результату, полученному ранее.
Для учета степени значимости (приоритета) тех или иных измерений в квадратичную форму Гаусса вводится матрица весовых коэффициентов. В рассматриваемой задаче квадратичная форма и ее производные будут иметь вид:


Умножая (15) на λi, i=1, 2, …, N, i≠j получаем с учетом (35):

Приравнивая верхние недиагональные элементы в (36), получаем уравнения в скалярном виде (16), (17), (18), где


Выше построен алгоритм однозначного определения векторов δi и матрицы 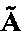 как результат однократной обработки исходных матриц ориентации Ai, i=1, 2, …, N, полученных на текущий момент времени. Для фильтрации случайных ошибок измерения результаты измерений осредняются на заданном временном интервале измерения построением линейного фильтра:
как результат однократной обработки исходных матриц ориентации Ai, i=1, 2, …, N, полученных на текущий момент времени. Для фильтрации случайных ошибок измерения результаты измерений осредняются на заданном временном интервале измерения построением линейного фильтра:

Для построения фильтра (39) необходимо построить переходную матрицу F, описывающую динамику изменения оцениваемых переменных х, определить вектор измерения z, построить матрицу связи Н и сформировать коэффициент усиления K в цепи обратной связи фильтра.
Поведение матриц ориентации Ai комплексируемых БИНС описывается линейными уравнениями Пуассона:

где ωi^ - кососимметрическая матрица, соответствующая вектору ωi абсолютных угловых скоростей приборного трехгранника i-го БИНС.
В силу линейности (40) и принципа суперпозиции поведение вектора δi может быть описано кинематическими уравнениями ошибок

где νi - скорости расхождения матриц  и Ai в осях приборного трехгранника i-го БИНС, вызванные наличием некомпенсированных инструментальных ошибок (дрейфов) системы.
и Ai в осях приборного трехгранника i-го БИНС, вызванные наличием некомпенсированных инструментальных ошибок (дрейфов) системы.
Поскольку скорости νi определены в осях приборного трехгранника, можно считать, что эти переменные не зависят от абсолютных скоростей ωi.

Обозначим:
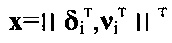
Тогда структура матрицы F в (39) будет определяться уравнениями (41), (42):

где
Е - единичная матрица размера 3×3,
dt - шаг интегрирования.
В качестве измерения используется вектор малых углов δi.
Тогда матрица связи будет определяться, как:

где Е - единичная матрица размера 3×3.
Коэффициент усиления K может вычисляться по стандартному алгоритму Калмана.
На блок-схеме (см. фиг. 2) приведена структурная схема функциональных компонентов блока обработки первичной информации (поз. 3), реализующая вычисление матрицы ориентации 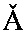 , которая состоит из последовательно соединенных блока вычисления переменных bi (k, r) (поз. 4), где k, r - номера строк и столбцов матриц ориентации A(k, r) комплексируемых систем, блока вычисления измерений zi (поз. 5), блока вычисления невязок δi (поз. 6), блока фильтрации невязок δi (поз. 7) и блока вычисления матрицы ориентации
, которая состоит из последовательно соединенных блока вычисления переменных bi (k, r) (поз. 4), где k, r - номера строк и столбцов матриц ориентации A(k, r) комплексируемых систем, блока вычисления измерений zi (поз. 5), блока вычисления невязок δi (поз. 6), блока фильтрации невязок δi (поз. 7) и блока вычисления матрицы ориентации 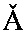 (поз. 8).
(поз. 8).
Задача обработки скоростной информации решается на уровне ускорений Wi (приращений скоростей за такт работы вычислителя), определенных в проекциях на оси приборного трехгранника (БЧЭ). Сформируем вектор измерений как:

Получаем переопределенную систему которую будем решать с использованием критерия Гаусса:

где λi - весовой коэффициент.
Приравнивая нулю частные производные по 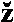 , получаем искомое решение (
, получаем искомое решение (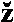 в проекциях на оси сопровождающего трехгранника).
в проекциях на оси сопровождающего трехгранника).

Полученный вектор 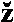 используется в дальнейшем для решения навигационных уравнений.
используется в дальнейшем для решения навигационных уравнений.
Для использования позиционной информации по текущим координатам и курсу ϕi, λi, εi определим матрицу направляющих косинусов i-го БИНС
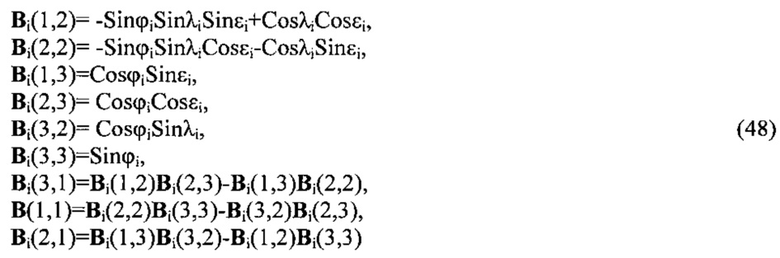
где индексы, стоящие в круглых скобках, определяют элементы матрицы Bi. Выполняя операции над матрицами направляющих косинусов Bi, аналогичные операциям, выполняемым над матрицами ориентации Ai:

где элементы матрицы Bij и вектора z определяются по (19) и (20), как:

(принимается во внимание, что сопровождающие трехгранники всех N БИНС имеют одинаковую ориентацию по северному направлению местного меридиана).
Искомый вектор γi определяется как:

Искомая матрица направляющих косинусов  определяется как:
определяется как:

Элементы γi(1), γi(2) вычисленного по (55) вектора γi будем использовать в качестве измерений при построении фильтра. Моделью оцениваемых ошибок является динамическая группа уравнений ошибок:

где
δp1, δp2 - скоростные импульсы,
α1, α2 - ошибки построения вертикали,
ε1, ε2 - приведенные ошибки масштабов акселерометров,
ν1, ν2 - скорости уходов, определяемые величиной некомпенсированных дрейфов БИНС,
ω02 - частота Шулера.
При интегрировании этих уравнений в правую часть будем подставлять значения углов δi и уходов νi, полученных по алгоритму, описанному выше и перепроектированных на оси сопровождающего трехгранника:


В результате получаем автономную систему уравнений ошибок оценки:
Δγ1'=Δδр1+ω3Δγ2

где Δγi, Δδpi, Δαi i=1, 2 - ошибки оценки 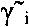 ,
, 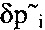 ,
, 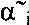 переменных γi, δpi, αi, получаемой на выходе фильтра.
переменных γi, δpi, αi, получаемой на выходе фильтра.

При определении коэффициентов усиления в цепи обратной связи фильтра пренебрежем слабыми перекрестными связями между каналами системы, что не приведет к нарушению устойчивости системы, а лишь к сдвигу корней ее характеристического уравнения. В результате получаем две тождественные системы уравнений третьего порядка:

i=1, 2
или в векторной форме:

где


с измерением:

и матрицей связи:

Выходными параметрами алгоритма являются вектор δi, по которому вычисляется откорректированное значение матрицы ориентации 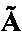 , и векторы x, (64). Компоненты γi векторов x, i=1, 2 используются для коррекции матрицы направляющих косинусов:
, и векторы x, (64). Компоненты γi векторов x, i=1, 2 используются для коррекции матрицы направляющих косинусов:

где

Компоненты δpi используются для вычисления откорректированных скоростей.
Структурная схема функциональных компонентов блока обработки поступающей с выхода БИНС первичной информации, реализующая вычисление матрицы приращения линейных скоростей Wi, представлена на Фиг. 2 в виде трех последовательно соединенных блоков (Фиг. 2) - блока вычисления по (47)-(55) переменных γi (поз. 9), блока фильтрации γi (поз. 10) и блока вычисления по (56) матрицы В направляющих косинусов (поз. 11). На выходе блока (поз. 3) получаем откорректированные значения линейных скоростей объекта V1, V2 и матрицы направляющих косинусов.
В блоке решения навигационных уравнений (поз. 12) решаются стандартные навигационные уравнения и интегрируется матрица ориентации А решением стандартных уравнений Пуассона. Входными величинами для интегрирования навигационных уравнений и матрицы ориентации в этом блоке являются матрицы 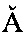 в осях приборного трехгранника и скорости V1, V2, полученные в блоке обработки первичной информации.
в осях приборного трехгранника и скорости V1, V2, полученные в блоке обработки первичной информации.
Блок решения навигационных уравнений (поз. 12) выходом подключается к входу блока контроля (поз. 13), другие входы которого подключаются к выходам БИНС (поз. 1, 2), входящих в состав комплекса.
Построим индикатор контроля скоростной информации. Определим разность приращения скоростей, поступающих с выходов интеграторов i-го и j-го БИНС в проекциях на оси j-го БИНС:

В качестве индикатора введем скалярное произведение:

Подставляя (70) в (71), получаем:

Аналогичным образом, для контроля выходной информации, поступающей с выходов лазерных гироскопов БИНС, в качестве индикатора введем скалярное произведение:

где

Индикаторы 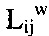 и
и  представляют собой матрицы размера 3×3.
представляют собой матрицы размера 3×3.
Величина элементов этих матриц определяет степень расхождения выходных сигналов i-го и j-го БИНС (лазерных гироскопов для 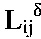 , или первых интеграторов для
, или первых интеграторов для  ) по соответствующему каналу - элемент матриц, стоящий на пересечении второй строки и третьего столбца определяет степень расхождения соответствующего устройства по первому каналу; элемент матриц, стоящий на пересечении первой строки и третьего столбца определяет степень расхождения соответствующего устройства по второму каналу; элемент матриц, стоящий на пересечении второй строки и первого столбца определяет степень расхождения соответствующего устройства по третьему каналу.
) по соответствующему каналу - элемент матриц, стоящий на пересечении второй строки и третьего столбца определяет степень расхождения соответствующего устройства по первому каналу; элемент матриц, стоящий на пересечении первой строки и третьего столбца определяет степень расхождения соответствующего устройства по второму каналу; элемент матриц, стоящий на пересечении второй строки и первого столбца определяет степень расхождения соответствующего устройства по третьему каналу.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМПЛЕКСИРОВАНИЯ БЕСПЛАТФОРМЕННЫХ ИНЕРЦИАЛЬНЫХ НАВИГАЦИОННЫХ СИСТЕМ | 2016 |
|
RU2634082C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2634071C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ОБЪЕКТА И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2017 |
|
RU2661446C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА, КОРРЕКТИРУЕМАЯ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668659C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБОК БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668658C1 |
| КОМБИНИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ АСТРОИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2017 |
|
RU2654965C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩИХ ПОПРАВОК В БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЕ | 2017 |
|
RU2654964C1 |
| КОМПЛЕКСНАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2010 |
|
RU2439498C1 |
| ЗАЩИЩЕННЫЙ СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2019 |
|
RU2713584C1 |
| Способ астрономической коррекции навигационных параметров летательного аппарата | 2021 |
|
RU2767449C1 |
Изобретение относится к навигационно-пилотажным комплексам, объединяющим несколько инерциальных навигационных систем (ИНС) для формирования обобщенной выходной информации о местонахождении объекта, его ориентации в пространстве и его скоростях, а также использующих внешнюю информацию для коррекции систем, входящих в состав комплекса. Технический результат - повышение точности выходной информации комплекса и глубины контроля систем, входящих в состав комплекса. Для этого в состав навигационно-пилотажного комплекса входят по меньшей мере две бесплатформенные навигационные системы и связанный с ними блок обработки первичной информации, при этом в состав комплекса дополнительно входят блок решения навигационных уравнений и блок контроля, первым входом подключенный к выходу блока решения навигационных уравнений, а вторым и третьим входами подключенный к первым выходам бесплатформенных навигационных систем, при этом блок обработки первичной информации включает последовательно соединенные по направлению сигнала блок вычисления переменных bi(k, r), входами подключенный к вторым выходам бесплатформенных навигационных систем, блок вычисления измерений zi, блок вычисления невязок δi, блок фильтрации невязок δi и блок вычисления матрицы ориентации, выходом подключенный к первому входу блока решения навигационных уравнений, а также последовательно соединенные по направлению сигнала блок вычисления переменных γi, входами подключенный к третьим выходам бесплатформенных навигационных систем, блок фильтрации уi и блок вычисления матрицы направляющих косинусов, выходом подключенный к второму входу блока решения навигационных уравнений. 2 ил.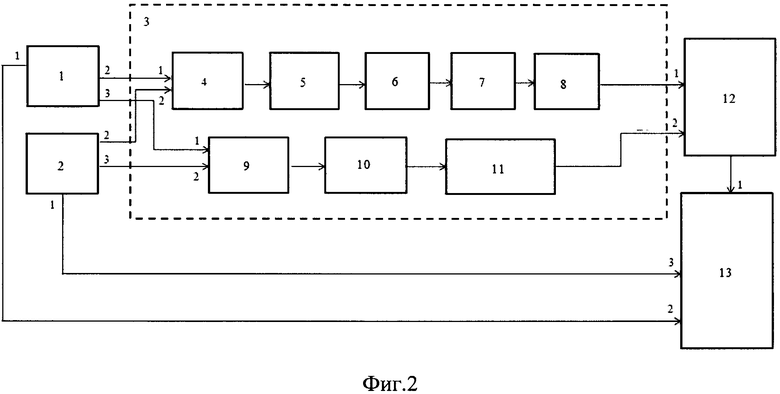
Навигационно-пилотажный комплекс, в состав которого входят по меньшей мере две бесплатформенные инерциальные системы и связанный с ними блок обработки первичной информации, отличающийся тем, что в состав комплекса дополнительно входят блок решения навигационных уравнений и блок контроля, первым входом подключенный к выходу блока решения навигационных уравнений, а вторым и третьим входами подключенный к первым выходам бесплатформенных инерциальных систем, при этом блок обработки первичной информации включает последовательно соединенные по направлению сигнала блок вычисления переменных bi(k,r), входами подключенный к вторым выходам бесплатформенных навигационных систем, блок вычисления измерений zi, блок вычисления невязок δi, блок фильтрации невязок δi и блок вычисления матрицы ориентации, выходом подключенный к первому входу блока решения навигационных уравнений, а также последовательно соединенные по направлению сигнала блок вычисления переменных γi, входами подключенный к третьим выходам бесплатформенных навигационных систем, блок фильтрации γi и блок вычисления матрицы направляющих косинусов, выходом подключенный к второму входу блока решения навигационных уравнений.
| КОМПЛЕКСИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА НАВИГАЦИИ НА "ГРУБЫХ" ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТАХ | 2008 |
|
RU2380656C1 |
| БАБИЧ О.А | |||
| Обработка информации в навигационных комплексах | |||
| - М.: Машиностроение, 1991, с.6-16, 391-507 | |||
| US 6408245 B1, 18.06.2002 | |||
| КОМПЛЕКСНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2004 |
|
RU2265190C1 |
| Устройство для испытания изделий на случайные вибрации | 1978 |
|
SU763714A1 |
| Способ многоканальной регистрации результатов измерений и устройство для его осуществления | 1990 |
|
SU1747905A1 |
Авторы
Даты
2017-10-23—Публикация
2016-06-02—Подача