1. Область применения. Изобретение относится к информационным системам обработки поискового запроса пользователя в Интернете, использующим гипертекстовые технологии.
2. Уровень техники. Известно устройство отыскания информации, применяемое на сервере по ключевым словам, введенным первым пользователем, и включающее модуль поиска ключа в алфавитном классификаторе, посредством использования поля ввода с автозаполнением (см. патентная заявка США №2010/0250524, МКИ: G06F 17/30, опуб. 30.09.2010 г), используемое во многих известных интернет-порталах, таких как google, yandex т.д. Недостатком известного устройства, использующего переход по ключу (с помощью поля ввода с автозаполнением), является отсутствие пользовательского интерфейса, предоставляющего возможность быстрого обзора всего ключевого массива на наличие или отсутствие ключей. В силу этого данное устройство использует поле ввода с большим количеством шагов перехода (нажатий клавиш на электронном устройстве) для ввода и набора символов на клавиатуре, что делает ее неудобной при поиске нужной информации, особенно при пользовании мобильными устройствами.
3. Задача изобретения. Задачей изобретения является создание применяемого на сервере устройства, обеспечивающего быстрый поиск ключа в ключевом массиве за счет минимизации числа шагов перехода к искомому ключу.
Для решения поставленной задачи применяемое на сервере устройство отыскания информации по ключевым словам, введенным первым пользователем, и включающее модуль поиска ключа в алфавитном классификаторе, дополнительно снабжено модулем генерации префиксного дерева сочетаний (ПДС), модулем подсчета частот префиксов, модулем подсчета общего числа операций в алфавитном классификаторе (АК), модулем выбора результата оптимальных параметров "nmax" и "n" и модулем генерации оптимального АК.
Указанный модуль генерации ПДС проводит первоначальную обработку ключевого массива для получения ПДС и определяет соответствующие частоты префиксных сочетаний, с помощью которых определяет число ключей, входящих в класс, для данного ключевого префикса. Модуль подсчета частот префиксов определяет количество терминальных узлов в каждом узле префиксного дерева сочетаний. После этого модуль подсчета общего числа операций в АК производит расчет общего числа операций [Sоп(nmax,n)] в АК для различных значений числа ключей в классе и группе по ПДС. Следующий модуль выбирает оптимальный АК по минимальному значению общего числа операций " nmax", "n". И последний модуль выводит оптимальный АК, уже используемый для отыскания искомого ключа.
Предложенное устройство, создав оптимальный АК, обеспечивает быстрый поиск ключа в ключевом массиве. Этот оптимальный АК позволяет за минимальное число шагов перейти к искомому ключу. В отличие от поля ввода созданный оптимальный АК не требует ввода символов, а состоит из системы иерархических меню или подсказок. При этом верхний уровень классификатора является точкой входа в оптимальный АК. Такое устройство оптимального АК позволяет успешно использовать его на устройствах без клавиатуры, например на мобильных устройствах, а также на обычных компьютерах. Современные обозреватели Интернета реализуют гипертекстовую технологию, которая позволяет успешно применять данный оптимальный АК для массивов данных, которые составляют часть БД и нередко содержат большое количество текстовых ключей, что и указывает на необходимость построения интерфейсов в виде алфавитных классификаторов для быстрого доступа к ключам массива.
Далее система поясняется более подробно со ссылкой на графические материалы, на которых
- на Фиг. 1 показана блок-схема предлагаемого устройства создания оптимального АК,
- на Фиг. 2 приведен фрагмент ключевого массива по полю ФИО: первые 20 ключей на префикс "Г",
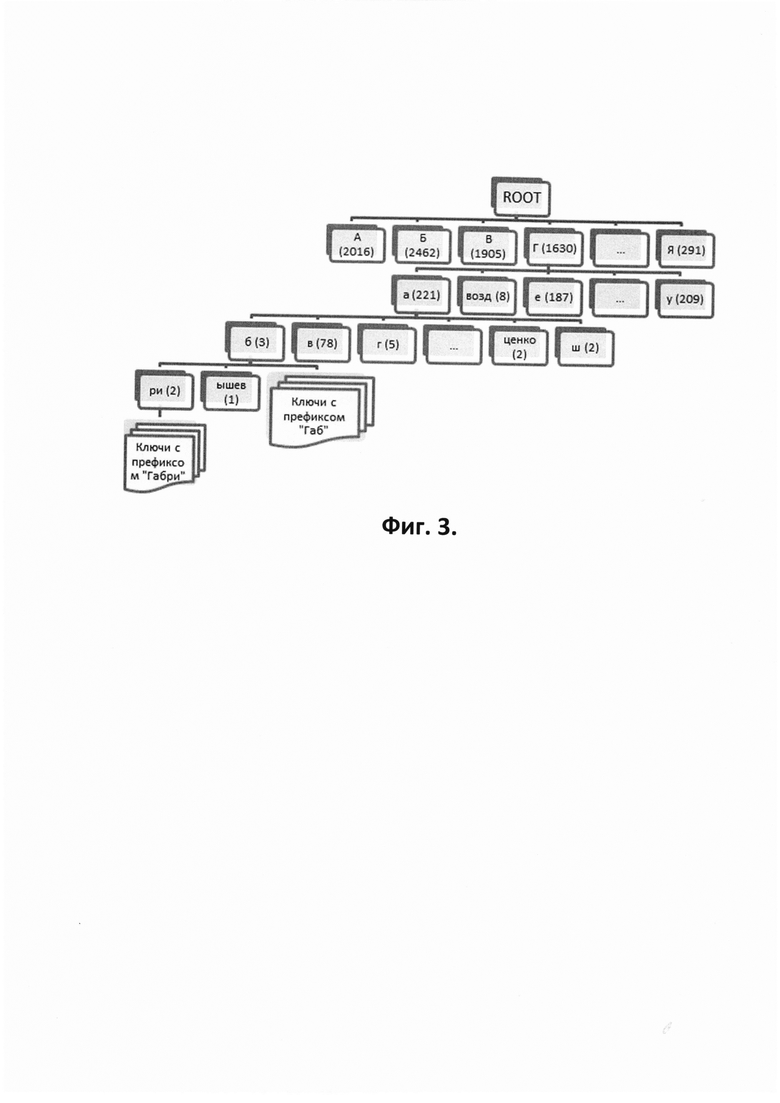
- на Фиг. 3 схематически представлена примерная структура сжатого ПДС (PATRICIA tree), используемого в устройстве построения алфавитного классификатора фигуры 1,
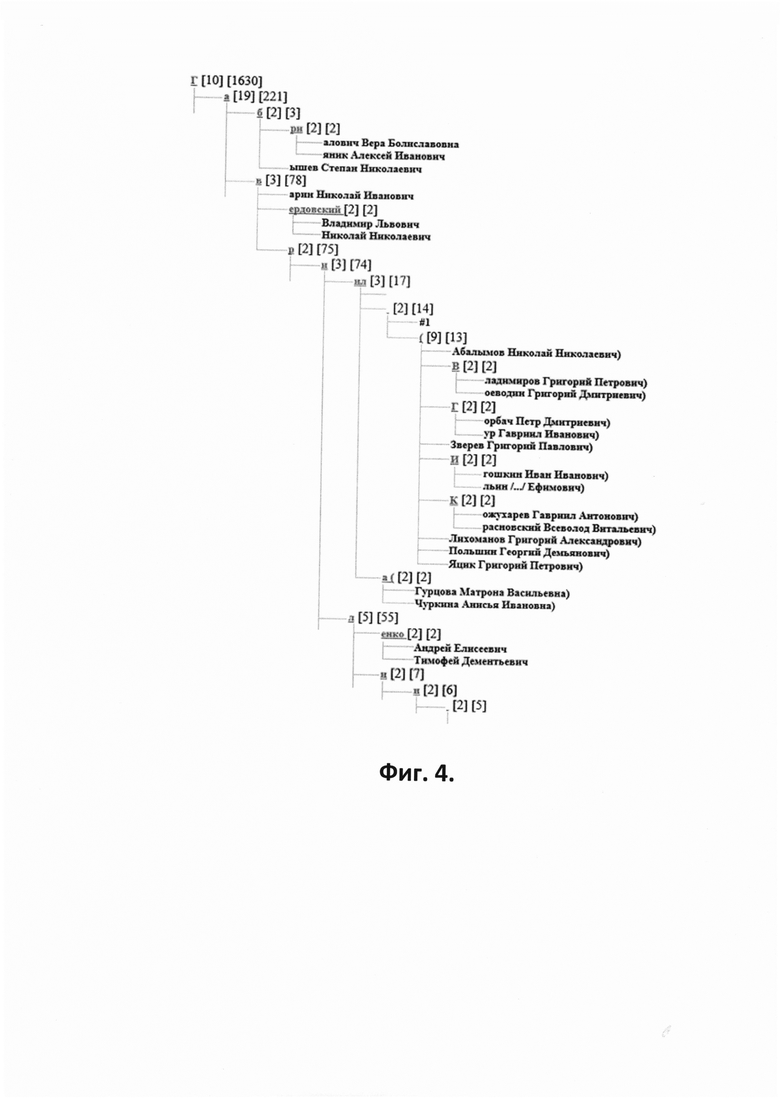
- на Фиг. 4 приведен фрагмент ПДС для ключевого массива по полю ФИО,
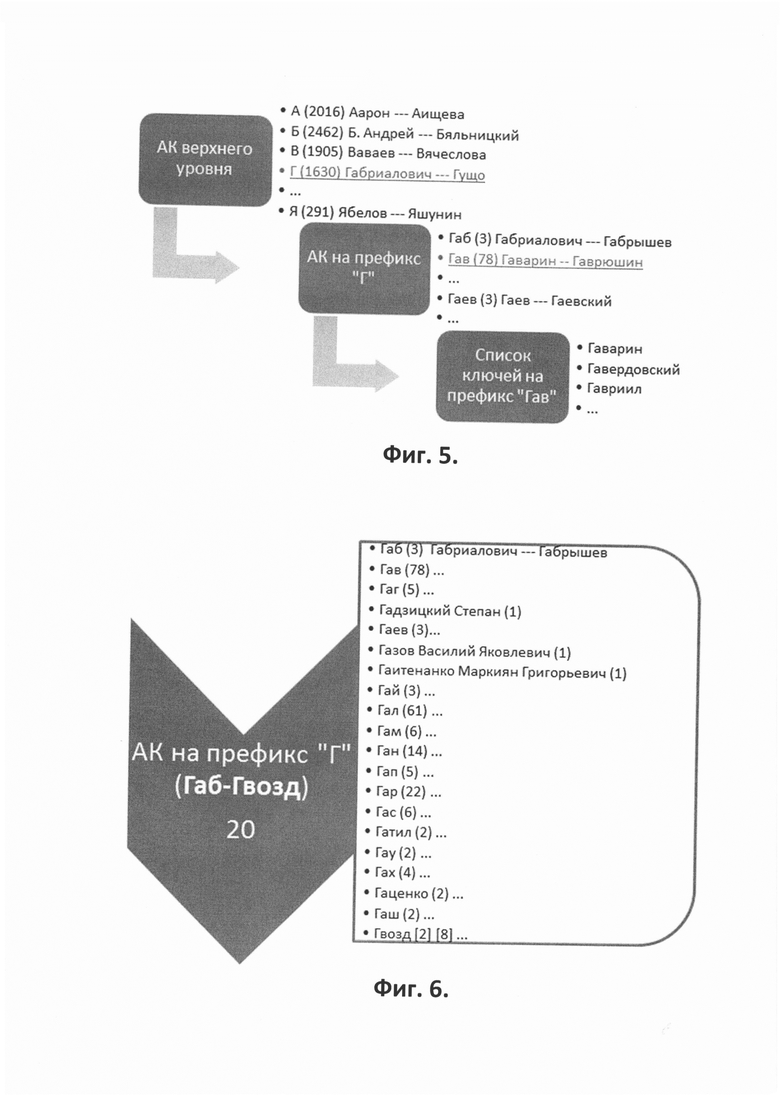
- на Фиг. 5 показан пример оптимального многоуровневого алфавитного классификатора в виде системы иерархических меню при 176 ключах в классе и 20 ключах в группе, полученного в результате применения системы построения фигуры 1,
- на Фиг. 6 показан АК на префикс "Г": первая группа из 20 префиксов (Габ-Гвозд),
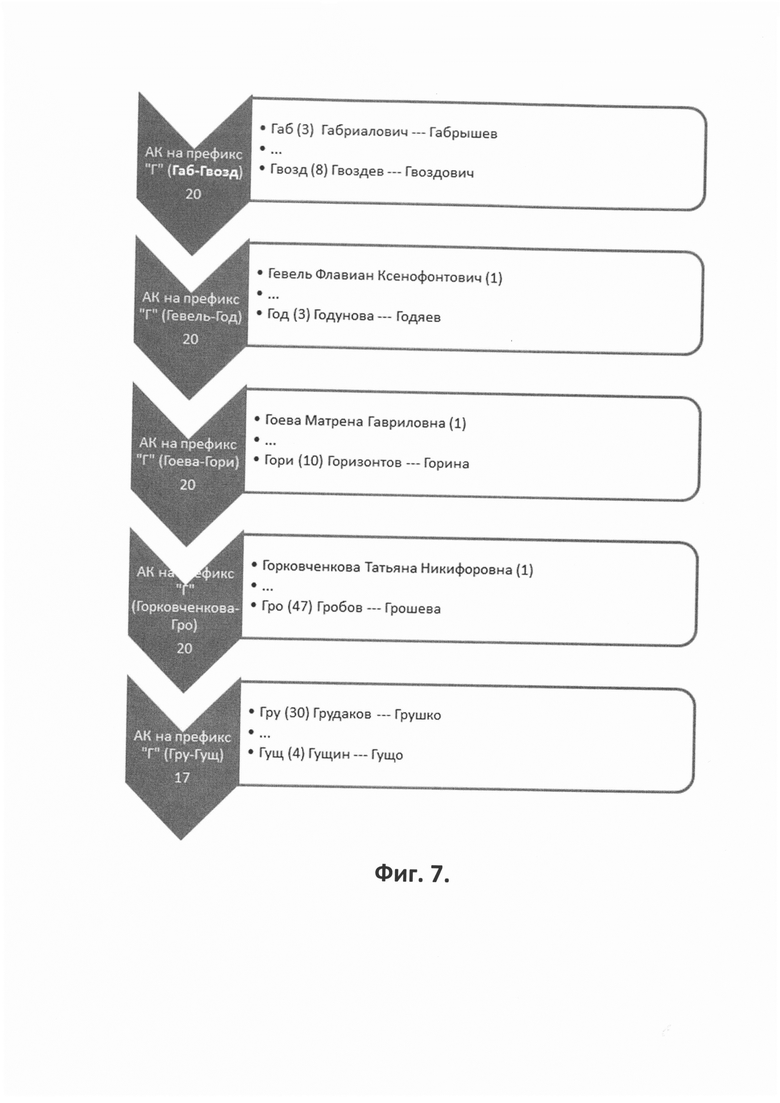
- на Фиг. 7 показан АК на префикс "Г, состоящий из 5 групп: 4 группы по 20 префиксов и последняя группа из 17 префиксов,
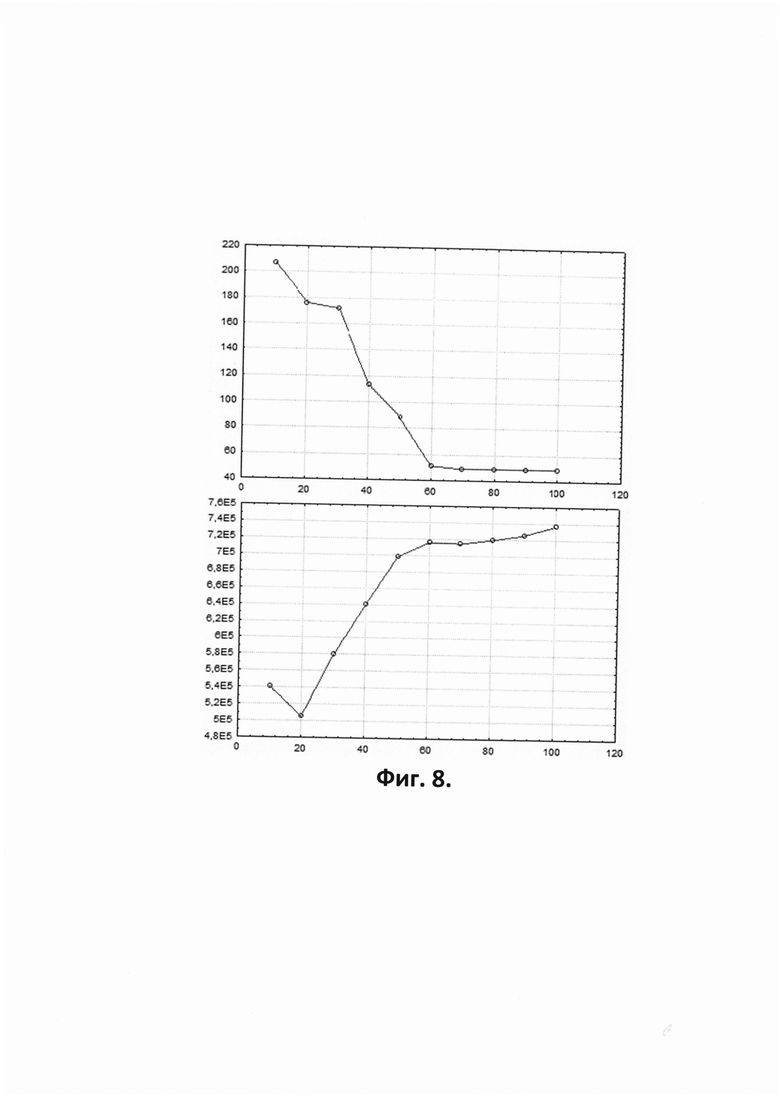
- на Фиг. 8 приведены графики nmax*(n) и S0n(nmax*,n),
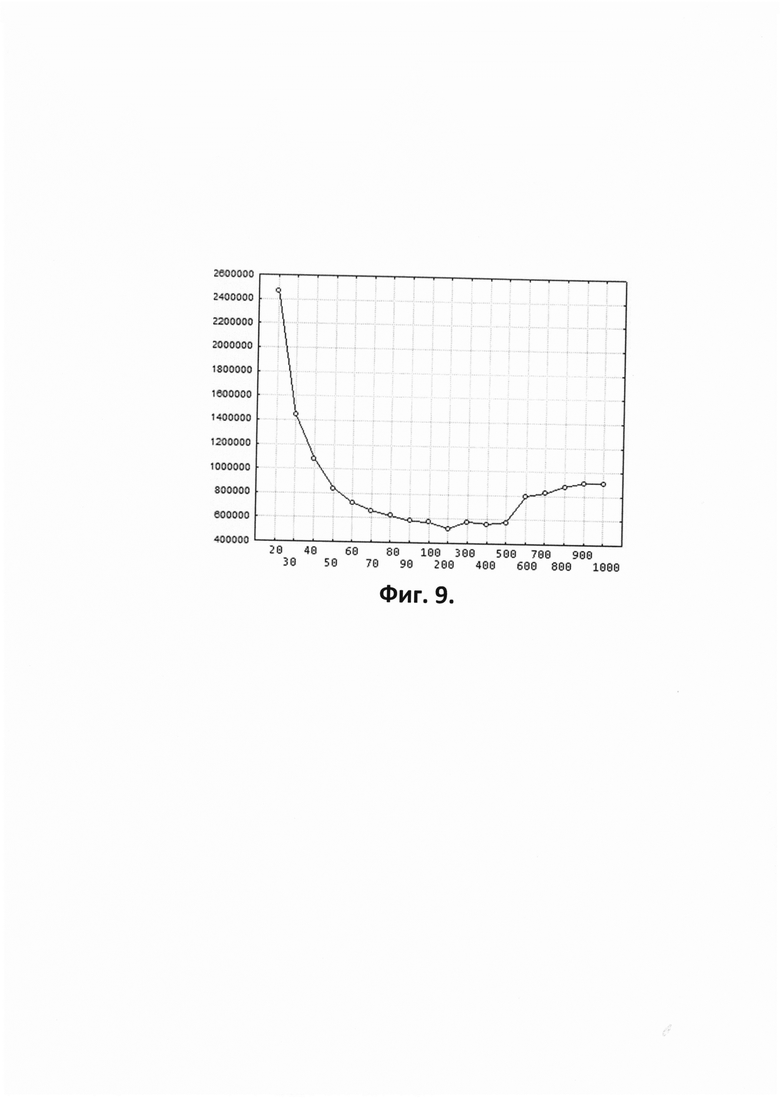
- на Фиг. 9 приведена схематичная форма графика Sоп(nmax,20).
Подробное описание работы устройства
На 1 этапе (см.Фиг. 1) происходит построение сжатого префиксного дерева сочетаний (ПДС) или PATRICIA tree по ключевому массиву (см.Фиг. 2) в виде последовательности следующих шагов:
Шаг 1. Переход к первому ключу массива.
Шаг 2. Модуль фиксирует первую букву текущего ключа массива. Если среди узлов ПДС первого уровня отсутствует узел с этой буквой, то узел с этой буквой он добавляет в дерево.
Шаг 3. Модуль выбирает следующую букву текущего ключа массива. Если среди узлов ПДС соответствующего уровня отсутствует узел с этой буквой, то модуль добавляет в дерево узел с этой буквой.
Шаг 4. Если есть следующая буква, то происходит переход к шагу 3.
Шаг 5. Переход к следующему ключу массива. Если он существует, то происходит переход к шагу 2.
Полученное в результате построения дерево или древовидная структура tree будет иметь во всех узлах по одной букве ключа массива. Такое дерево посредством объединения последовательно идущих узлов без ветвления в один узел дает дерево PATRICIA (ПДС), в котором узлы могут содержать более одной буквы (см.Фиг. 3, 4).
На 2 этапе происходит левый обход дерева ПДС, в результате которого в дерево в каждый узел (кроме терминальных) добавляется счетчик терминальных узлов (см.Фиг. 3, 4). На Фиг. 4 для каждого нетерминального узла показаны счетчик узлов непосредственно подчиненных данному и счетчик терминальных узлов.
На 3 этапе для каждого значения максимального числа ключей в классе nmax и числа вершин в группе n происходит обход дерева ПДС для расчета общего числа операций в АК - Soп с данными параметрами. Любой префикс в ПДС задает класс ключей, начинающихся с этого буквенного префикса.
Каждый класс ключей, содержащий не более nmax ключей, разбивают на группы по n ключей.
На 4 этапе среди всех полученных значений общего числа операций в АК Soп выбирают минимальное и по нему определяют значение параметров оптимального АК (см.Фиг. 5) - максимальное число ключей в классе nmax* и число ключей в группе n*.
В результате на основе исходного массива (Фиг. 2) создается префиксное дерево сочетаний (Фиг. 3, 4), посредством которого происходит построение оптимального АК (Фиг. 5).
Для подсчета общего числа операций на 3 этапе используют следующий функционал:
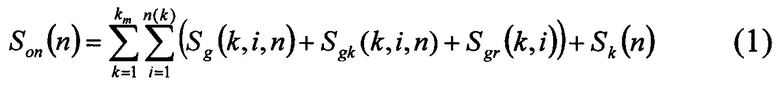
где n означает число ключей в группе. Число ключей в классе nmax неявно влияет на значения всех слагаемых, т.к. от nmax будет зависеть число групп на любой ключ или префикс. Первая сумма означает суммирование по всем длинам ключей от 1 до km, вторая сумма означает суммирование по всем ключам длины k от 1 до n(k), где n(k) - общее число ключей длины k.
Первое слагаемое Sg(k,i,n) - суммарное число операций прохода по группам вершин для класса с ключом длины k и номером i.
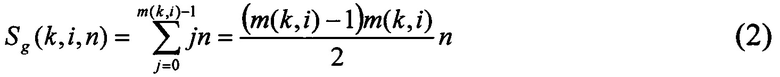
где m(k,i) - число групп по n ключей для префикса длиной k с номером i: 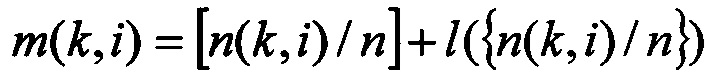 , где квадратные и фигурные скобки - это целая и дробная часть числа соответственно, l(0)=0, l(х)=1 при х>0; n(k,i) - число ключей под i-м префиксом классификатора длиной k
, где квадратные и фигурные скобки - это целая и дробная часть числа соответственно, l(0)=0, l(х)=1 при х>0; n(k,i) - число ключей под i-м префиксом классификатора длиной k
Второе слагаемое Sgk(k,i,n) - суммарное число операций прохода по вершинам групп для класса с ключом длины k и номером i, кроме последней группы, в которой может быть число вершин, меньшее n.
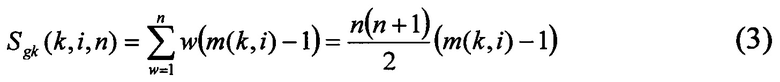
Третье слагаемые Sgr(k,i) - суммарное число операций прохода по вершинам последней группы числом r(k,i)≤n для класса с ключом длины k и номером i.

Эти три слагаемых стоят под двойной суммой. Последнее слагаемое Sk(n) - общее число операций для алфавитных ключей классификатора состоит из трех слагаемых (см. формулу 5), подобных (2), (3) и (4). Однако весь уровень алфавитных ключей представляет собой один класс, разбитый на группы по n алфавитных ключей. Таким образом, у величин mа числа групп по n алфавитных ключей и rа числа алфавитных ключей, входящих в последнюю группу, соответствующих величинам m(k,i) и r(k,i), будут отсутствовать индексы k и i.
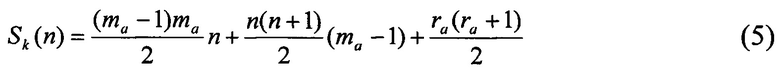
Другой, более общий вариант подсчета общего числа операций включает в себя подсчет числа операций по всем уровням многоуровневого АК. Вариант, представленный формулой (1), предполагает наличие одного уровня АК, который состоит из алфавитных ключей, ссылающихся на соответствующие классы вершин ключевого массива. В многоуровневом АК каждый более высокий уровень классификатора будет являться одноуровневым классификатором для подчиненного уровня. В этом случае в формулу (1) добавляется третья сумма по всем уровням АК, и значения всех слагаемых под суммами будут зависеть еще от номера уровня h в АК.
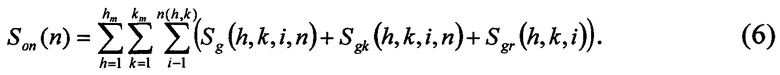
Формула (6) включает в себя слагаемое (5) при суммировании по уровням АК от 1 до hm. Верхний уровень алфавитного классификатора будет состоять из одного класса. Число уровней классификатора 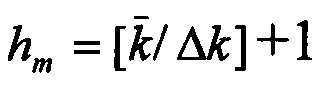 . Здесь
. Здесь 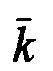 обозначает среднюю длину ключа на последнем уровне классификатора, а Δk - среднее число букв, которое добавляется к ключу на каждом уровне классификатора. В величину hm включается также ключевой уровень массива, поэтому добавляется 1. Величина n(h,k) общего числа ключей длины k будет зависеть от номера уровня h. Это же относится к величинам числу групп ключей m(h,k,i) и числу ключей в последней группе r(h,k,i). С учетом указанных особенностей слагаемые в формуле (6) Sg, Sgk, Sgr рассчитываются по формулам (2), (3) и (4) соответственно.
обозначает среднюю длину ключа на последнем уровне классификатора, а Δk - среднее число букв, которое добавляется к ключу на каждом уровне классификатора. В величину hm включается также ключевой уровень массива, поэтому добавляется 1. Величина n(h,k) общего числа ключей длины k будет зависеть от номера уровня h. Это же относится к величинам числу групп ключей m(h,k,i) и числу ключей в последней группе r(h,k,i). С учетом указанных особенностей слагаемые в формуле (6) Sg, Sgk, Sgr рассчитываются по формулам (2), (3) и (4) соответственно.
Для понимания работы устройства при построении оптимального АК ниже приведен пример в виде пояснений к Фиг. 2-9. На Фиг. 2 показан фрагмент ключевого массива по полю ФИО34 657 (первые 20 ключей на префикс "Г" с гипертекстовыми ссылками на биографические справки). В результате работы первых двух этапов алгоритма на Фиг. 1 на основе исходного ключевого массива создается ПДС или дерево PATRICIA, размеченное частотными счетчиками числа ключей в классе, фрагменты которого показаны на Фиг. З (частоты - числа в круглых скобках) и на Фиг. 4. На Фиг. 4 показаны счетчик префиксов, подчиненных данному, и счетчик ключей массива, начинающихся с данного префикса. В результате работы этапов 3 и 4 на Фиг. 1 происходит выбор параметров для оптимального АК по минимальному значению числа операций Sоп - максимального числа ключей в классе nmax* и числа ключей в группе n*. В данном случае получились следующие значения: Sоп*=505 080 при nmax*=176 и n=20.
Фрагмент оптимального АК показан на Фиг. 5. Более детальные примеры фрагментов оптимального АК показаны на Фиг. 6 и 7. Вначале на верхнем уровне АК выбирается префикс искомого ключа (Фиг. 5). В данном случае - это однобуквенный префикс "Г". Затем на втором уровне АК модуль выбирает префикс "Гав" и происходит переход на первую группу ключей, начинающихся с префикса "Гав", представленных, например, в виде списка (как показано на Фиг. 2).
На Фиг. 6 приведен пример первой группы классификатора на префикс "Г", состоящий из 20 префиксов различной длины.
На Фиг. 7 условно показаны все 5 групп на префикс "Г". Во всех группах, кроме последней, по 20 ключей, в последней - 17 ключей. Для данного примера показаны графики nmax*(n) и Sоп(nmax*,n) на Фиг. 8 и график Sоп(nmax,n*) на Фиг. 9. Здесь nmax*=176 и n*=20. Зависимости на графиках сглажены так, что минимум Sоп и соответствующие значения nmax* и n* несколько изменились. Зависимость показана на Фиг. 9 качественно (деления по оси абсцисс имеют разный шаг).
В результате применения системы на Фиг. 1 получается ПДС с частотами префиксов и оптимальные параметры АК - максимальное число ключей в классе nmax* и число ключей в группе n*. Оптимальный АК может быть задан посредством этих трех объектов: ПДС, nmax*, n*. Процесс получения оптимального АК из ПДС состоит в следующем. Посредством ПДС и величины nmax* выделяют классы ключей с префиксами, частоты которых не превосходят nmax* Пример такого уровня АК приведен на Фиг. 6. Это нижний уровень АК, надстроенный непосредственно над ключевым массивом. Далее процедура является итеративной. Получившийся очередной уровень АК модуль рассматривает также как исходный ключевой массив, т.е. этот уровень АК надстраивается более верхним уровнем АК с префиксами, имеющими меньшую длину. Процесс построения такой же как и в случае исходного ключевого массива. При этом все частоты в ПДС корректируются так, чтобы значения частот у префиксов на надстраиваемом уровне АК имели единичные значения (префиксы ниже этого уровня не рассматриваются). На верхнем уровне ПДС все префиксы, число которых не превосходит nmax*, составляют один класс. Это и является критерием окончания работы процедуры построения АК на основе ПДС с заданными параметрами. При выборе определенного префикса соответствующий класс будет состоять из групп по n префиксов или ключей. В последней группе класса число ключей может быть меньше, чем n.
В приведенном примере АК по полю ФИО34 657 число ключей в массиве таково (т.е. оно невелико), что получается два уровня в оптимальном АК, причем верхний уровень состоит из однобуквенных префиксов, т.е. букв алфавита. В этом случае достаточно применения функционала (1) для одноуровневого АК. Одноуровневый АК надстраивается посредством верхнего уровня из букв алфавита (при этом число префиксов в каждом однобуквенном классе не превосходит) nmax*.
Преимущества предложенной системы. Построенный предложенным устройством многоуровневый алфавитный классификатор (АК) обеспечивает быстрый поиск ключа в ключевом массиве. Он позволяет за минимальное число шагов перейти к искомому ключу. В отличие от поля ввода АК не требует ввода символов, а состоит из системы иерархических меню или подсказок. При этом верхний уровень классификатора является точкой входа в АК. Такое устройство АК позволяет успешно использовать его на устройствах без клавиатуры, например на мобильных устройствах, а также на обычных компьютерах. Современные обозреватели интернет реализуют гипертекстовую технологию, которая позволяет успешно применять АК для массивов данных, которые составляют часть БД и нередко содержат большое количество текстовых ключей, что и указывает на необходимость построения интерфейсов в виде алфавитных классификаторов для быстрого доступа к ключам массива.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ПОИСКА ИНФОРМАЦИИ | 1999 |
|
RU2149446C1 |
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ДАННЫХ | 2014 |
|
RU2679784C2 |
| УСТРОЙСТВО ПОИСКА ИНФОРМАЦИИ | 1997 |
|
RU2116670C1 |
| СПОСОБ ДЛЯ КОДИРОВАНИЯ КОЭФФИЦИЕНТА ПРЕОБРАЗОВАНИЯ НА ОСНОВЕ ВЫСОКОЧАСТОТНОГО ОБНУЛЕНИЯ И ОБОРУДОВАНИЕ ДЛЯ ЭТОГО | 2019 |
|
RU2789446C2 |
| СПОСОБ ДЛЯ КОДИРОВАНИЯ КОЭФФИЦИЕНТА ПРЕОБРАЗОВАНИЯ НА ОСНОВЕ ВЫСОКОЧАСТОТНОГО ОБНУЛЕНИЯ И ОБОРУДОВАНИЕ ДЛЯ ЭТОГО | 2023 |
|
RU2818967C1 |
| СПОСОБ ДЛЯ КОДИРОВАНИЯ КОЭФФИЦИЕНТА ПРЕОБРАЗОВАНИЯ НА ОСНОВЕ ВЫСОКОЧАСТОТНОГО ОБНУЛЕНИЯ И ОБОРУДОВАНИЕ ДЛЯ ЭТОГО | 2019 |
|
RU2776033C1 |
| СПОСОБ ДЛЯ КОДИРОВАНИЯ КОЭФФИЦИЕНТА ПРЕОБРАЗОВАНИЯ НА ОСНОВЕ ВЫСОКОЧАСТОТНОГО ОБНУЛЕНИЯ И ОБОРУДОВАНИЕ ДЛЯ ЭТОГО | 2023 |
|
RU2806796C1 |
| УСТРОЙСТВО И СПОСОБ ВЫПОЛНЕНИЯ ВЫСОКОСКОРОСТНОГО ПОИСКА МАРШРУТОВ ПРОТОКОЛА ИНТЕРНЕТ И УПРАВЛЕНИЯ ТАБЛИЦАМИ МАРШРУТИЗАЦИИ/ПЕРЕСЫЛКИ | 2001 |
|
RU2233473C2 |
| Классификатор логического вектора | 1989 |
|
SU1683003A1 |
| СПОСОБ УПЛОТНЕНИЯ СТРУКТУРЫ ДАННЫХ ПРЕФИКСНОГО ДЕРЕВА | 2013 |
|
RU2534368C2 |
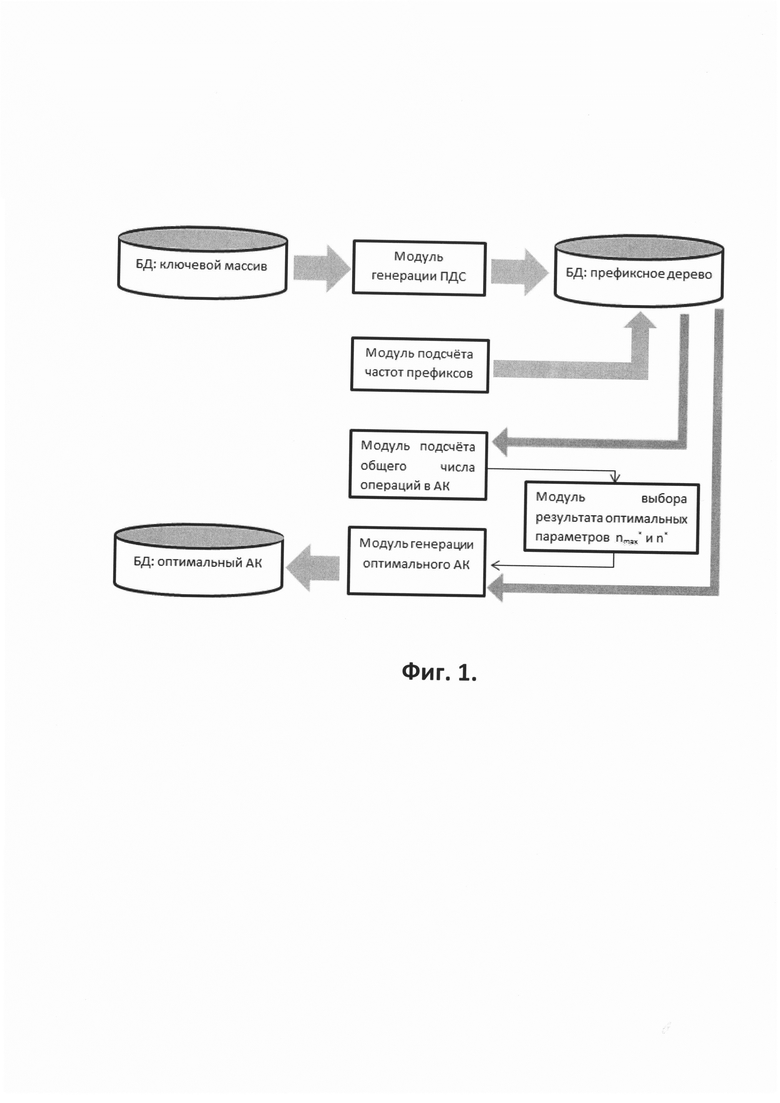

Изобретение относится к информационным системам обработки поискового запроса пользователей в Интернете. Технический результат заключается в обеспечении быстрого поиска ключа в ключевом массиве за счет минимизации числа шагов перехода к искомому ключу. Технический результат достигается за счет устройства отыскания информации по ключевым словам, применяемого на сервере и включающего модуль поиска ключа в алфавитном классификаторе, модуль генерации префиксного дерева сочетаний (ПДС), выполненный с возможностью проведения первоначальной обработки ключевого массива для получения ПДС и определения соответствующих частот префиксных сочетаний, с помощью которых определяет число ключей, входящих в класс, для данного ключевого префикса, модуль подсчета частот префиксов, модуль подсчета общего числа операций в алфавитном классификаторе (АК), модуль выбора результата оптимальных параметров "nmax" и "n" и модуль генерации оптимального АК, при этом вышеуказанный модуль генерации префиксного дерева сочетаний (ПДС) посредством базы данных, содержащей префиксное древо сочетаний (ПДС), связан с модулем подсчета общего числа операций в алфавитном классификаторе (АК), который, в свою очередь, соединен с указанным модулем выбора результата оптимальных параметров «nmax» и «n», причем последний соединен с модулем генераций оптимального АК. 9 ил.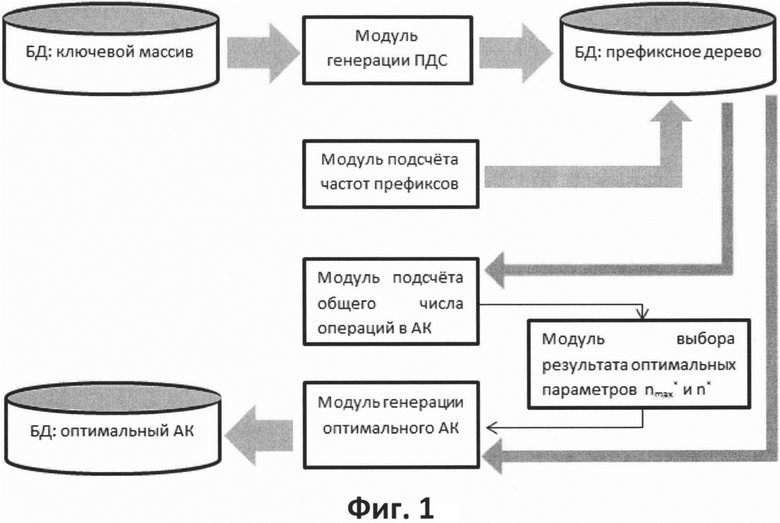
Устройство отыскания информации по ключевым словам, применяемое на сервере и включающее модуль поиска ключа в алфавитном классификаторе, отличающееся тем, что оно дополнительно содержит:
- модуль генерации префиксного дерева сочетаний (ПДС), выполненный с возможностью проведения первоначальной обработки ключевого массива для получения ПДС и определения соответствующих частот префиксных сочетаний, с помощью которых определяет число ключей, входящих в класс, для данного ключевого префикса,
- модуль подсчета частот префиксов,
- модуль подсчета общего числа операций в алфавитном классификаторе (АК),
- модуль выбора результата оптимальных параметров "nmax" и "n" и
- модуль генерации оптимального АК,
при этом вышеуказанный модуль генерации префиксного дерева сочетаний (ПДС) посредством базы данных, содержащей префиксное древо сочетаний (ПДС), связан с модулем подсчета общего числа операций в алфавитном классификаторе (АК), который, в свою очередь, соединен с указанным модулем выбора результата оптимальных параметров «nmax» и «n», причем последний соединен с модулем генераций оптимального АК.
| СПОСОБ ПОИСКА ИНФОРМАЦИОННЫХ РЕСУРСОВ С ИСПОЛЬЗОВАНИЕМ ПЕРЕАДРЕСАЦИЙ | 2011 |
|
RU2453916C1 |
| ОБЕСПЕЧЕНИЕ РУКОВОДСТВА ТЕМАТИЧЕСКИМ ПОИСКОМ | 2012 |
|
RU2628200C2 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
Авторы
Даты
2019-02-14—Публикация
2018-03-14—Подача