Изобретение относится к пассивным системам видения оптического, инфракрасного и миллиметрового диапазонов длин волн [1, 2], предназначенным для наблюдения за малоразмерными объектами. В системах оптического и инфракрасного диапазонов сигналы отражения и излучения от объектов проходят через оптические линзы, преобразуются в уровни амплитуды и отображаются в матрицах (кадрах) плоского изображения двух наблюдателей, взаимно удаленных в пространстве и образующих стереопару. В пассивной радиосистеме миллиметрового диапазона сигналы излучения от объектов принимается антеннами, сканирующими по пространству, проходят тракт первичной обработки и по результатам сканирования преобразуются в уровни амплитуды и отображаются в матрицах плоского изображения двух наблюдателей, также образующих стереопару.
Полученные в указанных системах изображения объектов в k-х матрицах (k=1, 2) сегментируются выделением однородных по амплитуде подобластей с помощью известных операций сегментации, например [3], и каждый сегмент представляется вектором параметров, включающим координаты центра сегмента, среднюю амплитуду и геометрические характеристики.
Для измерения дальности до объекта в системах с оптической линзой рассматривается пара сопряженных точек Vk=(xk, yk,1), k=1, 2 - центров сегментов, отображающих центр объекта в прямоугольных координатах двух матриц оптического изображения (единица замещает неизвестную третью координату). Для известных матриц внутренних параметров камер Ak, k=1, 2, зависящих от фокусных расстояний ƒk, устанавливается связь:
ZkVk=AkMk [1], где 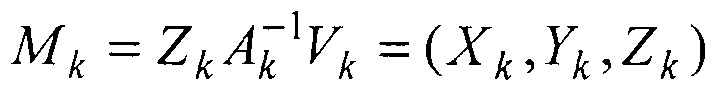 - центр объекта в прямоугольной системе k-го наблюдателя, совмещенной с центром оптической линзы.
- центр объекта в прямоугольной системе k-го наблюдателя, совмещенной с центром оптической линзы.
Для измерения дальности до объекта в радиосистемах со сканирующими антеннами рассматривается пара спряженных точек Vk=(ϕk, θk), k=1, 2 - центров сегментов, показывающих центр объекта в угловых координатах азимута и угла места двух матриц радиотеплового изображения. На основе измеренных координат ϕk, θk устанавливаются сопряженные орты ak, k=1, 2, векторов направления на центр объекта в прямоугольных координатах, совмещенных с центрами антенн: ak=(cosθk sinϕk, sin θk, cos θk cos ϕk). Использование ортов применимо также и для систем с оптическими линзами, в этом случае орты определятся как 
При известных наклонных дальностях r1 и r2 до объекта пространственные координаты объекта в системах координат наблюдателей находятся как Mk=rkak, k=1, 2. При известной взаимной ориентации наблюдателей - матрицы поворота осей Р и базового вектора b, соединяющего центры двух систем координат, для перехода из системы координат второго наблюдателя в систему первого устанавливается связь М1 и М2: М1=РМ2+b, r1a1=r2Pa2+b или с учетом вектора е ошибок сопряжения М1 и М2:
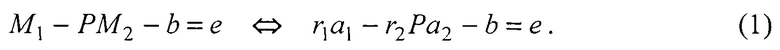
В реальности в пассивном режиме наблюдения дальности r1 и r2 до объекта неизвестны и требуется нахождение их оценок  Для определения оценок дальностей используется известный способ, основанный на методе [1] наименьших квадратов (МНК), а также способ геометрических построений с помощью теоремы синусов [4]. Рассмотрим в качестве прототипа способ [1, с. 174 - 176], который с учетом операций сегментации сводится к следующему.
Для определения оценок дальностей используется известный способ, основанный на методе [1] наименьших квадратов (МНК), а также способ геометрических построений с помощью теоремы синусов [4]. Рассмотрим в качестве прототипа способ [1, с. 174 - 176], который с учетом операций сегментации сводится к следующему.
1. Размещают в пространстве двух взаимно удаленных наблюдателей на базовом расстоянии, контролирующих объект при известной матрице Р поворота осей и базовом векторе b.
2. В двух матрицах оптического изображения выполняют операции сегментации изображений объекта.
3. Находят точки Vk(xk, yk, 1), k=1, 2, центра сегмента в координатах х, у плоских кадров изображения.
4. Определяют матрицы Ak, k=1, 2, внутренних параметров камер, зависящие от фокусных расстояний ƒk оптических линз, и устанавливают связь  где Mk - сопряженные точки, Zk - координаты центра объекта в системах наблюдателей, подлежащие оцениванию.
где Mk - сопряженные точки, Zk - координаты центра объекта в системах наблюдателей, подлежащие оцениванию.
5. Из условия минимума квадрата евклидовой нормы вектора ошибок сопряжения (1):
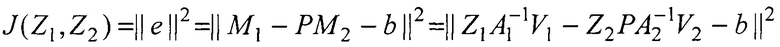 находят МНК-оценки
находят МНК-оценки  неизвестных координат Z1 и Z2.
неизвестных координат Z1 и Z2.
6. Вычисляют дальности как  k=1, 2.
k=1, 2.
Данный способ обладает следующими недостатками.
1. Способ рассчитан только на оптические системы, в том числе тепловые, с наличие оптических линз, позволяющих использовать фокусные расстояния ƒk в составе матриц Ak для нахождения оценок координат Zk, k=1, 2. Поэтому данный способ не применим для пассивных радиосистем с антеннами.
2. Способ-прототип не показывает операций нахождения сопряженных пар точек в матрицах наблюдателей и поэтому не применим для оценивания наклонных дальностей r1 и r2 при наблюдении за несколькими объектами.
Предлагаемое техническое решение направлено на устранение этих недостатков, а именно на определение дальностей r1 и r2 как в оптических, так и в радиосистемах при наличии нескольких объектов наблюдения.
Технический результат предлагаемого технического решения достигается применением способа определения дальностей до объектов в пассивных системах видения, который заключается в расположении двух наблюдателей, взаимно удаленных на базовое расстояние, выполнении операций сегментации изображений объектов в двух матрицах изображения наблюдателей и нахождении центров сегментов, отличающийся тем, что для найденных центров m сегментов определяют орты a1(i) векторов i-x направлений на центры объектов первого наблюдателя и орты a2(j) векторов j-x направлений на центры объектов второго наблюдателя, где 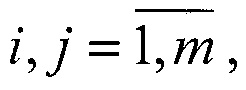 затем для всех m! вариантов соединения ортов а1 (j) и a2(j),
затем для всех m! вариантов соединения ортов а1 (j) и a2(j),  в m неповторяющихся сопряженных пар вычисляют оценки дальностей r1(i) и r2(ji),
в m неповторяющихся сопряженных пар вычисляют оценки дальностей r1(i) и r2(ji), 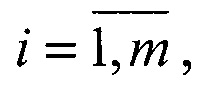 по критерию минимума суммы квадрата евклидовых норм векторов ei ошибок сопряжения ортов
по критерию минимума суммы квадрата евклидовых норм векторов ei ошибок сопряжения ортов  где Р - матрица поворота осей при пересчете координат орта a2(ji) в систему координат первого наблюдателя, b - базовый вектор, соединяющий центры систем координат наблюдателей, после чего выбирают вариант m пар соединения ортов a1 и a2(ji),
где Р - матрица поворота осей при пересчете координат орта a2(ji) в систему координат первого наблюдателя, b - базовый вектор, соединяющий центры систем координат наблюдателей, после чего выбирают вариант m пар соединения ортов a1 и a2(ji),  с наименьшим значениям показателя J и получают оценки дальностей r1(i) и r2(ji),
с наименьшим значениям показателя J и получают оценки дальностей r1(i) и r2(ji), 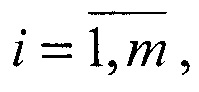 до m объектов, соответствующие данному показателю.
до m объектов, соответствующие данному показателю.
Алгоритмически способ осуществляют следующим образом.
1. Размещают в пространстве двух взаимно удаленных наблюдателей на базовом расстоянии, контролирующих несколько объектов при известной матрице Р поворота осей и базовом векторе b.
2. В двух матрицах изображения наблюдателей выполняют операции сегментации изображений объектов и находят координаты центров сегментов.
3. Для найденных центров m сегментов определяют орты а1 (i) векторов i-x направлений на центры объектов первого наблюдателя и орты а2 (j) векторов j-x направлений второго наблюдателя, где 
4. Для всех m! вариантов соединения ортов а1(i) и a2(ji) в m неповторяющихся сопряженных пар, где ji ∈ {1, 2, …, m}, находят оценки дальностей r1(i) и r2(ji) по критерию минимума квадрата евклидовой нормы вектора ei ошибок сопряжения ортов:

где Т - символ транспонирования вектора-столбца.
А именно, на этапе расчетов выполняют операции минимизации функции J(r1, r2) в (2) по r1 и r2 (символы i и ji для удобства опущены):
∂J/∂r1=2(r1a1-r2Pa2-b)Ta1=0Т, ∂J/∂r2=2(r1a1-r2Pa2-b)T(-Ра2)=0Т, или после транспонирования и группирования:

где учтено, что в силу ортогональности PTP=I, I - единичная матрица.
После записи (3) в матричной форме с учетом  имеем:
имеем:
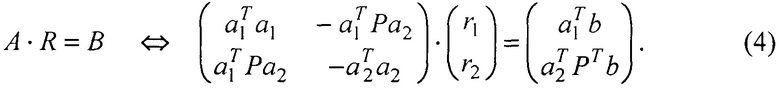
После обращения матрицы А в (4) вычисляют оценки дальностей:

5. Из m! вариантов соединения ортов в m неповторяющихся пар a1(i) и a2(ji),  ji ∈ {1, 2, …, m}, выбирают вариант с наименьшим значением показателя правильности сопряжения
ji ∈ {1, 2, …, m}, выбирают вариант с наименьшим значением показателя правильности сопряжения  При этом получают оценки (5) дальностей
При этом получают оценки (5) дальностей 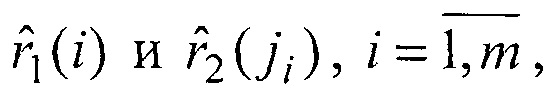 соответствующие показателю J.
соответствующие показателю J.
6. На основе оценок  вычисляют оценки пространственных координат m объектов в системах координат двух наблюдателей:
вычисляют оценки пространственных координат m объектов в системах координат двух наблюдателей:
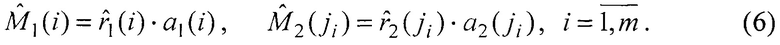
Замечание. Перебор m! вариантов из m пар можно сократить путем проверки компланарности - близости к нулю (с учетом ошибок) смешанного произведения трех векторов: а1(i), а2(ji)) и b.
Результаты моделирования. Моделировались два наблюдателя, разнесенные по координате X на 30 м, по координатам Y и 2 - на 2 и 3 м, наблюдались объекты, удаленные на 100 - 110 м. Координаты наблюдателей на множестве реализаций эксперимента менялись в пределах нескольких метров. Взаимная ориентация наблюдателей - матрица поворота осей Р и базовый вектор b были известны. При этом для пар сопряженных ортов направлений на объекты определялись дальности и пространственные координаты объектов по формулам (5) и (6). В таблице показана зависимость среднего расстояния dср между найденными и моделируемыми точками (центрами объектов) от среднеквадратической ошибки ах измерения координат ортов.

Предложенный способ определения дальностей до объектов может найти применение в существующих оптических и радиотехнических системах пассивного видения при наблюдении за несколькими объектами.
Литература
1. Цифровая обработка изображений в информационных системах: учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
2. Пассивная радиолокация: методы обнаружения объектов / Под ред. Р.П. Быстрова и А.В. Соколова. М.: Радиотехника, 2008. 320 с.
3. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB. М: Техносфера, 2006. 616 с.
4. Патент RU 2368918 С1. Способ формирования трехмерного изображения поверхности на базе бортового радиотеплолокатора / В.К. Клочко. МПК: G01S 13/89. Приоритет 07.04.2008. Опубл.: 27.09. 2009. Бюл. №27.
Изобретение относится к пассивным системам видения оптического, инфракрасного и миллиметрового диапазонов длин волн, предназначенным для наблюдения за малоразмерными объектами. Достигаемый технический результат - определение дальностей как в оптических, так и в радиосистемах при наличии нескольких объектов наблюдения. Указанный результат достигается за счет того, что способ определения дальностей в пассивных системах видения заключается в определении ортов векторов направлений на центры объектов в матрицах изображения двух взаимно удаленных наблюдателей и выборе неповторяющихся пар ортов, поставленных в соответствие друг другу, по критерию минимума квадрата евклидовой нормы вектора ошибок сопряжения ортов с одновременным вычислением оценок дальностей до объектов. На основе полученных оценок дальностей определяются пространственные координаты объектов. 1 табл.
Способ определения дальностей до объектов в пассивных системах видения, заключающийся в расположении двух наблюдателей, взаимно удаленных на базовое расстояние, выполнении операций сегментации изображений объектов в двух матрицах изображения наблюдателей и нахождении центров сегментов, отличающийся тем, что для найденных центров  сегментов определяют орты a1(i) векторов i-х направлений на центры объектов первого наблюдателя и орты a2(j) векторов j-x направлений на центры объектов второго наблюдателя, где i,
сегментов определяют орты a1(i) векторов i-х направлений на центры объектов первого наблюдателя и орты a2(j) векторов j-x направлений на центры объектов второго наблюдателя, где i,  затем для всех
затем для всех  1 вариантов соединения ортов а1(i) и а2(ji),
1 вариантов соединения ортов а1(i) и а2(ji),  в
в  неповторяющихся сопряженных пар вычисляют оценки дальностей r1(i) и r2(ji),
неповторяющихся сопряженных пар вычисляют оценки дальностей r1(i) и r2(ji),  по критерию минимума суммы квадрата евклидовых норм векторов еi ошибок сопряжения ортов
по критерию минимума суммы квадрата евклидовых норм векторов еi ошибок сопряжения ортов  где Р - матрица поворота осей при пересчете координат орта a2(ji) в систему координат первого наблюдателя, b - базовый вектор, соединяющий центры систем координат наблюдателей, после чего выбирают вариант
где Р - матрица поворота осей при пересчете координат орта a2(ji) в систему координат первого наблюдателя, b - базовый вектор, соединяющий центры систем координат наблюдателей, после чего выбирают вариант  пар соединения ортов a1(i) и а2(ji),
пар соединения ортов a1(i) и а2(ji),  с наименьшим значениям показателя J и получают оценки дальностей r1(i) и r2(ji),
с наименьшим значениям показателя J и получают оценки дальностей r1(i) и r2(ji),  до
до  объектов, соответствующие данному показателю.
объектов, соответствующие данному показателю.
| ГРУЗМАН И.С | |||
| и др | |||
| Цифровая обработка изображений в информационных системах: учебное пособие | |||
| Новосибирск, изд | |||
| НГТУ, 2002, с.174-176 | |||
| СПОСОБ НАБЛЮДЕНИЯ ЗА ОБЪЕКТАМИ НА ПОВЕРХНОСТИ БОРТОВОЙ РАДИОТЕПЛОЛОКАЦИОННОЙ СТАНЦИЕЙ, СОВМЕЩЕННОЙ С РАДИОЛОКАЦИОННОЙ СТАНЦИЕЙ | 2008 |
|
RU2379707C1 |
| Сборная железобетонная крепь для горных выработок | 1957 |
|
SU112446A1 |
| US 4179697 A, 18.12.1979 | |||
| US 6489922 B1, 03.12.2002 | |||
| WO 2016081271 A1, 26.05.2016 | |||
| Устройство для двухкординатного программного управления | 1974 |
|
SU549788A1 |
Авторы
Даты
2019-03-07—Публикация
2018-04-02—Подача