Изобретение относится к пассивным системам радиовидения [1], работающим по принципу стереопары. Эффект стереопары [2] позволяет определять дальности до объектов наблюдения без применения активных средств измерения при наличии двух взаимно удаленных на базовое расстояние наблюдателей. Для расчета дальностей требуется знание взаимной ориентации двух систем координат - матрицы Р поворота осей координат и вектора параллельного переноса t (базового вектора) [2]. При этом базовый вектор t, как правило, известен, а углы α, β, γ, включенные с состав матрицы Р, требуется найти. Для взаимной ориентации двух систем координат необходимо иметь n пар (n≥1) сопряженных векторов направлений на объекты, формируемых в системах наблюдения за объектами.
Рассмотрим в качестве прототипа способ [2] нахождения углов α, β, γ, который заключается в следующем.
1. Устанавливается стереопара из двух взаимно удаленных на базовое расстояние |t| наблюдателей при известном базовом векторе t.
2. В системах координат наблюдателей формируются n пар сопряженных ортов а1(i) и а2(i) векторов направлений на i-e объекты,  где
где
n - количество наблюдаемых объектов, и назначается матрица Р поворота осей координат с углами поворота α, β, γ в ее составе.
3. Для n пар сопряженных ортов а1(i) и 
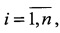 представленных в системе координат первого наблюдателя с помощью матрицы Р, вычисляется показатель J правильности сопряжения в виде суммы модулей смешанных произведений
представленных в системе координат первого наблюдателя с помощью матрицы Р, вычисляется показатель J правильности сопряжения в виде суммы модулей смешанных произведений 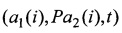 трех векторов a1(i),
трех векторов a1(i),  и t:
и t:
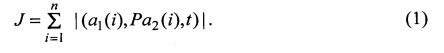
При этом вычисление (a1(i), Pa2(i), t) осуществляется с помощью определителя, строками которого являются координаты данных векторов.
4. Численным методом подбора находятся углы α, β, γ, при которых показатель (1) принимает наименьшее значение, близкое к нулю.
Данный способ обладает следующим недостатком. Близкое к нулю значение показателя (1) является признаком компланарности трех векторов a1(i), 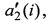 t и представляет необходимое условие сопряжения векторов a1(i) и
t и представляет необходимое условие сопряжения векторов a1(i) и 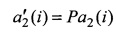 по принадлежности i-м объектам
по принадлежности i-м объектам 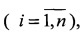 но не достаточное условие.
но не достаточное условие.
Предлагаемое техническое решение направлено на устранение этого недостатка, а именно на введение дополнительных операций проверки достаточности сопряжения i-x пар векторов a1(i) и 
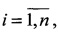 одновременно с определением дальностей до объектов.
одновременно с определением дальностей до объектов.
Технический результат предлагаемого технического решения достигается применением способа взаимной ориентации систем координат и определения дальностей до объектов в пассивной системе радиовидения, который заключается в установлении стереопары из двух взаимно удаленных на базовое расстояние |t| наблюдателей при известном базовом векторе t, формировании в системах координат наблюдателей n пар сопряженных ортов а1(i) и а2(i)
векторов направлений на i-e объекты, 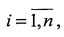 где n - количество наблюдаемых объектов, нахождении матрицы Р поворота осей координат на углы α, β, γ численным методом подбора по критерию минимума показателя
где n - количество наблюдаемых объектов, нахождении матрицы Р поворота осей координат на углы α, β, γ численным методом подбора по критерию минимума показателя  где
где 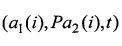 - смешанное произведение трех векторов, отличающийся тем, что с помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и
- смешанное произведение трех векторов, отличающийся тем, что с помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и 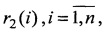 до i-x объектов по формуле (Т - символ транспонирования):
до i-x объектов по формуле (Т - символ транспонирования):
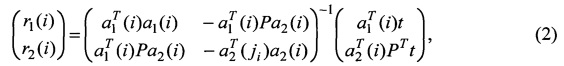
которые обеспечивают минимум показателя

где 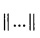 - норма вектора, после чего показатель I сравнивается с малым числом ε>0, и если I≤ε, то матрица Р принимается в качестве матрицы поворота, а на основе найденных дальностей вычисляются пространственные координаты объектов М1(i)=r1(i)a1(i) и M2(i)=r2(i)a2(i),
- норма вектора, после чего показатель I сравнивается с малым числом ε>0, и если I≤ε, то матрица Р принимается в качестве матрицы поворота, а на основе найденных дальностей вычисляются пространственные координаты объектов М1(i)=r1(i)a1(i) и M2(i)=r2(i)a2(i), 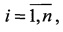 в системах координат наблюдателей.
в системах координат наблюдателей.
Алгоритмически способ заключается в следующем.
1. Устанавливается стереопара из двух взаимно удаленных на базовое расстояние ⏐t⏐ наблюдателей при известном базовом векторе t.
2. В системах координат наблюдателей формируются n пар сопряженных ортов a1(i) и a2(i) векторов направлений на i-e объекты,  где
где
n - количество наблюдаемых объектов, и назначается матрица Р поворота осей координат заданием в ее составе углов поворота α, β, γ.
3. Для n пар сопряженных ортов a1(i) и 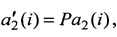
 представленных в системе координат первого наблюдателя, вычисляется показатель (1) правильности сопряжения векторов J в виде суммы модулей смешанных произведений (a1(i),Pa2(i),t) троек векторов a1(i),
представленных в системе координат первого наблюдателя, вычисляется показатель (1) правильности сопряжения векторов J в виде суммы модулей смешанных произведений (a1(i),Pa2(i),t) троек векторов a1(i), 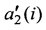 и t.
и t.
4. Численным методом подбора находятся углы α, β, γ в составе матрицы Р по критерию минимума показателя (1).
5. С помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и r2(i),  до i-х объектов по формуле (2), для которых показатель (3) принимает наименьшее значение.
до i-х объектов по формуле (2), для которых показатель (3) принимает наименьшее значение.
6. Наименьшее значение показателя I сравнивается с заданным порогом ε. Если I<ε, то матрица Р принимается в качестве матрицы поворота, а на основе найденных оценок дальностей вычисляются пространственные координаты центров объектов М1(i)=r1(i)a1(i) и M2(i)=r2(i)a2(i), 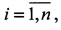 в системах координат наблюдателей.
в системах координат наблюдателей.
Пояснительная часть Показатель (1) представляет необходимое условие сопряжения векторов a1(i) и a2(i),  То есть, если векторы a1(i) и a2(i),
То есть, если векторы a1(i) и a2(i), 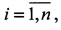 образуют n сопряженных пар, то отсюда следует, что тройки векторов a1(i), a2(i), t,
образуют n сопряженных пар, то отсюда следует, что тройки векторов a1(i), a2(i), t, 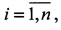 компланарны и их смешанные произведения равны нулю с точностью до ошибок измерения координат векторов. Соответственно показатель (1) не превышает малого числа ε>0: J≤ε. Как следствие, если J>ε, то векторы не образуют сопряженные пары.
компланарны и их смешанные произведения равны нулю с точностью до ошибок измерения координат векторов. Соответственно показатель (1) не превышает малого числа ε>0: J≤ε. Как следствие, если J>ε, то векторы не образуют сопряженные пары.
Однако условие компланарности не является достаточным для сопряжения при n>1, так как возможны случаи, когда для компланарных троек а1(i), а2(i), t векторы а1(i) и а2(i) не направлены на один и тот же объект. Поэтому дополнительно вводится достаточное условие сопряжения в виде показателя (3). Для сопряженных пар векторов r1(i)a1(i) и r2(i)Pa2(i), 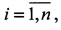 рассматриваемых в системе координат первого наблюдателя, тройки векторов r1(i)a1(i), r2(i)Pa2(i) и t замыкаются по правилу треугольника (с точностью до вектора ошибок), что дает значение показателя (3), близкое к нулю. Поэтому в случае выполнения неравенства I≤ε, где ε - малое положительное число, окончательно принимается решение о правильности сопряжения пар векторов и найденных оценок дальностей. Оценки дальностей (2) находятся по критерию минимума показателя (3) методом наименьших квадратов.
рассматриваемых в системе координат первого наблюдателя, тройки векторов r1(i)a1(i), r2(i)Pa2(i) и t замыкаются по правилу треугольника (с точностью до вектора ошибок), что дает значение показателя (3), близкое к нулю. Поэтому в случае выполнения неравенства I≤ε, где ε - малое положительное число, окончательно принимается решение о правильности сопряжения пар векторов и найденных оценок дальностей. Оценки дальностей (2) находятся по критерию минимума показателя (3) методом наименьших квадратов.
Результаты моделирования Разрабатывалась компьютерная программа моделирования работы алгоритма, основанного на предложенном способе. При наблюдении n объектов задавались углы взаимной ориентация систем координат наблюдателей. Поиск данных углов в составе матрицы Р осуществлялся численным методом Гаусса-Зейделя пошаговой минимизацией показателя (1). Начальные значения углов при поиске задавались случайным образом в окрестности заданных углов. С помощью найденной матрицы Р вычислялись дальности до объектов и пространственные координаты их центров. На множестве реализаций случайных величин определялись следующие характеристики: среднее расстояние dcp между моделируемыми и найденными на основе оценок дальностей центрами объектов; среднее значение Icp показателя (3) достаточного условия сопряжения. В таблице представлены dcp и Iср в зависимости от числа объектов n. Среднее значение Jср показателя (1) необходимого условия сопряжения получалось близким к нулю.
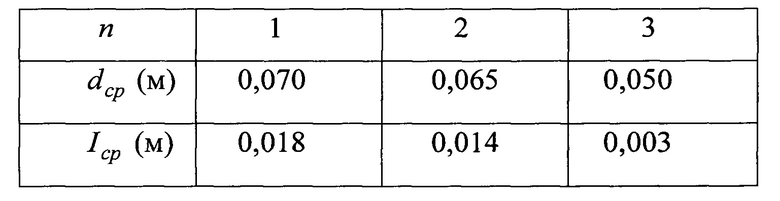
По результатам моделирования (таблица) можно отметить уменьшение средней ошибки dcp определения центров объектов и соответственно уменьшение показателя Iср с увеличением числа объектов n.
Предложенный способ может найти применение в существующих пассивных системах радиовидения, развертываемых на местности для наблюдения за объектами и определения их пространственных координат.
Литература
1. Пассивная радиолокация: методы обнаружения объектов / Под ред. Р.П. Быстрова и А.В. Соколова. М.: Радиотехника, 2008. 320 с.
2. Цифровая обработка изображений в информационных системах: учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
Изобретение относится к пассивным системам радиовидения, работающим по принципу стереопары. Для расчета дальностей требуется знание взаимной ориентации двух систем координат - матрицы поворота осей координат, которую находят из условия компланарности сопряженных векторов направлений на объекты и базового вектора. Предложенный способ заключается в установлении стереопары из двух взаимно удаленных на базовое расстояние наблюдателей при известном базовом векторе, формировании в системах координат наблюдателей n пар сопряженных ортов a1(i) и a2(i) векторов направлений на центры i-x объектов, нахождении матрицы Р поворота осей координат на углы α, β, γ численным методом подбора углов, при этом с помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и r2(i), на основе найденных дальностей вычисляются пространственные координаты центров объектов в системах координат наблюдателей. Предлагаемый способ позволяет прошедшие проверку на компланарность векторы дополнительно проверить на выполнение достаточного условия сопряжения и одновременно определить дальности до объектов. 1 табл.
Способ взаимной ориентации систем координат и определения дальностей до объектов в пассивной системе радиовидения, заключающийся в установлении стереопары из двух взаимно удаленных на базовое расстояние |t| наблюдателей при известном базовом векторе, формировании в системах координат наблюдателей n пар сопряженных ортов a1(i) и a2(i) векторов направлений на центры i-x объектов, 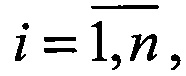 где n - количество наблюдаемых объектов, нахождении матрицы Р поворота осей координат на углы α, β, γ численным методом подбора углов по критерию минимума показателя
где n - количество наблюдаемых объектов, нахождении матрицы Р поворота осей координат на углы α, β, γ численным методом подбора углов по критерию минимума показателя 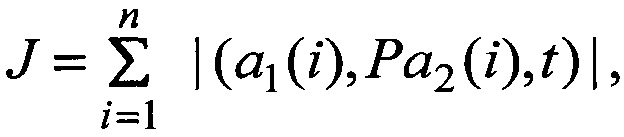 где (al(i),Pa2(i),t) - смешанное произведение трех векторов, отличающийся тем, что с помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и r2(i),
где (al(i),Pa2(i),t) - смешанное произведение трех векторов, отличающийся тем, что с помощью найденной матрицы Р и известного вектора t вычисляются оценки дальностей r1(i) и r2(i), 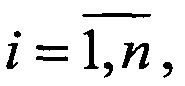 до i-x объектов по формуле (T - символ транспонирования):
до i-x объектов по формуле (T - символ транспонирования):
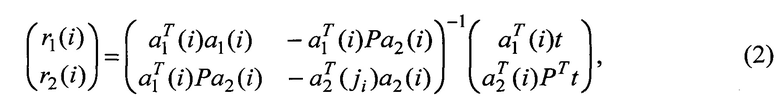
которые обеспечивают минимум показателя

где ||…|| - норма вектора, после чего показатель I сравнивается с малым числом ε>0 и если I≤ε, то матрица Р принимается в качестве матрицы поворота, а на основе найденных дальностей вычисляются пространственные координаты центров объектов М1(i)=r1(i)a1(i) и М2(i)=r2(i)a2(i),  в системах координат наблюдателей.
в системах координат наблюдателей.
| СПОСОБ ИЗМЕРЕНИЯ БОРТОВОЙ ПАССИВНОЙ СИСТЕМОЙ НАБЛЮДЕНИЯ ПЕРЕМЕЩЕНИЙ ДВИЖУЩЕГОСЯ ОБЪЕКТА И ДАЛЬНОСТИ ДО НЕГО | 2008 |
|
RU2381523C2 |
| СПОСОБ ИЗМЕРЕНИЯ ДАЛЬНОСТИ И ЛИНЕЙНЫХ РАЗМЕРОВ ОБЪЕКТОВ ПО ИХ ТЕЛЕВИЗИОННЫМ ИЗОБРАЖЕНИЯМ | 2008 |
|
RU2381521C2 |
| СПОСОБ СЕЛЕКЦИИ ПО ДАЛЬНОСТИ МНОЖЕСТВЕННЫХ ОБЪЕКТОВ | 2012 |
|
RU2498336C1 |
| US 9344701 B2, 17.05.2016 | |||
| WO 2012092246 A2, 05.07.2012 | |||
| В.К | |||
| КЛОЧКО "МЕТОДЫ ФОРМИРОВАНИЯ ТРЕХМЕРНЫХ ИЗОБРАЖЕНИЙ ПОВЕРХНОСТИ В БОРТОВЫХ СИСТЕМАХ РАДИОВИДЕНИЯ" // Сборник РАН Сибирское отделение "Автометрия", том 45 N 1, стр | |||
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
Авторы
Даты
2019-06-05—Публикация
2018-05-29—Подача