Изобретение относится к оптическим, тепловым и пассивным радиосистемам наблюдения за малоразмерными объектами [1, 2]. Целью наблюдения является оценивание пространственных координат объектов, которое основано на эффекте стереопары, что требует наличия как минимум двух взаимно удаленных наблюдателей и их взаимной ориентации - матрицы поворота осей координат Р и вектора параллельного переноса (базового вектора) t. При отсутствии или сбое работы навигационной системы взаимная ориентация двух систем координат осуществляется на основе нескольких пар сопряженных опорных точек, наблюдаемых в матрицах изображения.
Известен способ [2] оценивания параметров (углов поворота) матрицы Р и трех координат вектора t, рассчитанный на применение в системах видения с оптической линзой. Способ заключается в следующем.
1. Устанавливается стереопара из двух взаимно удаленных на базовое расстояние наблюдателей, и формируются две матрицы изображения одной и той же сцены, содержащей m точечных объектов наблюдения.
2. В полученных матрицах выбираются m пар сопряженных точек V1(i) и V2(i),  . Каждая i-я пара соответствует i-му точечному объекту, наблюдаемому в двух матрицах.
. Каждая i-я пара соответствует i-му точечному объекту, наблюдаемому в двух матрицах.
3. Определяются координаты x1(i),y1(i) и x2(i),y2(i) сопряженных точек V1(i) и V2(i), 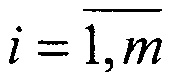 , в системах координат {о1,х1,у1} и {о2,х2,у2} двух матриц. Точки V1(i) и V2(i) представляются в параллельных системах координат {О1,Х1,Y1,Z1} и {O2,X2,Y2,Z2}, совмещенных с центрами О1 и O2 оптических линз, как точки M1(i) и M2(i):
, в системах координат {о1,х1,у1} и {о2,х2,у2} двух матриц. Точки V1(i) и V2(i) представляются в параллельных системах координат {О1,Х1,Y1,Z1} и {O2,X2,Y2,Z2}, совмещенных с центрами О1 и O2 оптических линз, как точки M1(i) и M2(i): 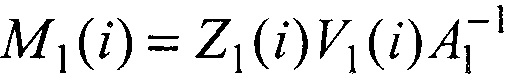 ,
, 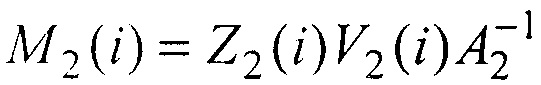 , где А1 и А2 - матрицы внутренних параметров камер, зависящие от фокусных расстояний ƒ1 и ƒ2; Z1 и Z2 - неизвестные третьи координаты сопряженных точек.
, где А1 и А2 - матрицы внутренних параметров камер, зависящие от фокусных расстояний ƒ1 и ƒ2; Z1 и Z2 - неизвестные третьи координаты сопряженных точек.
3. Для m пар сопряженных точек M1(i) и  ,
,  представленных в системе координат первого наблюдателя, где Р - матрица поворота осей, t - вектор параллельного переноса, записывается условие компланарности M1(i), M2(i) и t - равенство нулю их смешанного произведения в матричной форме для
представленных в системе координат первого наблюдателя, где Р - матрица поворота осей, t - вектор параллельного переноса, записывается условие компланарности M1(i), M2(i) и t - равенство нулю их смешанного произведения в матричной форме для 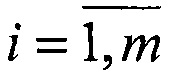 .
.
4. На основе смешанного произведения составляется квадратичная форма, зависящая от параметров матрицы Р (углов поворота), и численным методом подбора параметров находится минимальное собственное число матрицы квадратичной формы и соответствующий ему собственный вектор to - орт вектора t.
5. Найденные параметры (углы) дают оценку матрицы Р, а по известному расстоянию |t|=O1O2 определяется вектор t=|t|to.
Данный способ можно представить в универсальной форме, применимой как для оптических, так и для радиотехнических сканирующих систем с антеннами, заменив пары сопряженных точек M1(i), M2(i) на соответствующие им орты направлений a1(i) и a2(i) такие, что М1(i)=r1(i)a1(i), M2(i)=r2(i)a2(i), где r1=О1М1 и r2=O2M2 - наклонные дальности до объекта. Тогда для оптических систем орты определятся (символ i опустим):
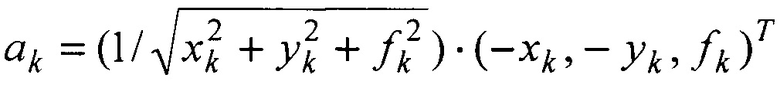 , k=1,2,
, k=1,2,
и для радиотехнических систем:
a k=(cosθk sinϕk, sinθk, cosθk cosϕk)T, k=1,2,
где ϕk,θk - угловые координаты (азимут и угол места) направления линии визирования антенны на объект наблюдения; Т - символ транспонирования.
В терминах ортов а1(i) и a2(i) направлений на M1(i) и M2(i), 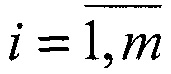 , представим способ-прототип следующим образом.
, представим способ-прототип следующим образом.
1. Операции п. 1 соответствуют выше изложенному.
2. В матрицах наблюдателей выбираются m пар сопряженных точек V1(i) и V2(i),  , и определяются для них орты a1(i) и a2(i) направлений на i-е объекты.
, и определяются для них орты a1(i) и a2(i) направлений на i-е объекты.
3. Для m пар сопряженных ортов a1(i) и  ,
,  , представленных в системе координат первого наблюдателя, записывается условие компланарности a1(i), a2(i) и t - равенство нулю их смешанного произведения в матричной форме для
, представленных в системе координат первого наблюдателя, записывается условие компланарности a1(i), a2(i) и t - равенство нулю их смешанного произведения в матричной форме для 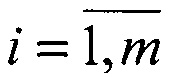 .
.
4,5. Операции пп. 4, 5 соответствуют выше изложенным.
Данный способ обладает следующими недостатками.
1. Способ не показывает правила нахождения пар сопряженных точек, без которого нельзя его реализовать. Условие компланарности указанных векторов не является достаточным условием сопряжения пар точек или ортов направлений на точки и может быть использовано только после установления факта их сопряжения.
2. Способ требует больших вычислительных затрат из-за применения численных методов подбора параметров матрицы Р и нахождения собственных чисел матрицы квадратичной формы.
Предлагаемое техническое решение направлено на устранение этих недостатков, а именно на введение правила выбора сопряженных пар точек или ортов направлений на эти точки и уменьшение вычислительных затрат на реализацию способа.
Технический результат предлагаемого технического решения достигается применением способа ориентации систем координат наблюдателей в пассивной системе видения, который заключается в установлении стереопары из двух взаимно удаленных на базовое расстояние наблюдателей и формировании двух матриц изображения одной и той же сцены, содержащей m точечных объектов наблюдения, отличающийся тем, что измеряют расстояния от центра каждого наблюдателя до m контрольных i-х объектов - наклонные дальности r1(i) и r2(j), 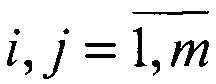 , определяют орты a1(i) и a2(j) направлений на объекты в системах координат двух наблюдателей, пересчитывают координаты ортов в координаты точек М1(i)=r1(i)a1(i) и M2(j)=r2(j)a1(j),
, определяют орты a1(i) и a2(j) направлений на объекты в системах координат двух наблюдателей, пересчитывают координаты ортов в координаты точек М1(i)=r1(i)a1(i) и M2(j)=r2(j)a1(j),  , затем рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар М1(i) и M2(j)
, затем рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар М1(i) и M2(j) 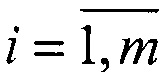 , ji∈{1,2,…,m}, и в системе координат первого наблюдателя составляют матричное уравнение М-В⋅С=Е, где М - блочный вектор, состоящий из М1(i),
, ji∈{1,2,…,m}, и в системе координат первого наблюдателя составляют матричное уравнение М-В⋅С=Е, где М - блочный вектор, состоящий из М1(i),  , В - матрица, составленная определенным образом из координат точек М2(ji),
, В - матрица, составленная определенным образом из координат точек М2(ji),  , Е - вектор ошибок сопряжения, С - вектор неизвестных параметров взаимной ориентации, при этом вычисляют оценку вектора С методом наименьших квадратов по формуле
, Е - вектор ошибок сопряжения, С - вектор неизвестных параметров взаимной ориентации, при этом вычисляют оценку вектора С методом наименьших квадратов по формуле  , далее среди m! вариантов соединения выбирают один вариант с наименьшей суммой квадратов невязок
, далее среди m! вариантов соединения выбирают один вариант с наименьшей суммой квадратов невязок 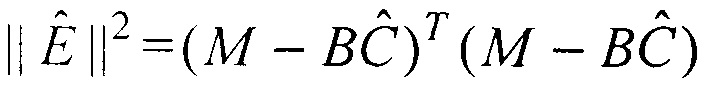 и из состава вектора
и из состава вектора  , соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы
, соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы  и вектора
и вектора 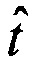 .
.
Алгоритмически предлагаемый способ сводится к следующей последовательности действий.
1. Два наблюдателя размещают в пространстве так, что прямоугольная система координат второго наблюдателя {O2,X2,Y2,Z2} приводится к системе координат первого {О1,X1,Y1,Z1} поворотом вокруг осей O2X2, O2Y2 и параллельным переносом t=(Δx,Δy,Δz).
2. Наблюдению подлежат m(m≥11) контрольных точечных объектов или m центров малоразмерных объектов, расстояния от которых r1(i) и r2(j) до центров O1 и O2 измеряют независимо для первого и второго наблюдателей ( ,
, 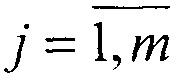 ), например, с помощью лазерного дальномера. При этом соответствие между i и j по принадлежности одному объекту неизвестно.
), например, с помощью лазерного дальномера. При этом соответствие между i и j по принадлежности одному объекту неизвестно.
3. Определяют орты а1(i) и a2(j) направлений на объекты в системах координат двух наблюдателей, которые пересчитывают в координаты точек М1(i)=r1(i),a1(i) и M2(j)=r2(j)a1(j),  .
.
4. Рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар М1(i) и M2(ji)  , ji∈{1,2,…,m}, и в системе координат первого наблюдателя составляют систему m уравнений связи координат сопряженных точек М1(i)-РМ2 (ji)-t=ei,
, ji∈{1,2,…,m}, и в системе координат первого наблюдателя составляют систему m уравнений связи координат сопряженных точек М1(i)-РМ2 (ji)-t=ei, 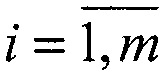 , где Р=PyPx - матрица поворота вокруг двух осей, ei - вектор ошибок сопряжения:
, где Р=PyPx - матрица поворота вокруг двух осей, ei - вектор ошибок сопряжения:

далее представляют систему (1) в матричной форме:

где М=(М1(1),М1(2),…,М1(m))T; В=(В1,В2,…,Bm)Т; Е=(е1,е2,…,em)T;
 ;
;
С=(sxsy cxsy cy cx sx sy sxcy cxcy Δx Δy Δz)T - вектор неизвестных параметров взаимной ориентации; cx=cosα; sx=sinα; cy=cosβ; sy=sinβ; α и β - углы поворота вокруг осей O2X2 и O2Y2.
При этом вычисляют оценку вектора С методом наименьших квадратов по формуле:

5. Среди m! вариантов соединения выбирают один вариант с наименьшим значением показателя сопряжения J, имеющего смысл суммы квадратов невязок при оценивании параметров по формуле (3):

и из состава вектора  , соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы
, соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы  и вектора
и вектора 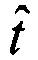 .
.
Замечания. 1. В случае известного вектора t вектор M1(i) в (1) заменяют на M1(i)-t, 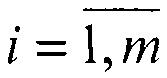 (m≥8), при этом из матрицы Bi в (2) убирают последние три столбца, а из вектора С - последние три строки.
(m≥8), при этом из матрицы Bi в (2) убирают последние три столбца, а из вектора С - последние три строки.
2. В случае поворота системы координат вокруг трех осей (Р=PzPyPx) возможна последовательная процедура поворота вокруг двух осей: XY, YZ, XZ и т.д. с оцениванием параметров (3) в сторону уменьшения показателя (4). Также возможен численный поиск минимума (4) подбором одного угла поворота вокруг OZ при вычислении остальных углов по формуле (3).
Результаты моделирования
При моделировании два наблюдателя, разнесенные по координате X на 30 м, по координатам Y и Z - на 2 и 3 м, наблюдали один объект, удаленный на 100-110 м. Координаты наблюдателей на множестве реализаций эксперимента менялись в пределах нескольких метров. Наблюдателя фиксировали несколько десятков пар сопряженных точек (контрольных объектов) при неизвестной матрице Р=PyPx, при этом дальности r1(i), r2(j) считались известными. Алгоритмом находилась оценка 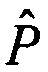 матрицы Р на основе оценок (3), и на множестве реализаций вычислялась средняя (по числу параметров) абсолютная ошибка Δср оценивания параметров матрицы Р путем сравнения найденных и моделируемых значений. Зависимость Δср от среднеквадратической ошибки измерения координат ортов σх представлена в таблице.
матрицы Р на основе оценок (3), и на множестве реализаций вычислялась средняя (по числу параметров) абсолютная ошибка Δср оценивания параметров матрицы Р путем сравнения найденных и моделируемых значений. Зависимость Δср от среднеквадратической ошибки измерения координат ортов σх представлена в таблице.

По результатам моделирования следует отметить, что требуется большое количество опорных точек (сопряженных пар) для получения удовлетворительных оценок параметров матрицы Р. Для повышения точности оценок следует увеличивать точность измерения координат ортов, то есть добиваться снижения σх.
Предложенный способ может найти применение в существующих оптических и пассивных радиотехнических системах видения, развертываемых на незнакомой местности для наблюдения за объектами при отсутствии или выходе из строя навигационных приборов.
Литература
1. Пассивная радиолокация: методы обнаружения объектов / Под ред. Р.П. Быстрова и А.В. Соколова. М.: Радиотехника, 2008. 320 с.
2. Цифровая обработка изображений в информационных системах: учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
Изобретение относится к области радиосистем наблюдения. Технический результат – уменьшение вычислительных затрат за счёт введения правила выбора сопряженных пар точек или ортов направлений на эти точки. Способ ориентации систем координат наблюдателей в пассивной системе видения заключается в установлении стереопары из двух взаимно удаленных на базовое расстояние наблюдателей и формировании двух матриц изображения одной и той же сцены, содержащей m точечных объектов наблюдения, причем измеряют расстояния от центра каждого наблюдателя до m контрольных i-x объектов - наклонные дальности, определяют орты направлений на объекты в системах координат двух наблюдателей, пересчитывают координаты ортов в координаты точек и затем рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар и в системе координат первого наблюдателя составляют матричное уравнение, при этом вычисляют оценку вектора методом наименьших квадратов, далее среди m! вариантов соединения выбирают один вариант с наименьшей суммой квадратов невязок и из состава вектора, соответствующего выбранному варианту, извлекают оценки параметров для матрицы и вектора, которые помещают в состав искомой матрицы и вектора.
Способ ориентации систем координат наблюдателей в пассивной системе видения, заключающийся в установлении стереопары из двух взаимно удаленных на базовое расстояние наблюдателей и формировании двух матриц изображения одной и той же сцены, содержащей m точечных объектов наблюдения, отличающийся тем, что измеряют расстояния от центра каждого наблюдателя до m контрольных i-x объектов - наклонные дальности r1(i) и r2(j),  определяют орты a1(i) и a2(j) направлений на объекты в системах координат двух наблюдателей, пересчитывают координаты ортов в координаты точек М1(i)=r1(i)а1(i) и М2(j)=r2(j)а1(j),
определяют орты a1(i) и a2(j) направлений на объекты в системах координат двух наблюдателей, пересчитывают координаты ортов в координаты точек М1(i)=r1(i)а1(i) и М2(j)=r2(j)а1(j),  затем рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар М1(i) и M2(ji)
затем рассматривают m! вариантов соединения точек первого и второго наблюдателей в m неповторяющихся сопряженных пар М1(i) и M2(ji)  ji∈{1,2, …, m}, и в системе координат первого наблюдателя составляют матричное уравнение М-В⋅С=Е, где М - блочный вектор, состоящий из М1(i),
ji∈{1,2, …, m}, и в системе координат первого наблюдателя составляют матричное уравнение М-В⋅С=Е, где М - блочный вектор, состоящий из М1(i),  В - матрица, составленная определенным образом из координат точек M2(ji),
В - матрица, составленная определенным образом из координат точек M2(ji),  Е - вектор ошибок сопряжения, С - вектор неизвестных параметров взаимной ориентации, при этом вычисляют оценку вектора С методом наименьших квадратов по формуле
Е - вектор ошибок сопряжения, С - вектор неизвестных параметров взаимной ориентации, при этом вычисляют оценку вектора С методом наименьших квадратов по формуле  , далее среди m! вариантов соединения выбирают один вариант с наименьшей суммой квадратов невязок
, далее среди m! вариантов соединения выбирают один вариант с наименьшей суммой квадратов невязок 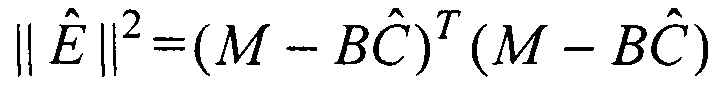 и из состава вектора
и из состава вектора  , соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы
, соответствующего выбранному варианту, извлекают оценки параметров для матрицы Р и вектора t, которые помещают в состав искомой матрицы 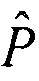 и вектора
и вектора 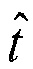 .
.
| СПОСОБ ОБНАРУЖЕНИЯ И ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСКОМОГО ОБЪЕКТА | 2008 |
|
RU2392635C2 |
| ПАРАЛЛАКТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТА | 1984 |
|
RU2027144C1 |
| ОСНОВАННОЕ НА АНАЛИЗЕ ИЗОБРАЖЕНИЙ ОТСЛЕЖИВАНИЕ ПЕРЕМЕЩЕНИЯ | 2005 |
|
RU2387011C2 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Токарный резец | 1924 |
|
SU2016A1 |
| RICHARD M | |||
| MARINO et al | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Найдено в Интернет по адресу: https://www.researchgate.net/profile/Richard_Marino/publication/284048532_Jigsaw_A_foliage-penetrating_3D_imaging_laser_radar_system/links/58d3da5892851c319e593f9c/Jigsaw-A-foliage-penetrating-3D-imaging-laser-radar-system.pdf. | |||
Авторы
Даты
2019-03-19—Публикация
2018-04-02—Подача