Изобретение относится к пассивным сканирующим системам видения оптического, инфракрасного и миллиметрового диапазонов длин волн [1, 2], предназначенным для наблюдения за движущимися объектами. Система состоит из нескольких приемных устройств - приемников, взаимно удаленных и ориентированных в пространстве. Сканирование осуществляется изменением углового положения линии визирования приемников во времени по определенному правилу. При каждом положении линии визирования принимаемый сигнал излучения в направлении линии визирования преобразуется в тракте первичной обработки и преобразуется в цифровую форму. При определенной мощности сигнала, превышающей порог обнаружения, фиксируются углы направления на объект и момент времени образования сигнала при данном направлении. Для определения пространственного положения объекта требуется наличие двух наблюдателей, образующих стереопару [1].
Известен способ определения пространственного положения объекта [1, с. 174-176], который применительно к сканирующим системам можно интерпретировать следующим образом.
1. Размещаются два приемника, сканирующих зону обзора и взаимно ориентированные базовым вектором b2=(b2x,b2y,b2z)T, соединяющим центры прямоугольных систем координат, и матрицей Р2 поворота осей координат второго наблюдателя относительно первого (T - символ транспонирования).
2. Формируются в одном периоде сканирования орты а1=(a1x,a1y,a1z) и a2=(a2x,a2y,a2z)T векторов М1=(x1,y1,z1)T и М2=(x2,y2,z2)T направлений на объект в системах координат наблюдателей на моменты времени t1 и t2. В общем случае t1≠t2 из-за различной ориентации приемников в пространстве и различии в правилах сканирования. Пространственное положение объекта определяется координатами векторов М1 и М2, связанных с ортами а1 и а2 через наклонные дальности до объекта r1 и r2:

3. Записывается достаточное условие сопряжения векторов М1 и М2, то есть направления на один и тот же объект в виде уравнения связи координат с точностью до ошибок сопряжения:

где е2=(e2x,e2y,e2z) - вектор ошибок сопряжения. С учетом (1) уравнение (2) принимает вид:

После обозначения  уравнение (3) представляется в матричном виде как запись трех уравнений с двумя неизвестными r1 и r2:
уравнение (3) представляется в матричном виде как запись трех уравнений с двумя неизвестными r1 и r2:
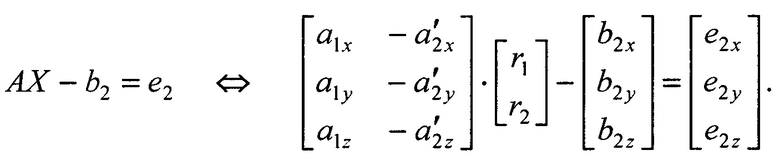
4. По критерию минимума квадрата нормы вектора ошибок сопряжения (метода наименьших квадратов - МНК):
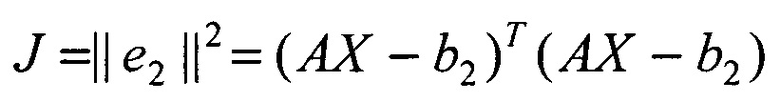
Находится вектор МНК-оценок дальностей 
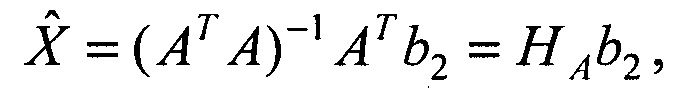
где НА=(ATA)-1AT - матрица весовых коэффициентов, и соответственно находятся оценки пространственных координат объекта на моменты времени t1 и t2 в системах координат наблюдателей:

5. Оценки положения объекта 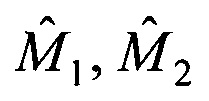 обновляются в последовательности периодов сканирования путем повторения операций пп. 2-4.
обновляются в последовательности периодов сканирования путем повторения операций пп. 2-4.
Однако данный способ обладает следующим недостатком - он справедлив только для неподвижного объекта. В случае движущегося объекта происходит смещение вектора М1 на промежутке времени [t1, t2], вследствие чего нарушается условие сопряжения (2). Объект, движущийся по линейному закону со скоростью V1=(ν1x,ν1y,ν1z)T на момент времени t1 в системе координат первого приемника, получает приращение ΔМ1=V1Δt за время Δt=t2-t1. С учетом этого условие сопряжения (2) запишем как:

Уравнение (4) представляет систему трех уравнений (по числу координат векторов) с пятью неизвестными r1, r2, ν1x, ν1y, ν1z и не имеет точного решения.
Объект, движущийся также с ускорением 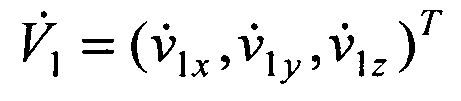 на момент времени t1, получает приращение
на момент времени t1, получает приращение 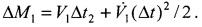 При этом уравнение (4) будет содержать восемь неизвестных и также не имеет решения.
При этом уравнение (4) будет содержать восемь неизвестных и также не имеет решения.
Предлагаемое техническое решение направлено на устранение этого недостатка, а именно на определение пространственного положения, скорости и ускорения движущегося объекта на момент времени t1.
Технический результат предлагаемого технического решения достигается применением способа определения пространственного положения, скорости и ускорения объекта в пассивной сканирующей системе видения, который заключается в размещении двух приемников, сканирующих зону обзора и взаимно ориентированных базовым вектором b2 и матрицей поворота осей Р2, формировании в одном периоде сканирования ортов векторов направлений на объект а1, а2 в системах координат приемников на моменты времени t1, t2, составлении матрицы А из координат векторов а1 и 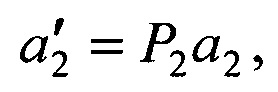 вычислении матрицы НА=(ATA)-1AT и умножении ее слева на вектор b2, получении вектора
вычислении матрицы НА=(ATA)-1AT и умножении ее слева на вектор b2, получении вектора 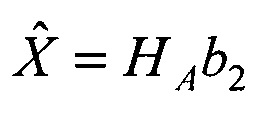 оценок дальностей до объекта
оценок дальностей до объекта  умножении оценок дальностей на орты и получении оценок пространственных координат объекта
умножении оценок дальностей на орты и получении оценок пространственных координат объекта 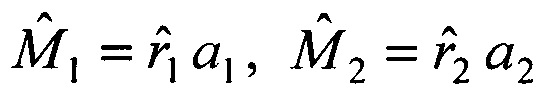 на моменты времени t1 и t2, повторении всех операций в последовательности периодов сканирования, отличающийся тем, что размещают третий приемник, сканирующий зону обзора, ориентированный относительно первого приеника базовым вектором b3 и матрицей поворота осей Р3, формируют орт а3 в момент времени t3 в направления на объект в третьей системе координат, составляют матрицу А из координат векторов а1,
на моменты времени t1 и t2, повторении всех операций в последовательности периодов сканирования, отличающийся тем, что размещают третий приемник, сканирующий зону обзора, ориентированный относительно первого приеника базовым вектором b3 и матрицей поворота осей Р3, формируют орт а3 в момент времени t3 в направления на объект в третьей системе координат, составляют матрицу А из координат векторов а1, 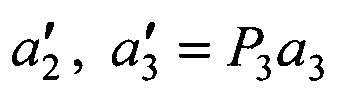 и приращений времени Δt2=t2-t1, Δt3=t3-t1, вычисляют матрицу НА=(ATA)-1AT, умножают ее слева на блочный вектор В, составленный из векторов b2 и b3, в результате получают вектор
и приращений времени Δt2=t2-t1, Δt3=t3-t1, вычисляют матрицу НА=(ATA)-1AT, умножают ее слева на блочный вектор В, составленный из векторов b2 и b3, в результате получают вектор 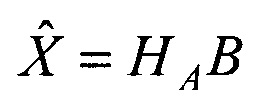 оценок дальностей
оценок дальностей  и координат вектора V1 скорости движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности
и координат вектора V1 скорости движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности  на орт а1 и получают оценку вектора пространственного положения объекта
на орт а1 и получают оценку вектора пространственного положения объекта 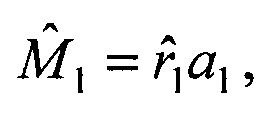 который вместе с вектором скорости движения объекта
который вместе с вектором скорости движения объекта 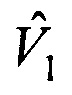 передают на сопровождение,
передают на сопровождение,
дополнительно размещают еще два приемника, сканирующих зону обзора, ориентированных относительно первого приемника базовыми векторами b4, b5 и матрицами поворота осей Р4, Р5, формируют орты направлений на объект а4, а5 в моменты времени t4, t5, составляют матрицу А из координат векторов а1, 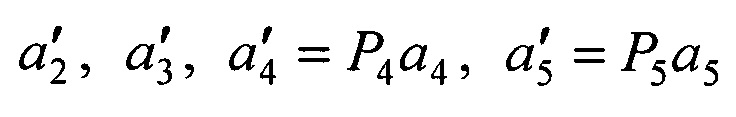 и приращений времени Δt2, Δt3, Δt4=t4-t1, Δt5=t5-t1, вычисляют матрицу НА=(АТА)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2, b3, b4, b5, в результате получают вектор
и приращений времени Δt2, Δt3, Δt4=t4-t1, Δt5=t5-t1, вычисляют матрицу НА=(АТА)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2, b3, b4, b5, в результате получают вектор 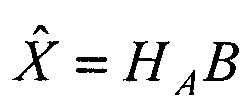 оценок дальностей
оценок дальностей 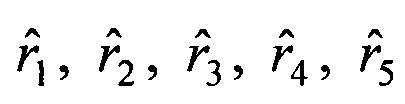 и координат векторов V1,
и координат векторов V1, 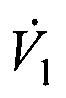 скорости и ускорения движения объекта на момент времени в системе координат первого наблюдателя, затем умножают оценку дальности
скорости и ускорения движения объекта на момент времени в системе координат первого наблюдателя, затем умножают оценку дальности  на орт а1 и получают оценку вектора пространственного положения объекта
на орт а1 и получают оценку вектора пространственного положения объекта 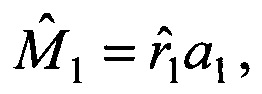 который вместе с оценками вектора скорости
который вместе с оценками вектора скорости 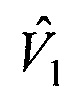 и ускорения
и ускорения 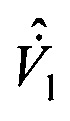 движения объекта передают на сопровождение.
движения объекта передают на сопровождение.
Алгоритмически способ осуществляется следующим образом.
1. Размещаются три приемника, сканирующих зону обзора и ориентированных относительно первого основного приемника базовыми векторами b2=(b2x,b2y,b2z)T, b3=(b3x,b3y,b3z)T и матрицами поворота осей координат Р2 и Р3 относительно первого приемника.
2. Формируются в одном периоде сканирования орты а1=(a1x,a1y,a1z)T, a2=(a2x,a2y,a2z)T, a3=(a3x,a3y,a3z)T векторов направлений на объект М1=(x1,y1,z1)T, М2=(x2,y2,z2)T, М3=(x3,y3,z3)T в системах координат приемников в моменты времени t1, t2, t3. Неизвестные векторы пространственного положения объекта М1, М2, М3 связанны с наблюдаемыми ортами через наклонные дальности r1, r2, r3:

3. Записывается достаточное условие сопряжения векторов М1, М2 и М1, М3 в виде системы уравнений связи координат:
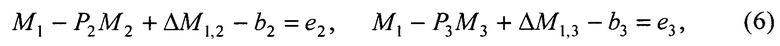
где ΔM1,2=V1Δt2 и ΔM1,3=V1Δt3 - приращения вектора М1 за счет изменения его координат за время Δt2=t2-t1 и Δt3=t3-t1 (Δt2≠0, Δt3≠0); V1=(ν1x,ν1y,ν1z)T - вектор скоростей изменения координат объекта в системе первого приемника на момент времени t1; е2=(e2x,e2y,e2z)T и е3=(e3x,e3y,e3z)T - векторы ошибок сопряжения. С учетом (5) система уравнений (6) принимает вид:
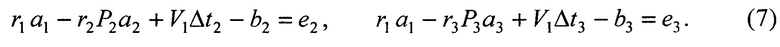
После обозначений 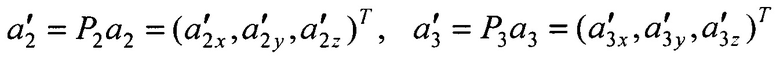 система (7) представляется как запись шести уравнений с шестью неизвестными r1, r2, r3, ν1x, ν1y, ν1z в матричной форме:
система (7) представляется как запись шести уравнений с шестью неизвестными r1, r2, r3, ν1x, ν1y, ν1z в матричной форме: 

4. По критерию минимума квадрата нормы ошибок сопряжения:

находятся МНК-оценки 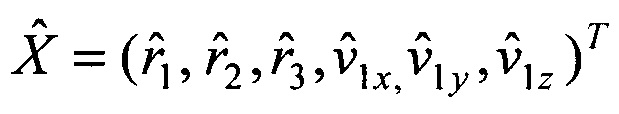 дальностей и скоростей:
дальностей и скоростей:

где НА=(ATA)-1AT - матрица весовых коэффициентов.
5. Оценка дальности 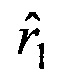 умножается на орт а1, получаются оценки вектора пространственного положения объекта
умножается на орт а1, получаются оценки вектора пространственного положения объекта 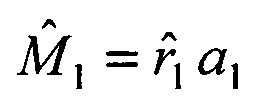 и скорости его движения
и скорости его движения 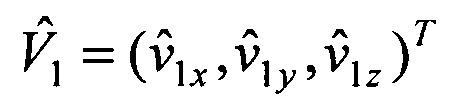 на момент времени t1 в первой системе координат.
на момент времени t1 в первой системе координат.
6. Полученные оценки положения и скорости объекта  передаются на сопровождение объекта и обновляются в последовательности периодов сканирования путем повторения операций пп. 2-4.
передаются на сопровождение объекта и обновляются в последовательности периодов сканирования путем повторения операций пп. 2-4.
7. Для повышения точности оценок (10) дальности и скорости предусматривается увеличение числа наблюдателей. При этом в матрице А выражения (8) появляются дополнительные строки и столбцы, а в векторах X, В и Е дополнительные строки. Так, при числе наблюдателей n=4 имеем систему 9 уравнений с 7 неизвестными, а при n=5 систему 12 уравнений с 8 неизвестными.
8. Дополнительно для получения оценки вектора ускорения  движения объекта в системе координат первого приемника на момент времени t1 размещаются еще два приемника, сканирующих зону обзора и ориентированных относительно первого наблюдателя базовыми векторами b4, b5 и матрицами поворота осей Р4, Р5. Формируются орты направлений на объект а4, а5 на моменты времени t4, t5.
движения объекта в системе координат первого приемника на момент времени t1 размещаются еще два приемника, сканирующих зону обзора и ориентированных относительно первого наблюдателя базовыми векторами b4, b5 и матрицами поворота осей Р4, Р5. Формируются орты направлений на объект а4, а5 на моменты времени t4, t5.
9. Записывается система уравнений
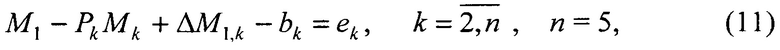
где 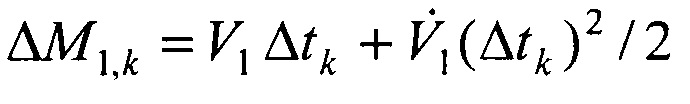 - приращения вектора М1 за счет изменения его координат за время Δtk=tk-t1 (Δtk≠0);
- приращения вектора М1 за счет изменения его координат за время Δtk=tk-t1 (Δtk≠0);  - вектор ускорений изменения координат объекта в системе первого приемника на момент времени t1. После преобразования (11) к виду:
- вектор ускорений изменения координат объекта в системе первого приемника на момент времени t1. После преобразования (11) к виду:
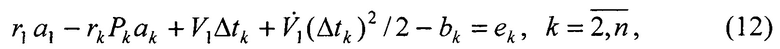
при n=5 имеем систему 3(n-1)=12 уравнений с n+6=11 неизвестными, которая записывается в матричной форме АХ-В=Е подобно (8), где матрица A имеет 3(n-1) строк и n+6 столбцов. Решение системы (12) дает вектор 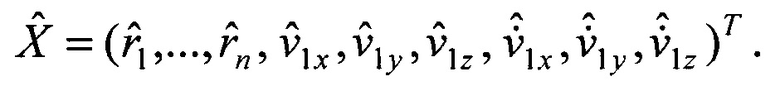
10. Для сопровождения объекта в каждом периоде сканирования выдаются векторы оценок его пространственного положения 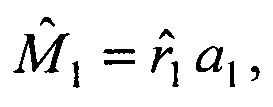 скорости
скорости  и ускорения
и ускорения 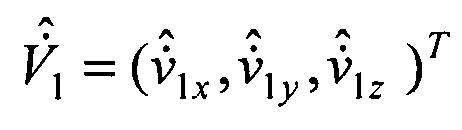 на момент времени t1.
на момент времени t1.
Предложенный способ определения пространственного положения, скорости и ускорения объекта в пассивной сканирующей системе может найти применение в существующих оптических и радиометрических системах пассивного видения при наблюдении за объектами.
При этом в радиометрической системе, состоящей из k-х радиометров 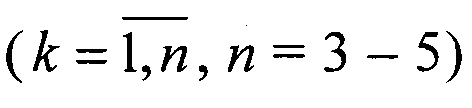 с антеннами, сканирующими в направлении угловых координат азимута ϕ и угла места θ, при ориентации осей Ох, Оу в вертикальной плоскости и оси Oz в горизонтальной орты векторов направлений на объект имеют вид: ak=(xk,yk,zk)T=(cosθk sinϕk, sinθk, cosθk cosϕk)T.
с антеннами, сканирующими в направлении угловых координат азимута ϕ и угла места θ, при ориентации осей Ох, Оу в вертикальной плоскости и оси Oz в горизонтальной орты векторов направлений на объект имеют вид: ak=(xk,yk,zk)T=(cosθk sinϕk, sinθk, cosθk cosϕk)T.
В оптической системе, состоящей из k-х видео приемников с фокусным расстоянием ƒk, наблюдающих объект в кадрах видео изображений в координатах xk, yk, орты векторов направлений на объект имеют вид:
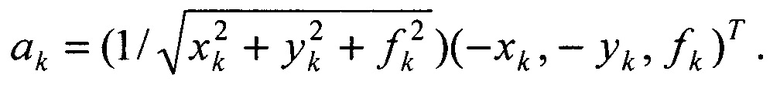
Литература
1. Цифровая обработка изображений в информационных системах: учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
2. Пассивная радиолокация: методы обнаружения объектов / Под ред. Р.П. Быстрова и А.В. Соколова. М.: Радиотехника, 2008. 320 с.
Изобретение относится к пассивным сканирующим системам видения оптического, инфракрасного и миллиметрового диапазонов длин волн, предназначенным для наблюдения за движущимися объектами. Достигаемый технический результат – определение пространственного положения, скорости и ускорения объекта в пассивной сканирующей системе видения. Система состоит из нескольких приемников, взаимно удаленных и ориентированных в пространстве. Сканирование осуществляется изменением углового положения линии визирования приемника во времени по определенному правилу. По результатам сканирования формируются орты направлений на объект в системах координат приемников и фиксируются моменты времени их образования. Предложенный способ позволяет в каждом периоде сканирования находить векторы пространственных координат положения объекта, скорости и ускорения его движения. Для этого из координат ортов и разностей моментов времени их образования составляется матрица системы уравнений и находится ее решение матричным методом.
Способ определения пространственного положения, скорости и ускорения объекта в пассивной сканирующей системе видения, заключающийся в размещении двух приемников, сканирующих зону обзора и взаимно ориентированных базовым вектором b2 и матрицей поворота осей Р2, формировании в одном периоде сканирования ортов векторов направлений на объект а1, а2 в системах координат приемников на моменты времени t1, t2, составлении матрицы А из координат векторов а1 и 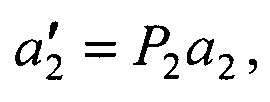 вычислении матрицы НА=(АТА)-1АТ и умножении ее слева на вектор b2, в результате получении вектора
вычислении матрицы НА=(АТА)-1АТ и умножении ее слева на вектор b2, в результате получении вектора 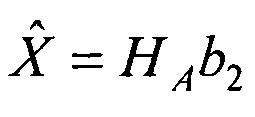 оценок дальностей до объекта
оценок дальностей до объекта 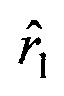 и
и 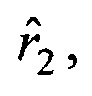 умножении оценок дальностей на орты и получении оценок пространственных координат объекта
умножении оценок дальностей на орты и получении оценок пространственных координат объекта  на моменты времени t1 и t2, повторении всех операций в последовательности периодов сканирования, отличающийся тем, что размещают третий приемник, сканирующий зону обзора, ориентированный относительно первого приемника базовым вектором b3 и матрицей поворота осей Р3, формируют орт а3 в момент времени t3 в направлении на объект в третьей системе координат, составляют матрицу А из координат векторов а1,
на моменты времени t1 и t2, повторении всех операций в последовательности периодов сканирования, отличающийся тем, что размещают третий приемник, сканирующий зону обзора, ориентированный относительно первого приемника базовым вектором b3 и матрицей поворота осей Р3, формируют орт а3 в момент времени t3 в направлении на объект в третьей системе координат, составляют матрицу А из координат векторов а1, 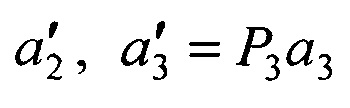 и приращений времени Δt2=t2-t1, Δt3=t3-t1, вычисляют матрицу HA=(ATA)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2 и b3, в результате получают вектор
и приращений времени Δt2=t2-t1, Δt3=t3-t1, вычисляют матрицу HA=(ATA)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2 и b3, в результате получают вектор 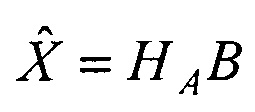 оценок дальностей
оценок дальностей  и координат вектора V1 скорости движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности
и координат вектора V1 скорости движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности 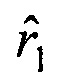 на орт a1 и получают оценку вектора пространственного положения объекта
на орт a1 и получают оценку вектора пространственного положения объекта 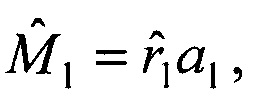 который вместе с вектором скорости движения объекта
который вместе с вектором скорости движения объекта 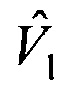 передают на сопровождение, дополнительно размещают еще два приемника, сканирующих зону обзора, ориентированных относительно первого приемника базовыми векторами b4, b5 и матрицами поворота осей Р4, Р5, формируют орты направлений на объект а4, а5 в моменты времени t4, t5, составляют матрицу А из координат векторов а1,
передают на сопровождение, дополнительно размещают еще два приемника, сканирующих зону обзора, ориентированных относительно первого приемника базовыми векторами b4, b5 и матрицами поворота осей Р4, Р5, формируют орты направлений на объект а4, а5 в моменты времени t4, t5, составляют матрицу А из координат векторов а1, 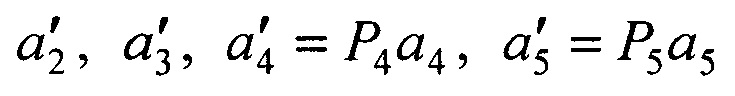 и приращений времени Δt2, Δt3, Δt4=t4-t1, Δt5=t5-t1, вычисляют матрицу НА=(АТА)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2, b3, b4, b5, в результате получают вектор
и приращений времени Δt2, Δt3, Δt4=t4-t1, Δt5=t5-t1, вычисляют матрицу НА=(АТА)-1АТ, умножают ее слева на блочный вектор В, составленный из векторов b2, b3, b4, b5, в результате получают вектор 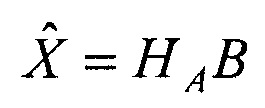 оценок дальностей
оценок дальностей 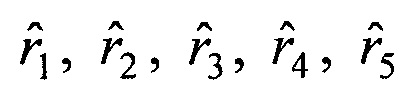 и координат векторов V1,
и координат векторов V1, 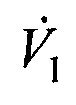 скорости и ускорения движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности
скорости и ускорения движения объекта на момент времени t1 в системе координат первого приемника, затем умножают оценку дальности  на орт a1 и получают оценку вектора пространственного положения объекта
на орт a1 и получают оценку вектора пространственного положения объекта 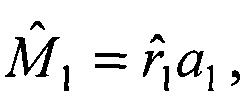 который вместе с оценками вектора скорости
который вместе с оценками вектора скорости  и ускорения
и ускорения  движения объекта передают на сопровождение.
движения объекта передают на сопровождение.
| ГРУЗМАН И.С | |||
| и др | |||
| Цифровая обработка изображений в информационных системах: учебное пособие | |||
| Новосибирск, Изд-во НГТУ | |||
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
| Система пассивной локации для определения координат летательного аппарата в ближней зоне аэродрома и на этапе захода на посадку с резервным каналом определения дальности | 2016 |
|
RU2633380C1 |
| СПОСОБ ОБНАРУЖЕНИЯ, ОПРЕДЕЛЕНИЯ КООРДИНАТ И СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ | 2014 |
|
RU2564385C1 |
| СПОСОБ ОЦЕНКИ ТЕКУЩИХ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2002 |
|
RU2231806C2 |
| EP 2990822 A1, 02.03.2016 | |||
| US 7315488 B2, 01.01.2008 | |||
| WO 2002091018 A1, 14.11.2002. | |||
Авторы
Даты
2019-09-16—Публикация
2018-11-12—Подача