Изобретение относится к многопозиционным радиотехническим системам наблюдения за группой движущихся объектов, разрешимых по доплеровской частоте. Система принимает отраженные сигналы, излучаемые внешним источником на определенной частоте в пассивном режиме, характерном для "Silent Sentry System".
Известны способы определения положения объекта в доплеровских наземных или бортовых системах, например, [1]. Однако они основаны на использовании приемо-передающих антенн активного излучения сигналов. Известен способ [2] пассивного определения положения и скорости объекта на основе эффекта стереопары в системе нескольких приемников, который рассмотрим в качестве прототипа. Способ сводится к следующему.
1. Размещают n=3 приемника, ориентированных относительно первого базовыми векторами b2, b3 и матрицами поворота осей координат Р2 и Р3 относительно первого приемника.
2. Формируют по результатам наблюдения орты а1, а2, а3 векторов направлений на объект в системах координат приемников последовательно в дискретные моменты времени t1, t2, t3, и составляют матрицу А из координат вектора а1, векторов а2, а3, пересчитанных в систему координат первого приемника с помощью матриц Р2, Р3, и моментов времени t1, t2, t3, после чего вычисляют матрицу весовых коэффициентов Н=(ATA)-1 AT, где “-1” и “T” - символы обращения матрицы и ее транспонирования.
3. Умножают матрицу Н справа на вектор В, составленный из координат векторов b2, b3, и получают вектор X=НВ оценок дальностей r1, r2, r3 до объекта от каждого приемника, а также координат νx, νy, νz скорости  в системе координат первого приемника. При этом оценки X отвечают минимуму показателя J=(АХ-В)Т(АХ-В) суммы квадратов ошибок сопряжения векторов а1, а2, а3, то есть их направления на один и тот же объект.
в системе координат первого приемника. При этом оценки X отвечают минимуму показателя J=(АХ-В)Т(АХ-В) суммы квадратов ошибок сопряжения векторов а1, а2, а3, то есть их направления на один и тот же объект.
4. Для получения оценок ускорения, а также повышения точности оценок X дополнительно включают четвертый и пятый приемники и фиксируют их орты направлений на объект а4, а5 в дискретные моменты времени t4, t5.
Данный способ обладает следующими недостатками.
1. Для определения положения и скорости объекта на момент времени t1 в системе координат первого приемника требуется наблюдение за объектом в разные моменты времени t1, t2, t3, разнесенные на большие промежутки. За время наблюдения скорость объекта может измениться.
2. Для определения ускорения объекта на момент времени t1 требуются дополнительные моменты времени наблюдения t4 и t5, что приводит к увеличению времени наблюдения.
3. Точность оценок положения, скорости и ускорения зависит от правильного выбора моментов времени формирования ортов направлений на объект при составлении матрицы А. При этом обращение матрицы АТ А в общем случае неустойчиво, что приводит к необходимости использования процедур регуляризации, а это снижает точность оценок.
4. Способ не предусматривает наблюдение за группой объектов.
Предлагаемое техническое решение направлено на устранение указанных недостатков, а именно, на получение оценок положения и скорости в группе объектов путем фиксации ортов направлений на объекты в один дискретный момент времени t1 при устойчиво обращаемой матрице.
Технический результат предлагаемого технического решения достигается применением способа определения пространственного положения и скорости в группе объектов системой доплеровских приемников, который заключается в размещении нескольких n приемников, принимающих сигнал отражения от объектов в зоне обзора приемников и ориентированных относительно первого приемника базовыми векторами b2, …, bn и матрицами Р2, …, Pn поворота осей координат, формировании ортов а1, а2, …, an векторов направлений на объекты в системах координат приемников в разные дискретные моменты времени t1, t2, …, tn, составлении матрицы из координат ортов, вычислении на ее основе матрицы весовых коэффициентов, умножении полученной матрицы слева на вектор, составленный из координат базовых векторов, и получении вектора оценок дальностей и координат скорости каждого объекта, отличающийся тем, что сигнал, излучаемый на несущей частоте ƒ0 внешним источником и отражаемый от объектов, принимают в антенных решетках нескольких приемников в один и тот же дискретный момент времени t1, выделяют фазы спектральных составляющих сигнала на одинаковых доплеровских частотах, зафиксированных в приемных каналах каждого приемника, определяют фазовым методом угловое направление прихода составляющих сигнала и орты а1, а2, …, an векторов этих направлений, составляют матрицу А из скалярных произведений пар ортов и умножают обратную матрицу А-1 слева на вектор В, составленный из скалярных произведений ортов и базовых векторов, и вычисляют вектор X оценок дальностей r1, r2, …, rn до объектов по формуле Х=А-1В=(r1, r2, …, rn)T, затем распределяют орты по принадлежности объектам путем выбора неповторяющихся вариантов соединения ортов с наименьшими показателями их сопряжения J=(АХ-В)T(АХ-В) и тем самым обнаруживают объекты, после чего для каждого i-го обнаруженного объекта (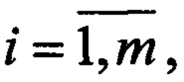 m - число объектов) умножают оценку дальности ri на орт a1 и получают вектор Mi=riai дооценок пространственных координат объекта в системе координат i-го приемника, затем составляют матрицу ΔА из разностей координат ортов направлений на этот объект, записанных в системе координат первого приемника, и вектор ΔF, составленный из разностей сдвигов доплеровских частот, измеренных в стереопарах приемников, и вычисляют вектор Vi оценок координат скорости каждого i-го объекта в системе координат первого приемника по формуле Vi=(c/ƒ0)ΔA-lΔF, где с - скорость света, далее векторы Vi и векторы Mi,
m - число объектов) умножают оценку дальности ri на орт a1 и получают вектор Mi=riai дооценок пространственных координат объекта в системе координат i-го приемника, затем составляют матрицу ΔА из разностей координат ортов направлений на этот объект, записанных в системе координат первого приемника, и вектор ΔF, составленный из разностей сдвигов доплеровских частот, измеренных в стереопарах приемников, и вычисляют вектор Vi оценок координат скорости каждого i-го объекта в системе координат первого приемника по формуле Vi=(c/ƒ0)ΔA-lΔF, где с - скорость света, далее векторы Vi и векторы Mi,  передают на сопровождение объектов.
передают на сопровождение объектов.
Алгоритмически способ осуществляется следующим образом.
1. Размещаются n=4 приемника, ориентированных относительно первого приемника базовыми векторами b2=(b2x, b2y, b2z)T, b3=(b3x, b3y, b3z)T, b4=(b4x, b4y, b3z)T и матрицами поворота осей координат Р2, Р3, Р4.
2. Сигнал s0(t)=U0cos(2πƒ0t+φ0), где U0 - амплитуда; ƒ0 - несущая частота: ƒ0=c/λ, λ - длина волны, с - скорость света; φ0 - начальная фаза (неизвестная величина при приеме сигнала); t - текущее время, излучаемый внешним источником и отражаемый от i-х объектов (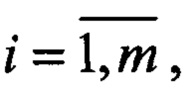 m - число объектов) принимается в q-x приемных элементах (
m - число объектов) принимается в q-x приемных элементах (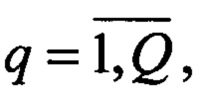 Q≥4 - число приемных элементов) антенной решетки (АР) каждого k-го приемника
Q≥4 - число приемных элементов) антенной решетки (АР) каждого k-го приемника  как сигнал sqik (t) с фазой ψqik=ψqik(t, ϕik, θik), описываемой моделью (символы i и k для удобства опускаем): ψq=2πƒ0(t-tq)+φ0+ε, где ε=ε(ϕ, θ) - случайное изменение фазы при отражении сигнала от i-го объекта в направлении угловых координат азимута ϕ и угла места θ; tq=[r0(t)+rq(t)]/c, r0(t) - расстояние, которое сигнал проходит от момента времени его излучения передатчиком до момента отражения от i-го объекта; rq(t)=rq(t, ϕ, θ) - расстояние, которое сигнал проходит после отражения от движущегося объекта в ϕ, θ-м угловом направлении до попадания на q-й элемент АР k-го приемника, причем r0(t)=R0+νr0t, rq(t)=R+δq+νrt, R0 и R - радиальные дальности до объекта соответственно от передатчика и от центра приемника, если бы объект был неподвижен; νr0 и νr - проекции вектора скорости
как сигнал sqik (t) с фазой ψqik=ψqik(t, ϕik, θik), описываемой моделью (символы i и k для удобства опускаем): ψq=2πƒ0(t-tq)+φ0+ε, где ε=ε(ϕ, θ) - случайное изменение фазы при отражении сигнала от i-го объекта в направлении угловых координат азимута ϕ и угла места θ; tq=[r0(t)+rq(t)]/c, r0(t) - расстояние, которое сигнал проходит от момента времени его излучения передатчиком до момента отражения от i-го объекта; rq(t)=rq(t, ϕ, θ) - расстояние, которое сигнал проходит после отражения от движущегося объекта в ϕ, θ-м угловом направлении до попадания на q-й элемент АР k-го приемника, причем r0(t)=R0+νr0t, rq(t)=R+δq+νrt, R0 и R - радиальные дальности до объекта соответственно от передатчика и от центра приемника, если бы объект был неподвижен; νr0 и νr - проекции вектора скорости 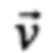 объекта в направлении передатчика и приемника; δq=δq(ϕ, θ) - отклонение сигнала, достигшего q-го элемента АР, относительно центра АР:
объекта в направлении передатчика и приемника; δq=δq(ϕ, θ) - отклонение сигнала, достигшего q-го элемента АР, относительно центра АР:
 где xq,yq - координаты центра q-го приемного элемента АР; х, у - координаты объекта отражения в системе АР; угол ϕ отсчитывается в горизонтальной плоскости OXZ относительно оси OZ, направленной в сторону объектов, а угол θ - относительно плоскости OXZ в направлении оси OY.
где xq,yq - координаты центра q-го приемного элемента АР; х, у - координаты объекта отражения в системе АР; угол ϕ отсчитывается в горизонтальной плоскости OXZ относительно оси OZ, направленной в сторону объектов, а угол θ - относительно плоскости OXZ в направлении оси OY.
Фаза сигнала, принятого в ϕ, θ-м направлении, запишется как
ψq=ψq(t,ϕ,θ)=2πƒ0[(1-νr∑)/c]t-2πƒ0[(R0+R)/c-2πƒ0δq/c+φ0+ε.
Дифференцированием ψq no t получается суммарная доплеровская частота

которая зависит от суммы радиальных скоростей νr∑=νr0+νr.
С учетом измеряемого доплеровского сдвига частот в k-м приемнике: Fk=ƒ0-ƒ∑=ƒ0νr∑/с фаза будет:
ψq(ϕ,θ)=2πƒ0t-2πFkt-(2π/λ)(R0+R)-(2π/λ)δq+φ0+ε.
В процессе прохождения тракта первичной обработки несущая частота ƒ0 снимается. После дискретизации по времени tj,  где N - количество временных отсчетов, фаза (2) принимает вид
где N - количество временных отсчетов, фаза (2) принимает вид

где ηq - фазовый шум; ξq=ξq (ϕ, θ) - случайная величина.
После того, как временная последовательность значений сигнала проходит через быстрое преобразование Фурье, получается частотная последовательность, из которой выделяются составляющие спектра с амплитудами, превышающими порог обнаружения полезного сигнала во всех q-x каналах  Фазы выделенных i-x составляющих (
Фазы выделенных i-x составляющих ( m - число выделенных частот Fik) в q-м элементе АР k-го приемника:
m - число выделенных частот Fik) в q-м элементе АР k-го приемника:

где δqik и ξqik даны в (2).
3. В соответствии с фазовым метолом измерения угловых координат берутся разности фаз ψq в (3) с учетом (1):
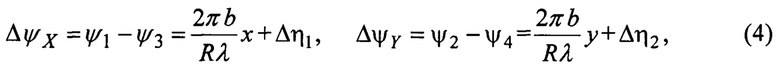
где Δη1=ξ1-ξ3 и Δη2=ξ2-ξ4, и находятся координаты х и у из (4), пренебрегая ошибками Δη1 и Δη2: х=ΔψXRλ/(πb), у=ΔψYRλ/(πb).
Затем вычисляются координаты орта aik=(ax, ay, az)T направления на i-й объект отражения сигнала в k-м приемнике:
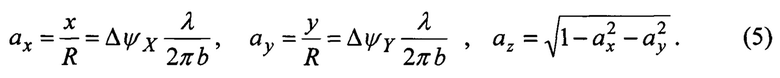
4. Составляется матрица А и вектор В вида
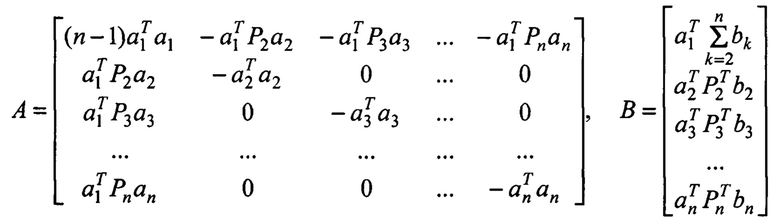
и вычисляется вектор X=(r1, r2, …, rn)T оценок дальностей до объектов по формуле X=А-1В, отвечающий критерию минимума показателя J суммы квадратов ошибок сопряжения ek:

При обращении матрицы А не требуется регуляризация.
5. Осуществляется перебор вариантов соединения ортов aik, 
 найденных в (5). Для каждого варианта вычисляются оценки дальностей до объектов rik,
найденных в (5). Для каждого варианта вычисляются оценки дальностей до объектов rik, 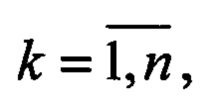 в соответствии с п. 4 и последовательно выбираются
в соответствии с п. 4 и последовательно выбираются 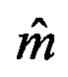 неповторяющихся вариантов соединения ортов с наименьшими показателями J. Для
неповторяющихся вариантов соединения ортов с наименьшими показателями J. Для  выбранных вариантов соединения ортов находятся пространственные координаты
выбранных вариантов соединения ортов находятся пространственные координаты 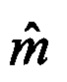 объектов Mik=rik aik1,
объектов Mik=rik aik1,  в системах k-х приемников, где
в системах k-х приемников, где 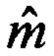 - оценка числа обнаруженных объектов.
- оценка числа обнаруженных объектов.
6. Для каждого i-го обнаруженного объекта фиксируются соответствующие ему доплеровские сдвиги частот Fk, измеренные в k-х приемниках:
Fk=ƒ0-ƒk=ƒ0νrk/с, или cFk=ƒ0 (νr0+νrk), где νrk=νr0+νrk.
Представляя радиальные скорости с помощью скалярных произведений векторов в системе координат 1-го приемника как

где νx, νy, νz - координаты вектора скорости в системе координат 1-го приемника; 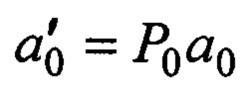 - орт вектора направления на объект в системе координат передатчика, пересчитанный в систему координат 1-го приемника с помощью матрицы поворота осей Р0 в матричной форме;
- орт вектора направления на объект в системе координат передатчика, пересчитанный в систему координат 1-го приемника с помощью матрицы поворота осей Р0 в матричной форме;  - орты векторов направлений на объект в системах координат k-х приемников, пересчитанные в систему координат 1-го приемника с помощью матриц поворота осей Pk, получаем систему n уравнений:
- орты векторов направлений на объект в системах координат k-х приемников, пересчитанные в систему координат 1-го приемника с помощью матриц поворота осей Pk, получаем систему n уравнений:

или систему n - 1 уравнений вида 
в матричной форме:

Для n=4 при измеренных значениях Fk, 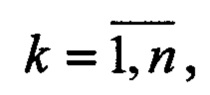 и известной несущей частоте ƒ0 из (6) получается уравнение в матричной форме относительно вектора
и известной несущей частоте ƒ0 из (6) получается уравнение в матричной форме относительно вектора 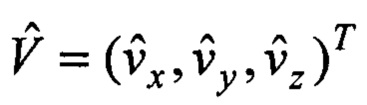 оценок координат вектора
оценок координат вектора 
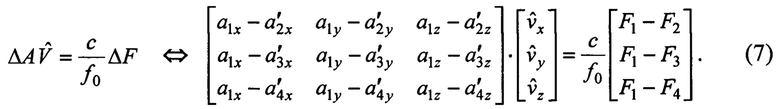
Методом обратной матрицы из (7) находится вектор оценок скорости i-го обнаруженного объекта в системе координат первого приемника:
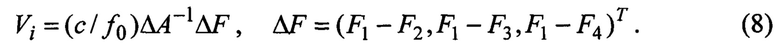
При обращении матрицы ΔА не требуется регуляризация.
7. С увеличением числа приемников (n>4) получается избыточность уравнений, вследствие чего сказываются ошибки Δ измерения разности доплеровских частот, и модель (7) принимает вид

где Δ=(Δ1, Δ2, …, Δn)T - вектор ошибок измерения разностей частот. Тогда решение находится минимизацией квадрата нормы вектора ошибок, что приводит к стандартным оценкам метода наименьших квадратов:
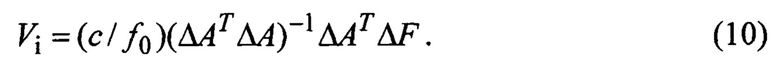
8. Векторы Vi, полученные для каждого объекта по формуле (10), вместе с векторами Mi оценок пространственных координат объектов  передаются на сопровождение объектов.
передаются на сопровождение объектов.
Для определения оценок ускорения достаточно повторить вычисления для двух дискретных моментов времени t1 и t2. Предложенный способ может найти применение в системах, работающих в режиме "Silent Sentry System".
Литература
1. Бакулев П.А. Радиолокационные системы: учебник для вузов. М.: Радиотехника, 2007. 376 с.
2. Патент RU 2700275. Способ определения пространственного положения, скорости и ускорения объекта в пассивной сканирующей системе видения / В.К. Клочко, X.К. Нгуен. Приоритет 12.11.2018.
Изобретение относится к многопозиционным радиотехническим системам наблюдения за группой движущихся объектов, разрешимых по доплеровской частоте. Способ может найти применение в существующих многопозиционных радиотехнических системах обнаружения и траекторного сопровождения объектов, работающих в режиме "Silent Sentry System". Техническим результатом изобретения является обеспечение возможности получения оценок положения и скорости в группе объектов путем фиксации ортов направлений на объекты в один дискретный момент времени при устойчиво обращаемой матрице. Предложенный способ позволяет получать оценки положения и скорости в группе объектов путем измерения угловых координат и ортов направлений на объекты отражения фазовым методом на основе спектральных составляющих принятых сигналов, выделенных на доплеровских частотах, обнаруживать объекты по критерию сопряжения векторов направлений на объекты в стереопарах приемников, находить оценки дальностей до обнаруженных объектов и их пространственные координаты, а также векторы скоростей объектов на основе решения систем алгебраических уравнений в один дискретный момент времени.
Способ определения пространственного положения и скорости в группе объектов системой доплеровских приемников, заключающийся в размещении нескольких n приемников, ориентированных относительно первого приемника базовыми векторами b2, …, bn и матрицами Р2, …, Pn поворота осей координат, формировании по результатам наблюдений ортов а1, а2, …, аn векторов направлений на объекты в системах координат приемников в разные дискретные моменты времени t1, t2, …, tn, составлении матрицы из координат ортов и моментов времени, вычислении на ее основе матрицы весовых коэффициентов, умножении полученной матрицы слева на вектор, составленный из координат базовых векторов, и получении вектора оценок дальностей и координат скорости объекта, отличающийся тем, что сигнал, излучаемый на несущей частоте ƒ0 внешним источником и отражаемый от группы объектов, принимают в антенных решетках нескольких приемников в дискретный момент времени t1, выделяют фазы спектральных составляющих сигнала на одинаковых доплеровских частотах, зафиксированных в приемных каналах каждого приемника, определяют фазовым методом угловые направления прихода составляющих сигнала и формируют орты а1, а2, …, аn векторов этих направлений, составляют матрицу А из скалярных произведений пар ортов и умножают обратную матрицу А-1 слева на вектор В, составленный из скалярных произведений ортов и базовых векторов, и вычисляют вектор X оценок дальностей r1, r2, …, rn до объектов по формуле Х=А-1В=(r1, r2, …, rn)T, где Т - символ транспонирования, затем распределяют орты по принадлежности объектам путем выбора неповторяющихся вариантов соединения ортов с наименьшими показателями сопряжения J=(АХ-В)T(АХ-В) и тем самым обнаруживают объекты, после чего для каждого i-го обнаруженного объекта ( m - число объектов) умножают оценку дальности ri на орт аi и получают вектор Mi=riаi оценок пространственных координат объекта в системе координат i-го приемника, затем составляют матрицу ΔА из разностей координат ортов направлений на этот объект, записанных в системе координат первого приемника, и вектор ΔF, составленный из разностей сдвигов доплеровских частот, измеренных в стереопарах приемников, и вычисляют вектор Vi оценок координат скорости каждого i-го объекта в системе координат первого приемника по формуле Vi=(с/ƒ0)ΔA-1ΔF, где с - скорость света, далее векторы Vi и векторы Mi,
m - число объектов) умножают оценку дальности ri на орт аi и получают вектор Mi=riаi оценок пространственных координат объекта в системе координат i-го приемника, затем составляют матрицу ΔА из разностей координат ортов направлений на этот объект, записанных в системе координат первого приемника, и вектор ΔF, составленный из разностей сдвигов доплеровских частот, измеренных в стереопарах приемников, и вычисляют вектор Vi оценок координат скорости каждого i-го объекта в системе координат первого приемника по формуле Vi=(с/ƒ0)ΔA-1ΔF, где с - скорость света, далее векторы Vi и векторы Mi,  передают на сопровождение объектов.
передают на сопровождение объектов.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ОБЪЕКТА В ПАССИВНОЙ СКАНИРУЮЩЕЙ СИСТЕМЕ ВИДЕНИЯ | 2018 |
|
RU2700275C1 |
| СПОСОБ ВЫДЕЛЕНИЯ СПЕКТРАЛЬНЫХ ОТСЧЕТОВ В МНОГОКАНАЛЬНОЙ ДОПЛЕРОВСКОЙ РЛС | 2017 |
|
RU2661913C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТЕЙ ДО ОБЪЕКТОВ В ПАССИВНЫХ СИСТЕМАХ ВИДЕНИЯ | 2018 |
|
RU2681518C1 |
| Способ адаптивной обработки сигналов в обзорных когерентно-импульсных радиолокационных станциях | 2019 |
|
RU2704789C1 |
| Способ обзорной пассивной однопозиционной моноимпульсной трёхкоординатной угломерно-разностно-доплеровской локации перемещающихся в пространстве радиоизлучающих объектов | 2017 |
|
RU2661357C1 |
| СПОСОБ ОРИЕНТАЦИИ СИСТЕМ КООРДИНАТ НАБЛЮДАТЕЛЕЙ В ПАССИВНОЙ СИСТЕМЕ ВИДЕНИЯ | 2018 |
|
RU2682382C1 |
| JP 2016142714 A, 08.08.2016 | |||
| US 10310066 B1, 04.06.2019 | |||
| JP 2009162726 A, 23.07.2009 | |||
| CN 105044709 A, 11.11.2015 | |||
| KR 101745995 B1, 13.06.2017. | |||
Авторы
Даты
2020-07-13—Публикация
2019-11-29—Подача