Изобретение относится к гироскопическому приборостроению и предназначено для повышения точности динамически настраиваемого гироскопа (ДНГ) по патенту №2235976 (Егоров В.Д., Тульчинский А.А. Динамически настраиваемый гироскоп - патент №2235976).
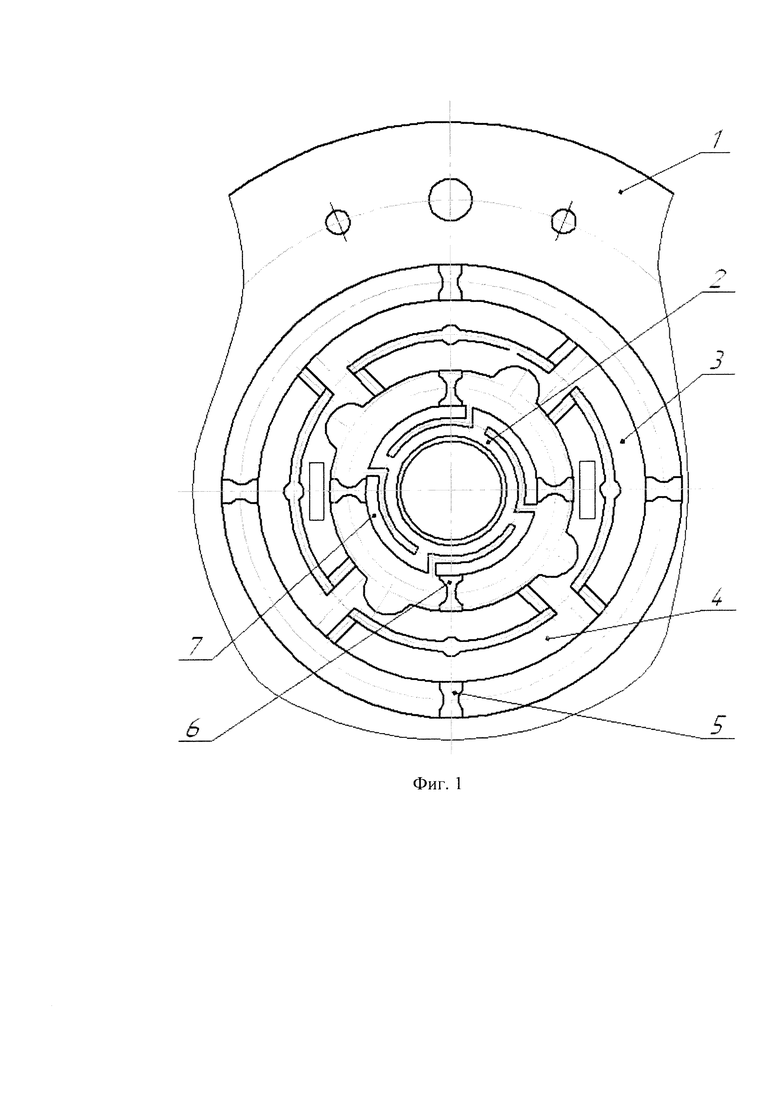
На фиг. 1 дан вид на чувствительный элемент такого ДНГ со стороны оси приводного вала.
Монолитный чувствительный элемент такого ДНГ представляет собой диск с центральным отверстием, по которому он устанавливается на приводной вал гироскопа. Маховик 1 связан со втулкой 2 (деталью приводного вала) упругим кардановым подвесом, состоящим из кардановых колец 3, 4 и упругих элементов - торсионов 5, 6. Каждое карданово кольцо связано одной парой торсионов 5 с маховиком 1, а другой парой 6 - со втулкой 2 через консольные балки 7, образованные во втулке 2 радиальными и кольцевыми щелями. Линейная податливость балок 7 выбирается такой, чтобы были равны первые главные собственные частоты колебаний гироскопа в осевом и радиальном направлениях. Достоинство такого гироскопа заключается в том, что он инвариантен к воздействию синхронных линейных вибраций в направлении оси приводного вала и в направлении, перпендикулярном оси вала (к воздействию "косых" вибраций).
Операции по балансировке ДНГ включают в себя статическую и динамическую балансировку ротора гироскопа и приводного вала (раздельно), балансировку ротора на упругом подвесе, заключающуюся в совмещении осей упругих элементов, совмещении центра масс ротора с центром подвеса и динамическую настройку гироскопа. Подробно такие операции описаны в статье (Виноградов Г.М., Родионов Е.М., Шабаев В.И. Регулировка и балансировка динамически настраиваемых гироскопов "Авиационная промышленность", 1977, №3).
Для монолитного чувствительного элемента ДНГ по патенту №22359976 балансировку ротора на упругом подвесе и динамическую настройку гироскопа целесообразно выполнять путем притирки торсионов по способу, приведенному в (Егоров В.Д., Тульчинский А.А. Способ статической балансировки гироскопа с торсионным подвесом типа универсальный шарнир - Авт. свид. №75561 от 11.12.1973 г.) с контролем притирки по периоду колебаний ротора в статике по способу (Егоров В.Д., Тульчинский А.А. Способ статической балансировки гироскопа - Авт. свид. №164364 от 08.09.1981 г.), которые взяты за прототип.
Балансировка ДНГ известными способами, включая прототипы, однозначно приводит к улучшению его точностных характеристик, кроме одной - при балансировке не уменьшается квадратурная составляющая скорости ухода гироскопа (Виноградов Г.М., Родионов Е.М., Шабаев В.И. О дрейфе динамически настраиваемого гироскопа от остаточных напряжений в торсионах и его диагностике. М., "Приборостроение", 1977, №2, Брозгуль Л.И. Динамически настраиваемые гироскопы, М., "Машиностроение", 1989), в чем и состоит недостаток известных способов.
Под квадратурной составляющей скорости ухода ДНГ понимается уход вокруг оси, которая лежит в плоскости вращения ротора и перпендикулярна линии действия в этой же плоскости внешней силы, приложенной к ротору. Это значит, что указанная сила вызывает момент вокруг оси действия этой силы (Виноградов Г.М., Родионов Е.М., Шабаев В.И. О дрейфе динамически настраиваемого гироскопа от остаточных напряжений в торсионах и его диагностике. М., "Приборостроение", 1977, №2).
Механизм возникновения такого ухода, который связан с начальной встречной закруткой торсионов, описан в статье (Виноградов Г.М., Родионов Е.М., Шабаев В.И. О дрейфе динамически настраиваемого гироскопа от остаточных напряжений в торсионах и его диагностике. М., "Приборостроение", 1977, №2). В монолитном чувствительном элементе ДНГ такая встречная закрутка торсионов вызвана внутренними напряжениями в торсионах, создаваемыми при их механической и термической обработке.
Целью настоящего изобретения является компенсация квадратурной составляющей скорости ухода. Цель достигается тем, что с торсионов 6, соединяющих кардановы кольца с консольными балками 7 (фиг. 1) снимаются фаски с контролем снятия по периоду колебаний в статике.
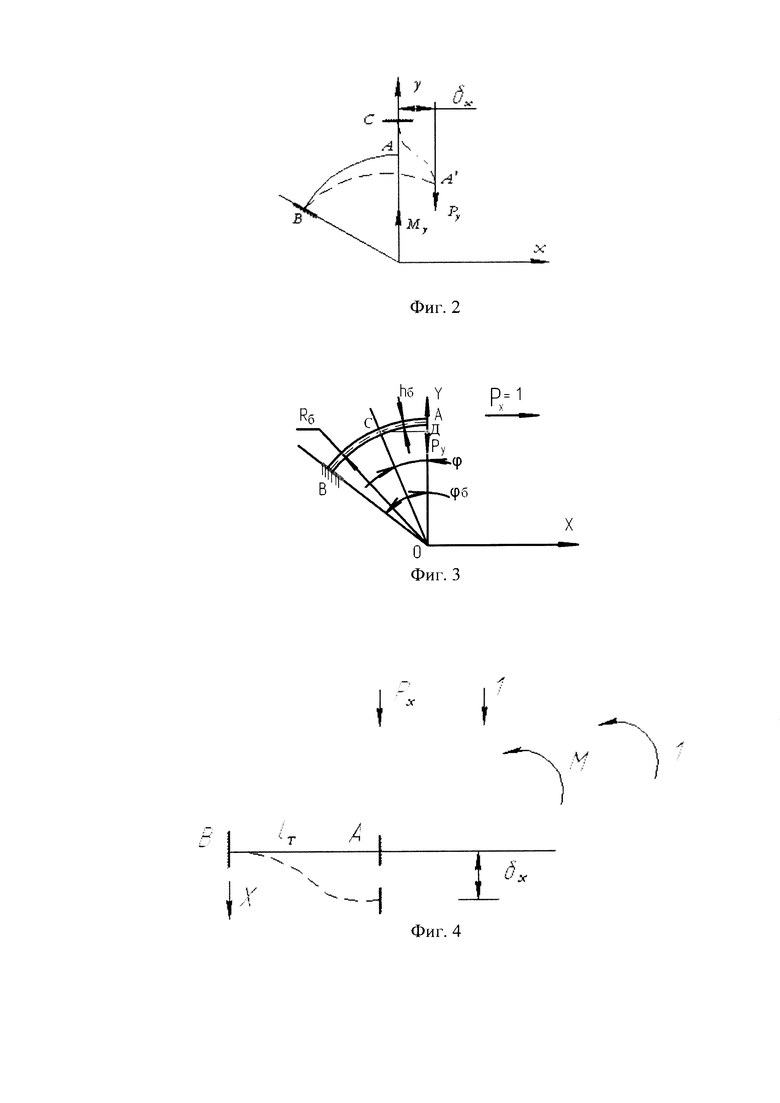
На фиг. 2 приведена схема приложения внешней силы Ру, вызываемой весом ротора, через торсион СА к концу А консольной балки 7, показанной на фиг. 1, связывающей торсион с приводным валом. Под действием силы Ру конец А балки получит перемещение не только вдоль оси Y, но также перемещение δx вдоль оси X, вызывая изгиб торсиона.
На фиг 3 показана консольная балка, связывающая торсион с кардановым кольцом
Rб - средний радиус балки,
hб - толщина балки,
bб - ширина балки (размер вдоль оси приводного вала),
ϕб - угловой размер балки.
Определим перемещение δx конца балки вдоль оси X под действием силы Ру. Далее в расчетах как балки, так и торсиона, будем учитывать только изгибающие моменты, пренебрегая деформацией от сдвига, что незначительно скажется на результатах расчета (Беляев Н.М. Сопротивление материалов. М., Физматгиз, 1959).
Изгибающий момент М(ϕ) в сечении С балки, расположенном под углом ϕ по отношению к оси OY, определяется выражением

Изгибающий момент М0 от единичной силы Рх=1, приложенной к концу А балки вдоль оси X:
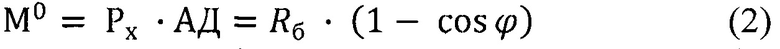
В соответствии с формулой Максвелла-Мора (Беляев Н.М. Сопротивление материалов. М., Физматгиз, 1959) перемещение δx определено выражением
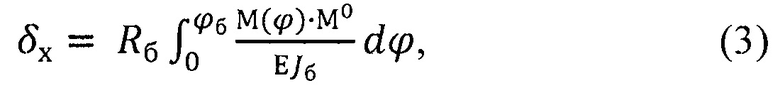
где Е - модуль упругости материала балки,
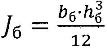 - момент инерции сечения балки.
- момент инерции сечения балки.
Подстановка в формулу (3) выражений (1) и (2) дает:
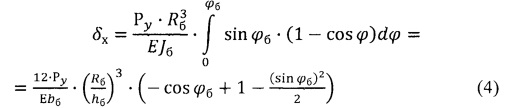
Конец А торсиона, связанного с жесткой балкой, получит такое же перемещение δx. Второй конец торсиона остается в жесткой заделке (кардановом кольце).
Схема деформации торсиона показана на фиг. 4
При расчете для простоты и наглядности вычислений реальный торсион, образованный перемычкой размера h0 в пластине толщиной bт между двумя отверстиями диаметра dт (фиг. 5) можно заменить торсионом, представляющим собой пластину прямоугольного сечения толщиной h0, шириной bт (размером вдоль оси приводного вала) и длиной 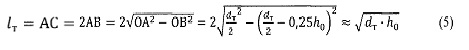
Такая замена вполне допустима, учитывая, что 95% процентов податливости реального торсиона определяется податливостью среднего участка, размер h сечения которого не превышает 1,5h0 (Егоров В.Д. Теоретическое и экспериментальное исследование погрешностей динамически настраиваемого гироскопа, обусловленных несовершенствами упругого подвеса - Диссертация на соискание ученой степени кандидата технических наук, 1984 г.).
Определим силу Рх, вызывающую перемещение δх. Система статически неопределима. Отбросим заделку торсиона в сечении А, ее действие заменим силой Рх и моментом М. На фиг. 6 показаны эпюры изгибающих моментов от силы Рх, момента М и единичных силовых факторов Рх=1, М=1.
В соответствии с правилом Верещагина (Беляев Н. М. Сопротивление материалов. М., Физматгиз, 1959) находим перемещение δx и угол поворота θ сечения А торсиона:
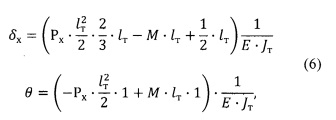
где 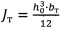 - момент инерции торсиона.
- момент инерции торсиона.
Угол θ поворота сечения А можно считать равным нулю, тогда из условия θ=0
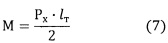
Подстановка выражения (7) в (6) дает:

откуда 
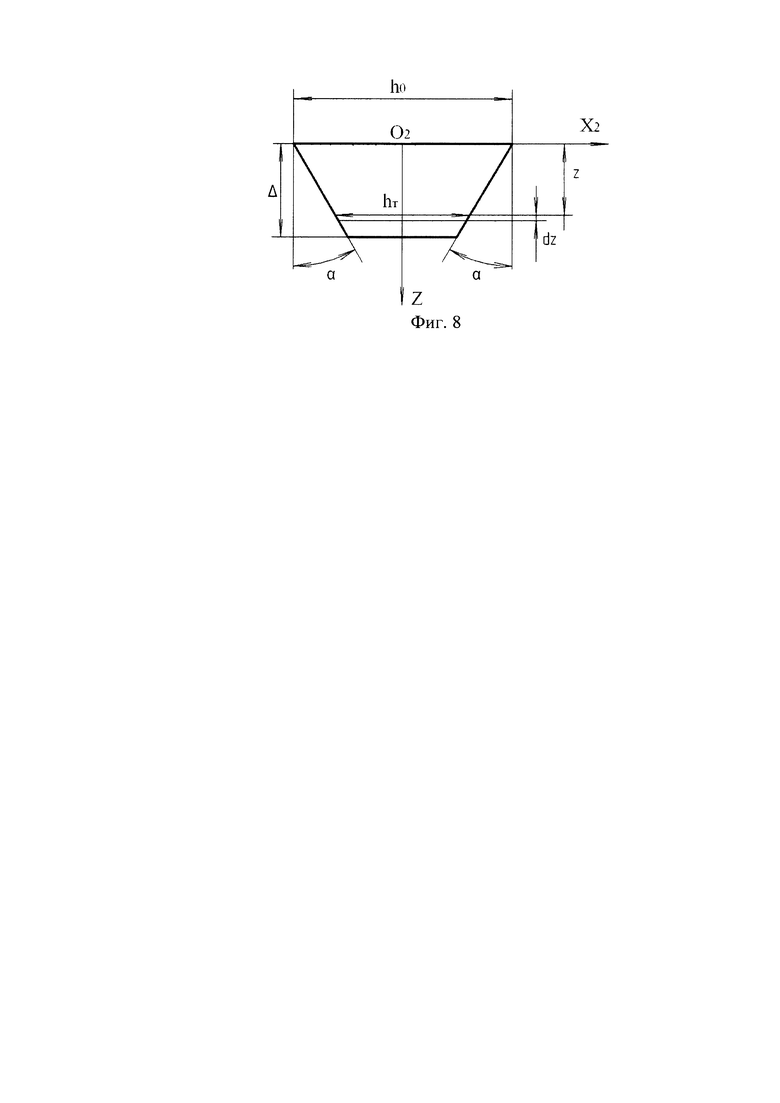
Рассмотрим торсион, показанный на фиг. 7 в системе координат XYZ. Ось Z параллельны оси приводного вала, оси X и Y параллельны осям упругого карданова подвеса. Плоскость XY делит торсион по размеру bт пополам. С торсиона снята фаска размером Δ по оси вала под углом α к этой оси.
Под действием на торсионы силы Ру связанная с консольной балкой сторона торсиона А'Д'С'В' получает перемещение δx вдоль оси X, как показано на фиг. 2, квадратурный момент Му (момент, вызывающий квадратурную составляющую скорости ухода) образуется из-за неравенства сил P1 и Р2, приложенных от торсиона к карданову кольцу от концевых участков торсиона, расположенных на расстоянии 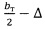 от оси Y.
от оси Y.
В соответствии с правилами механики
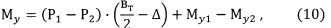
где Му1 (Му2) - момент силы Р1 (Р2), относительно оси Y1 (Y2).
Сила Р1 определяется выражением:
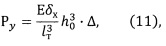
непосредственно вытекающего из выражения (9).
Момент Му1 этой силы относительно оси Y1 определяется выражением:
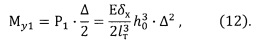
Для определения силы Р2 и момента Му2 рассмотрим часть торсиона с размером Δ по оси Z, примыкающую к торцевому сечению АА'ДД', в системе координат X2Y2Z, как показано на фиг. 8.
В этой системе координат толщина hт торсиона меняется по закону:
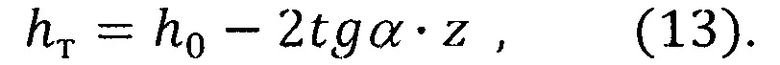
Рассмотрим элементарную пластину, находящуюся между двумя плоскостями, параллельными плоскости X2Y2 и отстоящую от этой плоскости на расстояниях z и z+Δz.
В соответствии с выражением (9), учитывая выражение (13), сила сопротивления перемещению δх этой пластины, приложенная к карданову кольцу, определяется выражением:
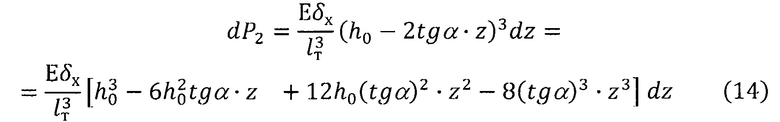
Момент, приложенный к карданову кольцу от этой силы относительно оси у2, определяется выражением:
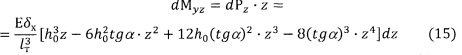
Интегрируя выражения (14) и (15), находим силу Р2 и момент М2:
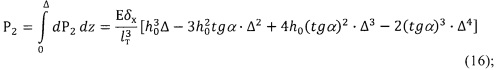
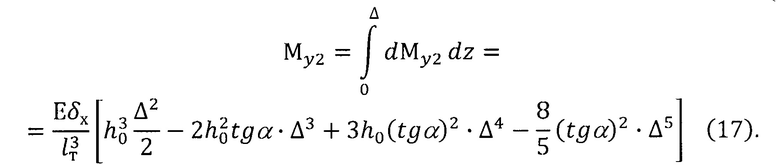
С учетом выражений (10), (11), (12), (15), (16) квадратурный момент My определяется зависимостью:
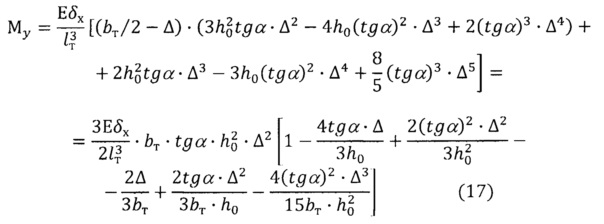
Оценим на реальном примере вес каждого слагаемого, стоящего в квадратных скобках сомножителя правой части выражения (17). При tgα=45°, Δ=0,02 мм, h0=0,13 мм, bт=0,8 мм слагаемые этого сомножителя принимают следующие числовые значения:
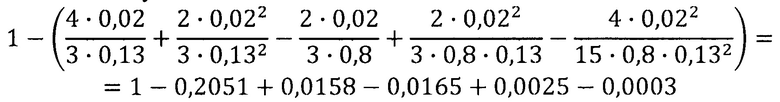
Из этого примера следует, что в данном сомножителе можно пренебречь всеми слагаемыми, кроме первых двух.
В этом случае выражение (17) принимает вид:
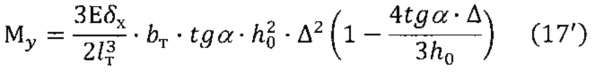
Связь момента Му с силой Ру определяется из выражения (17'), которое с учетом выражения (4) приобретает вид:
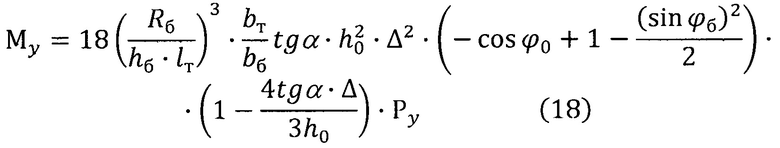
При горизонтальном положении оси приводного вала гироскопа сила Ру, приложенная к одному торсиону, связывающему карданово кольцо с приводным валом через консольную балку, изменяется по закону:
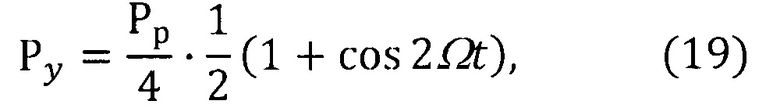
где Ω - угловая скорость вращения вала,
Рр - вес ротора ЧЭ (без внутреннего кольца).
Постоянная составляющая этой силы вызывает момент Му const, приводящий к квадратурной погрешности гироскопа:
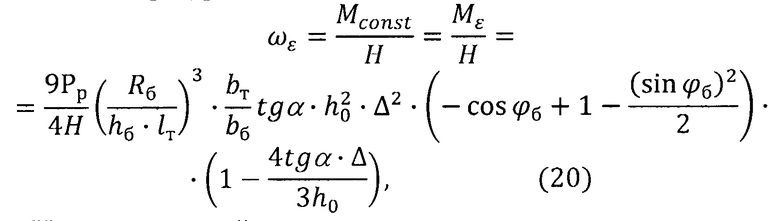
где Н - кинетический момент гироскопа.
Численная оценка этого выражения с учетом (5) при следующих реальных данных:
Рр=100 г, Rб=5,6 мм, hб=0,8 мм, bб=10 мм, ϕб=60°, bт=0,8 мм, dт=2 мм, h0=0,13 мм, 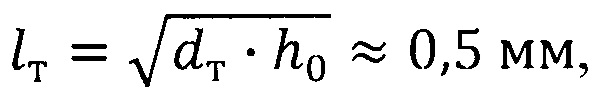 α=45°, Δ=0,02 мм, Н=850 г⋅см⋅сек дает:
α=45°, Δ=0,02 мм, Н=850 г⋅см⋅сек дает:
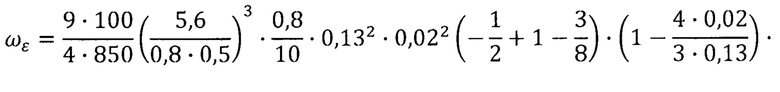
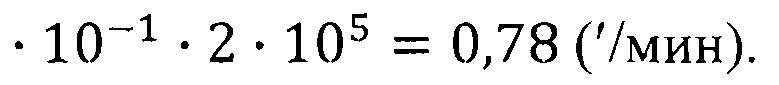
Если со всех четырех торсионов, соединяющих кардановы кольца с приводным валом, сняты со стороны одной торцевой поверхности ротора фаски размером Δ=0,02 мм по оси вала под углом 45° к этой оси, то квадратурная составляющая скорости ухода будет в 4 раза больше, т.е. составит 3,12'/мин.
Квадратурный момент Мε и квадратурная составляющая скорости ухода ωε поменяют знак, если с торсионов, соединяющих кардановы кольца с приводным валом, снять фаски с другой торцевой стороны ротора.
Из приведенной численной оценки выражения (20) следует, что можно пренебречь по сравнению с единицей вторым слагаемым последнего сомножителя этого выражения. В этом случае из выражения (20) вытекает следующая зависимость, по которой можно определить величину фасок, снимаемых с каждого из четырех торсионов, соединяющих кардановы кольца с консольными балками, для устранения измеренной квадратурной составляющей скорости ухода гироскопа:
где 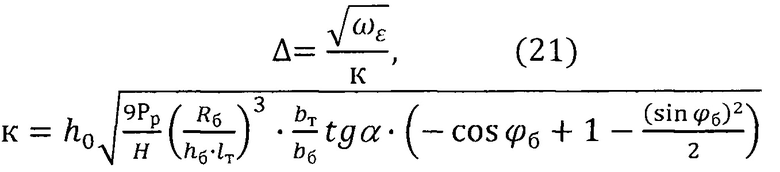
С учетом данных, приведенных для численных оценок выражения (20),
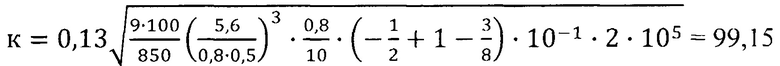
(Δ - мм, ωε - '/мин).
Для полученного по формуле (20) численного значения ωε=3,12'/мин при Δ=0,02 мм расчет по формуле (21) дает значение Δ

мало отличающееся от 0,02 мм.
Снятие фасок с торсионов можно контролировать по изменению периода невращающегося ротора относительно осей карданова подвеса.
Угловая жесткость торсионов, прямоугольного сечения с размером h0 меньшей и bт большей стороны определяется по теории чистого кручения (Ван Цзи-Де Прикладная теория упругости, М, "Физматгиз", 1959) выражением
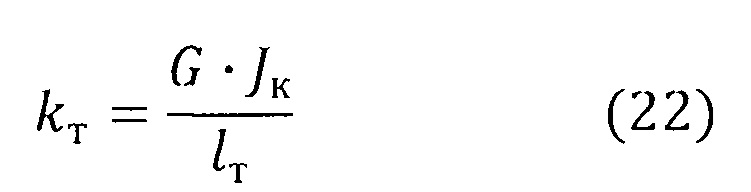
где G - модуль упругости при сдвиге материала торсиона,
Jк - момент инерции сечения на кручение

Для практических расчетов можно взять 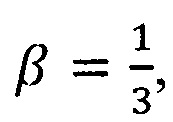 тогда
тогда 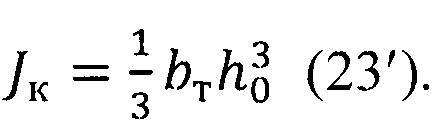
Из фиг 7 видно, что кромка торсиона, с которого снимается фаска, расположена относительно оси Y карданова подвеса на расстоянии

Снятие 2 фасок размером Δ под углом 45° по отношению к оси ротора ведет к уменьшению момента инерции сечения торсиона на кручение на величину
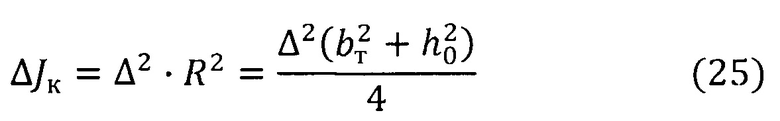
(пренебрегая моментами инерции участков сечения площадью 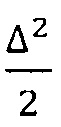 относительно их центральных осей, параллельных оси Y).
относительно их центральных осей, параллельных оси Y).
С учетом выражений (22), (23'), и (25) относительное изменение угловой жесткости kп 4-х торсионов, расположенных по оси карданова подвеса, при снятии фасок с двух торсионов, соединяющих кардановы кольца с консольными балками, определяется выражением:
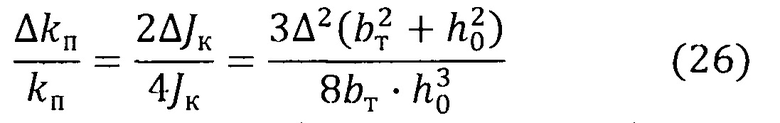
С учетом выражений (21) и (26) периоды колебаний ротора относительно осей карданова подвеса в начале Тн и в конце Тк притирки торсионов связаны следующим соотношением:
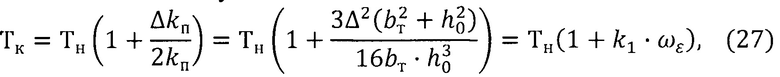
где
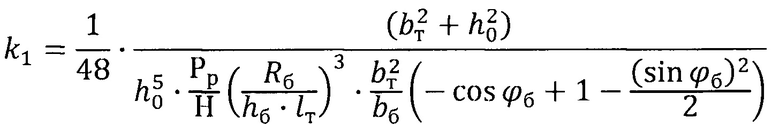
Для приведенных в выражении (20) данных k1=7,13⋅10-3 сек.
Контроль снятия фаски с каждой стороны торсиона должен осуществляться по изменению периода колебаний ротора на величину 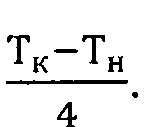
Предложенный способ балансировки ДНГ экспериментальна опробован с положительным результатом.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДИНАМИЧЕСКИ НАСТРАИВАЕМЫЙ ГИРОСКОП | 2002 |
|
RU2235976C2 |
| ДИНАМИЧЕСКИ НАСТРАИВАЕМЫЙ ГИРОСКОП | 1977 |
|
RU2107260C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ В СОСТАВЕ ГИРОСТАБИЛИЗАТОРА ДИНАМИЧЕСКИ НАСТРАИВАЕМОГО ГИРОСКОПА | 1989 |
|
RU2065574C1 |
| Установка для изучения режимов работы динамически настраиваемого гироскопа | 2024 |
|
RU2829671C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ДИНАМИЧЕСКИ НАСТРАИВАЕМОГО ГИРОСКОПА | 1988 |
|
RU2065575C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ В СОСТАВЕ ГИРОСТАБИЛИЗАТОРА ДИНАМИЧЕСКИ НАСТРАИВАЕМОГО ГИРОСКОПА И ДИНАМИЧЕСКИ НАСТРАИВАЕМЫЙ ГИРОСКОП | 1990 |
|
RU2120109C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПРОЕКЦИЙ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ВЕКТОРА УГЛОВОЙ СКОРОСТИ ВРАЩЕНИЯ ЗЕМЛИ ДЛЯ ОПРЕДЕЛЕНИЯ АЗИМУТАЛЬНОГО НАПРАВЛЕНИЯ (КОМПАСИРОВАНИЯ) | 2005 |
|
RU2300078C1 |
| ДИНАМИЧЕСКИ НАСТРАИВАЕМЫЙ ГИРОСКОП | 1999 |
|
RU2178142C2 |
| ДИНАМИЧЕСКИ НАСТРАИВАЕМЫЙ ГИРОСКОП | 1973 |
|
SU1840324A1 |
| СПОСОБ НАСТРОЙКИ ГИРОСКОПА | 2004 |
|
RU2253840C1 |

Изобретение относится к области гироскопического приборостроения. Сущность изобретения заключается в том, что способ регулирования динамически настраиваемого гироскопа дополнительно содержит этапы, на которых компенсируют квадратурную составляющую скорости ухода путем снятия фасок с торсионов, соединяющих кардановы кольца с консольными балками в местах, определяемых знаком квадратурной составляющей скорости ухода, с контролем снятия фасок по периодам колебаний невращающегося чувствительного элемента относительно осей карданова подвеса. Технический результат – повышение точности прецессионного динамически настраиваемого гироскопа (ДНГ). 8 ил.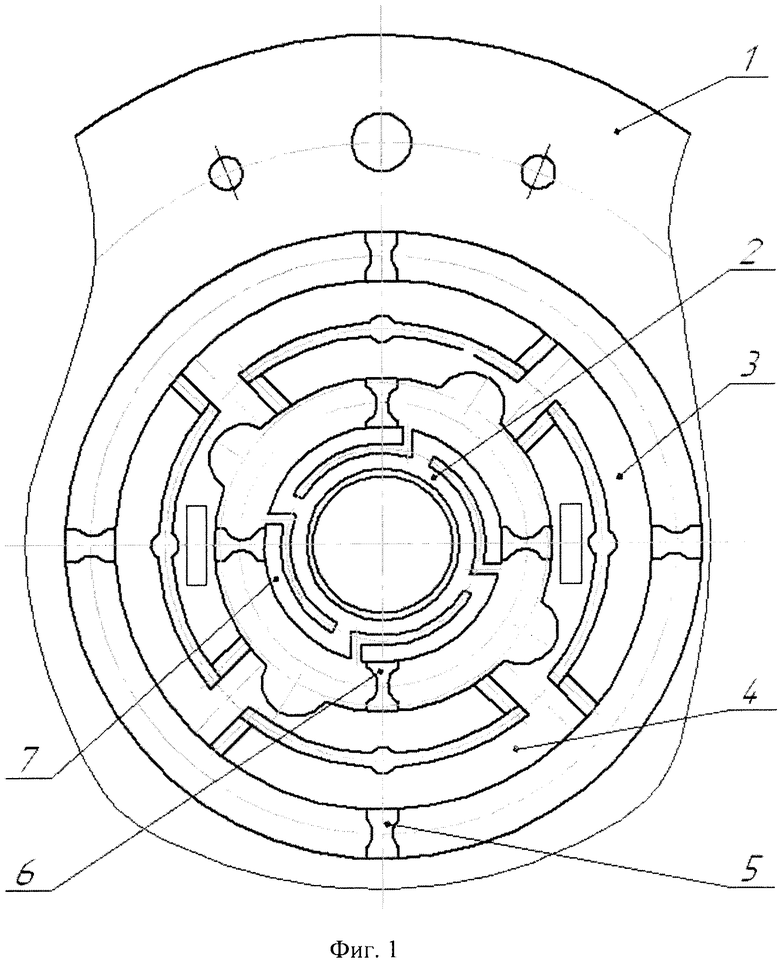
Способ регулирования динамически настраиваемого гироскопа, содержащего монолитный чувствительный элемент, включающий втулку приводного вала, кардановы кольца и упругие элементы - торсионы, соединяющие кольца со втулкой через упругие консольные балки, образованные вырезанными во втулке радиальными и кольцевыми щелями, включающий измерение квадратурной составляющей скорости ухода, отличающийся от известных способов регулирования тем, что с целью повышения точности гироскопа компенсируют квадратурную составляющую скорости ухода путем снятия фасок с торсионов, соединяющих кардановы кольца с консольными балками в местах, определяемых знаком квадратурной составляющей скорости ухода, с контролем снятия фасок по периодам колебаний невращающегося чувствительного элемента относительно осей карданова подвеса.
| СПОСОБ БАЛАНСИРОВКИ | 1987 |
|
SU1487627A1 |
| СПОСОБ ЮСТИРОВКИ ДИНАМИЧЕСКИ НАСТРАИВАЕМОГО ГИРОСКОПА | 1993 |
|
RU2036433C1 |
| CN 101907505 B, 25.01.2012 | |||
| US 2016161255 A1, 09.06.2016. | |||
Авторы
Даты
2019-05-30—Публикация
2018-08-03—Подача