Данное изобретение относится к области измерений линейных и угловых перемещений.
В настоящее время при измерениях линейных и угловых перемещений широкое применение получили преобразователи с так называемыми квадратурными выходными сигналами, под которыми подразумеваются гармонические сигналы, имеющие взаимный фазовый сдвиг на ±90°. В основе подобных преобразователей лежит процесс модуляции физических энергетических полей (магнитного, электрического, светового), возникающей при смещении чувствительного элемента преобразователя, жестко связанного с объектом измерений. При этом имеет место связь между смещениями объекта и числом периодов выходного сигнала преобразователя. В тех случаях, когда период структур чувствительного элемента достаточно мал, для целей регистрации величины смещения объекта бывает достаточным зафиксировать с необходимым знаком число периодов выходного сигнала преобразователя, сформированных преобразователем за время движения объекта измерения. Для этого в середине прошлого века был предложен способ реверсивного счета полос (см. Peck E.R. "Wavelength or length measurement by reversible fringe counting"/ E.R. Peck, S.W. Obetz // J. Opt. Soc. Am. - 1953. Vol. 43, pp 505-509), в основе которого лежит процедура регистрации числа моментов смены полярности одного из квадратурных сигналов на противоположную. При этом счет числа изменений полярности осуществляют с учетом знака направления изменения фазы сигналов. Для этого выходные аналоговые сигналы (Sin X и Cos X) предварительно преобразуют в дискретные, обозначаемые, например, как «S» и «С», которые в отличие от аналоговых имеют только два уровня: нижний и верхний, обозначаемые как «0» и «1». Для учета направления роста фазы сигналов отслеживают направление смены полярности одного из выходных сигналов при постоянстве фазы другого. Например, следят за изменениями полярности косинусной составляющей при постоянстве синусной, т.е. при S=1 выявляют знак сигнала на выходе звена, дифференцирующего сигнал «С». Изменению полярности косинусной составляющей с положительной на отрицательную ставят в соответствие импульсный сигнал «с», формируемый на выходе дифференцирующего звена, а изменению полярности с отрицательной на положительную - ставят в соответствие сигнал «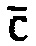 ». При этом и с, и
». При этом и с, и 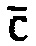 могут принимать значение «0» и «1». Тогда, если выполняется условие, что и «S», и «с» равны 1, то имеет место увеличение фазы квадратур на полный оборот (2π радиан) и надо в реверсивный счетчик добавить «1». И наоборот, если выполняется условие, что и S, и
могут принимать значение «0» и «1». Тогда, если выполняется условие, что и «S», и «с» равны 1, то имеет место увеличение фазы квадратур на полный оборот (2π радиан) и надо в реверсивный счетчик добавить «1». И наоборот, если выполняется условие, что и S, и 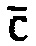 равны 1 то имеет место уменьшение фазы квадратур на полный оборот и надо вычесть из содержимого реверсивного счетчика «1». Сигналам управления счета в реверсивном счетчике соответствуют две логических функции F и В. Здесь F-forward (вперед) и В - back (назад):
равны 1 то имеет место уменьшение фазы квадратур на полный оборот и надо вычесть из содержимого реверсивного счетчика «1». Сигналам управления счета в реверсивном счетчике соответствуют две логических функции F и В. Здесь F-forward (вперед) и В - back (назад):
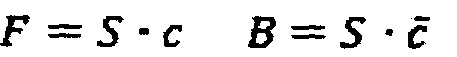
Достаточно скоро (уже в 60- е годы) упомянутый способ реверсивного счета полос был модифицирован с целью увеличения разрешающей способности процесса регистрации фазы (см. Cook H.D., "An automatic fringe counting interferometer for use in the calibration of line scales" / H.D. Cook, LA. Marietta // J. of Research of National Bureau of Standards. C: Engineering and Instrumentation. 1961, vol. 65C, N2, pp 129 -140.). В этом первоисточнике предложены модифицированные логические функции управления направлением счета в реверсивном счетчике, учитывающие все возможные состояния логических переменных S, С, s и с и их инверсий: 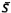 ,
, 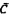 ,
, 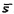 и
и 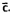 . Соответственно логические функции управления реверсивным счетчиком F и В выглядят теперь следующим образом:
. Соответственно логические функции управления реверсивным счетчиком F и В выглядят теперь следующим образом:
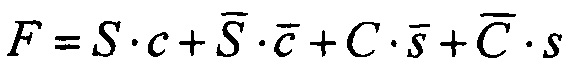 и
и 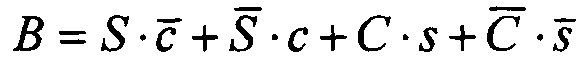
Модифицированный алгоритм позволяет регистрировать приращения фазы квадратур с разрешением до четверти периода. Подобную процедуру регистрации с повышенным разрешением назвали интерполяцией. Очень скоро стало ясно, что возможности модифицированного алгоритма также ограничены. Был предложен алгоритм удвоения чувствительности за счет получения дополнительных квадратур, сдвинутых относительно исходных на ±45° и применения к ним модифицированного алгоритма. Простое сложение двух импульсных последовательностей позволило удвоить число разрешаемых значений фазы до восьми на один период квадратур (т.е. фиксировать приращение фазы квадратур через каждые 45°).
Используя технологию сдвига фаз с помощью потенциометрических фазовращателей, были созданы модули умножения частоты квадратур на 10, 16, 20, 25 и 50. Однако, подобный подход ограничивал допустимую частоту исходных квадратурных сигналов. По мере развития микроэлектронной промышленностью были созданы коммерчески доступные, в интегральном исполнении, быстродействующие многоразрядные аналого-цифровые преобразователи и цифровые сигнальные процессоры. Благодаря им стали развиваться цифровые методы преобразования квадратурных сигналов, в т.ч. цифровые алгоритмы повышения разрешающей способности линейных и угловых преобразователей. В соответствии с этими алгоритмами аналоговые квадратурные сигналы с помощью аналого-цифровых преобразователей (АЦП) преобразуют в цифровые и на этой основе цифровые сигнальные процессоры (ЦСП) вычисляют фазу квадратур, в соответствии с известным выражением:
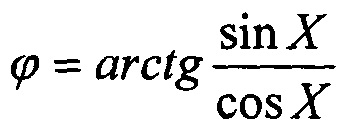
(см., например, Hercher М. "Ultra-high Resolution Interferometric Sensors" // Optics @ Photonics News, Nov., 1991. или Hosoe S. "Laser Interferometric System for Displacement Measurement with High Precision"// Nanotechnology, 1991. V.2, p.88). Для этого в ЦСП вычисляют значение tgϕ, выполнив операцию деления мгновенных значений Sin X и Cos X. Затем вычисляют численное значение фазы ϕ, используя представление функции arc tgϕ рядом Тейлора из 5 элементов разложения вида:
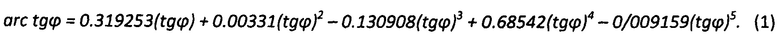
(см. например, J. Burke, J. F. Moynihan, K. Unterkofler «Extraction of high resolution position information from sinusoidal encoders».. Proc. PCIM-Europe 1999, Nuremberg. - P. 217-222).
Для этих алгоритмов интерполяции характерно то, что здесь необходимо выполнять достаточно много вычислительных операций. Разрешаемая способность используемого способа измерения фазы квадратурных сигналов определяется разрядностью аналого-цифровых преобразователей. Например, если разрядность АЦП равна 8, т.е. n=8, то разрешаемая способность регистрации изменений фазы N может достигать 256, а при n=12 число разрешаемых значений фазы достигает уже значения N=4096, т.е. фаза квадратур будет измеряться более точно. Основным недостатком данного способа повышения разрешающей способности является необходимость использования весьма быстродействующих логических элементов и оперативной памяти.
Чтобы существенно снизить требования к элементам схемы электронного блока преобразователя линейных или угловых перемещений одним из авторов данной заявки в свое время был предложен способ измерений, при котором снижение требований осуществлялось за счет распараллеливания процесса счета кратных долей периода квадратурных сигналов и интерполяции дробных частей внутри кратных долей периода квадратурных сигналов (см. Кирьянов В.П., Кокарев С.А. «Лазерно-интерферометрический преобразователь перемещений с субнанометровым разрешением» // Автометрия, 1998, №2, с. 3). Основное отличие данного способа измерения состояло в том, что выработка решения о добавлении или вычитании единицы в реверсивном счетчике преобразователя осуществляется параллельно процедуре получения значения arc tg X, не дожидаясь завершения процедуры вычисления текущего значения фазы квадратурных сигналов. Выработка решения производится на основе анализа значений знаковых (старших) разрядов аналого-цифровых преобразователей (АЦП), преобразующих синхронно квадратурные сигналы преобразователя. Это позволяло заметно снизить требования к быстродействию элементов схем, ответственных за вычисление мгновенных значений фазы квадратур, а процедура счета полос теперь уже не зависела от скорости вычисления функции arc tg X. Кроме того, синхронное и взаимозависимое изменение выходных кодов АЦП и реверсивного счетчика преобразователя снимает проблему стыковки отсчетов числа кратных долей периода и значений дробных долей, получаемых при интерполяции фазы внутри кратных долей.
Данный способ регистрации фазы квадратурных сигналов выбран в данной заявке за прототип. Для него отметим следующее. Основным недостатком процедуры интерполяции промежуточных значений фазы через операцию 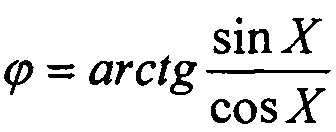 является сложность процедуры вычисления из-за наличия в ней промежуточной операции деления Sin X на Cos X и возведения во вторую, третью, четвертую и пятую степени значения tg X, являющегося результатом деления.
является сложность процедуры вычисления из-за наличия в ней промежуточной операции деления Sin X на Cos X и возведения во вторую, третью, четвертую и пятую степени значения tg X, являющегося результатом деления.
Перед авторами стояла задача упростить и ускорить операцию вычисления промежуточных значений фазы квадратурных сигналов.
Для этого предложен способ регистрации фазы квадратурных сигналов, согласно которому аналоговые квадратурные сигналы преобразуют в цифровые синхронно с помощью двух аналого-цифровых преобразователей, выходы старших разрядов обоих аналого-цифровых преобразователей используют для определения номера текущего квадранта фазовой плоскости квадратурных сигналов и формирования сигнала управления реверсивным счетчиком, который используют для регистрации числа целых периодов изменения фазы квадратурных сигналов, текущий номер квадранта фазовой плоскости запоминают как первый и второй разряды дробной части выходного кода фазы квадратурных сигналов отличающийся тем, что прямые и инверсные значения выходных кодов обоих аналого-цифровых преобразователей складывают между собой в комбинациях, определяемых текущим номером квадранта фазовой плоскости, результат сложения выходных кодов обоих аналого-цифровых преобразователей используют в качестве адреса ячеек памяти в блоке памяти, хранящем младшие разряды кодов дробной части фазы квадратур, которые после считывания заносят в третий и последующие разряды дробной части выходного кода фазы квадратурных сигналов.
Предлагаемый способ регистрации с высоким разрешением фазы квадратурных сигналов позволяет получать результат измерения всего за два рабочих такта цифрового сигнального процессора, используемого в составе блока регистрации, вместо сотни тактов, характерных для стандартных алгоритмов вычисления arctgϕ, таких как алгоритм (1).
На фигуре 1 приведена функциональная схема блока регистрации преобразователя линейных или угловых перемещений, реализующая предложенный способ регистрации фазы квадратурных сигналов. Здесь 1- входные усилители, 2- входные аналого-цифровые преобразователи (АЦП), 3 - инверторы, 4 - дискриминатор направления счета, 5 - регистр с входной логикой, 6 - реверсивный счетчик, 7 - кодировщик квадрантов, 8 - сумматор, 9 - блок памяти, 10 - выходной буферный регистр (в т.ч. 10 - 1 - часть регистра для целочисленных значений кода фазы, 10 - 2 - часть регистра для дробных значений кода фазы), 11 - выход блока регистрации, 12 - линия связи с управляющим компьютером.
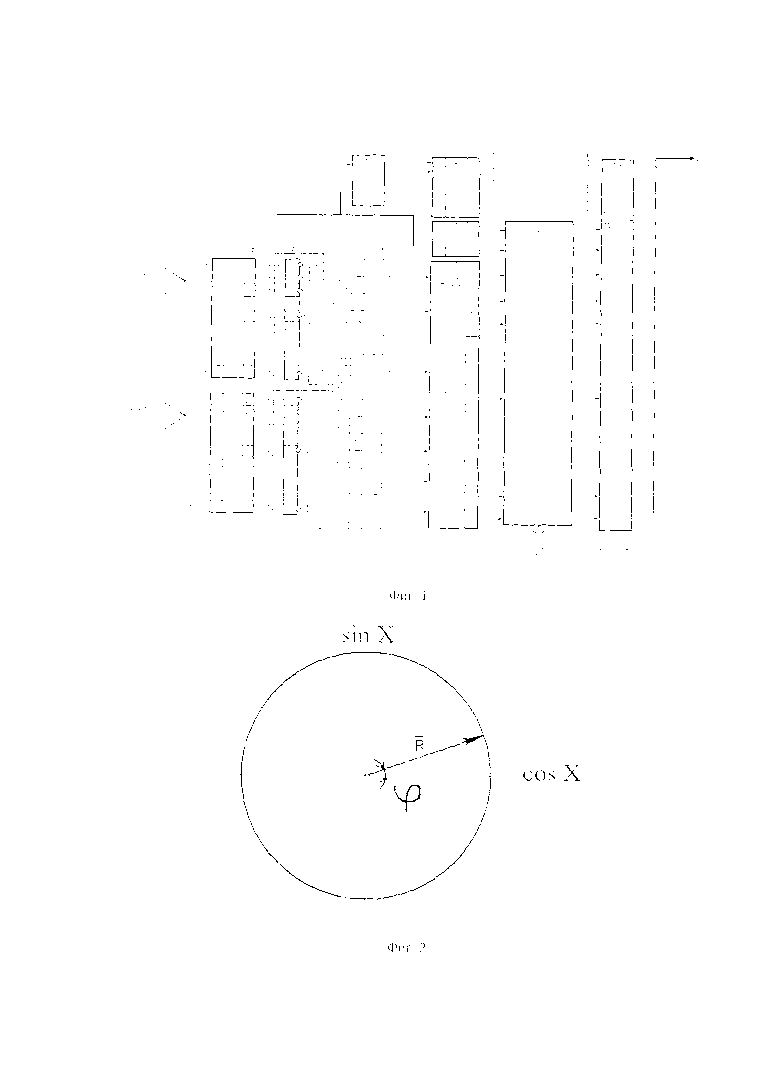
На фигуре 2 приведена фазовая плоскость квадратурных сигналов преобразователя.
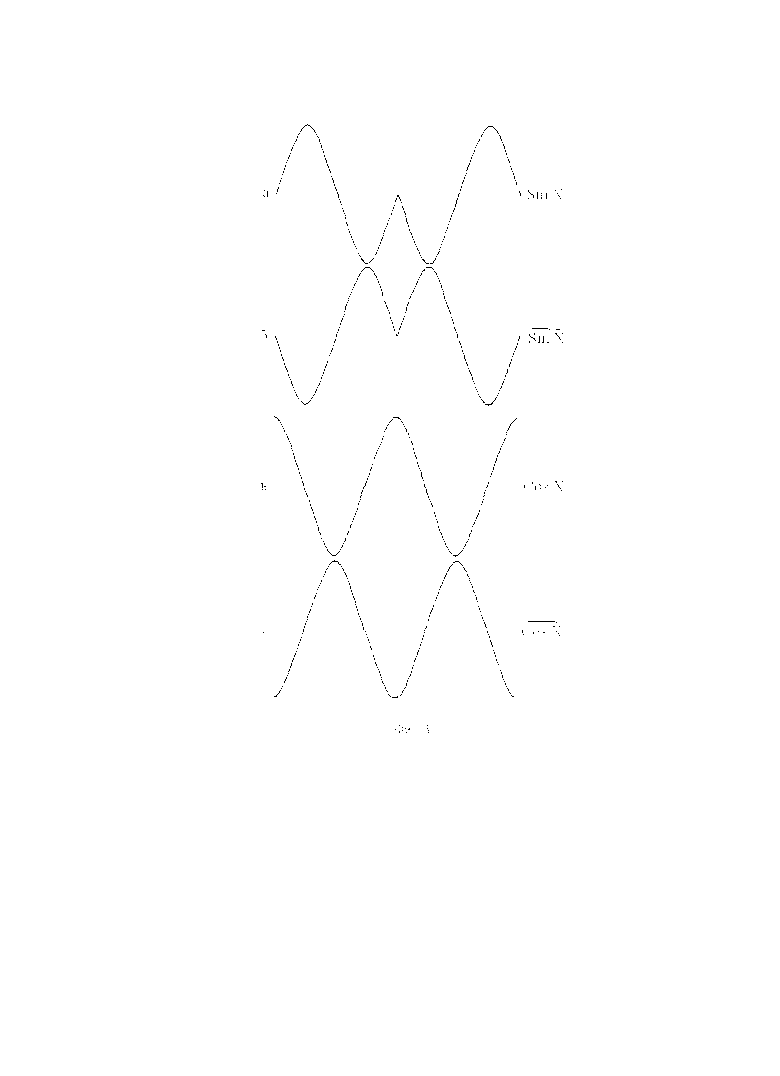
На фигуре 3 приведены эпюры выходных сигналов датчика с растровым сопряжением муарового типа при перемещении на один период растра вперед и на один период -назад. Здесь на фигуре 3, а представлен в аналоговой форме сигнал Sin X, на фигуре 3, б - инверсия от Sin X 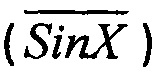 , на фигуре 3, в - Cos X и на фигуре 3, г - инверсия от
, на фигуре 3, в - Cos X и на фигуре 3, г - инверсия от 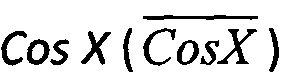 .
.
На фигуре 4 приведены (в аналоговой форме) эпюры формируемых сигналов, пропорциональных результату сложения исходных кодов мгновенных значений квадратур. Здесь на фигуре 4, а приведен сигнал, пропорциональный изменениям фазы в первом и втором разрядах дробной части выходного кода фазы квадратур. На фигуре 4, б - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода в первом квадранте фазовой плоскости, полученное как результат сложения кода Sin X и 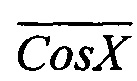 , на фигуре 4, в - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода во втором квадранте фазовой плоскости как результат сложения кода
, на фигуре 4, в - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода во втором квадранте фазовой плоскости как результат сложения кода 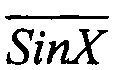 и
и 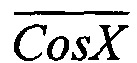 , на фигуре 4, г - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода в третьем квадранте фазовой плоскости как результат сложения кода
, на фигуре 4, г - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода в третьем квадранте фазовой плоскости как результат сложения кода 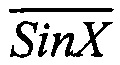 и Cos X,
и Cos X,
на фигуре 4, д - представлено приращение фазы в 3, 4 и т.д. младших разрядах выходного кода в четвертом квадранте фазовой плоскости как результат сложения кода Sin X и Cos X и на фигуре 4, е - представлено изменение фазы, пропорциональное кодам всех n разрядов дробной части выходного кода квадратур.
На фигуре 5 представлена систематическая составляющая погрешности преобразования мгновенных значений квадратур в фазу в интервале от 0° до 90° фазовой плоскости.
Заявляемый способ регистрации угловых или линейных перемещений с повышенным разрешением реализуется следующим образом. На фигуре 1 представлена функциональная схема блока регистрации преобразователя линейных или угловых перемещений, реализующая предложенный способ регистрации фазы квадратурных сигналов в соответствии с формулой изобретения.
Для однозначного описания процесса формирования выходных сигналов и последующего преобразования сигналов в соответствии с предложенным способом регистрации целесообразно ввести понятие фазовой плоскости квадратур (квадратурных сигналов) (см. фиг. 2.) Фазовая плоскость квадратур (ФПК) представляет собой ортогональную систему координат Sin X и Cos X, аналогичную декартовой системе координат, только в качестве координаты X используется переменная Cos X и вместо координаты Y-используется переменная Sin X. Далее вводится понятие радиуса-вектора  с углом поворота ϕ на фазовой плоскости. Проекция радиуса-вектора
с углом поворота ϕ на фазовой плоскости. Проекция радиуса-вектора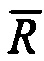 на горизонтальную ось - есть квадратура Cos X, а проекция на вертикальную ось - есть квадратура Sin X. Исходное состояние: ϕ=0. Приращение угла ϕ в сторону увеличения фазы квадратур происходит в направлении против движения часовой стрелки. Данным условиям соответствуют пространственные (временные) эпюры сигналов, представленные на фигуре 3, когда объект смещается в положительном направлении (т.е. в сторону увеличения значения фазового угла) на один период чувствительного элемента преобразователя, а затем - назад, в обратном направлении, также на один период. С выхода датчика (как углового, так и линейного) квадратурные сигналы поступают на входные усилители 1 блока регистрации, которые передают сигналы с линии связи на входы двух АЦП 2. Прямые выходные коды преобразователей 2 пропорциональны Sin X и Cos X. В табл. 1 представлены значения выходных кодов преобразователей 2 для обеих квадратур во всех четырех квадрантах базовой плоскости.
на горизонтальную ось - есть квадратура Cos X, а проекция на вертикальную ось - есть квадратура Sin X. Исходное состояние: ϕ=0. Приращение угла ϕ в сторону увеличения фазы квадратур происходит в направлении против движения часовой стрелки. Данным условиям соответствуют пространственные (временные) эпюры сигналов, представленные на фигуре 3, когда объект смещается в положительном направлении (т.е. в сторону увеличения значения фазового угла) на один период чувствительного элемента преобразователя, а затем - назад, в обратном направлении, также на один период. С выхода датчика (как углового, так и линейного) квадратурные сигналы поступают на входные усилители 1 блока регистрации, которые передают сигналы с линии связи на входы двух АЦП 2. Прямые выходные коды преобразователей 2 пропорциональны Sin X и Cos X. В табл. 1 представлены значения выходных кодов преобразователей 2 для обеих квадратур во всех четырех квадрантах базовой плоскости.

Текущие значения кодов старших разрядов обоих преобразователей 2 однозначно определяют текущий номер квадранта фазовой плоскости.
Процедуру дешифровки текущего значения кода квадранта осуществляет кодировщик 7 (см. фиг. 1), который передает со своих двух выходов текущий код квадранта для записи в ячейки выходного буферного регистра 10 с «весами» 2-1 и 2-2. Если текущий угол поворота ϕ радиуса-вектора 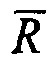 на фазовой плоскости находится в интервале от 0° до 90°, то согласно Табл. 1 в старших разрядах АЦП 2 обоих составляющих фиксируется «1». Это состояние выявляется логической функцией sn⋅cn=1, где sn - состояние выхода старшего разряда аналого-цифрового преобразователя 2 синусной квадратуры, а cn - то же, но для косинусной квадратуры. На это состояние кодировщик формирует код первого квадранта - 00, который и заносит его в ячейки буферного регистра 10. Во втором квадранте в старшем разряде АЦП 2 синусной составляющей фиксируется «1», а АЦП косинусной составляющей - «0». Это состояние выявляется логической функцией
на фазовой плоскости находится в интервале от 0° до 90°, то согласно Табл. 1 в старших разрядах АЦП 2 обоих составляющих фиксируется «1». Это состояние выявляется логической функцией sn⋅cn=1, где sn - состояние выхода старшего разряда аналого-цифрового преобразователя 2 синусной квадратуры, а cn - то же, но для косинусной квадратуры. На это состояние кодировщик формирует код первого квадранта - 00, который и заносит его в ячейки буферного регистра 10. Во втором квадранте в старшем разряде АЦП 2 синусной составляющей фиксируется «1», а АЦП косинусной составляющей - «0». Это состояние выявляется логической функцией 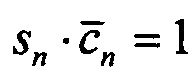 . Для этого состояния подключенные к выходам преобразователей 2 инверторы 3 формируют цифровые инверсные сигналы
. Для этого состояния подключенные к выходам преобразователей 2 инверторы 3 формируют цифровые инверсные сигналы 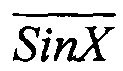 и
и 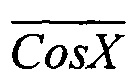 . На это состояние кодировщик формирует код второго квадранта - 01, который и заносит в ячейки буферного регистра 10. Аналогичным образом распознается нахождение радиуса-вектора в третьем и четвертом квадрантах фазовой плоскости квадратур и производится занесение в буферный регистр соответствующих кодов (10 и 11, соответственно).
. На это состояние кодировщик формирует код второго квадранта - 01, который и заносит в ячейки буферного регистра 10. Аналогичным образом распознается нахождение радиуса-вектора в третьем и четвертом квадрантах фазовой плоскости квадратур и производится занесение в буферный регистр соответствующих кодов (10 и 11, соответственно).
Более мелкие значения дробных долей полного оборота фазы, соответствующие ячейкам выходного регистра 10 с «весами» 2-3, 2-4 и т.д. до 2-n от полного оборота, выявляются путем сложения мгновенных значений кодов синусной и косинусной составляющих квадратур в комбинациях, определяемых положением радиуса-вектора 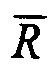 в текущем квадранте фазовой плоскости. При этом в первом квадранте складываются коды, пропорциональные Sin X и
в текущем квадранте фазовой плоскости. При этом в первом квадранте складываются коды, пропорциональные Sin X и 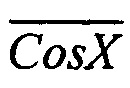 ; во втором квадранте - коды, пропорциональные
; во втором квадранте - коды, пропорциональные 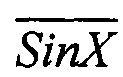 и
и 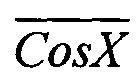 ; в третьем квадранте - коды, пропорциональные
; в третьем квадранте - коды, пропорциональные 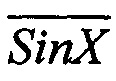 и Cos X, и в четвертом квадранте -складываются коды, пропорциональные Sin X и Cos X. Затем результат сложения смещается на половину его диапазона изменения и запоминается его в ячейках выходного буферного регистра 10 с «весами» 2-3, 2-4 и т.д. до 2-n.
и Cos X, и в четвертом квадранте -складываются коды, пропорциональные Sin X и Cos X. Затем результат сложения смещается на половину его диапазона изменения и запоминается его в ячейках выходного буферного регистра 10 с «весами» 2-3, 2-4 и т.д. до 2-n.
Суть выполнения указанных процедур рассмотрим с помощью эпюр квадратур Sin X, 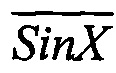 , Cos X и
, Cos X и 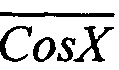 , представленных на фигуре 4.
, представленных на фигуре 4.
Здесь на эпюре 4, а приведен аналоговый ступенчатый сигнал, пропорциональный изменениям кода фазы в первом и втором разрядах дробной части выходного регистра (10-2) кода фазы квадратур. Одновременно с этим в младших разрядах регистра происходит формирование более мелких долей дробной части выходного кода.
При этом, если в первом квадранте фазовой плоскости складывать коды Sin X и 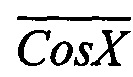 (фигура 4, б), то сумма мгновенных значений обеих квадратур представляет собой линейную функцию, которой можно поставить в соответствие изменение мгновенных значений фазы квадратур, если эту сумму предварительно отнормировать. В предлагаемом способе результат сложения кодов, пропорциональных Sin X и
(фигура 4, б), то сумма мгновенных значений обеих квадратур представляет собой линейную функцию, которой можно поставить в соответствие изменение мгновенных значений фазы квадратур, если эту сумму предварительно отнормировать. В предлагаемом способе результат сложения кодов, пропорциональных Sin X и 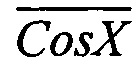 , нормируют за счет того, что результат сложения заносят в 3, 4 и последующие младшие разряды регистра (10-2), что эквивалентно сдвигу числа вправо на три разряда, т.е. делению на 8. Этот процесс описывается выражением (2) и легко формализуется:
, нормируют за счет того, что результат сложения заносят в 3, 4 и последующие младшие разряды регистра (10-2), что эквивалентно сдвигу числа вправо на три разряда, т.е. делению на 8. Этот процесс описывается выражением (2) и легко формализуется:

Например, в первом квадранте, согласно Таблице 1, в старшем разряде АЦП синусной составляющей присутствует «1», которая разрешает проходить на входы сумматора 9 коды, пропорциональные 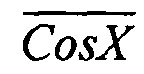 . Одновременно в старшем разряде АЦП косинусной составляющей также присутствует «1», которая разрешает проходить на входы сумматора 8 коды, пропорциональные Sin X. Результат сложения в сумматоре двух кодов дает в интервале (0°, 90°) знакопеременную кусочно-линейную функцию. Чтобы эта кусочно-линейная функция однозначно соответствовала изменению фазы квадратур в данном квадранте, результат сложения смещают в одну сторону на половину его диапазона изменения и делят на 8 для того, чтобы отнормировать результат сложения на диапазон изменения фазы в данном квадранте.
. Одновременно в старшем разряде АЦП косинусной составляющей также присутствует «1», которая разрешает проходить на входы сумматора 8 коды, пропорциональные Sin X. Результат сложения в сумматоре двух кодов дает в интервале (0°, 90°) знакопеременную кусочно-линейную функцию. Чтобы эта кусочно-линейная функция однозначно соответствовала изменению фазы квадратур в данном квадранте, результат сложения смещают в одну сторону на половину его диапазона изменения и делят на 8 для того, чтобы отнормировать результат сложения на диапазон изменения фазы в данном квадранте.
Фактически указанные выше операции реализуются, когда кодовый эквивалент результата сложения заносится в ячейки (2-3…2-n) выходного буферного регистра 10. В этом случае происходит смещение результата сложения в однополярную область изменений и деление на 8 за счет параллельного сдвига кода результата сложения вправо относительно кода числа полных оборотов фазы.
Аналогичные операции выполняют во втором, третьем и четвертом квадрантах фазовой плоскости.
Сигнал, пропорциональный изменению кодов во всех п разрядах регистра (10-2), представлен на фигуре 4, е.
Количественные показатели процедуры сложения кодов Sin X и 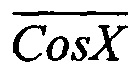 в соответствии с указанным алгоритмом оценены в Таблице 2 для восемнадцати значений фазы, взятых через 5°. Еще четыре значения фазы выбраны для определения экстремального отклонения результата преобразования мгновенных значений квадратур в мгновенные значения фазы от линейной зависимости. Для поиска значений Sin X и Cos X фаза квадратур приведена в третьем столбце в радианах, а для сличения результата преобразования в седьмом столбце пересчитана в относительных единицах. Результат преобразования согласно алгоритма (2) приведен в столбце 6. Погрешность преобразования мгновенных значений квадратур в мгновенные значения фазы представлена в 8-м столбце таблицы 2. В нем оценивается разность между истинным значением фазы (в относительных единицах) и значением фазы, полученным согласно предлагаемому алгоритму.
в соответствии с указанным алгоритмом оценены в Таблице 2 для восемнадцати значений фазы, взятых через 5°. Еще четыре значения фазы выбраны для определения экстремального отклонения результата преобразования мгновенных значений квадратур в мгновенные значения фазы от линейной зависимости. Для поиска значений Sin X и Cos X фаза квадратур приведена в третьем столбце в радианах, а для сличения результата преобразования в седьмом столбце пересчитана в относительных единицах. Результат преобразования согласно алгоритма (2) приведен в столбце 6. Погрешность преобразования мгновенных значений квадратур в мгновенные значения фазы представлена в 8-м столбце таблицы 2. В нем оценивается разность между истинным значением фазы (в относительных единицах) и значением фазы, полученным согласно предлагаемому алгоритму.
Согласно результатам, приведенным в восьмом столбце таблицы, погрешность регистрации имеет периодический характер. В интервале фаз от 0° до 45° разность значений -отрицательная, причем экстремум функции приходится на значение фазы, равное 19°, для которой величина ошибки составляет -0.005271, а в интервале фаз от 45° до 90° разность значений - положительная. Положительный экстремум функции приходится на значение фазы, равное 71°, для которой величина ошибки составляет +0.005271.
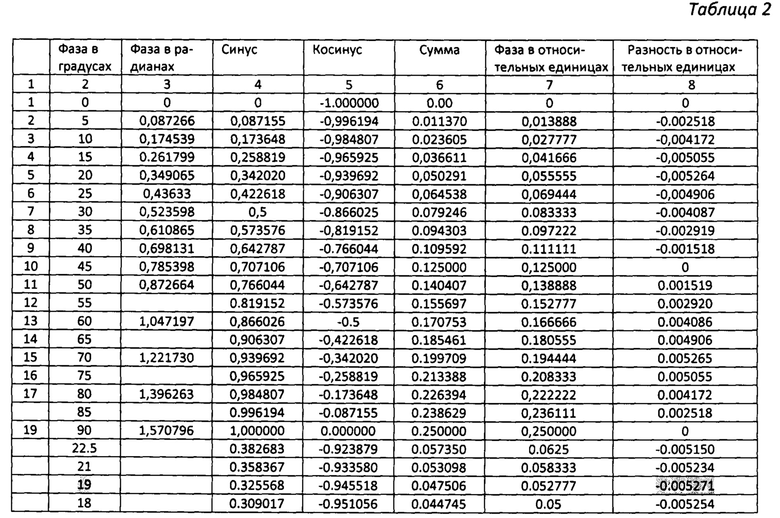
Графически отклонения от линейности процесса преобразования мгновенных значений квадратур в их фазу представлены на фигуре 5. Эти экстремальные значения (±0.005271) не превышают значения кванта ячейки выходного регистра с «весом» 2-7 (0.0078125). Т.е. методическая ошибка предлагаемого алгоритма не превышает 2-7 от 2π радиан фазы квадратур. Например, для углового датчика с числом штрихов N=36000 это составит неопределенность, не превышающую ±0,189''. Или для линейного датчика с периодом растра, равным 20 мкм, эта неопределенность составит 0,1 мкм. Для лазерного интерферометра с плоскими ретрорефлекторами, имеющему основное разрешение, равное 0,16820496 мкм, данная неопределенность не превысит 0.8 нм.
Однако, наличие указанной методической (систематической) погрешности не является сдерживающим фактором, когда требуется обеспечить более высокую точность позиционирования, т.к. она может быть устранена путем ее компенсации. Для этого в состав блока регистрации включен блок памяти 9, адресные шины которого управляются сигналами с выхода сумматора 8. На каждый входной сигнал из блока памяти считывается корректированное значение фазы. Если в блоке регистрации используются 12-тиразрядные АЦП, то имеется возможность реализовать регистрацию фазы квадратур с разрешением до 2-12 от базовой разрешающей способности датчик, что составляет 0,0002441 от полного оборота фазы квадратур.
Предлагаемый способ регистрации фазы квадратурных сигналов позволяет регистрировать как линейные, так и угловые перемещения с повышенным разрешением не только для случая гармонических (Sin X, 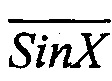 , Cos X и
, Cos X и 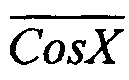 ) квадратурных сигналов, но и для случая генерации треугольных выходных сигналов.
) квадратурных сигналов, но и для случая генерации треугольных выходных сигналов.
Например, в случае т.н. «грубых» растров, имеющих период штрихов более 80 мкм, чаще всего реализуется т.н. обтюрационное сопряжение растров, при котором формируются квадратурные сигналы треугольной формы (см. «Фотоэлектрические преобразователи информации», под редакцией проф. Л.Н. Преснухина, / М.: «Машиностроение», 1974). Для таких сигналов интерполяция промежуточных значений фазы через операцию 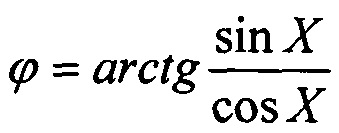 неприемлема из-за значительных отклонений формы обеих квадратур от синусоид. В принципе, квадратурные сигналы треугольной формы позволяют непосредственно повышать разрешающую способность преобразователя, и это можно было бы использовать, если бы линейная зависимость между мгновенными значениями выходного сигнала и фазой квадратур выдерживалось бы во всем диапазоне изменения фазы. Однако в случаях, когда окна сопрягаемых растров перекрыты значительно и остаются только узкие щели, то начинают отрицательно сказываться явления дифракции света на краях штрихов и законы полного внутреннего отражения света на границах раздела стекло/воздух. Они существенно перераспределяют потоки света непредусмотренным образом. Для света с длиной волны, порядка 0,8 мкм (наиболее часто используемой в фотоэлектрических преобразователях), ширина щели порядка 1,2 мкм и менее, начинает вносить существенную нелинейность, например, из-за явления полного отражения значительная часть света направляется внутрь стеклянного носителя и не попадает на фотоприемник.
неприемлема из-за значительных отклонений формы обеих квадратур от синусоид. В принципе, квадратурные сигналы треугольной формы позволяют непосредственно повышать разрешающую способность преобразователя, и это можно было бы использовать, если бы линейная зависимость между мгновенными значениями выходного сигнала и фазой квадратур выдерживалось бы во всем диапазоне изменения фазы. Однако в случаях, когда окна сопрягаемых растров перекрыты значительно и остаются только узкие щели, то начинают отрицательно сказываться явления дифракции света на краях штрихов и законы полного внутреннего отражения света на границах раздела стекло/воздух. Они существенно перераспределяют потоки света непредусмотренным образом. Для света с длиной волны, порядка 0,8 мкм (наиболее часто используемой в фотоэлектрических преобразователях), ширина щели порядка 1,2 мкм и менее, начинает вносить существенную нелинейность, например, из-за явления полного отражения значительная часть света направляется внутрь стеклянного носителя и не попадает на фотоприемник.
В результате они ограничивают возможность интерполяции фазы только тридцатью двумя промежуточными дискретными значениями (т.е. порядка 2-5 от полного периода изменения фазы квадратур).
Ситуацию можно заметно улучшить, если применить предлагаемый способ для регистрации квазитреугольных (т.е. почти треугольных) сигналов в преобразователях с растровым сопряжением обтюрационного типа. Цифровая обработка сигналов в соответствии с выражением (2) уменьшает вклад нелинейностей этого преобразователя до 2-9 от полного периода изменения фазы квадратур. Например, для линейного преобразователя с периодом растра, равным 80 мкм, это позволяет даже в усеченном виде (т.е. без коррекции) реализовать разрешение, равное 0,1 мкм.
Таким образом, технический эффект от использования предлагаемого способа проявляется в двух аспектах. Первый - заметное сокращение времени формирования цифрового значения фазы квадратур. Это позволит существенно снизить динамическую погрешность управления параметрами движения управляемого объекта. Даже в усеченном варианте реализации предлагаемого способа регистрации фазы квадратурных сигналов (т.е. без коррекции методической погрешности) возможно повышение разрешающей способности преобразователей как с гармоническими, так и с квазитреугольными выходными сигналами до (2-8-2-9) от полного периода изменения фазы квадратур. Использование полной версии способа позволяет довести разрешение до 2-12-2-14 от полного периода изменения фазы квадрату, в том числе и для квазитреугольных сигналов сопряжений обтюрационного типа.
| название | год | авторы | номер документа |
|---|---|---|---|
| Эталон единицы плоского угла | 2016 |
|
RU2637727C1 |
| Управляемое фазосдвигающее устройство | 1980 |
|
SU907460A1 |
| Способ определения мгновенных значений фазового сдвига электрических сигналов | 1987 |
|
SU1499265A1 |
| УСТРОЙСТВО ПРЕОБРАЗОВАНИЯ МНОГОФАЗНОГО ПЕРИОДИЧЕСКОГО СИГНАЛА | 1991 |
|
RU2017063C1 |
| Компенсационный анализатор гармо-НиК | 1974 |
|
SU822060A1 |
| Устройство для цифровой фильтрации на основе дискретного преобразования Фурье | 1990 |
|
SU1795475A1 |
| СПОСОБ ОБРАБОТКИ НЕКОГЕРЕНТНОГО ПАКЕТА РАДИОИМПУЛЬСОВ | 1992 |
|
RU2054691C1 |
| Преобразователь угла поворота вала в код | 1985 |
|
SU1312737A1 |
| СПОСОБ ИЗМЕРЕНИЯ АКТИВНОЙ И РЕАКТИВНОЙ СОСТАВЛЯЮЩИХ МОЩНОСТИ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА С УСТАНОВИВШИМСЯ СИНУСОИДАЛЬНЫМ РЕЖИМОМ | 1990 |
|
RU2039358C1 |
| ФАЗОМЕТР С ГЕТЕРОДИННЫМ ПРЕОБРАЗОВАНИЕМ ЧАСТОТЫ | 2013 |
|
RU2551837C2 |
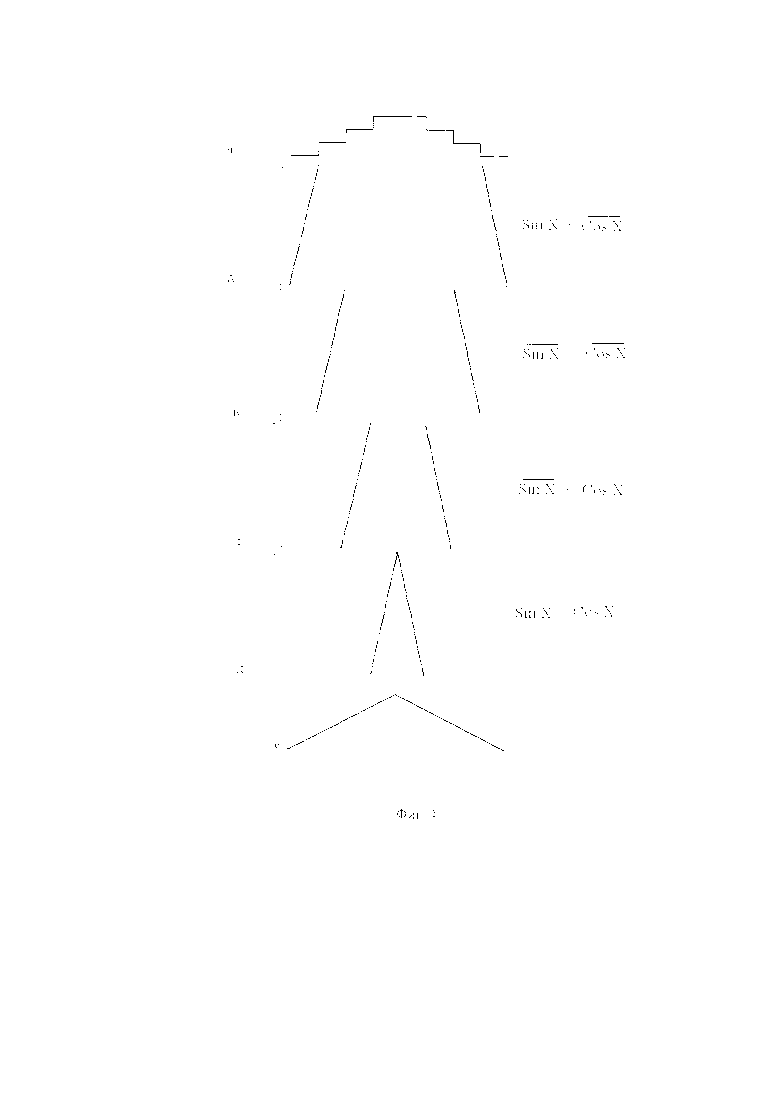

Изобретение относится к средствам измерений с помощью фотоэлектрических угловых и линейных преобразователей перемещений. Технический результат заключается в повышении скорости обработки сигналов. В способе аналоговые квадратурные сигналы преобразуют синхронно в цифровые и определяют номера текущего квадранта фазовой плоскости квадратурных сигналов и формируют сигналы управления реверсивным счетчиком, который используют для регистрации числа целых периодов изменения фазы квадратурных сигналов, текущий номер квадранта фазовой плоскости запоминают как первый и второй разряды дробной части выходного кода фазы квадратурных сигналов, результат сложения выходных кодов обоих аналого-цифровых преобразователей используют в качестве адреса ячеек памяти в блоке памяти, хранящем младшие разряды кодов дробной части фазы квадратур, которые после считывания из блока памяти заносят в третий и последующие разряды дробной части выходного кода фазы квадратурных сигналов. 2 табл., 5 ил.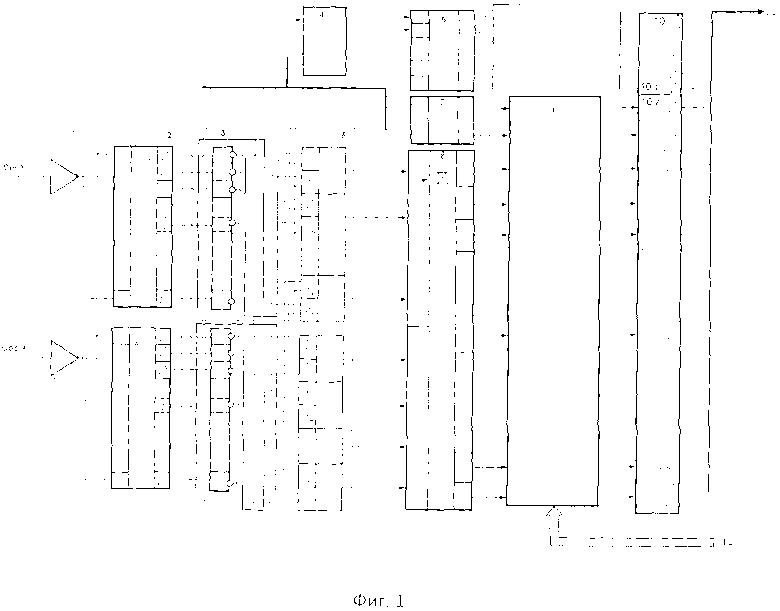
Способ регистрации фазы квадратурных сигналов, согласно которому аналоговые квадратурные сигналы преобразуют синхронно в цифровые с помощью двух аналого-цифровых преобразователей, выходы старших разрядов обоих аналого-цифровых преобразователей используют для определения номера текущего квадранта фазовой плоскости квадратурных сигналов и формирования сигналов управления реверсивным счётчиком, который используют для регистрации числа целых периодов изменения фазы квадратурных сигналов, текущий номер квадранта фазовой плоскости запоминают как первый и второй разряды дробной части выходного кода фазы квадратурных сигналов, отличающийся тем, что прямые и инверсные значения выходных кодов обоих аналого-цифровых преобразователей складывают между собой в комбинациях, определяемых текущим номером квадранта фазовой плоскости, результат сложения выходных кодов обоих аналого-цифровых преобразователей используют в качестве адреса ячеек памяти в блоке памяти, хранящем младшие разряды кодов дробной части фазы квадратур, которые после считывания из блока памяти заносят в третий и последующие разряды дробной части выходного кода фазы квадратурных сигналов.
| ВРЕМЯИМПУЛЬСНЫЙ КВАДРАТИЧНЫЙ ПРЕОБРАЗОВАТЕЛЬ | 1998 |
|
RU2149449C1 |
| ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНЫЙ СИНТЕЗАТОР С КВАДРАТУРНЫМИ ВЫХОДАМИ | 2005 |
|
RU2294054C1 |
| US 4349897, 14.09.1982 | |||
| Пюпитр для работы на пишущих машинах | 1922 |
|
SU86A1 |
Авторы
Даты
2019-06-28—Публикация
2018-06-18—Подача