Изобретение относится к области развивающих игр, а именно к трехмерным ручным головоломкам - конструкторам, применяемым для развития пространственного и логического мышления, мелкой моторики рук, а также пространственного воображения.
Известен (HU, патент 170062, опубл. 28.03.1977) кубик Рубика 3x3x3, содержащий 27 игровых элементов и крестообразную опору с тремя перпендикулярными осями на которой закреплены шесть из них, способных вращаться вокруг своей оси, и в совокупности с еще 21 игровым элементом сложной геометрической формы они собираются в механически жесткий куб 3x3x3 и образуют по каждой из трех осей три конструктивно связанных подвижных слоя игровых элементов, видимая поверхность которых представляет собой 54 игровые грани 1x1 окрашенных по 9 штук в 6 различных цветов в соответствии с принадлежностью к одной из шести граней 3x3 куба 3x3x3, при этом в любой игровой операции- повороте грани вокруг оси задействованы девять элементов для верхнего и нижнего слоя и восемь для среднего слоя.
Недостатком известной головоломки является конструкция механизма крепления подвижных элементов, который ограничивает изменение количества элементов и свободу их перемещения, например поворот одного углового элемента независимо относительно других или сдвиг слоя составных частей для послойного перемешивания, а так же и то что из 162 граней принадлежащих 27 кубикам в игре задействованы только 54 видимые грани, а 108 невидимых граней не задействованы в игре.
Известен также (CN, патент 2825035, опубл. 11.10.2006) КУБ ТАНГРАМ, состоящий из шести идентичных геометрических фигур в виде четырехгранных пирамид, объединенных вершинами к центру, каждая из которых состоит из соединенных между собой семи различных острых конических многогранников, основания каждой из пирамид являются одной из граней куба, а стороны основания образуют ребра куба.
Основным недостатков этой конструкции является то, что собираемая фигура - куб не имеет возможности преобразования в другие геометрические формы.
Известна (US, заявка 2009014954, опубл. 15.01.2009), трехмерная игрушка - головоломка, содержащая множество многогранников-тетраэдров (пазлов), представляющих собой правильные пирамиды с квадратным основанием, которые могут быть собраны в различные геометрические формы. Поверхности указанных компонентов могут быть снабжены магнитными элементами для удержания указанных компонентов в сложной форме.
Игрушка предназначена для складывания произвольных фигур (как из кубиков), а не - трансформации в разные формы, как единого объекта. Причем, в каждой отдельной фигуре может быть произвольное количество элементов, объединенных в разной последовательности и разными гранями. Магниты в элементах этой головоломки нужны только лишь для того, чтобы элементы держались вместе. Причем собрать можно только такие наборы фигур, которые способны жестко соединяться друг с другом плоскостями посредством магнитов. Например, нельзя компоновать такие фигуры, у которых плоскости не соприкасаются друг с другом вплотную, поскольку в этом случае, тетраэдры не способны стыковаться друг с другом. Причиной этого является отсутствие соединений между ребрами боковых граней соседних пирамид.
Известна игрушка - трансформер (GB, заявка 2107200, опубл. 27.041983), содержащая одинаковые сегменты (тетраэдры), где каждый соединен с двумя другими, при этом каждая пара из двух соседних соединена гибкими пленками. Трансформация происходит путем манипуляция блоками вокруг шарниров, образованных между соседними блоками. Основная форма игрушки - куб, который содержит 12 сегментов (тетраэдров), в основании которых лежат прямоугольные равнобедренные треугольники, при этом высотой сегмента является высота перпендикулярной к основанию грани.
Недостатком данного решения является соединение сегментов куба последовательно между собой парами ребер боковых граней соседних пирамид посредством конструктивного узла в виде гибкого соединения, что усложняет конструкцию, снижает надежность и срок эксплуатации гибкого соединения. К тому же гибкое соединение делает невозможным разъединение элементов между собой, отделение их друг от друга и всей конструкции в целом, сборку их в другой последовательности, что ограничивает число трансформаций геометрических фигур.
Известна (http://puzzlemochalov.narod.ru/3D/chess_cub.htm,) головоломка - шахматный куб. Предлагаемая головоломка существенно повышает занимательность головоломки шахматный куб, так как правила ее сборки соответствуют правилу притяжения магнитных полюсов и соблюдаются автоматически благодаря физическим силам магнитных взаимодействий.
Кроме шахматного куба, имеющего двухцветную раскраску элементов, существует развивающая игра широко известная в РФ под названием «кубики Никитина» (https://sovets.net/15374-kubiki-nikitina.html) с многоцветной окраской элементов, предлагаемая головоломка-конструктор расширяет возможности по развитию мелкой моторики и улучшает занимательность кубиков Никитина.
Наиболее близким аналогом разработанного технического решения можно признать (RU, патент 2597870, опубл. 20.09.016) головоломку, состоящую из подвижных выпуклых многогранников, имеющих разное оформление граней или одинаковое, скрепленных друг с другом и перемещаемых относительно друг друга в процессе игры, причем выпуклые многогранники скрепляются друг с другом посредством магнитов, без закрепления размещенных в полостях под гранями многогранников и закрытых сверху плоскостью грани, свободно поворачивающихся только в плоскости грани и имеющих оба магнитных полюса, обращенных к плоскости грани, при этом на внешних, видимых гранях элементов многогранника патента 2597870, магнитные крепления отсутствуют, что является препятствием для операции перестановки слоя элементов любой видимой грани путем отделения слоя от фигуры и последующим его переворотом на 180 вокруг оси лежащей в плоскости грани и стыковки с исходным многогранником.
Недостатком известных головоломок следует признать их ограниченные возможности по модификации взаимного положения многогранников, что ограничивает возможности их использования.
Техническая проблема, на решение которой направлена разработанная головоломка - конструктор, состоит в устранении ограничений на несколько типов теоретически возможных операции с составными элементами конструкции многогранника, накладываемых механическим шарниром.
Технический результат, достигаемый при реализации разработанного технического решения, состоит в возможности осуществления принципиально новых игровых операций с блоками, гранями и ребрами, составленных из элементов, допускающими перевороты со сменой поверхности контакта магнитной системы грани (слоя из элементов) или ребра (линейного отрезка из элементов) с многогранником (блоком из элементов), а так же, допускающих повороты единичных элементов на месте без изменения положения остальных элементов с сохранением механической устойчивости конструкции многогранника и может служить учебным пособием для изучающих группы симметрии геометрических объектов-комплексов наделенных физическими свойствами.
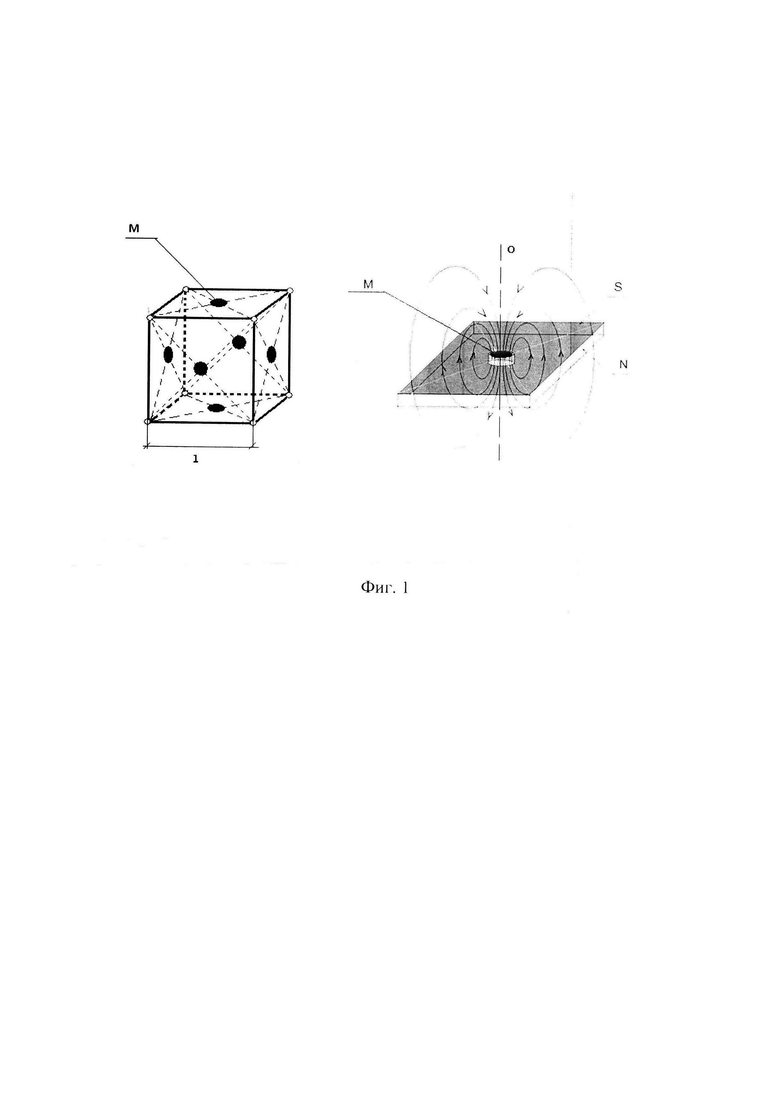
Для достижения указанного технического результата предложено использовать разработанную конструкцию настольной логической игры, магнитной головоломки с функцией конструктора. Указанная игра-головоломка предназначена для обучения и развития пользователей представляет собой многогранник W собранный из элементов магнитно-гранецентрированных ячеек-многогранников (см. фиг 1, на которой изображены элементы W - гексаэдра NxNxN), с гранями в виде правильных многоугольников (квадраты для гексаэдра), в центре которых жестко закреплены магнитные диски определенной полярности, причем элементарные ячейки - многогранники, входящие в состав элементов многогранника W, имеют различную геометрическую развертку магнитной полярности граней, а в собранном виде вступают в конструктивную связь благодаря магнитным силам и образуют механически жесткую фигуру многогранника W.
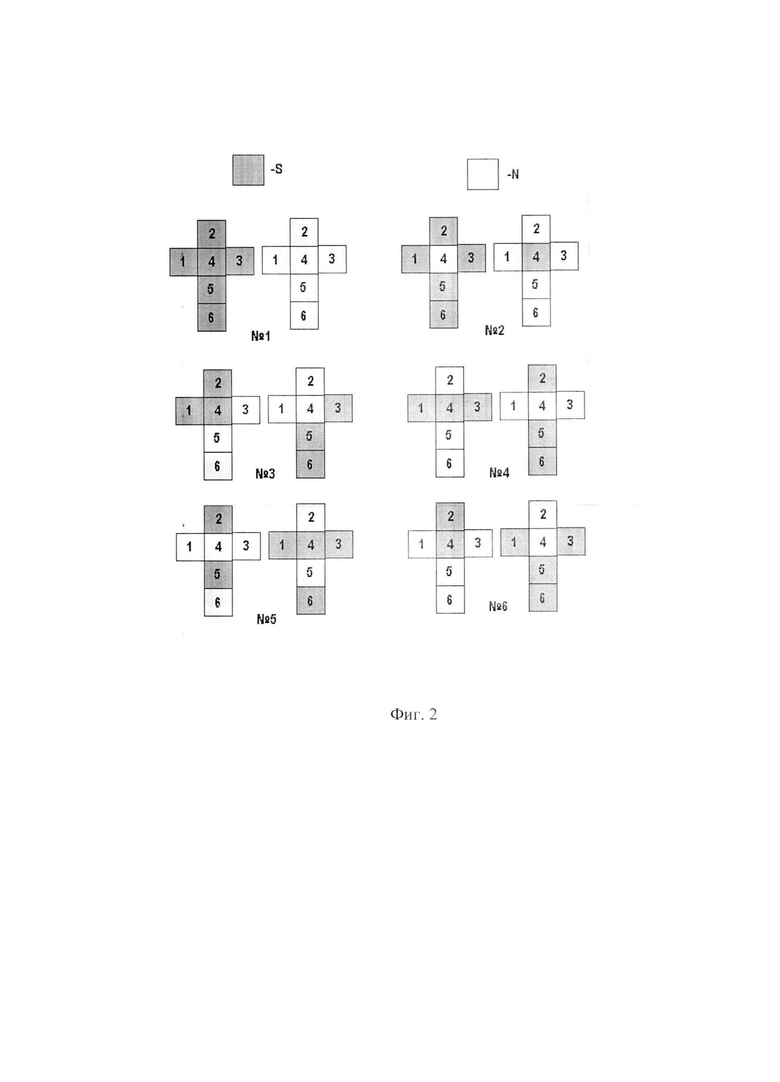
На фиг. 2 представлены шесть видов различных геометрических разверток магнитных полярности граней возможных для гексаэдра, и в каждый вид входит две развертки: исходная и антисимметричная ей, в которой полярность N меняется на полярность S, и соответственно полярность S заменяется на N для каждой из шести единичных грани исходной развертки.
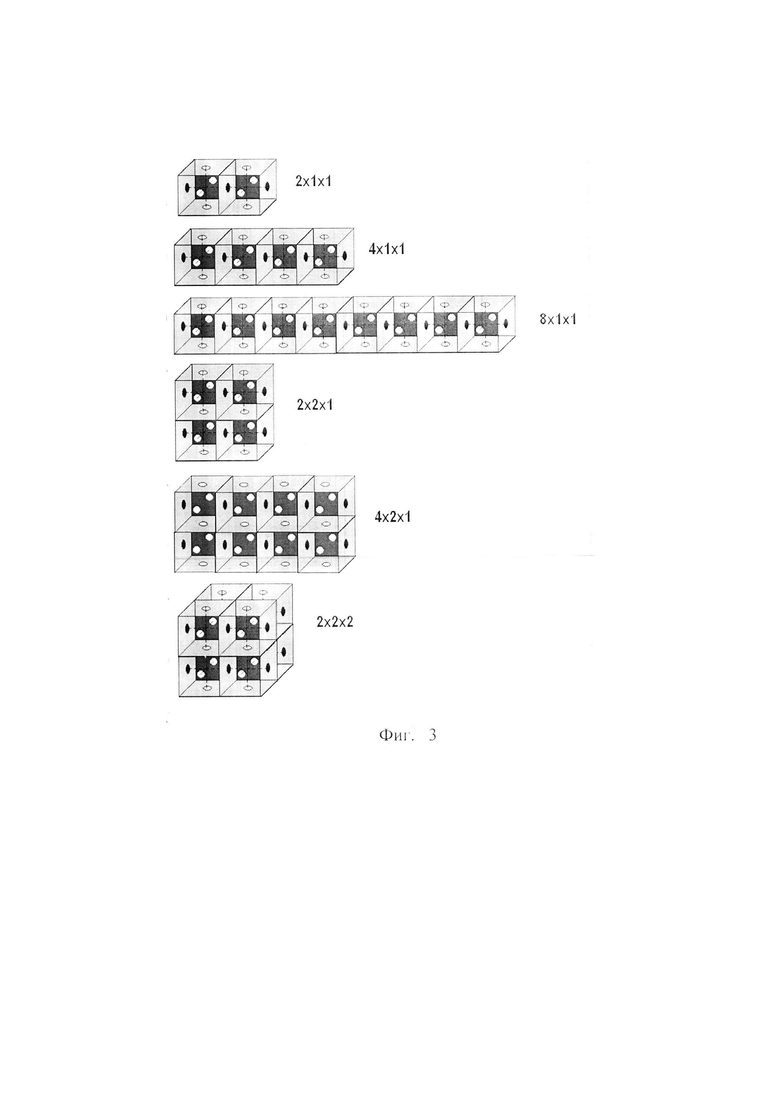
В простейшем случае многогранник W это куб 2x2x2, а его составные элементы - восемь кубических ячеек одного вида магнитной развертки, у которых антисимметричная развертка совпадает с исходной на фиг. 2 развертки №3 или №4. При этом, грани элементов 1x1x1 раскрашены в два цвета соответствующих полярности N,S и причем куб 2x2x2 содержит 48 магнитных диска М, 24 из которых находятся внутри куба 2x2x2 и обеспечивают конструктивную связь - магнитный замок между составными элементами и механическую жесткость куба 2x2x2, а остальные 24 диска расположены по четыре на внешней поверхности каждой из шести граней куба 2x2x2 см фиг. 3, и нужны для образования нового магнитного замка при манипуляциях с различными составными блоками и составления из них новых фигур W во время игры.
В более сложном случае куба 2x2x2 используются элементы, у которых исходная и антисимметричная магнитная развертка не совпадают, при этом его восемь элементов делятся на две группы по четыре элемента. В первой группе четыре элемента с исходной разверткой одного вида, во второй группе четыре элемента с антисимметричной разверткой этого же вида, например: четыре кубика с полярностями на шести гранях N,S,S,S,S,S и четыре S,N,N,N,N,N. Фиг 2 развертки №2 или то же самое для разверток №1, №5, №6 фиг. 2.
В самом общем случае игра-головоломка состоит, по меньшей мере, из одного вида одинаковых элементов - правильных многогранников, число которых равно Q и у каждого из которых m граней, причем каждый элемент несет на своих гранях магнитную систему, представляющую собой к одинаковых аксиально намагниченных дисков разной полярности, углубленных и закрепленных по одному в центре грани, параллельно ее поверхности, при этом, центры двух граней разной полярности, принадлежащих разным элементам, выполнены с возможностью притягиваются друг к другу с образованием пары, механически прочно связанных элементов, причем эта пара выполнена с возможностью независимого вращения вокруг оси связи О, проходящей через центр магнитного диска М перпендикулярно поверхности грани элемента, Фиг№1 (для куба NxNxN=Q) и, тем самым, при вращении менять набор знаков полярности на своих, открытых для связи с другими элементами гранях, лежащими в выбранной плоскости, при этом, магнитная система выполнена с возможностью разбиения Q элементов на одинаковые группы по j связанных элементов образующих механически связанные устойчивые геометрические фигуры Vj, Фиг №3 (Vj для куба 2x2x2) выполненные с возможностью изменения конфигураций и сбора всех фигур Vj в единую устойчивую геометрическую фигуру W с заданной игровой раскраской граней фигуры W, причем возможность взаимного перемещения многогранников Vj, при составлении фигуры W, определяет форма симметрии, в соответствии с которой распределены метки магнитных дисков различной полярности на гранях элементов образующих грани фигуры Vj или расположенных на поверхности их соединения/ разделения в фигуру W, при этом фигура W выполнена с возможностью разделения на части и в случае, когда k<m и эти части соприкасаются гранями, не содержащими элементов магнитной системы.
При использовании элементов - правильных многогранников с числом элементов Q=C3, где С - произвольное целое число, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, при этом каждый элемент имеет три грани с полярностью N и три грани с полярностью S и они расположены на развертке полярностей элемента так, что все три пары противоположных граней элемента имеют противоположные полярности, при этом фигуры Vj ребра Cx1x1 или грани CxCx1 фигура W - гексаэдр СхСхС. Фиг. 2 развертка №3
При использовании элементов - правильных многогранников с числом элементов Q=C3, где С - произвольное целое число, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, при этом каждый элемент имеет три грани с полярностью N и три грани с полярностью S и они расположены на развертке полярностей элемента так, что две пары противоположных граней элемента имеют одну и ту же полярность и одна пара противоположных граней имеет разную полярность, при этом фигуры Vj ребра Cx1x1 или грани CxCx1 фигура W - гексаэдр СхСхС. Фиг. 2 развертка №4
При использовании элементов - правильных многогранников с числом элементов Q=P3 где Р - четное, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элемента на всех гранях полярность одного знака, при этом фигуры Vj ребра Px1x1 или грани PxPx1 фигура W - гексаэдр РхРхР, причем число элементов с положительной полярностью равно числу элементов с отрицательной полярностью и равно Q/2. Фиг. 2 развертка №1
При использовании элементов - правильных многогранников с числом элементов Q=L3, где L-нечетное элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элемента на всех гранях полярность одного знака, при этом число элементов с положительной полярностью граней отличается от числа элементов с отрицательной полярностью на единицу, фигуры Vj ребра Lx1x1 или грани LxLx1 фигура W - гексаэдр LxLxL. В случае куба 3x3x3 собранного из таких элементов он отличается от кубика Рубика 3x3x3 тем, что помимо операций стандартных для граней и слоев кубика Рубика в нем возможны несколько дополнительных операций для граней и слоев, а так же для блоков 3x1x1 образующих ребра и тем самым получению невозможных для кубика Рубика конфигураций его составных элементов. Фиг. 2 развертка №1
В некоторых вариантах карманного исполнения при использовании элементов - правильных многогранников с числом элементов Q=8, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, фигуры Vj ребра 2x1x1 или грани 2x2x1 фигура W - гексаэдр 2x2x2, причем у каждого элемента на всех гранях, кроме одной полярность одинакова, при этом общее число дисков магнитной системы с положительной и отрицательной полярностью одинаково и равно 24, причем, окраска граней элементов выполнена в два цвета соответствующих их полярности. Фиг. 2 развертка №2.
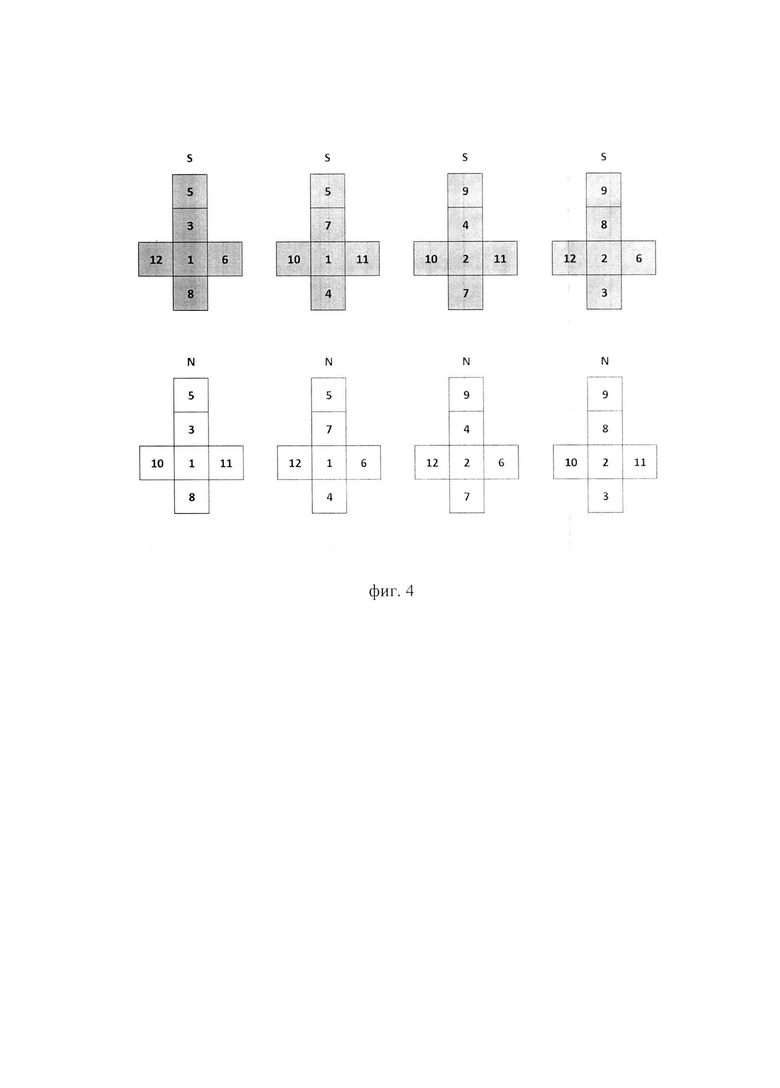
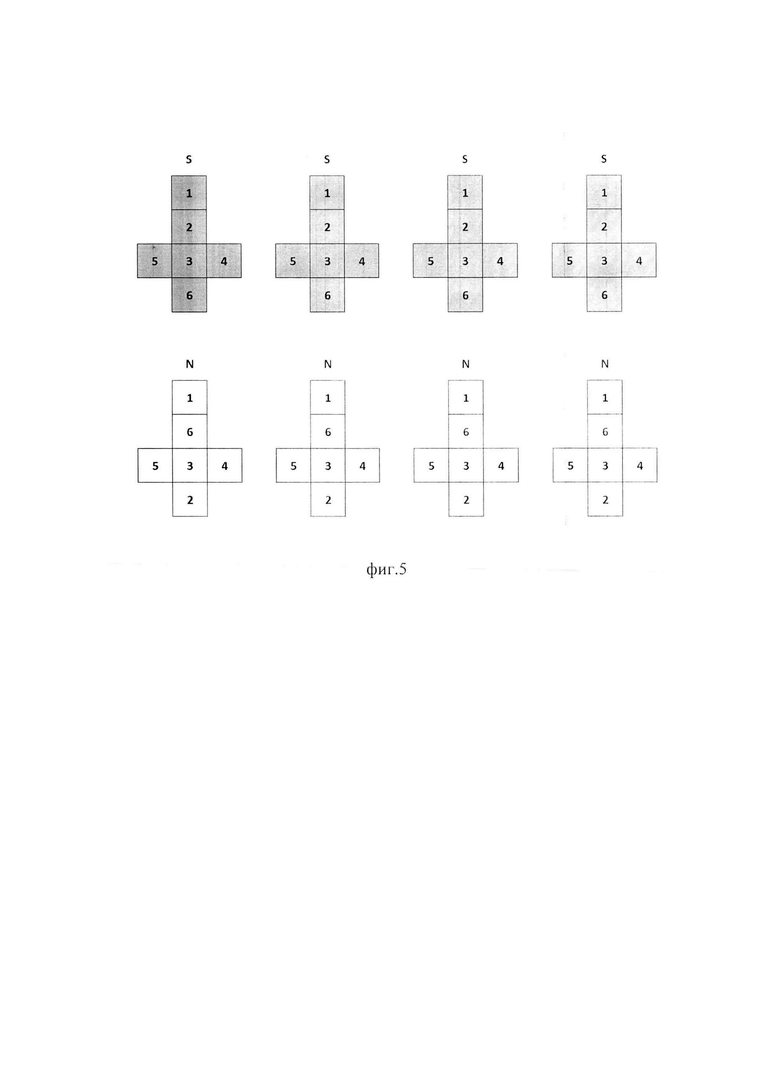
В других вариантах карманного исполнения при использовании элементов - правильных многогранников с числом элементов Q=8, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элемента на всех гранях полярность одного знака, при этом число элементов с положительной полярностью граней равно числу элементов с отрицательной полярностью и равно 4, фигуры Vj ребра 2x1x1 или грани 2x2x1 фигура W - гексаэдр 2x2x2, причем распределение полярности элементов в собранной фигуре W не меняется при любых взаимных перемещениях фигур Vj, при этом грани элементов не содержат меток полярности и окрашены в 12 различных цветов по 4 грани в один цвет. Фиг. 2 развертка полярности №1 (развертка цветов на фиг. 4.), и облегченный по сборке вариант с такой же магнитной разверткой, но окраской граней элементов в шесть цветов и допускающей сборку по цветам в блоке 8x1x1, с последующей трансформацией в блок 4x2x1 и затем в куб 2x2x2 у которого все внешние и внутренние грани 2x2 имеют один цвет из шести возможных, при этом окраска видимых граней куба 2x2x2 может меняться во время игровых манипуляций. Развертка цветов на фиг 5.
Также возможно при реализации разработанного технического решения в карманном исполнении при использовании элементов - правильных многогранников с числом элементов Q=8, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=2, распределение полярности у четырех элементов на соседних гранях одинаковая и у других четырех на соседних гранях разная, причем общее число магнитных элементов системы с разной полярностью одинаково, при этом фигуры Vj-ребра 2x1x1 или грани 2x2x1, фигура W гексаэдр 2x2x2 выполнена с возможностью разделения на две или четыре части, при этом грани элементов с магнитной системой окрашены в цвета соответствующие своей полярности, остальные грани элементов имеют игровой цвет, символ или одну четвертую часть рисунка.
Приведенные варианты реализации разработанного технического решения не ограничивают возможности «карманного исполнения» игры-головоломки.
При использовании элементов - правильных многогранников с числом элементов Q=20, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=2, при этом 6 элементов имеют разную полярность на противоположных гранях и 14 элементов разную полярность на соседних гранях, фигуры Vj-ребра 2x1x1 или грани 2x2x1, фигура W выполнена с возможностью разделения на две части, граничащие между собой гранями не содержащим магнитной системы, причем одна часть представляет собой гексаэдр 2x2x2, а вторая часть тороидальный многогранник, при этом грани элементов с магнитной системой окрашены в первый и второй цвета, а остальные в восемь различных цветов.
Конструкция магнитного куба трансформера 2x2x2 имеет шесть различных модификаций и состоит из восьми элементов - одинаковых по размеру пустотелых кубиков 1x1x1, каждая из шести плоских граней которых центрирована магнитным диском М, с аксиальной симметрией магнитного поля, на двух торцах которого противоположная полярность N или S, жестко закрепленным так, что торец диска М находится вровень с видимой плоскостью грани 1x1, в отверстии по центру грани фиг. 1, при этом грань окрашена в соответствии с полярностью видимого торца диска М или в игровой цвет, рисунок. Восемь элементов в собранном из них кубе 2x2x2 образуют конструктивную механическую связь за счет магнитных сил и допускают разрешенные в соответствии с правилом притяжения/отталкивания магнитных полюсов N и S перестановки отдельных единичных кубиков, блоков из двух, трех и четырех кубиков с последующей трансформацией куба в другую геометрическую фигуру с конструктивной магнитно-механической связью и состоящую из тех же элементов, причем, восемь элементов разбиты на антисимметричные по развертке полярностей пары кубиков 1x1x1, и принадлежат только одному неприводимому виду из шести возможных фиг. 2. Такой выбор развертки полярности граней элементов обеспечивает заданное число способов вступления в магнитный контакт кубиков 1x1x1, а так же составленных из них блоков 2x1x1,2x2x1,4x1x1 и прй этом каждая ассиметричная пара развертки кубиков 1x1x1x определяет одну из шести модификаций магнитного куба трансформера 2x2x2 с присущей ей раскраской по полярности на гранях 2x2 и другими особенностями трансформационных перестановок его составных частей-блоков 2x1x1 и 2x2x1.
Центры граней 1x1 любых двух элементов 1x1x1 выполнены с возможностью, притягиваться или отталкиваться, и соответственно, образовывать или препятствовать, образованию прочной на механический разрыв связи по линии О фиг. 1 и независимо вращаться вокруг оси О проходящей по линии магнитной связи без совершения механической работы против магнитных сил, благодаря аксиальной симметрии магнитного поля дисков М.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГОЛОВОЛОМКА-КОНСТРУКТОР | 2024 |
|
RU2824698C1 |
| ОБЪЕМНАЯ ИГРА-ГОЛОВОЛОМКА | 2009 |
|
RU2403946C1 |
| КОНСТРУКТОР | 1995 |
|
RU2133130C1 |
| КУБИК РУБИКА НА МАГНИТНЫХ КРЕПЛЕНИЯХ | 2015 |
|
RU2597820C1 |
| ОБЪЕМНАЯ ЛОГИЧЕСКАЯ ГОЛОВОЛОМКА | 1992 |
|
RU2009678C1 |
| Объемная игра-головоломка | 1989 |
|
SU1697863A1 |
| Объемная логическая головоломка | 1982 |
|
SU1087140A1 |
| Головоломка с магнитной системой (варианты) | 2022 |
|
RU2781298C1 |
| "Объемная головоломка "Граненая радуга" | 1990 |
|
SU1771789A1 |
| Объемная логическая головоломка | 1991 |
|
SU1780792A1 |
Головоломка - магнитный конструктор, содержащая магнитную систему с функцией магнитного конструктора, причем она состоит по меньшей мере из одного вида одинаковых элементов - правильных многогранников, число которых равно Q и у каждого из которых m граней, причем каждый элемент несет на своих гранях магнитную систему, представляющую собой k одинаковых аксиально намагниченных дисков разной полярности, углубленных и закрепленных по одному в центре грани, параллельно ее поверхности, при этом центры двух граней разной полярности, принадлежащих разным элементам, выполнены с возможностью притягиваются друг к другу с образованием пары механически прочно связанных элементов, причем эта пара выполнена с возможностью независимого вращения вокруг оси связи, проходящей через центр магнитного диска перпендикулярно поверхности грани элемента, и тем самым при вращении менять набор знаков полярности на своих открытых для связи с другими элементами гранях, лежащими в выбранной плоскости, при этом магнитная система выполнена с возможностью разбиения Q элементов на одинаковые группы по j связанных элементов, образующих механически связанные устойчивые геометрические фигуры Vj, выполненные с возможностью изменения конфигураций и сбора всех фигур Vj в единую устойчивую геометрическую фигуру с заданной игровой раскраской W, причем возможность взаимного перемещения многогранников Vj, при составлении фигуры W, определяет форму симметрии, в соответствии с которой распределены метки магнитных дисков различной полярности на гранях элементов, образующих грани Vj или расположенных на поверхности их соединения/разделения в фигуру W, при этом фигура W выполнена с возможностью разделения на части в случае, когда k<m, и эти части соприкасаются гранями, не содержащими элементов магнитной системы. Технический результат заключается в обеспечении игровых операций с блоками, гранями и ребрами, составленными из элементов и может служить учебным пособием для изучающих группы симметрии геометрических объектов-комплексов, наделенных физическими свойствами. 7 з.п. ф-лы, 5 ил.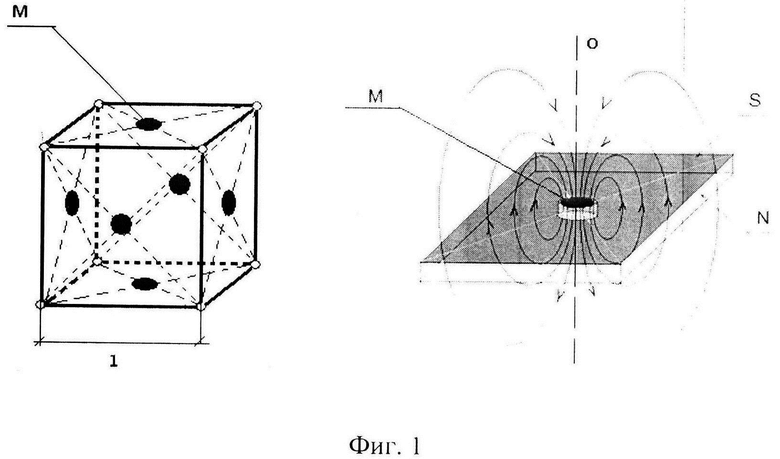
1. Головоломка - магнитный конструктор, содержащая магнитную систему с функцией магнитного конструктора, отличающаяся тем, что она состоит по меньшей мере из одного вида одинаковых элементов - правильных многогранников, число которых равно Q и у каждого из которых m граней, причем каждый элемент несет на своих гранях магнитную систему, представляющую собой k одинаковых аксиально намагниченных дисков разной полярности, углубленных и закрепленных по одному в центре грани, параллельно ее поверхности, при этом центры двух граней разной полярности, принадлежащих разным элементам, выполнены с возможностью притягиваются друг к другу с образованием пары механически прочно связанных элементов, причем эта пара выполнена с возможностью независимого вращения вокруг оси связи, проходящей через центр магнитного диска перпендикулярно поверхности грани элемента, и тем самым при вращении менять набор знаков полярности на своих открытых для связи с другими элементами гранях, лежащими в выбранной плоскости, при этом магнитная система выполнена с возможностью разбиения Q элементов на одинаковые группы по j связанных элементов, образующих механически связанные устойчивые геометрические фигуры Vj, выполненные с возможностью изменения конфигураций и сбора всех фигур Vj в единую устойчивую геометрическую фигуру с заданной игровой раскраской W, причем возможность взаимного перемещения многогранников Vj, при составлении фигуры W, определяет форма симметрии, в соответствии с которой распределены метки магнитных дисков различной полярности на гранях элементов, образующих грани Vj, или расположенных на поверхности их соединения/разделения в фигуру W, при этом фигура W выполнена с возможностью разделения на части в случае, когда k<m, и эти части соприкасаются гранями, не содержащими элементов магнитной системы.
2. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что при использовании элементов - правильных многогранников с числом элементов Q=C, где С - произвольное целое число, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, при этом каждый элементарный гексаэдр содержит три магнитных диска с полярностью N и три с полярностью S, причем у каждого элемента исходная и антисимметричная магнитная развертка одинаковы и принадлежат одному из шести неприводимых видов, фигуры Vj ребра Cx1x1 или грани CxCx1, фигура W - гексаэдр СхСхС, окраска граней элементов в цвет их полярности.
3. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что при использовании элементов - правильных многогранников с числом элементов Q=C3, где С - произвольное число, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элементарного гексаэдра на всех гранях полярность одного знака, при этом фигуры Vj ребра Cx1x1 или грани CxCx1, фигура W - гексаэдр СхСхС, причем если С четное, то число элементарных гексаэдров с положительной полярностью граней равно их числу с отрицательной полярностью и равно Q/2, и если С нечетное, то число элементарных гексаэдров с разной полярностью граней отличается на единицу, окраска граней элементов комбинированная, в цвет полярности и игровой цвет или рисунок.
4. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что в карманном исполнении при использовании элементов - правильных многогранников с числом элементов Q=8 элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, магнитная развертка граней у четырех элементов NSSSSS и NNNNNS у остальных четырех, грани элементов раскрашены в цвет их полярности, фигуры Vj ребра 2x1x1 или грани 2x2x1, фигура W - гексаэдр 2x2x2.
5. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что в карманном исполнении при использовании элементов - правильных многогранников с числом элементов Q=8, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элемента на всех гранях полярность одного знака, при этом число элементов с положительной полярностью граней равно числу элементов с отрицательной полярностью и равно 4, фигуры Vj ребра 2x1x1 или грани 2x2x1, фигура W - гексаэдр 2x2x2, причем распределение полярности элементов в собранной фигуре W не меняется при любых взаимных перемещениях фигур Vj, при этом грани элементов не содержат меток полярности и окрашены в 12 различных цветов по 4 грани 2x2 в один цвет.
6. Головоломка - магнитный конструктор по п. 5, отличающаяся тем, что в карманном исполнении шесть граней 1x1 каждого из восьми элементов 1x1x1 окрашены в шесть различных цветов, при этом сборка правильно окрашенного куба 2x2x2 имеет меньшую сложность, выполняется в блоке 8x1x1, который затем трансформируется в блок 4х2х1 и далее в куб 2x2x2, у которого видимые шесть граней 2x2 окрашены в три цвета, при этом противоположные видимые грани окрашены в один цвет, внутренние грани 2x2 окрашены так же в три цвета, отличающихся от цвета видимых граней.
7. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что в карманном исполнении при использовании элементов - правильных многогранников с числом элементов Q=27, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=6, причем у каждого элемента на всех гранях полярность одного знака, при этом общее число элементов с положительной S и отрицательной N полярностью граней отличается на единицу, фигура W - гексаэдр 3x3x3, Vj ребра 3x1x1 или грани 3x3x1, при этом видимые грани 3x3 собранного гексаэдра 3x3x3 окрашены в шесть различных цветов, остальные грани единичных элементов окрашены в цвета их полярности.
8. Головоломка - магнитный конструктор по п. 1, отличающаяся тем, что при использовании элементов - правильных многогранников с числом элементов Q=20, элементы представляют собой гексаэдры m=6, число элементов магнитной системы k=2, при этом 6 элементов имеют разную полярность на противоположных гранях и 14 элементов разную полярность на соседних гранях, фигуры Vj-ребра 2x1x1 или грани 2x2x1, фигура W выполнена с возможностью разделения на две части, граничащие между собой гранями не содержащим магнитной системы, причем одна часть представляет собой гексаэдр 2x2x2, а вторая - часть тороидальный многогранник, при этом грани элементов с магнитной системой окрашены в первый и второй цвета, а остальные - в восемь различных цветов.
| 0 |
|
SU178468A1 | |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОБЪЕМНОГО ТЕЛА | 1990 |
|
RU2018347C1 |
| US 20100308536 A1, 09.12.2010 | |||
| US 20080064461 A1, 13.03.2008. | |||
Авторы
Даты
2019-09-11—Публикация
2019-04-02—Подача