Описание известного уровня техники
В настоящее время все больше внимания уделяется автоматизированным системам распознавания изображений [22] вследствие их эффективности в различных областях, включая биометрию, медицинскую диагностику, беспилотные автомобили, контекстную рекламу и т.д. Задача многоклассового распознавания изображений [43] состоит в том, чтобы отнести объект, представленный на изображении, к любому из C > 2 возможных классов (категорий) [13]. Такая задача представляет сложность для многих интеллектуальных систем в связи с возможностью изменения объектов (позы, размера и т.д.) или условий наблюдений (освещенности, окклюзии, шума и т.д.). Наилучшие результаты во многих контекстах получают при использовании нейронных сетей прямого распространения [32] с глубокой архитектурой [6], таких как сверточные нейронные сети (CNN) [30, 33]. Эта ситуация значительно усложняется, если обучающая база данных информационной системы содержит небольшое количество изображений для каждой категории. В таком случае наиболее популярными решениями являются методы переноса обучения и доменной адаптации [6], в которых глубокую CNN обучают с использованием внешнего, очень большого набора данных, а выход одного из последних слоев этой сети для входного изображения используют в качестве его вектора признаков [29].
Если размер обучающей выборки относительно мал, то традиционные классификаторы, например, SVM (машина опорных векторов) или RF (случайный лес), обычно характеризуются слишком низкой точностью. В этом случае можно применить методы обучения на примерах, например, метод ближайшего соседа (NN), или статистический подход, в котором для принятия решения используется байесовский подход или критерий максимума апостериорной вероятности (MAP) [22, 24]. К сожалению, если требуется распознавать изображения в режиме реального времени (например, лица на видео), вектор признаков имеет высокую размерность, мера близости является сложной, и доступно только стандартное оборудование (например, ноутбук или даже мобильный телефон), то выполнение полного перебора по множеству всех классов недостаточно даже для сотен категорий.
Одним из возможных путей повышения вычислительной эффективности распознавания [23] является использование тернарных решений (TWD) [39], которые берут начало из модели теории принятия решений на основе приближенных множеств (DTRS). В отличие от обычных бинарных решений, TWD вводит третье, отложенное решение [39]. Например, при распознавании видео бывает невозможно достоверно классифицировать каждый видеокадр [27]. Поэтому можно отложить это решение до тех пор, пока не будет обработан следующий кадр.
Следует отметить, что отложенное решение не подходит для большинства задач распознавания изображений на замкнутом множестве классов, в которых необходимо выбрать одну из заданных категорий. На первый взгляд, теория TWD, основанная на байесовском подходе, не может помочь в данном случае, поскольку невозможно повысить точность (оптимальных) решений MAP. Однако в контексте иерархического представления изображений (гранулярности) [17] очень перспективной является сочетание TWD и теории гранулярных вычислений [20]. Она обеспечивает гибкость при дальнейшем изучении сомнительных объектов на различных уровнях гранулярности и тем самым снижает вероятность некорректного решения [45]. Фактически, в этом заключается основная идея глубоких сетей CNN, которые автоматически изучают иерархию визуальных признаков [6].
Вдохновившись последовательным статистическим анализом [34] и перспективой гранулярных вычислений на TWD, Yao и Deng [41] предложили последовательные тернарные решения (TWD) на основе вероятностных приближенных множеств и полного отношения порядка. Последовательные TWD - это динамическая процедура принятия решения, в которой особое внимание уделяется стратегии обновления для уменьшения временной сложности [37, 44]. Согласно идее последовательных TWD необходимо назначить три области принятия решения на каждом уровне гранулярности и рассматривать уровни более детальной гранулярности с более детальным описанием входного объекта только в тех случаях, когда в этом есть необходимость.
Несмотря на очевидный потенциал последовательного TWD, его применение при распознавании изображений все еще находится на стадии активных исследований. По существу, большинство многоклассовых TWD не применялись для сложных задач классификации с неконтролируемыми условиями съемки. Фактически, есть несколько исследований, посвященных распознаванию изображений, в которых рассматриваются только довольно простые задачи распознавания лиц в ограниченных условиях. Например, Li и др. [12] представили изображение лица на каждом уровне гранулярности, используя модификацию традиционной модели главных компонент [22], и продемонстрировали, что последовательный анализ может повысить точность для нескольких эталонов. В работе Savchenko [23] было предложено повысить вычислительную эффективность распознавания изображений путем последовательного анализа пирамиды традиционных визуальных признаков HOG (гистограмм ориентированных градиентов). В конечном итоге, оба этих метода невозможно применять непосредственно с современными методами на основе CNN [18, 19], которые являются единственным достаточно точным вариантом для неконтролируемых условий [10]. Даже недавнее исследование Li и др. [11] сфокусировано на простых сетях прямого распространения на основе автокодировщика посредством корректировки потерь при извлечении последовательных гранулярных признаков и не рассматривает гораздо более точные глубокие CNN. Насколько известно, в настоящее время не существует методов, основанных на TWD, с простой настройкой параметров, которые бы можно было применять вместе с существующими методами извлечения глубоких признаков [29].
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
В основу настоящего изобретения положен статистический подход к распознаванию изображений и предлагается обобщение тернарных решений (TWD) для случая многих классов, являющееся оптимальным с точки зрения теории множественных сравнений [7]. Это TWD используется в новом методе последовательного распознавания, который основан на определении информационных гранул в глубоких признаках CNN с помощью традиционного метода главных компонент (PCA). Возможности данного подхода в повышении эффективности распознавания продемонстрированы на экспериментах с множеством эталонов изображений и современными архитектурами CNN [19, 30, 33].
В настоящем изобретении разработаны возможные пути реализации многоклассовых TWD при распознавании изображений с глубокими признаками на выходе CNN. Экспериментальным путем продемонстрировано, что параметры известных аналогов очень сложно настроить с помощью анализа апостериорной вероятности [38] или отношения правдоподобия [31] для получения порогов, подходящих для совершенно разных наборов данных. Поэтому предложено новое определение многоклассовых TWD (21)-(23) на основе вычисления отношения расстояний между входным объектом и эталонами из обучающего множества. Показано, что это определение достаточно устойчиво к выбору параметров. Фактически, все результаты (см. таблицы 1 и 2 и фиг. 8-11) были получены для фиксированного значения порога δ1/*. Кроме того, особое внимание обращается на тот факт, что отношение расстояний хорошо согласуется с обычным тестированием достоверности сопоставления дескрипторов SIFT [16].
Особую важность представляет тот факт, что нет необходимости использовать многоклассовые TWD при распознавании изображений, если требуется получить всего одну метку класса для наблюдаемого изображения. При таком сценарии по существу невозможно улучшить байесовское решение. Согласно изобретению наибольших преимуществ TWD в данной задаче можно получить при его сочетании с теориями гранулярных вычислений и последовательных TWD [40]. Хотя существуют исследования, демонстрирующие возможность улучшения точности распознавания лиц [12, 11], данное изобретение направлено на повышение вычислительной эффективности классификации изображений. В основу нового метода (см. фиг. 2, 3) положено определение уровней гранулярности изображений на основе PCA. Показано, что в этом случае можно повторно использовать расстояния, вычисленные на предыдущих уровнях (25), так что соответствующая времени выполнения сложность обработки будет идентичной на каждом уровне. Эксперименты с несколькими наборами данных для лиц и категорий изображений подтвердили преимущества изобретательского подхода по сравнению с другими, базирующимися на методе ближайшего соседа, включая известные реализации многоклассового TWD.
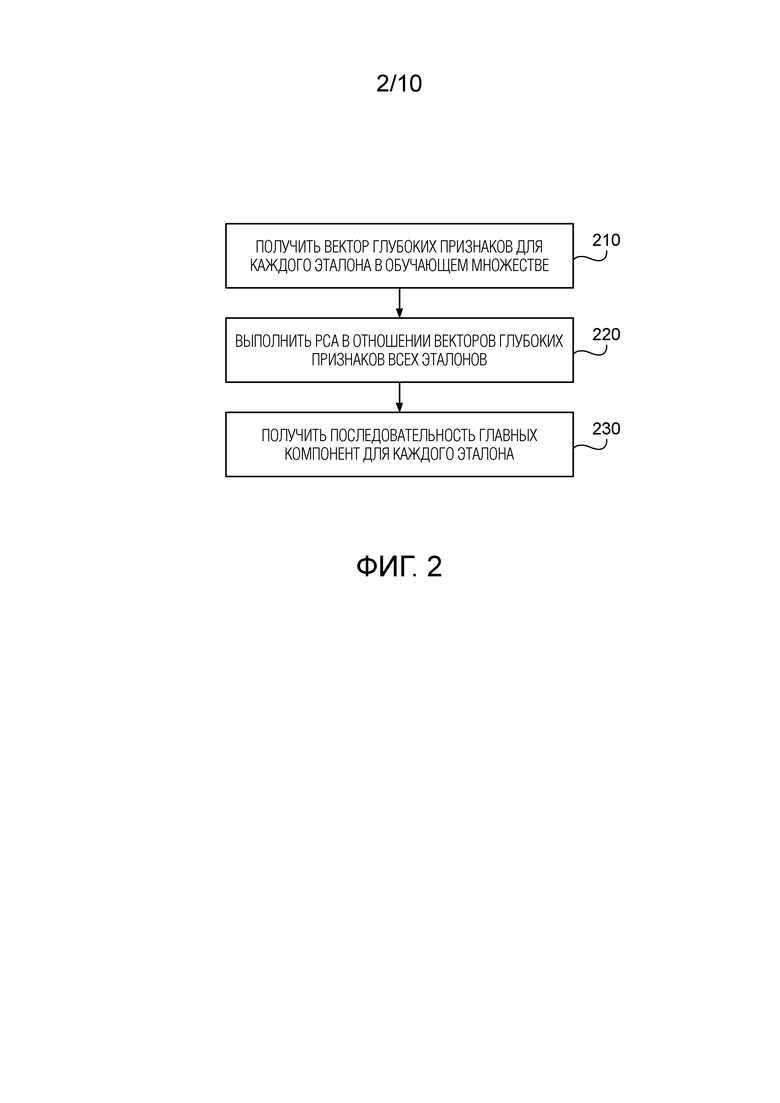
Согласно первому аспекту изобретения предложен способ распознавания изображений. Способ содержит этапы, на которых: получают вектор глубоких признаков входного изображения с помощью глубокой сверточной нейронной сети (CNN); применяют преобразование PCA (метод главных компонент) к данному вектору для получения последовательности главных компонент входного изображения; делят полученную последовательность главных компонент на заранее заданное количество смежных частей, каковое заранее заданное количество является количеством уровней гранулярности, так что каждая часть относится к отличающемуся от других уровню гранулярности; и сопоставляют входное изображение с эталонами из обучающего множества изображений, причем каждый эталон принадлежит конкретному классу из некоторого количества классов, составляющего, по меньшей мере, 2. При упомянутом сопоставлении для каждого уровня гранулярности, начиная с уровня самой грубой гранулярности, присоединяют часть упомянутой последовательности, относящуюся к этому уровню гранулярности, к подпоследовательности главных компонент входного изображения, которая вначале является пустой; вычисляют расстояния между упомянутой подпоследовательностью и соответствующими подпоследовательностями главных компонент эталонов из множества потенциально подходящих решений (решений-кандидатов), причем множество решений-кандидатов вначале включает в себя все эталоны обучающего множества изображений; оценивают отношения минимального расстояния ко всем другим расстояниям среди вычисленных расстояний; исключают из множества решений-кандидатов эталоны, каждый из которых имеет связанное с ним оцененное отношение, которое меньше заданного порога; и если множество решений-кандидатов включает в себя по меньшей мере один эталон из лишь одного класса, идентифицируют данное входное изображение как относящееся к этому классу. Один и тот же заранее заданный порог можно использовать для каждого уровня гранулярности.
Предпочтительно, перед получением вектора глубоких признаков входного изображения выполняют этапы, на которых: для каждого эталона обучающего множества изображений получают с помощью глубокой CNN вектор глубоких признаков данного эталона и нормируют полученный вектор в евклидовой норме; выполняют PCA в отношении векторов глубоких признаков всех эталонов из обучающего множества изображений для получения матрицы преобразования, причем матрица преобразования представляет собой квадратную матрицу, измерения которой совпадают с размерностью каждого вектора глубоких признаков; и получают последовательность главных компонент для каждого эталона путем умножения матрицы преобразования на вектор глубоких признаков данного эталона.
При получении вектора глубоких признаков входного изображения предпочтительно дополнительно нормируют полученный вектор в евклидовой норме, и при применении преобразования PCA предпочтительно умножают матрицу преобразования на вектор глубоких признаков входного изображения.
Главные компоненты в каждой полученной последовательности предпочтительно упорядочиваются по соответствующим собственным значениям.
Упомянутое заранее заданное количество уровней гранулярности можно выбрать таким образом, чтобы деление размерности каждого вектора глубоких признаков на это заранее заданное количество давало целое число. В этом случае смежные части последовательности главных компонент входного изображения имеют одинаковый размер.
Расстояния на (l+1)-ом уровне гранулярности, 1 ≤ l < L, где L - количество уровней гранулярности, предпочтительно вычисляют как
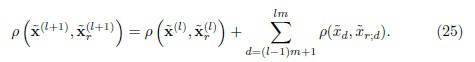 ,
,
где m = D/L, D - размерность каждого вектора глубоких признаков; 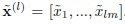 - подпоследовательность главных компонент входного изображения на l-ом уровне гранулярности;
- подпоследовательность главных компонент входного изображения на l-ом уровне гранулярности; 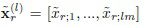 - подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-ом уровне гранулярности; и
- подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-ом уровне гранулярности; и 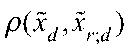
Предпочтительно, способ дополнительно содержит этапы, на которых: если для уровня самой детальной гранулярности множество решений-кандидатов включает в себя эталоны из более, чем одного класса, идентифицируют входное изображение как относящееся к классу, к которому относится эталон, имеющий максимальное оцененное отношение расстояний до входного объекта среди эталонов в множестве решений-кандидатов.
Согласно второму аспекту настоящего изобретения предложена вычислительная система, выполненная с возможностью распознавания изображений. Система содержит: один или более процессоров и одно или более машиночитаемых запоминающих устройств, на которых хранятся машиноисполняемые команды. Машиноисполняемые команды при их исполнении одним или несколькими процессорами предписывают одному или нескольким процессорам выполнять этапы способа распознавания изображений согласно первому аспекту.
Согласно третьему аспекту настоящего изобретения предложен машиночитаемый носитель данных. На машиночитаемом носителе данных сохранены машиноисполняемые команды. Упомянутые команды при их исполнении вычислительным устройством предписывают вычислительному устройству выполнять способ распознавания изображения согласно первому аспекту.
Технический результат, обеспечиваемый настоящим изобретением, заключается в значительном ускорении процесса распознавания изображений. В зависимости от количества классов в обучающей выборке процесс распознавания изображений можно ускорить в 1,5-10 раз по сравнению с известными аналогами.
Изобретение может найти применение в решении широкого круга задач распознавания изображений там, где имеется большое количество различных классов (категорий) и относительно небольшое количество имеющихся эталонных изображений (образов) для каждой категории. Эти задачи включают в себя, прежде всего, задачи, рассматриваемые в экспериментальном разделе идентификации лиц на фотографиях и видео, где выполняется потенциальный поиск среди фотографий тысяч разных людей. К другой области применения относятся различные задачи поиска изображений в огромных базах данных (поиск изображений по содержанию).
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг. 1 - предлагаемый подход для многоклассового распознавания изображений на основе последовательных TWD и гранулярных вычислений в соответствии с вариантом осуществления настоящего изобретения.
Фиг. 2 - блок-схема предварительной обработки множества эталонов в соответствии с вариантом осуществления настоящего изобретения.
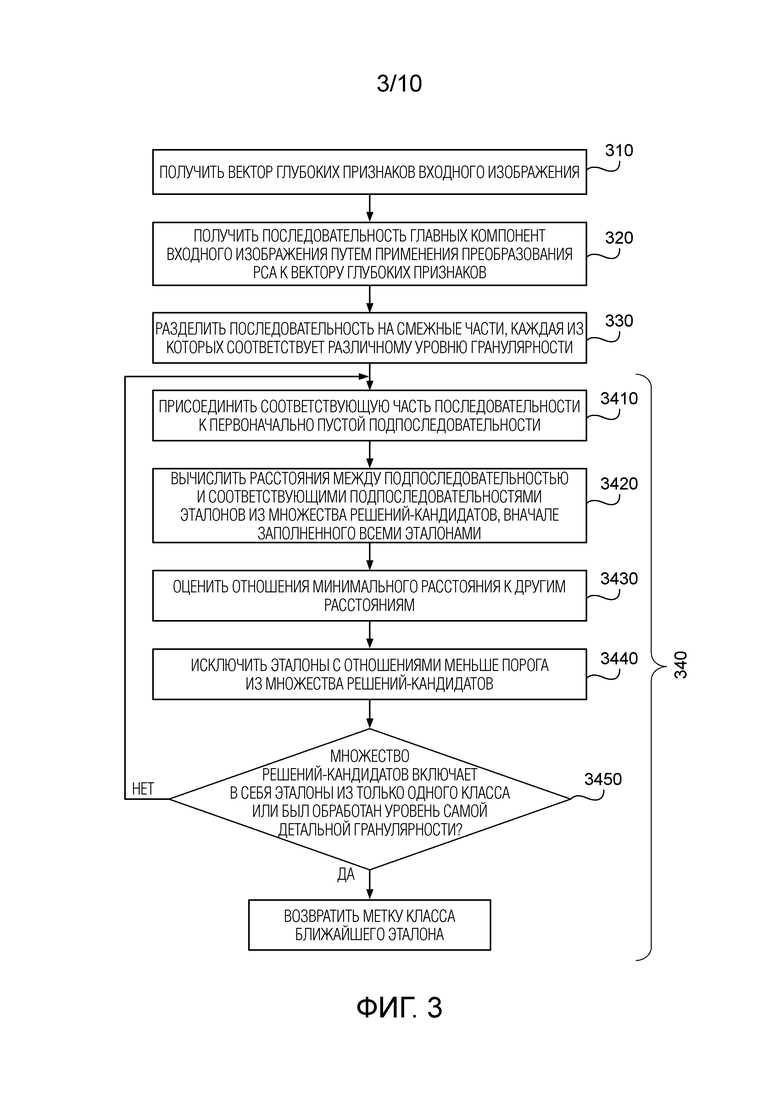
Фиг. 3 - блок-схема распознавания изображений в соответствии с вариантом осуществления настоящего изобретения.
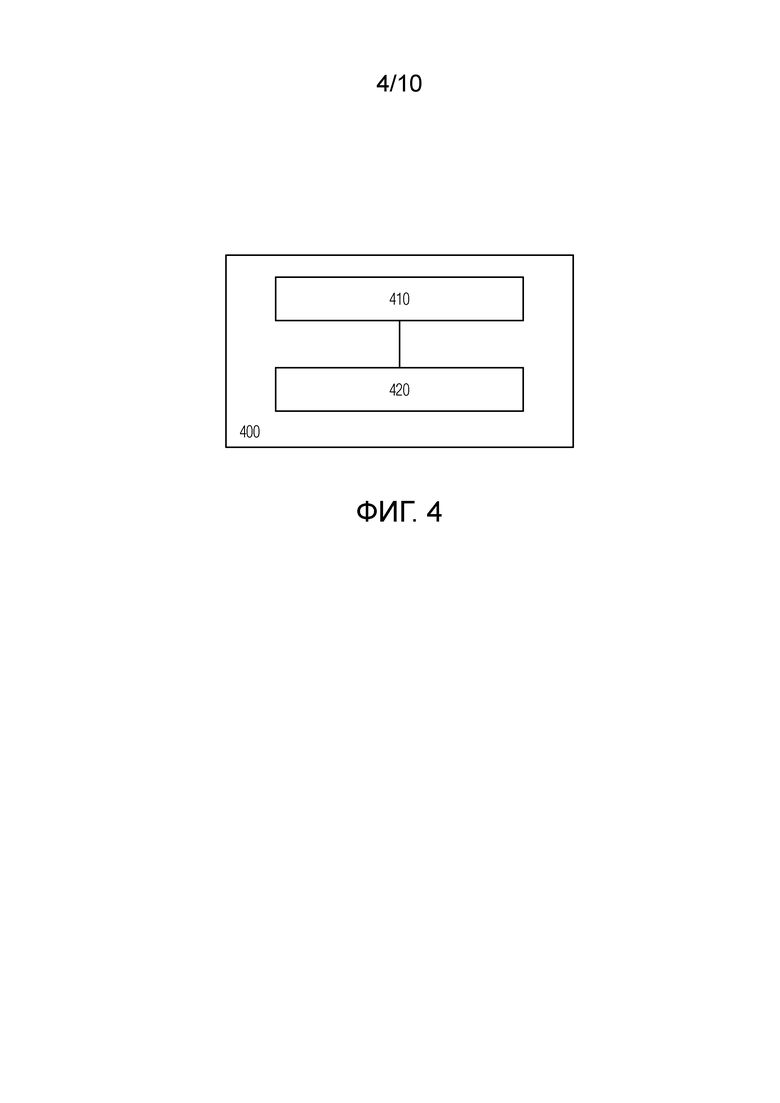
Фиг. 4 - высокоуровневая блок-схема вычислительного устройства, в котором могут быть реализованы аспекты настоящего изобретения.
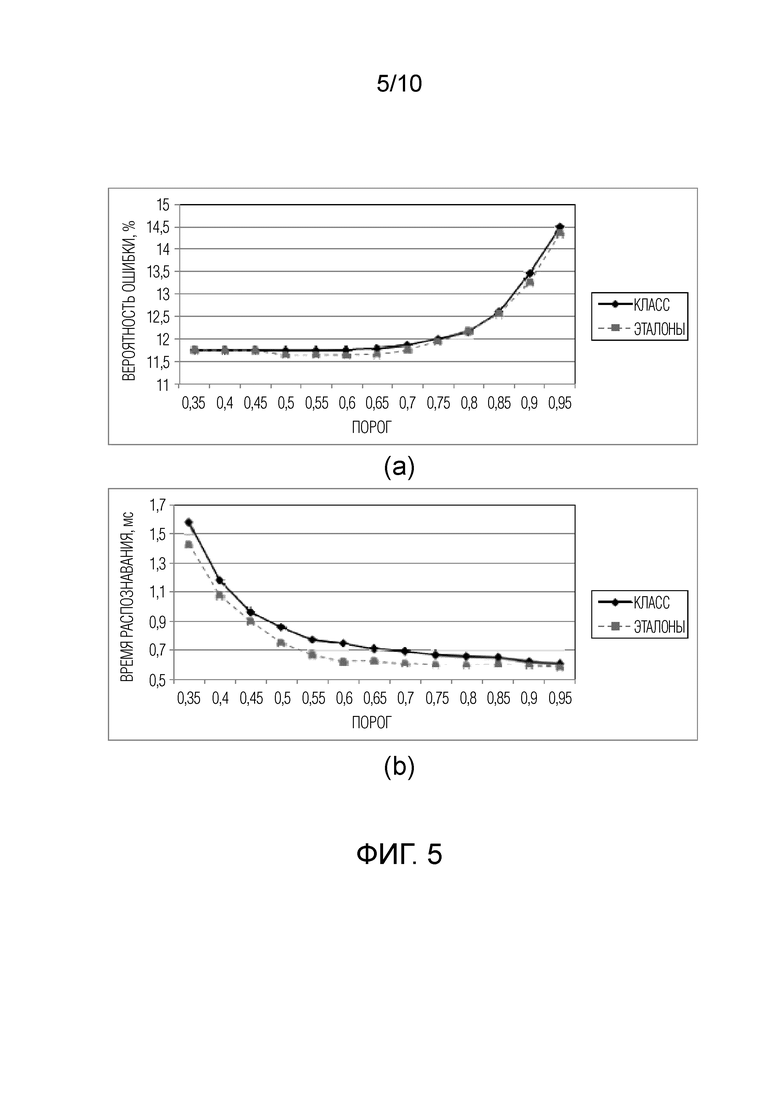
Фиг. 5 - зависимость (а) вероятности ошибки и (б) времени распознавания от порога δ1/*, для признаков VGGFace, набора данных LFW, m=32.
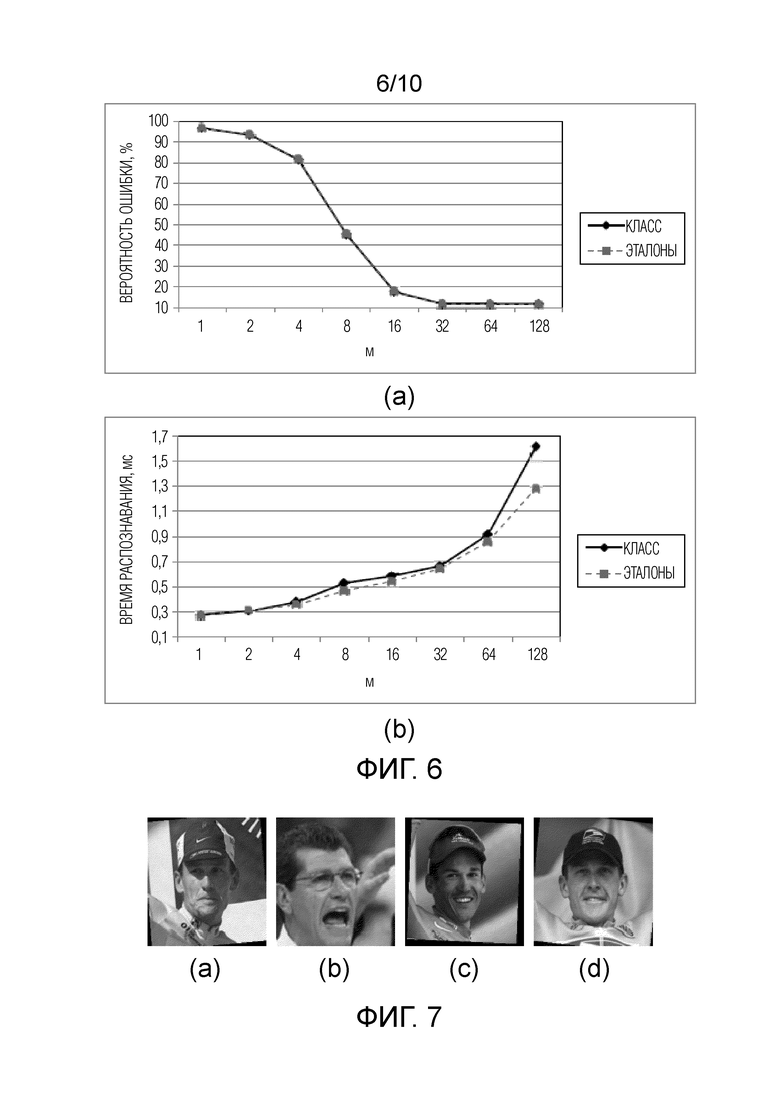
Фиг. 6 - зависимость (а) вероятности ошибки и (b) времени распознавания от параметра m, для признаков VGGFace, набора данных LFW, δ1/*=0.7.
Фиг. 7 - изображения из примера распознавания лиц: (a) пробная фотография, (b)-(d) ближайшие фотографии из галереи.
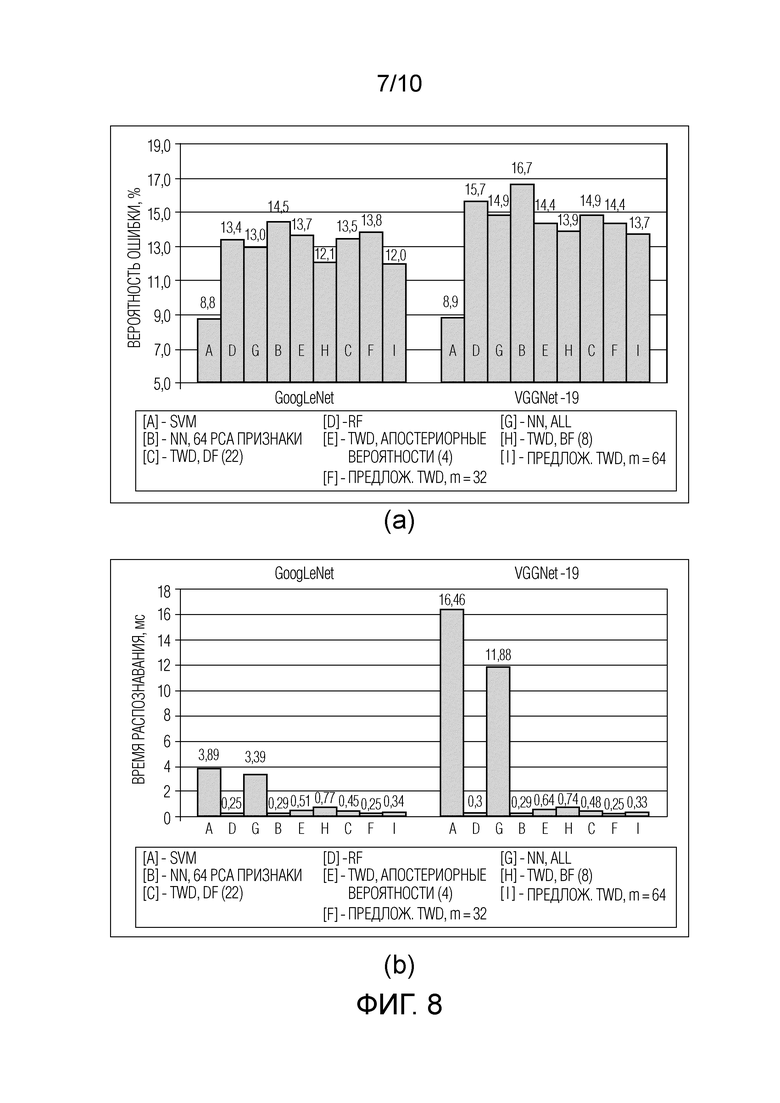
Фиг. 8 - результаты категоризации изображений, набор данных Caltech-101, (a) вероятность ошибки и (b) время распознавания.
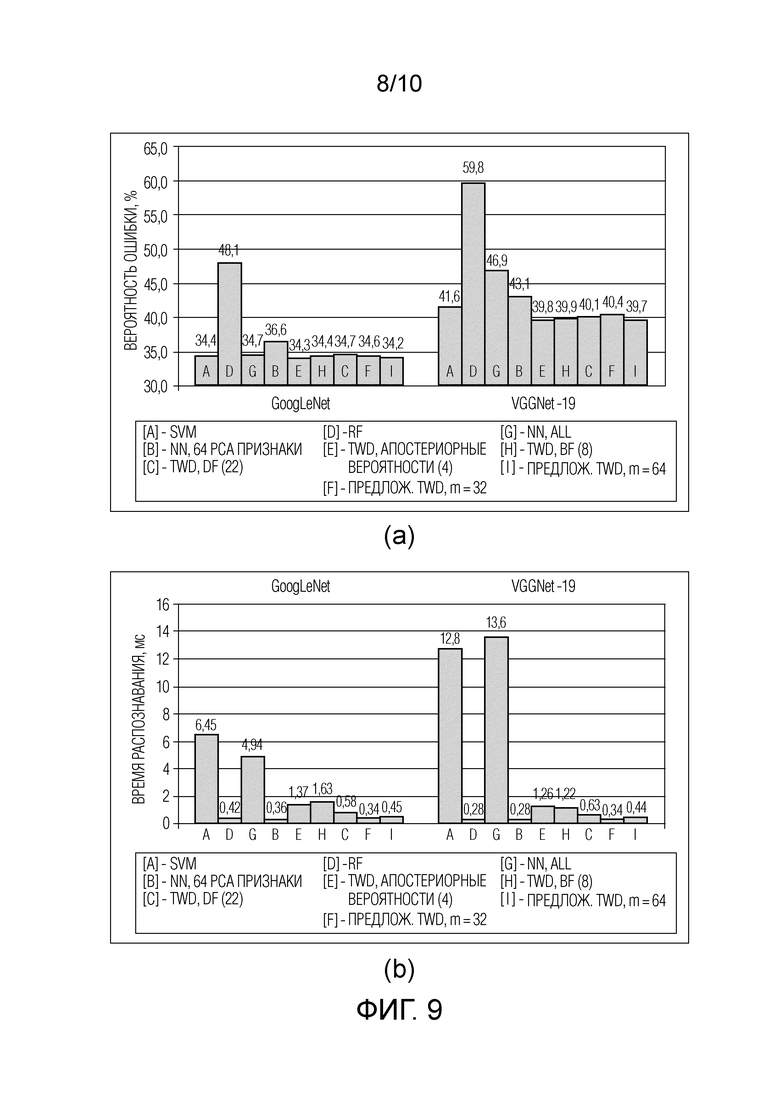
Фиг. 9 - результаты категоризации изображений, набор данных Caltech-256 (a) вероятность ошибки и (b) время распознавания.
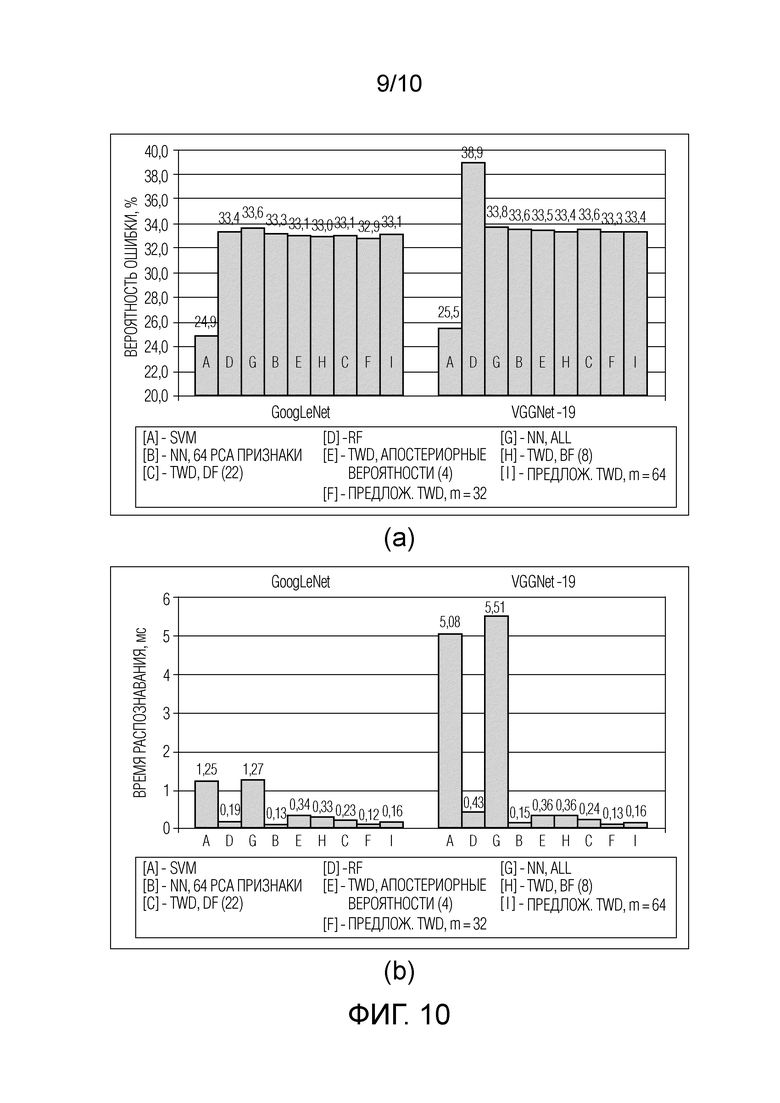
Фиг. 10 - результаты категоризации изображений, набор данных Stanford Dogs, (a) вероятность ошибки и (b) время распознавания.
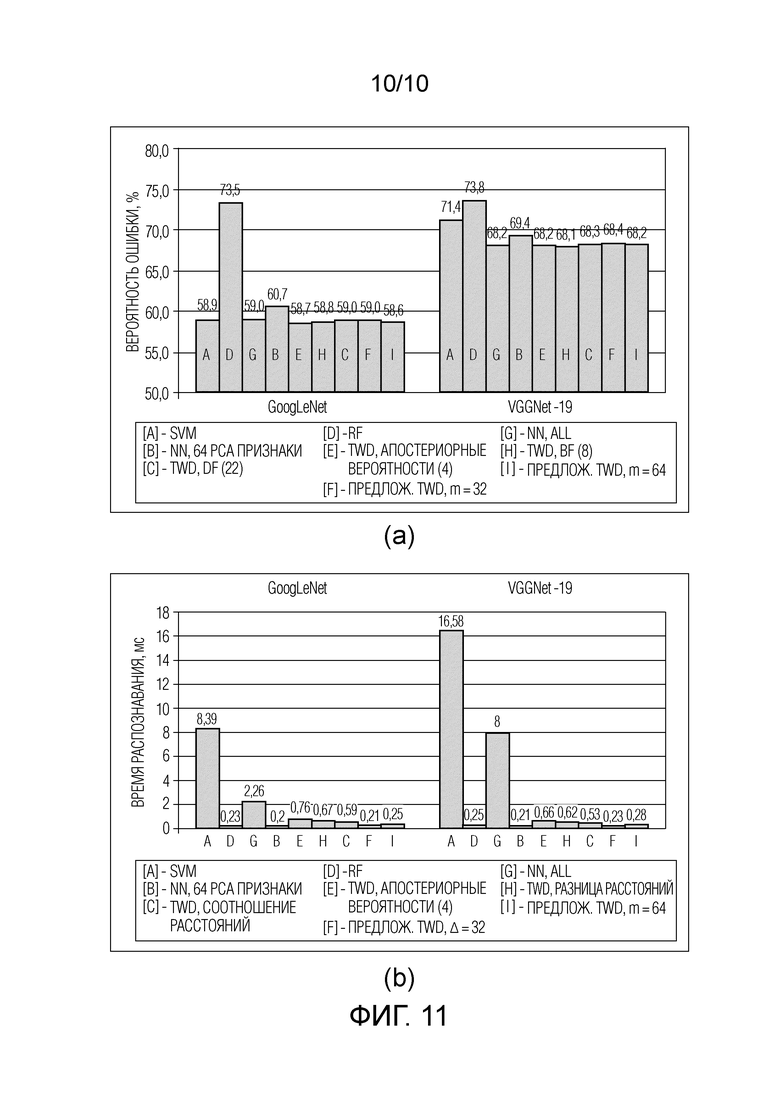
Фиг. 11 - результаты категоризации изображений, набор данных CUB-200-2011, (a) вероятность ошибки и (b) время распознавания.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
1. Статистическое распознавание изображений
Задача многоклассового распознавания изображений на замкнутом множестве состоит в том, чтобы отнести наблюдаемое изображение к одному из C > 2 классов (категорий). Эти классы задаются обучающим множеством R ≥ C эталонных изображений. В данном описании рассматривается случай обучения с учителем, в котором известна метка класса 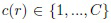 r-го изображения. При этом допускается, что обучающая выборка весьма мала
r-го изображения. При этом допускается, что обучающая выборка весьма мала 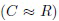 , чтобы обучать сложный классификатор (например, глубокую нейронную сеть) с нуля. Поэтому можно применить перенос обучения или доменную адаптацию [6]. В этих методах для обучения глубокой CNN используются большие внешние наборы данных, например, ImageNet или CASIA-WebFaces. Затем изменяют размер входного изображения и всех обучающих изображений из ограниченной выборки эталонов, чтобы обеспечить одинаковую ширину W и высоту H. Эти изображения передаются в заранее обученную CNN для извлечения признаков [29] с использованием выходов одного из ее последних слоев [27]. L1-нормированные выходы для входного изображения и каждого r-го эталонного изображения используются в качестве D-размерных векторов признаков
, чтобы обучать сложный классификатор (например, глубокую нейронную сеть) с нуля. Поэтому можно применить перенос обучения или доменную адаптацию [6]. В этих методах для обучения глубокой CNN используются большие внешние наборы данных, например, ImageNet или CASIA-WebFaces. Затем изменяют размер входного изображения и всех обучающих изображений из ограниченной выборки эталонов, чтобы обеспечить одинаковую ширину W и высоту H. Эти изображения передаются в заранее обученную CNN для извлечения признаков [29] с использованием выходов одного из ее последних слоев [27]. L1-нормированные выходы для входного изображения и каждого r-го эталонного изображения используются в качестве D-размерных векторов признаков 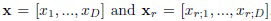 , соответственно. Такие средства извлечения признаков, основывающиеся на глубоком обучении, позволяют обучать общий классификатор, например, SVM, RF или просто NN, который работает почти так же хорошо, как если бы доступен большой набор данных изображений из этих C классов [6].
, соответственно. Такие средства извлечения признаков, основывающиеся на глубоком обучении, позволяют обучать общий классификатор, например, SVM, RF или просто NN, который работает почти так же хорошо, как если бы доступен большой набор данных изображений из этих C классов [6].
Если в CNN используются функции активации ReLU [6], то векторы извлеченных признаков являются положительными и суммируются до 1 за счет L1-нормировки. В результате векторы признаков входного изображения и каждого r-го эталона можно рассматривать как оценки дискретных распределений вероятностей (гипотетических) случайных переменных 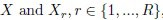 и
и 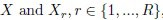 , соответственно [24]. Задача распознавания сводится к проверке простой статистической гипотезы о распределении X. Оптимальное решение MAP возвращает класс, соответствующий максимальной вероятности P(c|x) [22]. В случае малых выборок обычно предполагают, что каждый эталон в обучающем множестве представляет режим в плотности вероятности всего класса. Следовательно, P(c|x) можно оценить, используя правило Байеса:
, соответственно [24]. Задача распознавания сводится к проверке простой статистической гипотезы о распределении X. Оптимальное решение MAP возвращает класс, соответствующий максимальной вероятности P(c|x) [22]. В случае малых выборок обычно предполагают, что каждый эталон в обучающем множестве представляет режим в плотности вероятности всего класса. Следовательно, P(c|x) можно оценить, используя правило Байеса:
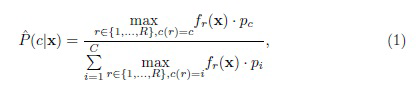
где pc - априорная вероятность c-го класса, а fr(x) - неизвестная плотность вероятности (правдоподобие) Xr. Используя идеи обучения представлениям [6], можно рассматривать выходы последних слоев глубокой CNN как независимые случайные величины. Следовательно, плотность fr(x) оценивается следующим образом:

где n - размер выборки, использованной для оценки распределения случайной переменной X. Его можно вычислить как общее число пикселей во входном изображении WH. Подставив (2) в (1) и разделив его числитель и знаменатель на 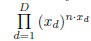 , можно получить следующую оценку апостериорной вероятности:
, можно получить следующую оценку апостериорной вероятности:
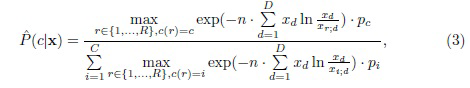
или
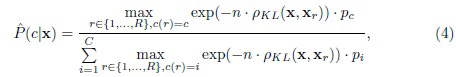
где 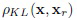 - рассогласование Кульбака-Лейблера (KL) между векторами x и xr признаков [9]. Фактически, это выражение эквивалентно функции активации softmax [6] с коэффициентом сглаживания n. Следовательно, критерий MAP можно записать в упрощенной форме:
- рассогласование Кульбака-Лейблера (KL) между векторами x и xr признаков [9]. Фактически, это выражение эквивалентно функции активации softmax [6] с коэффициентом сглаживания n. Следовательно, критерий MAP можно записать в упрощенной форме:
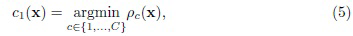
где расстояние между входным изображением и c-ым классом обозначается как
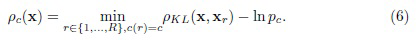
Следует отметить известный факт об эквивалентности критерия MAP и принципа минимальной информационной дискриминации KL для полиномиальных распределений [9]. Критерий (5) реализует стандартное правило ближайшего соседа, которое типично для проблемы малых выборок. Временная сложность такого классификатора определяется как O(RD). Поскольку размерность D глубоких признаков обычно имеет довольно большую величину (256 ... 4096), этот метод невозможно реализовать в режиме реального времени при большом числе различных классов C (следовательно, и размере обучающего множества R). В остальной части данного описания рассматриваются возможные способы повышения вычислительной эффективности распознавания путем использования теории TWD.
2. Многоклассовые тернарные решения в распознавании изображений
В данном разделе рассматриваются возможности использования TWD в описанной процедуре распознавания изображений. Три основных варианта принятых, отклоненных и отложенных решений лучше всего интерпретируются в задаче бинарной классификации. Она включает в себя три типа решений: положительное (принятие первого класса), отрицательное (отклонение первого класса и принятие второго класса) и граничное (отсрочка окончательного решения и непринятие ни первого, ни второго класса). Таким образом, концепция класса естественным образом проецируется на теорию TWD: каждый c-ый класс представлен положительной POS, отрицательной NEG и граничной BND попарно непересекающимися областями.
Хотя TWD не может решать многоклассовые задачи напрямую, существует несколько хорошо известных возможностей применения TWD с использованием многоклассовой DTRS [45]. Например, Lingras и др. [13] обсуждали подход "каждый против каждого" к многоклассовой байесовской процедуре принятия решения и специально построили 2C-1 функций потерь. Они пришли к заключению, что классификация "каждый класс с каждым" создает большое количество моделей классификации и может обусловить низкую скорость обучения из-за малого количества обучающих данных для каждой модели. Liu и др. [14] предложили двухэтапный алгоритм, в котором на первом этапе осуществляется традиционное преобразование "один против остальных", а на втором этапе выбирают наилучший класс-кандидат в положительной области, используя критерий минимальной вероятности ошибки с байесовским дискриминантным анализом. В работе Zhou [45] предложено зависящее от матрицы потерь решение для нескольких классов с использованием метода "один против остальных". Deng и Jia [4] определили несколько параметров в многоклассовой DTRS на основе матрицы стоимости и продемонстрировали, что их многоклассовый, зависящий от матрицы потерь алгоритм классификации, полученный из байесовской процедуры принятия решения, довольно точен в некоторых задачах классификации UCI.
Одним из наиболее широко используемых методов определения многоклассовых тернарных решений является приближенная байесовская модель [31], которая не требует информации об априорных и апостериорных вероятностях. В этой статье Slezak определил положительную, отрицательную и граничную области для каждого класса решений, используя коэффициент Байеса (BF), т.е. отношение условных плотностей (правдоподобий) (2) для попарно непересекающихся классов сравнивается с порогом 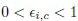 :
:
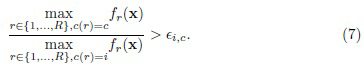
Используя преобразования (3)-(6) из предыдущего раздела, можно выяснить, что этот критерий эквивалентен следующему правилу
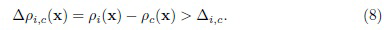
Используя такой подход, можно определить три области для каждого класса [31]:
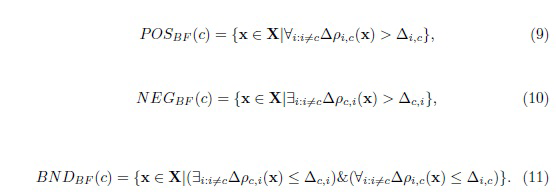
Здесь X - универсальное множество всех изображений с шириной W и высотой H. Эти определения реализуют известный, основанный на KL критерий для проверки гипотез о распределении [9] в случае полной априорной неопределенности pc = 1/C.
Другой подход к многоклассовым задачам был предложен Yao and Zhao [38]. Они следовали подходу "один против остальных" (или "один против всех") и преобразовали байесовскую процедуру принятия решений C-класса в C задач бинарной классификации, которые можно сформулировать независимо в терминах теории TWD, используя достоверность (апостериорную вероятность) каждого класса решений. В этом подходе используется разбиение n универсального множества X на два класса, указывающее на то, что объект находится в классе решения c и не в c. После этого TWD выполняется отдельно для каждого класса. Три множества решений определены на основе оценок апостериорных вероятностей 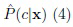 следующим образом:
следующим образом:
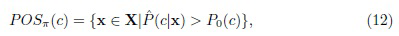
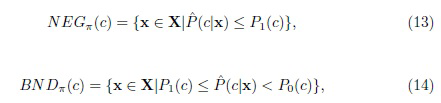
где пороги 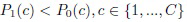 можно настроить на основе заданных функций потерь для выбора разных классов в разных состояниях.
можно настроить на основе заданных функций потерь для выбора разных классов в разных состояниях.
Фактически, такое определение очень похоже на известное статистически оптимальное правило для варианта отклонения, которое было введено Чоу (Chow) [3]. Единственное отличие подхода Yao и Zhao (12)-(14) состоит в том, что правило Чоу проверяет только достоверность оптимального решения (5), поэтому его можно рассматривать как решения с (C+1) альтернативами, которые принимают любой из C классов или откладывают процесс принятия решения в случае недостоверного результата (5). Применения таких решений изучались при распознавании лиц [23] и классификации речи [26]. Наиболее очевидным методом является отнесение признаков наблюдаемого изображения x к c-му классу, если данное изображение включено в положительную область (12) только этого класса. Таким образом, существуют C положительных областей
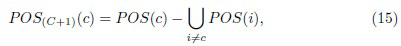
и всего одно граничное множество
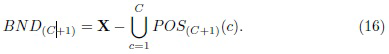
Если POS(c) определить методом Yao (12), то получается обычное правило Чоу [3], которое, как было показано эмпирически, эффективно снижает вероятность ошибочной классификации [21]. Однако в рассматриваемом случае можно также применить подход Slezak (9).
Наиболее сложной проблемой описанных многоклассовых моделей TWD является техническая сложность соответствующей настройки многих различных порогов, особенно для большого числа классов. Известно [31], что эти модели обладают значительной выразительной силой даже для унифицированных порогов 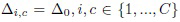 для BF (9)-(11) и
для BF (9)-(11) и 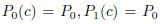 для подхода Yao (12)-(14). К сожалению, даже в этом случае настройка параметров затруднена при сопоставлении разности расстояний (8) или апостериорных вероятностей (12). Следовательно, ее необходимо аккуратно повторять для каждой задачи/меры близости и т.п. В следующем разделе рассматриваются способы преодоления недостатков этих методов на основании теории множественных сравнений [7].
для подхода Yao (12)-(14). К сожалению, даже в этом случае настройка параметров затруднена при сопоставлении разности расстояний (8) или апостериорных вероятностей (12). Следовательно, ее необходимо аккуратно повторять для каждой задачи/меры близости и т.п. В следующем разделе рассматриваются способы преодоления недостатков этих методов на основании теории множественных сравнений [7].
3. Предлагаемое изобретение
3.1. Тернарные решения, основанные на множественных сравнениях
В данном подразделе предлагается определить области TWD с помощью фиксации вероятности ошибки I рода 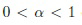 того, что заданное изображение представляет c-ый класс. В основу одного из возможных методов [26] для описанного статистического подхода положен известный факт, что 2n-кратная рассогласование KL между векторами признаков одного и того же класса имеет распределение хи-квадрат с (D-1) степенями свободы в асимптотике (для большого разрешения изображения n = W⋅H) [9, 28]. Таким образом, решение в пользу с-го класс принимается, если
того, что заданное изображение представляет c-ый класс. В основу одного из возможных методов [26] для описанного статистического подхода положен известный факт, что 2n-кратная рассогласование KL между векторами признаков одного и того же класса имеет распределение хи-квадрат с (D-1) степенями свободы в асимптотике (для большого разрешения изображения n = W⋅H) [9, 28]. Таким образом, решение в пользу с-го класс принимается, если

Здесь 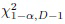 -
- 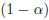 квантиль распределения хи-квадрат с (D-1) степенями свободы. В этом случае ошибка I рода появляется, если c-ый эталон не попадает в данную (положительную) область (17).
квантиль распределения хи-квадрат с (D-1) степенями свободы. В этом случае ошибка I рода появляется, если c-ый эталон не попадает в данную (положительную) область (17).
К сожалению, параметр α в данном определении не является вероятностью ошибки I рода при одновременной проверке всех C гипотез. На самом деле, при многоклассовом распознавании появляется проблема множественных сравнений, поэтому в (17) [7] требуется соответствующая коррекция. В настоящей заявке используется тест Бенджамини-Хохберга (Benjamini-Hochberg), который контролирует уровень ложноположительных результатов [1]. Сначала упорядочиваются все расстояния (6) и получаются метки классов 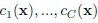 упорядоченной последовательности
упорядоченной последовательности 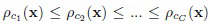 . Индекс kc(x) каждого класса с в этой упорядоченной последовательности сохраняется, так что:
. Индекс kc(x) каждого класса с в этой упорядоченной последовательности сохраняется, так что: 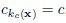 .
.
Согласно Benjamini и Hochberg [1], для принятия класса ci необходимо ввести коррекцию (C+1-i)/C вероятности ошибки I рода. Следовательно, TWD для множественных сравнений можно определить следующим образом:
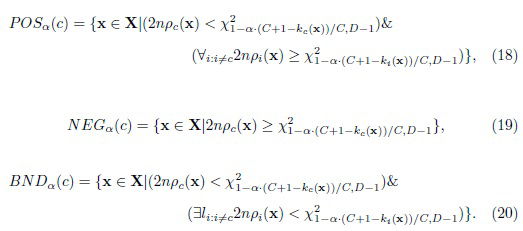
В отличие от систем принятия решений, которые могут рекомендовать несколько рекомендация для лица, принимающего решения, задача распознавания требует выбора всего одного класса для наблюдаемого изображения. Следовательно, в данном случае принимается не более одного класса, аналогично методу BF (9)-(11). Таким образом, вектор x признаков изображения принадлежит POSa(c) тогда и только тогда, когда c принят процедурой Бенджамини-Хохберга, а все другие классы отклонены. В этом случае класс c является оптимальным решением MAP (1), т.е. ближайшим соседом (5). Вектор x принадлежит NEGa(c) тогда и только тогда, когда гипотезы о классе c отклонены процедурой Бенджамини-Хохберга. Во всех других случаях вектор признаков x принадлежит BNDa(c).
К сожалению, предложенный TWD (18)-(20) затруднительно использовать на практике, поскольку расстояние между реальными изображениями одного и того же класса довольно велико и не удовлетворяет теоретическому распределению хи-квадрат с (D-1) степенями свободы [26]. Следовательно, процедура Бенджамини-Хохберга просто отклоняет все классы. Поэтому в настоящем изобретении рассмотрена небольшая модификация описанной процедуры с использованием известного распределения вероятностей рассогласования KL между различными гипотезами [9]. Если изображение x соответствует классу c, то 2n-кратное расстояние 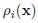 для каждого другого класса
для каждого другого класса 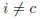 распределяется асимптотически как нецентральный хи-квадрат с (D-1) степенями свободы и параметром нецентральности
распределяется асимптотически как нецентральный хи-квадрат с (D-1) степенями свободы и параметром нецентральности 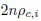 [24,25]. В данном случае
[24,25]. В данном случае 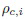 - это расстояние между классами c и i, которое можно определить как минимальное расстояние между эталонами этих классов. В результате, отношение расстояний (DF)
- это расстояние между классами c и i, которое можно определить как минимальное расстояние между эталонами этих классов. В результате, отношение расстояний (DF) 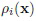 и
и 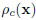 имеет нецентральное F-распределение
имеет нецентральное F-распределение 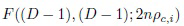 [28].
[28].
При статистическом распознавании образов имеются всего два возможных решения: принять класс MAP 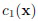 (5) или отложить процесс принятия решения [3]. Таким образом, в итоге получается следующее определение TWD:
(5) или отложить процесс принятия решения [3]. Таким образом, в итоге получается следующее определение TWD:
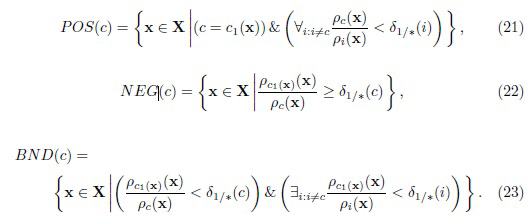
Пороги 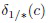 выбираются, исходя из предположения, что i-й класс является корректным, поэтому отношение
выбираются, исходя из предположения, что i-й класс является корректным, поэтому отношение 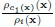 имеет нецентральное распределение F((D-1), (D-1); 2npi,c1(x)). Следовательно, пороги
имеет нецентральное распределение F((D-1), (D-1); 2npi,c1(x)). Следовательно, пороги 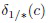 выбираются как
выбираются как 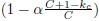 -квантиль этого нецентрального F-распределения.
-квантиль этого нецентрального F-распределения.
Предложенное TWD для распознавания изображений (21)-(23) аналогично модели Slezak [31], однако вместо отношения условных вероятностей (BF) используется отношение расстояния (DF). Следует подчеркнуть, что хотя эти уравнения были синтезированы с использованием асимптотических свойств рассогласования Кульбака-Лейблера (Kullback-Liebler), их можно использовать с произвольной мерой близости путем соответствующего выбора порогов 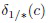 . Такую настройку можно реализовать гораздо более надежным способом по сравнению с BF (т.е. разностями расстояний (8)) и установлением порога апостериорных вероятностей (12), потому что данное отношение не зависит от масштаба меры близости. Например, DF использовался в обычном методе SIFT (масштабно-инвариантная трансформация признаков) [16] для выбора достоверных совпадений дескрипторов SIFT. Lowe продемонстрировал, что пороговое значение DF, равное 0,8, устраняет 90% ложных совпадений, в то же время отбрасывая менее 5% правильных совпадений во многих практических задачах обработки изображений [16].
. Такую настройку можно реализовать гораздо более надежным способом по сравнению с BF (т.е. разностями расстояний (8)) и установлением порога апостериорных вероятностей (12), потому что данное отношение не зависит от масштаба меры близости. Например, DF использовался в обычном методе SIFT (масштабно-инвариантная трансформация признаков) [16] для выбора достоверных совпадений дескрипторов SIFT. Lowe продемонстрировал, что пороговое значение DF, равное 0,8, устраняет 90% ложных совпадений, в то же время отбрасывая менее 5% правильных совпадений во многих практических задачах обработки изображений [16].
3.2. Последовательные тернарные решения
В типичных задачах распознавания изображений на замкнутом множестве категорий необходимо возвратить точно одну метку класса. Существующие многоклассовые TWD, включая описанный выше подход (21)-(23), по-видимому, бесполезны в данном случае, так как они не могут обеспечить что-либо точнее оптимального решения MAP (5). Тем не менее, основные достоинства TWD в задаче распознавания образов заключается в возможности значительно ускорить процедуру классификации [23, 26] при использовании последовательного TWD [40]. Согласно этой идее, объекты описываются L > 1 гранулами (представлением) [20], и на каждом уровне гранулярности назначаются три области принятия решения. Затем эти уровни гранулярности последовательно анализируются [34] от грубых к детальным гранулам до тех пор, пока представление наблюдаемого объекта на некотором уровне гранулярности не будет включено в положительную или отрицательную области. Если временная сложность для уровней более детальной гранулярности возрастает, то эта процедура реализует многоуровневую инкрементную обработку [36], которая может значительно повысить вычислительную эффективность анализа только представления самой детальной гранулярности.
Для реализации последовательного анализа с многоклассовым TWD (21)-(23) необходимо определить гранулярные аппроксимации изображений. В [23] предложено выделять признаки HOG из пирамид изображений. Однако это определение не подходит для признаков, извлеченных современными глубокими CNN [6], которые применяются в разделе 1 настоящего описания. Поэтому рассматриваются более типичные методы подпространств [12].
В частности, PCA будет выполняться в отношении всех векторов признаков из обучающего множества для получения матрицы Ф преобразования D × D [22]. Количество компонент в PCA равно размерности D глубоких элементов. В результате эталоны xr преобразуются в D-размерный вектор 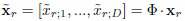 линейно независимых компонент, упорядоченных по соответствующим собственным значениям. Эту же процедуру повторяют для признаков x входного изображения, чтобы получить его PCA преобразование
линейно независимых компонент, упорядоченных по соответствующим собственным значениям. Эту же процедуру повторяют для признаков x входного изображения, чтобы получить его PCA преобразование 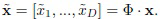 Более того, предложенный подход сосредоточен только на аддитивных мерах близости, так что их можно представить в виде суммы расстояний между соответствующими признаками:
Более того, предложенный подход сосредоточен только на аддитивных мерах близости, так что их можно представить в виде суммы расстояний между соответствующими признаками:
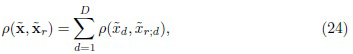
Такие расстояния типичны при распознавании изображений с глубокими признаками CNN. Что более важно, их плотности вероятности хорошо изучены [2] и могут быть аппроксимированы тем же самым распределением хи-квадрат, которое использовалось ранее для рассогласования KL [24].
Выберем количество уровней гранулярности L в качестве делителя общего числа признаков D, чтобы m = D/L было целым числом. Для такого случая предлагается определить представление входа на l-ом уровне гранулярности как вектора его первых lm главных компонент 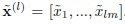 . Это представление совпадает с представлением
. Это представление совпадает с представлением 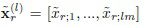 каждого эталона из обучающего множества. Кроме того, что данное определение гранулярности является простым, оно также является наименее затратным в вычислительном отношении, так как отсутствует необходимость сопоставления всех компонент при изучении следующего (l+1)-го уровня. Действительно, свойство аддитивности меры близости (24) позволяет вычислять только расстояния между m новыми компонентами:
каждого эталона из обучающего множества. Кроме того, что данное определение гранулярности является простым, оно также является наименее затратным в вычислительном отношении, так как отсутствует необходимость сопоставления всех компонент при изучении следующего (l+1)-го уровня. Действительно, свойство аддитивности меры близости (24) позволяет вычислять только расстояния между m новыми компонентами:
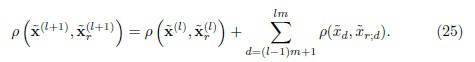
В результате, в отличие от известных реализаций последовательного TWD в распознавании образов [12, 23, 26], вычислительная эффективность последовательной обработки идентична на каждом уровне гранулярности. Даже наихудший сценарий с пустыми отрицательными областями для всех классов и каждым уровнем гранулярности лишь немного медленнее, чем бинарное решение на самом точном уровне, т.е. поиска методом полного перебора (5).
Таким образом, можно разработать процесс последовательного TWD при распознавании изображений (Фиг. 1). Сначала наблюдаемое изображение предварительно обрабатывается, и извлекаются глубокие признаки CNN. Затем анализируется только небольшое число m главных компонент в самом грубом приближении. Все эталонные эталоны с довольно большими (22) промежуточными расстояниями (25) отклоняются, и в дальнейшем не будут сопоставляться. Если можно получить всего один достоверный класс, т.е. положительная область (21) не пустая, то процесс завершается, и этот класс возвращается как результат. В противном случае, сопоставляются следующие m главных компонент, но наблюдаемое изображение сопоставляется с эталонами только тех классов, граничная область (23) которых включает в себя упомянутое наблюдаемое изображение. Этот процесс повторяется до тех пор, пока не будет получено единственное достоверное решение (21) на l-ом уровне. Если решения на всех L уровнях гранулярности недостоверны, то просто возвращается класс ближайшего соседа (5), как это делается при общем последовательном TWD с использованием бинарного решения на основном уровне [40].
Далее предложенный метод описывается полностью со ссылками на Фиг. 2, 3.
Прежде всего, важно отметить, что для уменьшения количества параметров аналогично применению показателя BF [31], все пороги DF приняты идентичными: 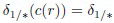 . Также важно отметить, что отношение между расстоянием до ближайшего соседа (5) и расстояниями до всех классов pc(x) было проверено в описанной ранее процедуре (21)-(23). Однако в обсуждаемом подходе это правило немного модифицировано посредством сопоставления минимального расстояния с расстояниями до всех эталонов ρ(x, xr). В последнем случае можно заранее предотвратить дальнейшее вычисление расстояний до некоторых эталонов с высоким ρ(x, xr), даже если входное изображение включено в положительные (21) или граничные (22) области их классов из-за близости к другому эталону(ам) этих классов.
. Также важно отметить, что отношение между расстоянием до ближайшего соседа (5) и расстояниями до всех классов pc(x) было проверено в описанной ранее процедуре (21)-(23). Однако в обсуждаемом подходе это правило немного модифицировано посредством сопоставления минимального расстояния с расстояниями до всех эталонов ρ(x, xr). В последнем случае можно заранее предотвратить дальнейшее вычисление расстояний до некоторых эталонов с высоким ρ(x, xr), даже если входное изображение включено в положительные (21) или граничные (22) области их классов из-за близости к другому эталону(ам) этих классов.
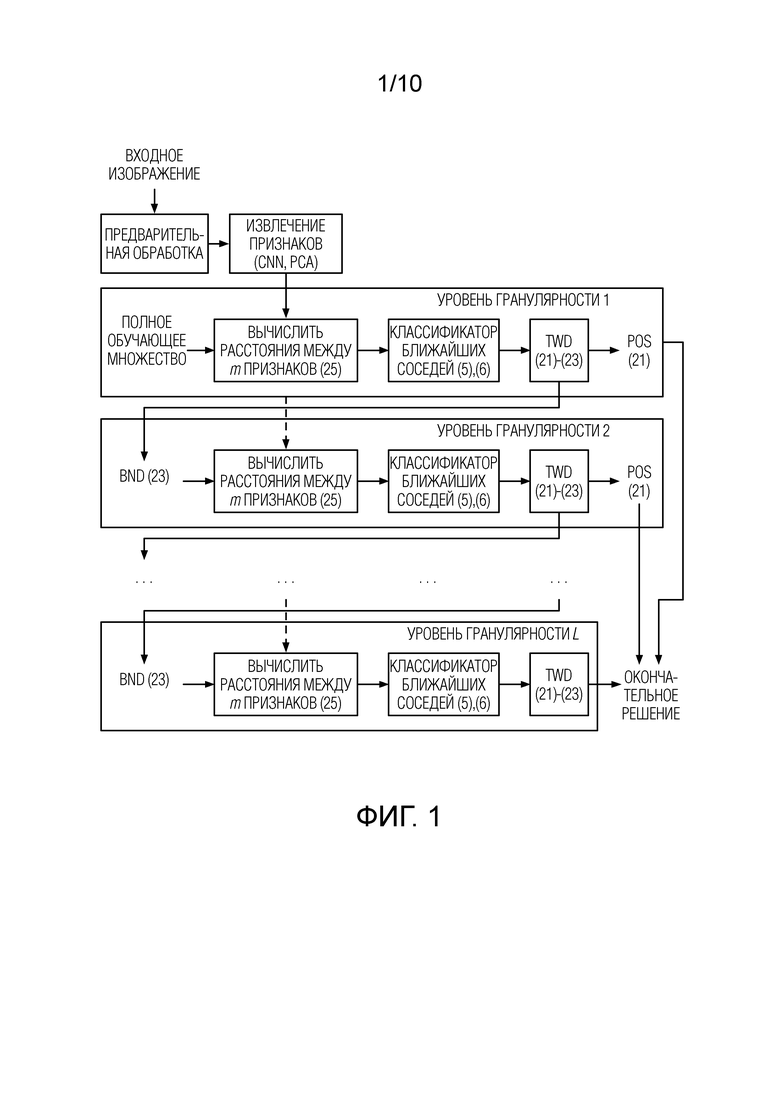
На Фиг.2 показана предварительная обработка обучающего множества изображений согласно варианту осуществления настоящего изобретения. Как отмечалось выше, обучающее множество изображений включает в себя эталонные изображения, каждый из которых принадлежит конкретному классу из заранее определенного количества (≥2) классов.
На этапе 210 для каждого эталона обучающего множества изображений получают вектор глубоких признаков данного эталона с помощью глубокой CNN, и полученный вектор нормируют в евклидовой норме. Как отмечалось ранее, указанный вектор извлекается на выходе предпоследнего слоя глубокой CNN.
На этапе 220 выполняют PCA по отношению к векторам глубоких признаков всех эталонов для получения матрицы преобразования. Матрица преобразования представляет собой квадратную матрицу D × D, где D - размерность каждого вектора глубоких признаков. После этого матрицу преобразования сохраняют.
На этапе 230 получают последовательность главных компонент для каждого эталона путем умножения матрицы преобразования на вектор глубоких признаков данного эталона. Главные компоненты в каждой полученной последовательности упорядочиваются по соответствующим собственным значениям.
На Фиг.3 показано распознавание изображения в соответствии с вариантом осуществления настоящего изобретения.
На этапе 310 получают вектор глубоких признаков входного изображения с помощью глубокой CNN, аналогично этапу 210. В частности, вектор извлеченных глубоких признаков также нормируют в евклидовой норме.
На этапе 320 к полученному вектору применяют преобразование PCA, чтобы получить последовательность главных компонент входного изображения. В частности, данную последовательность получают путем умножения ранее сохраненной матрицы преобразования (с этапа 220) на вектор глубоких признаков входного изображения. Главные компоненты в полученной последовательности также упорядочиваются по соответствующим собственным значениям.
На этапе 330 полученную последовательность главных компонент делят на некоторое количество смежных частей, где указанное количество является заданным количеством уровней гранулярности (L). В результате каждая часть относится к отличающемуся от других уровню гранулярности. В предпочтительном варианте L выбирают таким образом, чтобы деление размерности D каждого вектора глубоких признаков на L давало в результате целочисленное значение m. Иными словами, в предпочтительном варианте каждая из частей полученной последовательности имеет одинаковый размер m. Однако этот вариант не следует считать ограничительным; в частности, в некоторых вариантах можно разделить последовательность на неравные части.
На этапе 340 входное изображение сопоставляют с эталонами из обучающего множества изображений. Сопоставлению предшествует первоначальное заполнение множества решений-кандидатов всеми эталонами обучающего множества изображений. На этапе 340 выполняют цикл по уровням гранулярности, при этом для каждого уровня гранулярности (l ≤ L), начиная с уровня самой грубой гранулярности (l = 1), выполняют следующие подэтапы.
На подэтапе 3410 присоединяют l-ую часть последовательности главных компонент входного изображения к подпоследовательности главных компонент входного изображения. Эта подпоследовательность была пустой до начала цикла. В соответствии с вышеизложенным, указанная l-ая часть связана с l-ым (т.е. текущим) уровнем гранулярности и в предпочтительном варианте включает в себя m главных компонент.
На подэтапе 3420 вычисляют расстояния между этой подпоследовательностью и соответствующими подпоследовательностями главных компонент эталонов из множества решений-кандидатов.
На подэтапе 3430 вычисляют отношения минимального расстояния ко всем другим расстояниям среди вычисленных расстояний.
На подэтапе 3440 эталоны, каждый из которых имеет связанное с ним вычисленное значение, которое меньше заранее заданного порога, исключаются из множества решений-кандидатов. В предпочтительном варианте для всех уровней гранулярности используется один и тот же заранее заданный порог.
На подэтапе 3450, если множество решений-кандидатов включает в себя по меньшей мере один эталон из лишь одного класса, входное изображение идентифицируется как относящееся к данному классу, возвращается соответствующую метку класса, и цикл завершается. В противном случае, если для последнего уровня самой детальной гранулярности l = L множество решений-кандидатов все еще включает в себя эталоны из более чем одного класса, определяют эталон, имеющий максимальное вычисленное отношение, среди эталонов, присутствующих в множестве решений-кандидатов, и входное изображение идентифицируют как относящееся к классу, которому принадлежит данный эталон, и соответственно возвращают метку класса этого эталона.
Как обсуждалось выше, на подэтапе 3420 расстояния вычисляются в соответствии с уравнением (25). То есть, на (l+1)-ом уровне гранулярности, 1 ≤ l< L, расстояния вычисляются как:
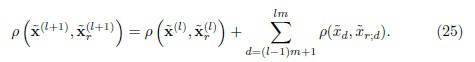 ,
,
где m = D/L; 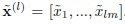 - подпоследовательность главных компонент входного изображения на l-ом уровне гранулярности;
- подпоследовательность главных компонент входного изображения на l-ом уровне гранулярности; 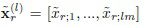 - подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-ом уровне гранулярности; и
- подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-ом уровне гранулярности; и 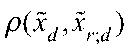
Временная сложность предложенного метода, составляющая в худшем случае O(RD), идентична полному перебору (5). Вычислительная эффективность в лучшем случае пустых граничных областей (23) для всех категорий на уровне самой грубой гранулярности можно определить как O(RD/L). Оценка вычислительной эффективности в среднем случае требует анализа значений функции распределения упомянутых выше нецентральных F-распределений в точке 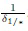 . Для простоты предполагается, что процент попавших в граничную область (23) эталонов на каждом уровне равен константе
. Для простоты предполагается, что процент попавших в граничную область (23) эталонов на каждом уровне равен константе 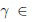 (0; 1]. Тогда временную сложность предложенного метода (см. Фиг. 2, 3) можно оценить как:
(0; 1]. Тогда временную сложность предложенного метода (см. Фиг. 2, 3) можно оценить как: 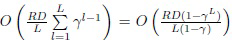 . Эта оценка обычно на порядок меньше сложности наихудшего случая, в котором
. Эта оценка обычно на порядок меньше сложности наихудшего случая, в котором 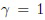 . Фактически, вычислительная эффективность предложенного метода должна быть намного выше, чем эффективность обычных классификаторов или известных реализаций многоклассового последовательного TWD (подраздел 2 настоящего описания).
. Фактически, вычислительная эффективность предложенного метода должна быть намного выше, чем эффективность обычных классификаторов или известных реализаций многоклассового последовательного TWD (подраздел 2 настоящего описания).
Специалистам будет понятно, что описанные выше методы согласно изобретению можно реализовать с помощью обычных компьютерных программных и аппаратных средств. В частности, на Фиг.4 показана высокоуровневая блок-схема обычного вычислительного устройства 400, в котором могут быть реализованы аспекты настоящего изобретения. Вычислительное устройство 400 включает в себя, по меньшей мере, блок 410 обработки данных и блок 420 хранения данных, подключенный к блоку 410 обработки данных. Блок 410 обработки данных обычно содержит один или несколько процессоров (ЦП), которые могут быть универсальными или специализированными, выпускаемыми серийно или заказными процессорами. Блок 420 хранения данных обычно содержит различные машиночитаемые носители и/или запоминающие устройства, как энергонезависимые (например, ПЗУ, жесткие диски, флэш-накопители и т.п.), так и энергозависимые (например, различные виды ОЗУ и т.п.).
В контексте настоящего изобретения блок 420 хранения данных содержит машиночитаемые носители данных, на которых записано соответствующее программное обеспечение. Это программное обеспечение содержит машиноисполняемые команды, которые при их исполнении блоком 410 обработки данных предписывают блоку 410 обработки данных выполнять способ в соответствии с изобретением. Такое программное обеспечение может быть соответствующим образом разработано и развернуто с использованием известных технологий и сред программирования.
Для специалиста будет очевидно, что вычислительное устройство 400, задействованное в реализации изобретения, также содержит другие известные аппаратные средства, такие как устройства ввода-вывода, интерфейсы связи и т. п., а также базовое программное обеспечение, такое как операционная система, стеки протоколов, драйверы и т.д., которые могут быть выпускаемыми серийно или заказными. Вычислительное устройство 400 может быть выполнено с возможностью сообщения с другими вычислительными устройствами, платформами и сетями посредством известных технологий проводной и/или беспроводной связи.
Следует понимать, что проиллюстрированные варианты осуществления изобретения являются всего лишь предпочтительными, а не единственно возможными примерами изобретения. Напротив, объем изобретения определяется нижеследующей формулой изобретения и ее эквивалентами. Раскрытие, содержащееся в документах, перечисленных ниже, включено в настоящее описание в качестве ссылки.
4. Экспериментальные результаты
В данном разделе рассматриваются задачи распознавания лиц и категоризации изображений. Для извлечения признаков изображения применяется платформа глубокого обучения Caffe. Все CNN предварительно обучены их авторами, поэтому они загружены с официальных сайтов, включая репозиторий Caffe Model Zoo. В данном контексте используется квадрат расстояния Евклида между главными компонентами, которое можно записать в форме (24), подходящей для аддитивного разложения (25).
Поскольку настоящее изобретение фокусируется, в основном, на вычислительной эффективности распознавания, предложенный метод (см. фиг. 2, 3) сравнивался с (C+1)-сторонними решениями (15), (16) [23] с предложенным определением уровней детализации. В последнем подходе достоверность решений проверялась с помощью следующих методов:
1. Традиционное правило Чоу [3] с оценкой (4) апостериорной вероятности (12)-(14) [38];
2. Сопоставление разности расстояний (8) с порогом, обусловленным многоклассовыми решениями BF [31];
3. Сопоставление DF (21)-(23), в котором все классы проверяются на каждом уровне гранулярности с использованием уравнений (15), (16).
В случае (C+1)-сторонних решений по принципу выполняются рекомендации из статьи [23] и используются только уровни гранулярности L=2. На уровне самой грубой гранулярности анализируются m=64 главных компонент. Уровень самой детальной гранулярности во всех последовательных TWD, включая предлагаемый метод (Фиг. 1), описывается главными компонентами, т.е. он обычно меньше, чем общее количество признаков D, чтобы максимально ускорить этот подход. Для простоты настройки все пороги установлены равными друг другу для каждого конкретного последовательного TWD, так что эти пороги не зависят от метки класса c.
Кроме того, метод ближайшего соседа (5) рассматривается в трех вариантах, в частности, сопоставление первых 64, 256 и всех D главных компонент. Также используются многоклассовые классификаторы, реализованные в библиотеке OpenCV, в частности, RF и SVM с ядром RBF. В большинстве случаев их параметры невозможно настроить с помощью только обучающих множеств, так как они слишком малы. Поэтому здесь используются дополнительные наборы данных VGG Flower и PubFig83 для настройки параметров в задачах категоризации изображений и распознавания лиц, соответственно. Хотя лучшие результаты можно получить при настройке параметров тем же набором данных, что и обучающее/тестовое множество, эта процедура не является корректной, поскольку она оказывает влияние на результаты тестирования. В то же время отсутствие такой настройки для каждого отдельного набора данных может привести к несколько худшим результатам, о которых сообщается в имеющихся публикациях.
Протокол тестирования для наборов данных, использованных в экспериментах, реализует следующий вариант случайной подвыборки в методе перекрестной проверки, который подходит для изучения случая малых выборок. Каждый набор данных делится произвольно 10 раз на обучающее и тестовое множество, так что отношение размера R обучающего множества к размеру всего набора данных T равно фиксированному числу. Каждый класс делится независимо, чтобы обеспечить примерно одинаковое соотношение количества изображений в обучающем и тестовом множествах. Изобретение сфокусировано на проблеме малых выборок, поэтому отношение R/T выбирается достаточно малым. Поскольку все наборы данных несбалансированы, точность классификации изображений из каждой категории оценивается отдельно, и вычисляется (макро) средняя вероятность ошибки a. Кроме того, измеряется среднее время классификации одного изображения 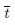 (в мс) на специальном сервере (24 ядерный Intel Xeon 3,47 ГГц, 96 ГБ ОЗУ)
(в мс) на специальном сервере (24 ядерный Intel Xeon 3,47 ГГц, 96 ГБ ОЗУ)
4.1. Распознавание лиц в неконтролируемых условиях съемки
В данном подразделе рассматривается идентификация лиц в неконтролируемых условиях съемки [15]. Используются три общедоступные модели CNN, а именно: сеть VGG-16 (VGGFace) [19], ResFace (ResNet-101 для распознавания лиц) [18] и Light CNN [35]. Слой "fc7" сети VGGFace извлекает D=4096 неотрицательных признаков из изображения RGB 224×224. Тот же самый формат изображения используется для извлечения D=2048 признаков из слоя "pool5" сети ResFace. Сеть Light CNN (версия C) извлекает D=256 признаков (возможно, отрицательных) на слое "eltwise_fc2" из полутонового изображения 128×128.
Первая часть этого подраздела посвящена набору данных LFW (Labeled Faces in the Wild, Размеченные лица в естественных условиях) [10] с T=13233 фотографиями C=5749 человек. Классы, имеющие всего одно эталонное изображение, были помещены в обучающее множество. Изображения всех остальных классов были разделены на две части одинакового размера, чтобы равномерно заполнить обучающее и тестовое множества. В результате, обучающее множество содержит в среднем R=8640 эталонов.
Предложенный подход (см. фиг. 1) был реализован в двух вариантах: раздельная обработка всех классов (21)-(23) и его упрощенная версия с отклонением отдельных эталонов (см. Фиг. 2, 3). Сначала демонстрируется возможность настройки параметров предложенного способа, а именно: порога DF 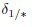 и шага гранулярности m. Результаты для дескриптора VGGFace показаны на Фиг. 5 и 6 соответственно.
и шага гранулярности m. Результаты для дескриптора VGGFace показаны на Фиг. 5 и 6 соответственно.
Как и ожидалось, чем больше порог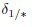 , тем меньше время распознавания (Фиг. 5b), но тем выше вероятность ошибки (Фиг. 5а). Однако точность не претерпевает существенных изменений, если
, тем меньше время распознавания (Фиг. 5b), но тем выше вероятность ошибки (Фиг. 5а). Однако точность не претерпевает существенных изменений, если 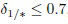 , поэтому в оставшейся части описания в качестве порога будет использоваться значение 0,7. Кроме того, очень большое количество уровней гранулярности L (и, следовательно, низкое m) приводит к неточным решениям, поскольку в простых экспериментах эти пороги не зависят от уровня гранулярности l, хотя, теоретически, следует использовать количество признаков ml как степени свободы в нецентральном F-распределении. Однако для точного распознавания изображений лица достаточно выбрать m=32 или m=64. Более того, хотя точность в случае отклонения обоих классов и эталонов примерно одинакова, время распознавания в последнем случае меньше на 0,1-0,2 мс. Поэтому в дальнейших экспериментах для отдельных эталонов будет использоваться только TWD, как описано со ссылками на Фиг. 2, 3).
, поэтому в оставшейся части описания в качестве порога будет использоваться значение 0,7. Кроме того, очень большое количество уровней гранулярности L (и, следовательно, низкое m) приводит к неточным решениям, поскольку в простых экспериментах эти пороги не зависят от уровня гранулярности l, хотя, теоретически, следует использовать количество признаков ml как степени свободы в нецентральном F-распределении. Однако для точного распознавания изображений лица достаточно выбрать m=32 или m=64. Более того, хотя точность в случае отклонения обоих классов и эталонов примерно одинакова, время распознавания в последнем случае меньше на 0,1-0,2 мс. Поэтому в дальнейших экспериментах для отдельных эталонов будет использоваться только TWD, как описано со ссылками на Фиг. 2, 3).
Результаты всех экспериментов с набором данных LFW сведены в Таблице 1.
При этом можно сделать следующие выводы. Во-первых, точность традиционных классификаторов RF и SVM недостаточна из-за эффектов, вызванных выборками очень малого размера.
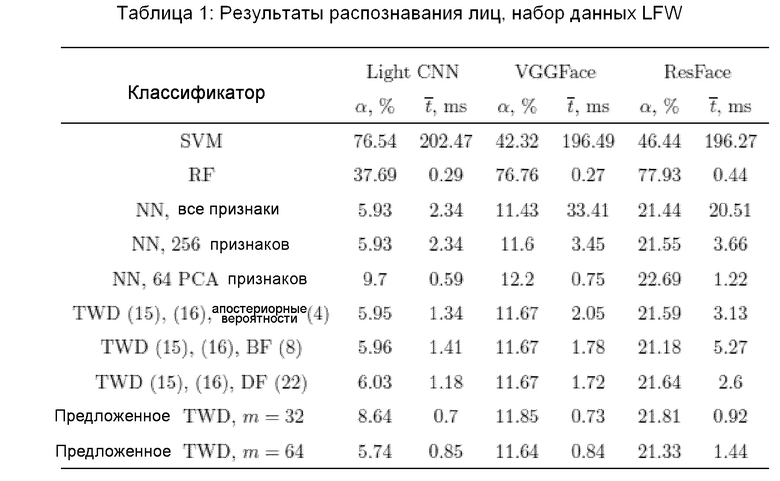
Более того, реализация многоклассового SVM по методу "один против остальных" очень медленная из-за последовательной обработки всех классов. Во-вторых, предварительная обработка PCA довольно эффективна, поскольку достаточно всего 256 основных компонент, чтобы распознавать изображения практически с такой же точностью, как при использовании метода полного перебора, в котором сопоставляются все D признаков. В-третьих, метод ближайшего соседа всего с 64 признаками на уровне самой грубой гранулярности не может обеспечить точное решение. Однако последовательное TWD с m=64 признаками на уровне самой грубой гранулярности может снизить вероятность ошибки без существенных потерь в вычислительной эффективности. Определение разности расстояний в BF (9)-(11) происходит немного быстрее, чем при обычном подходе (12)-(14), поскольку обычный подход включает в себя довольно сложные вычисления апостериорных вероятностей (4). Важно отметить, что отношение расстояний (21)-(23), предложенное в изобретении, является наиболее устойчивым к ошибкам методом определения многоклассового TWD. Например, хотя DF работает так же быстро, как и другие варианты дескриптора VGGFace, он намного быстрее, чем существующие варианты для признаков Light CNN и ResFace. Фактически, установка порога на 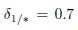 позволяет отфильтровывать недостоверные решения для всех используемых дескрипторов. И наконец, предложенная реализация последовательного TWD (см. фиг. 2, 3) с определениями DF TWD (21)-(23) позволяет увеличить скорость распознавания в 2,5-4 раза по сравнению с методом ближайшего соседа с 256 главными компонентами. Кроме того, предложенный метод в 1,5-2,5 раза быстрее, чем существующие последовательные решения по принципу (C+1) (15), (16). Примечательно, что m=32 в предложенном методе некорректно для малоразмерных признаков Light CNN, но достаточно для достижения довольно низкой вероятности ошибки для высокоразмерных дескрипторов VGGFace и ResFace.
позволяет отфильтровывать недостоверные решения для всех используемых дескрипторов. И наконец, предложенная реализация последовательного TWD (см. фиг. 2, 3) с определениями DF TWD (21)-(23) позволяет увеличить скорость распознавания в 2,5-4 раза по сравнению с методом ближайшего соседа с 256 главными компонентами. Кроме того, предложенный метод в 1,5-2,5 раза быстрее, чем существующие последовательные решения по принципу (C+1) (15), (16). Примечательно, что m=32 в предложенном методе некорректно для малоразмерных признаков Light CNN, но достаточно для достижения довольно низкой вероятности ошибки для высокоразмерных дескрипторов VGGFace и ResFace.
В следующем эксперименте рассматриваются T=81132 изображений из C=1000 первых классов набора данных для лиц CASIA-WebFace [42]. Около трети этого набора данных (R=25000 изображений) были помещены в обучающее множество, остальные изображения попали в тестовое множество. Результаты представлены в Таблице 2.
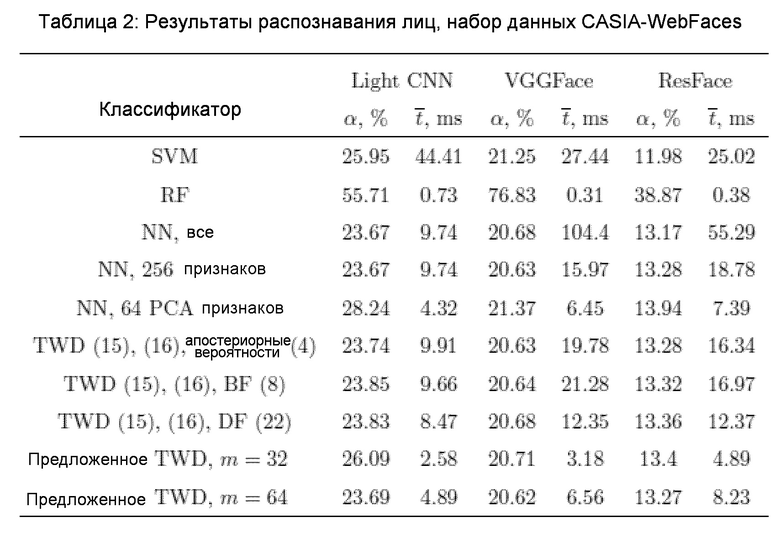
В отличие от предыдущих экспериментов, вероятность ошибки известной SVM здесь довольно низкая. Например, это лучший классификатор для признаков ResNet.
Однако вычислительная эффективность SVM остается низкой. Важно, что LightCNN, которая была наиболее точным дескриптором для набора данных LFW (Таблица 1), дает наихудшие признаки в этом эксперименте. По всей видимости, в настоящее время не существует общедоступного дескриптора лиц, который был бы лучшим во всех сценариях. При этом обычное сопоставление апостериорных вероятностей и отношения условных плотностей (разности расстояний) не позволяет улучшить характеристики основного уровня гранулярности (метод ближайшего соседа с 256 главными компонентами). Тем не менее, предложенный DF (22) даже в (C+1)-сторонних решениях в 1,2-2 раза эффективнее, чем традиционные многоклассовые определения TWD [31, 38]. Примечательно, что последние методы даже медленнее, чем обработка на основном уровне (метод ближайшего соседа с 256 признаками), из-за малого количества отклоненных решений. Это может объясняться вышеупомянутыми трудностями достоверной оценки порогов, которые представляются не такими сложными в критериях отношения расстояний (21)-(23). Кроме того, предлагаемая реализация последовательного TWD (см. фиг. 2, 3) и здесь является лучшим классификатором, основывающимся на поиске ближайшего соседа. Она в 2-4 раза быстрее, чем лучший из других алгоритмов, хотя точность приблизительно равна точности довольно медленного полного перебора (5).
4.2. Практический пример
Продемонстрируем на простом примере, как этот подход повышает точность распознавания лиц. Одно из тестовых изображений (Фиг. 7а) человека из набора данных LFW распознается с помощью схемы, описанной в предыдущем подразделе. Признаки извлекаются посредством Light CNN [35]. Рассматриваются L=4 уровней гранулярности с m=64 новых главных компонент на каждый уровень. В таблице 3 показаны минимальные расстояния и их отношения для нескольких ближайших человек из указанной галереи, установленные на разных уровнях.
Обработка первых 64 главных компонент на уровне самой грубой гранулярности l=1 дает некорректное решение (см. Фиг. 7b). Однако последовательный анализ в соответствии с предложенным методом (Фиг. 1) не прекращается, поскольку граничные области (23) 6 классов, представленных в Таблице 3, не являются пустыми, так как DF (столбец 3 в этой таблице) превышает порог 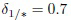 .
.
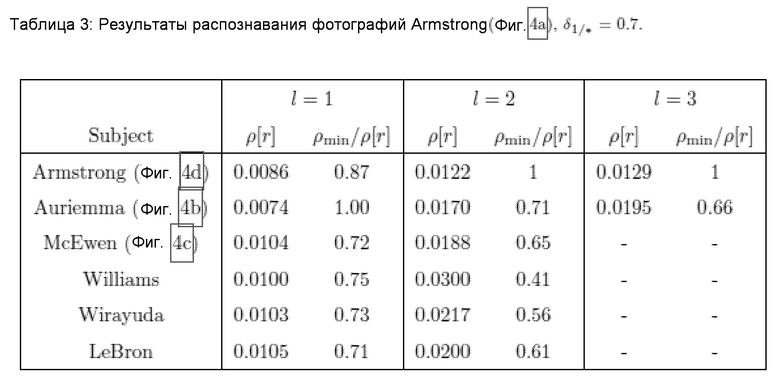
Принятие решения на втором уровне гранулярности позволило получить правильного ближайшего соседа (Фиг. 7d). Более того, ограничивающие области 4 классов на этом этапе становятся пустыми. Однако выполнение метода согласно изобретению (см. Фиг. 2, 3) не прекращается, поскольку все еще существует два возможных решения (фиг. 7b и 7d). Только информации о 192 главных компонентах на уровне l=3 достаточно для принятия достоверного решения, поскольку DF для изображения Geno Auriemma (0.66) меньше порога 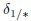 .
.
Важно подчеркнуть, что предлагаемый метод не требует анализа всех D=256 признаков в данном примере. Однако после обработки наблюдаемого изображения (Фиг. 7а) на уровне самой грубой гранулярности не было вынесено поспешное и некорректное решение. Таким образом, предлагаемый метод позволяет достичь компромисса между точностью и вычислительной эффективностью распознавания, как видно из экспериментов (Таблицы 1 и 2) в предыдущем подразделе.
4.3. Категоризация изображений
Данный подраздел посвящен задаче распознавания категории визуального объекта. Используются четыре набора данных с довольно большим количеством классов:
1. Набор данных Caltech 101 Object Category [5], который содержит T=8677 изображений C=102 классов, включая отвлекающий фоновый класс. Обучающее множество содержит R=3060 изображений.
2. Набор данных Caltech 256 с T=29780 изображений классов C=257, включая перенасыщенный класс. В обучающее множество было включено R=2570 изображений.
3. Набор данных Stanford Dogs [8] с T=20580 изображений C=120 классов, из которых R=1200 эталонов заполнили обучающее множество.
4. Набор данных CUB-200-2011 (Caltech-UCSD Birds) с T=11788 изображениями C=200 типов птиц. По 10 изображений из каждого класса помещены в обучающее множество (R=2000). Хотя этот набор данных используется, в основном, для задачи обнаружения объектов, изображения обрезаются с помощью ограничительных рамок, предоставленных его авторами, для решения обычной задачи распознавания изображений.
Для извлечения признаков изображения на предварительных этапах предложенного способа (см. Фиг. 2, 3) применялись обычные методы доменной адаптации. Две архитектуры глубоких CNN (19-слойная VGGNet [30] и Inception v1 (или GoogLeNet) [33]) были загружены из репозитория Caffe Model Zoo. Эти CNN уже были обучены распознавать изображения 1000 классов из набора данных ImageNet. Затем каждое RGB изображение из каждого набора данных подавалось на вход этих CNN. Выходы одного из последних уровней CNN ("pool5/7×7-s1" для Inception и "fc6" для VGGNet) подвергали L2-нормированию, чтобы получить окончательный вектор признаков, имеющий размерность D=1024 для Inception и D=4096 для VGGNet. Все результаты экспериментов показаны на Фиг. 8-11 для наборов данных Caltech-101, Caltech-256, Dogs и CUB-200-2011, соответственно.
Хотя в настоящем описании рассматриваются четыре разных набора данных, основные результаты остаются очень похожими. Во-первых, в отличие от предыдущего подраздела, в этих экспериментах имеется достаточно изображений для каждого класса, чтобы обучить традиционные классификаторы. Фактически, SVM является наиболее точным методом практически во всех случаях. Однако ее временная сложность слишком высока для реализации в режиме реального времени, в частности, аппаратные характеристики машины опорных векторов несопоставимы с характеристиками сервера. RF остается очень быстрым методом, но его точность приблизительно равна точности других методов только в экспериментах с наборами данных Caltech-101 (Фиг. 8) и Stanford Dogs (Фиг. 10), где SVM точнее на 5-10%. Кроме того, время распознавания TWD с отношением расстояний (21)-(23) остается на 20-100% меньше по сравнению с BF (9)-(11) и правилом Чоу (12)-(14) без существенного увеличения вероятности ошибки. Сопоставление разностей расстояний (8) в некоторых случаях происходит даже медленнее, чем поиск ближайшего соседа для рассматриваемой самой детальной гранулярности (256 признаков). И наконец, самый важный вывод относится к превосходству последовательного TWD (см. Фиг. 2, 3) над другими классификаторами на основе метода ближайшего соседа: предложенный способ в 4-10 раз быстрее, чем поиск ближайшего соседа на основном уровне (256 признаков) и в 1,5-3 раза быстрее, чем последовательные решения по принципу (C+1) с традиционными определениями трех областей (9)-(11) и (12)-(14). Следует подчеркнуть еще раз: достаточно начать с изучения всего m=32 главных компонент, уменьшая при этом количество уровней гранулярности (m=64 компонент на каждый уровень), чтобы в большинстве случаев повысить точность при неощутимом ухудшении времени принятия решений.
Сокращения
• BF - Коэффициент Байеса
• CNN - Сверточная нейронная сеть
• DF - Отношение расстояний
• DTRS - Теория принятия решений на основе приближенных множеств
• HOG - Гистограммы ориентированных градиентов
• MAP - Максимальная апостериорная вероятность
• NN - Ближайший сосед
• PCA - Метод главных компонент
• RF - Случайный лес
• SIFT - Масштабно-инвариантная трансформация характерных признаков
• SVM - Машина опорных векторов
• TWD - Тернарное решение
Литература
[1] Benjamini Y., Hochberg Y., 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the royal statistical society. Series B (Methodological), 289-300.
[2] Burghouts G., Smeulders A., Geusebroek J.-M., 2008. The distribution family of similarity distances. In: Proceedings of NIPS. pp. 201-208.
[3] Chow C. K., 1970. On optimum recognition error and reject tradeoff. IEEE Transactions on Information Theory 16 (1), 41-46.
[4] Deng G., Jia X., 2016. A decision-theoretic rough set approach to multiclass cost-sensitive classification. In: International Joint Conference on Rough Sets, LNCS/LNAI. Springer, pp. 250-260.
[5] Fei-Fei L., Fergus R., Perona P., 2006. One-shot learning of object categories. IEEE Transactions on Pattern Analysis and Machine Intelligence 28 (4), 594-611.
[6] Goodfellow I., Bengio Y., Courville A., 2016. Deep learning. MIT press.
[7] Hochberg Y., Tamhane A. C., 2009. Multiple comparison procedures.
[8] Khosla A., Jayadevaprakash N., Yao B., Li F.-F., 2011. Novel dataset for fine-grained image categorization: Stanford dogs. In: Proceedings of CVPRW on Fine-Grained Visual Categorization (FGVC). Vol.2. p. 1.
[9] Kullback S., 1997. Information Theory and Statistics. Dover Publications, Mineola, New York.
[10] Learned-Miller E., Huang G. B., RoyChowdhury A., Li H., Hua G., 2016. Labeled faces in the wild: A survey. In: Advances in Face Detection and Facial Image Analysis. Springer, pp. 189-248.
[11] Li H., Zhang L., Zhou X., Huang B., 2017. Cost-sensitive sequential three-way decision modeling using a deep neural network. International Journal of Approximate Reasoning 85, 68-78.
[12] Li H. X., Zhang L. B., Huang B., Zhou X. Z., 2016. Sequential three-way decision and granulation for cost-sensitive face recognition. Knowledge-Based Systems 91, 245-251.
[13] Lingras P., Chen M., Miao D., 2008. Rough multi-category decision theoretic framework. Rough Sets and Knowledge Technology, 676-683.
[14] Liu D., Li T., Li H., 2012. A multiple-category classification approach with decision-theoretic rough sets. Fundamenta Informaticae 115 (2-3), 173-188.
[15] Long Y., Zhu F., Shao L., Han J., 2018. Face recognition with a small occluded training set using spatial and statistical pooling. Information Sciences 430-431, 634-644.
[16] Lowe D. G., 2004. Distinctive image features from scale-invariant key-points. International Journal of Computer Vision 60 (2), 91-110.
[17] Lu J., Han J., Hu Y., Zhang G., 2016. Multilevel decision-making: a survey. Information Sciences 346, 463-487.
[18] Masi I., Tran A., Hassner T., Leksut J. T., Medioni G., 2016. Do we really need to collect millions of faces for effective face recognition? In: Proceedings of ECCV.
[19] Parkhi O. M., Vedaldi A., Zisserman A., 2015. Deep face recognition. In: Proceedings of BMVC. Vol.1. p.6.
[20] Pedrycz W., Succi G., Sillitti A., Iljazi J., 2015. Data description: a general framework of information granules. Knowledge-Based Systems 80, 98-108.
[21] Pillai I., Fumera G., Roli F., 2013. Multi-label classification with a reject option. Pattern Recognition 46 (8), 2256-2266.
[22] Prince S. J., 2012. Computer vision: models, learning, and inference. Cambridge University Press.
[23] Savchenko A. V., 2016. Fast multi-class recognition of piecewise regular objects based on sequential three-way decisions and granular computing. Knowledge-Based Systems 91, 252-262.
[24] Savchenko A. V., 2016. Search techniques in intelligent classification systems. Springer.
[25] Savchenko A. V., 2017. Maximum-likelihood approximate nearest neighbor method in real-time image recognition. Pattern Recognition 61, 459-469.
[26] Savchenko A. V., 2017. Sequential three-way decisions in efficient classification of piecewise stationary speech signals. In: International Joint Conference on Rough Sets, LNCS/LNAI. Springer, pp. 264-277.
[27] Savchenko A. V., Belova N. S., Savchenko L. V., 2018. Fuzzy analysis and deep convolution neural networks in still-to-video recognition. Optical Memory and Neural Networks (Information Optics) 27 (1), 23-31.
[28] Savchenko V. V., Savchenko A. V., 2016. Information-theoretic analysis of efficiency of the phonetic encoding-decoding method in automatic speech recognition. Journal of Communications Technology and Electronics 61 (4), 430-435.
[29] Sharif Razavian A., Azizpour H., Sullivan J., Carlsson S., 2014. CNN features off-the-shelf: an astounding baseline for recognition. In: Proceedings of CVPRW. IEEE Computer Society, pp. 806-813.
[30] Simonyan K., Zisserman A., 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
[31] Slezak D., 2005. Rough sets and bayes factor. Transactions on Rough Sets III, LNCS 3400, 202-229.
[32] Szczuka M., Slezak D., 2011. Feedforward neural networks for compound signals. Theoretical Computer Science 412 (42), 5960-5973.
[33] Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., 2015. Going deeper with convolutions. In: Proceedings of CVPR. IEEE Computer Society, pp. 1-9.
[34] Wald A., 2013. Sequential Analysis. Dover Publications, New York.
[35] Wu X., He R., Sun Z., Tan T., 2016. A light CNN for deep face representation with noisy labels. arXiv preprint arXiv:1511.02683.
[36] Yang X., Li T., Fujita H., Liu D., Yao Y., 2017. A unified model of sequential three-way decisions and multilevel incremental processing. Knowledge-Based Systems 134, 172-188.
[37] Yang X., Li T., Liu D., Chen H., Luo C., 2017. A unified framework of dynamic three-way probabilistic rough sets. Information Sciences, 126-147.
[38] Yao Y., Zhao Y., 2008. Attribute reduction in decision-theoretic rough set models. Information sciences 178 (17), 3356-3373.
[39] Yao Y. Y., 2010. Three-way decisions with probabilistic rough sets. Information Sciences 180, 341-353.
[40] Yao Y. Y., 2013. Granular computing and sequential three-way decisions. In: Proceedings of RSKT, LNCS. Vol. 8171. Springer, pp. 16-27.
[41] Yao Y. Y., Deng X. F., 2011. Sequential three-way decisions with probabilistic rough sets. In: Proceedings of ICCI*CC. IEEE Computer Society, pp. 120-125.
[42] Yi D., Lei Z., Liao S., Li S. Z., 2014. Learning face representation from scratch. arXiv preprint arXiv:1411.7923.
[43] Yu Z., Li T., Luo G., Fujita H., Yu N., Pan Y., 2018. Convolutional networks with cross-layer neurons for image recognition. Information Sciences 433-434, 241-254.
[44] Zhang Q., Lv G., Chen Y., Wang G., 2018. A dynamic three-way decision model based on the updating of attribute values. Knowledge-Based Systems 142, 71-84.
Zhou B., 2014. Multi-class decision-theoretic rough sets. International Journal of Approximate Reasoning 55 (1), 211-224.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ ОБУЧЕННЫМИ НЕЙРОННЫМИ СЕТЯМИ | 2021 |
|
RU2779281C1 |
| РАСПОЗНАВАНИЕ СОБЫТИЙ НА ФОТОГРАФИЯХ С АВТОМАТИЧЕСКИМ ВЫДЕЛЕНИЕМ АЛЬБОМОВ | 2020 |
|
RU2742602C1 |
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ СВЕРТОЧНЫМИ НЕЙРОННЫМИ СЕТЯМИ | 2020 |
|
RU2771442C1 |
| СПОСОБ АУДИОВИЗУАЛЬНОГО РАСПОЗНАВАНИЯ СРЕДСТВ ИНДИВИДУАЛЬНОЙ ЗАЩИТЫ НА ЛИЦЕ ЧЕЛОВЕКА | 2022 |
|
RU2791415C1 |
| СПОСОБ И СИСТЕМА ДЛЯ РАСПОЗНАВАНИЯ ЛИЦА С УЧЕТОМ СПИСКА ЛЮДЕЙ, НЕ ПОДЛЕЖАЩИХ ПРОВЕРКЕ | 2008 |
|
RU2381553C1 |
| ОДНОВРЕМЕННОЕ РАСПОЗНАВАНИЕ АТРИБУТОВ ЛИЦ И ИДЕНТИФИКАЦИИ ЛИЧНОСТИ ПРИ ОРГАНИЗАЦИИ ФОТОАЛЬБОМОВ | 2018 |
|
RU2710942C1 |
| Способ формирования архитектуры нейросети для классификации объекта, заданного в виде облака точек, способ ее применения для обучения нейросети и поиска семантически схожих облаков точек | 2017 |
|
RU2674326C2 |
| ВИЗУАЛИЗАЦИЯ РЕКОНСТРУКЦИИ 3D-СЦЕНЫ С ИСПОЛЬЗОВАНИЕМ СЕМАНТИЧЕСКОЙ РЕГУЛЯРИЗАЦИИ НОРМАЛЕЙ TSDF ПРИ ОБУЧЕНИИ НЕЙРОННОЙ СЕТИ | 2023 |
|
RU2825722C1 |
| СПОСОБ ФОРМИРОВАНИЯ СИСТЕМЫ УПРАВЛЕНИЯ МОЗГ-КОМПЬЮТЕР | 2019 |
|
RU2704497C1 |
| РАСПОЗНАВАНИЕ СИМВОЛОВ С ИСПОЛЬЗОВАНИЕМ ИЕРАРХИЧЕСКОЙ КЛАССИФИКАЦИИ | 2018 |
|
RU2693916C1 |
Изобретение относится к вычислительной технике. Технический результат заключается в повышении эффективности распознавания изображений. Способ распознавания изображений, в котором получают посредством глубокой сверточной нейронной сети (CNN) вектор глубоких признаков входного изображения; применяют преобразование PCA (метод главных компонент) к данному вектору для получения последовательности главных компонент входного изображения; делят последовательность главных компонент на заранее заданное количество смежных частей, каждая из которых относится к отличающемуся от других уровню гранулярности; и присоединяют часть последовательности, относящуюся к этому уровню гранулярности, к первоначально пустой подпоследовательности главных компонент входного изображения, вычисляют расстояния между подпоследовательностью и соответствующими подпоследовательностями главных компонент эталонов из множества решений-кандидатов, оценивают отношения минимального расстояния к другим расстояниям, исключают эталоны с отношениями меньше порога из множества решений-кандидатов, и если множество решений-кандидатов включает в эталоны только одного класса, идентифицируют входное изображение как относящееся к этому классу. 3 н. и 16 з.п. ф-лы, 11 ил., 3 табл.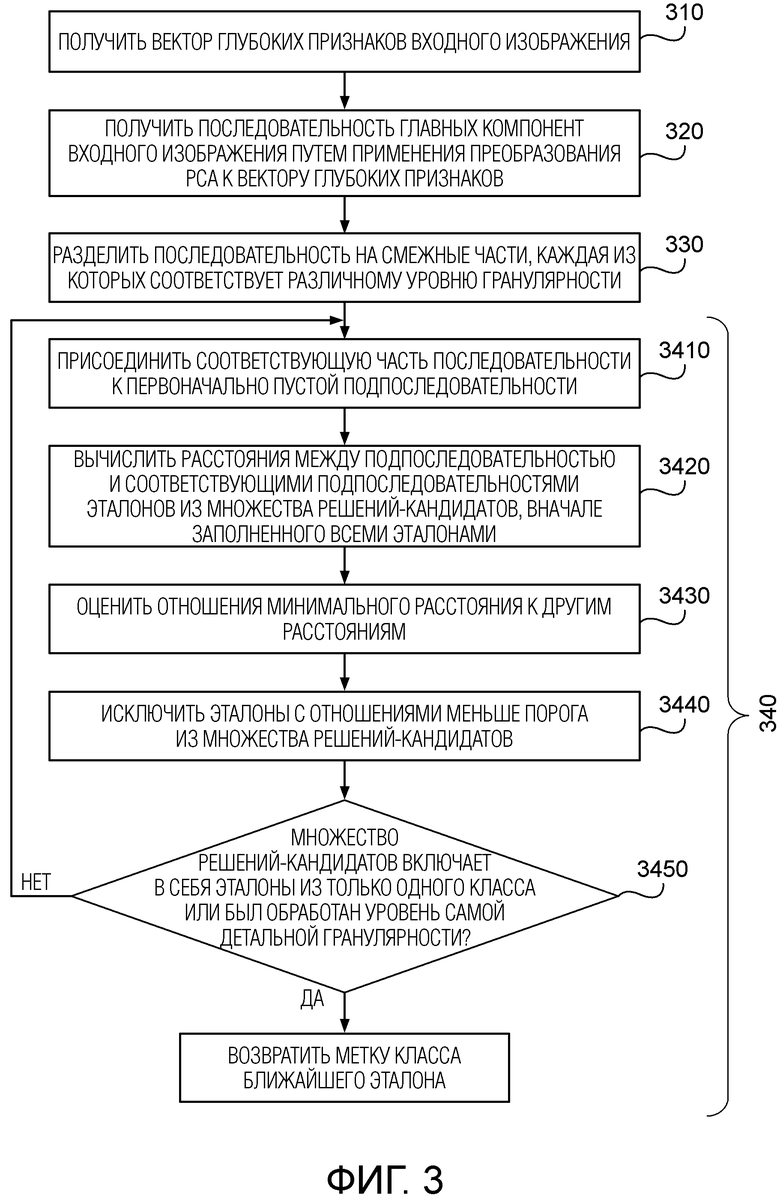
1. Способ распознавания изображений, содержащий этапы, на которых:
получают посредством глубокой сверточной нейронной сети (CNN) вектор глубоких признаков входного изображения;
применяют преобразование PCA (метод главных компонент) к данному вектору для получения последовательности главных компонент входного изображения;
делят полученную последовательность главных компонент на заранее заданное количество смежных частей, каковое заранее заданное количество представляет собой количество уровней гранулярности, так что каждая часть относится к отличающемуся от других уровню гранулярности; и
сопоставляют входное изображение с эталонами из обучающего множества изображений, причем каждый эталон принадлежит конкретному классу из числа классов, составляющего по меньшей мере 2, при этом при упомянутом сопоставлении:
для каждого уровня гранулярности, начиная с уровня самой грубой гранулярности:
присоединяют часть упомянутой последовательности, относящуюся к этому уровню гранулярности, к подпоследовательности главных компонент входного изображения, причем данная подпоследовательность вначале пустая,
вычисляют расстояния между этой подпоследовательностью и соответствующими подпоследовательностями главных компонент эталонов из множества потенциально подходящих решений, причем множество потенциально подходящих решений вначале включает в себя все эталоны обучающего множества изображений,
оценивают отношения минимального расстояния ко всем другим расстояниям среди вычисленных расстояний,
исключают из множества потенциально подходящих решений эталоны, каждый из которых имеет связанное с ним оцененное отношение, которое меньше заранее заданного порога, и
если множество потенциально подходящих решений включает в себя по меньшей мере один эталон только одного класса, идентифицируют входное изображение как относящееся к этому классу.
2. Способ по п.1, дополнительно содержащий, перед упомянутым получением вектора глубоких признаков входного изображения, этапы, на которых:
для каждого эталона обучающего множества изображений получают, посредством глубокой CNN, вектор глубоких признаков этого эталона и нормируют полученный вектор в евклидовой норме;
выполняют PCA в отношении векторов глубоких признаков всех эталонов из обучающего множества изображений для получения матрицы преобразования, представляющей собой квадратную матрицу, каждое измерение которой равно размерности каждого вектора глубоких признаков; и
получают последовательность главных компонент для каждого эталона путем умножения матрицы преобразования на вектор глубоких признаков данного эталона.
3. Способ по п.2, в котором упомянутое получение вектора глубоких признаков входного изображения дополнительно содержит этап, на котором нормируют полученный вектор в евклидовой норме, и упомянутое применение преобразования PCA содержит этап, на котором умножают матрицу преобразования на вектор глубоких признаков входного изображения.
4. Способ по п.2 или 3, в котором главные компоненты в каждой полученной последовательности упорядочиваются по соответствующим собственным значениям.
5. Способ по любому из пп.2-4, в котором упомянутое заранее заданное количество уровней гранулярности выбирают так, чтобы размерность каждого вектора глубоких признаков делилась нацело на это заранее заданное количество.
6. Способ по п.1, в котором для каждого уровня гранулярности используется один и тот же заранее заданный порог.
7. Способ по п.1, в котором каждая из упомянутых смежных частей последовательности главных компонент входного изображения имеет одинаковый размер.
8. Способ по п.1, дополнительно содержащий этап, на котором: если для уровня самой детальной гранулярности множество потенциально подходящих решений включает в себя эталоны из более чем одного класса, идентифицируют входное изображение как относящееся к классу, к которому относится эталон, имеющий максимальное оцененное отношение среди эталонов в множестве потенциально подходящих решений.
9. Способ по п.5, в котором расстояния на (l+1)-м уровне гранулярности, 1 ≤ l < L, где L - количество уровней гранулярности, вычисляют как
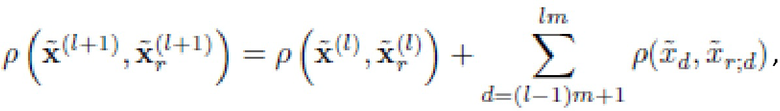
где
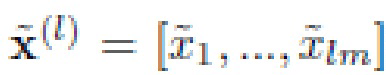 - подпоследовательность главных компонент входного изображения на l-м уровне гранулярности; m = D/L, D - размерность каждого вектора глубоких признаков;
- подпоследовательность главных компонент входного изображения на l-м уровне гранулярности; m = D/L, D - размерность каждого вектора глубоких признаков;
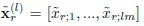 - подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-м уровне гранулярности; и
- подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-м уровне гранулярности; и
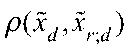
10. Вычислительная система, выполненная с возможностью распознавания изображений, при этом вычислительная система содержит:
один или более процессоров; и
одно или более машиночитаемых запоминающих устройств, на которых хранятся машиноисполняемые инструкции, которые при их исполнении одним или более процессорами предписывают одному или более процессорам выполнять операции, содержащие:
получение, посредством глубокой сверточной нейронной сети (CNN), вектора глубоких признаков входного изображения;
применение преобразования PCA (метод главных компонент) к этому вектору для получения последовательности главных компонент входного изображения;
разделение полученной последовательности главных компонент на заранее заданное количество смежных частей, каковое заранее заданное количество представляет собой количество уровней гранулярности, так что каждая часть относится к отличающемуся от других уровню гранулярности; и
сопоставление входного изображения с эталонами из обучающего множества изображений, причем каждый эталон принадлежит конкретному классу из числа классов, составляющего по меньшей мере 2, при этом данное сопоставление содержит:
для каждого уровня гранулярности, начиная с уровня самой грубой гранулярности:
присоединение части упомянутой последовательности, связанной с этим уровнем гранулярности, к подпоследовательности главных компонент входного изображения, причем данная подпоследовательность вначале пустая,
вычисление расстояний между этой подпоследовательностью и соответствующими подпоследовательностями главных компонент эталонов из множества потенциально подходящих решений, причем множество потенциально подходящих решений вначале включает в себя все эталоны обучающего множества изображений,
оценивание отношений минимального расстояния ко всем другим расстояниям среди вычисленных расстояний,
исключение из множества потенциально подходящих решений эталонов, с каждым из которых связано оцененное отношение, которое меньше заранее заданного порога, и
если множество потенциально подходящих решений включает в себя по меньшей мере один эталон только одного класса, идентификацию входного изображения в качестве относящегося к этому классу.
11. Система по п.10, в которой операции дополнительно содержат, перед получением вектора глубоких признаков входного изображения:
для каждого эталона обучающего множества изображений, получение, посредством глубокой CNN, вектора глубоких признаков этого эталона и нормировку полученного вектора в евклидовой норме;
выполнение PCA в отношении векторов глубоких признаков всех эталонов из обучающего множества изображений для получения матрицы преобразования, представляющей собой квадратную матрицу, каждое измерение которой равно размерности каждого вектора глубоких признаков; и
получение последовательности главных компонент для каждого эталона путем умножения матрицы преобразования на вектор глубоких признаков данного эталона.
12. Система по п.11, в которой упомянутое получение вектора глубоких признаков входного изображения дополнительно содержит нормировку полученного вектора в евклидовой норме, и упомянутое применение преобразования PCA содержит умножение матрицы преобразования на вектор глубоких признаков входного изображения.
13. Система по п.11 или 12, в которой главные компоненты в каждой полученной последовательности упорядочиваются по соответствующим собственным значениям.
14. Система по любому из пп.11-13, в которой упомянутое заранее заданное количество уровней гранулярности выбирается так, чтобы размерность каждого вектора глубоких признаков делилась нацело на это заранее заданное количество.
15. Система по п.10, в которой для каждого уровня гранулярности используется один и тот же заранее заданный порог.
16. Система по п.10, в которой каждая из упомянутых смежных частей последовательности главных компонент входного изображения имеет одинаковый размер.
17. Система по п.10, в которой операции дополнительно содержат: если для уровня самой детальной гранулярности множество потенциально подходящих решений включает в себя эталоны из более чем одного класса, идентификацию входного изображения в качестве относящегося к классу, к которому относится эталон, имеющий максимальное оцененное отношение среди эталонов в множестве потенциально подходящих решений.
18. Система по п.14, в которой расстояние на (l+1)-м уровне гранулярности, 1 ≤ l < L, где L - количество уровней гранулярности, вычисляется как
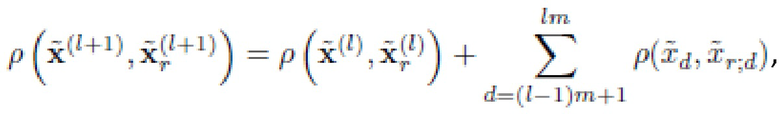
где
 - подпоследовательность главных компонент входного изображения на l-м уровне гранулярности; m = D/L, D - размерность каждого вектора глубоких признаков;
- подпоследовательность главных компонент входного изображения на l-м уровне гранулярности; m = D/L, D - размерность каждого вектора глубоких признаков;
 - подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-м уровне гранулярности; и
- подпоследовательность главных компонент r-го эталона обучающего множества изображений на l-м уровне гранулярности; и
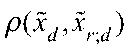
19. Машиночитаемый носитель данных, на котором хранятся машиноисполняемые команды, которые при их исполнении вычислительным устройством предписывают вычислительному устройству выполнять способ распознавания изображений по любому из пп.1-9.
| Токарный резец | 1924 |
|
SU2016A1 |
| Токарный резец | 1924 |
|
SU2016A1 |
| US 10025950 B1, 17.07.2018 | |||
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| СПОСОБ, УСТРОЙСТВО И СЕРВЕР РАСПОЗНАВАНИЯ КОНФИДЕНЦИАЛЬНОЙ ФОТОГРАФИИ | 2015 |
|
RU2622874C1 |
Авторы
Даты
2019-11-22—Публикация
2019-01-25—Подача