Изобретение относится к тепловым испытаниям, а именно к определению теплофизических характеристик материалов (теплопроводности и температуропроводности).
Известен способ определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца, приводят его в тепловой контакт с эталонным образцом, термостатируют исследуемый и эталонный образцы при заданной начальной температуре, подводят непрерывно теплоту к плоскости внутри эталонного образца, расположенной на известном расстоянии параллельно плоскости контакта, поддерживают температуры на внешних поверхностях исследуемого и эталонного образцов, равными заданной начальной температуре термостатирования, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру эталонного образца в заданном сечении, заканчивают испытания при достижении заданной минимальной скорости изменения температуры, вычисляют искомые теплофизические характеристики по зависимостям, приведенным в формуле изобретения (А.с. №1689825, МКИ G 01 N 25/18, 1991).
Недостатком способа является большая длительность экспериментального определения теплофизических характеристик, обусловленная необходимостью предварительного термостатирования образцов и определения интегральных характеристик.
Наиболее близким техническим решением является способ комплексного определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца и приводят его в тепловой контакт по плоскости с эталонным образцом, термостатируют исследуемый и эталонный образцы при начальной заданной температуре, затем подводят непрерывно теплоту к плоскости сечения внутри эталонного образца, расположенной на заданном расстоянии и параллельно плоскости контакта, при этом температуры на внешних поверхностях исследуемого и эталонного образцов поддерживают равными заданной начальной температуре термостатирования, регистрируют удельную мощность источника теплоты и измеряют с постоянным шагом во времени температуру эталонного образца в заданном сечении, на каждом шаге определяют величину динамического параметра, представляющего собой отношение температуры в заданном сечении эталонного образца на шаге измерения, номер которого на постоянное целое число меньше номера последнего шага измерения, к температуре в этом же сечении эталонного образца на последнем шаге измерения, сравнивают величину динамического параметра с заданным максимальным значением, испытания заканчивают при превышении максимального значения динамического параметра, задают максимальное значение динамического параметра в диапазоне 0,2... 0,8 и определяют искомые теплофизические характеристики по формулам (Патент РФ №2027172, МПК6 G 01 N 25/18. Способ комплексного определения теплофизических характеристик материалов и устройство для его осуществления./ Пономарев С.В., Мищенко С.В. и др. Опубл. 20.01.95. Бюл. №2). Принято за прототип.
Недостатками известного способа являются следующие факты. В прототипе необходимо использовать эталонный образец. При таком подходе возможно определение теплофизических характеристик материалов, имеющих значения теплофизических свойств, близкие со свойствами эталонного образца. Также в прототипе необходимо термостатирование образцов перед началом проведения испытаний, что увеличивает время проведения эксперимента.
Такие признаки прототипа, как измерение толщины исследуемого образца, подведение теплоты к образцам, поддерживание температуры на внешних поверхностях образцов, равной заданной температуре, регистрация удельной мощности источника теплоты, измерение с постоянным шагом во времени температуры в течение всего эксперимента, определение на каждом шаге величины динамического параметра и сравнение с максимальным значением, лежащим в заданном диапазоне, определение искомых теплофизических характеристик по формулам, совпадают с существенными признаками заявляемого изобретения.
Технической задачей является расширение диапазона определения теплофизических характеристик материалов и повышение точности измерения.
Данная техническая задача решается тем, что в способе комплексного определения теплофизических характеристик материалов, заключающимся в том, что измеряют толщину исследуемого образца, подводят теплоту к образцам, поддерживают температуру на внешних поверхностях образцов, равной заданной температуре, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру в течение всего эксперимента, определяют на каждом шаге величину динамического параметра и сравнивают с максимальным значением, лежащим в заданном диапазоне, определяют искомые теплофизические характеристики по формулам, дополнительно в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты, эксперимент проводят в два этапа, причем на первом этапе подводят постоянную мощность к объемному источнику теплоты, на каждом шаге во времени регистрируют среднеинтегральную температуру объемного источника теплоты и вычисляют величину динамического параметра как отношение разности скоростей изменения измеряемой среднеинтегральной температуры на первом и текущем шаге к скорости изменения среднеинтегральной температуры на первом шаге, заканчивают проведение первого этапа эксперимента при превышении заданного максимального значения динамического параметра из диапазона 0,87... 0,95, а на следующем шаге во времени начинают проведение второго этапа эксперимента, а именно прекращают подвод мощности к объемному источнику теплоты, на каждом j-м шаге второго этапа вычисляют безразмерную температуру 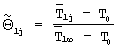 и число Фурье
и число Фурье 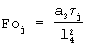 , проведение второго этапа эксперимента прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08, причем по зарегистрированным на первом этапе эксперимента данным вычисляют искомую теплопроводность λ по формуле
, проведение второго этапа эксперимента прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08, причем по зарегистрированным на первом этапе эксперимента данным вычисляют искомую теплопроводность λ по формуле
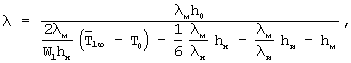
где h0, hH, hи, hм - соответственно толщины исследуемого образца, объемного источника теплоты, электрической изоляции, металлической оболочки, м;
λ H, λ и, λ м - соответственно теплопроводность объемного источника теплоты, электрической изоляции, металлической оболочки, Вт/(мК);
W1 - удельная мощность объемного источника теплоты, Вт/м3;
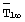 - среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
- среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
Т0 - заданная температура, поддерживаемая на внешних поверхностях образцов, К,
а по зарегистрированным на втором этапе эксперимента данным определяют тангенс 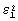 угла наклона прямолинейного участка графика функции
угла наклона прямолинейного участка графика функции 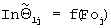 и определяют искомую температуропроводность а4 из решения задачи Штурма-Лиувилля
и определяют искомую температуропроводность а4 из решения задачи Штурма-Лиувилля
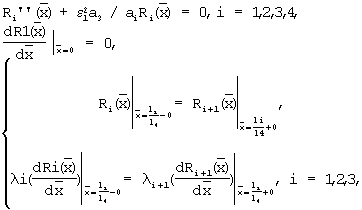
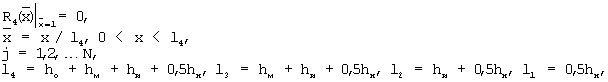
где а1, а2, а3, а4 - соответственно температуропроводность материала объемного источника теплоты, материала электрической изоляции, металлической оболочки, исследуемого образца, м2/с,
N – номер шага во времени при измерении температуры на втором этапе эксперимента, на котором текущее значение безразмерной температуры впервые стало меньше заданного значения,
l1, l2, l3, l4 - координаты, определяемые через толщины объемного источника теплоты, электрической изоляции, металлической оболочки и исследуемого образца,
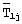 - среднеинтегральная температура, измеряемая на j-м шаге второго этапа эксперимента, К,
- среднеинтегральная температура, измеряемая на j-м шаге второго этапа эксперимента, К,
τ j - момент времени, отсчитываемый с начала второго этапа эксперимента и соответствующий j-му шагу второго этапа.
Использование двух одинаковых исследуемых образцов позволяет расширить диапазон измеряемых теплофизических характеристик. Упрощается проведение измерений, так как не нужен аттестованный образец с известными теплофизическими характеристиками.
Предложенная процедура определения величины динамического параметра позволяет наиболее полно получить информацию из значений изменения температуры во времени. Построение динамического параметра как отношение разности скоростей изменения измеряемой среднеинтегральной температуры на первом шаге во времени и текущем шаге во времени к скорости изменения среднеинтегральной температуры на первом шаге во времени позволяет относительно быстро и с погрешностью, не превышающей заданную величину, определить значение среднеинтегральной температуры в стационарном состоянии, по которому определяют искомую теплопроводность. Это обуславливает повышение точности измерения.
Полученные формулы, по которым вычисляются теплопроводность и температуропроводность, позволяют легко автоматизировать процесс проведения теплофизического эксперимента.
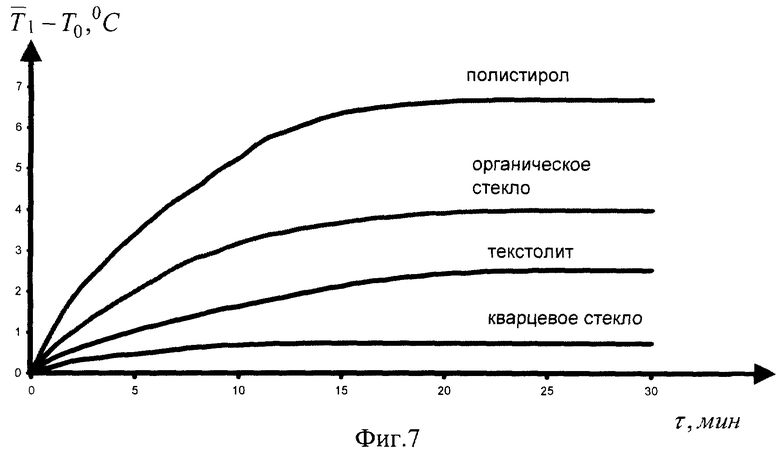
На фиг.1 приведена физическая модель измерительного устройства, реализующего предлагаемый способ. На фиг.2 изображена структурная схема измерительного устройства. На фиг.3 изображена схема измерительного блока. На фиг.4 изображена мостовая измерительная схема. На фиг.5 изображен график изменения среднеинтегральной температуры объемного источника теплоты на первом и втором этапах эксперимента. На фиг.6 изображен график функции 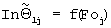 . На фиг.7 изображены графики изменения среднеинтегральных температур объемного источника теплоты при проведении экспериментов с различными материалами на первом этапе. На фиг.8 изображены графики изменения зависимости погрешности определения теплопроводности δ λ от величины динамического параметра γ . На фиг.9 изображены графики изменения среднеинтегральных температур объемного источника теплоты при проведении экспериментов с различными материалами на втором этапе. На фиг 10 приведены графики функции
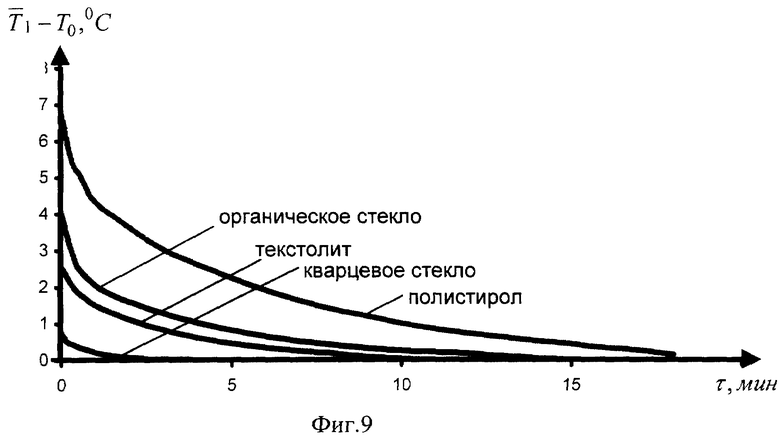
. На фиг.7 изображены графики изменения среднеинтегральных температур объемного источника теплоты при проведении экспериментов с различными материалами на первом этапе. На фиг.8 изображены графики изменения зависимости погрешности определения теплопроводности δ λ от величины динамического параметра γ . На фиг.9 изображены графики изменения среднеинтегральных температур объемного источника теплоты при проведении экспериментов с различными материалами на втором этапе. На фиг 10 приведены графики функции 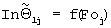 для различных материалов.
для различных материалов.
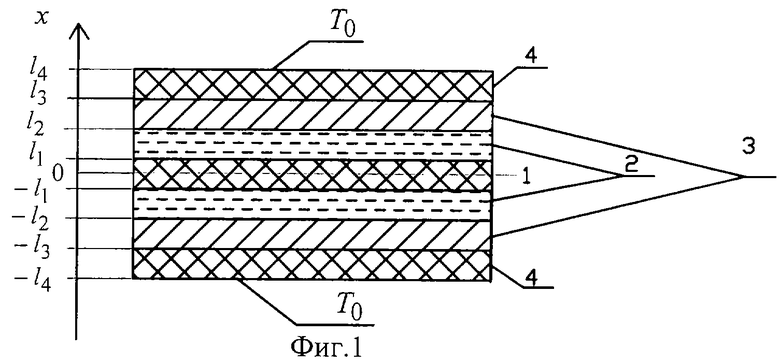
Физическая модель измерительного устройства представляет собой (фиг.1) плоскую симметричную многослойную систему. Первый слой 1 (объемный источник теплоты) системы, представляющий собой совокупность нагревателя и термометра сопротивления, навитых по спирали Архимеда, расположен между слоями электрической изоляции 2. Слои 3 представляют собой защитные металлические пластины, предотвращающие соприкосновение исследуемого материала (слои 4) со слоями электрической изоляции 2. На внешних границах модели при х=±l4 поддерживается постоянная температура Tо. Значения теплопроводности и температуропроводности слоев 1, 2 и 3 считаются известными. В силу того, что многослойная система симметрична относительно координаты х=0, математическую модель можно записать для половины системы (0≤ х≤ l4).
Математическая модель измерительного устройства была сформулирована, принимая во внимание следующие допущения:
1. Теплоперенос излучением в исследуемом веществе отсутствует.
2. При достаточно малой величине отношения толщины слоя исследуемого вещества к его диаметру температурное поле этого слоя можно считать одномерным.
3. Температура T0 на внешних границах плоской системы поддерживается постоянной.
4. Термическое сопротивление на поверхностях контакта слоев отсутствует.
5. Удельная мощность объемного источника теплоты (нагревателя) считается постоянной и равномерно распределенной по всему объему первого слоя.
6. Значения теплофизических свойств всех слоев системы считаются постоянными и не зависимыми от температуры.
На основании имеющейся симметричной физической модели измерительного устройства и принятых допущений сформулирована математическая модель в виде системы дифференциальных уравнений теплопроводности
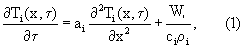
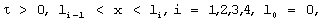
с начальными условиями
T1(x,0)=T2(x,0)=T3(x,0)=T4(x,0)=T0=const,
с граничными условиями
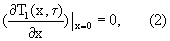
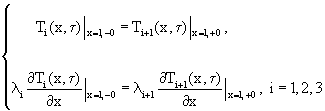 (3)
(3)
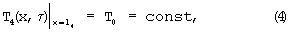
где ciρ i - объемная теплоемкость, λ i - теплопроводность, аi - температуропроводность и Wi - объемная плотность внутренних источников теплоты i-го слоя, причем W1=const, W2=W3=W4=0.
Стационарное температурное поле плоской системы описывается системой дифференциальных уравнений теплопроводности:
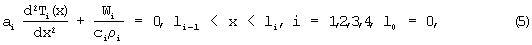
с граничными условиями
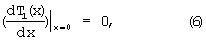
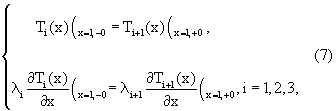
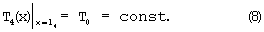
Решение стационарной задачи (5)-(8) имеет вид
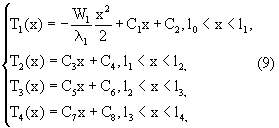
где Сj, 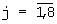 - постоянные коэффициенты, определяемые из граничных условий.
- постоянные коэффициенты, определяемые из граничных условий.
Из граничных условий получено: С1=0,
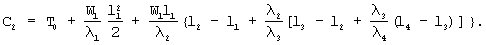
Таким образом, функция распределения стационарной температуры в первом слое имеет вид
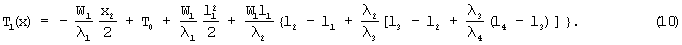
Значение стационарной среднеинтегральной температуры, измеряемое в конце первого этапа эксперимента, можно вычислить из выражения
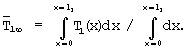
Подставив в последнее выражение T1(х) из выражения (10), получим формулу для нахождения искомой теплопроводности λ 4
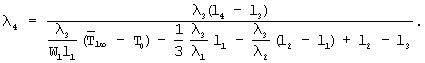
После преобразований получим
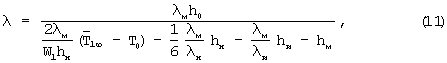
где h0, hн, hи, hм - соответственно толщины исследуемого образца, объемного источника теплоты, электрической изоляции, металлической оболочки, м;
λ н, λ и, λ м - соответственно теплопроводность объемного источника теплоты, электрической изоляции, металлической оболочки, Вт/(мК);
W1 - удельная мощность объемного источника теплоты, Вт/м3;
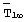 - среднеинтегральная температура объемного источника теплоты в стационарном режиме, К;
- среднеинтегральная температура объемного источника теплоты в стационарном режиме, К;
Т0 - заданная температура, поддерживаемая на внешних поверхностях образцов, К.
Температурное поле многослойной системы на втором этапе описывается дифференциальными уравнениями
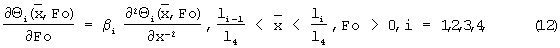
с начальными условиями 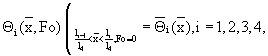
с граничными условиями
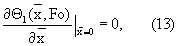
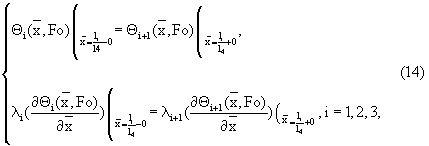
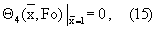
где 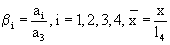 - безразмерная координата,
- безразмерная координата, 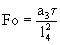 - безразмерное время,
- безразмерное время, 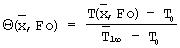 - безразмерная температура,
- безразмерная температура, 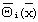 - распределение безразмерной температуры, полученное в конце первого этапа эксперимента.
- распределение безразмерной температуры, полученное в конце первого этапа эксперимента.
Решение нестационарной задачи (12)-(15), полученное методом разделения переменных, имеет вид
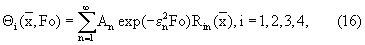
где 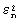 - собственные значения, a
- собственные значения, a 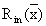 - собственные функции задачи Штурма-Лиувилля:
- собственные функции задачи Штурма-Лиувилля:
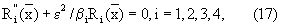
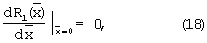
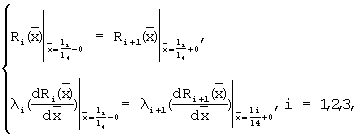 (19)
(19)

При значениях Fo, превышающих некоторое Fo* , сумма членов ряда (16) мало отличается от значения первого члена, т.е.
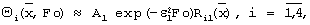
где 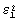 - первое собственное значение,
- первое собственное значение, 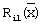 - первая собственная функция задачи Штурма-Лиувилля, А1 - постоянный множитель.
- первая собственная функция задачи Штурма-Лиувилля, А1 - постоянный множитель.
С учетом изложенного выше среднеинтегральная безразмерная температура первого слоя может быть вычислена по формуле
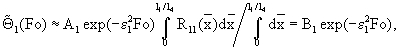
где 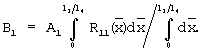
Прологарифмировав последнюю формулу, получим
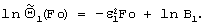
Построением графика последней функции или численным способом наименьших квадратов определяют величину ε
Объемную теплоемкость исследуемого материала можно вычислить по формуле (сρ )4=λ 4/а4.
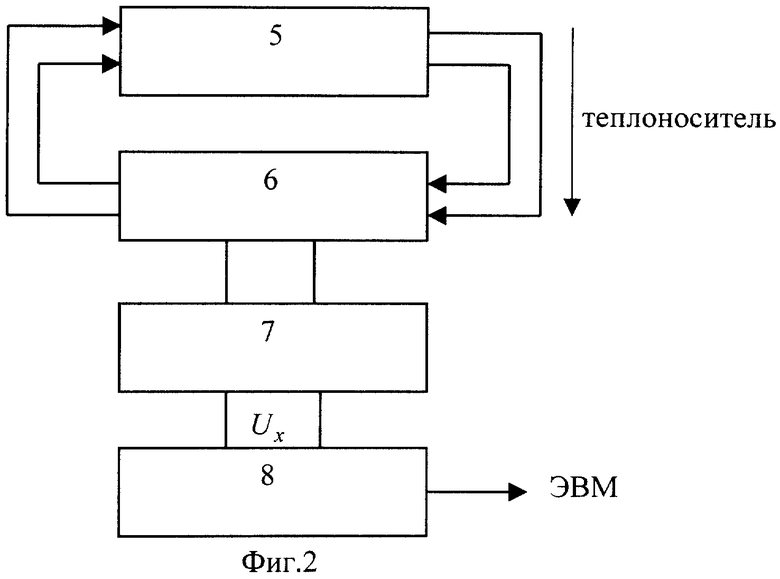
Измерительное устройство (фиг.2), реализующее предлагаемый способ, содержит жидкостный термостат 5, измерительный блок 6, измерительную схему 7, блок сопряжения 8.
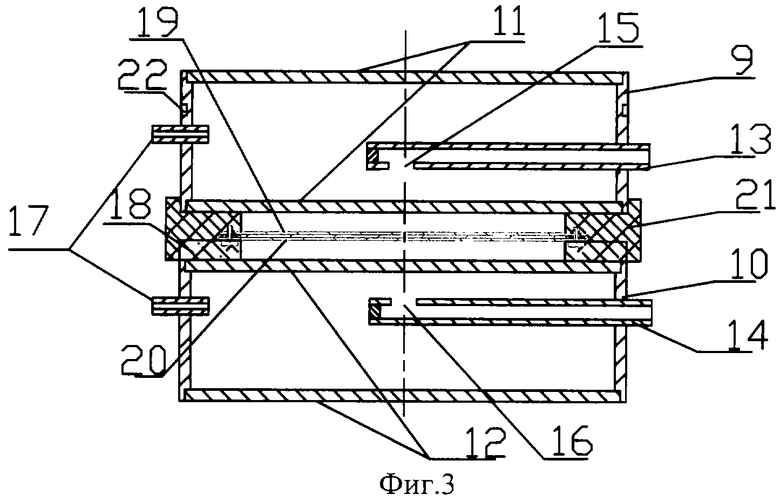
Измерительный блок 6 (фиг.3) включает в свой состав верхний и нижний теплообменники, образованные полыми цилиндрами 9 и 10, с торцевых сторон закрытых крышками 11 и 12. Теплообменники предназначены для поддержания постоянной температуры Т0 на внешней поверхности исследуемого вещества 4 (фиг.1). В каждый теплообменник вставлены трубки 13 и 14, предназначенные для подачи теплоносителя (воды). Трубки 13 и 14 запаяны с одного конца, а в каждой трубке сбоку сделаны отверстия 15 и 16, предназначенные для направления потока теплоносителя на рабочие поверхности теплообменников. Для отвода теплоносителя используются трубки 17. К нижнему теплообменнику приклеивается кольцо 18 из теплоизоляционного материала. Деталь 19 представляет собой металлический диск (слой 3 на фиг.1) с приклеенной к его поверхности полиэтилентерефталатной пленкой (слой 2 на фиг.1), на которую по спирали Архимеда приклеивается медная (термометр сопротивления RK1) и манганиновая (нагреватель) проволоки, образующие первый слой 1 физической модели. Деталь 20 также представляет собой металлический диск (нижний слой 3 на фиг.1) с приклеенной к его поверхности полиэтилентерефталатной пленкой (нижний слой 2 на фиг.1). Детали 19 и 20 скрепляются между собой и с кольцом 21 винтами. Кольцо 21 изготовлено из теплоизоляционного материала.
Пространство, образованное верхней поверхностью нижнего теплообменника, внутренней поверхностью кольца 18 и плоскостью диска 20, заполняется исследуемым материалом. Аналогично пространство, образованное нижней поверхностью верхнего теплообменника, внутренней поверхностью кольца 21 и плоскостью диска 19, заполняется исследуемым материалом. В кольцевой канавке 22 верхнего теплообменника намотана медная проволока, выполняющая функцию термометра сопротивления (RK2), измеряющего температуру теплообменника Т0.
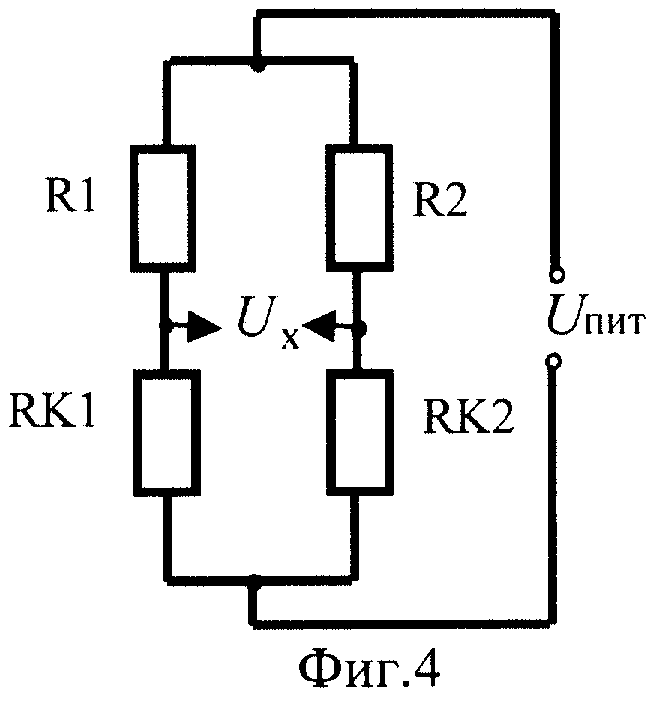
Термометры сопротивления RK1, RK2 включены в мостовую измерительную схему 7 (фиг.4), питаемую от источника стабилизированного напряжения Uпит, так, что выходное напряжение Uх пропорционально разности температур, измеряемых ими. Выходное напряжение Uх поступает на блок сопряжения 8, преобразующий аналоговый сигнал в цифровой.
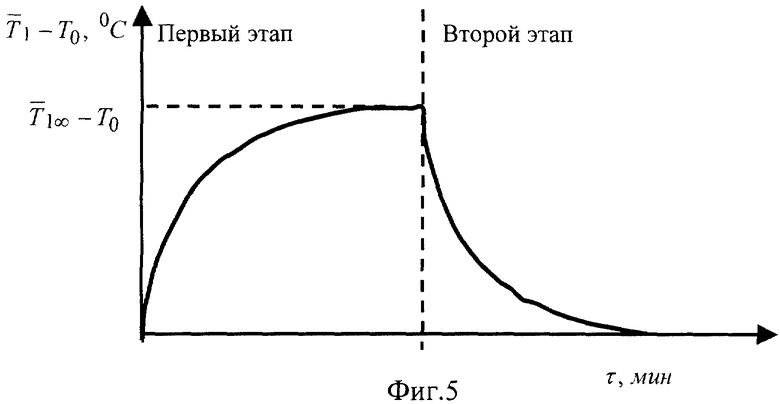
Способ комплексного определения теплофизических характеристик реализуется в два этапа (фиг.5): на первом этапе происходит нагрев, а на втором этапе нагрев прекращается (процесс охлаждения).
На первом этапе подают постоянное напряжение Uн на нагреватель измерительного блока 6 (фиг.2). В результате в первом слое 1 (фиг.1) начинает действовать внутренний источник тепла с объемной плотностью W1=U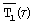 первого слоя.
первого слоя.
На каждом шаге определяют величину динамического параметра, которую сравнивают с максимальным значением, лежащим в заданном диапазоне 0,87... 0,95. Заканчивают измерение на первом этапе при превышении величины динамического параметра заданного максимального значения, взятого из диапазона 0,87... 0,95. Искомую теплопроводность λ вычисляют по формуле
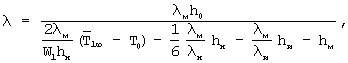
где h0, hн, hи, hм - соответственно толщины исследуемого образца, объемного источника теплоты, электрической изоляции, металлической оболочки, м;
λ н, λ и, λ м - соответственно теплопроводность объемного источника теплоты, электрической изоляции, металлической оболочки, Вт/(мК);
W1 - удельная мощность объемного источника теплоты, Вт/м3;
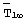 - среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
- среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
Т0 - заданная температура, поддерживаемая на внешних поверхностях образцов, К.
В ходе второго этапа эксперимента отключают нагреватель и измеряют значения среднеинтегральной температуры первого слоя 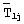 в моменты времени τ j, вычисляют безразмерную температуру
в моменты времени τ j, вычисляют безразмерную температуру 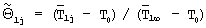 и число Фурье
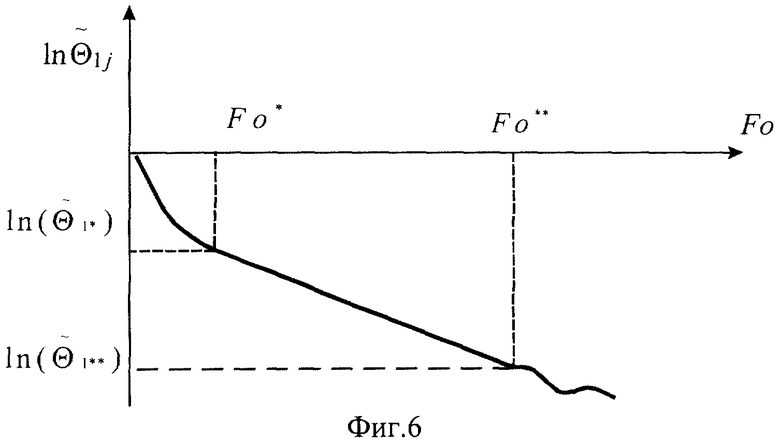
и число Фурье 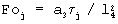 . Проведение второго этапа прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08. Определяют прямолинейный участок зависимости (21) (на фиг.6 начальная точка имеет координаты
. Проведение второго этапа прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08. Определяют прямолинейный участок зависимости (21) (на фиг.6 начальная точка имеет координаты 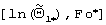 , а конечная
, а конечная 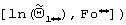 а затем находят значение, равное тангенсу угла наклона прямолинейного участка зависимости
а затем находят значение, равное тангенсу угла наклона прямолинейного участка зависимости
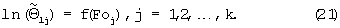
Подставив найденное значение ε
Рассмотрим конкретный пример реализации предложенного способа.
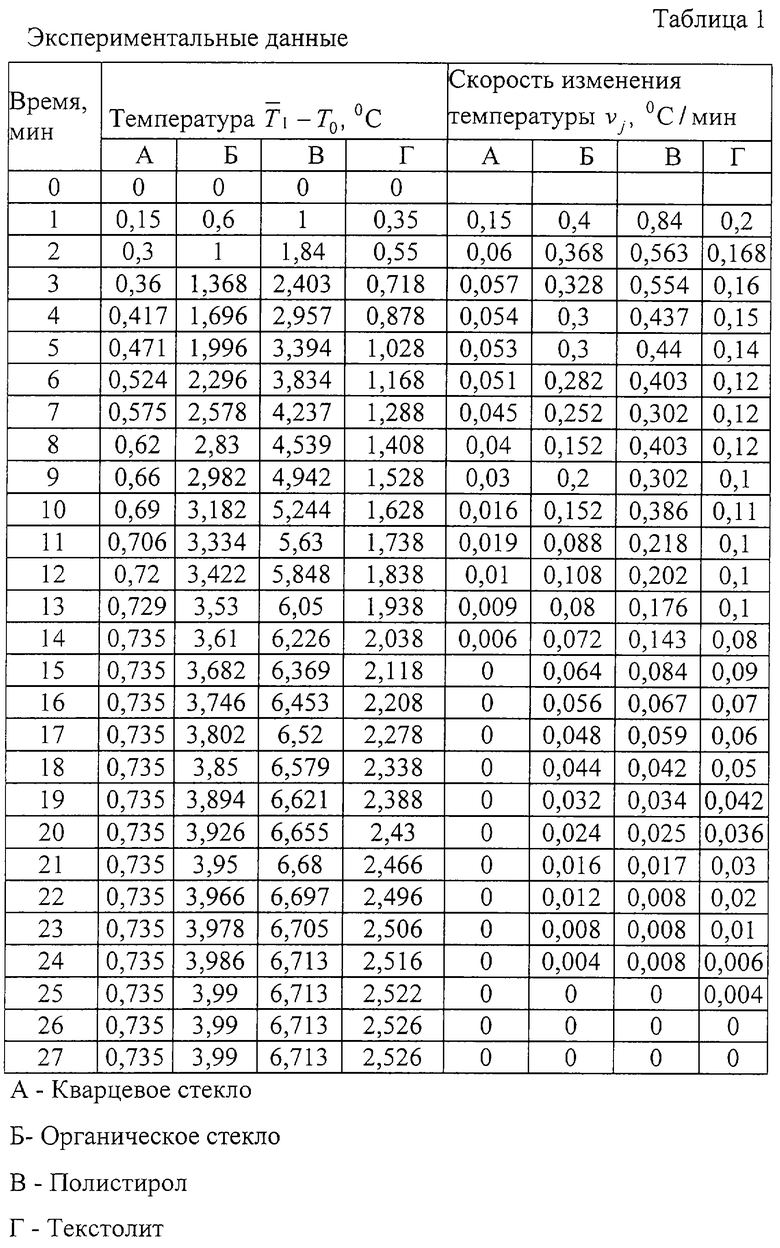
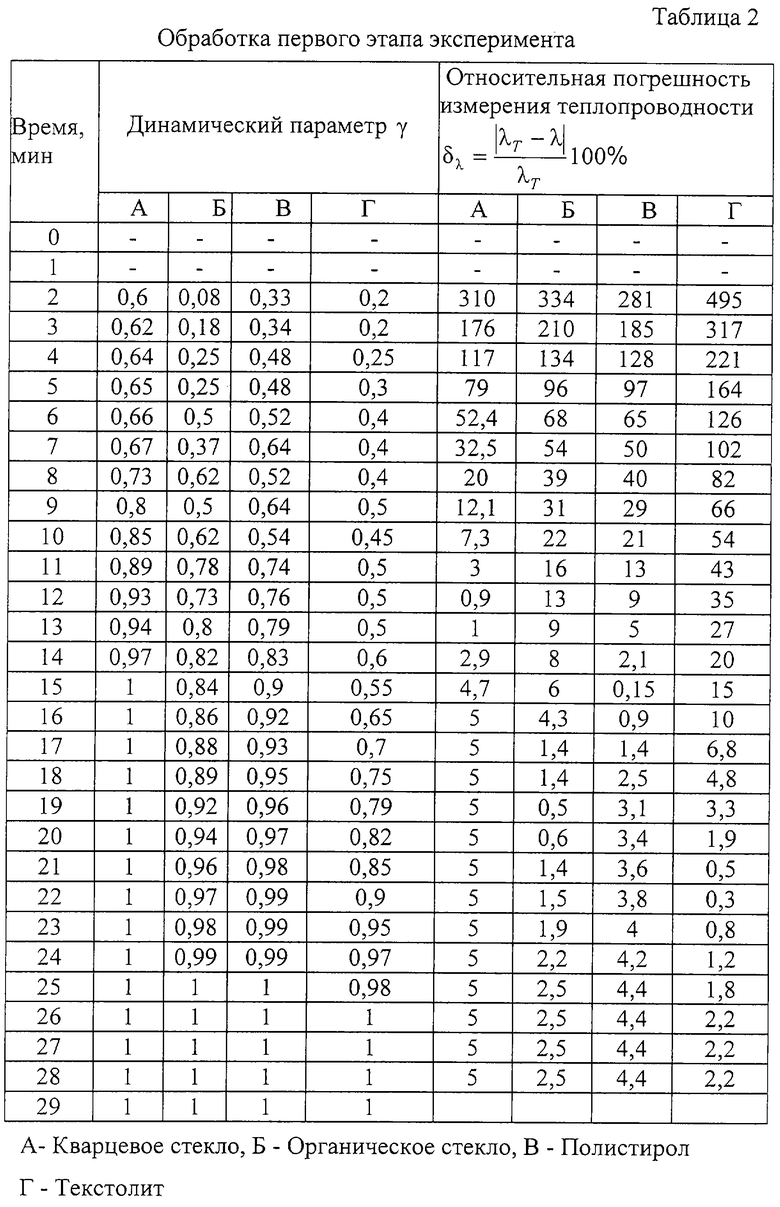
Для измерения теплофизических характеристик изготовлены по два образца из органического стекла, полистирола, текстолита и кварцевого стекла диаметром 116 мм и толщиной 8 мм. Толщины объемного источника теплоты, электрической изоляции и металлической оболочки равны 0,3; 0,3 мм и 1 мм, соответственно. На протяжении всего эксперимента (на первом и втором этапах) на внешних поверхностях исследуемых образцов поддерживалась постоянная температура Т0=20° С. На первом этапе эксперимента на нагреватель подавалось напряжение ~ 33 В. Сопротивление нагревателя 790 Ом, питание измерительной схемы 1,5 В, сопротивление термометров сопротивления RK1 и RK2 - 10 Ом, площадь объемного источника теплоты 0,00785 м2, удельная мощность объемного источника теплоты 585340 Вт/м3. На каждом временном шаге измерялась среднеинтегральная температура объемного источника теплоты (табл.1), на j-м временном шаге вычислялась скорость изменения температуры vj (табл.1) как отношение разности температур на j+1 временном шаге и j временном шаге к длине временного шага. Вычислялась величина динамического параметра λ (табл.2).
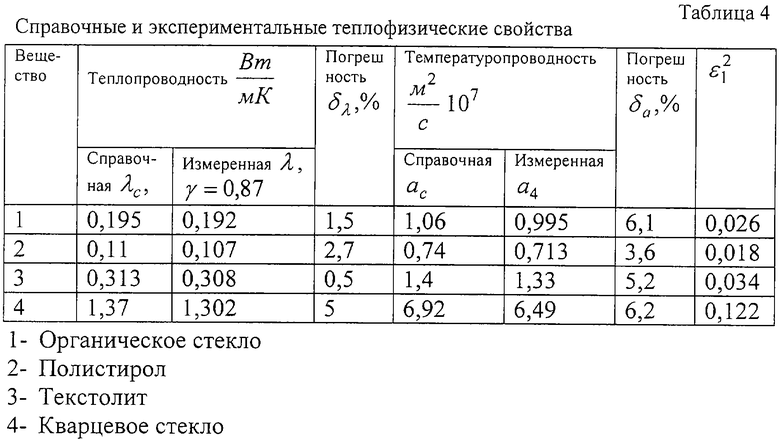
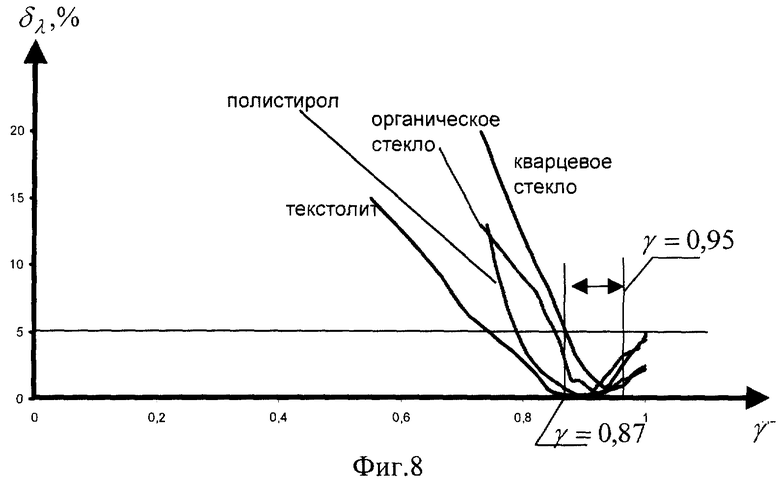
Первый этап эксперимента завершался при γ =0,95. По измеренной среднеинтегральной температуре 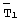 вычислялась теплопроводность λ по формуле (1), после чего вычислялась относительная погрешность (табл.2), где λ с - справочное значение теплопроводности измеряемых веществ (табл.4). По вычисленным значениям γ и δ λ построены графики (фиг.8), из которых определялся диапазон значений динамического параметра. Из фиг.8 видно, что для измеренных веществ, теплопроводность которых лежит в диапазоне
вычислялась теплопроводность λ по формуле (1), после чего вычислялась относительная погрешность (табл.2), где λ с - справочное значение теплопроводности измеряемых веществ (табл.4). По вычисленным значениям γ и δ λ построены графики (фиг.8), из которых определялся диапазон значений динамического параметра. Из фиг.8 видно, что для измеренных веществ, теплопроводность которых лежит в диапазоне 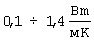 , относительная погрешность δ λ измерения теплопроводности (меньше или равна 5% если γ лежит в диапазоне 0,87... 0,95.
, относительная погрешность δ λ измерения теплопроводности (меньше или равна 5% если γ лежит в диапазоне 0,87... 0,95.
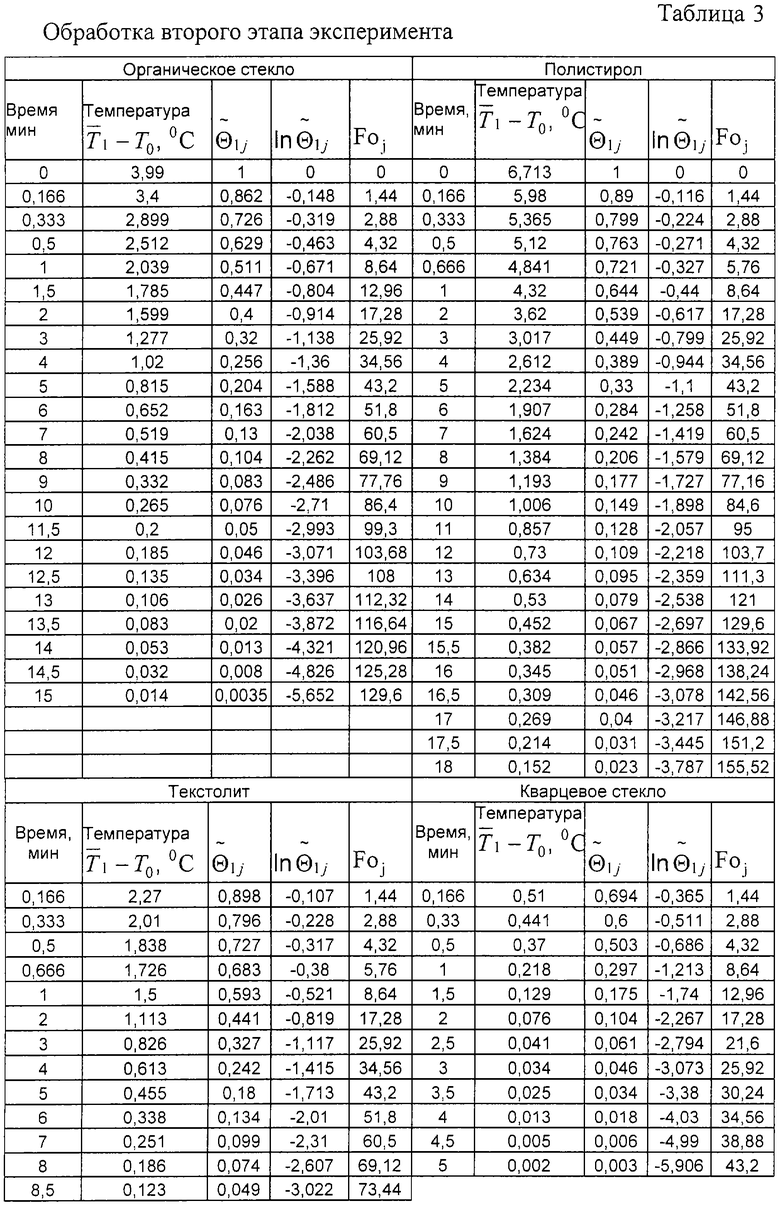
На втором этапе эксперимента прекратили подвод мощности к нагревателю, измеряли среднеинтегральную температуру объемного источника теплоты (табл.3), вычисляли безразмерную температуру 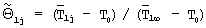 и число Фурье
и число Фурье 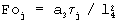 . Из графика функции
. Из графика функции 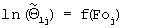 определяли величину
определяли величину 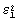 (табл.4) и подставляли найденное значение в задачу Штурма-Лиувилля (17)-(20). Численно подобрали величину а4 (табл. 4), удовлетворяющую указанной задаче.
(табл.4) и подставляли найденное значение в задачу Штурма-Лиувилля (17)-(20). Численно подобрали величину а4 (табл. 4), удовлетворяющую указанной задаче.
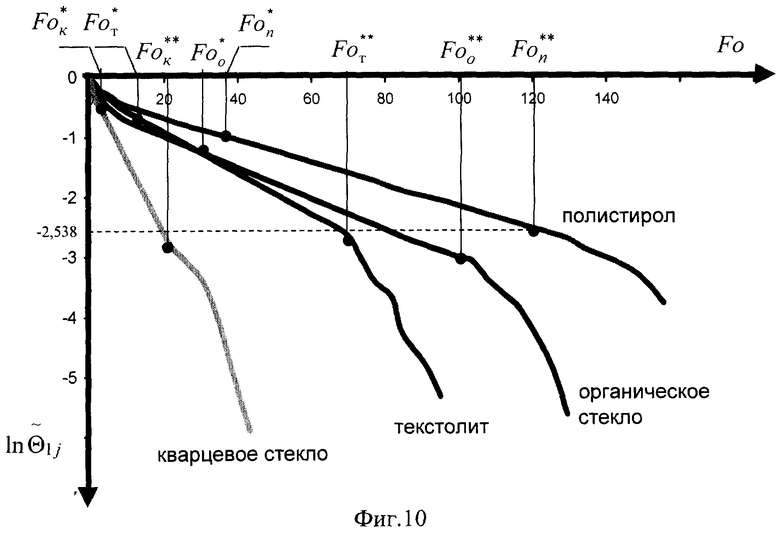
Для вычисления температуропроводности а4 используется прямолинейный участок графика функции 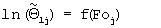 . На фиг.10 координаты
. На фиг.10 координаты 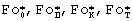 - есть координаты начальной точки прямолинейного участка графика функции
- есть координаты начальной точки прямолинейного участка графика функции 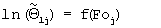 для органического стекла, полистирола, кварцевого стекла и текстолита, соответственно, а координаты
для органического стекла, полистирола, кварцевого стекла и текстолита, соответственно, а координаты 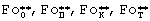 - есть координаты конечной точки прямолинейного участка. Второй этап эксперимента можно завершить, как только будет достигнута конечная точка прямолинейного участка кривой
- есть координаты конечной точки прямолинейного участка. Второй этап эксперимента можно завершить, как только будет достигнута конечная точка прямолинейного участка кривой 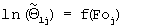 . Как видно из фиг.10, для исследуемых веществ с температуропроводностью в диапазоне
. Как видно из фиг.10, для исследуемых веществ с температуропроводностью в диапазоне 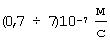 конечной точке прямолинейного участка соответствует значение безразмерной температуры
конечной точке прямолинейного участка соответствует значение безразмерной температуры 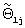 , равное 0,08.
, равное 0,08.
Таким образом, эксперимент показал (фиг.8), что правая граница диапазона максимального значения динамического параметра равна 0,95. Продолжение проведения первого этапа эксперимента не приводит к получению более точного результата измерения.
Левая граница рассматриваемого диапазона для различных материалов имеет следующее значение:
- для текстолита - 0,75;
- для полистирола - 0,80;
- для органического стекла - 0,85;
- для кварцевого стекла - 0,87.
Получаем диапазон [0,87... 0,95], в котором лежит максимальное значение динамического параметра для всех веществ, теплопроводность которых лежит в диапазоне 0,1... 1,4 Вт/(мК).
Для второго этапа эксперимента из графика зависимости 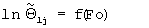 (фиг.10) следует, что координаты конечных точек прямолинейных участков
(фиг.10) следует, что координаты конечных точек прямолинейных участков 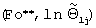 для рассматриваемых материалов имеют следующие значения:
для рассматриваемых материалов имеют следующие значения:
- кварцевого стекла (21,6; -2,794);
- текстолита (69,12; -2,607);
- органического стекла (103,68; -3,071);
- полистирола (121;-2,538).
Т.е. наибольшее значение 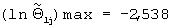 . Тогда заданное значение безразмерной температуры равно е-2,538=0,08.
. Тогда заданное значение безразмерной температуры равно е-2,538=0,08.
Таким образом, при значениях безразмерной температуры, больших заданного значения, равного 0,08, имеем прямолинейные участки зависимости 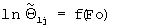 для всех рассматриваемых материалов, температуропроводность которых лежит в диапазоне (0,7... 7,0)10-7 м2/с. Поэтому на втором этапе следует прекращать эксперимент на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08.
для всех рассматриваемых материалов, температуропроводность которых лежит в диапазоне (0,7... 7,0)10-7 м2/с. Поэтому на втором этапе следует прекращать эксперимент на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, равного 0,08.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2009 |
|
RU2387981C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ МАТЕРИАЛОВ | 2013 |
|
RU2523090C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 1991 |
|
RU2018117C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ И ДИСПЕРСНЫХ МАТЕРИАЛОВ | 1999 |
|
RU2178166C2 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2027172C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2010 |
|
RU2439543C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТЕПЛОИЗОЛЯЦИОННЫХ МАТЕРИАЛОВ МЕТОДОМ ПЛОСКОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2601234C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ МАТЕРИАЛОВ МЕТОДОМ ЛИНЕЙНОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2613194C1 |
| Способ определения температуропроводности и коэффициента теплопроводности | 2022 |
|
RU2785084C1 |
| Способ определения теплофизических характеристик материалов | 1989 |
|
SU1689825A1 |
Изобретение относится к тепловым испытаниям. Способ включает измерение толщины исследуемого образца, подведение теплоты к двум идентичным образцам, поддерживание температуры на внешних поверхностях образцов, равной заданной температуре. При этом регистрируют удельную мощность источника теплоты и измеряют с постоянным шагом во времени температуру в течение всего эксперимента. Определяют на каждом шаге величину динамического параметра и сравнивают с максимальным значением, лежащим в заданном диапазоне. На первом этапе эксперимента подводят постоянную мощность к объемному источнику теплоты и по зарегистрированным данным вычисляют искомую теплопроводность. На втором этапе прекращают подвод мощности к объемному источнику теплоты и по зарегистрированным данным определяют искомую температуропроводность. Изобретение позволяет расширить диапазон определения теплофизических характеристик материалов и повысить точность измерения. 10 ил., 4 табл.
Способ комплексного определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца, подводят теплоту к образцам, поддерживают температуру на внешних поверхностях образцов равной заданной температуре, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру в течение всего эксперимента, определяют на каждом шаге величину динамического параметра и сравнивают с максимальным значением, лежащим в заданном диапазоне, определяют искомые теплофизические характеристики по формулам, отличающийся тем, что в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты, эксперимент проводят в два этапа, причем на первом этапе подводят постоянную мощность к объемному источнику теплоты, на каждом шаге во времени регистрируют среднеинтегральную температуру объемного источника теплоты и вычисляют величину динамического параметра как отношение разности скоростей изменения измеряемой среднеинтегральной температуры на первом и текущем шаге к скорости изменения среднеинтегральной температуры на первом шаге, заканчивают проведение первого этапа эксперимента при превышении заданного максимального значения динамического параметра из диапазона 0,87...0,95, а на следующем шаге во времени начинают проведение второго этапа эксперимента, а именно, прекращают подвод мощности к объемному источнику теплоты, на каждом j-м шаге второго этапа вычисляют безразмерную температуру 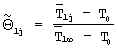 и число Фурье
и число Фурье 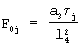 , проведение второго этапа эксперимента прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения из диапазона 0,08...0,10, причем по зарегистрированным на первом этапе эксперимента данным вычисляют искомую теплопроводность по формуле
, проведение второго этапа эксперимента прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения из диапазона 0,08...0,10, причем по зарегистрированным на первом этапе эксперимента данным вычисляют искомую теплопроводность по формуле
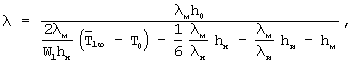
где h0, hн, hи, hм - соответственно толщины исследуемого образца, объемного источника теплоты, электрической изоляции, металлической оболочки, м;
λн, λи, λм - соответственно теплопроводность объемного источника теплоты, электрической изоляции, металлической оболочки, Вт/(мК);
W1 - удельная мощность объемного источника теплоты, Вт/м3;
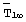 - среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
- среднеинтегральная температура объемного источника теплоты в стационарном режиме, за которую принимают значение измеряемой среднеинтегральной температуры в конце первого этапа эксперимента именно на том шаге во времени, на котором величина динамического параметра впервые превысила заданное максимальное значение параметра, К;
Т0 - заданная температура, поддерживаемая на внешних поверхностях образцов, К,
а по зарегистрированным на втором этапе эксперимента данным определяют тангенс 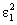 угла наклона прямолинейного участка графика функции
угла наклона прямолинейного участка графика функции
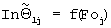 и определяют искомую температуропроводность А4 из решения задачи Штурма-Лиувилля
и определяют искомую температуропроводность А4 из решения задачи Штурма-Лиувилля
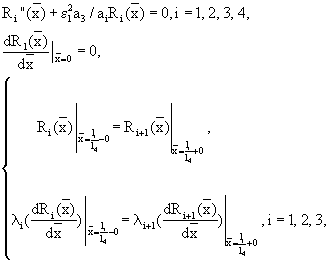
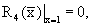
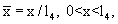
j=1, 2,...N,
l4=h0+hм+hu+0,5hн, l3=hм+hu+0,5hн, l2=hu+0,5hн, l1=0,5hн,
где a1, a2, a3, a4 - соответственно температуропроводность материала объемного источника теплоты, материала электрической изоляции, металлической оболочки, исследуемого образца, м2/с;
N - номер шага во времени при измерении температуры на втором этапе эксперимента, на котором текущее значение безразмерной температуры впервые стало меньше заданного значения;
l1, l2, l3, l4 - координаты, определяемые через толщины объемного источника теплоты, электрической изоляции, металлической оболочки и исследуемого образца;
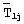 - среднеинтегральная температура, измеряемая на j-м шаге второго этапа эксперимента, К;
- среднеинтегральная температура, измеряемая на j-м шаге второго этапа эксперимента, К;
τj - момент времени, отсчитываемый с начала второго этапа эксперимента, и соответствующий j-му шагу второго этапа.
| ИЗМЕРИТЕЛЬ ДЛИТЕЛЬНОСТИ ПОДГОТОВИТЕЛЬНОЙ СТАДИИ РАЗРЯДА В СВЕЧАХ ЗАЖИГАНИЯ | 2000 |
|
RU2182339C2 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2027172C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 1991 |
|
RU2018117C1 |
| Способ комплексного определенияТЕплОфизичЕСКиХ ХАРАКТЕРиСТиКМАТЕРиАлОВ | 1979 |
|
SU817563A1 |
| Способ определения теплофизических характеристик материалов | 1989 |
|
SU1689825A1 |
| Способ определения теплофизических характеристик твердых материалов | 1983 |
|
SU1117512A1 |
Авторы
Даты
2004-12-27—Публикация
2003-04-08—Подача