Изобретение относится к робототехнике и может быть использовано в системах копирующего управления антропоморфными манипуляторами.
Известен комплекс копирующего управления с задающей рукояткой [Е.И. Юревич «Управление роботами и робототехническими системами». - СПб: СПбГТУ, 2000. - 171 с. - с. 131-133], который включает в себя блок механической системы задающего устройства, блок датчиков задающего устройства, блок решения обратной задачи кинематики, блок управления приводами исполнительного устройства. Данный комплекс позволяет организовать копирующее управление антропоморфным манипулятором.
Признаками аналога, совпадающими с признаками заявляемого устройства, являются блок механической системы задающего устройства, блок датчиков задающего устройства, блок решения обратной задачи кинематики, блок управления приводами исполнительного устройства.
Недостатками, препятствующими достижению в этом аналоге технического результата, обеспечиваемого изобретением, являются ограниченные функциональные возможности. В частности, данная система копирующего управления ориентирована на использование задающей рукоятки в качестве передаточного звена между оператором и устройством управления, что позволяет оператору управлять одной рукой только тремя степенями подвижности исполнительного манипулятора, в то время как антропоморфный исполнительный манипулятор имеет семь степеней подвижности. С другой стороны, использование задающей рукоятки не позволяет осуществлять интуитивное управление и контролировать положение локтевого узла исполнительного манипулятора.
Известно устройство для измерения углов поворота в суставах кисти оператора, защищенное патентом US №4986280, кл. А61В 5/103, B25J 19/02, B25J 9/00, G01D 5/14, G01D 5/12, G05B 19/427, G06F 3/00, 1991 г., система управления которого включает в себя блок механической системы задающего устройства, блок датчиков задающего устройства и вычислитель углов поворота в суставах руки оператора. Эта структура позволяет организовать измерение углов поворота в суставах кисти оператора и может быть использована для осуществления копирующего управления антропоморфным захватом манипулятора.
Признаками аналога, совпадающими с признаками заявляемого устройства, являются блок механической системы задающего устройства, блок датчиков задающего устройства и вычислитель углов поворота в суставах кисти оператора.
Недостатком, препятствующим достижению в этом аналоге технического результата, обеспечиваемого заявляемым изобретением, являются ограниченные функциональные возможности. В частности, вычислитель углов поворота ориентирован на расчет углов поворота в суставах только кисти оператора и не может быть использован для расчета углов поворота в остальных суставах руки оператора.
Известна структура комплекса управления на основе копирующего манипулятора [Е.И. Юревич «Управление роботами и робототехническими системами». - СПб: СПбГТУ, 2000. - 171 с. - с. 123-131], которая предполагает наличие блока механической системы задающего устройства, блока датчиков задающего устройства, блока управления приводами исполнительного манипулятора. Эта структура позволяет организовать копирующее управление антропоморфным манипулятором.
Существенными признаками аналога, совпадающими с признаками заявляемого изобретения, являются блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами исполнительного манипулятора.
Недостатками, препятствующими достижению в этом аналоге технического результата, обеспечиваемого изобретением, являются невозможность одновременного управления всеми степенями подвижности антропоморфного манипулятора, сложность интуитивного управления оператором всеми степенями подвижности исполнительного манипулятора, ограниченность рабочей зоны. Они обусловлены тем обстоятельством, что за счет позиционирования и ориентации рабочего окончания задающего манипулятора может быть осуществлено управление только шестью степенями подвижности исполнительного манипулятора, в то время как антропоморфный исполнительный манипулятор зачастую содержит семь степеней подвижности. Дополнительно, при использовании аналога производится копирование движений не руки оператора, а задающего манипулятора, приводимого в движение рукой оператора. Таким образом, теряется естественность и интуитивность управления исполнительным манипулятором, сужается рабочая зона.
Устройством, наиболее близким по технической сущности к предлагаемому изобретению (прототипом), является дистанционный манипулятор, защищенный патентом RU №125508, кл. B25J 3/04, 2011 г., из описания которого структура системы управления включает в себя блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами антропоморфного манипулятора. Эта структура позволяет организовать копирующее управления антропоморфным манипулятором.
Существенными признаками прототипа, совпадающими с признаками заявляемого изобретения, являются блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами антропоморфного манипулятора.
Недостатком, препятствующим достижению в прототипе технического результата, обеспечиваемого изобретением, является низкая точность измерения углов поворота руки оператора. Данный недостаток обусловлен тем, что в качестве целевых углов поворота антропоморфного манипулятора используются углы поворота не руки оператора, а задающего устройства. Вследствие того, что звенья задающего устройства параллельны частям руки оператора, однако оси вращения звеньев в общем случае не совпадают с осями вращения частей руки оператора, углы поворота задающего устройства коррелируют, но не совпадают с углами поворота руки оператора. Данное обстоятельство снижает точность копирующего управления антропоморфным манипулятором с помощью прототипа.
Техническим результатом данного изобретения является повышение точности копирующего управления антропоморфным манипулятором, за счет повышения точности определения углов поворота руки оператора.
Технический результат достигается тем, что в комплекс управления, содержащий блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами антропоморфного манипулятора, в котором выходы блока механической системы задающего устройства соединены со входами блока датчиков задающего устройства, введен блок расчета углов поворота руки оператора, при этом выходы блока датчиков задающего устройства соединены со входами блока расчета углов поворота руки оператора, выходы которого соединены со входами блока управления приводами антропоморфного манипулятора, блок расчета углов поворота руки оператора содержит блок памяти, вычислитель декартовых координат суставов руки оператора, блок решения обратной задачи кинематики, первый выход блока памяти соединен с первым входом вычислителя декартовых координат суставов руки оператора, второй выход блока памяти соединен с первым входом блока решения обратной задачи кинематики, второй вход вычислителя декартовых координат суставов руки оператора соединен со входом блока расчета углов поворота руки оператора, а выход соединен со вторым входом блока решения обратной задачи кинематики, выход которого соединен с выходом блока расчета углов поворота руки оператора, на первом выходе блока памяти формируются координаты точки B1, принятой за начало отсчета, координаты вектора жесткой сцепки B1C1, длины частей руки оператора 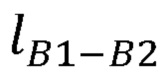 ,
, 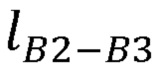 ,
, 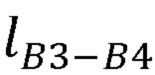 , длины звеньев задающего устройства
, длины звеньев задающего устройства 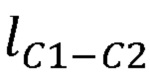 ,
, 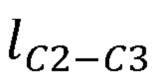 ,
, 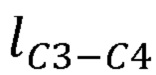 , длины сцепок В3С3, В4С4 и виртуальной сцепки
, длины сцепок В3С3, В4С4 и виртуальной сцепки 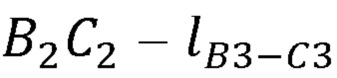 ,
, 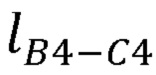 ,
, 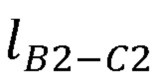 , координаты локтевого сустава
, координаты локтевого сустава 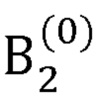 в заданном начальном положении руки оператора, на втором выходе блока памяти формируются координаты точки В1, принятой за начало отсчета, длины частей руки оператора
в заданном начальном положении руки оператора, на втором выходе блока памяти формируются координаты точки В1, принятой за начало отсчета, длины частей руки оператора 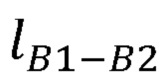 ,
, 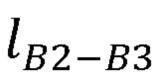 ,
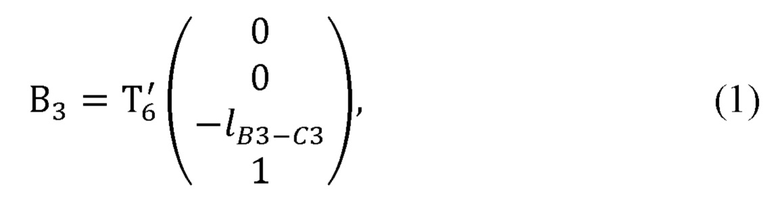
, 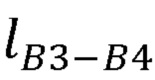 , вычислитель декартовых координат суставов руки оператора формирует представление Денавита-Хартенберга, рассчитывает декартовы координаты лучезапястного сустава руки оператора по формуле:
, вычислитель декартовых координат суставов руки оператора формирует представление Денавита-Хартенберга, рассчитывает декартовы координаты лучезапястного сустава руки оператора по формуле:
где В3 - радиус-вектор лучезапястного сустава руки оператора в глобальной системе координат;
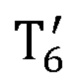 - матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты центра кисти оператора по формуле:
- матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты центра кисти оператора по формуле:
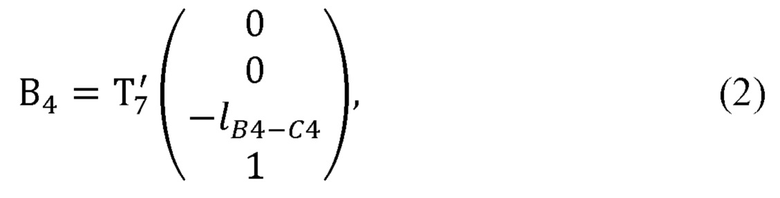
где В4 - радиус-вектор центра кисти оператора в глобальной системе координат;
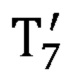 - матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты нормали к ладони оператора по формуле:
- матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты нормали к ладони оператора по формуле:


где С3 - радиус-вектор лучезапястного сочленения задающего устройства в глобальной системе координат;
N - вектор нормали к ладони оператора в глобальной системе координат;
рассчитывает расстояние между плечевым и лучезапястным суставами руки оператора по формуле:
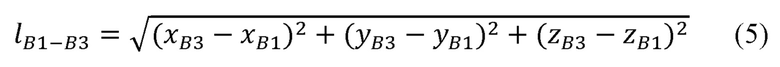
где 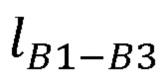 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
хВ1, уВ1, zB1 - декартовы координаты плечевого сустава В1;
xB3, yB3, zB3 - декартовы координаты лучезапястного сустава В3; рассчитывает радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3:
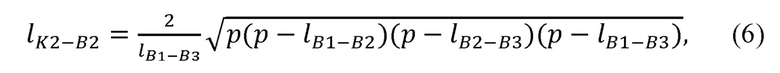
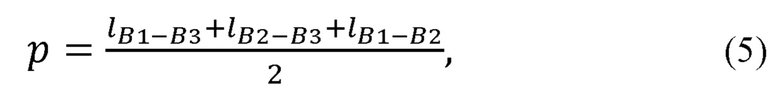
где р - полупериметр треугольника B1B2B3;
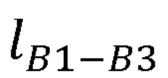 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
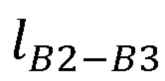 - длина предплечья руки оператора;
- длина предплечья руки оператора;
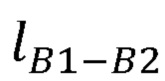 - длина плеча руки оператора;
- длина плеча руки оператора;
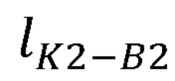 - радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3;
- радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3;
рассчитывает длину отрезка B1K2 соединяющего плечевой сустав В1 и центр K2 окружности, описываемой точкой В2 при вращении вокруг прямой B1B3, по формуле:
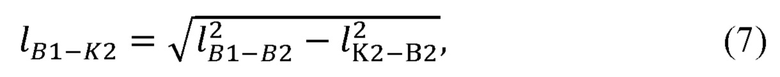
где 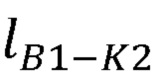 - длина отрезка B1K2;
- длина отрезка B1K2;
рассчитывает координаты точки K2 по формуле:
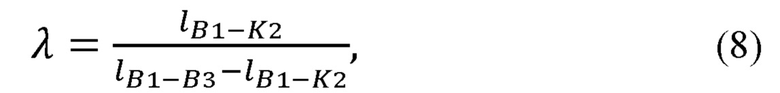
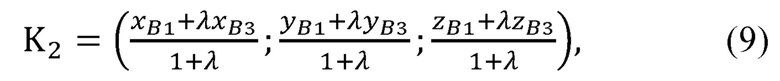
где λ - отношение, в котором точка K2 делит отрезок B1B3;
рассчитывает коэффициенты An, Bn, Cn, Dn плоскости, перпендикулярной отрезку В1В3, и проходящей через точку K2:
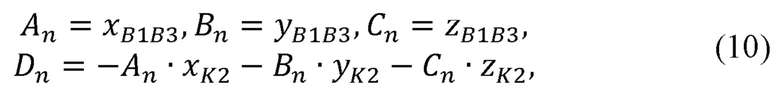
где хВ1ВЗ, уВ1ВЗ, zB1B3 - декартовы координаты вектора В1В3;
xK2, yK2, zK2 - декартовы координаты точки K2;
выполняет замену:
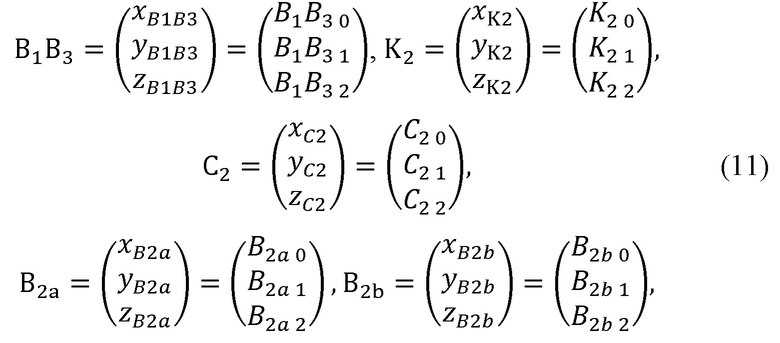
рассчитывает варианты положения В2а и B2b локтевого сустава В2 по формулам:
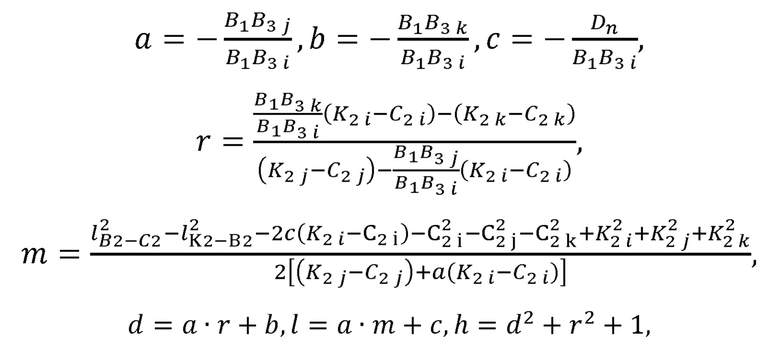
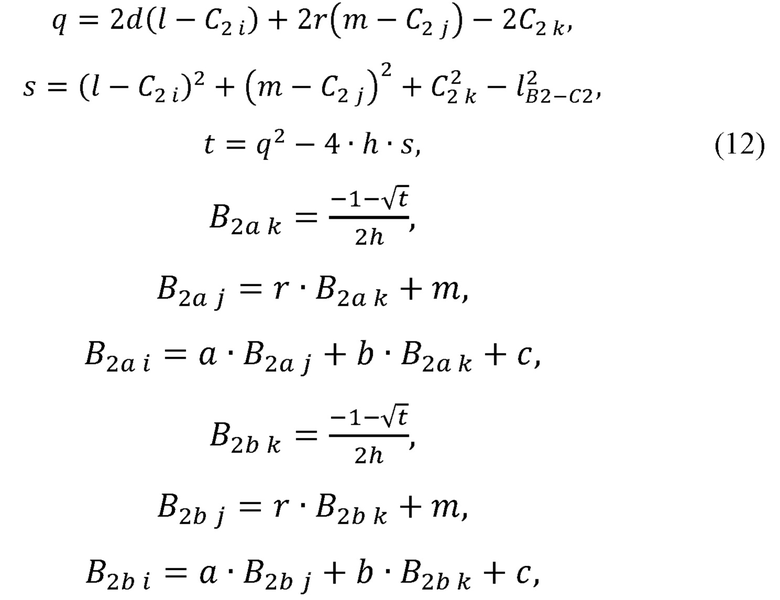
где а, b, с, r, m, d, 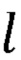 , h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
, h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
i, j, k - индексы, принимающие значения, определяемые следующим правилом: индекс i равен номеру ненулевой компоненты вектора B1B3 в выражении, j и k - номерам оставшихся компонент;
выбирает положение искомой точки В2 из двух возможных вариантов В2а и B2b по формуле:
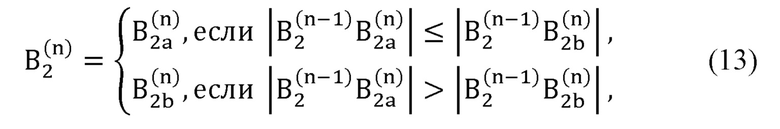
где 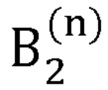 - радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
n - номер текущей итерации косвенного измерения углов поворота в суставах руки оператора;
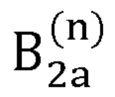 - первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
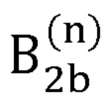 - второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
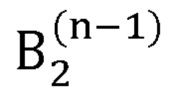 - радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации;
блок решения обратной задачи кинематики формирует представление Денавита-Хартенберга руки оператора, рассчитывает декартовы координаты различных точек в необходимых системах координат:
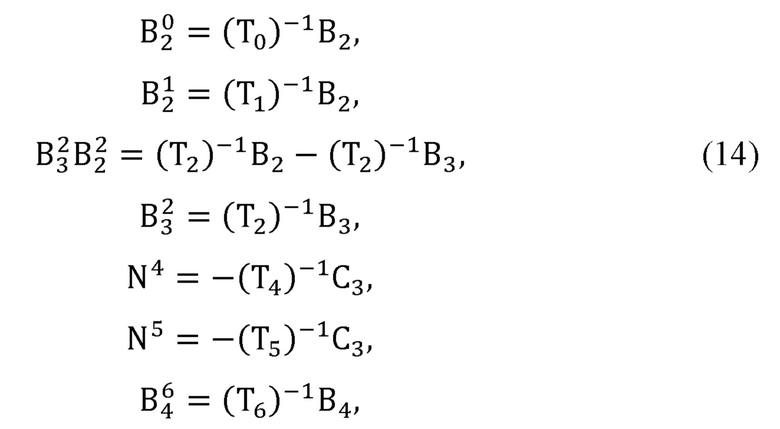
где 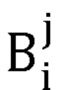 - координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
- координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
Ti - матрица преобразования из j-й системы координат в глобальную систему координат;
Bi - координаты точки Bi в глобальной системе координат;
Ni - координаты вектора нормали N в i-й системе координат;
рассчитывает углы поворота руки оператора по формулам:
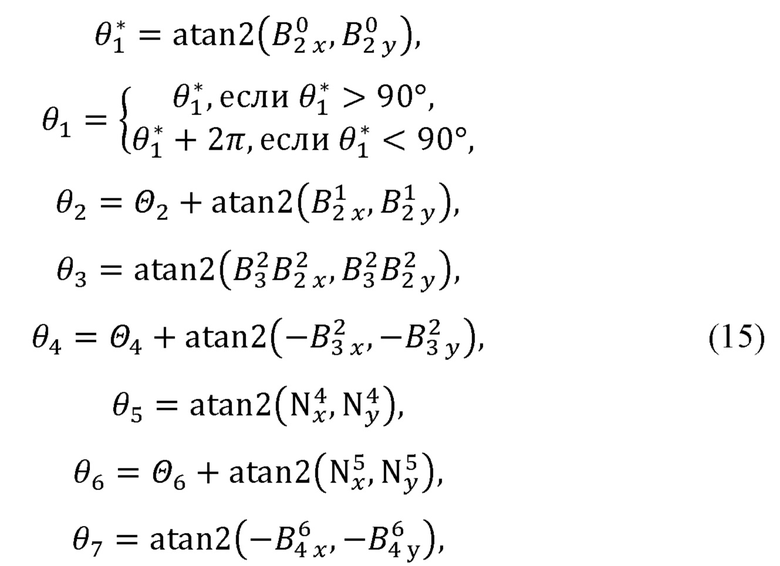
где 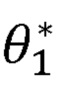 - ненормированное значение первого угла поворота руки оператора;
- ненормированное значение первого угла поворота руки оператора;
atan2(x,y) - функция арктангенса, учитывающая квадрант вычисляемого угла;
θi - i-й угол поворота руки оператора;
Θ2, Θ4, Θ6 - константы, отдельно определяемые для каждой модели задающего устройства;
формирует вектор углов поворота руки оператора по формуле:
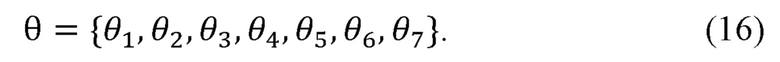
Теоретическое доказательство наличия причинно-следственной связи между заявляемыми признаками и достигаемым техническим результатом заключается в следующем.
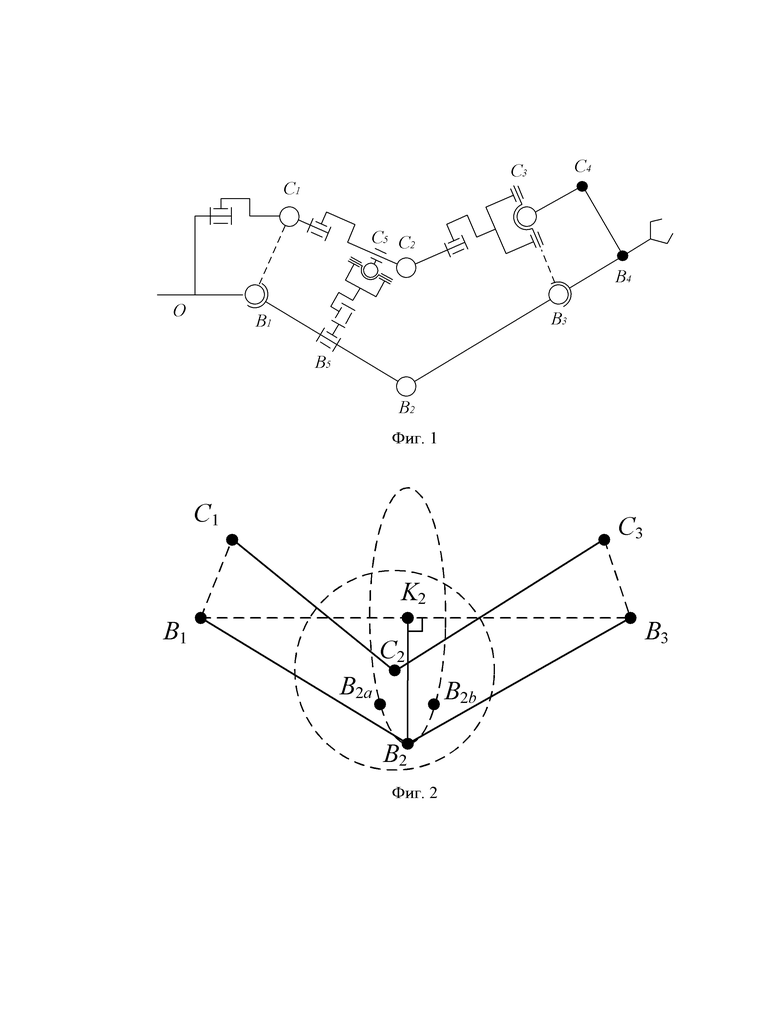
Рассмотрим кинематическую схему связанных между собой руки оператора и задающего устройства (фиг. 1). Плечевой, локтевой и лучезапястный суставы руки оператора, а также центр его кисти обозначены как В1, В2, В3, В4, соответственно. Аналогичные точки задающего устройства, имеющего кинематическую схему аналогичную кинематической схеме руки оператора, обозначены как С1, С2, С3, С4, соответственно. Точка O - неподвижная относительно тела оператора точка крепления задающего устройства. Непрерывными линиями на фиг. 1 обозначены жесткие физически существующие связи между точками. Пунктирными линиями обозначены жесткие связи, не существующие, но обусловленные другими жесткими физическими связями. Полыми точками обозначены кинематические пары руки оператора и задающего устройства. Заполненными точками обозначены жесткие соединения звеньев.
Рука оператора и задающее устройство сцеплены в нескольких местах жесткими сцепками. Жесткая сцепка В1ОС1 предотвращает взаимное движение плечевого сустава оператора В1 и плечевого сочленения задающего устройства C1. Сцепка В3В4С4С3 объединяет кистевые звенья оператора и задающего устройства для полного контроля над движением задающего устройства. Также существует гибкая сцепка, представленная на фиг. 1 как кинематическая цепь В5С5. Данная цепь удерживает звенья задающего устройства в положении, параллельном частям руки оператора. В противном случае для изображенного на фиг. 1 положения руки возможна ситуация, когда локтевой сустав направлен вниз, а локтевое сочленение задающего устройства - вверх.
Пусть известны:
- координаты точки В1 = (0; 0; 0), принятой за начало отсчета;
- координаты вектора жесткой сцепки B1C1 = (хВ1С1; yB1C1; zB1C1);
- длины частей руки оператора 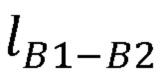 ,
, 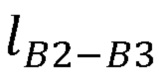 ,
, 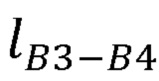 ;
;
- длины звеньев задающего устройства 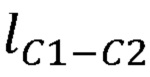 ,
, 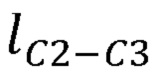 ,
, 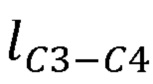 ;
;
- длины сцепок В3С3, В4С4 и виртуальной сцепки 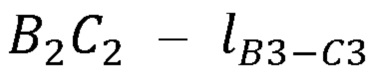 ,
, 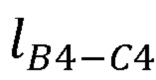 ,
, 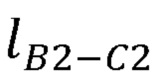 ;
;
- вектор измеренных значений обобщенных координат задающего устройства: 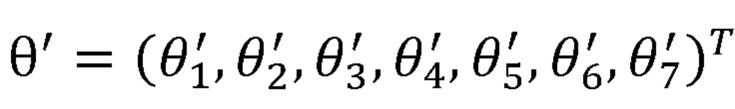
Сцепка В2С2 названа виртуальной, т.к. физически она не существует, однако расстояние между точками В2 и С2 изменяется в ограниченных пределах вследствие наличия реальной сцепки В5С5. Таким образом, из данных пределов может быть выбрано одно значение, позволяющее выполнять дальнейшие расчеты углов поворота руки оператора с некоторой погрешностью. Длина виртуальной сцепки может быть подобрана экспериментально с целью уменьшения данной погрешности.
На основе перечисленных известных величин могут быть рассчитаны декартовы координаты лучезапястного сустава руки оператора, центра ее кисти, а также вектора нормали к ладони оператора путем решения прямой задачи кинематики с помощью представления Денавита-Хартенберга. Для получения представления Денавита-Хартенберга выполняются следующие действия:
1. Задающее устройство представляется в виде эквивалентной кинематической цепи, состоящей из семи звеньев и семи кинематических пар пятого класса.
2. Вводится произвольная глобальная система координат, относительно которой необходимо получить радиус-векторы искомых точек кинематической цепи, состоящей из задающего устройства и руки оператора, а также системы координат, связанные со звеньями задающего устройства.
3. Формируются матрицы преобразования 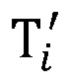 из i-й системы координат, связанной с i-м звеном в глобальную систему координат.
из i-й системы координат, связанной с i-м звеном в глобальную систему координат.
На основе полученного представления Денавита-Хартенберга декартовы координаты лучезапястного сустава руки оператора, центра ее кисти, а также вектора нормали к ладони оператора могут быть рассчитаны по следующим формулам:
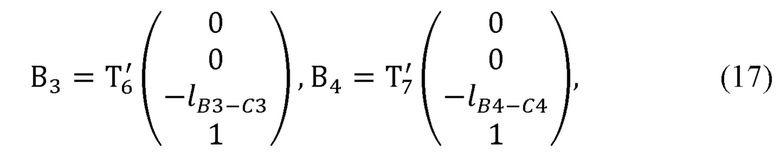
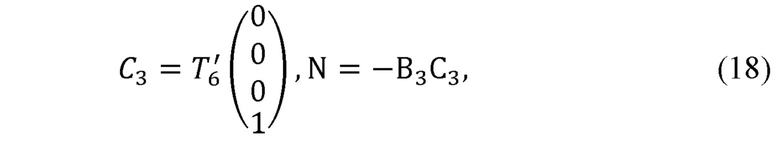
где В3 - радиус-вектор лучезапястного сустава руки оператора в глобальной системе координат;
В4 - радиус-вектор центра кисти оператора в глобальной системе координат;
С3 - радиус-вектор лучезапястного сочленения задающего устройства в глобальной системе координат;
N - вектор нормали к ладони оператора в глобальной системе координат;
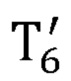 - матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат;
- матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат;
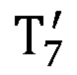 - матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат.
- матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат.
Локтевой сустав руки оператора не имеет жесткой сцепки с задающим устройством, поэтому его декартовы координаты не могут быть найдены путем решения прямой задачи кинематики. Однако его координаты могут быть приближенно найдены с помощью следующего способа.
Необходимо найти расстояние между соседними суставами, декартовы координаты которых известны вследствие их жесткой связи с задающим устройством:
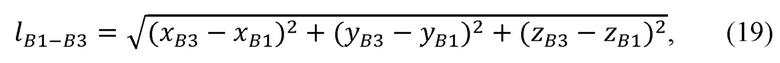
где 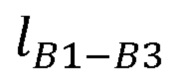 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
хВ1, уВ1, zB1 - декартовы координаты плечевого сустава В1;
xB3, yB3, zB3 - декартовы координаты лучезапястного сустава В3.
Для известных декартовых координат суставов В1 и В3 множество возможных положений неизвестного сустава В2 представляет собой окружность, изображенную на фиг. 2, описываемую точкой В2 при вращении вокруг прямой В1В3. Центр окружности K2 может быть получен из треугольника B1B2B3 путем проведения высоты из точки В2 к стороне B1B3.
Длина высоты 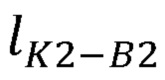 может быть найдена через площадь треугольника B1B2B3:
может быть найдена через площадь треугольника B1B2B3:
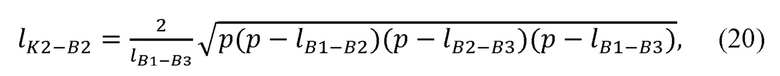
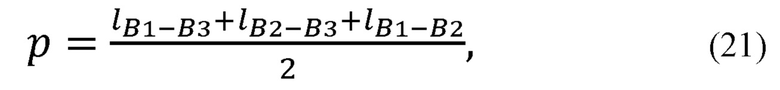
где р - полупериметр треугольника В1В2В3;
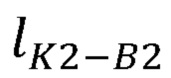 - длина высоты, проведенной в треугольнике B1B2B3 из точки В2.
- длина высоты, проведенной в треугольнике B1B2B3 из точки В2.
Длина отрезка B1K2 может быть найдена по формуле:
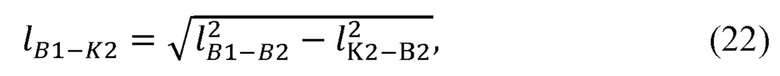
где 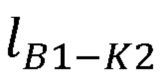 - длина отрезка B1K2.
- длина отрезка B1K2.
Координаты точки K2 могут быть найдены по формуле деления отрезка в заданном отношении:
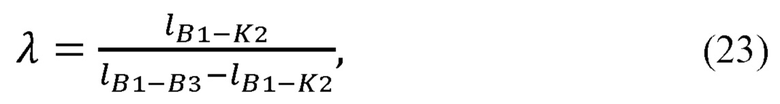
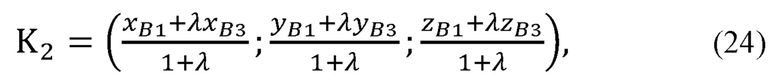
где λ - отношение, в котором точка K2 делит отрезок В1В3.
Обозначенная на фиг. 2 окружность возможных положений сустава В2 может быть найдена как пересечение сферы с центром в точке K2 и радиусом 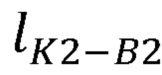 , и плоскости, перпендикулярной отрезку B1B3, и проходящей через точку K2:
, и плоскости, перпендикулярной отрезку B1B3, и проходящей через точку K2:
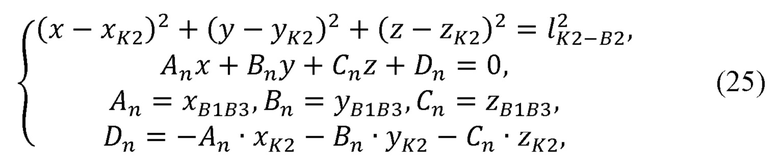
где xK2, yK2, zK2 - декартовы координаты точки K2;
An, Bn, Cn, Dn - коэффициенты плоскости, перпендикулярной отрезку В1В3, и проходящей через точку K2;
xB1B3, yB1B3, zB1B3 - значения проекций вектора B1B3 на оси декартовой системы координат.
Предлагаемый способ определения координат локтевого сустава основывается на допущении о том, что в целях расчета положения локтевого сустава можно считать расстояние между сочленением С2 и суставом В2 постоянным. Тогда выбор положения точки В2 на окружности, описывающей возможные положения локтевого сустава, может быть произведен из условия нахождения общих точек пересечения со сферой с центром в точке С2 и радиусом 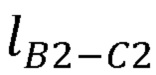 (фиг. 2). Уравнение данной сферы имеет вид:
(фиг. 2). Уравнение данной сферы имеет вид:
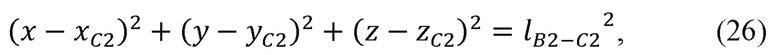
где хС2, уС2, zC2 - декартовы координаты сочленения С2;
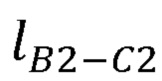 - эффективная длина нежесткого крепления.
- эффективная длина нежесткого крепления.
Варианты положения В2а и B2b локтевого сустава В2 могут быть найдены как точки пересечения описанных выше окружности и сферы. Примем, что:
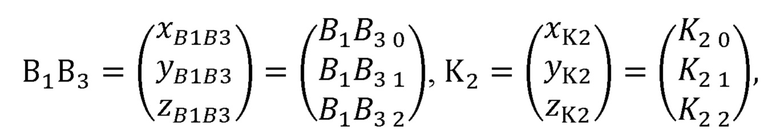
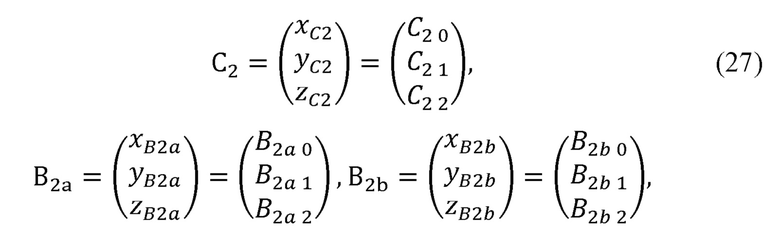
где B1B3, K2, С2, В2а, B2b - значения декартовых координат соответствующих векторов и точек.
Варианты положения В2а и B2b локтевого сустава В2 могут быть найдены по формулам:
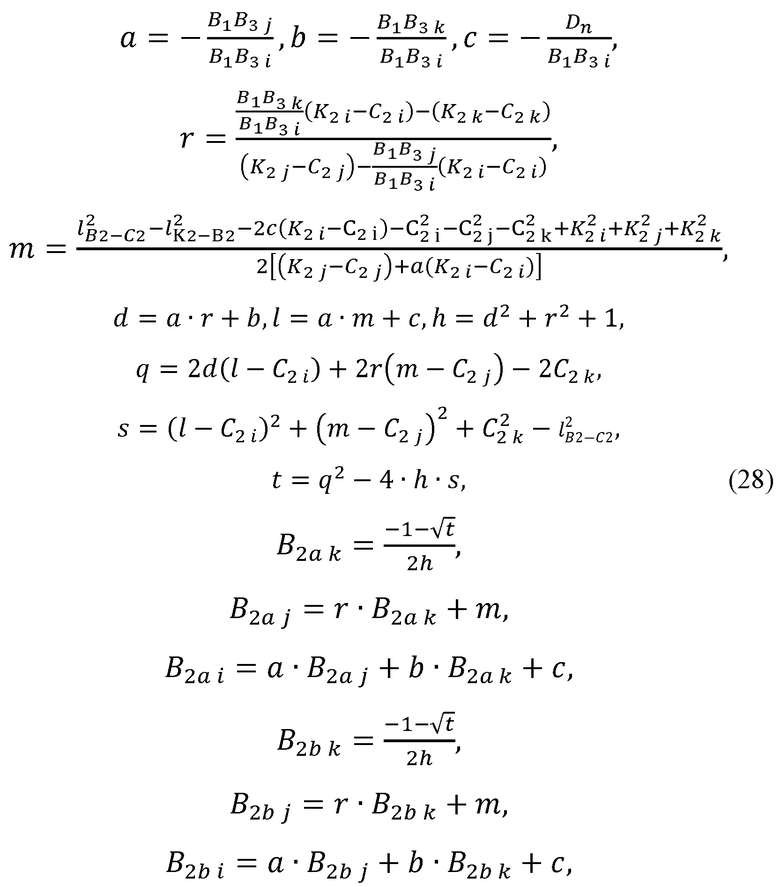
где а, b, с, r, m, d, 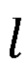 , h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
, h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
i, j, k - индексы, принимающие значения, определяемые следующим правилом: индекс i равен номеру ненулевой компоненты вектора В1В3 в выражении, индексы j и k - номерам оставшихся компонент. Данные индексы, динамически определяемые в процессе расчета, введены для гарантии, что при расчете величин а, b и с не будет деления на ноль.
Выбор положения искомой точки В2 из двух возможных вариантов В2а и B2b может выполняться из условия непрерывности перемещения сустава в процессе движения. Для этого в начале работы оператора с задающим устройством необходимо выбрать одну из двух рассчитанных точек положения локтевого сустава, как наиболее соответствующую его реальному положению. Для этого оператор должен выполнить постановку руки в некоторое заданное начальное положение, в котором декартовы координаты локтевого сустава соответствуют координатам, записанным в блоке памяти.
В процессе циклической работы алгоритма расчета выбор одной из двух точек производится из условия минимума расстояния до точки положения локтевого сустава, найденной на предыдущей итерации:
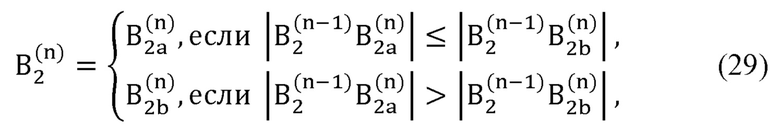
где 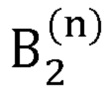 - радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
n - номер текущей итерации косвенного измерения углов поворота в суставах руки оператора;
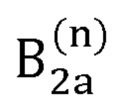 - первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
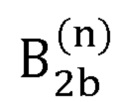 - второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
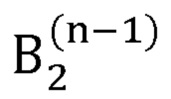 - радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации.
- радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации.
На основе декартовых координат суставов руки оператора, а также центра его кисти и нормали к ладони могут быть найдены углы поворота руки оператора путем решения обратной задачи кинематики, например, с помощью решения, предложенного в работе [Petrenko, V.I. Calculating rotation angles of the operator's arms based on generalized coordinates of the master device with following anthropomorphic manipulator in real time / V.I. Petrenko, F.B. Tebueva, V.B. Sychkov, V.O. Antonov, M.M. Gurchinsky // International Journal of Mechanical Engineering and Technology (IJMET). - 2018. - Vol. 9, Issue 7 (2018). - pp. 447-461].
Рассчитанные углы поворота руки оператора ближе к реальным значениям углов поворота руки оператора, чем измеренные значения углов поворота задающего устройства, используемые в прототипе в качестве приближенного значения углов поворота руки оператора. Вывод формул (17)÷(29), а также результаты испытаний, подтверждающие повышение точности расчета углов поворота руки оператора при их применении приведены в [Petrenko V.I., Tebueva F.B., Sychkov V.B., Antonov V.O., Gurchinsky M.M. Calculating rotation angles of the operator's arms based on generalized coordinates of the master device with following anthropomorphic manipulator in real time. International Journal of Mechanical Engineering and Technology, Volume 9, Issue 7, July 2018, Pages 447-461].
Таким образом, осуществление расчета по приведенным формулам с одной стороны позволяет достичь заявленного технического результата, а с другой - требует применения заявленных признаков, что обусловливает причинно-следственную связь между заявляемыми признаками и достигаемым техническим результатом.
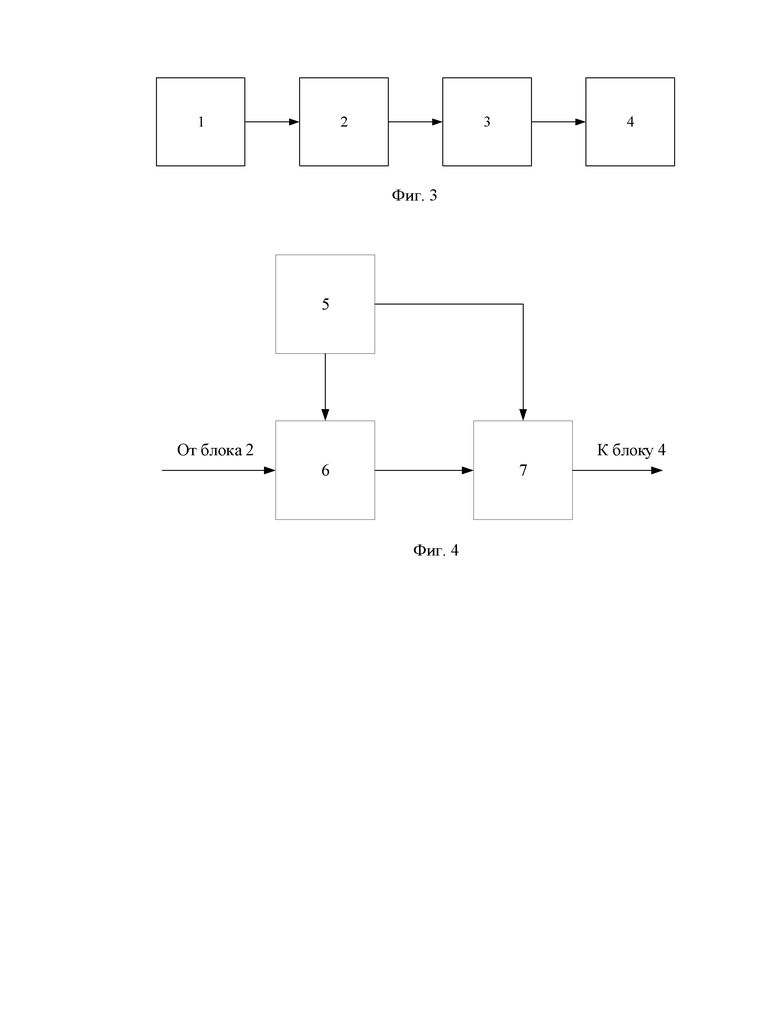
Комплекс управления антропоморфным манипулятором (см. фиг. 3) содержит блок механической системы задающего устройства 1, блок датчиков задающего устройства 2, блок расчета углов поворота руки оператора 3, блок управления приводами антропоморфного манипулятора 4.
Выходы блока механической системы задающего устройства 1 соединены со входами блока датчиков задающего устройства 2. Выходы блока датчиков задающего устройства 2 соединены со входами блока расчета углов поворота руки оператора 3. Выходы блока расчета углов поворота руки оператора 3 соединены с входами блока управления приводами антропоморфного манипулятора 4.
Блок расчета углов поворота руки оператора 3 (см. фиг. 4) содержит блока памяти 5, вычислитель декартовых координат суставов руки оператора 6 и блок решения обратной задачи кинематики 7.
Первый выход блока памяти 5 соединен с первым входом вычислителя декартовых координат суставов руки оператора 6. Второй выход блока памяти 5 соединен с первым входом блока решения обратной задачи кинематики 7. Второй вход вычислителя декартовых координат суставов руки оператора 6 соединен с входом блока расчета углов поворота руки оператора 3. Выход вычислителя декартовых координат суставов руки оператора 6 соединен со вторым входом блока решения обратной задачи кинематики 7, выход которого соединен с выходом блока расчета углов поворота руки оператора 3.
Принцип работы комплекса управления заключается в следующем (фиг. 3).
Рука оператора приводит в движение блок механической системы задающего устройства 1. Положение блока механической системы задающего устройства 1 в пространстве обобщенных координат определяется блоком датчиков задающего устройства 2 и на его выходе формируется вектор обобщенных координат задающего устройства θ', размерностью семь, равной количеству основных степеней подвижности руки оператора. Блок расчета углов поворота руки оператора 3 на основе входного вектора обобщенных координат задающего устройства θ' и хранящихся внутри блока параметров задающего устройства и руки оператора выполняет расчет углов поворота руки оператора θ. Рассчитанные значения углов поворота руки оператора θ обрабатываются блоком управления приводами антропоморфного манипулятора 4.
Процесс расчета углов поворота руки оператора блоком расчета углов поворота руки оператора 3 заключается в следующем.
На первом выходе блока памяти 5 формируются значения параметров, необходимых для расчетов декартовых координат суставов руки оператора:
- координаты точки В1 = (0; 0; 0), принятой за начало отсчета;
- координаты вектора жесткой сцепки B1C1 = (хВ1С1; yB1C1; zB1C1);
- длины частей руки оператора  ,
, 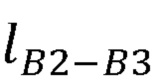 ,
, 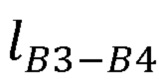 ;
;
- длины звеньев задающего устройства 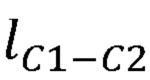 ,
, 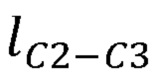 ,
, 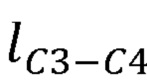 ;
;
- длины сцепок В3С3, В4С4 и виртуальной сцепки 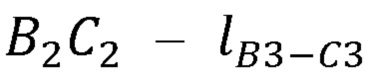 ,
, 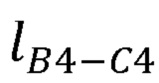 ,
, 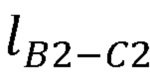 ;
;
- координаты локтевого сустава в начальном положении рассчитанные на предыдущей итерации расчета.
На втором выходе блока памяти 5 формируются значения параметров, необходимых для решения обратной задачи кинематики:
- координаты точки В1 = (0; 0; 0), принятой за начало отсчета;
- длины частей руки оператора 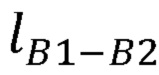 ,
, 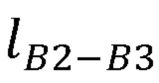 ,
, 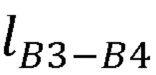 .
.
На основе параметров, хранимых в блоке памяти 5 (фиг. 4) и измеренных значений углов поворота задающего устройства θ', поступающих от входов блока расчета углов поворота руки оператора 3, вычислитель декартовых координат суставов руки оператора 6 рассчитывает декартовы координаты суставов руки оператора, центра его кисти и нормали к его ладони.
Для этого формируется представление Денавита-Хартенберга задающего устройства. Находятся декартовы координаты лучезапястного сустава руки оператора, центра ее кисти, а также вектора нормали к ладони оператора путем решения прямой задачи кинематики по формулам:
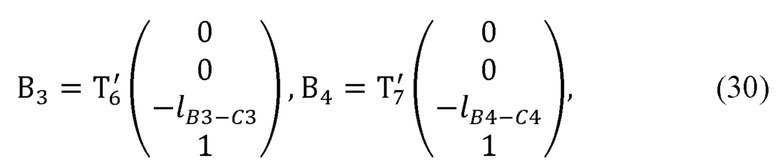
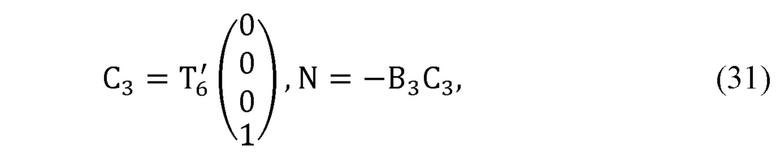
где В3 - радиус-вектор лучезапястного сустава руки оператора в глобальной системе координат;
В4 - радиус-вектор центра кисти оператора в глобальной системе координат;
С3 - радиус-вектор лучезапястного сочленения задающего устройства в глобальной системе координат;
N - вектор нормали к ладони оператора в глобальной системе координат;
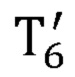 - матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга;
- матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга;
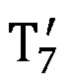 - матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга.
- матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга.
Для расчета декартовых координат локтевого сустава используют следующую методику.
Находят расстояние между плечевым и лучезапястным суставами, декартовы координаты которых известны вследствие их жесткой связи с задающим устройством:
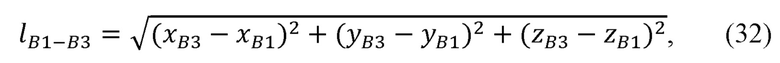
где 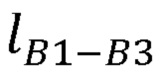 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
хВ1, уВ1, zB1 - декартовы координаты плечевого сустава В1;
xB3, yB3, zB3 - декартовы координаты лучезапястного сустава В3.
Рассчитывают радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3 (см. фиг. 2):
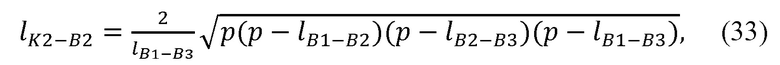
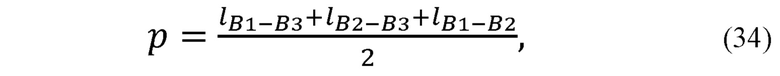
где р - полупериметр треугольника В1В2В3;
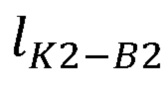 - радиус окружности, описываемой точкой точкой В2 при вращении вокруг прямой B1B3.
- радиус окружности, описываемой точкой точкой В2 при вращении вокруг прямой B1B3.
Рассчитывают длину отрезка B1K2 соединяющего плечевой сустав В1 и центр K2 окружности, описываемой точкой B2 при вращении вокруг прямой В1В3, по формуле:
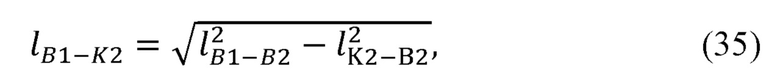
где 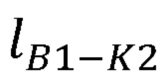 - длина отрезка B1K2.
- длина отрезка B1K2.
Рассчитывают координаты точки K2 по формуле:
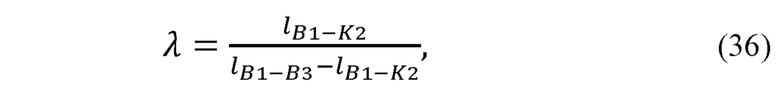
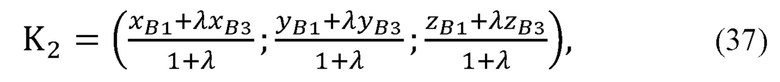
где λ - отношение, в котором точка K2 делит отрезок B1B3.
Рассчитывают коэффициенты An, Bn, Cn, Dn плоскости, перпендикулярной отрезку В1В3, и проходящей через точку K2:
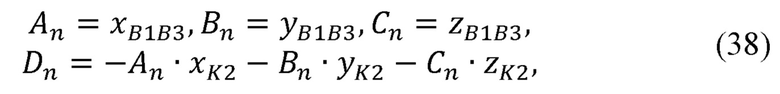
где хВ1В3, уВ1В3, zB1B3 - декартовы координаты вектора В1В3;
xK2, yK2, zK2 - декартовы координаты точки K2.
Варианты положения В2а и B2b локтевого сустава В2 могут быть найдены как точки пересечения описанных выше окружности и сферы. Примем, что:
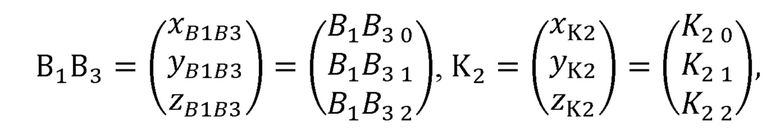
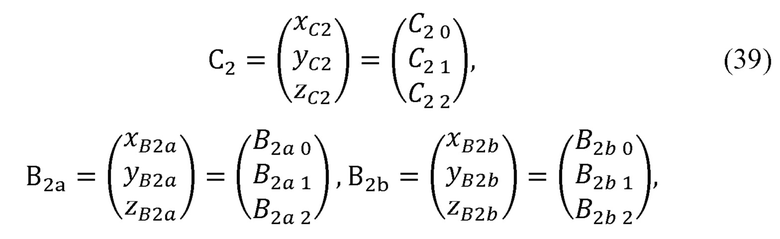
где B1B3, K2, С2, В2а, B2b - значения декартовых координат соответствующих векторов и точек.
Варианты положения В2а и B2b локтевого сустава В2 могут быть найдены по формулам:
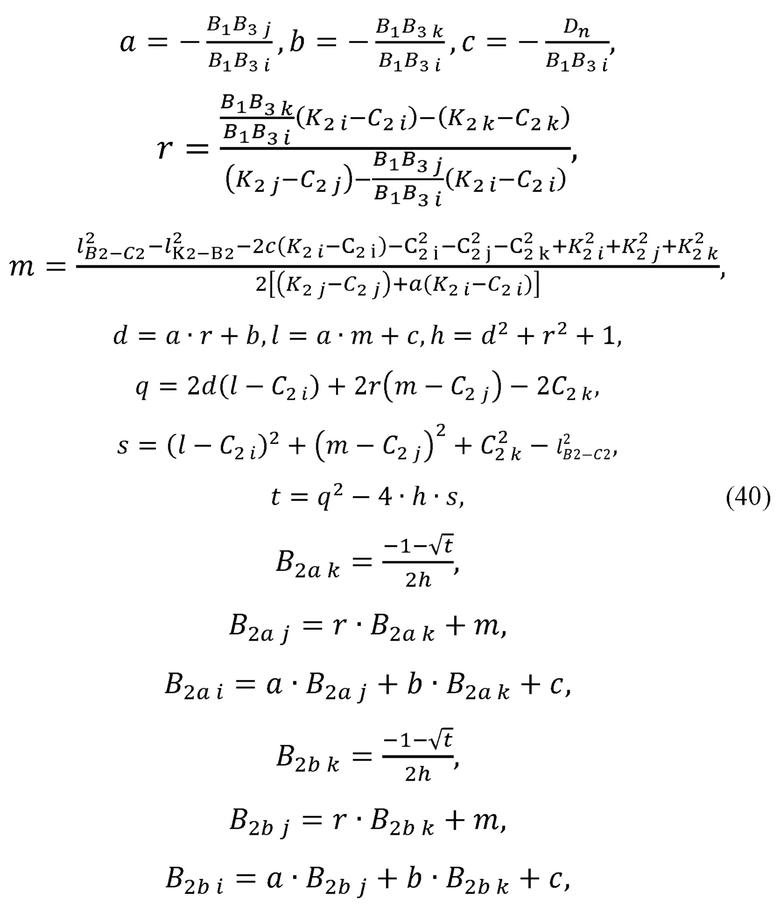
где а, b, с, r, m, d, 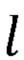 , h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
, h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
i, j, k - индексы, принимающие значения, определяемые следующим правилом: индекс i равен номеру ненулевой компоненты вектора В1В3 в выражении, j и k - номерам оставшихся компонент. Данные индексы, динамически определяемые в процессе расчета, введены для гарантии, что при расчете величин а, b и с не будет деления на ноль.
Выбор положения искомой точки В2 из двух возможных вариантов В2а и B2b может выполняться из условия непрерывности перемещения сустава в процессе движения. Для этого в начале работы оператора с задающим устройством необходимо выбрать одну из двух рассчитанных точек положения локтевого сустава, как наиболее соответствующую его реальному положению. Для этого оператор должен выполнить постановку руки в некоторое заданное начальное положение, в котором декартовы координаты локтевого сустава соответствуют координатам, записанным в блоке памяти.
В процессе циклической работы алгоритма расчета выбор одной из двух точек производится из условия минимума расстояния до точки положения локтевого сустава, найденной на прошлой итерации:
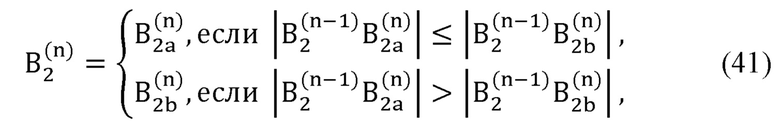
где 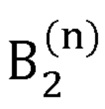 - радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
n - номер текущей итерации косвенного измерения углов поворота в суставах руки оператора;
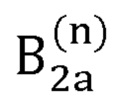 - первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
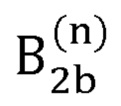 - второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
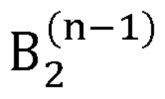 - радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации.
- радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации.
На основе формируемых декартовых координат суставов руки оператора В1, В2, В3, центра его кисти В4 и нормали к его ладони N на выходе вычислителя декартовых координат 6, блок решения обратной задачи кинематики 7 рассчитывает углы поворота руки оператора.
Для этого формируют представление Денавита-Хартенберга руки оператора.
Рассчитывают декартовы координаты различных точек в необходимых системах координат:
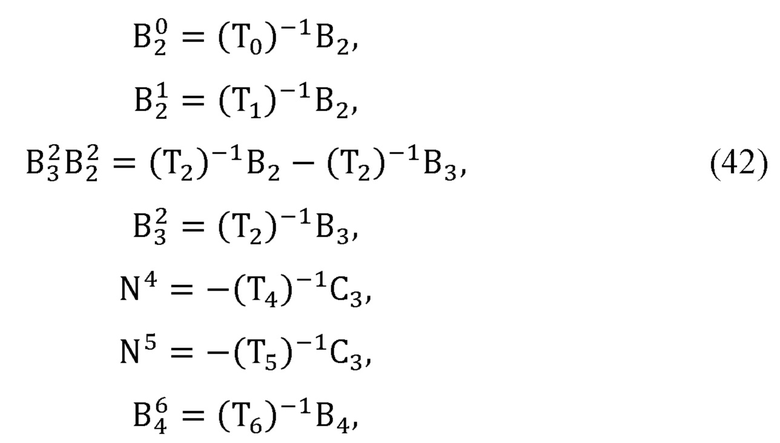
где 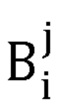 - координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
- координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
Ti - матрица преобразования из j-й системы координат в глобальную систему координат;
Bi - координаты точки Bi в глобальной системе координат;
Ni - координаты вектора нормали N в j-й системе координат.
Рассчитывают углы поворота руки оператора по формулам:

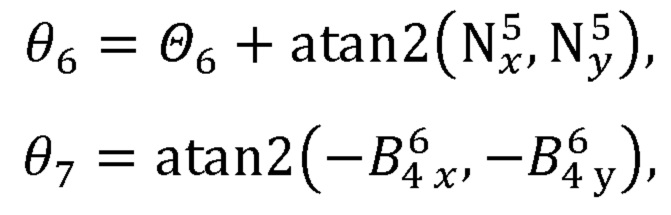
где 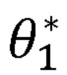 - ненормированное значение первого угла поворота руки оператора;
- ненормированное значение первого угла поворота руки оператора;
atan2(x,y) - функция арктангенса, учитывающая квадрант вычисляемого угла;
θi - i-й угол поворота руки оператора;
Θ2, Θ4, Θ6 - константы, отдельно определяемые для каждой модели задающего устройства.
Формируют вектор углов поворота руки оператора по формуле:
Таким образом, реализуемый заявляемым комплексом процесс управления антропоморфным манипулятором заключается в следующем:
1) Оператор приводит в движение механическую систему задающего устройства.
2) Измеряют обобщенные координаты 0' задающего устройства.
3) Рассчитывают декартовы координаты плечевого и лучезапястного суставов руки оператора, центра ладони оператора и вектора нормали к ней В1, В2, В3, В4, N, соответственно.
4) Решают обратную задачи кинематики для формирования сигнала управления антропоморфным манипулятором Э.
5) Осуществляют управление антропоморфным манипулятором на основе сформированного сигнала управления 0.
Описанный алгоритм расчета и уравнения (30)÷(44) соответствуют порядку расчета, приведенному в работе [Petrenko V.I., Tebueva F.B., Sychkov V.B., Antonov V.О., Gurchinsky M.M. Calculating rotation angles of the operator's arms based on generalized coordinates of the master device with following anthropomorphic manipulator in real time. International Journal of Mechanical Engineering and Technology, Volume 9, Issue 7, July 2018, Pages 447-461]. Данный порядок расчета обеспечивает формирование закона управления для копирующего управления антропоморфным манипулятором на основе перерасчета углов поворота задающего устройства в углы поворота руки оператора.
Таким образом, заявляемое изобретение, как и прототип обеспечивает копирующее управление антропоморфным манипулятором. Однако, в отличие от прототипа, заявляемое изобретение позволяет осуществлять более точное копирование движений оператора антропоморфным манипулятором. Данный факт может быть проиллюстрирован результатами испытаний. Параметры задающего устройства и руки оператора приведены в таблице 1, результаты испытаний приведены в таблице 2.
Предлагаемое изобретение промышленно применимо. В качестве блоков механической системы 1 и датчиков задающего устройства 2 могут использоваться существующие средства задающих устройств, реализованных в виде экзоскелета (например, дистанционный манипулятор, защищенный патентом RU №125508, кл. B25J 3/04, 2011 г.). В качестве блока управления приводами антропоморфного манипулятора 4 могут использоваться существующие блоки управления антропоморфными манипуляторами. В качестве блока расчета углов поворота руки оператора 3 может использоваться специализированная ЭВМ или вычислительные системы задающего или исполнительного устройства.

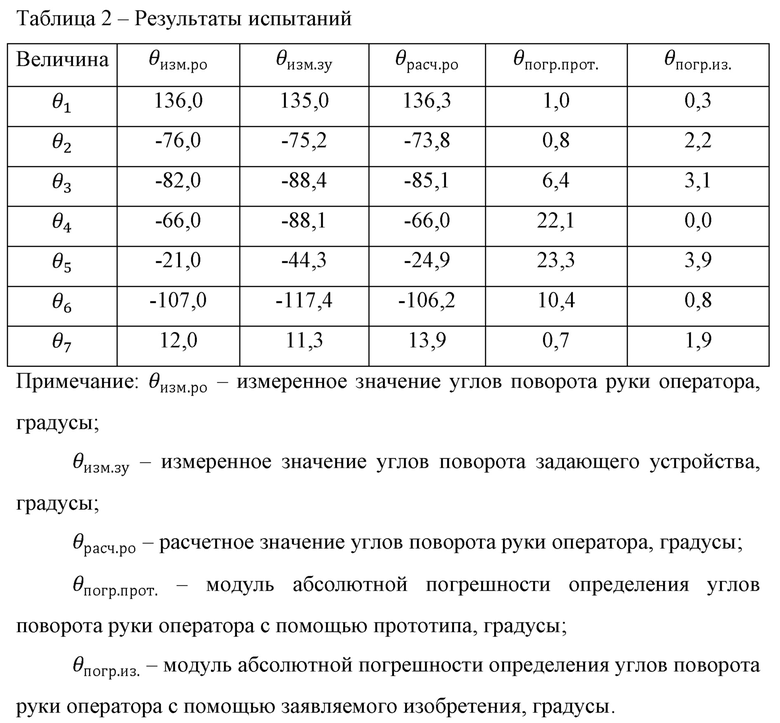
Результаты проведенных испытаний показывают, что использование предлагаемого комплекса позволит достичь более точного копирования движений оператора антропоморфным манипулятором по сравнению с устройством прототипом.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОМПЛЕКС КОПИРУЮЩЕГО УПРАВЛЕНИЯ МАНИПУЛЯТОРАМИ АНТРОПОМОРФНОГО РОБОТА | 2019 |
|
RU2725930C1 |
| СПОСОБ КОПИРУЮЩЕГО УПРАВЛЕНИЯ МАНИПУЛЯТОРАМИ АНТРОПОМОРФНОГО РОБОТА | 2019 |
|
RU2724769C1 |
| СПОСОБ КОСВЕННОГО ИЗМЕРЕНИЯ УГЛОВ ПОВОРОТА В СУСТАВАХ РУКИ ОПЕРАТОРА | 2018 |
|
RU2700118C1 |
| Способ калибровки кинематических параметров многостепенных манипуляторов | 2019 |
|
RU2719207C1 |
| КОМПЛЕКС ДИНАМИЧЕСКОГО УПРАВЛЕНИЯ АНТРОПОМОРФНЫМ МАНИПУЛЯТОРОМ | 2019 |
|
RU2724775C1 |
| Способ принудительной угловой ориентации головы и таза человека-оператора в механизме подвеса, применяемого для дистанционного управления антропоморфным роботом | 2019 |
|
RU2743952C2 |
| РОБОТИЗИРОВАННЫЙ ТРЕНАЖЕР ДЛЯ ЛЮДЕЙ С НАРУШЕНИЯМИ ФУНКЦИЙ ОПОРНО-ДВИГАТЕЛЬНОГО АППАРАТА | 2015 |
|
RU2604038C1 |
| Система и способ калибровки кинематических параметров роботизированного манипулятора | 2022 |
|
RU2810082C1 |
| СПОСОБ КАЛИБРОВКИ И ПРОГРАММИРОВАНИЯ РОБОТА | 2012 |
|
RU2605393C2 |
| СПОСОБ КАЛИБРОВКИ ЭНКОДЕРОВ РЫЧАЖНОЙ СИСТЕМЫ ЭКЗОСКЕЛЕТА | 2019 |
|
RU2724777C1 |
Изобретение относится к робототехнике и может быть использовано в системах копирующего управления антропоморфными манипуляторами. Комплекс содержит блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами антропоморфного манипулятора, блок расчета углов поворота руки оператора, который включает в себя блок памяти, вычислитель декартовых координат руки оператора, блок решения обратной задачи кинематики. Техническим результатом изобретения является повышение точности копирующего управления антропоморфным манипулятором за счет повышения точности определения углов поворота руки оператора. 4 ил., 2 табл.
Комплекс для управления движением антропоморфного манипулятора, содержащий блок механической системы задающего устройства, блок датчиков задающего устройства, блок управления приводами антропоморфного манипулятора, в котором выходы блока механической системы задающего устройства соединены со входами блока датчиков задающего устройства, отличающийся тем, что в него введен блок расчета углов поворота руки оператора, при этом выходы блока датчиков задающего устройства соединены со входами блока расчета углов поворота руки оператора, выходы которого соединены со входами блока управления приводами антропоморфного манипулятора, блок расчета углов поворота руки оператора содержит блок памяти, вычислитель декартовых координат суставов руки оператора, блок решения обратной задачи кинематики, первый выход блока памяти соединен с первым входом вычислителя декартовых координат суставов руки оператора, второй выход блока памяти соединен с первым входом блока решения обратной задачи кинематики, второй вход вычислителя декартовых координат суставов руки оператора соединен со входом блока расчета углов поворота руки оператора, а выход соединен со вторым входом блока решения обратной задачи кинематики, выход которого соединен с выходом блока расчета углов поворота руки оператора, на первом выходе блока памяти формируются координаты точки B1, принятой за начало отсчета, координаты вектора жесткой сцепки B1C1, длины частей руки оператора 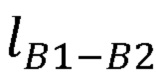 ,
, 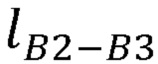 ,
, 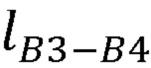 , длины звеньев задающего устройства
, длины звеньев задающего устройства 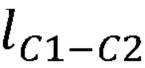 ,
, 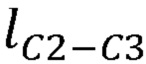 ,
, 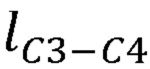 , длины сцепок В3С3, В4С4 и виртуальной сцепки
, длины сцепок В3С3, В4С4 и виртуальной сцепки 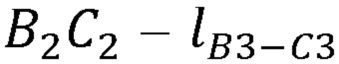 ,
, 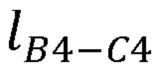 ,
, 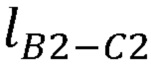 , координаты локтевого сустава
, координаты локтевого сустава 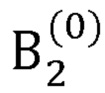 в заданном начальном положении руки оператора, на втором выходе блока памяти формируются координаты точки В1, принятой за начало отсчета, длины частей руки оператора
в заданном начальном положении руки оператора, на втором выходе блока памяти формируются координаты точки В1, принятой за начало отсчета, длины частей руки оператора 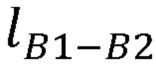 ,
, 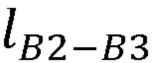 ,
, 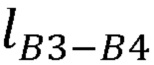 , вычислитель декартовых координат суставов руки оператора формирует представление Денавита-Хартенберга, рассчитывает декартовы координаты лучезапястного сустава руки оператора по формуле:
, вычислитель декартовых координат суставов руки оператора формирует представление Денавита-Хартенберга, рассчитывает декартовы координаты лучезапястного сустава руки оператора по формуле:
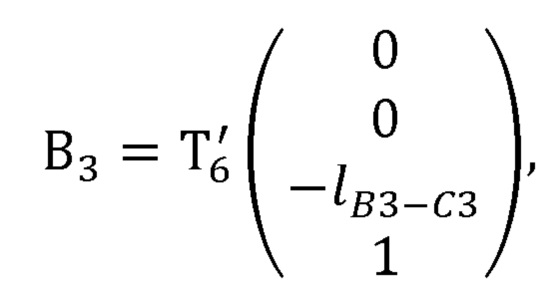
где В3 - радиус-вектор лучезапястного сустава руки оператора в глобальной системе координат;
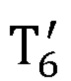 - матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты центра кисти оператора по формуле:
- матрица преобразования из системы координат, связанной с шестым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты центра кисти оператора по формуле:
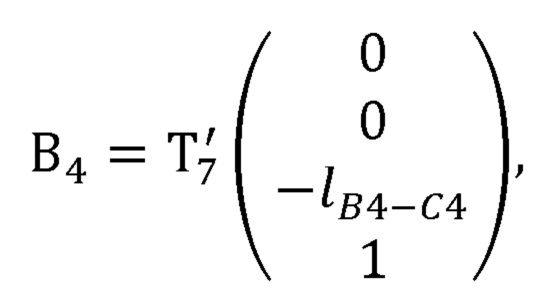
где В4 - радиус-вектор центра кисти оператора в глобальной системе координат;
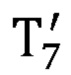 - матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты нормали к ладони оператора по формуле:
- матрица преобразования из системы координат, связанной с седьмым звеном задающего устройства, в глобальную систему координат, полученная с помощью представления Денавита-Хартенберга; рассчитывает декартовы координаты нормали к ладони оператора по формуле:
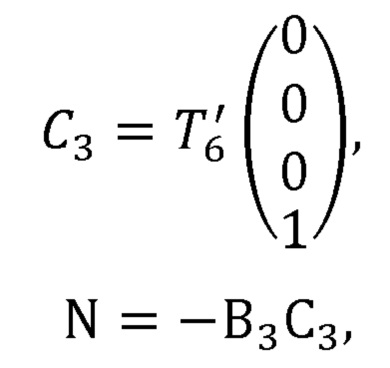
где С3 - радиус-вектор лучезапястного сочленения задающего устройства в глобальной системе координат;
N - вектор нормали к ладони оператора в глобальной системе координат;
рассчитывает расстояние между плечевым и лучезапястным суставами руки оператора по формуле:
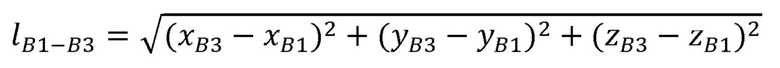 ,
,
где 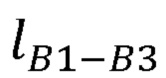 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
хВ1, yB1, zB1 - декартовы координаты плечевого сустава В1;
xB3, yB3, zB3 - декартовы координаты лучезапястного сустава В3;
рассчитывает радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3:
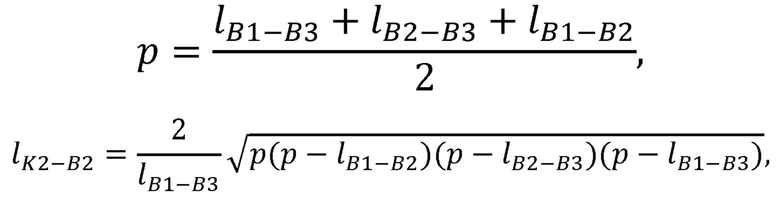
где р - полупериметр треугольника В1В2В3;
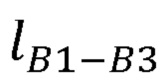 - расстояние между плечевым и лучезапястным суставами руки оператора;
- расстояние между плечевым и лучезапястным суставами руки оператора;
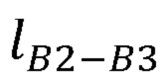 - длина предплечья руки оператора;
- длина предплечья руки оператора;
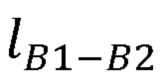 - длина плеча руки оператора;
- длина плеча руки оператора;
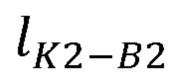 - радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3;
- радиус окружности, описываемой точкой В2 при вращении вокруг прямой B1B3;
рассчитывает длину отрезка B1K2 соединяющего плечевой сустав В1 и центр K2 окружности, описываемой точкой В2 при вращении вокруг прямой B1B3, по формуле:
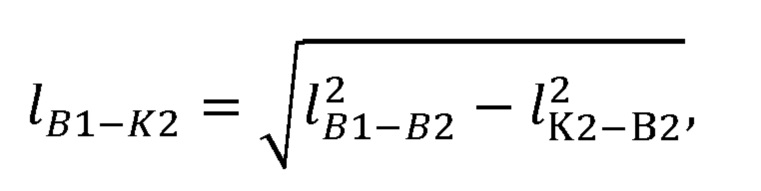
где 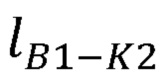 - длина отрезка B1K2;
- длина отрезка B1K2;
рассчитывает координаты точки K2 по формуле:
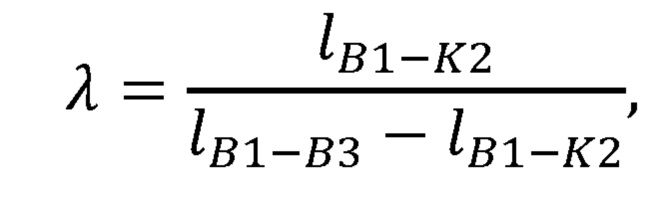
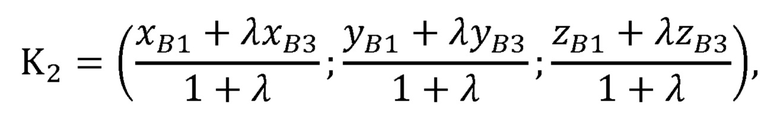
где λ - отношение, в котором точка K2 делит отрезок B1B3;
рассчитывает коэффициенты An, Bn, Cn, Dn плоскости, перпендикулярной отрезку В1В3 и проходящей через точку K2:
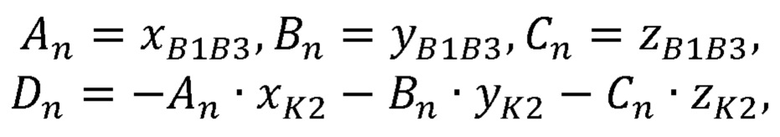
где хВ1В3, yB1B3, zB1B3 - декартовы координаты вектора В1В3;
xK2, yK2, zK2 - декартовы координаты точки K2;
выполняет замену:
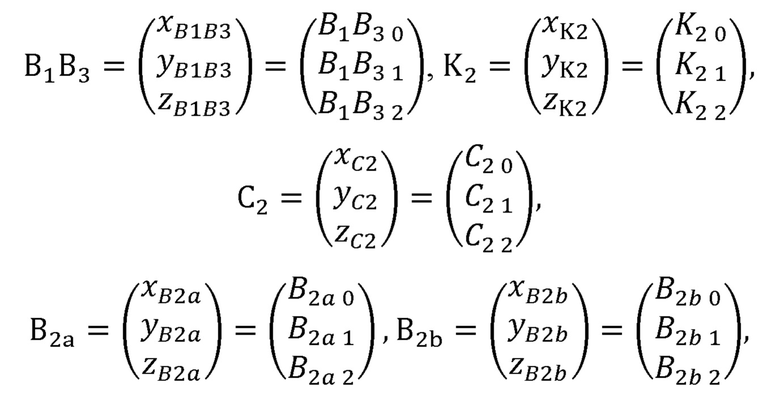
рассчитывает варианты положения В2а и B2b локтевого сустава В2 по формулам:
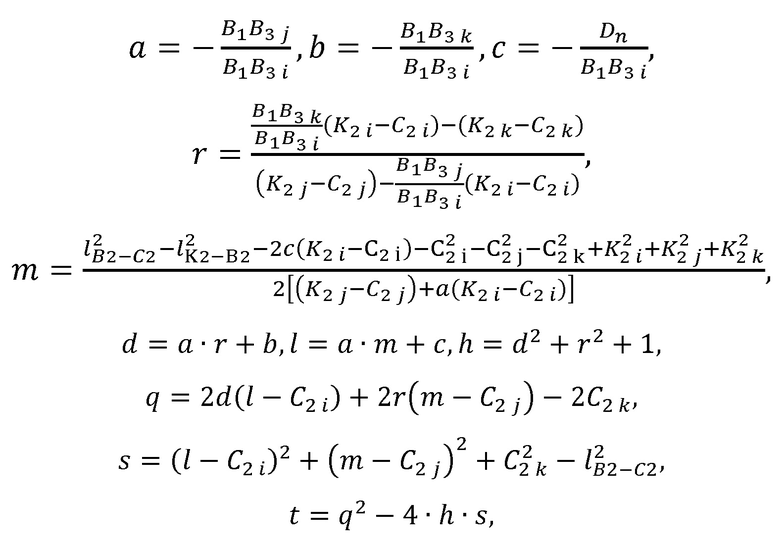
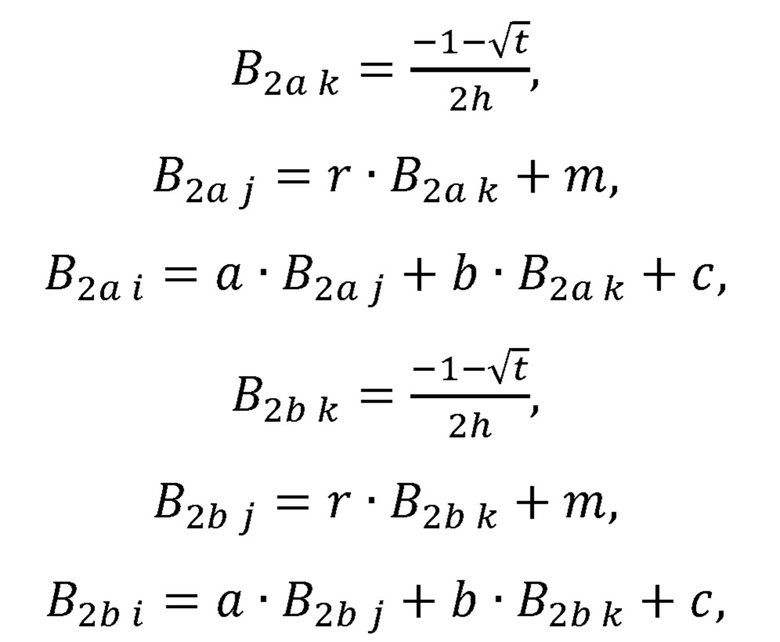
где а, b, с, r, m, d, 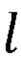 , h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
, h, q, s, t - промежуточные величины, необходимые для расчета декартовых координат точек В2а и B2b;
i, j, k - индексы, принимающие значения, определяемые следующим правилом: индекс i равен номеру ненулевой компоненты вектора B1B3 в выражении, j и k - номерам оставшихся компонент;
выбирает положение искомой точки В2 из двух возможных вариантов В2а и B2b по формуле:
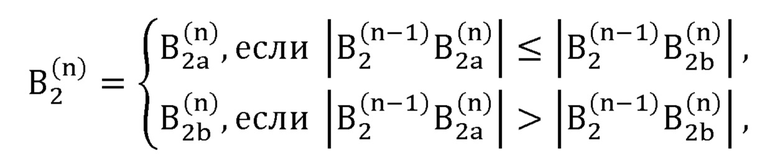
где 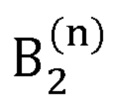 - радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисляемый на n-й итерации;
n - номер текущей итерации косвенного измерения углов поворота в суставах руки оператора;
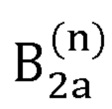 - первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- первый вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
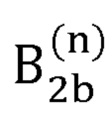 - второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
- второй вариант радиус-вектора декартовых координат сустава В2, вычисляемый на n-й итерации;
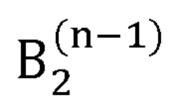 - радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации;
- радиус-вектор декартовых координат сустава В2, вычисленный на (n-1)-й итерации;
блок решения обратной задачи кинематики формирует представление Денавита-Хартенберга руки оператора, рассчитывает декартовы координаты различных точек в необходимых системах координат:
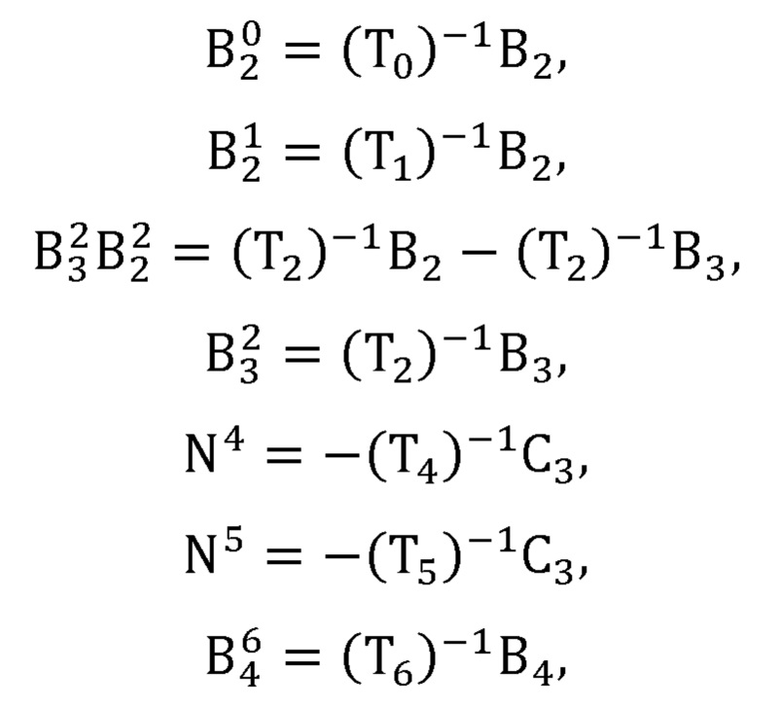
где 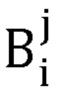 - координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
- координаты точки Bi в j-й системе координат представления Денавита-Хартенберга руки оператора;
Ti - матрица преобразования из j-й системы координат в глобальную систему координат;
Bi - координаты точки Bi в глобальной системе координат;
Ni - координаты вектора нормали N в i-й системе координат;
рассчитывает углы поворота руки оператора по формулам:
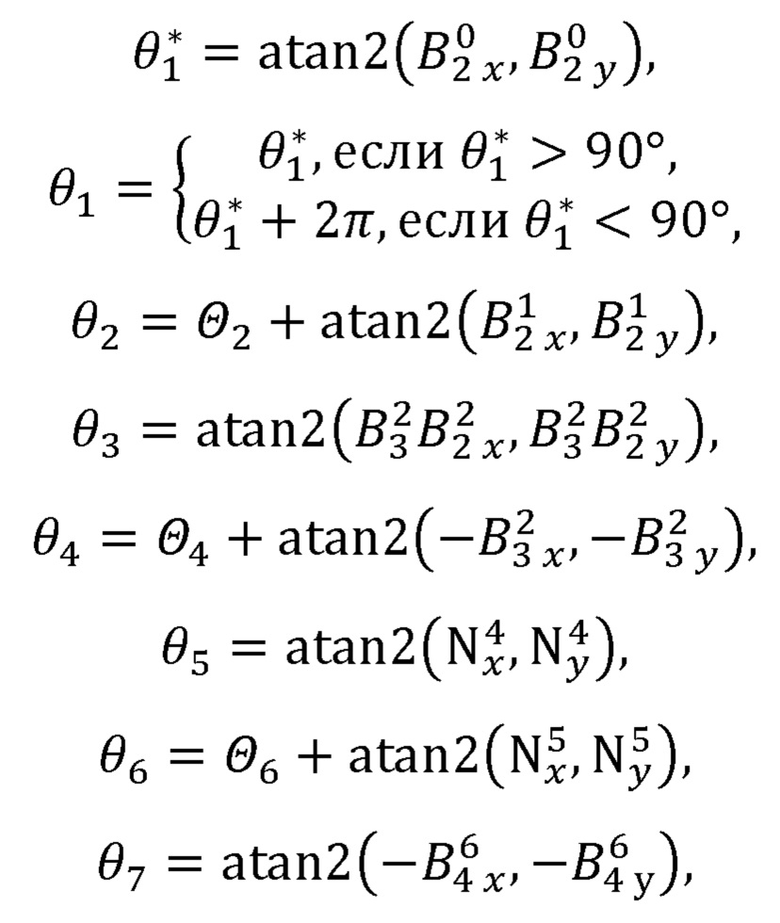
где 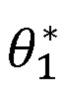 - ненормированное значение первого угла поворота руки оператора;
- ненормированное значение первого угла поворота руки оператора;
atan2(x,y) - функция арктангенса, учитывающая квадрант вычисляемого угла;
θi - i-й угол поворота руки оператора;
Θ2, Θ4, Θ6 _ константы, отдельно определяемые для каждой модели задающего устройства;
формирует вектор углов поворота руки оператора по формуле:
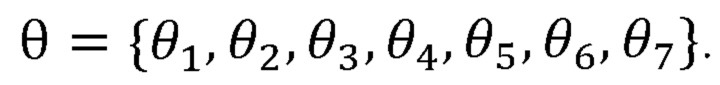
| Устройство для пропитки металлокерамических, графитовых и тому подобных изделий расплавленным металлом | 1959 |
|
SU125508A1 |
| Тарировочное устройство к торсиометрам | 1961 |
|
SU146552A1 |
| US 4986280 A1, 22.01.1991. | |||
Авторы
Даты
2019-12-25—Публикация
2018-12-25—Подача