Изобретение относится к измерительной технике для определения модуля упругости материала тонких покрытий.
Известен способ определения модуля упругости материала покрытий на изделии заключающийся в том, что в поверхность с покрытием с известной толщиной внедряют сферический индентор с известными упругими характеристиками и радиусом, записывают диаграмму изменения нагрузки от глубины внедрения и для участка диаграммы, отвечающей упругому деформированию материала покрытия, рассчитывают модуль упругости материала покрытия Епок из аналитического соотношения, связывающего обобщенный приведенный модуль упругости образца с покрытием E**, с толщиной покрытия, геометрией контакта, упругими свойствами материала основы и покрытия, а также эмпирическим параметром α:


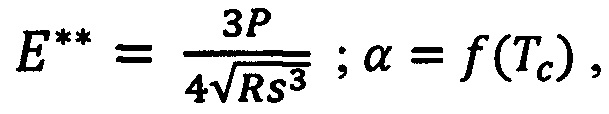
где  - модуль сдвига, s - глубина внедрения индентора в слоистое тело, h - толщина покрытия, Е* = Е/(1-μ2); Е* Е, μ - приведенные модули упругости, модули нормальной упругости и коэффициенты Пуассона образца с покрытием, индентора, подложки и покрытия, соответственно; а0 - радиус отпечатка в материале основы; «об», «и», «ос», «пок» - подстрочные индексы, обозначающие, что параметр, у которого они стоят, относится к образцу с покрытием, индентору, материалу основы или материалу покрытия, соответственно, α - экспериментально определяемая функция, учитывающая отличие характера распределения давления в отпечатке слоистого тела от Герцевского с изменением относительной толщины покрытия
- модуль сдвига, s - глубина внедрения индентора в слоистое тело, h - толщина покрытия, Е* = Е/(1-μ2); Е* Е, μ - приведенные модули упругости, модули нормальной упругости и коэффициенты Пуассона образца с покрытием, индентора, подложки и покрытия, соответственно; а0 - радиус отпечатка в материале основы; «об», «и», «ос», «пок» - подстрочные индексы, обозначающие, что параметр, у которого они стоят, относится к образцу с покрытием, индентору, материалу основы или материалу покрытия, соответственно, α - экспериментально определяемая функция, учитывающая отличие характера распределения давления в отпечатке слоистого тела от Герцевского с изменением относительной толщины покрытия  [1].
[1].
(Патент US 7 165 463 В2, от 23.01.2007).
Недостатком этого способа является низкая точность определения величины модуля упругости материала тонкого покрытия, связанные с трудностью точного определения области диаграммы нагружение - внедрение, отвечающей упругому деформированию только материала покрытия, а также низкой точностью определения функции а, учитывающей отличие характера распределения давления в контакте сферического индентора со слоистым телом от Герцевского с изменением толщины покрытия.
Известен способ определения модуля упругости материала покрытия на изделии, заключающийся в том, что измеряют толщину покрытия и модуль упругости материала основы изделия, помещают изделие в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора Виккерса в изделие, на глубину, превышающую толщину покрытия и записывают диаграмму изменения величины нагрузки с увеличением глубины внедрения индентора.
(Патент РФ №2618500, G 01N 3/42,2016 г. )
Данный способ по технической сущности и достигаемому результату наиболее близок к предложенному техническому решению и, поэтому, принят за его ближайший аналог- прототип.
Согласно этому способу измеряют толщину покрытия и модуль упругости материала основы изделия, помещают изделие в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора в изделие, на глубину, превышающую толщину покрытия, записывают диаграммы изменения величины нагрузки с увеличением глубины внедрения, строят массив данных (или функциональную зависимость) изменения параметра  значения входящих в данный параметр величин определяются при равных по величине значениях нагрузки, от относительной глубины внедрения
значения входящих в данный параметр величин определяются при равных по величине значениях нагрузки, от относительной глубины внедрения  сравнивают с теоретически рассчитанным массивом данных (или аналитическими зависимостями) изменения параметра Мтаб, для ряда дискретных значений величины контактной упругости К от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Мэкс, полученного из эксперимента, с набором значений параметра Мтаб в диапазоне от 0,2 до 1,0 значений относительной глубины внедрения индентора
сравнивают с теоретически рассчитанным массивом данных (или аналитическими зависимостями) изменения параметра Мтаб, для ряда дискретных значений величины контактной упругости К от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Мэкс, полученного из эксперимента, с набором значений параметра Мтаб в диапазоне от 0,2 до 1,0 значений относительной глубины внедрения индентора  используя следующие зависимости и обозначения:
используя следующие зависимости и обозначения:





где Ф - упруго-геометрический параметр, диапазон существования которого  для
для  t0 - толщина поверхностного слоя слоистого полупространства, моделирующего реальное слоистое тело с покрытием h;
t0 - толщина поверхностного слоя слоистого полупространства, моделирующего реальное слоистое тело с покрытием h;  - предельный радиус пятна контакта для материала основы;
- предельный радиус пятна контакта для материала основы;  - модули нормальной упругости материалов покрытия, основы (подложки) и индентора,
- модули нормальной упругости материалов покрытия, основы (подложки) и индентора,  - коэффициенты Пуассона материала основы, покрытия и индентора, h - толщина покрытия,
- коэффициенты Пуассона материала основы, покрытия и индентора, h - толщина покрытия,  - текущее значение относительной толщины покрытия, s0, sc - текущая глубина внедрения в материал основы и материал с покрытием (слоистое тело);
- текущее значение относительной толщины покрытия, s0, sc - текущая глубина внедрения в материал основы и материал с покрытием (слоистое тело);  - предельный радиус отпечатка для слоистого тела; А1, А2, А3, …Ai, B1, B2, B3, …Bj - коэффициенты двухточечной Паде аппроксиманты [2].
- предельный радиус отпечатка для слоистого тела; А1, А2, А3, …Ai, B1, B2, B3, …Bj - коэффициенты двухточечной Паде аппроксиманты [2].
Недостатком этого способа является высокая трудоемкость проведения измерительных процедур и невысокая точность рассчитываемого значения модуля упругости тонкого покрытия, связанные с необходимостью проведения экспериментального внедрения в материал основы изделия без покрытия и учета этих результатов в расчетах при определении модуля упругости материала покрытия.
Задача, решаемая в предлагаемом способе - снижение трудоемкости и повышение точности определения модуля упругости тонкого покрытия за счет обработки результатов экспериментального исследования только изделия с покрытием.
Согласно этому способу измеряют толщину покрытия и модуль упругости материала основы изделия, помещают изделие в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора в изделие, на глубину, равную толщине покрытия, записывают диаграмму внедрения (кривую нагружения) в координатах «усилие нагружения - глубина внедрения», получают массив данных параметра  сравнивают с теоретически рассчитанным массивом данных изменения параметра (Dтеор)i=[D{E*}⋅D{E*=1}] (или аппроксимирующей зависимостью Dтеор=ƒ(s/h)), для ряда дискретных значений величины контактной упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием и определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэксп, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора
сравнивают с теоретически рассчитанным массивом данных изменения параметра (Dтеор)i=[D{E*}⋅D{E*=1}] (или аппроксимирующей зависимостью Dтеор=ƒ(s/h)), для ряда дискретных значений величины контактной упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием и определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэксп, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора 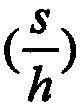 , используя следующие зависимости и обозначения:
, используя следующие зависимости и обозначения:



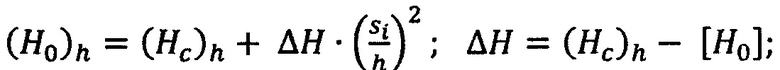

где h - толщина покрытия, s,. - текущая глубина внедрения в материал с покрытием (слоистое тело); (Hc)h - твердость покрытия, определяемая при глубине внедрения в материал с покрытием равной толщине покрытия; [H0] - твердость основы материала;  - модули нормальной упругости материалов покрытия, основы (подложки) и индентора. (D{E*})i и D{E*=1} - табулированные безразмерные значения (таблица 1) функции, теоретически определяемой по методике, изложенной в работах Воронина Н.А. [3, 4].
- модули нормальной упругости материалов покрытия, основы (подложки) и индентора. (D{E*})i и D{E*=1} - табулированные безразмерные значения (таблица 1) функции, теоретически определяемой по методике, изложенной в работах Воронина Н.А. [3, 4].

Отличительным признаком изобретения является то, что определение модуля нормальной упругости материала покрытия производят только по результатам исследования отклика изделия с покрытием (слоистое тело) на внедрение пирамидального алмазного индентора. Таким образом, предлагаемый способ позволяет существенно снизить трудоемкость и повысить точность определения модуля упругости тонкого покрытия, так как в заявляемом техническом решении осуществляется измерение модуля Юнга только по результатам экспериментального исследования изделия с покрытием, в то время как в прототипе экспериментальные данные получают в результате двух процедур инструментального внедрения - в изделие с покрытием и в изделие без покрытия.
Согласно изобретению набор значений параметра (Dтеор)i=[D{E*}i⋅D{E*=1}], рассчитываются по табулированным значениям [D{E*}i], взятым из таблицы 1 или в результате табулирования функции, теоретически определяемой по методике, изложенной в работах Воронина Н.А. [3, 4] (Теоретическая оценка композиционной и истинной твердости тонких покрытий. Трение и смазка в машинах и механизмах. 2011, №7. с. 11-21. и Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т. 23, №6. с. 583-596).
Проведенный заявителем анализ техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения, а определение из перечня выявленных аналогов прототипа, как наиболее близкого по совокупности признаков аналога, позволил выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявленном объекте, изложенных в формуле изобретения. Следовательно, заявленное изобретение соответствует требованию "новизна" по действующему законодательству.
Для проверки соответствия заявленного изобретения требованию изобретательского уровня заявитель провел дополнительный поиск известных решений, с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного изобретения, результаты которого показывает, что заявленное изобретение не следует для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения действий на достижение технического результата. Следовательно, заявленное изобретение соответствует требованию "изобретательский уровень" по действующему законодательству.
Предлагаемый способ поясняется чертежами, представленными на фиг. 1-7.
На фиг. 1 изображена диаграмма внедрения алмазного индентора в поверхность изделия с тонким покрытием, в виде зависимости изменения нагрузки Рэкс„ от величины глубины внедрения sc, полученной из экспериментального исследования. Маркеры обозначают ряд экспериментальных точек, используемых в дальнейшем для расчета переводного коэффициента, позволяющего совмещать на одном графике экспериментальные значения и теоретически рассчитываемые значения глубин внедрения.
На фиг. 2 изображена зависимость изменения параметра  от относительной величины глубины внедрения
от относительной величины глубины внедрения  алмазного индентора в основу изделия с покрытием толщиной h. Маркеры обозначают результаты расчета параметра (Dэксп)i для экспериментальных точек, указанных на фиг. 1. Здесь же приведена аппроксимирующая зависимость степенная функция и указана точность совпадения аппроксимирующей зависимости экспериментальным точкам.
алмазного индентора в основу изделия с покрытием толщиной h. Маркеры обозначают результаты расчета параметра (Dэксп)i для экспериментальных точек, указанных на фиг. 1. Здесь же приведена аппроксимирующая зависимость степенная функция и указана точность совпадения аппроксимирующей зависимости экспериментальным точкам.
На фиг. 3 изображена таблица теоретических значений параметра Dтеор для ряда значений упругого контактного параметра Е* в зависимости от значений относительной глубины внедрения  алмазного индентора в поверхность модельного слоистого материала, имитирующего изделие с покрытием.
алмазного индентора в поверхность модельного слоистого материала, имитирующего изделие с покрытием.
На фиг. 4 представлены в графическом виде зависимости изменения параметра Dтеор от относительной глубины внедрения 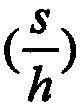 алмазного индентора для ряда дискретных значений упругого контактного параметра Е* (зависимости построены по некоторым значениям, приведенным в таблице на фиг. 3)
алмазного индентора для ряда дискретных значений упругого контактного параметра Е* (зависимости построены по некоторым значениям, приведенным в таблице на фиг. 3)
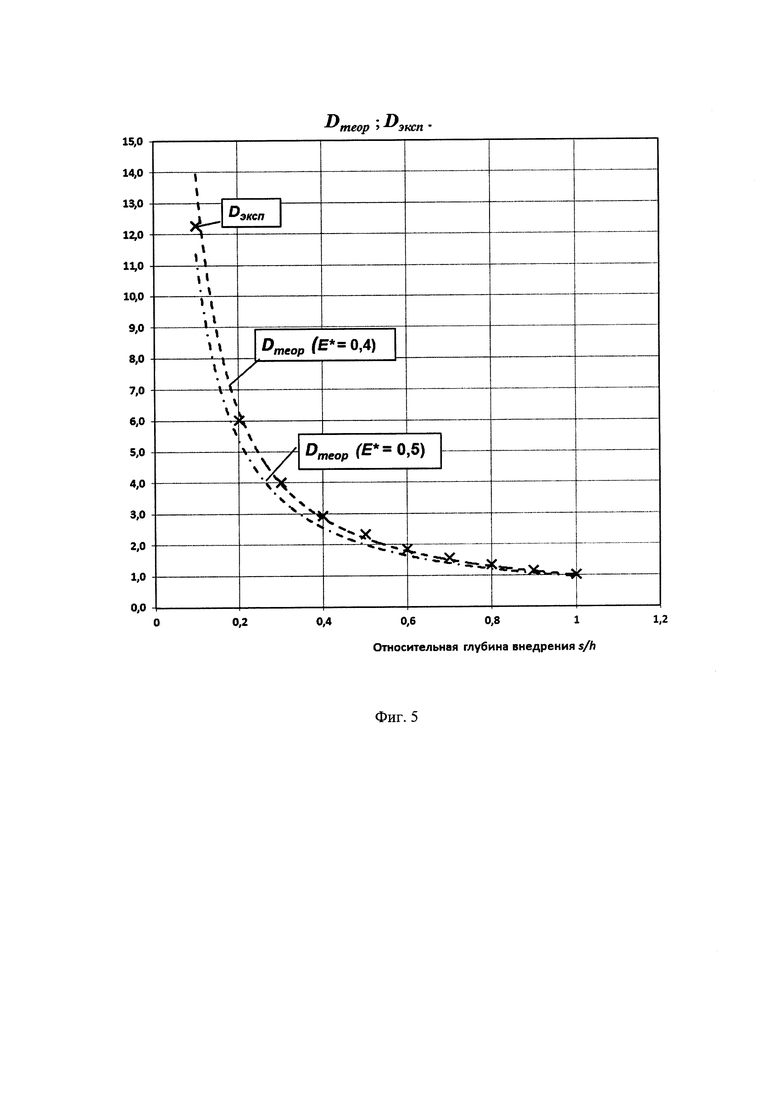
На фиг. 5 изображены зависимости изменения параметров Dэксп (см. фиг. 2) и Dтеор для двух значений Е* (см. фиг. 4) от относительной глубины внедрения 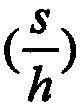 алмазного индентора в слоистое тело.
алмазного индентора в слоистое тело.
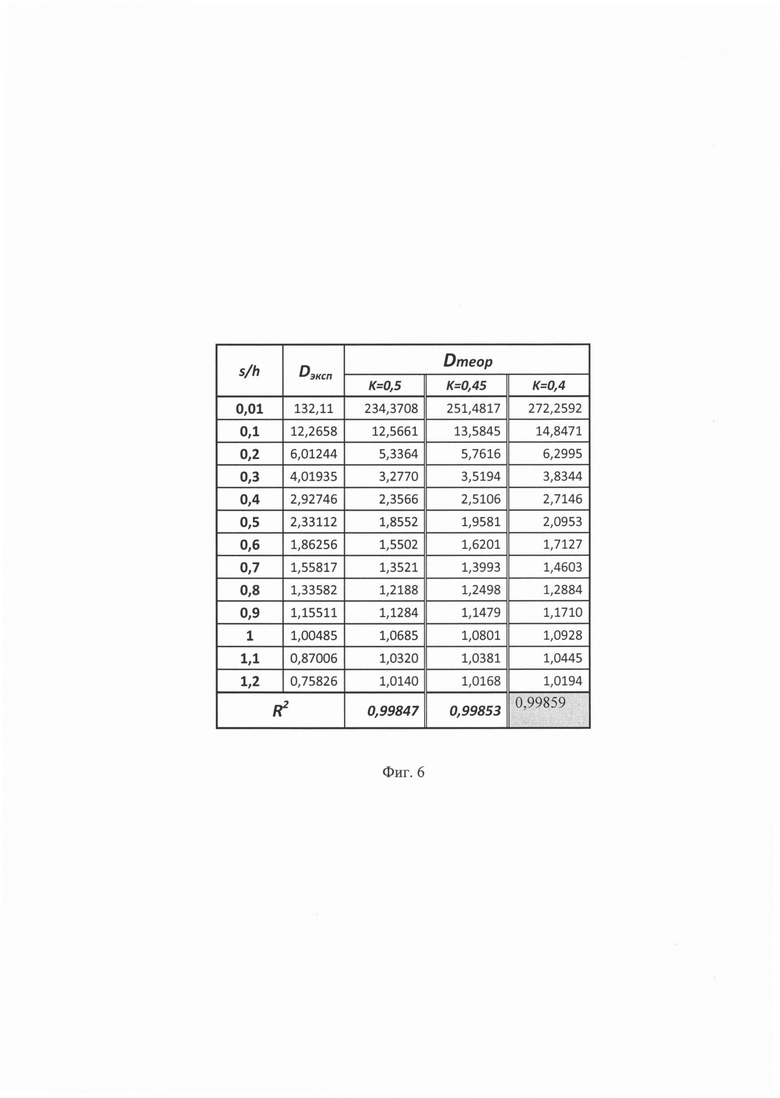
На фиг. 6 приведены результаты численного сравнения значений параметра Dэксп и теоретических параметров Dтеор для Е*=0,5, Е*=0,4 и для Е*=0,45 для диапазона изменения относительной глубины внедрения  в пределах от 0,01 до 1,0 в виде коэффициента корреляции R2 значений табличных параметров Dтеор и экспериментального параметра Dэксп,
в пределах от 0,01 до 1,0 в виде коэффициента корреляции R2 значений табличных параметров Dтеор и экспериментального параметра Dэксп,
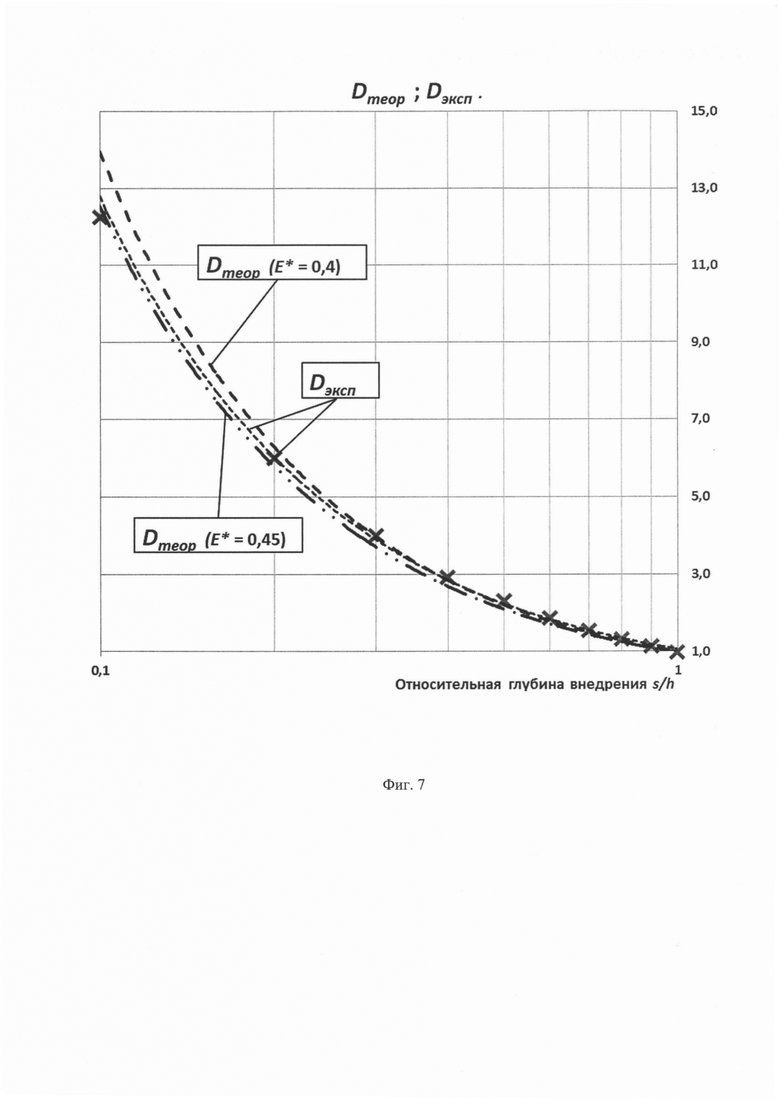
На фиг. 7 представлены результаты сравнения значений параметра Dэксп (виде экспериментальных точек и аппроксимирующей функции степенного вида) и теоретических параметров Dтеор для Е*=0,45 и Е*=0,45 от относительной глубины внедрения на графике в полулогарифмическом масштабе.
Способ определения модуля нормальной упругости тонких покрытий реализуется следующим образом.
Для исследуемой твердой поверхности с тонким покрытием (слоистой системы) измеряют толщину покрытия h. В случае использования стандартного материала в качестве подложки записывают значения модуля нормальной упругости Е0, коэффициента Пуассона μ0 и значение твердости [Н0] по Виккерсу из справочников. Если материал основы неизвестен, то производят измерение упругих характеристик и объемной твердости с использованием стандартизованных методик. Записывают известные значения упругих характеристик алмазного индентора: модуля Юнга  и коэффициента Пуассона
и коэффициента Пуассона 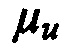 . С помощью прибора - микро- или нанотвердомера с непрерывной регистрацией нагрузки и глубины внедрения внедряют алмазный наконечник в виде четырехугольной (пирамида Виккерса) или треугольной пирамиды (пирамида Берковича) в исследуемую слоистую систему (поверхность с тонким твердым покрытием) и производят запись диаграммы «нагрузка Р - внедрение s» (см. фиг. 1). Внедрение в исследуемую поверхность производят на глубину не меньшую, чем толщина покрытия и всегда большую, чем 0,1 часть толщины покрытия.
. С помощью прибора - микро- или нанотвердомера с непрерывной регистрацией нагрузки и глубины внедрения внедряют алмазный наконечник в виде четырехугольной (пирамида Виккерса) или треугольной пирамиды (пирамида Берковича) в исследуемую слоистую систему (поверхность с тонким твердым покрытием) и производят запись диаграммы «нагрузка Р - внедрение s» (см. фиг. 1). Внедрение в исследуемую поверхность производят на глубину не меньшую, чем толщина покрытия и всегда большую, чем 0,1 часть толщины покрытия.
По экспериментальной диаграмме внедрения для слоистой системы рассчитывают значения твердости покрытия  при максимальной глубине внедрения, равной толщине покрытия, и определяют параметр
при максимальной глубине внедрения, равной толщине покрытия, и определяют параметр 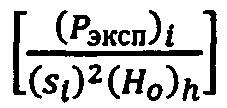 для всего диапазона нагрузки в данном испытании. Рассчитывают значения относительной величины внедрения индентора
для всего диапазона нагрузки в данном испытании. Рассчитывают значения относительной величины внедрения индентора  путем деления значений (sc)i на толщину покрытия h. Массиву значений
путем деления значений (sc)i на толщину покрытия h. Массиву значений  ставят в соответствие соответствующие значения
ставят в соответствие соответствующие значения  и называют параметром (Dэксп). Графически этот параметр (Dэксп) может быть представлен в виде набора экспериментальных точек в координатах
и называют параметром (Dэксп). Графически этот параметр (Dэксп) может быть представлен в виде набора экспериментальных точек в координатах  или аппроксимирован некоторой функцией, например полиномом или степенной функцией (см. фиг. 2).
или аппроксимирован некоторой функцией, например полиномом или степенной функцией (см. фиг. 2).
Массив значений  является конечным результатом обработки экспериментальных данных, полученных инструментальным индентированием изделия с тонким твердым покрытием (поверхностным слоем).
является конечным результатом обработки экспериментальных данных, полученных инструментальным индентированием изделия с тонким твердым покрытием (поверхностным слоем).
Известен аналитический способ определения теоретической композиционной твердости Нс поверхности твердого тела с покрытием на основе рассмотрения механики контактного взаимодействия в слоистую систему сферического индентора [3]:

где  - предельный упруго-геометрический параметр, диапазон существования которого
- предельный упруго-геометрический параметр, диапазон существования которого 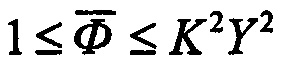 для
для  Ф - упруго-геометрический параметр, диапазон существования которого
Ф - упруго-геометрический параметр, диапазон существования которого 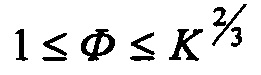 для
для 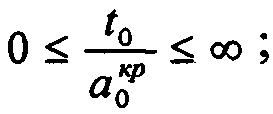 t0 - толщина поверхностного слоя слоистого полупространства, моделирующего реальное слоистое тело с покрытием h;
t0 - толщина поверхностного слоя слоистого полупространства, моделирующего реальное слоистое тело с покрытием h;  - предельный радиус пятна контакта для материала основы;
- предельный радиус пятна контакта для материала основы;  Н1, Н0 - значения микротвердости материала покрытия и основы, соответственно.
Н1, Н0 - значения микротвердости материала покрытия и основы, соответственно.
Предельный упруго-геометрический параметр  в общем случае зависит от геометрических
в общем случае зависит от геометрических  и упругих
и упругих  характеристик, а также величин твердости (Н0, Н1) компонентов слоистой системы.
характеристик, а также величин твердости (Н0, Н1) компонентов слоистой системы.
Предельный упруго-геометрический параметр  и связь модельного слоя t0 с толщиной покрытия в области глубин внедрения больших, чем 0,1 толщины покрытия могут быть рассчитаны по следующим аналитическим зависимостям:
и связь модельного слоя t0 с толщиной покрытия в области глубин внедрения больших, чем 0,1 толщины покрытия могут быть рассчитаны по следующим аналитическим зависимостям:

С учетом зависимости (2) выражение (1) для определения композиционной твердости слоистого тела в диапазоне глубин внедрения от 0,1 до 1,0 величины  может быть преобразовано к виду:
может быть преобразовано к виду:

Параметр Т в уравнении (3) зависит от относительной глубины внедрения и от величины контактного модуля упругости слоистой системы Е*. Величина H0 для идеальных компактных твердых тел и при моделировании принимается равной объемной твердости исследуемого материала. На практике при инструментальном индентировании объемных материалов установлен эффект повышения твердости с уменьшением глубины внедрения (так называемый размерный эффект). Одна из основных причин влияния размерного эффекта на сопротивление материала пластической деформации заключается в уровне удельной площади деформируемой поверхности [5].
Учесть влияние размерного эффекта на величину материал основы при индентировании слоистых тел можно, применив структуру уравнения (3) к однородному материалу, для которого параметр Г рассчитывается при значении величины Е*=1, то есть рассматривать однородное тело как слоистое тела с покрытием, у которого модуль упругости равен модулю упругости материала основы:

где (H0)h - твердость подложки при глубине внедрения индентора, равной толщине покрытия.
При индентировании слоистых покрытий с твердыми защитными поверхностными покрытиями также установлен эффект повышения напряжения в пластической области материала основы при индентировании пирамидального наконечника, за счет стеснения (дополнительного уплотнения) материала подложки твердым поверхностным слоем [6]. Эффект стеснения приводит к повышению значения твердости материала основы под покрытием, по сравнению с исходной объемной твердостью материала.
Учет указанных эффектов - размерного эффекта и эффекта стеснения -учитывается в параметре (H0)h следующим образом:
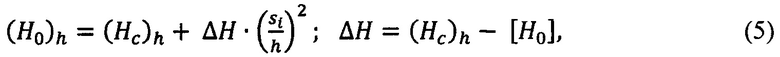
где (Hc)h - твердость покрытия, определяемая при глубине внедрения в материал с покрытием равной толщине покрытия; [H0] - объемная твердость основы материала (по справочнику на этот материал или измеренная по известной стандартной методике). Первый член уравнения (5) учитывает вклад размерного эффекта на глубине внедрения, равной толщине покрытия, а второй член уравнения (5) учитывает эффект стеснения материала основы при инструментальном индентировании с увеличением глубины внедрения от нуля до глубины, равной толщине покрытия.
Таким образом, уравнение (3) можно переписать в виде

Твердость слоистого тела может быть представлена в виде

Тогда параметры (Dэксп)i=(Dтеор)i, рассчитываемые при (Рс)эксп=(Рс)теор=(Р0)теор, можно вычислять по следующим выражениям


где в правая часть уравнения (6) представляет собой массив данных экспериментальных точек кривой нагружения диаграммы внедрения, а уравнения (7) массив данных точек теоретической кривой нагружения диаграммы внедрения при одинаковом значении относительной глубины внедрения  .
.
Сопоставляя массив значений Dэксп, полученных из эксперимента инструментального внедрения для исследуемого изделия с покрытием, с теоретически рассчитываемым массивом Dтеор, можно определить численно или графически контактный модуль упругости Е* (см. фиг. 5, 6 и 7).
Заявляемый способ определения модуля Юга материала покрытия предполагает проведение сопоставления экспериментальных Dэксп и теоретически рассчитываемых параметров Dтеор при значения относительных глубин внедрения  в диапазоне 0,1 до 1,0. Диапазон значений параметра
в диапазоне 0,1 до 1,0. Диапазон значений параметра  выбран не случайно. В диапазоне параметра
выбран не случайно. В диапазоне параметра  от 0 до 0,1 велика вероятность повышенной погрешности измерения глубины внедрения индентора при инструментальном индентировании, как из-за малости измеряемых линейных величин, так и за счет ошибки оценки точки начального касания индентора с исследуемой поверхности, принимаемой на диаграмме за нулевую точку. При значениях параметра
от 0 до 0,1 велика вероятность повышенной погрешности измерения глубины внедрения индентора при инструментальном индентировании, как из-за малости измеряемых линейных величин, так и за счет ошибки оценки точки начального касания индентора с исследуемой поверхности, принимаемой на диаграмме за нулевую точку. При значениях параметра  близких и больших 1,0, которые характеризуют физическое проникновение индентора на всю толщину покрытия, вероятность изменения характера деформирования становится значительна, за счет наличия границы раздела между покрытием и основой, представляющего собой протяженный макродефект, и измененных физико-механических характеристик материала покрытия и материала основы в прилегающих слоях к границе раздела, за счет термо-химических процессов синтеза покрытия в технологическом процессе получения последнего.
близких и больших 1,0, которые характеризуют физическое проникновение индентора на всю толщину покрытия, вероятность изменения характера деформирования становится значительна, за счет наличия границы раздела между покрытием и основой, представляющего собой протяженный макродефект, и измененных физико-механических характеристик материала покрытия и материала основы в прилегающих слоях к границе раздела, за счет термо-химических процессов синтеза покрытия в технологическом процессе получения последнего.
Из выражения для контактного модуля упругости Е* можно определить модуль Юнга материала покрытия:
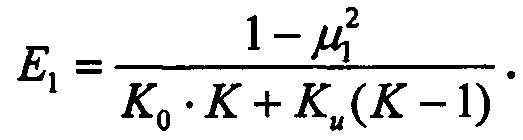
Пример. Для примера было произведено определение модуля Юнга материала слоистого тела, которое было использовано в изобретении-прототипе. Это было покрытие из нитрида алюминия, нанесенное магнетронным способом толщиной 5 мкм на нержавеющую сталь 12Х18Н10Т. Модуль Юнга и коэффициент Пуассона алмазной пирамиды Виккерса были  Упругие характеристики материала основы изделия Е0=180 ГПа, μ0=0,3. Принято было, что коэффициент Пуассона материала покрытия равен материалу основы. Запись диаграмм внедрения в поверхность с покрытием производилось на микроиндентометре МТИ 5 с достижением максимальной нагрузки в 2,5 Н (см. фиг. 1). Твердость покрытия при глубине внедрения 5 мкм, рассчитанная по диаграмме внедрения, составила 2,6 ГПа (260 кгс/мм2). Объемная твердость материала основы была измерена приборе ПМТЗ при максимальной нагрузке в 5 Н. Она составила 2 ГПа (200 кгс/мм2).
Упругие характеристики материала основы изделия Е0=180 ГПа, μ0=0,3. Принято было, что коэффициент Пуассона материала покрытия равен материалу основы. Запись диаграмм внедрения в поверхность с покрытием производилось на микроиндентометре МТИ 5 с достижением максимальной нагрузки в 2,5 Н (см. фиг. 1). Твердость покрытия при глубине внедрения 5 мкм, рассчитанная по диаграмме внедрения, составила 2,6 ГПа (260 кгс/мм2). Объемная твердость материала основы была измерена приборе ПМТЗ при максимальной нагрузке в 5 Н. Она составила 2 ГПа (200 кгс/мм2).
Результаты обработки экспериментальных диаграмм внедрения представлены в графическом виде (см. фиг. 2). Там же приведена аппроксимирующая зависимость степенного вида для параметра Dэксп в виде  полученная по экспериментальным точкам. Точность соответствия аппроксимирующей зависимости демонстрационным экспериментальным точкам равна R2=0,9953.
полученная по экспериментальным точкам. Точность соответствия аппроксимирующей зависимости демонстрационным экспериментальным точкам равна R2=0,9953.
Теоретические расчеты параметра (Dтеор)i представлены в таблице на фиг. 3 в виде массива данных и в графическом виде (см. фиг. 4) для ряда типовых значений контактного модуля упругости Е*.
Оценить совпадение экспериментально определенного параметра Dэксп с теоретически рассчитанным значением параметра Dтеор можно графически (см. фиг. 5) или по степени корреляции массива данных параметра Dэксп массиву расчетных данных Dтеор (см. фиг. 6). Из графиков, приведенных на фиг. 5 наглядно видно, что экспериментальные точки параметра Dэксп располагается между двумя кривыми, построенными по значениям параметра Dтеор для контактных модулей упругости K=0,5 и K=0,4. Если рассматривать аргумент полученных функциональных зависимостей в диапазоне от 0,1 до 1,0, то экспериментально полученному параметру Dэксп соответствует значение контактного модуля упругости, близкое к 0,4-0,45. Если судить по значению коэффициента корреляции Пирсона R2, то несколько лучшее соответствие экспериментальному массиву данных соответствует теоретически рассчитанный массив данных для K=0,40 (фиг. 6 и 7).
Расчет модуля Юнга покрытия по контактному модулю упругости слоистой системы E*=0,40 дал значение Е1=355 ГПа, что близко к значению, указанному в изобретении-прототипе, где Е1=342 ГПа.
Результаты экспериментальной проверки свидетельствуют о пригодности предлагаемого способа для практического использования. Следовательно, заявленное изобретение соответствует требованию "промышленная применимость" по действующему законодательству.
Литература
1. Герцевская эпюра распределения давления в контакте - эллиптический закон изменения давления в контакте при внедрении сферического штампа в поверхность однородного компактного материала, рассчитываемый по известным формулам Герца (см. Джонсон К. Механика контактного взаимодействия. М.: Мир, 1989. - 510 с.) Для слоистых твердых тел эпюра давления отличается от эллиптической и тем сильнее, чем большее различие в механических характеристиках материала покрытия и материала основы. Большинство исследователей используют эмпирические зависимости (как это сделано в аналоге в Патенте US 7165463) для учета этого различия.
2. Коэффициенты двухточечной Паде-аппроксиманты, рассчитываются по известным формулам (Н.А. Воронин. Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т. 23, №6. с. 583-596).
3. Воронин Н.А. Теоретическая оценка композиционной и истинной твердости тонких покрытий. Трение и смазка в машинах и механизмах. 2011, №7. с. 11-21.
4. Воронин Н.А. Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т. 23, №6. с. 583-596.
5. В.М. Матюнин. Индентирование в диагностике механических свойств материалов. М:, МЭИ, 2015, - 288 с.
6. Воронин Н.А. Моделирование диаграммы внедрения для топокомпозитов. Проблемы машиностроения и надежности машин. 2018, №3.




Изобретение относится к измерительной технике для определения модуля упругости материала тонких покрытий. Сущность: измеряют толщину покрытия и модуль упругости материала основы изделия, помещают изделие в микротвердомер, с помощью которого производят внедрение алмазного пирамидального индентора в изделие на глубину, равную толщине покрытия, записывают диаграмму внедрения (кривую нагружения) в координатах «усилие нагружения - глубина внедрения», получают массив данных параметра  сравнивают с теоретически рассчитанным массивом данных изменения параметра (Dтеор)i=[D{E*}⋅D{E*=1}] (или аппроксимирующей зависимостью Dтеор=ƒ (s/h)) для ряда дискретных значений величины контактной упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, и определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэксп, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора
сравнивают с теоретически рассчитанным массивом данных изменения параметра (Dтеор)i=[D{E*}⋅D{E*=1}] (или аппроксимирующей зависимостью Dтеор=ƒ (s/h)) для ряда дискретных значений величины контактной упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, и определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэксп, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора  используя зависимости. Технический результат: снижение трудоемкости и повышение точности определения модуля упругости тонкого покрытия. 1 табл., 7 ил.
используя зависимости. Технический результат: снижение трудоемкости и повышение точности определения модуля упругости тонкого покрытия. 1 табл., 7 ил.
Способ определения модуля упругости материала покрытия на изделии, заключающийся в том, что изделие, на поверхности которого имеется жестко связанное с материалом изделия покрытие известной толщины и которое имеет известное значение модуля упругости и объемной твердости, помещают в прибор-твердомер, с помощью которого производят нагружение путем внедрения алмазного пирамидального наконечника в поверхность изделия с покрытием на глубину, близкую толщине покрытия, записывают диаграмму изменения величины нагрузки с увеличением глубины внедрения, отличающийся тем, что по диаграмме «нагрузка - внедрение» получают массив данных или функциональную зависимость изменения параметра  от относительной глубины внедрения
от относительной глубины внедрения  сравнивают с теоретически рассчитанным массивом данных или аналитическими зависимостями изменения параметра Dтеор для ряда дискретных значений контактного модуля упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэкс, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора
сравнивают с теоретически рассчитанным массивом данных или аналитическими зависимостями изменения параметра Dтеор для ряда дискретных значений контактного модуля упругости Е* от относительной глубины внедрения индентора в поверхность модели слоистого тела, имитирующего поверхность изделия с покрытием, определяют модуль нормальной упругости материала покрытия Е1 по результатам максимального совпадения значений параметра Dэкс, полученного из эксперимента, с набором значений параметра Dтеор в диапазоне от 0,1 до 1,0 значений относительной глубины внедрения индентора 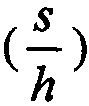 , используя следующие зависимости и обозначения:
, используя следующие зависимости и обозначения:

 i=1…n;
i=1…n; 
 (Dтеор)i=[(D{E*})i⋅D{E*=1}];
(Dтеор)i=[(D{E*})i⋅D{E*=1}];
i=1…n;  (E*)j=0,1…1,0; j=1…m;
(E*)j=0,1…1,0; j=1…m;
 ΔH=(Hc)h-[H0];
ΔH=(Hc)h-[H0];


где h - толщина покрытия,
si - текущая глубина внедрения в материал с покрытием (слоистое тело);
(Hc)h - твердость покрытия, определяемая при глубине внедрения в материал с покрытием, равной толщине покрытия;
[Н0] - твердость основы материала;
Е1, Е0, Eu - модули нормальной упругости материалов покрытия, основы (подложки) и индентора;
(D{E*})i и D{E*=1} - коэффициенты, в качестве которых использованы табличные табулированные безразмерные значения

| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА ПОКРЫТИЯ НА ИЗДЕЛИИ | 2016 |
|
RU2618500C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК МОДИФИЦИРОВАННОГО ПОВЕРХНОСТНОГО СЛОЯ МАТЕРИАЛА ИЗДЕЛИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2646442C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА ПОКРЫТИЯ НА ИЗДЕЛИИ | 2012 |
|
RU2489701C1 |
| US 20100024534 A1, 04.02.2010. | |||
Авторы
Даты
2019-03-29—Публикация
2018-05-23—Подача