Изобретение относится к измерительной технике для определения адгезионной прочности тонких защитных покрытий на изделиях машиностроения.
Известен способ определения адгезионной прочности покрытий, заключающийся в том, что в поверхность образца с покрытием известной толщины внедряют сферический индентор с известными упругими характеристиками и радиусом, осуществляют на поверхности серию отпечатков при дискретно возрастающей от отпечатка к отпечатку нормальной нагрузкой, разрезают образец в плоскости нахождения центра отпечатка, определяют с помощью оптической микроскопии отпечаток, в котором впервые обнаруживается отслаивание покрытия, фиксируют значение нагрузки, при которой был получен отпечаток с отслоением, как критическую нагрузку, методом конечных элементов моделируют процесс внедрения сферического индентора при критической нагрузке, определяют величину нормальных растягивающих напряжений на границе раздела покрытие - основной материал, которые считают ответственными за отслаивание покрытия, а значение которых принимают за величину адгезионной прочности.
(Патент US 6581441 В1 от 24.06 2003) Недостатками этого способа является высокая погрешность определения величины адгезионной прочности покрытия, связанная с дискретностью прилагаемой нагрузки при индентировании и с не учетом вклада в определямую величину адгезионной прочности остаточных напряжений, которые характерны для тонких покрытий, получаемых в вакууме.
Известен способ определения адгезионной прочности покрытия к основе, согласно которому в поверхность изделия с покрытием известной толщины внедряют пирамидальный жесткий индентор, записывают диаграммы внедрения после двух последовательных циклов индентирования в одно и тоже место при одинаковых условиях нагружения, рассчитывают площади диаграмм внедрения, рассчитывают разницу между площадями, определяют радиус круговой трещины области расслоения и рассчитывают значение адгезионной прочности покрытия к подложке по известной формуле.
(Xie Н., Huang Н. Characterization of the interfacial strength of SiNx/GaAs film/substrate systems using energy balance in nanoindentation. Journal of Materials Research. 2013, V. 28, No. 23, P. 3137-3145)
Данный способ по технической сущности и достигаемому результату наиболее близок к предложенному техническому решению и, поэтому, принят за его ближайший прототип.
Согласно этому способу в поверхность с покрытием известной толщины внедряют пирамидальный жесткий индентор, записывают диаграммы внедрения после двух последовательных циклов индентирования в одно и тоже место при одинаковых условиях нагружения, рассчитывают площади диаграмм внедрения, вычисляют разницу между площадями, определяют радиус круговой трещины области расслоения исходя из модели деформирования упругой мембраны с учетом упругого деформирования индентором материала покрытия в месте контакта и рассчитывают значение адгезионной прочности G покрытия по формуле:
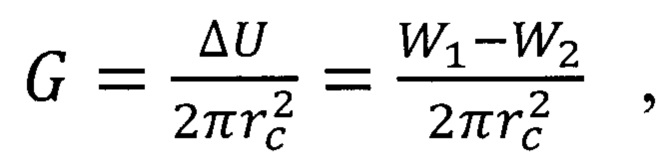
где ΔU - работа, затрачиваемая на межфазное расслоение; rc - радиус расслоения; W1 - площадь диаграммы внедрения первого цикла индентирования; W2 - площадь диаграммы внедрения второго цикла индентирования;
Недостатком этого способа является невысокая точность определения адгезионной прочности тонких покрытий, связанная с тем, процесс индентирования произходит в условиях упругого деформирования слоистого тела и не учитывается вклад остаточных напряжений в покрытии на величину рассчитываемой адгезионной прочности.
Задача, решаемая в предлагаемом способе, заключается в обеспечении возможности с высокой точностью определять адгезионную прочность тонких покрытий за счет исключения вклада остаточных напряжений в работу деформирования, направлемую на межфазное разрушение системы покрытие-подложка в процессе индентирования слоистой системы.
Решение поставленной задачи достигается за счет того, что предложен способ определения адгезионной прочности покрытия, заключающийся в том, что изделие, на поверхности которого имеется покрытие известной толщины, представляет собой слоистое тело, состоящее из основы (подложки) и покрытия, материалы которых (подложки и покрытия) имеют известные значения модулей упругости и твердостей, помещают в прибор-твердометр, с помощью которого производят внедрение алмазного пирамидального наконечника в поверхность покрытия в виде двух повторных циклов индентирования, последовательно производимых в одно и тоже место, на глубину, обеспечивающую отслаивание покрытия при разгружении в первом цикле индентирования, записывают диаграмму внедрения, представляющую собой графики изменения глубины внедрения при возрастании нагрузки и затем при снижении нагрузки, фиксируют значение конечной нагрузки при нагружении Р1 для первого цикла внедрения, фиксируют при разгружении значение нагрузки Р2 в районе 5% от значения Р1 в первом цикле деформирования, фиксируют значение конечной нагрузки при нагружении Р3 в районе 50% от значения Р1 во втором цикле нагружения, фиксируют значение глубины внедрения при разгружении до нуля во втором цикле индентирования и определяют по известной методике координаты точки на кривой разгружения второго цикла индентирования, в которой отсутствуют остаточные напряжения. Через эту точку по известной методике на диаграмме внедрения строят кривую нагружения только покрытия без остаточных напряжений, которая пересекает кривую разгружения первого цикла индентирования в некоторой точке, через которую можно провести кривую упругопластического нагружения исследуемого слоистого тела без остаточных напряжений в покрытии. Рассчитывают по известной методике и строят на экспериментальной диаграмме внедрения теоретическую диаграмму внедрения для идеального модельного слоистого тела с механическими характеристиками, соответствующими исследуемому топокомпозиту. Фиксируют значения координат точки пересечения теоретической кривой нагружения с кривой разгрузки первого цикла индентирования, которая в этом месте совпадает с кривой разгрузки теоретической диаграммы внедрения. Определяют площадь фигуры, образуемой теоретической кривой нагружения слоистого тела, кривой упругопластического деформирования исследуемого топокомпозита без остаточных напряжений в покрытии и частью теоретической кривой разгрузки. Фиксируют значение площади как значение работы, затраченной на межфазное разрушение границы раздела слоистого тела (ΔU), рассчитывают по известной формуле значение радиуса круговой трещины, ограничивающей область отслоения покрытия от основы и вычисляют значение величины адгезионной прочности G покрытия к основе по известной формуле.
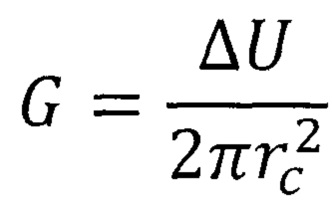
где ΔU - работа, затрачиваемая на межфазное расслоение; rc - радиус расслоения.
При этом теоретически кривая нагружения и разгружения слоистого тела рассчитывается по формулам
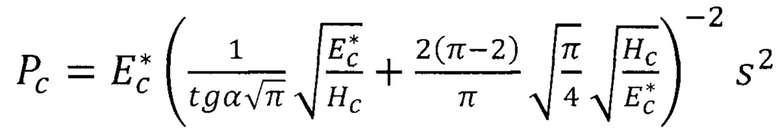 и
и
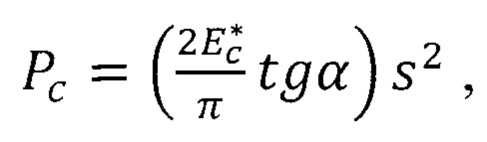
где 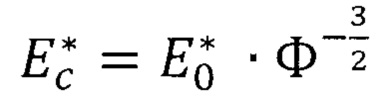 ,
, 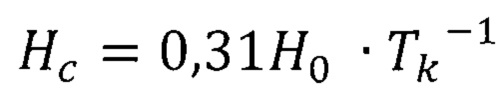 ,
,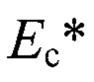 - эффективный модуль упругости слоистого тела;
- эффективный модуль упругости слоистого тела; 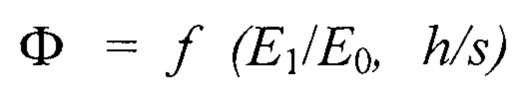 - упруго-геометрический параметр слоистой системы; h - толщина покрытия;
- упруго-геометрический параметр слоистой системы; h - толщина покрытия; 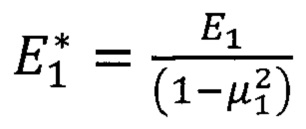 ,
, 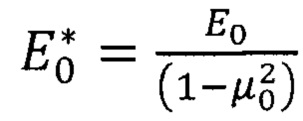 - приведенный модуль упругости материала покрытия и материала основы, соответственно; Е1, Е0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы;
- приведенный модуль упругости материала покрытия и материала основы, соответственно; Е1, Е0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы; 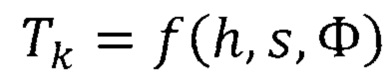 - весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
- весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
Радиус круговой трещины при межфазном разрушении адгезионной связи покрытия с подложкой в процессе индентирования рассчитывается из условия линейной связи величины центральной нагрузки (нагрузки на индентор) и прогиба покрытия как мембраны по оси действия силы по известной формуле:
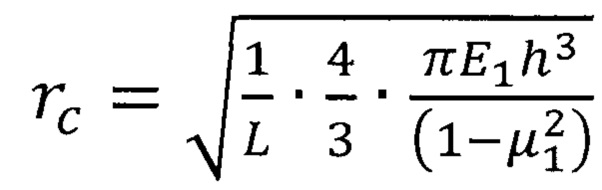
где rc - радиус круговой трещины, L - жесткость покрытия как упругой мембраны..
Сущность предлагаемого способа заключается в том, что изделие с покрытием рассматривают как слоистое тело, у которого при индентировании в процессе нагружения происходит межфазное расслоение по границе покрытие-подложка, энергия которого рассчитывается как разница между энергиями, затрачиваемыми на упругопластическоое деформирование идеального слоистого тела и исследуемиого слоистого тела без остаточных напряжений в покрытии (Н.А. Воронин. Адгезионная прочность тонких покрытий из нитрида алюминия в топокомпозите системы АШ-Д16Т. Проблемы машиностроения и автоматизации. 2023, в печати.), что позволяет с большей точностью и объективностью определить степень адгезионной связи покрытия к основе.
Отличительным признаком изобретения является то, что определение адгезионной прочности покрытия производят без учета вклада остаточных напряжений в покрытии, которые изменяют истинное значение адгезионной прочности в зависимости от вида и уровня остаточных напряжений в покрытии.
Таким образом, предлагаемый способ позволяет существенно повысить точность и объективность определения адгезионной прочности тонких покрытий за счет исключения вклада остаточных напряжений в покрытии, в то время как в прототипе рассчитываемая величина адгезионной прочности включает вклад остаточных напряжений в энергию, затрачиваемую на межфазное разрушение связи покрытия к подложке во время нагружения индентором поверхности слоистого тела..
Проведенный заявителем анализ техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения, а определение из перечня выявленных аналогов прототипа, как наиболее близкого по совокупности признаков аналога, позволил выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявленном объекте, изложенных в формуле изобретения. Следовательно, заявленное изобретение соответствует требованию "новизна" по действующему законодательству.
Для проверки соответствия заявленного изобретения требованию изобретательского уровня заявитель провел дополнительный поиск известных решений, с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного изобретения, результаты которого показывает, что заявленное изобретение не следует для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения действий на достижение технического результата. Следовательно, заявленное изобретение соответствует требованию "изобретательский уровень" по действующему законодательству.
Предлагаемый способ поясняется чертежами, представленными на фиг. 1-5
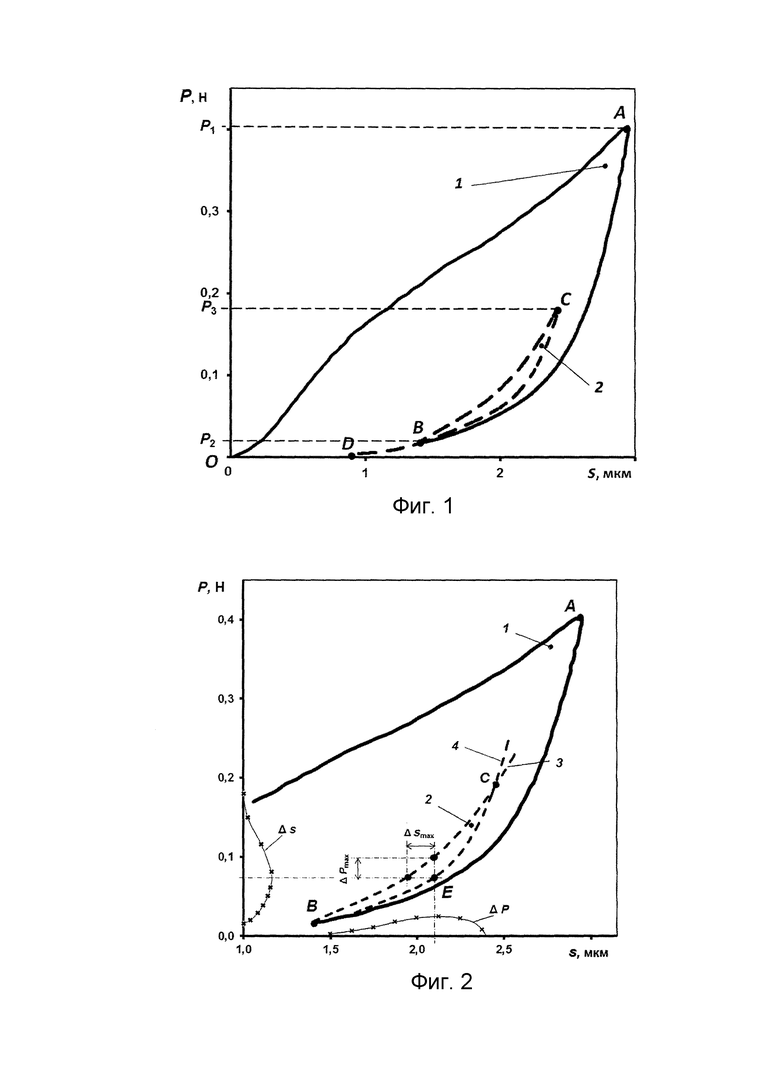
Фиг 1. Экспериментальная диаграмма внедрения с повторным циклом индентирования: 1 - первый цикл индентирования; 2 - второй цикл индентирования.
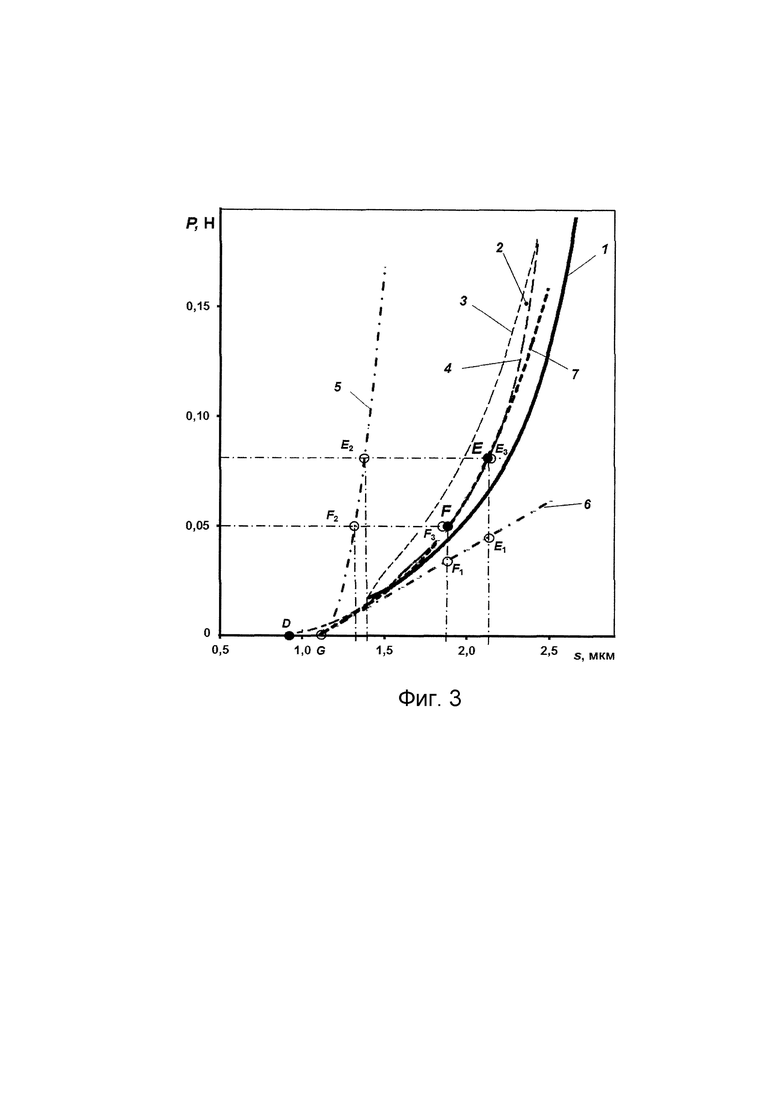
Фиг. 2. Анализ кривых диаграммы внедрения с повторным циклом индентирования в исследуемый топокомпозит.1 - первый цикл индентирования;2 - второй цикл индентирования, 3 - линия тренда кривой ВС; 4 - линия тренда кривой ВЕС
Фиг. 3. Определение расположения и координат начала кривой нагружения покрытия без остаточных напряжений. 1 - кривая разгрузки первого цикла индентирования; 2 - диаграмма внедрения второго цикла индентирования, 3 и 4 - кривые нагружения и разгружения второго цикла индентирования, соответственно; 5 - кривая упругого деформирования материала покрытия при индентировании; 6 - прямая упругого деформирования покрытия как мембраны; 7 - кривая упругого нагружения покрытия без остаточных напряжений
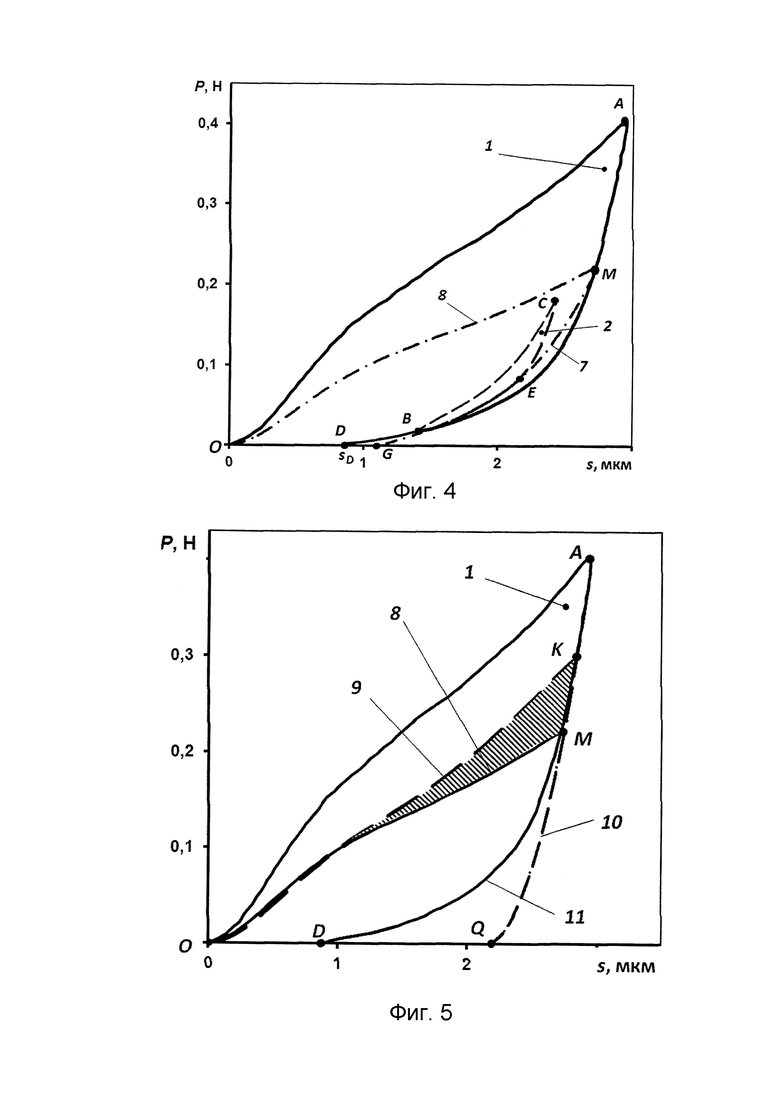
Фиг. 4. Определение вида и расположения кривой упругопластического деформирования слоистого тела без остаточных напряжений в покрытии: 1 -диаграмма внедрения первого цикла индентирования; 2 - диаграмма внедрения второго цикла индентирования; 7 - кривая упругого деформирования покрытия без остаточных напряжений; 8 - кривая упругопластического деформирования топокомпозита без остаточных напряжений в покрытии.
Фиг. 5. Расчетная схема определения работы, затрачиваемой на межфазное разрушение: 1 - диаграмма внедрения первого цикла индентирования; 8 - кривая упругопластического деформирования топокомпозита без остаточных напряжений в покрытии; 9 - теоретическая кривая нагружения упругопластического деформирования топокомпозита; 10 - теоретическая кривая разгрузки топокомпозит; 11 - экспериментальная кривая разгрузки топокомпозита первого цикла индентирования.
Способ определения адгезионной прочности напряженных тонких покрытий реализуется следующим образом.
Для исследуемого изделия с тонким твердым покрытием на пластичной подложке измеряют толщину покрытия h. В случае использования стандартного материала в качестве подложки записывают значения модуля нормальной упругости E0, коэффициента Пуассона μ0 из справочника. Если материал основы неизвестен, то производят измерение упругих характеристик и микротвердости твердости с использованием стандартных методик. Определение модуля упругости материала покрытия производят по одной из методик, описанной в технической и научной литературе (см. например, стандарт ISO (International Standard) 14577-4:2007). Коэффициент Пуассона материала покрытия записывают из известных опубликованных в научной литературе значений или принимают равной материалу основы. С помощью прибора - микро- или нанотвердометра с непрерывной регистрацией нагрузки и глубины внедрения внедряют алмазный наконечник в виде четырехугольной (пирамида Виккерса) или треугольной пирамиды (пирамида Берковича) в исследуемое слоистое тело (поверхность с тонким твердым покрытием - топокомпозит) на глубину, обеспечивающую межфазное отслаивание покрытия при разгружении и записывают экспериментальную диаграмму внедрения в координатах «нагрузка Р - внедрение 5». Диаграмма внедрения представляет собой два графика изменения глубины внедрения «s» при возрастании нагрузки «Р» и затем при снижении нагрузки, полученная в результате двух циклов индентирования (фиг. 1). Первый цикл индентирования состоит в нагружении до некоторой конечной нагрузки Р1 и разгружении индентора до величины нагрузки Р2, равной не более 5% величины предельной нагрузки Р1 при нагружении. Второй цикл индентирования осуществляется непосредственно сразу после окончания первого цикла и заключается во внедрении индентора в тот же отпечаток путем нагружения индентора до величины конечной нагрузки Р3, обеспечивающей значимое чисто упругое деформирование (прогиб) ранее (на этапе первичного цикла индентирования) отслоившегося от подложки покрытия. Как правило, значение Р3 не превышает величины 50% от величины Р1. Затем в рамках второго цикла индентирования следует полное снятие нагрузки с индентора вплоть до значения равного нулю. Координаты пересечения кривой разгрузки второго цикла деформирования указывают на величину остаточной глубины отпечатка в данном испытании. Эта глубина фиксируется (см. фиг. 1, точка D) и обозначает глубину отпечатка для топокомпозита с напряженным покрытием, то есть покрытием с остаточными напряжениями, полученными в результате предшествующей технологической операции изготовления топокомпозита. Величина конечной нагрузки Р1 выбирается из условия достижения максимального значения глубины внедрения, при котором на кривой разгружения диаграммы внедрения единичного цикла индентирования отмечается характерная нелинейность конца кривой разгружения и при этом отсутствуют видимые повреждения (трещины и сколы) поверхности покрытия. Обнаружение разрушений и повреждений в зоне отпечатка является основанием для отказа от применимости описываемого способа определения адгезионной прочности.
Наличие указанного выше характерного криволинейного вида конца кривой разгружения объясняется значительным различием пластических и упругих характеристик материалов подложки и покрытия (см. Abdul-Baqi A., Van der Giessen Е. Delamination of a strong film from a ductile substrate during indentation unloading //Journal of Materials Research. 2001. V. 16. N. 5. P. 1396-1407). Такой вид диаграмм внедрения связан с тремя параллельно идущими процессами, протекающими в процессе упругопластического деформирования индентором слоистой системы (см. Воронин Н.А. Анализ причин специфического деформационного поведения топокомпозита системы АШ-Д16Т при инструментальном индентировании. Восточно-Европейский научный журнал. 2021. №10(74). С. 42-52). Первый их них представляет собой процесс упругого прогиба покрытия по типу жесткой плиты, лежащей на податливой основе и нагружаемой в центре единичной силой. Второй - процесс упруго пластического деформирования слоистой системы. Оба этих процесса обеспечивают протекание третьего процесса -процесса межфазного расслоения на границе раздела «покрытие -подложка», которое ослабляет (разрывает) адгезионные связи между покрытием и подложкой. Прогиб усиливает процесс расслоения, что приводит к увеличению протяженности последнего (см. Abdul-Baqi A., Van der Giessen Е. Delamination of a strong film from a ductile substrate during indentation unloading // Journal of Materials Research. 2001. V. 16. N. 5. P. 1396-1407). При разгружении в единичном цикле индентирования под действием упругих сил в изогнутом под нагрузкой покрытии происходит отслаивание покрытия, его восстановление до горизонтального первоначального состояния и даже некоторое выпучивание покрытия, вследствие наличия остаточных напряжений.
При проведении двух циклового индентирования правильность выбора абсолютной величины максимальной конечной нагрузки Р3 для цикла повторного индентирования оценивается путем анализа диаграмм внедрения после нескольких (3-5 раза) повторных проведений нагружений и разгружений с достижением в каждом из них выбранного предельного значения Р3. Совпадение между собой по форме и виду кривых деформирования (гистерезисных петель) во втором цикле индентирования при их повторных циклах индентирования говорит о том, что покрытие-мембрана работает исключительно в упругой зоне деформирования и в зоне контакта индентора со слоистым телом отсутствуют дополнительные пластические деформации. Такой вывод говорит о возможности использования выбранной конечной нагрузки Р3 в предлагаемом методе оценки адгезионной прочности. В случае несовпадения кривых деформирования (гистерезисных петель) необходимо изменить величину конечной нагрузки нагружения во втором цикле индентирования в меньшую сторону.
Проводится анализ кривых деформирования повторного цикла индентирования (фиг. 2). Условия напряженно-деформационного состояния в области контакта индентора с покрытием описываются кривой нагружения ВС и кривой разгружения СВ. Форма диаграммы внедрения второго цикла индентирования характеризует упругий гистерезис деформирования покрытия. В процессе анализу устанавливается, что в точке Е кривой СВ происходит нейтрализация остаточных напряжений (см. Воронин Н.А. Анализ причин специфического деформационного поведения топокомпозита системы АШ-Д16Т при инструментальном индентировании. Восточно-Европейский научный журнал. 2021. №10(74). С. 42-52).
Определяем координаты точки Е. Для этого аппроксимируем кривые ВС и СВ полиномами и-степени (см. фиг. 2). Рассчитываем (аналитически или графически) значения разницы в глубинах внедрения Δs и величинах нагрузки ΔР между кривыми ВС и СВ при одинаковых величинах усилия индентирования и одинаковых значениях глубины внедрения, соответственно. Значения глубины внедрения и усилия нагружения, соответствующие максимальным значениям Δs и ΔР, будут координатами точки Е. Результаты процедура по графическому определению координат точки Е представлена кривыми Δs и ΔР (см. фиг 2).
Точка Е, принадлежащая кривой разгружения СВ одновременно принадлежит кривой упругого деформирования покрытия без остаточных напряжений при нагружении. Уравнение этой кривой включает в себя упругую деформацию материала покрытия в результате индентирования и упругую деформацию покрытия как мембраны при ее центральном нагружении. Как указывалось, координаты точки Е, принадлежат кривой разгрузки СВ и кривой упругого нагружения покрытия без остаточных напряжений. Более того координаты точек кривой СВ, лежащие ниже точки Е, по крайней мере, расположенные вблизи точки Е, также должны быть близки к кривой упругого нагружения покрытия без остаточных напряжений. Обстоятельством, которое ясно по умолчанию, является схождение кривых: кривой упругого нагружения покрытия без остаточных напряжений, кривой упругой деформации материала покрытия в результате индентирования и кривой упругой деформацию покрытия как мембраны, в одной точке на оси абсцисс. И нахождение этой точки на оси абсцисс детерминировано с местом нахождения точки Е на диаграмме повторного индентирования. Определяем вид кривой упругого нагружения покрытия без остаточных напряжений в результате проведения следующей процедуры. Уравнение кривой упругого деформирования материала покрытия при индентировании рассчитывается по формуле ((см. Fischer-Cripps А.С. Critical review of analysis and interpretation of nanoindentation test data. Surface & Coatings Technology, 2006. V. 200. P. 4153-4165):
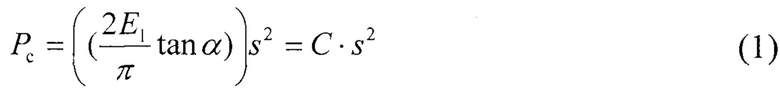
где α - эквивалентный угол конуса (70,3° для индентора Берковича), Е1 - модуль упругости материала покрытия, 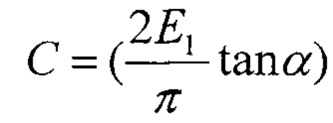 - константа жесткости материала покрытия. Уравнение (1) соответствует уравнению параболы в виде Рс=Cs2.
- константа жесткости материала покрытия. Уравнение (1) соответствует уравнению параболы в виде Рс=Cs2.
Уравнение кривой упругого деформирования покрытия как мембраны можеть быть рассчитано по формуле (см. Lu М., Huang Н. Interfacial energy release rates of SiN/GaAs film/substrate systems determined using a cyclic loading dual-indentation method. Thin Solid Films. 2015. V. 589. P. 822-830):
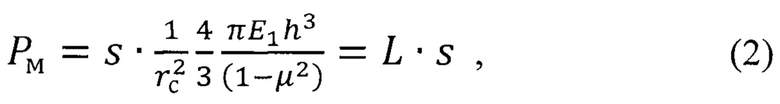
где rc - радиус отслаивания покрытия (радиус мембраны), h - толщина покрытия, μ - коэффициент Пуассона для материала покрытия,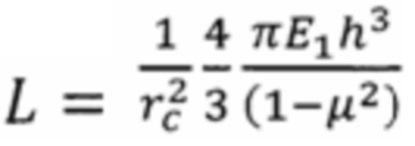 - жесткость покрытия как мембраны.
- жесткость покрытия как мембраны.
Графически уравнение упругого деформирования покрытия как мембраны представляет собой прямую линию.
Уравнение кривой упругого нагружения покрытия без остаточных напряжений представляет собой результат совместной деформации покрытия как материала и покрытия как мембраны. Кривая нагружения покрытия без остаточных напряжений может быть представлена полиномом вида

где К - константа покрытия, характеризующая суммарную жесткость упругого деформирования от индентирования и прогиба покрытия как мембраны.
При графическом изображении на экспериментальной диаграмме внедрения кривая нагружения без остаточных напряжений должна занимать промежуточное расположение между кривыми, рассчитываемыми по уравнениям (1) и (2) и касаться в точке Е кривую разгружения второго цикла индентирования.
В связи с отсутствием знаний значений констант жесткости L и K, а также координаты на оси абсциссы начала кривой упругого нагружения покрытия без остаточных напряжений, применяем метод графического определения начальной точки кривой упругого деформирования покрытия без остаточных напряжений, при аналитическом определении значений констант жесткости L и K.
На диаграмме внедрения (фиг. 3) выбираем координаты начала построения кривых упругого деформирования ненапряженного покрытия, руководствуясь следующей логикой. Из эксперимента на индентирование исследуемого топокомпозита с двумя циклами индентирования имеется значение точки окончания процесса деформирования. Координаты этой точки D [sD; 0.0]. Зная, что этой точке соответствует свободное состояние напряженного покрытия без нагрузки, и наличие в покрытии сжимающих остаточных напряжений, что видно из формы гистерезисной петли деформирования покрытия во втором цикле индентирования, выбираем начальную точку кривой упруго деформирования покрытия без напряжений в точке G [sD; 0.0] правее по оси абсцисс от точки D (см. фиг. 3).
По известным значениям параметров α и Е1 по формуле (1) рассчитываем константу жесткости С. Строим график параболы Рс=С⋅s2 из начальной точки G (см. рис. 3, кривая 5). Строим предполагаемый график прямой упругого деформирования покрытия как мембраны из точки G в виде прямой, проходящей в начальной части достаточно близко, почти по касательной к кривой разгрузки первого цикла индентирования (см. рис. 3, кривая 6). Особых требований к углу наклона этой прямой к оси абсцисс не предъявляем, так как на следующих этапах ее расположение на диаграмме внедрения будет математически уточнено. По ранее подобранной по экспериментальным данным, относящимся к кривой разгружения при повторном индентировании и аппроксимированной в виде полинома аналитической функцией (см. фиг. 3 кривая 4), фиксируем на кривой разгрузки координаты точки Е и точки F (черные маркеры). Если точка Е однозначно принадлежит кривой упругого деформирования покрытия без остаточных напряжений, то точка F выбирается на некотором расстоянии на кривой разгружения второго цикла деформирования и ниже точки Е. Это расстояние равно от 0,3 до 0,5 от длины дуги кривой разгружения ниже точки Е. Фиксация координат точек Е и F на кривой разгрузки позволяет применить аналитику для расчета констант кривой деформирования покрытия как мембраны без остаточных напряжений. Фиксируем значения абсцисс точек Е2 и F2, принадлежащие кривой упругого деформирования покрытия как материала, и значения абсцисс точек Е1 и F1, принадлежащих прямой упругого деформирования покрытия как мембраны (см. рис. 3, круглые открытые маркеры). Из представленного графического построения исследуемых кривых деформирования известны абсолютные значения абсцисс точек Е2,F2, Е1 и F1 С2, и В2.
Составляем два баланса энергии, затрачиваемой на совершение работы по упругому деформированию покрытия без остаточных напряжений для точек Е и F соответственно, как сумму работ, затрачиваемых на деформирование покрытия как материал и как мембрана:
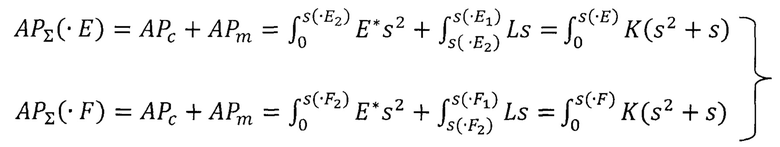
Из решения полученной системы уравнений, получаем значения коэффициентов L и K. Строим кривые упругого деформирования покрытия как мембраны и упругого нагружения покрытия без остаточных напряжений по уравнению 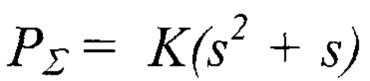 и убеждаемся, что точка Е3 совпадает с точкой Е, а точка F3 близко располагается к координатам точки F3 (см. рис. 3, круглые открытые маркеры).
и убеждаемся, что точка Е3 совпадает с точкой Е, а точка F3 близко располагается к координатам точки F3 (см. рис. 3, круглые открытые маркеры).
Если точка Е3 не совпадает с точкой Е, смещаем начальную точку G кривой упругого деформирования покрытия без остаточных напряжений правее на некоторую величину (шаг). Проводим повторное графоаналитическое построение новых кривых и вновь сравниваем степень совпадение точки Е3 с точкой Е. В результате некоторого числа итераций (шагов) определяем координаты точки G, для которой точка Е3 точно совпадает с точкой Е, а точка F3 близко располагается к координатам точки F. По координатам точек G, F3 и Е3 подбираем полином третий степени 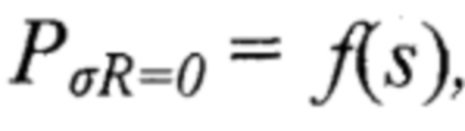 который являться уравнением кривой упругого деформирования покрытия без остаточных напряжений. Строим эту кривую на диаграмме внедрения (см. фиг. 3, кривая 7). Экстраполируем построенную кривую до пересечения с кривой разгрузки первого цикла индентирования (фиг. 4, точка М).
который являться уравнением кривой упругого деформирования покрытия без остаточных напряжений. Строим эту кривую на диаграмме внедрения (см. фиг. 3, кривая 7). Экстраполируем построенную кривую до пересечения с кривой разгрузки первого цикла индентирования (фиг. 4, точка М).
Точка М на кривой разгружения первого цикла индентирования характеризует, в соответствие с моделью Вонга (см. Воронин Н.А. Усовершенствованный способ определения остаточных напряжений в тонких твердых покрытиях. Проблемы машиностроения и автоматизации. 2022, №3, с. 24-32), точку пересечения кривой нагружения при индентировании топокомпозита с покрытием без остаточных напряжений.
Строим на диаграмме внедрения кривую упругопластического нагружения слоистого тела с покрытием без остаточных напряжений по точкам кривой нагружения топокомпозита первого цикла индентирования исходя из пропорциональности значений величин нагрузок для точки А относительно точки М. Расположение и вид кривой нагружения топокомпозита без остаточных напряжений в покрытии представлен на фиг. 4 кривой 8. Аппроксимируем кривую 8 полиноминальной функцией.
Строим теоретическую диаграмму внедрения для идеального модельного топокомпозита с механическими и геометрическими характеристиками, отвечающими исследуемому топокомпозиту, и совмещаем ее с экспериментальной диаграммой внедрения первого цикла индентирования, воспользовавшись зависимостями (4) и (5) (см. Н.А. Воронин. Теоретическая оценка композиционной и истинной твердости тонких покрытий. Трение и смазка в машинах и механизмах. 2011, №7. с. 11-21; Воронин Н.А. Моделирование диаграммы внедрения для топокомпозитов. Проблемы машиностроения и надежности машин, 2018, №5, с. 57-65.))
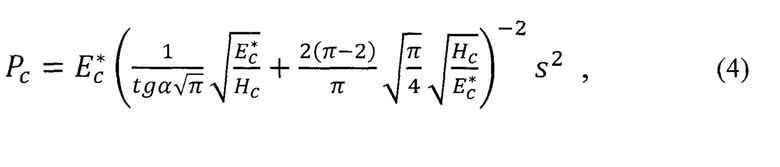

где 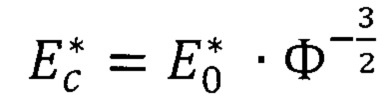 ,
, 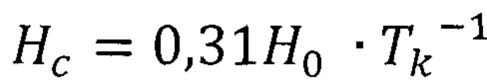 ,
,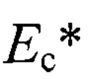 - эффективный модуль упругости слоистого тела;
- эффективный модуль упругости слоистого тела; 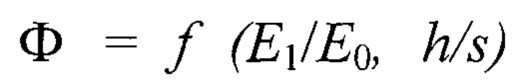 - упруго-геометрический параметр слоистой системы; h - толщина покрытия;
- упруго-геометрический параметр слоистой системы; h - толщина покрытия; 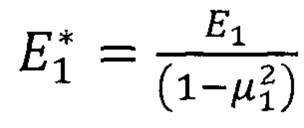 ,
,  - приведенный модуль упругости материала покрытия и материала основы, соответственно; E1, E0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы;
- приведенный модуль упругости материала покрытия и материала основы, соответственно; E1, E0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы; 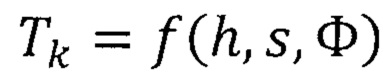 - весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
- весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
Эффективный модуль упругости слоистого тела может быть рассчитан с использованием табулированных значений функции 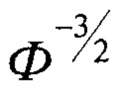 определенных для широкого круга значений параметра
определенных для широкого круга значений параметра 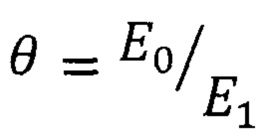 и представленных в таблице.
и представленных в таблице.
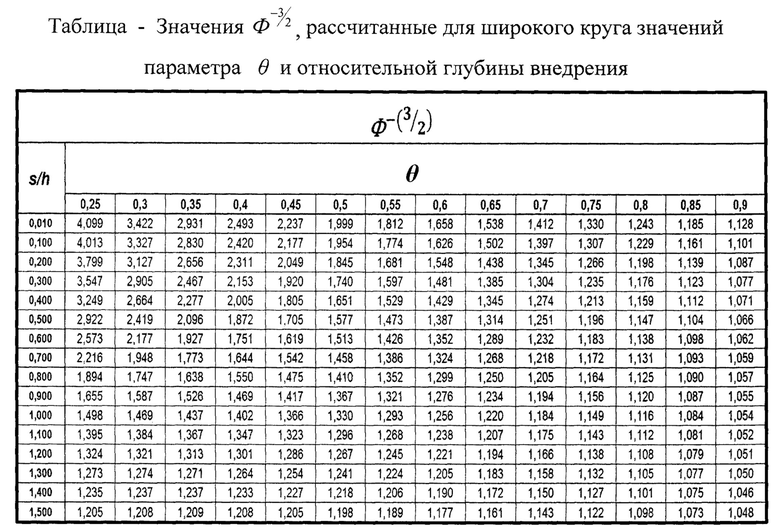
На фиг. 5 представлена теоретическая диаграмма внедрения - кривая ОК представляет теоретическую кривую нагружения модельного топокомпозита, кривая AQ - теоретическую кривую разгрузки. Фиксируем координаты точек К и Q. Теоретическая кривая разгружения на начальном этапе геометрически совпадает с экспериментальной кривой разгрузки первого цикла индентирования. Заштрихованная площадь диаграммы внедрения ОКМО (см. фиг. 5) соответствует работе пластической деформации (AU), затраченной на межфазное разрушения границы раздела покрытие-подложка в результате тангенциального пластического течения при индентировании в процессе первого цикла деформирования.
Интегрированием кривых диаграммы внедрения определяем и фиксируем значение работы пластической деформации (AU), затраченной на межфазное разрушение по величине площади ОКМО на диаграмме внедрения.
Рассчитываем радиус круговой трещины при межфазном разрушении адгезионной связи покрытия с подложкой в процессе индентирования используя выражение (2):
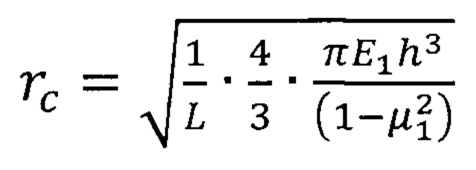
где rc - радиус круговой трещины, Е1 - модуль упругости материала покрытия, h - толщина покрытия, μ1 - коэффициент Пуассона, L -жесткость покрытия как упругой мембраны. Величина L была рассчитана при нахождении кривой деформирования покрытия без остаточных напряжений. Рассчитываем адгезионную прочность покрытия к подложке по зависимости (см. Xie Н, Huang Н. Characterization of the interfacial strength of SiNx/GaAs film/substrate systems using energy balance in nanoindentation. Journal of Materials Research. 2013, V. 28, No. 23, P. 3137-3145):

где ΔU - работа, затрачиваемая на межфазное расслоение,rc - радиус расслоения.
Пример. Для примера было произведено определение адгезионной прочности покрытия из нитрида алюминия (AIN), нанесенного магнетронным способом, толщиной 5 мкм на алюминиевый сплав Д16Т. Запись диаграммы внедрения производилось на наноиндентометре НаноСкан 4D при использовании пирамиды Берковича. Упругие характеристики материала основы изделия Е0=93 ГПа и материала покрытия Е1=320 ГПа, микротвердости 18 ГПа и 36 ГПа, соответственно. Диаграмма внедрения была получена при достижении в первичном цикле индентирования максимальной нагрузки Р1=0,4Н, в повторном цикле - Р2≈0,2Н. Минимальное значение усилия на индентор при разгрузке в первом цикле индентирования составляло Р3≈0,02Н.
Результаты расчета по формуле (6) для исследуемого в данной работе образца из покрытия нитрида алюминия на подложке из Д16Т дали значения адгезионной прочности G=3,0±0,1 Дж/м2, что близко к значениям, известным в литературе (см. например. Xie, Н.Т. and Н. Huang, Characterization of the interfacial strength of SiN/GaAs film/substrate systems using energy balance in nanoindentation. Journal of Materials Research, 2013. 28: p. 3137-3145).
Результаты экспериментальной проверки свидетельствуют о пригодности предлагаемого способа для практического использования. Следовательно, заявленное изобретение соответствует требованию "промышленная применимость" по действующему законодательству.
Изобретение относится к измерительной технике для определения адгезионной прочности тонких напряженных покрытий на изделии машиностроения. Сущность: изделие с покрытием, в котором присутствуют остаточные напряжения, подвергается микроиндентированию с получением диаграмм внедрения, содержащих два цикла индентирования. Первый цикл индентирования, обеспечивает межфазное отделение покрытие на некотором участке, без разрушения сплошности покрытия. Второй цикл нагружения проводится в тот же отпечаток, что и в первом цикле индентирования, но с нагружением, обеспечивающим упругое деформирование покрытие под индентором. По результатам анализа кривых повторного нагружения и разгрузки строится кривая упругопластического нагружения изделия с покрытием без присутствия в нем остаточных напряжений. Аналитическая обработка кривых нагружения покрытия с остаточными напряжениями и ненапряженного покрытия, позволяет определить радиус межфазной трещины. Построение теоретической диаграммы единичного цикла индентирования для исследуемого изделия позволяет по разности площадей теоретической диаграммы и рассчитанной диаграммы внедрения без остаточных напряжений, но с отслаиванием покрытия после индентирования, рассчитать величины энергии, затрачиваемой на межфазное разрушение в системе покрытие-основа изделия, С учетом известных данных по величине энергии, затрачиваемой на межфазное разрушение слоистой системы и радиуса межфазной трещины вычисляется величина адгезионной прочности покрытия к пластичной подложке по известной зависимости. Технический результат: возможность существенно повысить точность и объективность определения адгезионной прочности тонких покрытий. 8 з.п. ф-лы, 5 ил., 1 табл.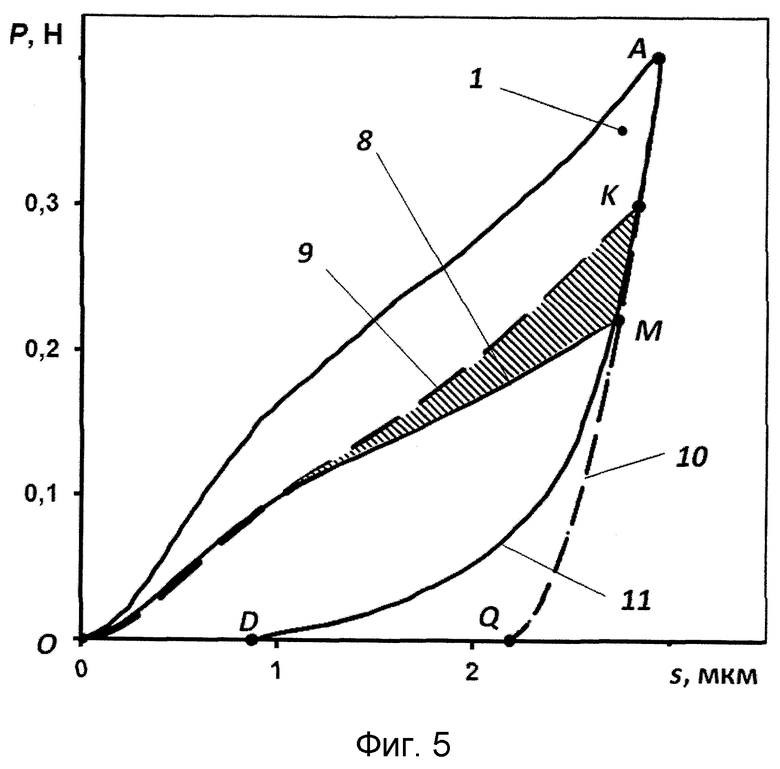
1. Способ определения адгезионной прочности тонких напряженных покрытий на изделии, заключающийся в том, что изделие, на поверхности которого имеется покрытие известной толщины, представляет собой слоистое тело, состоящее из основы и покрытия, материалы которых имеют известные физико-механические характеристики, помещают в прибор-твердометр, с помощью которого производят нагружение алмазного пирамидального наконечника в поверхность покрытия в виде двух повторных циклов индентирования, последовательно производимых в одно и тоже место, на глубину, обеспечивающую отслаивание покрытия при разгружении в первом цикле индентирования, записывают диаграммы внедрения, представляющую собой графики изменения глубины внедрения при возрастании нагрузки и затем при снижении нагрузки, анализируют площади диаграмм внедрения, рассчитывают размеры той части площади индентирования, которая соответствует работе, затрачиваемой на межфазное расслоение, определяют радиус круговой трещины области расслоения исходя из модели деформирования упругой мембраны с учетом упругого деформирования индентором материала покрытия в месте контакта и рассчитывают значение адгезионной прочности G покрытия по формуле:

где ΔU - работа, затрачиваемая на межфазное расслоение; rc - радиус расслоения, отличающийся тем, что в нем в точке А фиксируют значение конечной нагрузки при нагружении P1 для первого цикла внедрения, фиксируют значения нагрузки при разгружении Р2 равной не более 5% от значения P1 в первом цикле деформирования, фиксируют значение конечной нагрузки Р3 равной не более 50% от значения Р1 при нагружении во втором цикле нагружения, фиксируют значение глубины внедрения при разгружении до нуля во втором цикле индентирования, определяют координаты точки Е на кривой разгружения второго цикла индентирования, в которой отсутствуют остаточные напряжения в покрытии и через которую строят кривую нагружения ненапряженного покрытия, которая пересекает кривую разгружения первого цикла индентирования в некоторой точке М, через которую строят кривую упругопластического нагружения исследуемого слоистого тела без остаточных напряжений в покрытии, рассчитывают и строят на экспериментальной диаграмме внедрения теоретическую диаграмму внедрения для идеального слоистого тела с механическими характеристиками, соответствующими исследуемому слоистому телу, фиксируют значения координат точки К пересечения теоретической кривой нагружения с кривой разгрузки первого цикла индентирования, которая до этого места совпадает с кривой разгрузки теоретической диаграммы внедрения, определяют площадь фигуры ОКМО, образуемой теоретической кривой нагружения слоистого тела, кривой упругопластического деформирования исследуемого топокомпозита без остаточных напряжений в покрытии и частью теоретической кривой разгрузки, фиксируют значение рассчитанной площади как значение работы, затраченной на межфазное разрушение границы раздела слоистого тела (ΔU), рассчитывают значение радиуса rc круговой трещины, ограничивающей область отслоения покрытия от основы и вычисляют значение величины адгезионной прочности G покрытия к основе по формуле (Ф1);
2. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 1, отличающийся тем, что значением конечной нагрузки Р1 при первом цикле нагружения является максимальная нагрузка для данного слоистого тела, не приводящая к повреждениям в покрытии после индентирования в виде поперечных трещин, сколов и нарушения сплошности покрытия;
3. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 1, отличающийся тем, что конечная нагрузка Р2 второго цикла нагружения не вносит пластическую деформацию в покрытие и подложку;
4. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 1, отличающийся тем, что для определения координат точки Е на кривой разгружения второго цикла индентирования, в которой отсутствуют остаточные напряжения в покрытии, производят обработку данных, на основе которых строилось графическое изображение диаграммы внедрения второго цикла индентирования, подбирают полиноминальные функции кривых повторного нагружения и разгрузки, сравнивают аналитически или графически их между собой и по разнице в глубинах внедрения Δs и величинах нагрузки ΔР между кривыми нагружения и разгрузки при одинаковых величинах усилия индентирования и одинаковых значениях глубины внедрения, соответственно, устанавливают ординату и абсциссу максимальных значений Δs и ΔР, соответственно, фиксируют аналитически и графически на кривой повторного разгружения координаты точки Е, в которой отсутствуют остаточные напряжения в покрытии, и координаты которой, в свою очередь, принадлежат кривой упругого деформирования покрытия без остаточных напряжений;
5. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 4, отличающийся тем, что определяют координаты ряда точек кривой нагружения ненапряженного покрытия на основе итерационного процесса графоаналитической обработки, которая включает данные:
- кривой упругого деформирования ненапряженного покрытия как материального твердого тела, построенной по известной квадратичной зависимости:
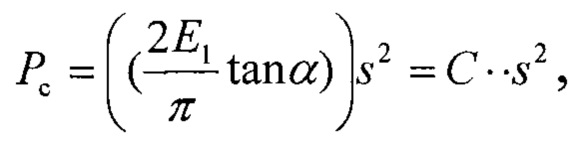
где Е1 - модуль упругости материала покрытия; α - эквивалентный угол конуса (70,3° для индентора Берковича); 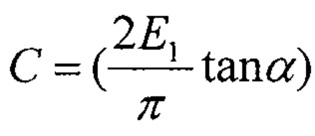 - жесткость покрытия как материала при индентировании острым индентором,
- жесткость покрытия как материала при индентировании острым индентором,
- прямой упругого деформирования ненапряженного покрытия как мембраны, нагруженной центральной силой и закрепленной по краю, описываемой известной линейной зависимостью:
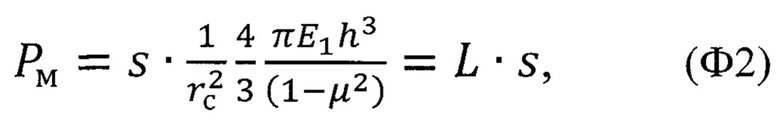
где rc - радиус отслаивания покрытия (радиус мембраны); h - толщина покрытия; μ - коэффициент Пуассона для материала покрытия; 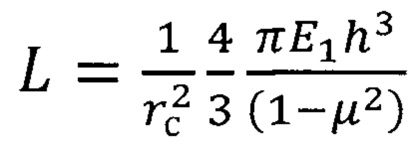 - жесткость покрытия как мембраны,
- жесткость покрытия как мембраны,
- кривой суммарного упругого деформирования ненапряженного покрытия как материала и мембраны, которая может быть описана некоторой нелинейной зависимостью вида,
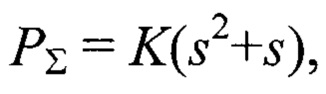
где К - суммарная жесткость покрытия как материала и мембраны,
- координаты двух точек кривой разгружения второго цикла индентирования, точки Е и точки F, принадлежащей нижней части ветви кривой повторной разгружения, и точки на кривой оси абсцисс, определяющей начало координат все упомянутых в данном пункте формулы кривых, и систему уравнений, описывающих баланс энергии, затрачиваемой на совершение работы по суммарному упругому деформированию ненапряженного покрытия как материала и мембраны в виде суммы затрачиваемой энергии отдельно при упругом деформировании покрытия как материал и как мембрана для известных координат точек Е и F;
6. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 5, отличающийся тем, что графически строят кривую нагружения ненапряженного покрытия по координатам точек, принадлежащим кривой нагружения ненапряженного покрытия, описывают кривую полиноминальной функцией, экстраполируют график этой функции до пересечения его с кривой разгружения первого цикла индентирования и фиксируют координаты точки пересечения М;
7. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 6, отличающийся тем, что определяем аналитически и строим графически на диаграмме внедрения кривую упругопластического нагружения слоистого тела с покрытием без остаточных напряжений по точкам кривой упругопластического нагружения слоистого тела первого цикла индентирования исходя из пропорциональности значений величин нагрузок для точки А относительно точки М;
8. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 1, отличающийся тем, что теоретическую диаграмму внедрения для идеального модельного слоистого тела строим на диаграмме внедрения, используя следующие зависимости:
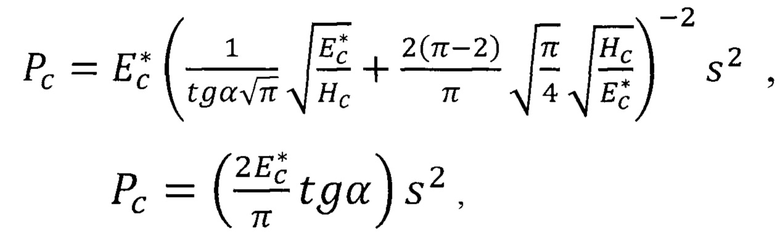
где 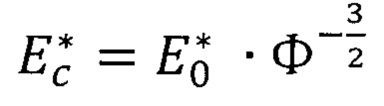 ,
, 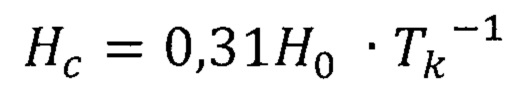 ,
, 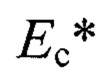 - эффективный модуль упругости слоистого тела;
- эффективный модуль упругости слоистого тела; 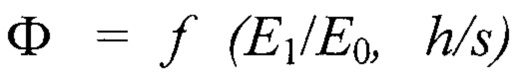 - упругогеометрический параметр слоистой системы; h - толщина покрытия;
- упругогеометрический параметр слоистой системы; h - толщина покрытия; 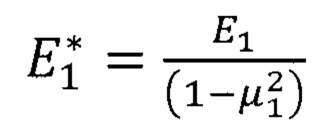 ,
, 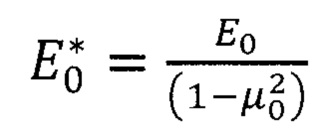 - приведенный модуль упругости материала покрытия и материала основы, соответственно; Е1, Е0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы;
- приведенный модуль упругости материала покрытия и материала основы, соответственно; Е1, Е0 - модули нормальной упругости материалов покрытия и основы, соответственно; μ1, μ0 - коэффициент Пуассона материалов покрытия и основы, соответственно, s - текущая глубина индентора, отсчитываемая от свободной поверхности; Н0 - твердость материала основы; 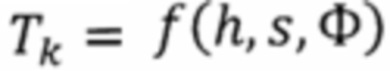 весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
весовая функция, учитывающая место зарождения пластической деформации в слоистом теле; α - эквивалентный угол конуса (70,3° для индентора Берковича).
9. Способ определения адгезионной прочности тонких напряженных покрытий на изделии по п. 1, отличающийся тем, что радиус круговой трещины при межфазном разрушении адгезионной связи покрытия с подложкой в процессе индентирования рассчитывают, используя выражение (Ф2):
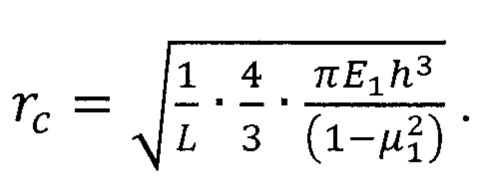
| СПОСОБ ОПРЕДЕЛЕНИЯ АДГЕЗИОННОЙ ПРОЧНОСТИ ТОНКИХ ТВЕРДЫХ ПОКРЫТИЙ НА ПОДАТЛИВЫХ ПОДЛОЖКАХ | 2020 |
|
RU2747709C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АДГЕЗИОННОЙ ПРОЧНОСТИ ТОНКИХ ТВЕРДЫХ ПОКРЫТИЙ НА ИЗДЕЛИЯХ | 2019 |
|
RU2710392C1 |
| Способ определения прочности сцепления покрытия с подложкой | 1987 |
|
SU1430835A1 |
| KR 1020160118852 A, 12.10.2016. | |||
Авторы
Даты
2023-12-22—Публикация
2023-03-01—Подача