Изобретение относится к измерительной технике для определения остаточных напряжений тонких защитных покрытий на изделиях машиностроения из пластичных металлических материалов.
Известен способ определения остаточных напряжений в тонких покрытиях по кривизне прямоугольного образца с покрытием. При этом на длинную, узкую и тонкую пластину (основной материал) наносят исследуемое покрытие. Остаточные напряжения деформируют пластину. По радиусу кривизны определяют средние остаточные напряжения в покрытии. Расчетные зависимости получают при следующих допущениях: 1) покрытие идеально соединено с основным материалом, и смещение на границе раздела не происходит; 2) сечение остается плоским и перпендикулярным оси образца. Для вычисления остаточных напряжений в тонких покрытиях, например вакуумных или гальванических, используют расчетные зависимости Бреннер-Стендерофа:
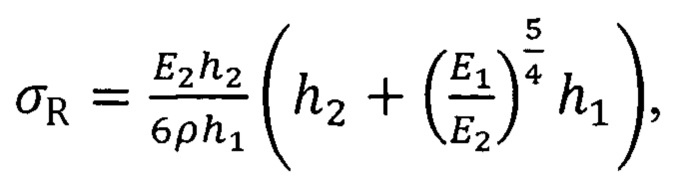
где Е1, Е2 - модули упругости материала покрытия и подложки, соответственно; h1, h2 - толщина покрытия и подложки, соответственно; ρ - радиус кривизны образца с покрытием.
(A. Brenner, S. Senderoff. Calculation of Stress in Electrodeposits from the Curvature of a Plated Strip.Journal of Research of the National Bureau of Standards. 1949, Vol. 42, Research Paper RP1954.)
Недостатком этого метода является то, что способ разрушающий.
Известен способ определения продольных остаточных напряжений в изделии некоторой линейной протяженности в результате вырезки части материала в виде балки (пластинки, полоски) параллельно оси протяженного изделия в интересующем месте. Вырезанный объект - балка (пластинка) в свободном состоянии деформируется под действием остаточных напряжений, принимая криволинейный вид с максимальным прогибом в центре пластинки (балки). Продольные остаточные напряжения рассчитывались по формуле:
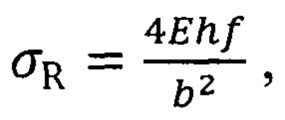
где Е - модуль упругости материала полоски, h - высота полоски, ƒ - прогиб, b - длина хорды.
(С.П. Буркин, Г.В. Шимов, Е.А. Андрюкова. Остаточные напряжения в металлопродукции: учебное пособие. Екатеринбург, Изд-во Урал. университета, 2015. - 248 с.: стр. 69)
Недостатком этого метода является то, что он разрушающий и малопригоден для тонких покрытий.
Известен способ определения остаточных напряжений, базирующийся на вырезки ламели (полоски) из тонкого покрытия и анализе профиля (прогиба) ламели, создаваемого за счет внутренних напряжений, с целью определения остаточных напряжений на основе теории балки.
(Z. Gao, X. Zhang, J. Kulczyk-Malecka et al. Ceramic buckling for determining the residual stress in thin films. Scripta Materialia. 2021, V. 201. P. 113949)
Данный способ по технической сущности и достигаемому результату наиболее близок к предлагаемому техническому решению и, поэтому, принят за его ближайший прототип.
Согласно этому способу из покрытия вырезалась ламель методом фрезерования фокусированным ионным пучком (FIB - Focused ion beam milling). Остаточные напряжения сжатия внутри ламели вызывали изгиб балки, после завершения подрезки. Изгиб и форма изогнутой балки визуализировались с помощью сканирующего электронного микроскопа. Величина остаточных напряжений рассчитывалась на основе элементарной теории балки, предполагающей, что деформация является чисто упругой и напряжение равномерно по толщине покрытия.
Профиль выпучивания покрытия описывался косинусоидальной функцией S:
S(X)=С(1 - cos(2πX)),
где 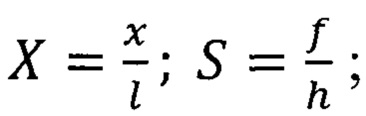 ƒ - максимальный прогиб ламели (балки) в центре.
ƒ - максимальный прогиб ламели (балки) в центре.
Множитель «С» получают путем подгонки профиля изгиба. Деформация балки связана с «С» через параметр λ:
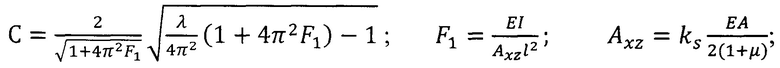
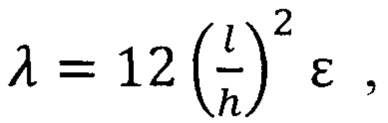
где ks - коэффициент сдвига Тимошенко, зависящий от геометрии: обычно ks=5/6 для прямоугольного сечения; l - длина балки; I - момент инерции; А - площадь поперечного сечения балки; Е - модуль упругости материала покрытия; μ - коэффициент Пуассона материала покрытия.
Величина остаточных напряжений может быть рассчитана по величине относительной деформации ε:
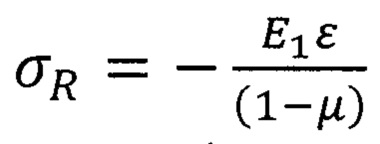
Недостатком этого способа является трудоемкость и дороговизна.
Задача, решаемая в предлагаемом способе, заключается в возможности существенно более проще определять величину остаточных напряжений в тонких покрытиях, нанесенных на податливые подложки путем применения микроиндентирования для которого характерно при определенных конечных нагрузках внедрения индентора обеспечивать межфазное расслоение на границе покрытие-подложка и при повторном нагружении в режиме упругого деформирования зафиксировать прогиб вздувшегося (выпуклового) покрытия.
Решение поставленной задачи достигается за счет того, что предложен способ определения остаточных напряжений в покрытии, заключающийся в проведении следующих процедур. Вначале изделие, на поверхности которого имеется покрытие известной толщины, представляющее собой слоистое тело, состоящее из основы (податливой подложки) и твердого покрытия, материалы которых (подложки и покрытия) имеют известные значения модулей упругости, коэффициентов Пуассона и пределов текучести (твердости) помещают в прибор-микротвердометр, с помощью которого производят нагружение (внедрение) алмазного пирамидального наконечника в поверхность покрытия, на глубину, обеспечивающую межфазное отслаивание покрытия при нагружении и записывают экспериментальную диаграмму внедрения. Диаграмма внедрения представляет собой график изменения глубины внедрения «s» при возрастании нагрузки «Р» и затем при снижении нагрузки, полученный в результате двух циклов индентирования. Первый цикл индентирования состоит в нагружении до некоторой конечной нагрузки Pmax и разгружении индентора до величины нагрузки не более 5% от величины предельной нагрузки Pmax при нагружении. Второй цикл индентирования осуществляется непосредственно сразу после окончания первого цикла и заключается во внедрении индентора в тот же отпечаток путем нагружения индентора до величины конечной нагрузки, обеспечивающей значимое чисто упругое деформирование (прогиб) ранее (на этапе нагружения первичного цикла индентирования) отслоившегося от подложки покрытия. Затем в рамках второго цикла индентирования следует полное снятие нагрузки с индентора вплоть до значения равного нулю. Координаты пересечения кривой разгрузки второго цикла деформирования указывают на величину остаточной глубины отпечатка в данном испытании. Эта глубина фиксируется как «sr» и обозначает глубину отпечатка для покрытия с остаточными напряжениями.
Кривые нагружения и разгрузки второго цикла индентирования подвергаются обработке в виде определения функциональных зависимостей между нагрузкой и глубиной внедрения. Функциональные зависимости получают в виде полиномиальных уравнений n-степени (как правило, не ниже шестой). Полученные функциональные зависимости используются для определения координат моды кривой разгрузки второго цикла индентирования. Это достигается установлением максимального значения разности глубины внедрения Δs и величины нагрузки ΔР между кривыми нагружения и разгрузки при одинаковых величинах усилия индентирования и одинаковых значениях глубины внедрения, соответственно. Значения глубины внедрения и усилия нагружения, соответствующие максимальным значениям Δs и ΔР, определяют координаты точки С - моды кривой разгрузки. Точка С, принадлежащая кривой разгружения, одновременно принадлежит кривой упругого деформирования покрытия без остаточных напряжений при нагружении. Из анализа природы кривой упругого деформирования покрытия без остаточных напряжений устанавливается вид и математическое уравнение кривой упругого деформирования покрытия без остаточных напряжений при нагружении. Координаты пересечения кривой упругого деформирования покрытия без остаточных напряжений при нагружении указывают на величину остаточной глубины отпечатка для случая испытания исследуемого покрытия без остаточных напряжений. Эта глубина фиксируется как «sr0». Анализ механики деформирования покрытия без остаточных напряжений позволяет рассчитать размер (радиус) трещины межфазного расслоения на границе покрытие - подложка. Разница глубин отпечатков для покрытия с остаточными напряжениями «sr» и для ненапряженного покрытия «sr0» значение прогиба покрытия при полном снятии нагрузки на индентор. Установленные в процессе анализа диаграммы внедрения с повторным циклом индентирования - длина трещины расслоения, равная двум радиусам межфазной трещины и прогиб покрытия - совместно с данными о толщине покрытия и упругими характеристиками материала покрытия позволяют рассчитать величину остаточных напряжений по зависимости, предложенной в прототипе.
Сущность предлагаемого способа заключается в том, изделие с покрытием, в котором присутствуют остаточные напряжения, подвергается микроиндентированию с получением диаграммы внедрения, содержащим два цикла индентирования. Первый цикл индентирования, обеспечивает межфазное отделение покрытие на некотором участке, без разрушения сплошности покрытия. Второй цикл нагружения проводится в тот же отпечаток, что и в первом цикле индентирования, но с нагружением, обеспечивающим упругое деформирование покрытие под индентором. По результатам анализа кривых повторного нагружения и разгрузки строится кривая нагружения для изделия с покрытием без присутствия в нем остаточных напряжений. Аналитическая обработка этих кривых нагружения покрытия с остаточными напряжениями и ненапряженного покрытия, позволяет определить радиус межфазной трещины и прогиб выпуклости покрытия. С учетом известных начальных данных о материале покрытия и толщине вычисляется величина остаточных напряжений в покрытии по известной зависимости, предложенной в прототипе.
Отличительным признаком изобретения является то, что определение величины остаточных напряжений в покрытии топокомпозита (поверхностно слоистого тела) производят за счет замены операции вырезки ламели путем фрезерования ионным пучком на процесс микроиндентирования и анализа диаграмм внедрения двумя циклами нагружения.
Таким образом, предлагаемый способ позволяет существенно упростить процедуру известного способа определения остаточных напряжений в тонких твердых покрытиях, наносимых на податливые подложки, за счет создания эффекта межфазного расслоения, сопровождаемого процесс индентирования, в то время как в прототипе процедура реализации трудоемкая, так как используется высокотехнологическое оборудование и сложная процедура изготовления и измерения геометрических параметров опытного образца.
Проведенный заявителем анализ техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения, а определение из перечня выявленных аналогов прототипа, как наиболее близкого по совокупности признаков аналога, позволил выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявленном объекте, изложенных в формуле изобретения. Следовательно, заявленное изобретение соответствует требованию "новизна" по действующему законодательству.
Для проверки соответствия заявленного изобретения требованию изобретательского уровня заявитель провел дополнительный поиск известных решений, с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного изобретения, результаты которого показывает, что заявленное изобретение не следует для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения действий на достижение технического результата. Следовательно, заявленное изобретение соответствует требованию "изобретательский уровень" по действующему законодательству.
Предлагаемый способ поясняется чертежами, представленными на фиг. 1-4.
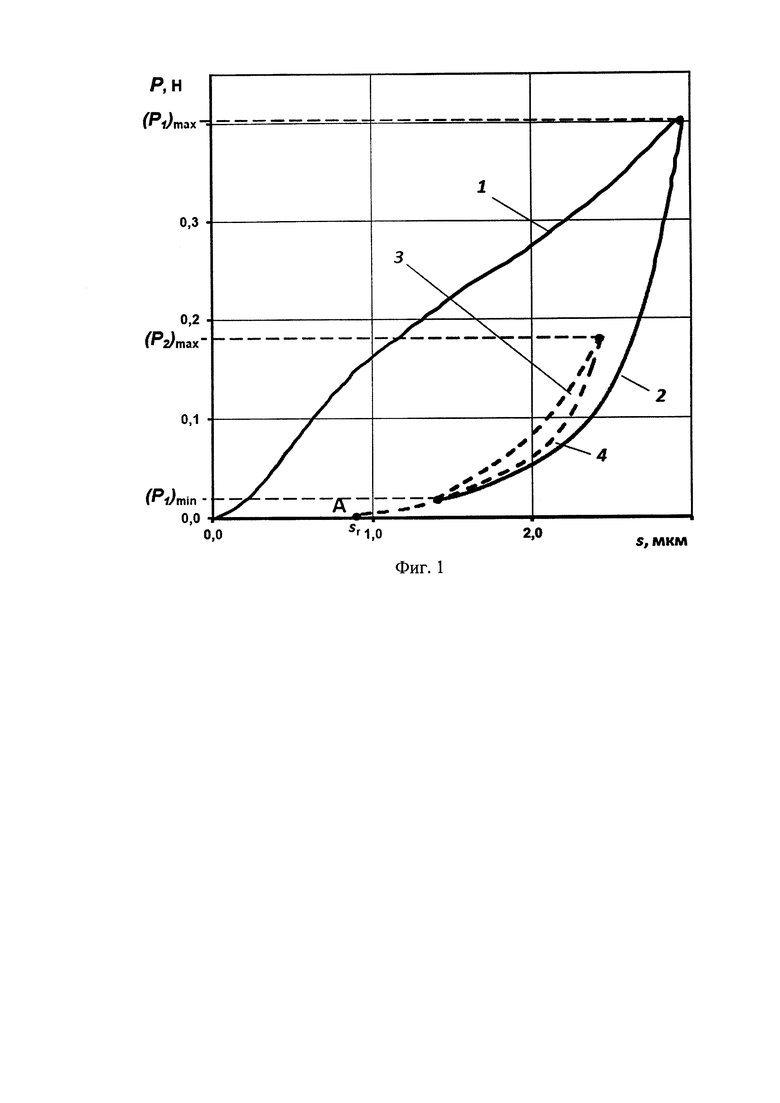
На фиг. 1 изображена диаграмма внедрения первичного и повторного циклов индентирования. 1 - кривая нагружения первичного цикла индентирования, 2 - кривая разгружения первичного цикла индентирования, 3 - кривая нагружения повторного цикла индентирования, 4 - кривая разгружения повторного цикла индентирования.
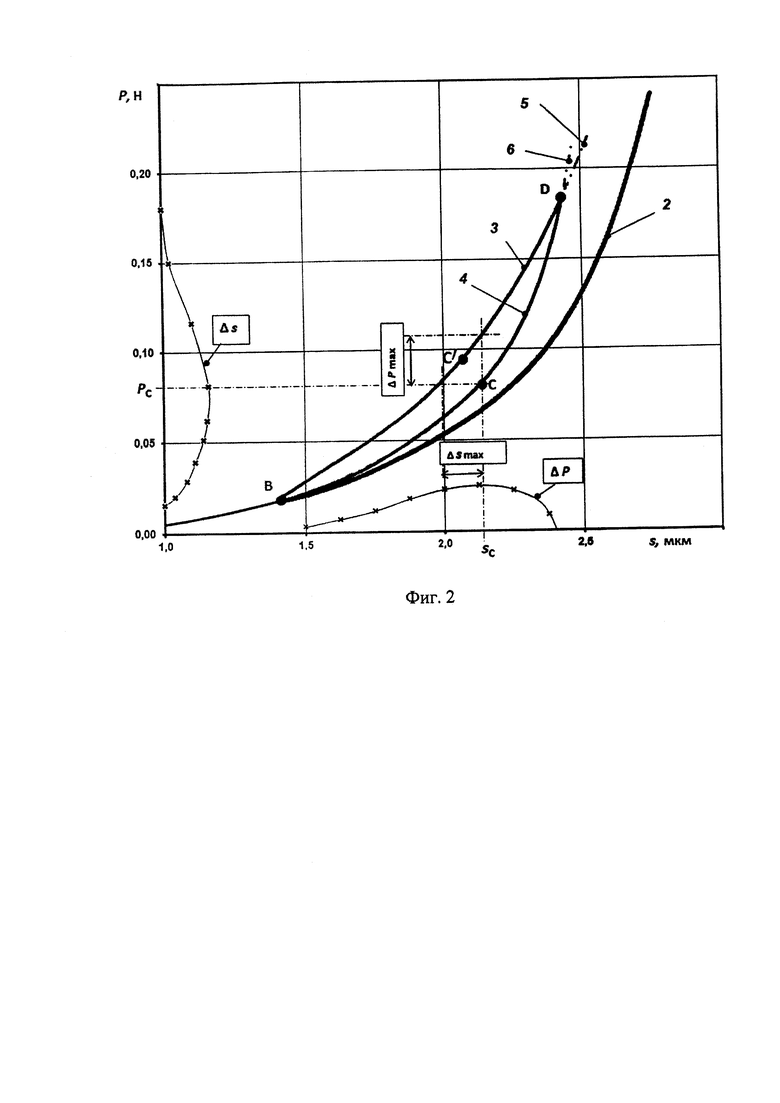
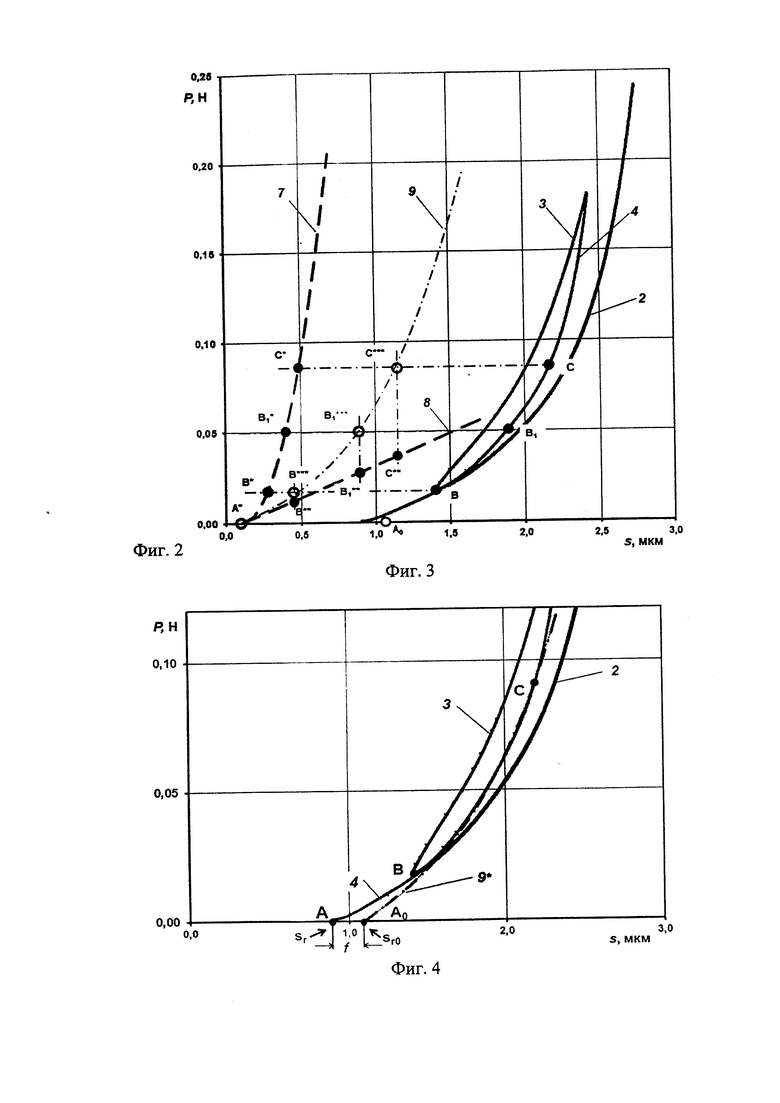
На фиг. 2 изображена часть диаграммы внедрения, представленной на фиг.1 и включающая часть кривой разгружения первичного цикла индентирования и повторный цикл упругого индентирования. 2 - кривая разгружения первичного цикла индентирования, 3 - кривая нагружения повторного цикла индентирования (кривая ВС/D), 4 - кривая разгружения повторного цикла индентирования (кривая BCD), 5 - аппроксимированная кривая 3 повторного нагружения, 6 - аппроксимированная кривая 4 повторного разгружения.
На фиг. 3 изображена расчетная схема определения координат начала кривой упругого нагружения покрытия для случая отсутствия остаточных напряжений в покрытии. 2 - кривая разгрузки первого цикла индентирования; 3 и 4 - кривые нагружения и разгружения второго цикла индентирования, соответственно; 7 - кривая упругого деформирования материала покрытия при индентировании; 8 - прямая упругого деформирования покрытия как мембраны; 9 - кривая упругого нагружения покрытия без остаточных напряжений
На фиг. 4 изображена часть графика фиг. 3 для демонстрации расчета величины прогиба покрытия от вздутия после снятия нагрузки на индентор. 2 - кривая разгрузки первого цикла индентирования, 3 - кривая повторного нагружения, 4 - кривая разгружения повторного разгружения, 9* - кривая упругого деформирования покрытия без остаточных напряжений.
Способ определения остаточных напряжений тонких твердых покрытий на пластических подложках реализуется следующим образом. Для исследуемого изделия с тонким твердым покрытием измеряют толщину покрытия h и модуль нормальной упругости Е. Определение модуля упругости материала покрытия производят по одной из методик, описанной в технической и научной литературе (см. например, стандарт ISO (International Standard) 14577-4:2007 или Oliver W.C, Pharr G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, №7, pp. 1564-1583). Коэффициент Пуассона материала покрытия выбирается из справочника.
С помощью прибора микротвердометра с непрерывной регистрацией нагрузки и глубины внедрения внедряют алмазный наконечник в виде четырехугольной (пирамида Виккерса) или треугольной пирамиды (пирамида Берковича) в исследуемое слоистое тело (поверхность с тонким твердым покрытием) и производят запись диаграмм внедрения «нагрузка Р - внедрение s» в некотором диапазоне конечных нагрузок, в порядке повышения их конечных нагрузок в каждом цикле нагружения (см. Воронин Н.А. Анализ причин специфического деформационного поведения топокомпозита системы AlN-Д16Т при инструментальном индентировании. Восточно-Европейский научный журнал. 2021. №10(74). С. 42 - 52). Как известно типовая диаграмма внедрения при инструментальном индентирования состоят из двух кривых: кривой нагружения и кривой разгрузки (см. Oliver W.C, Pharr G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, №7, pp. 1564-1583). Кривая нагружения описывает упругопластическую деформацию твердого тела под инденторов при его внедрении в поверхность этого тела. Кривая разгрузки описывает упругое деформирование (упругое восстановление) поверхности твердого тела при снятии нагрузки на индентор. Анализ диаграмм внедрения, для топокомпозитов на податливых подложках, показывает, что на всех кривых разгрузки можно выделить два характерных участка: в верхней части наблюдается кривая с малой кривизной - практически линейным изменением нагрузки с глубиной отпечатка, а в нижней части - участок кривой со значительным искривлением. Линейный участок кривой разгрузки с увеличением предельной нагрузки индентирования эквидистантно повторяется от одной диаграммы внедрения к другой, увеличиваясь по протяженности незначительно с увеличением конечной нагрузки. Кривизна нижнего участка кривой разгрузки с увеличением конечной нагрузки индентирования существенно изменяется - кривая разгрузки больше и раньше выгибается в сторону начала координат диаграммы внедрения. Наличие указанного характерного сильно криволинейного вида кривой разгружения связан с тремя параллельно идущими процессами, протекающими в процессе упругопластического нагружения индентором слоистой системы (см. Воронин Н.А. Анализ причин специфического деформационного поведения топокомпозита системы AlN-Д16Т при инструментальном индентировании. Восточно-Европейский научный журнал. 2021. №10(74). С. 42 - 52). Первый их них представляет собой процесс упругого прогиба покрытия по типу жесткой плиты, лежащей на податливой основе и нагружаемой в центре единичной силой. Второй - процесс упруго пластического деформирования слоистой системы. Оба этих процесса обеспечивают протекание третьего процесса - процесса межфазного расслоения на границе раздела «покрытие - подложка», которое ослабляет (разрывает) адгезионные связи между покрытием и подложкой. Прогиб усиливает процесс расслоения, что приводит к увеличению протяженности последнего (см. Abdul-Baqi A., Van der Giessen Е. Delamination of a strong film from a ductile substrate during indentation unloading. Journal of Materials Research. 2001. V. 16. N. 5. P. 1396-1407). При разгружении под действием упругих сил в изогнутом под нагрузкой покрытии происходит отслаивание покрытия от подложки, его восстановление до горизонтального первоначального состояния и даже некоторое выпучивание покрытия.
Для исследуемого топокомпозита переход от одной конечной нагрузки нагружения к последующей контролируется по величине глубины внедрения. Как правило, желательным диапазоном изменения глубины внедрения является (0,2 - 0,8) от толщины покрытия. При каждом цикле индентирования анализируют визуально поверхность покрытия вокруг отпечатков на расстоянии до пяти размеров диаметра отпечатка на предмет поврежденности покрытия (трещин, сколов, разрушений). Из диаграмм внедрения, для которых не обнаружено следов повреждения поверхности вокруг отпечатка, выбирается для последующих исследований максимальная по величине конечная нагрузка нагружения. До этой предельной нагрузки или близкой к ней, но меньшей по величине, производится индентирование с повторным нагружением в полученный отпечаток с записью диаграммы. Проводится не менее трех циклов повторных нагружений с разгружением в условиях реализации упругого деформирования. Конечная нагрузка повторных циклов индентирования проводится при достижении одной и той же величины нагрузки, но не превышающей 50% от конечной нагрузки первого цикла нагружения. Величина конечной нагрузки при повторных циклах нагружения выбирается из условия обеспечения отсутствия пластической деформации топокомпозита. Минимальные значения усилия на индентор при разгрузках как в первом цикле индентирования, так и в последующих повторных циклах нагружения устанавливался в районе не менее ~5% от конечной нагрузки первого цикла нагружения. Величина минимального усилия на индентор при разгрузке в повторных циклах индентирования выбирается из условия недопущения при разгружении перехода покрытия, как мембраны при восстановлении прогиба, через номинальное положение, соответствующее горизонтальному расположению покрытия на поверхности подложки. Последний цикл повторного индентирования заканчивается полной разгрузкой.
Из анализа расположения повторных кривых нагружения и разгрузки друг относительно друга делается вывод о правильности выбора величины конечной нагрузки повторных циклов индентирования. Полное совпадение (наложение друг на друга) кривых индентирования трех повторных циклов нагружения и разгрузки, позволяет говорить о том, что покрытие-мембрана работает исключительно в упругой зоне деформирования и отсутствует дополнительная пластическая деформация слоистого тела. Если совпадение не имеет место быть, то следует изменить величину конечной нагрузки нагружения для повторных циклов индентирования в меньшую сторону.
При совпадении между собой кривых индентирования трех повторных циклов выбираем третий цикл повторного индентирования и приступаем к анализу диаграммы. На фиг. 1 представлена диаграмма внедрения в поверхность покрытия (с неизвестными по величине остаточными напряжениями) с повторным циклом нагружения и разгрузки. Первый цикл нагружения проводится до достижения выбранной конечной нагрузки индентирования (Р1)max Выбранный дополнительный цикл повторного нагружения проводится до значения конечной нагрузки (Р2)max. Минимальное значение усилия на индентор при разгрузке в первом цикле индентирования устанавливается в районе (P1)min ≈ 0,05(P1)max.
Фиксируем значение величины глубины остаточного пластичного отпечатка по координатам конечной точки кривой разгружения повторного цикла индентирования (см. фиг. 1, точка А). Эта величина соответствует значению sr (см. фиг. 1).
Анализируем кривые деформирования повторного цикла индентирования (фиг. 2). При повторном нагружении покрытия условия напряженно-деформационного состояния в области контакта индентора с покрытием описываются кривой нагружения ВС/D. При этом в области ВС/ момент изгиба покрытия остаточными напряжениями в начальный момент интенсивно противодействует изгибному моменту от усилия нагружения индентора, а затем в меньшей степени оказывает сопротивление в связи с появлением растягивающих напряжений от удлинения покрытия при деформировании. На кривой существует точка С/, характеризующая моду изменения изгибного момента от остаточных напряжений с возрастания по величине к снижению по мере нагружения покрытия индентором. В точке D изменение направления действия усилия индентирования в связи с этапом разгружения имеет место перераспределение напряжений, действующих в контактной области. Это приводит к появлению упругого гистерезиса, описываемого кривой DCB. В точке С кривой DCB имеет место мода изменения величины изгибного момента от остаточных напряжений. При разгружении влияние остаточных напряжений на изгибающий момент начинает снижаться, снижается влияние усилие нагрузки, а влияние на суммарный изгибающий момент в покрытии от растягивающих сил изменяется в меньшей степени. В точке С происходит нейтрализация остаточных напряжений.
Определяются координаты точки С.Для этого аппроксимируем кривые ВС/D и DCB полиномами n-степени (как правило, не выше шестой) (см. фиг. 2). Рассчитываются значения разницы в глубинах внедрения Δs и величинах нагрузки ΔР между кривыми BCT/D и DCB при одинаковых величинах усилия индентирования и одинаковых значениях глубины внедрения, соответственно. Значения глубины внедрения и усилия нагружения, соответствующие максимальным значениям Δs и ΔР, будут координатами точки С. Аналогичная процедура по определению координат точки С может быть произведена графически, как это показано на фиг. 2 и представлена кривыми Δs и ΔР.
Точка С, принадлежащая кривой разгружения DCB одновременно принадлежит кривой упругого деформирования покрытия без остаточных напряжений при нагружении. Уравнение этой кривой нам неизвестно, но кривая упругого нагружения покрытия без остаточных напряжений включает упругую деформацию покрытия в результате индентирования и упругую деформацию покрытия как мембраны при ее центральном нагружении. Как указывалось, координаты точки С, принадлежат кривой разгрузки DCB и кривой упругого нагружения покрытия без остаточных напряжений. Более того координаты точек кривой DCB, лежащие ниже точки С, по крайней мере, расположенные вблизи точки С, также должны быть близки в к кривой упругого нагружения покрытия без остаточных напряжений. Обстоятельством, которое ясно по умолчанию, является схождение кривых упругого нагружения покрытия без остаточных напряжений, упругой деформации покрытия в результате индентирования и упругой деформацию покрытия как мембраны в одной точке на оси абсцисс. И нахождение этой точки на оси абсцисс детерминировано с местом нахождения точки С на диаграмме повторного индентирования. Нахождение вида кривой упругого нагружения покрытия без остаточных напряжений и координат точки начала этой кривой на оси абсцисс реализуется в результате проведения следующей процедуры.
Математически и графически анализируем предполагаемый вид кривых упругого нагружения покрытия без остаточных напряжений, упругого деформирования материала покрытия в результате индентирования и упругого деформирования покрытия как мембраны при ее центральном нагружении. Уравнение кривой упругого деформирования материала покрытия при индентировании рассчитывается по формуле (Fischer-Cripps А.С. Critical review of analysis and interpretation of nanoindentation test data. Surface & Coatings Technology, 2006. V. 200. P. 4153-4165):
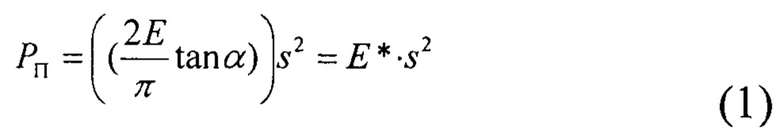
где α - эквивалентный угол конуса (70,3° для индентора Берковича), Е - модуль упругости материала покрытия, 
При подстановке известных значений параметров α и Е получаем уравнение параболы в виде 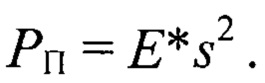
Уравнение кривой упругого деформирования покрытия как мембраны рассчитывается по формуле (Lu М., Huang Н. Interfacial energy release rates of SiN/GaAs film/substrate systems determined using a cyclic loading dual-indentation method. Thin Solid Films. 2015. V. 589. P. 822-830):
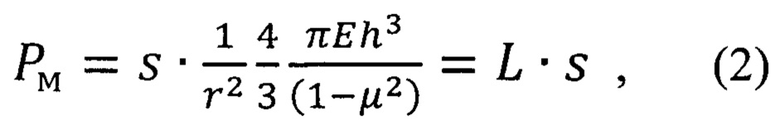
где rп - радиус отслаивания покрытия (радиус мембраны), h - толщина покрытия, μ - коэффициент Пуассона для материала покрытия, 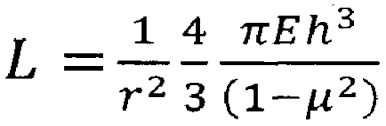 - жесткость покрытия как мембраны.
- жесткость покрытия как мембраны.
Графически уравнение упругого деформирования покрытия как мембраны представляет собой прямую линию.
Уравнение кривой упругого нагружения покрытия без остаточных напряжений представляет собой результат совместной деформации покрытия как материала и покрытия как мембраны. При графическом изображении она должна занимать промежуточное расположение между кривыми, рассчитываемыми по уравнениям (1) и (2). Кривая нагружения покрытия без остаточных напряжений может быть представлена полиномом вида

где K - константа покрытия, характеризующая суммарную жесткость упругого деформирования от индентирования и прогиба покрытия как мембраны.
Графически кривые (1), (2) и (3) можно представить на графике диаграммы внедрения (фиг. 3). В связи с отсутствием данных о значениях жесткости покрытия как мембраны и константы покрытия, характеризующей суммарную жесткость упругого деформирования от индентирования и прогиба покрытия как мембраны их истинное взаиморасположение возможно в результате графо-аналитического решения. В связи с эти, размещаем эти графики на диаграмме внедрения, смещеннной в свободное от места расположения истинной диаграммы внедрения, в начало координат.Строим кривую упругого деформирования материала покрытия при индентировании по уравнению (1). Аналитически рассчитываем жесткость покрытия как мембраны и суммарную жесткость упругого деформирования покрытия для известных значений координат точек С и В1, размещаемых на смещенной диаграмме внедрения в точках С*** и В1***. Выбор точек диктуется следующими условиями: точка С точно принадлежит кривой нагружения покрытия без остаточных напряжений, точка В1 достаточно отдалена от координат точки С (что бы получать значимое численное решение при ее использовании в аналитическом решении (4)), но функционально должна быть близка к траектории кривой нагружения покрытия без остаточных напряжений.
Составляем два баланса энергии, затрачиваемой на совершение работы по упругому деформированию покрытия без остаточных напряжений для точки С*** и точки В1***:
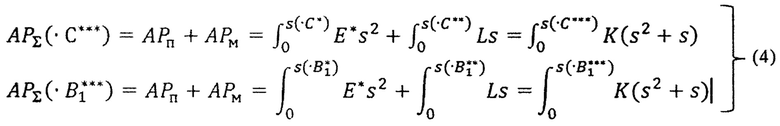
Из полученной системы уравнений, получаем значения множителей уравнений (2) и (3) L и K, так как значения абсцисс точек С, C*,С**,С*** и точек В1, B1*,B1**,B1*** известны. Строим прямую упругого деформирования покрытия как мембраны по уравнению (2). Строим кривую упругого нагружения покрытия без остаточных напряжений по уравнению (3) и проверяем, что три точки О, B1***, С*** принадлежат этой кривой. Если точки не совпадают с кривой, то смещаем начало координат всех кривых право, на некоторую величину, например, в точку А*. Строим все кривые из новой точки и убеждаемся, что три точки A*, B1***, С*** принадлежат кривой 9 (см. фиг. 3). Проводим проверку по точке В и убеждаемся что точки В** и В*** располагаются близко к соответствующим кривым, но не принадлежат им. Это является подтверждением правильности подбора кривой (9), так как только точка С и близкие к ней точки кривой В, B1, и С в районе В1С принадлежат кривой упругого нагружения покрытия без остаточных напряжений.
Смещаем кривую 9 в ее действительное положение на диаграмме внедрения, то есть совмещая точку С*** с точкой С (см. фиг. 3), рассчитываем по полученному уравнению координаты точек кривой нагружения покрытия без остаточных напряжений, аппроксимируем данные полиномом третьей степени и фиксируем координаты начало кривой в точке А0 (см. фиг. 3 и фиг. 4, кривая 9*). Абсцисса точки А0 характеризует остаточную глубину отпечатка (sr0) для топокомпозита с покрытием без остаточных напряжений.
Установленные значения величин глубины остаточного отпечатка для напряженного покрытия (sr) и для покрытия без остаточных напряжений (sr0) позволяют определить прогиб ƒ выпуклости отслоившегося покрытия после снятия нагрузки на индентор путем вычисления разницы между sr0 и sr.
Остаточные напряжения рассчитываются на основе элементарной теории балки, предполагающей, что деформация является чисто упругой и напряжение равномерно по толщине покрытия. Радиальный профиль выпученного покрытия, представляем в виде балки шириной а малой величины и высотой, равной толщине покрытия h. Такой профиль балки описывается косинусной функцией S в работе (Ma L.S.,. Lee D.W. Exact solutions for nonlinear static responses of a shear deformable FGM beam under an in-plane thermal loading. Eur. J. Mech. A Solids. 2012, V. 31(1), pp. 13-20):
S(X)=C[1- cos(2πX)],
где 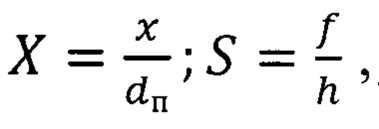 ƒ - максимальный прогиб покрытия как мембраны (балки) в центре.
ƒ - максимальный прогиб покрытия как мембраны (балки) в центре.
Множитель «С» получают путем подгонки профиля изгиба. Деформация балки связана с « С» через параметр λ:
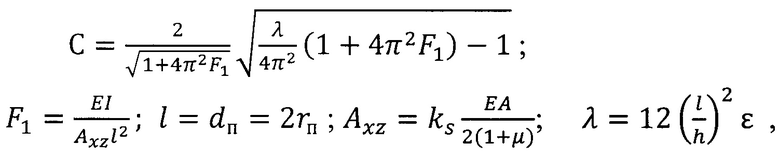
где ks - коэффициент сдвига Тимошенко, зависящий от геометрии: обычно ks=5/6 для прямоугольного сечения; l - длина балки; I - момент инерции; А - площадь поперечного сечения балки; Е1 - модуль упругости покрытия; μ - коэффициент Пуассона; dп=2 rп=l - диаметр межфазной трещины; rп - радиус межфазной трещины; ε - относительная деформация.
Радиус межфазной трещины определяется по формуле (2) по установленному ранее значению жесткости покрытия как мембраны.
Величина остаточных напряжений может быть рассчитана по величине относительной деформации ε:
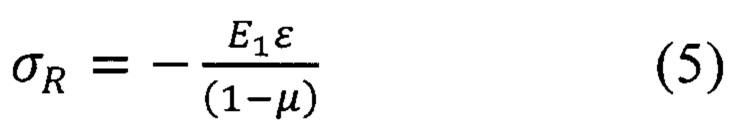
Пример. Для примера было произведено определение остаточных напряжений покрытия из нитрида алюминия (AlN), нанесенного магнетронным способом, толщиной 5 мкм на алюминиевый сплав Д16Т. Запись диаграммы внедрения производилось на наноиндентометре НаноСкан 4D при использовании пирамиды Берковича. Упругие характеристики материала основы изделия Е=93 ГПа и материала покрытия Е=320 ГПа, микротвердость 18 ГПа и 36 ГПа, соответственно, с достижением в первичном цикле индентирования максимальной нагрузки Значение конечной нагрузки в первом цикле индентирования составляло (P1)max=0,4Н, в повторном цикле - (P2)max ≈ 0,2Н. Минимальное значение усилия на индентор при разгрузке в первом цикле индентирования составляло (P1)min ≈ 0,02Н (см. фиг. 1).
Измеренное по диаграмме внедрения значение глубины пластического отпечатка в напряженном покрытии sr=0,89 мкм. Рассчитанные значения глубины отпечатка в покрытии без остаточных напряжений sr0=1,1 мкм, радиус межфазной трещины rп=72,5 мкм, прогиба покрытия ƒ=0,21 мкм. Значение коэффициента Пуассона для материала покрытия было принято μ=0,3.
Расчет остаточных напряжений в покрытии исследованного топокопозита проводился по формуле (5) и показал значение σR= -2,6 ГПа. Полученное значение достаточно близко совпадает со значениями остаточных напряжений, указываемых в научной литературе для покрытий из нитрида алюминия (см. например Greczyns ki G., Lu J., Johansson M.P. et al. Role of Tin+ and Aln+ ion irradiation (n=1,2) during Til-xAlxN alloy film growth in a hybrid HIPIMS/magnetron mode // Surface & Coatings Technology. 2012. V. 206. P. 4202-4211), где остаточные напряжения были измерены рентгеноструктурным методом и показали значение σR= -2,7 ГПа. Расчеты, сделанные в работе (Воронин Н.А. Усовершенствованный способ определения остаточных напряжений в тонких твердых покрытиях. Проблемы машиностроения и автоматизации, 202, №3 в печати), с использованием известных моделей S. Suresh и Q. Wang показали значения остаточных напряжений -2,25 ГПа и -2,65 ГПа, соответственно.
Результаты экспериментальной проверки свидетельствуют о пригодности предлагаемого способа для практического использования. Следовательно, заявленное изобретение соответствует требованию "промышленная применимость" по действующему законодательству.
Изобретение относится к измерительной технике для определения остаточных напряжений в тонком твердом напряженном покрытии, нанесенном на податливую подложку. Способ заключается в том, что изделие с покрытием, в котором присутствуют остаточные напряжения, подвергается микроиндентированию с получением диаграммы внедрения, содержащему два цикла индентирования. Первый цикл обеспечивает межфазное отделение покрытия на некотором участке без разрушения сплошности покрытия. Второй цикл нагружения проводится в тот же отпечаток, что и в первом цикле индентирования, но с нагружением, обеспечивающим упругое деформирование покрытия под индентором. По результатам анализа кривых повторного нагружения и разгрузки строится кривая нагружения для изделия с покрытием без присутствия в нем остаточных напряжений. Аналитическая обработка этих кривых нагружения покрытия с остаточными напряжениями и ненапряженного покрытия позволяет определить радиус межфазной трещины и прогиб выпуклости покрытия. С учетом известных начальных данных о материале покрытия и толщине вычисляется величина остаточных напряжений в покрытии по математической зависимости. Технический результат: упрощение процедуры определения остаточных напряжений за счет учета деформирования материала подложки и наличия эффекта межфазного расслоения. 7 з.п. ф-лы, 4 ил.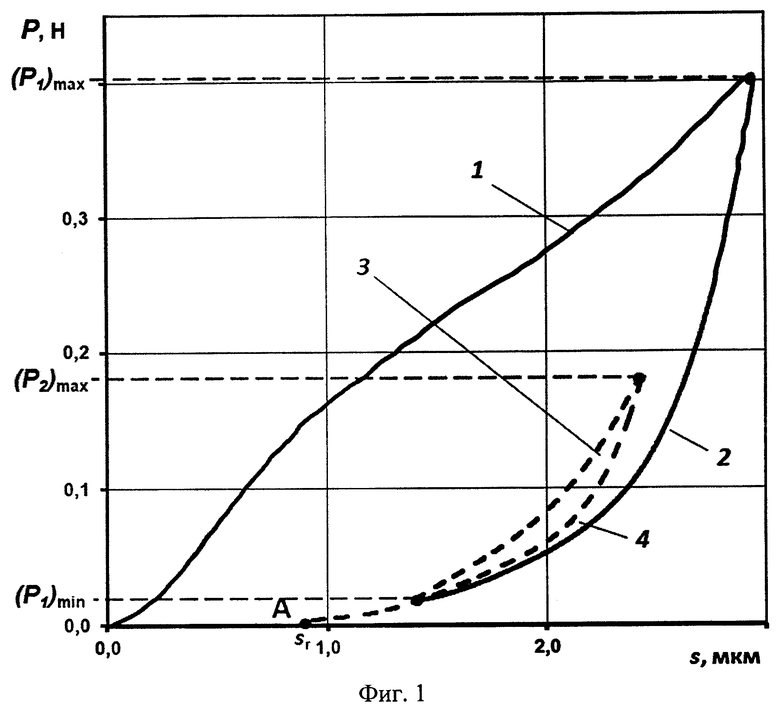
1. Способ определения остаточных напряжений в тонком твердом напряженном покрытии, нанесенном на податливую подложку, включающий выделение части покрытия, анализ профиля и расчет величины остаточных напряжений σR в покрытии по формуле (Ф1)
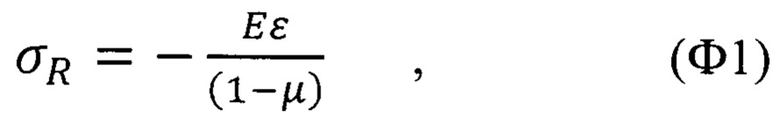
где Е - модуль упругости покрытия; μ - коэффициент Пуассона материала покрытия; ε - относительная деформация покрытия, связанная с параметром λ зависимостью 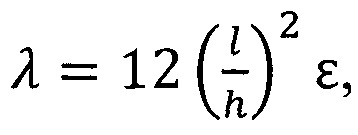 который в свою очередь связан с множителем С косинусоидальной функции S(X)=С[(1-cos(2πX)], описывающей профиль выпучивания части покрытия в радиальном сечении, рассчитываемый через следующие зависимости
который в свою очередь связан с множителем С косинусоидальной функции S(X)=С[(1-cos(2πX)], описывающей профиль выпучивания части покрытия в радиальном сечении, рассчитываемый через следующие зависимости
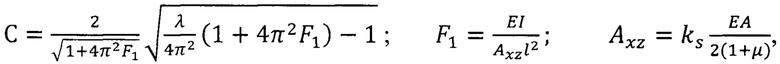 где
где 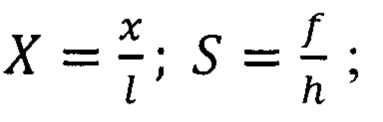 ƒ - максимальный прогиб покрытия; ks - коэффициент сдвига Тимошенко, зависящий от геометрии; l - длина балки; I - момент инерции; А - площадь поперечного сечения балки, отличающийся тем, что в нем отделение части покрытия от подложки производят путем индентирования в покрытие алмазного пирамидального наконечника в режиме нагружения, производимого до некоторой максимальной величины нагрузки (P1)max, и затем последующего разгружения, производимого до некоторой минимальной величины нагрузки (Р1)min на индентор, приводящих к межфазному отделению покрытия от подложки с радиусом rп=l/2, затем производят повторное внедрение индентора в тот же отпечаток путем нагружения индентора до некоторой конечной нагрузки (Р2)max, меньшей, чем (P1)max, и последующее разгружение, заканчивающееся полным снятием нагрузки на индентор, записывают диаграмму внедрения этих двух циклов индентирования в виде графиков кривых изменения нагрузки Р от глубины внедрения s при возрастании и затем снижении нагрузки, фиксируют глубину sr пластического отпечатка в напряженном покрытии по точке пересечения кривой повторной разгрузки с осью абсцисс диаграммы внедрения, описывают математические кривые повторного цикла нагружения и разгрузки в виде полиноминальных уравнений, обрабатывают эти уравнения, определяют на основе графоаналитической обработки ряда данных повторной кривой разгрузки, теоретического уравнения упругого деформирования материала покрытия при индентировании в ненапряженное покрытие, теоретического уравнения прямой, описывающей деформирование покрытия как мембраны, нагруженной центральной силой и закрепленной жестко по краю, координаты, а затем уравнение в виде полинома третьей степени кривой, описывающей суммарное упругое деформирование ненапряженного покрытия как материала и мембраны, фиксируют на диаграмме внедрения второго цикла индентирования вид и расположение кривой, описывающей суммарное упругое деформирование ненапряженного покрытия как материала и мембраны, фиксируют глубину пластического отпечатка в покрытии без остаточных напряжений, определяемую по точке пересечения кривой, описывающей упругое суммарное деформирование ненапряженного покрытия как материала и мембраны, с осью абсцисс диаграммы внедрения, рассчитывают радиус rп межфазного расслоения покрытия, рассчитывают величину прогиба выпучивания покрытия ƒ как разницу в размерах глубин пластического отпечатка для покрытия напряженного sr и без остаточных напряжений sr0 и, используя известные данные об упругих свойствах материала покрытия и его толщине, рассчитывают величину остаточных напряжений σR в покрытии по формуле (Ф1).
ƒ - максимальный прогиб покрытия; ks - коэффициент сдвига Тимошенко, зависящий от геометрии; l - длина балки; I - момент инерции; А - площадь поперечного сечения балки, отличающийся тем, что в нем отделение части покрытия от подложки производят путем индентирования в покрытие алмазного пирамидального наконечника в режиме нагружения, производимого до некоторой максимальной величины нагрузки (P1)max, и затем последующего разгружения, производимого до некоторой минимальной величины нагрузки (Р1)min на индентор, приводящих к межфазному отделению покрытия от подложки с радиусом rп=l/2, затем производят повторное внедрение индентора в тот же отпечаток путем нагружения индентора до некоторой конечной нагрузки (Р2)max, меньшей, чем (P1)max, и последующее разгружение, заканчивающееся полным снятием нагрузки на индентор, записывают диаграмму внедрения этих двух циклов индентирования в виде графиков кривых изменения нагрузки Р от глубины внедрения s при возрастании и затем снижении нагрузки, фиксируют глубину sr пластического отпечатка в напряженном покрытии по точке пересечения кривой повторной разгрузки с осью абсцисс диаграммы внедрения, описывают математические кривые повторного цикла нагружения и разгрузки в виде полиноминальных уравнений, обрабатывают эти уравнения, определяют на основе графоаналитической обработки ряда данных повторной кривой разгрузки, теоретического уравнения упругого деформирования материала покрытия при индентировании в ненапряженное покрытие, теоретического уравнения прямой, описывающей деформирование покрытия как мембраны, нагруженной центральной силой и закрепленной жестко по краю, координаты, а затем уравнение в виде полинома третьей степени кривой, описывающей суммарное упругое деформирование ненапряженного покрытия как материала и мембраны, фиксируют на диаграмме внедрения второго цикла индентирования вид и расположение кривой, описывающей суммарное упругое деформирование ненапряженного покрытия как материала и мембраны, фиксируют глубину пластического отпечатка в покрытии без остаточных напряжений, определяемую по точке пересечения кривой, описывающей упругое суммарное деформирование ненапряженного покрытия как материала и мембраны, с осью абсцисс диаграммы внедрения, рассчитывают радиус rп межфазного расслоения покрытия, рассчитывают величину прогиба выпучивания покрытия ƒ как разницу в размерах глубин пластического отпечатка для покрытия напряженного sr и без остаточных напряжений sr0 и, используя известные данные об упругих свойствах материала покрытия и его толщине, рассчитывают величину остаточных напряжений σR в покрытии по формуле (Ф1).
2. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что желательным значением предельной нагрузки (P1)max при первичном цикле нагружения является нагрузка, обеспечивающая отсутствие повреждений в покрытии после индентирования в виде поперечных трещин, сколов и нарушения сплошности покрытия.
3. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что минимальное значение усилия на индентор при разгрузке в первом цикле индентирования устанавливается в районе не более ~5% (Р1)тах, но не менее величины, при которой начинается выпучивание покрытия.
4. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что конечная нагрузка (Р2)max повторного цикла нагружения не превышает величины 0,5 (P1)max и не вносит пластическую деформацию в покрытие и подложку.
5. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что кривые повторного цикла нагружения и разгрузки описывают полиноминальными уравнениями n-й степени, не менее шестой.
6. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что обработка полиноминальных кривых повторного нагружения и разгрузки кривых заключается в сравнении аналитически или графически их между собой и по разнице в глубинах внедрения Δs и величинах нагрузки ΔР между кривыми нагружения и разгрузки при одинаковых величинах усилия индентирования и одинаковых значениях глубины внедрения соответственно, устанавливают ординату и абсциссу максимальных значений Δs и ΔР соответственно, фиксируют аналитически и графически координаты точки С на кривой повторного разгружения, которая является модой кривой повторного разгружения и координаты которой в свою очередь принадлежат кривой упругого деформирования покрытия без остаточных напряжений.
7. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что графоаналитической обработке подвергают:
- кривую упругого деформирования ненапряженного покрытия как материального твердого тела, построенную по известной квадратичной зависимости
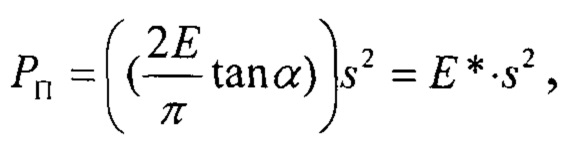
где Е - модуль упругости материала покрытия; α - эквивалентный угол конуса; 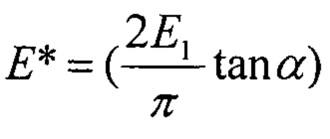 - жесткость покрытия как материала при индентировании острым индентором,
- жесткость покрытия как материала при индентировании острым индентором,
- прямую упругого деформирования ненапряженного покрытия как мембраны, нагруженной центральной силой и закрепленной по краю, описываемую известной линейной зависимостью
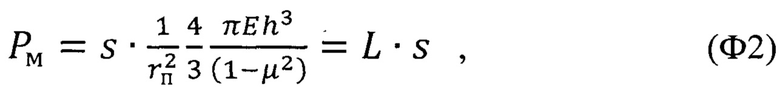
где rп - радиус отслаивания покрытия (радиус мембраны); h - толщина покрытия; μ - коэффициент Пуассона для материала покрытия; 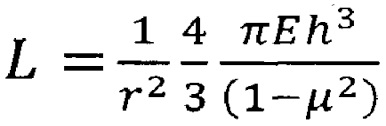 - жесткость покрытия как мембраны,
- жесткость покрытия как мембраны,
- кривую суммарного упругого деформирования ненапряженного покрытия как материала и мембраны, которая может быть описана некоторой нелинейной зависимостью вида
РΣ=K(s2+S),
где К - суммарная жесткость покрытия как материала и мембраны,
- координаты двух точек кривой повторного разгружения, точки С и точки В1, принадлежащей нижней части ветви кривой повторного разгружения, и точки на кривой оси абсцисс, определяющей начало координат всех упомянутых в данном пункте формулы кривых, и
- систему уравнений, описывающих баланс энергии, затрачиваемой на совершение работы по суммарному упругому деформированию ненапряженного покрытия как материала и мембраны в виде суммы затрачиваемой энергии отдельно при упругом деформировании покрытия как материала и как мембраны для известных координат точек С и В1, рассчитывают значения L и К, аналитически рассчитывают уравнение суммарного упругого деформирования ненапряженного покрытия и графически фиксируют на диаграмме внедрения.
8. Способ определения остаточных напряжений в тонком твердом напряженном покрытии по п. 1, нанесенном на податливую подложку, отличающийся тем, что для расчета радиуса rп межфазного расслоения используют зависимость, представленную формулой (Ф2).
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА ПОКРЫТИЯ НА ИЗДЕЛИИ | 2018 |
|
RU2683597C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА ПОКРЫТИЯ НА ИЗДЕЛИИ | 2016 |
|
RU2618500C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНОГО НАПРЯЖЕНИЯ С ПРИМЕНЕНИЕМ ИНСТРУМЕНТАЛЬНОГО ИНДЕНТИРОВАНИЯ, НОСИТЕЛЬ ИНФОРМАЦИИ С СООТВЕТСТВУЮЩЕЙ КОМПЬЮТЕРНОЙ ПРОГРАММОЙ И УСТРОЙСТВО ДЛЯ ИНСТРУМЕНТАЛЬНОГО ИНДЕНТИРОВАНИЯ, ПРЕДНАЗНАЧЕННОЕ ДЛЯ РЕАЛИЗАЦИИ ИНСТРУМЕНТАЛЬНОГО ИНДЕНТИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ НОСИТЕЛЯ ИНФОРМАЦИИ | 2013 |
|
RU2611078C1 |
| Способ определения вязкости микроразрушения тонких аморфно-нанокристаллических плёнок | 2018 |
|
RU2699945C1 |
| KR 1020050056177 A, 14.06.2005 | |||
| CN 104075941 A, 01.10.2014. | |||
Авторы
Даты
2023-07-20—Публикация
2022-08-19—Подача