Изобретение относится к навигационным приборам для контроля и управления летательными аппаратами (ЛА), а также к области приборостроения и может применяться в системах навигации ЛА.
Известен способ определения пространственного положения и курса летательного аппарата, патент №2505786, МПК G01C 23/00, опубликованный 27.01.2014 г., бюл. №3, принятый нами в качестве прототипа.
В известном способе для повышения надежности в полете при кратковременном отключении напряжения питания после его восстановления при вычислении углов пространственной ориентации используют тарировочные характеристики блока датчиков угловой скорости (БДУС), блока датчиков линейного ускорения (БДЛУ), трехкомпонентного магнитометра с учетом изменения температуры окружающей среды. Летательный аппарат выводят на горизонтальный прямолинейный участок полета без ускорения и активизируют режим ускоренной коррекции, при котором согласуют углы, вычисленные по информации от блока датчиков угловой скорости, с углами, вычисленными по информации от блока датчиков линейного ускорения и трехкомпонентного магнитометра.
Недостатком вышеприведенного способа является возможность коррекции углов только в процессе невозмущенного полета без ускорений. Так как в турбулентной атмосфере создать невозмущенный полет крайне сложно, определение улов пространственной ориентации летательного аппарата происходит со значительными ошибками.
Целью предлагаемого способа является расширение функциональных возможностей и повышение точности определения навигационных параметров в условиях маневрирования.
Поставленная цель достигается путем применения способа определения углов пространственной ориентации, заключающегося в использовании информации от блока датчиков угловой скорости, блока датчиков линейного ускорения, трехкомпонентного магнитометрического датчика (ТМД), режима коррекции, дополнительно осуществляют определение и списание девиации ТМД, включая круговую девиацию после набора высоты путем совершения полета по кругу, используют адаптированную к внешним возмущениям бесплатформенную инерциальную курсовертикаль (БИКВ) и ТМД со списанной в полете девиацией, осуществляют оптимизацию коэффициентов адаптивной коррекции углов, используя при этом введенные датчики динамического и статического давлений для определения воздушной скорости, с последующим дифференцированием и фильтрацией для получения сигнала, пропорционального линейному продольному ускорению, и дополнительную оптимизацию коэффициентов адаптивной коррекции, выполняя настройку на множестве обучающих последовательностей.
Ниже приведено описание работы способа определения углов пространственной ориентации.
После набора высоты совершают полный круг над аэродромом или в заданной зоне, где отсутствуют магнитные аномалии, в процессе которого запоминаются значения измеренного магнитного курса при помощи ТМД.
Как показывают расчеты, модель содержит шесть параметров Пуассона, которые устойчиво определяются по ограниченному объему полетных данных.
Используя упрощенную модель, которая позволяет учесть влияние второй по значимости четвертной девиации на ошибку определения магнитного курса и приведенные ниже алгоритмы, определяют коэффициенты магнитной девиации ТМД.

где:
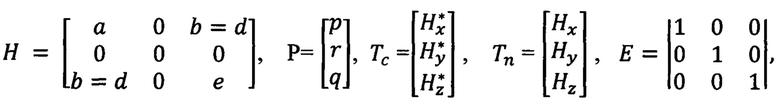
Коэффициенты p, q, r учитывают влияние магнитного поля твердого в магнитном отношении железа. Коэффициенты а, b, d, е учитывают влияние магнитного поля мягкого в магнитном отношении железа ЛА. Допущение о равенстве коэффициентов b и d является пренебрежением влияния индуктивного магнитного поля ЛА на постоянное смещение оценки магнитного курса.
С учетом направления связанных осей ЛА начальные матрица Н и вектор Р принимают вид
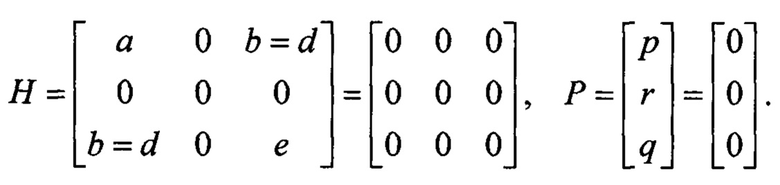
Далее определяют:
- Оценку модуля магнитного поля земли (МПЗ) 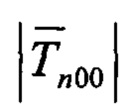 , усредненную на всем отрезке наблюдения из N отсчетов:
, усредненную на всем отрезке наблюдения из N отсчетов:
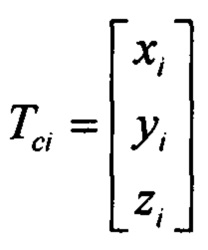 - полную совокупность измерений магнитометра;
- полную совокупность измерений магнитометра;
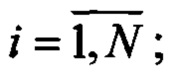
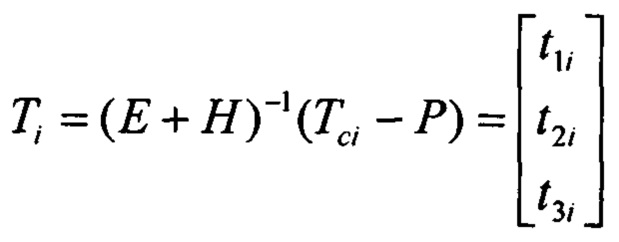 - совокупность оценок измерений магнитометра с учетом компенсации девиации;
- совокупность оценок измерений магнитометра с учетом компенсации девиации;
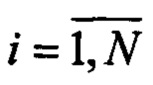
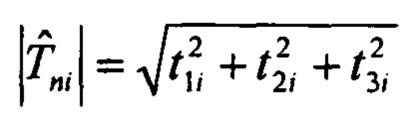 - совокупность оценок модуля МПЗ с учетом компенсации девиации;
- совокупность оценок модуля МПЗ с учетом компенсации девиации;
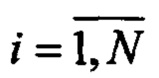
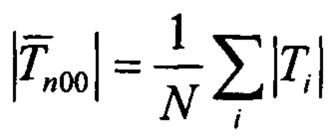 - оценку модуля МПЗ, усредненную по всему отрезку наблюдения;
- оценку модуля МПЗ, усредненную по всему отрезку наблюдения;
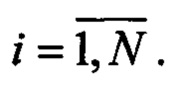
- Оценку средних значений модуля МПЗ 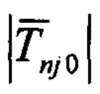 ,
, 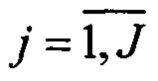 на J частных интервалах:
на J частных интервалах:
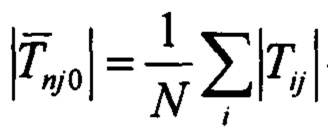 - совокупность оценок модуля МПЗ, усредненных на частных интервалах наблюдения;
- совокупность оценок модуля МПЗ, усредненных на частных интервалах наблюдения;
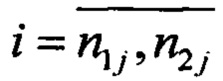 ,
, 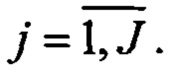
- Запоминают вектор частных оценок модуля МПЗ.
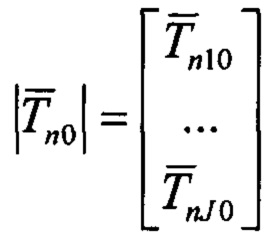 вектор
вектор 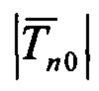 имеет размерность J.
имеет размерность J.
- Формируют вектор В разностей между оценкой модуля МПЗ, усредненной по всему отрезку наблюдения, и оценками, усредненными на частных интервалах:
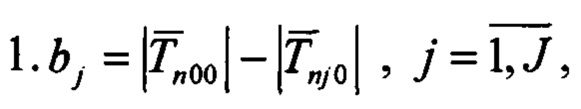
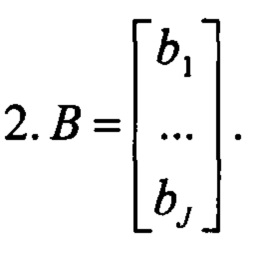
- Вычисляют функции чувствительности измерений модуля МПЗ к вариациям искомых коэффициентов.
Вычисление приращений оценок коэффициентов осуществляется путем формирования системы линейных алгебраических уравнений.
Аα=В,
где А - матрица функций чувствительности размерностью [j×6]
В=[φp φr φq φa φе φbd],
В - вектор размерностью J,
αT=[Δp Δr Δq Δa Δе Δb],
α - вектор приращений.
Вектор приращений определяется решением следующего выражения:
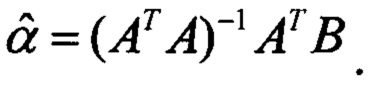
При правильном решении приращения Δp Δr Δq Δa Δе Δb по мере выполнения итераций стремятся к нулю. Итерационный процесс полагаем успешным, если на последней итерации выполняется условие:
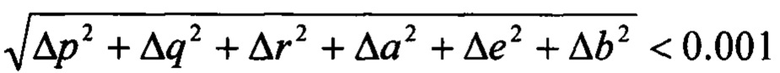
Текущее значение магнитного курса ЛА вычисляется с помощью соотношений:
Тψi=Сϑγ(Е+М)-1(Tci-Р),
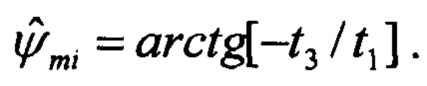
Основные положения способа списания девиации в полете приведены в работе [1].
Далее определяют круговую девиацию A0. Заметим, что модель (1) описывает все составляющие девиации, в том числе и круговую, которая неразличима с угловой ошибкой установки магнитометра в горизонтальной плоскости. В связи с этим при определении коэффициентов матрицы М модели (1) необходимо учитывать хотя бы одно измерение курса, которое наиболее просто выполнить перед взлетом ЛА.
Обозначим А=A0 - оценку приближенного коэффициента круговой девиации по измерению начального курса. Для нее имеют место соотношения

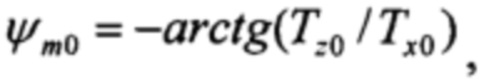
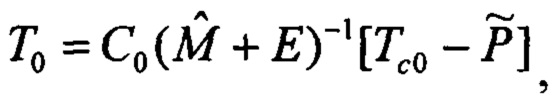
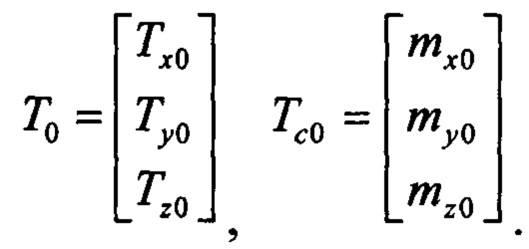
Здесь 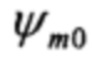 - оценка начального курса ψ0 по сигналам магнитометра, спроецированным на плоскость нормальной земной системы координат с учетом магнитного склонения и оценок М и P, полученных при условии b=d; С0 - матрица поворота.
- оценка начального курса ψ0 по сигналам магнитометра, спроецированным на плоскость нормальной земной системы координат с учетом магнитного склонения и оценок М и P, полученных при условии b=d; С0 - матрица поворота.
Поскольку оценивание А0 опирается на оценки М и Р, задачу идентификации надо решать повторно. Как показывают расчеты, достаточно двух решений.
Для этого используются известные соотношения Арчибальда Смита, связывающего коэффициенты модели (1) с коэффициентами девиации, как ошибки магнитного курса при горизонтальном положении магнитометра.
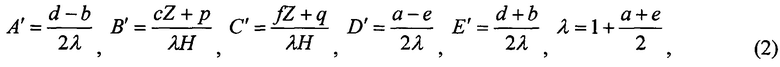
Здесь A',B',C',D',E' являются точными коэффициентами девиации 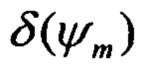 . Заметим, что приближенные коэффициенты девиации в (1) соответствуют δ=tgδ и определяются как А=А', В=В', С=С', D=D', Е=Е'.
. Заметим, что приближенные коэффициенты девиации в (1) соответствуют δ=tgδ и определяются как А=А', В=В', С=С', D=D', Е=Е'.
При первом решении алгоритма идентификации полагается А=А'=0. С учетом (2) это соответствует b=d и выполняется предварительная идентификация шести коэффициентов a, d, e, p, q, r.
При втором решении алгоритма идентификации коэффициенты a, d, e, p, q, r уточняются при условии b=A0d(2+а+е), которое следует из (2) для А≠0.
В целом реализация предлагаемого метода определения круговой девиации А0 состоит из следующих этапов.
1. Измерение |T0| с помощью откалиброванного магнитометра.
2. Измерение и запоминание начального курса, крена, тангажа и сигналов магнитометра при неподвижном положении ЛА перед взлетом.
3. Выполнение полета по замкнутой в плане траектории, и накопление измерений магнитометра на участке маневра.
4. Вычисление начального приближения оценок коэффициентов а, b, d, e, p, q, r при условии b=d путем решения алгоритма параметрической идентификации.
5. Определение оценки круговой девиации А0 с учетом измерений начального курса, крена, тангажа и известного магнитного склонения.
6. Вычисление результирующих оценок коэффициентов a, b, d, e, p, q, r при условии b=A0d(2+а+е).
Заметим, что измерение начального курса можно определить пеленгом на любой заданный ориентир.
Компенсация девиации с целью оценивания курса в процессе полета состоит в вычислении оценки текущего курса ЛА ψi по сигналам магнитометра 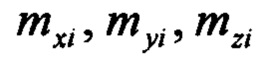 по модели (1) с идентифицированными коэффициентами.
по модели (1) с идентифицированными коэффициентами.

Здесь Ci - матрица поворота, учитывающая текущие значения крена, тангажа и магнитного склонения.
В описании работы БИКВ используют две модели ориентации. Модель 1 предназначена для учета изменения ориентации аппарата на шагах дискретизации измерений БДУС. Она является динамической, детерминированной и представлена в параметрах Родрига-Гамильтона:
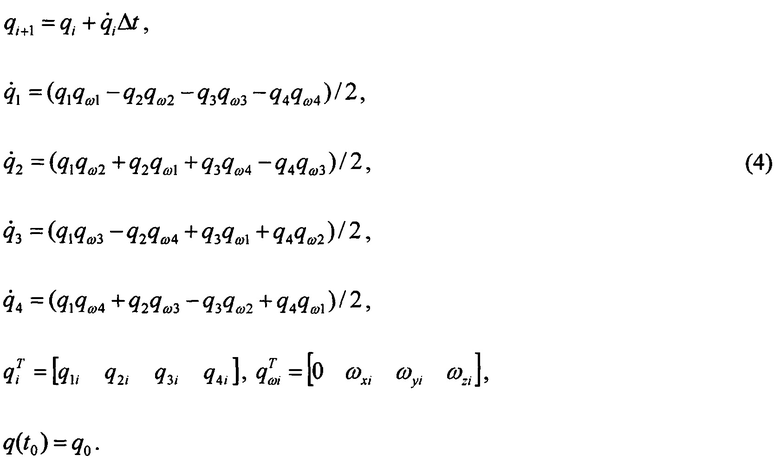
Здесь qi - кватернион ориентации ЛА; qωi - кватернион угловых скоростей; i - номер дискретного момента времени; Δt - шаг дискретизации измерений; q0 - кватернион ориентации для начального момента времени.
Кватернион q определяет ориентацию связанной системы координат ЛА относительно подвижной системы координат, роль которой играет нормальная система координат. С точки зрения теории бесплатформенных инерциальных систем соотношения (4) являются одношаговым алгоритмом ориентации.
Модель 2 предназначена для коррекции модели 1. Вектор состояния модели 2 учитывает три компоненты - крен, тангаж и скорость ЛА относительно Земли. Вектор состояния модели 2 подлежит оцениванию по текущим значениям сигналов БДЛУ. Модель 2 является стохастической и статической, поскольку ее состояние учитывается для текущего дискретного момента времени ti. Соотношения для модели 2 имеют вид:
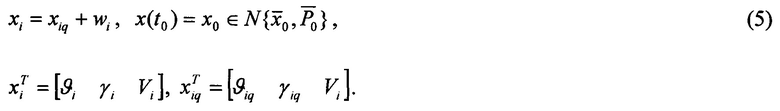
Здесь xi - вектор состояния; 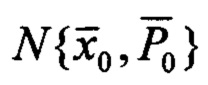 - его априорное нормальное распределение; V - земная скорость; wi - вектор возмущений; xiq - вспомогательный вектор, рассчитываемый по кватерниону ориентации модели 1 с помощью матрицы А поворота связанной системы координат относительно нормальной
- его априорное нормальное распределение; V - земная скорость; wi - вектор возмущений; xiq - вспомогательный вектор, рассчитываемый по кватерниону ориентации модели 1 с помощью матрицы А поворота связанной системы координат относительно нормальной
А(3×3)=[aij],
ϑ=arcsin(a(1,2)), γ=-acrtg(a(3,2)/a(2,2)).
Обозначим 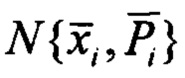 - априорное нормальное распределение вектора состояния модели 2 для момента времени ti;
- априорное нормальное распределение вектора состояния модели 2 для момента времени ti; 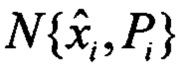 - апостериорное распределение, подлежащее оцениванию;
- апостериорное распределение, подлежащее оцениванию; 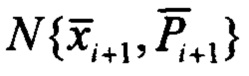 - априорное распределение для следующего момента времени ti+1. Тогда алгоритм БИКВ, решаемый на одном интервале дискретизации измерений Δt, представляется в виде последовательности следующих шагов.
- априорное распределение для следующего момента времени ti+1. Тогда алгоритм БИКВ, решаемый на одном интервале дискретизации измерений Δt, представляется в виде последовательности следующих шагов.
Шаг 1. Определение статистик апостериорной плотности 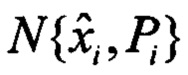 вектора состояния модели 2 с учетом
вектора состояния модели 2 с учетом 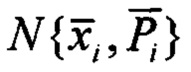 и текущих измерений гироскопов и акселерометров. Определение статистик апостериорной плотности
и текущих измерений гироскопов и акселерометров. Определение статистик апостериорной плотности 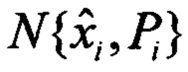 имеет вид известных соотношений байесовского оценивания вектора состояния по вектору его дискретных измерений.
имеет вид известных соотношений байесовского оценивания вектора состояния по вектору его дискретных измерений.
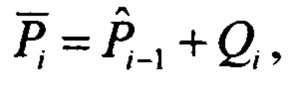
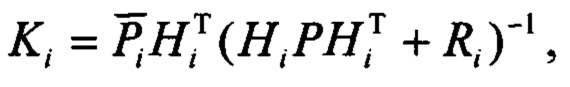
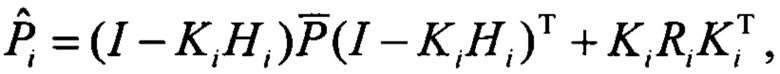
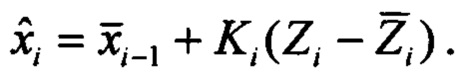
Здесь 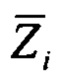 - оценка вектора наблюдений, которая имеет вид
- оценка вектора наблюдений, которая имеет вид
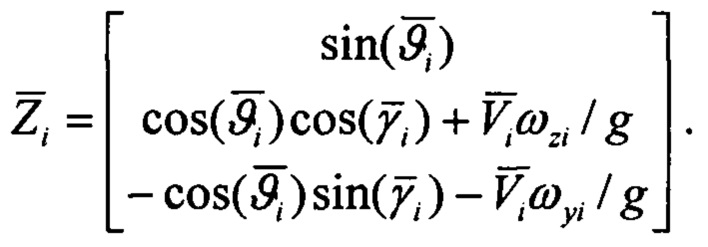
Шаг 2. Расчет кватерниона ориентации 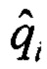 .
.
Шаг 3. Вычисление априорного кватерниона ориентации 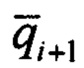 для следующего момента дискретного времени.
для следующего момента дискретного времени.
Шаг 4. Вычисление статистик априорной плотности 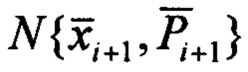 . Вычисление статистик априорной плотности
. Вычисление статистик априорной плотности 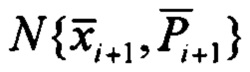 включает в себя расчет априорного математического ожидания и ковариационной матрицы. Априорное математическое ожидание компоненты скорости определяют с учетом допущения о постоянстве скорости и принимают равным ее оценке:
включает в себя расчет априорного математического ожидания и ковариационной матрицы. Априорное математическое ожидание компоненты скорости определяют с учетом допущения о постоянстве скорости и принимают равным ее оценке: 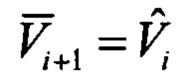 . Априорные математические ожидания тангажа
. Априорные математические ожидания тангажа 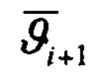 и крена
и крена 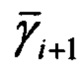 вычисляют по кватерниону
вычисляют по кватерниону 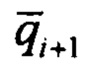 и соотношениям (1). Априорную ковариационную матрицу приближенно принимают равной апостериорной ковариационной матрице
и соотношениям (1). Априорную ковариационную матрицу приближенно принимают равной апостериорной ковариационной матрице 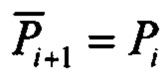 . Применение более сложных соотношений для ее расчета представляется неоправданным в силу приближенности модели 2.
. Применение более сложных соотношений для ее расчета представляется неоправданным в силу приближенности модели 2.
Указанные вычисления выполняют на каждом шаге Δt по мере поступления новых измерений БДУС и БДЛУ [2,3].
В предлагаемом способе осуществляют оптимизацию адаптации коэффициентов фильтра БИКВ в зависимости от турбулентности. Полные выражения для перегрузок, зависящих от параметров полета ЛА, определяются следующими выражениями:
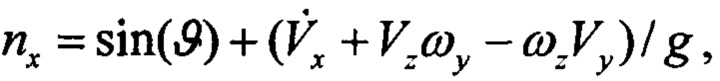
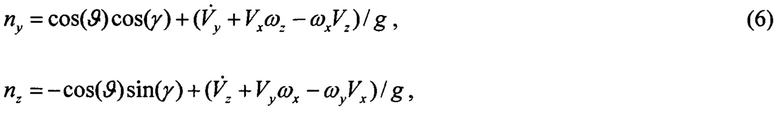
где: Vx, Vy, Vz - проекции скорости ЛА на связанную систему координат,
g - ускорение силы тяжести.
Степень влияния слагаемых в правых частях (6) зависит от режима полета.
В режиме прямолинейного горизонтального полета с постоянной скоростью имеет место 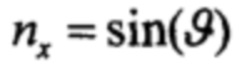 ,
, 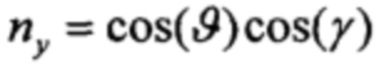 ,
, 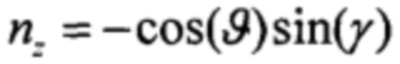 . Данные соотношения используются в простейших вариантах коррекции, когда ускорения, создаваемые ЛА значительно меньше гравитационных.
. Данные соотношения используются в простейших вариантах коррекции, когда ускорения, создаваемые ЛА значительно меньше гравитационных.
Слагаемые (Vzωy-ωzVy)/g, (Vxωz-ωxVz)/g, (Vyωx-ωyVx)/g обусловлены появлением кориолисовых сил и имеют значимость при разворотах ЛА.
Слагаемые 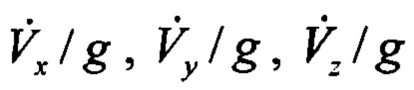 имеют значимость при появлении линейных ускорений по связанным осям ЛА.
имеют значимость при появлении линейных ускорений по связанным осям ЛА.
В рамках вектора состояния модели (2) учитывают наиболее значимые члены в (6). При относительно небольших углах атаки и скольжения скорость направлена в основном по строительной оси ЛА, тогда можно сделать допущение:
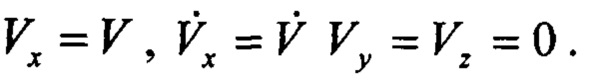
Тогда (6) представляются в упрощенном виде:

Приближенность (7) и допущения снижают точность учета составляющих кажущегося ускорения (6). Однако строгое выполнение (7) не требуется, в чем и состоит преимущество исходной идеи. Суть заключается в том, что всякое отклонение измеренного модуля перегрузки от единицы и всякие неточности в (7) учитываются снижением доверия к наблюдениям перегрузок путем увеличения дисперсий в ковариационной матрице Ri. При этом снижается интенсивность коррекции, следовательно, снижаются ее ошибки.
На участках разгона и торможения значительный вклад в изменение параметра кажущегося ускорения вносит производная скорости. Учитывая то, что изменение скорости ЛА относится к длиннопериодическому движению, производная скорости выделяется из оценки скорости с помощью сглаживающего фильтра нижних частот
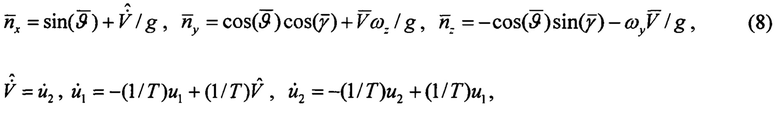
где Т - постоянная времени фильтра нижних частот.
Из рассмотрения Якобиана выражения (7) следует, что оценивание скорости ЛА происходит при выполнении разворотов, когда присутствуют одна или обе угловые скорости ωz, ωу. При этом слагаемые ωxV/g, - ωyV/g в соотношениях для 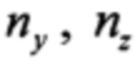 (7) обеспечивают оценивание крена. Из первого уравнения в (7) следует, что слагаемое
(7) обеспечивают оценивание крена. Из первого уравнения в (7) следует, что слагаемое 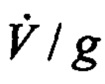 в выражении для
в выражении для 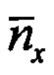 влияет на оценивание тангажа.
влияет на оценивание тангажа.
На участках полета при взлете и посадке, когда скорость изменяется наиболее интенсивно, а ЛА не выполняет разворотов, скорость не оценивается, но при этом учитывают 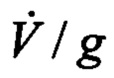 для повышения точности оценивания тангажа.
для повышения точности оценивания тангажа.
Определение барометрической высоты и воздушной скорости осуществляют по выходным сигналам микромеханических датчиков статического и динамического давлений по известным соотношениям:
Т=Т0-0,065 h,
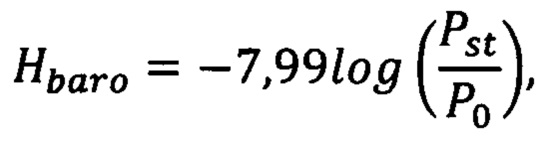
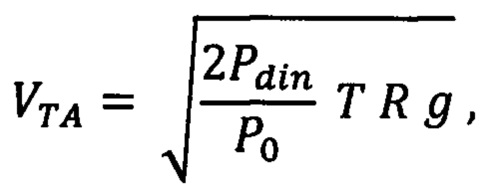
Где:
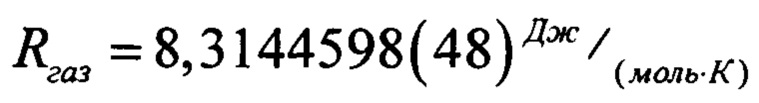
T0=273 К
λ=0,065 К/м
Hbaro, VTA - барометрическая высота и воздушная скорость,
Pst, Pdyn - статическое и динамическое давление,
Т - температура воздуха на заданной высоте h.
Выделение производной 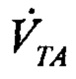 выполняют аналогично (8) с помощью фильтра нижних частот:
выполняют аналогично (8) с помощью фильтра нижних частот:
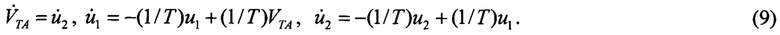
Заметим, что при этом постоянные рассогласования между земной и истинной воздушной скоростями не вносят ошибок в определение производной. Динамические ошибки измерения VTA на малых высотах взлета и посадки незначительны. Шумовые погрешности сглаживаются фильтром. Поэтому с достаточной точностью правомерно полагать 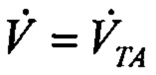 .
.
Дополнительную оптимизацию коэффициентов фильтра БИКВ выполняют с учетом уровня погрешностей датчиков. Путем анализа ошибок инерциальных датчиков с помощью спектральной плотности мощности и дисперсии Алана выделяют шумы квантования, случайное блуждание (дрейф), нестабильность смещения нуля (фликкер шум), а также случайное блуждание (дрейф) скорости, мультипликативную систематическую погрешность и синусоидальный шум.
С учетом того, что основной вклад в ошибки ориентации вносят смещения нулей БДУС, настройку коэффициентов фильтра БИКВ выполняют на множестве обучающих последовательностей, формируемых для набора сочетаний знаков смещений. Для каждого полета формируют девять обучающих последовательностей. Варианты знаков смещений нулей гироскопов представлены в таблице 1, где с0 - абсолютная величина смещения. Величина с0 задается с учетом класса точности используемых ДУС.
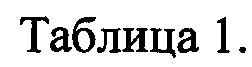
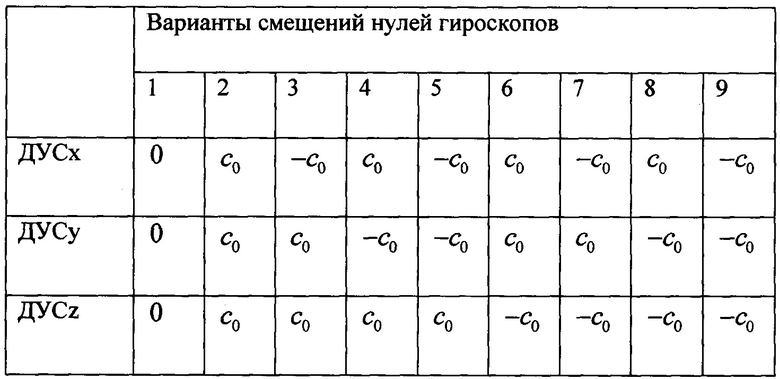
Всего в алгоритме присутствует шесть коэффициентов, подлежащих настройке: q1, q2, q3 - диагональные элементы ковариационной матрицы возмущений Q, a=d1, 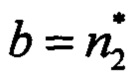 ,
, 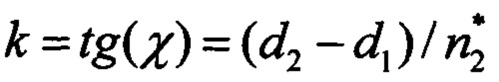 - коэффициенты нелинейной функции
- коэффициенты нелинейной функции 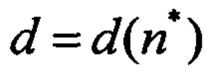 , определяющей диагональные элементы ковариационной матрицы ошибок наблюдения R.
, определяющей диагональные элементы ковариационной матрицы ошибок наблюдения R.
Критерием качества J1, назначают взвешенную среднеквадратическую ошибку ориентации по крену и тангажу, усредненную по времени и по множеству всех девяти обучающих последовательностей.
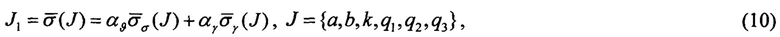
где 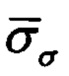 - среднеквадратическая ошибка оценивания тангажа;
- среднеквадратическая ошибка оценивания тангажа; 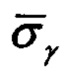 - среднеквадратическая ошибка оценивания крена; αϑ=0.5 и αγ=0.5 - весовые коэффициенты; J={а,b,k,q1,q2,q3} - множество из шести искомых коэффициентов алгоритма.
- среднеквадратическая ошибка оценивания крена; αϑ=0.5 и αγ=0.5 - весовые коэффициенты; J={а,b,k,q1,q2,q3} - множество из шести искомых коэффициентов алгоритма.
Идентификацию турбулентности в смысле выявления ее наличия выполняют по величине среднеквадратичного отклонения 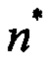 на скользящем интервале небольшой длины порядка 1-2 секунд. При превышении некоторого заданного порога
на скользящем интервале небольшой длины порядка 1-2 секунд. При превышении некоторого заданного порога 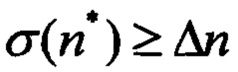 принимают решение о наличии турбулентности.
принимают решение о наличии турбулентности.
Оптимизацию коэффициентов осуществляют в три этапа.
1. Численная минимизация критерия качества minJ1 и определение коэффициентов {а1,b1,k1,q11,q21,q31} для полетов в спокойной атмосфере, 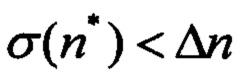 .
.
2. Численная минимизация критерия качества minJ1 и определение коэффициентов {а2,b2,k2,q12,q22,q32} для полетов в условиях турбулентности, 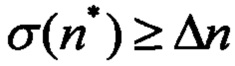 .
.
3. Определение процедуры вычисления дисперсий d, q1 ,q2, q3, удовлетворяющей с достаточной точностью полетам, как в спокойной атмосфере, так и в турбулентности. Наиболее просто данная процедура реализуется с помощью линейной интерполяции коэффициентов фильтра по результатам этапов 1, 2, и текущим значениям 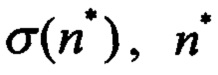 .
.
Предложенный Способ определения углов пространственной ориентации может быть использован как на высокоманевренных, так и на маломаневренных летательных аппаратах. Техническим результатом является повышение точности определения истинного курса, достигнутого путем списания девиации в полете и постоянной адаптивной коррекцией углов крена и тангажа по сигналам акселерометров, а также оптимизацией коэффициентов фильтрации в зависимости от турбулентности и при осуществлении настройки на множестве обучающих последовательностей. Заметим, что списание девиации может быть осуществлено периодически, в случае отсутствия замены бортового и подвесного оборудования ЛА. За счет подавления влияния кажущегося ускорения, зависимость маятниковой коррекции от вида движения объекта ослабляется до уровня, позволяющего использовать датчики ДУС и ДЛУ средней и низкой точности, в том числе микромеханического типа.
Литература:
1. Патент №2550774, Способ определения и компенсации девиации магнитометрических датчиков и устройство для его осуществления, МПК G01C 21/08. Бюллетень №13, 2015 г. Авторы Заец В.Ф., Кулабухов В.С., Качанов Б.О., Туктарев Н.А., Гришин Д.В.
2. Патент №2564380, Способ коррекции бесплатформенной инерциальной навигационной системы, МПК G01C 21/06. Бюллетень. №27, 2015 г. Авторы Заец В.Ф., Кулабухов В.С., Качанов Б.О., Туктарев Н.А., Гришин Д.В.
3. Патент №2564379, Бесплатформенная инерциальная курсовертикаль, МПК G01C 21/16. Бюллетень №27, 2015 г. Авторы Заец В.Ф., Кулабухов В.С., Качанов Б.О., Туктарев Н.А.
| название | год | авторы | номер документа |
|---|---|---|---|
| Малогабаритная адаптивная курсовертикаль | 2016 |
|
RU2714144C2 |
| Комплексный способ навигации летательных аппаратов | 2016 |
|
RU2646957C1 |
| Малогабаритный навигационный комплекс | 2016 |
|
RU2644632C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2643201C2 |
| Адаптивный корректор углов ориентации для БИНС | 2020 |
|
RU2749152C1 |
| Адаптивная бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2647205C2 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ НА ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТАХ ВЫСОКОЙ ТОЧНОСТИ | 2015 |
|
RU2615032C1 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
Изобретение относится к области навигационного приборостроения и может найти применение в системах контроля и управления летательными аппаратами (ЛА). Технический результат - расширение функциональных возможностей и повышение точности определения навигационных параметров. Для этого осуществляют определение и списание девиации трехкомпонентного магнитометрического датчика (ТМД), включая круговую девиацию, после набора высоты путем совершения полета по кругу, используя адаптированную к внешним возмущениям бесплатформенную инерциальную курсовертикаль (БИКВ) и ТМД со списанной в полете девиацией на основе оптимизации коэффициентов адаптивной коррекцией углов, используя при этом введенные датчики динамического и статического давлений для определения воздушной скорости, с последующим ее дифференцированием и фильтрацией для получения сигнала, пропорционального линейному продольному ускорению, и используют дополнительную оптимизацию коэффициентов адаптивной коррекции, выполняя настройку на множестве обучающих последовательностей. При этом повышение точности определения истинного курса достигается путем списания девиации в полете и постоянной адаптивной коррекцией углов крена и тангажа по сигналам акселерометров, а также на основе оптимизации коэффициентов фильтрации в зависимости от турбулентности и осуществления настройки на множестве обучающих последовательностей. Причем списание девиации может быть осуществлено периодически, в случае отсутствия замены бортового и подвесного оборудования ЛА. В результате представляется возможность использовать датчики угловых скоростей и линейных ускорений средней и низкой точности, в том числе микромеханического типа. 1 табл.
Способ определения углов пространственной ориентации, заключающийся в использовании информации с блока датчиков угловой скорости, блока датчиков линейного ускорения, трехкомпонентного магнитометрического датчика (ТМД), применении режима коррекции, отличающийся тем, что дополнительно осуществляют определение и списание девиации ТМД, включая и круговую девиацию, после набора высоты путем совершения полета по кругу, используют адаптированную к внешним возмущениям бесплатформенную инерциальную курсовертикаль (БИКВ) и ТМД со списанной в полете девиацией, осуществляют оптимизацию коэффициентов адаптивной коррекции углов, используя при этом введенные датчики динамического и статического давлений для определения воздушной скорости, с последующим ее дифференцированием и фильтрацией для получения сигнала, пропорционального линейному продольному ускорению, и осуществляют дополнительную оптимизацию коэффициентов адаптивной коррекции, выполняя настройку на множестве обучающих последовательностей.
| СИСТЕМА И СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ И КУРСА ЛЕТАТЕЛЬНОГО АППАРАТА | 2012 |
|
RU2505786C2 |
| US 6522992 B1, 18.02.2003 | |||
| СИСТЕМА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ ОБЪЕКТА | 2004 |
|
RU2282869C1 |
| Авиационная радионавигация | |||
| Справочник под ред | |||
| Сосновского А.А | |||
| - М.: Транспорт, 1990, с.151 | |||
| US 6901331 В1, 31.05.2005. | |||
Авторы
Даты
2020-02-03—Публикация
2016-12-22—Подача