Предлагаемое изобретение относится к области космической техники и может быть использовано для приведения космического аппарата (КА) к долготе стояния на геостационарной орбите (ГСО) при больших начальных отклонениях орбитальных параметров от заданных значений и для перевода КА на другую долготу.
Известен способ приведения КА к долготе стояния на ГСО, описанный в статье [1] А.Е. Назаров «Использование комбинированного метода расчета программы коррекций приведения геостационарного КА для минимизации эксцентриситета орбиты», Вестник ФГУП НПО им. С.А. Лавочкина, 2009, №2, стр. 23-33. В нем приведение выполняется тремя импульсными коррекциями. Этот способ принципиально не может быть применен, если используются двигатели малой тяги.
Известен способ, описанный в книге [2] Г.М. Чернявский, В.А. Бартенев, В.А. Малышев «Управление орбитой стационарного спутника». М.: Машиностроение, 1984 г., стр. 120-126. В нем выполняют многошаговый процесс приведения двигателями малой тяги. На каждом шаге во время полета КА выполняют измерения орбитальных параметров и по результатам измерений вычисляют время начала и длительность воздействия коррекций на этом шаге. При вычислении прогнозируют результат путем решения дифференциальных уравнений движения КА с учетом корректирующего воздействия.
Недостатки этого способа в следующем. Способ не предусматривает ограничений на длительность работы двигателей при очередном включении.
Точные измерения на каждом шаге приведения требуют от одних до трех суток времени между коррекциями. Поскольку при применении двигателей с тягой порядка 0,1 Н и ограниченной длительностью работы могут потребоваться десять и более шагов приведения, то его общая длительность будет недопустимо большой, особенно при больших начальных отклонениях периода и, соответственно, при большой начальной скорости дрейфа КА вдоль ГСО. Расчет коррекций согласно данному способу достаточно сложен и выполнение этого расчета в автономном режиме полета КА проблематично. Кроме этого в [3] на стр. 92 также отмечена плохая сходимость алгоритмов расчета для этого способа [2].
В качестве прототипа принят способ, описанный в статье [3] В.В. Салмин, А.С. Четвериков «Управление плоскими параметрами орбиты геостационарного космического аппарата с помощью двигателей малой тяги», Вестник Самарского государственного аэрокосмического университета, Т. 14, №4, 2015 г., стр. 92-100. В этом способе приведение реализуется тремя протяженными коррекциями. Способ прост и может быть реализован в автономном режиме полета КА. Однако для приведения с реальными начальными отклонениями тяга двигателей должна быть много больше 0,1 Н. Это видно и по описанию примера расчета в [2]. Из длительности коррекций около 12000 с ([2], стр. 96) и расхода скорости 12 м/с ([2], рис. 6) ускорение можно оценить как 10-3 м/с2. Отсюда следует, что при характерной массе КА около 2500 кг тяга должна быть 2,5 Н.
Прототип имеет следующий недостаток. При больших начальных отклонениях и при ограничениях длительности непрерывной работы двигателей приведение нельзя выполнить за три коррекции эффективными электроракетными двигателями с большим удельным импульсом. Такие двигатели применяются при большом сроке существования КА, но величина их тяги порядка 0,1 Н. Данные о таких двигателях приведены в книге [4] Ю.Г. Сухой «Коррекции орбит геостационарных спутников», Часть 1, М., Спутник, 2011 г., стр. 17-19, где они отнесены к двигателям сверхмалой тяги. При тяге 0,1 Н и необходимом расходе скорости не менее 10 м/с в случае больших начальных отклонений, на приведение требуется около 12 коррекций по 6 часов каждая с учетом ограничения на длительность работы двигателя в течение суток. В таком случае прототип не может быть использован.
Техническим результатом изобретения является приведение КА на заданную долготу ГСО двигателями сверхмалой тяги, порядка 0,1 Н, за минимальное время с учетом ограничений на длительность работы двигателей и на расход характеристической скорости, при этом расчет приведения может быть выполнен на КА.
Существо изобретения состоит в том, что изменяют период систематическими максимальными коррекциями, возможными для данного КА в течение суток, и используют зависимость отклонения периода, оптимального для скорейшего приведения, от текущего отклонения долготы.
Для пояснения изобретения рассмотрим взаимозависимость отклонений геодезической долготы КА и периода орбиты при равномерном изменении периода во времени. Для этого введем обозначения:
t - время движения от начального отклонения;
W - угловая скорость движения КА;
ΔW0 - начальное отклонение скорости W от номинальной для ГСО;
Т - период орбиты;
ΔТ - отклонение периода;
ΔТ0 - начальное отклонение периода;
ΔTmax - заданное максимальное допустимое отклонение периода;
ΔL - отклонение долготы;
ΔL0 - начальное отклонение долготы;
δТ - изменение периода коррекцией за сутки;
δTmax - максимальное изменение периода коррекцией за сутки;
δL - изменение долготы за сутки при отклонении периода δТ.
При движении КА вдоль ГСО от некоторого начального отклонения долготы ΔL0 с небольшим равномерным увеличением угловой скорости вдоль орбиты отклонение долготы ΔL изменяется согласно соотношению:
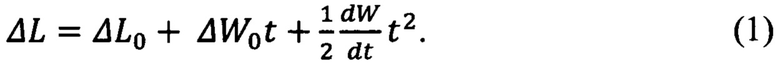
Выражая угловую скорость и ее отклонение через период как W=2π/Т, ΔW0=W×(-ΔT0/T), дифференцируя и используя приближенные соотношения dT/dt=δТ/Т, из (1) получим:
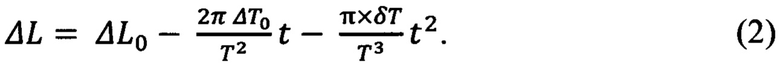
Время t выразим через разность отклонений периода ΔT-ΔТ0, посуточное изменение δТ периода и период Т, тогда t=(ΔT-ΔТ0)×(Т/δТ). После подстановки этого выражения для времени t в соотношение (2) и упрощения простыми преобразованиями получим соотношение, связывающее отклонение долготы ΔL и отклонение периода ΔT при номинальном для ГСО значении периода Т=86164,09 с:
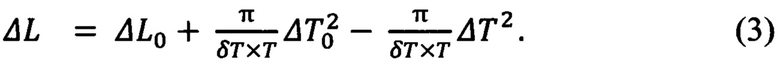
Соотношение (3) зависит от КА только через возможную величину изменения периода δТ, определяемую массой КА, тягой двигателей и ограничениями их работы.
Чтобы в результате посуточной коррекции δТ периода получить нулевые отклонения долготы и периода, необходимо в (3) положить ΔL=0, ΔT=0. В таком случае с учетом (3) начальная долгота и начальное отклонение периода должны удовлетворять соотношениям:
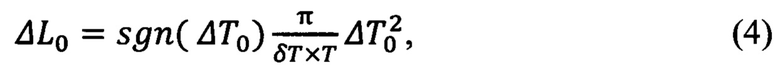
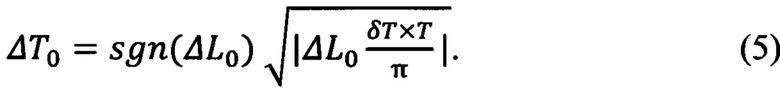
Значение функции sgn(x) равно единице со знаком аргумента х.
Чтобы при постоянном ежесуточном изменении периода получить нулевые отклонения долготы и периода, на очередных сутках отклонения ΔL, ΔT должны удовлетворять соотношениям (6, 7), аналогичным (4, 5):
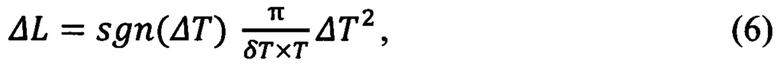
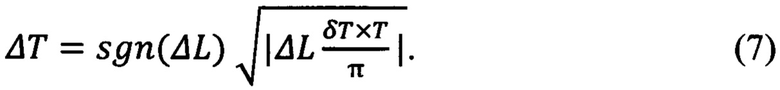
Если период отличается от номинального значения Т=86164,09 секунд на постоянную величину ΔT, то долгота в течение суток изменяется на

На фазовой диаграмме кривые, отражающие взаимозависимость отклонений долготы и периода, являются параболами.
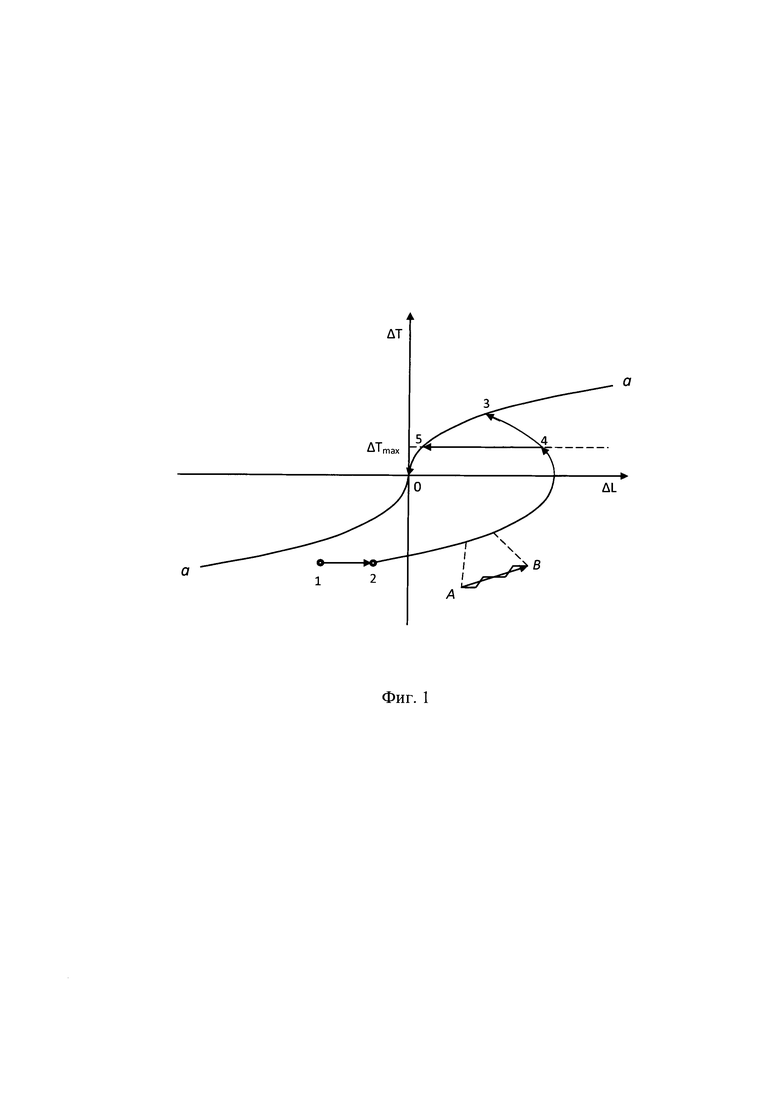
На фиг. 1 схематически показан пример такой диаграммы изменения отклонений ΔL, ΔT долготы и периода от их начальных значений до нулевых значений при приведении.
Кривая a является сопряжением двух половин парабол с вершинами в начале координат. Она в соответствии с (7) определяет при отклонении ΔL величину оптимального отклонения ΔT, начиная с которой при посуточном приближении периода к номинальному значению с максимальной возможной для данного КА скоростью в конечном итоге отклонения ликвидируются. На кривой a, если ΔL положительно, то для приближения к началу координат период уменьшают, если ΔL отрицательно, то увеличивают.
Исходными данными для приведения являются орбитальные параметры КА по результатам измерений. На фиг. 1 этим параметрам соответствуют отклонения в точке 1. Начало коррекций возможно только после некоторой задержки, необходимой для выполнения расчетов, передачи информации на КА и приведения его в состояние готовности к коррекциям. В течение этой задержки КА дрейфует от точки 1 к точке 2. От точки 2 период посуточно увеличивают на максимальную возможную величину и отклонения изменяются от точки 2 по параболе до приближения к кривой a в точке 3, если необходимо минимизировать длительность приведения. От точки 3 период ежесуточно уменьшают на такую же величину до окончания приведения в точке 0. Для уменьшения расхода скорости можно уменьшить число коррекций, ограничив величину отклонения периода. На фиг. 1 этому соответствует увеличение отклонения периода от точки 2 не до точки 3, а до точки 4, где отклонение периода достигает заданной ограничивающей величины ΔTmax. После этого коррекции не выполняют, пока КА дрейфует до приближения к кривой а в точке 5. Далее период уменьшают, как описано выше. Такое движение с ограничением периода обеспечивает приведение за минимальное время при заданном ограничении расхода скорости и с минимальным расходом при заданном времени. При приближении к конечной точке и к точкам 3, 4 период изменяют на величину его оставшегося отклонения.
Расчет всех коррекций приведения, выполняемых на фиг. 1 от точки 2 до его окончания, можно выполнить до начала коррекций. Более точно можно обеспечить приведение, выполнив измерения и по ним новый расчет во время предусмотренного дрейфа. Ему в примере на фиг. 1 соответствует движение от точки 4 к точке 5. Во время дрейфа также можно выполнить коррекции эксцентриситета или наклонения. Коррекции периода вблизи перигея и апогея орбиты могут совмещаться с коррекциями эксцентриситета без дополнительного расхода характеристической скорости.
При реальном исполнении коррекций чередуются короткие отрезки времени, в пределах нескольких часов, когда непрерывно изменяется период, с отрезками без коррекций, на которых изменяется практически только долгота КА из-за отклонения периода от номинального периода ГСО. Это схематически показано на выноске А-В, отражающей на фиг. 1 движение на одном шаге. Если число коррекций достаточно велико, то соотношения (2-7) соблюдаются с приемлемой точностью, несмотря на то, что период изменяется не равномерно, а на отдельных отрезках времени.
Коррекции периода и совмещенные с ними коррекции эксцентриситета выполняют в апсидальных точках орбиты, т.е. в ее апогее и перигее. При таких коррекциях окончание последней коррекции, начавшейся в течение текущих суток, может выйти за их пределы. Поэтому в изобретении управление КА осуществляют не по суткам, а по интервалам управления, длительность которых равна или суткам, или превышает их на величину, необходимую для завершения коррекции, начатой в этих сутках. В изобретении в качестве таких суток применяют звездные сутки, но точно также можно применять солнечные или календарные сутки. Далее в описании изобретения словосочетание «интервал управления» используется как термин с описанным выше содержанием.
При реализации предлагаемого способа движение КА между точками 2,3; 3,0 или точками 2,4; 4,5; 5,0 может выполняться не за целое, а за дробное число интервалов управления. Однако при большой общей длительности приведения это не дает существенных преимуществ по длительности и точности, но усложняет планирование и исполнение коррекций. При целом числе интервалов управления можно обеспечить конечное отклонение долготы, не превышающее величину δL в выражении (8) при Т=86164,09 секунд. Тогда при реальной величине отклонения периода ΔT=50 секунд отклонение долготы не превысит 0,2 градуса. Этого достаточно для дальнейшего уменьшения долготы в процессе ее поддержания с заданной точностью. Следует отметить, что на практике при длительном приведении конечное отклонение определяется преимущественно ошибками исполнения коррекций.
Технический результат изобретения достигается тем, что способ приведения КА к долготе стояния на геостационарной орбите, включающий измерения орбитальных параметров, расчет и планирование коррекций движения КА и выполнение коррекций, имеет следующие отличия.
Определяют момент времени готовности КА к выполнению коррекций путем добавления к моменту времени измеренных орбитальных параметров также времени, необходимого для выполнения расчетов, передачи команд на КА и изменения ориентации КА, далее вычисляют орбитальные параметры на момент времени готовности КА путем численного прогнозирования движения КА до этого момента, задают величину максимального допустимого отклонения периода и промежутки времени, на которых запрещено выполнение коррекций, в процессе полета КА от момента времени готовности последнего к выполнению коррекций управляют полетом по последовательным интервалам управления, окончание каждого интервала управления соответствует началу следующего интервала управления, длительность интервалов управления равна звездным суткам или превышает их на величину, необходимую для завершения коррекции, начатой на этих сутках, коррекции на интервалах управления выполняют вблизи апсидальных точек орбиты и в зависимости от выполнения условий в начале интервала управления, а именно, если это начало находится в пределах промежутка времени, запрещенного для коррекций, то коррекции не выполняют, иначе при одновременном выполнении условий
|ΔТ|<δTmax
|ΔL|<δLmax
е<δemax
коррекциями изменяют период орбиты на величину
δT=-ΔT
также коррекциями уменьшают эксцентриситет орбиты на величину
δe=е
и завершают коррекции приведения к долготе стояния,
при выполнении условия
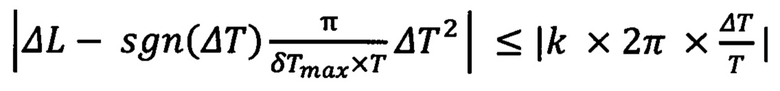
коррекциями изменяют период орбиты на величину
δT=-sgn(ΔL)δTmax,
при одновременном выполнении условий
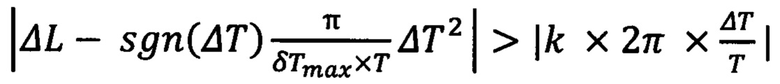
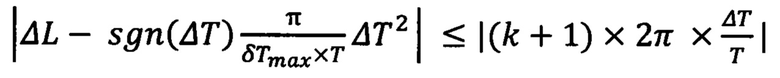
или одновременном выполнении условий
|ΔTmax|≤|ΔТ|
sgn(ΔT)sgn(ΔL)>0
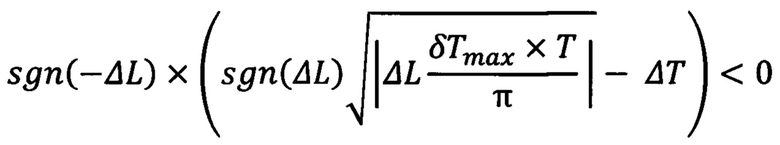
или условия
|ΔT-sgn(ΔL)ΔTmax|<δTmax
не изменяют коррекциями период орбиты,
при выполнении условия
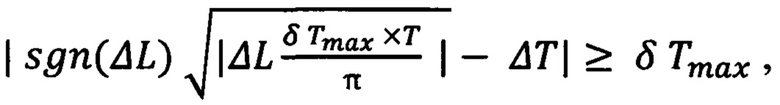
коррекциями изменяют период орбиты на величину
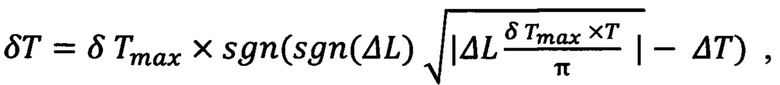
при выполнении условия
e≥δemax
коррекциями уменьшают эксцентриситет орбиты на величину
δe=δemax,
при выполнении условия
e<δemax
коррекциями уменьшают эксцентриситет орбиты на величину
δе=e,
где
ΔT - отклонение периода орбиты,
δTmax - максимальное изменение периода орбиты коррекцией за сутки,
δLmax - изменение долготы, при изменении периода орбиты на δTmax,
δТ - изменение периода орбиты коррекцией,
ΔTmax - заданное максимальное допустимое отклонение периода;
ΔL - отклонение долготы,
e - эксцентриситет орбиты,
δemax - максимальное уменьшение эксцентриситета орбиты коррекцией за сутки,
δe - уменьшение эксцентриситета орбиты коррекцией,
k - коэффициент, k≥1,
Т - номинальный период орбиты, Т=86164,09 с.
Предлагаемый способ реализуется следующим образом.
Из момента времени измеренных орбитальных параметров добавлением времени, необходимого для выполнения расчетов, передачи команд на КА и изменения ориентации КА, определяют момент времени готовности КА к выполнению коррекций, прогнозируют численным методом движение КА до этого момента времени готовности КА и тем самым вычисляют орбитальные параметры на этот момент.
Задают величину максимального допустимого отклонения периода.
Задают промежутки времени, на которых коррекция запрещена, за исключением затенений. Например, с целью резервирования этих промежутков времени для контрольных измерений орбитальных параметров, задают время начала и окончания таких промежутков, при этом учитывают, что фактически реализуемый промежуток времени запрета может превышать заданный на величину до суток.
Вычисляют время начала и длительность всех непрерывных корректирующих воздействий, необходимых от момента готовности КА к выполнению коррекций до окончания приведения к долготе стояния. Такие вычисления проводят путем имитационного моделирования движения КА численным методом с использованием достаточно точной модели движения. Это моделирование выполняют в цикле по непрерывной последовательности интервалов управления. Длительность такого очередного интервала управления равна длительности звездных суток или превышает ее на величину, необходимую для завершения коррекции, запланированной на этом интервале управления и начинающейся до истечения звездных суток от его начала. На очередном шаге цикла моделирования, соответствующем такому очередному интервалу управления, проверяют выполнение условий в момент начала интервала управления и по результатам проверки определяют последующие действия для этого интервала управления. Если коррекции запрещены для времени начала этого интервала управления согласно заданию, то коррекции на этом интервале управления не планируют. Иначе из орбитальных параметров КА на начало интервала управления проверяют выполнение условий, определяющих необходимость и величину коррекций на этом интервале управления. Коэффициент k≥1 в соответствующих описанных условиях предназначен для исключения нежелательного перехода через границу, отражаемую кривой а на фиг. 1, а также для обеспечения запаса времени для выполнения измерений орбитальных параметров, если такие измерения предусмотрены в процессе полета помимо измерений во время длительного дрейфа. Они могут быть предусмотрены, например, при приближении к завершению приведения с постоянным отклонением периода порядка δTmax в течение k-1 полных суток, так что на практике может быть 1≤k≤4, если для измерений требуется трое суток.
Если по результатам проверки условий на интервале управления необходима коррекция, то для времени до окончания звездных суток от начала текущего интервала управления рассчитывают время начала, окончания или длительность исполнения трансверсальных воздействий и определяют их направление, т.е. знак воздействий. Максимальную длительность воздействий определяют заранее по известным данным: по тяге двигателей и массе КА, по ограничению на длительность работы двигателей в сутках. Воздействия планируют вблизи апсидальных точек орбиты, т.е. вблизи ее перигея и апогея, середины воздействий соответствуют этим точкам. Время их прохождения вычисляют по аргументу широты и истинной аномалии из параметров орбиты в начале интервала управления. По этому времени и длительности воздействий вычисляют время начала воздействий. Длительность интервала управления равна звездным суткам, если запланированное на интервале корректирующее воздействие, начинающиеся ранее истечения звездных суток от начала интервала, заканчивается до завершения этих суток. Иначе окончанием интервала считается окончание такого воздействия.
Вычисляют промежутки времени затенения КА Землей и Луной, затем при необходимости сдвигают или сокращают рассчитанные воздействия во времени для исключения затенений при воздействиях.
Временем начала, длительностью и знаком воздействий на интервале управления дополняют данные, полученные аналогично для всех предшествующих интервалов управления, начиная от момента готовности КА к выполнению коррекций.
Выполняют прогнозирование численным методом с учетом корректирующих воздействий от начала интервала управления до его окончания и в результате вычисляют орбитальные параметры КА на начало следующего интервала управления.
Продолжая цикл по интервалам управления, выполняют описанные выше действия от проверки выполнения условий, определяющих необходимость коррекций на интервале управления, до вычисления орбитальных параметров КА на начало следующего интервала управления.
Цикл вычислений заканчивают при выполнении условий окончания приведения к долготе стояния:
|ΔТ|<δTmax
|ΔL|<δLmax
е<δemax
Кроме вычисления начала и окончания или длительности воздействий, а также их знака, в результате имитационного моделирования получают длительность приведения и величину расхода характеристической скорости, пропорциональную суммарной длительности воздействий.
Описанное имитационное моделирование от начала задания величины максимального допустимого отклонения периода до окончания цикла вычислений можно выполнять неоднократно, например, для выбора компромисса между длительностью приведения и расходом скорости.
В процессе полета КА при приведении исполняют корректирующие воздействия по данным о началах, окончаниях и знаках воздействий, полученным при имитационном моделировании. Тем самым обеспечивают управление движением КА.
Благодаря простоте расчета коррекций для приведения предлагаемым способом этот расчет может быть выполнен на КА. При наличии на КА средств достаточно точного измерения отклонений орбитальных параметров КА от заданных значений предлагаемый способ можно применять без предварительного расчета коррекций.
Работоспособность и эффективность предлагаемого способа подтверждена имитационным моделированием с учетом возможных ошибок измерений и ошибок исполнения коррекций.
Источники информации
1. А.Е. Назаров Использование комбинированного метода расчета программы коррекций приведения геостационарного КА для минимизации эксцентриситета орбиты. Вестник ФГУП НПО им. С.А. Лавочкина, 2009, №2, стр. 23-33.
2. Г.М. Чернявский, В.А. Бартенев, В.А. Малышев «Управление орбитой стационарного спутника», М., Машиностроение, 1984 г., стр. 120-126.
3. В.В. Салмин, А.С. Четвериков «Управление плоскими параметрами орбиты геостационарного космического аппарата с помощью двигателей малой тяги». Вестник Самарского государственного аэрокосмического университета, Т. 14, №4, 2015 г., стр. 92-100.
4. Ю.Г. Сухой «Коррекции орбит геостационарных спутников», Часть 1, М., Спутник, 2011 г., стр. 17-19.
Изобретение относится к управлению движением космического аппарата (КА) на геостационарной орбите (ГСО) с помощью двигателей преимущественно сверхмалой тяги (~ 0,1 Н). Отклонения орбитальных параметров от заданных начальных значений считаются большими. Способ состоит в изменении периода обращения и эксцентриситета ГСО систематическими максимальными коррекциями, возможными для данного КА в течение суток. При этом используют зависимость отклонения периода, оптимального для скорейшего приведения КА к заданной долготе стояния, от текущего её отклонения. Техническим результатом является приведение КА на заданную долготу стояния на ГСО за минимальное время, с учетом характерных ограничений, при этом расчет приведения может быть выполнен на борту КА. 1 ил.
Способ приведения космического аппарата (КА) к долготе стояния на геостационарной орбите, включающий измерения орбитальных параметров, расчет и планирование коррекций движения КА и выполнение коррекций, отличающийся тем, что определяют момент времени готовности КА к выполнению коррекций путем добавления к моменту времени измеренных орбитальных параметров также времени, необходимого для выполнения расчетов, передачи команд на КА и изменения ориентации КА, далее вычисляют орбитальные параметры на момент времени готовности КА путем численного прогнозирования движения КА до этого момента, задают величину максимального допустимого отклонения периода и промежутки времени, на которых запрещено выполнение коррекций, в процессе полета КА от момента времени готовности последнего к выполнению коррекций управляют полетом по последовательным интервалам управления, причём окончание каждого интервала управления соответствует началу следующего интервала управления, длительность интервалов управления равна звездным суткам или превышает их на величину, необходимую для завершения коррекции, начатой на этих сутках, коррекции на интервалах управления выполняют вблизи апсидальных точек орбиты и в зависимости от выполнения условий в начале интервала управления, а именно, если это начало находится в пределах промежутка времени, запрещенного для коррекций, то коррекции не выполняют, в противном случае при одновременном выполнении условий
|ΔT|<δTmax,
|ΔL|<δLmax,
e<δemax
коррекциями изменяют период орбиты на величину
δT=-ΔТ,
коррекциями также уменьшают эксцентриситет орбиты на величину
δe=е
и завершают коррекции приведения к долготе стояния, при выполнении условия
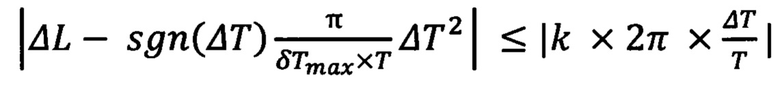
коррекциями изменяют период орбиты на величину
δТ=-sgn(ΔL)δTmax,
при одновременном выполнении условий
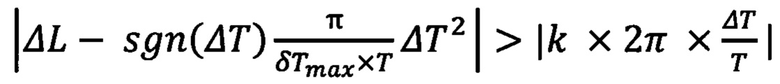 ,
,
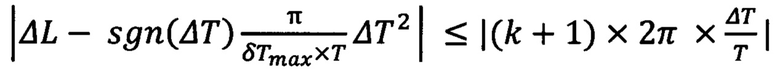
или при одновременном выполнении условий
|ΔTmax|≤|ΔT|,
sgn(ΔT)sgn(ΔL)>0,
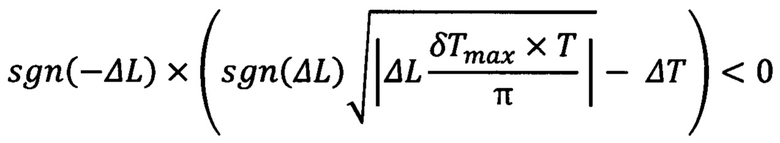
или при выполнении условия
|ΔТ-sgn(ΔL)ΔTmax|<δTmax
не изменяют коррекциями период орбиты, а при выполнении условия
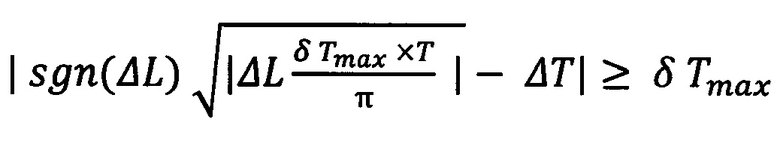
коррекциями изменяют период орбиты на величину
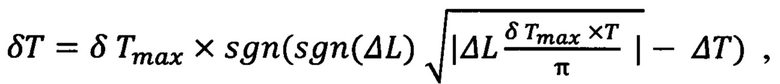
при выполнении условия
e≥δemax
коррекциями уменьшают эксцентриситет орбиты на величину
δe=δemax,
при выполнении условия
e<δemax
коррекциями уменьшают эксцентриситет орбиты на величину
δe=е,
где:
ΔT - отклонение периода орбиты,
δTmax - максимальное изменение периода орбиты коррекцией за сутки,
δLmax - изменение долготы, при изменении периода орбиты на δTmax,
ΔTmax - заданное максимальное допустимое отклонение периода,
δТ - изменение периода орбиты коррекцией,
ΔL - отклонение долготы,
е - эксцентриситет орбиты,
δemax - максимальное уменьшение эксцентриситета орбиты коррекцией за сутки,
δe - уменьшение эксцентриситета орбиты коррекцией,
k - коэффициент, k≥1,
Т - номинальный период орбиты, Т=86164,09 с.
| В | |||
| В | |||
| Салмин, А | |||
| С | |||
| Четвериков | |||
| Управление плоскими параметрами орбиты геостационарного космического аппарата с помощью двигателя малой тяги | |||
| Вестник СГАУ, Т.14, N4, 2015, с.92-99 | |||
| Г.М.Чернявский, В.А.Бартенев, В.А.Малышев | |||
| Управление орбитой стационарного спутника | |||
| М., Машиностроение, 1984, с.92, 93, 120-122 | |||
| СПОСОБ УДЕРЖАНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСИНХРОННОЙ 24-ЧАСОВОЙ ОРБИТЕ | 2013 |
|
RU2535353C2 |
| US | |||
Авторы
Даты
2020-02-13—Публикация
2018-11-30—Подача