Предлагаемое изобретение относится к области вторичной цифровой обработки сигналов и может быть использовано в телевизионных, радиолокационных, инфракрасных информационных системах (ИС) беспилотных летательных аппаратов (БПЛА) для определения положения точки их промаха относительно выбранного объекта наведения по информации только угломерного канала системы управления, в том числе, при минимальных расстояниях между БПЛА и объектом, а также в момент ослепления ИС беспилотного летательного аппарата.
Известен способ определения мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала [1], заключающийся в том, что при минимальных расстояниях между БПЛА и объектом, а также в момент ослепления ИС беспилотного летательного аппарата ее угломерный канал (угломер интенсивно маневрирующих объектов) формирует значения положения линии визирования БПЛА на объект по азимуту 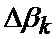

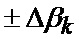
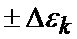
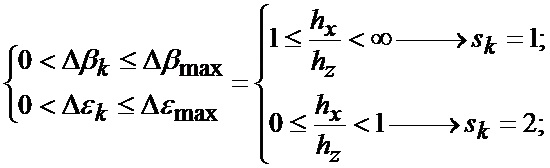
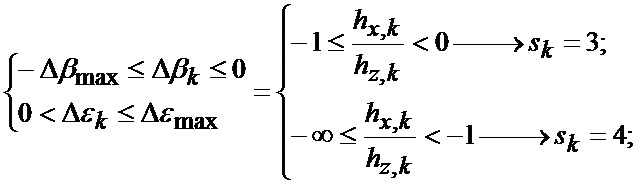
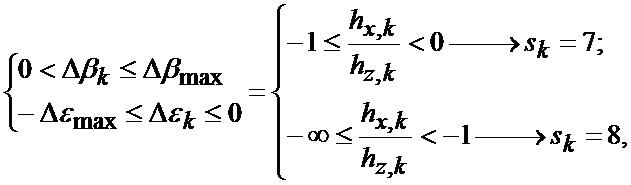
где
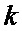
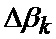
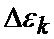
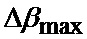
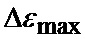
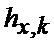

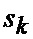
формируется вектор измерения в соответствии с выражением
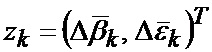
где
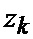
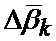
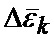
а также показание 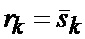
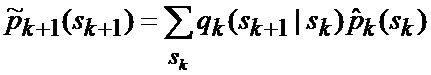
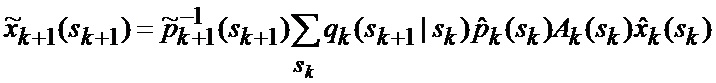
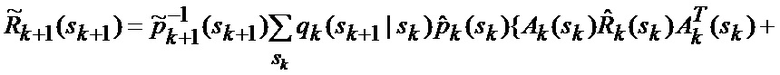
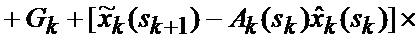
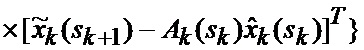
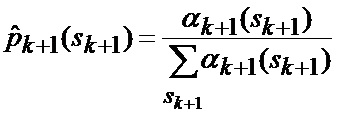
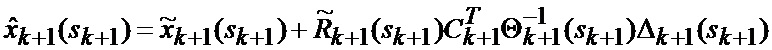
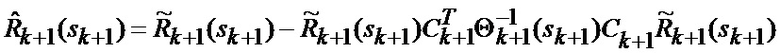
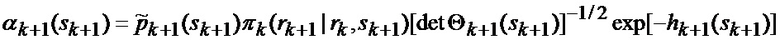
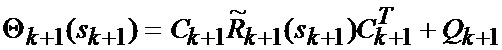

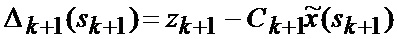
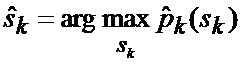
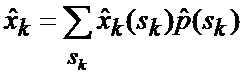

основанной на априорных данных в виде математической модели (ММ) системы «БПЛА - объект наведения - ИС - индикатор» со случайной скачкообразной структурой (ССС), включающей линейную модель динамики положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования
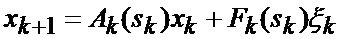
модель измерений этих фазовых координат в ИС
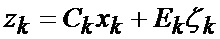
модель смены сектора нахождения точки мгновенного промаха БПЛА
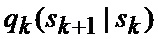
модель индикатора сектора (при его наличии) нахождения точки мгновенного промаха БПЛА
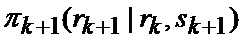
модель неуправляемых случайных возмущений и помех
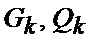
при начальных условиях
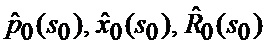
где
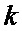
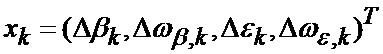
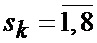
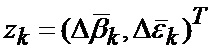
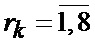
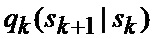
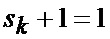
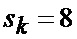
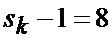
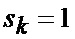
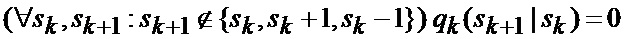
что отражает возможные альтернативы смены сектора нахождения точки мгновенного промаха БПЛА, а именно на следующем шаге дискретизации может произойти или сохранение положения точки мгновенного промаха БПЛА в текущем секторе картинной плоскости, или переход этой точки в один из соседних секторов, помимо этого при допущении об отсутствии смены секторов полагается 
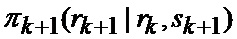
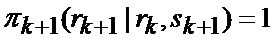
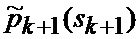
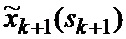
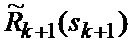
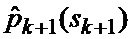
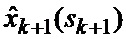
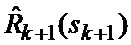
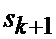

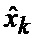
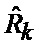
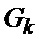
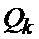
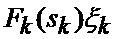
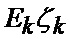

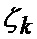
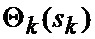
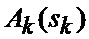
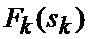

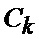
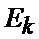
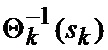

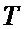
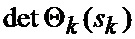

определяется оценка 
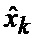
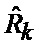
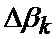

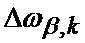
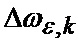
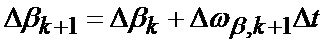
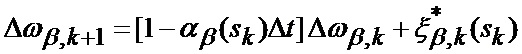
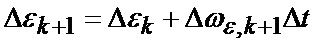
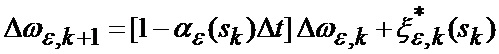
или в векторно-матричном представлении (16)
отдельно для параметров положения и движения по азимуту (22), (23)
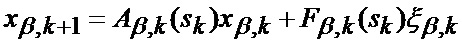
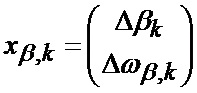
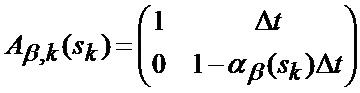
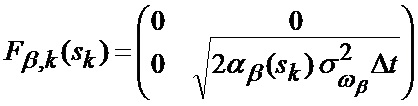
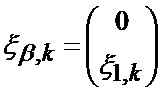
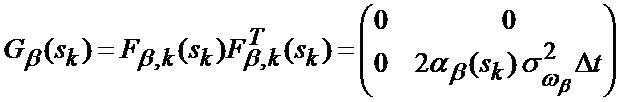
отдельно для параметров положения и движения по углу места (24), (25)
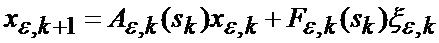
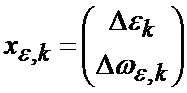
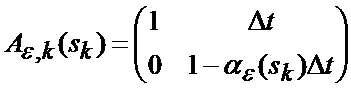
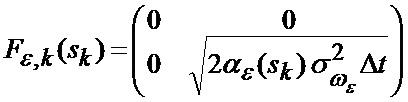
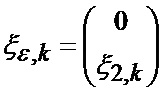
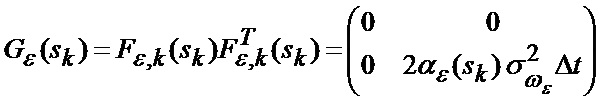
или совместно для рассматриваемых фазовых координат
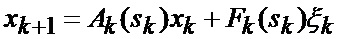
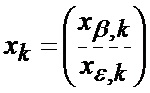
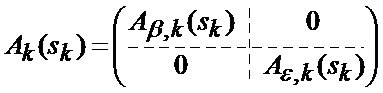
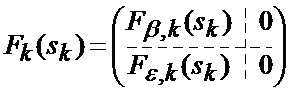
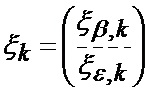
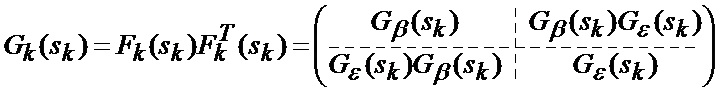
где
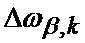
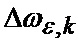
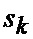
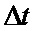
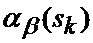
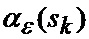
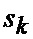
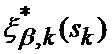
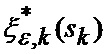
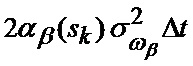
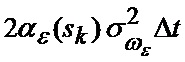
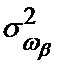
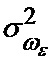
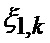
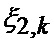
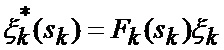
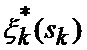
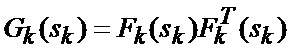
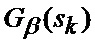
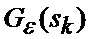
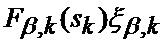
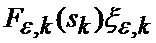
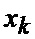
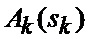
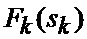
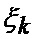
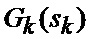
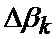

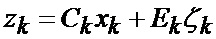

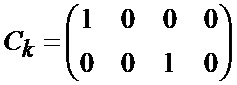
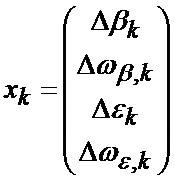
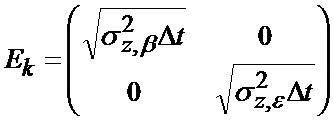
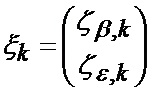
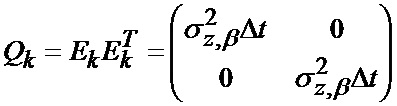
где

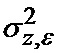
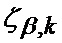
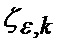
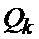
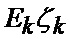
Существенными признаками известного способа определения мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала [1] являются:
1. Применение многоканального, по числу секторов картинной плоскости, фильтра совместных оценивания положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, и распознавания сектора нахождения точки мгновенного промаха БПЛА, функционирующего в соответствии с процедурой (3)-(15) квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния марковской структуры линейной стохастической динамической системы.
2. Комплексирование в (6) показаний ИС, измеряющей фазовые координаты, и индикатора сектора нахождения точки мгновенного промаха БПЛА с моделью (19).
3. Учет априорных данных о смене сектора нахождения точки мгновенного промаха БПЛА в виде условных вероятностей переходов (18).
4. Коррекция оценок (4), (5), (14), (15) фазовых координат, полученных на основе модели (16) и измерений (17), по оцененным вероятностям (6) нахождения точки мгновенного промаха БПЛА в соответствующем секторе картинной плоскости объекта и априорным данным (18) о смене этого сектора (адаптация фильтра к различным тактическим ситуациям - относительному положению БПЛА и объекта).
5. Прогнозирование (3) вероятностей 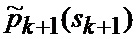
6. Прогнозирование (4) условных математических ожиданий 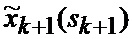
7. Прогнозирование (5) условных КМ 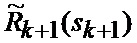
8. Оценка (6) апостериорных вероятностей 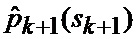
9. Оценка (7) условных апостериорных математических ожиданий 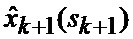
10. Оценка (8) условных апостериорных КМ 
11. Идентификация (13) такого 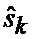
12. Нахождение (14) безусловной оценки 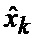
13. Нахождение (15) безусловной КМ 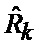
Недостатком известного способа определения мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала является низкая достоверность распознавания сектора нахождения точки мгновенного промаха БПЛА и оценки фазовых координат взаимного перемещения объекта и БПЛА вследствие:
1. Допущения о линейном характере зависимости фазовых координат от времени, в то время как фактически динамика фазовых координат носит нелинейный характер.
2. Допущения о статистической независимости смены секторов нахождения точки мгновенного промаха БПЛА от фазовых координат, в то время как фактически вероятности смены таких секторов зависят от фазовых координат, в частности, с приближением фактического положения линии визирования БПЛА на объект к границам секторов возрастают вероятности переходов точки мгновенного промаха БПЛА в соседние сектора.
3. Допущения о нормальности аппроксимирующей условной плотности вероятности фазовых координат при фиксированном секторе нахождения точки мгновенного промаха БПЛА - значительное отличие вида фактической плотности вероятности фазовых координат от нормального вида аппроксимирующей плотности приводит к возрастанию ошибок оценивания.
Технической задачей изобретения является повышение достоверности распознавания сектора нахождения точки мгновенного промаха БПЛА и оценки фазовых координат взаимного перемещения объекта и БПЛА путем адаптивной двухмоментной параметрической аппроксимации неизвестной плотности вероятности фазовых координат смесью априорно заданных законов распределения и приближением получаемых оценок к их оптимальным значениям за счет учета нелинейностей в динамике фазовых координат и их измерений и учета статистической зависимости вероятностей смены секторов нахождения точки мгновенного промаха БПЛА от фазовых координат.
Для решения технической задачи в способе определения мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала [1], заключающемся в том, что при минимальных расстояниях между БПЛА и объектом, а также в момент ослепления ИС беспилотного летательного аппарата ее угломерный канал (угломер интенсивно маневрирующих объектов) формирует значения положения линии визирования БПЛА на объект по азимуту и углу места, знаки положения этой линии визирования относительно направления на объект по азимуту и по углу места, задаются верхние и нижние границы секторов картинной плоскости объекта, выбранного для наведения, по соотношениям (1), формируется вектор измерения в соответствии с выражением (2), а также показание индикатора (при его наличии) нахождения точки мгновенного промаха БПЛА в конкретном секторе, которые дополнительно поступают на вход многоканального фильтра, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания [3] на основе метода адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно заданных законов распределения, в соответствии с выражениями
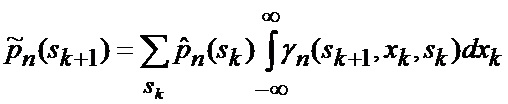
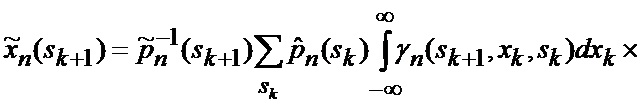
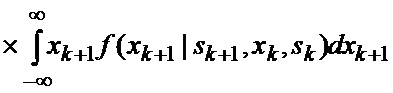
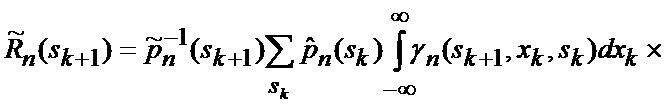
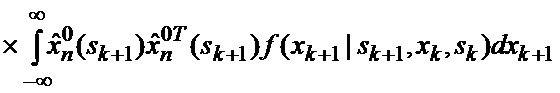
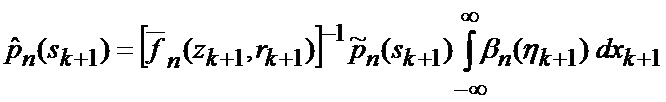


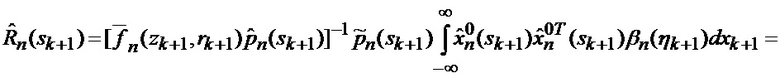
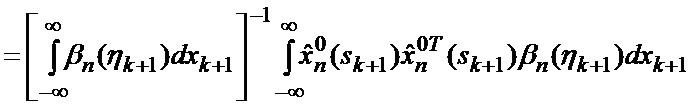
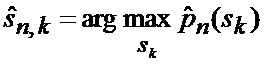
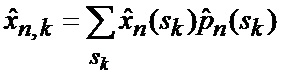
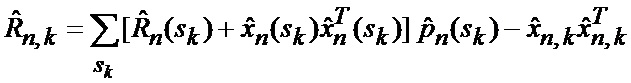
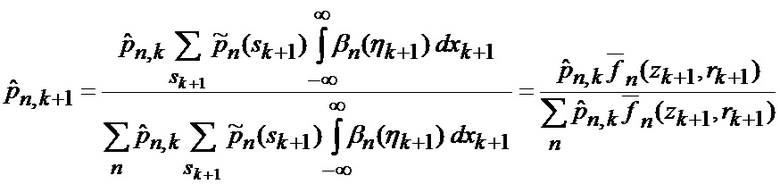
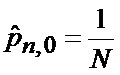
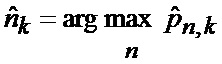
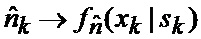

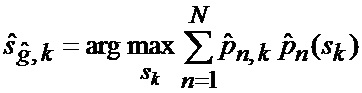
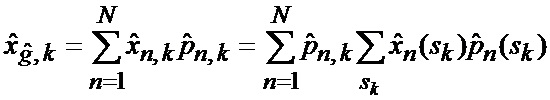
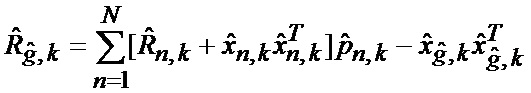
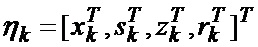
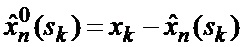
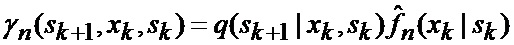
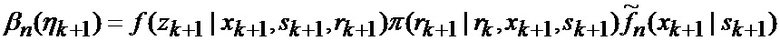
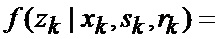
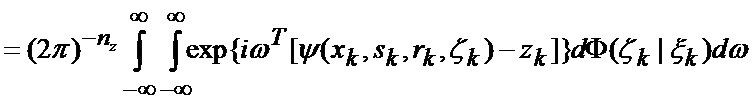
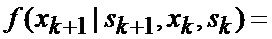
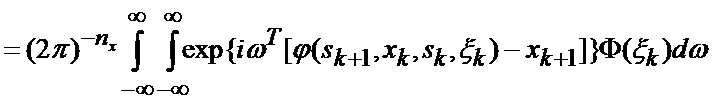
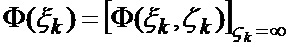
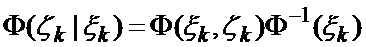
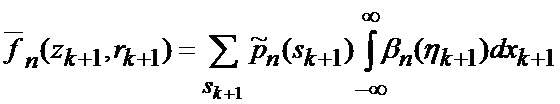
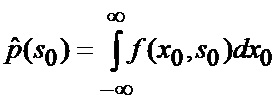
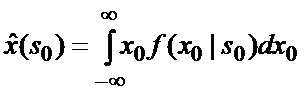
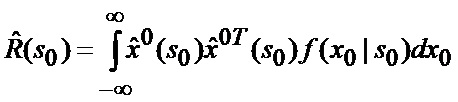
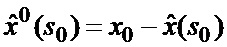
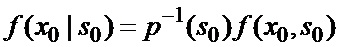
основанной на априорных данных в виде ММ системы «БПЛА - объект наведения - ИС - индикатор» со ССС, включающей нелинейную модель динамики положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования
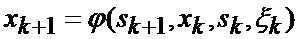
нелинейную модель измерений этих фазовых координат в ИС
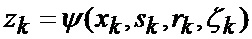
модель смены сектора нахождения точки мгновенного промаха БПЛА
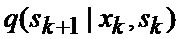
модель индикатора сектора (при его наличии) нахождения точки мгновенного промаха БПЛА
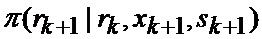
модель неуправляемых случайных возмущений и помех
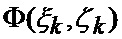
при начальных условиях
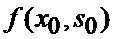
с множеством альтернативных видов аппроксимирующих функций
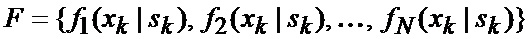
где
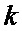
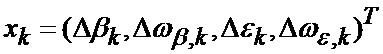
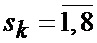
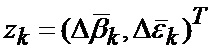
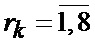
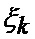
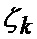
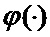
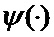
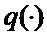
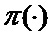
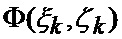
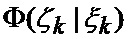
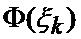
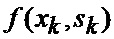
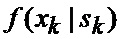
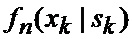
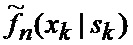
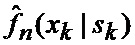
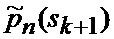
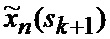
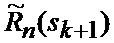
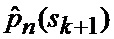
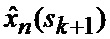
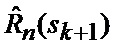
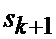
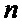

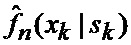
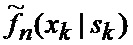
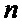

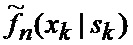
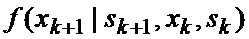
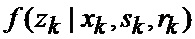
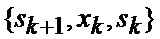
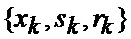
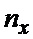
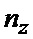
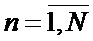
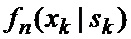
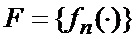
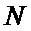
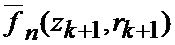

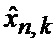
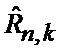
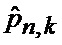

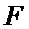
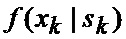
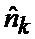
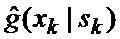
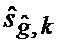
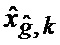
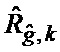
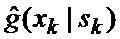
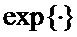
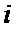
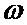
определяется оценка 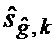
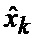
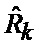
Новыми признаками, обладающими существенными отличиями, являются:
1. Применение многоканального, как по числу секторов картинной плоскости, так и по числу видов аппроксимирующих функций, фильтра совместных оценивания положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, и распознавания сектора нахождения точки мгновенного промаха БПЛА, функционирующего в соответствии с процедурой (30)-(56) квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания на основе нового метода адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно заданных законов распределения, вместо одноканального, по числу видов аппроксимирующих функций, фильтра, функционирующего на основе известного метода двухмоментной параметрической аппроксимации плотностей вероятности [2].
2. Автоматический выбор (40) вида аппроксимирующей функции из априорно заданного их множества непосредственно в процессе функционирования фильтра (реализует разработанный авторами метод адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности на основе идентификации вида аппроксимирующей функции из априорно заданного их множества).
3. Автоматическое формирование (41) смеси аппроксимирующих функций из априорно заданного их множества непосредственно в процессе функционирования фильтра (реализует разработанный авторами метод адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно заданных аппроксимирующих функций).
4. Совместное оценивание фазовых координат (31), (32), (34), (35), (37), (38) и распознавание сектора нахождения точки мгновенного промаха БПЛА (30), (33), (36) на основе метода двухмоментной параметрической аппроксимации [2] в N многоканальных, по числу секторов картинной плоскости объекта, квазиоптимальных фильтрах, отличающихся видом аппроксимирующих функций 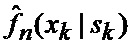
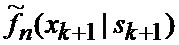
5. Прогнозирование (30) вероятностей 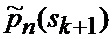
6. Прогнозирование (31) условных математических ожиданий 
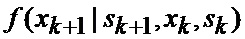
7. Прогнозирование (32) условных КМ 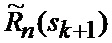
8. Оценивание (33) апостериорных вероятностей 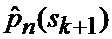
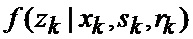
9. Оценивание (34) условных апостериорных математических ожиданий 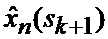
10. Оценивание (35) условных апостериорных КМ 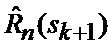
11. Идентификация (36) такого 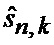
12. Нахождение (37) безусловной, по отношению к секторам нахождения точки мгновенного промаха БПЛА, оценки фазовых координат 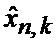
13. Нахождение (38) безусловной, по отношению к секторам нахождения точки мгновенного промаха БПЛА, КМ 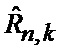
14. Коррекция (39) апостериорных вероятностей 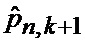

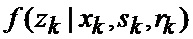
15. Идентификация (40) такого вида аппроксимирующей плотности вероятности 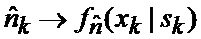
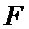
16. Оценивание (41) условной плотности вероятности фазовых координат 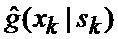
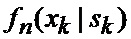
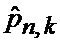
17. Идентификация (42) сектора 
18. Оценивание (43) фазовых координат 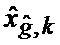
19. Оценивание (44) безусловной по отношению к видам аппроксимирующих функций КМ 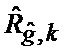
Данные признаки являются существенными и в известных технических решениях не обнаружены.
Применение всех новых существенных признаков позволит достоверно распознать сектор нахождения точки мгновенного промаха БПЛА с одновременным формированием достоверных безусловных оценок положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования путем адаптивной двухмоментной параметрической аппроксимации неизвестной плотности вероятности фазовых координат оптимальной смесью априорно заданных законов распределения за счет учета нелинейностей в динамике фазовых координат и их измерений и учета статистической зависимости вероятностей смены секторов нахождения точки мгновенного промаха БПЛА от фазовых координат.
Заявляемый способ является результатом научно-исследовательской и экспериментальной работы, выполненной авторами.
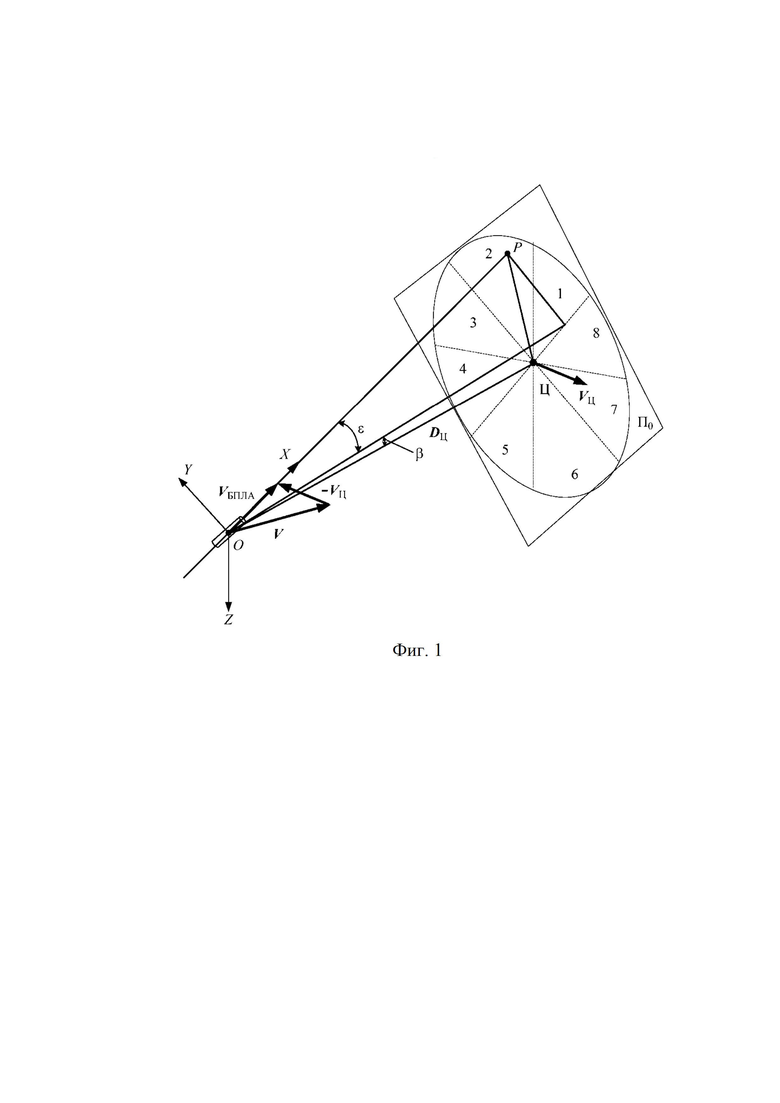
На фиг. 1 представлена схема относительного положения БПЛА и объекта, где О, Ц - соответственно центры масс БПЛА и объекта;
OXYZ - связанная система координат БПЛА;
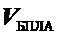 ,
, 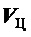 ,V - скорости соответственно БПЛА, цели и взаимного сближения;
,V - скорости соответственно БПЛА, цели и взаимного сближения;
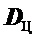 - дальность до цели;
- дальность до цели;
β, ε - соответственно азимут и угол места цели;
П0 - картинная плоскость объекта;
Р - точка промаха;
1-8 - номера секторов.
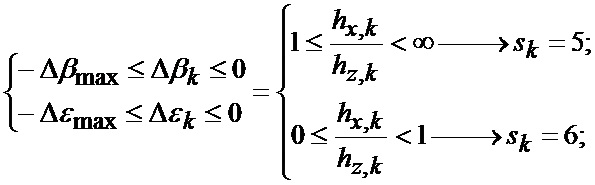
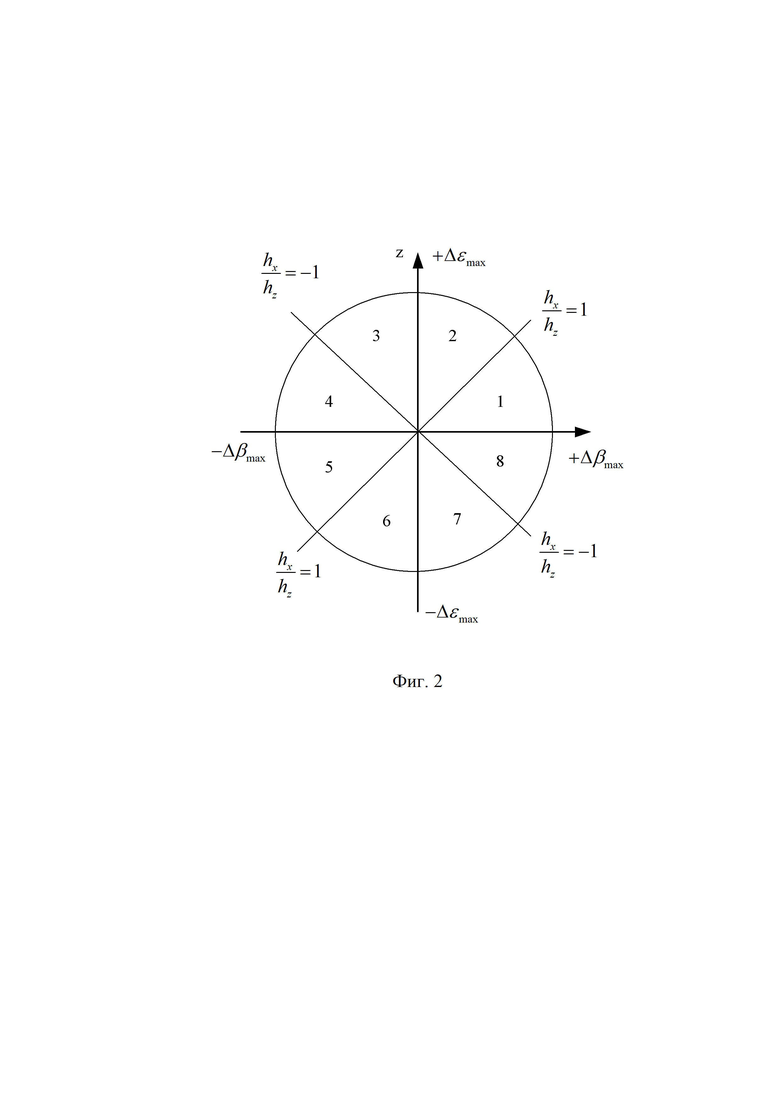
На фиг. 2 приведены верхние и нижние границы секторов картинной плоскости объекта, выбранного для наведения, где 1-8 - номера секторов;
hx - продольный промах БПЛА;
hz - поперечный промах БПЛА.
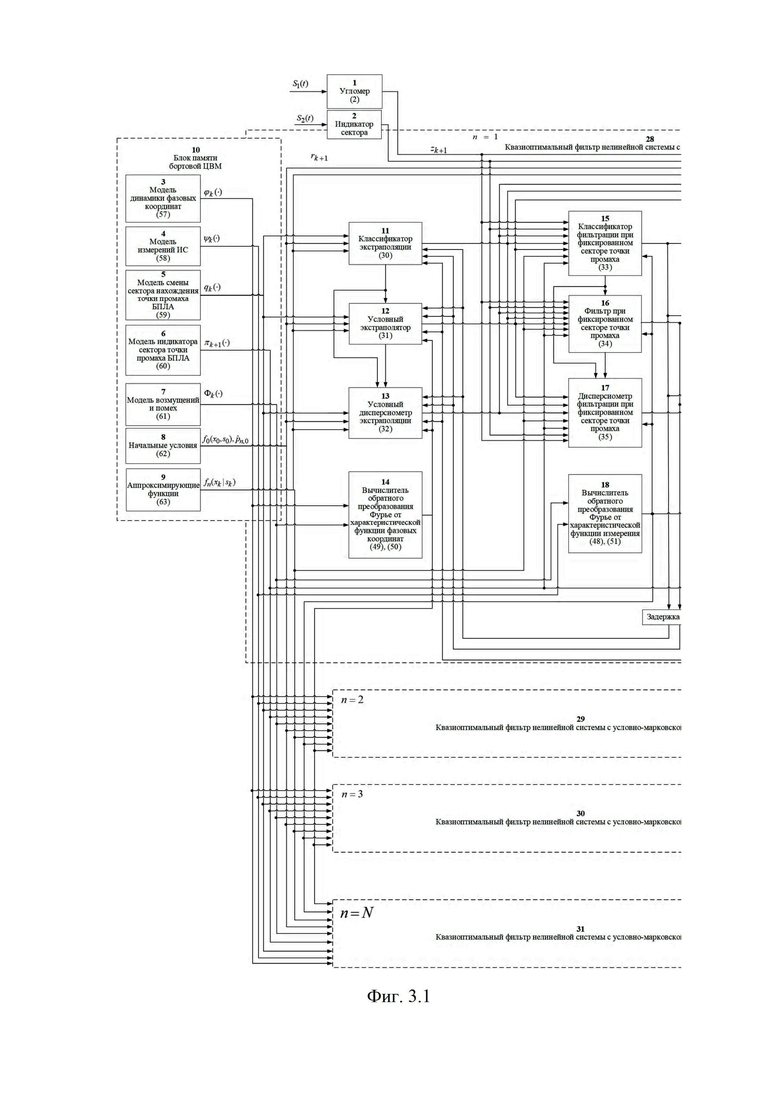
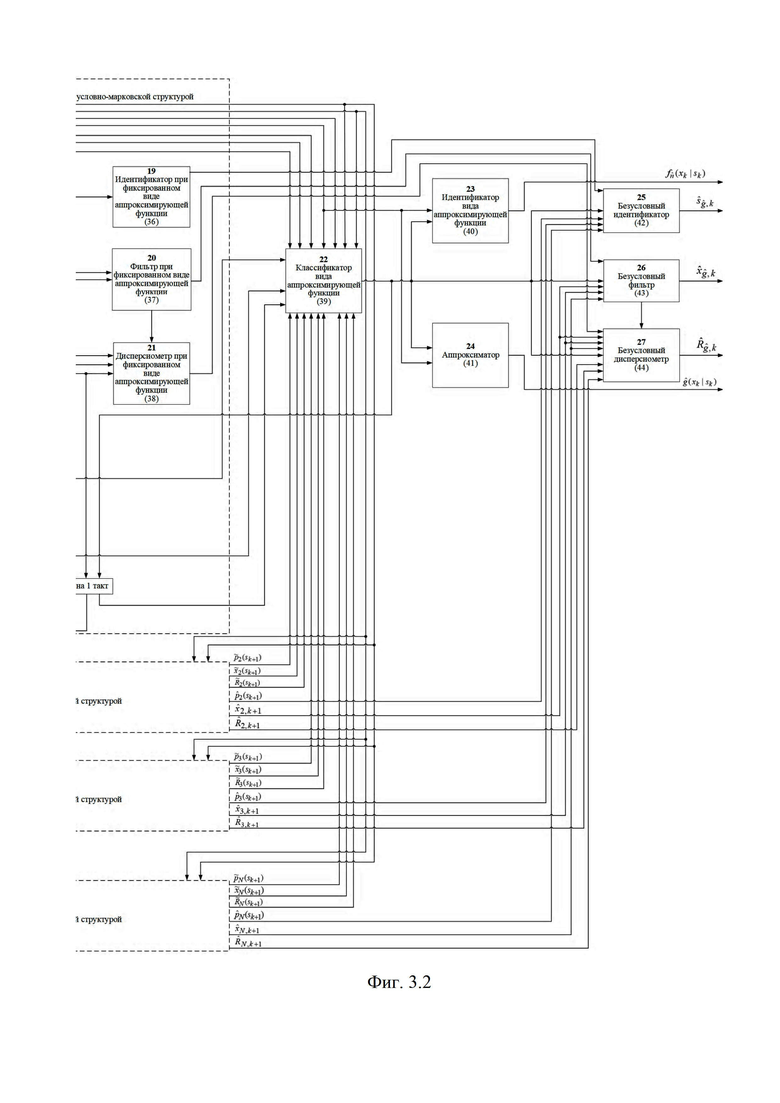
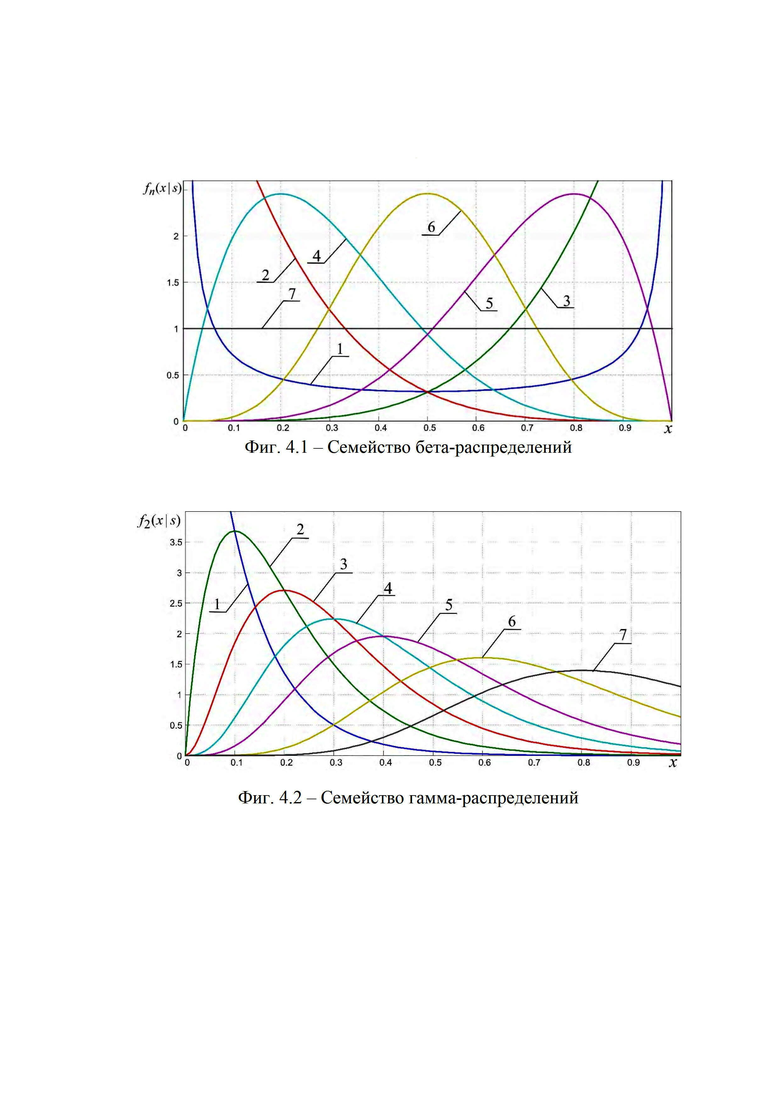
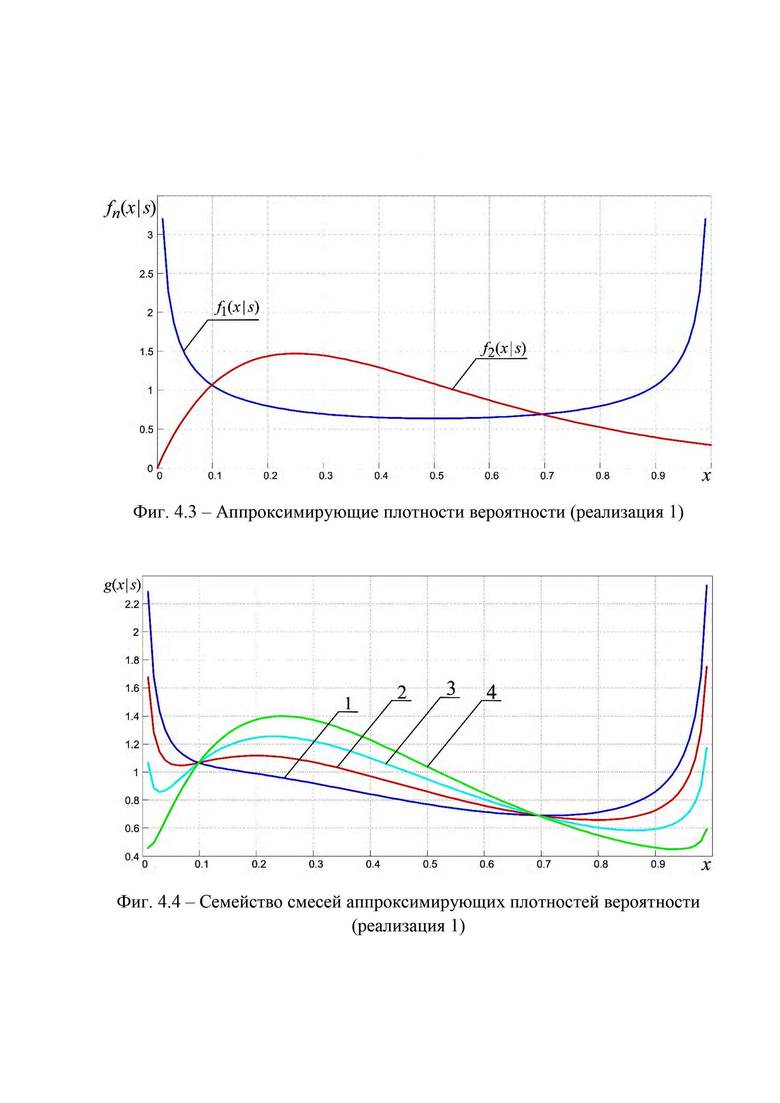
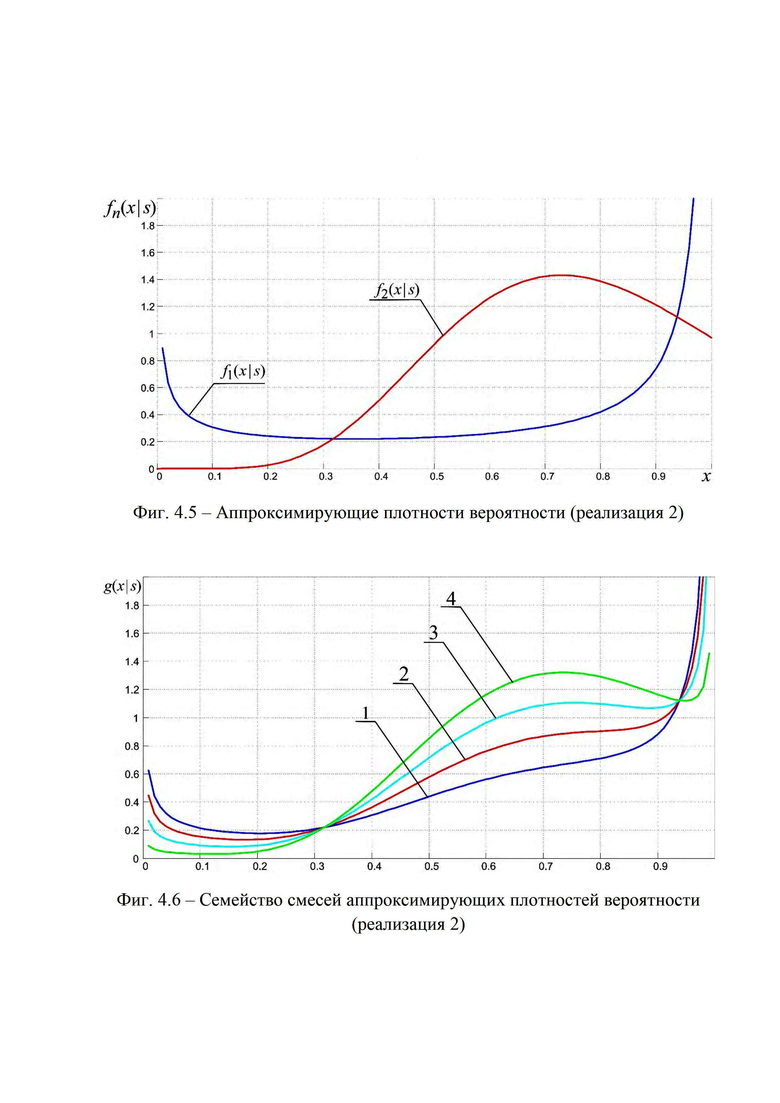
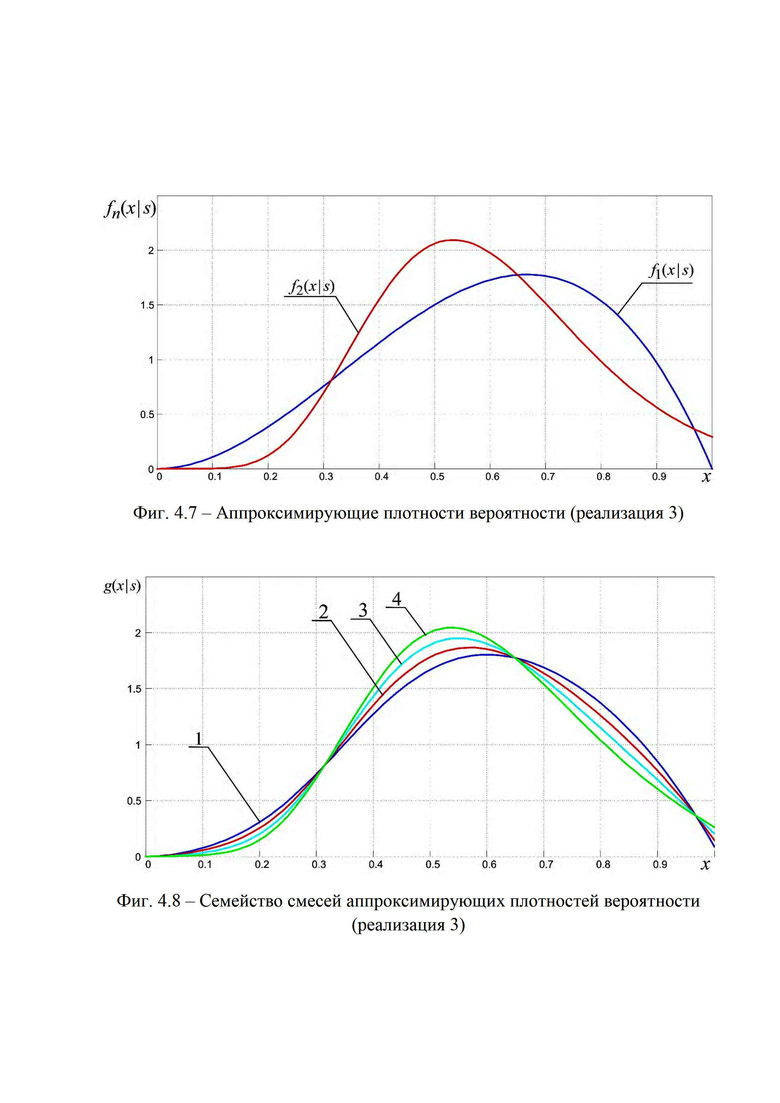
На фиг. 3.1, 3.2 приведена блок-схема, поясняющая реализацию предлагаемого способа определения мгновенного положения точки промаха БПЛА по информации угломерного канала. На фиг. 4.1 и 4.2 приведен пример семейства плотностей вероятности бета- и гамма- распределений соответственно (значения параметров распределений представлены соответственно в табл. 1 и 2), которые рассматриваются в качестве элементов множества альтернативных видов аппроксимирующих функций (63), а также конкретные реализации этих альтернативных аппроксимирующих плотностей (фиг. 4.3, 4.5, 4.7) и соответствующих им семейств смесей из этих плотностей (фиг. 4.4, 4.6, 4.8) при различных значениях вероятностей 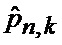
Способ определения мгновенного положения точки промаха БПЛА по информации угломерного канала осуществляется следующим образом.
Сформированные на выходе угломера 1 интенсивно маневрирующих объектов ИС [3] измерения (2) совместно с выходными показаниями индикатора (60) сектора нахождения точки мгновенного промаха БПЛА поступают на вход нового многоканального фильтра 28, 29, 30, 31 совместного оценивания положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, каждый канал которого функционирует в соответствии с известной процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания, структурная схема которой и описание приводятся в [2], и отличается только видом аппроксимирующей функции, положенной в основу этой процедуры. Многоканальный фильтр работает на основе априорных данных (57)-(63) в виде ММ системы «БПЛА - объект наведения - ИС - индикатор» со ССС, включающей (блок 10 памяти бортовой ЦВМ) модель нелинейной динамики фазовых координат 3 взаимного перемещения объекта и БПЛА, представленную функцией 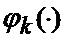
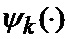
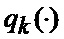
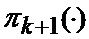
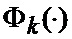
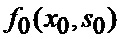

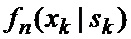
Сформированные на выходе многоканального фильтра 28, 29, 30, 31 прогнозируемые на один шаг дискретности вперед вероятности 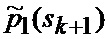

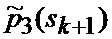
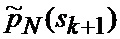
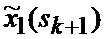
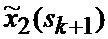
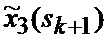
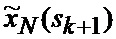
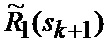
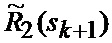

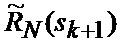
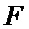
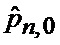
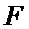
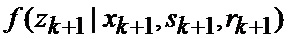
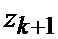
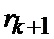

В результате на выходе блока 22 формируются вероятности 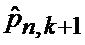
Помимо этого на вход идентификатора 23 и аппроксиматора 24 поступает множество 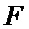
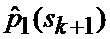
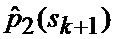
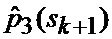
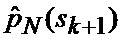

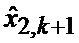
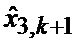
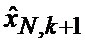
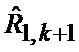
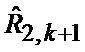
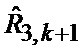
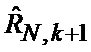

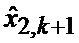
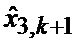
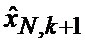
Сформированные на выходе идентификатора 23 оценка 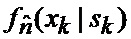
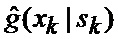
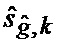
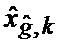
Табл. 1 - Значения параметров аппроксимирующего бета-распределения
Табл. 2 - Значения параметров аппроксимирующего гамма-распределения
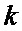
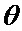
Табл. 3 - Исходные данные для построения смеси бета- и гамма- распределений
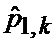
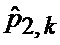
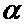
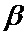
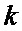
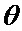
При этом сущность разработанного авторами метода адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно заданных аппроксимирующих функций заключается в следующем.
1. Выдвигается гипотеза об альтернативных видах 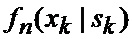
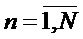
2. С учетом выдвинутой гипотезы в соответствии с (30)-(39) находятся апостериорные вероятности 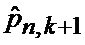
3. С учетом найденных вероятностей в соответствии с (41) оценивается условная плотность вероятности фазовых координат при нахождении точки мгновенного промаха БПЛА в фиксированном секторе, смесью 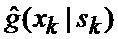
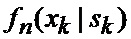
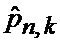
Основную суть метода отражает выражение (39), которое выводится следующим образом. Рассмотрим известное [2] выражение для процедуры квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания
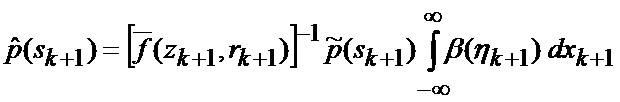
После подстановки 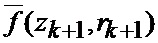
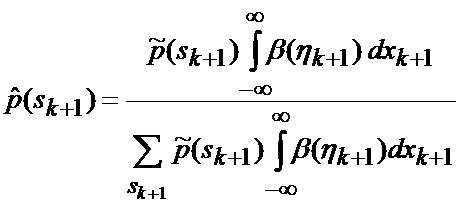
После подстановки 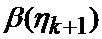
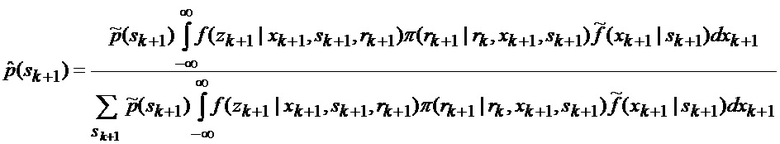
Произведем расширение векторов состояния структуры системы со ССС и индикации этого состояния, включив в них помимо векторов 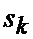
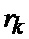
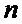
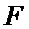
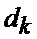
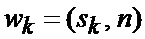
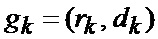
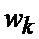
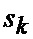

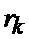
имеем
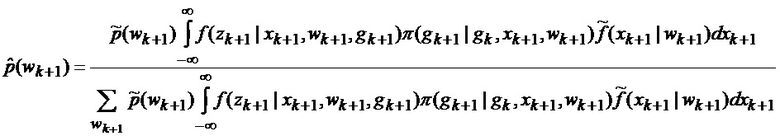
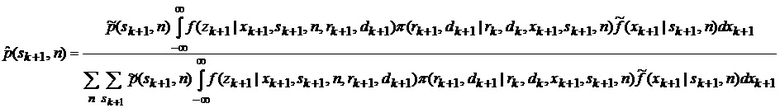
По теореме умножения вероятностей
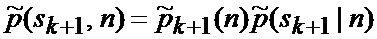
Вследствие постоянства фактического вида условной плотности вероятности фазовых координат, имеем
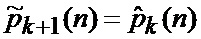
С учетом того, что вектора измерения фазовых координат и индикации состояния структуры не зависят от фактического вида условной плотности вероятности фазовых координат, получаем
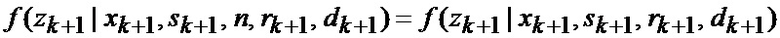

Так как индикатор вида аппроксимирующей функции отсутствует, то
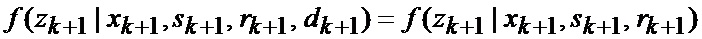
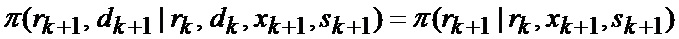
Обозначив 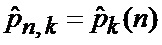

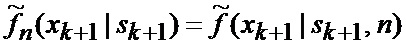
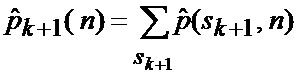
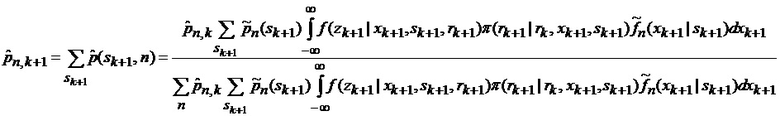
Тогда, воспользовавшись вспомогательными обозначениями, окончательно получаем

где
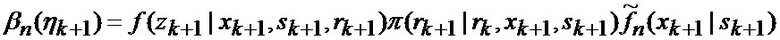
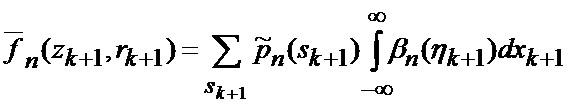
При отсутствии априорных данных о степени соответствия видов аппроксимирующих функций фактическому виду условной плотности вероятности фазовых координат при фиксированном состоянии структуры, начальные условия в (66) принимаются равновероятными
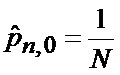
Результаты сравнительного моделирования предлагаемого способа определения мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала на основе многоканального фильтра совместных оценивания положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, и распознавания сектора нахождения точки мгновенного промаха БПЛА, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания на основе адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно заданных законов распределения, и известного способа определения мгновенного положения точки промаха БПЛА по информации угломерного канала [1] свидетельствуют с доверительной вероятностью 0,95 о снижении СКО ошибки фильтрации на 14±0,1% и о повышении вероятности правильного распознавания сектора нахождения точки мгновенного промаха БПЛА на 12±0,1%.
Таким образом, применение предлагаемого изобретения позволит повысить достоверность распознавания сектора нахождения точки мгновенного промаха БПЛА и оценки фазовых координат взаимного перемещения объекта и БПЛА путем адаптивной двухмоментной параметрической аппроксимации неизвестной плотности вероятности фазовых координат смесью априорно заданных законов распределения и приближением получаемых оценок к их оптимальным значениям за счет учета нелинейностей в динамике фазовых координат и их измерений и учета статистической зависимости вероятностей смены секторов нахождения точки мгновенного промаха БПЛА от фазовых координат.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Определение мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала / С.М. Мужичек, В.И. Павлов, О.В. Ермолин, А.А. Скрынников // Журнал «Вестник компьютерных и информационных технологий» - 2017. - № 5. - С. 23-27 (прототип)
2. Бухалев, В.А. Оптимальное сглаживание в системах со случайной скачкообразной структурой / В.А. Бухалев. М.: ФИЗМАТЛИТ, 2013, С. 115-120.
3. Определение направления на объект и предполагаемого промаха на борту беспилотного летательного аппарата мгновенного положения точки промаха беспилотного летательного аппарата по информации угломерного канала / Г.Г. Себряков, С.М. Мужичек, В.И. Павлов, О.В. Ермолин, А.А. Скрынников // Журнал «Вестник компьютерных и информационных технологий»- 2018. - № 12. - С. 11-18.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ комплексирования информации при определении направления беспилотного летательного аппарата на воздушный объект и величины предполагаемого промаха | 2022 |
|
RU2794733C1 |
| Способ сопровождения воздушной цели из класса "самолёт с турбореактивным двигателем" при воздействии уводящих по дальности и скорости помех | 2020 |
|
RU2764781C1 |
| Способ распознавания варианта наведения подвижного объекта на один из летательных аппаратов группы | 2019 |
|
RU2713212C1 |
| СПОСОБ ДОСТАВКИ ПОЛЕЗНОЙ НАГРУЗКИ НА ВОЗДУШНЫЙ ОБЪЕКТ | 2022 |
|
RU2784492C1 |
| Способ сопровождения крылатой ракеты при огибании рельефа местности в различных тактических ситуациях | 2021 |
|
RU2760951C1 |
| СПОСОБ ДОСТАВКИ ПОЛЕЗНОЙ НАГРУЗКИ НА ВОЗДУШНЫЙ ОБЪЕКТ | 2023 |
|
RU2804765C1 |
| Способ распознавания функционального назначения летательных аппаратов пары по принципу "ведущий-ведомый" | 2019 |
|
RU2726869C1 |
| Способ комплексирования информации радиолокационной станции и радиолокационных головок самонаведения ракет, пущенных носителем по воздушной цели при воздействии уводящих по дальности и скорости помех | 2021 |
|
RU2765145C1 |
| Способ сопровождения в радиолокационной станции воздушной цели из класса "самолёт с турбореактивным двигателем" при воздействии уводящих по дальности и скорости помех | 2019 |
|
RU2713635C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СИСТЕМЫ САМОНАВЕДЕНИЯ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2024 |
|
RU2830544C1 |
Изобретение относится к области вторичной цифровой обработки сигналов и может быть использовано в телевизионных, радиолокационных, инфракрасных информационных системах (ИС) беспилотных летательных аппаратов (БПЛА) для определения положения точки их промаха относительно выбранного объекта наведения по информации только угломерного канала системы управления, в том числе, при минимальных расстояниях между БПЛА и объектом, а также в момент ослепления ИС БПЛА. Достигаемый технический результат - повышение достоверности распознавания сектора нахождения точки мгновенного промаха БПЛА в картинной плоскости объекта наведения и оценки фазовых координат взаимного перемещения объекта и БПЛА. Способ заключается в распознавании сектора нахождения точки мгновенного промаха БПЛА с одновременным формированием достоверных безусловных оценок положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, путем адаптивной двухмоментной параметрической аппроксимации (АДПА) неизвестной плотности вероятности фазовых координат оптимальной смесью априорно заданных законов распределения за счет учета нелинейностей в динамике фазовых координат и их измерений и учета статистической зависимости вероятностей смены секторов нахождения точки мгновенного промаха БПЛА от фазовых координат на основе измерений в угломере положения линии визирования БПЛА на объект по азимуту и углу места, формирования границ секторов картинной плоскости объекта наведения, обработки измерений угломера и показаний индикатора сектора в многоканальном фильтре, функционирующем в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания на основе нового метода АДПА неизвестных плотностей вероятности смесью априорно заданных законов распределения, основанной на априорных данных в виде математической модели ММ) системы «БПЛА - объект наведения - информационная система - индикатор» со случайной скачкообразной структурой, включающей нелинейную модель динамики положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, нелинейную модель измерений этих фазовых координат в ИС, модель смены сектора нахождения точки мгновенного промаха БПЛА, модель индикатора сектора нахождения точки мгновенного промаха БПЛА, модель неуправляемых случайных возмущений и помех, при начальных условиях, с множеством альтернативных видов аппроксимирующих функций, и на выходе которого формируются оценки вида аппроксимирующей функции, аппроксимирующей смеси априорно заданных функций, сектора нахождения точки мгновенного промаха БПЛА, безусловных математических ожиданий фазовых координат и ковариационных матриц ошибок их оценивания. 3 табл., 12 ил.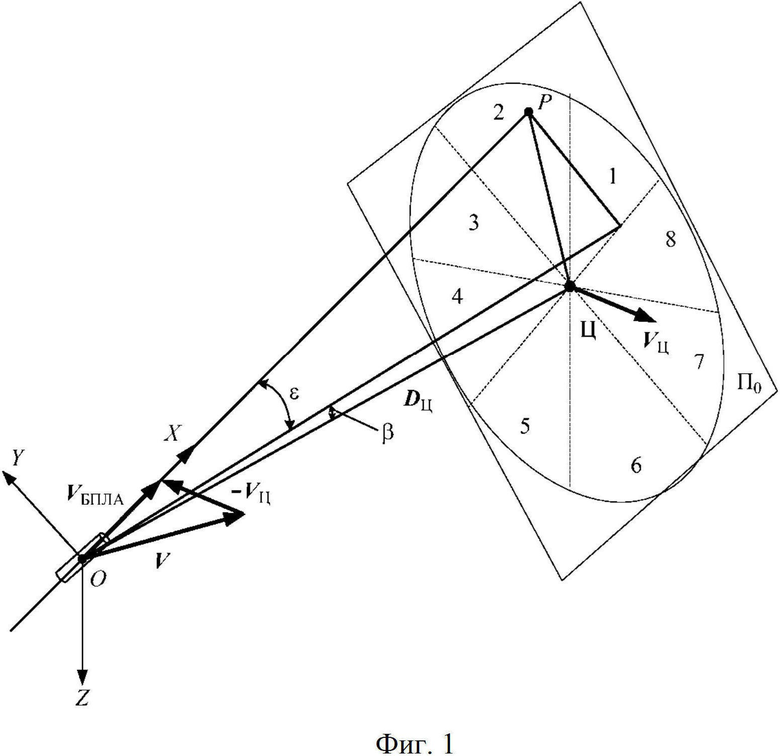
Способ определения мгновенного положения точки промаха беспилотного летательного аппарата (БПЛА) по информации угломерного канала, заключающийся в том, что угломер БПЛА формирует значения положения линии визирования на объект по азимуту и углу места, задаются верхние и нижние границы секторов картинной плоскости объекта, выбранного для наведения, формируется вектор измерения и показание индикатора нахождения точки мгновенного промаха БПЛА в конкретном секторе, отличающийся тем, что сформированные измерения и показания поступают на вход многоканального фильтра, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания на основе нового метода адаптивной двухмоментной параметрической аппроксимации (АДПА) неизвестных плотностей вероятности смесью априорно заданных законов распределения, основанной на априорных данных в виде математической модели (ММ) системы «БПЛА – объект наведения – информационная система (ИС) – индикатор» со случайной скачкообразной структурой (ССС), включающей нелинейную модель динамики положения линии визирования БПЛА на объект по азимуту и углу места, а также составляющих угловой скорости этой линии визирования, нелинейную модель измерений этих фазовых координат в ИС, модель смены сектора нахождения точки мгновенного промаха БПЛА, модель индикатора сектора нахождения точки мгновенного промаха БПЛА, модель неуправляемых случайных возмущений и помех, при начальных условиях, с множеством альтернативных видов аппроксимирующих функций, на основе априорных данных о смене положения точки мгновенного промаха БПЛА по секторам и динамике фазовых координат, представленных соответственно начальными и переходными вероятностями условной цепи Маркова и альтернативными моделями динамики фазовых координат, соответствующих различному положению по секторам точки мгновенного промаха БПЛА относительно объекта, по результатам измерений и показаниям индикатора сектора осуществляется совместное оценивание фазовых координат и распознавание сектора нахождения точки мгновенного промаха БПЛА на основе нового метода АДПА в нескольких многоканальных, по числу секторов картинной плоскости объекта, квазиоптимальных фильтрах, различающихся видом примененной аппроксимирующей функции, при этом в каждом фильтре на основе априорных данных о смене положения точки мгновенного промаха БПЛА по секторам картинной плоскости объекта, представленных соответственно начальными и переходными вероятностями условной цепи Маркова, прогнозируются вероятности нахождения точки мгновенного промаха БПЛА в каждом из секторов картинной плоскости объекта на один шаг дискретности вперед при фиксированном виде аппроксимирующей функции, с учетом найденных вероятностей на основе априорных данных о смене положения точки мгновенного промаха БПЛА по секторам картинной плоскости объекта и динамике фазовых координат взаимного перемещения объекта и БПЛА, с учетом, найденной как обратное преобразование Фурье от характеристической функции фазовых координат, условной плотности вероятности фазовых координат, прогнозируются условные математические ожидания (МО) фазовых координат на один шаг дискретности вперед при фиксированном виде аппроксимирующей функции и нахождении точки мгновенного промаха БПЛА в фиксированном секторе, с учетом найденных вероятностей и математических ожиданий прогнозируются условные ковариационные матрицы (КМ) ошибок оценивания фазовых координат на один шаг дискретности вперед при фиксированном виде аппроксимирующей функции и нахождении точки мгновенного промаха БПЛА в фиксированном секторе, по степени согласованности, представленной функцией правдоподобия, спрогнозированных вероятностей, МО фазовых координат и КМ ошибок их оценивания с результатами измерений и показаниями индикатора сектора, с учетом найденной, как обратное преобразование Фурье от характеристической функции измерений, условной плотности вероятности этих измерений оцениваются апостериорные вероятности нахождения точки мгновенного промаха БПЛА в каждом из секторов картинной плоскости объекта при фиксированном виде аппроксимирующей функции, для каждой альтернативной модели динамики фазовых координат, отличающейся гипотезой о положении точки мгновенного промаха БПЛА относительно объекта, на основе спрогнозированных МО и КМ ошибок прогноза с учетом результатов измерения и показаний индикатора находятся условные апостериорные МО фазовых координат взаимного перемещения объекта и БПЛА при фиксированном виде аппроксимирующей функции и нахождении точки мгновенного промаха БПЛА в фиксированном секторе, для каждой альтернативной модели динамики фазовых координат, отличающейся гипотезой о положении точки мгновенного промаха БПЛА относительно объекта, на основе спрогнозированных МО и КМ ошибок прогноза с учетом результатов измерения и показаний индикатора находятся условные апостериорные КМ ошибок оценивания фазовых координат при фиксированном виде аппроксимирующей функции и нахождении точки мгновенного промаха БПЛА в фиксированном секторе, из возможных секторов нахождения точки мгновенного промаха БПЛА идентифицируется тот, для которого при фиксированном виде аппроксимирующей функции найденная апостериорная вероятность окажется больше, безусловная, по отношению к секторам нахождения точки мгновенного промаха БПЛА, оценка фазовых координат при фиксированном виде аппроксимирующей функции вычисляется на основе апостериорных вероятностей нахождения точки мгновенного промаха БПЛА в каждом из секторов картинной плоскости объекта и условных апостериорных оценок фазовых координат, как безусловного математического ожидания, с учетом найденных апостериорных вероятностей нахождения точки мгновенного промаха БПЛА в каждом из секторов картинной плоскости объекта, условных МО фазовых координат, условных КМ ошибок их оценивания и безусловных оценок фазовых координат находится безусловная, по отношению к секторам нахождения точки мгновенного промаха БПЛА, КМ ошибок оценивания фазовых координат при фиксированном виде аппроксимирующей функции, для каждого из многоканальных по числу видов аппроксимирующих функций фильтров, по степени согласованности, представленной функцией правдоподобия, спрогнозированных вероятностей нахождения точки мгновенного промаха БПЛА в каждом из секторов картинной плоскости объекта, условных МО фазовых координат и КМ ошибок их оценивания при различных видах аппроксимирующих функций с результатами измерений и показаниями индикатора сектора, с учетом найденной, как обратное преобразование Фурье от характеристической функции измерений, условной плотности вероятности этих измерений корректируются апостериорные вероятности соответствия вида аппроксимирующей функции плотности вероятности из заданного их множества фактическому виду плотности вероятности фазовых координат, из возможных видов аппроксимирующих плотностей вероятности идентифицируется тот, для которого скорректированная вероятность окажется больше, оценивается условная плотность вероятности фазовых координат при нахождении точки мгновенного промаха БПЛА в фиксированном секторе картинной плоскости объекта, смесью априорно заданных аппроксимирующих функций, взятых с весовыми коэффициентами, пропорциональными скорректированным вероятностям соответствия вида этих функций фактическому виду плотности вероятности фазовых координат, с учетом оценок вероятностей соответствия видов аппроксимирующих функций из заданного их множества фактическому виду плотности вероятности фазовых координат и апостериорных вероятностей идентифицируется сектор нахождения точки мгновенного промаха БПЛА, с учетом найденных оценок фазовых координат при фиксированном виде аппроксимирующей функции и вероятностей соответствия видов аппроксимирующих функций из заданного их множества фактическому виду плотности вероятности фазовых координат, определяется оценка фазовых координат, как безусловное по отношению к видам аппроксимирующих функций МО, с учетом найденных апостериорных вероятностей соответствия видов аппроксимирующих функций из заданного их множества фактическому виду плотности вероятности фазовых координат, условных МО фазовых координат и КМ ошибок их оценивания при фиксированном виде аппроксимирующей функции, и безусловных оценок этих фазовых координат находится безусловная по отношению к видам аппроксимирующих функций КМ ошибок оценивания фазовых координат.
| СЕБРЯКОВ Г.Г., МУЖИЧЕК С.М., СКРЫННИКОВ А.А., ПАВЛОВ В.И., ЕРМОЛИН О.В | |||
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Кипятильник для воды | 1921 |
|
SU5A1 |
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ЛЕТАТЕЛЬНОГО АППАРАТА | 2012 |
|
RU2496081C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРАЕКТОРИИ ПОЛЕТА ИНФОРМАЦИОННОГО ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2597309C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ МОДИФИЦИРОВАННОЙ, ИНВАРИАНТНОЙ К РЕЛЬЕФУ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ УГЛОМЕСТНОЙ ПРОЦЕДУРЫ РАСЧЁТА ДАЛЬНОСТИ | 2016 |
|
RU2617373C1 |
Авторы
Даты
2020-05-21—Публикация
2019-09-30—Подача