Область техники, к которой относится изобретение
[0001] Варианты осуществления настоящей заявки относятся к области технологий связи и, в частности, к способу и устройству кодирования полярным кодом.
Уровень техники
[0002] В качестве самой фундаментальной технологии беспроводного доступа, канальное кодирование играет ключевую роль в обеспечении надежной передачи данных. В существующей системе беспроводной связи канальное кодирование обычно выполняется с использованием турбокода, кода проверки на четность с низкой плотностью (low-density parity-check, LDPC) и полярного (Polar) кода. Турбокод не может поддерживать передачу информации с чрезмерно низкой или чрезмерно высокой скоростью передачи данных. Для передачи среднего/короткого пакета из–за характеристик кодирования/декодирования турбокода и кода LDPC для турбокода и кода LDPC оказывается очень сложно достичь идеальной производительности в случае ограниченной кодовой длины. С точки зрения реализации турбокод и код LDPC имеют относительно высокую вычислительную сложность в процессе реализации кодирования/декодирования. Полярный код – это хороший код, который теоретически доказал, что он способен достигать пропускную способность Шеннона и имеет относительно низкую сложность кодирования/декодирования, и поэтому применяется более широко.
[0003] Однако с быстрым развитием систем беспроводной связи системы будущей связи, такие как системы связи 5–го поколения (5th generation, 5G), будут иметь некоторые новые характеристики. Например, три наиболее типичных сценария связи включают в себя расширенную широкополосную мобильную связь (enhance mobile broadband, eMBB), массовую связь машинного типа (massive machine type communication, mMTC) и сверхнадежную связь с малой задержкой (ultra reliable low latency communication, URLLC). Сценарии связи предъявляют более высокие требования к производительности кодирования/декодирования полярным кодом.
[0004] Упорядочение надежности для поляризованных каналов играет ключевую роль в производительности кодирования/декодирования полярным кодом. Однако в настоящее время точность упорядочения надежности для поляризованных каналов нежелательна, что препятствует дальнейшему улучшению характеристик кодирования/декодирования полярным кодом во время применения.
Сущность изобретения
[0005] Варианты осуществления настоящей заявки предоставляют способ и устройство кодирования полярным кодом для повышения точности упорядочения надежности для поляризованных каналов.
[0006] Конкретные технические решения, представленные в вариантах осуществления настоящей заявки, являются следующими:
[0007] Согласно первому аспекту предоставлен способ кодирования полярным кодом. Способ включает в себя: получение, посредством устройства кодирования, подлежащих кодированию битов, где длина подлежащих кодированию битов равна K, и K является положительным целым числом; получение последовательности, используемой для кодирования K подлежащих кодированию битов, где последовательность обозначена как первая последовательность, первая последовательность используется для представления порядка надежности N поляризованных каналов, первая последовательность включает в себя порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N является базовой кодовой длиной полярного кода, N является положительной целочисленной степенью 2, и K≤N; выбор в порядке убывания надежности первых K порядковых номеров, надежность которых имеет высокий ранг в первой последовательности; и отображение подлежащих кодированию битов информации в поляризованные каналы, соответствующие первым K порядковым номерам, и выполнение кодирования полярным кодом над подлежащими кодированию битами. Следовательно, позиции информационных битов и фиксированных битов определяются путем вычисления надежности поляризованных каналов полярного кода без учета параметра канала и битовой скорости. Таким образом, вычислительная сложность кодирования полярным кодом может быть уменьшена.
[0008] В одном возможном варианте реализации первая последовательность является всей или поднабором второй последовательности, при этом вторая последовательность включает в себя порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, Nmax является положительным целым числом, Nmax≥N, и порядок, в котором расположены порядковые номера поляризованных каналов в первой последовательности, согласован с порядком, в котором расположены порядковые номера, меньшие N, в порядковых номерах поляризованные каналы во второй последовательности.
[0009] В одном возможном варианте реализации вторая последовательность может быть частью или всей любой последовательностью, показанной в последовательностях с Q1 по Q30 в описании, порядковые номера N поляризованных каналов во второй последовательности расположены в порядке возрастания надежности N поляризованных каналов, а минимальное значение порядкового номера поляризованного канала равно 0.
[0010] В одном возможном варианте реализации вторая последовательность является частью или всей любой последовательностью, показанной в таблицах с Q1 по Q30 в описании, порядковые номера N поляризованных каналов во второй последовательности расположены в порядке возрастания надежности N поляризованных каналов, и минимальное значение порядкового номера поляризованного канала равно 0.
[0011] В одном возможном варианте реализации вторая последовательность может быть частью или всей любой последовательностью, показанной в последовательностях с Z1 по Z30 в описании, каждый из порядковых номеров N поляризованных каналов во второй последовательности соответствует порядку надежности порядкового номера во всей последовательности, и минимальное значение порядкового номера поляризованного канала равно 0.
[0012] В одном возможном варианте реализации вторая последовательность является частью или всей любой последовательностью, показанной в таблицах с Z1 по Z30 в описании, каждый из порядковых номеров N поляризованных каналов во второй последовательности соответствует порядку надежности порядкового номера во всей последовательности, и минимальное значение порядкового номера поляризованного канала равно 0.
[0013] Согласно второму аспекту предоставляется устройство кодирования полярным кодом. Устройство имеет функцию реализации способа согласно любому из первого аспекта и возможных вариантов реализации первого аспекта. Функция может быть реализована с использованием аппаратного обеспечения или может быть реализована с использованием аппаратного обеспечения для исполнения соответствующего программного обеспечения. Аппаратное обеспечение или программное обеспечение включает в себя один или более модулей, соответствующих вышеуказанной функции.
[0014] В одном возможном варианте реализации, когда часть или вся функция реализуется с использованием аппаратного обеспечения, устройство кодирования полярным кодом включает в себя: схему интерфейса ввода, выполненную с возможностью получения подлежащих кодированию битов; логическую схему, выполненную с возможностью выполнения способа в соответствии с любым из первого аспекта и возможных вариантов реализации первого аспекта; и схему интерфейса вывода, выполненную с возможностью вывода битовой последовательности после кодирования.
[0015] В необязательном порядке, устройство кодирования полярным кодом может быть микросхемой или интегральной схемой.
[0016] В одном возможном варианте реализации, когда часть или вся функция реализуется с использованием программного обеспечения, устройство кодирования полярным кодом включает в себя: память, выполненную с возможностью хранения программы; и процессор, выполненный с возможностью выполнения программы, хранящейся в памяти. Когда программа исполняется, устройство кодирования полярным кодом может реализовать способ в соответствии с любым из первого аспекта и возможных вариантов осуществления первого аспекта.
[0017] В необязательном порядке, память может быть физически независимым блоком. В качестве альтернативы, память интегрирована с процессором.
[0018] В одном возможном варианте реализации, когда часть или вся функция реализуется с использованием программного обеспечения, устройство кодирования полярным кодом включает в себя процессор. Память, выполненная с возможностью хранения программы, расположена вне устройства кодирования. Процессор соединен с памятью с помощью схемы/проводников и выполнен с возможностью считывания и исполнение программы, хранящейся в памяти.
[0019] Согласно третьему аспекту предоставляется система связи. Система связи включает в себя сетевое устройство и терминал. Сетевое устройство или терминал может выполнять способ в соответствии с любым из первого аспекта и возможных вариантов реализации первого аспекта.
[0020] Согласно четвертому аспекту предоставляется компьютерный носитель данных, хранящий компьютерную программу. Компьютерная программа включает в себя инструкцию, используемую для выполнения способа в соответствии с любым из первого аспекта и возможных вариантов реализации первого аспекта.
[0021] Согласно пятому аспекту предоставляется компьютерный программный продукт, включающий в себя инструкцию. При исполнении на компьютере инструкция предписывает компьютеру выполнять способы в соответствии с вышеизложенными аспектами.
[0022] Согласно шестому аспекту предоставляется беспроводное устройство. Беспроводное устройство включает в себя устройство кодирования, выполненное с возможностью реализации способа, описанного в любом из первого аспекта и возможных вариантов реализации первого аспекта, модулятор и приемопередатчик, при этом
модулятор выполнен с возможностью модуляции битовой последовательности после кодирования для получения модулированной последовательности; и
приемопередатчик выполнен с возможностью обработки модулированной последовательности.
[0023] В одном возможном варианте реализации беспроводное устройство представляет собой терминал или сетевое устройство.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
[0024] Фиг.1 является схематической архитектурной схемой системы связи, применяемой в одном варианте осуществления настоящей заявки;
[0025] Фиг.2 является схематической блок–схемой последовательности операций способа кодирования полярным кодом в соответствии с одним вариантом осуществления настоящей заявки;
[0026] Фиг.3 является первой структурной схемой устройства кодирования полярным кодом в соответствии с одним вариантом осуществления настоящей заявки;
[0027] Фиг.4 является второй структурной схемой устройства кодирования полярным кодом в соответствии с одним вариантом осуществления настоящей заявки;
[0028] Фиг.5 является третьей структурной схемой устройства кодирования полярным кодом в соответствии с одним вариантом осуществления настоящей заявки; и
[0029] Фиг.6 является четвертой структурной схемой устройства кодирования полярным кодом в соответствии с одним вариантом осуществления настоящей заявки.
Описание вариантов осуществления
[0030] Далее подробно описываются варианты осуществления настоящей заявки со ссылкой на прилагаемые чертежи.
[0031] Варианты осуществления настоящей заявки предоставляют способ и устройство кодирования полярным кодом. Порядок надежности получается на основе надежности поляризованных каналов, порядковые номера поляризованных каналов, используемых для отправки информационных битов, выбираются на основе порядка надежности, а кодирование полярным кодом выполняется на основе порядковых номеров, выбранных для информационных битов. В вариантах осуществления настоящей заявки надежность каждого подканала полярного кода может быть вычислена более точно. Способ и устройство кодирования, предусмотренные в вариантах осуществления настоящего изобретения, подробно описаны ниже со ссылкой на прилагаемые чертежи.
[0032] Чтобы облегчить понимание вариантов осуществления настоящей заявки, ниже кратко описан полярный код.
[0033] В схеме кодирования полярным кодом бесшумный канал используется для передачи информации, полезной для пользователя, а канал с белым шумом используется для передачи согласованной информации или не используется для передачи информации. Полярный код представляет собой линейный блочный код со своей матрицей кодирования 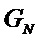


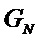

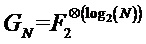

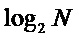
Вышеприведенная матрица 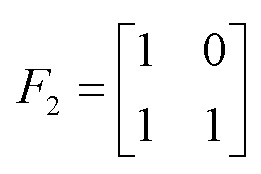 .
.

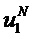
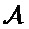
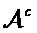
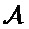
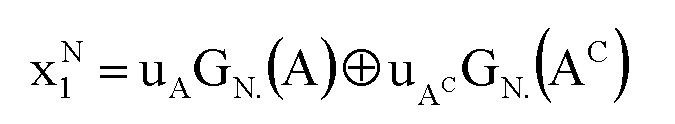
где GN(A) является подматрицей, полученной из строк, которые соответствуют индексам в наборе 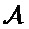
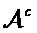
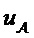
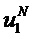
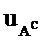
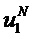
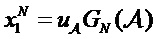
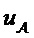
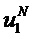
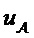
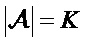

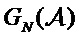
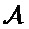
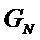

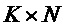
[0035] Процесс построения полярного кода, то есть процесс выбора набора 
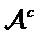
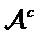

[0036] Решения, предоставленные в вариантах осуществления настоящей заявки, относятся к тому, как определять надежность поляризованного канала. Основная идея изобретения вариантов осуществления настоящей заявки состоит в том, что надежность поляризованного канала может быть представлена с использованием некоторой надежности. С точки зрения спектрального анализа сигналов приближение существующей надежности к надежности поляризованного канала можно понимать как преобразование области сигнала. Подобно преобразованию Фурье, в котором преобразование между временной областью и частотной областью сигнала реализуется с использованием ядра 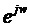

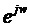
[0037] Фиг.1 является структурной схемой сети беспроводной связи в соответствии с одним вариантом осуществления настоящего изобретения. Фиг.1 является всего лишь примером. Другие беспроводные сети, к которым могут применяться способ или устройство кодирования в соответствии с вариантами осуществления настоящего изобретения, должны входить в объем охраны настоящего изобретения.
[0038] Как показано на Фиг.1, сеть 100 беспроводной связи включает в себя сетевое устройство 110 и терминал 112. Когда сеть 100 беспроводной связи включает в себя базовую сеть 102, сетевое устройство 110 может быть дополнительно соединено с базовой сетью 102. Сетевое устройство 110 может дополнительно осуществлять связь с IP–сетью 104, например, Интернетом (Internet), частной IP–сетью или другой сетью передачи данных. Сетевое устройство предоставляет обслуживание для терминала в зоне действия сетевого устройства. Например, как показано на Фиг.1, сетевое устройство 110 обеспечивает беспроводной доступ для одного или более терминалов 112 в зоне покрытия сетевого устройства 110. Кроме того, может существовать перекрывающаяся область между покрытием сетевых устройств, например, сетевым устройством 110 и сетевым устройством 120. Сетевые устройства могут дополнительно осуществлять связь друг с другом, например, сетевое устройство 110 может осуществлять связь с сетевым устройством 120.
[0039] Вышеупомянутое сетевое устройство может быть устройством, выполненным с возможностью осуществления связи с терминальным устройством. Например, сетевое устройство может быть базовой приемопередающей станцией (Base Transceiver Station, BTS) в системе GSM или системе CDMA или может быть Узлом B (NodeB, NB) в системе WCDMA, или может дополнительно представлять собой развитый NodeB (Evolved Node B, eNB или eNodeB) в системе LTE или устройство на стороне сети в будущей сети 5G. Альтернативно, сетевое устройство может быть ретрансляционной станцией, точкой доступа, находящимся в транспортном средстве устройством или тому подобным. В системе связи устройство–устройство (Device to Device, D2D) сетевое устройство может альтернативно быть терминалом, который играет роль базовой станции.
[0040] Вышеупомянутый терминал может относиться к пользовательскому оборудованию (User Equipment, UE), терминалу доступа, пользовательскому блоку, мобильной станции, удаленной станции, удаленному терминалу, мобильному устройству, пользовательскому терминалу, устройству беспроводной связи, пользовательскому агенту или пользовательскому устройству. Терминал доступа может быть сотовым телефоном, беспроводным телефоном, телефоном с протоколом инициирования сеанса (SIP), станцией с беспроводной абонентской линией (Wireless Local Loop, WLL), персональным цифровым помощником (Personal Digital Assistant, PDA), портативным устройством, имеющим функцию беспроводной связи, вычислительным устройством, другим устройством обработки, соединенным с беспроводным модемом, находящимся в транспортном средстве устройством, носимым устройством, терминальным устройством в будущей сети 5G и т.п. На основе архитектуры системы связи, показанной на Фиг.1, в этом варианте осуществления настоящей заявки способ кодирования полярным кодом может выполняться вышеупомянутым сетевым устройством или терминалом. Способ кодирования полярным кодом может использоваться, когда сетевое устройство или терминал служит в качестве передающей стороны для отправки данных или информации. Соответственно, когда сетевое устройство или терминал служит в качестве принимающей стороны для приема данных или информации, последовательность подканала должна сначала определяться на основе способа настоящего изобретения. Далее подробно описан способ кодирования полярным кодом, предоставленный в вариантах осуществления настоящей заявки.
[0041] На основе архитектуры системы связи, показанной на Фиг.1, как показано на Фиг.2, конкретная процедура способа кодирования полярным кодом, предоставленная в одном варианте осуществления настоящей заявки, заключается в следующем.
[0042] Этап 201. Получение первой последовательности, используемой для кодирования K подлежащих кодированию битов.
[0043] Первая последовательность включает в себя порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, K является положительным целым числом, N является базовой кодовой длиной полярного кода, и N представляет собой положительную целочисленную степень 2.
[0044] Этап 202. Порядковые номера K поляризованных каналов выбираются из первой последовательности в порядке убывания надежности.
[0045] Этап 203. Размещение подлежащих кодированию битов на основе выбранных порядковых номеров K поляризованных каналов и выполнение кодирования полярным кодом над подлежащими кодированию битами.
[0046] K подлежащих кодированию битов отображаются в K поляризованных каналов в N поляризованных каналах. Надежность K поляризованных каналов выше, чем надежность остальных N–K поляризованных каналов.
[0047] В необязательном порядке, первая последовательность является всей или поднабором второй последовательности, вторая последовательность включает в себя порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, то есть порядок, в котором расположены порядковые номера поляризованных каналов в первой последовательности, соответствует порядку, в котором расположены порядковые номера, меньшие N, в порядковых номерах поляризованных каналов во второй последовательности. Nmax может быть положительной целочисленной степенью 2 или может не быть положительной целочисленной степенью 2, и Nmax≥N. Способ вычисления надежности Nmax поляризованных каналов аналогичен способу вычисления надежности N поляризованных каналов. Расположение, основанное на надежности, в данном документе может быть расположением, выполненным в порядке возрастания надежности, или может быть расположением, выполненным в порядке убывания надежности. Альтернативно, порядковые номера поляризованных каналов группируются в две или более групп, и порядковые номера в каждой группе располагаются в порядке убывания или в порядке возрастания надежности. Конкретным вариантом группировки может быть группировка на основе значений порядковых номеров поляризованных каналов или группировка на основе конгруэнтных порядковых номеров (например, три группы делятся, а порядковые номера, которые являются конгруэнтными по модулю 3, группируются в одну группу). Это конкретно не ограничено в данном документе.
[0048] В необязательном порядке, согласование скорости выполняется на основе целевой кодовой длины в отношении последовательности, полученной после кодирования полярным кодом.
[0049] Согласно способу кодирования, предоставленному в этом варианте осуществления, после приема входных информационных битов определяется количество K подлежащих кодированию битов на основе целевой кодовой длины N полярного кода. Независимо от оперативного вычисления или способа, которым вычисление и хранение выполняются заранее, если известна вторая последовательность, то первая последовательность может быть получена из второй последовательности, и когда Nmax=N, то вторая последовательность является первой последовательностью. Вторая последовательность включает в себя порядок надежности Nmax поляризованных каналов, где Nmax – максимальная кодовая длина, поддерживаемая системой связи. В необязательном порядке, первая последовательность может быть получена из предварительно сохраненной второй последовательности, затем информационные биты определяются на основе первой последовательности, и, наконец, выполняется полярное кодирование над K подлежащими кодированию битами, чтобы получить битовую последовательность, полученную после полярного кодирования. Следовательно, позиции информационных битов и фиксированных битов определяются путем получения надежности поляризованного канала полярного кода посредством комбинации оперативного вычисления и автономного хранения.
[0050] Далее конкретно описывается последовательность порядковых номеров поляризованных каналов, которая получается посредством расположения, основанного на надежности i–го поляризованного канала в N (или Nmax) поляризованных каналах. Порядковые номера N поляризованных каналов могут быть от 0 до N–1 или от 1 до N. В этом варианте осуществления настоящей заявки, когда определяется надежность i–го поляризованного канала из N поляризованных каналов, то значение i может быть 1, 2,… и N, или может быть 0, 1,… и N–1.
[0051] Можно понять, что формулы, используемые в вариантах осуществления настоящей заявки, являются просто примерами. Любое решение, которое может быть получено специалистами в данной области техники путем внесения простых изменений в формулы, не влияющих на эффективность формул, должно попадать в объем охраны вариантов осуществления настоящей заявки.
[0052] Конкретные примеры последовательностей см. в следующих шести группах последовательностей, найденных на основе различных критериев. Вторая последовательность может быть частью или всей любой последовательностью, показанной в последовательностях с Q1 по Q30. Эти последовательности также могут быть представлены с использованием соответствующих таблиц с Таблицы Q1 до Таблицы Q30. «Надежность или порядковый номер надежности» – это естественная последовательность надежности в порядке возрастания, а «порядковый номер поляризованного канала» – это порядковые номера поляризованного канала в соответствующих последовательностях. Здесь «часть» имеет три разных значения:
(1) Nmax не является положительной целочисленной степенью 2, но кодовые длины в приведенных примерах являются положительными целочисленными степенями 2; поэтому вторая последовательность может быть только частью любой последовательности, показанной в последовательностях с Q1 по Q30; или же
(2) Nmax_encoding_device, поддерживаемое устройством кодирования, меньше, чем Nmax_protocol, регулируемого протоколом, и поэтому необходимо выбирать только Nmax_encoding_device в любой последовательности, показанной в последовательностях с Q1 по Q30; или
(3) Часть фактически используемой последовательности, имеющей длину Nmax, полностью соответствует части любой последовательности, показанной в последовательностях с Q1 по Q30.
[0053] Эти последовательности также могут быть представлены с использованием Z–последовательностей, то есть порядок надежности поляризованных каналов, который соответствует естественному порядку порядкового номера поляризованного канала, используется в качестве Z–последовательности. Более конкретно, вторая последовательность может быть частью или всей любой последовательностью, показанной в последовательностях от Z1 до Z30. Аналогично, Z–последовательности также могут быть представлены с использованием соответствующих таблиц с Z1 по Z30, где порядковые номера поляризованных каналов последовательно расположены в порядке возрастания, а «надежность или порядковый номер надежности» представляет собой порядковый номер порядка надежности поляризованного канала, который соответствует порядковому номеру поляризованного канала.
[0054] Например, x–я последовательность Q представляет собой последовательность Qx и таблицу Qx, и последовательность Qx эквивалентна таблице Qx. Соответствующими Z-последовательностями являются Последовательность Zx и Таблица Zx, и Последовательность Zx эквивалентна Таблице Zx, где x=1, 2,… и 30.
[0055] Первая группа последовательностей (получена с использованием критерия, который всесторонне учитывает производительность с кодовой длиной в 64, 128, 256, 512 и 1024 и преимущественно учитывает производительность с базовой кодовой длиной в 256).
[0056] Последовательность Q1, имеющая длину последовательности 1024:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 512, 3, 12, 5, 18, 128, 9, 33, 17, 10, 256, 20, 34, 24, 65, 7, 36, 66, 129, 11, 40, 19, 132, 513, 13, 68, 48, 14, 72, 257, 21, 130, 26, 35, 80, 258, 136, 38, 22, 260, 516, 37, 25, 96, 67, 264, 41, 144, 28, 69, 49, 74, 160, 42, 520, 272, 192, 70, 44, 131, 81, 15, 288, 50, 134, 73, 514, 23, 52, 320, 133, 76, 82, 137, 56, 27, 259, 528, 97, 39, 384, 138, 84, 29, 261, 145, 544, 43, 98, 140, 30, 88, 262, 146, 71, 518, 265, 161, 45, 100, 148, 51, 46, 576, 75, 266, 104, 273, 164, 193, 53, 515, 162, 268, 77, 152, 274, 54, 524, 83, 57, 112, 85, 135, 289, 517, 194, 78, 290, 58, 276, 168, 530, 99, 139, 196, 86, 176, 640, 60, 89, 280, 101, 147, 292, 521, 141, 321, 142, 90, 200, 545, 31, 102, 263, 105, 529, 322, 149, 296, 47, 522, 92, 208, 267, 385, 324, 304, 536, 768, 532, 163, 153, 150, 106, 55, 165, 386, 577, 328, 548, 269, 113, 154, 79, 224, 166, 275, 108, 578, 270, 59, 114, 195, 169, 156, 87, 546, 61, 277, 291, 519, 278, 116, 170, 197, 641, 177, 281, 91, 552, 201, 388, 293, 198, 523, 62, 143, 336, 584, 172, 282, 120, 644, 103, 178, 294, 531, 202, 93, 323, 560, 392, 297, 151, 580, 209, 284, 180, 525, 107, 94, 204, 769, 298, 352, 325, 526, 155, 109, 533, 400, 305, 300, 642, 210, 184, 326, 538, 115, 167, 592, 157, 225, 306, 547, 329, 110, 770, 212, 117, 171, 550, 330, 226, 648, 387, 308, 158, 608, 416, 337, 534, 216, 271, 549, 118, 279, 537, 332, 389, 173, 579, 121, 199, 776, 179, 228, 553, 338, 656, 312, 540, 390, 174, 581, 393, 283, 772, 122, 672, 554, 784, 63, 340, 704, 448, 561, 353, 800, 394, 232, 203, 527, 582, 556, 295, 285, 181, 124, 205, 240, 643, 585, 562, 286, 299, 354, 182, 401, 211, 396, 344, 586, 832, 564, 95, 185, 206, 327, 645, 535, 402, 593, 186, 356, 588, 568, 307, 646, 418, 213, 301, 227, 302, 896, 594, 360, 111, 649, 771, 417, 539, 214, 404, 309, 188, 449, 331, 217, 159, 609, 596, 551, 650, 119, 229, 333, 408, 541, 773, 610, 657, 310, 420, 600, 218, 368, 230, 652, 391, 175, 313, 339, 542, 334, 123, 555, 774, 233, 314, 658, 612, 341, 777, 450, 220, 424, 355, 673, 583, 125, 234, 183, 395, 241, 557, 660, 616, 316, 342, 345, 778, 563, 403, 287, 397, 452, 674, 558, 785, 432, 187, 357, 207, 664, 587, 780, 705, 676, 236, 346, 565, 361, 126, 242, 589, 405, 215, 398, 566, 303, 597, 358, 801, 419, 624, 456, 786, 348, 244, 569, 189, 590, 219, 647, 311, 706, 362, 595, 464, 802, 406, 680, 421, 788, 248, 598, 190, 570, 369, 651, 409, 834, 410, 708, 480, 613, 231, 572, 315, 659, 364, 422, 335, 688, 370, 792, 221, 611, 451, 601, 425, 804, 412, 653, 453, 833, 317, 712, 235, 602, 343, 543, 372, 654, 222, 614, 426, 775, 433, 559, 237, 898, 617, 347, 808, 243, 720, 454, 665, 318, 604, 376, 661, 428, 779, 238, 675, 359, 836, 458, 625, 399, 662, 677, 434, 567, 457, 816, 245, 618, 349, 787, 127, 781, 897, 407, 666, 436, 591, 363, 620, 465, 736, 350, 678, 571, 246, 681, 249, 626, 460, 707, 840, 411, 782, 365, 789, 440, 599, 374, 668, 628, 423, 900, 466, 848, 803, 250, 790, 371, 709, 191, 573, 689, 481, 682, 413, 603, 793, 366, 713, 468, 710, 373, 574, 655, 427, 806, 414, 684, 904, 252, 615, 482, 632, 805, 429, 794, 864, 223, 690, 455, 714, 835, 472, 809, 377, 605, 619, 435, 663, 721, 319, 796, 484, 692, 912, 430, 606, 716, 488, 810, 459, 838, 667, 239, 817, 621, 378, 837, 722, 437, 696, 461, 737, 679, 380, 812, 627, 247, 899, 841, 441, 622, 928, 351, 724, 783, 469, 629, 818, 438, 669, 462, 738, 683, 251, 842, 849, 496, 901, 820, 728, 467, 633, 902, 367, 670, 791, 442, 844, 630, 474, 685, 850, 483, 691, 711, 379, 865, 795, 415, 824, 960, 740, 253, 905, 634, 444, 693, 744, 485, 807, 686, 906, 470, 575, 715, 375, 866, 913, 473, 852, 636, 797, 431, 694, 811, 486, 752, 723, 798, 489, 856, 908, 254, 717, 607, 930, 476, 697, 725, 914, 439, 819, 839, 868, 492, 718, 698, 381, 813, 623, 814, 498, 872, 739, 929, 671, 916, 821, 463, 726, 961, 843, 490, 631, 729, 700, 382, 741, 845, 920, 471, 822, 851, 730, 497, 880, 742, 443, 903, 687, 825, 500, 445, 932, 846, 635, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 915, 964, 477, 909, 719, 799, 699, 493, 504, 748, 944, 858, 873, 638, 754, 255, 968, 869, 491, 478, 383, 910, 815, 917, 727, 870, 701, 931, 860, 499, 756, 731, 823, 922, 874, 976, 918, 502, 933, 743, 760, 881, 494, 702, 921, 876, 501, 847, 992, 447, 733, 827, 882, 934, 963, 505, 937, 747, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 859, 755, 479, 966, 830, 888, 940, 750, 871, 970, 911, 757, 946, 969, 861, 977, 875, 919, 639, 758, 948, 862, 761, 508, 972, 923, 877, 952, 886, 935, 978, 762, 503, 883, 703, 993, 925, 878, 980, 941, 764, 495, 926, 885, 994, 735, 939, 984, 967, 889, 947, 831, 507, 942, 751, 973, 996, 890, 949, 759, 892, 971, 1000, 953, 509, 863, 981, 950, 974, 763, 1008, 979, 879, 954, 986, 995, 891, 927, 510, 765, 956, 997, 982, 887, 985, 943, 998, 1001, 766, 988, 951, 1004, 893, 1010, 957, 975, 511, 1002, 894, 983, 1009, 955, 987, 1012, 958, 999, 1005, 989, 1016, 990, 1011, 767, 1003, 1014, 1006, 1017, 895, 1013, 991, 1018, 959, 1020, 1015, 1007, 1019, 1021, 1022, 1023]
[0057] Таблица Q1, имеющая длину последовательности 1024:
[0058] Последовательность No2, имеющая длину последовательности 512:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 128, 9, 33, 17, 10, 256, 20, 34, 24, 65, 7, 36, 66, 129, 11, 40, 19, 132, 13, 68, 48, 14, 72, 257, 21, 130, 26, 35, 80, 258, 136, 38, 22, 260, 37, 25, 96, 67, 264, 41, 144, 28, 69, 49, 74, 160, 42, 272, 192, 70, 44, 131, 81, 15, 288, 50, 134, 73, 23, 52, 320, 133, 76, 82, 137, 56, 27, 259, 97, 39, 384, 138, 84, 29, 261, 145, 43, 98, 140, 30, 88, 262, 146, 71, 265, 161, 45, 100, 148, 51, 46, 75, 266, 104, 273, 164, 193, 53, 162, 268, 77, 152, 274, 54, 83, 57, 112, 85, 135, 289, 194, 78, 290, 58, 276, 168, 99, 139, 196, 86, 176, 60, 89, 280, 101, 147, 292, 141, 321, 142, 90, 200, 31, 102, 263, 105, 322, 149, 296, 47, 92, 208, 267, 385, 324, 304, 163, 153, 150, 106, 55, 165, 386, 328, 269, 113, 154, 79, 224, 166, 275, 108, 270, 59, 114, 195, 169, 156, 87, 61, 277, 291, 278, 116, 170, 197, 177, 281, 91, 201, 388, 293, 198, 62, 143, 336, 172, 282, 120, 103, 178, 294, 202, 93, 323, 392, 297, 151, 209, 284, 180, 107, 94, 204, 298, 352, 325, 155, 109, 400, 305, 300, 210, 184, 326, 115, 167, 157, 225, 306, 329, 110, 212, 117, 171, 330, 226, 387, 308, 158, 416, 337, 216, 271, 118, 279, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 63, 340, 448, 353, 394, 232, 203, 295, 285, 181, 124, 205, 240, 286, 299, 354, 182, 401, 211, 396, 344, 95, 185, 206, 327, 402, 186, 356, 307, 418, 213, 301, 227, 302, 360, 111, 417, 214, 404, 309, 188, 449, 331, 217, 159, 119, 229, 333, 408, 310, 420, 218, 368, 230, 391, 175, 313, 339, 334, 123, 233, 314, 341, 450, 220, 424, 355, 125, 234, 183, 395, 241, 316, 342, 345, 403, 287, 397, 452, 432, 187, 357, 207, 236, 346, 361, 126, 242, 405, 215, 398, 303, 358, 419, 456, 348, 244, 189, 219, 311, 362, 464, 406, 421, 248, 190, 369, 409, 410, 480, 231, 315, 364, 422, 335, 370, 221, 451, 425, 412, 453, 317, 235, 343, 372, 222, 426, 433, 237, 347, 243, 454, 318, 376, 428, 238, 359, 458, 399, 434, 457, 245, 349, 127, 407, 436, 363, 465, 350, 246, 249, 460, 411, 365, 440, 374, 423, 466, 250, 371, 191, 481, 413, 366, 468, 373, 427, 414, 252, 482, 429, 223, 455, 472, 377, 435, 319, 484, 430, 488, 459, 239, 378, 437, 461, 380, 247, 441, 351, 469, 438, 462, 251, 496, 467, 367, 442, 474, 483, 379, 415, 253, 444, 485, 470, 375, 473, 431, 486, 489, 254, 476, 439, 492, 381, 498, 463, 490, 382, 471, 497, 443, 500, 445, 446, 475, 487, 477, 493, 504, 255, 491, 478, 383, 499, 502, 494, 501, 447, 505, 506, 479, 508, 503, 495, 507, 509, 510, 511]
[0059] Таблица No2, имеющая длина последовательности 512:
[0060] Последовательность Q3, имеющая длину последовательности 256:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 128, 9, 33, 17, 10, 20, 34, 24, 65, 7, 36, 66, 129, 11, 40, 19, 132, 13, 68, 48, 14, 72, 21, 130, 26, 35, 80, 136, 38, 22, 37, 25, 96, 67, 41, 144, 28, 69, 49, 74, 160, 42, 192, 70, 44, 131, 81, 15, 50, 134, 73, 23, 52, 133, 76, 82, 137, 56, 27, 97, 39, 138, 84, 29, 145, 43, 98, 140, 30, 88, 146, 71, 161, 45, 100, 148, 51, 46, 75, 104, 164, 193, 53, 162, 77, 152, 54, 83, 57, 112, 85, 135, 194, 78, 58, 168, 99, 139, 196, 86, 176, 60, 89, 101, 147, 141, 142, 90, 200, 31, 102, 105, 149, 47, 92, 208, 163, 153, 150, 106, 55, 165, 113, 154, 79, 224, 166, 108, 59, 114, 195, 169, 156, 87, 61, 116, 170, 197, 177, 91, 201, 198, 62, 143, 172, 120, 103, 178, 202, 93, 151, 209, 180, 107, 94, 204, 155, 109, 210, 184, 115, 167, 157, 225, 110, 212, 117, 171, 226, 158, 216, 118, 173, 121, 199, 179, 228, 174, 122, 63, 232, 203, 181, 124, 205, 240, 182, 211, 95, 185, 206, 186, 213, 227, 111, 214, 188, 217, 159, 119, 229, 218, 230, 175, 123, 233, 220, 125, 234, 183, 241, 187, 207, 236, 126, 242, 215, 244, 189, 219, 248, 190, 231, 221, 235, 222, 237, 243, 238, 245, 127, 246, 249, 250, 191, 252, 223, 239, 247, 251, 253, 254, 255]
[0061] Таблица No3, имеющая длину последовательности 256:
[0062] Последовательность Q4, имеющая длину последовательности 128:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 9, 33, 17, 10, 20, 34, 24, 65, 7, 36, 66, 11, 40, 19, 13, 68, 48, 14, 72, 21, 26, 35, 80, 38, 22, 37, 25, 96, 67, 41, 28, 69, 49, 74, 42, 70, 44, 81, 15, 50, 73, 23, 52, 76, 82, 56, 27, 97, 39, 84, 29, 43, 98, 30, 88, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 85, 78, 58, 99, 86, 60, 89, 101, 90, 31, 102, 105, 47, 92, 106, 55, 113, 79, 108, 59, 114, 87, 61, 116, 91, 62, 120, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0063] Таблица No4, имеющая длину последовательности 128:
[0064] Последовательность Q5, имеющая длину последовательности 64:
[0, 1, 4, 8, 2, 16, 32, 6, 3, 12, 5, 18, 9, 33, 17, 10, 20, 34, 24, 7, 36, 11, 40, 19, 13, 48, 14, 21, 26, 35, 38, 22, 37, 25, 41, 28, 49, 42, 44, 15, 50, 23, 52, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0065] Таблица No5, имеющая длину последовательности 64:
[0066] Последовательность Z1, имеющая длину последовательности 1024:
[0, 1, 4, 10, 2, 12, 7, 24, 3, 15, 18, 28, 11, 33, 36, 70, 5, 17, 13, 30, 20, 39, 47, 76, 22, 51, 41, 84, 57, 92, 99, 161, 6, 16, 21, 42, 25, 50, 46, 88, 29, 55, 62, 96, 67, 107, 111, 169, 35, 59, 72, 110, 77, 119, 126, 184, 83, 129, 138, 200, 148, 207, 225, 322, 8, 23, 26, 53, 34, 58, 66, 103, 37, 74, 60, 113, 80, 123, 136, 193, 43, 69, 81, 128, 91, 131, 145, 205, 100, 149, 158, 218, 171, 238, 250, 355, 52, 87, 97, 142, 108, 151, 162, 233, 115, 164, 183, 249, 197, 258, 276, 377, 130, 191, 201, 268, 212, 279, 295, 394, 231, 302, 318, 415, 338, 430, 463, 573, 14, 27, 40, 68, 31, 79, 73, 132, 45, 82, 90, 143, 98, 155, 157, 226, 56, 94, 102, 152, 109, 167, 182, 243, 124, 181, 192, 257, 204, 271, 287, 389, 61, 106, 121, 180, 117, 185, 195, 269, 140, 203, 213, 280, 229, 300, 313, 410, 146, 216, 234, 305, 247, 337, 347, 432, 265, 356, 363, 451, 385, 481, 497, 612, 65, 118, 135, 202, 144, 214, 223, 303, 159, 220, 237, 331, 251, 339, 357, 453, 172, 245, 264, 349, 278, 370, 382, 467, 292, 388, 405, 483, 425, 517, 535, 640, 194, 272, 283, 372, 306, 395, 407, 507, 330, 418, 431, 529, 459, 541, 556, 666, 340, 434, 464, 546, 479, 569, 587, 680, 495, 589, 608, 697, 632, 726, 756, 843, 19, 38, 44, 85, 48, 93, 101, 163, 54, 105, 114, 173, 122, 190, 199, 293, 64, 116, 125, 196, 139, 208, 211, 296, 150, 217, 230, 316, 246, 336, 344, 444, 71, 133, 137, 209, 153, 222, 235, 335, 168, 242, 253, 345, 262, 371, 373, 470, 176, 261, 273, 367, 286, 384, 402, 485, 310, 411, 419, 509, 438, 527, 550, 653, 78, 156, 166, 239, 175, 255, 266, 358, 188, 275, 282, 387, 298, 396, 414, 513, 227, 290, 308, 412, 323, 422, 439, 531, 351, 440, 460, 544, 478, 571, 584, 686, 254, 327, 346, 427, 364, 452, 472, 558, 376, 462, 487, 580, 511, 596, 620, 707, 406, 499, 515, 610, 533, 624, 600, 739, 552, 647, 669, 719, 677, 771, 790, 848, 89, 174, 186, 285, 221, 299, 312, 409, 241, 315, 329, 433, 350, 445, 468, 562, 260, 348, 361, 443, 383, 466, 491, 576, 397, 501, 503, 594, 523, 617, 629, 722, 289, 380, 369, 474, 403, 493, 512, 603, 426, 521, 537, 627, 554, 637, 658, 746, 450, 539, 565, 650, 578, 672, 692, 764, 598, 683, 710, 801, 729, 806, 813, 877, 325, 386, 424, 519, 446, 525, 548, 642, 476, 567, 560, 663, 591, 674, 694, 782, 489, 582, 605, 704, 622, 689, 736, 794, 645, 742, 713, 816, 760, 830, 847, 898, 505, 615, 634, 716, 655, 732, 749, 821, 661, 753, 786, 846, 768, 835, 870, 937, 700, 798, 775, 857, 805, 874, 865, 928, 836, 883, 893, 948, 919, 960, 974, 992, 9, 32, 75, 120, 49, 134, 104, 210, 63, 154, 170, 224, 127, 248, 256, 332, 86, 165, 141, 236, 179, 259, 291, 360, 177, 297, 267, 381, 311, 398, 413, 532, 95, 160, 206, 274, 189, 294, 281, 392, 219, 307, 320, 416, 334, 435, 448, 540, 240, 326, 343, 442, 354, 461, 469, 566, 366, 480, 498, 586, 508, 613, 625, 737, 112, 187, 198, 301, 244, 314, 333, 429, 228, 342, 352, 455, 365, 465, 482, 579, 270, 362, 375, 488, 391, 471, 496, 599, 404, 520, 530, 618, 551, 648, 659, 758, 288, 390, 400, 518, 421, 506, 536, 633, 437, 543, 570, 649, 581, 668, 684, 773, 475, 561, 590, 679, 602, 690, 712, 787, 635, 705, 728, 809, 744, 819, 841, 914, 147, 215, 263, 341, 232, 359, 368, 484, 284, 378, 393, 500, 408, 524, 534, 626, 309, 401, 420, 510, 436, 553, 563, 651, 454, 549, 577, 665, 601, 693, 708, 779, 319, 428, 447, 557, 458, 564, 585, 676, 492, 588, 616, 696, 630, 714, 734, 803, 514, 614, 641, 717, 656, 730, 747, 822, 673, 761, 770, 834, 789, 854, 871, 930, 324, 457, 486, 592, 504, 611, 623, 718, 528, 621, 643, 738, 660, 757, 769, 832, 547, 652, 671, 751, 687, 762, 783, 852, 703, 788, 797, 859, 812, 878, 888, 941, 583, 675, 695, 777, 725, 791, 800, 867, 731, 810, 823, 885, 837, 894, 903, 950, 750, 825, 842, 897, 858, 907, 915, 955, 868, 918, 927, 965, 936, 975, 984, 1007, 178, 252, 277, 379, 317, 399, 417, 538, 304, 423, 441, 555, 456, 574, 595, 688, 321, 449, 477, 572, 494, 597, 609, 709, 516, 619, 638, 721, 654, 745, 752, 833, 328, 473, 490, 607, 522, 636, 628, 733, 545, 646, 662, 748, 678, 772, 774, 850, 568, 667, 691, 765, 702, 781, 795, 860, 723, 804, 811, 879, 824, 889, 900, 947, 353, 526, 502, 644, 559, 670, 664, 766, 593, 682, 698, 785, 711, 792, 808, 875, 606, 699, 715, 796, 743, 817, 826, 886, 754, 827, 839, 896, 856, 910, 917, 961, 639, 720, 740, 818, 767, 845, 853, 904, 776, 840, 862, 912, 873, 922, 933, 968, 799, 869, 880, 929, 892, 939, 924, 979, 901, 945, 953, 972, 956, 988, 994, 1012, 374, 575, 542, 681, 604, 701, 706, 802, 631, 727, 735, 820, 755, 831, 849, 906, 657, 741, 763, 828, 780, 851, 864, 913, 793, 872, 861, 921, 887, 932, 938, 973, 685, 778, 759, 855, 807, 866, 881, 925, 815, 884, 891, 942, 902, 935, 949, 981, 838, 895, 908, 946, 916, 954, 963, 986, 923, 959, 969, 997, 976, 990, 1000, 1016, 724, 784, 814, 882, 829, 890, 899, 944, 844, 909, 905, 957, 920, 951, 964, 991, 863, 911, 926, 967, 934, 962, 978, 995, 943, 980, 970, 998, 985, 1003, 1005, 1014, 876, 931, 940, 971, 952, 977, 982, 1001, 958, 983, 993, 1008, 987, 1002, 1010, 1019, 966, 996, 989, 1006, 999, 1013, 1009, 1018, 1004, 1011, 1015, 1020, 1017, 1021, 1022, 1023]
[0067] Таблица Z1, имеющая длину последовательности 1024:
[0068] Последовательность Z2, имеющая длину последовательности 512:
[0, 1, 4, 9, 2, 11, 7, 23, 3, 14, 17, 27, 10, 31, 34, 66, 5, 16, 12, 29, 19, 37, 45, 71, 21, 48, 39, 79, 54, 86, 92, 145, 6, 15, 20, 40, 24, 47, 44, 82, 28, 52, 59, 89, 63, 99, 103, 152, 33, 56, 68, 102, 72, 110, 116, 163, 78, 118, 126, 176, 134, 182, 196, 263, 8, 22, 25, 50, 32, 55, 62, 96, 35, 70, 57, 104, 75, 113, 124, 170, 41, 65, 76, 117, 85, 120, 132, 181, 93, 135, 143, 191, 153, 206, 215, 284, 49, 81, 90, 129, 100, 137, 146, 202, 106, 148, 162, 214, 174, 221, 234, 298, 119, 168, 177, 228, 186, 236, 247, 308, 201, 252, 262, 322, 273, 330, 349, 406, 13, 26, 38, 64, 30, 74, 69, 121, 43, 77, 84, 130, 91, 140, 142, 197, 53, 88, 95, 138, 101, 150, 161, 210, 114, 160, 169, 220, 180, 230, 242, 307, 58, 98, 111, 159, 108, 164, 172, 229, 128, 179, 187, 237, 199, 251, 259, 318, 133, 189, 203, 254, 213, 272, 279, 332, 226, 285, 289, 343, 303, 360, 368, 423, 61, 109, 123, 178, 131, 188, 195, 253, 144, 192, 205, 269, 216, 274, 286, 345, 154, 211, 225, 281, 235, 293, 300, 352, 245, 306, 314, 361, 327, 379, 388, 434, 171, 231, 239, 295, 255, 309, 316, 373, 268, 323, 331, 385, 346, 391, 398, 444, 275, 334, 350, 393, 359, 404, 412, 449, 367, 413, 421, 455, 431, 464, 473, 493, 18, 36, 42, 80, 46, 87, 94, 147, 51, 97, 105, 155, 112, 167, 175, 246, 60, 107, 115, 173, 127, 183, 185, 248, 136, 190, 200, 261, 212, 271, 276, 339, 67, 122, 125, 184, 139, 194, 204, 270, 151, 209, 217, 277, 224, 294, 296, 354, 158, 223, 232, 291, 241, 302, 312, 362, 257, 319, 324, 374, 335, 384, 395, 439, 73, 141, 149, 207, 157, 219, 227, 287, 166, 233, 238, 305, 249, 310, 321, 377, 198, 244, 256, 320, 264, 325, 336, 386, 283, 337, 347, 392, 358, 405, 411, 451, 218, 266, 278, 329, 290, 344, 355, 399, 297, 348, 363, 409, 375, 416, 426, 458, 315, 369, 378, 422, 387, 428, 418, 468, 396, 437, 445, 462, 448, 477, 481, 496, 83, 156, 165, 240, 193, 250, 258, 317, 208, 260, 267, 333, 282, 340, 353, 401, 222, 280, 288, 338, 301, 351, 365, 407, 311, 370, 371, 415, 382, 425, 430, 463, 243, 299, 292, 356, 313, 366, 376, 419, 328, 381, 389, 429, 397, 433, 441, 470, 342, 390, 402, 438, 408, 446, 453, 475, 417, 450, 459, 484, 465, 486, 487, 501, 265, 304, 326, 380, 341, 383, 394, 435, 357, 403, 400, 443, 414, 447, 454, 479, 364, 410, 420, 457, 427, 452, 467, 482, 436, 469, 460, 488, 474, 490, 495, 504, 372, 424, 432, 461, 440, 466, 471, 489, 442, 472, 480, 494, 476, 491, 499, 507, 456, 483, 478, 497, 485, 500, 498, 506, 492, 502, 503, 508, 505, 509, 510, 511]
[0069] Таблица Z2, имеющая длину последовательности 512:
[0070] Последовательность Z3, имеющая длину последовательности 256:
[0, 1, 4, 9, 2, 11, 7, 22, 3, 14, 17, 26, 10, 30, 33, 60, 5, 16, 12, 28, 18, 35, 42, 64, 20, 44, 37, 71, 49, 76, 81, 122, 6, 15, 19, 38, 23, 43, 41, 73, 27, 47, 54, 78, 57, 86, 90, 126, 32, 51, 61, 89, 65, 95, 99, 133, 70, 101, 107, 141, 114, 147, 155, 192, 8, 21, 24, 46, 31, 50, 56, 84, 34, 63, 52, 91, 67, 97, 106, 137, 39, 59, 68, 100, 75, 103, 112, 146, 82, 115, 120, 152, 127, 162, 167, 201, 45, 72, 79, 109, 87, 116, 123, 159, 92, 124, 132, 166, 140, 170, 177, 207, 102, 135, 142, 173, 148, 179, 184, 212, 158, 186, 191, 217, 196, 220, 227, 243, 13, 25, 36, 58, 29, 66, 62, 104, 40, 69, 74, 110, 80, 118, 119, 156, 48, 77, 83, 117, 88, 125, 131, 163, 98, 130, 136, 169, 145, 175, 182, 211, 53, 85, 96, 129, 93, 134, 139, 174, 108, 144, 149, 180, 157, 185, 190, 216, 113, 151, 160, 188, 165, 195, 199, 222, 172, 202, 204, 224, 209, 231, 234, 247, 55, 94, 105, 143, 111, 150, 154, 187, 121, 153, 161, 194, 168, 197, 203, 225, 128, 164, 171, 200, 178, 205, 208, 229, 183, 210, 214, 232, 219, 236, 238, 249, 138, 176, 181, 206, 189, 213, 215, 235, 193, 218, 221, 237, 226, 239, 241, 250, 198, 223, 228, 240, 230, 242, 244, 251, 233, 245, 246, 252, 248, 253, 254, 255]
[0071] Таблица No3, имеющая длину последовательности 256:
[0072] Последовательность Z4, имеющая длину последовательности 128:
[0, 1, 4, 9, 2, 11, 7, 21, 3, 13, 16, 24, 10, 27, 30, 51, 5, 15, 12, 26, 17, 32, 37, 54, 19, 39, 33, 59, 43, 63, 66, 90, 6, 14, 18, 34, 22, 38, 36, 61, 25, 42, 47, 64, 49, 69, 72, 93, 29, 45, 52, 71, 55, 75, 77, 96, 58, 79, 83, 100, 86, 103, 106, 119, 8, 20, 23, 41, 28, 44, 48, 68, 31, 53, 46, 73, 56, 76, 82, 98, 35, 50, 57, 78, 62, 81, 85, 102, 67, 87, 89, 105, 94, 109, 111, 121, 40, 60, 65, 84, 70, 88, 91, 108, 74, 92, 95, 110, 99, 112, 114, 122, 80, 97, 101, 113, 104, 115, 116, 123, 107, 117, 118, 124, 120, 125, 126, 127]
[0073] Таблица Z4, имеющая длину последовательности 128:
[0074] Последовательность Z5, имеющая длину последовательности 64:
[0, 1, 4, 8, 2, 10, 7, 19, 3, 12, 15, 21, 9, 24, 26, 39, 5, 14, 11, 23, 16, 27, 31, 41, 18, 33, 28, 44, 35, 46, 48, 57, 6, 13, 17, 29, 20, 32, 30, 45, 22, 34, 37, 47, 38, 49, 51, 58, 25, 36, 40, 50, 42, 52, 53, 59, 43, 54, 55, 60, 56, 61, 62, 63]
[0075] Таблица Z5, имеющая длину последовательности 64:
[0076] Вторая группа группы последовательностей (полученных с помощью критерия, который всесторонне учитывает производительность, полученную в списке (List), размеры которого соответственно 1, 2, 4, 8 и 16, и преимущественно учитывает исполнение списков 1 и 16).
[0077] Последовательность Q6, имеющая длину последовательности 1024:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 256, 36, 24, 20, 65, 34, 7, 129, 66, 512, 11, 40, 68, 13, 19, 130, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 38, 260, 96, 514, 264, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 70, 131, 544, 192, 44, 81, 50, 73, 133, 15, 52, 320, 23, 134, 76, 82, 56, 384, 137, 97, 27, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 31, 292, 200, 263, 90, 149, 321, 322, 102, 545, 105, 532, 92, 47, 296, 163, 150, 546, 208, 385, 267, 304, 324, 153, 165, 536, 386, 106, 55, 328, 577, 548, 113, 154, 79, 224, 108, 269, 166, 578, 519, 552, 195, 270, 641, 523, 580, 560, 275, 59, 169, 156, 291, 277, 114, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 151, 209, 284, 180, 107, 94, 204, 770, 648, 298, 352, 533, 325, 608, 155, 210, 400, 305, 547, 300, 109, 184, 534, 772, 326, 656, 115, 167, 157, 537, 225, 306, 329, 110, 117, 212, 171, 330, 226, 549, 776, 538, 387, 308, 216, 416, 672, 337, 158, 271, 118, 279, 550, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 122, 554, 581, 393, 283, 174, 203, 340, 448, 561, 353, 394, 181, 527, 582, 556, 63, 295, 285, 232, 124, 643, 585, 562, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 186, 404, 213, 418, 539, 568, 594, 649, 771, 227, 832, 588, 646, 302, 111, 360, 214, 551, 609, 896, 188, 309, 449, 331, 217, 408, 229, 541, 159, 420, 596, 650, 773, 310, 333, 119, 339, 218, 368, 657, 230, 391, 542, 610, 233, 313, 334, 774, 658, 612, 175, 123, 314, 555, 600, 583, 341, 450, 652, 220, 557, 424, 395, 777, 673, 355, 287, 183, 234, 125, 241, 563, 660, 558, 616, 778, 674, 316, 342, 345, 397, 452, 432, 207, 785, 403, 357, 187, 587, 565, 664, 624, 780, 236, 126, 242, 398, 705, 346, 456, 358, 405, 303, 569, 595, 244, 786, 189, 676, 589, 566, 647, 361, 706, 215, 348, 419, 406, 464, 801, 590, 409, 680, 788, 362, 570, 597, 572, 311, 708, 219, 598, 601, 651, 611, 410, 802, 421, 792, 231, 602, 653, 248, 688, 369, 190, 480, 335, 364, 613, 659, 654, 422, 315, 221, 370, 425, 235, 451, 412, 343, 372, 317, 614, 775, 222, 543, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 376, 567, 618, 665, 736, 898, 840, 781, 428, 625, 238, 359, 458, 399, 245, 434, 677, 457, 591, 349, 127, 666, 787, 678, 620, 782, 626, 571, 191, 407, 350, 436, 465, 246, 460, 363, 681, 599, 249, 411, 668, 707, 573, 789, 803, 790, 682, 365, 440, 628, 709, 374, 423, 466, 250, 371, 689, 793, 481, 413, 603, 574, 366, 468, 655, 900, 805, 429, 615, 710, 252, 373, 848, 684, 713, 605, 690, 632, 482, 794, 806, 427, 414, 663, 835, 904, 809, 714, 619, 796, 472, 223, 455, 692, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 817, 435, 812, 319, 484, 430, 621, 838, 667, 239, 461, 378, 459, 627, 622, 437, 488, 380, 818, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 811, 697, 866, 798, 379, 431, 913, 607, 489, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 872, 381, 930, 497, 821, 463, 726, 961, 843, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 903, 687, 825, 932, 471, 635, 846, 500, 745, 962, 826, 732, 446, 936, 255, 853, 475, 753, 695, 867, 637, 907, 487, 746, 828, 854, 504, 799, 909, 857, 964, 719, 477, 915, 699, 493, 748, 944, 858, 873, 638, 968, 478, 383, 754, 869, 491, 910, 815, 917, 727, 870, 701, 931, 499, 860, 756, 922, 731, 976, 918, 874, 823, 502, 933, 743, 760, 881, 494, 702, 921, 827, 876, 501, 847, 992, 934, 447, 733, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 884, 938, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023]
[0078] Таблица Q6, имеющая длину последовательности 1024:
[0079] Последовательность Q7, имеющая длину последовательности 512:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 256, 36, 24, 20, 65, 34, 7, 129, 66, 11, 40, 68, 13, 19, 130, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 38, 260, 96, 264, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 70, 131, 192, 44, 81, 50, 73, 133, 15, 52, 320, 23, 134, 76, 82, 56, 384, 137, 97, 27, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 31, 292, 200, 263, 90, 149, 321, 322, 102, 105, 92, 47, 296, 163, 150, 208, 385, 267, 304, 324, 153, 165, 386, 106, 55, 328, 113, 154, 79, 224, 108, 269, 166, 195, 270, 275, 59, 169, 156, 291, 277, 114, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 151, 209, 284, 180, 107, 94, 204, 298, 352, 325, 155, 210, 400, 305, 300, 109, 184, 326, 115, 167, 157, 225, 306, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 337, 158, 271, 118, 279, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 122, 393, 283, 174, 203, 340, 448, 353, 394, 181, 63, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 186, 404, 213, 418, 227, 302, 111, 360, 214, 188, 309, 449, 331, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 233, 313, 334, 175, 123, 314, 341, 450, 220, 424, 395, 355, 287, 183, 234, 125, 241, 316, 342, 345, 397, 452, 432, 207, 403, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 409, 362, 311, 219, 410, 421, 231, 248, 369, 190, 480, 335, 364, 422, 315, 221, 370, 425, 235, 451, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 458, 399, 245, 434, 457, 349, 127, 191, 407, 350, 436, 465, 246, 460, 363, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 472, 223, 455, 377, 435, 319, 484, 430, 239, 461, 378, 459, 437, 488, 380, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 381, 497, 463, 492, 443, 382, 498, 445, 471, 500, 446, 255, 475, 487, 504, 477, 493, 478, 383, 491, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511]
[0080] Таблица Q7, имеющая длину последовательности 512:
[0081] Последовательность Q8, имеющая длину последовательности 256:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 36, 24, 20, 65, 34, 7, 129, 66, 11, 40, 68, 13, 19, 130, 48, 14, 72, 21, 132, 35, 26, 80, 37, 25, 22, 136, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 160, 70, 131, 192, 44, 81, 50, 73, 133, 15, 52, 23, 134, 76, 82, 56, 137, 97, 27, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 31, 200, 90, 149, 102, 105, 92, 47, 163, 150, 208, 153, 165, 106, 55, 113, 154, 79, 224, 108, 166, 195, 59, 169, 156, 114, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 151, 209, 180, 107, 94, 204, 155, 210, 109, 184, 115, 167, 157, 225, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 122, 174, 203, 181, 63, 232, 124, 205, 182, 211, 185, 240, 206, 95, 186, 213, 227, 111, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 244, 189, 215, 219, 231, 248, 190, 221, 235, 222, 237, 243, 238, 245, 127, 191, 246, 249, 250, 252, 223, 239, 251, 247, 253, 254, 255]
[0082] Таблица Q8, имеющая длину последовательности 256:
[0083] Последовательность Q9, имеющая длину последовательности 128:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 12, 33, 36, 24, 20, 65, 34, 7, 66, 11, 40, 68, 13, 19, 48, 14, 72, 21, 35, 26, 80, 37, 25, 22, 38, 96, 67, 41, 28, 69, 42, 49, 74, 70, 44, 81, 50, 73, 15, 52, 23, 76, 82, 56, 97, 27, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 31, 90, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0084] Таблица Q9, имеющая длина последовательности 128:
[0085] Последовательность Q10, имеющая длину последовательности 64:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 9, 6, 17, 10, 18, 12, 33, 36, 24, 20, 34, 7, 11, 40, 13, 19, 48, 14, 21, 35, 26, 37, 25, 22, 38, 41, 28, 42, 49, 44, 50, 15, 52, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0086] Таблица Q10, имеющая длину последовательности 64:
[0087] Последовательность Z6, имеющая длину последовательности 1024:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 28, 16, 31, 35, 77, 5, 12, 14, 32, 21, 38, 47, 80, 20, 46, 42, 88, 57, 95, 101, 159, 6, 17, 23, 40, 19, 45, 49, 89, 29, 55, 59, 96, 72, 108, 113, 172, 34, 61, 74, 111, 78, 120, 129, 187, 84, 131, 141, 208, 146, 218, 236, 333, 9, 22, 26, 54, 30, 58, 68, 103, 36, 75, 62, 114, 82, 123, 135, 193, 44, 73, 83, 130, 91, 138, 145, 214, 99, 148, 163, 228, 171, 242, 254, 357, 51, 87, 97, 144, 109, 154, 167, 239, 118, 169, 186, 253, 195, 269, 282, 380, 133, 191, 213, 275, 216, 283, 299, 401, 233, 307, 317, 417, 337, 435, 460, 577, 15, 25, 33, 69, 39, 76, 81, 134, 48, 86, 92, 143, 100, 153, 157, 238, 56, 93, 102, 155, 112, 164, 175, 249, 122, 182, 192, 263, 210, 277, 297, 394, 64, 106, 119, 174, 124, 183, 197, 276, 142, 209, 217, 285, 232, 306, 322, 416, 156, 225, 240, 311, 252, 329, 342, 433, 270, 348, 366, 453, 386, 473, 511, 585, 71, 121, 137, 201, 152, 215, 231, 309, 161, 234, 244, 323, 255, 341, 356, 449, 177, 250, 264, 346, 284, 368, 382, 480, 293, 390, 403, 496, 425, 520, 531, 648, 194, 279, 287, 375, 312, 392, 406, 505, 336, 410, 434, 523, 459, 535, 567, 670, 355, 436, 461, 552, 471, 571, 590, 695, 508, 595, 611, 690, 627, 714, 743, 816, 18, 37, 41, 90, 50, 94, 104, 162, 53, 105, 115, 179, 126, 196, 202, 298, 63, 116, 127, 207, 139, 212, 223, 300, 147, 222, 237, 321, 251, 335, 343, 432, 66, 136, 149, 211, 160, 226, 241, 334, 173, 248, 258, 344, 268, 364, 379, 468, 180, 266, 280, 363, 292, 387, 399, 494, 314, 411, 418, 519, 443, 528, 555, 664, 79, 165, 166, 246, 181, 261, 273, 358, 188, 281, 286, 389, 302, 400, 412, 513, 235, 296, 313, 402, 324, 422, 444, 526, 350, 445, 464, 550, 481, 576, 587, 686, 259, 327, 345, 431, 362, 452, 466, 568, 381, 478, 490, 592, 514, 604, 619, 707, 404, 510, 521, 612, 527, 628, 608, 721, 557, 660, 672, 750, 678, 778, 794, 845, 85, 178, 185, 291, 227, 305, 316, 407, 247, 320, 328, 428, 349, 446, 462, 570, 265, 347, 361, 451, 367, 467, 483, 586, 391, 487, 501, 596, 525, 616, 639, 725, 294, 365, 369, 482, 395, 503, 518, 609, 427, 522, 533, 638, 565, 624, 666, 751, 448, 546, 572, 662, 588, 676, 688, 770, 605, 693, 692, 790, 722, 801, 814, 879, 325, 388, 423, 524, 447, 534, 554, 649, 465, 574, 569, 673, 591, 671, 691, 782, 484, 589, 610, 687, 620, 694, 723, 806, 647, 729, 740, 818, 760, 834, 844, 905, 512, 615, 635, 724, 665, 726, 756, 824, 677, 754, 772, 848, 786, 837, 870, 924, 680, 780, 798, 856, 809, 875, 865, 930, 828, 885, 893, 946, 909, 954, 963, 984, 27, 43, 52, 98, 60, 117, 128, 199, 65, 132, 140, 204, 151, 220, 224, 330, 67, 150, 158, 219, 170, 260, 271, 354, 184, 278, 290, 370, 304, 393, 408, 532, 70, 168, 176, 267, 190, 288, 301, 383, 200, 308, 318, 419, 332, 426, 439, 536, 206, 326, 340, 437, 359, 455, 476, 558, 371, 469, 491, 584, 493, 599, 618, 745, 107, 189, 198, 303, 205, 319, 331, 421, 229, 339, 351, 454, 377, 475, 486, 575, 245, 353, 372, 470, 396, 492, 497, 594, 420, 498, 506, 617, 545, 632, 656, 753, 262, 384, 409, 500, 415, 515, 529, 625, 440, 544, 559, 645, 581, 667, 675, 773, 457, 566, 583, 674, 606, 685, 709, 787, 634, 712, 730, 807, 741, 822, 842, 903, 110, 203, 221, 338, 243, 352, 378, 477, 257, 373, 397, 499, 424, 507, 517, 621, 274, 405, 414, 516, 438, 541, 553, 640, 456, 560, 578, 669, 597, 681, 700, 774, 295, 430, 442, 556, 474, 573, 580, 682, 488, 593, 603, 696, 630, 710, 718, 803, 509, 613, 633, 715, 650, 735, 742, 820, 659, 747, 764, 836, 789, 854, 871, 925, 315, 463, 479, 598, 495, 607, 626, 713, 539, 631, 644, 738, 653, 744, 758, 833, 547, 651, 658, 755, 683, 763, 783, 852, 704, 788, 797, 860, 813, 880, 888, 933, 561, 689, 698, 775, 719, 791, 800, 867, 731, 810, 825, 884, 838, 894, 907, 949, 766, 819, 846, 897, 858, 911, 916, 961, 868, 921, 929, 966, 940, 974, 983, 1003, 125, 230, 256, 374, 272, 398, 413, 530, 289, 429, 441, 543, 458, 564, 582, 701, 310, 450, 472, 579, 489, 600, 602, 706, 504, 614, 636, 728, 646, 736, 749, 829, 360, 485, 502, 601, 538, 623, 637, 739, 542, 643, 655, 746, 663, 759, 769, 850, 548, 661, 679, 768, 703, 781, 795, 864, 716, 804, 812, 873, 826, 889, 900, 944, 376, 537, 540, 641, 549, 652, 668, 762, 563, 684, 697, 785, 711, 792, 808, 876, 629, 702, 720, 796, 732, 817, 827, 886, 761, 831, 840, 898, 857, 910, 915, 960, 654, 734, 748, 821, 767, 847, 853, 902, 777, 841, 863, 914, 874, 922, 932, 969, 799, 869, 881, 928, 891, 935, 943, 976, 904, 947, 953, 981, 958, 989, 991, 1011, 385, 551, 562, 699, 622, 708, 717, 802, 642, 727, 737, 823, 757, 830, 849, 901, 657, 752, 765, 835, 776, 851, 862, 913, 793, 872, 859, 919, 887, 931, 939, 972, 705, 771, 779, 855, 805, 866, 878, 926, 815, 882, 892, 936, 899, 941, 950, 980, 839, 895, 906, 945, 917, 955, 959, 987, 923, 965, 968, 993, 975, 996, 998, 1008, 733, 784, 811, 883, 832, 890, 896, 942, 843, 908, 912, 952, 920, 956, 967, 990, 861, 918, 927, 964, 938, 970, 971, 997, 948, 977, 979, 999, 985, 1004, 1006, 1016, 877, 934, 937, 973, 951, 978, 982, 1001, 957, 986, 988, 1005, 994, 1007, 1012, 1018, 962, 992, 995, 1009, 1000, 1010, 1013, 1019, 1002, 1014, 1015, 1020, 1017, 1021, 1022, 1023]
[0088] Таблица Z6, имеющая длину последовательности 1024:
[0089] Последовательность Z7, имеющая длину последовательности 512:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 27, 16, 30, 34, 70, 5, 12, 14, 31, 21, 37, 45, 73, 20, 44, 41, 81, 54, 88, 93, 141, 6, 17, 23, 39, 19, 43, 47, 82, 28, 52, 56, 89, 65, 99, 103, 152, 33, 57, 67, 101, 71, 109, 116, 165, 77, 118, 126, 177, 131, 187, 199, 269, 9, 22, 26, 51, 29, 55, 62, 95, 35, 68, 58, 104, 75, 112, 121, 169, 42, 66, 76, 117, 84, 124, 130, 183, 91, 133, 145, 193, 151, 205, 215, 286, 49, 80, 90, 129, 100, 137, 149, 202, 107, 150, 164, 214, 171, 225, 234, 299, 119, 167, 182, 228, 185, 235, 247, 313, 196, 252, 259, 323, 273, 334, 347, 406, 15, 25, 32, 63, 38, 69, 74, 120, 46, 79, 85, 128, 92, 136, 140, 201, 53, 86, 94, 138, 102, 146, 155, 210, 111, 161, 168, 220, 179, 230, 245, 309, 60, 98, 108, 154, 113, 162, 173, 229, 127, 178, 186, 237, 195, 251, 262, 322, 139, 190, 203, 254, 213, 268, 275, 332, 226, 281, 293, 345, 302, 356, 372, 407, 64, 110, 123, 174, 135, 184, 194, 253, 143, 197, 206, 263, 216, 274, 285, 342, 156, 211, 221, 279, 236, 295, 301, 358, 242, 306, 315, 366, 327, 378, 387, 435, 170, 231, 239, 297, 255, 308, 317, 369, 272, 319, 333, 381, 346, 390, 398, 442, 284, 335, 348, 393, 355, 402, 412, 458, 370, 415, 422, 453, 429, 460, 469, 488, 18, 36, 40, 83, 48, 87, 96, 144, 50, 97, 105, 158, 114, 172, 175, 246, 59, 106, 115, 176, 125, 181, 189, 248, 132, 188, 200, 261, 212, 271, 276, 331, 61, 122, 134, 180, 142, 191, 204, 270, 153, 209, 217, 277, 224, 291, 298, 354, 159, 223, 232, 290, 241, 303, 311, 365, 257, 320, 324, 377, 336, 386, 395, 439, 72, 147, 148, 207, 160, 219, 227, 287, 166, 233, 238, 305, 249, 312, 321, 374, 198, 244, 256, 314, 264, 325, 337, 384, 283, 338, 350, 392, 359, 405, 409, 450, 218, 266, 278, 330, 289, 344, 352, 399, 300, 357, 364, 414, 375, 417, 426, 459, 316, 371, 379, 423, 385, 430, 419, 461, 396, 437, 444, 470, 448, 477, 482, 495, 78, 157, 163, 240, 192, 250, 258, 318, 208, 260, 267, 329, 282, 339, 349, 401, 222, 280, 288, 343, 294, 353, 361, 408, 307, 363, 367, 416, 383, 425, 433, 465, 243, 292, 296, 360, 310, 368, 376, 420, 328, 380, 388, 432, 397, 428, 441, 471, 341, 391, 403, 438, 410, 446, 452, 475, 418, 456, 455, 481, 462, 484, 487, 501, 265, 304, 326, 382, 340, 389, 394, 436, 351, 404, 400, 445, 413, 443, 454, 479, 362, 411, 421, 451, 427, 457, 463, 485, 434, 467, 468, 489, 474, 492, 494, 504, 373, 424, 431, 464, 440, 466, 473, 490, 447, 472, 476, 496, 480, 493, 499, 506, 449, 478, 483, 497, 486, 500, 498, 507, 491, 502, 503, 508, 505, 509, 510, 511]
[0090] Таблица Z7, имеющая длину последовательности 512:
[0091] Последовательность Z8, имеющая длину последовательности 256:
[0, 1, 2, 7, 3, 8, 11, 23, 4, 10, 13, 26, 16, 29, 33, 63, 5, 12, 14, 30, 20, 35, 42, 65, 19, 41, 38, 72, 49, 77, 82, 120, 6, 17, 22, 37, 18, 40, 44, 73, 27, 47, 51, 78, 58, 86, 90, 127, 32, 52, 60, 88, 64, 94, 99, 134, 69, 101, 107, 142, 112, 150, 157, 194, 9, 21, 25, 46, 28, 50, 55, 84, 34, 61, 53, 91, 67, 97, 104, 137, 39, 59, 68, 100, 74, 106, 111, 146, 80, 113, 122, 152, 126, 161, 167, 203, 45, 71, 79, 110, 87, 116, 124, 159, 92, 125, 133, 166, 139, 171, 177, 207, 102, 135, 145, 173, 148, 178, 184, 213, 155, 186, 190, 218, 196, 222, 227, 243, 15, 24, 31, 56, 36, 62, 66, 103, 43, 70, 75, 109, 81, 115, 119, 158, 48, 76, 83, 117, 89, 123, 129, 163, 96, 131, 136, 169, 144, 175, 183, 212, 54, 85, 93, 128, 98, 132, 140, 174, 108, 143, 149, 180, 154, 185, 191, 217, 118, 151, 160, 188, 165, 193, 198, 220, 172, 200, 204, 225, 209, 230, 235, 244, 57, 95, 105, 141, 114, 147, 153, 187, 121, 156, 162, 192, 168, 197, 202, 224, 130, 164, 170, 199, 179, 205, 208, 231, 182, 210, 214, 232, 219, 236, 238, 249, 138, 176, 181, 206, 189, 211, 215, 233, 195, 216, 221, 237, 226, 239, 241, 250, 201, 223, 228, 240, 229, 242, 245, 252, 234, 246, 247, 251, 248, 253, 254, 255]
[0092] Таблица Z8, имеющая длину последовательности 256:
[0093] Последовательность Z9, имеющая длину последовательности 128:
[0, 1, 2, 7, 3, 8, 11, 22, 4, 10, 13, 24, 15, 27, 30, 53, 5, 12, 14, 28, 19, 32, 38, 55, 18, 37, 34, 60, 43, 63, 67, 89, 6, 16, 21, 33, 17, 36, 39, 61, 25, 42, 45, 64, 49, 69, 72, 94, 29, 46, 51, 71, 54, 75, 77, 96, 58, 79, 83, 100, 86, 104, 107, 119, 9, 20, 23, 41, 26, 44, 48, 68, 31, 52, 47, 73, 56, 76, 81, 98, 35, 50, 57, 78, 62, 82, 85, 102, 66, 87, 90, 105, 93, 109, 111, 121, 40, 59, 65, 84, 70, 88, 91, 108, 74, 92, 95, 110, 99, 112, 114, 122, 80, 97, 101, 113, 103, 115, 116, 123, 106, 117, 118, 124, 120, 125, 126, 127]
[0094] Таблица Z9, имеющая длину последовательности 128:
[0095] Последовательности Z10, имеющая длину последовательности 64:
[0, 1, 2, 7, 3, 8, 10, 20, 4, 9, 12, 21, 14, 23, 26, 40, 5, 11, 13, 24, 18, 27, 32, 42, 17, 31, 29, 44, 35, 46, 48, 57, 6, 15, 19, 28, 16, 30, 33, 45, 22, 34, 36, 47, 38, 49, 51, 58, 25, 37, 39, 50, 41, 52, 53, 59, 43, 54, 55, 60, 56, 61, 62, 63]
[0096] Таблица Z10, имеющая длину последовательности 64:
[0097] Третья группа последовательностей (критерий, который всесторонне учитывает производительность, полученную в списке (list), размеры которого соответственно 1, 2, 4, 8 и 16, и преимущественно учитывает производительность Списков 2, 4 и 8).
[0098] Последовательность Q11, имеющая длину последовательности 1024:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 260, 264, 38, 514, 96, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 192, 544, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 31, 200, 90, 545, 292, 322, 532, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 546, 324, 208, 386, 150, 153, 165, 106, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 59, 169, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 608, 352, 325, 533, 155, 210, 305, 547, 300, 109, 184, 534, 537, 115, 167, 225, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 776, 330, 226, 549, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 174, 554, 581, 393, 283, 122, 448, 353, 561, 203, 63, 340, 394, 527, 582, 556, 181, 295, 285, 232, 124, 205, 182, 643, 562, 286, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 568, 832, 588, 186, 646, 404, 227, 896, 594, 418, 302, 649, 771, 360, 539, 111, 331, 214, 309, 188, 449, 217, 408, 609, 596, 551, 650, 229, 159, 420, 310, 541, 773, 610, 657, 333, 119, 600, 339, 218, 368, 652, 230, 391, 313, 450, 542, 334, 233, 555, 774, 175, 123, 658, 612, 341, 777, 220, 314, 424, 395, 673, 583, 355, 287, 183, 234, 125, 557, 660, 616, 342, 316, 241, 778, 563, 345, 452, 397, 403, 207, 674, 558, 785, 432, 357, 187, 236, 664, 624, 587, 780, 705, 126, 242, 565, 398, 346, 456, 358, 405, 303, 569, 244, 595, 189, 566, 676, 361, 706, 589, 215, 786, 647, 348, 419, 406, 464, 680, 801, 362, 590, 409, 570, 788, 597, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 410, 231, 688, 653, 248, 369, 190, 364, 654, 659, 335, 480, 315, 221, 370, 613, 422, 425, 451, 614, 543, 235, 412, 343, 372, 775, 317, 222, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 591, 678, 434, 677, 349, 245, 458, 666, 620, 363, 127, 191, 782, 407, 436, 626, 571, 465, 681, 246, 707, 350, 599, 668, 790, 460, 249, 682, 573, 411, 803, 789, 709, 365, 440, 628, 689, 374, 423, 466, 793, 250, 371, 481, 574, 413, 603, 366, 468, 655, 900, 805, 615, 684, 710, 429, 794, 252, 373, 605, 848, 690, 713, 632, 482, 806, 427, 904, 414, 223, 663, 692, 835, 619, 472, 455, 796, 809, 714, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 435, 817, 319, 621, 812, 484, 430, 838, 667, 488, 239, 378, 459, 622, 627, 437, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 913, 798, 811, 379, 697, 431, 607, 489, 866, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 255, 964, 909, 719, 477, 915, 638, 748, 944, 869, 491, 699, 754, 858, 478, 968, 383, 910, 815, 976, 870, 917, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 922, 874, 918, 502, 933, 743, 760, 881, 494, 702, 921, 501, 876, 847, 992, 447, 733, 827, 934, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023]
[0099] Таблица Q11, имеющая длину последовательности 1024:
[0100] Последовательность Q12, имеющая длину последовательности 512:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 260, 264, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 192, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 31, 200, 90, 292, 322, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 324, 208, 386, 150, 153, 165, 106, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 59, 169, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 448, 353, 203, 63, 340, 394, 181, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 360, 111, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 313, 450, 334, 233, 175, 123, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 316, 241, 345, 452, 397, 403, 207, 432, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 362, 409, 219, 311, 421, 410, 231, 248, 369, 190, 364, 335, 480, 315, 221, 370, 422, 425, 451, 235, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 245, 458, 363, 127, 191, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 223, 472, 455, 377, 435, 319, 484, 430, 488, 239, 378, 459, 437, 380, 461, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 255, 477, 491, 478, 383, 493, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511]
[0101] Таблица Q12, имеющая длину последовательности 512:
[0102] Последовательность Q13, имеющая длину последовательности 256:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 21, 132, 35, 26, 80, 37, 25, 22, 136, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 160, 192, 70, 44, 131, 81, 50, 73, 15, 133, 52, 23, 134, 76, 137, 82, 56, 27, 97, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 31, 200, 90, 149, 102, 105, 163, 92, 47, 208, 150, 153, 165, 106, 55, 113, 154, 79, 108, 224, 166, 195, 59, 169, 114, 156, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 107, 180, 151, 209, 94, 204, 155, 210, 109, 184, 115, 167, 225, 157, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 174, 122, 203, 63, 181, 232, 124, 205, 182, 211, 185, 240, 206, 95, 213, 186, 227, 111, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 244, 189, 215, 219, 231, 248, 190, 221, 235, 222, 237, 243, 238, 245, 127, 191, 246, 249, 250, 252, 223, 239, 251, 247, 253, 254, 255]
[0103] Таблица Q13, имеющая длину последовательности 256:
[0104] Последовательность Q14, имеющая длину последовательности 128:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 12, 33, 65, 20, 34, 24, 36, 7, 66, 11, 40, 68, 19, 13, 48, 14, 72, 21, 35, 26, 80, 37, 25, 22, 38, 96, 67, 41, 28, 69, 42, 49, 74, 70, 44, 81, 50, 73, 15, 52, 23, 76, 82, 56, 27, 97, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 31, 90, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0105] Таблица Q14, имеющая длину последовательности 128:
[0106] Последовательность Q15, имеющая длину последовательности 64:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 9, 6, 17, 10, 18, 12, 33, 20, 34, 24, 36, 7, 11, 40, 19, 13, 48, 14, 21, 35, 26, 37, 25, 22, 38, 41, 28, 42, 49, 44, 50, 15, 52, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0107] Таблица Q15, имеющая длину последовательности 64:
[0108] Последовательность Z11, имеющая длину последовательности 1024:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 28, 16, 33, 35, 76, 5, 12, 14, 32, 19, 38, 47, 80, 22, 46, 42, 87, 57, 95, 101, 160, 6, 17, 21, 40, 23, 45, 51, 89, 29, 55, 59, 96, 71, 108, 113, 175, 34, 61, 74, 111, 79, 120, 129, 186, 86, 131, 141, 208, 146, 218, 236, 327, 9, 18, 26, 54, 30, 58, 70, 103, 36, 75, 62, 114, 83, 123, 135, 193, 44, 73, 85, 130, 91, 138, 145, 214, 99, 148, 162, 228, 174, 242, 256, 357, 53, 88, 97, 144, 109, 154, 169, 239, 118, 170, 185, 250, 195, 269, 282, 382, 133, 191, 211, 273, 216, 283, 301, 403, 233, 307, 322, 419, 337, 434, 460, 582, 15, 25, 31, 72, 39, 78, 81, 134, 48, 84, 92, 143, 100, 153, 157, 238, 56, 93, 102, 155, 112, 168, 182, 252, 122, 183, 192, 264, 213, 279, 297, 395, 64, 106, 119, 173, 124, 184, 198, 274, 142, 209, 217, 285, 232, 306, 317, 418, 156, 225, 240, 311, 251, 333, 339, 432, 270, 348, 370, 453, 386, 472, 511, 583, 68, 121, 137, 201, 152, 215, 231, 309, 161, 234, 244, 326, 257, 338, 356, 447, 180, 253, 265, 346, 284, 366, 384, 478, 293, 388, 406, 494, 424, 518, 532, 641, 197, 275, 288, 373, 312, 394, 409, 506, 336, 415, 433, 526, 454, 535, 567, 671, 355, 440, 461, 552, 470, 577, 591, 695, 509, 598, 613, 690, 629, 714, 743, 830, 20, 37, 41, 90, 49, 94, 104, 167, 50, 105, 115, 176, 126, 194, 202, 295, 63, 116, 127, 205, 139, 212, 223, 296, 147, 222, 237, 321, 254, 335, 342, 431, 66, 136, 149, 207, 164, 226, 241, 334, 172, 248, 258, 344, 268, 364, 377, 468, 171, 266, 277, 363, 292, 385, 397, 495, 314, 411, 425, 517, 439, 531, 555, 663, 77, 159, 165, 246, 179, 262, 276, 358, 187, 281, 287, 383, 302, 402, 414, 515, 235, 298, 313, 405, 328, 422, 438, 528, 350, 443, 464, 550, 481, 576, 593, 686, 261, 324, 345, 430, 362, 452, 466, 568, 380, 475, 487, 581, 512, 605, 619, 707, 407, 510, 519, 614, 529, 630, 609, 721, 560, 660, 672, 749, 677, 779, 794, 846, 82, 177, 181, 291, 227, 305, 316, 410, 247, 320, 329, 427, 349, 445, 463, 570, 259, 347, 361, 446, 372, 467, 483, 585, 389, 489, 505, 601, 527, 617, 640, 725, 294, 365, 376, 482, 396, 500, 521, 610, 426, 522, 533, 638, 561, 627, 667, 751, 451, 546, 574, 661, 586, 676, 688, 770, 606, 693, 692, 790, 722, 801, 813, 877, 323, 387, 412, 523, 444, 534, 554, 647, 465, 569, 578, 673, 597, 679, 691, 777, 484, 589, 611, 687, 620, 694, 723, 802, 646, 729, 740, 816, 760, 834, 844, 905, 516, 615, 636, 724, 666, 726, 756, 821, 670, 753, 772, 840, 786, 853, 870, 924, 680, 780, 798, 859, 808, 873, 865, 930, 828, 885, 893, 946, 909, 954, 963, 984, 27, 43, 52, 98, 60, 117, 128, 199, 65, 132, 140, 204, 151, 220, 224, 330, 67, 150, 158, 219, 166, 263, 271, 354, 188, 272, 290, 381, 304, 398, 413, 525, 69, 163, 178, 267, 190, 289, 299, 392, 200, 308, 318, 416, 332, 435, 449, 536, 210, 325, 341, 442, 359, 462, 473, 564, 367, 469, 490, 588, 493, 600, 616, 745, 107, 189, 196, 303, 206, 319, 331, 429, 229, 343, 351, 457, 369, 477, 488, 572, 245, 353, 375, 471, 391, 492, 497, 594, 404, 498, 504, 618, 545, 631, 656, 752, 260, 390, 400, 503, 421, 520, 524, 624, 437, 544, 557, 645, 580, 664, 674, 773, 456, 566, 587, 675, 607, 685, 709, 787, 635, 712, 730, 803, 741, 819, 836, 903, 110, 203, 221, 340, 243, 352, 371, 480, 255, 378, 393, 499, 408, 508, 513, 621, 280, 401, 420, 514, 436, 541, 553, 642, 455, 562, 579, 669, 595, 681, 700, 774, 300, 428, 448, 556, 474, 575, 573, 682, 485, 590, 599, 696, 625, 710, 718, 805, 507, 608, 633, 715, 643, 735, 742, 822, 659, 750, 764, 841, 789, 855, 871, 925, 315, 459, 476, 592, 496, 604, 626, 713, 539, 634, 650, 738, 653, 744, 758, 833, 547, 651, 658, 755, 683, 763, 783, 852, 704, 788, 797, 860, 812, 878, 888, 933, 563, 689, 698, 775, 719, 791, 800, 867, 731, 810, 823, 884, 837, 894, 907, 949, 766, 825, 842, 897, 857, 911, 916, 961, 868, 921, 929, 966, 940, 974, 983, 1003, 125, 230, 249, 379, 278, 399, 417, 530, 286, 423, 441, 543, 458, 559, 584, 701, 310, 450, 479, 571, 491, 603, 596, 706, 501, 612, 628, 728, 648, 736, 747, 829, 360, 486, 502, 602, 538, 623, 637, 739, 542, 649, 655, 748, 665, 759, 769, 848, 548, 662, 678, 768, 703, 782, 795, 861, 716, 807, 811, 879, 824, 889, 900, 944, 368, 537, 540, 644, 549, 652, 668, 762, 565, 684, 697, 778, 711, 792, 809, 875, 632, 702, 720, 796, 732, 817, 826, 886, 761, 827, 843, 898, 858, 910, 915, 960, 654, 734, 754, 818, 767, 839, 850, 902, 785, 854, 863, 914, 874, 922, 932, 969, 799, 869, 881, 928, 892, 935, 943, 976, 904, 947, 953, 981, 958, 989, 991, 1011, 374, 551, 558, 699, 622, 708, 717, 806, 639, 727, 737, 820, 757, 832, 847, 901, 657, 746, 765, 835, 776, 851, 864, 913, 793, 872, 862, 919, 887, 931, 939, 972, 705, 771, 781, 856, 804, 866, 880, 926, 815, 882, 891, 936, 899, 941, 950, 980, 838, 895, 906, 945, 917, 955, 959, 987, 923, 965, 968, 993, 975, 996, 998, 1008, 733, 784, 814, 883, 831, 890, 896, 942, 845, 908, 912, 952, 920, 956, 967, 990, 849, 918, 927, 964, 938, 970, 971, 997, 948, 977, 979, 999, 985, 1004, 1006, 1016, 876, 934, 937, 973, 951, 978, 982, 1001, 957, 986, 988, 1005, 994, 1007, 1012, 1018, 962, 992, 995, 1009, 1000, 1010, 1013, 1019, 1002, 1014, 1015, 1020, 1017, 1021, 1022, 1023]
[0109] Таблица Z11, имеющая длину последовательности 1024:
[0110] Последовательность Z12, имеющая длину последовательности 512:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 27, 16, 32, 34, 69, 5, 12, 14, 31, 19, 37, 45, 73, 22, 44, 41, 80, 54, 88, 93, 142, 6, 17, 21, 39, 23, 43, 49, 82, 28, 52, 56, 89, 64, 99, 103, 155, 33, 57, 67, 101, 72, 109, 116, 165, 79, 118, 126, 178, 131, 187, 199, 266, 9, 18, 26, 51, 29, 55, 63, 95, 35, 68, 58, 104, 76, 112, 121, 169, 42, 66, 78, 117, 84, 124, 130, 183, 91, 133, 144, 193, 154, 205, 215, 286, 50, 81, 90, 129, 100, 137, 149, 202, 107, 150, 164, 210, 171, 225, 234, 300, 119, 167, 180, 227, 185, 235, 248, 313, 196, 252, 262, 324, 273, 334, 347, 407, 15, 25, 30, 65, 38, 71, 74, 120, 46, 77, 85, 128, 92, 136, 140, 201, 53, 86, 94, 138, 102, 148, 161, 212, 111, 162, 168, 221, 182, 232, 246, 309, 60, 98, 108, 153, 113, 163, 173, 228, 127, 179, 186, 237, 195, 251, 259, 323, 139, 190, 203, 254, 211, 269, 275, 332, 226, 281, 294, 345, 304, 356, 372, 408, 62, 110, 123, 174, 135, 184, 194, 253, 143, 197, 206, 265, 216, 274, 285, 342, 159, 213, 222, 279, 236, 293, 302, 358, 242, 306, 315, 365, 326, 377, 387, 434, 172, 229, 239, 296, 255, 308, 317, 369, 272, 322, 333, 382, 346, 390, 398, 443, 284, 337, 348, 393, 355, 404, 412, 458, 370, 415, 422, 453, 429, 460, 469, 491, 20, 36, 40, 83, 47, 87, 96, 147, 48, 97, 105, 156, 114, 170, 175, 244, 59, 106, 115, 176, 125, 181, 189, 245, 132, 188, 200, 261, 214, 271, 276, 331, 61, 122, 134, 177, 145, 191, 204, 270, 152, 209, 217, 277, 224, 291, 298, 354, 151, 223, 231, 290, 241, 303, 311, 366, 257, 319, 327, 376, 336, 386, 395, 439, 70, 141, 146, 207, 158, 220, 230, 287, 166, 233, 238, 301, 249, 312, 321, 374, 198, 247, 256, 314, 267, 325, 335, 384, 283, 338, 350, 392, 359, 403, 413, 450, 219, 264, 278, 330, 289, 344, 352, 399, 299, 357, 363, 406, 373, 417, 426, 459, 316, 371, 378, 423, 385, 430, 419, 461, 396, 437, 444, 470, 447, 478, 482, 495, 75, 157, 160, 240, 192, 250, 258, 318, 208, 260, 268, 329, 282, 340, 349, 401, 218, 280, 288, 341, 295, 353, 361, 409, 307, 364, 368, 416, 383, 425, 433, 465, 243, 292, 297, 360, 310, 367, 379, 420, 328, 380, 388, 432, 397, 428, 441, 471, 343, 391, 402, 438, 410, 446, 452, 475, 418, 456, 455, 481, 462, 484, 487, 501, 263, 305, 320, 381, 339, 389, 394, 436, 351, 400, 405, 445, 414, 448, 454, 477, 362, 411, 421, 451, 427, 457, 463, 485, 435, 467, 468, 488, 474, 492, 494, 504, 375, 424, 431, 464, 440, 466, 473, 489, 442, 472, 476, 493, 480, 496, 499, 506, 449, 479, 483, 497, 486, 500, 498, 507, 490, 502, 503, 508, 505, 509, 510, 511]
[0111] Таблица Z12, имеющая длину последовательности 512:
[0112] Последовательность Z13, имеющая последовательность длина 256:
[0, 1, 2, 7, 3, 8, 11, 23, 4, 10, 13, 26, 16, 31, 33, 62, 5, 12, 14, 30, 19, 35, 42, 65, 21, 41, 38, 71, 49, 77, 82, 120, 6, 17, 20, 37, 22, 40, 44, 73, 27, 47, 51, 78, 57, 86, 90, 128, 32, 52, 60, 88, 64, 94, 99, 134, 70, 101, 107, 142, 112, 150, 157, 193, 9, 18, 25, 46, 28, 50, 56, 84, 34, 61, 53, 91, 67, 97, 104, 137, 39, 59, 69, 100, 74, 106, 111, 146, 80, 113, 122, 152, 127, 161, 167, 203, 45, 72, 79, 110, 87, 116, 124, 159, 92, 125, 133, 163, 138, 171, 177, 207, 102, 135, 144, 173, 148, 178, 184, 213, 155, 186, 191, 218, 196, 222, 227, 243, 15, 24, 29, 58, 36, 63, 66, 103, 43, 68, 75, 109, 81, 115, 119, 158, 48, 76, 83, 117, 89, 123, 130, 165, 96, 131, 136, 169, 145, 176, 183, 212, 54, 85, 93, 126, 98, 132, 140, 174, 108, 143, 149, 180, 154, 185, 190, 217, 118, 151, 160, 188, 164, 194, 198, 220, 172, 200, 205, 225, 209, 230, 235, 244, 55, 95, 105, 141, 114, 147, 153, 187, 121, 156, 162, 192, 168, 197, 202, 224, 129, 166, 170, 199, 179, 204, 208, 231, 182, 210, 214, 232, 219, 236, 238, 249, 139, 175, 181, 206, 189, 211, 215, 233, 195, 216, 221, 237, 226, 239, 241, 250, 201, 223, 228, 240, 229, 242, 245, 252, 234, 246, 247, 251, 248, 253, 254, 255]
[0113] Таблица Z13, имеющая длину последовательности 256:
[0114] Последовательность Z14, имеющая последовательность длина 128:
[0, 1, 2, 7, 3, 8, 11, 22, 4, 10, 13, 24, 15, 28, 30, 53, 5, 12, 14, 27, 18, 32, 38, 55, 20, 37, 34, 59, 43, 63, 67, 89, 6, 16, 19, 33, 21, 36, 39, 61, 25, 42, 45, 64, 49, 69, 72, 94, 29, 46, 51, 71, 54, 75, 77, 96, 58, 79, 83, 100, 86, 104, 107, 119, 9, 17, 23, 41, 26, 44, 48, 68, 31, 52, 47, 73, 56, 76, 81, 98, 35, 50, 57, 78, 62, 82, 85, 102, 66, 87, 90, 105, 93, 109, 111, 121, 40, 60, 65, 84, 70, 88, 91, 108, 74, 92, 95, 110, 99, 112, 114, 122, 80, 97, 101, 113, 103, 115, 116, 123, 106, 117, 118, 124, 120, 125, 126, 127]
[0115] Таблица Z14, имеющая длину последовательности 128:
[0116] Последовательность Z15, имеющая длину последовательности 64:
[0, 1, 2, 7, 3, 8, 10, 20, 4, 9, 12, 21, 14, 24, 26, 40, 5, 11, 13, 23, 16, 27, 32, 42, 18, 31, 29, 44, 35, 46, 48, 57, 6, 15, 17, 28, 19, 30, 33, 45, 22, 34, 36, 47, 38, 49, 51, 58, 25, 37, 39, 50, 41, 52, 53, 59, 43, 54, 55, 60, 56, 61, 62, 63]
[0117] Таблица Z15, имеющая длину последовательности 64:
[0118] Четвертая группа последовательностей (критерий, который учитывает баланс производительности при ограничении частичного порядка (partial-order).
[0119] Последовательность Q16, имеющая длину последовательности 1024:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 22, 80, 136, 513, 25, 37, 260, 264, 26, 96, 514, 38, 67, 41, 144, 28, 69, 516, 42, 272, 49, 70, 520, 160, 44, 131, 73, 288, 528, 192, 50, 74, 544, 52, 15, 133, 320, 81, 23, 134, 384, 76, 56, 259, 82, 137, 27, 97, 39, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 90, 200, 31, 545, 292, 322, 532, 263, 149, 102, 105, 296, 304, 163, 92, 47, 267, 150, 208, 385, 546, 386, 324, 106, 153, 165, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 169, 59, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 352, 608, 325, 533, 155, 210, 305, 547, 300, 109, 184, 115, 534, 167, 225, 537, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 330, 226, 549, 776, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 390, 122, 554, 448, 312, 581, 393, 283, 704, 174, 394, 181, 340, 203, 353, 561, 527, 582, 556, 63, 295, 285, 232, 124, 286, 562, 205, 182, 643, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 186, 539, 404, 227, 594, 568, 771, 418, 649, 302, 832, 551, 111, 896, 360, 588, 609, 331, 214, 309, 188, 449, 217, 646, 408, 229, 541, 159, 420, 596, 650, 773, 310, 333, 119, 657, 658, 610, 368, 339, 391, 313, 218, 334, 542, 230, 233, 774, 612, 175, 123, 652, 600, 450, 583, 341, 220, 555, 314, 557, 424, 395, 777, 673, 355, 287, 183, 234, 125, 616, 342, 563, 778, 660, 558, 452, 674, 397, 785, 432, 316, 345, 241, 207, 403, 357, 187, 587, 565, 664, 624, 780, 236, 126, 242, 398, 705, 346, 456, 358, 405, 303, 569, 189, 595, 215, 566, 676, 361, 706, 589, 244, 786, 647, 348, 419, 406, 464, 801, 590, 362, 570, 409, 680, 597, 788, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 369, 190, 688, 653, 248, 231, 410, 364, 654, 659, 335, 480, 315, 221, 613, 422, 370, 425, 235, 451, 543, 614, 412, 343, 222, 775, 317, 372, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 677, 434, 349, 458, 678, 245, 666, 363, 591, 127, 620, 407, 782, 436, 465, 626, 571, 246, 681, 350, 707, 460, 599, 668, 789, 249, 411, 682, 573, 365, 803, 790, 709, 440, 466, 793, 574, 371, 423, 689, 603, 366, 628, 250, 413, 468, 655, 481, 900, 805, 191, 373, 615, 684, 427, 710, 794, 605, 414, 252, 713, 374, 848, 690, 632, 806, 482, 429, 904, 809, 455, 223, 663, 835, 692, 619, 472, 714, 796, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 817, 435, 484, 621, 812, 319, 430, 838, 667, 239, 378, 459, 437, 622, 627, 488, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 247, 462, 441, 442, 469, 251, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 905, 415, 485, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 811, 697, 866, 798, 379, 431, 913, 607, 489, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 909, 719, 638, 915, 477, 255, 964, 699, 748, 869, 944, 491, 754, 910, 858, 917, 478, 968, 870, 815, 383, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 702, 918, 921, 874, 494, 976, 760, 933, 881, 501, 743, 922, 876, 847, 934, 827, 733, 882, 502, 447, 992, 937, 963, 747, 505, 855, 924, 734, 829, 938, 884, 506, 965, 749, 945, 966, 755, 859, 940, 830, 911, 871, 888, 479, 946, 750, 969, 861, 757, 970, 919, 875, 758, 508, 862, 639, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 895, 1011, 1013, 959, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023]
[0120] Таблица Q16, имеющая длину последовательности 1024:
[0121] Последовательность Q17, имеющая последовательность длина 512:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 22, 80, 136, 25, 37, 260, 264, 26, 96, 38, 67, 41, 144, 28, 69, 42, 272, 49, 70, 160, 44, 131, 73, 288, 192, 50, 74, 52, 15, 133, 320, 81, 23, 134, 384, 76, 56, 259, 82, 137, 27, 97, 39, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 90, 200, 31, 292, 322, 263, 149, 102, 105, 296, 304, 163, 92, 47, 267, 150, 208, 385, 386, 324, 106, 153, 165, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 169, 59, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 390, 122, 448, 312, 393, 283, 174, 394, 181, 340, 203, 353, 63, 295, 285, 232, 124, 286, 205, 182, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 111, 360, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 368, 339, 391, 313, 218, 334, 230, 233, 175, 123, 450, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 452, 397, 432, 316, 345, 241, 207, 403, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 189, 215, 361, 244, 348, 419, 406, 464, 362, 409, 219, 311, 421, 369, 190, 248, 231, 410, 364, 335, 480, 315, 221, 422, 370, 425, 235, 451, 412, 343, 222, 317, 372, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 458, 245, 363, 127, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 466, 371, 423, 366, 250, 413, 468, 481, 191, 373, 427, 414, 252, 374, 482, 429, 455, 223, 472, 377, 435, 484, 319, 430, 239, 378, 459, 437, 488, 380, 461, 496, 351, 467, 438, 247, 462, 441, 442, 469, 251, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 477, 255, 491, 478, 383, 493, 499, 494, 501, 502, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511]
[0122] Таблица Q17, имеющая длину последовательности 512:
[0123] Последовательность Q18, имеющая длину последовательности 256:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 21, 132, 35, 22, 80, 136, 25, 37, 26, 96, 38, 67, 41, 144, 28, 69, 42, 49, 70, 160, 44, 131, 73, 192, 50, 74, 52, 15, 133, 81, 23, 134, 76, 56, 82, 137, 27, 97, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 90, 200, 31, 149, 102, 105, 163, 92, 47, 150, 208, 106, 153, 165, 55, 113, 154, 79, 108, 224, 166, 195, 169, 59, 114, 156, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 107, 180, 151, 209, 94, 204, 155, 210, 109, 184, 115, 167, 225, 157, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 122, 174, 181, 203, 63, 232, 124, 205, 182, 211, 185, 240, 206, 95, 213, 186, 227, 111, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 189, 215, 244, 219, 190, 248, 231, 221, 235, 222, 237, 243, 238, 245, 127, 246, 249, 250, 191, 252, 223, 239, 247, 251, 253, 254, 255]
[0124] Таблица Q18, имеющая длину последовательности 256:
[0125] Последовательность Q19, имеющая длину последовательности 128:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 12, 33, 65, 20, 34, 24, 36, 7, 66, 11, 40, 68, 19, 13, 48, 14, 72, 21, 35, 22, 80, 25, 37, 26, 96, 38, 67, 41, 28, 69, 42, 49, 70, 44, 73, 50, 74, 52, 15, 81, 23, 76, 56, 82, 27, 97, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 90, 31, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0126] Таблица Q19, имеющая длину последовательности 128:
[0127] Последовательность Q20, имеющая длину последовательности 64:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 9, 6, 17, 10, 18, 12, 33, 20, 34, 24, 36, 7, 11, 40, 19, 13, 48, 14, 21, 35, 22, 25, 37, 26, 38, 41, 28, 42, 49, 44, 50, 52, 15, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0128] Таблица Q20, имеющая длину последовательности 64:
[0129] Последовательность Z16, имеющая длину последовательности 1024:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 28, 16, 33, 35, 76, 5, 12, 14, 32, 19, 38, 42, 80, 22, 46, 50, 88, 57, 95, 101, 162, 6, 17, 21, 40, 23, 47, 53, 90, 29, 55, 60, 96, 66, 108, 113, 175, 34, 62, 72, 111, 75, 120, 129, 186, 84, 131, 141, 209, 146, 218, 236, 333, 9, 18, 26, 54, 30, 58, 63, 103, 36, 68, 73, 114, 83, 123, 135, 193, 43, 79, 86, 130, 91, 138, 145, 214, 99, 148, 160, 228, 174, 242, 256, 357, 51, 89, 97, 144, 109, 154, 169, 239, 118, 170, 183, 250, 195, 269, 282, 379, 133, 191, 211, 271, 216, 283, 301, 401, 233, 307, 315, 417, 337, 435, 460, 581, 15, 25, 31, 67, 39, 77, 81, 134, 44, 87, 92, 143, 100, 153, 157, 238, 56, 93, 102, 155, 112, 168, 177, 252, 122, 184, 192, 264, 213, 279, 297, 394, 65, 106, 119, 173, 124, 185, 198, 273, 142, 208, 217, 285, 232, 306, 323, 416, 156, 225, 240, 311, 251, 325, 341, 433, 270, 348, 367, 453, 387, 470, 506, 622, 71, 121, 137, 201, 152, 215, 231, 309, 161, 234, 244, 327, 257, 340, 356, 450, 178, 253, 265, 346, 284, 366, 385, 472, 293, 389, 409, 494, 423, 518, 529, 643, 197, 274, 287, 370, 312, 392, 412, 510, 336, 413, 434, 523, 459, 535, 567, 670, 355, 449, 461, 552, 478, 577, 589, 690, 509, 597, 615, 695, 631, 714, 743, 835, 20, 37, 41, 85, 48, 94, 104, 167, 49, 105, 115, 176, 126, 194, 202, 295, 61, 116, 127, 205, 139, 212, 223, 296, 147, 222, 237, 321, 254, 335, 338, 432, 69, 136, 149, 207, 164, 226, 241, 334, 171, 248, 258, 344, 268, 364, 376, 468, 172, 266, 277, 363, 292, 386, 399, 495, 318, 408, 425, 517, 447, 531, 555, 666, 78, 159, 165, 246, 182, 262, 276, 358, 187, 281, 286, 384, 302, 400, 410, 515, 235, 298, 313, 406, 326, 422, 437, 528, 350, 448, 464, 550, 481, 574, 591, 686, 260, 328, 345, 431, 362, 452, 466, 568, 381, 475, 487, 579, 512, 601, 613, 707, 405, 505, 521, 609, 532, 623, 633, 721, 560, 660, 671, 750, 677, 779, 794, 850, 82, 179, 181, 291, 227, 305, 314, 407, 247, 320, 324, 428, 349, 444, 462, 570, 259, 347, 361, 451, 369, 467, 483, 583, 391, 489, 511, 598, 527, 616, 630, 726, 294, 365, 374, 482, 395, 500, 520, 610, 427, 522, 533, 626, 561, 639, 667, 751, 446, 546, 573, 662, 585, 673, 688, 770, 605, 692, 693, 790, 722, 801, 813, 880, 317, 388, 420, 524, 442, 534, 554, 642, 465, 569, 575, 672, 593, 679, 691, 777, 484, 586, 606, 687, 617, 694, 723, 802, 648, 729, 740, 816, 760, 834, 846, 904, 516, 619, 638, 724, 663, 727, 756, 821, 676, 754, 772, 841, 786, 852, 865, 924, 680, 780, 798, 858, 808, 870, 879, 930, 828, 885, 892, 946, 914, 954, 963, 984, 27, 45, 52, 98, 59, 117, 128, 199, 64, 132, 140, 204, 151, 220, 224, 330, 70, 150, 158, 219, 166, 263, 272, 354, 188, 275, 290, 368, 304, 393, 411, 525, 74, 163, 180, 267, 190, 288, 299, 378, 200, 308, 316, 424, 332, 426, 441, 536, 210, 329, 339, 438, 359, 455, 473, 564, 372, 469, 488, 588, 493, 600, 608, 745, 107, 189, 196, 303, 206, 319, 331, 421, 229, 343, 351, 454, 382, 477, 486, 580, 245, 353, 371, 471, 396, 491, 497, 594, 419, 498, 504, 612, 545, 629, 656, 753, 261, 383, 404, 503, 415, 519, 526, 624, 436, 544, 557, 647, 582, 664, 674, 773, 457, 566, 587, 675, 614, 685, 709, 787, 636, 712, 730, 803, 741, 819, 832, 916, 110, 203, 221, 342, 243, 352, 390, 480, 255, 375, 397, 499, 418, 508, 513, 618, 280, 402, 403, 514, 440, 541, 553, 644, 456, 562, 578, 669, 595, 681, 700, 774, 300, 430, 443, 556, 474, 572, 576, 682, 490, 590, 599, 696, 625, 710, 718, 805, 507, 611, 635, 715, 646, 735, 742, 822, 659, 747, 764, 837, 789, 854, 861, 925, 322, 463, 476, 592, 496, 604, 627, 713, 539, 632, 649, 738, 653, 744, 758, 831, 547, 651, 658, 755, 683, 763, 783, 851, 704, 788, 797, 859, 812, 877, 888, 933, 563, 689, 698, 775, 719, 791, 800, 871, 731, 810, 823, 884, 838, 894, 906, 949, 766, 825, 842, 897, 856, 909, 913, 961, 867, 921, 929, 966, 940, 974, 983, 1003, 125, 230, 249, 373, 278, 398, 414, 530, 289, 429, 439, 543, 458, 559, 584, 701, 310, 445, 479, 571, 492, 596, 603, 706, 501, 607, 628, 728, 650, 736, 749, 829, 360, 485, 502, 602, 538, 621, 637, 739, 542, 641, 655, 746, 665, 759, 769, 849, 548, 661, 678, 768, 703, 782, 795, 860, 716, 807, 811, 876, 824, 889, 900, 944, 377, 537, 540, 645, 549, 652, 668, 762, 565, 684, 697, 778, 711, 792, 809, 874, 634, 702, 720, 796, 732, 817, 826, 886, 761, 827, 844, 898, 857, 908, 915, 960, 654, 734, 748, 818, 767, 839, 848, 902, 785, 853, 864, 912, 873, 922, 932, 969, 799, 869, 878, 928, 891, 935, 943, 976, 903, 947, 953, 981, 958, 989, 991, 1008, 380, 551, 558, 699, 620, 708, 717, 806, 640, 725, 737, 820, 757, 830, 843, 901, 657, 752, 765, 833, 776, 845, 862, 911, 793, 863, 872, 919, 887, 931, 939, 972, 705, 771, 781, 855, 804, 868, 875, 926, 815, 882, 890, 936, 899, 941, 950, 980, 840, 895, 905, 945, 917, 955, 959, 987, 923, 965, 968, 993, 975, 996, 998, 1011, 733, 784, 814, 883, 836, 893, 896, 942, 847, 907, 910, 952, 920, 956, 967, 990, 866, 918, 927, 964, 938, 970, 971, 997, 948, 977, 979, 999, 985, 1004, 1006, 1016, 881, 934, 937, 973, 951, 978, 982, 1001, 957, 986, 988, 1005, 994, 1007, 1012, 1018, 962, 992, 995, 1009, 1000, 1010, 1013, 1019, 1002, 1014, 1015, 1020, 1017, 1021, 1022, 1023]
[0130] Таблица Z16, имеющая длину последовательности 1024:
[0131] Последовательность Z17, имеющая длину последовательности 512:
[0, 1, 2, 7, 3, 8, 11, 24, 4, 10, 13, 27, 16, 32, 34, 69, 5, 12, 14, 31, 19, 37, 41, 73, 22, 44, 48, 81, 54, 88, 93, 144, 6, 17, 21, 39, 23, 45, 50, 83, 28, 52, 56, 89, 61, 99, 103, 155, 33, 58, 66, 101, 68, 109, 116, 165, 77, 118, 126, 179, 131, 187, 199, 269, 9, 18, 26, 51, 29, 55, 59, 95, 35, 63, 67, 104, 76, 112, 121, 169, 42, 72, 79, 117, 84, 124, 130, 183, 91, 133, 142, 193, 154, 205, 215, 286, 49, 82, 90, 129, 100, 137, 149, 202, 107, 150, 162, 210, 171, 225, 234, 299, 119, 167, 180, 227, 185, 235, 248, 313, 196, 252, 258, 323, 273, 334, 347, 407, 15, 25, 30, 62, 38, 70, 74, 120, 43, 80, 85, 128, 92, 136, 140, 201, 53, 86, 94, 138, 102, 148, 157, 212, 111, 163, 168, 221, 182, 232, 246, 309, 60, 98, 108, 153, 113, 164, 173, 228, 127, 178, 186, 237, 195, 251, 263, 322, 139, 190, 203, 254, 211, 265, 276, 332, 226, 281, 294, 345, 304, 355, 369, 426, 65, 110, 123, 174, 135, 184, 194, 253, 143, 197, 206, 267, 216, 275, 285, 342, 158, 213, 222, 279, 236, 293, 302, 356, 242, 306, 318, 365, 326, 377, 385, 435, 172, 229, 239, 296, 255, 308, 320, 371, 272, 321, 333, 381, 346, 390, 398, 442, 284, 341, 348, 393, 358, 405, 411, 453, 370, 414, 422, 458, 430, 460, 469, 492, 20, 36, 40, 78, 46, 87, 96, 147, 47, 97, 105, 156, 114, 170, 175, 244, 57, 106, 115, 176, 125, 181, 189, 245, 132, 188, 200, 262, 214, 271, 274, 331, 64, 122, 134, 177, 145, 191, 204, 270, 151, 209, 217, 277, 224, 291, 298, 354, 152, 223, 231, 290, 241, 303, 311, 366, 260, 317, 327, 376, 339, 386, 395, 440, 71, 141, 146, 207, 161, 220, 230, 287, 166, 233, 238, 301, 249, 312, 319, 374, 198, 247, 256, 315, 266, 325, 335, 384, 283, 340, 350, 392, 359, 403, 412, 450, 219, 268, 278, 330, 289, 344, 352, 399, 300, 357, 363, 406, 373, 416, 421, 459, 314, 368, 379, 419, 387, 427, 431, 461, 396, 437, 443, 470, 447, 478, 482, 495, 75, 159, 160, 240, 192, 250, 257, 316, 208, 261, 264, 329, 282, 337, 349, 401, 218, 280, 288, 343, 295, 353, 361, 408, 307, 364, 372, 415, 383, 423, 429, 465, 243, 292, 297, 360, 310, 367, 378, 420, 328, 380, 388, 428, 397, 433, 441, 471, 338, 391, 402, 438, 409, 445, 452, 475, 417, 455, 456, 481, 462, 484, 487, 501, 259, 305, 324, 382, 336, 389, 394, 434, 351, 400, 404, 444, 413, 448, 454, 477, 362, 410, 418, 451, 424, 457, 463, 485, 436, 467, 468, 488, 474, 491, 494, 504, 375, 425, 432, 464, 439, 466, 473, 489, 446, 472, 476, 493, 480, 496, 498, 506, 449, 479, 483, 497, 486, 499, 500, 507, 490, 502, 503, 508, 505, 509, 510, 511]
[0132] Таблица Z17, имеющая длину последовательности 512:
[0133] Последовательность Z18, имеющая длину последовательности 256:
[0, 1, 2, 7, 3, 8, 11, 23, 4, 10, 13, 26, 16, 31, 33, 62, 5, 12, 14, 30, 19, 35, 38, 65, 21, 41, 43, 71, 49, 77, 82, 122, 6, 17, 20, 37, 22, 42, 45, 73, 27, 47, 51, 78, 55, 86, 90, 128, 32, 52, 59, 88, 61, 94, 99, 134, 68, 101, 107, 143, 112, 150, 157, 194, 9, 18, 25, 46, 28, 50, 53, 84, 34, 57, 60, 91, 67, 97, 104, 137, 39, 64, 69, 100, 74, 106, 111, 146, 80, 113, 120, 152, 127, 161, 167, 203, 44, 72, 79, 110, 87, 116, 124, 159, 92, 125, 131, 163, 138, 171, 177, 207, 102, 135, 144, 173, 148, 178, 184, 213, 155, 186, 190, 218, 196, 222, 227, 243, 15, 24, 29, 56, 36, 63, 66, 103, 40, 70, 75, 109, 81, 115, 119, 158, 48, 76, 83, 117, 89, 123, 129, 165, 96, 132, 136, 169, 145, 176, 183, 212, 54, 85, 93, 126, 98, 133, 140, 174, 108, 142, 149, 180, 154, 185, 191, 217, 118, 151, 160, 188, 164, 192, 198, 220, 172, 200, 205, 225, 209, 229, 233, 247, 58, 95, 105, 141, 114, 147, 153, 187, 121, 156, 162, 193, 168, 197, 202, 224, 130, 166, 170, 199, 179, 204, 208, 230, 182, 210, 214, 232, 219, 236, 238, 249, 139, 175, 181, 206, 189, 211, 215, 235, 195, 216, 221, 237, 226, 239, 241, 250, 201, 223, 228, 240, 231, 242, 244, 251, 234, 245, 246, 252, 248, 253, 254, 255]
[0134] Таблица Z18, имеющая длину последовательности 256:
[0135] Последовательность Z19, имеющая длину последовательности 128:
[0, 1, 2, 7, 3, 8, 11, 22, 4, 10, 13, 24, 15, 28, 30, 53, 5, 12, 14, 27, 18, 32, 34, 55, 20, 36, 38, 59, 43, 63, 67, 90, 6, 16, 19, 33, 21, 37, 40, 61, 25, 42, 45, 64, 48, 69, 72, 94, 29, 46, 50, 71, 52, 75, 77, 96, 57, 79, 83, 100, 86, 104, 107, 119, 9, 17, 23, 41, 26, 44, 47, 68, 31, 49, 51, 73, 56, 76, 81, 98, 35, 54, 58, 78, 62, 82, 85, 102, 66, 87, 89, 105, 93, 109, 111, 121, 39, 60, 65, 84, 70, 88, 91, 108, 74, 92, 95, 110, 99, 112, 114, 122, 80, 97, 101, 113, 103, 115, 116, 123, 106, 117, 118, 124, 120, 125, 126, 127]
[0136] Таблица Z19, имеющая длину последовательности 128:
[0137] Последовательность Z20, имеющая длину последовательности 64:
[0, 1, 2, 7, 3, 8, 10, 20, 4, 9, 12, 21, 14, 24, 26, 41, 5, 11, 13, 23, 16, 27, 29, 42, 18, 30, 32, 44, 35, 46, 48, 57, 6, 15, 17, 28, 19, 31, 33, 45, 22, 34, 36, 47, 38, 49, 51, 58, 25, 37, 39, 50, 40, 52, 53, 59, 43, 54, 55, 60, 56, 61, 62, 63]
[0138] Таблица Z20, имеющая длину последовательности 64:
[0139] Пятая группа последовательностей (критерий, который преимущественно учитывает минимальное кодовое расстояние).
[0140] Последовательность Q21, имеющая длину последовательности 1024:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 6, 9, 17, 10, 18, 128, 12, 33, 256, 20, 34, 24, 65, 36, 7, 129, 66, 512, 11, 40, 68, 19, 13, 130, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 96, 260, 38, 514, 264, 67, 41, 144, 28, 69, 42, 516, 49, 160, 272, 70, 520, 288, 528, 131, 44, 544, 73, 192, 50, 74, 52, 15, 133, 320, 81, 23, 134, 76, 137, 82, 384, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 517, 161, 45, 576, 518, 100, 51, 148, 521, 46, 75, 640, 266, 273, 522, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 530, 57, 112, 529, 524, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 89, 768, 196, 290, 141, 101, 280, 545, 546, 532, 147, 176, 142, 90, 536, 292, 200, 263, 31, 149, 321, 322, 577, 102, 105, 296, 163, 92, 47, 150, 548, 208, 324, 385, 304, 267, 578, 106, 153, 386, 165, 55, 328, 113, 519, 552, 641, 154, 79, 108, 224, 269, 166, 523, 560, 580, 195, 277, 169, 275, 291, 59, 270, 114, 156, 87, 197, 116, 170, 61, 525, 531, 177, 278, 281, 526, 642, 293, 388, 91, 584, 769, 198, 172, 120, 201, 62, 143, 336, 282, 103, 178, 294, 93, 533, 644, 534, 547, 770, 392, 297, 592, 323, 202, 284, 151, 209, 180, 107, 325, 94, 537, 400, 298, 204, 352, 305, 155, 300, 210, 608, 648, 109, 184, 115, 167, 225, 326, 157, 110, 772, 549, 656, 538, 117, 212, 330, 171, 550, 329, 306, 226, 387, 308, 271, 579, 416, 216, 337, 158, 776, 118, 540, 553, 279, 332, 389, 173, 121, 199, 179, 228, 283, 122, 393, 174, 312, 672, 390, 554, 556, 203, 561, 181, 295, 448, 353, 338, 63, 581, 340, 285, 394, 232, 124, 354, 582, 784, 704, 527, 286, 182, 562, 643, 585, 205, 299, 211, 401, 185, 396, 240, 586, 645, 593, 535, 301, 402, 344, 206, 564, 800, 327, 356, 307, 95, 417, 213, 186, 404, 111, 539, 568, 594, 649, 771, 302, 832, 588, 646, 227, 360, 214, 188, 551, 609, 896, 331, 309, 418, 449, 217, 408, 229, 541, 159, 420, 596, 650, 773, 310, 333, 119, 368, 339, 391, 657, 313, 218, 542, 610, 334, 230, 233, 774, 658, 612, 175, 123, 450, 652, 341, 220, 557, 314, 555, 600, 583, 424, 395, 777, 673, 355, 287, 183, 234, 125, 342, 563, 674, 616, 558, 660, 778, 452, 397, 432, 316, 345, 241, 207, 785, 403, 357, 187, 587, 565, 664, 624, 780, 236, 126, 242, 398, 705, 346, 456, 358, 405, 303, 569, 595, 189, 786, 215, 676, 589, 566, 647, 361, 706, 244, 348, 419, 406, 311, 708, 219, 598, 601, 651, 611, 409, 680, 788, 362, 570, 597, 572, 464, 801, 590, 421, 802, 369, 792, 190, 602, 653, 248, 688, 231, 410, 364, 335, 422, 613, 659, 654, 315, 221, 370, 425, 235, 451, 480, 775, 412, 614, 343, 222, 317, 372, 543, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 376, 428, 625, 238, 359, 567, 618, 665, 736, 898, 457, 399, 781, 591, 666, 678, 349, 434, 677, 840, 782, 626, 571, 620, 787, 363, 245, 458, 127, 407, 436, 465, 350, 246, 681, 460, 249, 599, 411, 365, 668, 707, 573, 789, 803, 790, 682, 440, 709, 466, 628, 371, 423, 366, 250, 413, 574, 468, 603, 481, 689, 793, 191, 373, 655, 900, 805, 427, 615, 710, 414, 252, 848, 684, 713, 605, 690, 632, 482, 794, 806, 472, 223, 663, 835, 904, 809, 714, 619, 796, 374, 429, 455, 692, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 817, 435, 812, 484, 319, 430, 621, 838, 667, 239, 378, 459, 437, 627, 622, 488, 380, 461, 679, 841, 818, 724, 669, 496, 629, 928, 737, 899, 783, 738, 901, 842, 438, 467, 247, 820, 849, 683, 351, 791, 441, 728, 670, 462, 469, 442, 251, 367, 630, 740, 902, 711, 844, 850, 905, 685, 691, 824, 633, 483, 795, 744, 470, 852, 686, 444, 473, 253, 634, 485, 415, 375, 960, 865, 575, 807, 906, 715, 913, 693, 797, 866, 811, 717, 474, 254, 694, 723, 636, 486, 798, 607, 697, 489, 431, 379, 908, 752, 914, 856, 868, 839, 929, 813, 718, 819, 476, 916, 725, 698, 490, 739, 814, 843, 623, 497, 439, 381, 671, 463, 726, 930, 872, 821, 920, 700, 729, 492, 932, 961, 741, 903, 845, 498, 880, 382, 822, 851, 631, 443, 825, 730, 471, 445, 687, 635, 742, 846, 500, 745, 826, 732, 446, 962, 936, 255, 853, 504, 637, 907, 475, 746, 867, 487, 695, 799, 854, 828, 753, 857, 964, 909, 719, 477, 915, 869, 699, 748, 944, 638, 754, 491, 910, 858, 478, 815, 727, 917, 870, 493, 873, 701, 968, 383, 860, 756, 918, 931, 976, 499, 921, 874, 702, 823, 494, 731, 760, 881, 933, 501, 743, 922, 876, 847, 934, 827, 733, 502, 992, 882, 447, 963, 937, 747, 505, 855, 924, 734, 829, 884, 938, 506, 965, 749, 945, 966, 940, 969, 911, 946, 755, 888, 830, 859, 639, 871, 970, 750, 508, 948, 977, 757, 479, 919, 861, 875, 972, 978, 758, 862, 952, 761, 993, 923, 703, 495, 935, 877, 883, 980, 762, 925, 994, 878, 503, 885, 939, 984, 764, 996, 926, 735, 967, 886, 941, 507, 947, 889, 831, 1000, 942, 971, 751, 509, 949, 890, 973, 1008, 510, 950, 979, 759, 892, 863, 953, 974, 981, 954, 763, 995, 879, 982, 956, 985, 765, 997, 927, 887, 986, 766, 998, 1001, 943, 891, 988, 1002, 1009, 511, 951, 893, 1004, 975, 1010, 894, 955, 1012, 983, 957, 1016, 958, 987, 767, 999, 989, 1003, 990, 1005, 1011, 895, 1006, 1013, 1014, 1017, 959, 1018, 1020, 991, 1007, 1015, 1019, 1021, 1022, 1023]
[0141] Таблица Q21, имеющая длину последовательности 1024:
[0142] Последовательность Q22, имеющая длину последовательности 512:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 6, 9, 17, 10, 18, 128, 12, 33, 256, 20, 34, 24, 65, 36, 7, 129, 66, 11, 40, 68, 19, 13, 130, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 96, 260, 38, 264, 67, 41, 144, 28, 69, 42, 49, 160, 272, 70, 288, 131, 44, 73, 192, 50, 74, 52, 15, 133, 320, 81, 23, 134, 76, 137, 82, 384, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 89, 196, 290, 141, 101, 280, 147, 176, 142, 90, 292, 200, 263, 31, 149, 321, 322, 102, 105, 296, 163, 92, 47, 150, 208, 324, 385, 304, 267, 106, 153, 386, 165, 55, 328, 113, 154, 79, 108, 224, 269, 166, 195, 277, 169, 275, 291, 59, 270, 114, 156, 87, 197, 116, 170, 61, 177, 278, 281, 293, 388, 91, 198, 172, 120, 201, 62, 143, 336, 282, 103, 178, 294, 93, 392, 297, 323, 202, 284, 151, 209, 180, 107, 325, 94, 400, 298, 204, 352, 305, 155, 300, 210, 109, 184, 115, 167, 225, 326, 157, 110, 117, 212, 330, 171, 329, 306, 226, 387, 308, 271, 416, 216, 337, 158, 118, 279, 332, 389, 173, 121, 199, 179, 228, 283, 122, 393, 174, 312, 390, 203, 181, 295, 448, 353, 338, 63, 340, 285, 394, 232, 124, 354, 286, 182, 205, 299, 211, 401, 185, 396, 240, 301, 402, 344, 206, 327, 356, 307, 95, 417, 213, 186, 404, 111, 302, 227, 360, 214, 188, 331, 309, 418, 449, 217, 408, 229, 159, 420, 310, 333, 119, 368, 339, 391, 313, 218, 334, 230, 233, 175, 123, 450, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 452, 397, 432, 316, 345, 241, 207, 403, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 189, 215, 361, 244, 348, 419, 406, 311, 219, 409, 362, 464, 421, 369, 190, 248, 231, 410, 364, 335, 422, 315, 221, 370, 425, 235, 451, 480, 412, 343, 222, 317, 372, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 349, 434, 363, 245, 458, 127, 407, 436, 465, 350, 246, 460, 249, 411, 365, 440, 466, 371, 423, 366, 250, 413, 468, 481, 191, 373, 427, 414, 252, 482, 472, 223, 374, 429, 455, 377, 435, 484, 319, 430, 239, 378, 459, 437, 488, 380, 461, 496, 438, 467, 247, 351, 441, 462, 469, 442, 251, 367, 483, 470, 444, 473, 253, 485, 415, 375, 474, 254, 486, 489, 431, 379, 476, 490, 497, 439, 381, 463, 492, 498, 382, 443, 471, 445, 500, 446, 255, 504, 475, 487, 477, 491, 478, 493, 383, 499, 494, 501, 502, 447, 505, 506, 508, 479, 495, 503, 507, 509, 510, 511]
[0143] Таблица Q22, имеющая длину последовательности 512:
[0144] Последовательность Q23, имеющая длину последовательности 256:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 6, 9, 17, 10, 18, 128, 12, 33, 20, 34, 24, 65, 36, 7, 129, 66, 11, 40, 68, 19, 13, 130, 48, 14, 72, 21, 132, 35, 26, 80, 37, 25, 22, 136, 96, 38, 67, 41, 144, 28, 69, 42, 49, 160, 70, 131, 44, 73, 192, 50, 74, 52, 15, 133, 81, 23, 134, 76, 137, 82, 56, 27, 97, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 90, 200, 31, 149, 102, 105, 163, 92, 47, 150, 208, 106, 153, 165, 55, 113, 154, 79, 108, 224, 166, 195, 169, 59, 114, 156, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 151, 209, 180, 107, 94, 204, 155, 210, 109, 184, 115, 167, 225, 157, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 122, 174, 203, 181, 63, 232, 124, 182, 205, 211, 185, 240, 206, 95, 213, 186, 111, 227, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 189, 215, 244, 219, 190, 248, 231, 221, 235, 222, 237, 243, 238, 245, 127, 246, 249, 250, 191, 252, 223, 239, 247, 251, 253, 254, 255]
[0145] Таблица Q23, имеющая длину последовательности 256:
[0146] Последовательность Q24, имеющая длину последовательности 128:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 6, 9, 17, 10, 18, 12, 33, 20, 34, 24, 65, 36, 7, 66, 11, 40, 68, 19, 13, 48, 14, 72, 21, 35, 26, 80, 37, 25, 22, 96, 38, 67, 41, 28, 69, 42, 49, 70, 44, 73, 50, 74, 52, 15, 81, 23, 76, 82, 56, 27, 97, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 90, 31, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0147] Таблица Q24, имеющая длину последовательности 128:
[0148] Последовательность Q25, имеющая длину последовательности 64:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 6, 9, 17, 10, 18, 12, 33, 20, 34, 24, 36, 7, 11, 40, 19, 13, 48, 14, 21, 35, 26, 37, 25, 22, 38, 41, 28, 42, 49, 44, 50, 52, 15, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0149] Таблица Q25, имеющая длину последовательности 64:
[0150] Последовательность Z21, имеющая длину последовательности 1024:
[0, 1, 2, 7, 3, 8, 10, 24, 4, 11, 13, 28, 16, 32, 35, 76, 5, 12, 14, 31, 19, 38, 47, 80, 21, 46, 42, 87, 57, 95, 101, 167, 6, 17, 20, 40, 23, 45, 51, 89, 29, 55, 59, 96, 69, 108, 115, 177, 34, 61, 73, 112, 75, 123, 130, 190, 86, 133, 143, 210, 148, 218, 235, 327, 9, 22, 26, 54, 30, 58, 64, 103, 36, 71, 74, 116, 82, 126, 138, 197, 44, 79, 84, 131, 91, 141, 147, 214, 99, 149, 162, 228, 176, 242, 259, 364, 49, 88, 97, 146, 111, 154, 172, 239, 121, 173, 186, 257, 198, 271, 278, 369, 134, 192, 212, 273, 216, 283, 300, 401, 233, 307, 312, 417, 333, 435, 460, 585, 15, 25, 33, 68, 39, 77, 81, 137, 48, 83, 92, 145, 100, 153, 161, 236, 56, 93, 102, 159, 113, 168, 178, 254, 125, 187, 196, 266, 213, 277, 298, 394, 62, 107, 122, 175, 127, 189, 201, 274, 144, 207, 217, 286, 232, 306, 314, 416, 160, 221, 240, 309, 256, 322, 340, 433, 272, 348, 367, 453, 382, 471, 505, 619, 72, 124, 140, 205, 151, 215, 231, 308, 165, 234, 252, 320, 263, 344, 358, 449, 180, 255, 268, 346, 284, 366, 381, 473, 296, 390, 407, 486, 421, 519, 529, 639, 199, 275, 290, 379, 310, 392, 411, 510, 332, 412, 434, 522, 459, 535, 560, 670, 350, 448, 461, 552, 480, 583, 590, 695, 508, 593, 611, 707, 628, 728, 746, 816, 18, 37, 41, 90, 50, 94, 104, 166, 53, 105, 118, 184, 128, 200, 211, 293, 63, 119, 129, 208, 142, 206, 222, 303, 155, 223, 238, 311, 253, 330, 339, 432, 66, 139, 152, 209, 164, 226, 241, 323, 174, 249, 262, 345, 267, 355, 375, 468, 183, 265, 289, 363, 292, 387, 399, 484, 315, 406, 423, 518, 446, 530, 555, 665, 78, 169, 170, 251, 181, 258, 276, 361, 191, 288, 285, 386, 304, 400, 410, 513, 237, 297, 326, 403, 329, 420, 436, 528, 357, 447, 464, 550, 481, 573, 589, 699, 264, 325, 334, 431, 362, 452, 466, 561, 380, 478, 494, 582, 512, 596, 610, 708, 402, 503, 520, 608, 531, 620, 647, 732, 557, 660, 671, 756, 677, 778, 796, 854, 85, 182, 188, 291, 227, 305, 317, 404, 248, 313, 331, 428, 349, 444, 462, 568, 261, 347, 356, 451, 368, 467, 483, 586, 391, 491, 511, 595, 526, 612, 627, 731, 295, 365, 388, 482, 395, 501, 514, 609, 427, 521, 533, 624, 558, 648, 666, 755, 445, 546, 574, 662, 587, 673, 693, 777, 604, 701, 706, 800, 726, 804, 813, 881, 324, 389, 418, 523, 443, 534, 554, 649, 465, 567, 584, 672, 592, 678, 704, 780, 498, 588, 606, 694, 614, 705, 723, 803, 638, 727, 745, 821, 767, 834, 845, 913, 524, 616, 635, 720, 664, 730, 750, 824, 676, 754, 771, 842, 788, 850, 865, 926, 684, 776, 794, 860, 809, 870, 878, 935, 818, 885, 892, 946, 909, 954, 959, 988, 27, 43, 52, 98, 60, 106, 110, 193, 65, 114, 120, 202, 136, 219, 224, 338, 67, 135, 132, 220, 158, 243, 245, 354, 163, 260, 282, 370, 301, 393, 408, 532, 70, 156, 157, 246, 179, 280, 287, 383, 194, 302, 318, 424, 319, 422, 440, 536, 203, 321, 341, 437, 359, 455, 476, 562, 371, 469, 495, 579, 497, 599, 613, 735, 109, 171, 185, 294, 204, 328, 335, 426, 229, 343, 351, 454, 377, 475, 500, 570, 250, 353, 372, 470, 396, 496, 487, 594, 425, 488, 506, 615, 545, 632, 656, 752, 269, 384, 409, 490, 415, 515, 527, 625, 439, 544, 563, 645, 580, 667, 675, 775, 457, 559, 578, 674, 607, 685, 709, 799, 634, 719, 729, 806, 749, 819, 840, 905, 117, 195, 225, 342, 244, 352, 378, 477, 270, 373, 397, 489, 419, 507, 517, 621, 281, 405, 414, 516, 441, 541, 553, 640, 456, 564, 571, 669, 597, 683, 703, 779, 316, 430, 438, 556, 474, 575, 572, 679, 492, 591, 603, 698, 630, 716, 725, 805, 509, 617, 633, 717, 650, 740, 747, 825, 659, 753, 770, 837, 786, 852, 863, 925, 337, 463, 479, 598, 485, 605, 626, 712, 539, 631, 644, 738, 653, 744, 765, 833, 547, 651, 658, 748, 682, 769, 781, 847, 702, 787, 802, 866, 812, 877, 888, 942, 565, 687, 690, 772, 710, 791, 807, 871, 722, 810, 822, 884, 838, 894, 908, 953, 758, 829, 841, 901, 856, 912, 919, 962, 867, 922, 931, 969, 939, 975, 980, 1002, 150, 230, 247, 374, 279, 398, 413, 525, 299, 429, 442, 543, 458, 569, 577, 689, 336, 450, 472, 581, 493, 600, 602, 700, 504, 618, 636, 721, 646, 741, 751, 826, 360, 499, 502, 601, 538, 623, 637, 736, 542, 643, 655, 743, 663, 764, 773, 846, 548, 661, 681, 766, 696, 784, 797, 864, 718, 801, 811, 876, 828, 889, 903, 949, 376, 537, 540, 641, 549, 652, 668, 762, 576, 680, 692, 774, 713, 793, 808, 874, 629, 697, 714, 798, 724, 817, 827, 886, 760, 830, 844, 904, 855, 915, 920, 964, 654, 734, 742, 823, 761, 836, 849, 906, 783, 851, 862, 916, 873, 928, 934, 971, 795, 868, 880, 929, 890, 936, 944, 978, 902, 948, 956, 984, 963, 990, 994, 1009, 385, 551, 566, 688, 622, 691, 711, 792, 642, 715, 737, 820, 757, 832, 843, 899, 657, 739, 759, 835, 768, 848, 857, 914, 785, 861, 872, 924, 887, 932, 941, 977, 686, 763, 782, 858, 789, 869, 875, 927, 815, 883, 891, 937, 897, 945, 951, 983, 839, 895, 900, 947, 910, 955, 960, 989, 921, 965, 968, 995, 973, 998, 1000, 1014, 733, 790, 814, 882, 831, 893, 896, 943, 853, 898, 907, 952, 917, 957, 966, 992, 859, 911, 918, 961, 930, 967, 972, 997, 938, 974, 979, 1001, 985, 1004, 1006, 1017, 879, 923, 933, 970, 940, 976, 981, 1003, 950, 982, 986, 1005, 991, 1007, 1010, 1018, 958, 987, 993, 1008, 996, 1011, 1012, 1019, 999, 1013, 1015, 1020, 1016, 1021, 1022, 1023]
[0151] Таблица Z21, имеющая длину последовательности 1024:
[0152] Последовательность Z22, имеющая длину последовательности 512:
[0, 1, 2, 7, 3, 8, 10, 24, 4, 11, 13, 27, 16, 31, 34, 69, 5, 12, 14, 30, 19, 37, 45, 73, 21, 44, 41, 80, 54, 88, 93, 145, 6, 17, 20, 39, 23, 43, 49, 82, 28, 52, 56, 89, 63, 99, 103, 154, 33, 57, 66, 101, 68, 109, 116, 165, 79, 118, 126, 179, 131, 187, 198, 268, 9, 22, 26, 51, 29, 55, 60, 95, 35, 64, 67, 104, 75, 112, 121, 169, 42, 72, 77, 117, 84, 124, 130, 183, 91, 132, 141, 193, 153, 205, 216, 291, 47, 81, 90, 129, 100, 136, 149, 202, 107, 150, 161, 214, 170, 225, 232, 296, 119, 167, 181, 227, 185, 233, 247, 313, 196, 252, 257, 323, 273, 334, 347, 407, 15, 25, 32, 62, 38, 70, 74, 120, 46, 76, 85, 128, 92, 135, 140, 199, 53, 86, 94, 138, 102, 146, 155, 211, 111, 162, 168, 222, 182, 231, 246, 309, 58, 98, 108, 152, 113, 164, 173, 228, 127, 176, 186, 236, 195, 251, 259, 322, 139, 188, 203, 254, 213, 263, 276, 332, 226, 281, 294, 345, 301, 355, 369, 426, 65, 110, 123, 174, 133, 184, 194, 253, 143, 197, 209, 262, 219, 277, 287, 342, 156, 212, 224, 279, 234, 293, 300, 356, 244, 306, 318, 363, 326, 377, 385, 433, 171, 229, 239, 298, 255, 308, 320, 371, 272, 321, 333, 380, 346, 390, 398, 442, 283, 341, 348, 393, 358, 405, 412, 452, 370, 414, 422, 458, 430, 464, 469, 488, 18, 36, 40, 83, 48, 87, 96, 144, 50, 97, 105, 160, 114, 172, 180, 242, 59, 106, 115, 177, 125, 175, 189, 248, 137, 190, 201, 256, 210, 270, 275, 331, 61, 122, 134, 178, 142, 191, 204, 264, 151, 207, 218, 278, 223, 284, 297, 354, 159, 221, 238, 290, 241, 303, 311, 362, 260, 317, 327, 376, 339, 386, 395, 440, 71, 147, 148, 208, 157, 215, 230, 288, 166, 237, 235, 302, 249, 312, 319, 374, 200, 245, 267, 315, 269, 325, 335, 384, 286, 340, 350, 392, 359, 402, 411, 453, 220, 266, 274, 330, 289, 344, 352, 399, 299, 357, 365, 404, 373, 416, 421, 459, 314, 368, 378, 419, 387, 427, 434, 467, 396, 437, 443, 473, 447, 478, 482, 496, 78, 158, 163, 240, 192, 250, 261, 316, 206, 258, 271, 329, 282, 337, 349, 401, 217, 280, 285, 343, 295, 353, 361, 408, 307, 364, 372, 415, 383, 423, 429, 466, 243, 292, 304, 360, 310, 367, 375, 420, 328, 379, 388, 428, 397, 435, 441, 472, 338, 391, 403, 438, 409, 445, 450, 477, 417, 454, 457, 483, 462, 485, 487, 501, 265, 305, 324, 381, 336, 389, 394, 436, 351, 400, 406, 444, 413, 448, 455, 479, 366, 410, 418, 451, 424, 456, 461, 484, 432, 463, 468, 490, 474, 492, 494, 505, 382, 425, 431, 460, 439, 465, 470, 491, 446, 471, 475, 493, 480, 495, 498, 506, 449, 476, 481, 497, 486, 499, 500, 507, 489, 502, 503, 508, 504, 509, 510, 511]
[0153] Таблица Z22, имеющая длину последовательности 512:
[0154] Последовательность Z23, имеющая длину последовательности 256:
[0, 1, 2, 7, 3, 8, 10, 23, 4, 11, 13, 26, 16, 30, 33, 62, 5, 12, 14, 29, 18, 35, 42, 65, 20, 41, 38, 71, 49, 77, 82, 122, 6, 17, 19, 37, 22, 40, 45, 73, 27, 47, 51, 78, 56, 86, 90, 128, 32, 52, 59, 88, 61, 94, 99, 134, 70, 101, 107, 143, 112, 150, 157, 194, 9, 21, 25, 46, 28, 50, 54, 84, 34, 57, 60, 91, 67, 97, 104, 137, 39, 64, 69, 100, 74, 106, 111, 146, 80, 113, 120, 152, 127, 161, 167, 203, 44, 72, 79, 110, 87, 116, 124, 159, 92, 125, 131, 166, 138, 171, 177, 206, 102, 135, 144, 173, 148, 178, 184, 213, 155, 186, 190, 218, 196, 222, 227, 243, 15, 24, 31, 55, 36, 63, 66, 103, 43, 68, 75, 109, 81, 115, 119, 158, 48, 76, 83, 117, 89, 123, 129, 163, 96, 132, 136, 169, 145, 176, 183, 212, 53, 85, 93, 126, 98, 133, 140, 174, 108, 142, 149, 180, 154, 185, 191, 217, 118, 151, 160, 188, 165, 193, 197, 220, 172, 200, 205, 225, 209, 229, 233, 247, 58, 95, 105, 141, 114, 147, 153, 187, 121, 156, 162, 192, 168, 198, 202, 224, 130, 164, 170, 199, 179, 204, 208, 230, 182, 210, 214, 232, 219, 236, 238, 249, 139, 175, 181, 207, 189, 211, 215, 235, 195, 216, 221, 237, 226, 239, 241, 250, 201, 223, 228, 240, 231, 242, 244, 251, 234, 245, 246, 252, 248, 253, 254, 255]
[0155] Таблица Z23, имеющая длину последовательности 256:
[0156] Последовательность Z24, имеющая длину последовательности 128:
[0, 1, 2, 7, 3, 8, 10, 22, 4, 11, 13, 24, 15, 28, 30, 53, 5, 12, 14, 27, 17, 32, 38, 55, 19, 37, 34, 59, 43, 63, 67, 90, 6, 16, 18, 33, 21, 36, 40, 61, 25, 42, 45, 64, 48, 69, 72, 94, 29, 46, 50, 71, 52, 75, 77, 96, 58, 79, 83, 100, 86, 104, 107, 119, 9, 20, 23, 41, 26, 44, 47, 68, 31, 49, 51, 73, 56, 76, 81, 98, 35, 54, 57, 78, 62, 82, 85, 102, 66, 87, 89, 105, 93, 109, 111, 121, 39, 60, 65, 84, 70, 88, 91, 108, 74, 92, 95, 110, 99, 112, 114, 122, 80, 97, 101, 113, 103, 115, 116, 123, 106, 117, 118, 124, 120, 125, 126, 127]
[0157] Таблица Z24, имеющая длину 128:
[0158] Последовательность Z25, имеющая длину последовательности 64:
[0, 1, 2, 7, 3, 8, 9, 20, 4, 10, 12, 21, 14, 24, 26, 41, 5, 11, 13, 23, 16, 27, 32, 42, 18, 31, 29, 44, 35, 46, 48, 57, 6, 15, 17, 28, 19, 30, 33, 45, 22, 34, 36, 47, 38, 49, 51, 58, 25, 37, 39, 50, 40, 52, 53, 59, 43, 54, 55, 60, 56, 61, 62, 63]
[0159] Таблица Z25, имеющая длину последовательности 64:
[0160] Шестая группа последовательностей (критерий, который учитывает оптимальную производительность списка 4).
[0161] Последовательность Q26, имеющая длину последовательности 1024:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 512, 3, 12, 5, 18, 128, 9, 33, 17, 10, 36, 66, 24, 256, 20, 65, 34, 7, 129, 40, 11, 72, 132, 513, 19, 48, 68, 13, 257, 14, 21, 130, 26, 80, 35, 258, 38, 136, 96, 22, 516, 37, 25, 67, 264, 41, 144, 28, 69, 260, 49, 74, 160, 42, 520, 134, 70, 44, 81, 272, 15, 50, 131, 192, 73, 23, 514, 137, 52, 288, 76, 133, 82, 27, 97, 259, 39, 528, 56, 138, 84, 29, 145, 261, 43, 320, 544, 98, 140, 265, 30, 88, 146, 262, 100, 518, 161, 71, 45, 273, 51, 148, 266, 576, 46, 75, 104, 164, 193, 53, 162, 515, 384, 268, 77, 152, 54, 85, 524, 289, 112, 274, 57, 78, 135, 517, 194, 83, 290, 168, 276, 86, 530, 58, 139, 322, 196, 101, 640, 60, 147, 176, 280, 99, 89, 521, 292, 141, 321, 200, 90, 545, 31, 142, 102, 263, 529, 47, 386, 105, 296, 208, 522, 153, 92, 149, 267, 548, 163, 324, 113, 150, 578, 165, 55, 304, 106, 275, 536, 269, 385, 154, 768, 79, 108, 224, 166, 532, 59, 169, 114, 195, 577, 328, 270, 277, 87, 546, 156, 116, 388, 519, 336, 291, 278, 197, 641, 61, 177, 170, 552, 91, 281, 201, 198, 523, 62, 143, 294, 584, 172, 392, 103, 644, 120, 293, 282, 531, 352, 178, 202, 560, 323, 297, 93, 580, 107, 151, 209, 525, 284, 180, 400, 769, 94, 204, 298, 526, 326, 155, 533, 305, 109, 325, 642, 210, 184, 225, 538, 167, 300, 592, 115, 387, 329, 547, 110, 416, 770, 212, 271, 117, 550, 306, 157, 648, 226, 171, 330, 608, 337, 389, 534, 308, 216, 549, 121, 390, 537, 158, 279, 332, 579, 118, 173, 776, 338, 179, 553, 199, 353, 656, 283, 312, 540, 448, 228, 581, 393, 122, 181, 772, 232, 295, 561, 174, 394, 586, 63, 203, 672, 354, 554, 401, 340, 646, 124, 285, 582, 182, 299, 556, 240, 211, 593, 286, 344, 784, 396, 205, 527, 95, 418, 562, 185, 643, 213, 402, 704, 307, 327, 585, 356, 535, 206, 186, 649, 301, 111, 564, 302, 800, 360, 227, 588, 417, 159, 645, 404, 594, 309, 214, 539, 449, 331, 609, 119, 771, 217, 188, 551, 229, 568, 333, 408, 650, 310, 596, 339, 420, 541, 218, 657, 368, 773, 123, 230, 555, 175, 832, 391, 313, 610, 241, 652, 450, 334, 777, 220, 542, 341, 600, 424, 314, 658, 183, 774, 233, 612, 355, 673, 125, 287, 583, 395, 557, 234, 785, 316, 345, 563, 187, 660, 452, 778, 403, 558, 342, 397, 587, 207, 616, 236, 676, 432, 705, 346, 565, 361, 674, 126, 242, 896, 357, 780, 405, 589, 215, 664, 398, 566, 303, 597, 358, 801, 419, 624, 456, 786, 348, 189, 569, 244, 590, 410, 647, 219, 706, 311, 595, 362, 802, 464, 680, 406, 788, 421, 598, 231, 570, 248, 651, 369, 834, 190, 708, 409, 613, 315, 572, 364, 659, 422, 335, 221, 688, 451, 792, 370, 611, 425, 601, 235, 804, 343, 653, 412, 833, 480, 712, 222, 602, 317, 543, 453, 654, 426, 614, 372, 775, 433, 559, 237, 898, 617, 347, 808, 243, 720, 454, 665, 318, 604, 376, 661, 428, 779, 238, 675, 359, 836, 458, 625, 399, 662, 677, 245, 567, 434, 816, 457, 618, 349, 787, 465, 781, 897, 363, 666, 407, 591, 127, 620, 246, 736, 436, 678, 571, 350, 681, 249, 626, 460, 707, 840, 411, 782, 365, 789, 440, 599, 374, 668, 628, 423, 900, 466, 848, 803, 250, 790, 371, 709, 191, 573, 689, 481, 682, 413, 603, 793, 366, 713, 468, 710, 429, 574, 655, 252, 806, 414, 684, 904, 373, 615, 482, 632, 805, 223, 794, 864, 427, 690, 472, 714, 835, 455, 809, 377, 605, 619, 435, 663, 721, 319, 796, 430, 692, 912, 239, 606, 716, 461, 810, 484, 838, 667, 378, 817, 621, 437, 837, 722, 247, 696, 380, 737, 679, 459, 812, 627, 488, 899, 841, 441, 622, 928, 351, 724, 783, 469, 629, 818, 438, 669, 462, 738, 683, 251, 842, 849, 496, 901, 820, 728, 467, 633, 902, 367, 670, 791, 442, 844, 630, 474, 685, 850, 483, 691, 711, 379, 865, 795, 415, 824, 960, 740, 253, 905, 634, 444, 693, 744, 485, 807, 686, 906, 470, 575, 715, 375, 866, 913, 473, 852, 636, 797, 431, 694, 811, 486, 752, 723, 798, 489, 856, 908, 254, 717, 607, 930, 476, 697, 725, 914, 439, 819, 839, 868, 492, 718, 698, 381, 813, 623, 814, 498, 872, 739, 929, 445, 671, 916, 821, 463, 726, 961, 843, 490, 631, 729, 700, 382, 741, 845, 920, 471, 822, 851, 932, 730, 497, 880, 635, 742, 443, 687, 903, 825, 475, 753, 962, 846, 732, 500, 853, 936, 826, 446, 695, 745, 867, 637, 487, 799, 907, 746, 828, 493, 857, 699, 964, 915, 477, 854, 909, 719, 504, 748, 944, 858, 873, 638, 478, 754, 869, 917, 727, 499, 910, 815, 870, 931, 255, 968, 860, 701, 756, 922, 491, 731, 823, 874, 976, 918, 502, 933, 743, 760, 881, 494, 702, 921, 827, 876, 934, 847, 505, 733, 963, 882, 937, 747, 383, 855, 924, 992, 734, 829, 965, 501, 938, 884, 945, 749, 859, 755, 479, 966, 830, 888, 940, 750, 871, 506, 970, 911, 757, 946, 969, 861, 977, 447, 875, 919, 639, 758, 948, 862, 761, 508, 972, 923, 877, 952, 886, 935, 978, 762, 503, 883, 703, 993, 925, 878, 980, 941, 764, 495, 926, 885, 994, 735, 939, 984, 967, 889, 947, 831, 507, 942, 751, 973, 996, 890, 949, 759, 892, 971, 1000, 953, 509, 863, 981, 950, 974, 763, 1008, 979, 879, 954, 986, 995, 891, 927, 510, 765, 956, 997, 982, 887, 985, 943, 998, 1001, 766, 988, 951, 1004, 893, 1010, 957, 975, 511, 1002, 894, 983, 1009, 955, 987, 1012, 958, 999, 1005, 989, 1016, 990, 1011, 767, 1003, 1014, 1006, 1017, 895, 1013, 991, 1018, 959, 1020, 1015, 1007, 1019, 1021, 1022, 1023]
[0162] Таблица Q26, имеющая длину последовательности 1024:
[0163] Последовательность Q27, имеющая длину последовательности 512:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 128, 9, 33, 17, 10, 36, 66, 24, 256, 20, 65, 34, 7, 129, 40, 11, 72, 132, 19, 48, 68, 13, 257, 14, 21, 130, 26, 80, 35, 258, 38, 136, 96, 22, 37, 25, 67, 264, 41, 144, 28, 69, 260, 49, 74, 160, 42, 134, 70, 44, 81, 272, 15, 50, 131, 192, 73, 23, 137, 52, 288, 76, 133, 82, 27, 97, 259, 39, 56, 138, 84, 29, 145, 261, 43, 320, 98, 140, 265, 30, 88, 146, 262, 100, 161, 71, 45, 273, 51, 148, 266, 46, 75, 104, 164, 193, 53, 162, 384, 268, 77, 152, 54, 85, 289, 112, 274, 57, 78, 135, 194, 83, 290, 168, 276, 86, 58, 139, 322, 196, 101, 60, 147, 176, 280, 99, 89, 292, 141, 321, 200, 90, 31, 142, 102, 263, 47, 386, 105, 296, 208, 153, 92, 149, 267, 163, 324, 113, 150, 165, 55, 304, 106, 275, 269, 385, 154, 79, 108, 224, 166, 59, 169, 114, 195, 328, 270, 277, 87, 156, 116, 388, 336, 291, 278, 197, 61, 177, 170, 91, 281, 201, 198, 62, 143, 294, 172, 392, 103, 120, 293, 282, 352, 178, 202, 323, 297, 93, 107, 151, 209, 284, 180, 400, 94, 204, 298, 326, 155, 305, 109, 325, 210, 184, 225, 167, 300, 115, 387, 329, 110, 416, 212, 271, 117, 306, 157, 226, 171, 330, 337, 389, 308, 216, 121, 390, 158, 279, 332, 118, 173, 338, 179, 199, 353, 283, 312, 448, 228, 393, 122, 181, 232, 295, 174, 394, 63, 203, 354, 401, 340, 124, 285, 182, 299, 240, 211, 286, 344, 396, 205, 95, 418, 185, 213, 402, 307, 327, 356, 206, 186, 301, 111, 302, 360, 227, 417, 159, 404, 309, 214, 449, 331, 119, 217, 188, 229, 333, 408, 310, 339, 420, 218, 368, 123, 230, 175, 391, 313, 241, 450, 334, 220, 341, 424, 314, 183, 233, 355, 125, 287, 395, 234, 316, 345, 187, 452, 403, 342, 397, 207, 236, 432, 346, 361, 126, 242, 357, 405, 215, 398, 303, 358, 419, 456, 348, 189, 244, 410, 219, 311, 362, 464, 406, 421, 231, 248, 369, 190, 409, 315, 364, 422, 335, 221, 451, 370, 425, 235, 343, 412, 480, 222, 317, 453, 426, 372, 433, 237, 347, 243, 454, 318, 376, 428, 238, 359, 458, 399, 245, 434, 457, 349, 465, 363, 407, 127, 246, 436, 350, 249, 460, 411, 365, 440, 374, 423, 466, 250, 371, 191, 481, 413, 366, 468, 429, 252, 414, 373, 482, 223, 427, 472, 455, 377, 435, 319, 430, 239, 461, 484, 378, 437, 247, 380, 459, 488, 441, 351, 469, 438, 462, 251, 496, 467, 367, 442, 474, 483, 379, 415, 253, 444, 485, 470, 375, 473, 431, 486, 489, 254, 476, 439, 492, 381, 498, 445, 463, 490, 382, 471, 497, 443, 475, 500, 446, 487, 493, 477, 504, 478, 499, 255, 491, 502, 494, 505, 383, 501, 479, 506, 447, 508, 503, 495, 507, 509, 510, 511]
[0164] Таблица Q27, имеющая длину последовательности 512:
[0165] Последовательность Q28, имеющая длину последовательности 256:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 128, 9, 33, 17, 10, 36, 66, 24, 20, 65, 34, 7, 129, 40, 11, 72, 132, 19, 48, 68, 13, 14, 21, 130, 26, 80, 35, 38, 136, 96, 22, 37, 25, 67, 41, 144, 28, 69, 49, 74, 160, 42, 134, 70, 44, 81, 15, 50, 131, 192, 73, 23, 137, 52, 76, 133, 82, 27, 97, 39, 56, 138, 84, 29, 145, 43, 98, 140, 30, 88, 146, 100, 161, 71, 45, 51, 148, 46, 75, 104, 164, 193, 53, 162, 77, 152, 54, 85, 112, 57, 78, 135, 194, 83, 168, 86, 58, 139, 196, 101, 60, 147, 176, 99, 89, 141, 200, 90, 31, 142, 102, 47, 105, 208, 153, 92, 149, 163, 113, 150, 165, 55, 106, 154, 79, 108, 224, 166, 59, 169, 114, 195, 87, 156, 116, 197, 61, 177, 170, 91, 201, 198, 62, 143, 172, 103, 120, 178, 202, 93, 107, 151, 209, 180, 94, 204, 155, 109, 210, 184, 225, 167, 115, 110, 212, 117, 157, 226, 171, 216, 121, 158, 118, 173, 179, 199, 228, 122, 181, 232, 174, 63, 203, 124, 182, 240, 211, 205, 95, 185, 213, 206, 186, 111, 227, 159, 214, 119, 217, 188, 229, 218, 123, 230, 175, 241, 220, 183, 233, 125, 234, 187, 207, 236, 126, 242, 215, 189, 244, 219, 231, 248, 190, 221, 235, 222, 237, 243, 238, 245, 127, 246, 249, 250, 191, 252, 223, 239, 247, 251, 253, 254, 255]
[0166] Таблица Q28, имеющая длину последовательности 256:
[0167] Последовательность Q29, имеющая длину последовательности 128:
[0, 1, 4, 8, 2, 16, 32, 6, 64, 3, 12, 5, 18, 9, 33, 17, 10, 36, 66, 24, 20, 65, 34, 7, 40, 11, 72, 19, 48, 68, 13, 14, 21, 26, 80, 35, 38, 96, 22, 37, 25, 67, 41, 28, 69, 49, 74, 42, 70, 44, 81, 15, 50, 73, 23, 52, 76, 82, 27, 97, 39, 56, 84, 29, 43, 98, 30, 88, 100, 71, 45, 51, 46, 75, 104, 53, 77, 54, 85, 112, 57, 78, 83, 86, 58, 101, 60, 99, 89, 90, 31, 102, 47, 105, 92, 113, 55, 106, 79, 108, 59, 114, 87, 116, 61, 91, 62, 103, 120, 93, 107, 94, 109, 115, 110, 117, 121, 118, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127]
[0168] Таблица Q29, имеющая длину последовательности 128:
[0169] Последовательность Q30, имеющая длину последовательности 64:
[0, 1, 4, 8, 2, 16, 32, 6, 3, 12, 5, 18, 9, 33, 17, 10, 36, 24, 20, 34, 7, 40, 11, 19, 48, 13, 14, 21, 26, 35, 38, 22, 37, 25, 41, 28, 49, 42, 44, 15, 50, 23, 52, 27, 39, 56, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63]
[0170] Таблица Q30, имеющая длину последовательности 64:
[0171] Последовательность Z26, имеющая длину последовательности 1024:
[0, 1, 4, 10, 2, 12, 7, 26, 3, 15, 18, 29, 11, 36, 38, 69, 5, 17, 13, 33, 23, 39, 48, 74, 21, 51, 41, 82, 56, 90, 99, 161, 6, 16, 25, 43, 19, 50, 45, 85, 28, 54, 62, 93, 66, 107, 113, 166, 34, 59, 70, 109, 77, 118, 125, 183, 87, 131, 142, 197, 148, 216, 225, 327, 8, 24, 20, 52, 35, 57, 65, 106, 30, 73, 60, 114, 79, 123, 132, 192, 42, 67, 81, 136, 89, 126, 140, 205, 100, 153, 159, 220, 173, 243, 253, 350, 47, 83, 96, 152, 103, 146, 163, 231, 115, 168, 185, 245, 193, 261, 275, 367, 129, 179, 199, 271, 208, 280, 302, 385, 233, 295, 318, 404, 335, 430, 459, 580, 14, 27, 40, 71, 31, 80, 64, 133, 46, 76, 88, 143, 97, 156, 162, 226, 55, 91, 101, 149, 110, 174, 180, 246, 124, 172, 190, 258, 207, 283, 298, 375, 61, 105, 119, 177, 116, 182, 195, 268, 138, 198, 218, 286, 229, 303, 324, 407, 150, 217, 238, 306, 250, 319, 338, 424, 265, 353, 364, 440, 388, 479, 503, 612, 72, 117, 135, 200, 145, 214, 223, 308, 158, 222, 239, 328, 254, 348, 363, 449, 170, 247, 264, 342, 278, 355, 380, 466, 293, 387, 400, 485, 417, 513, 529, 637, 194, 266, 285, 372, 315, 390, 405, 497, 321, 426, 435, 521, 451, 541, 556, 658, 341, 412, 460, 546, 481, 565, 582, 672, 499, 589, 608, 697, 627, 726, 756, 852, 22, 37, 44, 84, 58, 92, 102, 164, 53, 98, 111, 175, 122, 188, 203, 279, 68, 108, 130, 186, 139, 204, 213, 299, 151, 221, 235, 311, 249, 336, 344, 431, 78, 128, 137, 212, 155, 234, 227, 322, 169, 242, 255, 339, 269, 366, 369, 470, 184, 260, 282, 358, 292, 379, 395, 487, 312, 410, 422, 507, 437, 531, 550, 653, 94, 157, 144, 241, 178, 262, 257, 359, 202, 273, 287, 383, 300, 392, 415, 512, 211, 289, 305, 397, 333, 419, 446, 523, 345, 438, 455, 544, 478, 571, 587, 686, 237, 309, 330, 428, 361, 462, 472, 558, 371, 457, 489, 576, 509, 596, 620, 707, 402, 501, 517, 610, 537, 632, 600, 739, 552, 647, 666, 719, 674, 771, 791, 882, 121, 189, 167, 272, 209, 290, 296, 409, 230, 317, 325, 433, 347, 447, 468, 562, 251, 332, 356, 444, 377, 464, 493, 578, 393, 505, 483, 594, 525, 617, 629, 722, 276, 374, 351, 474, 398, 495, 511, 603, 421, 519, 535, 640, 554, 624, 655, 746, 453, 539, 567, 650, 584, 669, 692, 764, 598, 683, 710, 804, 729, 779, 817, 911, 314, 382, 414, 515, 442, 533, 548, 645, 476, 569, 560, 677, 591, 661, 694, 783, 491, 573, 605, 704, 622, 689, 736, 795, 642, 742, 713, 808, 760, 832, 842, 896, 527, 615, 634, 716, 663, 732, 749, 822, 680, 753, 787, 858, 768, 827, 869, 937, 700, 800, 775, 847, 813, 889, 864, 928, 836, 876, 903, 948, 919, 960, 974, 992, 9, 32, 75, 120, 49, 134, 104, 210, 63, 154, 171, 224, 127, 248, 256, 349, 86, 165, 141, 236, 196, 259, 291, 362, 187, 297, 267, 381, 313, 399, 418, 532, 95, 160, 206, 274, 176, 294, 281, 389, 219, 307, 331, 406, 340, 434, 445, 540, 240, 323, 352, 439, 368, 456, 469, 566, 391, 480, 498, 586, 508, 613, 625, 737, 112, 201, 181, 301, 244, 316, 337, 432, 228, 360, 326, 448, 373, 465, 482, 579, 270, 343, 378, 488, 396, 471, 496, 599, 420, 520, 530, 618, 551, 648, 659, 758, 288, 384, 411, 518, 427, 506, 536, 633, 450, 543, 570, 649, 581, 668, 684, 773, 475, 561, 590, 679, 602, 690, 712, 788, 635, 705, 728, 802, 744, 821, 841, 914, 147, 215, 263, 354, 232, 376, 334, 484, 284, 365, 394, 500, 413, 524, 534, 626, 310, 401, 423, 510, 441, 553, 563, 651, 467, 549, 577, 665, 601, 693, 708, 780, 329, 429, 458, 557, 452, 564, 585, 676, 492, 588, 616, 696, 630, 714, 734, 805, 514, 614, 641, 717, 656, 730, 747, 818, 673, 761, 770, 829, 790, 855, 870, 930, 357, 454, 486, 592, 504, 611, 623, 718, 528, 621, 643, 738, 660, 757, 769, 835, 547, 652, 671, 751, 687, 762, 784, 846, 703, 789, 799, 859, 812, 877, 886, 941, 583, 675, 695, 777, 725, 792, 803, 866, 731, 819, 825, 881, 837, 893, 901, 950, 750, 809, 843, 895, 856, 906, 915, 955, 867, 918, 927, 965, 936, 975, 984, 1007, 191, 252, 277, 386, 320, 403, 425, 538, 304, 416, 443, 555, 463, 574, 595, 688, 346, 436, 477, 572, 494, 597, 609, 709, 516, 619, 638, 721, 654, 745, 752, 823, 370, 473, 490, 607, 522, 636, 628, 733, 545, 646, 662, 748, 678, 772, 774, 849, 568, 667, 691, 765, 702, 782, 796, 860, 723, 807, 816, 872, 826, 887, 898, 947, 408, 526, 502, 644, 559, 670, 664, 766, 593, 682, 698, 786, 711, 793, 811, 875, 606, 699, 715, 797, 743, 814, 833, 883, 754, 828, 839, 894, 854, 909, 917, 961, 639, 720, 740, 820, 767, 844, 850, 902, 776, 840, 861, 912, 873, 922, 933, 968, 801, 868, 879, 929, 891, 939, 924, 979, 899, 945, 953, 972, 956, 988, 994, 1012, 461, 575, 542, 681, 604, 701, 706, 806, 631, 727, 735, 824, 755, 834, 848, 905, 657, 741, 763, 831, 781, 845, 863, 913, 794, 871, 857, 921, 884, 932, 938, 973, 685, 778, 759, 851, 798, 865, 874, 925, 815, 880, 890, 942, 900, 935, 949, 981, 838, 892, 907, 946, 916, 954, 963, 986, 923, 959, 969, 997, 976, 990, 1000, 1016, 724, 785, 810, 878, 830, 888, 897, 944, 853, 908, 904, 957, 920, 951, 964, 991, 862, 910, 926, 967, 934, 962, 978, 995, 943, 980, 970, 998, 985, 1003, 1005, 1014, 885, 931, 940, 971, 952, 977, 982, 1001, 958, 983, 993, 1008, 987, 1002, 1010, 1019, 966, 996, 989, 1006, 999, 1013, 1009, 1018, 1004, 1011, 1015, 1020, 1017, 1021, 1022, 1023]
[0172] Таблица Z26, имеющая длину последовательности 1024:
[0173] Последовательность Z27, имеющая длину последовательности 512:
[0, 1, 4, 9, 2, 11, 7, 25, 3, 14, 17, 28, 10, 34, 36, 65, 5, 16, 12, 31, 22, 37, 46, 70, 20, 48, 39, 77, 53, 84, 92, 145, 6, 15, 24, 41, 18, 47, 43, 80, 27, 51, 59, 87, 62, 99, 104, 149, 32, 56, 66, 101, 72, 109, 115, 163, 81, 120, 129, 174, 134, 189, 196, 269, 8, 23, 19, 49, 33, 54, 61, 98, 29, 69, 57, 105, 74, 113, 121, 170, 40, 63, 76, 124, 83, 116, 128, 181, 93, 139, 144, 192, 155, 210, 217, 284, 45, 78, 89, 138, 96, 133, 147, 201, 106, 151, 165, 211, 171, 223, 233, 295, 118, 160, 176, 230, 183, 237, 252, 306, 202, 247, 263, 317, 274, 332, 348, 409, 13, 26, 38, 67, 30, 75, 60, 122, 44, 71, 82, 130, 90, 141, 146, 197, 52, 85, 94, 135, 102, 156, 161, 212, 114, 154, 169, 221, 182, 239, 249, 300, 58, 97, 110, 158, 107, 162, 173, 228, 126, 175, 191, 241, 199, 253, 267, 319, 136, 190, 206, 255, 215, 264, 276, 329, 226, 286, 293, 338, 308, 359, 371, 423, 68, 108, 123, 177, 132, 188, 195, 256, 143, 194, 207, 270, 218, 283, 292, 343, 153, 213, 225, 279, 235, 287, 303, 352, 246, 307, 315, 362, 325, 377, 385, 433, 172, 227, 240, 298, 261, 309, 318, 368, 265, 330, 335, 381, 344, 391, 398, 441, 278, 322, 349, 393, 360, 402, 410, 446, 369, 413, 421, 455, 429, 464, 473, 495, 21, 35, 42, 79, 55, 86, 95, 148, 50, 91, 103, 157, 112, 167, 179, 236, 64, 100, 119, 166, 127, 180, 187, 250, 137, 193, 204, 258, 214, 275, 280, 333, 73, 117, 125, 186, 140, 203, 198, 266, 152, 209, 219, 277, 229, 294, 296, 354, 164, 222, 238, 289, 245, 302, 312, 363, 259, 321, 328, 373, 336, 386, 395, 439, 88, 142, 131, 208, 159, 224, 220, 290, 178, 232, 242, 305, 251, 310, 324, 376, 185, 243, 254, 313, 273, 326, 341, 382, 281, 337, 346, 392, 358, 405, 412, 451, 205, 257, 271, 331, 291, 350, 355, 399, 297, 347, 364, 407, 374, 416, 426, 458, 316, 370, 379, 422, 389, 431, 418, 468, 396, 437, 444, 462, 447, 477, 482, 500, 111, 168, 150, 231, 184, 244, 248, 320, 200, 262, 268, 334, 282, 342, 353, 401, 216, 272, 288, 340, 301, 351, 366, 408, 311, 372, 361, 415, 383, 425, 430, 463, 234, 299, 285, 356, 314, 367, 375, 419, 327, 380, 388, 434, 397, 428, 440, 470, 345, 390, 403, 438, 411, 445, 453, 475, 417, 450, 459, 485, 465, 479, 488, 504, 260, 304, 323, 378, 339, 387, 394, 436, 357, 404, 400, 448, 414, 442, 454, 480, 365, 406, 420, 457, 427, 452, 467, 483, 435, 469, 460, 486, 474, 491, 493, 502, 384, 424, 432, 461, 443, 466, 471, 489, 449, 472, 481, 496, 476, 490, 498, 507, 456, 484, 478, 494, 487, 501, 497, 506, 492, 499, 503, 508, 505, 509, 510, 511]
[0174] Таблица Z27, имеющая длину последовательности 512:
[0175] Последовательность Z28, имеющая длину последовательности 256:
[0, 1, 4, 9, 2, 11, 7, 24, 3, 14, 17, 27, 10, 33, 34, 59, 5, 16, 12, 30, 21, 35, 43, 64, 20, 45, 37, 70, 49, 76, 81, 121, 6, 15, 23, 39, 18, 44, 40, 72, 26, 47, 54, 78, 57, 87, 90, 124, 31, 51, 60, 88, 66, 95, 99, 134, 73, 102, 109, 141, 113, 149, 155, 194, 8, 22, 19, 46, 32, 50, 56, 86, 28, 63, 52, 91, 67, 97, 103, 137, 38, 58, 69, 106, 75, 100, 108, 145, 82, 117, 120, 152, 128, 162, 167, 201, 42, 71, 79, 116, 84, 112, 123, 158, 92, 125, 135, 163, 138, 170, 176, 206, 101, 131, 143, 175, 147, 178, 185, 210, 159, 183, 190, 215, 196, 222, 227, 243, 13, 25, 36, 61, 29, 68, 55, 104, 41, 65, 74, 110, 80, 118, 122, 156, 48, 77, 83, 114, 89, 129, 132, 164, 98, 127, 136, 169, 146, 179, 184, 208, 53, 85, 96, 130, 93, 133, 140, 174, 107, 142, 151, 181, 157, 186, 193, 217, 115, 150, 160, 187, 166, 191, 197, 220, 172, 202, 205, 224, 212, 230, 235, 247, 62, 94, 105, 144, 111, 148, 154, 188, 119, 153, 161, 195, 168, 200, 204, 225, 126, 165, 171, 199, 177, 203, 209, 229, 182, 211, 214, 232, 219, 236, 238, 249, 139, 173, 180, 207, 189, 213, 216, 233, 192, 221, 223, 237, 226, 239, 241, 250, 198, 218, 228, 240, 231, 242, 244, 251, 234, 245, 246, 252, 248, 253, 254, 255]
[0176] Таблица Z28, имеющая длину последовательности 256:
[0177] Последовательность Z29, имеющая длину последовательности 128:
[0, 1, 4, 9, 2, 11, 7, 23, 3, 13, 16, 25, 10, 30, 31, 51, 5, 15, 12, 27, 20, 32, 38, 54, 19, 40, 33, 58, 43, 63, 66, 90, 6, 14, 22, 35, 17, 39, 36, 60, 24, 42, 47, 64, 49, 70, 72, 92, 28, 45, 52, 71, 55, 75, 77, 96, 61, 80, 84, 100, 86, 104, 106, 119, 8, 21, 18, 41, 29, 44, 48, 69, 26, 53, 46, 73, 56, 76, 81, 98, 34, 50, 57, 82, 62, 78, 83, 102, 67, 88, 89, 105, 94, 109, 111, 121, 37, 59, 65, 87, 68, 85, 91, 107, 74, 93, 97, 110, 99, 112, 114, 122, 79, 95, 101, 113, 103, 115, 117, 123, 108, 116, 118, 124, 120, 125, 126, 127]
[0178] Таблица Z29, имеющая длину последовательности 128:
[0179] Последовательность Z30, имеющая длину последовательности 64:
[0, 1, 4, 8, 2, 10, 7, 20, 3, 12, 15, 22, 9, 25, 26, 39, 5, 14, 11, 23, 18, 27, 31, 41, 17, 33, 28, 43, 35, 46, 48, 57, 6, 13, 19, 29, 16, 32, 30, 44, 21, 34, 37, 47, 38, 49, 51, 58, 24, 36, 40, 50, 42, 52, 53, 59, 45, 54, 55, 60, 56, 61, 62, 63]
[0180] Таблица Z30, имеющая длину последовательности 64:
[0181] Следует отметить, что, приведенные выше последовательности являются лишь некоторыми примерами. Использование приведенных выше последовательностей в процессе кодирования полярным кодом помогает улучшить эффективность кодирования/декодирования полярным кодом. В любой из описанных последовательностей, корректировки или эквивалентные замены в следующих аспектах могут быть внесены без влияния на общий результат.
[0182] 1. Позиции небольшого количества элементов в последовательности взаимозаменяются. Например, позиция порядкового номера может быть отрегулирована в пределах заданного диапазона. Например, указанный диапазон составляет 5, и позиция элемента, порядковый номер которого составляет 10, может быть отрегулирована в пределах пяти позиций влево или вправо.
[0183] 2. Некоторые элементы последовательности регулируются, но наборы каналов для передачи T информационных битов, которые выбраны на основе последовательности являются последовательными или аналогичными.
[0184] 3. Последовательность включает в себя N элементов, начиная с 0 и заканчивая N–1, и N элементов, начиная с 0 и заканчивая N–1 представляют собой порядковые номера N поляризованных каналов. На самом деле, порядковые номера N поляризованных каналов могут также начинаться с 1 и заканчиваться на N. Это может быть достигнуто путем добавления 1 к каждому порядковому номеру в приведенной выше последовательности, и это также является формой порядкового номера в вышеупомянутых способах вычисления. Конечно, порядковый номер или идентификатор вышеупомянутого поляризованного канала может быть представлен с помощью другого способа. Конкретный способ представления не влияет на конкретную позицию поляризованного канала в последовательности;
[0185] 4. Порядковые номера N поляризованных каналов в вышеупомянутой последовательности расположены в порядке возрастания надежности N поляризованных каналов. В этом случае выбор K поляризованных каналов в порядке убывания надежности является выбором поляризованных каналов, которые соответствуют последним K порядковым номерам в любой из вышеупомянутых последовательностей. На самом деле, порядковые номера N поляризованных каналов также могут быть расположены в порядке убывания надежности N поляризованных каналов. Это может быть достигнуто путем расположения элементов в вышеупомянутой последовательности в обратном или реверсном порядке. В этом случае выбор K поляризованных каналов в порядке убывания надежности является выбором поляризованных каналов, которые соответствуют первым K порядковым номерам; и
[0186] 5. Вышеупомянутые последовательности могут далее представляться с помощью нормированной надежности или эквивалентной надежности каждого канала. Например, если последовательная позиция канала x в вышеупомянутой последовательности представляет собой n (крайняя левая позиция обозначается как 1), надежность канала может быть представлена как n или нормированная n/N, где N является длиной последовательности.
[0187] Основываясь на той же концепции изобретения способа кодирования полярным кодом, показанного на Фиг.2, как показано на Фиг.3, один вариант осуществления настоящей заявки дополнительно обеспечивает устройство 300 кодирования полярным кодом. Устройство 300 кодирования полярным кодом выполнено с возможностью осуществления способа кодирования полярным кодом, показанного на Фиг.2. Часть или весь способ кодирования полярным кодом, показанный на Фиг.3, может быть реализован с помощью аппаратного обеспечения или может быть реализован с помощью программного обеспечения. Когда часть или весь способ кодирования полярным кодом реализуется с помощью аппаратного обеспечения, устройство 300 кодирования полярным кодом включает в себя: схему 301 интерфейса ввода, выполненную с возможностью получения подлежащих кодированию битов; логическую схему 302, выполненную с возможностью осуществления способа кодирования полярным кодом, показанного на Фиг.2, причем для получения подробной информации, необходимо обратиться к описанию в вышеупомянутых вариантах осуществления способа, и подробности не описаны здесь повторно; и схему 303 интерфейса вывода, выполненную с возможностью вывода битовой последовательности после кодирования.
[0188] Кроме того, битовая последовательность, полученная после кодирования и выводимая из устройства 300 кодирования, выводится в приемопередатчик 320 после модуляции модулятором 310. Приемопередатчик 320 выполняет соответствующую обработку (включающую в себя, но не ограничивающуюся этим, такую обработку, как цифро-аналоговое преобразование и/или частотное преобразование) над модулированной последовательностью и отправляет обработанную последовательность с помощью антенны 330.
[0189] В необязательном порядке, устройство 300 кодирования полярным кодом может быть микросхемой или интегральной схемой в конкретном варианте реализации.
[0190] В необязательном порядке, когда часть или весь способ кодирования полярным кодом в вышеупомянутом варианте осуществления реализуется с использованием программного обеспечения, как показано на Фиг.4, устройство 300 кодирования полярным кодом включает в себя: память 401, выполненную с возможностью хранения программы; процессор 402, выполненный с возможностью выполнения программы, хранящейся в памяти 401. Когда программа исполняется, устройству 300 кодирования полярным кодом предписывается реализовывать способ кодирования полярным кодом, предоставленный в варианте осуществления на Фиг.2.
[0191] В необязательном порядке, память 401 может быть физически независимым блоком. В качестве альтернативы, как показано на Фиг.5, память 501 интегрирована с процессором 502.
[0192] В необязательном порядке, когда часть или весь способ кодирования в варианте осуществления на Фиг.2 реализуется с использованием программного обеспечения, устройство 300 передачи полярного кода может включать в себя только процессор 402. Память 401, выполненная с возможностью хранения программы, расположена вне устройства 300 передачи полярного кода. Процессор 402 соединен с памятью 401 с помощью схемы/проводников и выполнен с возможностью считывания и исполнения программы, хранящейся в памяти 401.
[0193] Процессор 402 может быть центральным блоком обработки (central processing unit, CPU), сетевым процессором (network processor, NP) или сочетанием CPU и NP.
[0194] Процессор 402 может дополнительно включать в себя аппаратную микросхему. Вышеупомянутая аппаратная микросхема может быть специализированной интегральной схемой (application-specific integrated circuit, ASIC), программируемым логическим устройством (programmable logic device, PLD) или сочетанием ASIC и PLD. Вышеупомянутое PLD может представлять собой комплексное программируемое логическое устройство (complex programmable logic device, CPLD), полевую программируемую вентильную матрицу (field-programmable gate array, FPGA), типовую матричную логику (generic array logic, GAL) или любое их сочетание.
[0195] Память в вышеупомянутом варианте осуществления может включать в себя энергозависимую (недолговременную) память (volatile memory), например, запоминающее устройство с произвольным доступом (random-access memory, RAM). Альтернативно, память может включать в себя энергонезависимую (долговременную) память (non-volatile memory), например, флэш–память (flash memory), накопитель на жестком диске (hard disk drive, HDD) или твердотельный накопитель (solid-state drive, SSD). Альтернативно, память может включать в себя комбинацию вышеупомянутых типов памяти.
[0196] На основании способа кодирования полярным кодом, показанного на Фиг.2, как показано на Фиг.6, вариант осуществления настоящей заявки дополнительно предоставляет устройство 300 кодирования полярным кодом. Устройство 300 кодирования полярным кодом выполнено с возможностью осуществления способа кодирования полярным кодом, показанного на Фиг.2. Устройство 300 кодирования полярным кодом включает в себя:
блок 601 получения, выполненный с возможностью получения первой последовательности, используемой для кодирования K подлежащих кодированию битов, при этом первая последовательность включает в себя порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, K является положительным целым числом, N является базовой кодовой длиной полярного кода, N является положительной целочисленной степенью 2, и K≤N;
блок 602 выбора, выполненный с возможностью выбора порядковых номеров K поляризованных каналов из первой последовательности в порядке возрастания надежности; и
блок 603 кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом над подлежащими кодированию битами.
[0197] Первая последовательность может быть любой из последовательностей, описанных выше, или может быть последовательностью, полученной путем выбора, из второй последовательности, имеющей длину Nmax, порядковых номеров (начиная с 0), меньших N. Вторая последовательность может быть любой из последовательностей, описанных выше. Надежность i–го поляризованного канала в N поляризованных каналах может быть определена с использованием любой из формул, описанных выше.
[0198] Один вариант осуществления настоящей заявки дополнительно предоставляет компьютерный носитель данных, хранящий компьютерную программу. Компьютерная программа приспособлена для выполнения способа кодирования полярным кодом, показанного на Фиг.2.
[0199] Один вариант осуществления настоящей заявки дополнительно предоставляет компьютерный программный продукт, включающий в себя инструкцию. При исполнении на компьютере инструкция предписывает компьютеру выполнять способ кодирования полярным кодом, показанный на Фиг.2.
[0200] Специалистам в данной области техники должно быть понятно, что варианты осуществления настоящей заявки могут быть предоставлены как способ, система или компьютерный программный продукт. Следовательно, настоящая заявка может использовать форму вариантов осуществления только аппаратных средств, вариантов осуществления только программных средств или вариантов осуществления с комбинацией программного обеспечения и аппаратных средств. Кроме того, настоящая заявка может использовать форму компьютерного программного продукта, который реализован на одном или более компьютерных носителях данных (включающих в себя, помимо прочего, дисковое запоминающее устройство, CD–ROM, оптическое запоминающее устройство и т.п.), которые включают в себя компьютерный программный код.
[0201] Настоящая заявка описана со ссылкой на блок–схемы последовательностей операций и/или блок–схемы способа, устройства (системы) и компьютерного программного продукта согласно вариантам воплощения настоящей заявки. Следует понимать, что инструкции компьютерной программы могут быть использованы для реализации каждого процесса и/или каждого блока в блок–схемах последовательностей операций и/или блок–схемах и комбинации процесса и/или блока в блок–схемах последовательностей операций и/или блок–схемах. Эти инструкции компьютерной программы могут предоставляться для компьютера общего назначение, компьютера специального назначения, встроенного процессора или процессора любого другого программируемого устройства обработки данных для генерации машины, так чтобы инструкции, выполняемые компьютером или процессором любого другого программируемого устройства обработки данных, генерировали устройство для реализации конкретной функции в одном или более процессах на блок–схемах последовательностей операций и/или в одном или более блоках на блок–схемах.
[0202] Эти инструкции компьютерной программы могут храниться в машиночитаемой памяти, которая может предписывать компьютеру или любому другому программируемому устройству обработки данных работать определенным образом, так что инструкции, хранящиеся в машиночитаемой памяти, генерируют средство, которое включает в себя устройство с инструкциями. Устройство с инструкциями реализует конкретную функцию в одном или более процессах на блок–схемах последовательностей операций и/или в одном или более блоках на блок–схемах.
[0203] Эти инструкции компьютерной программы могут быть загружены в компьютер или другое программируемое устройство обработки данных, так чтобы последовательность операций и этапов выполнялись на компьютере или другом программируемом устройстве, тем самым генерируя реализуемую компьютером обработку. Следовательно, инструкции, исполняемые на компьютере или другом программируемом устройстве, предоставляют этапы для реализации конкретной функции в одном или более процессах в блок–схемах последовательностей операций и/или в одном или более блоках на блок–схемах.
[0204] Несмотря на то, что были описаны некоторые предпочтительные варианты осуществления настоящей заявки, специалисты в данной области техники могут внести изменения и модификации в эти варианты осуществления, как только они изучат основную концепцию изобретения. Следовательно, нижеследующая формула изобретения предназначена толковаться как охватывающая предпочтительные варианты осуществления и все изменения и модификации, попадающие в объем данной заявки.
[0205] Очевидно, что специалисты в данной области техники могут внести различные модификации и изменения в варианты осуществления настоящей заявки, не отступая от сущности и объема вариантов осуществления настоящей заявки. Настоящая заявка предназначена для охвата этих модификаций и изменений при условии, что они попадают в объем охраны, определенный последующей формулой изобретения и ее эквивалентными технологиями.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПОЛЯРНОГО КОДИРОВАНИЯ | 2018 |
|
RU2760317C2 |
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ | 2018 |
|
RU2739582C1 |
| УСТРОЙСТВО КОДИРОВАНИЯ И СПОСОБ КОДИРОВАНИЯ ПОЛЯРНЫМ КОДОМ | 2014 |
|
RU2685034C2 |
| УСТРОЙСТВО СЕТИ МОБИЛЬНОЙ КОММУНИКАЦИИ | 2004 |
|
RU2292646C2 |
| МАШИНА ДЛЯ МЕХАНИЧЕСКОЙ ОБРАБОТКИ КОЖ | 1991 |
|
RU2019566C1 |
| Способ и устройство кодирования данных, носитель данных и процессор | 2018 |
|
RU2742912C1 |
| Полюсопереключаемая трехфазная двухслойная обмотка совмещенного типа | 1988 |
|
SU1674317A1 |
| КОЭФФИЦИЕНТЫ LDPC-СДВИГА ДЛЯ НОВОГО СТАНДАРТА РАДИОСВЯЗИ | 2018 |
|
RU2731883C1 |
| СПОСОБ ОЦЕНКИ ПЛЕМЕННЫХ КАЧЕСТВ СВИНЕЙ | 2008 |
|
RU2384058C2 |
| Двуслойная полюсопереключаемая трехфазная обмотка совмещенного типа | 1988 |
|
SU1585878A1 |
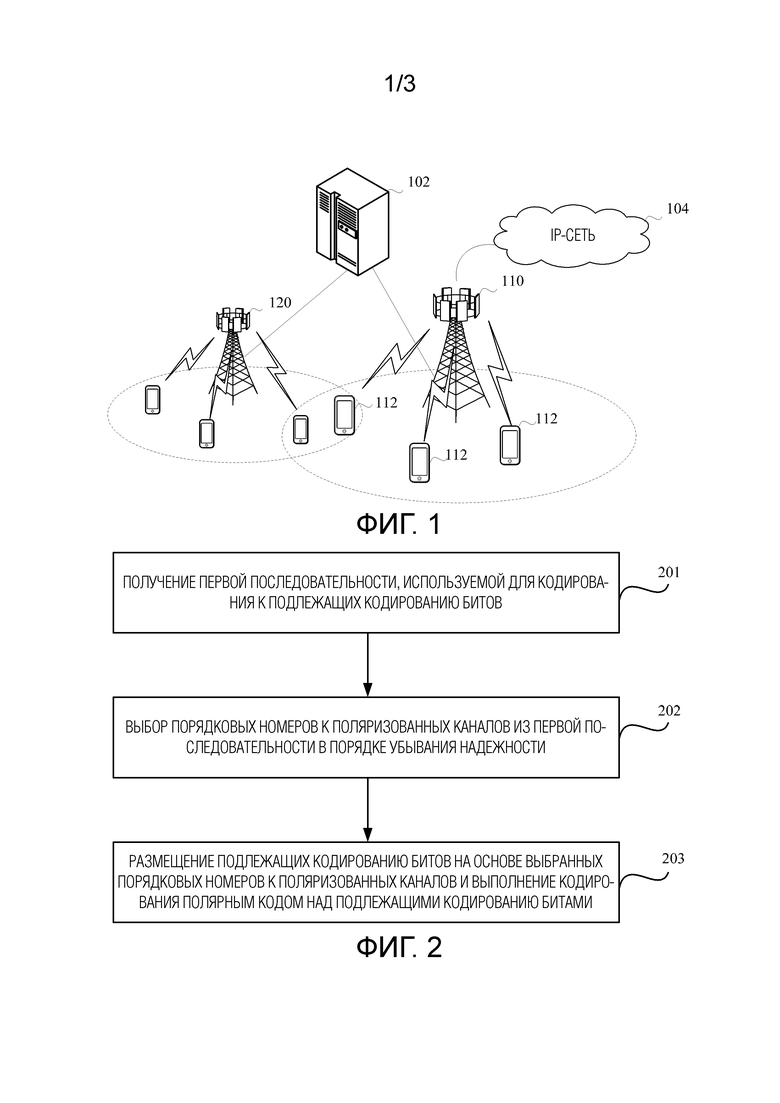

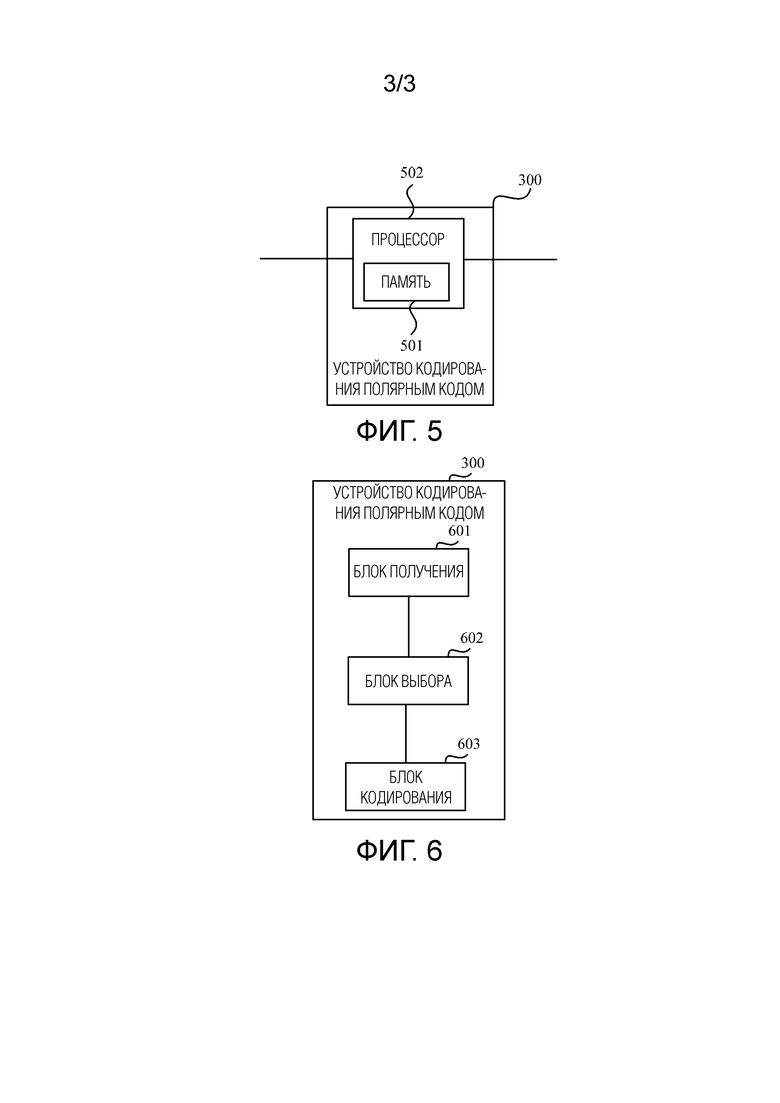
Изобретение относится к области технологий связи. Технический результат - повышение надежности передачи в поляризованных каналах при кодировании полярным кодом. Для этого предусмотрено получение первой последовательности для кодирования K подлежащих кодированию битов, которая включает в себя порядковые номера N поляризованных каналов, которые расположены в первой последовательности на основе надежности N поляризованных каналов, K является положительным целым числом, N является базовой кодовой длиной полярного кода, N является положительной целочисленной степенью 2, и K≤N; выбор порядковых номеров K поляризованных каналов из первой последовательности в порядке убывания надежности; и размещение подлежащих кодированию битов на основе выбранных порядковых номеров K поляризованных каналов и выполнение кодирования полярным кодом над подлежащими кодированию битами. 18 н. и 10 з.п. ф-лы, 6 ил., 60 табл.
1. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N; при этом первая последовательность является точно такой же, что и вторая последовательность, или первая последовательность является поднабором второй последовательности, вторая последовательность содержит порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, Nmax является положительным целым числом, N≤Nmax;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом Nmax=1024, вторая последовательность является Последовательностью Q11 или последовательностью, показанной в Таблице Q11;
при этом Последовательность Q11 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 260, 264, 38, 514, 96, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 192, 544, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 31, 200, 90, 545, 292, 322, 532, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 546, 324, 208, 386, 150, 153, 165, 106, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 59, 169, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 608, 352, 325, 533, 155, 210, 305, 547, 300, 109, 184, 534, 537, 115, 167, 225, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 776, 330, 226, 549, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 174, 554, 581, 393, 283, 122, 448, 353, 561, 203, 63, 340, 394, 527, 582, 556, 181, 295, 285, 232, 124, 205, 182, 643, 562, 286, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 568, 832, 588, 186, 646, 404, 227, 896, 594, 418, 302, 649, 771, 360, 539, 111, 331, 214, 309, 188, 449, 217, 408, 609, 596, 551, 650, 229, 159, 420, 310, 541, 773, 610, 657, 333, 119, 600, 339, 218, 368, 652, 230, 391, 313, 450, 542, 334, 233, 555, 774, 175, 123, 658, 612, 341, 777, 220, 314, 424, 395, 673, 583, 355, 287, 183, 234, 125, 557, 660, 616, 342, 316, 241, 778, 563, 345, 452, 397, 403, 207, 674, 558, 785, 432, 357, 187, 236, 664, 624, 587, 780, 705, 126, 242, 565, 398, 346, 456, 358, 405, 303, 569, 244, 595, 189, 566, 676, 361, 706, 589, 215, 786, 647, 348, 419, 406, 464, 680, 801, 362, 590, 409, 570, 788, 597, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 410, 231, 688, 653, 248, 369, 190, 364, 654, 659, 335, 480, 315, 221, 370, 613, 422, 425, 451, 614, 543, 235, 412, 343, 372, 775, 317, 222, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 591, 678, 434, 677, 349, 245, 458, 666, 620, 363, 127, 191, 782, 407, 436, 626, 571, 465, 681, 246, 707, 350, 599, 668, 790, 460, 249, 682, 573, 411, 803, 789, 709, 365, 440, 628, 689, 374, 423, 466, 793, 250, 371, 481, 574, 413, 603, 366, 468, 655, 900, 805, 615, 684, 710, 429, 794, 252, 373, 605, 848, 690, 713, 632, 482, 806, 427, 904, 414, 223, 663, 692, 835, 619, 472, 455, 796, 809, 714, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 435, 817, 319, 621, 812, 484, 430, 838, 667, 488, 239, 378, 459, 622, 627, 437, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 913, 798, 811, 379, 697, 431, 607, 489, 866, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 255, 964, 909, 719, 477, 915, 638, 748, 944, 869, 491, 699, 754, 858, 478, 968, 383, 910, 815, 976, 870, 917, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 922, 874, 918, 502, 933, 743, 760, 881, 494, 702, 921, 501, 876, 847, 992, 447, 733, 827, 934, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023];
при этом Таблица Q11 представляет собой следующее:
2. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N; при этом первая последовательность является точно такой же, что и вторая последовательность, или первая последовательность является поднабором второй последовательности, вторая последовательность содержит порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, Nmax является положительным целым числом, N≤Nmax;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом Nmax=512, вторая последовательность является Последовательностью Q12 или последовательностью, показанной в Таблице Q12;
при этом Последовательность Q12 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 260, 264, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 192, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 31, 200, 90, 292, 322, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 324, 208, 386, 150, 153, 165, 106, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 59, 169, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 448, 353, 203, 63, 340, 394, 181, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 360, 111, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 313, 450, 334, 233, 175, 123, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 316, 241, 345, 452, 397, 403, 207, 432, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 362, 409, 219, 311, 421, 410, 231, 248, 369, 190, 364, 335, 480, 315, 221, 370, 422, 425, 451, 235, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 245, 458, 363, 127, 191, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 223, 472, 455, 377, 435, 319, 484, 430, 488, 239, 378, 459, 437, 380, 461, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 255, 477, 491, 478, 383, 493, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511];
при этом Таблица Q12 представляет собой следующее:
3. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=1024, первая последовательность является последовательностью, показанной в Последовательности Q11 или в Таблице Q11;
при этом Последовательность Q11 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 260, 264, 38, 514, 96, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 192, 544, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 31, 200, 90, 545, 292, 322, 532, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 546, 324, 208, 386, 150, 153, 165, 106, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 59, 169, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 608, 352, 325, 533, 155, 210, 305, 547, 300, 109, 184, 534, 537, 115, 167, 225, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 776, 330, 226, 549, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 174, 554, 581, 393, 283, 122, 448, 353, 561, 203, 63, 340, 394, 527, 582, 556, 181, 295, 285, 232, 124, 205, 182, 643, 562, 286, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 568, 832, 588, 186, 646, 404, 227, 896, 594, 418, 302, 649, 771, 360, 539, 111, 331, 214, 309, 188, 449, 217, 408, 609, 596, 551, 650, 229, 159, 420, 310, 541, 773, 610, 657, 333, 119, 600, 339, 218, 368, 652, 230, 391, 313, 450, 542, 334, 233, 555, 774, 175, 123, 658, 612, 341, 777, 220, 314, 424, 395, 673, 583, 355, 287, 183, 234, 125, 557, 660, 616, 342, 316, 241, 778, 563, 345, 452, 397, 403, 207, 674, 558, 785, 432, 357, 187, 236, 664, 624, 587, 780, 705, 126, 242, 565, 398, 346, 456, 358, 405, 303, 569, 244, 595, 189, 566, 676, 361, 706, 589, 215, 786, 647, 348, 419, 406, 464, 680, 801, 362, 590, 409, 570, 788, 597, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 410, 231, 688, 653, 248, 369, 190, 364, 654, 659, 335, 480, 315, 221, 370, 613, 422, 425, 451, 614, 543, 235, 412, 343, 372, 775, 317, 222, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 591, 678, 434, 677, 349, 245, 458, 666, 620, 363, 127, 191, 782, 407, 436, 626, 571, 465, 681, 246, 707, 350, 599, 668, 790, 460, 249, 682, 573, 411, 803, 789, 709, 365, 440, 628, 689, 374, 423, 466, 793, 250, 371, 481, 574, 413, 603, 366, 468, 655, 900, 805, 615, 684, 710, 429, 794, 252, 373, 605, 848, 690, 713, 632, 482, 806, 427, 904, 414, 223, 663, 692, 835, 619, 472, 455, 796, 809, 714, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 435, 817, 319, 621, 812, 484, 430, 838, 667, 488, 239, 378, 459, 622, 627, 437, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 913, 798, 811, 379, 697, 431, 607, 489, 866, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 255, 964, 909, 719, 477, 915, 638, 748, 944, 869, 491, 699, 754, 858, 478, 968, 383, 910, 815, 976, 870, 917, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 922, 874, 918, 502, 933, 743, 760, 881, 494, 702, 921, 501, 876, 847, 992, 447, 733, 827, 934, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023];
при этом Таблица Q11 представляет собой следующее:
4. Способ кодирования, отличающийся тем, что содержит этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=512, первая последовательность является последовательностью, показанной в Последовательности Q12 или Таблице Q12;
при этом Последовательность Q12 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 260, 264, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 192, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 31, 200, 90, 292, 322, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 324, 208, 386, 150, 153, 165, 106, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 59, 169, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 448, 353, 203, 63, 340, 394, 181, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 360, 111, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 313, 450, 334, 233, 175, 123, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 316, 241, 345, 452, 397, 403, 207, 432, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 362, 409, 219, 311, 421, 410, 231, 248, 369, 190, 364, 335, 480, 315, 221, 370, 422, 425, 451, 235, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 245, 458, 363, 127, 191, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 223, 472, 455, 377, 435, 319, 484, 430, 488, 239, 378, 459, 437, 380, 461, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 255, 477, 491, 478, 383, 493, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511];
при этом Таблица Q12 представляет собой следующее:
5. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=256, первая последовательность является последовательностью, показанной в Последовательности Q13 или в Таблице Q13;
при этом Последовательность Q13 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 21, 132, 35, 26, 80, 37, 25, 22, 136, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 160, 192, 70, 44, 131, 81, 50, 73, 15, 133, 52, 23, 134, 76, 137, 82, 56, 27, 97, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 31, 200, 90, 149, 102, 105, 163, 92, 47, 208, 150, 153, 165, 106, 55, 113, 154, 79, 108, 224, 166, 195, 59, 169, 114, 156, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 107, 180, 151, 209, 94, 204, 155, 210, 109, 184, 115, 167, 225, 157, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 174, 122, 203, 63, 181, 232, 124, 205, 182, 211, 185, 240, 206, 95, 213, 186, 227, 111, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 244, 189, 215, 219, 231, 248, 190, 221, 235, 222, 237, 243, 238, 245, 127, 191, 246, 249, 250, 252, 223, 239, 251, 247, 253, 254, 255];
при этом Таблица Q13 представляет собой следующее:
6. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=128, первая последовательность является последовательностью, показанной в Последовательности Q14 или Таблице Q14;
при этом Последовательность Q14 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 12, 33, 65, 20, 34, 24, 36, 7, 66, 11, 40, 68, 19, 13, 48, 14, 72, 21, 35, 26, 80, 37, 25, 22, 38, 96, 67, 41, 28, 69, 42, 49, 74, 70, 44, 81, 50, 73, 15, 52, 23, 76, 82, 56, 27, 97, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 31, 90, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127];
при этом Таблица Q14 представляет собой следующее:
7. Способ кодирования, содержащий этапы, на которых:
получают первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом, и K≤N;
выбирают порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
размещают K подлежащих кодированию битов на основе выбранных порядковых номеров K поляризованных каналов; и
выполняют кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=64, первая последовательность является последовательностью, показанной в Последовательности Q15 или в Таблице Q15;
при этом Последовательность Q15 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 9, 6, 17, 10, 18, 12, 33, 20, 34, 24, 36, 7, 11, 40, 19, 13, 48, 14, 21, 35, 26, 37, 25, 22, 38, 41, 28, 42, 49, 44, 50, 15, 52, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63];
при этом Таблица Q15 представляет собой следующее:
8. Способ по п.1 или 2, в котором вторая последовательность является предварительно сохраненной.
9. Способ по любому одному из пп.1–7, в котором K подлежащих кодированию битов содержат бит проверки циклическим избыточным кодом.
10. Способ по любому одному из пп.1–7, в котором K подлежащих кодированию битов содержат бит проверки на четность.
11. Способ по любому одному из пп.1–7, в котором после выполнения кодирования полярным кодом в отношении подлежащих кодированию битов устройство кодирования выполняет на основе целевой кодовой длины согласование скорости в отношении последовательности, полученной после кодирования полярным кодом.
12. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N; при этом первая последовательность является точно такой же, что и вторая последовательность, или первая последовательность является поднабором второй последовательности, вторая последовательность содержит порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, Nmax является положительным целым числом, N≤Nmax;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом Nmax=1024, вторая последовательность является Последовательностью Q11 или последовательностью, показанной в Таблице Q11;
при этом Последовательность Q11 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 260, 264, 38, 514, 96, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 192, 544, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 31, 200, 90, 545, 292, 322, 532, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 546, 324, 208, 386, 150, 153, 165, 106, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 59, 169, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 608, 352, 325, 533, 155, 210, 305, 547, 300, 109, 184, 534, 537, 115, 167, 225, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 776, 330, 226, 549, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 174, 554, 581, 393, 283, 122, 448, 353, 561, 203, 63, 340, 394, 527, 582, 556, 181, 295, 285, 232, 124, 205, 182, 643, 562, 286, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 568, 832, 588, 186, 646, 404, 227, 896, 594, 418, 302, 649, 771, 360, 539, 111, 331, 214, 309, 188, 449, 217, 408, 609, 596, 551, 650, 229, 159, 420, 310, 541, 773, 610, 657, 333, 119, 600, 339, 218, 368, 652, 230, 391, 313, 450, 542, 334, 233, 555, 774, 175, 123, 658, 612, 341, 777, 220, 314, 424, 395, 673, 583, 355, 287, 183, 234, 125, 557, 660, 616, 342, 316, 241, 778, 563, 345, 452, 397, 403, 207, 674, 558, 785, 432, 357, 187, 236, 664, 624, 587, 780, 705, 126, 242, 565, 398, 346, 456, 358, 405, 303, 569, 244, 595, 189, 566, 676, 361, 706, 589, 215, 786, 647, 348, 419, 406, 464, 680, 801, 362, 590, 409, 570, 788, 597, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 410, 231, 688, 653, 248, 369, 190, 364, 654, 659, 335, 480, 315, 221, 370, 613, 422, 425, 451, 614, 543, 235, 412, 343, 372, 775, 317, 222, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 591, 678, 434, 677, 349, 245, 458, 666, 620, 363, 127, 191, 782, 407, 436, 626, 571, 465, 681, 246, 707, 350, 599, 668, 790, 460, 249, 682, 573, 411, 803, 789, 709, 365, 440, 628, 689, 374, 423, 466, 793, 250, 371, 481, 574, 413, 603, 366, 468, 655, 900, 805, 615, 684, 710, 429, 794, 252, 373, 605, 848, 690, 713, 632, 482, 806, 427, 904, 414, 223, 663, 692, 835, 619, 472, 455, 796, 809, 714, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 435, 817, 319, 621, 812, 484, 430, 838, 667, 488, 239, 378, 459, 622, 627, 437, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 913, 798, 811, 379, 697, 431, 607, 489, 866, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 255, 964, 909, 719, 477, 915, 638, 748, 944, 869, 491, 699, 754, 858, 478, 968, 383, 910, 815, 976, 870, 917, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 922, 874, 918, 502, 933, 743, 760, 881, 494, 702, 921, 501, 876, 847, 992, 447, 733, 827, 934, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023];
при этом Таблица Q11 представляет собой следующее:
13. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N; при этом первая последовательность является точно такой же, что и вторая последовательность, или первая последовательность является поднабором второй последовательности, вторая последовательность содержит порядковые номера Nmax поляризованных каналов, порядковые номера Nmax поляризованных каналов расположены во второй последовательности на основе надежности Nmax поляризованных каналов, Nmax является положительным целым числом, N≤Nmax;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом Nmax=512, вторая последовательность является Последовательностью Q12 или последовательностью, показанной в Таблице Q12;
при этом Последовательность Q12 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 260, 264, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 192, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 31, 200, 90, 292, 322, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 324, 208, 386, 150, 153, 165, 106, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 59, 169, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 448, 353, 203, 63, 340, 394, 181, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 360, 111, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 313, 450, 334, 233, 175, 123, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 316, 241, 345, 452, 397, 403, 207, 432, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 362, 409, 219, 311, 421, 410, 231, 248, 369, 190, 364, 335, 480, 315, 221, 370, 422, 425, 451, 235, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 245, 458, 363, 127, 191, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 223, 472, 455, 377, 435, 319, 484, 430, 488, 239, 378, 459, 437, 380, 461, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 255, 477, 491, 478, 383, 493, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511];
при этом Таблица Q12 представляет собой следующее:
14. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=1024, вторая последовательность является Последовательностью Q11 или последовательностью, показанной в Таблице Q11;
при этом Последовательность Q11 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 512, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 513, 80, 37, 25, 22, 136, 260, 264, 38, 514, 96, 67, 41, 144, 28, 69, 42, 516, 49, 74, 272, 160, 520, 288, 528, 192, 544, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 515, 88, 140, 30, 146, 71, 262, 265, 161, 576, 45, 100, 640, 51, 148, 46, 75, 266, 273, 517, 104, 162, 53, 193, 152, 77, 164, 768, 268, 274, 518, 54, 83, 57, 521, 112, 135, 78, 289, 194, 85, 276, 522, 58, 168, 139, 99, 86, 60, 280, 89, 290, 529, 524, 196, 141, 101, 147, 176, 142, 530, 321, 31, 200, 90, 545, 292, 322, 532, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 546, 324, 208, 386, 150, 153, 165, 106, 55, 328, 536, 577, 548, 113, 154, 79, 269, 108, 578, 224, 166, 519, 552, 195, 270, 641, 523, 275, 580, 291, 59, 169, 560, 114, 277, 156, 87, 197, 116, 170, 61, 531, 525, 642, 281, 278, 526, 177, 293, 388, 91, 584, 769, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 644, 202, 592, 323, 392, 297, 770, 107, 180, 151, 209, 284, 648, 94, 204, 298, 400, 608, 352, 325, 533, 155, 210, 305, 547, 300, 109, 184, 534, 537, 115, 167, 225, 326, 306, 772, 157, 656, 329, 110, 117, 212, 171, 776, 330, 226, 549, 538, 387, 308, 216, 416, 271, 279, 158, 337, 550, 672, 118, 332, 579, 540, 389, 173, 121, 553, 199, 784, 179, 228, 338, 312, 704, 390, 174, 554, 581, 393, 283, 122, 448, 353, 561, 203, 63, 340, 394, 527, 582, 556, 181, 295, 285, 232, 124, 205, 182, 643, 562, 286, 585, 299, 354, 211, 401, 185, 396, 344, 586, 645, 593, 535, 240, 206, 95, 327, 564, 800, 402, 356, 307, 301, 417, 213, 568, 832, 588, 186, 646, 404, 227, 896, 594, 418, 302, 649, 771, 360, 539, 111, 331, 214, 309, 188, 449, 217, 408, 609, 596, 551, 650, 229, 159, 420, 310, 541, 773, 610, 657, 333, 119, 600, 339, 218, 368, 652, 230, 391, 313, 450, 542, 334, 233, 555, 774, 175, 123, 658, 612, 341, 777, 220, 314, 424, 395, 673, 583, 355, 287, 183, 234, 125, 557, 660, 616, 342, 316, 241, 778, 563, 345, 452, 397, 403, 207, 674, 558, 785, 432, 357, 187, 236, 664, 624, 587, 780, 705, 126, 242, 565, 398, 346, 456, 358, 405, 303, 569, 244, 595, 189, 566, 676, 361, 706, 589, 215, 786, 647, 348, 419, 406, 464, 680, 801, 362, 590, 409, 570, 788, 597, 572, 219, 311, 708, 598, 601, 651, 421, 792, 802, 611, 602, 410, 231, 688, 653, 248, 369, 190, 364, 654, 659, 335, 480, 315, 221, 370, 613, 422, 425, 451, 614, 543, 235, 412, 343, 372, 775, 317, 222, 426, 453, 237, 559, 833, 804, 712, 834, 661, 808, 779, 617, 604, 433, 720, 816, 836, 347, 897, 243, 662, 454, 318, 675, 618, 898, 781, 376, 428, 665, 736, 567, 840, 625, 238, 359, 457, 399, 787, 591, 678, 434, 677, 349, 245, 458, 666, 620, 363, 127, 191, 782, 407, 436, 626, 571, 465, 681, 246, 707, 350, 599, 668, 790, 460, 249, 682, 573, 411, 803, 789, 709, 365, 440, 628, 689, 374, 423, 466, 793, 250, 371, 481, 574, 413, 603, 366, 468, 655, 900, 805, 615, 684, 710, 429, 794, 252, 373, 605, 848, 690, 713, 632, 482, 806, 427, 904, 414, 223, 663, 692, 835, 619, 472, 455, 796, 809, 714, 721, 837, 716, 864, 810, 606, 912, 722, 696, 377, 435, 817, 319, 621, 812, 484, 430, 838, 667, 488, 239, 378, 459, 622, 627, 437, 380, 818, 461, 496, 669, 679, 724, 841, 629, 351, 467, 438, 737, 251, 462, 442, 441, 469, 247, 683, 842, 738, 899, 670, 783, 849, 820, 728, 928, 791, 367, 901, 630, 685, 844, 633, 711, 253, 691, 824, 902, 686, 740, 850, 375, 444, 470, 483, 415, 485, 905, 795, 473, 634, 744, 852, 960, 865, 693, 797, 906, 715, 807, 474, 636, 694, 254, 717, 575, 913, 798, 811, 379, 697, 431, 607, 489, 866, 723, 486, 908, 718, 813, 476, 856, 839, 725, 698, 914, 752, 868, 819, 814, 439, 929, 490, 623, 671, 739, 916, 463, 843, 381, 497, 930, 821, 726, 961, 872, 492, 631, 729, 700, 443, 741, 845, 920, 382, 822, 851, 730, 498, 880, 742, 445, 471, 635, 932, 687, 903, 825, 500, 846, 745, 826, 732, 446, 962, 936, 475, 853, 867, 637, 907, 487, 695, 746, 828, 753, 854, 857, 504, 799, 255, 964, 909, 719, 477, 915, 638, 748, 944, 869, 491, 699, 754, 858, 478, 968, 383, 910, 815, 976, 870, 917, 727, 493, 873, 701, 931, 756, 860, 499, 731, 823, 922, 874, 918, 502, 933, 743, 760, 881, 494, 702, 921, 501, 876, 847, 992, 447, 733, 827, 934, 882, 937, 963, 747, 505, 855, 924, 734, 829, 965, 938, 884, 506, 749, 945, 966, 755, 859, 940, 830, 911, 871, 639, 888, 479, 946, 750, 969, 508, 861, 757, 970, 919, 875, 862, 758, 948, 977, 923, 972, 761, 877, 952, 495, 703, 935, 978, 883, 762, 503, 925, 878, 735, 993, 885, 939, 994, 980, 926, 764, 941, 967, 886, 831, 947, 507, 889, 984, 751, 942, 996, 971, 890, 509, 949, 973, 1000, 892, 950, 863, 759, 1008, 510, 979, 953, 763, 974, 954, 879, 981, 982, 927, 995, 765, 956, 887, 985, 997, 986, 943, 891, 998, 766, 511, 988, 1001, 951, 1002, 893, 975, 894, 1009, 955, 1004, 1010, 957, 983, 958, 987, 1012, 999, 1016, 767, 989, 1003, 990, 1005, 959, 1011, 1013, 895, 1006, 1014, 1017, 1018, 991, 1020, 1007, 1015, 1019, 1021, 1022, 1023];
при этом Таблица Q11 представляет собой следующее:
15. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом над подлежащими кодированию битами;
при этом N=512, вторая последовательность является Последовательностью Q12 или последовательностью, показанной в Таблице Q12;
при этом Последовательность Q12 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 256, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 257, 21, 132, 35, 258, 26, 80, 37, 25, 22, 136, 260, 264, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 272, 160, 288, 192, 70, 44, 131, 81, 50, 73, 15, 320, 133, 52, 23, 134, 384, 76, 137, 82, 56, 27, 97, 39, 259, 84, 138, 145, 261, 29, 43, 98, 88, 140, 30, 146, 71, 262, 265, 161, 45, 100, 51, 148, 46, 75, 266, 273, 104, 162, 53, 193, 152, 77, 164, 268, 274, 54, 83, 57, 112, 135, 78, 289, 194, 85, 276, 58, 168, 139, 99, 86, 60, 280, 89, 290, 196, 141, 101, 147, 176, 142, 321, 31, 200, 90, 292, 322, 263, 149, 102, 105, 304, 296, 163, 92, 47, 267, 385, 324, 208, 386, 150, 153, 165, 106, 55, 328, 113, 154, 79, 269, 108, 224, 166, 195, 270, 275, 291, 59, 169, 114, 277, 156, 87, 197, 116, 170, 61, 281, 278, 177, 293, 388, 91, 198, 172, 120, 201, 336, 62, 282, 143, 103, 178, 294, 93, 202, 323, 392, 297, 107, 180, 151, 209, 284, 94, 204, 298, 400, 352, 325, 155, 210, 305, 300, 109, 184, 115, 167, 225, 326, 306, 157, 329, 110, 117, 212, 171, 330, 226, 387, 308, 216, 416, 271, 279, 158, 337, 118, 332, 389, 173, 121, 199, 179, 228, 338, 312, 390, 174, 393, 283, 122, 448, 353, 203, 63, 340, 394, 181, 295, 285, 232, 124, 205, 182, 286, 299, 354, 211, 401, 185, 396, 344, 240, 206, 95, 327, 402, 356, 307, 301, 417, 213, 186, 404, 227, 418, 302, 360, 111, 331, 214, 309, 188, 449, 217, 408, 229, 159, 420, 310, 333, 119, 339, 218, 368, 230, 391, 313, 450, 334, 233, 175, 123, 341, 220, 314, 424, 395, 355, 287, 183, 234, 125, 342, 316, 241, 345, 452, 397, 403, 207, 432, 357, 187, 236, 126, 242, 398, 346, 456, 358, 405, 303, 244, 189, 361, 215, 348, 419, 406, 464, 362, 409, 219, 311, 421, 410, 231, 248, 369, 190, 364, 335, 480, 315, 221, 370, 422, 425, 451, 235, 412, 343, 372, 317, 222, 426, 453, 237, 433, 347, 243, 454, 318, 376, 428, 238, 359, 457, 399, 434, 349, 245, 458, 363, 127, 191, 407, 436, 465, 246, 350, 460, 249, 411, 365, 440, 374, 423, 466, 250, 371, 481, 413, 366, 468, 429, 252, 373, 482, 427, 414, 223, 472, 455, 377, 435, 319, 484, 430, 488, 239, 378, 459, 437, 380, 461, 496, 351, 467, 438, 251, 462, 442, 441, 469, 247, 367, 253, 375, 444, 470, 483, 415, 485, 473, 474, 254, 379, 431, 489, 486, 476, 439, 490, 463, 381, 497, 492, 443, 382, 498, 445, 471, 500, 446, 475, 487, 504, 255, 477, 491, 478, 383, 493, 499, 502, 494, 501, 447, 505, 506, 479, 508, 495, 503, 507, 509, 510, 511];
при этом Таблица Q12 представляет собой следующее:
16. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=256, вторая последовательность является Последовательностью Q13 или последовательностью, показанной в Таблице Q13;
при этом Последовательность Q13 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 128, 12, 33, 65, 20, 34, 24, 36, 7, 129, 66, 11, 40, 68, 130, 19, 13, 48, 14, 72, 21, 132, 35, 26, 80, 37, 25, 22, 136, 38, 96, 67, 41, 144, 28, 69, 42, 49, 74, 160, 192, 70, 44, 131, 81, 50, 73, 15, 133, 52, 23, 134, 76, 137, 82, 56, 27, 97, 39, 84, 138, 145, 29, 43, 98, 88, 140, 30, 146, 71, 161, 45, 100, 51, 148, 46, 75, 104, 162, 53, 193, 152, 77, 164, 54, 83, 57, 112, 135, 78, 194, 85, 58, 168, 139, 99, 86, 60, 89, 196, 141, 101, 147, 176, 142, 31, 200, 90, 149, 102, 105, 163, 92, 47, 208, 150, 153, 165, 106, 55, 113, 154, 79, 108, 224, 166, 195, 59, 169, 114, 156, 87, 197, 116, 170, 61, 177, 91, 198, 172, 120, 201, 62, 143, 103, 178, 93, 202, 107, 180, 151, 209, 94, 204, 155, 210, 109, 184, 115, 167, 225, 157, 110, 117, 212, 171, 226, 216, 158, 118, 173, 121, 199, 179, 228, 174, 122, 203, 63, 181, 232, 124, 205, 182, 211, 185, 240, 206, 95, 213, 186, 227, 111, 214, 188, 217, 229, 159, 119, 218, 230, 233, 175, 123, 220, 183, 234, 125, 241, 207, 187, 236, 126, 242, 244, 189, 215, 219, 231, 248, 190, 221, 235, 222, 237, 243, 238, 245, 127, 191, 246, 249, 250, 252, 223, 239, 251, 247, 253, 254, 255];
при этом Таблица Q13 представляет собой следующее:
17. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом над подлежащими кодированию битами;
при этом N=128, вторая последовательность является Последовательностью Q14 или последовательностью, показанной в Таблице Q14;
при этом Последовательность Q14 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 64, 9, 6, 17, 10, 18, 12, 33, 65, 20, 34, 24, 36, 7, 66, 11, 40, 68, 19, 13, 48, 14, 72, 21, 35, 26, 80, 37, 25, 22, 38, 96, 67, 41, 28, 69, 42, 49, 74, 70, 44, 81, 50, 73, 15, 52, 23, 76, 82, 56, 27, 97, 39, 84, 29, 43, 98, 88, 30, 71, 45, 100, 51, 46, 75, 104, 53, 77, 54, 83, 57, 112, 78, 85, 58, 99, 86, 60, 89, 101, 31, 90, 102, 105, 92, 47, 106, 55, 113, 79, 108, 59, 114, 87, 116, 61, 91, 120, 62, 103, 93, 107, 94, 109, 115, 110, 117, 118, 121, 122, 63, 124, 95, 111, 119, 123, 125, 126, 127];
при этом Таблица Q14 представляет собой следующее:
18. Устройство кодирования, содержащее:
блок получения, выполненный с возможностью получать первую последовательность, используемую для кодирования K подлежащих кодированию битов, где K является положительным целым числом, причем первая последовательность содержит порядковые номера N поляризованных каналов, порядковые номера N поляризованных каналов расположены в первой последовательности на основе надежности N поляризованных каналов, N=2n, n является положительным целым числом и K≤N;
блок выбора, выполненный с возможностью выбирать порядковые номера K поляризованных каналов из первой последовательности на основе надежности; и
блок кодирования, выполненный с возможностью размещать подлежащие кодированию биты на основе выбранных порядковых номеров K поляризованных каналов и выполнять кодирование полярным кодом в отношении подлежащих кодированию битов;
при этом N=64, вторая последовательность является Последовательностью Q15 или последовательностью, показанной в Таблице Q15;
при этом Последовательность Q15 представляет собой следующее:
[0, 1, 2, 4, 8, 16, 32, 3, 5, 9, 6, 17, 10, 18, 12, 33, 20, 34, 24, 36, 7, 11, 40, 19, 13, 48, 14, 21, 35, 26, 37, 25, 22, 38, 41, 28, 42, 49, 44, 50, 15, 52, 23, 56, 27, 39, 29, 43, 30, 45, 51, 46, 53, 54, 57, 58, 60, 31, 47, 55, 59, 61, 62, 63];
при этом Таблица Q15 представляет собой следующее:
19. Устройство по п.12 или 13, при этом вторая последовательность является предварительно сохраненной.
20. Устройство по любому одному из пп.12–17, при этом K подлежащих кодированию битов содержат бит проверки циклическим избыточным кодом.
21. Устройство по любому одному из пп.12–17, при этом K подлежащих кодированию битов содержат бит проверки на четность.
22. Устройство по любому одному из пп.12–17, при этом после выполнения кодирования полярным кодом в отношении подлежащих кодированию битов, устройство кодирования выполняет на основе целевой кодовой длины согласование скорости в отношении последовательности, полученной после кодирования полярным кодом.
23. Устройство кодирования, содержащее:
процессор, выполненный с возможностью осуществлять способ по любому одному из пп.1-11.
24. Устройство по п.21, при этом устройство дополнительно содержит память, приспособленную для хранения программы, причем способ реализуется, когда программа исполняется процессором.
25. Устройство кодирования, содержащее:
схему интерфейса ввода, выполненную с возможностью получать подлежащие кодированию биты;
логическую схему, выполненную с возможностью осуществлять способ по любому одному из пп.1–11 на основе полученных подлежащих кодированию битов, для получения битовой последовательности; и
схему интерфейса вывода, выполненную с возможностью выводить битовую последовательность.
26. Беспроводное устройство, содержащее устройство кодирования по пп.12–22, модулятор и приемопередатчик, в котором
модулятор выполнен с возможностью модулировать битовую последовательность, полученную после полярно–полярного кодирования, для получения модулированной последовательности; и
приемопередатчик выполнен с возможностью передавать модулированную последовательность.
27. Устройство по п.26, при этом беспроводное устройство является терминалом или сетевым устройством.
28. Компьютерный носитель данных, при этом носитель данных хранит компьютерную программу, и компьютерная программа содержит инструкции, используемые для выполнения способа по любому одному из пп.1–11.
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ В СКРУЧЕННОМ ПОЛЯРНОМ КОДЕ | 2014 |
|
RU2571587C2 |
| CN 103746708 A, 23.04.2014 | |||
| CN 103023518 A, 03.04.2013 | |||
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| KR 20110060635 A, 08.06.2011. | |||
Авторы
Даты
2020-08-12—Публикация
2018-05-04—Подача