Область техники, к которой относится изобретение
Варианты осуществления настоящего изобретения относятся к области технологий связи и, в частности, к способу и устройству для полярного кодирования.
Уровень техники
В самой базовой технологии беспроводного доступа канальное кодирование играет решающую роль в обеспечении надежной передачи данных. В существующей системе беспроводной связи обычно осуществляется канальное кодирование с использованием турбо-кода, кода с малой плотностью проверок на четность (low density parity check, LDPC) и полярного (polar) кода. Турбо-код не может поддерживать передачу информации при слишком низкой или слишком высокой скорости передачи данных. Однако, для передачи среднего пакета или короткого пакета сложно получить требуемую производительность турбо-кода и LDPC кода, когда длины кодов ограничены из-за характеристик кодирования/декодирования турбо-кода и LDPC кода. С точки зрения реализации, турбо-код и LDPC код имеют относительно высокую сложность вычислений в процессе кодирования/декодирования. Теоретически доказано, что полярный код является подходящим кодом, который может достичь предела Шеннона, и имеет относительно низкую сложность кодирования/декодирования и, по этой причине, полярный код получает все более широкое применение.
Однако, с быстрым развитием системы беспроводной связи, перспективные системы связи, такие как системы связи пятого поколения (5th generation, 5G), имеют некоторые новые характеристики. Например, три наиболее типичные сценарии связи включают в себя усовершенствованную мобильной широкополосной связи (enhance mobile broadband, eMBB) интернет, массивной связи машинного типа (massive machine type communication, mMTC) и сверхнадежную связь с низкой задержкой (ultra reliable low latency communication, URLLC). Эти сценарии связи накладывают более высокое требование на производительность кодирования/декодирования полярного кода.
Порядок надежности поляризованных каналов играет важную роль в производительности кодирования/декодирования полярного кода. Тем не менее, в настоящее время не требуется точность порядка надежности поляризованных каналов. Следовательно, процесс реализации оказывает влияние на дополнительное повышение производительности кодирования/декодирования полярного кода.
Сущность изобретения
Варианты осуществления настоящего изобретения предоставляют способ и устройство для полярного кодирования для повышения точности порядка надежности поляризованных каналов.
В соответствии с первым аспектом предоставлен способ полярного кодирования. По меньшей мере, выбирают две последовательности с относительно хорошей производительностью на основании правила определения производительности. Определяют те же самые номера последовательности в одном и том же местоположении сортировки, по меньшей мере, в двух последовательностях. Определенные те же номера последовательности определены как номера последовательности, чья надежность остается неизменной в последовательности, и сортируют номера последовательности, чья надежность остается неизменной в последовательностях, на основании порядков номеров последовательности, по меньшей мере, в двух последовательностях. Сравнивают номера последовательности, по меньшей мере, в двух последовательностях, в отличных от определенных номеров последовательности, чья надежность остается неизменной, для выбора некоторых подпоследовательностей, и местоположения элементов в подпоследовательностях могут быть взаимно обменены. Используют последовательность сортировки, полученную из вышеизложенного, в качестве последовательности сортировки, используемой для полярного кодирования в этом варианте осуществления настоящего изобретения. Таким образом, для последовательности сортировки, полученной с помощью вышеописанного способа, может быть всесторонне рассмотрено множество последовательностей с относительно хорошей производительностью, и определяет номер последовательности, надежность которой остается неизменным, с использованием набора пересечений между различными последовательностями. Это помогает повысить точность порядка надежности поляризованных каналов и повысить производительность кодирования/декодирования полярного кода.
В возможной реализации, определяют последовательность, используемую для кодирования битов, подлежащих кодированию, где последовательность используют для представления порядка надежности N поляризованных каналов; и полярное кодирование выполняется на битах, подлежащих кодированию, с использованием последовательности для получения кодированных битов, где N является длиной материнского кода полярного кода, и N является положительным целым числом степени 2.
В возможной реализации, длина битов, подлежащих кодированию, равна К, К битов, подлежащих кодированию, отображают на К поляризованные каналы в N поляризованных каналах, и надежность K поляризованных каналов выше, чем надежность остальных N-K поляризованных каналов.
В одной из возможных реализаций, определяют последовательность, используемую для кодирования битов, подлежащих кодированию, на основании длины N и заданной последовательности.
В одном из возможных реализаций, последовательность, используемая для кодирования битов, подлежащих кодированию, является всеми или поднабором другой последовательности, другая последовательность включает в себя Nmax номера последовательности, Nmax номера последовательности организованы в другой последовательности на основании надежности Nmax поляризованных каналов, Nmax является положительным целым числом степени 2, и Nmax ≥ N.
В возможной реализации, последовательность удовлетворяет характеристикам вложенности, и характеристика вложенности представляет собой следующее: получают последовательность с относительно короткой длиной N2 материнского кода на основании последовательности с относительно большой длиной N1 материнского кода. Элементы, чьи номера последовательности меньше или равны N2, извлекают из последовательности с относительно большой длиной N1 материнского кода, и полученная подпоследовательность представляет собой последовательность с относительно короткой длиной N2 материнского кода. Порядок элементов в полученной последовательности с относительно короткой длиной N2 материнского кода является таким же, как порядок этих элементов в последовательности с относительно большой длиной N1 материнского кода.
В возможной реализации, Nmax является максимальной длиной материнского кода полярного кода, например, Nmax = 1024 или Nmax = 512. Последовательность должна удовлетворять характеристики вложенности. Когда определяют последовательность с максимальной длиной материнского кода, может быть получена другая последовательность с относительно короткой длиной материнского кода, на основании последовательности с максимальной длиной материнской кода. Например, определяют последовательность с длиной 1024, и чья максимальная длина материнского кода равна 1024. Извлекают элементы, чьи значения элемента меньше или равны 64, из последовательности с длиной 1024, чтобы сформировать подпоследовательность с длиной 64. Порядок элементов в полученной подпоследовательности с длиной 64 является таким же, как порядок этих элементов в последовательности с длиной 1024. То есть, Извлеченная подпоследовательность удовлетворяет характеристике вложенности. Аналогично, последовательности длиной 128, 256 и 512 могут быть извлечены из последовательности с длиной 1024. В данном варианте осуществления настоящего изобретения применяют полученные последовательности с короткой длиной материнского кода для кодирования подлежащих кодированию битов.
В возможной реализации, последовательность может быть частично или полностью любой из последовательностей (1) до (30) в спецификации. Если N=1024, последовательность может быть полностью или частично какой-либо одной из последовательностей S1-S20 в спецификации.
В возможной реализации, когда значение N равно 64, 128, 256 или 512, последовательность может быть извлечена из заданной последовательности с максимальной длиной материнского кода на основании характеристики вложенности или последовательности, соответствующей длине кода в последовательности (1) до (30) в описании, может быть непосредственно использована.
Выполняют построение полярного кода с использованием последовательности, чтобы помочь повысить точность оценки надежности поляризованного канала, тем самым, повышая производительность кодирования/декодирования полярного кода.
Минимальное значение номера последовательности в любой одной из последовательностей S1-S20 в спецификации равно 1, и номера последовательности расположены в порядке возрастания надежности N поляризованных каналов. В возможной реализации, если номера последовательности в последовательности расположены в порядке возрастания надежности N поляризованных каналов и минимальное значение номеров последовательности равно 0, получают новую последовательность путем последовательного вычитания 1 из номеров последовательности в любой последовательности, что не оказывает влияния на производительность последовательности.
Аналогично, в возможной реализации, если числа последовательности в последовательности расположены в нисходящем порядке надежности N поляризованных каналов, новая последовательность может быть получена путем размещения чисел последовательности в любой из последовательностей S1-S20 в спецификации в обратном порядке, что не оказывает влияния на производительность последовательности.
В возможной реализации может также быть представлена последовательность с использованием последовательности нормированной надежности или эквивалентной надежности каналов. Например, если местоположение сортировки канала х в последовательности составляет n (минимальный номер последовательности в последовательности обозначаются как 1), надежность канала может быть представлена посредством n или нормализованным n/N.
В возможной реализации местоположения нескольких элементов в любой одной из последовательностей S1-S20 в описании, могут быть взаимно обменены. Например, местоположение номера последовательности можно корректировать в пределах указанной амплитуды. Например, указанная амплитуда равна 5, и местоположение элемента, чей номер последовательности равен 10, может быть скорректировано в диапазоне от пяти местоположений слева элемента до пяти местоположений справа от элемента.
В соответствии со вторым аспектом представлено устройство для полярного кодирования, и устройство имеет функции выполнения способа по любому из первого аспекта или возможных реализаций первого аспекта. Эти функции могут быть реализованы с использованием аппаратных средств, или могут быть реализованы с помощью аппаратных средств, исполняющих соответствующее программное обеспечение. Аппаратные средства или программное обеспечение включают в себя один или несколько модулей, соответствующие функциям.
В возможной реализации, когда некоторые или все функции реализуют с использованием аппаратных средств, устройство для полярного кодирования включает в себя: схему интерфейса ввода, выполненную с возможностью получать биты, подлежащие кодированию; логическую схему, выполненную с возможностью выполнять описанные в любом одном из первого аспекта или возможных реализаций согласно первого аспекту функции; и схему интерфейса вывода, выполненную с возможностью выводить кодированную битовую последовательность.
Возможно, устройство для полярного кодирования может быть микросхемой или интегральной схемой.
В возможной реализации, когда некоторые или все функции реализованы с помощью программного обеспечения, устройство для полярного кодирования включает в себя: память, выполненную с возможностью хранить программу; и процессор, выполненный с возможностью исполнять программу, хранящуюся в памяти. Когда программа выполняется, устройство для полярного кодирования может реализовывать способ по любому одному из первого аспекта или возможных реализаций первого аспекта.
Возможно, память может быть физически независимым блоком или может быть интегрирована в процессор.
В возможной реализации, когда некоторые или все функции реализованы с помощью программного обеспечения, устройство для полярного кодирования включает в себя процессор. Память, выполненная с возможностью хранить программу, находится вне устройства для кодирования. Процессор соединен с памятью с помощью схемы/проводки и выполнен с возможностью считывать и выполнять программу, хранящуюся в памяти.
В соответствии с третьим аспектом обеспечивают систему связи, в котором система связи включает в себя сторону передачи и сторону приема, и сторона передачи может выполнять способ в соответствии с первым аспектом или возможной реализацией первого аспекта.
В соответствии с четвертым аспектом предоставлен машиночитаемый носитель данных, в котором машиночитаемый носитель данных хранит компьютерную программу, и компьютерная программа включает в себя инструкцию, используемую для выполнения способа согласно любому из первого аспекта или возможных реализаций первого аспекта.
В соответствии с пятым аспектом, вариант осуществления настоящего изобретения предоставляет компьютерный программный продукт, включающий в себя инструкцию. При выполнении инструкции на компьютере, компьютер выполняет способ, описанный в предшествующем аспекте.
Краткое описание чертежей
Фиг. 1 представляет собой архитектурная схему системы связи по варианту осуществления настоящего изобретения;
фиг. 2 представляет собой блок-схему алгоритма способа полярного кодирования согласно варианту осуществления настоящего изобретения;
фиг. 3 представляет собой первую структурную схему устройства для полярного кодирования согласно варианту осуществления настоящего изобретения;
фиг. 4 представляет собой вторую структурную схему устройства для полярного кодирования согласно варианту осуществления настоящего изобретения;
фиг. 5 является третьей структурной схемой устройства для полярного кодирования согласно варианту осуществления настоящего изобретения; и
фиг. 6 является четвертой схемой устройства для полярного кодирования в соответствии с вариантом осуществления настоящего изобретения.
Описание вариантов осуществления
Ниже подробно описаны варианты осуществления настоящего изобретения со ссылкой на прилагаемые чертежи.
Варианты осуществления настоящего изобретения предоставляют способ и устройство для полярного кодирования. По меньшей мере, выбирают две последовательности с относительно хорошей производительностью на основании правила определения производительности. Определяют те же самые номера последовательности в одном и том же местоположении сортировки, по меньшей мере, в двух последовательностях. Определенные одинаковые номера последовательности определены как номера последовательности, надежность которых остается неизменной в последовательностях, и сортируют номера последовательности, надежность которой остается неизменной в последовательности, на основании порядков чисел последовательности в, по меньшей мере, двух последовательностях. Сравнивают номера последовательности в, по меньшей мере, двух последовательностях, отличные от определенных номеров последовательности, надежность которых остается неизменной, для выбора некоторых подпоследовательностей и местоположение элементов в подпоследовательностях могут быть взаимно обменены. Последовательность сортировки, полученная, как указано выше, используют в качестве последовательности сортировки, используемой для полярного кодирования в вариантах осуществления настоящего изобретения. Таким образом, для последовательности сортировки, полученной с помощью вышеописанного способа, могут всесторонне рассматривать множество последовательностей с относительно хорошей производительностью, и определять номер последовательности, надежность которой остается неизменной, с использованием набора пересечений между различными последовательностями. Это помогает повысить точность порядка надежности поляризованных каналов и повысить производительность кодирования/декодирования полярного кода.
Для облегчения понимания вариантов осуществления настоящего изобретения далее приведено краткое описание полярного кода.
Политика кодирования полярного кода состоит в передаче полезной информации пользователя с использованием бесшумного канала, и передачи согласованной информации или без информации по всем каналам с шумом. Полярный код также является линейным блочным кодом, кодирующая матрица полярного кода представляет собой  , процесс кодирования является
, процесс кодирования является  , где
, где  представляет собой вектор бинарной строки, длина
представляет собой вектор бинарной строки, длина  (а именно, длина кода) является N,
(а именно, длина кода) является N, 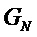 представляет собой
представляет собой 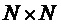 матрицу, и
матрицу, и  .
.  определяется как произведение Кронекера (Kronecker)
определяется как произведение Кронекера (Kronecker) 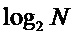 матриц
матриц 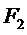 . Матрица
. Матрица 
В процессе кодирования полярного кода, некоторые биты в  используются для передачи информации, и также упоминаются как набор информационных бит, и набор индексов информационных бит обозначаются как
используются для передачи информации, и также упоминаются как набор информационных бит, и набор индексов информационных бит обозначаются как  . Другие биты устанавливаются на фиксированные значения, которые согласовывают сторона приема и сторона передачи, и упоминаются как набор фиксированных бит или набор замороженных бит (frozen bits), и набор индексов этих бит представлен с помощью дополнительного набора
. Другие биты устанавливаются на фиксированные значения, которые согласовывают сторона приема и сторона передачи, и упоминаются как набор фиксированных бит или набор замороженных бит (frozen bits), и набор индексов этих бит представлен с помощью дополнительного набора 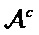
 . Процесс кодирования полярного кода эквивалентен
. Процесс кодирования полярного кода эквивалентен 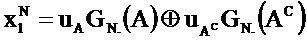
 , GN(AC) является суб-матрицей, полученной с использованием строк, соответствующих индексам в наборе
, GN(AC) является суб-матрицей, полученной с использованием строк, соответствующих индексам в наборе 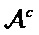 .
.  представляет собой набор информационных битов в
представляет собой набор информационных битов в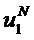 , и количество информационных битов равно К.
, и количество информационных битов равно К. 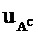
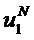 , количество фиксированных битов равно (N-K), и фиксированные биты являются известными битами. Эти фиксированные биты обычно устанавливают равным 0. Однако, фиксированные биты могут быть установлены на любое значение, согласованное между стороной приема и стороной передачи. Следовательно, кодирование выходного полярного кода может быть упрощено как
, количество фиксированных битов равно (N-K), и фиксированные биты являются известными битами. Эти фиксированные биты обычно устанавливают равным 0. Однако, фиксированные биты могут быть установлены на любое значение, согласованное между стороной приема и стороной передачи. Следовательно, кодирование выходного полярного кода может быть упрощено как  , где
, где  является набором информационных битов в
является набором информационных битов в 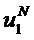 ,
,  является вектором строки с длиной
является вектором строки с длиной  , а именно,
, а именно, 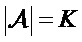 ,
,  указывает количество элементов в наборе, K является размером информационного блока, GN(A) является суб-матрицей, которая находится в матрице GN, и которую получают при использовании строк, соответствующих индексам в наборе А, и GN(A) представляет собой
указывает количество элементов в наборе, K является размером информационного блока, GN(A) является суб-матрицей, которая находится в матрице GN, и которую получают при использовании строк, соответствующих индексам в наборе А, и GN(A) представляет собой  матрицу.
матрицу.
Процесс построения полярного кода представляет собой процесс выбора набора A, и определяет производительность полярного кода. Процесс построения полярного кода обычно включает в себя: определение, на основании длины N материнского кода, наличия N поляризованных каналов, где N поляризованных каналов соответствуют N строкам в кодирующей матрице; и вычисление надежности поляризованных каналов, используя индексы из первых K поляризованных каналов с относительно высокой надежностью в качестве элементов в наборе А, а также с помощью индексов, соответствующих остальным (N-K) поляризованным каналам, в качестве элементов в наборе Ас индексов фиксированных бит. Набор  определяет местоположения информационных битов, и набор Ас определяет местоположения фиксированных битов.
определяет местоположения информационных битов, и набор Ас определяет местоположения фиксированных битов.
Для представления порядка надежности N поляризованных каналов в вариантах осуществления настоящего изобретения используют последовательность. N является длиной материнского кода полярного кода, и N является положительным целым числом степени 2.
В одном случае, последовательность может включать в себя последовательность номеров N поляризованных каналов, и последовательность номеров N поляризованных каналов расположены в последовательности, основанной на надежности N поляризованных каналов, например, могут быть организованы в убывающем порядке надежности, или могут быть расположены в порядке возрастания надежности. Для простоты описания, такая последовательность называется Q последовательностью.
В другом случае, последовательность может включать в себя значения надежности N поляризованных каналов. Возможно, значение надежности может быть значением нормированной надежности или значением эквивалентной надежности. Например, если местоположение сортировки канала х в последовательности является у и минимальный номер последовательности в последовательности обозначают как 1, надежность канала может быть представлена посредством у или нормализованным значением y/N. Аналогичным образом, значения надежности N поляризованных каналов могут быть расположены в той последовательности, в порядке убывания надежности, или могут быть расположены в порядке возрастания надежности. Для простоты описания, такая последовательность называется Z последовательностью.
Очевидно, что Q последовательность и Z последовательность могут быть взаимно преобразованы. Другими словами, Z последовательность может быть получена, если известна Q последовательность и vice versa.
Значение элемента в последовательности может находиться в диапазоне от 0 до N-1, или может находиться в диапазоне от 1 до N. В вариантах осуществления настоящего изобретения приведен пример, в котором значение элемента в последовательности находится в диапазоне от 1 до N. Очевидно, что может быть получена другая последовательность, элементы которой имеют значение в диапазоне от 0 до N-1. путем последовательного вычитания 1 из значений элементов в последовательности. Эти две последовательности имеют одинаковую производительность, и каждая из них может представлять порядок надежности N поляризованных каналов. В вариантах осуществления настоящего изобретения описан пример, в котором элементы в последовательности расположены в порядке возрастания надежности. Очевидно, что может быть получена последовательность, в которой элементы расположены в порядке убывания надежности путем размещения элементов в последовательности в обратном порядке. Эти две последовательности имеют одинаковую производительность, и каждая из них может представлять порядок надежности N поляризованных каналов.
Как показано на фиг. 1, система 100 связи применительно к варианту осуществления настоящего изобретения включает в себя сторону 101 передачи и сторону 102 приема. Сторона 101 передачи может быть альтернативно упоминаться как сторона кодирования, и сторона 102 приема может быть альтернативно упоминаться как сторона декодирования. Сторона 101 передачи может быть базовой станцией, сторона 102 приема представляет собой оконечное устройство; или сторона 101 передачи представляет собой оконечное устройство, сторона 102 приема является базовой станцией. Базовая станция представляет собой устройство, которое развернуто в сети радиодоступа, и которое выполнено с возможностью обеспечивать функции беспроводной связи для оконечного устройства. Базовая станция может включать в себя различные формы макро базовой станции, микро базовой станции, ретрансляционной станции или точки доступа, или тому подобное. Базовая станция может быть применена к системам с различными беспроводными технологиями доступа, такими как «Долгосрочное развитие» (Long Term Evolution, LTE) системы или более возможных систем связи, таких как система связи пятого поколения (5th generation, 5G). Базовая станция может дополнительно иметь другое сетевое устройство, которое имеет функцию базовой станции и специально, дополнительно может быть оконечным устройством, которое служит в качестве базовой станции в D2D связи. Оконечное устройство может включать в себя различные портативные устройства, устройства, установленные в транспортном средстве, носимые устройства или вычислительные устройства, которые имеют функцию беспроводной связи, или другое устройство обработки, соединенное с беспроводным модемом, различные формы устройства пользователя (user equipment, UE) или мобильные станции (mobile station, MS) или тому подобное.
Основываясь на архитектуре системы связи, показанной на фиг. 1, в вариантах осуществления настоящего изобретения, способ полярного кодирования может быть выполнен на стороне 101 передачи. Ниже приведено подробное описание способа полярного кодирования, представленного в вариантах осуществления настоящего изобретения.
Основываясь на архитектуре системы связи, показанной на фиг. 1, как показано на фиг. 2, конкретная процедура способа полярного кодирования, представленного в варианте осуществления настоящего изобретения, заключается в следующем.
Этап 201: определить последовательность, используемую для кодирования бит, подлежащих кодированию.
Для представления порядка надежности N поляризованных каналов используют последовательность, N является длиной материнского кода полярного кода, и N является положительным целым числом степени 2.
Этап 202: выполняют полярное кодирование битов, подлежащих кодированию, с использованием последовательности для получения кодированных битов.
Если длина бит, подлежащих кодированию, равна К, то К биты, подлежащие кодированию, отображают на К поляризованные каналы в N поляризованных каналах, и надежность K поляризованных каналов выше, чем надежность остальных N-K поляризованных каналов.
В частности, номера последовательности K поляризованных каналов выбирают в порядке убывания надежности на основании определенной последовательности, используемой для кодирования бит, подлежащих кодированию, и K биты, подлежащие кодированию, размещают в выбранных K поляризованных каналах.
В практическом применении, последовательность, используемая для кодирования бит, подлежащих кодированию, может быть сохранена в автономном порядке. После установления параметра (например, длины кода и скорость передачи бит), набор информационных бит и набор замороженных бит, которые используются для построения полярного кода определяются с использованием предварительно сохраненной последовательности. Для конкретного определения может быть сделана ссылка на вышеизложенное описание процесса полярного кодирования, и подробности не описаны здесь еще раз. Кроме того, в этом варианте осуществления настоящего изобретения, если последовательность, используемая для кодирования битов, подлежащих кодированию, представляет собой последовательность с относительно короткой длиной кода, последовательность с относительно короткой длиной кода может быть извлечена из хранимой последовательности с относительно большой длиной материнского кода на основании характеристики вложенности последовательности.
Далее приведены примеры Q последовательностей и Z последовательностей с различными длинами материнского кода, предоставленные Q последовательности и Z последовательности обе могут быть использованы для кодирования бит, подлежащих кодированию. В следующем примере, элементы в последовательности расположены в порядке возрастания надежности N поляризованных каналов.  представляет собой подпоследовательность в последовательности, n является номером последовательности подпоследовательности в последовательности, 1≤N≤ N, n является положительным целым числом, m представляет собой длину n-й подпоследовательности в последовательности, расположение элементов в подпоследовательности
представляет собой подпоследовательность в последовательности, n является номером последовательности подпоследовательности в последовательности, 1≤N≤ N, n является положительным целым числом, m представляет собой длину n-й подпоследовательности в последовательности, расположение элементов в подпоследовательности  являются изменяемые, и номера последовательности на местоположениях за пределами подпоследовательности в последовательности фиксированы. Когда местоположения элементов в подпоследовательности
являются изменяемые, и номера последовательности на местоположениях за пределами подпоследовательности в последовательности фиксированы. Когда местоположения элементов в подпоследовательности  происходит обмен в
происходит обмен в  , последовательность, полученная после обмена, может быть получена на основе последовательностей, приведенных ниже.
, последовательность, полученная после обмена, может быть получена на основе последовательностей, приведенных ниже.
Пример 1
(1) Если N = 64, последовательность представляет собой Q последовательность и Q последовательность может включать в себя 11 подпоследовательность, чей элемент местоположений изменчивы. Значение n изменяется от 1 до 11, и последовательность может быть:
[1, 2,  , 17, 33,
, 17, 33,  , 21, 35, 25,
, 21, 35, 25, 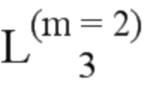 ,
, 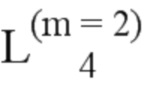 ,
,  , 15, 22,
, 15, 22, 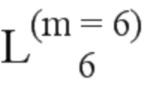 , 42, 29,
, 42, 29, 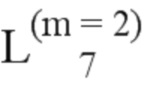 , 45,
, 45,  ,
,  ,
, 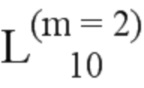 , 40, 30,
, 40, 30,  , 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64].
, 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (7, 4, 13, 6, 19, 10, 34, 18, 11);
= (7, 4, 13, 6, 19, 10, 34, 18, 11); 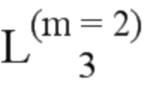 = (8, 37);
= (8, 37); 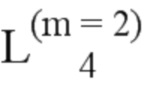 = (12, 41);
= (12, 41);  = (20, 14, 49
= (20, 14, 49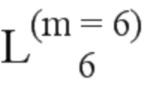 = (27, 36, 39, 23, 38, 26);
= (27, 36, 39, 23, 38, 26); 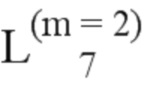 = (50, 43);
= (50, 43);  = (16, 51);
= (16, 51);  = (24, 53);
= (24, 53); 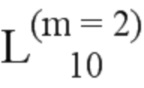 = (57, 28); и
= (57, 28); и  = (44, 31).
= (44, 31).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, 33, (7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), 42, 29, (50, 43), 45, (16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64].
(2) Если N = 64, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя две подпоследовательности, местоположения элементов которых, изменчивы. Значение n равно 1 или 2. Последовательность может быть [1, 2, 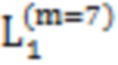 ,
, , 55, 56, 61, 57, 62, 63, 64].
, 55, 56, 61, 57, 62, 63, 64].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3, 11, 8, 20, 4); и
= (5, 9, 3, 11, 8, 20, 4); и  = (13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44).
= (13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44).
В этом примере Z последовательность конкретно является: [1, 2, (5, 9, 3, 11, 8, 20, 4), (13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44), 55, 56, 61, 57, 62, 63, 64].
(3) Если N = 128, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 23 подпоследовательности местоположения элемента которой изменяемы. Значение n изменяют в диапазоне от 1 до 23. Последовательность может быть: [1, 2,  , 17, 33,
, 17, 33, 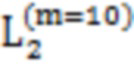 , 21, 35, 25,
, 21, 35, 25,  ,
,  ,
, 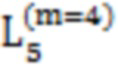 ,
,  , 22,
, 22, 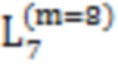 , 68, 42, 29, 70,
, 68, 42, 29, 70, 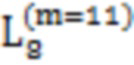 , 77,
, 77,  ,
,  ,
,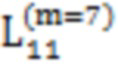 , 52,
, 52, 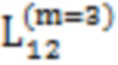 , 54, 78,
, 54, 78, 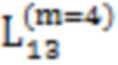 ,
,  ,
,  , 90,
, 90,  , 103, 106,
, 103, 106,  , 107,
, 107,  ,
, 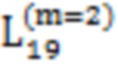 ,
,  ,
,  ,
,  , 94, 108, 95, 110, 116, 111, 118, 119, 122,
, 94, 108, 95, 110, 116, 111, 118, 119, 122,  , 125, 96, 112, 120, 124, 126, 127, 128].
, 125, 96, 112, 120, 124, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (7, 65, 4, 13, 6, 19, 10, 34, 18, 11);
= (7, 65, 4, 13, 6, 19, 10, 34, 18, 11);  = (66, 8, 37, 67);
= (66, 8, 37, 67); 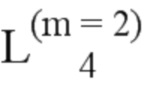 = (12, 41);
= (12, 41);  = (20, 14, 69, 49);
= (20, 14, 69, 49); 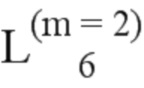 = (15, 73);
= (15, 73); 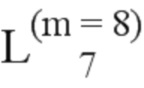 = (27, 36, 81, 39, 23, 38, 26, 97);
= (27, 36, 81, 39, 23, 38, 26, 97); 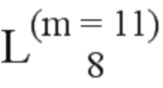 = (50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);
= (50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);  = (83, 57, 28, 98, 40);
= (83, 57, 28, 98, 40); 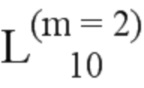 = (85, 30);
= (85, 30);  = (44, 99, 31, 89, 72, 46, 101);
= (44, 99, 31, 89, 72, 46, 101);  = (47, 76, 105);
= (47, 76, 105);  = (55, 84, 58, 113);
= (55, 84, 58, 113); 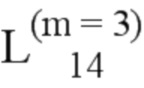 = (86, 79, 59);
= (86, 79, 59);  = (100, 87, 61);
= (100, 87, 61);  = (102, 91, 32);
= (102, 91, 32);  = (48, 93);
= (48, 93);  = (56, 114);
= (56, 114); 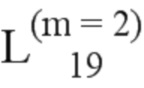 = (80, 109);
= (80, 109);  = (60, 115);
= (60, 115);  = (88, 62, 117);
= (88, 62, 117);  = (92, 63, 121, 104); и
= (92, 63, 121, 104); и  = (123, 64).
= (123, 64).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, 33, (7, 65, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (66, 8, 37, 67), (12, 41), (20, 14, 69, 49), (15, 73), 22, (27, 36, 81, 39, 23, 38, 26, 97), 68, 42, 29, 70, (50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53), 77, (83, 57, 28, 98, 40), (85, 30), (44, 99, 31, 89, 72, 46, 101), 52, (47, 76, 105), 54, 78, (55, 84, 58, 113), ( 86, 79, 59), (100, 87, 61), 90, (102, 91, 32), 103, 106, (48, 93), 107, (56, 114), (80, 109), (60, 115), (88, 62, 117), (92, 63, 121, 104), 94, 108, 95, 110, 116, 111, 118, 119, 122, (123, 64), 125, 96, 112, 120, 124, 126, 127, 128].
(4) Если N = 128, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну подпоследовательности, местоположения элемента которого изменчивы. Значение n равно 1. Последовательность может быть: [1, 2,  , 125, 121, 126, 127, 128].
, 125, 121, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим: 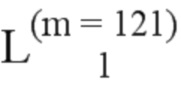 = (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119).
= (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119), 125, 121, 126, 127, 128].
(5) Если N = 256, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 25 подпоследовательности, местоположения элемента которой, изменчивы. Значение n колеблется от 1 до 25. Последовательность может быть: [1, 2,  , 17, 33,
, 17, 33,  , 21, 35, 25,
, 21, 35, 25, 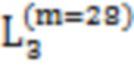 , 29,
, 29,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 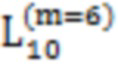 ,
, 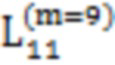 ,
,  ,
, 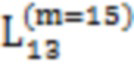 ,
,  ,
,  ,
,  ,
,  , 215, 189,
, 215, 189, 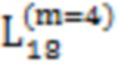 , 219,
, 219,  ,
,  ,
, 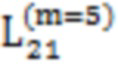 ,
,  ,
,  , 222, 236, 223,
, 222, 236, 223, 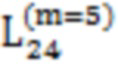 ,
,  , 253, 224, 240, 248, 252, 254, 255, 256].
, 253, 224, 240, 248, 252, 254, 255, 256].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3); 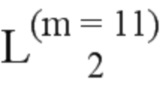 = (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11);
= (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11);  = (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145);
= (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145);  = (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77);
= (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77);  = (83, 138, 57, 28, 98, 40);
= (83, 138, 57, 28, 98, 40);  = (139, 85, 30, 146);
= (139, 85, 30, 146);  = (44, 99, 141, 31, 89, 147, 72, 162, 46, 101);
= (44, 99, 141, 31, 89, 147, 72, 162, 46, 101);  = (149, 52);
= (149, 52); 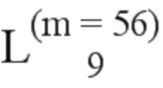 = (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157);
= (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157);  = (88, 62, 117, 171, 198, 178);
= (88, 62, 117, 171, 198, 178);  = (92, 202, 199, 63, 144, 173, 121, 104, 179);
= (92, 202, 199, 63, 144, 173, 121, 104, 179); 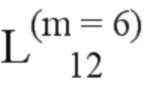 = (203, 94, 152, 210, 181, 108);
= (203, 94, 152, 210, 181, 108);  = (95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227);
= (95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227);  = (159, 217, 119, 174, 122, 200, 180, 229);
= (159, 217, 119, 174, 122, 200, 180, 229);  = (175, 123, 64, 233, 204, 182);
= (175, 123, 64, 233, 204, 182);  = (125, 206, 241, 183, 212, 96, 186, 207, 187, 214);
= (125, 206, 241, 183, 212, 96, 186, 207, 187, 214);  = (228, 112);
= (228, 112); 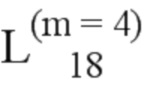 = (218, 160, 120, 230);
= (218, 160, 120, 230); 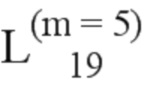 = (231, 176, 124, 234, 221);
= (231, 176, 124, 234, 221); 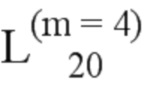 = (126, 235, 184, 242);
= (126, 235, 184, 242); 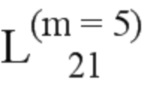 = (188, 208, 237, 127, 243);
= (188, 208, 237, 127, 243); 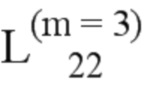 = (216, 245, 190);
= (216, 245, 190);  = (220, 249, 191, 232);
= (220, 249, 191, 232);  = (238, 244, 239, 246, 128); и
= (238, 244, 239, 246, 128); и  = (247, 250, 251, 192).
= (247, 250, 251, 192).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, 33, (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11), 21, 35, 25, (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145), 29, (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77), (83, 138, 57, 28, 98, 40), (139, 85, 30, 146), (44, 99, 141, 31, 89, 147, 72, 162, 46, 101), (149, 52), (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157), (88, 62, 117, 171, 198, 178), (92, 202, 199, 63, 144, 173, 121, 104, 179), (203, 94, 152, 210, 181, 108), (95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227), (159, 217, 119, 174, 122, 200, 180, 229), (175, 123, 64, 233, 204, 182), (125, 206, 241, 183, 212, 96, 186, 207, 187, 21 4), (228, 112), 215, 189, (218, 160, 120, 230), 219, (231, 176, 124, 234, 221), (126, 235, 184, 242), (188, 208, 237, 127, 243), (216, 245, 190), (220, 249, 191, 232), 222, 236, 223, (238, 244, 239, 246, 128), (247, 250, 251, 192), 253, 224, 240, 248, 252, 254, 255, 256].
(6) Если N = 256, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которой, изменчивы. Последовательность может быть: [1, 2, 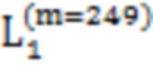 , 253, 249, 254, 255, 256].
, 253, 249, 254, 255, 256].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247).
= (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247).
В этом примере Q последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 20 1, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247), 253, 249, 254, 255, 256].
(7) Если N = 512, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 10 подпоследовательностей, местоположения элемента которой, изменчивы. Значение n колеблется от 1 до 10. Последовательность может быть: [1, 2,  , 17, 33,
, 17, 33,  ,
,  ,
, 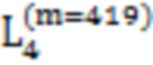 ,
,  ,
,  ,
, 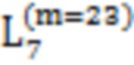 ,
,  , 507,
, 507,  ,
,  508, 510, 511, 512].
508, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3); 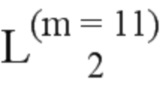 = (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11);
= (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11);  = (257, 21, 35, 25);
= (257, 21, 35, 25); 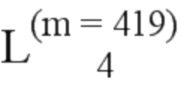 = (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 1 11, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485);
= (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 1 11, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485);  = (431, 489, 460, 240, 379, 438);
= (431, 489, 460, 240, 379, 438);  = (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);
= (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477); 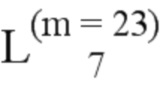 = (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500);
= (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500);  = (503, 495, 502, 448, 506);
= (503, 495, 502, 448, 506);  = (480, 509); и
= (480, 509); и 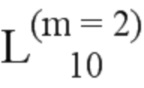 = (504, 496).
= (504, 496).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, 33, (7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11), (257, 21, 35, 25), (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 4 66, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485), (431, 489, 460, 240, 379, 438), (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477), (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500), (503, 495, 502, 448, 506), 507, (480, 509), (504, 496), 508, 510, 511, 512].
(8) Если N = 512, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность местоположения элемента которой изменчивы. Последовательность может быть: [1, 2, 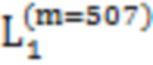 , 510, 511, 512].
, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
= (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 34 6, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506), 510, 511, 512].
(9) Если N = 1024, последовательность представляет собой Q последовательность и Q последовательность может включать в себя три подпоследовательности, чьи местоположения элемента изменчивы. Значение n колеблется от 1 до 3. Последовательность может быть: [1, 2,  , 17, 33,
, 17, 33,  ,
,  , 1020, 1022 1023, 1024].
, 1020, 1022 1023, 1024].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726,915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и
= (7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726,915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и 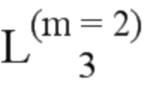 = (1016, 1008).
= (1016, 1008).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, 33, (7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 27 8, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018 896, 1014, 992, 1019, 960, 1021), (1016, 1008), 1020, 1022, 1023, 1024].
(10) Если N = 1024, последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n = 1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть: [1, 2,  ,1022 1023, 1024].
,1022 1023, 1024].
В возможном примере,  может быть следующим:
может быть следующим: 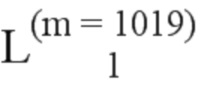 = (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 4 54, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 89 4, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 82 1, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 979, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
= (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 4 54, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 89 4, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 82 1, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 979, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
В этом примере Z последовательность конкретно является: [1, 2, (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 35 8, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895,904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 979, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018), 1022, 1023, 1024] .
Пример 2
(11) Когда N = 64, последовательность является Q последовательностью и Q последовательность может включать в себя 12 подпоследовательностей, местоположения элемента которого, изменяются. Значение n находится в диапазоне от 1 до 12. Последовательность может быть: [1, 2,  , 17,
, 17, 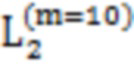 , 21, 35, 25,
, 21, 35, 25,  ,
,  ,
, 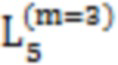 , 15, 22,
, 15, 22,  ,
,  ,
,  ,
,  ,
,  , 40, 30,
, 40, 30,  , 46, 52, 47, 54, 55, 58, 59,
, 46, 52, 47, 54, 55, 58, 59, 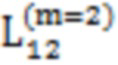 , 48, 56, 60, 62, 63, 64].
, 48, 56, 60, 62, 63, 64].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 4, 13, 6, 19, 10, 34, 18, 11);
= (33, 7, 4, 13, 6, 19, 10, 34, 18, 11); 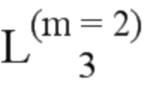 = (8, 37);
= (8, 37); 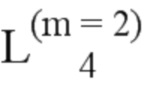 = (12, 41);
= (12, 41);  = (20, 14, 49);
= (20, 14, 49); 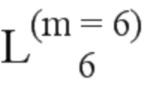 = (27, 36, 39, 23, 38, 26);
= (27, 36, 39, 23, 38, 26); 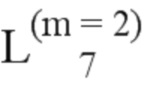 = (42, 29);
= (42, 29);  = (50, 43, 45, 16, 51);
= (50, 43, 45, 16, 51);  = (24, 53);
= (24, 53); 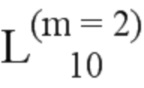 = (57, 28);
= (57, 28);  = (44, 31); и
= (44, 31); и  = (61, 32).
= (61, 32).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64].
(12) Если N = 64, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n = 1) подпоследовательность, местоположения элемента которой, изменчивы. Последовательность может быть: [1, 2, 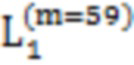 , 62, 63, 64].
, 62, 63, 64].
В возможном примере,  может быть следующим:
может быть следующим: 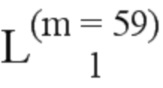 = (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57).
= (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57).
В этом примере Z последовательность конкретно является: [1, 2, (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57), 62, 63, 64].
(13) Если N = 128, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 23 (n=23) подпоследовательности, местоположения элемента которой, изменчивы. Последовательность может быть: [1, 2,  , 17,
, 17,  , 21, 35, 25,
, 21, 35, 25,  ,
,  ,
, 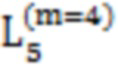 ,
,  , 22,
, 22,  ,
,  ,
, 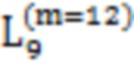 , 77,
, 77, 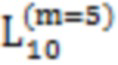 ,
,  ,
, 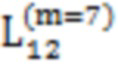 , 52,
, 52,  , 54,
, 54,  ,
,  ,
, 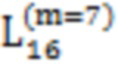 , 103,
, 103,  ,
,  ,
, 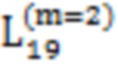 ,
,  ,
,  ,
,  , 94, 108, 95, 110, 116, 111, 118, 119,
, 94, 108, 95, 110, 116, 111, 118, 119,  , 112, 120, 124, 126, 127, 128].
, 112, 120, 124, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3); 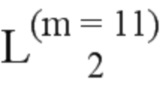 = (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11);
= (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11);  = (66, 8, 37, 67);
= (66, 8, 37, 67); 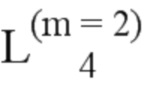 = (12, 41);
= (12, 41);  = (20, 14, 69, 49);
= (20, 14, 69, 49); 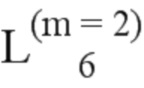 = (15, 73);
= (15, 73);  = (27, 36, 81, 39, 23, 38, 26, 97, 68);
= (27, 36, 81, 39, 23, 38, 26, 97, 68);  = (42, 29);
= (42, 29); 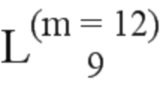 = (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);
= (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);  = (83, 57, 28, 98, 40);
= (83, 57, 28, 98, 40);  = (85, 30);
= (85, 30); 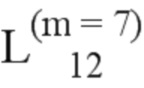 = (44, 99, 31, 89, 72, 46, 101);
= (44, 99, 31, 89, 72, 46, 101); 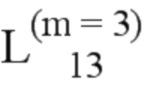 = (47, 76, 105);
= (47, 76, 105); 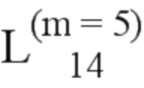 = (78, 55, 84, 58, 113);
= (78, 55, 84, 58, 113);  = (86, 79, 59);
= (86, 79, 59); 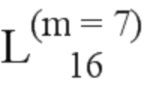 = (100, 87, 61, 90, 102, 91, 32);
= (100, 87, 61, 90, 102, 91, 32);  = (106, 48, 93);
= (106, 48, 93);  = (107, 56, 114);
= (107, 56, 114); 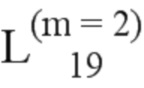 = (80, 109);
= (80, 109);  = (60, 115);
= (60, 115);  = (88, 62, 117);
= (88, 62, 117);  = (92, 63, 121, 104); и
= (92, 63, 121, 104); и  = (122, 123, 64, 125, 96).
= (122, 123, 64, 125, 96).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (66, 8, 37, 67), (12, 41), (20, 14, 69, 49), (15, 73), 22, (27, 36, 81, 39, 23, 38, 26, 97, 68), (42, 29), (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53), 77, (83, 57, 28, 98, 40), (85, 30), (44, 99, 31, 89, 72, 46, 101), 52, (47, 76, 105), 54, (78, 55, 84, 58, 113), (86, 79, 59), (100, 87, 61, 90, 102, 91, 32), 103, (106, 48, 93), (107, 56, 114), (80, 109), ( 60, 115), (88, 62, 117), (92, 63, 121, 104), 94, 108, 95, 110, 116, 111, 118, 119, (122, 123, 64, 125, 96), 112, 120, 124, 126, 127, 128].
(14) Если N = 128, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которой, изменчивы. Последовательность может быть: [1, 2,  , 126, 127, 128].
, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим: 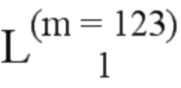 = (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121).
= (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121).
В этом примере последовательность Z именно: [1, 2, (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121), 126, 127, 128].
(15) Если N = 256, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 16 подпоследовательностей, местоположения элемента которой, изменчивы. Значение n может изменяться в пределах от 1 до 16. Последовательность может быть:
[1, 2,  , 17,
, 17,  , 21, 35, 25,
, 21, 35, 25, 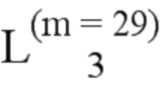 ,
,  ,
, 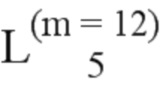 ,
, 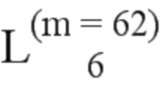 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , 222, 236, 223,
, 222, 236, 223, 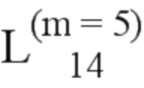 ,
,  ,
,  , 240, 248, 252, 254, 255, 256].
, 240, 248, 252, 254, 255, 256].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11);
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11); 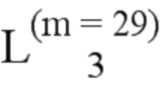 = (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29);
= (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29);  = (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146);
= (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146); 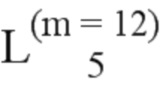 = (44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52);
= (44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52); 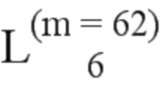 = (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178);
= (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178);  = (92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214);
= (92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214);  = (228, 112, 215, 189, 218, 160, 120, 230, 219);
= (228, 112, 215, 189, 218, 160, 120, 230, 219);  = (231, 176, 124, 234, 221);
= (231, 176, 124, 234, 221);  = (126, 235, 184, 242);
= (126, 235, 184, 242);  = (188, 208, 237, 127, 243);
= (188, 208, 237, 127, 243);  = (216, 245, 190);
= (216, 245, 190);  = (220, 249, 191, 232);
= (220, 249, 191, 232); 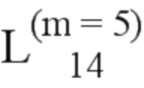 = (238, 244, 239, 246, 128);
= (238, 244, 239, 246, 128);  = (247, 250, 251, 192); и
= (247, 250, 251, 192); и  = (253, 224).
= (253, 224).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11), 21, 35, 25, (66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29), (70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146), (44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52), (47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178), (92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214), (228, 112, 215, 189, 218, 160, 120, 230, 219), (231, 176, 124, 234, 221), (126, 235, 184, 242), (188, 208, 237, 127, 243), (216, 245, 190), (220, 249, 191, 232), 222, 236, 223, (238, 244, 239, 246, 128), (247, 250, 251, 192), (253, 224), 240, 248, 252, 254, 255, 256].
(16) Если N = 256, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которой, изменчивы. Последовательность может быть: [1, 2,  , 254, 255, 256].
, 254, 255, 256].
В возможном примере,  может быть следующим: [
может быть следующим: [ = (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 17 2, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249)].
= (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 17 2, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249)].
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 20 1, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249), 254, 255, 256].
(17) Если N = 512, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя шесть подпоследовательностей, местоположения элемента которой, изменчивы. Значение n колеблется от 1 до 6. Последовательность может быть: [1, 2,  , 17,
, 17,  ,
, 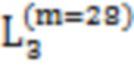 ,
, 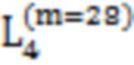 , 507,
, 507, 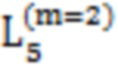 ,
,  , 508, 510, 511, 512].
, 508, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438) ;
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438) ;  = (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);
= (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);  = (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506);
= (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506); 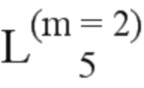 = (480, 509); и
= (480, 509); и 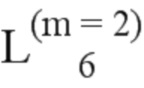 = (504, 496).
= (504, 496).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438), (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477), (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506), 507, (480, 509), (504, 496), 508, 510, 511, 512].
(18) Если N = 512, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть: [1, 2, 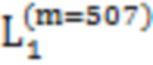 , 510, 511, 512].
, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
= (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 34 6, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506), 510, 511, 512].
(19) Если N = 1024, последовательность представляет собой Q последовательность и Q последовательность может включать в себя три подпоследовательности, чьи местоположения элемента, изменчивы. Значение n колеблется от 1 до 3. Последовательность может быть: [1, 2,  17,
17,  ,
,  , 1020, 1022 1023, 1024].
, 1020, 1022 1023, 1024].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698,726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018 896, 1014, 992, 1019, 960, 1021); и
= (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698,726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018 896, 1014, 992, 1019, 960, 1021); и 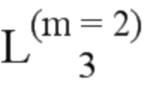 = (1016, 1008).
= (1016, 1008).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018 896, 1014 992, 1019, 960, 1021), (1016 1008), 1020, 1022, 1023, 1024].
(20) Если N = 1024, последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну подпоследовательность, чьи местоположения элемента, изменчивы. Последовательность может быть: [1, 2,  , 1022, 1023, 1024].
, 1022, 1023, 1024].
В возможном примере,  может представлять собой:
может представлять собой: 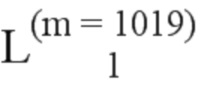 = (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 3 20, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, +935, +963, +979, +996, +944, +981, +971, +999, +986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
= (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 3 20, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, +935, +963, +979, +996, +944, +981, +971, +999, +986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
В этом примере Z последовательность конкретно является: [1, 2, (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 35 8, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 65 2, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 9 62, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 979, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018), 1022, 1023, 1024].
Пример 3
(21) Если N = 64, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 11 подпоследовательностей, местоположения элемента которого, изменчивы. Значение n колеблется от 1 до 11. Последовательность может быть:
[1, 2,  , 17,
, 17,  ,
, 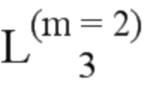 ,
,  , 15, 22,
, 15, 22,  ,
, 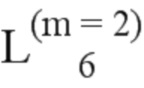 ,
,  ,
,  ,
, 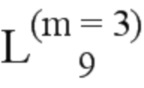 , 30,
, 30, 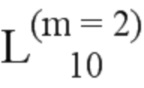 , 46, 52, 47, 54, 55, 58, 59,
, 46, 52, 47, 54, 55, 58, 59,  , 48, 56, 60, 62, 63, 64],
, 48, 56, 60, 62, 63, 64],
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 8, 37);
= (33, 7, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 8, 37); 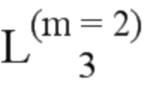 = (12, 41);
= (12, 41);  = (20, 14, 49);
= (20, 14, 49);  = (27, 36, 39, 23, 38, 26);
= (27, 36, 39, 23, 38, 26); 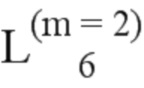 = (42, 29);
= (42, 29);  = (50, 43, 45, 16, 51);
= (50, 43, 45, 16, 51);  = (24, 53);
= (24, 53); 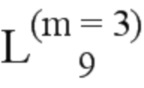 = (57, 28, 40);
= (57, 28, 40); 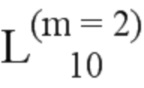 = (44, 31); и
= (44, 31); и  = (61, 32).
= (61, 32).
N = 64, и местоположения элементов могут в подпоследовательности  в Q последовательности могут быть изменены в подпоследовательности
в Q последовательности могут быть изменены в подпоследовательности  , например, могут быть (5, 9, 3) и могут быть заменены на (3, 9, 5) или (5, 3, 9).
, например, могут быть (5, 9, 3) и могут быть заменены на (3, 9, 5) или (5, 3, 9).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28, 40), 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64]. Набор в скобках является подпоследовательностью  .
.
(22) Если N = 64, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть:
[1, 2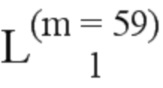 , 62, 63, 64].
, 62, 63, 64].
В возможном примере,  может быть следующим:
может быть следующим: 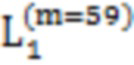 = (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57). Местоположения элементов в
= (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57). Местоположения элементов в  могут быть изменены в подпоследовательности.
могут быть изменены в подпоследовательности.
В этом примере Z последовательность конкретно является: [1, 2, (5, 9, 3, 11, 8, 20, 4, 13, 16, 22, 10, 25, 27, 40, 6, 15, 12, 24, 17, 28, 32, 42, 19, 34, 29, 45, 36, 47, 49, 58, 7, 14, 18, 30, 21, 33, 31, 46, 23, 35, 38, 48, 39, 50, 52, 59, 26, 37, 41, 51, 43, 53, 54, 60, 44, 55, 56, 61, 57), 62, 63, 64].
(23) Если N = 128, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя 17 подпоследовательностей, местоположения элемента которого, изменчивы. Значение n колеблется от 1 до 17. Последовательность может быть:
[1, 2,  , 17,
, 17,  ,
, 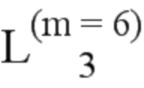 , 22,
, 22,  ,
, 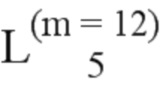 , 77,
, 77,  ,
, 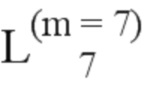 , 52,
, 52, 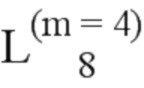 ,
,  ,
,  ,
,  ,
,  ,
, 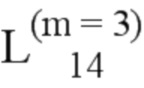 ,
,  , 94,
, 94,  , 110, 116, 111, 118,
, 110, 116, 111, 118,  , 112, 120, 124, 126, 127, 128].
, 112, 120, 124, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 12, 41);
= (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 12, 41); 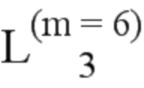 = (20, 14, 69, 49, 15, 73);
= (20, 14, 69, 49, 15, 73);  = (27, 36, 81, 39, 23, 38, 26, 97, 68, 42, 29);
= (27, 36, 81, 39, 23, 38, 26, 97, 68, 42, 29); 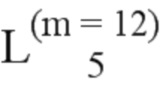 = (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);
= (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53);  = (83, 57, 28, 98, 40, 85, 30);
= (83, 57, 28, 98, 40, 85, 30); 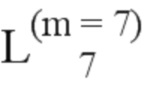 = (44, 99, 31, 89, 72, 46, 101);
= (44, 99, 31, 89, 72, 46, 101); 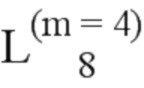 = (47, 76, 105, 54);
= (47, 76, 105, 54);  = (78, 55, 84, 58, 113, 86, 79, 59, 100, 87, 61, 90, 102, 91, 32);
= (78, 55, 84, 58, 113, 86, 79, 59, 100, 87, 61, 90, 102, 91, 32);  = (103, 106, 48, 93);
= (103, 106, 48, 93);  = (107, 56, 114);
= (107, 56, 114);  = (80, 109);
= (80, 109);  = (60, 115);
= (60, 115); 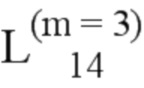 = (88, 62, 117);
= (88, 62, 117);  = (92, 63, 121, 104);
= (92, 63, 121, 104);  = (108, 95); и
= (108, 95); и  = (119, 122, 123, 64, 125, 96).
= (119, 122, 123, 64, 125, 96).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 12, 41), (20, 14, 69, 49, 15, 73), 22, (27, 36, 81, 39, 23, 38, 26, 97, 68, 42, 29), (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53), 77, (83, 57, 28, 98, 40, 85, 30), (44, 99, 31, 89, 72, 46, 101), 52, (47, 76, 105, 54), (78, 55, 84, 58, 113, 86, 79, 59, 100, 87, 61, 90, 102, 91, 32), (103, 106, 48, 93), (107, 56, 114), (80, 109), (60, 115), (88, 62, 117), ( 92, 63, 121, 104), 94, (108, 95), 110, 116, 111, 118, (119, 122, 123, 64, 125, 96), 112, 120, 124, 126, 127, 128].
(34) Если N = 128, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть:
[1, 2, 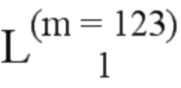 , 126, 127, 128].
, 126, 127, 128].
В возможном примере,  может быть следующим:
может быть следующим: 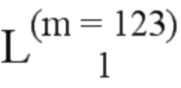 = (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121).
= (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 22, 4, 14, 17, 25, 11, 28, 31, 52, 6, 16, 13, 27, 18, 33, 38, 55, 20, 40, 34, 60, 44, 64, 67, 91, 7, 15, 19, 35, 23, 39, 37, 62, 26, 43, 48, 65, 50, 70, 73, 94, 30, 46, 53, 72, 56, 76, 78, 97, 59, 80, 84, 101, 87, 104, 107, 120, 9, 21, 24, 42, 29, 45, 49, 69, 32, 54, 47, 74, 57, 77, 83, 99, 36, 51, 58, 79, 63, 82, 86, 103, 68, 88, 90, 106, 95, 110, 112, 122, 41, 61, 66, 85, 71, 89, 92, 109, 75, 93, 96, 111, 100, 113, 115, 123, 81, 98, 102, 114, 105, 116, 117, 124, 108, 118, 119, 125, 121), 126, 127, 128].
(25) Если N = 256, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя девять подпоследовательностей, местоположения элемента которого, изменчивы. Значение n колеблется от 1 до 9. Последовательность может быть:
[1, 2,  , 17,
, 17, 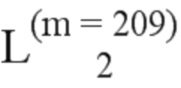 ,
,  ,
,  ,
,  , 222,
, 222, 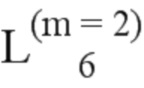 ,
,  ,
, 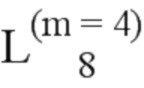 ,
,  , 240, 248, 252, 254, 255, 256].
, 240, 248, 252, 254, 255, 256].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3); 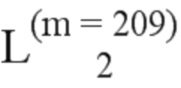 = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29, 70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146, 44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52, 47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178, 92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214, 228, 112, 215, 189, 218, 160, 120, 230, 219);
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29, 70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146, 44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52, 47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178, 92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214, 228, 112, 215, 189, 218, 160, 120, 230, 219);  = (231, 176, 124, 234, 221, 126, 235, 184, 242, 188, 208, 237, 127, 243);
= (231, 176, 124, 234, 221, 126, 235, 184, 242, 188, 208, 237, 127, 243);  = (216, 245, 190);
= (216, 245, 190);  = (220, 249, 191, 232);
= (220, 249, 191, 232); 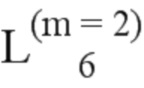 = (236, 223);
= (236, 223);  = (238, 244, 239, 246, 128);
= (238, 244, 239, 246, 128); 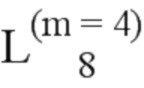 = (247, 250, 251, 192); и
= (247, 250, 251, 192); и  = (253, 224).
= (253, 224).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29, 70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146, 44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52, 47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178, 92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214, 228, 112, 215, 189, 218, 160, 120, 230, 219), (231, 176, 124, 234, 221, 126, 235, 184, 242, 188, 208, 237, 127, 243), (216, 245, 190), (220, 249, 191, 232), 222, (236, 223), (238, 244, 239, 246, 128), (247, 250, 251, 192), (253, 224), 240, 248, 252, 254, 255, 256].
(26) Если N = 256, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента, которого, изменчивы. Последовательность может быть:
[1, 2,  , 254, 255, 256].
, 254, 255, 256].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249).
= (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 201, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 23, 4, 15, 18, 27, 11, 31, 34, 61, 6, 17, 13, 29, 19, 36, 43, 65, 21, 45, 38, 72, 50, 77, 82, 123, 7, 16, 20, 39, 24, 44, 42, 74, 28, 48, 55, 79, 58, 87, 91, 127, 33, 52, 62, 90, 66, 96, 100, 134, 71, 102, 108, 142, 115, 148, 156, 193, 9, 22, 25, 47, 32, 51, 57, 85, 35, 64, 53, 92, 68, 98, 107, 138, 40, 60, 69, 101, 76, 104, 113, 147, 83, 116, 121, 153, 128, 163, 168, 202, 46, 73, 80, 110, 88, 117, 124, 160, 93, 125, 133, 167, 141, 171, 178, 208, 103, 136, 143, 174, 149, 180, 185, 213, 159, 187, 192, 218, 197, 221, 228, 244, 14, 26, 37, 59, 30, 67, 63, 105, 41, 70, 75, 111, 81, 119, 120, 157, 49, 78, 84, 118, 89, 126, 132, 164, 99, 131, 137, 170, 146, 176, 183, 212, 54, 86, 97, 130, 94, 135, 140, 175, 109, 145, 150, 181, 158, 186, 191, 217, 114, 152, 161, 189, 166, 196, 200, 223, 173, 203, 205, 225, 210, 232, 235, 248, 56, 95, 106, 144, 112, 151, 155, 188, 122, 154, 162, 195, 169, 198, 204, 226, 129, 165, 172, 20 1, 179, 206, 209, 230, 184, 211, 215, 233, 220, 237, 239, 250, 139, 177, 182, 207, 190, 214, 216, 236, 194, 219, 222, 238, 227, 240, 242, 251, 199, 224, 229, 241, 231, 243, 245, 252, 234, 246, 247, 253, 249), 254, 255, 256].
(27) Если N = 512, то последовательность представляет собой Q последовательность и Q последовательность может включать в себя четыре подпоследовательности, чьи местоположения элемента изменчивы. Значение n колеблется от 1 до 4. Последовательность может быть:
[1, 2,  , 17,
, 17,  ,
,  ,
, 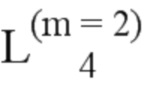 , 508, 510, 511, 512].
, 508, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);  = (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и
= (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и 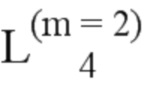 = (504, 496).
= (504, 496).
В этом примере Q последовательность конкретно является: [1, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 39 1, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477), (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509), (504, 496), 508, 510, 511, 512].
(28) Если N = 512, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть: [1, 2, 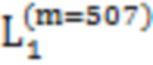 , 510, 511, 512].
, 510, 511, 512].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
= (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 416, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506).
В этом примере Z последовательность конкретно является: [1, 2, (5, 10, 3, 12, 8, 24, 4, 15, 18, 28, 11, 32, 35, 67, 6, 17, 13, 30, 20, 38, 46, 72, 22, 49, 40, 80, 55, 87, 93, 146, 7, 16, 21, 41, 25, 48, 45, 83, 29, 53, 60, 90, 64, 100, 104, 153, 34, 57, 69, 103, 73, 111, 117, 164, 79, 119, 127, 177, 135, 183, 197, 264, 9, 23, 26, 51, 33, 56, 63, 97, 36, 71, 58, 105, 76, 114, 125, 171, 42, 66, 77, 118, 86, 121, 133, 182, 94, 136, 144, 192, 154, 207, 216, 285, 50, 82, 91, 130, 101, 138, 147, 203, 107, 149, 163, 215, 175, 222, 235, 299, 120, 169, 178, 229, 187, 237, 248, 309, 202, 253, 263, 323, 274, 331, 350, 407, 14, 27, 39, 65, 31, 75, 70, 122, 44, 78, 85, 131, 92, 141, 143, 198, 54, 89, 96, 139, 102, 151, 162, 211, 115, 161, 170, 221, 181, 231, 243, 308, 59, 99, 112, 160, 109, 165, 173, 230, 129, 180, 188, 238, 200, 252, 260, 319, 134, 190, 204, 255, 214, 273, 280, 333, 227, 286, 290, 344, 304, 361, 369, 424, 62, 110, 124, 179, 132, 189, 196, 254, 145, 193, 206, 270, 217, 275, 287, 346, 155, 212, 226, 282, 236, 294, 301, 353, 246, 307, 315, 362, 328, 380, 389, 435, 172, 232, 240, 296, 256, 310, 317, 374, 269, 324, 332, 386, 347, 392, 399, 445, 276, 335, 351, 394, 360, 405, 413, 450, 368, 414, 422, 456, 432, 465, 474, 494, 19, 37, 43, 81, 47, 88, 95, 148, 52, 98, 106, 156, 113, 168, 176, 247, 61, 108, 116, 174, 128, 184, 186, 249, 137, 191, 201, 262, 213, 272, 277, 340, 68, 123, 126, 185, 140, 195, 205, 271, 152, 210, 218, 278, 225, 295, 297, 355, 159, 224, 233, 292, 242, 303, 313, 363, 258, 320, 325, 375, 336, 385, 396, 440, 74, 142, 150, 208, 158, 220, 228, 288, 167, 234, 239, 306, 250, 311, 322, 378, 199, 245, 257, 321, 265, 326, 337, 387, 284, 338, 348, 393, 359, 406, 412, 452, 219, 267, 279, 330, 291, 345, 356, 400, 298, 349, 364, 410, 376, 417, 427, 459, 316, 370, 379, 423, 388, 429, 419, 469, 397, 438, 446, 463, 449, 478, 482, 497, 84, 157, 166, 241, 194, 251, 259, 318, 209, 261, 268, 334, 283, 341, 354, 402, 223, 281, 289, 339, 302, 352, 366, 408, 312, 371, 372, 41 6, 383, 426, 431, 464, 244, 300, 293, 357, 314, 367, 377, 420, 329, 382, 390, 430, 398, 434, 442, 471, 343, 391, 403, 439, 409, 447, 454, 476, 418, 451, 460, 485, 466, 487, 488, 502, 266, 305, 327, 381, 342, 384, 395, 436, 358, 404, 401, 444, 415, 448, 455, 480, 365, 411, 421, 458, 428, 453, 468, 483, 437, 470, 461, 489, 475, 491, 496, 505, 373, 425, 433, 462, 441, 467, 472, 490, 443, 473, 481, 495, 477, 492, 500, 508, 457, 484, 479, 498, 486, 501, 499, 507, 493, 503, 504, 509, 506), 510, 511, 512].
(29) Если N = 1024, последовательность представляет собой Q последовательность и Q последовательность может включать в себя три (n=3) подпоследовательности, местоположения элемента которого, изменчивы. Последовательность может быть:
[1, 2,  , 17,
, 17,  ,
, 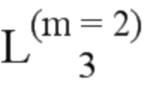 , 1020, 1022, 1023, 1024].
, 1020, 1022, 1023, 1024].
В возможном примере,  может быть следующим:
может быть следующим:  = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и
= (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и 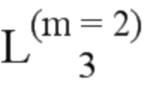 = (1016, 1008).
= (1016, 1008).
В этом примере Q последовательность конкретно является: [1, 2, (5, 9, 3), 17, (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 27 8, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820,840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018 896, 1014 992, 1019, 960, 1021), (1016, 1008), 1020, 1022, 1023, 1024].
(30) Если N = 1024, то последовательность представляет собой Z последовательность и Z последовательность может включать в себя одну (n=1) подпоследовательность, местоположения элемента которого, изменчивы. Последовательность может быть: [1, 2,  , 1022, 1023, 1024].
, 1022, 1023, 1024].
В возможном примере,  может быть следующим:
может быть следующим: 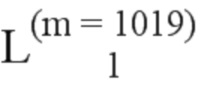 = (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 9 79, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
= (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362, 444, 384, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 9 79, 996, 944, 981, 971, 999, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018).
В этом примере, Z последовательность конкретно является: [1, 2, (5, 11, 3, 13, 8, 25, 4, 16, 19, 29, 12, 34, 37, 71, 6, 18, 14, 31, 21, 40, 48, 77, 23, 52, 42, 85, 58, 93, 100, 162, 7, 17, 22, 43, 26, 51, 47, 89, 30, 56, 63, 97, 68, 108, 112, 170, 36, 60, 73, 111, 78, 120, 127, 185, 84, 130, 139, 201, 149, 208, 226, 323, 9, 24, 27, 54, 35, 59, 67, 104, 38, 75, 61, 114, 81, 124, 137, 194, 44, 70, 82, 129, 92, 132, 146, 206, 101, 150, 159, 219, 172, 239, 251, 356, 53, 88, 98, 143, 109, 152, 163, 234, 116, 165, 184, 250, 198, 259, 277, 378, 131, 192, 202, 269, 213, 280, 296, 395, 232, 303, 319, 416, 339, 431, 464, 574, 15, 28, 41, 69, 32, 80, 74, 133, 46, 83, 91, 144, 99, 156, 158, 227, 57, 95, 103, 153, 110, 168, 183, 244, 125, 182, 193, 258, 205, 272, 288, 390, 62, 107, 122, 181, 118, 186, 196, 270, 141, 204, 214, 281, 230, 301, 314, 411, 147, 217, 235, 306, 248, 338, 348, 433, 266, 357, 364, 452, 386, 482, 498, 613, 66, 119, 136, 203, 145, 215, 224, 304, 160, 221, 238, 332, 252, 340, 358, 454, 173, 246, 265, 350, 279, 371, 383, 468, 293, 389, 406, 484, 426, 518, 536, 641, 195, 273, 284, 373, 307, 396, 408, 508, 331, 419, 432, 530, 460, 542, 557, 667, 341, 435, 465, 547, 480, 570, 588, 681, 496, 590, 609, 698, 633, 727, 757, 844, 20, 39, 45, 86, 49, 94, 102, 164, 55, 106, 115, 174, 123, 191, 200, 294, 65, 117, 126, 197, 140, 209, 212, 297, 151, 218, 231, 317, 247, 337, 345, 445, 72, 134, 138, 210, 154, 223, 236, 336, 169, 243, 254, 346, 263, 372, 374, 471, 177, 262, 274, 368, 287, 385, 403, 486, 311, 412, 420, 510, 439, 528, 551, 654, 79, 157, 167, 240, 176, 256, 267, 359, 189, 276, 283, 388, 299, 397, 415, 514, 228, 291, 309, 413, 324, 423, 440, 532, 352, 441, 461, 545, 479, 572, 585, 687, 255, 328, 347, 428, 365, 453, 473, 559, 377, 463, 488, 581, 512, 597, 621, 708, 407, 500, 516, 611, 534, 625, 601, 740, 553, 648, 670, 720, 678, 772, 791, 849, 90, 175, 187, 286, 222, 300, 313, 410, 242, 316, 330, 434, 351, 446, 469, 563, 261, 349, 362 444 3 84, 467, 492, 577, 398, 502, 504, 595, 524, 618, 630, 723, 290, 381, 370, 475, 404, 494, 513, 604, 427, 522, 538, 628, 555, 638, 659, 747, 451, 540, 566, 651, 579, 673, 693, 765, 599, 684, 711, 802, 730, 807, 814, 878, 326, 387, 425, 520, 447, 526, 549, 643, 477, 568, 561, 664, 592, 675, 695, 783, 490, 583, 606, 705, 623, 690, 737, 795, 646, 743, 714, 817, 761, 831, 848, 899, 506, 616, 635, 717, 656, 733, 750, 822, 662, 754, 787, 847, 769, 836, 871, 938, 701, 799, 776, 858, 806, 875, 866, 929, 837, 884, 894, 949, 920, 961, 975, 993, 10, 33, 76, 121, 50, 135, 105, 211, 64, 155, 171, 225, 128, 249, 257, 333, 87, 166, 142, 237, 180, 260, 292, 361, 178, 298, 268, 382, 312, 399, 414, 533, 96, 161, 207, 275, 190, 295, 282, 393, 220, 308, 321, 417, 335, 436, 449, 541, 241, 327, 344, 443, 355, 462, 470, 567, 367, 481, 499, 587, 509, 614, 626, 738, 113, 188, 199, 302, 245, 315, 334, 430, 229, 343, 353, 456, 366, 466, 483, 580, 271, 363, 376, 489, 392, 472, 497, 600, 405, 521, 531, 619, 552, 649, 660, 759, 289, 391, 401, 519, 422, 507, 537, 634, 438, 544, 571, 650, 582, 669, 685, 774, 476, 562, 591, 680, 603, 691, 713, 788, 636, 706, 729, 810, 745, 820, 842, 915, 148, 216, 264, 342, 233, 360, 369, 485, 285, 379, 394, 501, 409, 525, 535, 627, 310, 402, 421, 511, 437, 554, 564, 652, 455, 550, 578, 666, 602, 694, 709, 780, 320, 429, 448, 558, 459, 565, 586, 677, 493, 589, 617, 697, 631, 715, 735, 804, 515, 615, 642, 718, 657, 731, 748, 823, 674, 762, 771, 835, 790, 855, 872, 931, 325, 458, 487, 593, 505, 612, 624, 719, 529, 622, 644, 739, 661, 758, 770, 833, 548, 653, 672, 752, 688, 763, 784, 853, 704, 789, 798, 860, 813, 879, 889, 942, 584, 676, 696, 778, 726, 792, 801, 868, 732, 811, 824, 886, 838, 895, 904, 951, 751, 826, 843, 898, 859, 908, 916, 956, 869, 919, 928, 966, 937, 976, 985, 1008, 179, 253, 278, 380, 318, 400, 418, 539, 305, 424, 442, 556, 457, 575, 596, 689, 322, 450, 478, 573, 495, 598, 610, 710, 517, 620, 639, 722, 655, 746, 753, 834, 329, 474, 491, 608, 523, 637, 629, 734, 546, 647, 663, 749, 679, 773, 775, 851, 569, 668, 692, 766, 703, 782, 796, 861, 724, 805, 812, 880, 825, 890, 901, 948, 354, 527, 503, 645, 560, 671, 665, 767, 594, 683, 699, 786, 712, 793, 809, 876, 607, 700, 716, 797, 744, 818, 827, 887, 755, 828, 840, 897, 857, 911, 918, 962, 640, 721, 741, 819, 768, 846, 854, 905, 777, 841, 863, 913, 874, 923, 934, 969, 800, 870, 881, 930, 893, 940, 925, 980, 902, 946, 954, 973, 957, 989, 995, 1013, 375, 576, 543, 682, 605, 702, 707, 803, 632, 728, 736, 821, 756, 832, 850, 907, 658, 742, 764, 829, 781, 852, 865, 914, 794, 873, 862, 922, 888, 933, 939, 974, 686, 779, 760, 856, 808, 867, 882, 926, 816, 885, 892, 943, 903, 936, 950, 982, 839, 896, 909, 947, 917, 955, 964, 987, 924, 960, 970, 998, 977, 991, 1001, 1017, 725, 785, 815, 883, 830, 891, 900, 945, 845, 910, 906, 958, 921, 952, 965, 992, 864, 912, 927, 968, 935, 963, 979, 996, 944, 981, 971, 99 9, 986, 1004, 1006, 1015, 877, 932, 941, 972, 953, 978, 983, 1002, 959, 984, 994, 1009, 988, 1003, 1011, 1020, 967, 997, 990, 1007, 1000, 1014, 1010, 1019, 1005, 1012, 1016, 1021, 1018), 1022, 1023, 1024].
В вышеупомянутом примере последовательностях, местоположения элементов в подпоследовательности  может быть в подпоследовательности скорректировано. Например, в примере (1), описанной в примере 1,
может быть в подпоследовательности скорректировано. Например, в примере (1), описанной в примере 1,  = (5, 9, 3), и затем местоположения элементов в первой подпоследовательности
= (5, 9, 3), и затем местоположения элементов в первой подпоследовательности  в последовательности могут быть скорректированы на (5, 3, 9), (3, 5, 9), (3, 9, 5), (5, 9, 3), (9, 3, 5), (9, 5, 3) или тому подобное. После корректировки получают новую последовательность. В приведенных выше конкретных последовательностях, набор элементов в скобках представляет собой вышеупомянутую подпоследовательность
в последовательности могут быть скорректированы на (5, 3, 9), (3, 5, 9), (3, 9, 5), (5, 9, 3), (9, 3, 5), (9, 5, 3) или тому подобное. После корректировки получают новую последовательность. В приведенных выше конкретных последовательностях, набор элементов в скобках представляет собой вышеупомянутую подпоследовательность  , и местоположения элементов в скобках могут быть заменены друг с другом, но местоположения элементов в скобках, не могут быть обменены с местоположениями элементов вне скобок.
, и местоположения элементов в скобках могут быть заменены друг с другом, но местоположения элементов в скобках, не могут быть обменены с местоположениями элементов вне скобок.
Способ выполнения полярного кодирования на основе последовательности в данном варианте осуществления настоящего изобретения описан ниже с помощью примера.
Последовательность, в этом варианте осуществления настоящего изобретения удовлетворяет простой характеристики вложенности, то есть, другая последовательность с относительно короткой длиной материнского кода может быть получена на основе последовательности с относительно большой длиной материнского кода. В частности, например, последовательность, с относительно короткой длиной N2 материнского кода, получают на основе последовательности с относительно большой длиной N1 материнского кода. Элементы, чью номера последовательности меньше или равны N2, извлекается из последовательности с относительно большой длиной N1 материнского кода, и полученная подпоследовательность представляет собой последовательность с относительно короткой длиной N2 материнского кода. Порядок элементов в полученной последовательности с относительно короткой длиной N2 материнского кода является таким же, как порядок этих элементов в последовательности с относительно большой длиной N1 материнского кода. Предполагают, что биты, подлежащие кодированию, с длиной K включает в себя информационные биты с длиной Kinfo и бит проверки с длиной KCRC, длина кода равна М, и длина материнского кода равна N, где К = 27, Kinfo = 8, KCRC = 19, М = 60 и N = 64. При построении параметра для полярного кода, необходимо получить последовательность N=64. Предполагают, что полученная последовательность представляет собой Q последовательность. Q последовательность в предшествующем примере последовательностей N = 64 может быть непосредственно использована в данном варианте осуществления настоящего изобретения, или Q последовательность N=64 может быть получена на основании характеристики вложенности из Q последовательностей N> 64. Например, в примере 1 используют Q последовательность N=128. Получают все номера последовательности, чьи номера последовательности субканала меньше или равно 64, и порядок полученных номеров последовательностей остается неизменным, чтобы сформировать новую последовательность N = 64: [1, 2, (5, 9, 3), 17, 33, (7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), 42, 29, (50, 43, 45, 16, 51, 24, 53), (57, 28, 40), 30, (44, 31, 46), 52, 47, 54, (55, 58), 59, 61, 32, 48, 56, 60, 62, 63, 64]. Местоположения элементов в некоторых подпоследовательностях в последовательности могут быть изменены. Таким образом, новая последовательность N = 64, полученная на основе характеристики вложенности из последовательности N = 128 немного отличается от последовательности N = 64 в примере (1), описанных в примере 1: Диапазон скобок больше, и могут быть получены больше последовательностей.
Например, Q последовательность N = 64 в примере (1), описанной в примере 1, получают непосредственно. Местоположения K поляризованных каналов выбирают в порядке убывания надежности на основании полученной Q последовательности для размещения бит, подлежащих кодированию где К = 27. Более конкретно, биты, подлежащие кодированию, размещают на местах поляризованных каналов, чьи номера последовательности равны (43, 45, 16, 51, 24, 53, 57, 28, 40, 30, 44, 31, 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64) или в местоположениях поляризованных каналов, чьи номера последовательности равны (50, 45, 16, 51, 24, 53, 57, 28, 40, 30, 44, 31, 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64). В полученной непосредственно Q последовательности N = 64, местоположения двух элементов (50, 43) в подпоследовательности  = (50, 43) могут быть взаимно обменены. Таким образом, может быть две возможные комбинации. Биты, подлежащие кодированию, размещают, с равными позициями, в поляризованных каналах, соответствующих подпоследовательностям
= (50, 43) могут быть взаимно обменены. Таким образом, может быть две возможные комбинации. Биты, подлежащие кодированию, размещают, с равными позициями, в поляризованных каналах, соответствующих подпоследовательностям  . Поэтому, не следует рассматривать случай, в котором изменен элементы.
. Поэтому, не следует рассматривать случай, в котором изменен элементы.
Предпосылкой для приведенного выше примера размещения информационных битов является одинаковые приоритеты отправки 27 бит, подлежащих кодированию. Если приоритеты бит, подлежащие кодированию, различны, например, 18 бит проверки должны быть размещены в местах 18 поляризованных каналов с высокой надежностью в отобранных 27 поляризованных каналах, и один бит проверки должен быть помещен на позицию с более низкой надежностью ниже, чем у некоторых информационных битов. В этом случае, когда бит проверки помещают, могут быть рассмотрены порядки бита проверки в четыре подпоследовательностях с  по
по  . Например, бит проверки должен быть помещен на первом месте в
. Например, бит проверки должен быть помещен на первом месте в  . Когда
. Когда  первое местоположение равно 16, и после порядки 16 и 51обмениваются, первое местоположение равно 51. Таким образом, было ли выбрано местоположение 16 или местоположение 51 для бита проверки, что может повлиять на конечную производительность.
первое местоположение равно 16, и после порядки 16 и 51обмениваются, первое местоположение равно 51. Таким образом, было ли выбрано местоположение 16 или местоположение 51 для бита проверки, что может повлиять на конечную производительность.
Местоположения, отличные от местоположений, на которых помещены биты, подлежащие кодированию, являются местоположениями замороженных бит. Выполняют полярное кодирование и согласование скорости на основании местоположений бит, подлежащих кодированию, и местоположений замороженных бит.
Дополнительно, может быть получена новая последовательность N = 64 на основании характеристики вложенности, используя следующие последовательности: последовательность N = 256, последовательность N = 512 или последовательности N = 1024.
Пример N = 64, используемый для вышеизложенного описания, и способ кодирования другой длины кода аналогичен этому. Подробности не описаны здесь снова.
Последовательности (1) до (30), в приведенных выше примерах, в этом варианте осуществления настоящего изобретения, могут быть получены путем использования набора пересечений нескольких групп последовательностей. Например, получают последовательность (1) в предшествующем примере, применяя набор пересечений нескольких групп последовательностей, чьи длины материнского кода равны 64. Конечно, эта последовательность может быть получена другим способом.
В одном из возможных примерах могут быть получены следующие последовательности S1-S20 с помощью моделирования. Последовательности S1-S20 представляют собой последовательности, чьи длины материнского кода равны 1024. На основании характеристики вложенности, последовательности, чьи длины материнского кода равны 64, 128, 256 и 512 могут быть отдельно получены на основе последовательностей S1-S20, чтобы получить 20 групп последовательностей с длинами материнского кода по отдельности 64, 128, 256, 512 и 1024. Последовательности в примерах (1) до (10) и в примере 1, может быть получены на основе первой группы последовательностей по пятую группу последовательностей. Последовательности в примерах (11)-(20) в примере 2, могут быть получены на основе первой группы последовательностей по десятую группу последовательностей. Последовательности в примерах (21) до (30) в примере 3, могут быть получены на основании первой группы последовательностей по двадцатую группу последовательностей. Очевидно, что большее количество комбинированных последовательностей указывает на меньшее количество элементов, местоположение которых остаются неизменными в полученной последовательности, большего количества элементов, местоположения которых изменчивы, и большим диапазоном полученной последовательности.
В этом варианте осуществления настоящего изобретения, способ полярного кодирования, показанный на фиг. 2, дополнительно может быть выполнен с использованием любой из последовательностей S1-S20.
В частности, последовательности S1-S20 могут быть следующими:
Последовательность S1: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 18, 129, 13, 19, 34, 21, 35, 25, 257, 37, 66, 8, 67, 41, 12, 69, 130, 14, 49, 20, 131, 513, 73, 15, 22, 36, 133, 81, 23, 26, 258, 38, 137, 97, 27, 259, 39, 68, 42, 145, 29, 261, 70, 43, 50, 71, 161, 132, 265, 514, 45, 74, 16, 51, 134, 515, 75, 273, 53, 82, 24, 193, 135, 517, 77, 83, 138, 57, 289, 98, 28, 260, 40, 85, 139, 521, 146, 30, 99, 262, 44, 141, 147, 529, 89, 321, 101, 31, 263, 72, 162, 266, 46, 52, 149, 163, 545, 105, 267, 516, 47, 76, 274, 54, 153, 385, 165, 194, 136, 269, 518, 78, 113, 275, 55, 84, 58, 290, 195, 577, 519, 79, 169, 277, 86, 140, 522, 59, 291, 100, 197, 87, 142, 523, 177, 148, 281, 530, 61, 90, 293, 322, 102, 32, 264, 641, 201, 143, 525, 150, 531, 91, 323, 103, 164, 297, 546, 106, 268, 48, 209, 151, 533, 93, 325, 154, 386, 166, 547, 107, 270, 305, 114, 276, 56, 225, 155, 537, 387, 769, 167, 549, 196, 329, 578, 109, 271, 520, 80, 115, 170, 278, 60, 292, 157, 389, 198, 579, 337, 117, 171, 279, 553, 88, 52 4, 178, 282, 62, 294, 199, 581, 393, 642, 173, 202, 144, 526, 179, 561, 121, 353, 283, 532, 63, 92, 295, 324, 104, 298, 643, 203, 585, 401, 527, 181, 210, 152, 285, 534, 94, 326, 299, 548, 108, 645, 306, 205, 211, 593, 535, 95, 327, 185, 417, 226, 156, 538, 388, 770, 168, 301, 550, 330, 110, 272, 307, 116, 213, 649, 158, 227, 609, 539, 390, 771, 551, 331, 580, 111, 309, 338, 118, 172, 280, 554, 657, 217, 449, 229, 159, 541, 391, 773, 200, 333, 582, 339, 119, 394, 174, 555, 180, 313, 562, 122, 354, 284, 64, 296, 583, 673, 233, 341, 395, 644, 777, 175, 557, 204, 586, 402, 528, 182, 563, 123, 286, 355, 300, 397, 646, 206, 587, 241, 403, 785, 183, 565, 212, 345, 594, 125, 357, 287, 536, 96, 328, 186, 418, 302, 705, 647, 308, 207, 589, 405, 214, 595, 650, 187, 569, 419, 801, 228, 361, 610, 540, 772, 303, 552, 332, 112, 310, 215, 597, 651, 409, 658, 189, 218, 421, 450, 230, 160, 542, 611, 392, 774, 334, 369, 311, 340, 120, 556, 653, 314, 659, 219, 601, 451, 833, 231, 613, 543, 775, 335, 584, 425, 674, 234, 342, 396, 778, 176, 558, 315, 564, 124, 661, 356, 221, 453, 675, 235, 343, 617, 398, 779, 433, 559, 588, 242, 404, 786, 184, 317, 566, 346, 126, 358, 288, 665, 897, 677, 457, 706, 237, 399, 648, 781, 208, 590, 243, 625, 406, 787, 567, 347, 596, 127, 359, 188, 570, 420, 802, 362, 304, 707, 465, 591, 245, 407, 681, 789, 216, 349, 598, 652, 410, 190, 571, 422, 803, 363, 612, 709, 370, 312, 599, 654, 689, 249, 481, 411, 660, 793, 191, 573, 220, 423, 602, 805, 452, 834, 232, 365, 614, 544, 776, 336, 371, 426, 713, 655, 316, 413, 662, 222, 603, 454, 835, 615, 373, 427, 676, 809, 236, 344, 618, 780, 434, 560, 318, 721, 663, 223, 605, 455, 837, 666, 898, 429, 678, 458, 238, 619, 400, 782, 435, 817, 244, 377, 626, 788, 319, 568, 348, 128, 360, 737, 667, 899, 679, 459, 708, 841, 239, 621, 783, 437, 466, 592, 246, 627, 408, 682, 790, 350, 572, 804, 669, 364, 901, 461, 710, 467, 849, 247, 629, 683, 791, 351, 600, 441, 690, 250, 482, 412, 794, 192, 574, 424, 806, 366, 711, 372, 469, 905, 685, 714,656, 691, 251, 633, 414, 483, 865, 795, 575, 604, 807, 836, 367, 616, 374, 428, 810, 715, 913, 693, 473, 722, 253, 485, 415, 664, 797, 224, 606, 456, 838, 375, 430, 811, 620, 436, 818, 717, 378, 320, 723, 607, 839, 697, 929, 489, 738, 668, 900, 431, 680, 813, 460, 842, 240, 622, 784, 438, 819, 379, 628, 725, 670, 739, 902, 462, 843, 497, 623, 439, 821, 468, 850, 248, 381, 630, 684, 792, 352, 442, 729, 961, 741, 671, 903, 463, 712, 845, 470, 851, 631, 906, 686, 443, 692, 825, 252, 634, 484, 866, 796, 576, 808, 368, 471, 745, 853, 907, 687, 716, 914, 445, 694, 474, 254, 635, 486, 416, 798, 867, 376, 812, 909, 718, 753, 915, 695, 475, 724, 857, 255, 637, 487, 869, 799, 608, 840, 698, 930, 490, 432, 814, 820, 719, 380, 917, 477, 726, 699, 931, 491, 740, 873, 815, 844, 498, 624, 440, 822, 382, 727, 921, 701, 730, 933, 962, 493, 742, 672, 904, 464, 846, 499, 881, 823, 852, 383, 632, 444, 826, 731, 963, 743, 847, 501, 937, 472, 746, 854, 908, 688, 446, 827, 636, 868, 733, 965, 747, 855, 910,945, 505, 754, 916, 447, 696, 829, 476, 858, 256, 638, 488, 870, 800, 969, 749, 911, 720, 755, 918, 478, 859, 639, 871, 700, 932, 492, 874, 816, 977, 757, 919, 479, 728, 861, 922, 702, 934, 494, 875, 500, 882, 824, 384, 761, 993, 923, 703, 732, 935, 964, 495, 744, 877, 848, 502, 883, 938, 828, 925, 734, 966, 503, 885, 939, 748, 856, 946, 506, 448, 830, 735, 967, 941, 970, 750, 912, 947, 507, 756, 889, 831, 860, 640, 872, 971, 751, 949, 978, 509, 758, 920, 480, 862, 876, 973, 979, 759, 863, 953, 762, 994, 924, 704, 936, 496, 878, 884, 981, 763, 926, 995, 879, 504, 886, 940, 985, 765, 997, 927, 736, 968, 887, 942, 948, 508, 890, 832, 1001, 943, 972, 752, 950, 510, 891, 974, 1009, 951, 980, 511, 760, 893, 864, 954, 975, 982, 955, 764, 996, 880, 983, 957, 986, 766, 998, 928, 888, 987, 767, 999, 1002, 944, 892, 989, 1003, 1010, 952, 512, 894, 1005, 976, 1011, 895, 956, 1013, 984, 958, 1017, 959, 988, 768, 1000, 990, 1004, 991, 1006, 1012, 896, 1007, 1014, 1015, 1018, 960, 1019, 1021, 992, 1 008, 1016, 1020, 1022 1023, 1024];
последовательность S2: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 513, 8, 12, 130, 41, 69, 14, 20, 131, 49, 15, 73, 258, 22, 133, 36, 81, 23, 259, 26, 137, 38, 261, 97, 145, 27, 514, 39, 515, 265, 68, 42, 29, 161, 70, 43, 517, 50, 75, 273, 193, 521, 529, 71, 45, 132, 16, 74, 289, 545, 51, 24, 53, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 40, 98, 385, 30, 85, 139, 262, 146, 31, 99, 516, 44, 89, 141, 263, 147, 72, 266, 46, 101, 162, 518, 577, 519, 52, 149, 522, 47, 76, 267, 163, 274, 523, 641, 105, 54, 153, 78, 269, 194, 165, 275, 55, 84, 530, 525, 531, 136, 58, 113, 195, 290, 79, 169, 277, 59, 86, 61, 87, 140, 100, 197, 90, 291, 281, 546, 769, 142, 177, 91, 102, 148, 143, 533, 547, 537, 32, 103, 264, 106, 322, 293, 201, 323, 578, 150, 297, 48, 93, 209, 549, 579, 268, 386, 325, 305, 164, 151, 107, 56, 154, 225, 387, 329, 270, 114, 520, 553, 642, 80, 166, 109, 155, 276, 60, 271, 115, 167, 524, 581, 561, 157, 196, 170, 198, 171, 278, 292, 279, 1 17, 88, 62, 178, 282, 526, 643, 532, 527, 63, 92, 585, 770, 144, 389, 294, 199, 104, 337, 173, 283, 202, 121, 179, 295, 94, 534, 645, 535, 593, 548, 771, 152, 324, 393, 298, 203, 108, 285, 181, 210, 538, 95, 205, 299, 353, 649, 609, 326, 185, 211, 401, 306, 301, 110, 156, 327, 116, 111, 773, 550, 657, 539, 551, 168, 213, 307, 330, 158, 226, 118, 172, 331, 227, 388, 309, 217, 417, 338, 159, 777, 272, 580, 119, 541, 554, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 123, 394, 284, 64, 175, 341, 449, 354, 395, 233, 204, 673, 555, 557, 562, 582, 296, 286, 182, 206, 125, 785, 705, 183, 287, 528, 583, 644, 586, 563, 300, 355, 212, 402, 186, 397, 345, 207, 302, 801, 96, 187, 241, 536, 587, 565, 646, 594, 328, 403, 214, 357, 308, 303, 833, 589, 647, 112, 540, 569, 595, 650, 772, 228, 418, 332, 215, 405, 310, 189, 552, 610, 897, 160, 218, 361, 419, 409, 369, 230, 450, 421, 542, 597, 651, 774, 658, 311, 120, 334, 219, 543, 611, 176, 392, 231, 314, 124, 340, 335, 221, 451, 425, 315, 556, 601, 653, 234, 775, 659, 613, 235, 288, 453, 126, 342, 396, 778, 584, 558, 674, 356, 343, 564, 661, 559, 617, 779, 675, 184, 398, 433, 317, 346, 242, 208, 404, 358, 786, 188, 588, 566, 665, 625, 781, 237, 127, 243, 347, 399, 706, 216, 677, 787, 590, 567, 648, 406, 359, 304, 570, 596, 362, 707, 190, 457, 349, 465, 802, 420, 407, 245, 410, 591, 681, 789, 571, 598, 363, 573, 220, 422, 599, 652, 612, 709, 602, 803, 370, 793, 312, 191, 654, 689, 603, 411, 232, 249, 365, 336, 423, 614, 660, 655, 316, 222, 371, 426, 452, 413, 481, 236, 223, 344, 318, 544, 373, 615, 427, 776, 128, 454, 238, 560, 834, 805, 713, 835, 662, 809, 605, 618, 721, 780, 434, 898, 319, 455, 837, 817, 676, 663, 348, 429, 400, 377, 244, 239, 458, 435, 360, 568, 619, 666, 737, 899, 841, 782, 626, 350, 246, 459, 592, 678, 621, 667, 788, 572, 783, 627, 679, 408, 364, 351, 437, 192, 247, 466, 412, 461, 250, 366, 600, 708, 574, 669, 682, 790, 804, 791, 710, 683, 629, 441, 690, 794, 604, 575, 467, 424, 372, 251, 414, 367, 469, 482, 374, 656, 901, 806, 711, 428, 415, 253, 616, 849, 685, 795, 714, 633, 691, 807, 606, 483, 473, 224, 664, 836, 905, 810, 715, 620, 797, 693, 375, 485, 430, 456, 722, 607, 717, 811, 865, 838, 697, 723, 913, 818, 378, 436, 813, 320, 622, 240, 431, 460, 379, 668, 839, 489, 438, 628, 623, 462, 381, 439, 352, 497, 680, 725, 819, 842, 670, 738, 630, 468, 248, 442, 463, 470, 443, 252, 684, 843, 739, 900, 821, 729, 929, 850, 671, 784, 631, 792, 845, 902, 686, 368, 634, 712, 254, 692, 741, 851, 825, 903, 687, 471, 416, 484, 445, 376, 474, 906, 796, 486, 635, 745, 853, 961, 866, 907, 716, 694, 808, 475, 798, 637, 695, 255, 718, 576, 799, 812, 867, 432, 380, 698, 914, 487, 724, 909, 857, 719, 477, 814, 608, 490, 699, 753, 840, 915, 726, 869, 820, 815, 440, 491, 624, 382, 498, 493, 464, 672, 930, 844, 740, 917, 822, 727, 632, 701, 873, 931, 921, 881,730, 383, 499, 444, 446, 472, 962, 933, 823, 742, 846, 731, 447, 688, 904, 636, 826, 743, 852, 847, 256, 476, 733, 963, 937, 827, 746, 501, 488, 638, 505, 800, 696, 854, 908, 868, 855, 747, 910, 829, 965, 858, 754, 720, 916, 870, 478, 700, 749, 639, 816, 945, 755, 859, 911, 492, 479, 728, 918, 871, 384, 494, 500, 874, 702, 969, 495, 861, 502, 932, 919, 757, 922, 875, 732, 977, 934, 882, 761, 824, 703, 923, 744, 877, 848, 935, 828, 734, 883, 448, 938, 503, 964, 925, 993, 748, 735, 856, 885, 939, 506, 966, 507, 830, 750, 946, 860, 831, 967, 756, 941, 912, 872, 751, 889, 480, 970, 947, 862, 758, 971, 509, 920, 640, 876, 863, 759, 949, 978, 924, 973, 762, 878, 979, 496, 936, 704, 884, 953, 763, 504, 926, 879, 981, 994, 886, 940, 927, 765, 736, 887, 995, 942, 968, 985, 508, 890, 948, 832, 752, 943, 997, 972, 891, 1001, 510, 950, 974, 893, 951, 864, 760, 1009, 511, 980, 954, 764, 975, 955, 880, 982, 983, 928, 996, 766, 957, 888, 986, 998, 987, 944, 892, 999, 767, 512, 989, 1002, 952, 1003, 8 94, 976, 895, 1010, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S3: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 8, 130, 67, 513, 12, 41, 69, 20, 14, 131, 49, 15, 73, 258, 22, 133, 36, 23, 259, 81, 26, 137, 38, 27, 514, 97, 261, 39, 515, 265, 68, 42, 145, 29, 70, 43, 517, 50, 161, 273, 71, 289, 545, 45, 193, 521, 529, 132, 74, 51, 134, 82, 75, 16, 24, 53, 321, 135, 77, 57, 83, 28, 138, 98, 40, 385, 260, 85, 139, 262, 30, 146, 44, 99, 516, 89, 141, 31, 147, 46, 263, 72, 266, 101, 162, 518, 577, 519, 52, 149, 522, 47, 76, 267, 105, 274, 523, 641, 163, 54, 153, 78, 269, 194, 165, 275, 55, 84, 530, 525, 531, 136, 58, 113, 79, 277, 195, 290, 59, 169, 86, 140, 100, 87, 197, 142, 291, 61, 281, 546, 769, 90, 102, 148, 177, 91, 143, 533, 547, 537, 293, 201, 264, 32, 150, 322, 323, 578, 103, 106, 93, 48, 297, 164, 151, 209, 549, 579, 386, 268, 305, 325, 107, 154, 387, 166, 56, 329, 114, 520, 553, 642, 155, 80, 109, 225, 270, 167, 524, 581, 561, 60, 276, 271, 115, 196, 170, 292, 278, 157, 88, 171, 117, 27 9, 198, 62, 282, 526, 643, 532, 527, 178, 294, 389, 92, 585, 770, 199, 144, 63, 121, 202, 283, 173, 104, 337, 179, 295, 94, 534, 645, 535, 593, 548, 771, 298, 393, 324, 285, 203, 181, 108, 152, 210, 538, 95, 205, 299, 401, 326, 353, 649, 609, 306, 301, 156, 211, 110, 168, 185, 116, 226, 327, 158, 111, 773, 550, 657, 539, 551, 307, 213, 330, 118, 172, 331, 227, 388, 309, 272, 580, 417, 217, 338, 159, 777, 119, 541, 554, 280, 333, 390, 174, 122, 200, 180, 229, 394, 284, 391, 175, 313, 123, 673, 555, 557, 562, 582, 354, 204, 64, 182, 339, 296, 449, 341, 286, 395, 233, 125, 785, 705, 206, 183, 287, 528, 583, 644, 586, 563, 300, 355, 212, 402, 186, 397, 241, 536, 587, 565, 646, 594, 207, 302, 801, 345, 403, 328, 357, 308, 96, 418, 214, 187, 405, 112, 540, 569, 595, 650, 772, 303, 833, 589, 647, 228, 361, 215, 189, 552, 610, 897, 332, 310, 419, 409, 218, 450, 230, 160, 421, 542, 597, 651, 774, 658, 392, 334, 311, 369, 340, 120, 314, 219, 543, 611, 335, 231, 234, 775, 659, 613, 176, 124, 315, 556, 601, 653, 342, 221, 425, 451, 396, 778, 584, 558, 674, 356, 288, 184, 235, 126, 343, 564, 661, 559, 617, 779, 675, 317, 242, 346, 453, 398, 404, 208, 433, 358, 786, 188, 588, 566, 665, 625, 781, 237, 127, 243, 399, 706, 347, 457, 359, 406, 304, 570, 596, 190, 216, 677, 787, 590, 567, 648, 362, 707, 245, 349, 420, 407, 465, 802, 410, 591, 681, 789, 571, 598, 312, 363, 573, 220, 422, 599, 652, 612, 709, 602, 803, 370, 793, 191, 654, 689, 603, 249, 232, 411, 336, 365, 423, 614, 660, 655, 316, 222, 371, 426, 236, 452, 481, 413, 344, 223, 318, 544, 373, 615, 427, 776, 454, 238, 560, 834, 805, 713, 835, 662, 809, 605, 618, 721, 780, 348, 319, 244, 434, 898, 455, 837, 817, 676, 663, 360, 568, 619, 666, 737, 899, 841, 782, 626, 429, 377, 400, 239, 458, 435, 128, 350, 246, 459, 592, 678, 621, 667, 788, 572, 783, 627, 679, 437, 408, 466, 364, 247, 351, 412, 461, 250, 366, 600, 708, 574, 669, 682, 790, 804, 791, 710, 683, 629, 467, 192, 441, 690, 794, 604, 575, 372, 424, 251, 482, 469, 367, 414, 374, 656, 901, 806, 711, 428, 415, 253, 616, 849, 685, 795, 714, 633, 691, 807, 606, 483, 473, 224, 664, 836, 905, 810, 715, 620, 797, 693, 375, 430, 456, 722, 607, 717, 811, 865, 838, 697, 723, 913, 818, 378, 436, 813, 485, 320, 622, 431, 240, 379, 668, 839, 460, 438, 628, 623, 489, 381, 462, 497, 680, 725, 819, 842, 670, 738, 630, 352, 439, 468, 248, 442, 463, 470, 443, 252, 684, 843, 739, 900, 821, 729, 929, 850, 671, 784, 631, 792, 845, 902, 686, 368, 634, 712, 254, 692, 741, 851, 825, 903, 687, 471, 416, 484, 445, 376, 474, 906, 796, 486, 635, 745, 853, 961, 866, 907, 716, 694, 808, 475, 798, 637, 695, 255, 718, 576, 799, 812, 867, 432, 380, 698, 914, 487, 724, 909, 857, 719, 477, 814, 608, 490, 699, 753, 840, 915, 726, 869, 820, 815, 440, 491, 624, 382,498, 493, 464, 672, 930, 844, 740, 917, 822, 727, 632, 701, 873, 931, 921, 881, 730, 383, 499, 444, 446, 472, 962, 933, 823, 742, 846, 731, 447, 688, 904, 636, 826, 743, 852, 847, 256, 476, 733, 963, 937, 827, 746, 501, 488, 638, 505, 800, 696, 854, 908, 868, 855, 747, 910, 829, 858, 754, 720, 916, 870, 478, 700, 749, 639, 816, 965, 945, 755, 859, 911, 492, 479, 728, 918, 871, 384, 494, 500, 874, 702, 969, 495, 861, 502, 932, 919, 757, 922, 875, 732, 977, 934, 882, 761, 824, 703, 923, 744, 877, 848, 935, 828, 734, 883, 448, 938, 503, 964, 925, 993, 748, 735, 856, 885, 939, 506, 966, 507, 830, 750, 946, 860, 831, 967, 756, 941, 912, 872, 751, 889, 480, 970, 947, 862, 758, 971, 509, 920, 640, 876, 863, 759, 949, 978, 924, 973, 762, 878, 979, 496, 936, 704, 884, 953, 763, 504, 926, 879, 981, 994, 886, 940, 927, 765, 736, 887, 995, 942, 968, 985, 508, 890, 948, 832, 752, 943, 997, 972, 891, 1001, 510, 950, 974, 893, 951, 864, 760, 1009, 511, 980, 954, 764, 975, 955, 880, 982, 983, 928, 996, 766, 957, 888, 986, 998, 987, 944, 892, 999, 767, 512, 989, 1002, 952, 1003, 894, 976, 895, 1010, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024 ];
последовательность S4: [1, 2, 3, 5, 9, 17, 33, 4, 6, 513, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 8, 130, 67, 12, 41, 69, 20, 514, 14, 131, 49, 15, 73, 258, 22, 133, 36, 23, 259, 81, 26, 137, 38, 27, 515, 97, 261, 39, 265, 68, 42, 145, 29, 70, 43, 50, 161, 273, 517, 71, 289, 45, 193, 132, 74, 51, 134, 82, 75, 16, 521, 24, 53, 321, 135, 77, 57, 83, 28, 138, 98, 529, 40, 385, 260, 85, 139, 262, 30, 146, 545, 44, 99, 89, 141, 31, 147, 46, 263, 516, 72, 266, 101, 162, 52, 149, 47, 518, 76, 267, 105, 274, 163, 54, 153, 577, 78, 269, 194, 165, 275, 55, 519, 84, 136, 58, 113, 79, 277, 522, 195, 290, 59, 169, 86, 140, 523, 100, 87, 197, 142, 291, 641, 61, 281, 90, 102, 148, 177, 530, 91, 143, 293, 201, 264, 525, 32, 150, 322, 323, 531, 103, 106, 93, 48, 297, 546, 164, 151, 209, 386, 769, 268, 305, 325, 107, 533, 154, 387, 166, 56, 329, 547, 114, 155, 80, 537, 109, 225, 270, 167, 578, 60, 276, 271, 115, 549, 196, 170, 292, 278, 520, 157, 88, 171, 642, 117, 279, 198, 62, 579, 282, 178, 294, 524, 389, 92, 199, 144, 553, 63, 121, 202, 581, 283, 173, 104, 532, 337, 179, 295, 526, 94, 298, 393, 643, 324, 285, 203, 561, 181, 108, 152, 527, 210, 95, 205, 585, 299, 401, 326, 770, 353, 306, 534, 301, 156, 211, 645, 110, 168, 185, 548, 116, 226, 535, 327, 158, 111, 771, 307, 213, 593, 330, 118, 172, 538, 331, 227, 649, 388, 309, 272, 550, 417, 217, 539, 338, 159, 609, 119, 280, 773, 333, 390, 174, 551, 122, 200, 777, 180, 229, 580, 394, 284, 554, 391, 175, 657, 313, 123, 541, 354, 204, 64, 582, 182, 339, 555, 296, 449, 562, 341, 286, 673, 395, 785, 233, 125, 583, 206, 183, 801, 287, 300, 557, 355, 212, 705, 402, 186, 644, 397, 241, 586, 207, 302, 563, 345, 646, 403, 328, 594, 357, 308, 587, 96, 528, 418, 214, 536, 187, 405, 565, 112, 833, 303, 228, 647, 361, 215, 589, 189, 569, 332, 310, 595, 419, 409, 540, 218, 650, 450, 230, 610, 160, 552, 421, 392, 897, 334, 772, 311, 369, 597, 340, 651, 120, 774, 314, 219, 542, 335, 658, 231, 234, 556, 176, 611, 124, 315, 601, 342, 653, 221, 543, 425, 451, 659, 396, 558, 356, 775, 288, 584, 184, 235, 778, 126, 613, 343, 674, 317, 242, 564, 346, 661, 453, 559, 398, 588, 404, 208, 779, 433, 617, 358, 786, 188, 675, 237, 566, 127, 665, 243, 399, 590, 347, 781, 457, 706, 35 9, 677, 406, 787, 304, 567, 190, 596, 216, 648, 362, 570, 245, 349, 625, 420, 591, 407, 789, 465, 707, 410, 802, 312, 571, 363, 681, 220, 598, 422, 652, 370, 612, 191, 599, 249, 709, 232, 654, 411, 803, 336, 573, 365, 793, 423, 316, 222, 602, 371, 614, 426, 660, 236, 689, 452, 603, 481, 655, 413, 805, 344, 713, 223, 776, 318, 544, 373, 662, 427, 834, 454, 835, 238, 615, 348, 618, 605, 319, 560, 244, 809, 434, 676, 455, 663, 360, 721, 429, 898, 377, 780, 400, 817, 239, 837, 458, 619, 666, 435, 899, 128, 678, 350, 568, 246, 841, 459, 626, 667, 437, 592, 408, 621, 466, 737, 364, 782, 247, 679, 572, 351, 788, 412, 783, 461, 627, 708, 250, 682, 366, 804, 467, 790, 192, 669, 600, 441, 683, 372, 629, 791, 424, 710, 251, 574, 482, 794, 690, 469, 806, 367, 901, 604, 414, 711, 374, 656, 428, 575, 633, 415, 714, 253, 795, 685, 483, 616, 473, 849, 691, 224, 807, 606, 375, 810, 430, 905, 836, 456, 797, 378, 715, 693, 436, 620, 664, 485, 722, 320, 607, 717, 431, 811, 913, 240, 838, 379, 865, 818, 46 0, 813, 668, 438, 723, 622, 489, 680, 381, 697, 628, 462, 738, 839, 497, 670, 623, 352, 819, 725, 439, 842, 630, 468, 684, 843, 248, 739, 442, 900, 821, 463, 784, 929, 470, 729, 850, 671, 443, 631, 792, 252, 845, 902, 368, 686, 634, 254, 712, 692, 471, 741, 906, 416, 796, 903, 484, 687, 825, 635, 445, 866, 716, 376, 576, 694, 474, 851, 808, 961, 486, 853, 798, 475, 907, 745, 255, 637, 718, 695, 432, 799, 812, 380, 867, 724, 914, 487, 698, 909, 477, 753, 719, 814, 490, 857, 915, 840, 440, 869, 820, 608, 491, 930, 726, 382, 699, 917, 624, 498, 815, 740, 873, 493, 727, 701, 844, 464, 822, 931, 921, 383, 730, 962, 742, 499, 672, 933, 904, 444, 846, 823, 881, 852, 446, 632, 826, 731, 472, 847, 743, 746, 447, 688, 636, 827, 854, 256, 733, 937, 963, 476, 908, 868, 800, 696, 501, 747, 638, 855, 829, 488, 754, 858, 965, 910, 505, 916, 720, 945, 478, 870, 700, 749, 639, 755, 492, 911, 859, 969, 871, 479, 918, 816, 702, 728, 384, 874, 757, 861, 932, 919, 494, 977, 922, 824, 875, 732, 500, 934, 882, 703, 761, 495, 744, 923, 848, 877, 935, 828, 502, 734, 883, 938, 748, 964, 448, 993, 925, 856, 735, 830, 885, 503, 939, 966, 750, 860, 831, 756, 506, 946, 967, 872, 941, 889, 912, 507, 751, 970, 947, 640, 862, 758, 971, 480, 949, 920, 978, 876, 759, 863, 924, 509, 973, 762, 878, 979, 704, 953, 884, 936, 496, 763, 994, 981, 879, 926, 886, 940, 927, 504, 765, 995, 985, 736, 887, 942, 968, 890, 948, 997, 508, 832, 943, 752, 891, 972, 950, 1001, 893, 974, 1009, 864, 510, 951, 980, 760, 954, 975, 982, 955, 764, 880, 766, 983, 928, 996, 511, 957, 888, 986, 998, 987, 767, 944, 892, 999, 989, 1002, 952, 1003, 894, 1010, 1005, 976, 512, 895, 1011, 956, 958, 984, 959, 768, 988, 1013, 1000, 1017, 990, 1004, 991, 896, 1006, 1012, 1007, 1014, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022 1023, 1024];
последовательность S5: [1, 2, 5, 9, 3, 17, 33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629,424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904,688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 10 00, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021, 1016, 1008, 1020, 1022, 1023, 1024];
последовательность S6: [1, 2, 3, 5, 9, 17, 33, 4, 257, 513, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 21, 35, 25, 66, 37, 258, 67, 8, 12, 130, 41, 69, 514, 14, 20, 131, 49, 15, 73, 259, 22, 133, 36, 81, 23, 26, 137, 38, 97, 515, 261, 145, 27, 39, 68, 42, 29, 161, 70, 265, 43, 50, 75, 517, 193, 71, 45, 273, 132, 16, 74, 51, 24, 53, 289, 521, 134, 82, 77, 135, 28, 57, 260, 83, 138, 40, 529, 98, 262, 30, 85, 139, 146, 31, 321, 545, 99, 44, 89, 141, 263, 147, 72, 46, 516, 101, 266, 162, 52, 149, 47, 267, 769, 76, 163, 105, 385, 54, 153, 78, 518, 194, 274, 165, 55, 84, 269, 577, 136, 58, 113, 275, 195, 79, 519, 169, 290, 59, 86, 61, 277, 522, 87, 140, 291, 100, 197, 523, 90, 281, 142, 177, 322, 91, 641, 102, 148, 293, 143, 32, 530, 323, 103, 106, 264, 525, 201, 150, 48, 268, 93, 531, 209, 386, 164, 151, 546, 297, 107, 56, 325, 533, 154, 225, 270, 114, 80, 547, 276, 166, 109, 537, 387, 155, 60, 305, 578, 115, 167, 271, 157, 549, 329, 196, 170, 278, 770, 198, 171, 389, 579, 117, 292, 88, 62, 520, 337, 178, 63, 524, 279, 92, 282, 144, 642, 199, 393, 104, 553, 294, 173, 353, 581, 202, 121, 401, 526, 179, 283, 94, 532, 152, 295, 203, 643, 324, 108, 298, 561, 181, 210, 285, 527, 95, 417, 205, 585, 326, 185, 771, 299, 211, 110, 534, 306, 156, 331, 645, 116, 449, 548, 111, 327, 168, 593, 301, 213, 535, 388, 158, 272, 538, 226, 118, 649, 330, 172, 307, 550, 227, 280, 609, 217, 309, 773, 159, 390, 657, 119, 338, 174, 539, 333, 122, 551, 391, 200, 580, 180, 229, 554, 284, 123, 541, 313, 64, 673, 339, 175, 394, 582, 233, 296, 777, 204, 354, 555, 182, 286, 562, 341, 587, 206, 395, 705, 125, 402, 583, 183, 287, 557, 212, 355, 785, 186, 300, 644, 207, 345, 528, 96, 397, 586, 187, 563, 403, 328, 536, 241, 302, 565, 214, 801, 357, 112, 646, 418, 228, 594, 308, 589, 405, 215, 647, 303, 189, 540, 332, 569, 160, 419, 772, 361, 218, 595, 310, 650, 230, 409, 552, 334, 610, 120, 450, 774, 219, 542, 421, 176, 597, 311, 651, 340, 658, 231, 392, 543, 314, 833, 124, 369, 611, 221, 556, 451, 335, 601, 234, 653, 425, 775, 235, 315, 659, 342, 584, 126, 558, 317, 613, 343, 184, 778, 396, 674, 356, 564, 242, 453, 661, 208, 559, 346, 779, 398, 588, 188, 433, 675, 347, 617, 237, 897, 358, 566, 404, 665, 127, 590, 399, 288, 706, 243, 786, 359, 677, 362, 567, 216, 596, 457, 781, 406, 648, 190, 570, 304, 625, 349, 245, 787, 465, 707, 420, 591, 407, 681, 220, 802, 363, 571, 312, 598, 191, 573, 410, 789, 481, 599, 232, 652, 370, 803, 336, 612, 422, 709, 249, 602, 365, 793, 411, 222, 316, 654, 371, 689, 423, 834, 236, 603, 413, 614, 452, 660, 426, 805, 223, 655, 454, 544, 427, 835, 128, 615, 373, 618, 344, 776, 318, 713, 238, 662, 560, 434, 780, 319, 605, 348, 721, 244, 898, 400, 676, 455, 663, 360, 809, 429, 619, 239, 568, 458, 837, 666, 377, 737, 435, 782, 246, 626, 350, 592, 408, 788, 678, 459, 621, 192, 899, 364, 667, 437, 572, 466, 817, 627, 351, 679, 247, 783, 461, 669, 841, 441, 708, 467, 682, 366, 790, 250, 710, 683, 412, 901, 372, 629, 804, 367, 600, 424, 574, 251, 849, 690, 469, 575, 414, 791, 604, 482, 794, 374, 656, 428, 711, 905, 253, 616, 483, 806, 685, 473, 865, 415, 714, 633, 375, 913, 691, 224, 795, 430, 606, 664, 378, 807, 456, 715, 836, 436, 620, 810, 485, 693, 379, 722, 797, 240, 607, 929, 320, 717, 431, 838, 697, 489, 811, 723, 460, 622, 818, 438, 668, 462, 843, 628, 248, 961, 623, 381, 839, 680, 439, 813, 725, 468, 900, 670, 442, 784, 738, 463, 630, 352, 842, 684, 252, 819, 739, 443, 792, 729, 821, 497, 671, 902, 470, 631, 850, 368, 686, 845, 484, 634, 903, 471, 712, 692, 445, 741, 796, 416, 635, 825, 576, 254, 851, 687, 474, 906, 745, 486, 808, 716, 866, 376, 694, 798, 475, 853, 718, 432, 907, 637, 914, 487, 695, 799, 380, 724, 867, 698, 477, 812, 719, 490, 857, 608, 909, 255, 699, 915, 840, 491, 753, 814, 726, 382, 869, 624, 440, 930, 740, 820, 498, 917, 727, 815, 464, 701, 844, 672, 444, 931, 873, 730, 493, 822, 742,921, 383, 846, 632, 962, 499, 731, 933, 688, 823, 472, 852, 743, 904, 446, 826, 636, 881, 501, 733, 963, 847, 746, 256, 937, 747, 827, 476, 854, 638, 829, 855, 447, 696, 908, 868, 754, 488, 965, 720, 858, 910, 505, 700, 945, 859, 478, 749, 870, 916, 639, 911, 492, 800, 755, 871, 874, 479, 728, 969, 918, 702, 384, 816, 861, 757, 977, 932, 494, 919, 732, 875, 824, 703, 500, 922, 993, 744, 882, 495, 848, 934, 761, 877, 923, 734, 502, 828, 883, 935, 748, 925, 448, 964, 938, 735, 966, 939, 640, 503, 885, 856, 830, 750, 946, 831, 506, 860, 756, 912, 967, 872, 941, 507, 751, 970, 889, 947, 758, 862, 920, 509, 971, 704, 876, 949, 978, 863, 759, 480, 973, 953, 979, 878, 762, 924, 884, 879, 496, 936, 763, 981, 926, 994, 886, 940, 765, 504, 995, 985, 927, 887, 736, 942, 890, 968, 948, 997, 508, 891, 752, 832, 943, 1001, 972, 950, 974, 760, 893, 951, 510, 980, 954, 975, 864, 764, 955, 1009, 982, 880, 996, 983, 957, 928, 511, 766, 986, 998, 888, 987, 944, 999, 892, 989, 1002, 767, 1003, 894, 952, 1 010, 976, 956, 512, 1005, 895, 1011, 984, 958, 1013, 768, 988, 959, 1000, 1017 990, 1004, 991, 896, 1006, 1012, 1007, 1014, 960, 1015, 1018, 1019, 1021, 992, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S7: [1, 2, 3, 5, 9, 17, 4, 33, 6, 7, 65, 10, 11, 18, 13, 19, 129, 34, 21, 35, 25, 8, 37, 66, 257, 67, 12, 41, 69, 14, 20, 49, 130, 15, 73, 22, 131, 513, 36, 23, 133, 81, 26, 38, 27, 258, 137, 39, 68, 97, 42, 259, 29, 145, 43, 70, 261, 50, 71, 16, 45, 74, 51, 265, 132, 161, 514, 75, 24, 53, 134, 82, 515, 273, 77, 135, 83, 28, 57, 193, 138, 517, 40, 98, 85, 260, 30, 139, 289, 521, 146, 99, 44, 31, 262, 141, 89, 147, 72, 101, 46, 263, 529, 321, 52, 266, 162, 149, 47, 76, 105, 267, 54, 163, 516, 274, 153, 545, 78, 55, 269, 136, 165, 84, 113, 58, 194, 275, 518, 385, 79, 59, 86, 195, 140, 290, 169, 519, 277, 577, 522, 100, 87, 32, 291, 61, 197, 142, 90, 523, 281, 148, 177, 102, 264, 143, 293, 530, 91, 322, 201, 525, 150, 103, 48, 531, 106, 641, 323, 93, 268, 297, 164, 151, 209, 154, 546, 107, 533, 325, 56, 270, 166, 114, 276, 155, 547, 305, 386, 80, 109, 271, 537, 167, 115, 329, 60, 196, 225, 170, 520, 278, 387, 157, 549, 578, 769, 88, 117, 292, 62, 171, 198, 279, 389, 579, 337, 524, 282, 553, 178, 63, 199, 144, 294, 173, 92, 121, 202, 283, 581, 526, 179, 393, 104, 295, 532, 561, 642, 324, 94, 203, 353, 298, 527, 285, 152, 181, 585, 210, 108, 534, 643, 401, 95, 299, 326, 205, 211, 156, 548, 306, 185, 535, 110, 645, 327, 272, 593, 301, 538, 168, 116, 330, 226, 307, 213, 388, 158, 550, 417, 111, 539, 770, 649, 331, 118, 227, 172, 280, 159, 551, 309, 390, 580, 338, 217, 609, 554, 771, 541, 119, 333, 64, 200, 229, 174, 391, 122, 657, 339, 284, 555, 313, 582, 449, 180, 394, 773, 296, 175, 562, 123, 204, 354, 233, 583, 341, 528, 286, 395, 557, 182, 586, 563, 777, 644, 402, 96, 673, 355, 125, 300, 206, 287, 183, 397, 587, 345, 212, 241, 186, 536, 403, 565, 646, 328, 207, 357, 594, 302, 785, 589, 308, 187, 214, 418, 112, 647, 405, 595, 303, 540, 569, 705, 650, 332, 361, 228, 215, 160, 552, 310, 419, 189, 218, 610, 597, 772, 542, 651, 409, 801, 120, 334, 230, 311, 392, 421, 658, 340, 219, 611, 369, 556, 314, 450, 543, 774, 653, 335, 601, 231, 176, 124, 659, 234, 315, 584, 342, 451, 221, 613, 396, 558, 425, 775, 833, 564, 778, 674, 356, 126, 235, 661, 343, 288, 559, 317, 453, 184, 398, 588, 346, 617, 242, 779, 404, 566, 675, 433, 127, 208, 358, 237, 399, 786, 665, 347, 590, 243, 457, 188, 567, 781, 648, 406, 677, 359, 596, 304, 625, 570, 706, 787, 362, 897, 591, 349, 216, 245, 420, 190, 407, 571, 598, 707, 465, 652, 410, 802, 681, 363, 789, 312, 191, 422, 220, 612, 370, 249, 599, 544, 411, 803, 573, 709, 654, 336, 365, 602, 232, 793, 423, 660, 689, 371, 316, 452, 222, 614, 481, 426, 776, 655, 413, 805, 603, 834, 713, 236, 662, 344, 223, 615, 373, 560, 318, 427, 454, 618, 835, 605, 780, 809, 676, 434, 128, 663, 238, 319, 455, 400, 721, 429, 666, 348, 619, 377, 244, 458, 837, 568, 782, 435, 678, 360, 239, 626, 788, 667, 817, 898, 592, 350, 459, 621, 246, 783, 408, 679, 437, 627, 841, 572, 708, 466, 737, 682, 364, 790, 899, 669, 351, 247, 461, 192, 250, 600, 467, 629, 412, 804, 574, 683, 441, 710, 791, 366, 901, 849, 794, 424, 690, 372, 251, 482, 575, 711, 469, 656, 414, 806, 685, 367, 604, 633, 714, 795, 691, 905, 224, 616, 374, 483, 253, 428, 415, 807, 836, 606, 715, 473, 865, 810, 797, 664, 693, 375, 320, 456, 485, 722, 430, 620, 378, 913, 607, 811, 838, 717, 436, 240, 723, 431, 668, 818, 697, 379, 460, 622, 489, 839, 784, 813, 680, 438, 628, 842, 738, 819, 725, 900, 670, 352, 929, 623, 381, 248, 462, 439, 843, 468, 630, 739, 497, 684, 442, 792, 671, 821, 902, 463, 850, 729, 252, 631, 845, 576, 443, 712, 470, 741, 686, 368, 903, 634, 851, 796, 825, 961, 692, 906, 484, 254, 471, 416, 808, 687, 445, 635, 716, 474, 866, 745, 853, 798, 907, 694, 376, 255, 486, 914, 608, 475, 867, 637, 812, 718, 799, 695, 909, 857, 487, 724, 432, 753, 698, 380, 915, 490, 840, 719, 477, 869, 814, 820, 699, 726, 930, 624, 382, 491, 917, 815, 440, 844, 873, 740, 498, 727, 672, 822, 931, 701, 383, 464, 493, 730, 921, 632, 846, 499, 444, 742, 823, 904, 933, 852, 731, 881, 826, 962, 847, 472, 743, 501, 688, 446, 636, 746, 827, 854, 963, 733, 908, 937, 256, 447, 476, 868, 638, 747, 505, 855, 800, 829, 965, 696, 910, 858, 488, 754, 916, 945, 639, 720, 478, 870, 749, 911, 859, 755, 969, 700, 492, 918, 479, 871, 816, 874, 861, 728, 757, 932, 702, 384, 919, 494,977, 922, 875, 500, 824, 703, 934, 495, 732, 882, 761, 923, 848, 877, 744, 502, 935, 883, 828, 964, 734, 993, 938, 925, 503, 448, 748, 506, 856, 735, 885, 830, 939, 966, 946, 640, 507, 750, 831, 967, 912, 941, 860, 889, 756, 970, 947, 480, 872, 751, 509, 862, 971, 758, 920, 949, 978, 876, 863, 759, 973, 704, 496, 762, 979, 924, 953, 878, 936, 884, 763, 994, 981, 926, 879, 504, 736, 886, 995, 765, 940, 927, 985, 508, 887, 832, 968, 997, 942, 890, 948, 752, 510, 943, 891, 972, 1001, 950, 511, 864, 893, 760, 974, 951, 980, 1009, 954, 975, 764, 955, 982, 880, 996, 766, 983, 928, 957, 986, 888, 767, 998, 987, 999, 944, 892, 1002, 989, 512, 894, 1003, 952, 1010, 895, 976, 1005, 1011, 956, 984, 1013, 958, 768, 959, 988, 1017, 1000, 990, 1004, 991, 896, 1006, 1012, 1007, 1014, 1015, 960, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S8: [1, 2, 3, 5, 9, 17, 33, 4, 6, 7, 65, 10, 11, 18, 13, 129, 19, 34, 21, 35, 25, 257, 37, 8, 66, 67, 41, 12, 69, 14, 130, 49, 20, 15, 73, 513, 131, 22, 133, 36, 23, 81, 26, 258, 38, 137, 27, 259, 39, 97, 68, 42, 29, 145, 261, 70, 43, 50, 71, 265, 45, 16, 74, 514, 161, 132, 51, 75, 515, 134, 273, 53, 24, 82, 77, 517, 135, 193, 83, 138, 57, 28, 289, 260, 40, 98, 521, 139, 85, 30, 146, 262, 99, 141, 44, 31, 89, 529, 147, 263, 321, 101, 72, 266, 46, 162, 149, 52, 267, 47, 105, 545, 76, 516, 163, 274, 54, 153, 269, 385, 78, 518, 165, 136, 275, 194, 55, 113, 84, 58, 79, 519, 577, 290, 195, 277, 522, 169, 140, 86, 59, 291, 197, 100, 523, 87, 142, 281, 61, 32, 90, 530, 177, 148, 293, 264, 322, 102, 525, 143, 201, 641, 91, 531, 150, 323, 103, 297, 268, 48, 106, 546, 164, 93, 533, 151, 209, 325, 154, 270, 107, 547, 386, 166, 305, 276, 56, 114, 537, 155, 271, 329, 769, 109, 549, 387, 80, 520, 167, 578, 225, 196, 278, 115, 170, 157, 60, 579, 389, 292, 553, 279, 198, 524, 337, 171, 117, 8 8, 282, 62, 178, 581, 294, 199, 393, 526, 173, 144, 283, 202, 642, 63, 121, 561, 92, 532, 179, 295, 353, 324, 104, 527, 585, 298, 203, 643, 285, 401, 94, 534, 181, 152, 210, 326, 299, 205, 108, 645, 548, 95, 535, 593, 306, 211, 538, 327, 185, 156, 301, 272, 330, 770, 417, 110, 550, 388, 168, 307, 226, 649, 213, 116, 539, 158, 331, 771, 111, 551, 609, 580, 390, 227, 309, 554, 280, 338, 172, 118, 541, 159, 217, 657, 333, 773, 391, 449, 582, 229, 555, 200, 339, 394, 119, 174, 313, 284, 64, 122, 562, 180, 583, 296, 354, 777, 557, 395, 528, 341, 175, 586, 233, 673, 204, 644, 286, 123, 563, 402, 182, 355, 587, 397, 300, 287, 206, 646, 345, 785, 125, 565, 403, 96, 536, 183, 594, 241, 212, 357, 328, 186, 589, 302, 207, 647, 705, 418, 595, 405, 308, 650, 569, 214, 540, 187, 303, 361, 801, 332, 772, 419, 112, 552, 610, 228, 651, 597, 310, 215, 409, 542, 189, 160, 218, 658, 334, 774, 611, 421, 392, 450, 311, 230, 653, 556, 369, 340, 120, 543, 601, 314, 219, 659, 335, 775, 833, 613, 451, 584, 231, 778, 425, 558, 396, 342, 176, 315, 234, 674, 221, 124, 661, 564, 453, 356, 779, 559, 617, 343, 588, 398, 235, 675, 317, 288, 346, 786, 433, 126, 566, 404, 184, 242, 665, 358, 781, 399, 457, 897, 590, 237, 677, 208, 648, 347, 787, 706, 127, 567, 625, 596, 406, 243, 570, 359, 188, 591, 304, 362, 802, 707, 420, 349, 789, 681, 407, 652, 465, 598, 245, 571, 216, 410, 190, 363, 803, 709, 612, 422, 599, 312, 65 4, 370, 793, 573, 411, 544, 191, 602, 249, 689, 220, 660, 365, 805, 336, 776, 423, 834, 481, 614, 452, 232, 655, 371, 713, 426, 603, 413, 316, 222, 662, 835, 615, 809, 454, 780, 427, 560, 373, 618, 344, 236, 676, 605, 318, 223, 663, 721, 434, 837, 666, 455, 782, 619, 429, 400, 458, 898, 319, 238, 678, 377, 817, 348, 788, 435, 128, 568, 626, 244, 667, 360, 783, 841, 621, 459, 899, 592, 239, 679, 737, 708, 350, 790, 627, 437, 682, 408, 466, 246, 669, 572, 461, 364, 901, 804, 351, 791, 710, 849, 683, 629, 467, 600, 247, 794, 441, 574, 412, 192, 250, 690, 366, 806, 711, 424, 482, 905, 685, 656, 469, 372, 795, 714, 575, 633, 604, 414, 251, 691, 367, 807, 865, 836, 483, 616, 810, 715, 428, 374, 797, 415, 473, 913, 606, 253, 693, 224, 664, 722, 838, 485, 811, 456, 375, 717, 620, 430, 607, 320, 378, 818, 723, 436, 839, 697, 668, 813, 784, 431, 842, 489, 929, 622, 460, 900, 240, 680, 379, 819, 738, 725, 628, 438, 670, 843, 623, 462, 902, 739, 381, 821, 352, 792, 439, 850, 684, 497, 630, 468, 24 8, 671, 729, 442, 845, 463, 903, 961, 741, 712, 851, 906, 631, 686, 825, 470, 796, 443, 576, 634, 252, 692, 368, 808, 866, 484, 907, 853, 687, 745, 471, 716, 798, 635, 445, 416, 474, 914, 254, 694, 867, 486, 909, 812, 376, 799, 718, 857, 637, 475, 915, 608, 255, 695, 753, 724, 869, 840, 698, 487, 814, 719, 432, 490, 930, 477, 380, 917, 820, 726, 699, 815, 873, 844, 491, 931, 624, 740, 382, 822, 727, 440, 498, 921, 701, 672, 730, 846, 493, 933, 464, 904, 962, 383, 823, 742, 881, 852, 499, 632, 826, 731, 444, 847, 963, 743, 937, 908, 854, 688, 501, 827, 746, 472, 733, 636, 446, 965, 868, 855, 910, 747, 829, 800, 447, 858, 505, 945, 638, 476, 916, 256, 696, 754, 870, 488, 911, 969, 749, 720, 859, 639, 478, 918, 755, 871, 700, 816, 874, 492, 932, 861, 479, 919, 977, 757, 728, 922, 702, 875, 494, 934, 384, 824, 882, 500, 923, 703, 761, 732, 877, 848, 495, 935, 993, 964, 744, 883, 938, 502, 925, 828, 734, 966, 939, 885, 856, 503, 748, 830, 735, 448, 506, 946, 967, 941, 912, 970, 831, 750, 88 9, 860, 507, 947, 640, 756, 872, 971, 751, 862, 509, 949, 480, 920, 978, 758, 973, 876, 863, 979, 759, 953, 924, 704, 762, 878, 496, 936, 994, 981, 884, 926, 763, 879, 995, 940, 886, 504, 927, 985, 765, 736, 997, 968, 887, 942, 832, 890, 508, 948, 943, 1001, 972, 752, 891, 510, 950, 974, 893, 864, 511, 951, 1009, 980, 760, 954, 975, 982, 955, 764, 880, 996, 983, 957, 928, 986, 766, 998, 888, 987, 767, 999, 944, 1002, 989, 892, 1003, 894, 512, 952, 1010, 1005, 976, 895, 1011, 956, 1013, 984, 958, 959, 1017, 988, 768, 1000, 990, 1004, 991, 1006, 896, 1012, 1007, 1014, 1015, 960, 1018, 1019, 1021, 992, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S9: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 513, 8, 41, 130, 12, 69, 49, 14, 131, 20, 15, 73, 258, 22, 133, 23, 81, 36, 259, 26, 137, 97, 261, 38, 145, 27, 514, 39, 515, 265, 68, 29, 42, 161, 43, 45, 517, 50, 70, 273, 193, 521, 529, 16, 71, 132, 74, 51, 289, 545, 24, 75, 53, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 40, 98, 385, 30, 85, 139, 262, 146, 31, 99, 516, 44, 89, 141, 263, 147, 101, 266, 72, 46, 162, 518, 577, 519, 52, 149, 522, 47, 105, 267, 163, 274, 523, 641, 76, 54, 153, 113, 269, 194, 165, 275, 78, 55, 530, 525, 531, 136, 58, 84, 195, 290, 79, 169, 277, 59, 86, 61, 87, 140, 100, 197, 90, 291, 281, 546, 769, 142, 177, 91, 102, 148, 143, 533, 547, 537, 32, 103, 264, 48, 322, 293, 201, 323, 578, 150, 297, 93, 106, 209, 549, 579, 268, 386, 325, 305, 164, 151, 56, 107, 154, 225, 387, 329, 270, 114, 520, 553, 642, 80, 166, 109, 155, 276, 60, 271, 115, 167, 524, 581, 561, 88, 196, 62, 157, 170, 278, 292, 279, 198, 171, 117, 178, 282, 526, 643, 532, 527, 92, 63, 585, 770, 144, 389, 294, 199, 104, 337, 173, 283, 202, 121, 179, 295, 94, 534, 645, 535, 593, 548, 771, 152, 324, 393, 298, 203, 108, 285, 181, 210, 538, 95, 205, 299, 353, 649, 609, 326, 185, 211, 401, 306, 301, 110, 156, 327, 116, 111, 773, 550, 657, 539, 551, 168, 213, 307, 330, 158, 226, 118, 172, 331, 227, 388, 309, 217, 417 338, 159, 777 272, 580, 119 541, 554, 280 333, 390, 174 122, 200, 180 229, 339, 313 391, 175, 394 284, 123, 233, 341, 449, 354, 395, 204, 182, 673, 555, 557, 562, 582, 296, 286, 125, 183, 206, 785, 705, 64, 287, 528, 583, 644, 586, 563, 300, 355, 186, 402, 212, 397, 345, 207, 302, 801, 96, 187, 241, 536, 587, 565, 646, 594, 328, 403, 214, 357, 308, 303, 833, 589, 647, 112, 540, 569, 595, 650, 772, 160, 418, 332, 228, 405, 310, 215, 552, 610, 897, 120, 189, 361, 419, 409, 369, 218, 450, 421, 542, 597, 651, 774, 658, 311, 230, 334, 219, 543, 611, 176, 392, 124, 314, 231, 340, 335, 221, 451, 425, 315, 556, 601, 653, 234, 775, 659, 613, 126, 288, 184, 342, 396, 356, 778, 584, 558, 674, 343, 235, 564, 661, 559, 617, 779, 675, 398, 317, 346, 242, 208, 404, 358, 188, 237, 786, 127, 588, 566, 665, 625, 781, 304, 453, 433, 243, 347, 706, 399, 677, 787, 590, 567, 648, 216, 406, 359, 570, 596, 362, 707, 190, 457, 349, 420, 802, 407, 245, 410, 363, 591, 681, 789, 571, 598, 220, 573, 422, 370, 599, 652, 612, 709, 602, 803, 312, 793, 191, 411, 654, 689, 603, 232, 249, 365, 465, 336, 423, 614, 660, 655, 316, 222, 371, 426, 452, 413, 236, 223, 344, 373, 427, 544, 481, 615, 454, 776, 318, 238, 434, 560, 834, 805, 713, 835, 662, 809, 605, 618, 721, 780, 348, 898, 319, 455, 837, 817, 676, 663, 244, 429, 400, 360, 239, 377, 458, 435, 350, 568, 619, 666, 737, 899, 841, 782, 626, 246, 459, 408, 592, 678, 621, 667, 788, 572, 783, 627, 679, 128, 364, 351, 247, 437, 466, 412, 461, 250, 366, 467, 600, 708, 574, 669, 682, 790, 804, 791, 710, 683, 629, 424, 690, 794, 604, 575, 192, 372, 441, 251, 414, 367, 469, 482, 374, 656, 901, 806, 711, 428, 415, 253, 616, 849, 685, 795, 714, 633, 691, 807, 606, 224, 375, 483, 664, 836, 905, 810, 715, 620, 797, 693, 430, 456, 473, 378, 722, 607, 717, 811, 865, 838, 697, 723, 913, 818, 436, 320, 813, 240, 622, 431, 485, 460, 379, 668, 839, 438, 489, 628, 623, 462, 381, 439, 352, 248, 680, 725, 819, 842, 670, 738, 630, 468, 442, 252, 463, 497, 443, 368, 684, 843, 739, 900, 821, 729, 929, 850, 671, 784, 631, 792, 845, 902, 686, 470, 634, 712, 471, 692, 741, 851, 825, 903, 687, 416,484, 254, 445, 376, 474, 906, 796, 486, 635, 745, 853, 961, 866, 907, 716, 694, 808, 475, 798, 637, 695, 432, 718, 576, 799, 812, 867, 380, 487, 698, 914, 255, 724, 909, 857, 719, 477, 814, 608, 490, 699, 753, 840, 915, 726, 869, 820, 815, 440, 491, 624, 382, 464, 383, 498, 672, 930, 844, 740, 917, 822, 727, 632, 701, 873, 931, 921, 881, 730, 444, 493, 499, 446, 472, 962, 933, 823, 742, 846, 731, 447, 688, 904, 636, 826, 743, 852, 847, 733, 963, 937, 827, 746, 476, 501, 638, 488, 505, 800, 696, 854, 908, 868, 855, 747, 910, 829, 858, 754, 720, 916, 870, 700, 749, 639, 816, 965, 945, 755, 859, 911, 256, 478, 492, 479, 728, 918, 871, 494, 874, 702, 969, 500, 861, 495, 932, 919, 757, 922, 875, 732, 934, 882, 824, 703, 502, 923, 384, 744, 761, 877, 977, 848, 935, 828, 734, 883, 938, 964, 925, 748, 735, 856, 885, 939, 993, 448, 503, 506, 966, 507, 830, 750, 946, 860, 831, 967, 756, 941, 912, 872, 751, 889, 480, 970, 947, 862, 758, 971, 509, 920, 640, 876, 863, 759, 949, 978, 924, 973, 762,878, 979, 496, 936, 704, 884, 953, 763, 504, 926, 879, 981, 994, 886, 940, 927, 765, 736, 887, 995, 942, 968, 985, 508, 890, 948, 832, 752, 943, 997, 972, 891, 950, 1001, 974, 893, 510, 951, 864, 760, 511, 980, 954, 764, 975, 1009, 955, 880, 982, 983, 928, 996, 766, 957, 888, 986, 998, 987, 944, 892, 999, 767, 989, 1002, 952, 1003, 894, 976, 895, 1010, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 512, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S10: [1, 2, 3, 5, 9, 17, 33, 4, 257, 513, 6, 65, 7, 10, 11, 18, 129, 13, 19, 34, 21, 35, 25, 37, 66, 258, 8, 67, 41, 12, 69, 130, 514, 14, 49, 20, 73, 131, 15, 259, 22, 133, 36, 81, 23, 26, 137, 38, 27, 515, 261, 97, 39, 68, 42, 145, 29, 70, 43, 265, 50, 71, 161, 517, 45, 74, 132, 273, 16, 51, 75, 134, 53, 82, 289, 521, 24, 193, 77, 135, 83, 138, 260, 57, 28, 98, 529, 139, 262, 40, 85, 146, 30, 99, 321, 545, 141, 44, 89, 147, 263, 31, 101, 72, 516, 162, 266, 46, 149, 52, 105, 267, 769, 163, 47, 76, 274, 153, 54, 165, 518, 194, 385, 78, 113, 136, 269, 577, 55, 84, 58, 275, 195, 79, 519, 169, 290, 140, 86, 59, 277, 522, 197, 100, 291, 87, 142, 523, 177, 281, 61, 90, 293, 148, 530, 32, 201, 322, 102, 143, 641, 264, 91, 150, 323, 525, 103, 106, 164, 297, 209, 531, 48, 268, 93, 151, 546, 325, 154, 107, 386, 533, 166, 114, 270, 155, 56, 547, 305, 225, 109, 537, 276, 167, 196, 329, 549, 80, 115, 387, 170, 578, 271, 157, 60, 278, 770, 198, 171, 389, 520, 117, 292, 88, 178, 579, 337, 6 2, 199, 553, 279, 173, 282, 202, 524, 121, 393, 144, 581, 294, 179, 283, 642, 63, 92, 353, 526, 203, 295, 104, 561, 181, 324, 210, 532, 298, 94, 401, 585, 152, 205, 285, 643, 108, 326, 211, 527, 299, 95, 771, 306, 185, 156, 534, 327, 226, 417, 645, 110, 301, 548, 168, 330, 213, 593, 388, 116, 535, 272, 158, 307, 538, 227, 111, 649, 331, 172, 390, 550, 217, 309, 539, 118, 338, 773, 159, 280, 609, 229, 449, 200, 551, 333, 119, 580, 391, 174, 554, 122, 180, 657, 339, 64, 541, 394, 233, 582, 313, 175, 284, 555, 204, 354, 777, 123, 395, 562, 182, 296, 583, 341, 673, 206, 402, 557, 241, 286, 586, 125, 355, 644, 183, 397, 785, 212, 300, 528, 96, 345, 563, 186, 403, 587, 207, 646, 287, 357, 565, 214, 328, 594, 187, 801, 418, 228, 536, 302, 112, 705, 405, 589, 308, 215, 647, 361, 189, 595, 419, 650, 218, 303, 772, 332, 160, 569, 409, 540, 230, 310, 610, 421, 651, 219, 450, 774, 120, 552, 334, 231, 597, 369, 658, 392, 542, 234, 311, 611, 340, 833, 176, 314, 653, 221, 556, 451, 335, 601, 124, 659, 425, 775, 235, 396, 543, 342, 613, 242, 584, 315, 674, 453, 126, 778, 356, 558, 343, 661, 184, 398, 564, 237, 617, 433, 779, 317, 675, 208, 346, 559, 404, 588, 243, 786, 288, 665, 457, 566, 127, 677, 358, 399, 706, 188, 897, 347, 590, 406, 625, 245, 648, 359, 781, 362, 567, 216, 596, 420, 570, 465, 190, 787, 304, 707, 349, 591, 407, 681, 249, 802, 410, 652, 363, 598, 191, 571, 422, 789, 370, 709, 220, 612, 411, 803, 312, 599, 481, 654, 232, 689, 365, 793, 423, 222, 452, 573, 336, 602, 371, 805, 236, 660, 426, 544, 413, 713, 316, 834, 223, 614, 454, 655, 427, 776, 238, 603, 373, 662, 344, 835, 434, 615, 244, 618, 676, 318, 809, 455, 721, 429, 560, 128, 780, 458, 605, 377, 663, 400, 837, 435, 666, 239, 619, 319, 898, 678, 348, 626, 459, 782, 246, 667, 360, 568, 437, 817, 737, 466, 621, 247, 788, 350, 679, 408, 708, 461, 841, 592, 364, 627, 250, 899, 467, 682, 783, 351, 669, 441, 572, 412, 790, 192, 710, 683, 482, 901, 366, 629, 804, 424, 600, 469, 690, 251, 849, 574, 372, 711, 414, 791, 685, 483, 794, 367, 714, 428, 633, 905, 253, 656, 473, 806, 691, 374, 795, 415, 575, 604, 485, 865, 715, 224, 807, 456, 616, 693, 375, 836, 430, 722, 810, 378, 606, 913, 436, 664, 320, 717, 797, 240, 620, 838, 489, 723, 431, 811, 607, 460, 818, 697, 379, 668, 839, 438, 738, 462, 929, 622, 248, 813, 680, 497, 842, 725, 381, 900, 628, 439, 784, 670, 468, 819, 739, 352, 623, 442, 843, 684, 252, 902, 729, 463, 821, 630, 850, 470, 671, 792, 443, 741, 961, 484, 712, 845, 368, 631, 903, 471, 686, 634, 445, 692, 851, 474, 576, 906, 745, 254, 825, 687, 416, 796, 716, 486, 866, 635, 907, 475, 694, 808, 376, 853, 718, 487, 914, 753, 798, 490, 637, 867, 432, 695, 909, 724, 477, 812, 608, 380, 857, 698, 915, 255, 719, 799, 869, 491, 726, 840, 699, 498, 930, 740, 382, 814, 624, 917, 440, 820, 727, 873, 493, 701, 931, 730, 464, 815, 844, 672, 499, 921, 742, 822, 383, 933, 731, 962, 444, 632, 846, 743, 881, 501, 904, 746, 823, 472, 852, 688, 826, 446, 733, 963, 847, 636, 256, 937, 747, 908, 505, 854, 754, 827, 965, 447, 638, 868, 855, 696, 476, 910, 749, 945, 829, 488, 720, 858, 916, 478, 755, 800, 969, 639, 870, 492, 911, 700, 859, 918, 479, 757, 871, 874, 728, 494, 932, 977, 702, 816, 861, 500,919, 761, 922, 875, 703, 384, 934, 882, 732, 923, 495, 824, 993, 744, 877, 935, 734, 502, 964, 848, 883, 748, 938, 503, 925, 828, 735, 966, 939, 750, 506, 885, 856, 946, 756, 830, 967, 448, 941, 640, 970, 889, 912, 947, 507, 751, 831, 860, 971, 758, 872, 949, 509, 978, 759, 862, 920, 973, 876, 762, 480, 979, 863, 953, 924, 704, 994, 878, 936, 496, 981, 763, 884, 926, 995, 879, 940, 765, 504, 985, 886, 927, 997, 736, 968, 887, 942, 890, 948, 508, 832, 752, 1001, 943, 972, 891, 950, 974, 760, 1009, 893, 510, 951, 980, 864, 954, 764, 975, 982, 955, 996, 880, 983, 957, 986, 511, 766, 928, 998, 987, 888, 999, 1002, 944, 989, 892, 767, 1003, 1010, 894, 952, 1005, 976, 512, 1011, 895, 956, 1013, 984, 958, 768, 1017, 959, 988, 1000, 990, 1004, 991, 1006, 1012, 896, 1007, 1014, 1015, 1018, 960, 1019, 1021, 992, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S11: [1, 2, 3, 5, 9, 17, 4, 33, 6, 7, 65, 10, 11, 18, 13, 19, 129, 34, 21, 35, 25, 8, 37, 66, 257, 67, 12, 41, 69, 14, 20, 49, 130, 15, 73, 131, 22, 513, 36, 23, 133, 81, 26, 38, 27, 258, 137, 39, 68, 97, 42, 259, 29, 145, 43, 70, 261, 50, 71, 16, 45, 74, 51, 265, 132, 161, 514, 75, 24, 53, 134, 82, 515, 273, 77, 135, 83, 28, 57, 193, 138, 517, 40, 98, 85, 260, 139, 30, 289, 521, 146, 99, 44, 31, 262, 141, 89, 147, 72, 101, 46, 263, 529, 321, 52, 266, 162, 149, 47, 76, 105, 267, 163, 54, 516, 274, 153, 545, 78, 55, 269, 136, 165, 84, 113, 58, 194, 275, 518, 385, 79, 59, 195, 86, 140, 290, 169, 519, 277, 577, 522, 100, 87, 32, 291, 61, 197, 142, 90, 523, 281, 148, 177, 102, 264, 143, 293, 530, 91, 322, 201, 525, 150, 103, 48, 531, 106, 641, 323, 93, 268, 297, 164, 151, 209, 154, 546, 107, 533, 325, 56, 270, 166, 114, 276, 155, 547, 305, 386, 80, 109, 271, 537, 167, 115, 329, 60, 196, 225, 170, 520, 387, 278, 157, 549, 578, 769, 88, 117, 292, 171, 62, 198, 279, 389, 579, 337, 52 4, 282, 553, 178, 63, 199, 144, 294, 173, 92, 121, 202, 283, 581, 526, 179, 393, 104, 295, 532, 561, 642, 324, 203, 94, 353, 298, 527, 285, 152, 181, 585, 210, 108, 643, 534, 401, 95, 299, 326, 205, 211, 156, 548, 306, 185, 535, 110, 645, 327, 272, 593, 301, 538, 168, 116, 330, 226, 307, 213, 388, 158, 550, 417, 111, 539, 770, 649, 331, 227, 118, 172, 280, 159, 551, 309, 390, 580, 338, 217, 609, 554, 771, 541, 119, 333, 64, 200, 229, 174, 391, 122, 657, 339, 284, 555, 313, 582, 449, 180, 394, 773, 296, 175, 562, 123, 204, 354, 233, 583, 341, 528, 395, 286, 557, 182, 586, 563, 777, 644, 402, 96, 673, 355, 125, 300, 206, 287, 183, 397, 587, 345, 212, 241, 186, 536, 403, 565, 646, 328, 207, 357, 594, 302, 785, 589, 308, 187, 214, 418, 112, 647, 405, 595, 303, 540, 569, 705, 650, 332, 361, 228, 215, 160, 552, 419, 310, 189, 218, 610, 597, 772, 651, 542, 409, 801, 120, 334, 230, 311, 392, 421, 658, 340, 219, 611, 369, 556, 314, 450, 543, 774, 653, 335, 601, 231, 176, 124, 659, 234, 315, 584, 451, 342, 221, 613, 396, 558, 425, 775, 833, 564, 778, 674, 356, 235, 126, 661, 343, 288, 559, 317, 453, 184, 398, 588, 346, 617, 242, 779, 404, 675, 566, 433, 127, 208, 358, 237, 399, 786, 665, 347, 590, 243, 457, 188, 567, 781, 648, 406, 677, 359, 596, 304, 625, 570, 706, 787, 362, 897, 591, 349, 216, 245, 420, 190, 407, 571, 707, 598, 465, 652, 410, 802, 681, 363, 789, 312, 191, 422, 220, 612, 370, 249, 599, 544, 411, 803, 573, 709, 654, 336, 365, 602, 232, 793, 423, 660, 689, 371, 3 16, 452, 222, 614, 481, 426, 776, 655, 413, 805, 603, 834, 713, 236, 662, 344, 223, 615, 373, 560, 427, 318, 454, 618, 835, 605, 780, 809, 676, 434, 128, 663, 238, 319, 455, 400, 721, 429, 666, 348, 619, 377, 244, 458, 837, 568, 782, 435, 678, 360, 239, 626, 788, 667, 817, 898, 592, 459, 350, 621, 246, 783, 408, 679, 437, 627, 841, 572, 708, 466, 737, 682, 364, 899, 790, 669, 351, 247, 461, 192, 250, 600, 467, 629, 412, 804, 683, 574, 441, 710, 791, 366, 901, 849, 794, 424, 690, 372, 251, 482, 575, 711, 469, 656, 414, 806, 685, 367, 604, 633, 714, 795, 691, 905, 224, 616, 483, 374, 253, 428, 415, 807, 836, 715, 606, 473, 865, 810, 797, 664, 693, 375, 320, 456, 485, 722, 430, 620, 378, 913, 607, 811, 838, 717, 436, 240, 723, 431, 668, 818, 697, 379, 460, 622, 489, 839, 784, 813, 680, 438, 628, 842, 738, 819, 725, 900, 670, 352, 929, 623, 381, 248, 462, 439, 843, 468, 739, 630, 497, 684, 442, 792, 671, 821, 902, 463, 850, 729, 252, 631, 845, 576, 443, 712, 470, 741, 686, 368, 903, 634, 8 51, 796, 825, 961, 692, 906, 484, 254, 471, 416, 808, 687, 445, 635, 716, 474, 866, 745, 853, 907, 798, 694, 376, 255, 486, 914, 608, 475, 867, 637, 812, 718, 799, 695, 909, 857, 487, 724, 432, 753, 698, 380, 915, 490, 840, 719, 477, 869, 814, 820, 699, 726, 930, 624, 491, 382, 917, 815, 440, 844, 873, 740, 498, 727, 672, 931, 822, 701, 383, 464, 493, 730, 921, 632, 846, 499, 444, 742, 823, 904, 933, 852, 731, 881, 826, 962, 847, 472, 743, 501, 688, 446, 636, 746, 827, 963, 854, 733, 908, 937, 256, 447, 476, 868, 747, 638, 505, 855, 800, 829, 965, 696, 910, 858, 488, 754, 916, 945, 639, 720, 478, 870, 749, 911, 859, 755, 969, 700, 492, 918, 479, 871, 816, 874, 861, 728, 757, 932, 702, 384, 919, 494, 977, 922, 875, 500, 824, 703, 934, 495, 732, 882, 761, 923, 848, 877, 744, 502, 935, 883, 828, 964, 734, 993, 938, 925, 503, 448, 748, 506, 856, 735, 885, 939, 830, 966, 946, 640, 507, 750, 831, 967, 912, 941, 860, 889, 756, 970, 947, 480, 872, 751, 509, 971, 862, 758, 920, 949, 978, 876, 8 63, 759, 973, 704, 496, 762, 979, 924, 953, 878, 936, 884, 763, 994, 981, 926, 879, 504, 736, 995, 886, 765, 940, 927, 985, 508, 887 832, 968 997, 942 890, 948 752, 510 943, 891 972, 1001, 950, 511, 864, 893, 760, 974, 951, 980, 1009, 954, 975, 764, 955, 982, 880, 996, 766, 983, 928, 957, 986, 888, 767, 998, 987, 999, 944, 892, 1002, 989, 512, 1003, 894, 952, 1010, 895, 976, 1005, 1011, 956, 984, 1013, 958, 768, 959, 988, 1017, 1000, 990, 1004, 991, 896, 1006, 1012, 1007, 1014, 1015, 960, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S12: [1, 2, 3, 5, 9, 17, 4, 33, 6, 7, 10, 65, 11, 18, 13, 19, 129, 21, 34, 35, 25, 8, 37, 66, 257, 12, 67, 41, 14, 69, 20, 49, 15, 130, 73, 22, 131, 23, 36, 513, 133, 26, 81, 38, 27, 137, 39, 258, 29, 68, 42, 97, 259, 43, 145, 70, 261, 50, 16, 71, 45, 74, 51, 265, 132, 161, 75, 24, 53, 514, 134, 82, 77, 515, 273, 135, 28, 83, 57, 138, 40, 193, 517, 30, 85, 98, 139, 260, 289, 31, 44, 521, 99, 146, 141, 89, 262, 147, 72, 46, 101, 263, 52, 529, 47, 266, 149, 321, 162, 76, 105, 54, 267, 163, 153, 78, 55, 516, 274, 545, 269, 136, 84, 165, 58, 113, 79, 275, 194, 518, 59, 385, 86, 140, 195, 169, 519, 277, 290, 32, 87, 61, 522, 100, 577, 142, 291, 197, 90, 523, 281, 148, 177, 102, 143, 91, 264, 293, 530, 48, 201, 525, 103, 150, 322, 93, 531, 106, 268, 151, 323, 297, 164, 641, 107, 154, 56, 209, 533, 546, 270, 325, 166, 114, 155, 80, 276, 109, 547, 305, 271, 167, 60, 386, 537, 115, 157, 329, 196, 170, 520, 278, 225, 549, 387, 88, 62, 117, 578, 171, 279, 292, 198, 769, 63, 524, 389, 282, 579, 337, 553, 178, 144, 199, 92, 173, 121, 294, 283, 202, 526, 179, 104, 581, 393, 295, 94, 532, 203, 561, 527, 285, 152, 324, 298, 181, 353, 642, 95, 108, 585, 210, 534, 299, 205, 643, 401, 326, 156, 211, 185, 535, 110, 548, 306, 272, 327, 301, 168, 645, 538, 116, 593, 111, 158, 330, 307, 213, 226, 550, 388, 539, 417, 118, 159, 331, 172, 280, 649, 227, 551, 309, 770, 64, 217, 390, 541, 119, 580, 338, 554, 609, 333, 200, 771, 174, 229, 122, 391, 284, 339, 555, 313, 180, 657, 582, 175, 394, 123, 296, 449, 773, 204, 562, 528, 286, 233, 583, 341, 557, 182, 354, 395, 96, 125, 586, 563, 287, 300, 206, 777, 183, 355, 644, 402, 673, 397, 587, 345, 212, 186, 536, 241, 207, 565, 403, 328, 302, 357, 646, 594, 187, 112, 589, 308, 214, 785, 303, 647, 540, 405, 418, 595, 569, 160, 332, 215, 189, 361, 650, 228, 552, 310, 705, 419, 218, 542, 120, 597, 610, 651, 409, 334, 311, 772, 230, 801, 219, 392, 543, 340, 556, 421, 314, 611, 369, 658, 335, 176, 653, 231, 124, 450, 601, 774, 315, 221, 659, 234, 584, 342, 558, 396, 613, 451, 425, 775, 126, 564, 288, 235, 343, 559, 317, 778, 184, 356, 661, 833, 674, 398, 127, 588, 453, 346, 617, 242, 208, 566, 779, 404, 237, 675, 433, 358, 399, 347, 188, 665, 590, 243, 567, 786, 304, 457, 781, 359, 648, 406, 596, 677, 570, 625, 591, 349, 216, 787, 190, 362, 245, 706, 407, 420, 571, 897, 598, 191, 363, 652, 410, 312, 707, 465, 681, 789, 802, 220, 544, 249, 422, 599, 573, 612, 370, 411, 336, 365, 654, 232, 803, 709, 602, 423, 316, 222, 793, 371, 660, 689, 614, 655, 413, 452, 426, 603, 776, 481, 805, 223, 236, 344, 560, 318, 713, 615, 373, 662, 834, 427, 128, 454, 605, 618, 319, 780, 663, 835, 238, 809, 676, 434, 400, 455, 348, 429, 619, 377, 666, 244, 568, 721, 239, 458, 782, 435, 360, 837, 678, 626, 667, 592, 350, 788, 621, 246, 459, 817, 783, 408, 679, 572, 437, 898, 627, 351, 192, 364, 669, 841, 247, 708, 466, 682, 790, 737, 461, 899, 250, 600, 574, 412, 629, 467, 683, 441, 791, 366, 804, 710, 251, 424, 575, 901, 794, 372, 849, 690, 367, 656, 414, 711, 604, 469, 685, 482, 633, 806, 224, 795, 253, 714, 691, 616, 374, 415, 428, 905, 483, 807, 606, 320, 715, 473, 797, 375, 664, 836, 810, 693, 865, 456, 430, 607, 620, 485, 378, 722, 240, 811, 717, 436, 913, 838, 431, 379, 668, 723, 697, 622, 460, 818, 784, 489, 839, 813, 680, 438, 628, 352, 623, 381, 670, 842, 248, 819, 725, 738, 462, 439, 900, 929, 630, 671, 843, 468, 684, 442, 792, 739, 497, 463, 821, 252, 576, 729, 902, 631, 850, 443, 368, 845, 712, 470, 686, 741, 634, 903, 796, 851, 254, 825, 692, 416, 471, 687, 445, 906, 484, 635, 808, 961, 255, 716, 474, 798, 376, 745, 853, 694, 866, 907, 608, 486, 637, 475, 799, 812, 718, 695, 867, 914, 432, 909, 487, 380, 857, 724, 698, 753, 719, 477, 915, 490, 840, 814, 869, 699, 624, 382, 820, 726, 491, 815, 440, 917, 930, 383, 672, 844, 727, 701, 873, 740, 498, 464, 822, 493, 931, 730, 632, 444, 921, 846, 499, 823, 742, 731, 904, 852, 933, 826, 881, 847, 472, 688, 446, 743, 636, 501, 962, 256, 827, 733, 746, 854, 447, 908, 963, 937, 638, 476, 800, 747, 505, 855, 829, 696, 868, 910, 488, 639, 965, 858, 754, 720, 478, 916, 749, 945, 870, 911, 859, 700, 755, 479, 492, 816, 969, 871, 918, 384, 861, 728, 702, 874, 757, 919, 494, 932, 703, 875, 922, 500, 824, 977, 495, 732, 761, 934, 882, 923, 848, 877, 744, 502, 935,828, 734, 883, 448, 925, 503, 964, 938, 993, 735, 748, 506, 856, 830, 885, 939, 640, 966, 507, 831, 750, 946, 912, 967, 860, 941, 889, 756, 480, 751, 509, 970, 947, 872, 862, 758, 971, 920, 949, 863, 704, 876, 759, 978, 496, 973, 762, 924, 979, 953, 878, 763, 936, 884, 879, 926, 504, 981, 994, 736, 765, 886, 927, 940, 995, 508, 832, 985, 887, 968, 942, 997, 890, 752, 510, 948, 943, 891, 511, 972, 1001, 950, 864, 893, 760, 974, 951, 980, 954, 1009, 975, 764, 955, 880, 982, 766, 928, 983, 957, 996, 767, 986, 888, 998, 987, 944, 999, 892, 512, 989, 1002, 894, 1003, 952, 895, 1010, 976, 1005, 956, 1011, 984, 958, 1013, 768, 959, 988, 1017, 1000, 990, 991, 1004, 896, 1006, 1012, 1007, 1014, 960, 1015, 1018 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S13: [1, 2, 3, 5, 9, 17, 33, 4, 6, 513, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 8, 41, 130, 12, 69, 49, 514, 14, 131, 20, 15, 73, 258, 22, 133, 23, 81, 36, 259, 26, 137, 97, 261, 515, 38, 145, 27, 39, 265, 68, 29, 42, 161, 43, 45, 50, 70, 517, 273, 193, 16, 71, 132, 74, 51, 289, 24, 75, 53, 521, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 529, 40, 98, 385, 30, 85, 139, 262, 146, 545, 31, 99, 44, 89, 141, 263, 147, 101, 516, 266, 72, 46, 162, 52, 149, 47, 518, 105, 267, 163, 274, 76, 54, 153, 577, 113, 269, 194, 165, 275, 78, 519, 55, 136, 58, 84, 195, 290, 522, 79, 169, 277, 59, 86, 61, 523, 87, 140, 100, 197, 90, 641, 291, 281, 142, 177, 91, 102, 530, 148, 143, 32, 103, 264, 525, 48, 322, 293, 201, 531, 323, 150, 297, 93, 106, 546, 209, 268, 386, 325, 769, 305, 164, 151, 56, 533, 107, 154, 225, 387, 329, 547, 270, 114, 80, 537, 166, 109, 155, 276, 578, 60, 271, 115, 167, 549, 88, 196, 62, 157, 579, 170, 278, 292, 520, 279, 198, 171, 117, 553, 178, 28 2, 92, 642, 63, 144, 389, 294, 524, 199, 104, 337, 581, 173, 283, 202, 561, 121, 179, 295, 526, 94, 152, 324, 643, 393, 298, 203, 532, 108, 285, 181, 527, 210, 95, 205, 585, 299, 353, 326, 770, 185, 211, 534, 401, 306, 301, 645, 110, 156, 327, 535, 116, 111, 593, 168, 213, 307, 548, 330, 158, 771, 226, 118, 172, 538, 331, 227, 649, 388, 309, 217, 609, 417, 338, 773, 159, 272, 550, 119, 280, 657, 333, 390, 174, 539, 122, 200, 551, 180, 229, 777, 339, 313, 580, 391, 175, 541, 394, 284, 554, 123, 233, 341, 673, 449, 354, 555, 395, 204, 557, 182, 296, 562, 286, 582, 125, 183, 785, 206, 64, 705, 287, 300, 528, 355, 186, 583, 402, 212, 644, 397, 345, 586, 207, 302, 563, 96, 801, 187, 241, 536, 328, 403, 587, 214, 565, 357, 308, 646, 303, 112, 594, 160, 833, 418, 332, 589, 228, 405, 647, 310, 540, 215, 120, 569, 189, 361, 595, 419, 650, 409, 369, 772, 218, 552, 450, 421, 610, 311, 897, 230, 334, 542, 219, 597, 176, 651, 392, 124, 774, 314, 658, 231, 340, 543, 335, 611, 221, 451, 556, 425, 601, 315, 653, 234, 126, 775, 288, 659, 184, 613, 342, 778, 396, 356, 584, 343, 558, 235, 674, 398, 317, 564, 346, 661, 242, 559, 208, 617, 404, 358, 779, 188, 675, 237, 786, 127, 588, 304, 566, 453, 665, 433, 243, 625, 347, 781, 399, 706, 216, 677, 406, 787, 359, 590, 362, 567, 190, 648, 457, 570, 349, 420, 596, 407, 707, 245, 802, 410, 591, 363, 681, 220, 789, 422, 571, 370, 598, 312, 573, 191, 599, 411, 652, 232, 612, 249, 709, 365, 602, 465, 803, 336, 793, 423, 316, 222, 654, 371, 689, 426, 603, 452, 614, 413, 660, 236, 655, 223, 544, 344, 615, 373, 776, 427, 560, 481, 834, 454, 805, 318, 713, 238, 835, 434, 662, 809, 348, 605, 319, 618, 455, 721, 244, 780, 429, 898, 400, 837, 360, 817, 239, 676, 377, 663, 458, 568, 619, 435, 666, 350, 737, 246, 899, 459, 841, 408, 782, 626, 128, 592, 364, 678, 351, 621, 247, 667, 437, 788,572, 466, 783, 412, 627, 461, 679, 600, 250, 708, 366, 574, 467, 669, 424, 682, 790, 192, 804, 372, 791, 710, 441, 683, 251, 629, 414, 690, 794, 367, 604, 469, 575, 656, 482, 901, 374, 806, 428, 711, 616, 415, 849, 253, 685, 795, 224, 714, 375, 633, 691, 483, 807, 606, 430, 664, 456, 836, 905, 473, 810, 378, 715, 620, 436, 797, 693, 320, 722, 240, 607, 717, 431, 811, 865, 485, 838, 460, 697, 723, 379, 913, 818, 438, 813, 622, 489, 668, 462, 839, 628, 381, 623, 680, 439, 725, 819, 352, 842, 670, 248, 738, 630, 468, 684, 843, 442, 739, 252, 900, 821, 463, 729, 929, 497, 850, 671, 784, 443, 631, 792, 368, 845, 902, 470, 686, 634, 471, 712, 692, 416, 741, 851, 484, 825, 903, 254, 687, 906, 796, 445, 635, 745, 376, 853, 961, 474, 866, 907, 716, 486, 694, 808, 475, 798, 637, 432, 695, 718, 576, 380, 799, 812, 487, 867, 698, 914, 255, 724, 909, 477, 857, 719, 814, 490, 608, 699, 753, 440, 840, 915, 726, 491, 869, 820, 382, 815, 624, 672, 464, 930, 844, 740, 383, 917, 822, 727, 498, 632, 701,873, 444, 931, 921, 881, 493, 730, 962, 933, 499, 823, 742, 846, 731, 446, 688, 904, 636, 472, 826, 743, 852, 447, 847, 733, 963, 937, 476, 827, 746, 638, 501, 800, 696, 854, 908, 488, 868, 855, 747, 910, 505, 829, 858, 754, 720, 256, 916, 870, 700, 478, 749, 639, 816, 965, 945, 492, 755, 859, 911, 728, 479, 918, 871, 874, 702, 494, 969, 861, 932, 919, 757, 500, 922, 875, 732, 934, 882, 495, 824, 703, 923, 744, 502, 761, 877, 977, 848, 935, 828, 384, 734, 883, 938, 964, 925, 448, 748, 735, 856, 885, 939, 993, 503, 966, 830, 750, 946, 860, 831, 506, 967, 756, 941, 912, 872, 751, 507, 889, 970, 947, 862, 758, 971, 920, 480, 640, 876, 863, 759, 949, 978, 924, 509, 973, 762, 878, 979, 936, 704, 884, 953, 496, 763, 926, 879, 981, 994, 886, 940, 927, 504, 765, 736, 887, 995, 942, 968, 985, 890, 948, 832, 508, 752, 943, 997, 972, 891, 950, 1001, 974, 893, 951, 864, 510, 760, 980, 954, 764, 975, 1009, 955, 880, 982, 983, 928, 996, 766, 511, 957, 888, 986, 998, 987, 944, 892, 999, 767, 989, 100 2, 952, 1003, 894, 976, 895, 1010, 512, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S14: [1, 2, 5, 9, 3, 17, 33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 37, 67, 25, 257, 21, 66, 35, 8, 130, 41, 12, 73, 133, 514, 20, 49, 69, 14, 258, 15, 22, 131, 27, 81, 36, 259, 39, 137, 97, 23, 517, 38, 26, 68, 265, 42, 145, 29, 70, 261, 50, 75, 161, 43, 521, 135, 71, 45, 82, 273, 16, 51, 132, 193, 74, 24, 515, 138, 53, 289, 77, 134, 83, 28, 98, 260, 40, 529, 57, 139, 85, 30, 146, 262, 44, 321, 545, 99, 141, 266, 31, 89, 147, 263, 101, 519, 162, 72, 46, 274, 52, 149, 267, 577, 47, 76, 105, 165, 194, 54, 163, 516, 385, 269, 78, 153, 55, 86, 525, 290, 113, 275, 58, 79, 136, 518, 195, 84, 291, 169, 277, 87, 531, 59, 140, 323, 197, 102, 641, 61, 148, 177, 281, 100, 90, 522, 293, 142, 322, 201, 91, 546, 32, 143, 103, 264, 530, 48, 387, 106, 297, 209, 523, 154, 93, 150, 268, 549, 164, 325, 114, 151, 579, 166, 56, 305, 107, 276, 537, 270, 386, 155, 769, 80, 109, 225, 167, 533, 60, 170, 115, 196, 578, 329, 271, 278, 88, 547, 157, 117, 389, 520, 337, 292, 279, 198, 642, 62, 17 8, 171, 553, 92, 282, 202, 199, 524, 63, 144, 295, 585, 173, 393, 104, 645, 121, 294, 283, 532, 353, 179, 203, 561, 324, 298, 94, 581, 108, 152, 210, 526, 285, 181, 401, 770, 95, 205, 299, 527, 327, 156, 534, 306, 110, 326, 643, 211, 185, 226, 539, 168, 301, 593, 116, 388, 330, 548, 111, 417, 771, 213, 272, 118, 551, 307, 158, 649, 227, 172, 331, 609, 338, 390, 535, 309, 217, 550, 122, 391, 538, 159, 280, 333, 580, 119, 174, 777, 339, 180, 554, 200, 354, 657, 284, 313, 541, 449, 229, 582, 394, 123, 182, 773, 233, 296, 562, 175, 395, 587, 64, 204, 673, 355, 555, 402, 341, 647, 125, 286, 583, 183, 300, 557, 241, 212, 594, 287, 345, 785, 397, 206, 528, 96, 419, 563, 186, 644, 214, 403, 705, 308, 328, 586, 357, 536, 207, 187, 650, 302, 112, 565, 303, 801, 361, 228, 589, 418, 160, 646, 405, 595, 310, 215, 540, 450, 332, 610, 120, 772, 218, 189, 552, 230, 569, 334, 409, 651, 311, 597, 340, 421, 542, 219, 658, 369, 774, 124, 231, 556, 176, 833, 392, 314, 611, 242, 653, 451, 335, 778, 221, 543, 342, 601, 425, 315, 659, 184, 775, 234, 613, 356, 674, 126, 288, 584, 396, 558, 235, 786, 317, 346, 564, 188, 661, 453, 779, 404, 559, 343, 398, 588, 208, 617, 237, 677, 433, 706, 347, 566, 362, 675, 127, 243, 897, 358, 781, 406, 590, 216, 665, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 190, 570, 245, 591, 411, 648, 220, 707, 312, 596, 363, 803, 465, 681, 407, 789, 422, 599, 232, 571, 249, 652, 370, 835, 191, 709, 410, 614, 316, 573, 365, 660, 423, 336, 222, 689, 452, 793, 371, 612, 426, 602, 236, 805, 344, 654, 413, 834, 481, 713, 223, 603, 318, 544, 454, 655, 427, 615, 373, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 246, 568, 435, 817, 458, 619, 350, 788, 466, 782, 898, 364, 667, 408, 592, 128, 621, 247, 737, 437, 679, 572, 351, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 430, 575, 656, 253, 807, 415, 685, 905, 374, 616, 483, 633, 806, 224, 795, 865, 428, 691, 473, 715, 836, 456, 810, 378, 606, 620, 436, 664, 722, 320, 797, 431, 693, 913, 240, 607, 717, 462, 811, 485, 839, 668, 379, 818, 622, 438, 838, 723, 248, 697, 381, 738, 680, 460, 813, 628, 489, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 446, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 933, 731, 498, 881, 636, 743, 444, 688, 904, 826, 476, 754, 963, 847, 733, 501, 854, 937, 827, 447, 696, 746, 868, 638, 488, 800, 908, 747, 829, 494, 858, 700, 965, 916, 478, 855, 910, 720, 505, 749, 945, 859, 874,639, 479, 755, 870, 918, 728, 500, 911, 816, 871, 932, 256, 969, 861, 702, 757, 923, 492, 732, 824, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 828, 877, 935, 848, 506, 734, 964, 883, 938, 748, 384, 856, 925, 993, 735, 830, 966, 502, 939, 885, 946, 750, 860, 756, 480, 967, 831, 889, 941, 751, 872, 507, 971, 912, 758, 947, 970, 862, 978, 448, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021, 1016, 1008, 1020, 1022 1023, 1024];
последовательность S15: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 513, 8, 12, 130, 41, 69, 14, 20, 131, 49, 15, 73, 258, 22, 133, 36, 81, 23, 259, 26, 137, 38, 261, 97, 145, 27, 514, 39, 515, 265, 68, 42, 29, 161, 70, 43, 517, 50, 71, 273, 193, 521, 529, 45, 16, 132, 74, 51, 289, 545, 24, 75, 53, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 40, 98, 385, 30, 85, 139, 262, 146, 31, 99, 516, 44, 89, 141, 263, 147, 101, 266, 72, 46, 162, 518, 577, 519, 52, 149, 522, 47, 76, 267, 163, 274, 523, 641, 105, 54, 153, 78, 269, 194, 165, 275, 55, 84, 530, 525, 531, 136, 58, 113, 195, 290, 79, 169, 277, 59, 86, 61, 87, 140, 100, 197, 90, 291, 281, 546, 769, 142, 177, 91, 102, 148, 143, 533, 547, 537, 32, 103, 264, 48, 322, 293, 201, 323, 578, 150, 297, 93, 106, 209, 549, 579, 268, 386, 325, 305, 164, 151, 107, 56, 154, 225, 387, 329, 270, 114, 520, 553, 642, 80, 166, 109, 155, 276, 60, 271, 115, 167, 524, 581, 561, 157, 196, 170, 198, 171, 278, 292, 279, 117, 88, 62, 178, 282, 526, 643, 532, 527, 63, 92, 585, 770, 144, 389, 294, 199, 104, 337, 173, 283, 202, 121, 179, 295, 94, 534, 645, 535, 593, 548, 771, 152, 324, 393, 298, 203, 108, 285, 181, 210, 538, 95, 205, 299, 353, 649, 609, 326, 185, 211, 401, 306, 301, 110, 156, 327, 116, 111, 773, 550, 657, 539, 551, 168, 213, 307, 330, 158, 226, 118, 172, 331, 227, 388, 309, 217, 417, 338, 159, 777, 272, 580, 119, 541, 554, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 64, 394, 284, 175, 233, 341, 449, 354, 395, 204, 123, 673, 555, 557, 562, 582, 296, 286, 182, 206, 125, 785, 705, 183, 287, 528, 583, 644, 586, 563, 300, 355, 212, 402, 186, 397, 345, 207, 302, 801, 96, 187, 241, 536, 587, 565, 646, 594, 328, 403, 214, 357, 308, 303, 833, 589, 647, 112, 540, 569, 595, 650, 772, 228, 418, 332, 215, 405, 310, 189, 552, 610, 897, 160, 218, 361, 419, 409, 369, 230, 450, 421, 542, 597, 651, 774, 658, 311, 120, 334, 219, 543, 611, 176, 392, 231, 314, 124, 340, 335, 221, 451, 425, 315, 556, 601, 653, 234, 775, 659, 613, 235, 288, 453, 126, 342, 396, 778, 584, 558, 674, 356, 343, 564, 661, 559, 617, 779, 675, 184, 398, 433, 317, 346, 242, 208, 404, 358, 786, 188, 588, 566, 665, 625, 781, 237, 127, 243, 347, 399, 706, 216, 677, 787, 590, 567, 648, 406, 359, 304, 570, 596, 362, 707, 190, 457, 349, 465, 802, 420, 407, 245, 410, 591, 681, 789, 571, 598, 363, 573, 220, 422, 599, 652, 612, 709, 602, 803, 370, 793, 312, 191, 654, 689, 603, 411, 232, 249, 365, 336, 423, 614, 660, 6 55, 316, 222, 371, 426, 452, 413, 481, 236, 223, 344, 318, 544, 373, 615, 427, 776, 128, 454, 238, 560, 834, 805, 713, 835, 662, 809, 605, 618, 721, 780, 434, 898, 319, 455, 837, 817, 676, 663, 348, 429, 400, 377, 244, 239, 458, 435, 360, 568, 619, 666, 737, 899, 841, 782, 626, 350, 246, 459, 592, 678, 621, 667, 788, 572, 783, 627, 679, 408, 364, 351, 192, 247, 437, 466, 412, 461, 250, 366, 600, 708, 574, 669, 682, 790, 804, 791, 710, 683, 629, 441, 690, 794, 604, 575, 467, 424, 372, 251, 414, 367, 469, 482, 374, 656, 901, 806, 711, 428, 415, 253, 616, 849, 685, 795, 714, 633, 691, 807, 606, 483, 473, 224, 664, 836, 905, 810, 715, 620, 797, 693, 375, 485, 430, 456, 722, 607, 717, 811, 865, 838, 697, 723, 913, 818, 378, 436, 813, 320, 622, 240, 431, 460, 379, 668, 839, 489, 438, 628, 623, 462, 381, 439, 352, 497, 680, 725, 819, 842, 670, 738, 630, 468, 248, 442, 463, 470, 443, 252, 684, 843, 739, 900, 821, 729, 929, 850, 671, 784, 631, 792, 845, 902, 686, 368, 634, 712, 254, 692, 741, 8 51, 825, 903, 687, 471, 416, 484, 445, 376, 474, 906, 796, 486, 635, 745, 853, 961, 866, 907, 716, 694, 808, 475, 798, 637, 695, 255, 718, 576, 799, 812, 867, 432, 380, 698, 914, 487, 724, 909, 857, 719, 477, 814, 608, 490, 699, 753, 840, 915, 726, 869, 820, 815, 440, 491, 624, 382, 498, 493, 464, 672, 930, 844, 740, 917, 822, 727, 632, 701, 873, 931, 921, 881, 730, 383, 499, 444, 446, 472, 962, 933, 823, 742, 846, 731, 447, 688, 904, 636, 826, 743, 852, 847, 256, 476, 733, 963, 937, 827, 746, 501, 488, 638, 505, 800, 696, 854, 908, 868, 855, 747, 910, 829, 858, 754, 720, 916, 870, 478, 700, 749, 639, 816, 965, 945, 755, 859, 911, 492, 479, 728, 918, 871, 384, 494, 500, 874, 702, 969, 495, 861, 502, 932, 919, 757, 922, 875, 732, 977, 934, 882, 761, 824, 703, 923, 744, 877, 848, 935, 828, 734, 883, 448, 938, 503, 964, 925, 993, 748, 735, 856, 885, 939, 506, 966, 507, 830, 750, 946, 860, 831, 967, 756, 941, 912, 872, 751, 889, 480, 970, 947, 862, 758, 971, 509, 920, 640, 876, 863, 759, 949, 978, 924, 973, 762, 878, 979, 496, 936, 704, 884, 953, 763, 504, 926, 879, 981, 994, 886, 940, 927, 765, 736, 887, 995, 942, 968, 985, 508, 890, 948, 832, 752, 943, 997, 972, 891, 1001, 510, 950, 974, 893, 951, 864, 760, 1009, 511, 980, 954, 764, 975, 955, 880, 982, 983, 928, 996, 766, 957, 888, 986, 998, 987, 944, 892, 999, 767, 512, 989, 1002, 952, 1003, 894, 976, 895, 1010, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022 1023, 1024];
последовательность S16: [1, 2, 5, 9, 3, 17, 33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 25, 21, 35, 257, 66, 37, 8, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 73, 258, 15, 22, 131, 81, 27, 36, 259, 137, 39, 97, 23, 517, 38, 26, 68, 265, 42, 145, 29, 70, 261, 50, 43, 161, 71, 521, 45, 75, 82, 132, 273, 193, 16, 51, 74, 53, 24, 515, 135, 138, 289, 77, 134, 83, 28, 98, 260, 40, 529, 57, 139, 85, 30, 146, 262, 44, 321, 545, 99, 141, 266, 31, 89, 147, 263, 72, 519, 162, 46, 101, 385, 149, 52, 47, 577, 76, 267, 54, 274, 165, 194, 105, 516, 163, 269, 78, 153, 275, 55, 525, 58, 113, 136, 86, 79, 290, 518, 195, 84, 291, 59, 277, 169, 531, 100, 140, 323, 197, 87, 641, 177, 61, 90, 281, 102, 148, 522, 293, 142, 322, 91, 143, 546, 32, 201, 103, 264, 530, 106, 387, 48, 297, 523, 209, 154, 93, 150, 268, 164, 537, 769, 533, 325, 151, 56, 166, 107, 305, 114, 578, 276, 549, 270, 386, 155, 80, 109, 225, 167, 60, 579, 170, 115, 196, 329, 271, 278, 157, 547, 88, 117, 389, 520, 337, 292, 279, 198, 642, 62, 17 8, 171, 553, 92, 282, 199, 63, 524, 144, 173, 295, 585, 202, 393, 104, 645, 121, 294, 283, 532, 353, 179, 203, 561, 324, 298, 94, 581, 152, 210, 181, 526, 285, 108, 401, 770, 95, 205, 299, 527, 327, 156, 534, 306, 110, 326, 643, 211, 116, 185, 539, 168, 301, 593, 226, 388, 330, 548, 111, 417, 771, 158, 272, 213, 551, 307, 118, 649, 172, 227, 331, 609, 338, 390, 535, 309, 217, 550, 159, 391, 538, 119, 280, 333, 580, 174, 122, 777, 339, 200, 554, 180, 657, 354, 284, 541, 313, 449, 582, 229, 394, 773, 123, 175, 673, 555, 785, 204, 562, 395, 182, 341, 583, 557, 64, 296, 286, 233, 125, 183, 206, 287, 300, 355, 212, 402, 186, 397, 587, 345, 594, 647, 528, 96, 563, 241, 644, 207, 705, 328, 586, 403, 536, 214, 357, 308, 419, 565, 801, 589, 187, 302, 646, 112, 569, 303, 595, 361, 228, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 610, 597, 552, 651, 160, 230, 120, 334, 409, 311, 421, 219, 542, 369, 658, 231, 774, 392, 176, 556, 314, 833, 340, 221, 611, 653, 335, 451, 778, 124, 543, 342, 601, 425, 234, 659, 235, 775, 315, 613, 126, 674, 356, 184, 584, 288, 558, 396, 564, 661, 242, 779, 559, 317, 346, 617, 675, 897, 404, 343, 398, 188, 453, 208, 433, 786, 237, 588, 566, 665, 781, 347, 362, 127, 243, 358, 706, 406, 677, 590, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 410, 652, 370, 835, 411, 709, 232, 614, 316, 573, 365, 660, 423, 336, 222, 689, 452, 793, 371, 612, 426, 602, 236, 805, 413, 654, 481, 834, 223, 713, 344, 603, 318, 544, 454, 655, 427, 615, 373, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 400, 626, 246, 663, 678, 435, 568, 458, 817, 350, 619, 459, 788, 466, 782, 898, 364, 667, 408, 592, 128, 621, 437, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 424, 669, 629, 467, 901, 251, 849, 804, 372, 791, 192, 710, 482, 574, 690, 414, 683, 367, 604, 794, 469, 714, 374, 711, 253, 575, 656, 483, 807, 415, 685, 905, 375, 616, 224, 633, 806, 428, 795, 865, 430, 691, 473, 715, 836, 456, 810, 378, 606, 620, 436, 664, 722, 485, 797, 320, 693, 913, 431, 607, 717, 240, 811, 379, 839, 668, 438, 818, 622, 460, 838,723, 248, 697, 381, 738, 680, 462, 813, 628, 489, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 826, 501, 688, 446, 933, 847, 636, 963, 733, 937, 476, 854, 827, 447, 746, 868, 638, 908, 800, 488, 696, 747, 829, 858, 754, 855, 916, 965, 478, 910, 720, 505, 749, 945, 639, 755, 870, 256, 911, 700, 859, 479, 918, 871, 728, 494, 874, 969, 932, 702, 816, 861, 500, 757, 492, 875, 732, 923, 824, 977, 919, 934, 744, 761, 882, 495, 703, 922,877, 935, 828, 848, 734, 503, 883, 938, 384, 964, 748, 506, 856, 925, 993, 735, 502, 830, 966, 939, 885, 946, 750, 860, 756, 480, 967, 831, 889, 941, 751, 872, 507, 971, 912, 758, 947, 970, 862, 978, 448, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021, 1016, 1008, 1020, 1022 1023, 1024];
последовательность S17: [1, 2, 5, 9, 3, 17, 33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 37, 8, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 161, 70, 50, 75, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 134, 321, 53, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 164, 268, 386, 325, 305, 537, 769, 533, 209, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 198, 178, 642, 171, 28 2, 92, 553, 202, 199, 389, 294, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 211, 185, 534, 401, 306, 301, 643, 156, 110, 327, 539, 116, 168, 593, 158, 111, 307, 548, 330, 213, 771, 226, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 180, 777, 200, 229, 554, 339, 657, 313, 541, 391, 123, 582, 394, 284, 773, 233, 673, 555, 785, 175, 341, 705, 449, 562, 354, 801, 395, 204, 182, 528, 583, 557, 296, 286, 64, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 214, 594, 357, 308, 419, 187, 589, 569, 302, 647, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 160, 218, 610, 597, 552, 651, 230, 120, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 176, 653, 392, 231, 314, 340, 543, 335, 234, 556, 775, 124, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 350, 619, 128, 788, 246, 782, 898, 437, 667, 466, 592, 408, 621, 364, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382,814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 933, 847, 446, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 639, 755, 256, 969, 479, 384, 870, 492, 911, 816, 918, 728, 871, 874, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 848, 993, 448, 502, 877, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021, 1016, 1008, 1020, тысяча двадцать-две, 1023, 1024];
последовательность S18: [1, 2, 3, 5, 9, 17, 33, 4, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 513, 8, 12, 130, 41, 69, 14, 20, 131, 49, 15, 73, 258, 22, 133, 36, 81, 23, 259, 26, 137, 38, 261, 97, 145, 27, 514, 39, 515, 265, 68, 42, 29, 161, 70, 43, 517, 50, 71, 273, 45, 521, 529, 16, 132, 74, 193, 51, 289, 545, 24, 75, 53, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 40, 98, 385, 85, 30, 139, 262, 146, 31, 99, 516, 44, 89, 141, 263, 147, 101, 266, 72, 46, 162, 518, 577, 519, 52, 149, 522, 47, 76, 267, 163, 274, 523, 641, 105, 54, 153, 78, 269, 194, 165, 275, 55, 84, 530, 525, 531, 136, 58, 113, 195, 290, 79, 169, 277, 59, 86, 100, 87, 140, 61, 197, 90, 291, 281, 546, 769, 142, 177, 91, 102, 148, 143, 533, 547, 537, 32, 103, 264, 106, 322, 293, 201, 323, 578, 150, 297, 48, 93, 209, 549, 579, 268, 386, 325, 305, 164, 151, 107, 56, 154, 225, 387, 329, 270, 114, 520, 553, 642, 80, 166, 109, 155, 276, 60, 271, 115, 167, 524, 581, 561, 157, 196, 170, 198, 171, 278, 292, 279, 117, 88, 62, 178, 282, 526, 643, 532, 527, 63, 92, 585, 770, 144, 389, 294, 199, 104, 337, 173, 283, 202, 121, 179, 295, 94, 534, 645, 535, 593, 548, 771, 152, 324, 393, 298, 203, 108, 285, 181, 210, 538, 95, 205, 299, 353, 649, 609, 326, 185, 211, 401, 306, 301, 110, 156, 327, 116, 111, 773, 550, 657, 539, 551, 168, 213, 307, 330, 158, 226, 118, 172, 331, 227, 388, 309, 217, 417, 338, 159, 777, 272, 580, 119, 541, 554, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 64, 394, 284, 175, 123, 341, 449, 354, 395, 233, 204, 673, 555, 557, 562, 582, 296, 286, 182, 206, 125, 785, 705, 183, 287, 528, 583, 644, 586, 563, 300, 355, 212, 402, 186, 397, 345, 207, 302, 801, 96, 187, 241, 536, 587, 565, 646, 594, 328, 403, 214, 357, 308, 303, 833, 589, 647, 112, 540, 569, 595, 650, 772, 228, 418, 332, 215, 405, 310, 189, 552, 610, 897, 160, 218, 361, 419, 409, 369, 230, 450, 421, 542, 597, 651, 774, 658, 311, 120, 334, 219, 543, 611, 231, 392, 234, 314, 176, 340, 335, 221, 451, 425, 315, 556, 601, 653, 124, 775, 659, 613, 235, 288, 453, 126, 342, 396, 778, 584, 558, 674, 356, 343, 564, 661, 559, 617, 779, 675, 184, 398, 433, 317, 346, 242, 208, 404, 358, 786, 188, 588, 566, 665, 625, 781, 237, 127, 243, 347, 399, 706, 216, 677, 787, 590, 567, 648, 406, 359, 304, 570, 596, 362, 707, 190, 457, 349, 465, 802, 420, 407, 245, 410, 591, 681, 789, 571, 598, 363, 573, 220, 422, 599, 652, 612, 709, 602, 803, 370, 793, 312, 191, 654, 689, 603, 411, 232, 249, 365, 336, 423, 614, 660, 655, 316, 222, 371, 426, 452, 413, 481, 236, 223, 344, 318, 544, 373, 615, 427, 776, 128, 454, 238, 560, 834, 805, 713, 835, 662, 809, 605, 618, 721, 780, 434, 898, 319, 455, 837, 817, 676, 663, 348, 429, 400, 377, 244, 239, 458, 435, 360, 568, 619, 666, 737, 899, 841, 782, 626, 350, 246, 459, 592, 678, 621, 667, 788, 572, 783, 627, 679, 408, 364, 351, 192, 247, 437, 466, 412, 461, 250, 366, 600, 708, 574, 669, 682, 790, 804, 791, 710, 683, 629, 441, 690, 794, 604, 575, 467, 424, 372, 251, 482, 414, 469, 367, 374, 656, 901, 806, 711, 428, 415, 253, 616, 849, 685, 795, 714, 633, 691, 807, 606, 483, 473, 224, 664, 836, 905, 810, 715, 620, 797, 693, 375, 485, 430, 456, 722, 607, 717, 811, 865, 838, 697, 723, 913, 818, 378, 436, 813, 320, 622, 240, 431, 460, 379, 668, 839, 489, 438, 628, 623, 462, 381, 439, 352, 497, 680, 725, 819, 842, 670, 738, 630, 468, 248, 442, 463, 470, 443, 252, 684, 843, 739, 900, 821, 729, 929, 850, 671, 784, 631, 792, 845, 902, 686, 368, 634, 712, 254, 692, 741, 851, 825, 903, 687, 471, 416, 484, 445, 376, 474, 906, 796, 486, 635, 745, 853, 961, 866, 907, 716, 694, 808, 475, 798, 637, 695, 255, 718, 576, 799, 812, 867, 432, 380, 698, 914, 487, 724, 909, 857, 719, 477, 814, 608, 490, 699, 753, 840, 915, 726, 869, 820, 815, 440, 491, 624, 382, 498, 493, 464, 672, 930, 844, 740, 917, 822, 727, 632, 701, 873, 931, 921, 881, 730, 383, 499, 444, 446, 472, 962, 933, 823, 742, 846, 731, 447, 688, 904, 636, 826, 743, 852, 847, 256, 476, 733, 963, 937, 827, 746, 501, 488, 638, 505, 800, 696, 854,908, 868, 855, 747, 910, 829, 858, 754, 720, 916, 870, 478, 700, 749, 639, 816, 965, 945, 755, 859, 911, 492, 479, 728, 918, 871, 384, 494, 500, 874, 702, 969, 495, 861, 502, 932, 919, 757, 922, 875, 732, 977, 934, 882, 761, 824, 703, 923, 744, 877, 848, 935, 828, 734, 883, 448, 938, 503, 964, 925, 993, 748, 735, 856, 885, 939, 506, 966, 507, 830, 750, 946, 860, 831, 967, 756, 941, 912, 872, 751, 889, 480, 970, 947, 862, 758, 971, 509, 920, 640, 876, 863, 759, 949, 978, 924, 973, 762, 878, 979, 496, 936, 704, 884, 953, 763, 504, 926, 879, 981, 994, 886, 940, 927, 765, 736, 887, 995, 942, 968, 985, 508, 890, 948, 832, 752, 943, 997, 972, 891, 1001, 510, 950, 974, 893, 951, 864, 760, 1009, 511, 980, 954, 764, 975, 955, 880, 982, 983, 928, 996, 766, 957, 888, 986, 998, 987, 944, 892, 999, 767, 512, 989, 1002, 952, 1003, 894, 976, 895, 1010, 956, 1005, 1011, 958, 984, 959, 988, 1013, 1000, 1017, 768, 990, 1004, 991, 1006, 1012, 1007, 1014, 896, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024];
последовательность S19: [1, 2, 3, 5, 9, 17, 33, 4, 257, 513, 6, 65, 7, 10, 11, 129, 18, 13, 19, 34, 21, 35, 25, 66, 37, 258, 8, 130, 67, 12, 41, 69, 514, 20, 14, 131, 49, 15, 73, 259, 22, 133, 36, 23, 81, 26, 137, 38, 27, 515, 261, 97, 39, 68, 42, 145, 29, 70, 43, 265, 50, 161, 71, 517, 45, 193, 132, 273, 74, 51, 134, 82, 75, 16, 289, 521, 24, 53, 135, 77, 57, 83, 260, 28, 138, 98, 529, 40, 262, 85, 139, 30, 146, 44, 321, 545, 99, 89, 141, 31, 263, 147, 46, 72, 516, 101, 266, 162, 52, 149, 47, 267, 769, 76, 105, 163, 385, 54, 153, 78, 518, 194, 274, 165, 55, 84, 269, 577, 136, 58, 113, 275, 79, 195, 519, 59, 290, 169, 86, 140, 277, 522, 100, 87, 291, 197, 142, 523, 61, 281, 90, 102, 322, 148, 641, 177, 91, 293, 143, 201, 530, 264, 32, 150, 386, 525, 103, 106, 93, 323, 48, 531, 164, 268, 151, 209, 546, 297, 107, 154, 325, 533, 166, 56, 276, 114, 155, 547, 270, 80, 109, 537, 387, 225, 167, 305, 578, 60, 115, 271, 196, 549, 329, 170, 157, 278, 770, 88, 171, 389, 520, 117, 292, 198, 62, 642, 279, 17 8, 92, 579, 337, 199, 282, 144, 524, 63, 393, 121, 553, 294, 202, 283, 581, 173, 104, 353, 532, 179, 295, 94, 526, 203, 324, 181, 643, 298, 108, 401, 561, 152, 210, 285, 527, 95, 326, 205, 585, 299, 156, 771, 306, 211, 110, 534, 417, 168, 327, 645, 185, 301, 548, 116, 449, 226, 535, 388, 158, 593, 330, 111, 307, 538, 213, 118, 649, 390, 172, 338, 550, 227, 331, 539, 217, 272, 773, 159, 280, 609, 119, 309, 174, 551, 391, 122, 580, 333, 200, 554, 180, 229, 657, 313, 175, 541, 339, 123, 582, 284, 204, 394, 555, 64, 354, 777, 182, 296, 562, 233, 341, 673, 395, 583, 125, 286, 557, 206, 402, 705, 183, 300, 644, 212, 355, 785, 186, 345, 586, 241, 397, 563, 207, 287, 646, 96, 594, 403, 302, 587, 214, 328, 528, 187, 801, 357, 112, 536, 418, 228, 565, 308, 647, 405, 215, 589, 303, 189, 569, 332, 595, 218, 361, 772, 419, 230, 540, 310, 650, 160, 409, 610, 334, 552, 120, 450, 774, 219, 597, 421, 231, 651, 311, 542, 340, 658, 234, 392, 556, 314, 833, 176, 369, 611, 124, 601, 335, 451, 653, 221, 543, 315, 775, 184, 425, 659, 342, 558, 235, 584, 396, 613, 356, 126, 778, 343, 674, 453, 564, 242, 398, 661, 208, 559, 317, 779, 346, 588, 188, 358, 617, 404, 675, 237, 897, 433, 566, 347, 665, 127, 590, 399, 457, 706, 243, 786, 288, 677, 406, 567, 190, 596, 359, 781, 362, 648, 216, 570, 349, 625, 304, 245, 787, 420, 591, 407, 707, 465, 571, 220, 802, 363, 681, 410, 598, 191, 652, 422, 789, 312, 612, 249, 599, 370, 803, 411, 709, 336, 654, 232, 573, 365, 793, 481, 222, 423, 602, 316, 61 4, 371, 834, 236, 660, 452, 689, 426, 603, 413, 805, 223, 655, 344, 713, 427, 776, 238, 544, 373, 662, 454, 898, 318, 615, 244, 618, 605, 434, 835, 348, 560, 455, 676, 239, 780, 400, 663, 319, 721, 377, 809, 458, 619, 128, 666, 429, 837, 678, 360, 568, 435, 788, 246, 626, 350, 667, 459, 782, 592, 437, 621, 247, 899, 364, 737, 408, 679, 466, 817, 572, 351, 627, 250, 783, 461, 708, 841, 412, 682, 467, 669, 366, 790, 192, 600, 683, 424, 901, 441, 629, 804, 372, 710, 482, 574, 251, 791, 690, 414, 604, 367, 849, 711, 469, 794, 374, 656, 428, 575, 905, 253, 633, 483, 806, 714, 473, 795, 415, 685, 616, 375, 865, 691, 224, 807, 430, 606, 715, 378, 836, 456, 693, 810, 436, 620, 913, 485, 664, 431, 722, 797, 240, 607, 838, 379, 717, 460, 811, 668, 320, 818, 723, 438, 622, 929, 489, 680, 381, 839, 697, 248, 813, 628, 462, 961, 738, 439, 900, 670, 468, 842, 623, 442, 819, 725, 497, 630, 463, 902, 684, 252, 850, 739, 352, 843, 729, 784, 470, 671, 792, 443, 631, 821, 368, 686, 903, 484, 634, 845, 47 1, 712, 692, 445, 741, 825, 474, 687, 851, 635, 254, 796, 716, 486, 906, 576, 416, 866, 694, 808, 376, 745, 853, 475, 907, 637, 487, 798, 718, 914, 490, 695, 812, 432, 724, 867, 698, 380, 857, 753, 477, 909, 719, 799, 255, 608, 915, 814, 440, 726, 840, 699, 491, 869, 624, 382, 930, 740, 820, 498, 917, 727, 815, 464, 701, 844, 730, 444, 873, 931, 742, 493, 822, 672, 921, 383, 846, 632, 962, 499, 731, 933, 743, 823, 446, 852, 746, 904, 472, 826, 688, 881, 501, 636, 847, 963, 733, 256, 827, 696, 937, 476, 854, 747, 908, 868, 447, 638, 855, 965, 754, 505, 910, 720, 829, 858, 488, 700, 870, 916, 478, 749, 945, 859, 639, 911, 492, 969, 755, 800, 918, 479, 702, 871, 874, 728, 494, 861, 816, 757, 932, 919, 500, 977, 732, 875, 922, 703, 495, 934, 824, 761, 882, 384, 923, 848, 744, 877, 993, 734, 502, 935, 828, 883, 748, 964, 503, 938, 925, 735, 856, 939, 750, 506, 885, 966, 830, 756, 946, 860, 448, 967, 751, 912, 831, 889, 970, 507, 640, 941, 872, 947, 758, 862, 971, 509, 949, 759, 876, 920, 978, 863, 762, 480, 973, 924, 979, 878, 704, 936, 953, 884, 496, 994, 763, 926, 879, 981, 886, 940, 765, 504, 995, 985, 927, 887, 736, 942, 890, 968, 948, 997, 508, 943, 752, 891, 972, 832, 950, 1001, 893, 760, 974, 951, 510, 980, 954, 1009, 975, 764, 864, 982, 955, 880, 996, 983, 957, 986, 511, 766, 998, 928, 888, 987, 999, 1002, 944, 892, 989, 767, 952, 1003, 894, 1010, 976, 956, 512, 1005, 895, 1011, 958, 984, 1013, 768, 988, 959, 1017 1000, 990, 1004, 991, 1006, 1012, 1007, 896, 1014, 1015, 1018, 960, 1019, 1021, 992, 1008, 1016, 1020, 1022 1023, 1024]; и
последовательность S20: [1, 2, 3, 5, 9, 17, 33, 4, 6, 513, 65, 7, 10, 11, 129, 18, 13, 19, 34, 257, 21, 35, 25, 66, 37, 67, 8, 12, 130, 41, 69, 14, 514, 20, 131, 49, 15, 73, 258, 22, 133, 36, 81, 23, 259, 26, 137, 38, 261, 515, 97, 145, 27, 39, 265, 68, 42, 29, 161, 70, 43, 50, 75, 517, 273, 193, 71, 45, 132, 16, 74, 289, 51, 24, 53, 521, 134, 82, 321, 77, 135, 28, 57, 83, 138, 260, 529, 40, 98, 385, 30, 85, 139, 262, 146, 545, 31, 99, 44, 89, 141, 263, 147, 72, 516, 266, 46, 101, 162, 52, 149, 47, 518, 76, 267, 163, 274, 105, 54, 153, 577, 78, 269, 194, 165, 275, 55, 519, 84, 136, 58, 113, 195, 290, 522, 79, 169, 277, 59, 86, 61, 523, 87, 140, 100, 197, 90, 641, 291, 281, 142, 177, 91, 102, 530, 148, 143, 32, 103, 264, 525, 106, 322, 293, 201, 531, 323, 150, 297, 48, 93, 546, 209, 268, 386, 325, 769, 305, 164, 151, 107, 533, 56, 154, 225, 387, 329, 547, 270, 114, 80, 537, 166, 109, 155, 276, 578, 60, 271, 115, 167, 549, 157, 196, 170, 198, 579, 171, 278, 292, 520, 279, 117, 88, 62, 524, 178, 28 2, 63, 642, 92, 144, 389, 294, 553, 199, 104, 337, 581, 173, 283, 202, 526, 121, 179, 295, 532, 94, 152, 324, 643, 393, 298, 203, 561, 108, 285, 181, 527, 210, 95, 205, 585, 299, 353, 326, 770, 185, 211, 534, 401, 306, 301, 645, 110, 156, 327, 548, 116, 111, 593, 168, 213, 307, 535, 330, 158, 771, 226, 118, 172, 538, 331, 227, 649, 388, 309, 217, 550, 417, 338, 773, 159, 272, 609, 119, 280, 657, 333, 390, 174, 539, 122, 200, 551, 180, 229, 777, 339, 313, 580, 391, 123, 554, 394, 284, 541, 64, 175, 341, 673, 449, 354, 582, 395, 233, 555, 204, 296, 562, 286, 587, 182, 206, 785, 125, 183, 705, 287, 300, 583, 355, 212, 557, 402, 186, 644, 397, 345, 528, 207, 302, 586, 96, 801, 187, 241, 563, 328, 403, 536, 214, 565, 357, 308, 646, 303, 112, 594, 228, 833, 418, 332, 589, 215, 405, 647, 310, 540, 189, 160, 569, 218, 361, 595, 419, 650, 409, 369, 772, 230, 552, 450, 421, 610, 311, 897, 120, 334, 542, 219, 597, 176, 651, 392, 231, 774, 314, 658, 124, 340, 543, 335, 611, 221, 451, 556, 425, 601, 315, 653, 234, 235, 775, 288, 659, 453, 584, 126, 778, 342, 396, 558, 356, 613, 343, 674, 184, 398, 564, 433, 661, 317, 559, 346, 588, 242, 208, 779, 404, 675, 358, 786, 188, 617, 237, 566, 127, 665, 243, 347, 590, 399, 781, 216, 706, 406, 677, 359, 787, 304, 567, 362, 596, 190, 648, 457, 570, 349, 465, 625, 420, 707, 407, 802, 245, 591, 410, 681, 363, 789, 220, 571, 422, 598, 370, 573, 312, 599, 191, 652, 411, 612, 232, 709, 249, 602, 365, 803, 336, 793, 423, 316, 222, 654, 371, 689, 426, 603, 452, 614, 413, 660, 481, 655, 236, 544, 223, 615, 344, 776, 318, 618, 373, 834, 427, 805, 128, 713, 454, 835, 238, 662, 809, 434, 560, 319, 605, 455, 721, 348, 780, 429, 898, 400, 837, 377, 817, 244, 676, 239, 663, 458, 619, 568, 435, 666, 360, 737, 350, 899, 246, 841, 459, 782, 626, 408, 592, 364, 678, 351, 621, 437, 667, 192, 788, 572, 247, 783, 466, 627, 412, 679, 669, 461, 708, 250, 682, 366, 710, 441, 683, 790, 467, 804, 424, 791, 629, 372, 600, 251, 574, 414, 690, 794, 367, 575, 469, 604, 656, 482, 901, 374, 806, 428, 711, 616, 415, 849, 253, 685, 795, 483, 714, 473, 633, 691, 224, 807, 606, 375, 664, 485, 836, 905, 430, 810, 456, 715, 620, 378, 797, 693, 436, 722, 320, 607, 717, 240, 811, 865, 431, 838, 460, 697, 723, 379, 913, 818, 489, 813, 622, 438, 668, 462, 839, 628, 381, 623, 680, 439, 725, 819, 352, 842, 670, 497, 738, 630, 468, 684, 843, 248, 739, 442, 900, 821, 463, 729, 929, 470, 850, 671, 784, 443, 631, 792, 252, 845, 902, 368, 686, 634, 254, 712, 692, 471, 741, 851, 416, 825, 903,484, 635, 906, 796, 445, 576, 687, 376, 853, 961, 474, 866, 907, 745, 486, 716, 808, 475, 798, 694, 255, 718, 637, 695, 432, 799, 812, 380, 867, 724, 914, 487, 698, 909, 477, 857, 719, 814, 490, 608, 699, 753, 440, 840, 915, 726, 491, 869, 820, 382, 815, 624, 740, 498, 930, 844, 727, 493, 917, 822, 701, 464, 672, 730, 873, 383, 931, 921, 881, 499, 742, 962, 933, 444, 823, 632, 846, 731, 446, 688, 904, 743, 472, 826, 636, 852, 447, 847, 733, 963, 937, 256, 827, 746, 747, 476, 800, 965, 638, 854, 501, 908, 868, 855, 696, 488, 910, 945, 829, 858, 505, 754, 720, 916, 478, 870, 700, 749, 639, 755, 492, 859, 911, 728, 918, 479, 871, 816, 874, 702, 384, 969, 861, 977, 932, 919, 494, 757, 922, 875, 732, 934, 500, 882, 824, 703, 923, 495, 744, 761, 877, 848, 935, 828, 502, 734, 883, 938, 964, 925, 448, 993, 748, 735, 856, 830, 885, 503, 939, 640, 966, 750, 946, 831, 506, 967, 860, 941, 912, 889, 756, 507, 751, 970, 947, 872, 862, 758, 971, 480, 920, 876, 863, 949, 704, 759, 978, 509, 924, 973,762, 878, 953, 979, 936, 884, 496, 763, 926, 879, 981, 994, 886, 940, 927, 504, 765, 995, 985, 736, 887, 997, 942, 968, 890, 948, 508, 832, 752, 943, 972, 891, 1001, 950, 974, 893, 951, 864, 510, 1009, 980, 760, 954, 975, 982, 955, 764, 880, 766, 983, 928, 996, 511, 957, 888, 986, 998, 987, 767, 944, 892, 999, 989, 1002, 952, 1003, 894, 1010, 1005, 976, 512, 895, 1011, 956, 958, 984, 959, 768, 988, 1013, 1000, 1017, 990, 1004, 991, 896, 1006, 1012, 1007, 1014, 960, 1015, 1018, 1019, 992, 1021, 1008, 1016, 1020, 1022, 1023, 1024].
Указанные выше последовательности с относительно хорошей производительностью, полученный с помощью моделирования, можно сравнить с использованием заданного правила определения производительности. Возможно, этот вариант осуществление настоящего изобретения представляет собой пример правила определения производительности, но настоящее изобретение этим не ограничивается.
Далее приведено описание возможного правила определения производительности.
Оценка измерения: при достижении коэффициента блочной ошибки (block error rate, BLER) 10-2 и 10-3 требуется отношение сигнал-шум (signal-to-noise, SNR).
Моделирование условия:

K является значением, которое обеспечивает значение битовой скорости меньше 1/8 не рассматривается.
Оценивают значение SNR, требуемое при достижении BLER 10-2 и 10-3 соответственно. Более конкретно, заданы последовательности А и В. Исследуют каждую комбинацию (N, K) на основании параметра моделирования в приведенной выше таблице. Так, например, N = 64, К = 10. Значение SNR требуется при BLER = 10-2 полярным кодом с использованием последовательности A, обозначается как HA, и значение SNR, когда требуется BLER=10-2 полярным кодом с использованием последовательности B, обозначается как HB. Интерполяция HA-НВ значений SNR сравнивается с заданным пороговым значением. Если интерполяция HA-НВ, больше, чем пороговое значение, то записывается, что выбирают последовательность B, подсчет выигрыша в последовательности В увеличивается на 1, и счетчик проигрыша последовательности А увеличивается на 1. Если интерполяция HA-HB меньше, чем отрицательное пороговое значение, то записывают выигрыш последовательности А, счетчик выигрыша последовательности А увеличивается на 1, и счетчик проигрыша последовательности B увеличивается на 1. Если интерполяция HA-НВ является меньше или равно пороговому значению, или больше или равно отрицательному пороговому значению, то записывают, что эти две последовательности имеют одинаковую производительность, и ни один из счетчиков выигрыша двух последовательностей не увеличивается. Кроме того, SNR значения, необходимые для последовательностей А и В, при достижении значения BLER = 10-3, дополнительно исследована, интерполяция сравнивается с пороговым значением, и операция дополнительно выполняется на подсчете выигрыша.
Этапы определения приведенного выше порогового значения заключаются в следующем.
Когда длина К подлежащей кодированию информации была меньше или равна 200, PerfThresh_K = 0,1 дБ; или когда К больше, чем 200, то PerfThresh_K = 0,3 дБ.
Когда количество списков декодирования L = 1, PerfThresh_L = 0,4 дБ; когда L = 2, PerfThresh_L = 0,2 дБ; или, когда L является другим значением, PerfThresh_L = 0,1 дБ.
В качестве конечного порогового значения из двух пороговых значений выбирают наибольшее, то есть, PerfThresh = макс (PerfThresh_K, PerfThresh_L).
Процедура сравнения конкретных последовательностей представляет собой следующее.
Этап 1: вычислить значение счетчика выигрыша значение счетчика проигрыша и общее количество проигрыша для каждой последовательности. Выбирают последовательность А и последовательность А сравнивают с последовательностью B в каждом случае моделирования. Для каждого случая моделирования, если производительность А хуже, чем у B посредством PerfThresh, то значение счетчика проигрыша FailCount_AB A versus B увеличивают на 1; или, если производительность А лучше, чем у B посредством PerfThresh, то значение счетчика выигрыша WinCountAB A versus B увеличивают на 1. Если (FailCount_AB - WinCountAB)/общее количество случаев моделирования > 2%, то общее значение счетчика проигрыша OverallFail_A А увеличивается на 1. Последовательность А сравнивают с последовательностью C в каждом случае моделирования. Для каждого случая моделирования, если производительность А хуже, чем у C посредством PerfThresh, то значение счетчика проигрыша FailCount_AC А versus С увеличивают на 1; или, если производительность А лучше, чем С посредством PerfThresh, то значение счетчика выигрыша WinCount_AC А versus C увеличивается на 1. Если (FailCount_AC - WinCountAC)/общее количество случаев моделирования > 2%, то общее значение счетчика проигрыша OverallFail_A А увеличивают на 1. Этот процесс повторяется для последовательностей D на N. Выбирают последовательность B и последовательность В сравнивают с последовательностью B в каждом случае моделирования, и так далее. Выбирают последовательность N и последовательность N сравнивают с последовательностью А и так далее. Выбирают последовательность с минимальным общим значением счетчика проигрыша OverallFail.
Этап 2: если множество последовательностей A - М каждое имеет минимальное общее значение счетчика проигрыша OverallFail, для последовательности А, последовательность А сравнивают с последовательностью B в каждом случае моделирования. Для каждого случая моделирования, если производительность А лучше, чем у B посредством PerfThresh, то значение счетчика выигрыша WinCount_AB A versus B увеличивается на 1. Последовательность А сравнивают с последовательностью C в каждом случае моделирования. Для каждого случая моделирования, если производительность А лучше, чем С посредством PerfThresh, значение счетчика выигрыша WinCount_AC А versus C увеличивается на 1, и общее значение счетчика выигрыш А равно WinCount А = ΣWinCount_AB ... AM. Процесс повторяется до тех пор, пока последовательность А сравнивается с последовательностью М. Процесс повторяется для последовательностей В до последовательности М. Выбирают А последовательность с максимумом общего значения счетчика выигрыша WinCount, и предполагают, что последовательность представляет собой последовательность W.
Этап 3: задана последовательность W с максимумом общего значения счетчика выигрыша. Если существует последовательность х и значение счетчика выигрыша х для W больше, чем значение счетчика выигрыша W для х, а именно, WinCount_xW> WinCount Wx, выбирают также последовательность х для использования в следующем раунде.
Этап 4: если выбирают множество последовательностей, то конечная последовательность определяется путем голосования.
Следует отметить, что приведенные выше последовательности S1-S20 могут быть применены в способе полярного кодирования, показанного на фиг. 2 в этом варианте осуществления настоящего изобретения. В любой последовательности, корректировка или эквивалентные замены, включают в себя, но не ограничиваясь ими, следующие несколько аспектов может быть сделана, не затрагивая общий эффект последовательности.
1. Местоположения нескольких элементов в последовательности сортировки взаимно обмениваются. Например, местоположение номера последовательности можно корректировать в пределах указанной амплитуды. Например, указанная амплитуда равна 5, и местоположение элемента, чей номер последовательности равен 10, может быть откорректировано в диапазоне от пяти местоположений слева элемента до пяти местоположений справа от элемента.
2. Некоторые элементы в последовательности сортировки корректируется, но наборы каналов, которые используются для передачи Т-битной информации и которые были выбраны на основе последовательности сортировки, могут быть одинаковыми или аналогичными.
3. Последовательность сортировки включает в себя N элементов от 1 до N, и N элементов от 1 до N представляют номера последовательности N поляризованных каналов. На самом деле, номера последовательности N поляризованных каналов могут начинаться с 0 и заканчиваться N-1, и номер последовательности может быть получен путем вычитания 1 из каждого номера последовательности в последовательности сортировки. Это также является формой номера последовательности в предшествующем способе вычисления. Конечно же, в качестве альтернативы, может быть использован другой способ представления номеров последовательности или идентификаторов поляризованных каналов, и конкретный способ выражения не влияет на конкретные местоположения поляризованных каналов, представленных в последовательности сортировки.
4. Номера последовательности N поляризованных каналов в последовательности сортировки расположены в порядке убывания надежности N поляризованных каналов. На самом деле, номера последовательности N поляризованных каналов могут быть альтернативно расположены в порядке возрастания надежности N поляризованных каналов. Элементы в последовательности сортировки расположены в обратном порядке.
5. Последовательность сортировки может дополнительно быть представлена с помощью последовательности сортировки нормированной надежности или эквивалентной надежности всех каналов. Например, если местоположение сортировки канала х в последовательности является у (минимальный номер последовательности в последовательности сортировки обозначается как 1), то надежность канала может быть представлена у или нормализованной величиной y/N, где N представляет собой длину последовательности сортировки.
На основе способа полярного кодирования, показанного на фиг. 2, как показано на фиг. 3, где показан вариант осуществления настоящего изобретения, который дополнительно обеспечивает устройство 300 для полярного кодирования. Устройство 300 для полярного кодирования выполнено с возможностью выполнять способ полярного кодирования, показанный на фиг. 2. Устройство 300 для полярного кодирования включает в себя:
блок 301 определения, выполненный с возможностью определять последовательность, используемую для кодирования битой, подлежащих кодированию, где последовательность используют для представления порядка надежности N поляризованных каналов, N является длиной материнского кода полярного кода, и N представляет собой целое положительное число степени 2; и
блок 302 кодирования, выполненный с возможностью выполнять полярное кодирование бит, подлежащих кодированию, с использованием последовательности для получения кодированных бит.
Возможно, длина подлежащих кодированию бит равна К, К подлежащих кодированию бит отображают на К поляризованные каналы в N поляризованных каналах, и надежность K поляризованных каналов выше, чем надежность остальных N-К поляризованных каналов.
Возможно, последовательность может быть полностью или частично какой-либо одной из последовательностей (1) до (30) в вышеизложенном способе, или может представлять собой часть или все из любой одной из последовательностей S1-S20 в вышеприведенном способе.
Основываясь на той же концепции изобретения в качестве способа полярного кодирования, показанного на фиг. 2, как показано на фиг. 4, где показан вариант осуществления настоящего изобретения, который дополнительно обеспечивает устройство 400 для полярного кодирования. Устройство 400 для полярного кодирования выполнено с возможностью выполнять способа полярного кодирования, показанный на фиг. 2. Часть или весь способ полярного кодирования, показанный на фиг. 2, может быть реализован с помощью аппаратных средств или может быть реализован с помощью программного обеспечения. Когда способ реализуют с использованием аппаратных средств, устройство 400 для полярного кодирования включает в себя: схему 401 интерфейса ввода, выполненную с возможностью получать биты, подлежащие кодированию; логическую схему 402, выполненную с возможностью выполнять способ полярного кодирования, показанный на фиг. 2, где может быть сделана ссылка на описание в варианте осуществления вышеупомянутого способа и подробности не описаны здесь снова; и схему 403 интерфейса вывода, выполненную с возможностью выводить кодированную битовую последовательность.
Возможно, в конкретной реализации устройство 400 для полярного кодирования может представлять собой микросхему или интегральную схему.
Возможно, когда часть или весь способ полярного кодирования в предшествующем варианте осуществления реализован с помощью программного обеспечения, как показано на фиг. 5, устройство 400 для полярного кодирования включает в себя: память 501, выполненную с возможностью хранить программу; и процессор 502, выполненный с возможностью выполнять программу, хранящуюся в памяти 501. Когда программа выполнена, устройство 400 для полярного кодирования может реализовывать способ полярного кодирования, представленный в вышеупомянутом варианте осуществления на фиг. 2.
Возможно, память 501 может быть физически независимым блоком или, как показано на фиг. 6, память 501 может быть встроена в процессор 502.
Возможно, когда часть или весь способ полярного кодирования в предшествующем варианте осуществления на фиг. 2 реализован с помощью программного обеспечения, устройство 400 для полярного кодирования может включать в себя только процессор 502. Память 501, выполненная с возможностью хранить программу, расположена вне устройства 400 для полярного кодирования. Процессор 502 соединен с памятью 501, используя схему/проводку, и выполнен с возможностью считывать и выполнять программу, хранящуюся в памяти 501.
Процессор 502 может представлять собой центральный блок обработки (central processing unit, CPU), сетевой процессор (network processor, NP) или сочетание CPU и NP.
Процессор 502 может дополнительно включать в себя аппаратную микросхему. Аппаратная микросхема может быть специализированной интегральной схемой (application-specific integrated circuit, ASIC), программируемым логическим устройством (programmable logic device, PLD) или их комбинации. PLD может быть сложным программируемым логическим устройством (complex programmable logic device, CPLD), программируемой пользователем вентильной матрицей (field-programmable gate array, FPGA), типовой матричной логикой (generic array logic, GAL) или любой их комбинацией.
Память 501 может включать в себя энергозависимую память (volatile memory), например, оперативное запоминающее устройство (random-access memory, RAM); память 501 может включать в себя энергонезависимую память (non- volatile memory), такую как флэш-память (flash memory), жесткий диск (hard disk drive, HDD) или твердотельный накопитель (solid-state drive, SSD); или память 501 может включать в себя комбинацию из указанных выше типов памяти.
Вариант осуществления настоящего изобретения дополнительно обеспечивает машиночитаемый носитель данных. Машиночитаемый носитель данных хранит компьютерную программу, и программа включает в себя инструкцию, используемую для выполнения способа полярного кодирования, показанного на фиг. 2.
Вариант осуществления настоящего изобретения дополнительно предусматривает компьютерный программный продукт, включающий в себя инструкцию. Когда компьютерный программный продукт выполняется на компьютере, компьютер выполняет способ полярного кодирования, показанный на фиг. 2.
Специалисту в данной области техники должно быть понятно, что варианты осуществления настоящего изобретения могут быть предусмотрены в качестве способа, системы или компьютерного программного продукта. Таким образом, настоящее изобретение может использовать только варианты осуществления аппаратных средств, только варианты осуществления программного обеспечения или варианты осуществления с комбинацией программных и аппаратных средств. Кроме того, настоящее изобретение может использовать форму компьютерного программного продукта, который реализуется на одном или более машиночитаемых носителей данных (включающий в себя, но не ограничиваясь, дисковую память, CD-ROM, оптическую память и тому подобное), которые включают в себя используемый компьютером программный код.
Настоящее изобретение описано со ссылкой на блок-схемы алгоритма и/или блок-схемы способа, устройства (системы) и компьютерный программный продукт в соответствии с вариантами осуществления настоящего изобретения. Следует понимать, что инструкция компьютерной программы может быть использована для реализации каждого процесса и/или каждый этап в блок-схемах алгоритма и/или блок-схемах и комбинации процесса и/или этапа блок-схемах алгоритма и/или блок-схемы. Эти инструкции компьютерной программы могут быть предусмотрены для компьютера общего назначения, выделенного компьютера, встроенного процессора или процессора любого другого программируемого устройства обработки данных, чтобы сгенерировать машину, так что инструкции, исполняемые компьютером или процессором любого другого программируемого устройства обработки данных, генерируют устройство для реализации конкретной функции в одном или нескольких процессах в блок-схемах алгоритма и/или в одном или нескольких блоках в блок-схемах.
Эти инструкции компьютерной программы могут храниться в машиночитаемой памяти, которая может инструктировать компьютер или любые другие программируемые устройства выполнять конкретный процесс обработки данных, так что инструкции, сохраненные в машиночитаемой памяти, генерируют артефакт, который включает в себя инструкцию устройства. Инструкция устройства реализует конкретную функцию в одном или нескольких процессов в блок-схемах алгоритма и/или в одном или нескольких блоков в блок-схемах.
Эти инструкции компьютерной программы могут быть загружены в компьютер или другое программируемое устройство обработки данных, так что последовательность операций и этапов выполняются на компьютере или другом программируемом устройстве, тем самым, генерируя выполняемый компьютером процесс обработки. Таким образом, инструкции, выполняемые на компьютере или другом программируемом устройстве, обеспечивают этапы для реализации конкретной функции в одном или нескольких процессах в блок-схемах алгоритма и/или в одном или нескольких блоках в блок-схемах.
Хотя были описаны некоторые предпочтительные варианты осуществления настоящего изобретения, специалист в данной области техники может вносить изменения и модификации в эти варианты осуществления, после ознакомления с основной концепции изобретения. Таким образом, прилагаемую формулу изобретения следует рассматривать как охватывающую предпочтительные варианты осуществления и все изменения, и модификации, входящие в объем настоящего изобретения.
Очевидно, что специалист в данной области техники может внести различные модификации и вариации в варианты осуществления настоящего изобретения без отхода от сущности и объема вариантов осуществления настоящего изобретения. Настоящее изобретение охватывает эти модификации и вариации при условии, что они находятся в пределах объема защиты, определенного в следующей формуле изобретения и их эквивалентных технологий.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ ПОЛЯРНЫМ КОДОМ, БЕСПРОВОДНОЕ УСТРОЙСТВО И МАШИНОЧИТАЕМЫЙ НОСИТЕЛЬ | 2018 |
|
RU2729773C1 |
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ | 2018 |
|
RU2739582C1 |
| РАСПРЕДЕЛЕНИЕ УКАЗАНИЙ РАЗМЕРА ГРУППЫ МОБИЛЬНЫМ СТАНЦИЯМ | 2010 |
|
RU2559761C2 |
| СПОСОБ ПОБАЙТНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ С ПОМОЩЬЮ ПОТОЧНОГО ШИФРОВАНИЯ | 2023 |
|
RU2811065C1 |
| Способ и устройство кодирования данных, носитель данных и процессор | 2018 |
|
RU2742912C1 |
| КОЭФФИЦИЕНТЫ LDPC-СДВИГА ДЛЯ НОВОГО СТАНДАРТА РАДИОСВЯЗИ | 2018 |
|
RU2731883C1 |
| УСТРОЙСТВО КОДИРОВАНИЯ И СПОСОБ КОДИРОВАНИЯ ПОЛЯРНЫМ КОДОМ | 2014 |
|
RU2685034C2 |
| ПРОИЗВОДНЫЕ ПУРИНА, ПРЕДНАЗНАЧЕННЫЕ ДЛЯ ПРИМЕНЕНИЯ В КАЧЕСТВЕ АГОНИСТОВ АДЕНОЗИНОВОГО РЕЦЕПТОРА А | 2007 |
|
RU2457209C2 |
| МУТАНТНЫЙ КАЛЬРЕТИКУЛИН ДЛЯ ДИАГНОСТИКИ МИЕЛОИДНЫХ НОВООБРАЗОВАНИЙ | 2014 |
|
RU2668808C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ, ПРИСПОСОБЛЕНИЕ И УСТРОЙСТВО СВЯЗИ | 2018 |
|
RU2769096C2 |
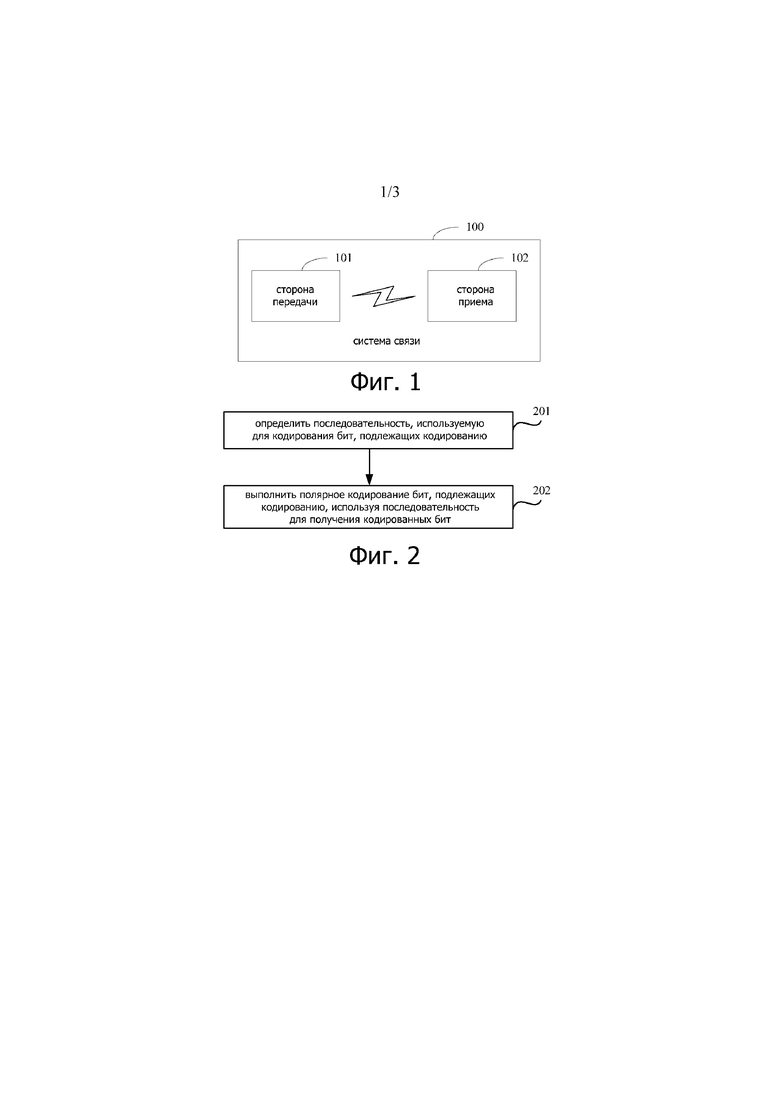

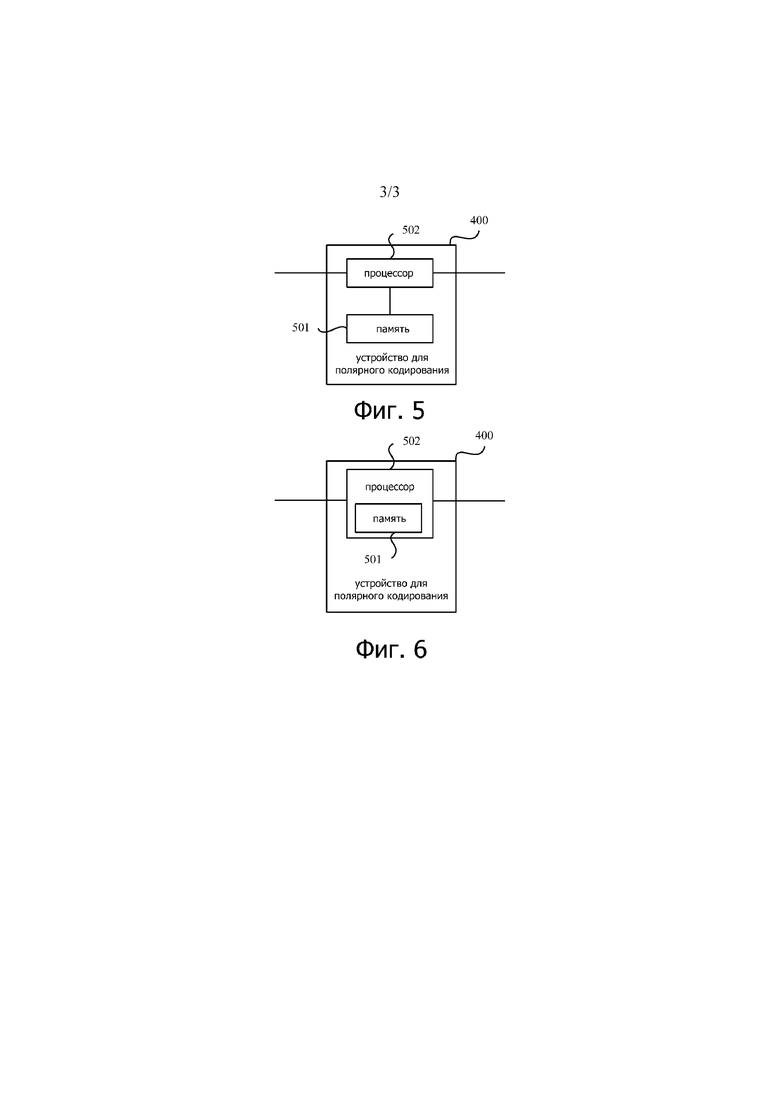
Группа изобретений относится к технологиям связи и, в частности, к технологиям полярного кодирования. Техническим результатом является повышение производительности кодирования/декодирования полярного кода. Предложен способ полярного кодирования. Способ содержит этап, на котором осуществляют определение последовательности, используемой для кодирования бит, подлежащих кодированию, в котором последовательность имеет длину N и используется для представления порядка надежности N поляризованный каналов и N является положительным целым числом степени 2. Далее выполняют полярное кодирование битов, подлежащих кодированию, с использованием последовательности для получения кодированных битов. Способ содержит этап, на котором определение последовательности, используемой для кодирования бит, подлежащих кодированию, содержит определение, на основании длины N материнского кода и заданной последовательности, последовательности, используемой для кодирования бит, подлежащих кодированию. 5 н. и 21 з.п. ф-лы, 6 ил.
1. Способ полярного кодирования, содержащий определение последовательности, используемой для кодирования бит, подлежащих кодированию, в котором последовательность имеет длину N и используется для представления порядка надежности N поляризованный каналов и N является положительным целым числом степени 2, последовательность является [1, 2, 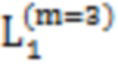 , 17,
, 17, 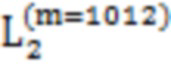 ,
,  , 1020, 1022, 1023, 1024]; и
, 1020, 1022, 1023, 1024]; и 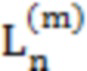 представляет собой подпоследовательность в последовательности, n представляет собой номер последовательности подпоследовательности в заданной последовательности, n ∈ {1, 2, 3}, m указывает длину n-й подпоследовательности, местоположения элементов в подпоследовательности могут взаимно обмениваться в подпоследовательности; и выполнение полярного кодирования битов, подлежащих кодированию, с использованием последовательности для получения кодированных битов.
представляет собой подпоследовательность в последовательности, n представляет собой номер последовательности подпоследовательности в заданной последовательности, n ∈ {1, 2, 3}, m указывает длину n-й подпоследовательности, местоположения элементов в подпоследовательности могут взаимно обмениваться в подпоследовательности; и выполнение полярного кодирования битов, подлежащих кодированию, с использованием последовательности для получения кодированных битов.
2. Способ по п. 1, в котором определение последовательности, используемой для кодирования бит, подлежащих кодированию, содержит определение, на основании длины N материнского кода и заданной последовательности, последовательности, используемой для кодирования бит, подлежащих кодированию.
3. Способ по п. 1 или 2, в котором последовательность, используемая для кодирования бит, подлежащих кодированию, представляет собой всю или подмножество другой последовательности, другая последовательность содержит номера последовательности Nmax поляризованных каналов, Nmax номера последовательности расположены в другой последовательности, основанной на надежности Nmax поляризованных каналов, Nmax является положительным целым числом степени 2 и Nmax ≥ N.
4. Способ по п. 3, в котором Nmax = 1024.
5. Способ по любому из пп. 1-4, в котором длина бит, подлежащих кодированию, равна К и К бит, подлежащих кодированию, отображают на К поляризованные каналы в N поляризованных каналах.
6. Способ по любому из пп. 1-5, в котором 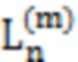 удовлетворяет по меньшей мере одному из следующих условий:
удовлетворяет по меньшей мере одному из следующих условий:
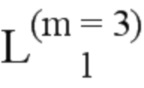 = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и
= (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и  = (1016, 1008).
= (1016, 1008).
7. Способ по любому из пп. 1-5, в котором, когда N = 64, последовательность является любой одной из следующих последовательностей:
[1, 2, (5, 9, 3), 17, 33, (7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), 42, 29, (50, 43), 45, (16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64];
[1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64]; или
[1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28, 40), 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
8. Способ по любому из пп. 1-5, в котором, когда N = 128, последовательность представляет собой
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 12, 41), (20, 14, 69, 49, 15, 73), 22, (27, 36, 81, 39, 23, 38, 26, 97, 68, 42, 29), (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53), 77, (83, 57, 28, 98, 40, 85, 30), (44, 99, 31, 89, 72, 46, 101), 52, (47, 76, 105, 54), (78, 55, 84, 58, 113, 86, 79, 59, 100, 87, 61, 90, 102, 91, 32), (103, 106, 48, 93), (107, 56, 114), (80, 109), (60, 115), (88, 62, 117), (92, 63, 121, 104), 94, (108, 95), 110, 116, 111, 118, (119, 122, 123, 64, 125, 96), 112, 120, 124, 126, 127, 128],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
9. Способ по любому из пп. 1-5, в котором при N = 256 последовательность представляет собой
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29, 70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146, 44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52, 47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178, 92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214, 228, 112, 215, 189, 218, 160, 120, 230, 219), (231, 176, 124, 234, 221, 12 6, 235, 184, 242, 188, 208, 237, 127, 243), (216, 245, 190), (220, 249, 191, 232), 222, (236, 223), (238, 244, 239, 246, 128), (247, 250, 251, 192), (253, 224), 240, 248, 252, 254, 255, 256],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
10. Способ по любому из пп. 1-5, в котором, когда N=512, последовательность является любой одной из следующих последовательностей:
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 15 6, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438), (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477), (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506), 507, (480, 509), (504, 496), 508, 510, 511, 512]; или
[1, 2, 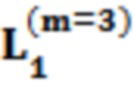 , 17,
, 17,  ,
,  ,
, 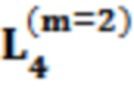 , 508, 510, 511, 512], в котором
, 508, 510, 511, 512], в котором 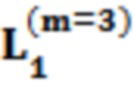 = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);  = (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и
= (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и 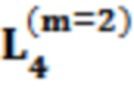 = (504, 496),
= (504, 496),
в котором местоположения элементов в скобках могут быть взаимно обменены в скобках.
11. Способ по любому из пп. 1-10, дополнительно содержащий выполнение согласования скорости на кодированных битах.
12. Устройство для полярного кодирования, содержащее блок определения, выполненный с возможностью определять последовательность, используемую для кодирования бит, подлежащих кодированию, в котором последовательность имеет длину N и используется для представления порядка надежности N поляризованных каналов, N является длиной материнского кода полярного кода и N является положительным целым числом степени 2, последовательность является [1, 2, 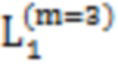 , 17,
, 17, 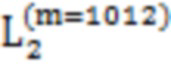 ,
,  , 1020, 1022, 1023, 1024]; и
, 1020, 1022, 1023, 1024]; и 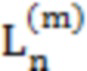 представляет собой подпоследовательность в последовательности, n представляет собой номер последовательности подпоследовательности в заданной последовательности, n ∈ {1, 2, 3}, m указывает длину n-й подпоследовательности, местоположения элементов в подпоследовательности могут взаимно обмениваться в подпоследовательности; и блок кодирования, выполненный с возможностью выполнять полярное кодирование бит, подлежащих кодированию, с использованием последовательности для получения кодированных бит.
представляет собой подпоследовательность в последовательности, n представляет собой номер последовательности подпоследовательности в заданной последовательности, n ∈ {1, 2, 3}, m указывает длину n-й подпоследовательности, местоположения элементов в подпоследовательности могут взаимно обмениваться в подпоследовательности; и блок кодирования, выполненный с возможностью выполнять полярное кодирование бит, подлежащих кодированию, с использованием последовательности для получения кодированных бит.
13. Устройство по п. 12, в котором блок определения выполнен с возможностью определять, на основании длины N материнского кода и заданной последовательности, последовательность, используемую для кодирования бит, подлежащих кодированию.
14. Устройство по п. 12 или 13, в котором последовательность, используемая для кодирования бит, подлежащих кодированию, является всей или подмножеством другой последовательности, другая последовательность содержит номера последовательности Nmax поляризованных каналов, Nmax номера последовательности расположены в другой последовательности, основанной на надежности Nmax поляризованных каналов, Nmax является положительным целым числом степени 2 и Nmax ≥ N.
15. Устройство по п. 14, в котором Nmax = 1024.
16. Устройство по любому из пп. 12-15, в котором длина бит, подлежащих кодированию, равна К и К бит, подлежащие кодированию, отображают на K поляризованные каналы в N поляризованных каналах.
17. Устройство по любому из пп. 12-16, в котором 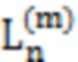 удовлетворяет по меньшей мере одному из следующих условий:
удовлетворяет по меньшей мере одному из следующих условий:
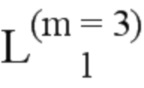 = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и
= (33, 7, 65, 513, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 514, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 517, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 521, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 515, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 529, 98, 40, 385, 139, 85, 30, 262, 146, 545, 44, 99, 141, 31, 89, 263, 147, 72, 519, 266, 162, 46, 101, 149, 52, 47, 577, 76, 267, 105, 274, 165, 194, 54, 516, 163, 269, 78, 153, 275, 55, 525, 84, 58, 113, 86, 136, 290, 518, 195, 79, 291, 59, 277, 169, 531, 100, 140, 197, 87, 177, 641, 61, 90, 281, 102, 148, 293, 522, 142, 322, 143, 91, 201, 546, 32, 103, 264, 106, 530, 323, 150, 297, 48, 523, 93, 209, 268, 386, 325, 305, 537, 769, 533, 164, 154, 151, 107, 56, 166, 387, 578, 329, 549, 270, 114, 155, 80, 225, 167, 276, 109, 579, 271, 60, 115, 196, 170, 157, 88, 547, 62, 278, 292, 520, 279, 117, 171, 198, 642, 178, 282, 92, 553, 202, 389, 294, 199, 524, 63, 144, 337, 585, 173, 283, 121, 645, 104, 179, 295, 532, 203, 94, 324, 561, 393, 298, 152, 581, 210, 285, 181, 526, 108, 95, 205, 770, 299, 353, 326, 527, 156, 110, 534, 401, 306, 301, 643, 211, 185, 327, 539, 116, 168, 593, 158, 226, 307, 548, 330, 111, 771, 213, 118, 172, 551, 331, 227, 649, 388, 309, 159, 609, 417, 338, 535, 217, 272, 550, 119, 280, 538, 333, 390, 174, 580, 122, 200, 777, 180, 229, 554, 339, 657, 313, 541, 391, 175, 582, 394, 284, 773, 123, 673, 555, 785, 64, 341, 705, 449, 562, 354, 801, 395, 233, 204, 528, 583, 557, 296, 286, 182, 125, 206, 241, 644, 586, 563, 287, 300, 355, 183, 402, 212, 397, 345, 587, 833, 565, 96, 186, 207, 328, 646, 536, 403, 594, 187, 357, 589, 569, 308, 647, 419, 214, 302, 228, 303, 897, 595, 361, 112, 650, 772, 418, 540, 215, 405, 310, 189, 450, 332, 218, 160, 610, 597, 552, 651, 120, 230, 334, 409, 542, 774, 611, 658, 311, 421, 601, 219, 369, 231, 653, 392, 176, 314, 340, 543, 335, 124, 556, 775, 234, 315, 659, 613, 342, 778, 451, 221, 425, 356, 674, 584, 126, 235, 184, 396, 242, 558, 661, 617, 317, 343, 346, 779, 564, 404, 288, 398, 453, 675, 559, 786, 433, 188, 358, 208, 665, 588, 781, 706, 677, 237, 347, 566, 362, 127, 243, 590, 406, 216, 399, 567, 304, 598, 359, 802, 420, 625, 457, 787, 349, 245, 570, 190, 591, 220, 648, 312, 707, 363, 596, 465, 803, 407, 681, 422, 789, 249, 599, 191, 571, 370, 652, 410, 835, 411, 709, 481, 614, 232, 573, 316, 660, 365, 423, 336, 689, 371, 793, 222, 612, 452, 602, 426, 805, 413, 654, 454, 834, 318, 713, 236, 603, 344, 544, 373, 655, 223, 615, 427, 776, 434, 560, 238, 899, 618, 348, 809, 244, 721, 455, 666, 319, 605, 377, 662, 429, 780, 239, 676, 360, 837, 459, 626, 400, 663, 678, 435, 568, 458, 817, 246, 619, 350, 788, 128, 782, 898, 408, 667, 437, 592, 364, 621, 466, 737, 351, 679, 572, 247, 682, 250, 627, 461, 708, 841, 412, 783, 366, 790, 441, 600, 375, 669, 629, 424, 901, 467, 849, 804, 251, 791, 372, 710, 192, 574, 690, 482, 683, 414, 604, 794, 367, 714, 469, 711, 374, 575, 656, 428, 807, 415, 685, 905, 253, 616, 483, 633, 806, 430, 795, 865, 224, 691, 456, 715, 836, 473, 810, 378, 606, 620, 436, 664, 722, 320, 797, 485, 693, 913, 431, 607, 717, 489, 811, 460, 839, 668, 240, 818, 622, 379, 838, 723, 438, 697, 462, 738, 680, 381, 813, 628, 248, 900, 842, 442, 623, 929, 352, 725, 784, 470, 630, 819, 439, 670, 463, 739, 684, 252, 843, 850, 497, 902, 821, 729, 468, 634, 903, 368, 671, 792, 443, 845, 631, 475, 686, 851, 484, 692, 712, 380, 866, 796, 416, 825, 961, 741, 254, 906, 635, 445, 694, 745, 486, 808, 687, 907, 471, 576, 716, 376, 867, 914, 474, 853, 637, 798, 432, 695, 812, 487, 753, 724, 799, 490, 857, 909, 255, 718, 608, 931, 477, 698, 726, 915, 440, 820, 840, 869, 493, 719, 699, 382, 814, 624, 815, 499, 873, 740, 930, 672, 917, 822, 464, 727, 962, 844, 491, 632, 730, 701, 383, 742, 846, 921, 472, 823, 852, 731, 498, 881, 743, 444, 904, 688, 826, 501, 446, 933, 847, 636, 746, 827, 733, 447, 963, 937, 476, 854, 868, 638, 908, 488, 696, 747, 829, 754, 855, 858, 916, 965, 478, 910, 720, 800, 700, 494, 505, 749, 945, 859, 874, 639, 755, 256, 969, 870, 492, 479, 384, 911, 816, 918, 728, 871, 702, 932, 861, 500, 757, 732, 824, 923, 875, 977, 919, 503, 934, 744, 761, 882, 495, 703, 922, 877, 502, 848, 993, 448, 734, 828, 883, 935, 964, 506, 938, 748, 856, 925, 735, 830, 966, 939, 885, 507, 750, 946, 860, 756, 480, 967, 831, 889, 941, 751, 872, 971, 912, 758, 947, 970, 862, 978, 876, 920, 640, 759, 949, 863, 762, 509, 973, 924, 878, 953, 887, 936, 979, 763, 504, 884, 704, 994, 926, 879, 981, 942, 765, 496, 927, 886, 995, 736, 940, 985, 968, 890, 948, 832, 508, 943, 752, 974, 997, 891, 950, 760, 893, 972, 1001, 954, 510, 864, 982, 951, 975, 764, 1009, 980, 880, 955, 987, 996, 892, 928, 511, 766, 957, 998, 983, 888, 986, 944, 999, 1002, 767, 989, 952, 1005, 894, 1011, 958, 976, 512, 1003, 895, 984, 1010, 956, 988, 1013, 959, 1000, 1006, 990, 1017, 991, 1012, 768, 1004, 1015, 1007, 1018, 896, 1014, 992, 1019, 960, 1021); и  =(1016, 1008).
=(1016, 1008).
18. Устройство по любому из пп. 12-16, в котором при N = 64 последовательность является любой одной из следующих последовательностей:
[1, 2, (5, 9, 3), 17, 33, (7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), 42, 29, (50, 43), 45, (16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, 61, 32, 48, 56, 60, 62, 63, 64];
[1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11), 21, 35, 25, (8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28), 40, 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64]; или
[1, 2, (5, 9, 3), 17, (33, 7, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 8, 37), (12, 41), (20, 14, 49), 15, 22, (27, 36, 39, 23, 38, 26), (42, 29), (50, 43, 45, 16, 51), (24, 53), (57, 28, 40), 30, (44, 31), 46, 52, 47, 54, 55, 58, 59, (61, 32), 48, 56, 60, 62, 63, 64],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
19. Устройство по любому из пп. 12-16, в котором при N = 128 последовательность представляет собой:
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 12, 41), (20, 14, 69, 49, 15, 73), 22, (27, 36, 81, 39, 23, 38, 26, 97, 68, 42, 29), (70, 50, 75, 43, 71, 45, 82, 16, 51, 74, 24, 53), 77, (83, 57, 28, 98, 40, 85, 30), (44, 99, 31, 89, 72, 46, 101), 52, (47, 76, 105, 54), (78, 55, 84, 58, 113, 86, 79, 59, 100, 87, 61, 90, 102, 91, 32), (103, 106, 48, 93), (107, 56, 114), (80, 109), (60, 115), (88, 62, 117), (92, 63, 121, 104), 94, (108, 95), 110, 116, 111, 118, (119, 122, 123, 64, 125, 96), 112, 120, 124, 126, 127, 128],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
20. Устройство по любому из пп. 12-16, в котором при N = 256 последовательность представляет собой:
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 22, 131, 27, 36, 81, 137, 39, 23, 38, 26, 97, 68, 42, 145, 29, 70, 50, 75, 161, 43, 193, 71, 45, 132, 82, 16, 51, 135, 74, 24, 53, 134, 77, 83, 138, 57, 28, 98, 40, 139, 85, 30, 146, 44, 99, 141, 31, 89, 147, 72, 162, 46, 101, 149, 52, 47, 76, 105, 165, 194, 54, 163, 78, 153, 55, 84, 58, 113, 86, 136, 195, 79, 59, 169, 100, 140, 197, 87, 177, 61, 90, 102, 148, 142, 143, 91, 201, 32, 103, 106, 150, 48, 93, 209, 164, 154, 151, 107, 56, 166, 114, 155, 80, 225, 167, 109, 60, 115, 196, 170, 157, 88, 62, 117, 171, 198, 178, 92, 202, 199, 63, 144, 173, 121, 104, 179, 203, 94, 152, 210, 181, 108, 95, 205, 156, 110, 211, 185, 116, 168, 158, 226, 111, 213, 118, 172, 227, 159, 217, 119, 174, 122, 200, 180, 229, 175, 123, 64, 233, 204, 182, 125, 206, 241, 183, 212, 96, 186, 207, 187, 214, 228, 112, 215, 189, 218, 160, 120, 230, 219), (231, 176, 124, 234, 221, 12 6, 235, 184, 242, 188, 208, 237, 127, 243), (216, 245, 190), (220, 249, 191, 232), 222, (236, 223), (238, 244, 239, 246, 128), (247, 250, 251, 192), (253, 224), 240, 248, 252, 254, 255, 256],
в котором местоположение элементов в скобках могут быть взаимно обменены в скобках.
21. Устройство по любому из пп. 12-16, в котором при N = 512 последовательность является любой одной из следующих последовательностей:
[1, 2, (5, 9, 3), 17, (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 15 6, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438), (462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477), (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506), 507, (480, 509), (504, 496), 508, 510, 511, 512]; или
[1, 2, 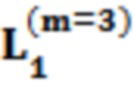 , 17,
, 17,  ,
,  ,
, 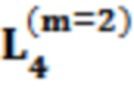 , 508, 510, 511, 512], в котором
, 508, 510, 511, 512], в котором 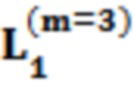 = (5, 9, 3);
= (5, 9, 3);  = (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);
= (33, 7, 65, 4, 13, 6, 19, 129, 10, 34, 18, 11, 257, 21, 35, 25, 66, 8, 37, 67, 130, 12, 41, 20, 133, 14, 69, 49, 15, 73, 258, 22, 131, 27, 36, 81, 259, 137, 39, 23, 261, 38, 26, 97, 68, 265, 42, 145, 29, 70, 50, 75, 161, 43, 273, 193, 71, 45, 132, 82, 16, 289, 51, 135, 74, 24, 53, 321, 134, 77, 83, 138, 57, 28, 260, 98, 40, 385, 139, 85, 30, 262, 146, 44, 99, 141, 31, 89, 263, 147, 72, 266, 162, 46, 101, 149, 52, 47, 76, 267, 105, 274, 165, 194, 54, 163, 269, 78, 153, 275, 55, 84, 58, 113, 86, 136, 290, 195, 79, 291, 59, 277, 169, 100, 140, 197, 87, 177, 61, 90, 281, 102, 148, 293, 142, 322, 143, 91, 201, 32, 103, 264, 106, 323, 150, 297, 48, 93, 209, 268, 386, 325, 305, 164, 154, 151, 107, 56, 166, 387, 329, 270, 114, 155, 80, 225, 167, 276, 109, 271, 60, 115, 196, 170, 157, 88, 62, 278, 292, 279, 117, 171, 198, 178, 282, 92, 202, 389, 294, 199, 63, 144, 337, 173, 283, 121, 104, 179, 295, 203, 94, 324, 393, 298, 152, 210, 285, 181, 108, 95, 205, 299, 353, 326, 156, 110, 401, 306, 301, 211, 185, 327, 116, 168, 158, 226, 307, 330, 111, 213, 118, 172, 331, 227, 388, 309, 159, 417, 338, 217, 272, 119, 280, 333, 390, 174, 122, 200, 180, 229, 339, 313, 391, 175, 394, 284, 123, 64, 341, 449, 354, 395, 233, 204, 296, 286, 182, 125, 206, 241, 287, 300, 355, 183, 402, 212, 397, 345, 96, 186, 207, 328, 403, 187, 357, 308, 419, 214, 302, 228, 303, 361, 112, 418, 215, 405, 310, 189, 450, 332, 218, 160, 120, 230, 334, 409, 311, 421, 219, 369, 231, 392, 176, 314, 340, 335, 124, 234, 315, 342, 451, 221, 425, 356, 126, 235, 184, 396, 242, 317, 343, 346, 404, 288, 398, 453, 433, 188, 358, 208, 237, 347, 362, 127, 243, 406, 216, 399, 304, 359, 420, 457, 349, 245, 190, 220, 312, 363, 465, 407, 422, 249, 191, 370, 410, 411, 481, 232, 316, 365, 423, 336, 371, 222, 452, 426, 413, 454, 318, 236, 344, 373, 223, 427, 434, 238, 348, 244, 455, 319, 377, 429, 239, 360, 459, 400, 435, 458, 246, 350, 128, 408, 437, 364, 466, 351, 247, 250, 461, 412, 366, 441, 375, 424, 467, 251, 372, 192, 482, 414, 367, 469, 374, 428, 415, 253, 483, 430, 224, 456, 473, 378, 436, 320, 485, 431, 489, 460, 240, 379, 438, 462, 381, 248, 442, 352, 470, 439, 463, 252, 497, 468, 368, 443, 475, 484, 380, 416, 254, 445, 486, 471, 376, 474, 432, 487, 490, 255, 477);  = (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и
= (440, 493, 382, 499, 464, 491, 383, 472, 498, 444, 501, 446, 447, 476, 488, 478, 494, 505, 256, 492, 479, 384, 500, 503, 495, 502, 448, 506, 507, 480, 509); и 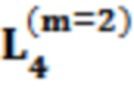 = (504, 496),
= (504, 496),
в котором местоположения элементов в скобках могут быть взаимно обменены в скобках.
22. Устройство по любому из пп. 12-21, в котором блок кодирования выполнен с возможностью выполнять согласование скорости на кодированных битах.
23. Устройство для полярного кодирования, содержащее память, выполненную с возможностью хранить программу; процессор, выполненный с возможностью выполнять программу, хранящуюся в памяти, в котором, когда программа выполняется, процессор выполнен с возможностью выполнять способ по любому из пп. 1-11.
24. Устройство по п. 23, в котором устройство для полярного кодирования представляет собой микросхему или интегральную схему.
25. Устройство для полярного кодирования, содержащее схему интерфейса ввода, выполненную с возможностью получать биты, подлежащие кодированию; логическую схему, выполненную с возможностью выполнять способ по любому из пп. 1-11; и схему интерфейса вывода, выполненную с возможностью выводить биты, полученные после полярного кодирования.
26. Машиночитаемый носитель данных, в котором машиночитаемый носитель данных хранит компьютерную программу, компьютерная программа содержит инструкцию, в котором, при выполнении устройством, инструкция побуждает выполнить способ по любому из пп. 1-11.
| СПОСОБ И УСТРОЙСТВО ГЕНЕРИРОВАНИЯ ГИБРИДНОГО ПОЛЯРНОГО КОДА | 2013 |
|
RU2610251C2 |
| CN 103281166 B, 25.05.2016 | |||
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| Токарный резец | 1924 |
|
SU2016A1 |
Авторы
Даты
2021-11-23—Публикация
2018-06-26—Подача