ОБЛАСТЬ ТЕХНИКИ
[0001] Заявленное изобретение относится к области информационных технологий, в частности к способу получения низкоразмерных числовых представлений последовательностей событий.
УРОВЕНЬ ТЕХНИКИ
[0002] Создание семантически значимых числовых представлений из огромного количества неразмеченых данных событий жизненного потока является сложной задачей для машинного обучения. Эти предварительно обученные числовые представления извлекают сложную информацию из исходных данных в виде низкоразмерных числовых векторов фиксированной длины и могут быть легко применены в различных последующих задачах машинного обучения в качестве признаков или дообучены под конкретную целевую переменную.
[0003] Традиционно для подхода метрического обучения или метрик лернинг (англ. Metric learning) требуются пары объектов, помеченные как похожие, но эти пары часто недоступны для данных жизненного потока событий. Данные о последовательности событий генерируются во многих бизнес-приложениях, некоторые примеры - транзакции по кредитным картам и данные о посещениях интернет-сайтов, а анализ последовательности событий - очень распространенная проблема машинного обучения [1] - [4]. Lifestream - это последовательность событий, которая присваивается человеку и фиксирует его / ее регулярные и рутинные действия определенного типа, например транзакции, поисковые запросы, телефонные звонки и сообщения.
[0004] Метрик лернинг подход к обучению, лежащий в основе заявленного способа MeLES, широко используется в различных областях, включая такие домены как компьютерное зрение, НЛП и аудио. В частности, метрик лернинг подход к обучению для распознавания лиц был первоначально предложен в [5], где контрастивная функция потерь (англ. contrastive loss) использовалась для обучения функции сопоставления входных данных с их низкоразмерными представления, используя некоторые предварительные знания об отношении похожести между обучающими выборками или ручную разметку. Кроме того, в [6] авторы представили FaceNet, метод, который обучает отображение изображений лиц на 128-мерные представления с использованием функции потери триплет (англ. triplet loss), основанной на классификации ближайших соседей с большим маржином (LMNN) [7]. В FaceNet авторы также представили онлайн-метод выбора троек объектов - триплетов и технику hard-positive и hard-negative майнинга для процедуры обучения.
[0005] Кроме того, метрик лернинг использовался для задачи распознавания голоса [8], где конрастивная функция потери (contrastive loss) определяется как близость численного представления каждого высказывания к центроиду численных представлений всех высказываний этого говорящего (positive pair - положительная пара) и дальность от центроидов численных представлений высказываний других говорящих, выбранных по наибольшей близости среди всех других говорящих (hard negative pair - жесткая отрицательная пара).
[0006] Наконец, в [9] авторы предложили дообучение модели BERT [10], которая использует метрик лернинг в форме сиамских и триплет нейронных сетей для обучения численных представлений предложений для задач семантического текстового сходства с использованием семантической близости аннотаций пар предложений.
[0007] Хотя метрик лернинг использовался во всех этих областях, он не был применен к анализу событий жизненного потока, связанных с транзакционными данными, кликстримом и другими типами данных событий жизненного потока, что является предметом данной статьи.
[0008] Важно отметить, что в предыдущей литературе подход метрик лернинг применялся в своих областях как обучение с учителем, в то время как заявленный способ MeLES внедряет идеи метрик лернинга совершенно новым способом, способом обучения без учителя в области последовательностей событий.
[0009] Другая идея применения обучения без учителя к последовательным данным была ранее предложена в методе контрастного прогнозирующего кодирования (англ. contrastive predicting coding - СРС) [11], где значимые представления извлекаются путем прогнозирования будущего в скрытом пространстве с использованием авторегрессивных методов. Представления СРС продемонстрировали высокую эффективность в четырех различных областях: аудио, компьютерное зрение, естественный язык и обучение с подкреплением.
[0010] В области компьютерного зрения существует множество других подходов к обучению с учителем, которые хорошо обобщены в источнике [12]. Есть несколько способов определить задачу обучения с учителем (аналогично заданию предсказания следующего слова в тексте) для изображения. Один из вариантов - изменить изображение, а затем попытаться восстановить исходное изображение. Примерами этого подхода являются супер-разрешение, изменение цвета изображения и восстановление поврежденного изображения. Другой вариант - предсказать контекстную информацию из локальных признаков, например, предсказать место патча изображения на изображении с несколькими отсутствующими патчами.
[0011] При этом почти каждый подход к обучению без учителя может быть использован для получения численных представлений исходных данных в форме эмбеддингов. Существует несколько примеров применения полученного набора численных представлений исходных данных для нескольких последующих задач [13], [14].
[0012] Одним из распространенных подходов к изучению представлений без учителя является либо традиционный автокодировщик (автоэнкодер) [15], либо вариационный автоэнкодер [16]. Он широко используется для изображений, текста и аудио или агрегированных данных событий жизненного потока ([17]). Хотя автоэнкодеры успешно использовались в нескольких перечисленных выше областях, они не применялись к необработанным данным событий жизненного потока в виде последовательностей событий, в основном из-за проблем определения расстояний между входом и восстановленными через автоэнкодер входными последовательностями.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[0013] В настоящем решении предлагается новый метод: метрик лернинг (метрическое обучение от англ. metric learning) для последовательностей событий (MeLES), используемый для получения представления данных жизненного потока в скрытом пространстве.
[0014] В настоящем решении воплощен новый метод - метрик лернинг на последовательностях событий (MeLES) для получения низкоразмерных числовых представлений последовательностей событий, который может хорошо работать со специфическими свойствами жизненных потоков событий, такими как их дискретная природа.
[0015] В широком смысле метод MeLES адаптирует подход метрик лернинг [18]-[19]. Метрик лернинг часто ставится как задача обучения с учителем для отображения многомерных объектов в пространство низкоразмерных числовых представлений. Целью метрик лернинга является представление семантически похожих объектов (изображений, видео, аудио и т.д.) ближе друг к другу, а разнородных - дальше. Большинство подходов метрик лернинга используются в таких приложениях, как распознавание речи [8], компьютерное зрение [20]-[21] и анализ текста [9].
[0016] В этих областях метрик лернинг успешно применяется как задача обучения с учителем к датасетам (наборам данных), где пары многомерных экземпляров помечены как один и тот же объект или разные объекты. В отличие от всех предыдущих методов метрик лернинга, MeLES полностью обучается без учителя и не требует никаких меток. Он основан на наблюдении, что данные жизненного потока событий подчиняются периодичности и повторяемости событий в последовательности. Поэтому некоторые подпоследовательности одного и того же жизненного потока можно рассматривать как многомерные представления одного и того же человека. Идея MeLES заключается в том, что в скрытом низкоразмерном пространстве численные представления таких подпоследовательностей должны быть ближе друг к другу.
[0017] Обучение без учителя позволяет обучать модели, используя внутреннюю структуру больших неразмеченных или частично размеченных обучающих датасетов. Обучение без учителя продемонстрировало эффективность в различных областях машинного обучения, таких как обработка естественного языка (например, ELMO, BERT, и компьютерное зрение).
[0018] Модель MeLES, обученная без учителя, может использоваться двумя способами. Представления, создаваемые моделью, могут непосредственно использоваться в качестве фиксированного вектора признаков в некоторой последующей задаче машинного обучения с учителем (например, задаче классификации), аналогично решению из источника [22]. В качестве альтернативы, обученная модель может быть дообучена [10] для конкретной последующей задачи машинного обучения с учителем.
[0019] Проведенные эксперименты с двумя открытыми датасетами с банковскими транзакциями позволили оценить эффективность заявленного метода для последующих задач машинного обучения. Когда численные представления MeLES непосредственно используются в качестве признаков, метод обеспечивает высокую производительность, сопоставимую с базовыми методами (бейзлайном).
[0020] Дообученные под конкретную задачу обучения с учителем представления позволяют достигать самых высоких показателей качества, значительно превосходя несколько других методов обучения с учителем и методов с предварительным обучением без учителя. Далее в настоящих материалах будет также представлено превосходство представлений MeLES над методами обучения с учителем в применении к частично размеченным данным по причине недостаточного количества разметки для обучения достаточно сложной модели с нуля.
[0021] Существующая техническая проблема состоит в том, что генерация численных представлений событийных данных является необратимым преобразованием, поэтому невозможно восстановить точную последовательность событий из ее представления. Следовательно, использование представлений приводит к большей конфиденциальности и безопасности данных для конечных пользователей, чем при работе непосредственно с необработанными данными событий, и все это достигается без потери качества моделирования.
[0022] Техническим результатом является повышение эффективности формирования признаков для моделей машинного обучения с помощью формирования низкоразмерных числовых представлений последовательностей событий.
[0023] Заявленный технический результат достигается за счет компьютерно-реализуемого способа получения низкоразмерных числовых представлений последовательностей событий, содержащего этапы, на которых:
- получают набор входных данных, характеризующий события, агрегированные в последовательность и связанные с по меньшей мере одной информационной сущностью, причем упомянутые данные содержат набор атрибутов, включающий: категориальные переменные, числовые переменные и временную метку;
при этом выполняется предобработка упомянутого набора входных данных, при которой:
 формируют позитивные пары последовательностей транзакционных событий, которые представляют собой подпоследовательности, принадлежащие последовательности транзакционных событий одной информационной сущности;
формируют позитивные пары последовательностей транзакционных событий, которые представляют собой подпоследовательности, принадлежащие последовательности транзакционных событий одной информационной сущности;
 формируют негативные пары подпоследовательностей транзакционных событий, которые являются подпоследовательностями, принадлежащими последовательностям транзакционных событий разных информационных сущностей;
формируют негативные пары подпоследовательностей транзакционных событий, которые являются подпоследовательностями, принадлежащими последовательностям транзакционных событий разных информационных сущностей;
- с помощью кодировщика транзакционных событий формируют векторное представление каждого транзакционного события из упомянутого набора атрибутов, при этом кодировщик содержит первичный набор параметров и выполняет этапы, на которых:
 осуществляют кодирование категориальных переменных в виде векторных представлений;
осуществляют кодирование категориальных переменных в виде векторных представлений;
 осуществляют нормирование числовых переменных;
осуществляют нормирование числовых переменных;
 осуществляют обработку временных меток для выстраивания упорядоченной по времени последовательности транзакционных событий;
осуществляют обработку временных меток для выстраивания упорядоченной по времени последовательности транзакционных событий;
 осуществляют конкатенацию полученных векторных представлений категориальных переменных и нормированных числовых переменных;
осуществляют конкатенацию полученных векторных представлений категориальных переменных и нормированных числовых переменных;
 формируют единый числовой вектор одного транзакционного события по итогам выполненной конкатенации;
формируют единый числовой вектор одного транзакционного события по итогам выполненной конкатенации;
- с помощью кодировщика подпоследовательности формируют векторное представление подпоследовательности транзакционных событий из набора числовых векторов транзакционных событий, полученных с помощью кодировщика транзакционных событий, при этом кодировщик содержит первичный набор параметров;
- осуществляют фильтрацию негативных пар векторов подпоследовательностей транзакционных событий, значение векторного расстояния между которыми не выше заданного порогового значения;
- корректируют первичные параметры упомянутых кодировщика транзакционных событий и кодировщика подпоследовательности с помощью применения функции потерь вида маржинальных или контрастивных потерь; и
- формируют низкоразмерные числовых представления последовательностей событий, связанных с одной информационной сущностью, на основании выполненной корректировки.
[0024] В одном из частных вариантов реализации способа информационная сущность представляет собой транзакционные данные физического или юридического лица.
[0025] В другом частном варианте реализации способа создание позитивных пар осуществляется с помощью алгоритма формирования несвязных подпоследовательностей.
[0026] В другом частном варианте реализации способа создание позитивных пар осуществляется с помощью алгоритма генерации случайных срезов последовательности.
[0027] В другом частном варианте реализации способа формируемые подпоследовательности не пересекаются между собой.
[0028] В другом частном варианте реализации способа формируемые подпоследовательности не пересекаются и/или пересекаются между собой.
[0029] В другом частном варианте реализации способа кодировщик подпоследовательности представляет собой рекуррентную нейронную сеть (РНС).
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
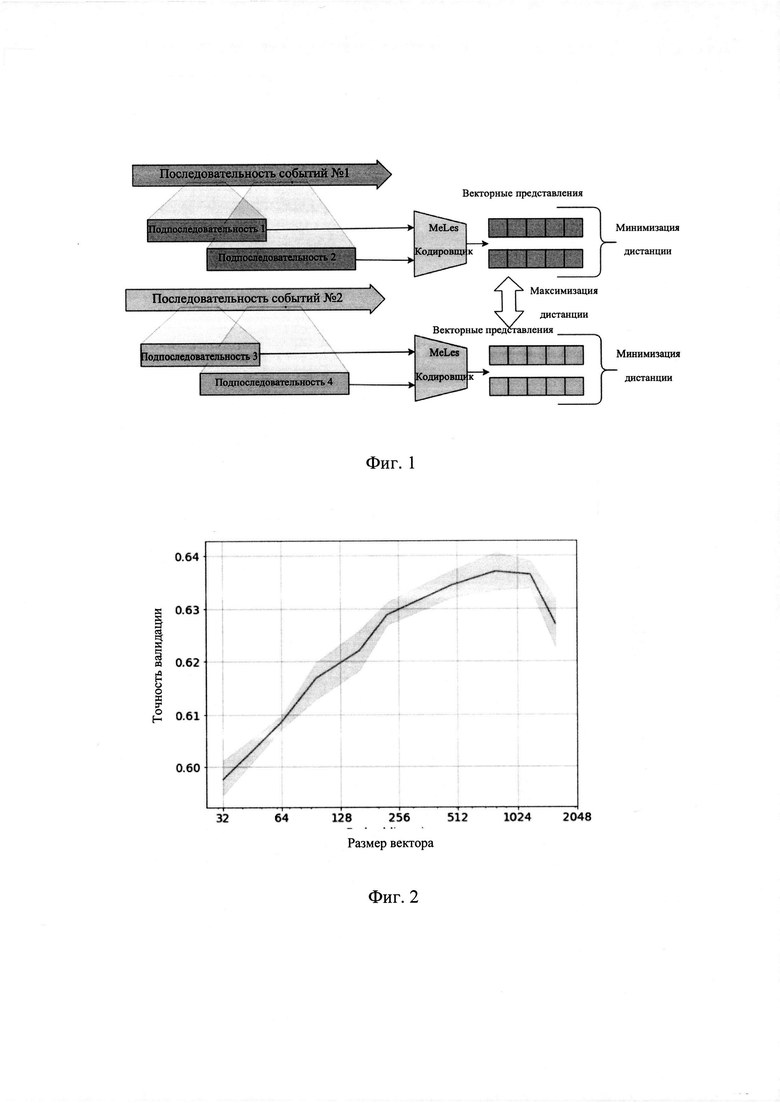
[0030] Фиг. 1 иллюстрирует концептуальную схему заявленного решения.
[0031] Фиг. 2 - Фиг. 3 иллюстрируют графики зависимостей размерности векторов в задачах прогнозирования.
[0032] Фиг. 4 иллюстрирует распределение векторов в задаче прогнозирования возрастной группы.
[0033] Фиг. 5 - Фиг. 8 иллюстрируют примеры прогнозирования на различных датасетах.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
[0034] Заявленный способ создан специально для данных событий жизненного потока. Такие данные состоят из отдельных событий информационной сущности, например, человека или юридического лица в непрерывном времени, например, поведения на веб-сайтах, выполнением транзакций и т.д.
[0035] Принимая во внимание транзакции, например, транзакции по кредитным картам, каждая транзакция имеет набор атрибутов, категориальных или числовых, включая временную метку транзакции. Пример последовательности трех операций с их атрибутами представлен в Таблице 1. Поле типа продавца представляет категорию продавца, такую как «авиакомпания», «гостиница», «ресторан» и т.д.
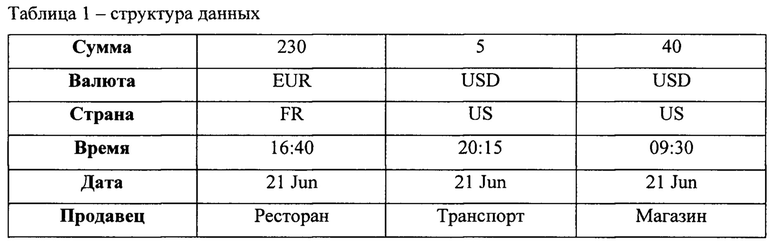
[0036] Другим примером данных жизненного потока является кликстрим (от англ. click-stream) - журнал посещений интернет-страниц. Пример журнала посещений интернет-страниц для одного пользователя представлен в Таблице 2.

[0037] На Фиг. 1 представлен общий принцип заявленного способа. Задано количество дискретных событий 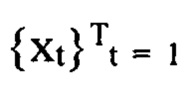 в заданном интервале наблюдения [1, Т] конечной целью является получение численного представления последовательности ct для временной метки Т в скрытое пространство Rd. Чтобы обучить кодировщик последовательности
в заданном интервале наблюдения [1, Т] конечной целью является получение численного представления последовательности ct для временной метки Т в скрытое пространство Rd. Чтобы обучить кодировщик последовательности 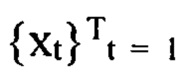 генерировать осмысленное численное представление ct из
генерировать осмысленное численное представление ct из 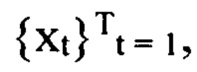 необходимо применить подход метрик лернинг так, чтобы расстояние между представлениями одной и той же информационной сущности было небольшим, тогда как представления разных сущностей (отрицательные пары) велики.
необходимо применить подход метрик лернинг так, чтобы расстояние между представлениями одной и той же информационной сущности было небольшим, тогда как представления разных сущностей (отрицательные пары) велики.
[0038] Одними из трудностей применения подхода метрик лернинг для данных жизненного потока заключается в том, что понятие семантического сходства как и различий требует знания базовых областей, а также процесса разметки положительных и отрицательных примеров является трудоемким. Ключевым свойством предметной области событий жизненного потока является периодичность и повторяемость событий в последовательности событий, что позволяет нам переформулировать задачу метрик лернинг как задачу обучения без учителя. MeLES изучает низкоразмерные представления из последовательных данных о выбранной информационной сущности, например, о человеке, отбирая положительные пары как подпоследовательности одной и той же последовательности одного человека и отрицательные пары как подпоследовательности из последовательностей разных людей. Соответствующие пары формируются с помощью обработки входных данных кодировщиками, формирующими векторные представления транзакционных событий, о чем будет более детально раскрыто далее.
[0039] Представление последовательности ct, полученное на основе метрик лернинг, затем используется в различных задачах машинного обучения в качестве вектора признаков. Кроме того, одним из возможных способов повышения качества задачи в которой применяются численные представления событийных данных является встраивание предварительно обученного ct (например, выходного вектора последнего слоя рекуррентной нейронной сети RNN) в задачу классификации с конкретной целевой переменной, а затем совместно обучать, то есть настраивать веса сети кодировщиков и классификатора.
[0040] Чтобы построить представление последовательности событий в виде вектора фиксированного размера ct ∈ Rd, используется подход, аналогичный энкодеру транзакций карты E.T.-RNN, описанному в работе авторов [15]. Вся сеть кодировщиков состоит из двух концептуальных частей: кодировщик событий и подсети кодировщика последовательности событий.
[0041] Кодировщик событий берет на вход набор атрибутов одного события xt и выводит его представление в скрытое пространство Z ∈ Rm: zt=e(xt). Кодировщик последовательности s принимает скрытые представления последовательности событий: z1:Т=z1, z2, zT и выводит представление всей последовательности ct на временном шаге t: ct = s (z1:t).
[0042] Сеть кодировщика событий состоит из нескольких эмбеддинг слоев и слоя батч нормализации [16]. Каждый эмбеддинг слой используется для кодирования каждого категориального атрибута события. Батч нормализация применяется к числовым атрибутам события. Наконец, выходные данные каждого эмбеддинг слоя и слоя батч нормализации конкатенируются для создания представления zt одного события в скрытом пространстве.
[0043] Последовательность скрытых представлений событий z1:t передается в кодировщик последовательности s для получения вектора ct фиксированного размера. Несколько подходов могут быть использованы для кодирования последовательности. Одним из возможных подходов является использование рекуррентной сети (RNN), как в [17]. Другой подход заключается в использовании кодирующей части архитектуры Transformer, представленной в [18]. В обоих случаях вектор последнего события может использоваться для представления всей последовательности событий. В случае RNN последний выход ht является представлением последовательности событий.
[0044] Кодировщик, основанный на архитектуре RNN-типа, такой как GRU [18], позволяет вычислять представление Ct+k путем обновления представления ct вместо расчета представления ct+k из всей последовательности прошлых событий z1:t: ck=rnn (ct, zt+1:k). Эта опция позволяет сократить время инференса, когда необходимо обновить уже существующие расчитанные клиентские представления новыми событиями, произошедшими после расчета. Это возможно из-за периодического характера сетей, подобных RNN.
[0045] Функция потери в метрик лернинге изменяют численные представления таким образом, что расстояние между представлениями из одного класса уменьшается, а между представлениями из другого класса увеличивается. Было рассмотрено несколько функций потерь метрик лернинга - contrastive loss (конрастивных потерь) [19], binomial deviance (потерь биномиального отклонения) [20], triplet loss (триплетных потерь) [21], histogram loss (гистограммных потерь) [22] и margin loss (маржинальных потерь) [23].
[0046] Все вышеуказанные функции потерь решают следующую проблему подхода метрик лернинга: использование всех пар выборок неэффективно, например, расстояние между представлениями некоторых из отрицательных пар уже достаточно большое, поэтому эти пары не пригодны для обучения ([24]-[25]).
[0047] Далее рассмотрим два вида функций потерь, которые концептуально просты, но в то же время продемонстрировали высокую эффективность при валидации в экспериментах с заявленным способом, а именно, функции контрастивных потерь и маржинальных потерь.
[0048] Функция контрастивных потерь имеет контрастивное слагаемое для отрицательной пары представлений, которое штрафует модель только в том случае, если отрицательная пара недостаточно удалена и расстояние между представлениями меньше, чем маржин m:
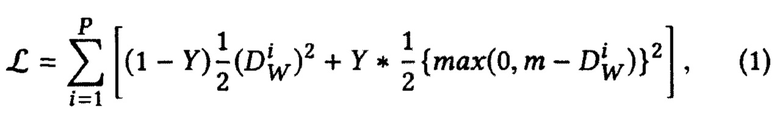
где Р - количество всех пар в батче, 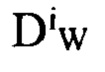 - функция расстояния между i-й помеченной выборкой пары представлений X1 и Х2, Y - бинарная метка, назначенная паре: Y=0 означает позитивная пара, Y=1 означает негативную пару, m>0 - маржин. Как предложено в [26], используется евклидово расстояние как функция расстояния:
- функция расстояния между i-й помеченной выборкой пары представлений X1 и Х2, Y - бинарная метка, назначенная паре: Y=0 означает позитивная пара, Y=1 означает негативную пару, m>0 - маржин. Как предложено в [26], используется евклидово расстояние как функция расстояния:
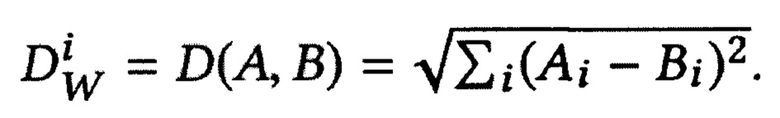
[0049] Функция маржинальных потерь похожа на контрастивных потерь, основное отличие заключается в том, что не существует штрафа для положительных пар, которые находятся ближе, чем порог в функции маржинальных потерь.
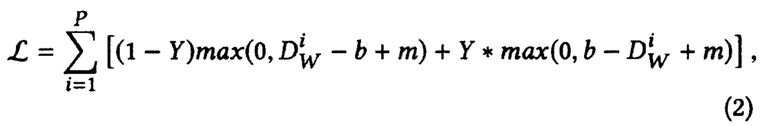
Где Р - количество всех пар в батче, 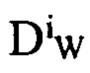 - функция расстояния между i-й помеченной выборочной парой представлений X1 и Х2, Y - бинарная метка, назначенная паре: Y=0 означает позитивную пару, Y=1 означает негативную пару, ш>0 и b>0 определитель порогового значения маржина
- функция расстояния между i-й помеченной выборочной парой представлений X1 и Х2, Y - бинарная метка, назначенная паре: Y=0 означает позитивную пару, Y=1 означает негативную пару, ш>0 и b>0 определитель порогового значения маржина
[0050] Выборка негативных пар - это еще один способ решения проблемы, заключающейся в том, что некоторые из негативных пар уже достаточно отдалены, поэтому эти пары не пригодны для обучения ([24]-[26]). Следовательно, при расчете функции потерь учитывается только часть возможных негативных пар. При этом рассматриваются только текущие пары в батче. Существует несколько возможных стратегий выбора наиболее подходящих для обучения негативных пар:
• Случайная выборка негативных пар;
• Жесткий негативный майнинг пар: генерировать k самых сложных негативых пар для каждой положительной пары;
• взвешенная по расстоянию выборка пар, где негативные к рассматриваемому примеры семплируются равномерно в соответствии с их относительным расстоянием от этого рассматриваемого примера [27];
• полу-жесткий отбор, при котором осуществляется выбор ближайшего к рассматриваемому примеру негативный пример из набора всех негативных примеров, которые находятся дальше от рассматриваемого примера, чем его позитивный пример ([28]).
[0051] Чтобы выбрать негативные пары, необходимо вычислить попарно расстояние между всеми возможными парами векторов представлений в батче. Чтобы сделать эту процедуру более вычислительно эффективной, мы выполняем нормализацию векторов представлений, то есть проецируем их на гиперсферу единичного радиуса. Поскольку 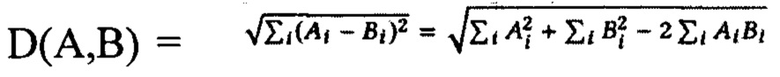 и
и 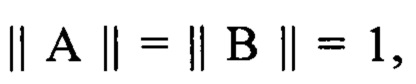 чтобы вычислить евклидово расстояние, то необходимо вычислить:
чтобы вычислить евклидово расстояние, то необходимо вычислить: 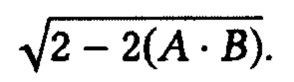
[0052] Чтобы вычислить скалярное произведение между всеми парами в батче, необходимо умножить матрицу всех векторов представлений батча на саму себя транспонированную, что является высоко оптимизированной вычислительной процедурой в большинстве современных сред разработки для глубокого обучения. Следовательно, вычислительная сложность выбора негативной пары составляет О (n2h), где h - размер представления, a n - размер батча.
[0053] Процедура генерации позитивных пар используется для создания батча для обучения MeLES. N начальных последовательностей взяты для генерации батча. Затем производится K подпоследовательностей для каждой начальной последовательности.
[0054] Пары подпоследовательностей, полученных из одной и той же последовательности, рассматриваются как положительные образцы, а пары из разных последовательностей рассматриваются как отрицательные образцы. Следовательно, после генерации положительной пары каждый батч содержит N×K подпоследовательностей, используемых в качестве обучающих выборок. В партии имеется K-1 положительных пар и (N-1) × K отрицательных пар на образец.
[0055] Существует несколько возможных стратегий генерации подпоследовательности. Простейшей стратегией является случайная выборка без замены. Другой стратегией является создание подпоследовательности от случайной последовательности расщепления до нескольких подпоследовательностей без пересечения между ними (см. Алгоритм 1). Третий вариант - использовать случайно выбранные срезы событий с возможным пересечением между срезами (см. Алгоритм 2). Порядок событий в сгенерированных подпоследовательностях всегда сохраняется.
[0056] Алгоритм 1: Стратегия генерации несвязных подпоследовательностей, гиперпараметры: k - число генерируемых подпоследовательностей.
вход: последовательность S длины l
выход: Sl,…,Sk - подпоследовательности сгенерированные из S.
Сформировать вектор inds длины l со случайными числами из [l,k].
для i←l to k выполнять:
Si=S[inds=i]
Конец.
[0057] Алгоритм 2: Стратегия генерации случайных срезов последовательности.
гиперпараметры: m, М - минимальная и максимально возможная длина подпоследовательности, k - количество подпоследовательностей, которые будут произведены.
вход: последовательность S длины l
выход: Sl,…,Sk - подпоследовательности сгенерированные из S.
для i←l to k выполнять
Сгенерировать случайное число li, 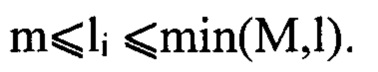
Сгенерировать случайное число s, 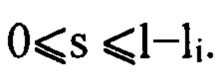
Si=S[s:s+li]
Конец.
[0058] Датасеты:
(1) Соревнование по предсказанию возрастной группы клиента - задача предсказать возрастную группу клиента в пределах 4 классов как целевые переменные, и точность используется в качестве показателя качества. Датасет состоит из 44 млн анонимных транзакций, представляющих 50 тыс. клиентов с целевой переменной, размеченной только для 30 тыс. из них (27 млн из 44 млн транзакций), для остальных 20 тыс. клиентов (17 млн из 44 млн транзакций) метка неизвестна. Каждая транзакция включает дату, тип (например, продуктовый магазин, одежду, заправку, товары для детей и т.Д.) и сумму. Мы используем все доступные 44М транзакций для метрик лернинга, за исключением 10% - для тестовой части датасета и 5% для валидации метрик лернинга.
(2) Соревнование по предсказания пола клиента - задача представляет собой бинарную классификационную задачу прогнозирования пола клиента, и используется метрика ROC-AUC. Датасет состоит из 6,8 млн анонимных транзакций, представляющих 15 тыс.клиентов, из которых только 8,4 тыс.из них размечены. Каждая транзакция характеризуется датой, типом (например, «депозит наличными через банкомат»), суммой и кодом категории продавца (также известный как МСС).
[0059] Для каждого набора данных мы выделяем 10% клиентов из размеченной части данных как тестовую выборку, на которой мы сравнивали качество различных моделей. В представленных экспериментах используется функция контрастивных потерь и стратегия генерации случайных срезов последовательности. Для всех методов гиперпараметры были выбраны с использованием случайного поиска с 5-фолдовой кросс-валидацией на тренировочной выборке с точки зрения качества на отложенной выборке.
[0060] Результаты настройки гиперпараметров, полученные для MeLES, показан в Таблице 3.
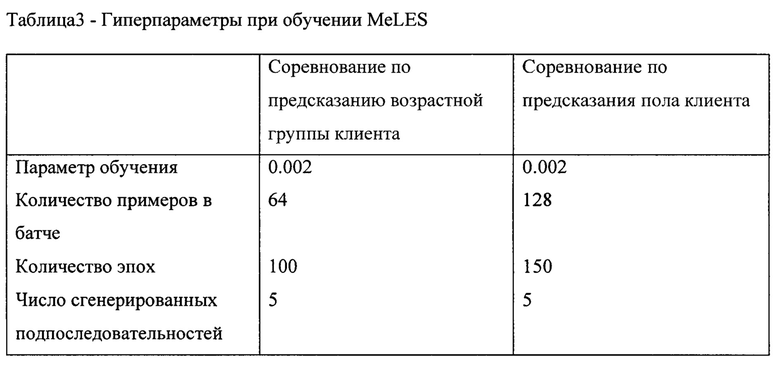
[0061] Для оценки методов обучения без учителя (включая MeLES) были использованы все транзакции, включая неразмеченные данные, кроме тестовой выборки, поскольку эти методы подходят для датасетов с частичной разметкой или вообще не требуют разметки.
[0062] Обучение архитектуры нейронной сети, пригодной для реализации заявленного способа, проводилось на одной видеокарте Tesla Р-100. При обучении нейронной сети MeLES один батч тренировочной выборки обрабатывается за 142 миллисекунды. Для датасета прогнозирования возраста один один батч тренировочной выборки содержит 64 уникальных клиента с 5 подвыборками на каждого клиента, то есть в общей сложности 320 обучающих выборок, среднее число транзакций на выборку составляет 90, следовательно, каждый батч содержит около 28800 транзакций.
[0063] Заявленный способ сравнивался со следующими двумя базовыми моделями. Во-первых, будет проанализирован метод Gradient Boosting Machine (GBM) на вручную построенных признаках. GBM можно рассматривать как надежную базовую модель в случае табличных данных с разнородными признаками. В частности, подходы, основанные на GBM, позволяют достигать самых современных результатов в различных практических задачах, включая поиск в Интернете, прогнозирование погоды, обнаружение мошенничества и многие другие.
[0064] Во-вторых, применяется недавно предложенный метод контрастного прогнозирования (СРС), метод обучения без учителя, который показал высокое качество для последовательных данных таких традиционных областей, как аудио, компьютерное зрение, естественный язык и обучение с подкреплением. Модель, основанная на GBM, требует большого количества вручную подготовленных из необработанных данных транзакций агрегатных признаков. Примером агрегатных признаков может служить средняя сумма расходов в некоторых категориях продавцов, таких как отели, рассчитанная за всю историю транзакций. Применялась LightGBM реализация алгоритма GBM с почти 1 тыс. признаков, подготовленных вручную для данной задачи.
[0065] В дополнение к упомянутым базовым моделям заявленный способ сравнивался с методом обучения с учителем, когда подсеть кодировщика и подсеть классификатора совместно обучаются под целевую переменную данной задачи. При этом в данном случае предварительная подготовка агрегатных признаков не производится.
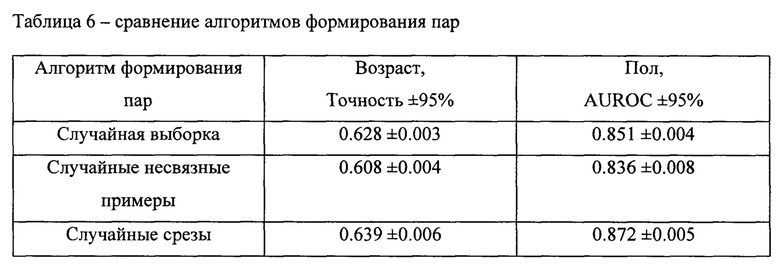
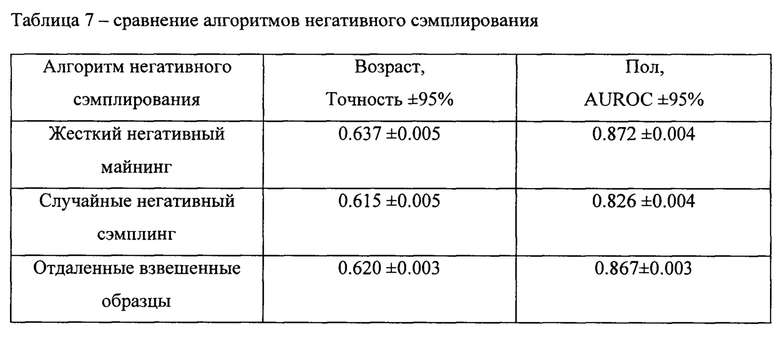
[0066] Далее в таблицах 4, 5, 6 и 7 будут представлены результаты экспериментов по различным вариантам заявленного способа.
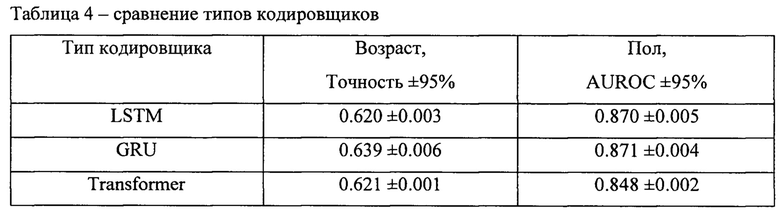
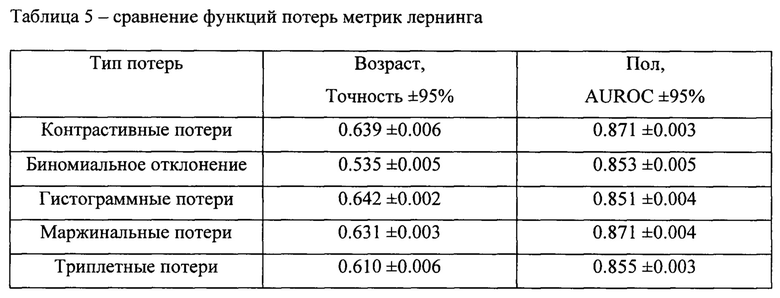
[0067] Как показано в Таблице 4, различные варианты архитектур кодировщиков показывают сопоставимое качество в данных задачах. При этом функция контрастивных потерь, которая может рассматриваться как основной вариант функции потери метрик лернинга, позволяет получить высокие результаты при использовании представлений в задачах машинного обучения (см. Таблицу 5). Это позволяет отразить тот факт, что увеличение качества модели для задачи метрик лернинга не всегда приводит к увеличению качества при использовании представлений в задачах машинного обучения.
[0068] Жесткий негативный майнинг приводит к значительному повышению качества при использовании представлений в задачах машинного обучения по сравнению со случайной негативной выборкой (см. Таблицу 7). Другое наблюдение состоит в том, что более сложная стратегия генерации подпоследовательности (например, случайные срезы) демонстрирует немного более низкое качество при использовании представлений в задачах машинного обучения по сравнению со случайной выборкой событий (см. Таблицу 6)
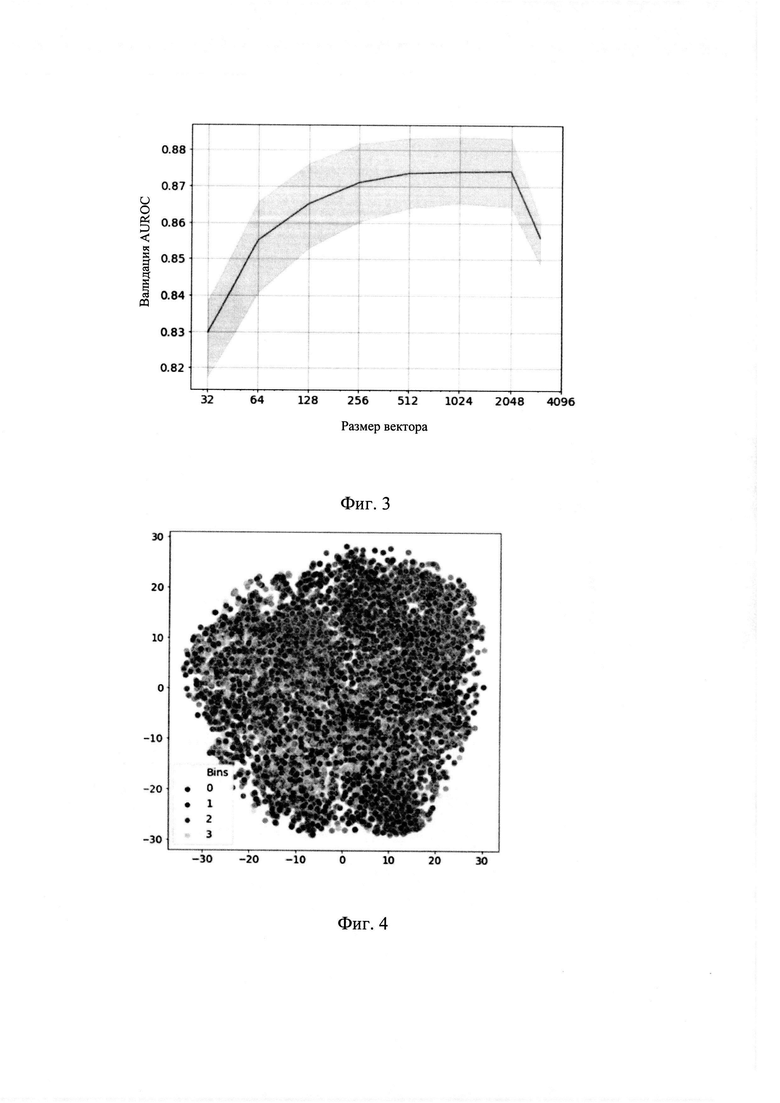
[0069] На Фиг. 2 показано, что при использовании представлений в задачах машинного обучения качество задачи увеличивается с размерностью представления. Наилучшее качество достигается при размерности представления 800. Дальнейшее увеличение размерности представления снижает качество. Результаты могут быть интерпретированы как проблема компромисса смещения-отклонения. Когда размерность представления слишком мала, можно отбросить слишком много информации (высокое смещение уклон). С другой стороны, когда размерность представления слишком велика, добавляется слишком много шума (высокая дисперсия).
[0070] На Фиг. 3 представлена схожая зависимость, отображающую плато между размерностью 256 и 2048, когда качество в задачах не увеличивается. Во всех экспериментах, кроме тех, что представлены на графике использовался размер векторов (эмбеддингов) равный 256.
[0071] Увеличение размерности представления также будет линейно увеличивать время обучения и объем используемой памяти на GPU.
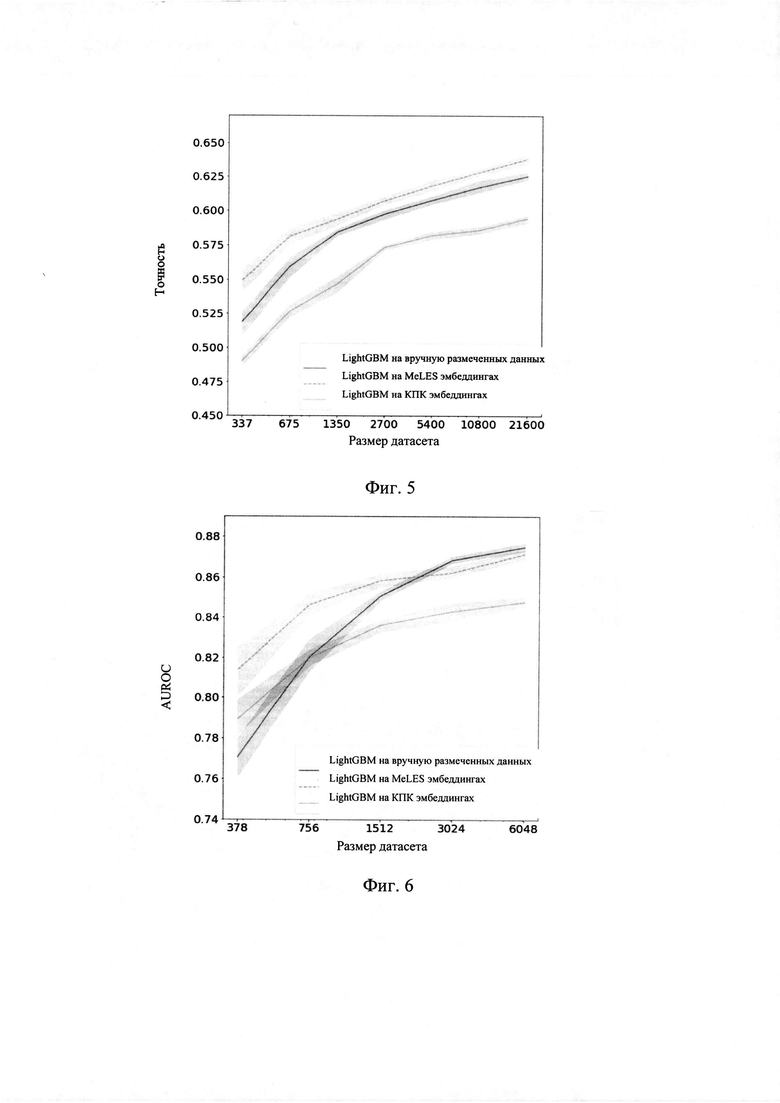
[0072] Чтобы визуализировать представления MeLES в двумерном пространстве, был применен метод преобразования tSNE. tSNE преобразует многомерное пространство в низкоразмерное на основе локальных отношений между точками, поэтому соседние векторы представлений в многомерном пространстве представлений оказываются близкими в 2-мерном пространстве.
[0073] Представления были получены полностью обучением без учителя из необработанных пользовательских транзакций без какой-либо информации о целевой переменной. Последовательность транзакций отражает поведение пользователя, поэтому модель MeLES фиксирует поведенческие паттерны и выводит представления пользователей с похожими паттернами поблизости. Векторы tSNE из набора данных прогнозирования возраста представлены на Фиг. 4. На Фиг. 4 можно наблюдать 4 кластера: кластеры для группы '1' и '2' находятся на противоположной стороне облака, кластеры для групп '2' и '3' в середине.
[0074] Сравнение с базовыми методами. Как показано в Таблице 8, заявленный способ генерирует представления последовательностей данных жизненного потока, которые обеспечивают высокое качество, сравнимое с вручную подготовленными признаками при использовании в последующих задачах. Более того представления, полученные с помощью нашего метода, дообученные под целевую переменную позволяют достигать самое высокое качество в обоих датасетах банковских транзакций, значительно опережая все часто используемые методы обучения.
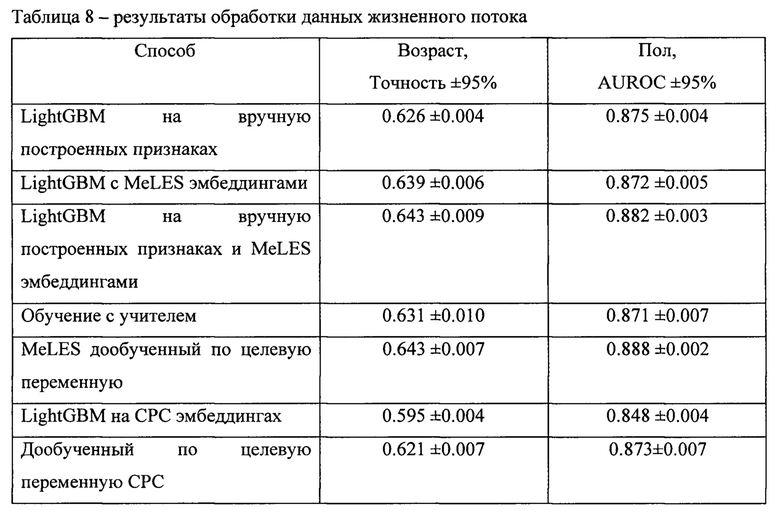
[0075] Кроме того, использование представлений последовательностей вместе с подготовленными вручную агрегатными признаками приводит к лучшему качеству, чем использование только агрегатных признаков или только представлений последовательностей, то есть возможно комбинировать различные подходы, чтобы получить еще более лучшую модель.
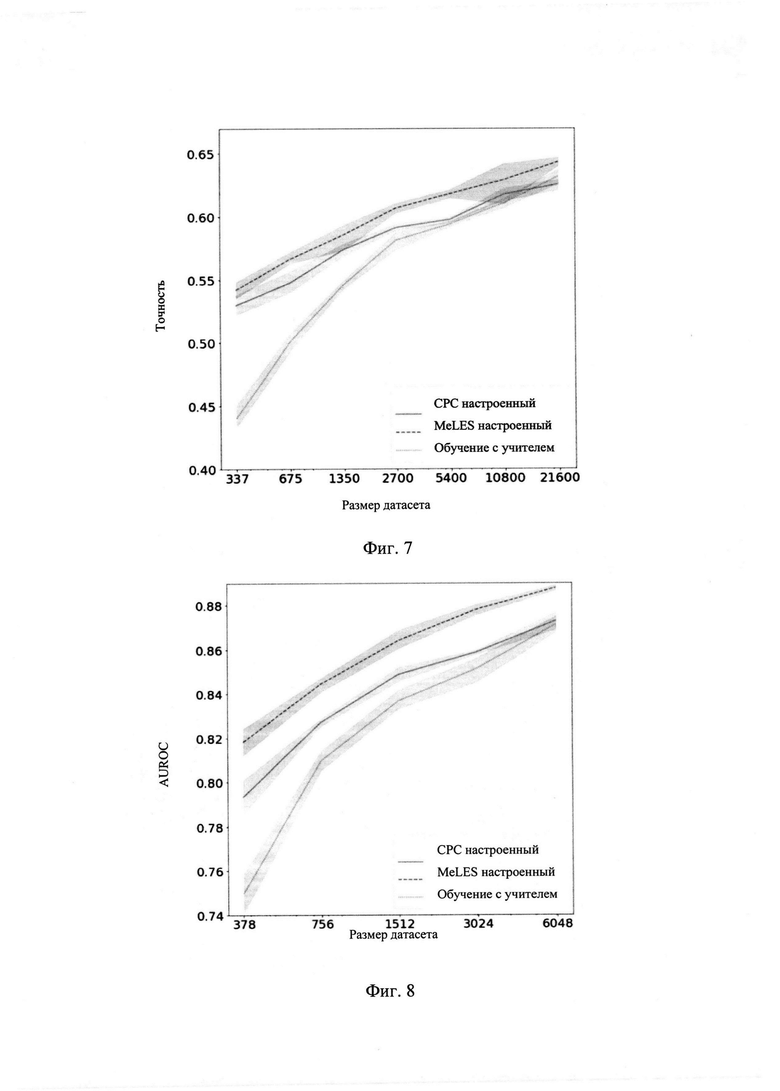
[0076] Чтобы оценить заявленный способ в условиях ограниченного количества размеченных данных, используется только часть доступной разметки для эксперимента с обучением без учителя. Так же как и в подходе обучения с учителем, выполняется сравнение предложенного метода с ligthGBM по вручную подготовленными агрегатным признакам и методом контрастного прогнозирующего кодирования СРС. Для обоих методов генерации представлений (MeLES и СРС) оценивается качество lightGBM как на представлениях, так и дообученных под целевую переменную представлений. В дополнение к этим экспериментам заявленный способ сравнивается с обучением с учителем на размеченной части датасета.
[0077] На Фиг. 5 - Фиг. 6 сравнивается качество подготовленных вручную агрегатных признаков и представлений, накладывая метод lightGBM поверх них. Кроме того, на Фиг. 7 - Фиг. 8 можно найти сравнение отдельных моделей на задачах, рассмотренных в статье. Как видно на рисунках, если количество разметки ограничено, MeLES значительно превосходит подходы обучения с учителем и другие. Также MeLES неизменно превосходит СРС для данных с разным объемом разметки.
[0078] В настоящем способе был применен подход на основе метрик лернинга для анализа данных жизненного потока новым образом, обучением без учителя. В рамках этого был разработан метод Metric Learning for Sequences (MeLES), основанный на обучении без учителя. В частности, метод MeLES может использоваться для создания представлений последовательностей событий со сложной структурой, которые могут эффективно использоваться в различных последующих задачах машинного обучения. Кроме того, заявленный метод может быть использован для предобработки признаков в условиях обучения без учителя. С помощью эмпирических экспериментов демонстрируется эффективность заявленного способа за счет достижения высоких результатов в качестве для нескольких задач, существенно опережая как классические базовые модели машинного обучения на основе созданных вручную признаков, так и подходы, основанные на нейронных сетях.
[0079] В среде с ограниченной разметкой, заявленный способ демонстрирует еще более сильные результаты при сравнении с методами на основании обучения с учителем. Предложенный метод генерации представлений удобен для использования в продуктиве, поскольку для получения сложных компактных представлений почти не требуется предварительной обработки признаков на основе сложных потоков событий. Предварительно рассчитанные представления могут быть легко использованы для различных последующих задач без выполнения сложных и трудоемких вычислений агрегатных признаков на основе необработанных данных о событиях. Для некоторых архитектур кодировщиков становится возможно постепенно обновлять уже рассчитанные представления, когда поступают дополнительные новые данные событий жизненного потока. Другое преимущество использования представлений на основе последовательности событий вместо явных данных о событиях заключается в том, что невозможно восстановить точную входную последовательность из ее представлений. Следовательно, использование представлений приводит к конфиденциальности и безопасности данных для конечных пользователей, чем непосредственно при работе с необработанными данными событий, и все это достигается без потери информации при использования последующих задачах машинного обучения.
Источники информации:
1. Srivatsan Laxman, Vikram Tankasali, and RyenWWhite. 2008. Stream prediction using a generative model based on frequent episodes in event sequences. In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. 453-461.
2.  Wiese and Christian Omlin. 2009. Credit card transactions, fraud detection, and machine learning: Modelling time with LSTM recurrent neural networks. In Innovations in neural information paradigms and applications. Springer, 231-268.
Wiese and Christian Omlin. 2009. Credit card transactions, fraud detection, and machine learning: Modelling time with LSTM recurrent neural networks. In Innovations in neural information paradigms and applications. Springer, 231-268.
3. Yishen Zhang, Dong Wang, Yuehui Chen, Huijie Shang, and Qi Tian. 2017. Credit risk assessment based on long short-term memory model. In International conference on intelligent computing. Springer, 700-712.
4. Luca Bigon, Giovanni Cassani, Ciro Greco, Lucas Lacasa, Mattia Pavoni, Andrea Polonioli, and Jacopo Tagliabue. 2019. Prediction is very hard, especially about conversion. Predicting user purchases from clickstream data in fashion e-commerce. arXiv preprint arXiv: 1907.00400 (2019).
5. Sumit Chopra, Raia Hadsell, and Yann LeCun. 2005. Learning a similarity metric discriminatively, with application to face verification. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05), Vol. 1. IEEE, 539-546.
6. Florian Schroff, Dmitry Kalenichenko, and James Philbin. 2015. FaceNet: A unified embedding for face recognition and clustering. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2015), 815-823.
7. Kilian Q Weinberger, John Blitzer, and Lawrence K Saul. 2006. Distance metric learning for large margin nearest neighbor classification. In Advances in neural information processing systems. 1473-1480.
8. Li Wan, Quan Wang, Alan Papir, and Ignacio Lopez Moreno. 2017. Generalized End-to-End Loss for Speaker Verification. (2017). arXiv:eess.AS/1710.10467
9. Nils Reimers and Iryna Gurevych. 2019. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics. http://arxiv.org/abs/l908.10084
10. Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In NAACL-HLT
11.  van den Oord, Yazhe Li, and Oriol Vinyals. 2018. Representation Learning with Contrastive Predictive Coding. CoRR abs/1807.03748 (2018). arXiv: 1807.03748 http://arxiv.org/abs/1807.03748
van den Oord, Yazhe Li, and Oriol Vinyals. 2018. Representation Learning with Contrastive Predictive Coding. CoRR abs/1807.03748 (2018). arXiv: 1807.03748 http://arxiv.org/abs/1807.03748
12. Longlong Jing and Yingli Tian. 2019. Self-supervised Visual Feature Learning with Deep Neural Networks: A Survey. (2019). arXiv:cs.CV/l 902.06162.
13. Yang Song, Yuan Li, BoWu, Chao-Yeh Chen, Xiao Zhang, and HartwigAdam. 2017. Learning Unified Embedding for Apparel Recognition. 2017 IEEE International Conference on Computer Vision Workshops (ICCVW) (2017), 2243-2246.
14. Andrew Zhai, Hao-Yu Wu, Eric Tzeng, Dong Huk Park, and Charles Rosenberg. 2019. Learning a Unified Embedding for Visual Search at Pinterest. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD '19). ACM, New York, NY, USA, 2412-2420. https://doi.org/10.1145/3292500.3330739.
15. David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. 1985. Learning internal representations by error propagation. Technical Report. California Univ San Diego La Jolla Inst for Cognitive Science.
16. Diederik P Kingma and Max Welling. 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114 (2013).
17. Rogelio A Mancisidor, Michael Kampffmeyer, Kjersti Aas, and Robert Jenssen. 2019. Learning Latent Representations of Bank Customers With The Variational Autoencoder. (2019). arXiv:stat.ML/l903.06580.
18. Eric P Xing, Michael I Jordan, Stuart J Russell, and Andrew Y Ng. 2003. Distance metric learning with application to clustering with side-information. In Advances in neural information processing systems. 521-528.
19. Raia Hadsell, Sumit Chopra, and Yann LeCun. 2006. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Volume 2 (CVPR '06). IEEE Computer Society, Washington, DC, USA, 1735-1742. https://doi.org/10.1109/CVPR.2006.100.
20. Florian Schroff, Dmitry Kalenichenko, and James Philbin. 2015. FaceNet: A unified embedding for face recognition and clustering. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2015), 815-823.
21. Chengzhi Mao, Ziyuan Zhong, Junfeng Yang, Carl Vondrick, and Baishakhi Ray. 2019. Metric learning for adversarial robustness. In Advances in Neural Information Processing Systems (2019), 478-489.
22. Tomas Mikolov, G.s Corrado, Kai Chen, and Jeffrey Dean. 2013. Efficient Estimation of Word Representations in Vector Space. 1-12.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РАСЧЕТА КРЕДИТНОГО РЕЙТИНГА КЛИЕНТА | 2019 |
|
RU2723448C1 |
| НЕЙРОСЕТЕВОЙ ПЕРЕНОС ВЫРАЖЕНИЯ ЛИЦА И ПОЗЫ ГОЛОВЫ С ИСПОЛЬЗОВАНИЕМ СКРЫТЫХ ДЕСКРИПТОРОВ ПОЗЫ | 2020 |
|
RU2755396C1 |
| ОБУЧЕНИЕ GAN (ГЕНЕРАТИВНО-СОСТЯЗАТЕЛЬНЫХ СЕТЕЙ) СОЗДАНИЮ ПОПИКСЕЛЬНОЙ АННОТАЦИИ | 2019 |
|
RU2735148C1 |
| МОДЕЛИРОВАНИЕ ЧЕЛОВЕЧЕСКОЙ ОДЕЖДЫ НА ОСНОВЕ МНОЖЕСТВА ТОЧЕК | 2021 |
|
RU2776825C1 |
| СПОСОБ ОТЛАДКИ ОБУЧЕННОЙ РЕКУРРЕНТНОЙ НЕЙРОННОЙ СЕТИ | 2019 |
|
RU2715024C1 |
| СПОСОБ ПОСТРОЕНИЯ КАРТЫ ГЛУБИНЫ ПО ПАРЕ ИЗОБРАЖЕНИЙ | 2022 |
|
RU2806009C2 |
| СПОСОБ СОЗДАНИЯ КОМБИНИРОВАННЫХ КАСКАДОВ НЕЙРОННЫХ СЕТЕЙ С ЕДИНЫМИ СЛОЯМИ ИЗВЛЕЧЕНИЯ ПРИЗНАКОВ И С НЕСКОЛЬКИМИ ВЫХОДАМИ, КОТОРЫЕ ОБУЧАЮТСЯ НА РАЗНЫХ ДАТАСЕТАХ ОДНОВРЕМЕННО | 2021 |
|
RU2779408C1 |
| СПОСОБ И СИСТЕМА СЕГМЕНТАЦИИ СЦЕН ВИДЕОРЯДА | 2022 |
|
RU2783632C1 |
| СПОСОБ И СИСТЕМА ВЫЯВЛЕНИЯ ДАННЫХ, ПОДВЕРЖЕННЫХ ДЕАНОНИМИЗАЦИИ, В ОБЕЗЛИЧЕННОМ НАБОРЕ ДАННЫХ | 2024 |
|
RU2837785C1 |
| СПОСОБ ОБУЧЕНИЯ ГЛУБОКИХ НЕЙРОННЫХ СЕТЕЙ НА ОСНОВЕ РАСПРЕДЕЛЕНИЙ ПОПАРНЫХ МЕР СХОЖЕСТИ | 2016 |
|
RU2641447C1 |
Изобретение относится к области информационных технологий, в частности к способу получения низкоразмерных числовых представлений последовательностей событий. Техническим результатом является повышение эффективности формирования признаков для моделей машинного обучения с помощью формирования низкоразмерных числовых представлений последовательностей событий. Предлагается компьютерно-реализуемый способ получения низкоразмерных числовых представлений последовательностей событий, содержащий этапы, на которых: получают набор входных данных, характеризующий события, агрегированные в последовательность и связанные с по меньшей мере одной информационной сущностью, при этом выполняется предобработка упомянутого набора входных данных, при которой: формируют позитивные и негативные пары последовательностей транзакционных событий, с помощью кодировщика транзакционных событий формируют векторное представление каждого транзакционного события из упомянутого набора атрибутов, осуществляют нормирование числовых переменных; осуществляют обработку временных меток, осуществляют конкатенацию полученных векторных представлений категориальных переменных и нормированных числовых переменных; формируют единый числовой вектор события по итогам выполненной конкатенации. 6 з.п. ф-лы, 8 ил., 8 табл.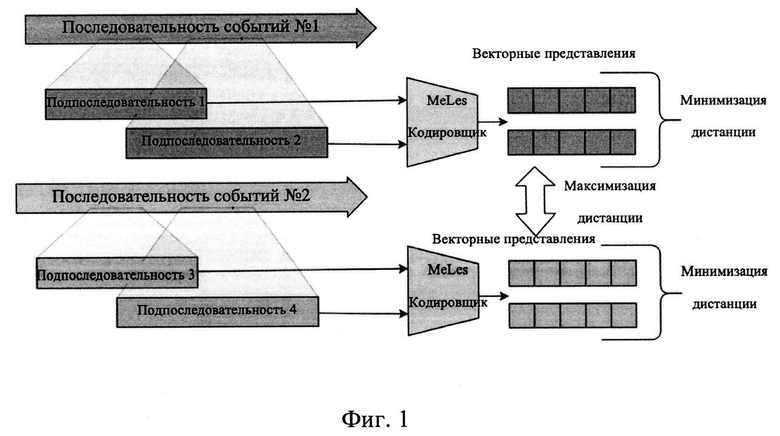
1. Компьютерно-реализуемый способ получения низкоразмерных числовых представлений последовательностей событий, содержащий этапы, на которых:
- получают набор входных данных, характеризующий события, агрегированные в последовательность и связанные с по меньшей мере одной информационной сущностью, причем упомянутые данные содержат набор атрибутов, включающий: категориальные переменные, числовые переменные и временную метку;
при этом выполняется предобработка упомянутого набора входных данных, при которой:
 формируют позитивные пары последовательностей транзакционных событий, которые представляют собой подпоследовательности, принадлежащие последовательности транзакционных событий одной информационной сущности;
формируют позитивные пары последовательностей транзакционных событий, которые представляют собой подпоследовательности, принадлежащие последовательности транзакционных событий одной информационной сущности;
 формируют негативные пары подпоследовательностей транзакционных событий, которые являются подпоследовательностями, принадлежащими последовательностям транзакционных событий разных информационных сущностей;
формируют негативные пары подпоследовательностей транзакционных событий, которые являются подпоследовательностями, принадлежащими последовательностям транзакционных событий разных информационных сущностей;
- с помощью кодировщика транзакционных событий формируют векторное представление каждого транзакционного события из упомянутого набора атрибутов, при этом кодировщик содержит первичный набор параметров и выполняет этапы, на которых:
 осуществляют кодирование категориальных переменных в виде векторных представлений;
осуществляют кодирование категориальных переменных в виде векторных представлений;
 осуществляют нормирование числовых переменных;
осуществляют нормирование числовых переменных;
 осуществляют обработку временных меток для выстраивания упорядоченной по времени последовательности транзакционных событий;
осуществляют обработку временных меток для выстраивания упорядоченной по времени последовательности транзакционных событий;
 осуществляют конкатенацию полученных векторных представлений категориальных переменных и нормированных числовых переменных;
осуществляют конкатенацию полученных векторных представлений категориальных переменных и нормированных числовых переменных;
 формируют единый числовой вектор одного транзакционного события по итогам выполненной конкатенации;
формируют единый числовой вектор одного транзакционного события по итогам выполненной конкатенации;
- с помощью кодировщика подпоследовательности формируют векторное представление подпоследовательности транзакционных событий из набора числовых векторов транзакционных событий, полученных с помощью кодировщика транзакционных событий, при этом кодировщик содержит первичный набор параметров;
- осуществляют фильтрацию негативных пар векторов подпоследовательностей транзакционных событий, значение векторного расстояния между которыми не выше заданного порогового значения;
- корректируют первичные параметры упомянутых кодировщика транзакционных событий и кодировщика подпоследовательности с помощью применения функции потерь вида маржинальных или контрастивных потерь; и
- формируют низкоразмерные числовые представления последовательностей событий, связанных с одной информационной сущностью, на основании выполненной корректировки.
2. Способ по п. 1, характеризующийся тем, что информационная сущность представляет собой транзакционные данные физического или юридического лица.
3. Способ по п. 1, характеризующийся тем, что создание позитивных пар осуществляется с помощью алгоритма формирования несвязных подпоследовательностей.
4. Способ по п. 1, характеризующийся тем, что создание позитивных пар осуществляется с помощью алгоритма генерации случайных срезов последовательности.
5. Способ по п. 3, характеризующийся тем, что формируемые подпоследовательности не пересекаются между собой.
6. Способ по п. 4, характеризующийся тем, что формируемые подпоследовательности не пересекаются и/или пересекаются между собой.
7. Способ по п. 1, характеризующийся тем, что кодировщик подпоследовательности представляет собой рекуррентную нейронную сеть (РНС).
| US 20170228731 A1, 10.08.2017 | |||
| US 20120131139 A1, 24.05.2012 | |||
| US 20180183650 A1, 28.06.2018 | |||
| Бур для ударного бурения | 1932 |
|
SU34474A1 |
| СИСТЕМА ИНФОРМАЦИОННОГО ОБМЕНА | 1995 |
|
RU2148856C1 |
| СИСТЕМЫ И СПОСОБЫ ДЛЯ ОТСЛЕЖИВАНИЯ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ПРЕДОСТАВЛЕННЫХ ПОЛЬЗОВАТЕЛЕМ ИНФОРМАЦИОННЫХ МЕТОК | 2016 |
|
RU2678659C1 |
Авторы
Даты
2021-01-28—Публикация
2020-02-14—Подача