ОБЛАСТЬ ТЕХНИКИ
[001] Данное техническое решение в общем относится к вычислительным системам, основанным на биологических моделях, а конкретно к способам обучения глубоких нейронных сетей на основе распределений попарных мер схожести.
УРОВЕНЬ ТЕХНИКИ
[002] Понятие глубокого обучения (deep learning) относится к задачам распознавания и обозначает подход к обучению так называемых глубоких структур, к которым можно отнести многоуровневые нейронные сети. Простой пример из области распознавания образов: необходимо научить вычислительную систему выделять все более абстрактные признаки в терминах других абстрактных признаков, то есть определить зависимость между абстрактными характерными особенностями (признаками), например, такими как выражение всего лица, глаз и рта и, в конечном итоге, скопления цветных пикселов математически, на основании которых можно, например, определять, пол, возраст человека или насколько он похож на другого человека.
[003] По сравнению с классическим машинным обучением глубокое обучение делает шаг вперед и исключает необходимость формализации знаний экспертов на начальном этапе. Все важные закономерности система определяет самостоятельно на основании введенных данных (как, например, в нейронных сетях).
[004] Из уровня техники известна статья S. Chopra, R. Hadsell, and Y. LeCun. Learning a similarity metric discriminatively, with application to face verification. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), 20-26 June 2005, San Diego, CA, USA, pp. 539-546, 2005.
[005] Данное техническое решение использует при глубоком обучении функцию потерь для пар примеров из тренировочных данных и вычисляет ее независимо. Для пар тренировочных примеров, которые относятся к одному классу (положительные пары), Евклидово расстояние между векторами их глубоких представлений минимизируется, а для пар примеров разных классов (отрицательные примеры) - максимизируется до того момента, пока расстояния между положительными примерами будут меньше расстояния между отрицательными примерами на величину параметра зазора (margin).
[006] Такой подход может вызывать проблемы с переобучением. Помимо этого, выбор значения параметра зазора является нетривиальной задачей, т.к. в процессе обучения происходит сильное изменение распределений значений расстояний.
[007] Также известна статья Weinberger, Kilian Q., and Lawrence К. Saul. "Distance metric learning for large margin nearest neighbor classification." Journal of Machine Learning Research 10. Feb (2009): 207-244.
[008] Данный метод использует при глубоком обучении функцию потерь для триплета примеров из тренировочных данных и вычисляет ее независимо. Триплет состоит из двух пар примеров, одна из которых является положительной (оба примера принадлежат одному классу), а другая - отрицательной (примеры принадлежат разным классам). Таким образом ищется такое представление, которое позволяет получать подходящие относительные расстояния между примерами в положительной и отрицательной парах - у положительных пар они должны быть меньше. Однако в этом методе также приходится задавать параметр зазора между расстояниями в положительных и отрицательных парах. С одной стороны, данный метод является достаточно гибким, поскольку характерная разница между расстояниями внутри положительных и отрицательных пар для примера может меняться в зависимости от расположения его представления в пространстве.
[009] Однако это может так же быть причиной переобучения. Помимо этого, выбор самих триплетов является непростой задачей, требующей иногда значительных вычислительных ресурсов.
СУЩНОСТЬ ТЕХНИЧЕСКОГО РЕШЕНИЯ
[0010] Данное техническое решение направлено на устранение недостатков, свойственных решениям, известным из уровня техники.
[0011] Технической проблемой, решаемой в данном техническом решении, является обучение модели глубокой нейронной сети.
[0012] Техническим результатом, проявляющимся при решении вышеуказанной проблемы, является повышение точности обучения и уменьшение временных затрат для настройки параметров обучения глубоких представлений входных данных.
[0013] Указанный технический результат достигается благодаря реализации способа обучения глубоких нейронных сетей на основе распределений попарных мер схожести, в котором получают размеченную обучающую выборку, где каждый элемент обучающей выборки имеет метку класса, к которому он принадлежит; формируют набор непересекающихся случайных подмножеств обучающей выборки входных данных для глубокой нейронной сети таким образом, что при объединении они представляют собой обучающую выборку; передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети, получая на выходе глубокое представление данного подмножества обучающей выборки; определяют все попарные меры схожести между полученными на предыдущем шаге глубокими представлениями элементов каждого подмножества; определенные на предыдущем шаге меры схожести между элементами, которые имеют одинаковые метки классов, относят к мерам схожести положительных пар, а меры схожести между элементами, которые имеют разные метки классов, относят к мерам схожести отрицательных пар; определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар посредством использования гистограммы; формируют функцию потерь на основе определенных на предыдущем шаге вероятностных распределений мер схожести для положительных пар и отрицательных пар; минимизируют сформированную функцию на предыдущем шаге потерь с помощью метода обратного распространения ошибки.
[0014] В некоторых вариантах осуществления получают размеченную обучающую выборку из хранилища данных.
[0015] В некоторых вариантах осуществления метка класса является числовой или символьной.
[0016] В некоторых вариантах осуществления передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети последовательно или параллельно.
[0017] В некоторых вариантах осуществления глубоким представлением подмножества является набор векторов вещественных чисел, каждый из которых соответствует элементу подмножества.
[0018] В некоторых вариантах осуществления перед получением на выходе глубокого представления каждого подмножества обучающей выборки выполняют L2-нормализацию последнего слоя глубокой нейронной сети.
[0019] В некоторых вариантах осуществления при определении мер схожести между глубокими представлениями элементов каждого подмножества используют косинусную меру схожести.
[0020] В некоторых вариантах осуществления определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар непараметрическим способом с помощью линейной интерполяции значений интервалов гистограммы.
[0021] В некоторых вариантах осуществления формируют функцию потерь, которая является дифференцируемой относительно парных схожестей.
[0022] В некоторых вариантах осуществления минимизируют функцию потерь на основе гистограмм с помощью метода обратного распространения ошибки до тех пор, пока значение функции потерь не перестанет уменьшаться.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
[0023] Признаки и преимущества настоящего технического решения станут очевидными из приводимого ниже подробного описания и прилагаемых чертежей, на которых:
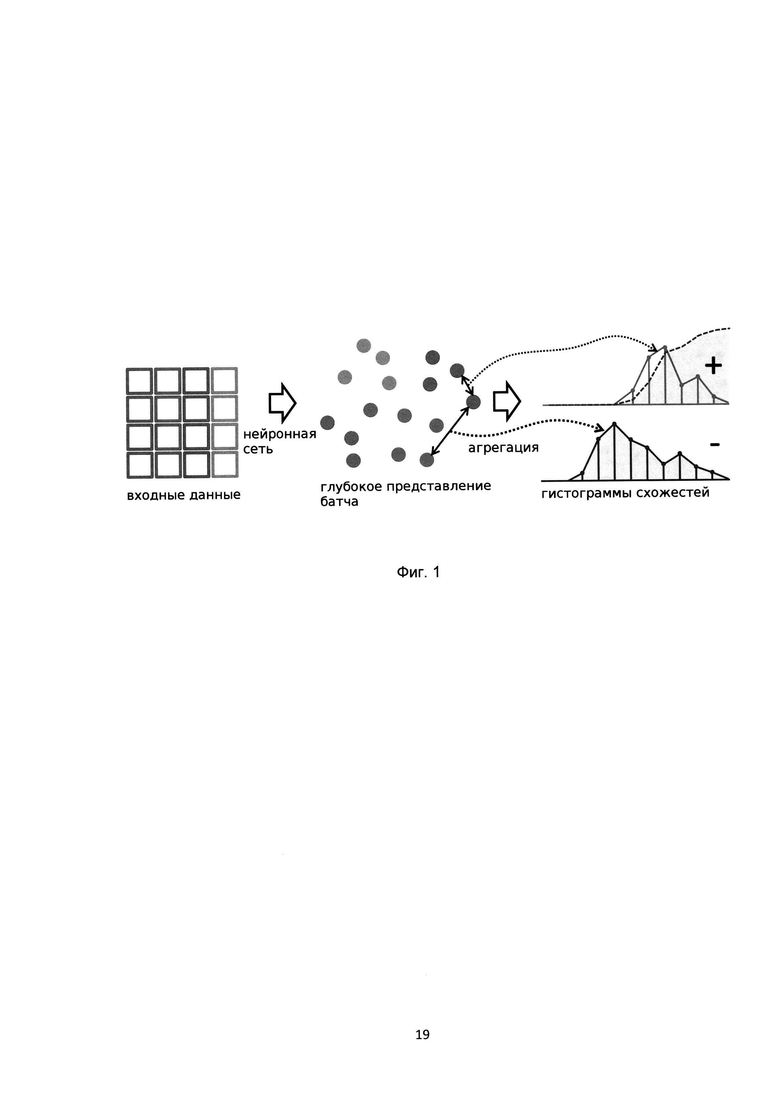
[0024] На Фиг. 1 показан пример вычисления функции потерь на основе гистограмм;
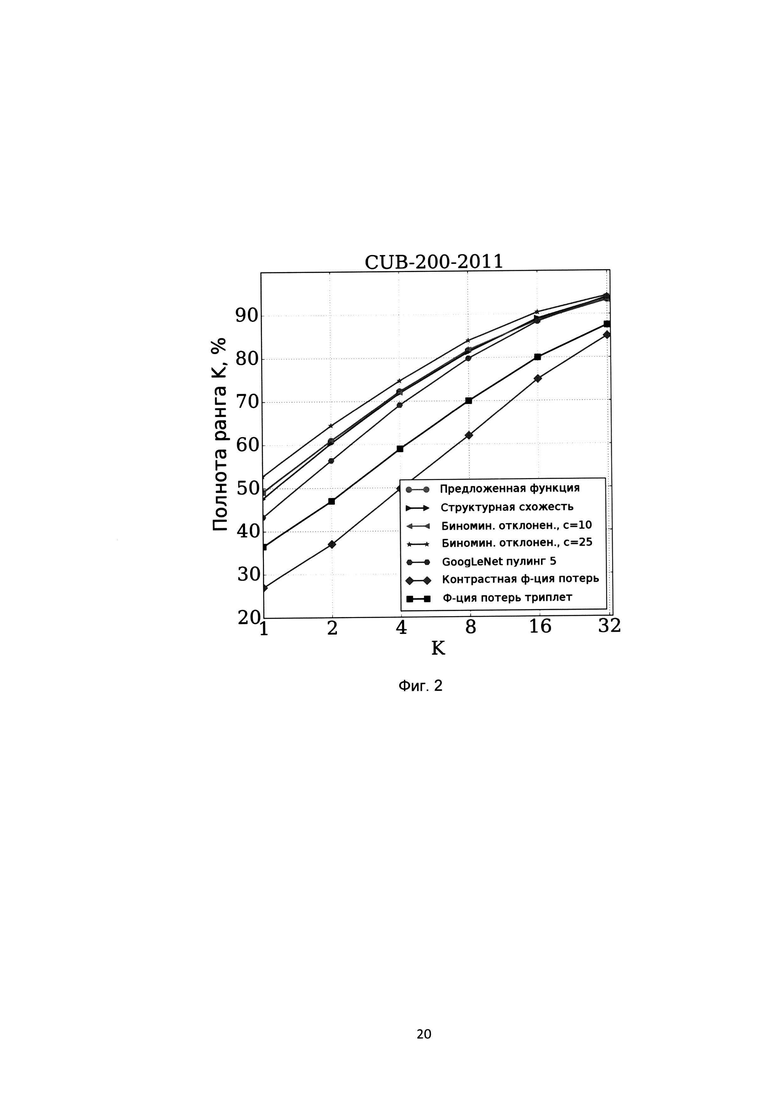
[0025] На Фиг. 2 показаны показатели полноты ранга K различных методов на базе CUB-200-2011;
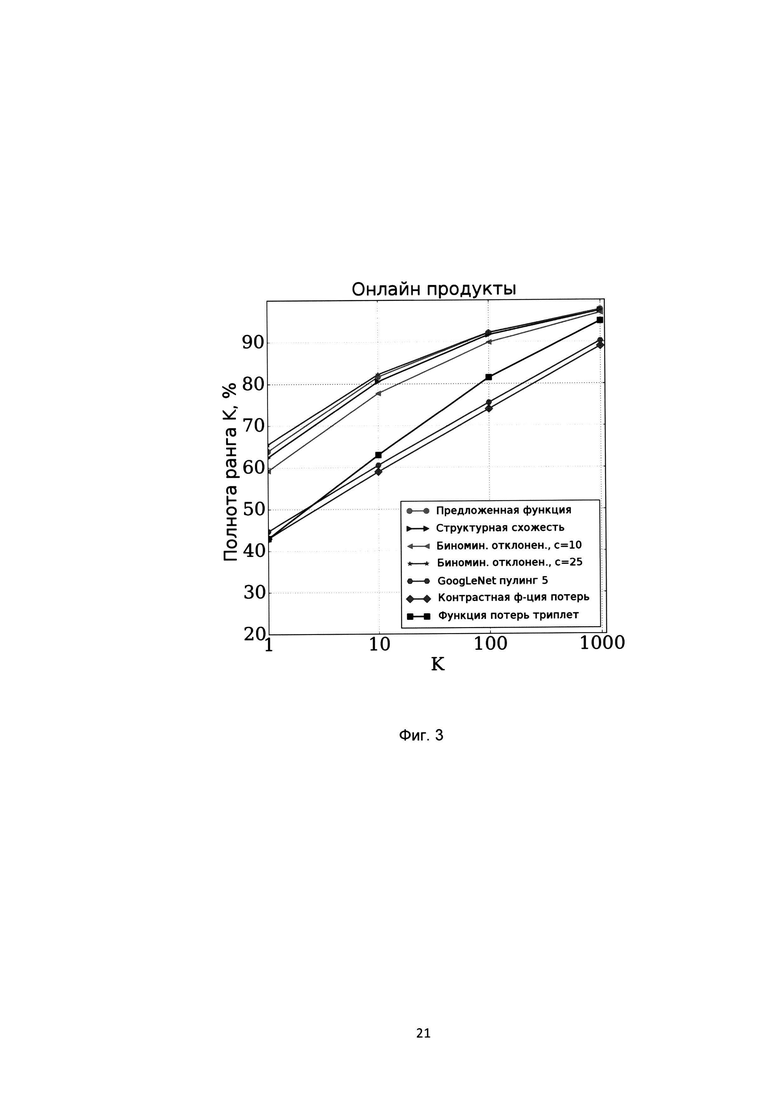
[0026] На Фиг. 3 показаны показатели полноты ранга K различных методов на базе онлайн продуктов;
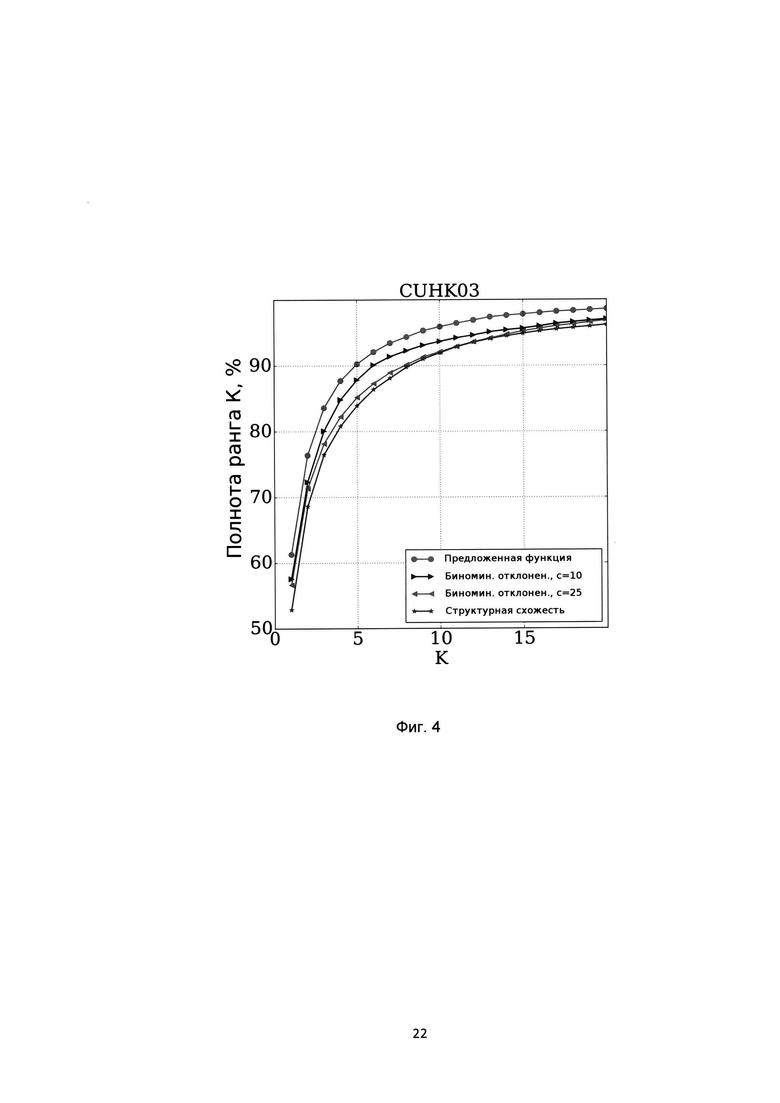
[0027] На Фиг. 4 показаны показатели полноты ранга K различных методов на базе CUHK03;
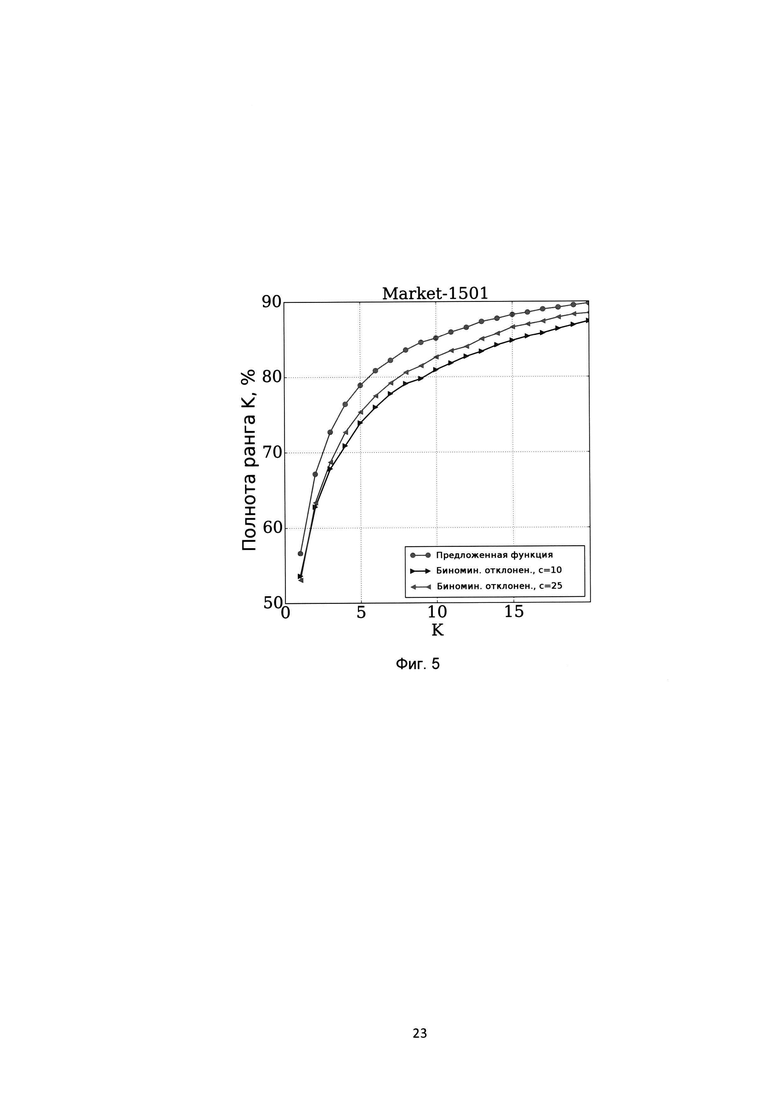
[0028] На Фиг. 5 показаны показатели полноты ранга K различных методов на базе Market-1501;
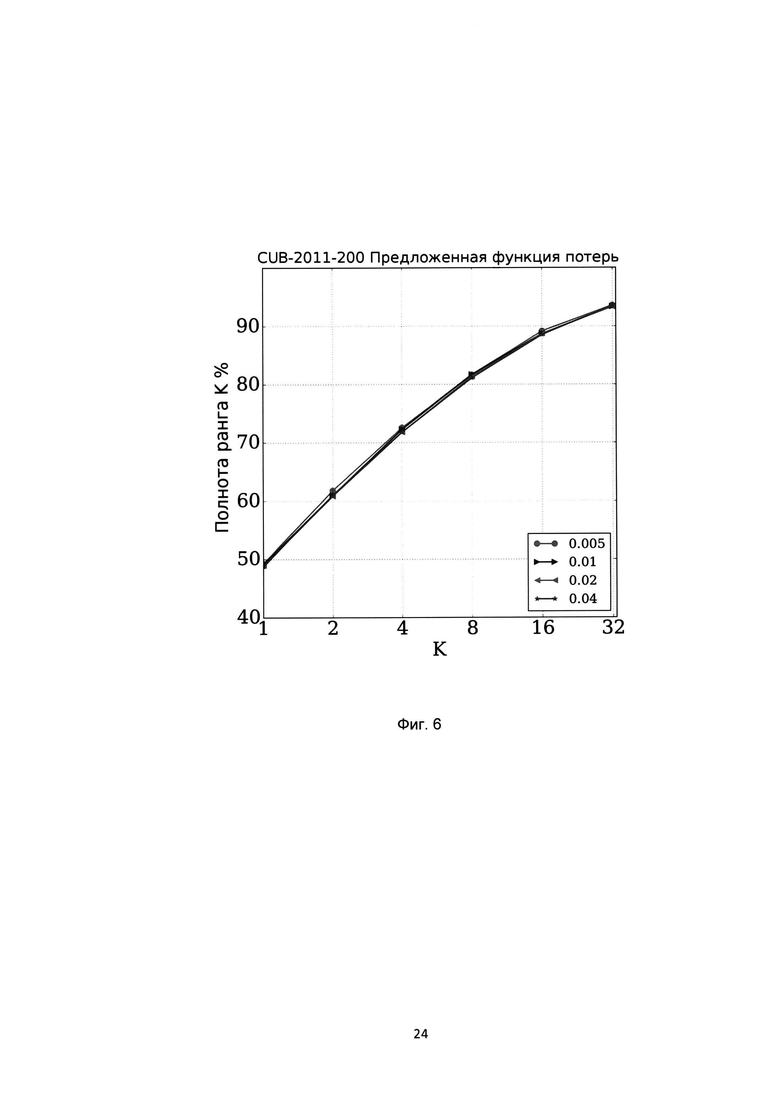
[0029] На Фиг. 6 показаны показатели полноты ранга K различных методов на базе CUB-2011-200 при использовании различных размеров корзин гистограмм в предложенной функции потерь.
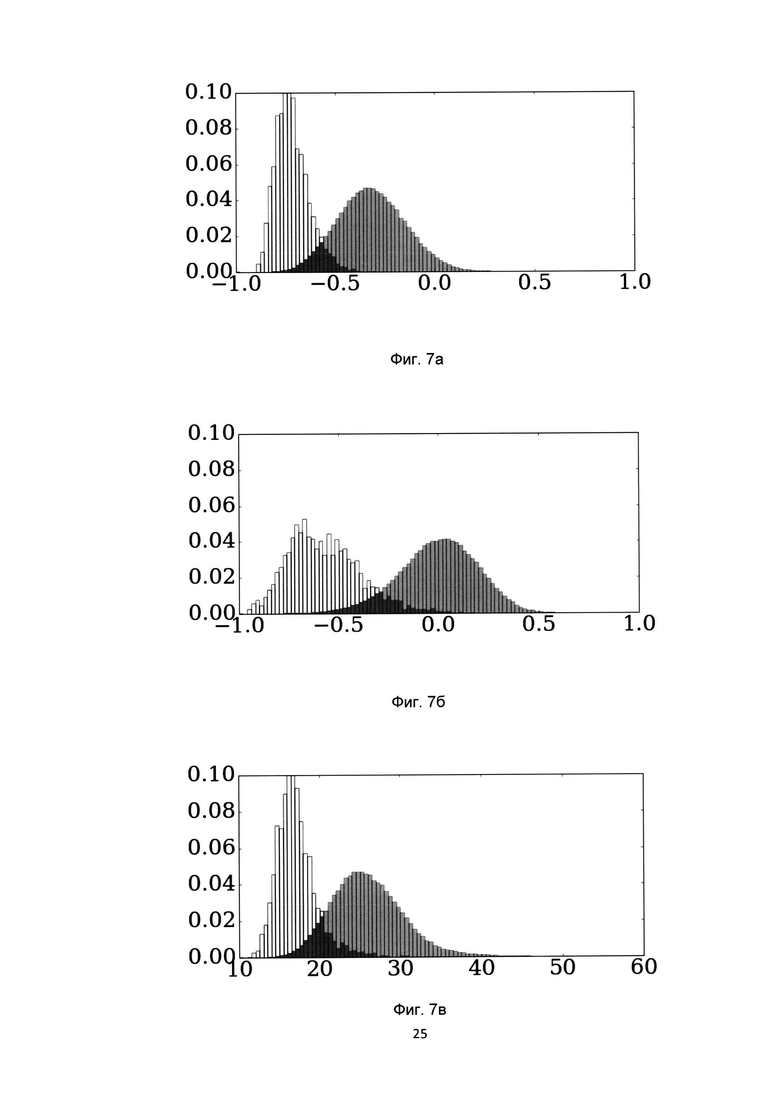
[0030] На Фиг. 7 показаны гистограммы распределений значений схожестей положительных пар (белый цвет) и отрицательных пар (серый цвет) при использовании различных функций потерь;
[0031] На Фиг. 7а показаны гистограммы распределений при использовании предложенной функции потерь;
[0032] На Фиг. 7б показаны гистограммы распределений при использовании биноминального отклонения при использовании структурной схожести;
[0033] На Фиг. 7в показаны гистограммы распределений при использовании структурной схожести.
ПОДРОБНОЕ ОПИСАНИЕ
[0034] Ниже будут описаны понятия и определения, необходимые для подробного раскрытия осуществляемого технического решения.
[0035] Техническое решение может быть реализовано в виде распределенной компьютерной системы.
[0036] В данном решении под системой подразумевается компьютерная система, ЭВМ (электронно-вычислительная машина), ЧПУ (числовое программное управление), ПЛК (программируемый логический контроллер), компьютеризированные системы управления и любые другие устройства, способные выполнять заданную, четко определенную последовательность операций (действий, инструкций).
[0037] Под устройством обработки команд подразумевается электронный блок либо интегральная схема (микропроцессор), исполняющая машинные инструкции (программы).
[0038] Устройство обработки команд считывает и выполняет машинные инструкции (программы) с одного или более устройства хранения данных. В роли устройства хранения данных могут выступать, но, не ограничиваясь, жесткие диски (HDD), флеш-память, ПЗУ (постоянное запоминающее устройство), твердотельные накопители (SSD), оптические носители (CD, DVD и т.п.). [0039] Программа - последовательность инструкций, предназначенных для исполнения устройством управления вычислительной машины или устройством обработки команд.
[0040] Глубокое обучение (англ. Deep learning) - набор алгоритмов машинного обучения, которые пытаются моделировать высокоуровневые абстракции в данных, используя архитектуры, состоящие из множества нелинейных трансформаций.
[0041] Другими словами, глубокое обучение - это часть более широкого семейства методов машинного обучения - обучения представлениям, где векторы признаков располагаются сразу на множестве уровней. Эти признаки определяются автоматически и связывают друг с другом, формируя выходные данные. На каждом уровне представлены абстрактные признаки, основанные на признаках предыдущего уровня. Таким образом, чем глубже мы продвигаемся, тем выше уровень абстракции. В нейронных сетях множество слоев представляет собой множество уровней с векторами признаков, которые генерируют выходные данные.
[0042] Выборка - часть генеральной совокупности элементов, которая охватывается экспериментом (наблюдением, опросом).
[0043] Глубокое представление - это представление исходных данных в некотором пространстве, которое получается на выходе обученной модели глубокой нейронной сети, при подаче на ее вход исходных данных.
[0044] Мера схожести - это вещественное значение, которое показывает, насколько объекты похожи друг на друга, например, принадлежат одному семантическому классу.
[0045] Вероятностное распределение - это закон, описывающий область значений случайной величины и вероятности их исхода (появления).
[0046] Гистограмма - способ графического представления табличных данных.
[0047] Функция потерь - функция, которая в теории статистических решений характеризует потери при неправильном принятии решений на основе наблюдаемых данных.
[0048] Зазор (англ. margin) - расстояние от некоторой точки до границы решения, которое используется, например, в машине опорных векторов. Также может быть величиной разницы между расстоянием между представлениями одного класса и расстоянием между представлениями разных классов
[0049] Пороги - это некоторые контрольные значения, которые позволяют задавать функции потерь параметрически.
[0050] Сверточная нейронная сеть (англ. convolutional neural network, CNN) - специальная архитектура искусственных нейронных сетей, предложенная Яном Лекуном и нацеленная на эффективное распознавание изображений за счет учета пространственной корреляции изображений с помощью сверточных фильтров с обучаемыми параметрами весов, входит в состав технологий глубокого обучения (англ. deep learning).
[0051] Косинусная мера схожести (англ. cosine similarity) - это мера сходства (или схожести) между двумя векторами предгильбертового пространства, которая используется для измерения косинуса угла между ними.
[0052] Если даны два вектора признаков, А и B, то косинусная мера схожести cos(θ), может быть представлена посредством использования скалярного произведения и нормы:
[0053] 
[0054] Способ обучения глубоких нейронных сетей на основе распределений попарных мер схожести может быть реализован в некоторых вариантах следующим образом.
[0055] Шаг 101: получают размеченную обучающую выборку, где каждый элемент обучающей выборки имеет метку класса, к которому он принадлежит;
[0056] Под классом понимается семантический класс объекта (например, лицо Пети или фото собаки). Каждый элемент из выборки имеет свою метку класса после классификации, выполненной человеком. Метка класса может принимать как числовое, так и символьное значение. Например, если объектами являются собака и кошка. В символьном искусственном интеллекте - это два разных символа, не имеющие никакой взаимосвязи между собой.
[0057] Обучающую выборку формируют предварительно и передают на устройство обработки данных, на котором выполняется данный способ, из хранилища данных.
[0058] Шаг 102: формируют набор непересекающихся случайных подмножеств обучающей выборки входных данных для глубокой нейронной сети таким образом, что при объединении они представляют собой обучающую выборку;
[0059] На данном этапе осуществляют разбиение всей обучающей выборки на случайные подмножества. Набор непересекающихся случайных подмножеств обучающей выборки входных данных можно представить в виде X={x1, x2, …, xn}, а глубокую нейронную сеть в виде ƒ(⋅, θ), где θ являются обучаемыми параметрами нейронной сети, схема которой показана на Фиг. 1. В некоторых источниках информации подмножество обучающей выборки называют батч (англ. batch).
[0060] Шаг 103: передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети, получая на выходе глубокое представление данного подмножества обучающей выборки;
[0061] Передавать подмножества обучающей выборки в некоторых вариантах осуществления могут как последовательно, так и параллельно.
[0062] Примером глубокого представления подмножества является набор векторов вещественных чисел, каждый из которых соответствует элементу подмножества.
[0063] Слой выхода в глубокой нейронной сети не дает результат классификации, а выдает n-мерный вектор глубоких представлений, где n - число нейронов на выходе модели глубокой нейронной сети. В некоторых вариантах реализации выполняют L2-нормализацию выходов последнего слоя глубокой нейронной сети. L2-нормализация (или регуляризация) выполняется для того, чтобы уменьшить степень переобучения модели и исключить параметр масштаба значений глубоких представлений. Таким образом, расстояние между представлениями ограничено и гистограмму можно задать, используя всего один параметр, например ширину интервала. L2-нормализацию проводят посредством деления вектора глубоких представлений на его L2-норму 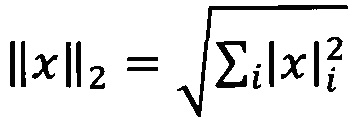 , которая является геометрическим расстоянием между двумя точками в многомерном пространстве, вычисляемым, например, в двумерном пространстве по теореме Пифагора. В некоторых вариантах реализации может использоваться иная нормализация, которая может быть дифференцируема.
, которая является геометрическим расстоянием между двумя точками в многомерном пространстве, вычисляемым, например, в двумерном пространстве по теореме Пифагора. В некоторых вариантах реализации может использоваться иная нормализация, которая может быть дифференцируема.
[0064] Шаг 104: определяют все попарные меры схожести между полученными на предыдущем шаге глубокими представлениями элементов каждого подмножества;
[0065] Если f1, f2, …, fn - полученные глубокие представления, то попарные меры схожести di,j определяются как di,j=D(fi, fj) (i и j могут принимать любые значения от 0 до N), где D(fi, fj) - это функция схожести между двумя векторами (например, косинусная мера схожести). Косинусная мера схожести D(x, y) между точками x=(x1, x2, …, xn) и y=(y1m y2, …, yn) в пространстве размерности n определяется как 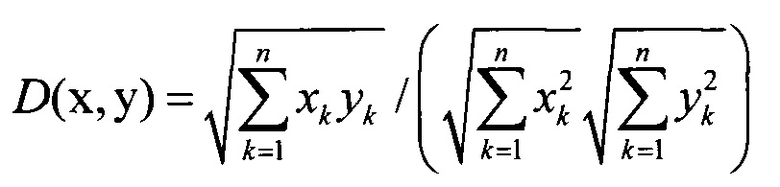
[0066] Если пары относятся к одному классу, то они являются положительными, а если пары относятся к разным классам, то отрицательными.
[0067] Шаг 105: определенные на предыдущем шаге меры схожести между элементами, которые имеют одинаковые метки классов, относят к мерам схожести положительных пар, а меры схожести между элементами, которые имеют разные метки классов, относят к мерам схожести отрицательных пар;
[0068] Например, работая с семантическими классами изображений "собака" и "кошка", мера схожести глубоких представлений 2-ух изображений собаки или 2-ух изображений кошки будет относиться к положительной паре, а мера схожести глубоких представлений из одного изображения собаки и одного изображения кошки будет относится к отрицательной паре.
[0069] Шаг 106: определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар посредством использования гистограммы;
На данном шаге определяют два одномерных вероятностных распределения мер схожести между примерами в пространстве их глубоких представлений, одно из которых относится к значениям мер схожести пар примеров с одинаковыми метками (положительные пары), а другая - к значениям мер схожести пар примеров с разными метками (отрицательные пары). Эти распределения вычисляются непараметрическим способом с помощью линейной интерполяции значений интервалов гистограммы. Пусть mij=1, если xi и xj являются одним и тем же объектом (положительная пара) mij=-1 в противном случае (отрицательная пара). Зная {mij} и выходы нейронной сети {yi=ƒ{xi; θ)}, есть возможность определить распределения вероятностей p+ и p-, которые соответствуют мерам схожести между положительными и отрицательными парами соответственно. В частности, значения S+={sij=〈xi,хj〉|mij=+1} и S-={sij=〈xi,хj|mij=-1〉} могут быть рассмотрены как выборки из этих двух распределений, где sij=〈хi,xj〉 - пара объектов.
[0070] Имея выборки S+ и S- можно использовать любой известный статистический подход для определения значений p+ и p-. Одномерность этих распределений и ограниченность значений в интервале [-1; +1] упрощает данную задачу.
[0071] В некоторых вариантах осуществления могут использовать гистограммы Н+ и Н- размерности R и с узлами t1=-1, …, tR=-1, равномерно расположенными на интервале [-1; +1] с шагом Δ=2/(R-1). В каждом узле гистограммы Н+ можно определить ее значение  :
:
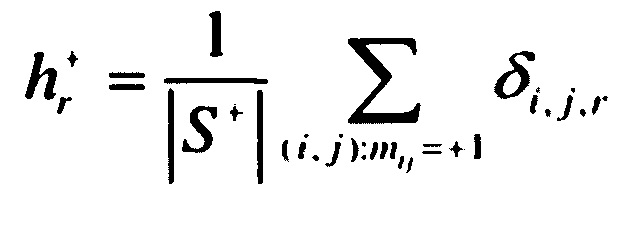 ,
,
где (i, j) обозначает все положительные примеры в подмножестве обучающей выборки. Веса δi,j,r выбираются следующим образом (где r - номер узла гистограммы):
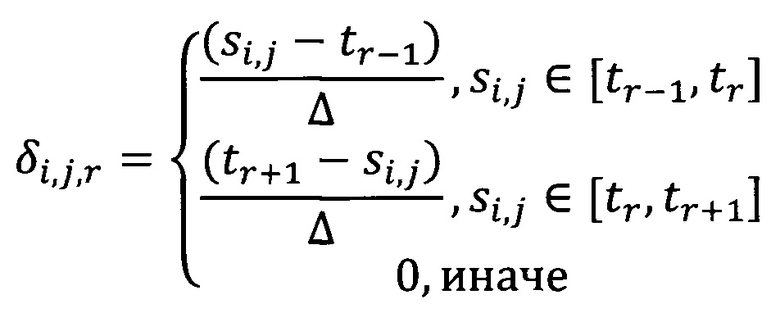
Таким образом, линейная интерполяция используется для каждой пары. Значения гистограммы Н- определяются аналогично.
[0072] Имея оценки для распределений p+ и p-, оценивают вероятность того, что мера схожести между двумя примерами в случайной отрицательной паре больше меры схожести между двумя примерами в случайной положительной паре (вероятность обратного) следующим образом:
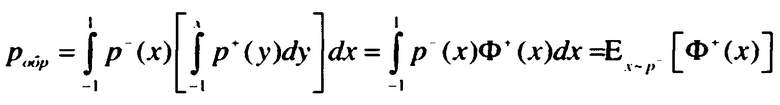
[0073] где Ф+(х) - кумулятивная плотность вероятности от p+(x). Этот интеграл может быть аппроксимирован и вычислен как:
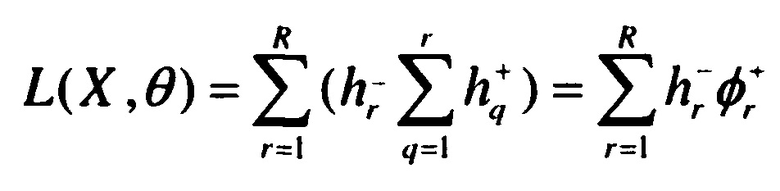 ,
,
[0074] где L - предложенная функция потерь на основе гистограмм, посчитанная по подмножеству выборки X с использованием выходных параметров сети θ, причем функция потерь аппроксимирует вероятность обратного.
 ,
,
является кумулятивной суммой гистограммы Н+.
[0075] Шаг 107: формируют функцию потерь на основе определенных на предыдущем шаге вероятностных распределений мер схожести для положительных пар и отрицательных пар;
[0076] Предложенная функция потерь является дифференцируемой относительно парных схожестей s∈S+ и s∈S-:
[0077] 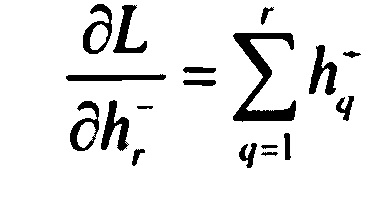 ,
,
[0078] 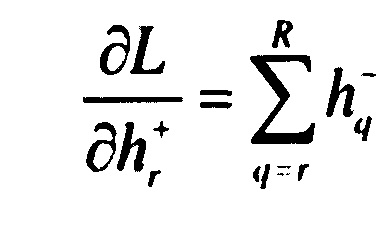 ,
,
[0079]  ,
,
[0080] для любого sij такого, что mij=+1 (аналогично для 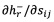 ). Также
). Также
[0081] 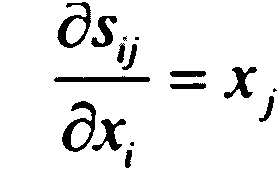
[0082] 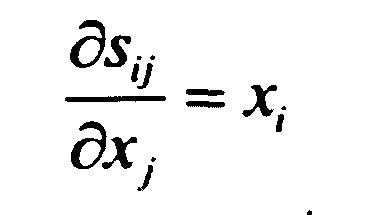
[0083] Шаг 108: минимизируют сформированную на предыдущем шаге функцию потерь на основе гистограмм с помощью метода обратного распространения ошибки [1].
[0084] При прямом проходе случайное подмножество обучающей выборки входных данных X={x1, x2, …, xN} подается на вход глубокой нейронной сети, после чего выполняется ее последовательные преобразования в слоях глубокой нейронной сети, которые определяются ее параметрами. В результате получается набор глубоких представлений входных данных, который подается на вход предложенной функции потерь вместе с метками классов, соответствующих элементам выборки. На основании этих входных данных вычисляется значение функции потерь (ошибка) и выполняется обратное распространение ошибки на выходы глубокой нейронной сети согласно формулам, описанным на шагах 107-108. Далее ошибка распространяется в обратном направлении от выхода ко входу глубокой нейронной сети через ее слои, при этом происходит обновление параметров слоев глубокой нейронной сети для минимизации этой ошибки. После этого происходит аналогичная обработка следующего случайного подмножества обучающей выборки входных данных. Процесс повторяется до тех пор, пока ошибка (значений функции потерь) не перестанет уменьшаться.
ПРИМЕРЫ ОСУЩЕСТВЛЕНИЯ
[0085] Для осуществления данного технического решения были выполнены экспериментальные сравнения предложенной функции потерь данного технического решения на основе гистограммы с функцией потерь биноминального отклонения (Binomial Deviance loss) [2], Softmax функции потерь структурной схожести (Lifted Structured Similarity Softmax loss) [3], контрастную функцию потерь [7] и функцию потерь на основе триплетов [8]. Моделирование выполнялось с помощью библиотеки для глубокого обучения Caffe. Сравнение выполнялось для задач поиска похожих вещей по их изображениям на базе Online products dataset [3], классификации видов птиц по их фотографиям на базе CUB-200-2011 [4], повторного детектирования объектов (ре-идентификации) на базах CHUNK03 [5] и Market-1501 [6]. В экспериментах с базами Online products и CUB-200-2011 использовалась одинаковая архитектура нейронной сети GoogLeNet с использованием признаков пятого слоя пулинга (пулинг - пространственное объединение активаций выходов предыдущего слоя). В экспериментах на базах CHUNK03 и Market-1501 использовалась архитектура глубокого обучения метрики, которая состоит из трех нейронных сетей для нижней, средней и верхней части изображения человека.
[0086] На примере данной реализации рассмотрим подробнее вариант осуществления данного способа. Входные изображения поступают в формате RGB в виде трехмерных матриц I таким образом, что у пикселя с координатами i и j значение R компоненты равно Ii,j,1, значение G компоненты равно Ii,j,2, а значение B - Ii,j,2, т.е. в этой матрице первые два измерения отвечают за геометрические координаты, а 3-е - за цветовую координату. С использованием билинейной интерполяции по геометрическим координатам данная матрица приводится к размеру по высоте 128 пикселей и шириной, равной 48 пикселям. Из полученной матрицы выделяются три подматрицы таким образом, что новые подматрицы имеют одинаковую высоту и ширину, равную 48 пикселям, а вертикальные координаты верхних границ полученных матриц равны соответственно 1, 41 и 81. Каждая из полученных подматриц передается на вход первого слоя глубокой нейронной сети для этой части (для каждой части обучается своя нейронная сеть), причем слой является сверточным и имеет ядро свертки размера 7×7×64, таким образом для каждой подматрицы на выходе получается карта признаков (трехмерная матрица) размера 48×48×64. Далее рассмотрим, что будет происходить в каждой глубокой нейронной сети. Для полученной карты признаков выполняется пространственный пулинг с шагом, равным 2 пикселя, в результате чего получается карта признаков размера 24×24×64. Над полученной картой признаков выполняется нелинейное преобразование, которое обнуляет все отрицательные значения. Полученный результат идет на вход сверточного слоя глубокой нейронной сети с ядром свертки размера 5×5×64 в результате чего получается карта признаков размера 24×24×64 и выполняется пулинг с шагом 2. В результате получается карта признаков размера 12×12×64. Таким образом, мы получили 3 карты признаков из каждой нейронной сети. Эти карты объединяются в один вектор глубокого представления исходного изображения длиной 500 элементов с использованием полносвязного слоя, у которого каждый элемент выходного вектора имеет связи с каждым элементом карты признаков каждой части. Далее выполняется L2-нормализация. Полученные глубокие представления входных изображений вместе с метками классов используются для нахождения мер схожести для всех возможных пар через вычисление косинусной меры схожести между глубокими представлениями, после чего на основании меток классов формируются вероятностные распределения мер схожести положительных и отрицательных пар на основе гистограмм. Полученные распределения используются для вычисления предложенной функции потерь, после чего выполняется обратное распространение производной потерь для коррекции параметров нейронной сети. Процесс обучения глубоких нейронных сетей на всех базах отличался только выбранной функцией потерь. Обучение с биноминальной функцией потерь выполнялось с двумя значениями величины потерь для негативных пар: с=10 и с=25.
[0087] Результаты значений коэффициента полноты ранга K (Recall@K) показаны на Фиг. 2 для базы CUB-200-2011, на Фиг. 3 для базы Online products, на Фиг. 4 для базы CHUNK03, на Фиг.5 для базы Market-1501. Из графика для баз CUB-200-2011 и Online products видно, что предложенная функция потерь незначительно уступает функции потерь на основе биноминального отклонения, однако превосходит остальные функции потерь. Для баз CHUNK03 и Market-1501 предложенная функция потерь позволяет добиться наилучшего результата. На базе CUB-200-211 был также проведен эксперимент по оценки влияния значения параметра интервала гистограммы на итоговую точность, результат которого показан на Фиг. 6. Из этого графика мы видим, что выбор значения параметра размера корзины гистограммы в предложенной функции потерь не оказывает влияния на показатели точности полученной модели. На Фиг. 5 представлены гистограммы распределений значений схожестей положительных пар (белый цвет) и отрицательных пар (серый цвет) на базе CHUNK03 при использовании предложенной функции потерь на основе гистограмм (Поз. 1), биноминального отклонения (Поз. 2) и структурной схожести (Поз. 3). Из этих графиков видно, что предложенная функция потерь обеспечивает наименьшее пересечение между распределениями значений схожестей положительных и отрицательных пар, что явным образом показывает достижение заявленного технического результата.
ИСПОЛЬЗУЕМЫЕ ИСТОЧНИКИ ИНФОРМАЦИИ
1. Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318-362. Cambridge, MA, MIT Press. 1986.
2. Yi, Dong, Zhen Lei, and Stan Z. Li. "Deep metric learning for practical person re-identification." arXiv preprint arXiv: 1407.4979 (2014).
3. H.O. Song, Y. Xiang, S. Jegelka, and S. Savarese. Deep metric learning via lifted structured feature embedding. Computer Vision and Pattern Recognition (CVPR), 2016.
4. C. Wah, S. Branson, P. Welinder, P. Perona, and S. Belongie. The Caltech-UCSD Birds-200-2011 Dataset. (CNS-TR-2011-001), 2011.
5. W. Li, R. Zhao, T. Xiao, and X. Wang. Deepreid: Deep filter pairing neural network for person re-identification. 2014 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2014, Columbus, OH, USA, June 23-28, 2014, pp. 152-159, 2014.
6. L. Zheng, L. Shen, L. Tian, S. Wang, J. Wang, and Q. Tian. Scalable person reidentification: A benchmark. Computer Vision, IEEE International Conference on, 2015.
7. S. Chopra, R. Hadsell, and Y. LeCun. Learning a similarity metric discriminatively, with application to face verification. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), 20-26 June 2005, San Diego, CA, USA, pp. 539-546, 2005.
8. Weinberger, Kilian Q., and Lawrence K. Saul. "Distance metric learning for large margin nearest neighbor classification." Journal of Machine Learning Research 10.Feb (2009): 207-244.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОЛУЧЕНИЯ НИЗКОРАЗМЕРНЫХ ЧИСЛОВЫХ ПРЕДСТАВЛЕНИЙ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СОБЫТИЙ | 2020 |
|
RU2741742C1 |
| ВЫЧИСЛИТЕЛЬНО ЭФФЕКТИВНОЕ МНОГОКЛАССОВОЕ РАСПОЗНАВАНИЕ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА НЕЙРОСЕТЕВЫХ ПРИЗНАКОВ | 2019 |
|
RU2706960C1 |
| РАСПОЗНАВАНИЕ СОБЫТИЙ НА ФОТОГРАФИЯХ С АВТОМАТИЧЕСКИМ ВЫДЕЛЕНИЕМ АЛЬБОМОВ | 2020 |
|
RU2742602C1 |
| Способ диагностики острого коронарного синдрома | 2020 |
|
RU2733077C1 |
| СПОСОБ РАСЧЕТА КРЕДИТНОГО РЕЙТИНГА КЛИЕНТА | 2019 |
|
RU2723448C1 |
| СИСТЕМА И СПОСОБ ДИАГНОСТИКИ ПАТОЛОГИЙ ЛЕГКИХ ПО РЕНТГЕНОВСКИМ ИЗОБРАЖЕНИЯМ | 2023 |
|
RU2840011C1 |
| СИСТЕМА И СПОСОБ ОБНАРУЖЕНИЯ ПАТОЛОГИЙ ЛЕГКИХ ПО РЕНТГЕНОВСКИМ ИЗОБРАЖЕНИЯМ | 2023 |
|
RU2840009C1 |
| АВТОМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ НАБОРА КАТЕГОРИЙ ДЛЯ КЛАССИФИКАЦИИ ДОКУМЕНТА | 2018 |
|
RU2701995C2 |
| Система и способ диагностики синуситов по рентгеновским изображениям | 2023 |
|
RU2828554C1 |
| СПОСОБ И СИСТЕМА РАСПОЗНАВАНИЯ ЭМОЦИОНАЛЬНОГО СОСТОЯНИЯ СОТРУДНИКОВ | 2021 |
|
RU2768545C1 |
Изобретение относится к вычислительным системам, основанным на биологических моделях, а именно к обучению глубоких нейронных сетей на основе распределений попарных мер схожести. Технический результат - повышение точности обучения и уменьшение временных затрат для настройки параметров обучения глубоких представлений входных данных. Способ обучения глубоких нейронных сетей на основе распределений попарных мер схожести заключается в том, что получают размеченную обучающую выборку, где каждый элемент обучающей выборки имеет метку класса, к которому он принадлежит; формируют набор непересекающихся случайных подмножеств обучающей выборки входных данных для глубокой нейронной сети таким образом, что при объединении они представляют собой обучающую выборку; передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети, получая на выходе глубокое представление данного подмножества обучающей выборки; определяют все попарные меры схожести между полученными на предыдущем шаге глубокими представлениями элементов каждого подмножества; определенные на предыдущем шаге меры схожести между элементами, которые имеют одинаковые метки классов, относят к мерам схожести положительных пар, а меры схожести между элементами, которые имеют разные метки классов, относят к мерам схожести отрицательных пар; определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар посредством использования гистограммы; формируют функцию потерь на основе определенных на предыдущем шаге вероятностных распределений мер схожести для положительных пар и отрицательных пар; минимизируют сформированную функцию на предыдущем шаге потерь с помощью метода обратного распространения ошибки. 9 з.п. ф-лы, 7 ил.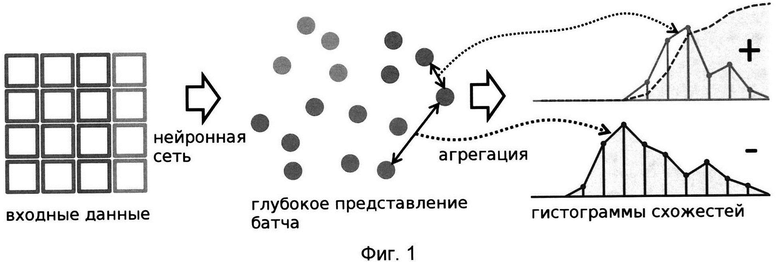
1. Способ обучения глубоких нейронных сетей на основе распределений попарных мер схожести, включающий следующие шаги:
- получают размеченную обучающую выборку, где каждый элемент обучающей выборки имеет метку класса, к которому он принадлежит;
- формируют набор непересекающихся случайных подмножеств обучающей выборки входных данных для глубокой нейронной сети таким образом, что при объединении они представляют собой обучающую выборку;
- передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети, получая на выходе глубокое представление данного подмножества обучающей выборки;
- определяют все попарные меры схожести между полученными на предыдущем шаге глубокими представлениями элементов каждого подмножества;
- определенные на предыдущем шаге меры схожести между элементами, которые имеют одинаковые метки классов, относят к мерам схожести положительных пар, а меры схожести между элементами, которые имеют разные метки классов, относят к мерам схожести отрицательных пар;
- определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар посредством использования гистограммы;
- формируют функцию потерь на основе определенных на предыдущем шаге вероятностных распределений мер схожести для положительных пар и отрицательных пар;
- минимизируют сформированную на предыдущем шаге функцию потерь с помощью метода обратного распространения ошибки.
2. Способ по п. 1, характеризующийся тем, что получают размеченную обучающую выборку из хранилища данных.
3. Способ по п. 1, характеризующийся тем, что метка класса является числовой или символьной.
4. Способ по п. 1, характеризующийся тем, что передают каждое сформированное подмножество обучающей выборки на вход глубокой нейронной сети последовательно или параллельно.
5. Способ по п. 1, характеризующийся тем, что глубоким представлением подмножества является набор векторов вещественных чисел, каждый из которых соответствует элементу подмножества.
6. Способ по п. 1, характеризующийся тем, что перед получением на выходе глубокого представления каждого подмножества обучающей выборки выполняют L2-нормализацию последнего слоя глубокой нейронной сети.
7. Способ по п. 1, характеризующийся тем, что при определении мер схожести между глубокими представлениями элементов каждого подмножества используют косинусную меру схожести.
8. Способ по п. 1, характеризующийся тем, что определяют вероятностное распределение значений мер схожести для положительных пар и вероятностное распределение значений мер схожести для отрицательных пар непараметрическим способом с помощью линейной интерполяции значений интервалов гистограммы.
9. Способ по п. 1, характеризующийся тем, что формируют функцию потерь, которая является дифференцируемой относительно парных схожестей.
10. Способ по п. 1, характеризующийся тем, что минимизируют функцию потерь на основе гистограмм с помощью метода обратного распространения ошибки до тех пор, пока значение функции потерь не перестанет уменьшаться.
| Токарный резец | 1924 |
|
SU2016A1 |
| KILIAN Q | |||
| WEINBERGER, DISTANCE METRIC LEARNING FOR LARGE MARGIN NEAREST NEIGHBOR CLASSIFICATION, JOURNAL OF MACHINE LEARNING RESEARCH 10 (2009) | |||
| Токарный резец | 1924 |
|
SU2016A1 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| СПОСОБ ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ | 2014 |
|
RU2566979C1 |
Авторы
Даты
2018-01-17—Публикация
2016-12-27—Подача