Область техники, к которой относится изобретение
Варианты осуществления, описанные здесь, относятся к способам и устройствам для вычисления решений вычислительных задач с использованием квантовой системы и, более конкретно, квантовой системы, включающей в себя множество квантовых бит (кубитов).
Уровень техники
Вычислительные устройства, основанные на классическом способе обработки информации, то есть, вычислительные устройства, не использующие квантово-механические эффекты, когда-то представляли собой калькуляторы с жесткой логикой, которые могли выполнять только конкретные операции. Переход на полностью программируемые компьютеры являлся поворотным моментом в развитии технологии, и положили начало информационной эпохе. В настоящее время квантовые вычислительные устройства, т.е. вычислительные устройства, которые, возможно, в дополнение к использованию классического способа обработки информации, используют квантово-механические эффекты для решения вычислительных задач, в каком-то смысле, находятся на этапах калькуляторов с жесткой логикой, поскольку они могут решать только вычислительные задачи, для которых они специально разработаны, т.е. «жесткие». В частности, все существующие квантовые вычислительные устройства, на всех платформах и дисциплинах, все еще не могут быть полностью программируемыми и масштабируемыми.
Например, квантовое вычислительное устройство, произведенное D-WAVE SYSTEMS Inc., основанное на сверхпроводящих кубитах, образует две группы кубитов, в котором произвольные взаимодействия могут иметь место между кубитами в разных группах, но не происходит взаимодействия между кубитами в той же группе. Могут быть добавлены дополнительные группы кубитов, но с теми же ограничениями. Поэтому это квантовое вычислительное устройство ограничено его жесткими ограничениями, которые не позволяют реализовать необходимые взаимодействия, как полностью программируемую, так и масштабируемую архитектуру.
Следовательно, существует потребность в усовершенствованных способах и устройствах для решения вычислительных задач с использованием квантовой системы.
Раскрытие сущности изобретения
Согласно варианту осуществления предлагается способ вычисления решения вычислительной задачи с использованием квантовой системы, включающей в себя множество кубитов. Этот способ включает в себя кодирование вычислительной задачи в гамильтониан задачи квантовой системы, в котором гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров, и в котором кодирование включает в себя определение из вычислительной задачи конфигурации кодирования с задачей для множества регулируемых параметров. Способ дополнительно включает в себя совершенствование квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана квантовой системы, в котором конечный гамильтониан представляет собой сумму гамильтониана задачи и гамильтониана ближнего порядка, в котором множество регулируемых параметров гамильтониана задачи находятся в конфигурации кодирования задачи, и в котором гамильтониан ближнего порядка является гамильтонианом d-тела, в котором d не зависит от вычислительной задачи. Способ дополнительно включает в себя измерение, по меньшей мере, участка множества кубитов для получения данных считывания квантовой системы. Способ дополнительно включает в себя определение решения вычислительной задачи из данных считывания.
Согласно еще одному варианту осуществления предлагается способ вычисления решения вычислительной задачи с использованием квантовой системы, содержащей множество кубитов. Этот способ включает в себя кодирование вычислительной задачи в гамильтониан задачи квантовой системы, в котором гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров, и в котором, кодирование включает в себя определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров. Этот способ дополнительно включает в себя инициализацию квантовой системы в начальном квантовом состоянии. Способ дополнительно включает в себя совершенствование квантовой системы из начального квантового состояния в конечное квантовое состояние путем выполнения квантового отжига, в котором выполнение квантового отжига включает в себя переход от начального гамильтониана квантовой системы к конечному гамильтониану квантовой системы. В этом случае, конечным гамильтонианом является сумма гамильтониана задачи и гамильтониана ближнего порядка, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи и, в котором ближний гамильтониан является гамильтонианом d-тела, в котором d не зависит от вычислительной задачи. Способ дополнительно включает в себя измерение, по меньшей мере, участка множества кубитов для получения данных считывания конечного квантового состояния. Способ дополнительно включает в себя определение решения вычислительной задачи из считывания.
Согласно еще одному варианту осуществления предлагается устройство для вычисления решений вычислительных задач. Устройство включает в себя квантовую систему, содержащую множество кубитов. Устройство дополнительно включает в себя блок охлаждения, выполненный с возможностью охлаждать квантовую систему в основное состояние квантовой системы. Устройство дополнительно включает в себя программируемый блок квантового отжига, выполненный с возможностью совершенствовать путем квантового отжига начальный гамильтониан квантовой системы в конечный гамильтониан квантовой системы, в котором конечный гамильтониан представляет собой сумму гамильтониана задачи и гамильтониана ближнего порядка, в котором гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров. Устройство дополнительно включает в себя измерительное устройство, выполненное с возможностью измерять, по меньшей мере, участок множества кубитов. Устройство дополнительно включает в себя классическую вычислительную систему, подключенную к программируемому блоку квантового отжига и измерительному устройству. Классическая вычислительная система выполнена с возможностью: принимать в качестве входных данных вычислительную задачу; кодировать вычислительную задачу в гамильтониан задачи, в котором кодирование содержит определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи; и выполнять коммуникацию конфигурации кодирования задачи в блок квантового отжига. Программируемый блок квантового отжига выполнен с возможностью: принимать конфигурацию кодирования задачи из классической вычислительной системы; и путем квантового отжига совершенствовать начальный гамильтониан в конечный гамильтониан, в котором множество регулируемых параметров гамильтониана задачи находятся в конфигурации кодирования задачи. Классическая вычислительная система дополнительно выполнена с возможностью: принимать данные считывания квантовой системы из измерительного устройства; и определять решение вычислительной задачи из данных считывания.
В соответствии с дополнительным вариантом осуществления предлагается программируемое устройство квантового отжига для вычисления решений вычислительных задач. Программируемое устройство квантового отжига включает в себя квантовую систему, включающую в себя множество сверхпроводящих кубитов, расположенных в соответствии с двумерной решеткой. Программируемое устройство квантового отжига дополнительно включает в себя узел смещения магнитного потока, включающий в себя множество блоков смещения магнитного потока, выполненных с возможностью генерировать множество регулируемых магнитных потоков. В этом случае каждый регулируемый магнитный поток воздействует на один сверхпроводящий кубит во множестве сверхпроводящих кубитов. Программируемое устройство квантового отжига дополнительно включает в себя блок соединения, включающий в себя, по меньшей мере, один сверхпроводящий квантовый интерференционный датчик, выполненный с возможностью соединять множество сверхпроводящих кубитов в соответствии с гамильтонианом плакетки. Программируемое устройство квантового отжига дополнительно включает в себя контроллер, подключенный к блоку смещения магнитного потока и к блоку соединения. Контроллер выполнен с возможностью принимать конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи квантовой системы, в котором гамильтониан задачи является гамильтонианом одного тела, и конфигурация кодирования задачи кодирует вычислительную задачу. Контроллер дополнительно выполнен с возможностью управлять блоком смещения магнитного потока и блока соединения для совершенствования начального гамильтониана квантовой системы в конечный гамильтониан квантовой системы путем квантового отжига. Конечным гамильтонианом является сумма гамильтониана плакетки и гамильтониана задачи, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи.
Варианты осуществления также относятся к способам работы раскрытых систем и устройств и к способам использования раскрытой системы для выполнения способов в соответствии с описанными здесь вариантами осуществления.
Дополнительные преимущества, признаки, аспекты и детали, которые могут быть объединены с вариантами осуществления, описанными здесь, очевидны из зависимых пунктов формулы изобретения, описания и чертежей.
Краткое описание чертежей
Полное и достаточное для воспроизведения раскрытие для специалиста в данной области техники более конкретно изложено в остальной части описания, включающей в себя ссылку на сопроводительные чертежи, на которых:
фиг. 1 показывает устройство для вычисления решений вычислительных задач с использованием квантовой системы в соответствии с описанными здесь вариантами осуществления;
фиг. 2-4 показывают примеры компоновки множества кубитов в соответствии с описанными здесь вариантами осуществления;
фиг. 5 иллюстрирует понятие гамильтониана одного тела в соответствии с описанными здесь вариантами осуществления;
фиг. 6-7 иллюстрируют понятие гамильтониана ближнего порядка в соответствии с вариантами осуществления, описанными здесь;
фиг. 8 показывает способ вычисления решения вычислительной задачи с использованием квантовой системы, содержащей множество кубитов;
фиг. 9-16 иллюстрируют конкретные кодировки вычислительной задачи в гамильтониан задачи и соответствующий конечный гамильтониан в соответствии с описанными здесь вариантами осуществления;
фиг. 17 показывает преимущества описанных здесь вариантов осуществления, относящихся к устойчивости квантовой системы к ошибкам.
Осуществление изобретения
Далее будут подробно описаны различные примерные варианты осуществления, один или несколько примеров которых, проиллюстрированы на каждом чертеже. Каждый пример представлен путем объяснения и не предназначен для ограничения. Например, признаки, проиллюстрированные или описанные как часть одного варианта осуществления, могут использоваться или в сочетании с другими вариантами осуществления для получения еще дополнительных вариантов осуществления. Предполагается, что настоящее изобретение включает в себя такие модификации и изменения.
В нижеследующем описании чертежей одни и те же ссылочные позиции относятся к одним и тем же компонентам. Как правило, описываются только различия в отношении отдельных вариантов осуществления. Структуры, показанные на чертежах, не обязательно изображены в соответствии с масштабом и могут содержать детали, выполненные в преувеличенном виде, чтобы обеспечить лучшее понимание вариантов осуществления.
Варианты осуществления, описанные здесь, относятся к квантовой системе, включающей в себя множество кубитов. Кубит, как описано здесь, может относиться к квантово-механической двухуровневой системе. Кубит может включать в себя два квантовых базисных состояния |0> и |1>, представляющих возможные квантовые состояния кубита. В соответствии с принципом суперпозиции квантовой механики любая суперпозиция вида a|0> + b|1> является возможным квантовым состоянием кубита. В этом случае a и b являются комплексными числами. Математически кубит может быть представлен двумерным векторным пространством. Множество кубитов может иметь квантовые базисные состояния, соответствующие конфигурациям, в которых каждый кубит множества кубитов находится, либо в квантовом состоянии |0>, либо в квантовом состоянии |1>. Учитывая, например, множество из пяти кубитов, примерное квантовое базисное состояние для 5-кубитов, может быть |00101>. В этом случае, квантовое состояние |00101> представляет собой конфигурацию, в которой первый, второй и четвертый кубиты находятся в квантовом состоянии |0> и третий и пятый кубиты находятся в квантовом состоянии |1>. Для множества m кубитов имеется 2m квантовых базисных состояний. Учитывая принцип суперпозиции, заданы два квантовых состояния для множества кубитов, суперпозиция квантовых базисных состояний также является квантовым состоянием для множества кубитов. Например, суперпозиция вида a | 00101> + b | 11110> + c | 11111> с комплексными числами a, b и c является квантовым состоянием для множества кубитов. Математически квантовая система, состоящая из множества m кубитов, может быть представлена 2m -мерным векторным пространством.
Множество кубитов может включать в себя или состоять из множества сверхпроводящих кубитов, например, трансмон или потоковые кубиты. Сверхпроводящий кубит может включать в себя первичную и вторичную сверхпроводящую петлю. Сверхпроводящие токи, распространяющиеся по часовой стрелке и против часовой стрелки, соответственно, в первичной сверхпроводящей петле, могут образовывать квантовые базисные состояния | 1> и | 0> сверхпроводящего кубита. Кроме того, смещение магнитного потока через вторичную сверхпроводящую петлю может связывать квантовые базисные состояния | 0> и | 1>.
Альтернативно, квантовая система может быть реализована с использованием системы захваченных ионов. В этом случае квантовые базисные состояния | 0> и | 1> кубита формируются двумя уровнями зеемановского или сверхтонкого многообразия или через запрещенный оптический переход щелочноземельных или щелочноземельных положительно заряженных ионов, таких как Ca40 +.
Еще одна дополнительная альтернатива, квантовая система может быть реализована с использованием ультрахолодных атомов, например, ультрахолодные нейтральные атомы щелочей, которые захватываются в оптической решетке или в решётках с большим шагом, из лазерных полей. Атомы могут быть переведены в основное состояние с использованием лазерного охлаждения. Квантовые базисные состояния кубита образованы основным состоянием атома и высоким ридберговским состоянием. Кубиты могут быть адресованы лазерным излучением.
Еще одна альтернатива, квантовая система может быть реализована посредством квантовых точек. Кубиты на базе квантовых точек могут быть изготовлены из GaAs / AlGaAs гетероструктур. Кубиты кодируются в спиновых состояниях, которые могут быть получены путем адиабатической настройкой потенциала из одной ямы в потенциал двойной ямы.
Еще одна альтернатива, квантовая система может быть реализована с примесями в кристаллах твердого тела, таких как NV центры, которые являются точечными дефектами в кристаллах алмаза. Изучаются другие примеси, например, центры окраски, связанные с примесями хрома, редкоземельные ионы в кристаллах твердого тела или дефектные центры в карбиде кремния. NV центры имеют два неспаренных электрона, которые обеспечивают основное состояние спина-1, которое позволяет идентифицировать два резких уровня дефекта с большим временем жизни, которые могут быть использованы для реализации кубита, возможно, в сочетании с окружающими ядерными спинами.
Согласно вариантам осуществления квантовая система может включать в себя одну или несколько или множество отдельных квантовых систем q-уровня, где q может быть константой. Например, q может находиться в диапазоне от 2 до 8, например, 3, 4, 5 или 6. Отдельная квантовая система q-уровня может включать в себя основу, состоящую из q состояний | 0>, | 1>, .. . | q-1>. Отдельная трехуровневая квантовая система будет называться «кутрит».
Гамильтониан квантовой системы может представлять собой взаимодействие или множество взаимодействий для квантовой системы. Гамильтониан является оператором, действующим на квантовую систему. Собственные значения гамильтониана соответствуют энергетическому спектру квантовой системы. Основным состоянием гамильтониана является квантовое состояние квантовой системы с минимальной энергией. Основным состоянием гамильтониана может быть квантовое состояние при нулевой температуре.
Классическая вычислительная система, как описано здесь, может относиться к вычислительной системе, работающей с классическими битами. Классическая вычислительная система может включать в себя центральный процессор (CPU) для обработки информации с классическими битами и/или память для хранения информации с классическими битами. Классическая вычислительная система может включать в себя один или несколько обычных компьютеров и/или сеть обычных компьютеров, таких как персональные компьютеры (PCs).
Прежде чем предоставить подробное описание вариантов осуществления, некоторые аспекты настоящего раскрытия будут теперь пояснены со ссылкой на фиг. 1, которая иллюстрирует примерное устройство 400 для вычисления решений вычислительных задач, в соответствии с вариантами осуществления, описанными здесь.
Устройство 400, показанное на фиг. 1, выполнено с возможностью вычислять решения вычислительных задач с использованием квантовой системы 420. Квантовая система 420 включает в себя множество кубитов 100, каждый из которых представлен на фиг. 1 черной точкой. Согласно варианту осуществления, показанному на фиг. 1, множество кубитов 100 расположены в соответствии с двумерной решеткой 120, в частности, с двумерной квадратной решеткой.
На фиг. 1 дополнительно показан блок 410 охлаждения, выполненный с возможностью охлаждать квантовую систему 420. Блок 410 охлаждения может охлаждать квантовую систему 420 до рабочей температуры.
На фиг. 1 дополнительно показана классическая вычислительная система 450. Классическая вычислительная система 450 выполнена с возможностью принимать в качестве входа вычислительную задачу 452, которая должна быть решена. Вычислительная задача 452 может, например, быть NP-сложной задачей, такой как, например, задача коммивояжера или задача минимизации изинговского спина. В этом случае «NP» означает «недетерминированное полиномиальное время».
Классическая вычислительная система 450 дополнительно выполнена с возможностью кодировать вычислительную задачу 452 в гамильтониан 472 задачи квантовой системы 420. Согласно примерному варианту осуществления, проиллюстрированному на фиг. 1, гамильтониан 472 задачи имеет вид Hprob = Σk Jk σz(k), где σz(k) является оператором Паули, действующим на k-м кубите множества кубитов 100, в котором каждый Jk является регулируемым параметром, определяемым одним или множеством внешних объектов, например, магнитными полями, которые можно регулировать в каждом кубите k индивидуально. Например, Jk может быть величиной силы регулируемого магнитного поля, влияющего на k-й кубит. Множество регулируемых внешних объектов, например, могут быть предусмотрены магнитные поля, в котором каждый регулируемый внешний объект воздействует на один кубит множества кубитов. Регулируя внешние объекты, можно отрегулировать параметры Jk в зависимости от вычислительной задачи 452.
Кодирование вычислительной задачи 452 в гамильтониане 472 задачи, выполненное классической вычислительной системой 450, включает в себя определение из вычислительной задачи 452 конфигурации кодирования задачи для множества регулируемых параметров Jk. Для каждого из регулируемых параметров Jk значение параметра может быть определено в зависимости от вычислительной задачи 452. Соответственно, конфигурация кодирования задачи зависит от вычислительной задачи.
На фиг. 1 дополнительно показан программируемый блок 430 квантового отжига, выполненный с возможностью выполнять квантовый отжиг, путем перехода от начального гамильтониана квантовой системы 420 к конечному гамильтониану квантовой системы 420.
Согласно варианту осуществления, описанному со ссылкой на фиг. 1, начальный гамильтониан имеет вид Hinit = Σk ak σx(k), где ak - коэффициент и в котором σx(k) является оператором Паули, действующим на k-го кубита во множестве кубитов 100. Операторы σz(k) и σx(k) Паули могут быть некоммутирующими, в частности, антикоммутирующими, операторами Паули. Начальный гамильтониан Hinit может быть не зависящим от вычислительной задачи 452.
Конечным гамильтонианом является суммой гамильтониана 472 задачи и гамильтониана 474 ближнего порядка. Согласно иллюстративному варианту осуществления, гамильтониан 474 ближнего порядка является гамильтонианом плакетки, представляющим взаимодействия между группами кубитов, соответствующих плакеток. Плакетки, например, являются элементарными квадратами двумерной квадратной решетки, согласно которой расположены кубиты. На фиг. 7, где показано более подробно, проиллюстрирован пример плакетки 370 двумерной решетки в соответствии с вариантами осуществления, описанными здесь. Гамильтониан ближнего порядка является гамильтонианом d-тела, например, гамильтониан плакетки 4-го тела, где d не зависит от вычислительной задачи 452. Согласно вариантам осуществления гамильтониан 474 ближнего порядка может быть независимым от вычислительной задачи 452.
Как упоминалось выше, вычислительная задача 452 кодируется в гамильтониане 472 задачи, в частности, в конфигурации кодирования задачи регулируемых параметров Jk. Согласно вариантам осуществления кодирование таково, что конечный гамильтониан 470, являющийся суммой гамильтониана 472 задачи и гамильтониана 474 ближнего порядка, имеет основное состояние, содержащее информацию о решении вычислительной задачи 452. Соответственно, если квантовая система 420 находится в основном состоянии конечного гамильтониана 470, то информация о вычислительной задаче может быть обнаружена путем измерения квантовой системы 420.
В соответствии с вариантами осуществления, описанными здесь, и как показано стрелкой 499 на фиг. 1, квантовая система 420 совершенствуется в направлении основного состояния конечного гамильтониана 470, в котором множество регулируемых параметров гамильтониана 472 задачи находится в конфигурации кодирования задачи. Согласно варианту осуществления, показанному на фиг. 1, квантовая система 420 развивается в основное состояние конечного гамильтониана 470 посредством блока 430 квантового отжига, осуществляющий квантовый отжиг. В этом случае, квантовый отжиг включает в себя переход от начального гамильтониана к конечному гамильтониану 470.
В соответствии с примерным вариантом осуществления квантовая система 420 инициализируется в начальном квантовом состоянии путем охлаждения квантовой системы 420 в основное состояние начального гамильтониана. Кроме того, программируемый блок 430 квантового отжига выполнен с возможностью совершенствовать квантовую систему 420 от начального квантового состояния в начальное время до конечного квантового состояния в конечное время. Квантовый отжиг может включать в себя переход от начального гамильтониана в начальное время к конечному гамильтониану 470 в конечное время для эволюции квантовой системы 420 от начального квантового состояния до конечного квантового состояния. Квантовый отжиг может быть выполнен, в то время как квантовая система 420 поддерживается, по существу, при рабочей температуре блоком 410 охлаждения.
Квантовый отжиг может включать в себя постепенно, например, адиабатически, переход от начального гамильтониана Hinit к конечному гамильтониану Hfinal = Hprob + HSR, где HSR - гамильтониан ближнего порядка, через интерполяционный гамильтониан H(t). В соответствии с примерным вариантом осуществления, проиллюстрированным на фиг. 1, интерполяционный гамильтониан имеет вид H (t) = A (t) Hinit + B (t) Hprob + C (t) HSR. В этом случае Hinit может относится к начальному гамильтониану, Hfinal может относится к конечному гамильтониану, t может быть временным параметром, и A (t), B (t) и C (t) могут быть интерполяционными коэффициентами в зависимости от временного параметра t. Для t, являющегося начальным временем t0, коэффициент A (t0) интерполяции может быть равен начальному значению 1, и коэффициент B (t0) интерполяции может быть равен начальному значению 0. В качестве альтернативы, t является начальным временем t0, коэффициент A (t0) интерполяции может быть намного больше коэффициента B (t0) интерполяции. Когда t является конечным временем tfin коэффициенты A (tfin) интерполяции могут быть равны конечному значению 0, и B (tfin) и C (tfin) могут быть равны конечному значению 1, соответственно, так что интерполяционный гамильтониан H (tfin) равен Hfinal. Альтернативно, когда t является конечным временем tfin, коэффициент A (tfin) интерполяции может быть намного меньше, чем коэффициенты B (tfin) и C (tfin) интерполяции. Выполнение квантового отжига может включать в себя постепенное, например, адиабатическое, изменение коэффициентов A (t), B (t) и C (t) интерполяции от их начальных значений в начальное время до их конечных значений в конечное время. Соответственно, интерполяционный гамильтониан постепенно меняется от начального гамильтониана в начальный момент времени до конечного гамильтониана в конечное время. В частности, процедура квантового отжига, как описано здесь, может выполняться так, что всегда C (t) = B (t).
С учетом, например, адиабатической теоремы квантовой механики, но, не желая обсуждать какую-либо конкретную теорию, квантовое состояние квантовой системы 420 будет основным состоянием или, по меньшей мере, хорошо аппроксимированным основным состоянием интерполяционного гамильтониана H(t) для всех значений временного параметра t от начального времени до конечного времени, если переход от начального гамильтониана к конечному гамильтониану 470 выполняется достаточно медленно. Соответственно, квантовый отжиг в исходное время совершенствует начальное квантовое состояние в конечное квантовое состояние, в котором конечное квантовое состояние является основным состоянием конечного гамильтониана или, по меньшей мере, хорошо аппроксимируется основным состоянием конечного гамильтониана 470.
На фиг. 1 дополнительно показано измерительное устройство 440, выполненное с возможностью измерять квантовую систему 420. Как показано, измерительное устройство 440 может быть выполнено с возможностью измерять участок 425 кубитов из множества кубитов 100. Использование измерительного устройства 440, участок 425 может быть измерен для получения данных считывания конечного квантового состояния. Конечное квантовое состояние, хорошо аппроксимируемое основным состоянием конечного гамильтониана, содержит информацию о решении вычислительной задачи 452. Чтение конечного квантового состояния может выявить информацию о решении. Согласно варианту осуществления, показанному на фиг. 1, данные считывания могут быть предоставлены из измерительного устройства 440 в классическую вычислительную систему 450, как показано на фиг. 1 стрелкой 445. Классическая вычислительная система 450 может определять решение 490 вычислительной задачи из данных считывания. Классическая вычислительная система 450 может, по меньшей мере, определять пробное решение вычислительной задачи и проверять, действительно ли пробное решение является решением вычислительной задачи. Для NP задач верификация представляет собой вычисление, которое может быть выполнено в полиномиальное время и обычно может быть легко вычислено. Если окажется, что решение вычислительной задачи не найдено, то процесс повторяется до тех пор, пока не будет найдено решение вычислительной задачи.
В свете вышеизложенного, в соответствии с вариантом осуществления, предлагается способ вычисления решения вычислительной задачи с использованием квантовой системы, включающей в себя множество кубитов. Способ включает в себя кодирование вычислительной задачи в гамильтониан задачи квантовой системы, как показано на фиг. 8, блоком 510. Гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров, и кодирование включает в себя определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров. Этот способ дополнительно включает в себя совершенствование квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана квантовой системы, как показано на фиг. 8 с помощью блока 520. Конечным гамильтонианом является сумма гамильтониана задачи и гамильтониана ближнего порядка, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи. В некоторых вариантах осуществления ближний гамильтониан является гамильтонианом d-тела с d, не зависящим от вычислительной задачи. Способ дополнительно включает в себя измерение, по меньшей мере, участка множества кубитов для получения данных считывания квантовой системы, как показано на фиг. 8 посредством блока 530. Способ дополнительно включает в себя определение решения вычислительной задачи из данных считывания, как показано на фиг. 8 блоком 540.
Варианты осуществления, описанные здесь, позволяют, таким образом, определять решение вычислительной задачи, например, NP-сложная задача, использующая квантовую систему. По сравнению с определением решения вычислительной задачи, использующей исключительно классическую вычислительную систему, то есть, без квантовой системы, описанные здесь варианты осуществления могут обеспечить уменьшение вычислительного времени, необходимого для решения вычислительной задачи. Другими словами, по сравнению с классическими вычислительными системами варианты осуществления, описанные здесь, могут позволить быстрее решать вычислительные задачи или даже позволить найти такое решение вообще, поскольку вычисление решения может занять слишком много времени для вычисления классической вычислительной системы.
Еще одно преимущество относится к аспекту, согласно которому гамильтониан задачи является гамильтонианом одного тела. В то время, как другие типы гамильтонианов задачи, в частности, гамильтонианы задачи, включающие в себя взаимодействия между большими группами кубитов или взаимодействия между удаленными друг от друга кубитами (дальние взаимодействия), могут быть неосуществимыми или, по меньшей мере, требуют очень сложной установки квантовой системы и компонентов, участвующих в квантовом вычислении, гамильтониан задачи одного тела, как описано здесь, может быть реализован с использованием гораздо более простой настройки, т.е. гораздо более простого устройства квантовой обработки. Кроме того, гамильтониан задачи вариантов осуществления, описанных здесь с его регулируемыми параметрами, обеспечивает полностью программируемую систему, с которой может быть закодирован широкий спектр вычислительных задач. Таким образом, устройства и способы в соответствии с описанными здесь вариантами осуществления позволяют вычислить решение широкого спектра вычислительных задач, таких как жесткая логика. По сравнению с системами, где может быть закодировано только ограниченное число задач, поскольку определенные взаимодействия, требуемые гамильтонианом задачи, являются жесткими в системе, тем самым, обеспечивается повышенная гибкость и гораздо более мощное устройство и способ.
Еще одно преимущество относится к аспекту, согласно которому конечным гамильтонианом является сумма гамильтониана задачи и гамильтониана ближнего порядка. Гамильтониан ближнего порядка может быть суммой слагаемых гамильтонианов, где слагаемые гамильтонианов могут быть гамильтонианами ограничения, как описано здесь. Наличие гамильтониана ближнего порядка дает преимущество в том, что никакие взаимодействия между отдаленными кубитами не нуждаются в разработке. Это снова контрастирует с гамильтонианами, требующими дальних взаимодействий, которые могут быть неосуществимы для реализации на квантовой системе или могут потребовать, по меньшей мере, очень сложную настройку устройства квантовой обработки.
Когда параметр d гамильтониана ближнего порядка d-тела не зависит от вычислительной задачи, это означает, что вычисление может быть реализовано с помощью одного и того же устройства квантовой обработки, независимо от которого кодируется вычислительная задача. Если гамильтониан ближнего порядка не зависит от вычислительной задачи, то дополнительное преимущество заключается в том, что взаимодействия между кубитами, определяемыми гамильтонианом ближнего порядка, не нужно менять для разных вычислительных задач.
Варианты осуществления, описанные здесь, обеспечивают масштабируемую архитектуру для решения вычислительных задач. Для данной квантовой системы можно вычислить решения широкого круга вычислительных задач определенного максимального размера, в котором максимальный размер определяется числом кубитов квантовой системы. Для вычисления решений вычислительных задач, выходящих за этот максимальный размер, может быть обеспечена более большая квантовая система, т.е. Квантовая система, содержащая большее количество кубитов, с соответствующим гамильтонианом задачи, гамильтонианом ближнего порядка и конечным гамильтонианом, в соответствии с описанными здесь вариантами осуществления, обрабатывает вычислительные задачи большего размера. Выбирая квантовую систему, имеющую достаточно большое количество кубитов, можно вычислить решения для вычислительных задач любого желаемого размера. Независимо от количества кубитов квантовой системы, гамильтониан задачи является гамильтонианом одного тела, и конечный гамильтониан представляет собой сумму гамильтониана задачи и гамильтониана ближнего порядка, в соответствии с описанными здесь вариантами осуществления. Соответственно, предоставляется масштабируемая архитектура для решения вычислительных задач.
Согласно некоторым вариантам осуществления вычислительная задача может быть задачей принятия решения. Задача принятия решения может относиться к вычислительной задаче, сформулированной как вопрос «да/нет». Решение задачи принятия решения может быть либо «да», либо «нет». Альтернативно, решение задачи принятия решения может быть одним классическим битом, то есть, 0 или 1. В соответствии с другими вариантами осуществления вычислительная задача может быть сформулирована иначе, чем задача принятия решения.
Вычислительная задача может быть любой из множества вычислительных задач, рассмотренных, например, в областях информатики, физики, химии или инженерии. В целях объяснения, но не намереваясь ограничить область охвата, ниже приведено описание трех примеров вычислительных задач. Три примера, рассмотренные ниже, являются примерами задачи принятия решения.
Первым примером вычислительной задачи, в соответствии с вариантами осуществления, описанными здесь, является задачей коммивояжеров. Задача коммивояжера включает в себя первый список городов и второй список расстояний между каждой парой городов в первом списке. Задача коммивояжера задает следующий вопрос: «Учитывая первый список, второй список и константу K, существует ли поездка длиной не более K, в которой при поездке (i) посещает каждый город в первом списке только один раз, и (ii) возвращается в город, в котором начинается поездка?»
Второй пример вычислительной задачи, в соответствии с вариантами осуществления, описанных здесь, является «задачей 3-красочности», относящейся к окраске математических графиков. Математический граф может включать в себя набор вершин и набор ребер, представляющих связи между парами вершин. 3-окраска математического графа представляет собой назначение каждой вершины математического графа одному из трех возможных цветов (например, «красный», «зеленый» или «синий»), где назначается любая пара вершин, связанных ребром к разным цветам. Для некоторых математических графов 3-окраска может отсутствовать. Задача 3-красочности задает вопрос: «Учитывая математический граф, присутствует ли 3-окраска?»
Третий пример вычислительной задачи в соответствии с вариантами осуществления, описанные здесь, относится к модели Изинга спина. Модель Изинг спина представляет собой физическую модель, представляющую взаимодействия между множеством спинов s1, s2, ..., sn, в котором каждый спин si представляет собой переменную, которая может иметь либо значение 1, либо значение -1, причем i варьируется от 1 к n. Для множества спинов можно рассмотреть функцию H (s1, s2, ..., sn) энергии в модели Изинга, в котором функция энергии в модели Изинга имеет вид
H(s1, s2, ..., sn) = Σij cijsisj + Σi cisi
Где каждый cij представляет собой коэффициент соединения, и каждый ci является полевым коэффициентом. Энергетическая функция Изинга включает в себя парные взаимодействия, где парное взаимодействие между спинами si и sj представлено термином cijsisj в энергетической функции Изинга. Абсолютное значение коэффициента cij соединения отражает силу попарного взаимодействия между спинами si и sj. Знак коэффициента cij соединения отражает характер попарного взаимодействия, например, ферромагнитные или антиферромагнитные взаимодействия. Модель спина Изинга может быть моделью Изинга дальнего порядка. Модель спина Изинга дальнего порядка может включать в себя взаимодействие между парами спинов, которые далеки друг от друга в соответствии с величиной расстояния. Модель спина Изинга дальнего порядка может включать в себя взаимодействия между парами спинов, которые удалены друг от друга на расстояние, составляющее, по меньшей мере, логарифм максимального расстояния между двумя спинами. Некоторые модели Изинга дальнего порядка, например, все-все модели спина Изинга, могут включать в себя взаимодействия между всеми парами спинов. Например, модель спина Изинга, где каждый из коэффициентов cij соединения отличен от нуля, может рассматриваться как модель спина Изинга дальнего порядка.
Энергетическая функция Изинга дополнительно включает в себя термины cisi, представляющие взаимодействие между спином si и внешним полем, влияющим на спин si, но не влияющим на другие спины. Сила и направление поля, влияющего на спин si, представлены абсолютной величиной и знаком коэффициента поля ci соответственно. Вычислительная задача, ассоциированная с моделью Изинга-спина, называемая здесь задачей модели Изинга, может быть сформулирована следующим образом: «Учитывая набор коэффициентов cij соединения, набор полевых коэффициентов ci и константу K, существует ли конфигурация (s1, s2, ..., sN) спинов так, что H (s1, s2, ..., sn) меньше, чем K?».
В соответствии с вариантами осуществления, описанными здесь, вычислительная задача может включать в себя множество входных переменных. Множество входных переменных может представлять информацию о решаемой вычислительной задаче. Например, ссылаясь на три описанные выше примера вычислительных задач, множество входных переменных может включать в себя: первый список городов и второй список расстояний (для задачи коммивояжера); наборы вершин и ребер графа (для задачи 3-красочности); наборов коэффициентов cij соединений и полевых коэффициентов ci (для задачи модели Изинга-спина).
В соответствии с вариантами осуществления, вычисление решения вычислительной задачи может включать в себя вычисление пробного решения для вычислительной задачи. Пробное решение может быть или не быть истинным решением вычислительной задачи. Для вариантов осуществления, согласно которым вычислительная задача относится к классу сложности NP, вычисление решения вычислительной задачи может включать в себя вычисление набора переменных свидетеля, как описано ниже.
В соответствии с вариантами осуществления, описанными здесь, решение вычислительной задачи вычисляется с использованием квантовой системы, содержащей множество кубитов. Множество кубитов может содержать, по меньшей мере, 8 кубитов, в частности, по меньшей мере, 3 кубита. Дополнительно или альтернативно, множество кубитов может включать в себя N кубитов, в котором N составляет от 100 до 10 000 кубитов, предпочтительно даже больше. Следует понимать, что множество кубитов 100, показанных на фигурах, описанных здесь, показано для иллюстративных и пояснительных целей, и фактическое количество кубитов может отличаться.
Кубиты квантовой системы могут быть расположены на двумерной поверхности или на трехмерной поверхности, которая может быть плоской или может включать в себя кривизну. Фиг. 2-4 показывают различные пространственные расположения множества кубитов 100, в соответствии с вариантами осуществления, описанными здесь. Эти пространственные расположения могут быть компоновками квантовых вычислительных устройств, например, квантовых микросхем, на которых могут быть реализованы кубиты и/или другие отдельные квантовые системы (q-уровневые системы, такие как кутриты). Как показано на фиг. 2, множество кубитов 100 может быть расположено в соответствии с двумерной плоской поверхностью 110, как показано на фиг. 2 пунктирными линиями. Следует понимать, что двумерная поверхность 110, показанная на фиг. 2, предназначена для визуального представления двухмерного пространственного расположения множества кубитов, но двумерная поверхность 110 не обязательно должна быть физической, осязаемой поверхностью, на которой расположено множество кубитов 100. Аналогичные соображения применимы к вариантам осуществления, согласно которым множество кубитов расположено в соответствии с 2-мерной решеткой или 3-мерной решеткой, как описано ниже.
В соответствии с дополнительными вариантами осуществления и, как показано на фиг. 3, множество кубитов 100 могут быть расположено в соответствии с двумерной решеткой 120, как показано пунктирными линиями. Решетку, такую как, например, 2-мерная решетка или трехмерная решетка, может включать в себя множество узлов, пространственно расположенных в соответствии с регулярной сеткой. На фиг. 3 множество кубитов 100, представленных множеством черных точек, соответствуют узлам двумерной решетки 120. Как показано, каждый кубит множества кубитов 100 может быть расположен в узле 2-мерной решетки 120. В иллюстративном варианте осуществления, показанном на фиг. 3, двумерная решетка 120 представляет собой двумерную квадратную решетку. В соответствии с альтернативными вариантами осуществления двумерная решетка 120 может быть, например, гексагональной решеткой или треугольной решеткой или любым другим типом двумерной решетки.
Согласно вариантам осуществления множество кубитов могут быть расположены в соответствии с трехмерной решеткой. Подобно обсуждению, представленному со ссылкой на фиг. 3, множество кубитов может соответствовать узлам трехмерной решетки. Каждый кубит множества кубитов может быть расположен на узле трехмерной решетки. Трехмерная решетка может быть трехмерной квадратной решеткой. Как и в случае двумерных решеток, можно рассмотреть и другие типы трехмерных решеток.
Двумерная решетка представляет собой плоскую структуру, которая может обеспечить более простую пространственную компоновку кубитов по сравнению с, например, трехмерной решеткой или некоторой нерегулярной пространственной компоновкой.
Согласно вариантам осуществления множество кубитов могут быть расположены в соответствии с участком двумерной решетки или в соответствии с участком трехмерной решетки. Фиг. 4 иллюстрирует примерный вариант осуществления, согласно которому множество кубитов 100 расположено в соответствии с треугольным участком 121 двумерной решетки. На фиг. 4 показан вид сверху участка 121. Треугольная форма соответствует расположению квантового вычислительного устройства в соответствии с некоторыми вариантами осуществления, которые выполнены с возможностью реализовать описанные здесь способы. Можно также рассмотреть участки решеток, имеющих разную форму.
Гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров. Гамильтониан одного тела квантовой системы, как описано здесь, может относиться к гамильтониану, в котором взаимодействия между группами из двух или более кубитов отсутствуют. Гамильтониан одного тела может быть суммой множества слагаемых гамильтонианов. Каждый слагаемый гамильтониана может действовать на один кубит множества кубитов. Гамильтониан одного тела может иметь вид H = Σi Hi, в котором каждый Hi - слагаемый гамильтониан, действующий исключительно на i-й кубит. Гамильтониан одного тела может представлять взаимодействия между множеством кубитов и внешним объектом, например, магнитное поле или электрическое поле, в котором каждый кубит взаимодействует индивидуально с внешним объектом.
На фиг. 5 показана схематическая иллюстрация гамильтониана одного тела в соответствии с вариантами осуществления, описанными здесь. С целью конкретизации, но не намереваясь ограничить объем, множество кубитов, показанных на фиг. 5, включает в себя 10 кубитов, а именно кубиты с 201 по 210, расположенные на участке двумерной квадратной решетки, которая образует треугольник, аналогичный как показано на фиг. 4. Гамильтониан одного тела, описанный со ссылкой на фиг. 5, представляет собой сумму 10 слагаемых гамильтонианов с 221 по 230. На фиг. 5 каждый из слагаемых гамильтонианов 221-230 схематически изображен как квадрат, окружающий один кубит, что указывает на то, что каждый слагаемый гамильтониан действует на одном кубите. Например, слагаемый гамильтониан 221 представлен как квадрат, окружающий кубит 201 и только один кубит 201, указывая, что слагаемый гамильтониан 221 действует на кубите 201, но не действует ни на одном из оставшихся кубитов с 202 по 210.
Гамильтониан задачи, являющийся гамильтонианом одного тела, может быть суммой слагаемых гамильтонианов, как описано выше. Множество регулируемых параметров гамильтониана задачи может включать в себя множество регулируемых параметров слагаемых гамильтонианов. Один или более слагаемых гамильтонианов гамильтониана одного тела, в частности, каждый из слагаемых гамильтонианов, может включать в себя один или более регулируемых параметров.
Регулируемый параметр гамильтониана задачи, как описано здесь, может относиться к параметру, представляющему силу и/или направление взаимодействия между кубитом множества кубитов и внешним объектом. Внешний объект может, например, включать в себя, по меньшей мере, одно из следующего: одно или более магнитных полей; одно или более электрических полей и/или одно или более лазерных полей, микроволн или фазовых сдвигов от механических деформаций. Регулировка регулируемого параметра гамильтониана задачи может быть реализована путем регулировки внешнего объекта и/или путем изменения силы и/или типа взаимодействия между кубитом и внешним объектом. Соответственно, регулируемый параметр может представлять собой регулируемое взаимодействие, например, взаимодействие, которое не является жестким в квантовой системе.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, множество регулируемых параметров гамильтониана задачи может включать в себя множество напряжений поля и/или множество направлений поля полей одного тела, действующих на множество кубитов. Поля, действующие на множество кубитов, могут включать в себя одно или более магнитных полей и/или одно или более электрических полей, например, в вариантах осуществления, относящихся к сверхпроводящим кубитам.
Поле одного тела может относиться к полю, влияющему на один кубит во множестве кубитов. В соответствии с вариантами осуществления множество полей одного тела могут включать в себя различные поля одного тела, влияющие на соответствующие кубиты, в зависимости от, возможно, различной напряженности поля и/или, возможно, разных направлений поля. Например, первое поле одного тела и второе поле одного тела могут влиять на первый кубит и второй кубит, соответственно, во множестве кубитов. В нем первое поле одного тела и второе поле одного тела, оба являются, например, магнитными полями, которые могут иметь разную напряженность поля и/или направления поля.
Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, гамильтониан одного тела имеет вид Σk Jk σz(k), в котором σz(k) является оператором Паули k-го кубита множества кубитов, в котором каждый Jk является коэффициентом, и в котором коэффициенты Jk образуют множество регулируемых параметров гамильтониана одного тела. Согласно некоторым вариантам осуществления оператор σz(k) Паули может быть оператором Паули, ассоциированным с первым пространственным направлением.
Для квантовой системы, включающей в себя множество сверхпроводящих кубитов, гамильтониан одного тела, такой как, например, гамильтониан задачи, может быть реализован множеством магнитных потоков, взаимодействующих с множеством сверхпроводящих кубитов. Магнитный поток или смещение магнитного потока могут проходить через первичную сверхпроводящую петлю и через вторичную сверхпроводящую петлю сверхпроводящего кубита. Множество регулируемых параметров гамильтониана задачи можно регулировать путем регулирования множества магнитных потоков или смещений магнитного потока.
Для квантовой системы, реализуемой захваченными ионами, отдельные ионы могут быть адресованы пространственным разделением или разделением по энергии. Случай пространственного разделения включает в себя использование лазерного луча, который прошел и/или отразился от акустооптического отражателя, акустооптического модулятора, микрозеркальных устройств и т.п. Случай разделения энергии связан с использованием градиента магнитного поля, который изменяет частоты внутреннего перехода, позволяя выбирать по разности энергий, т.е. отстройки применяемых полей. Гамильтониан одного тела может быть реализован лазерными полями или микроволнами, резонансными или нерезонансными с внутренним переходом или разностями пространственного магнитного поля.
Для квантовой системы, реализуемой квантовыми точками, гамильтониан одного тела может быть реализован электрическими полями.
Для квантовой системы, реализованной с NV центрами, используя магнитный резонанс посредством применения микроволновых импульсов, кубитные состояния могут когерентно манипулировать на наносекундной временной шкале. Селективная манипуляция состояниями кубитов также может быть обусловлена состоянием близких ядерных спинов.
Вычислительная проблема может быть отображена на конфигурацию кодирования задачи. Конфигурация кодирования задачи может зависеть от и/или содержать информацию о вычислительной задаче. Действие определения конфигурации кодирования задачи может включать в себя определение и/или вычисление значения для каждого из множества регулируемых параметров. Каждое значение может быть определено и/или вычислено из вычислительной задачи.
В соответствии с вариантами осуществления различные вычислительные задачи могут быть закодированы в гамильтониан задачи путем определения соответствующих различных конфигураций кодирования задачи. Например, первая вычислительная задача и вторая вычислительная задача могут быть закодированы в гамильтониан задач, что приводит к первой конфигурации кодирования задачи и второй конфигурации кодирования задачи для множества регулируемых параметров. Если вторая вычислительная задача отличается от первой вычислительной задачи, то вторая конфигурация кодирования задачи регулируемых параметров может отличаться от первой конфигурации кодирования задачи.
В соответствии с вариантами осуществления способ может включать в себя предоставление вычислительной задачи или, по меньшей мере, информации о вычислительной задаче, в классическую вычислительную систему, такую как, например, классическую вычислительную систему 450, показанную на фиг. 1. Например, в классическую вычислительную систему может быть предоставлено множество входных переменных вычислительной задачи, как описано здесь. Согласно вариантам осуществления вычислительная задача может быть закодирована в конфигурации кодирования задачи классической вычислительной системой. Классическая вычислительная система может быть выполнена с возможностью вычислять конфигурации кодирования задачи из вычислительной задачи, например, из множества входных переменных вычислительной задачи.
Терминология гамильтониана ближнего порядка, как используется здесь, может относиться к гамильтониану, представляющему взаимодействия множества кубитов, в котором отсутствует взаимодействие между кубитами, которые удалены друг от друга на расстояние, большее, чем расстояние прекращения взаимодействия. Расстояние прекращения взаимодействия может быть постоянной величиной. Расстояние прекращения взаимодействия может быть намного меньше по сравнению с максимальным расстоянием кубита между кубитами во множестве кубитов. Например, расстояние прекращения взаимодействия может составлять 30% или ниже максимального расстояния кубита, в частности 20% или ниже, более предпочтительно 10% или ниже. Для множества кубитов, расположенные в соответствии с решеткой, гамильтониан ближнего порядка может быть гамильтонианом r-диапазона, в котором не происходит взаимодействия между кубитами, которые удалены друг от друга на расстояние, большее, чем r раз элементарного расстояния (постоянная решетки) решетки. В этом случае, r может быть от 1 до 5, например, r = √2, 2, 3, 4 или 5. Понятие элементарного расстояния решетки в соответствии с вариантами осуществления, описанными здесь, проиллюстрировано ниже со ссылкой, например, на фиг. 6 и 7.
Независимо от количества кубитов квантовой системы гамильтониан плакетки и парный гамильтониан ближайших соседей квантовой системы, как описано здесь, следует рассматривать как гамильтонианы ближнего порядка.
Примером гамильтониана ближнего порядка является гамильтониан одного тела, как описано здесь. Для гамильтониана одного тела расстояние прекращения взаимодействия можно считать равным нулю, поскольку между группами из двух или более кубитов нет взаимодействия, и только взаимодействия между отдельными кубитами и внешним объектом, например, магнитного поля или электрического поля.
Фиг. 6 и 7 показывают дополнительные примеры гамильтонианов ближнего порядка для вариантов осуществления, в которых множество кубитов 100 расположено в соответствии с двумерной квадратной решеткой 120 и лежат на позициях узлов двумерной квадратной решетки, которые образуют треугольный участок 2-мерной квадратной решетки. С целью конкретизации, но не намереваясь ограничить объем, примерная двумерная квадратная решетка 120, показанная на фиг. 6 и 7 включает в себя 55 кубитов, расположенных в треугольнике в квадратной решетке 10 × 10, содержащей 10 рядов и 10 колонок. При прохождении любой строки кубитов двумерной решетки 120 вдоль х-направления 310, например, строка 391, обозначенная пунктирными линиями, последовательные кубиты в строке расположены на элементарном расстоянии D друг от друга, что также называется постоянной решетки в х-направлении. Элементарное расстояние D обозначено ссылочной позицией 350. Аналогично, при обходе любого столбца кубитов двумерной решетки 120 вдоль у-направления 320, например, столбец 392, последовательные кубиты в столбце находятся на элементарном расстоянии, которое также называется постоянной решетки в у-направлении. На фиг. 6 и 7 решетка представляет собой квадратную решетку, и элементарное расстояние (постоянные решетки) в направлении х и у - одинаковые. Однако постоянные решетки в х-направлении и в у-направлении также могут быть разными. Как показано, х-направление 310 перпендикулярно у-направлению 320. Максимальное расстояние кубита из множества кубитов 100, показанных на фиг. 6 и фиг. 7, представляет собой расстояние между кубитами 301 и 302. Максимальное расстояние кубита составляет (9√2) D.
Примером гамильтониана ближнего порядка, описанного со ссылкой на фиг. 6, является парный гамильтониан ближайшего соседа. Парный гамильтониан ближайшего соседа может включать в себя только взаимодействия между парами соседних кубитов на двумерной решетке 120, причем пара соседних кубитов может относиться к паре кубитов, удаленных друг от друга на элементарном расстоянии D. Кубиты 362 и 364, показанные на фиг. 6, представляет собой пример пары соседних кубитов. Парный гамильтониан ближайших соседей может быть суммой множества слагаемых гамильтонианов, причем каждый слагаемый гамильтониан представляет собой взаимодействие между парой соседних кубитов. Для парного гамильтониана ближайшего соседа, описанного со ссылкой на фиг. 6, расстояние прекращения взаимодействия равно элементарному расстоянию D. Соответственно, расстояние прекращения взаимодействия намного меньше по сравнению с максимальным расстоянием кубита, а именно расстояние D прекращения взаимодействия составляет менее 10% от максимального расстояния кубита.
Примером гамильтониана ближнего действия, описанного со ссылкой на фиг. 7, является гамильтониан плакетки. На фиг. 7 55 кубитов, показанные в виде черных кругов, снова расположены в двумерной квадратной решетке 120 и образуют в ней треугольник. Плакетка двумерной квадратной решетки 120 представляет собой элементарный квадрат двумерной квадратной решетки 120, как показано на фиг. 7 с позицией 370. Плакетка 370 содержит кубиты 371, 372, 373 и 374, где кубит 371 расположен на элементарном расстоянии D от кубита 372 и от кубита 374 и где кубит 373 также расположен на элементарном расстоянии D от кубитов 372 и 374. Кроме того, вспомогательные кубиты, показанные черными прямоугольниками, добавляются в дополнительную линию, чтобы завершите плакетки кубитов. Например, вспомогательный кубит 305 завершает плакетку кубитов 302, 303 и 304. Вспомогательные кубиты могут быть получены в определенном квантовом состоянии, например, | 1>. Для этой геометрии решетки гамильтониан плакетки может включать в себя только взаимодействия между группами из четырех кубитов или группами из трех кубитов и одного анциллы кубита, что соответствует плакеткам двумерной квадратной решетки 120. Гамильтониан плакетки может быть суммой множества слагаемых гамильтонианов. Каждый слагаемый гамильтониан может представлять собой взаимодействие, соответствующее плакетки кубитов на решетке, или взаимодействие, соответствующее плакетке кубитов и вспомогательного кубита. Альтернативно, никакие вспомогательные кубиты не могут быть использованы, и гамильтониан плакетки тогда включает в себя слагаемые гамильтонианов, описывающие взаимодействия только трех кубитов. Для гамильтониана плакетки, описанного со ссылкой на фиг. 7, расстояние прекращения взаимодействия составляет √2D, так как максимальное расстояние между двумя кубитами в плакетке составляет √2D. Например, расстояние между кубитами 371 и 373 составляет √2D. Соответственно, расстояние прекращения взаимодействия намного меньше по сравнению с максимальным расстоянием кубита, а именно расстоянием √2D прекращения взаимодействия ниже 12% от максимального расстояния кубита.
Для квантовой системы, включающей в себя множество сверхпроводящих кубитов, гамильтониан плакетки может быть реализован с использованием множества вспомогательных кубитов, где вспомогательный кубит может быть расположен внутри каждой плакетки, например, в центре каждой плакетки. Взаимодействие между кубитами вида Kkmσz(k)σz(m) может быть реализовано с помощью блока соединения, например, блока индуктивного соединения, как описано здесь. Блок соединения включает в себя сверхпроводящий квантовый интерференционный датчик. Применение регулируемого смещения магнитного потока к сверхпроводящему квантовому интерференционному датчику позволяет настроить коэффициент Kkm. Тогда слагаемый гамильтониан гамильтониана плакетки может быть реализован посредством Hsr,p=C(σz(1)+ σz(2)+ σz(3)+ σz(4)-2σz(p)-1)2, который включает в себя только парные взаимодействия вида σz(k)σz(m) однотелого σz(l) , соответствующих наложенным разностям в энергии между квантовыми базисными состояниями | 0> и | 1>. Здесь σz(l) представляет анцилл кубит. Гамильтониан ближнего действия представляет собой сумму слагаемых гамильтонианов Hsr,p. Для вариантов осуществления, с использованием вспомогательных кубитов, к начальному гамильтониану добавляется гамильтониан одного тела вида hΣpσx(p) для множества вспомогательных кубитов.
В качестве альтернативы гамильтониан плакетки может быть реализован без вспомогательных кубитов, например, с использованием трех островковых сверхпроводящих устройств в виде транскон-кубитов. Интегрируя два дополнительных сверхпроводящих квантовых интерференционных датчиков в блоке соединения и путем соединения четырех кубитов плакетки емкостным образом к копланарному резонатору, слагаемый гамильтониан вида -Cσz(1)σz(2)σz(3)σz(4) может быть реализован. Коэффициент C соединения может быть настроен посредством временно-зависимых смещений магнитного потока через два дополнительных сверхпроводящих квантовых интерференционных датчиков.
Для квантовой системы, реализуемой с захваченными ионами, взаимодействие между двумя ионами передаются через фононную шину. Для этого используются лазеры или микроволны, которые не настроены по отношению к полосовому переходу синей и/или красной зоны фононов. Сила излучения лазера и расстройка позволяют регулировать силу взаимодействия. Также можно использовать прямые взаимодействия через ридберговские возбуждения.
Для квантовой системы, реализуемой с холодными атомами, взаимодействие между кубитами может контролироваться путем расстройки лазера, который возбуждает d атомов. В этом случае гамильтониан является гамильтонианом d-тела. Гамильтонианы плакетки могут быть реализованы либо из взаимодействий d-тела, либо из вспомогательных кубитов с двухтельными взаимодействиями.
Для квантовой системы, реализуемой квантовыми точками, взаимодействие между двумя кубитами регулируется градиентом электрического поля и магнитным полем. Гамильтониан ближнего действия может быть реализован импульсной последовательностью и магнитными полями. Гамильтониан плакетки может быть реализован с использованием дополнительного вспомогательного кубита с гамильтонианом ближнего действия, действующим на все пары плакетки.
Для квантовой системы, реализуемой с NV центрами, взаимодействие между NV центрами может передаваться путем их соединения со световыми полями.
Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, множество кубитов может быть расположено в соответствии с двумерной решеткой. Гамильтониан ближнего действия может включать в себя взаимодействие между группами из четырех кубитов, соответствующих плакеткам двумерной решетки. Согласно вариантам осуществления, гамильтониан ближнего порядка может быть гамильтонианом плакетки, как описано здесь.
В соответствии с некоторыми вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, гамильтониан ближнего порядка представляет собой гамильтониан d-тела, где d может быть 2, 3, 4, 5, 6, 7 или 8. Гамильтониан d-тела, как описано здесь, может относиться к гамильтониану, представляющему взаимодействие множества кубитов, в котором не происходит взаимодействия соединений между группами, содержащими d + 1 или более кубитов. Гамильтониан d-тела может включать в себя взаимодействия между группами, содержащими d или менее кубитов. Гамильтониан d-тела может быть суммой множества слагаемых гамильтонианов, в котором каждый слагаемый гамильтониан представляет собой совместное взаимодействие между группой d-кубитов или меньше.
Например, гамильтониан одного тела, как описано здесь, можно рассматривать как гамильтониан d-тела с d = 1. В качестве дополнительного примера парный гамильтониан ближайших соседей, как описано здесь, можно рассматривать как гамильтониан d-тела с d = 2. В качестве еще одного примера гамильтониан плакетки, как описано здесь, можно рассматривать как гамильтониан d-тела с d = 4. Согласно вариантам осуществления, которые могут быть объединены с другими описанными вариантами осуществления, гамильтониан ближнего порядка может быть гамильтонианом d-тела, где d = 4. Значение d может зависеть от геометрии решетки. Например, для гексагональной решетки плакетка будет включать в себя шесть кубитов, и гамильтониан плакетки может быть гамильтонианом из 6 тел.
Предпочтительно иметь гамильтониан ближнего порядка, который является гамильтонианом d-тела с малым d, например, d = 4, так как соответствующие взаимодействия между кубитами могут быть легче сконструированы по сравнению с гамильтонианами d-тела с большим d.
Размер вычислительной задачи, как описано здесь, может относиться к измерению количества классических информационных блоков, необходимых для задания вычислительной задачи. Размер вычислительной задачи может зависеть от количества входных переменных вычислительной задачи. Размер вычислительной задачи может увеличиваться по мере увеличения числа входных переменных. Размер вычислительной задачи может быть равен числу входных переменных. Например, для задачи коммивояжера, как описано здесь, размер может относиться к сумме длин первого списка и второго списка. В качестве еще одного примера для задачи модели Изинга-спина размер может относиться к числу n спинов si.
Для первой вычислительной задачи, имеющей первый размер, соответствующий конечный гамильтониан может быть суммой первого гамильтониана задачи и первого гамильтониана ближнего порядка. Для второй вычислительной задачи, имеющей второй размер, соответствующий конечный гамильтониан может быть суммой второго гамильтониана задачи и второго гамильтониана ближнего порядка. Если второй размер совпадает с первым размером, то второй гамильтониан ближнего порядка может быть таким же, как и первый гамильтониан ближнего порядка. Если второй размер отличается от первого размера, то второй гамильтониан ближнего порядка может отличаться от первого гамильтониана ближнего порядка. Например, применительно к модели Изинга-спина, описанной выше, первая вычислительная задача может относиться к первой задаче модели Изинга-спина для N спинов с первым набором коэффициентов соединения и полевыми коэффициентами, и вторая вычислительная задача может относиться ко второй модели Извинга-спина, также для N спинов, со вторым набором коэффициентов соединения и полевыми коэффициентами, отличными от первого набора коэффициентов соединения и полевых коэффициентов. В этом случае, размеры первой и второй задачи модели Изинга-спина могут считаться равными числу N. Согласно вариантам осуществления гамильтониан ближнего порядка для первой задачи модели Изинга-спина такой же, как гамильтониан ближнего порядка для второй задачи модели Изинга-спина.
Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, гамильтониан ближнего порядка может быть гамильтонианом d-тела, где d может быть независимым от вычислительной задачи. Кроме того, расстояние прекращения взаимодействия может быть не зависящим от вычислительной задачи. Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, гамильтониан ближнего порядка может быть независимым от вычислительной задачи.
В соответствии с вариантами осуществления, описанными здесь, способ включает в себя совершенствование квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана. Основным состоянием конечного гамильтониана является квантовое состояние квантовой системы, минимизирующее энергию для конечного гамильтониана. Основное состояние конечного гамильтониана является собственным состоянием конечного гамильтониана, в частности, собственным состоянием с минимальным собственным значением. Поскольку вычислительная задача кодируется в гамильтониан задачи, и поскольку конечный гамильтониан является суммой гамильтониана задачи и гамильтониана ближнего порядка, то основное состояние конечного гамильтониана содержит информацию о вычислительной задаче и/или может кодировать решение вычислительной задачи.
Основным состоянием конечного гамильтониана может быть состояние квантовой системы при нулевой температуре. Не желая связывать себя какой-либо конкретной теорией, согласно познаниям в области квантовой физики, для квантовой системы невозможно достичь температуры абсолютного нуля. Тем не менее, процесс совершенствования квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана, включает в себя, например, охлаждение квантовой системы до рабочей температуры Tmax, может позволить приближаться к основному состоянию конечного гамильтониана. Рабочая температура Tmax может сильно зависеть от типа кубитов, используемых в квантовой системе. Например, для сверхпроводящих кубитов Tmax может составлять 50 mК или ниже, предпочтительно 1 mК или ниже. Квантовая система может быть усовершенствована из начального квантового состояния в конечное квантовое состояние квантовой системы, чтобы приблизиться к основному состоянию конечного гамильтониана. Конечным квантовым состоянием может быть состояние квантовой системы при рабочей температуре Tmax или при более низкой температуре, то есть, это может быть тепловое состояние конечного гамильтониана при рабочей температуре или при более низкой температуре. Соответственно, конечное квантовое состояние может аппроксимировать основное состояние конечного гамильтониана. Конечное квантовое состояние может содержать информацию об основном состоянии конечного гамильтониана. Конечное квантовое состояние может содержать информацию о решении вычислительной задачи.
Квантовая система может быть охлажденной, например, с помощью блока охлаждения, как описано здесь, до рабочей температуры Tmax или до более низкой температуры. Рабочая температура может быть отличной от нуля.
Согласно вариантам осуществления, которые объединены с другими вариантами осуществления, описанными здесь, способ может включать в себя инициализацию квантовой системы в начальном квантовом состоянии путем охлаждения квантовой системы до основного состояния начального гамильтониана. Основным состоянием начального гамильтониана является квантовое состояние квантовой системы, минимизирующее энергию для начального гамильтониана. Основным состоянием начального гамильтониана является собственное состояние начального гамильтониана, в частности, собственное состояние с минимальным собственным значением. Основным состоянием начального гамильтониана является состояние квантовой системы при нулевой температуре. Охлаждение квантовой системы в основное состояние начального гамильтониана может позволить приближаться к основному состоянию начального гамильтониана. Начальное квантовое состояние может аппроксимировать основное состояние начального гамильтониана.
Начальный гамильтониан может быть не зависящим от вычислительной задачи. Начальный гамильтониан может быть гамильтонианом d-тела с d, равным 1, 2, 3 или 4. Начальный гамильтониан может быть гамильтонианом одного тела, как описано здесь. Имея начальный гамильтониан, являющийся гамильтонианом одного тела, позволяет просто установить для реализации начального гамильтониана, например, для квантовой системы сверхпроводящих кубитов.
Начальным гамильтонианом может быть гамильтониан одного тела, имеющий вид Hinit = Σk ak σx(k). В этом случае ak может быть коэффициентом для k-го кубита во множестве кубитов, и σx(k) может быть оператором Паули, действующим на k-м кубите. В частности, σx(k) может быть оператором Паули, соответствующим второму пространственному направлению. Второе пространственное направление может быть ортогональным первому пространственному направлению, как описано здесь. Оператор σx(k) Паули и оператор σz (k) Паули могут быть некоммутирующими, в частности, антикоммутирующими операторами. Согласно вариантам осуществления каждый из коэффициентов ak равен единому общему коэффициенту h. Начальным гамильтонианом может быть гамильтониан одного тела, имеющий вид Hinit = h Σk σx(k).
Для сверхпроводящего кубита смещение магнитного потока через первичную сверхпроводящую петлю сверхпроводящего кубита может быть задано так, что базисные состояния | 0> и | 1> имеют одинаковую энергию, т.е. разность энергий для этих базисных состояний равна нуль. Кроме того, смещение магнитного потока через вторичную сверхпроводящую петлю может связывать базисные состояния | 0> и | 1>. Соответственно, для сверхпроводящего кубита может быть реализован слагаемый гамильтониан вида hσx(k). Соответственно, начальный гамильтониан вида Hinit = h Σk σx(k) может быть реализован для множества сверхпроводящих кубитов. Основное состояние начального гамильтониана может быть выполнено с некоторой вероятностью, установив коэффициент h на величину, которая намного больше, чем энергетический масштаб, определяемый температурой квантовой системы.
Для квантовой системы, реализуемой захваченными ионами, ионы могут быть инициализированы оптической накачкой с использованием лазера, который детерминированно переносит ионы в одно из двух квантовых базисных состояний кубита. Это уменьшает энтропию и, следовательно, охлаждает во внутренних состояниях.
Для квантовой системы, реализуемой с холодными атомами, начальное квантовое состояние может быть получено возбуждающими атомами, находящимися в основном состоянии, в ридберговское состояние с большой расстройкой.
Для квантовой системы, реализованной с NV центрами, NV центры могут быть адресованы индивидуально с использованием стандартных способов оптической конфокальной микроскопии. Инициализация и измерение могут выполняться за счет нерезонансного или резонансного оптического возбуждения.
Согласно вариантам осуществления квантовая система совершенствуется из начального квантового состояния в основное состояние конечного гамильтониана. Согласно вариантам воплощения квантовая система может включать в себя выполнение квантового отжига. Квантовый отжиг может выполняться программируемым блоком квантового отжига, как описано здесь.
Выполнение квантового отжига может включать переход от начального гамильтониана квантовой системы к конечному гамильтониану. Выполнение квантового отжига может включать переход от начального гамильтониана к конечному гамильтониану через интерполяционный гамильтониан. Интерполяционный гамильтониан может быть зависящим от времени гамильтонианом. Интерполяционный гамильтониан может иметь один или несколько интерполяционных параметров для интерполяции между начальным гамильтонианом и конечным гамильтонианом. Например, интерполяционный гамильтониан может иметь вид H(t) = A(t) Hinit + B(t) Hfinal. В этом случае, Hinit может ссылаться на начальный гамильтониан, Hfinal может ссылаться на конечный гамильтониан, t может быть временным параметром и A (t) и B (t) могут быть коэффициентами интерполяции в зависимости от временного параметра t.
Выполнение квантового отжига может включать в себя переход от начального гамильтониана в начальный момент времени к конечному гамильтониану в конечное время. В начальный момент времени один или несколько интерполяционных параметров интерполяционного гамильтониана могут быть установлены на одно или несколько соответствующих начальных значений. В начальный момент интерполяционный гамильтониан может быть равен начальному гамильтониану. Например, в варианте, в котором интерполяционный гамильтониан имеет вид H(t) = A(t) Hinit + B(t) Hfinal, интерполяционный параметр A (t) может быть установлен на начальное значение 1 в начальное время и интерполяционный параметр B (t) может быть установлен на начальное значение 0 в начальное время. Соответственно, интерполяционный гамильтониан равен Hinit в начальный момент времени.
Выполнение квантового отжига может включать в себя постепенный переход от начального гамильтониана к конечному гамильтониану. Выполнение квантового отжига может включать в себя постепенное изменение одного или нескольких интерполяционных параметров интерполяционного гамильтониана. В промежуточные моменты времени между начальным и конечным временем интерполяционный гамильтониан отличается от начального гамильтониана и/или конечного гамильтониана. Интерполяционный параметр интерполяционного гамильтониана может постепенно изменяться от начального значения, например, в начальный момент времени, до конечного значения, например, в конечное время. В конечный момент времени интерполяционный гамильтониан равен конечному гамильтониану. Например, для вариантов осуществления, согласно которым интерполяционный гамильтониан имеет вид H(t) = A(t) Hinit + B(t) Hfinal, интерполяционный параметр A (t) может постепенно изменяться с начального значения 1 в начальном времени до конечного значения 0 в конечное время. Аналогично, интерполяционный параметр B (t) может быть постепенно изменен от начального значения 0 в начальное время до конечного значения 1 в конечное время. Соответственно, интерполяционный гамильтониан H(t) равен конечному гамильтониану в конечное время.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, квантовая система поддерживается при рабочей температуре 50 mК или ниже, в частности 1 mК или ниже во время выполнения квантового отжига.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, выполнение квантового отжига от начального гамильтониана до конечного гамильтониана включает в себя адиабатическое совершенствование начального гамильтониана в конечный гамильтониан.
Для квантовой системы, включающей в себя множество сверхпроводящих кубитов с начальным гамильтонианом вида hΣk σx(k), гамильтониан задачи вида Σk Jk σz(k) и гамильтониан ближнего действия вида CΣl Cl со слагаемыми гамильтонианов Cl, соответствующие плакеткам, квантовый отжиг можно выполнить следующим образом. После инициализации, где C = Jk = 0, медленно увеличивается C и Jk, медленно снижая коэффициент a до a = 0.
Альтернативно или в дополнение к вариантам осуществления, включающим в себя квантовый отжиг, совершенствование квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана может включать в себя охлаждение квантовой системы от начального квантового состояния до конечного квантового состояния. Начальным квантовым состоянием может быть состояние квантовой системы при начальной температуре. Конечным квантовым состоянием может быть состояние квантовой системы при конечной температуре. Конечная температура ниже начальной. Охлаждение квантовой системы из начального квантового состояния при начальной температуре до конечного квантового состояния при конечной температуре может включать в себя уменьшение, например, постепенное снижение температуры от начальной температуры до конечной температуры. Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, конечная температура может составлять 50 mК или ниже, в частности 1 mК или ниже. Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, начальная температура может составлять комнатную температуру или ниже, в частности 200 Кельвинов или ниже.
В соответствии с вариантами осуществления способ включает в себя измерение, по меньшей мере, участка множества кубитов для получения данных считывания конечного квантового состояния. В соответствии с некоторыми вариантами осуществления измеряется участок множества кубитов, так что измеряются не все кубиты во множестве кубитов. Участок множества кубитов может содержать 70% или менее из множества кубитов, в частности, 60% или менее, более предпочтительно, 50% или менее. Согласно некоторым вариантам осуществления, если общее количество кубитов во множестве кубитов обозначено N, то количество кубитов в этой части масштабируется в соответствии с √N.
Измерение, по меньшей мере, участка множества кубитов может включать в себя измерение каждого кубита, по меньшей мере, в участке отдельно. Измерение, по меньшей мере, участка может включать в себя измерение оператора Паули, например, оператор σz Паули, для каждого из кубитов, по меньшей мере, на участке кубитов. Измерение, по меньшей мере, участка может включать в себя выполнение измерения двух результатов для каждого кубита, по меньшей мере, на участке множества кубитов. Измерение с двумя результатами может обеспечить один из двух возможных результатов, например, 0 или 1. По меньшей мере, участок кубитов может быть измерен измерительным устройством, как описано здесь.
Измерение, по меньшей мере, участка может обеспечить считывание конечного квантового состояния. Данные чтения могут иметь форму классической информации, представленной множеством классических бит. Данные считывания могут отображать информацию о конечном квантовом состоянии и/или об основном состоянии конечного гамильтониана. Данные считывания могу предоставлять информацию о решении, например, пробном решении, истинном решении или наборе переменных свидетеля, для вычислительной задачи. Чтение может быть решением вычислительной задачи.
Для квантовой системы, включающей в себя множество N сверхпроводящих кубитов, кубитные состояния | 0> и | 1> для множества кубитов могут быть измерены с высокой точностью с использованием измерительного устройства, включающего в себя множество сверхпроводящих квантовых интерференционных датчиков, в частности, N гистерезисных DC сверхпроводящих квантовых интерференционных датчиков и N RF сверхпроводящих квантовых интерференционных датчиков, управляемые линиями управления, в котором количество линий управления масштабируется в соответствии с √N.
Для квантовой системы, реализуемой с захваченными ионами, измерение квантовой системы может быть выполнено с помощью флуоресцентной спектроскопии. В этом случае, ионы приводятся на переход с коротким временем жизни, если они находятся в одном из двух состояний спина. В результате ионы в управляемом состоянии испускают много фотонов, в то время как другие ионы остаются темными. Испускаемые фотоны могут регистрироваться коммерческими CCD-камерами. Измерение в любом из направлений на блоховской сфере достигается с помощью соответствующих однокубитных импульсов перед флуоресцентной спектроскопией.
Для квантовой системы, реализуемой с холодными атомами, кубиты можно измерить, выполняя выборочную развертку атомов основного состояния и визуализацию флуоресценции с разрешениями одного узла.
Для квантовой системы, реализуемой с квантовыми точками, кубиты можно считывать из последовательности импульсов быстрым адиабатическим проходом.
В соответствии с вариантами осуществления способ включает в себя определение решения вычислительной задачи из данных считывания. Способ может включать в себя вычисление решения из данных считывания. Данные считывания могут быть предоставлены классической вычислительной системе, как описано здесь. Классическая вычислительная система может определять или вычислять решение вычислительной задачи из отсчета.
Вычислительная проблема, как описано здесь, может относиться к классу NP сложности, рассматриваемому в области информатики, где «NP» означает «недетерминированное полиномиальное время». Согласно вариантам осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, вычислительная задача относится к классу NP сложности. Класс NP сложности включает в себя решения задачи. Неформально говоря, для вычислительной задачи, принадлежащей классу NP сложности, существует множество переменных свидетеля, на основе которых можно проверить, что решение вычислительной задачи является «да». В этом случае, для вычислительных задач в NP процесс проверки того, что решение является «да», может быть выполнен с помощью алгоритма проверки, имеющего время выполнения, которое масштабируется только полиномиально с размером вычислительной задачи. Другими словами, набор переменных свидетеля содержит информацию о решении, в котором информация может обрабатываться в полиномиальной среде выполнения с помощью алгоритма проверки, чтобы убедиться, что решение является «да». Для формального определения класса NP сложности ссылка делается на соответствующую литературу по информатике.
Например, задача коммивояжера, задача 3-красочности и задача модели Изинга-спина, как описано здесь, являются примерами решения задач в классе NP сложности. Например, рассмотрим задачу модели Изинга. Если решение задачи модели Изинга-спина для заданного набора коэффициентов соединения и полевых коэффициентов и для заданной константы K является «да», то конфигурация спинов (s1, s2, ..., sn), для которых ассоциированная Изиновая энергетическая функция H (s1, s2, ..., sn) меньше, чем K, можно рассматривать как набор переменных свидетеля. Учитывая переменные свидетеля (s1, s2, ..., sn), в полиномиальное время может быть проверено, что энергия H (s1, s2, ..., sn) действительно меньше K, вычисляя число H (s1, s2, ..., sn) и сравнивая его с K. Соответственно, задача модели Изинга-спина содержится в классе NP сложности.
Задача определения того, является ли решение «да» или «нет» для задачи принятия решения, может не иметь алгоритма полиномиального времени для некоторых вычислительных задач в NP или может даже иметь экспоненциальную продолжительность выполнения, тогда как алгоритм проверки может иметь полиномиальное время выполнения. Считается, что некоторые вычислительные задачи класса NP сложности являются вычислительно неразрешимыми для классических вычислительных систем. В этом случае терминология «труднорешаемое вычисление» вычислительной задачи может относиться к вычислительной задаче, для которой не существует алгоритма, работающего на классической вычислительной системе с полиномиальным временем выполнения, чтобы определить, является ли решение вычислительной задачи «да», или «нет». В частности, задача коммивояжера, задача 3-красочности и задача модели Изин-спина считаются неразрешимыми для классических вычислительных систем, или, по меньшей мере, ни один алгоритм не может решить любую из этих задач в полиномиальной среде выполнения.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, вычислительная задача, для которой решение вычисляется с использованием квантовой системы, как описано здесь, является NP-полной задачей или NP-сложной задачей. NP-полные задачи относятся к классу NP и считаются вычислительно неразрешимыми для классических вычислительных систем. Хотя не каждая NP-сложная задача относится к NP, NP-сложные задачи также считаются вычислительно неразрешимыми для классических вычислительных систем.
Для вариантов осуществления, согласно которым вычислительная система принадлежит классу NP сложности, т.е. NP-полные задачи, данные считывания измерения могут включать в себя набор переменных свидетеля вычислительной задачи или, по меньшей мере, часть этого набора.
В соответствии с некоторыми вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, определение конфигурации кодирования задачи может включать в себя отображение вычислительной задачи на вспомогательную вычислительную задачу, в котором вспомогательная вычислительная задача включает в себя определение основного состояния модели спина дальнего действия. Вспомогательная вычислительная задача зависит от вычислительной задачи. Отображение вычислительной задачи на вспомогательную вычислительную задачу может включать в себя отображение входных параметров вычислительной задачи на входные параметры вспомогательной вычислительной задачи. Отображение вычислительной задачи на вспомогательную задачу может быть таково, что решение вычислительной задачи может быть определено из решения вспомогательной вычислительной задачи.
В соответствии с вариантами осуществления вспомогательная вычислительная задача может относиться к задаче модели Изинга-спина, как описано здесь. В соответствии с дополнительными вариантами осуществления вычислительная задача может быть задачей в классе NP сложности, например, задача коммивояжера, как описано здесь. Поскольку задача модели спина Изинга является NP-полной задачей, то каждая задача класса NP сложности, такая как, например, задача коммивояжера, может быть отображена на задачу модели Изинга. Например, для задачи коммивояжера, включающей в себя первый список и второй список, как описано здесь, первый список и второй список могут быть отображены на набор коэффициентов соединения и полевых коэффициентов, как описано здесь, для задачи модели Изинга-спина. Решение задачи коммивояжера может быть вычислено из решения для задачи модели Изинга с соответствующими коэффициентами соединения и полевыми коэффициентами. Такие отображения известны.
В соответствии с вариантами осуществления определение конфигурации кодирования задачи может включать в себя определение конфигурации кодирования задачи из модели спина дальнего действия, например, из модели спина Изинга. Конкретный способ выполнения этого определения более подробно описан со ссылкой на фиг. 9-16.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, модель спина дальнего порядка может быть моделью спина дальнего порядка с взаимодействием m-телом, где m равно 1, 2 или 3.
В соответствии с вариантами осуществления, которые могут быть объединены с другими вариантами осуществления, описанными здесь, способ дополнительно включает в себя определение гамильтониана ближнего порядка из множества замкнутых петель спинов в модели спина дальнего порядка.
Согласно еще одному варианту осуществления предлагается способ вычисления решения вычислительной задачи с использованием квантовой системы содержащий множество кубитов.
Способ включает в себя кодирование вычислительной задачи в гамильтониан задачи квантовой системы, как описано здесь. Гамильтониан задачи является гамильтонианом одного тела, включающим в себя множество регулируемых параметров, как описано здесь. Кодирование включает в себя определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров, как описано здесь.
Способ дополнительно включает в себя инициализацию квантовой системы в начальном квантовом состоянии. Способ дополнительно включает в себя совершенствование квантовой системы от начального квантового состояния до конечного квантового состояния путем выполнения квантового отжига. Выполнение квантового отжига включает в себя переход от начального гамильтониана квантовой системы к конечному гамильтониану квантовой системы, как описано здесь. Конечным гамильтонианом является сумма гамильтониана задачи и гамильтониана ближнего действия, как описано здесь, где множество регулируемых параметров гамильтониана задачи находятся в конфигурации кодирования задачи, и где гамильтониан ближнего порядка является гамильтонианом d-тела, где d не зависит от вычислительной задачи.
Способ дополнительно включает в себя измерение, по меньшей мере, участка из множества кубитов для получения данных считывания конечного квантового состояния, как описано здесь.
Способ дополнительно включает в себя определение решения вычислительной задачи из данных считывания, как описано здесь.
В соответствии с дополнительным вариантом осуществления устройство для вычисления решений вычислительных задач, такое как, например, устройство 400, показано на фиг. 1.
Устройство включает в себя квантовую систему, содержащую множество кубитов, как описано здесь.
Устройство дополнительно включает в себя блок охлаждения, такой как, например, блок 410 охлаждения, показанный на фиг. 1, выполненный с возможностью охлаждать квантовую систему в основном состоянии квантовой системы, как описано здесь. Блок охлаждения может быть выполнен с возможностью охлаждать квантовые системы в основном состоянии начального гамильтониана, как описано здесь, для инициализации квантовой системы в начальном квантовом состоянии, как описано здесь. Блок охлаждения может быть выполнен с возможностью поддерживать рабочую температуру квантовых систем, которая сильно зависит от типа кубитов, используемых в устройстве. Например, для сверхпроводящих кубитов рабочая температура составляет 50 mК или ниже, в частности, 1 mК или ниже.
Устройство дополнительно включает в себя программируемый блок квантового отжига, такой как, например, программируемый блок 430 квантового отжига, показанный на фиг. 1, выполненный с возможностью совершенствовать путем квантового отжига начальный гамильтониан квантовой системы в конечный гамильтониан квантовой системы, как описано здесь. Конечным гамильтонианом является сумма гамильтониана задачи и гамильтониана ближнего порядка, как описано здесь.
Блок охлаждения может быть выполнен с возможностью поддерживать квантовую систему при рабочей температуре во время выполнения квантового отжига программируемым блоком квантового отжига.
Устройство дополнительно включает в себя измерительное устройство, такое как, например, измерительное устройство 440, показанное на фиг. 1, выполненное с возможностью измерять, по меньшей мере, участок множества кубитов.
Устройство дополнительно включает в себя классическую вычислительную систему, такую как, например, классическую вычислительную систему 450, показанную на фиг. 1, соединенную с программируемым блоком квантового отжига и с измерительным устройством. Классическая вычислительная система может быть выполнена с возможностью принимать в качестве входных данных вычислительную задачу. Классическая вычислительная система может быть дополнительно выполнена с возможностью кодировать вычислительные задачи в гамильтониан задачи. В этом случае кодирование может включать в себя определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи, как описано здесь. Классическая вычислительная система может дополнительно быть выполнена с возможностью передавать конфигурацию кодирования задачи в блок квантового отжига.
Программируемый блок квантового отжига может быть выполнен с возможностью принимать конфигурации кодирования задач из классической вычислительной системы. Программируемый блок квантового отжига может быть выполнен с возможностью выполнять переход посредством квантового отжига из начального гамильтониана в конечный гамильтониан, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи.
Классическая вычислительная система может дополнительно быть выполнена с возможностью принимать данные считывания квантовой системы из измерительного устройства. Классическая вычислительная система может быть дополнительно выполнена с возможностью определять решения вычислительной задачи из данных считывания.
В соответствии с дополнительным вариантом осуществления предусмотрено программируемое устройство квантового отжига для вычисления решений вычислительных задач. Программируемое устройство квантового отжига включает в себя квантовую систему, включающую в себя множество сверхпроводящих кубитов, расположенных в соответствии с двумерной решеткой.
Программируемое устройство квантового отжига дополнительно включает в себя узел смещения магнитного потока, включающий в себя множество блоков смещения магнитного потока, выполненных с возможностью генерировать множество регулируемых магнитных потоков. Каждый регулируемый магнитный поток действует на один сверхпроводящий кубит во множестве сверхпроводящих кубитов.
Программируемое устройство квантового отжига дополнительно включает в себя блок соединения, включающий в себя, по меньшей мере, один сверхпроводящий квантовый интерференционный датчик, выполненный с возможностью соединять множества сверхпроводящих кубитов в соответствии с гамильтонианом плакетки.
Программируемое устройство квантового отжига дополнительно включает в себя контроллер, подключенный к блоку смещения магнитного потока и к блоку соединения. Контроллер выполнен возможностью принимать конфигурацию кодирования задачи для множества регулируемых параметров гамильтониана задачи квантовой системы, в котором гамильтониан задачи является гамильтонианом одного тела, и конфигурация кодирования задачи кодирует вычислительную задачу. Контроллер дополнительно выполнен с возможностью управлять блоком смещения магнитного потока и блоком соединения для совершенствования начального гамильтониана квантовой системы в конечный гамильтониан квантовой системы путем квантового отжига. Конечным гамильтонианом является сумма гамильтониана плакетки и гамильтониана задачи, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи.
Термин «программируемый блок квантового отжига» используется в синониме термина «программируемое устройство квантового отжига» в данном документе.
Дополнительные аспекты настоящего раскрытия описаны со ссылкой на фиг. 9-16. Приведено описание конкретного процесса кодирования вычислительной задачи в гамильтониан задачи и соответствующий конечный гамильтониан, а именно, кодирование задачи модели Изинга-спина с взаимодействиями дальнего действия в конечный квантовый гамильтониан, являющийся суммой гамильтониана задачи одного тела и гамильтониана плакетки. (Классическая) задача модели Изинга-спина с взаимодействиями дальнего порядка является NP-полной, и ее квантование тривиально, так что, здесь не будет никакого различия между классической и квантовой моделью изинговского спина. Известны сопоставления других классических вычислительных задач с задачей модели Изинга. Таким образом, основное состояние конечного квантового гамильтониана или тепловое состояние при низкой рабочей температуре может содержать информацию о решении задачи модели Изинга-спина и, путем обратного отображения, многих классических NP-сложных вычислительных задач. Конкретное отображение на конечный квантовый гамильтониан позволяет реализовать устройство для квантовой обработки (квантовый процессор) на двумерной поверхности, в частности, двумерной решетке, если задача модели Изинга-спина включает в себя только взаимодействия d-тела с d меньшим или равным два, и позволяет реализовать устройство для квантовой обработки в трехмерном пространстве, в частности, на трехмерной решетке, если задача модели Изинга-спина включает в себя только взаимодействия d-тела с d меньшим или равным трем. Отображение может быть расширено до задач модели Изинга-спина с взаимодействиями d-тела и произвольного d. Устройства для квантовой обработки полностью программируются с помощью гамильтониана задачи одного тела и являются масштабируемыми архитектурами.
В первую очередь рассматривается случай задачи модели Изинга-спина, включающей в себя только взаимодействия d-тела с d, меньшим или равным двум. Конкретное кодирование начинается с задачи модели Изинга-спина для n спинов, как описано здесь, с не более чем двумя взаимодействиями тела и соответствующими коэффициентами cij соединения. Индексы i и j могут находиться в диапазоне от 1 до n, причем j меньше i. В первом случае все полевые коэффициенты ci равны нулю. На фиг. 9 показана задача модели Изинга-спина для n = 6 спинов, в котором спины помечены от 1 до 6. Существует n (n-1) / 2 = 15 парных взаимодействий между спинами, как показано на фиг. 9 с помощью линий, соединяющие пары спинов. Например, линия, обозначенная 12, представляет собой попарное взаимодействие между спинами 1 и 2. 15 попарных взаимодействий соответствуют 15 коэффициентам cij соединения. Взаимодействия являются взаимодействиями дальнего действия.
Для каждой пары спинов в модели Изинга-спина предусмотрен соответствующий кубит в квантовой системе. Например, для 6 спинов с 15 парными взаимодействиями, показанных на фиг. 9, соответствующая квантовая система включает в себя 15 кубитов. Конфигурация спинов в модели Изин-спина сопоставляется с конфигурацией соответствующих кубитов. В этом случае конфигурация кубитов зависит от относительной ориентации спинов. Пара спинов, указывающих в одном направлении (параллельное выравнивание), отображается в кубит в квантовом базисном состоянии «| 1>». Кроме того, пара спинов, указывающих в противоположных направлениях (антипараллельное выравнивание), отображается в кубит в квантовом базовом состоянии «| 0>». Это отображение показано на фиг. 10. На фиг. 10 метки 0 и 1 соответствуют квантовым базисным состояниям | 0> и | 1> соответственно.
Коэффициенты cij соединения отображаются на множество регулируемых параметров Jk гамильтониана задачи, кодирующего вычислительную задачу, в данном случае задачи модели Изинга-спина. Гамильтониан задачи имеет вид Σk Jk σz(k), в котором k = n*i + j и где k находится в диапазоне от 1 до M и M = n (n-1) / 2. Задача модели Изинга-спина отображается на гамильтониан задачи таким образом, что регулируемые параметры Jk гамильтониана задачи представляют собой взаимодействия между спинами в модели Изинга-спина, соответствующие коэффициентам cij соединения.
Число кубитов, необходимых для кодирования задачи модели Изинга в гамильтониане задачи, квадратично возрастает по сравнению с задачей модели Изинга для n спинов, так как число двухтельных взаимодействий между спинами равно M = n (n - 1) / 2. В соответствии с некоторыми вариантами осуществления могут быть рассмотрены дополнительные степени свободы. Общее количество кубитов в квантовой системе может быть M + n - 2 или более, где n-2 дополнительные вспомогательные кубиты и/или дополнительные вспомогательные кубиты могут быть добавлены по причинам, объясненным ниже. Соответственно, количество кубитов может быть больше числа спинов n. В частности, число кубитов может быть числом спинов n плюс M - 2 дополнительных степеней свободы. Гамильтониан задачи позволяет программировать устройство для квантовой обработки только с локальными взаимодействиями, в частности, однотелесные взаимодействия с внешними полями.
Увеличенное число степеней свободы квантовой системы по сравнению с моделью Изинга-спина компенсируется гамильтонианом ближнего порядка, который является суммой M-n-суммарных слагаемых гамильтонианов Cl 4-тел, называемых гамильтонианами ограничения, представляющими ограничения для фиксации участка кубитов. Гамильтониан ближнего порядка имеет вид Σl Cl, в котором индекс l находится в диапазоне от 1 до (n2 - 3n) / 2 и где каждый слагаемый гамильтониан Cl является гамильтонианом ограничения, который может иметь вид
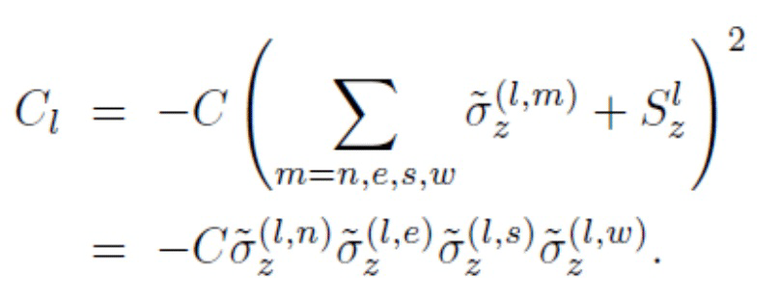
Ссылаясь на приведенное выше уравнение, можно рассмотреть две возможные реализации гамильтонианов ограничения. Сумма в приведенном выше уравнении может представлять собой дополнительную реализацию. Сумма вычисляется по четырем членам плакетки (север, восток, юг, запад) двумерной решетки, согласно которой расположены кубиты. Кроме того, каждый Szl является оператором, действующим на вспомогательный кутрит, включенный в состав квантовой системы. Вспомогательный кутрит имеет основу, состоящую из трех базовых состояний, которые в этом варианте будут обозначены | 0>, | 2> и | 4>. Вторая реализация гамильтонианов ближнего действия является реализацией на основе взаимодействия, которая не требует вспомогательных кутритов. Согласно реализации на основе взаимодействия, Cl представляет собой четырехтельное взаимодействие между кубитами, образующими плакетку решетки. Кроме того, в приведенном выше уравнении C представляет собой силу ограничения, например, постоянная величина ограничения.
Как описано выше, кодирование модели Изинга-спина в гамильтониане задачи включает в себя сопоставление конфигурации спинов модели Изинга-спина на конфигурации кубитов в квантовой системе, в котором конфигурация кубитов зависит от относительной ориентации пар спинов в соответствующей конфигурации спинов. Для обеспечения согласованного сопоставления учитываются аспекты, связанные с замкнутыми петлями в модели Изин-спина, как описано ниже. В каждой замкнутой петле спинов в модели Изин-спина число пар спинов, имеющих антипараллельное выравнивание, является четным числом. Например, со ссылкой на фиг. 9, рассмотрите, например, замкнутую петлю, образованную соединениями 14, 24, 23 и 13, как показано пунктирными линиями. Замкнутая петля включает в себя спины 1, 2, 3 и 4. Любая конфигурация спинов 1, 2, 3 и 4 включает в себя ноль, две или четыре пары антипараллельных спинов. Никакая конфигурация спинов 1, 2 3 и 4 не имеет одной или трех пар антипараллельных спинов. Соответственно, каждая конфигурация спинов 1, 2, 3 и 4 имеет четное число антипараллельных спинов.
Поскольку пары антипараллельных спинов отображаются на кубиты, находящиеся в квантовом базисном состоянии | 0>, то каждый набор кубитов в квантовой системе, соответствующий замкнутой петле спинов в модели Изинского спина, имеет четное число квантовых базисных состояний | 0>. Это обеспечивает набор ограничений для, по меньшей мере, участка кубитов квантовой системы. Например, для замкнутой петли, рассмотренной выше со ссылкой на фиг. 9, соответствующая группа из четырех кубитов показана на фиг. 11, обозначенная ссылочными позициями 14, 24, 23 и 13 с учетом соответствия между парами спинов в модели Изинга, и кубиты в квантовой системе. A, показанные на фиг. 11, кубиты 14, 24, 23 и 13 соответствуют плакетке двумерной решетки 120. Ввиду ограничения на замкнутой петле, как описано выше, любая конфигурация квантовых базисных состояний для кубитов 14, 24, 23 и 13 включают в себя либо нулевые, либо 2, либо четыре квантовых базисных состояния | 0>, как показано на фиг. 12.
Чтобы гарантировать, что ограничения, соответствующие всем замкнутым петлям, выполнены, достаточно обеспечить ограничения, связанные с подходящим подмножеством замкнутых петель. В соответствии с этим вариантом осуществления конкретные структурные блоки замкнутых петель, включающие в себя группы не более четырех спинов, достаточны для обеспечения того, чтобы все ограничения были выполнены, так что обеспечивается согласованное отображение модели Изинга-спина в квантовую систему. Структурные блоки включают в себя замкнутые петли, состоящие из четырех спинов, соединенные четырьмя соединениями, в котором одно соединение имеет индексное расстояние s, два соединения имеют индексное расстояние s + 1 и одно соединение имеет индексное расстояние s + 2. В этом случае, s варьируется от 1 до N - 2, и понятие «индексного расстояния» между спинами si и sj относится к числу | i - j |. Набор структурных блоков замкнутых петель с s = 1 обеспечивает n - 2 ограничения. Например, замкнутая петля, включающая в себя соединения 14, 24, 23 и 13 между спинами 1, 2, 3 и 4, как показано на фиг. 9 и как описано выше, представляет собой структурный блок замкнутой петли с s = 1.
Дополнительный аспект относится к границе квантовой системы. Некоторые структурные блоки замкнутых петель включают в себя группу из трех спинов, соединенных тремя соединениями, вместо четырех спинов, соединенных четырьмя соединениями. Например, со ссылкой на фиг. 9, в этом отношении можно рассмотреть замкнутую петлю, включающую в себя соединения 12, 23 и 13 между спинами 1, 2 и 3. Соответствующая группа кубитов в квантовой системе включает в себя три кубита 12, 23 и 13, расположенных по форме треугольника плакетки двумерной решетки. Для обеспечения ограничения, соответствующего замкнутой петле из трех спинов, гамильтониан Cl ограничения 3-тела можно считать действующим на соответствующей группе из трех кубитов. Альтернативно, в квантовую систему может быть добавлена дополнительная линия из n-2 вспомогательных кубитов, зафиксированных в квантовом базисном состоянии | 1>, как показано на фиг. 11 кругами с пунктирными линиями. Для применения ограничения, соответствующего замкнутой петле из трех спинов, например, замкнутая петля, соответствующая кубитам 12, 23 и 13, ограничительный гамильтониан С1 можно считать действующим на соответствующих трех кубитах и на одном из вспомогательных кубитов, а именно, вспомогательном кубите 1101, показанном на фиг. 11. Соответственно ограничительный гамильтониан Cl является гамильтонианом с 4 телами, действующий на плакетке увеличенной двумерной решетки, имеющий тот же вид, что и описанный выше. Последняя реализация имеет то преимущество, что все ограничительные гамильтонианы можно рассматривать на одной и той же основе, поскольку все ограничительные гамильтонианы являются гамильтонианами 4-тел, соответствующими плакеткам двумерной решетки.
Ограничительные гамильтонианы Cl гарантируют, что выполняются ограничения, соответствующие структурным блокам замкнутых петель и, следовательно, ограничения, соответствующие всем замкнутым петлям, выполняются. Соответственно, гамильтониан ближнего действия обеспечивает согласованное отображение ограничений на спины в модели Изинга-спина на ограничения, налагаемые на квантовую систему.
Для обеспечения данных считывания может быть измерен участок кубитов, такой как, например, участок 425, показанный на фиг. 11. Если квантовая система находится в основном состоянии конечного гамильтониана, то кубиты на участке 425 будут находиться в конфигурации квантовых состояний, соответствующих конфигурации спинов в основном состоянии модели Изинг-спина. Если квантовая система находится в тепловом состоянии конечного гамильтониана вблизи основного состояния, т.е. при достаточно низкой температуре, то это верно с большой вероятностью. Соответственно, измерение участка 425 позволяет определить решение задачи модели Изинг-спина, по меньшей мере, с высокой вероятностью. Если квантовая система находится в конечном состоянии, как описано здесь, в котором конечное состояние хорошо аппроксимируется основным состоянием конечного гамильтониана, то измерение участка 425, таким образом, будет, по меньшей мере, предоставлять информацию об основном состоянии модели Изинга, из которого можно вычислить пробное решение. Затем, он может быть проверен классическими вычислениями в полиномиальное время, является ли пробное решение истинным решением, а если нет, то вычисление может быть повторено до тех пор, пока не будет найдено истинное решение.
В качестве дополнительного преимущества описанных здесь вариантов осуществления, поскольку информация о модели Изинг-спина закодирована избыточным образом в квантовой системе, то можно измерить множество возможных групп кубитов, чтобы обеспечить считывание, из которого было получено решение вычислительной задачи.
В свете вышесказанного конструкция гамильтониана ближнего действия в соответствии с этим вариантом осуществления такова, что (i) ограничения охватывают все взаимодействия между спинами, (ii) число ограничений равно (n2 - 3n) / 2 и (iii) гамильтониан ближнего действия может быть реализован на простой двумерной геометрии с взаимодействием d-тела, где d = 4, и где взаимодействия соответствуют плакеткам двумерной решетки. Кроме того, этот вариант осуществления обеспечивает масштабируемую реализацию, поскольку добавление одного спина в модели Изин-спина эквивалентно добавлению линии из n спинов в квантовую систему.
Вариант осуществления, описанный со ссылкой на фиг. 9-12 относится к модели Изин-спина, включающую в себя парные взаимодействия между n спинами, в котором полевые коэффициенты равны нулю. Аналогичная кодировка может быть рассмотрена для модели Изин-спина с ненулевыми полевыми коэффициентами. Дополнительный спин sn + 1 может быть включен в состав модели Изинга, в котором sn + 1 фиксируется на значение +1. Затем ненулевые полевые коэффициенты могут быть переформулированы как коэффициенты соединения между n спинами и дополнительным спином sn + 1 . Таким образом, модель Изинг-спина с ненулевыми полевыми коэффициентами отображается на модель Изинг-спина, где полевые коэффициенты равны нулю. Таким образом, можно применить отображение к квантовой системе описанным выше образом. Добавление дополнительного спина sn + 1 включает в себя дополнительную линию n кубитов в квантовой системе.
Кроме того, кодирование также может быть рассмотрено для модели Изин-спина, включающей в себя взаимодействия между группами из трех спинов. В этом случае, функция энергии Изинга может иметь вид
H(s1, s2, ..., sn) = Σijk cijksisjsk
в котором коэффициенты cijk представляют собой трехтельные взаимодействия между спинами si, sj и sk и где i> j> k. Отображение такой модели Изинга с тремя телами на квантовую систему и кодирование соответствующей задачи модели Изинга в гамильтониан задачи квантовой системы проиллюстрированы на фиг. 13-16. В этом варианте осуществления кубиты в квантовой системе соответствуют тройкам спинов в модели Изинга с тремя телами. В модели Изинга с тремя телами существуют R = n (n-1) (n-2) / 6 тройки спинов. Соответственно, количество кубитов равно R или больше, в котором могут быть использованы дополнительные кубиты, например, вспомогательные кубиты и/или вспомогательные кубиты по аналогии с отображением для модели Изинг-спина с двумя телами, описанной выше. В этом варианте осуществления множество кубитов расположено в соответствии с 3-мерной квадратной решеткой 1601, показанной на фиг. 16. Гамильтониан задачи может иметь вид Σk Jk σz(k), аналогичный случаю модели Изин-спина, большинство двухтельных взаимодействий между спинами. Гамильтониан ближнего действия может иметь вид Σl Cl, в котором ограничительные гамильтонианы С1 соответствуют плакеткам трехмерной квадратной решетки. Число ограничительных гамильтонианов может быть 2 (R - n). Аналогично, это относится к границе квантовой системы, включающей в себя ограничительные гамильтонианы трех тел и/или использование дополнительных кубитов и/или вспомогательных кубитов, применимы и к этому варианту осуществления.
Дополнительным преимуществом описанных здесь вариантов осуществления является предотвращение и/или исправление ошибок в квантовой системе. Например, для небольшой квантовой системы с 4 кубитами, статические ошибки уменьшаются или даже исчезают при С, превышающем 1,5 J, где J = max (| cij |), в частности, для C равным около 1,5 J. Как правило, статические ошибки уменьшается или могут даже исчезнуть, если C больше (n - 2) max (| cij |), где n представляет число спинов в модели Изинга-спина. Кроме того, число кубитов N в квантовой системе больше, чем число спинов в модели Изинга-спина, например, N - n (n-1) / 2 или более. Соответственно, информация о модели Изин-спина кодируется в квантовой системе избыточным образом. Эта избыточность позволяет реализовать измерение с исправлением ошибок с уменьшенной чувствительностью к ошибкам из декогерирования. Измерение нескольких возможных комбинаций кубитов позволяет обнаруживать и корректировать декогеренцию в квантовой системе, подобно схемам коррекции ошибок в топологической квантовой памяти. На фиг. 17 показаны преимущества описанных здесь вариантов осуществления, относящиеся к предотвращению и/или коррекции ошибок в квантовой системе. На фиг. 17 ось 1701 относится к числу спинов n. Ось 1702 относится к масштабированию ошибок. Кроме того, кривые 1710, 1720 и 1730 показывают поведение ошибки, потерю информации и количество переворотов спина соответственно. На вставке ось 1703 относится к числу спинов и ось 1703 относится к числу отсчетов.
В соответствии с дополнительным вариантом осуществления предоставляется блок квантовой обработки [QPU]. Блок квантовой обработки выполнен с возможностью функционировать в качестве центрального процессора в устройствах для решения вычислительных задач. Блок квантовой обработки [QPU] включает в себя квантовую систему, как описано здесь. Квантовая система [QS] включает в себя множество кубитов, как описано здесь. Блок квантовой обработки выполнен с возможностью выполнять способы в соответствии с вариантами осуществления, описанными здесь.
Блок квантовой обработки может быть выполнен с возможностью реализовывать начальный гамильтониан Hinit в начальный момент t = t0. Блок квантовой обработки может дополнительно быть выполнен с возможностью реализовывать конечный гамильтониан Hfinal в конечное время t = tfin. В этом случае, формулировка «реализация гамильтониана» означает, что эти квантовые состояния квантовой системы [QS], которые имеют отношение к квантовой вычислительной функциональности изобретения, в основном определяются соответствующим гамильтонианом, в соответствии с теорией квантовой физики, т.е. свойствами квантовых вычислений квантовой системы [QS], достаточно определяются упомянутыми гамильтонианами, и дополнительные условия в фактическом гамильтониане квантовой системы [QS] пренебрежимо малы относительно функционального принципа изобретения.
Конечным гамильтонианом Hfinal может быть сумма гамильтониана Hprob задачи и гамильтониана HSR ближнего действия, т.е. Hfinal = Hprob + HSR. В этом случае гамильтониан Hprob задачи может быть гамильтонианом одного тела, содержащим (т.е. являющимся функцией) множество регулируемых параметров Jk. Регулируемые параметры Jk могут настраиваться индивидуально таким образом, чтобы кодировать вычислительную задачу.
Гамильтониан HSR ближнего действия может быть гамильтонианом d-тела с d равным или большим, чем 2, и где d может быть независимым от вычислительной задачи. В этом случае термин «гамильтониан ближнего порядка» может относиться к гамильтониану, представляющему взаимодействия нескольких кубитов, в котором происходят взаимодействия между кубитами, которые дистанцированы друг от друга на расстояние больше расстояния Lcut прекращения взаимодействия. Термин «гамильтониан d-тела» может относиться к гамильтониану, представляющему взаимодействие множества кубитов, в котором между группами, содержащими d + 1 или более кубитов, не происходит совместных взаимодействий.
Блок квантовой обработки [QPU] может быть выполнен с возможностью измерять квантовое состояние, по меньшей мере, участка множества кубитов квантовой системы [QS] после времени t = tfin.
Блок квантовой обработки [QPU] может быть выполнен с возможностью реализовывать интерполяционный гамильтониан H (t) вида H(t) = A(t)·H0 + B(t)·Hprob + C(t)·HSR, где A (t), B (t) и C (t) являются интерполяционными коэффициентами, зависящими от временного параметра t, где H0 является инициализирующим гамильтонианом, подходящим для инициализации квантовой системы для требуемого вычислительного процесса. В этом случае A (t), B (t) и C (t) удовлетворяют условиям A (t0) = 1, A (tfin) = 0, B (t0) = 0, B (tfin) = 1, C (tfin) = 1, так что H (t0) = Hinit = H0 + C (t0) • HSR и H (tfin) = Hfin = Hprob + HSR и в котором C (t0) является произвольным значением и может также быть 0 или 1.
Кубиты множества кубитов могут быть расположены в соответствии с 2-мерной решеткой или в соответствии с 3-мерной решеткой.
Кубиты множества кубитов могут быть расположены в углах плакетки соответствующей решетки, где термин «плакетка» может относиться к сеткам соответствующей решетки.
Гамильтониан задачи может иметь вид Hprob = Σk[Jk·σz(k)], где σz(k) может быть оператором Паули, ассоциированным с первым пространственным направлением z (rk), упомянутым оператором σz(k) Паули, действующим на k-ом кубите множества кубитов, и где z может относиться к вектору направления упомянутого первого пространственного направления и где rk обозначает вектор положения k-го кубита.
Инициализирующий гамильтониан H0 может иметь форму, которая подходит для инициализации квантовой системы для желаемого вычислительного процесса и которая предпочтительно легко реализуется. Например, инициализирующий гамильтониан может иметь вид H0 = h Σk[σx(k)], где h - коэффициент, где σx(k) является оператором Паули, ассоциированный со вторым пространственным направлением x (rk), причем упомянутый оператор σx(k) Паули действует на k-м кубите множества кубитов, и где x обозначает вектор направления второго пространственного направления и где rk обозначает вектор положения k-го кубита, где z (rk) и x (rk) предпочтительно взаимно ортогональны и в котором операторы σz(k) и σx(k) Паули предпочтительно являются некоммутирующими, в частности, антикоммутирующими.
Гамильтониан HSR ближнего действия может быть гамильтонианом НР плакетки, который может иметь вид HSR = HP := Σl[Cl(σz(l,1),…,σz(l,m),…,σz(l,M[l]))], где l обозначает номер l-ой плакетки, (l, 1) обозначает кубит, расположенный в первом углу l-ой плакетки, (l, m) обозначает кубит, расположенный в m-ом углу l-ой плакетки и (l, M [l]) обозначает кубит, расположенный на последнем (т.е. M [l]-м) углу l-ой плакетки, где σz(l,m) обозначает оператор Паули соответствующего кубита, и где соответствующий M [l] -тела- слагаемое Cl(σz(l,1),…,σz(l,m),…,σz(l,M)) обозначает дополнение l-ой плакетки в гамильтониан HP плакетки.
Гамильтониан HSR ближнего действия может быть реализован так, что только группы кубитов, образующих плакетку соответствующей кубит-решетки, дополняют слагаемые в HSR = HP и что, например, для кубит-решетки, состоящей только из треугольных плакеток, HSR = НР является гамильтонианом d-тела с d = M = 3, и для кубит-решетки, состоящей из треугольных и четырехугольных плакеток, НР является гамильтонианом, содержащим слагаемые 3-тела и 4 тела и, следовательно, гамильтониан 4-тела.
Блок квантовой обработки [QPU] может включать в себя дополнительные кубиты и/или кутриты и/или q-уровневые квантовые системы и/или другие компоненты и устройства, выполненные с возможностью реализации желаемых характеристик квантовой системы, в частности требуемые признаки гамильтониана HSR ближнего действия и гамильтониана плакетки соответственно.
Решетка, в соответствии с которой расположены кубиты, может представлять собой, по существу, плоскую двумерную решетку или трехмерную решетку, состоящую, по существу, из плоских двумерных подрешеток, которые, по существу, взаимно параллельны и которые уложены по отношению к третьему размеру.
Кубиты могут быть расположены, по существу, на участке треугольной формы 2-мерной решетки, соответственно, в основном на участке треугольной формы каждой двумерной подрешетки.
Множество плакеток, образованных соответствующей компоновкой кубитов, может состоять из (большинства) наборов четырехугольных плакеток и (меньшего) набора треугольных плакеток. Альтернативно или дополнительно, множество плакеток, образованных посредством соответствующей компоновки кубитов, может состоять только из четырехугольных плакеток, например, путем добавления дополнительных кубитов к квантовой системе, которые заполняют все плакетки до четырехугольных.
Слагаемые Cl гамильтониана HP = Σl[Cl] плакеток могут быть одной из двух форм:
i) 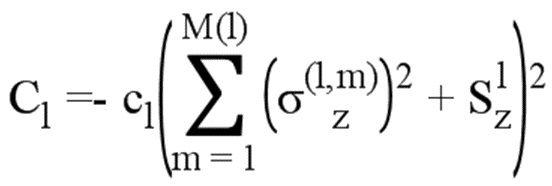 , или
, или
ii) 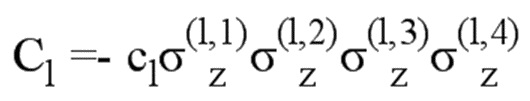 для четырехугольных плакеток и
для четырехугольных плакеток и
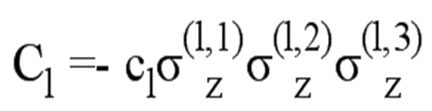 для треугольных плакеток
для треугольных плакеток
где cl является коэффициентом,
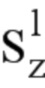 является оператором Паули вспомогательного кутрита.
является оператором Паули вспомогательного кутрита.
Пространственная компоновка кубитов квантовой системы и/или присвоение коэффициентов Jk гамильтониана Hprob задачи пространственным координатам кубитов квантовой системы и/или реализация гамильтониана ближнего порядка и/или выгодное определение участка кубитов, которые измеряются для обеспечения считывания, может выполняться в соответствии с отображением известной модели двухтельного квантового взаимодействия или известной модели квантового взаимодействия трех тел (например, двухтельной или трехтельной модели спина Изинга) на квантовую систему [QS], в частности, в соответствии с ограничениями (например, ограничениями замкнутой петли), выводимыми из упомянутого отображения.
Блок квантовой обработки может быть выполнен с возможностью охлаждать квантовую систему [QS] в основное состояние Hinit: = H (t0).
Блок квантовой обработки может быть выполнен с возможностью охлаждать квантовую систему [QS] в основном состоянии Hfin: = H (tfin).
Блок квантовой обработки может быть выполнен с возможностью охлаждать квантовую систему [QS] в основном состоянии H (t) в любое одно или все время между t = t0 и t = tfin.
Блок квантовой обработки может быть выполнен с возможностью совершенствовать интерполяционный гамильтониан H (t) от Hinit до Hfin, в частности, выполнять упомянутое совершенствование в соответствии с протоколом адиабатического квантового отжига.
Блок квантовой обработки может включать в себя множество сверхпроводящих кубитов, расположенных в соответствии с двумерной решеткой.
Блок квантовой обработки может включать в себя блок смещения магнитного потока, включающий в себя множество блоков смещения магнитного потока, выполненных с возможностью генерировать множества регулируемых магнитных потоков, в котором каждый регулируемый магнитный поток воздействует на один сверхпроводящий кубит во множестве сверхпроводящих кубитов.
Блок квантовой обработки может включать в себя блок соединения, включающий в себя, по меньшей мере, один сверхпроводящий квантовый интерференционный датчик, выполненный с возможностью соединять множества сверхпроводящих кубитов в соответствии с гамильтонианом HP плакетки.
Блок квантовой обработки может включать в себя контроллер, подключенный к блоку смещения магнитного потока и к блоку соединения.
Контроллер может быть выполнен с возможностью принимать конфигурации кодирования задачи для множества регулируемых параметров гамильтониана HP задачи квантовой системы, в котором гамильтониан задачи является гамильтонианом одного тела и в котором конфигурация кодирования задачи кодирует вычислительную задачу, как описано здесь.
Контроллер может быть выполнен с возможностью управлять блоком смещения магнитного потока и блока соединения для совершенствования начального гамильтониана Hinit квантовой системы в конечный гамильтониан Hfin квантовой системы путем квантового отжига, в котором конечным гамильтонианом Hfin является сумма гамильтониана HP плакетки и гамильтониана Hprob задачи, в котором множество регулируемых параметров Jk гамильтониана Hprob задачи находятся в конфигурации кодирования задачи.
В соответствии с вариантами осуществления, описанное здесь устройство выполнено с возможностью выполнять способы в соответствии с описанными в настоящем документе вариантами осуществления.
В соответствии с дополнительными вариантами осуществления предусмотрено устройство для квантовой обработки. Устройство для квантовой обработки может быть выполнено с возможностью вычислять решения вычислительных задач, как описано здесь. Устройство для квантовой обработки включает блок квантовой обработки (QPU). Блок квантовой обработки включает в себя плакетки кубитов. Плакетками могут быть элементарные соты двумерной или трехмерной решетки. Плакетки могут включать в себя не более четырех или не более трех кубитов. Блок квантовой обработки может включать в себя плакетки, включающие в себя кубиты и один или несколько вспомогательных кубитов, например, один вспомогательный кубит, приготовленный в конкретном квантовом состоянии. Кубиты или кубиты и вспомогательный кубит (-ы), в зависимости от обстоятельств, могут быть расположены по углам плакеток. Устройство для квантовой обработки может включать в себя вспомогательные системы q-уровня, например, вспомогательные кутриты, расположенные внутри некоторых или всех плакеток. Вспомогательные системы q-уровня могут опосредовать взаимодействия между кубитами или кубитами и вспомогательным кубитом (-ами) плакеток. Плакетки могут быть расположены так, чтобы образовывать квадратную решетку или ее часть. В частности, плакетки могут быть расположены с образованием треугольного участка квадратной решетки.
Блок квантовой обработки может дополнительно включать в себя первое устройство, включающее в себя блоки, которые взаимодействуют с одиночными кубитами или вспомогательными кубитами, и второе устройство, включающее в себя блоки, которые взаимодействуют с кубитами плакетки или кубитами и вспомогательным кубитом (-ми) плакетки. Первое устройство может быть выполнено с возможностью реализовывать гамильтониан одного тела на кубитах плакеток, или кубитах и вспомогательном кубите (ах) плакеток. Второе устройство может быть выполнено с возможностью реализовывать гамильтониан плакетки на кубитах плакетки или кубитах и вспомогательном кубите (ах) плакеток.
В соответствии с некоторыми вариантами осуществления кубиты представляют собой сверхпроводящие кубиты. Вспомогательный кубит (ы), если они имеются, также могут быть сверхпроводящими кубитами. Плакетки устроены так, чтобы образовывать двумерную квадратную решетку или участок из них, в частности, ее треугольный участок. Блок квантовой обработки включает в себя блок смещения магнитного потока, содержащий множество блоков смещения магнитного потока, выполненные с возможностью генерировать множества регулируемых магнитных потоков, в котором каждый регулируемый магнитный поток воздействует на один сверхпроводящий кубит плакетки. Узел смещения магнитного потока может быть выполнен с возможностью реализовывать гамильтониан одного тела на сверхпроводящих кубитах или сверхпроводящих кубитах и сверхпроводящем вспомогательном кубите (кубитах) плакеток 2-мерной или трехмерной решетки. Блок квантовой обработки включает в себя сверхпроводящие квантовые интерференционные датчики, в котором каждый квантовый интерференционный датчик соединяет сверхпроводящие кубиты плакетки или сверхпроводящие кубиты и сверхпроводящий вспомогательный кубит (кубиты) плакетки. Квантовый интерференционный датчик может обеспечивать контролируемое взаимодействие сверхпроводящих кубитов плакетки или сверхпроводящих кубитов и сверхпроводящего вспомогательного кубита (ов) плакетки. Квантовые интерференционные датчики могут быть компонентами блока квантового соединения, выполненного с возможностью реализовывать гамильтониан плакетки на плакетках двумерной или трехмерной решетки.
Блок квантовой обработки (QPU) может быть выполнен с возможностью выполнять способы вычисления решения вычислительных задач, как описано здесь. Устройство для квантовой обработки может дополнительно включать в себя такие компоненты, как блок охлаждения, классическое вычислительное устройство и контроллер, как описано здесь. Например, контроллер может быть подключен к блоку смещения магнитного потока и к блоку соединения и может быть выполнен с возможностью: (i) принимать конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи квантовой системы, где гамильтониан задачи является гамильтонианом одного тела и в котором конфигурация кодирования задачи кодирует вычислительную задачу; и (ii) управлять блоком смещения магнитного потока и блоком соединения для совершенствования начального гамильтониана квантовой системы в конечный гамильтониан квантовой системы путем квантового отжига, в котором конечным гамильтонианом является сумма гамильтониана плакетки и гамильтониан задачи, в котором множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи.
Варианты осуществления, описанные здесь, могут быть реализованы не только с помощью кубитов (т.е. двухуровневых квантовых битов), но также с кутритами или квантовых систем q-уровня с произвольным q. Различные способы реализации квантовой системы с использованием, например, сверхпроводящих кубитов, захваченных ионов, квантовых точек и NV-центров могут быть распространены на системы q-уровня, в частности на кутрит-системы, посредством учета более двух состояний. Манипулирование и считывание систем q-уровня и взаимодействия между ними могут быть реализованы посредством расширений вариантов осуществления, описанных выше.
Хотя вышеизложенное относится к некоторым вариантам осуществления изобретения, могут быть разработаны другие и дополнительные варианты осуществления, не выходящие за пределы объема, определенного формулой изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА И МЕТОД КОНТРОЛЯ ВЗАИМОДЕЙСТВИЯ МЕЖДУ СВЕРХПРОВОДНИКОВЫМИ КУБИТАМИ НА ОСНОВЕ ВЫСОКОЙ КИНЕТИЧЕСКОЙ ИНДУКТИВНОСТИ | 2022 |
|
RU2803401C1 |
| СПОСОБ И СИСТЕМА КОМПЕНСАЦИИ ШУМОВ НА КВАНТОВОМ ПРОЦЕССОРЕ С ПОМОЩЬЮ КВАНТОВОЙ ТОМОГРАФИИ ОПЕРАЦИЙ | 2022 |
|
RU2786349C1 |
| Способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов | 2023 |
|
RU2825968C1 |
| СПОСОБ ФОРМИРОВАНИЯ КУБИТА | 2018 |
|
RU2716028C1 |
| СПОСОБ И СИСТЕМА РАСПРЕДЕЛЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ В ОБЛАЧНОЙ СРЕДЕ | 2024 |
|
RU2826431C1 |
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| Устройство для реализации двухкубитного вентиля CZ между сверхпроводниковыми кубитами на основе высокой кинетической индуктивности | 2022 |
|
RU2795679C1 |
| ДВУХЭЛЕКТРОДНЫЙ БЫСТРОПЕРЕСТРАИВАЕМЫЙ ПО ПОТОКУ СВЕРХПРОВОДНИКОВЫЙ КУБИТ НА ОСНОВЕ КИНЕТИЧЕСКОЙ ИНДУКТИВНОСТИ | 2021 |
|
RU2780666C1 |
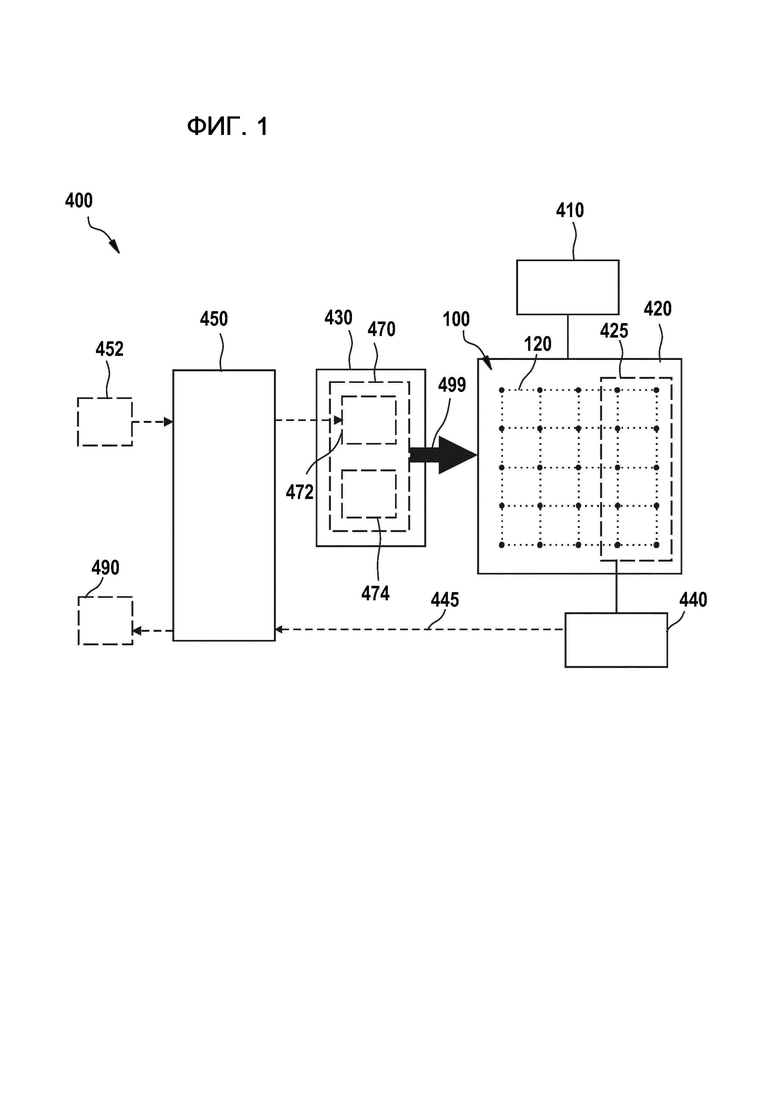
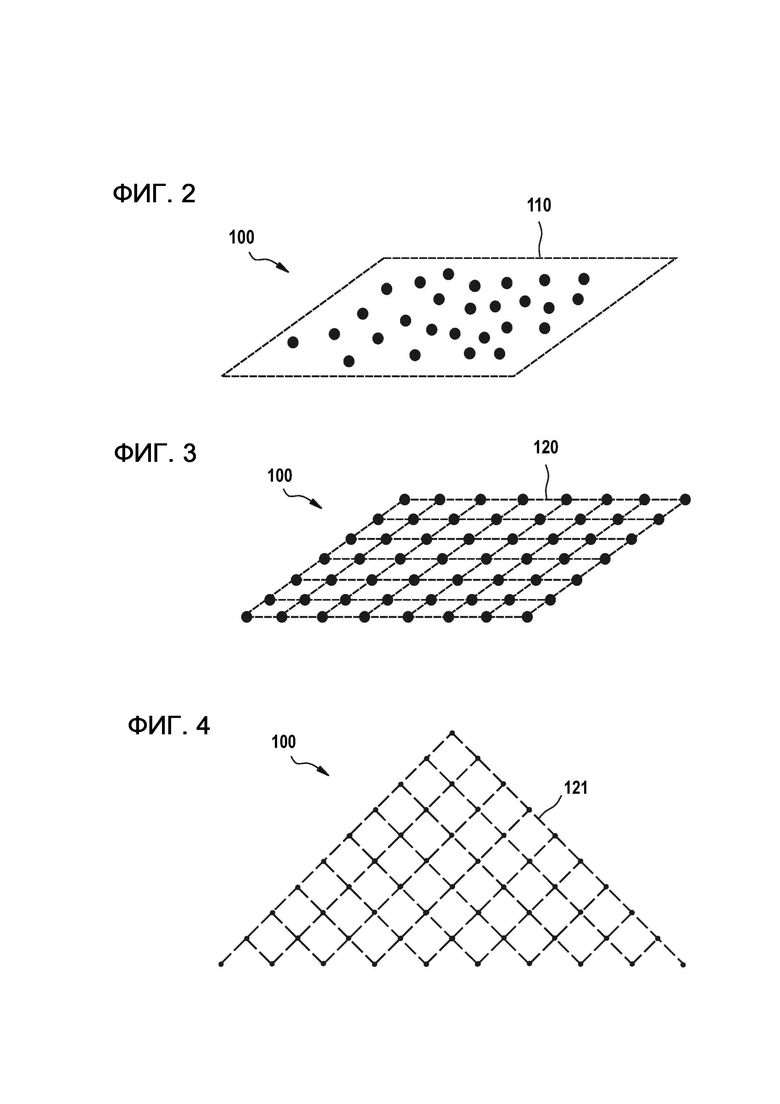
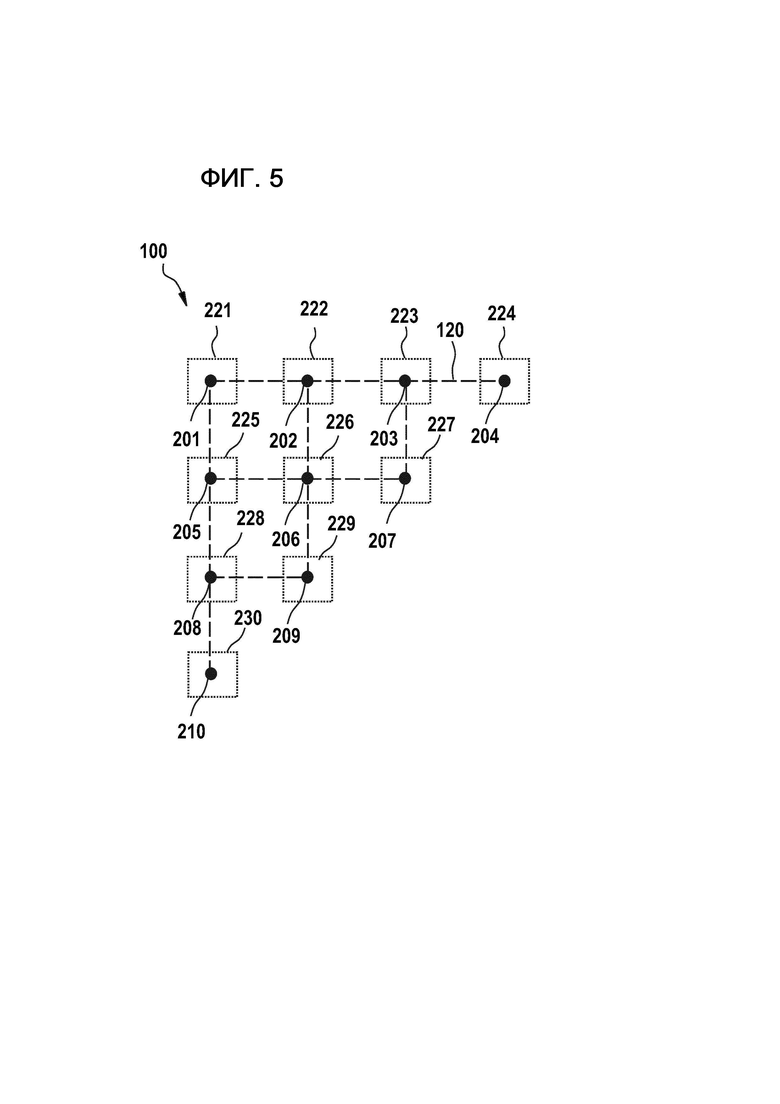
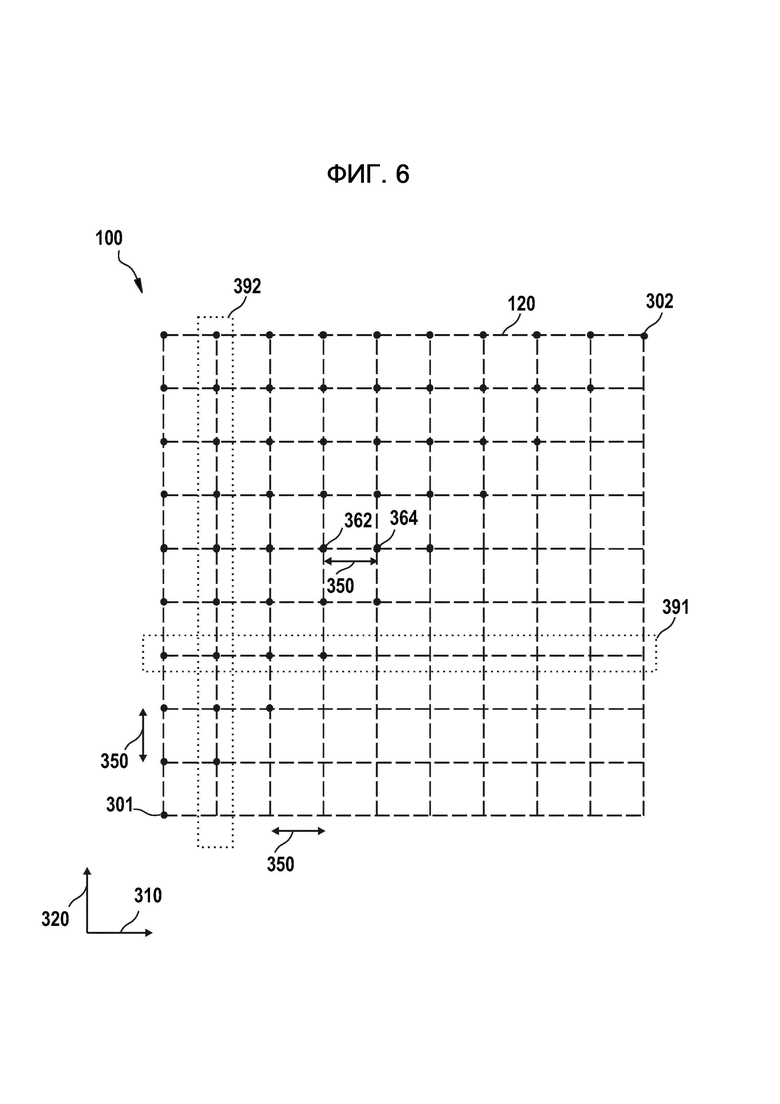
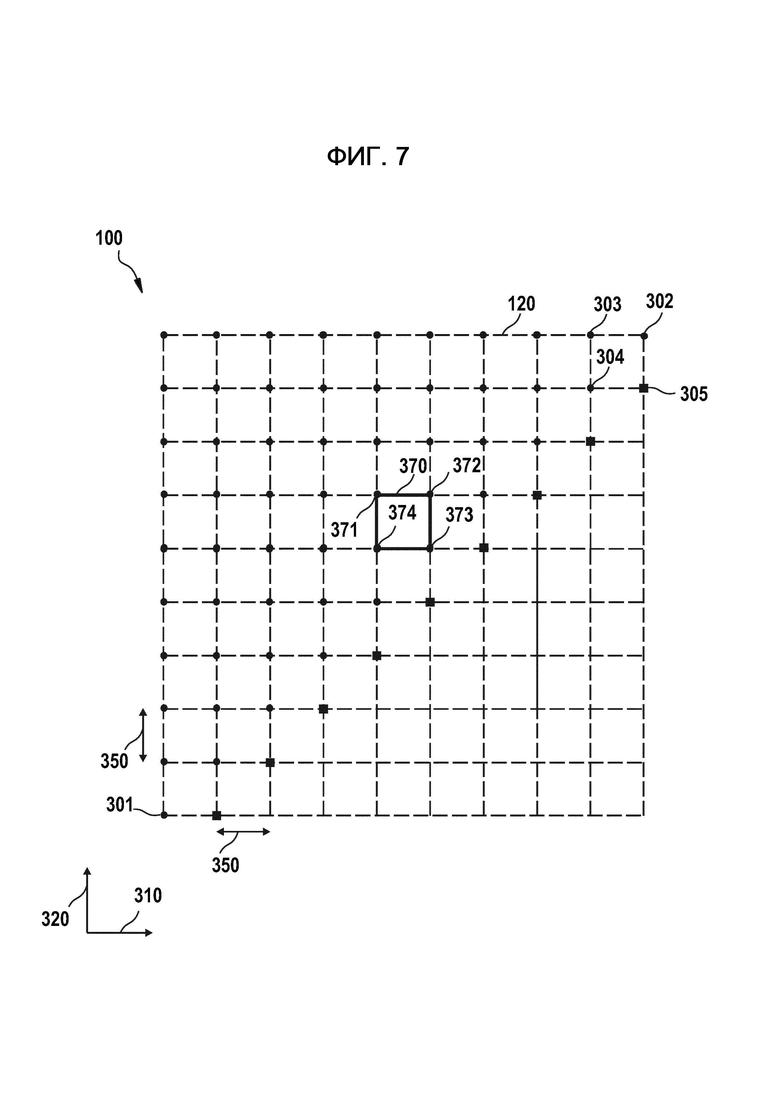
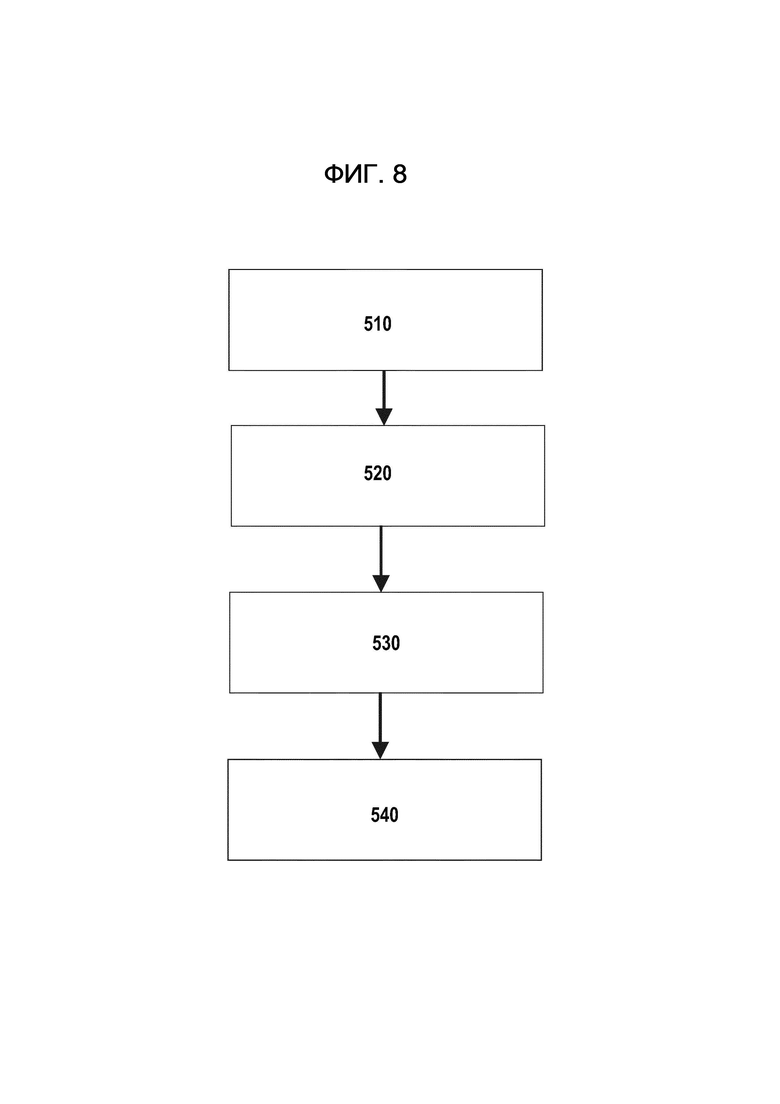
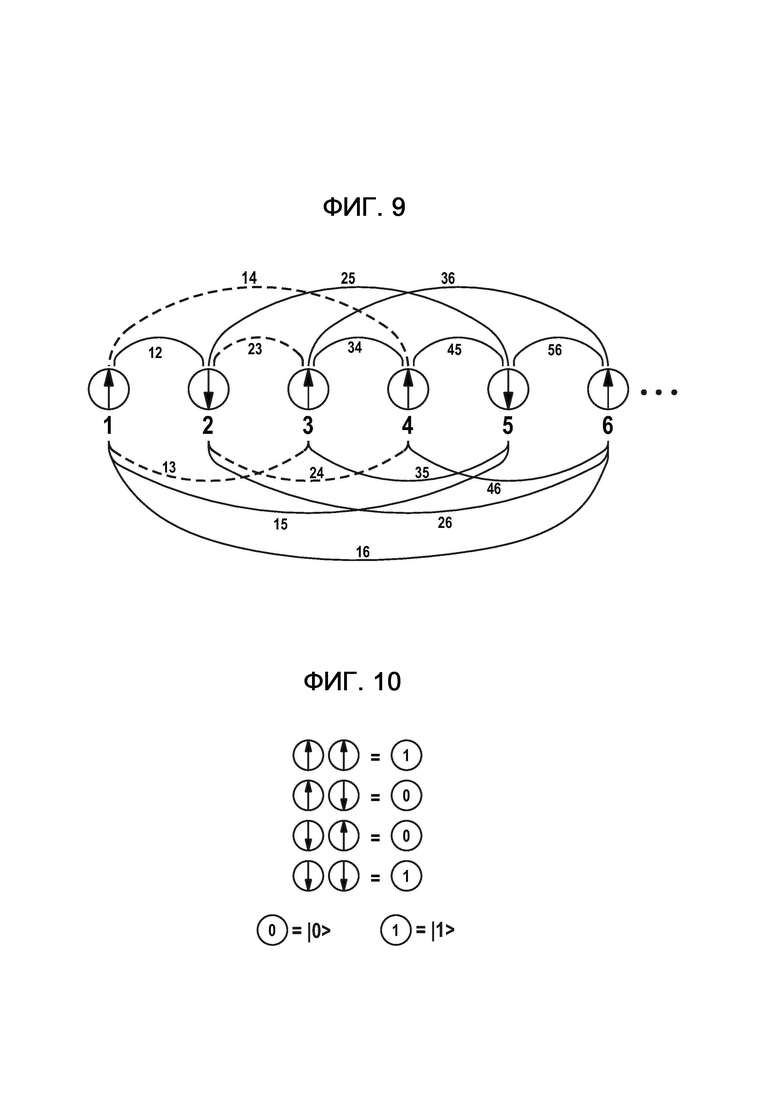
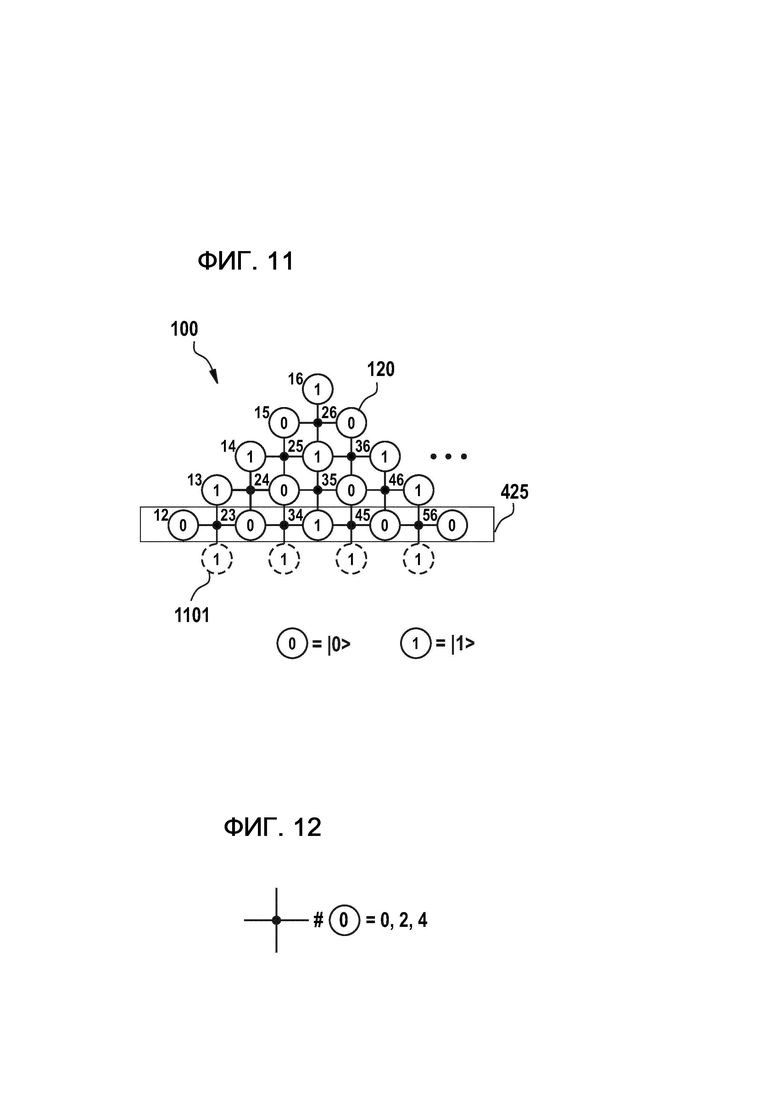
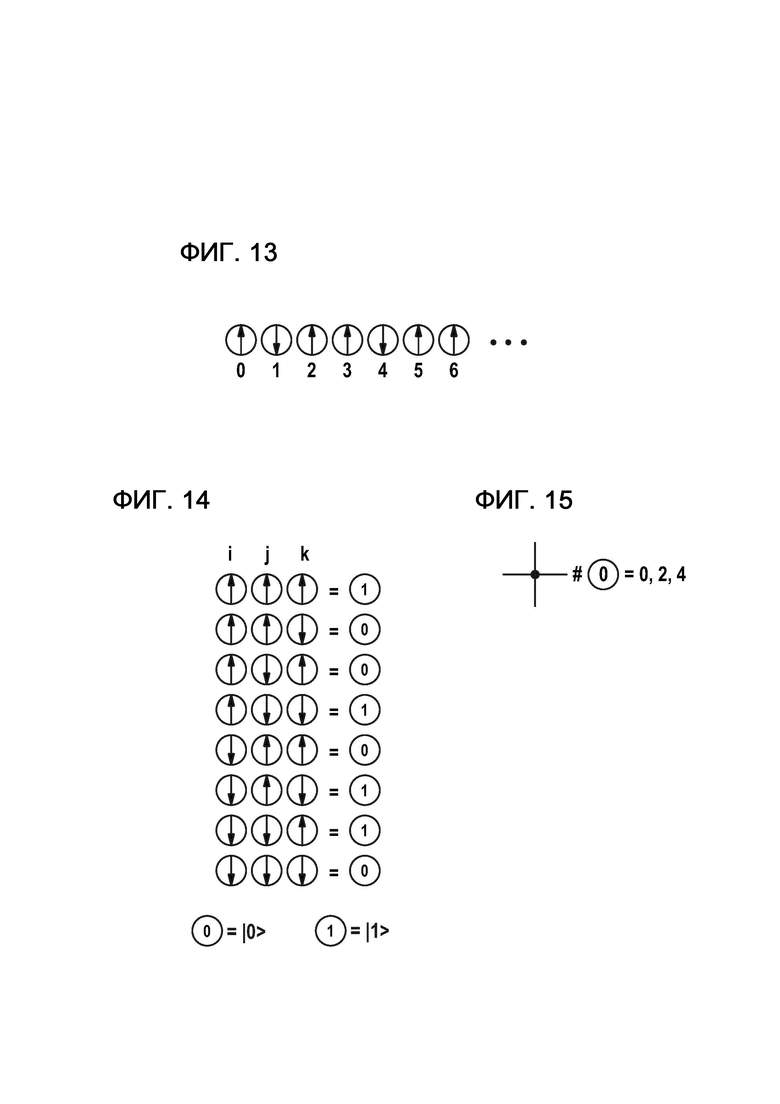
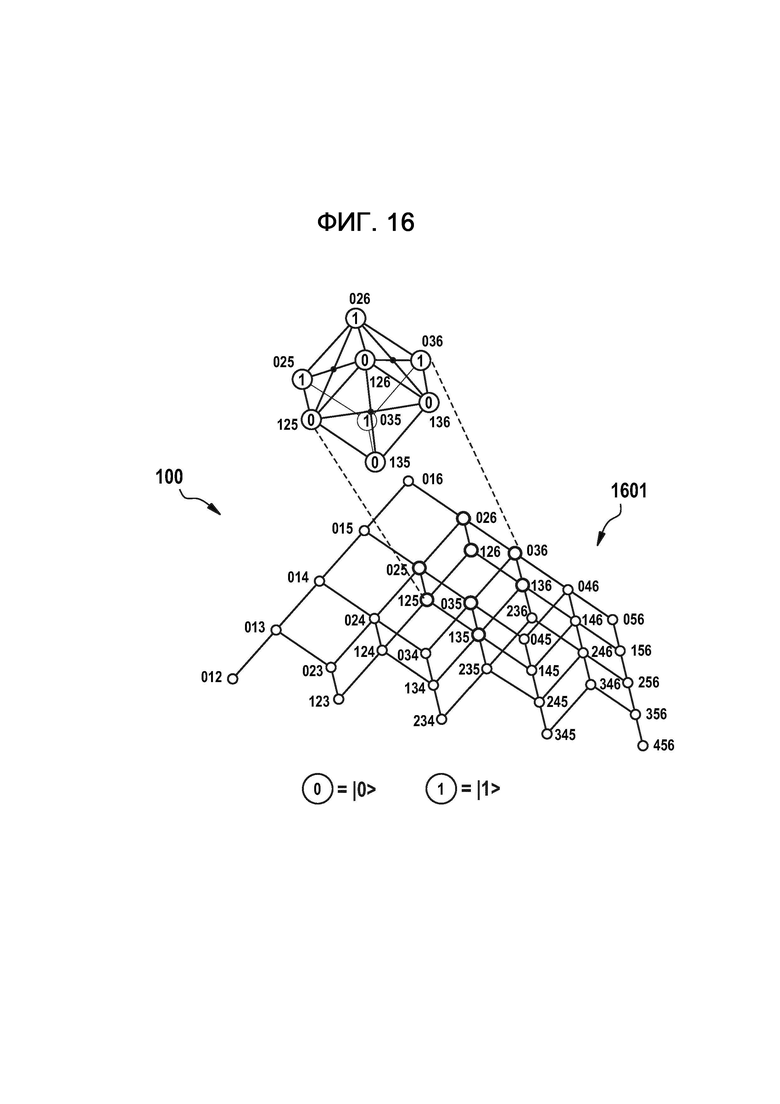
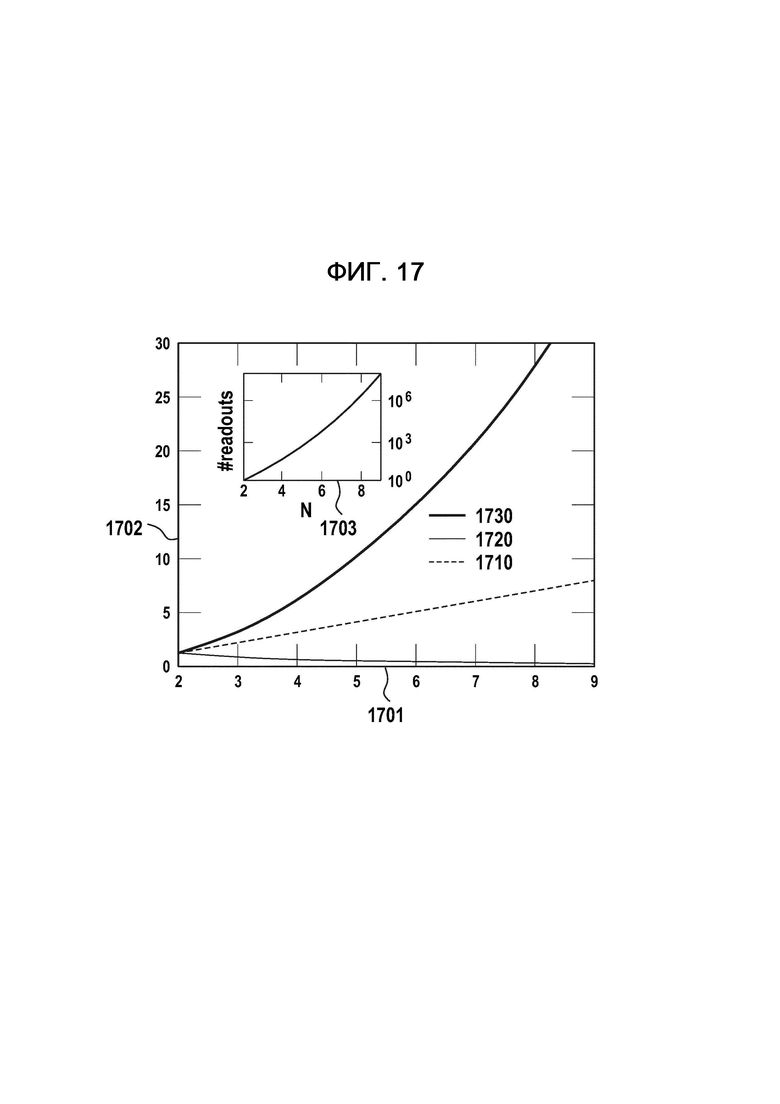
Изобретение относится к квантовым вычислительным системам. Технический результат направлен на расширение арсенала технических средств вычисления и решения вычислительной задачи с использованием квантовой системы. Технический результат достигается за счет кодирования вычислительной задачи в гамильтониан задачи квантовой системы, совершенствования квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана квантовой системы, измерения по меньшей мере участка множества кубитов для получения данных считывания квантовой системы и определения решения вычислительной задачи из данных считывания, причем множество регулируемых параметров гамильтониана задачи находятся в конфигурации кодирования задачи, при этом гамильтониан ближнего порядка является гамильтонианом d-тела и d не зависит от вычислительной задачи. 3 н. и 12 з.п. ф-лы, 17 ил.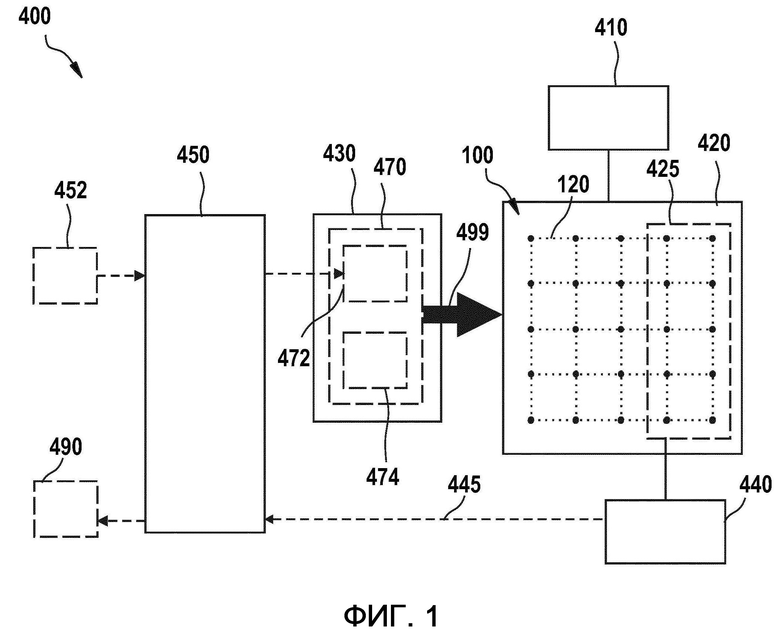
1. Способ вычисления решения вычислительной задачи с использованием квантовой системы, содержащей множество кубитов, содержащий этапы, на которых:
кодируют вычислительную задачу в гамильтониан задачи квантовой системы, причем гамильтониан задачи является гамильтонианом одного тела, содержащим множество регулируемых параметров, а этап кодирования содержит подэтап, на котором определяют, из вычислительной задачи, конфигурации кодирования задачи для множества регулируемых параметров;
совершенствуют квантовую систему из начального квантового состояния в основное состояние конечного гамильтониана квантовой системы, причем конечный гамильтониан представляет собой сумму гамильтониана задачи и гамильтониана ближнего порядка, а множество регулируемых параметров гамильтониана задачи находятся в конфигурации кодирования задачи, при этом гамильтониан ближнего порядка является гамильтонианом d-тела и d не зависит от вычислительной задачи;
измеряют по меньшей мере участок множества кубитов для получения данных считывания квантовой системы и
определяют решение вычислительной задачи из данных считывания.
2. Способ по п. 1, в котором этап совершенствования квантовой системы из начального квантового состояния в основное состояние конечного гамильтониана содержит подэтап, на котором осуществляют переход от начального гамильтониана квантовой системы к конечному гамильтониану посредством квантового отжига.
3. Способ по п. 2, дополнительно содержащий этап, на котором инициализируют квантовую систему в начальном квантовом состоянии посредством охлаждения квантовой системы до основного состояния начального гамильтониана.
4. Способ по любому из пп. 1-3, в котором множество регулируемых параметров содержит множество напряжений поля и/или множество направлений поля полей одного тела, действующих на множество кубитов.
5. Способ по любому из пп. 1-4, в котором этап квантового отжига от начального гамильтониана до конечного гамильтониана содержит подэтап, на котором осуществляют адиабатическое совершенствование начального гамильтониана в конечный гамильтониан.
6. Способ по любому из пп. 1-5, в котором гамильтониан ближнего порядка представляет собой гамильтониан d-тела, при этом d = 4.
7. Способ по любому из пп. 1-6, в котором гамильтониан ближнего порядка не зависит от вычислительной задачи.
8. Способ по любому из пп. 1-7, в котором множество кубитов расположены в соответствии с двумерной решеткой или в соответствии с трехмерной решеткой.
9. Способ по любому из пп. 1-8, в котором множество кубитов расположены в соответствии с двумерной решеткой, а гамильтониан ближнего порядка включает в себя взаимодействия между группами из четырех кубитов, соответствующих плакеткам двумерной решетки.
10. Способ по любому из пп. 1-9, в котором вычислительная задача является NP-сложной задачей.
11. Способ по любому из пп. 1-10, в котором гамильтониан задачи имеет вид Σk Jk σz(k), в котором σz(k) является оператором Паули k-го кубита множества кубитов, где каждый Jk является коэффициентом и коэффициенты Jk образуют множество регулируемых параметров гамильтониана задачи.
12. Способ по любому из пп. 1-11, в котором этап определения конфигурации кодирования задачи содержит подэтапы, на которых:
отображают вычислительную задачу на вспомогательную вычислительную задачу, причем вспомогательная вычислительная задача содержит определение основного состояния модели спина дальнего порядка, в частности модели спина дальнего порядка с взаимодействием m-тела, в котором m равно 1, 2 или 3; и
определяют конфигурацию кодирования задачи из модели спина дальнего порядка.
13. Способ по п. 12, дополнительно содержащий этап, на котором:
определяют гамильтониан ближнего порядка из множества замкнутых петель спинов в модели спина дальнего порядка.
14. Устройство решения вычислительных задач, содержащее:
квантовую систему, содержащую множество кубитов;
блок охлаждения, выполненный с возможностью охлаждения квантовой системы в основное состояние квантовой системы;
программируемый блок квантового отжига, выполненный с возможностью совершенствования, посредством квантового отжига начального гамильтониана квантовой системы в конечный гамильтониан квантовой системы, при этом конечный гамильтониан представляет собой сумму гамильтониана задачи и гамильтониана ближнего порядка, при этом гамильтониан задачи является гамильтонианом одного тела, содержащим множество регулируемых параметров;
измерительное устройство, выполненное с возможностью измерения по меньшей мере участка множества кубитов и
классическую вычислительную систему, соединенную с программируемым блоком квантового отжига и измерительным устройством, при этом классическая вычислительная система выполнена с возможностью:
приема в качестве входных данных вычислительной задачи;
кодирования вычислительной задачи в гамильтониан задачи, причем кодирование содержит определение из вычислительной задачи конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи; и
передачи конфигурации кодирования задачи в блок квантового отжига; а
программируемый блок квантового отжига выполнен с возможностью:
приема конфигурации кодирования задачи от классической вычислительной системы и
совершенствования, посредством квантового отжига, начального гамильтониана в конечный гамильтониан, при этом множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи; при этом
классическая вычислительная система дополнительно выполнена с возможностью:
приема данных считывания квантовой системы от измерительного устройства и
определения решения вычислительной задачи из данных считывания.
15. Программируемое устройство квантового отжига для вычисления решений вычислительных задач, содержащее:
квантовую систему, содержащую множество сверхпроводящих кубитов, расположенных в соответствии с двумерной решеткой;
узел смещения магнитного потока, содержащий множество блоков смещения магнитного потока, выполненных с возможностью генерирования множества регулируемых магнитных потоков, при этом каждый регулируемый магнитный поток выполнен с возможностью воздействия на один сверхпроводящий кубит из множества сверхпроводящих кубитов;
блок соединения, содержащий по меньшей мере один сверхпроводящий квантовый интерференционный датчик, выполненный с возможностью соединения множества сверхпроводящих кубитов в соответствии с гамильтонианом плакетки; и
контроллер, соединенный с блоком смещения магнитного потока и блоком соединения и выполненный с возможностью:
приема конфигурации кодирования задачи для множества регулируемых параметров гамильтониана задачи квантовой системы, причем гамильтониан задачи является гамильтонианом одного тела, а конфигурация кодирования задачи кодирует вычислительную задачу; и
управления узлом смещения магнитного потока и блоком соединения для совершенствования начального гамильтониана квантовой системы в конечный гамильтониан квантовой системы посредством квантового отжига, причем конечный гамильтониан представляет собой сумму гамильтониана плакетки и гамильтониана задачи, при этом множество регулируемых параметров гамильтониана задачи находится в конфигурации кодирования задачи.
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| US 8190548 B2, 29.03.2012 | |||
| US 8195596 B2, 05.06.2012 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ КУБИТА | 2013 |
|
RU2538296C2 |
| Самоходный погрузчик | 1958 |
|
SU119479A1 |
Авторы
Даты
2021-02-08—Публикация
2016-06-28—Подача