Область техники
Изобретение относится к области управления движением космических аппаратов с помощью реактивной силы, создаваемой двигательной установкой большой тяги, и с использованием возмущений от Луны, Солнца, нецентральности (или синоним: несферичности потенциала) земного гравитационного поля»земного гравитационного поля, светового давления, приводящих к долгопериодическим колебаниям наклонения орбит пассивных объектов в окрестности геостационарной орбиты.
Уровень техники
Известен аналог - патент RU 2531679 С2 (Опубликовано: 27.10.2014 Бюл. №30). Изобретение относится к ракетно-космической технике и может быть использовано для увода с рабочих орбит объектов космического мусора (ОКМ) на орбиты утилизации. Способ включает выведение космического аппарата-буксира (КАБ) и автономного стыковочного модуля (АСМ) в области орбит, предназначенных для очистки от ОКМ. Выбор последовательности увода ОКМ осуществляют путем сравнения критерия, например, вероятности столкновения ОКМ с другими космическими объектами, для каждого ОКМ. Компенсацию накопленных ошибок параметров движения КАБ при предыдущих маневрах, а также системы целеуказания распределяют между корректирующими импульсами КАБ на этапе дальнего наведения и АСМ на участке самонаведения.
Недостатком является то, что выбор последовательности увода ОКМ осуществляют путем сравнения вероятности столкновения ОКМ с другими космическими объектами. При этом никак не учитывается геометрическая конфигурация орбитальных плоскостей ОКМ, которая определяет величину импульсов скорости, необходимых для перелета между орбитами. На длительном временном интервале, требуемом для перелета к очередному ОКМ, точно определить вероятность столкновения невозможно.
Известен аналог - патент RU 2562908 С2 (Опубликовано: 10.09.2015 Бюл. №25). Изобретение относится к космической технике и может быть использовано при сближении и последующей стыковке двух космических объектов. Способ включает определение величины и места приложения отлетного импульса перед переводом активного космического аппарата (АКО) на траекторию полета к другому небесному телу, исходя из условия пересечения АКО орбиты пассивного космического аппарата (ПКО). Затем АКО переводят на орбиту другого небесного тела путем одновременного приложения к нему тормозного импульса (для обеспечения заданных параметров по высоте орбиты) и бокового импульса (для совмещения плоскостей орбит стыкующихся объектов). На фоне большого тормозного импульса незначительный боковой импульс практически не приведет к увеличению затрат топлива АКО, но существенно сократит время полета АКО до стыковки с ПКО.
Недостатком является то, что орбиты активного и пассивного объектов должны обязательно пересекаться. В задаче облета объектов крупногабаритного космического мусора орбиты в общем случае не пересекаются. Кроме того, в случае предлагаемого способа величина корректируемого угла между плоскостями АКО и ПКО варьируется от долей градуса до нескольких десятков градусов, следовательно, прямая коррекция этого угла потребует приложения больших (порядка 1 км/с) боковых импульсов скорости.
Известен аналог - патент RU 2688120 С1 (Опубликовано: 17.05.2019 Бюл. №14). Изобретение относится к пространственным маневрам космических аппаратов (КА) в нецентральном гравитационном поле Земли при сближении с объектами космического мусора (ОКМ). Схему облета ОКМ выбирают на основе портрета эволюции отклонений долгот восходящих узлов (ДВУ) орбит ОКМ. Если данный портрет имеет вид квазипараллельных линий, то применяют последовательную схему, переводя активный КА на орбиту ожидания с измененной скоростью прецессии линии узлов. При многократном пересечении указанных линий на портрете применяют диагональную схему - когда орбита очередного уводимого ОКМ служит орбитой ожидания КА для достижения следующего ОКМ.
Недостатком является то, что указанный способ применим только для низких орбит, где изменение ДВУ за виток может достигать нескольких десятых градуса. В окрестности геостационарной орбиты скорость прецессии ДВУ необходимо учитывать, но она чрезвычайно мала, поэтому этот способ непригоден.
Известен аналог - статья Alfriend K.Т., Lee D.-J., Creamer N.G. "Optimal Servicing of Geosynchronous Satellites" // Journal of Guidance, Control and Dynamics, 2006, Vol. 29, No. 1, pp. 203-206. В статье рассмотрена задача обслуживания спутников, находящихся на геостационарной орбите (ГСО). Критерием оптимальности исполняемых маневров выбрана минимизация массы расходуемого топлива, а сама последовательность перелета определяется на основе решения задачи коммивояжера. С учетом малости компланарных составляющих маневров, анализ проводится только по бинормальным составляющим.
Недостатком является то, что рассмотрены преимущественно орбиты с фиксированным малым наклонением, в то время как наклонение пассивного объекта в окрестности ГСО под действием возмущений от Земли, Луны и Солнца совершает долгопериодические колебания от 0 до примерно 17 градусов. Кроме того, в классической задаче коммивояжера не учитывается изменение положения объектов с течением времени. Так как активный КА выполняет перелеты не вдоль идеальной ГСО, а внутри ее окрестности (при этом большая полуось орбиты может изменяться на несколько сотен километров), то пренебрегать компланарными составляющими импульсов скорости некорректно.
Известен аналог - статья Jing Yu, Xiao-qian Chen, Li-hu Chen. "Biobjective planning of GEO debris removal mission with multiple servicing spacecraft" // Acta Astronautica, Vol. 105 (2014), pp. 311-320. В статье предполагается, что увод объекта на орбиту захоронения выполняется активным космическим аппаратом (КА), который затем возвращается за новым объектом, при этом количество КА-сборщиков варьируется. Для поиска оптимальной последовательности перелета используется гибридно-оптимальное управление, позволяющее получить последовательность двухимпульсных маневров с одновременной оптимизацией затрат СХС и продолжительности перелетов.
Недостатком является полное отсутствие наглядности полученного решения: используются громоздкие численные методы, которые не позволяют объяснить физические основы полученного решения. В работе не рассмотрен сценарий, при котором активный КА выполняет только перелеты между ОКМ, а их увод на орбиту захоронения происходит за счет специальных двигательных модулей, хранящихся на борту активного КА и закрепляемых на уводимом объекте.
Известен более близкий аналог - статья Баранов А.А., Гришко Д.А. и др. "Перелеты между объектами космического мусора в окрестности геостационарной орбиты" // Препринты ИПМ им. М.В. Келдыша РАН, 2018, №190, 27 с. http://library.keldysh.ru/preprint.asp?id=2018-190. В препринте введен портрет эволюции наклонений, предложены схемы облета крупных ОКМ в окрестности ГСО, основанные на свойствах эволюции наклонения орбит. Составлены перелетные пары начальных и конечных орбит для каждой рассмотренной схемы облета.
Недостатком является то, что были получены только оценки маневров активного КА: расчеты выполнены с использованием предельно простых формул, не учитывающих нюансы некомпланарных переходов между околокруговыми орбитами, где присутствует необходимость коррекции вектора эксцентриситета. В работе приведены вычисления только для сценария, при котором активный КА выполняет перелеты между ОКМ, не уводя их на орбиту захоронения.
Известен еще один более близкий аналог - статья Baranov А.А., Grishko D.A. et al. "Optimal transfer schemes between space debris objects in geostationary orbit" // Acta Astronautica, 2020, Vol. 169, pp. 23-31. В статье рассмотрены схемы перелета, основанные на использовании портрета эволюции наклонений. Маневры перехода между орбитами выполняются в приэкваториальной области и рассчитываются по формулам околокругового движения. Рассмотрен как сценарий облета ОКМ в окрестности ГСО, так и облет с их уводом на орбиту захоронения.
Недостатком является то, что параметры маневров не уточняются в точной модели движения. В данной работе решается задача перехода, которая эквивалентна задаче встречи только при оптимальном значении фазовой разницы между активным космическим аппаратом и ОКМ. Кроме того, в качестве крупных ОКМ рассмотрены только разгонные блоки, в то время как заявляемый способ можно применить к группе любых пассивных космических объектов.
Раскрытие изобретения
Задачей предлагаемого способа является устранение недостатков аналогов, а именно:
- распространение способа определения последовательности перелета на все типы ОКМ в окрестности ГСО;
- создание единой методики для поиска близких к оптимальным схем облета группы ОКМ в окрестности ГСО;
- определение продолжительности миссии по уводу ОКМ из защищаемой зоны ГСО при минимальных затратах СХС на ее осуществление;
- обеспечение точного расчета маневров встречи активного КА и ОКМ при некомпланарном перелете между двумя околокруговыми орбитами в окрестности ГСО.
Задачей является построение наиболее выгодных схем облета группы объектов космического мусора (ОКМ) при точном расчете маневров активного космического аппарата (КА) и, таким образом, уменьшение затрат суммарной характеристической скорости (СХС) при осуществлении перелетов между каждой парой и всеми ОКМ. Это позволяет при заданных возможностях конкретного КА облететь наибольшее число ОКМ.
Для решения задачи предлагается способ определения последовательности перелетов активного КА между объектами космического мусора в окрестности геостационарной орбиты. При этом схемы облета и последовательность перелетов выбираются на основе вида портрета эволюции наклонений орбит ОКМ. Он представляет собой совокупность линий, описывающих изменение угла между экватором и плоскостью орбиты каждого ОКМ с течением времени. Для ОКМ из окрестности ГСО такой портрет представляет собой долгопериодические (около 50 лет) колебания наклонения в диапазоне примерно [0°-17°]. Схему облета строят так, чтобы активный КА не покидал приэкваториальную область, то есть в процессе перелетов между объектами наклонение его орбиты не превышало 1°.
В основе способа лежит использование свойств сферического треугольника, который образуют плоскость экватора, а также плоскости начальной и конечной орбит на небесной сфере. Угол между двумя последними плоскостями зависит от наклонения орбит, а также от их отличия в долготе восходящего узла (ДВУ). При околонулевых наклонениях угол между плоскостями орбит также близок к нулю и мало чувствителен к отличию в ДВУ, что позволяет поворачивать орбитальную плоскость с минимальными затратами СХС. Это дает возможность предложить две схемы облета. Схема А (первая схема) подразумевает перелеты между объектами, когда наклонения их орбит близки к нулю и равны. В схеме В (вторая схема) активный КА находится на орбите текущего ОКМ до тех пор, пока наклонение орбиты следующего объекта не достигнет минимума, при этом в этот момент времени обе орбиты должны располагаться в приэкваториальной области. Так как обе описанные схемы основаны на одном и том же принципе маневрировании при близких нулю наклонениях, то рекомендуется выполнить расчет отдельно по каждой схеме.
Если активный КА должен только облететь ОКМ, то далее для конкретной схемы облета составляют перелетные пары, содержащие актуальные Кеплеровы элементы начальной и конечной орбит для каждого перелета между двумя объектами. После этого определяют параметры маневров, которые обеспечивают перелет между этими объектами, уточнение параметров маневров осуществляют с использованием итерационной процедуры, позволяющей решить задачу встречи.
Если активный КА должен увести ОКМ на орбиту захоронения, а уже с нее возвращаться за новым объектом, то в расчет маневров вносятся изменения, при этом схемы и последовательность облета остаются теми же. Находясь на орбите текущего объекта, активный КА захватывает его и ждет, когда выполнится основное условие из первой схемы А или второй схемы В. Незадолго до этого момента он осуществляет увод текущего объекта на орбиту захоронения и с нее потом перелетает к следующему объекту. Вследствие того, что эволюция наклонения орбит в окрестности ГСО происходит с очень малой скоростью (изменение не более 0.1° в течение 5 суток), такая последовательность действий не изменяет величину бинормальных составляющих маневров по сравнению со случаем последовательного облета объектов. Трансверсальные составляющие маневров, обеспечивающие перелет с орбиты захоронения к следующему объекту, также практически не изменяются. Добавляются только отдельно исполняемые трансверсальные маневры, обеспечивающие перевод объекта на орбиту захоронения без поворота плоскости движения активного КА.
Перечень фигур
На фиг. 1 представлен портрет эволюции наклонений, характерный для крупных ОКМ из окрестности ГСО. Под действием различного рода возмущений наклонения орбит совершают долгопериодические колебания.
На фиг. 2 представлен сферический треугольник, который связывает угол между плоскостями двух орбит с их наклонениями, а также отличием в долготе восходящего узла.
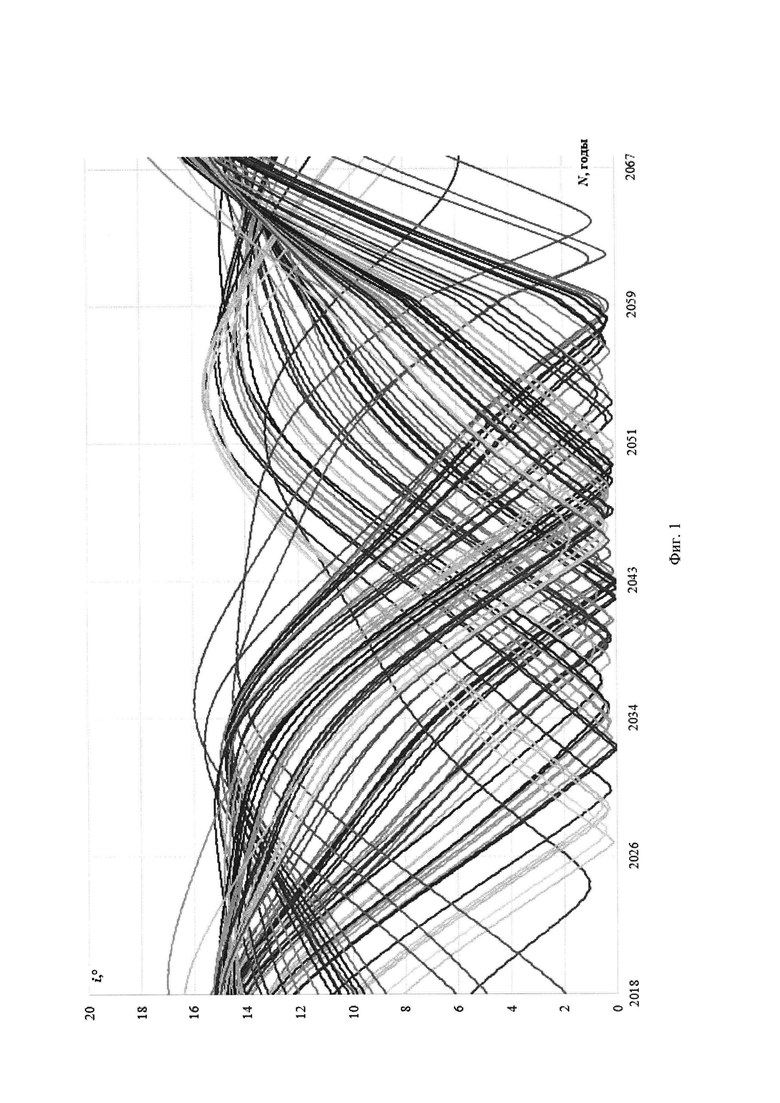
На фиг. 3 представлена в сильном увеличении нижняя (приэкваториальная) часть портрета эволюции наклонений, на которой показан принцип составления схемы облета А: перелеты между объектами выполняются в момент равенства наклонений их орбит, при этом сами наклонения близки к нулю.
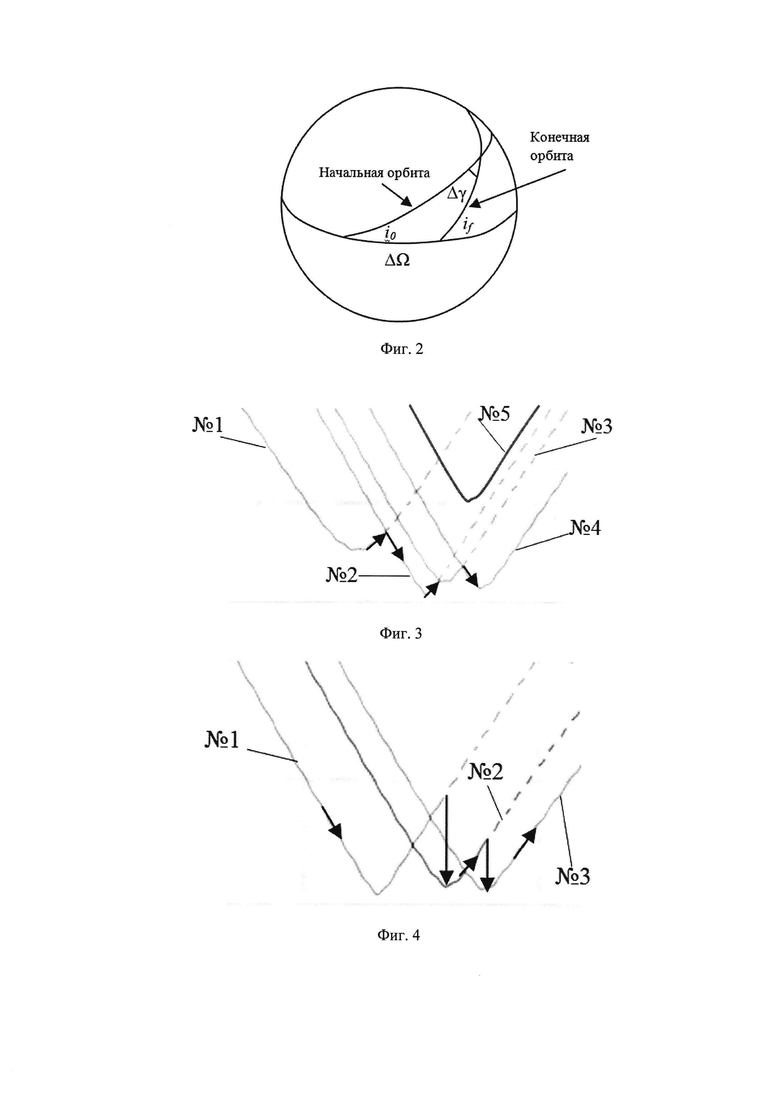
На фиг. 4 представлена в сильном увеличении нижняя (приэкваториальная) часть портрета эволюции наклонений, на которой показан принцип составления схемы облета В: перелеты между объектами выполняются в момент времени, когда наклонение орбиты следующего объекта достигает минимума, при этом сами наклонения близки к нулю.
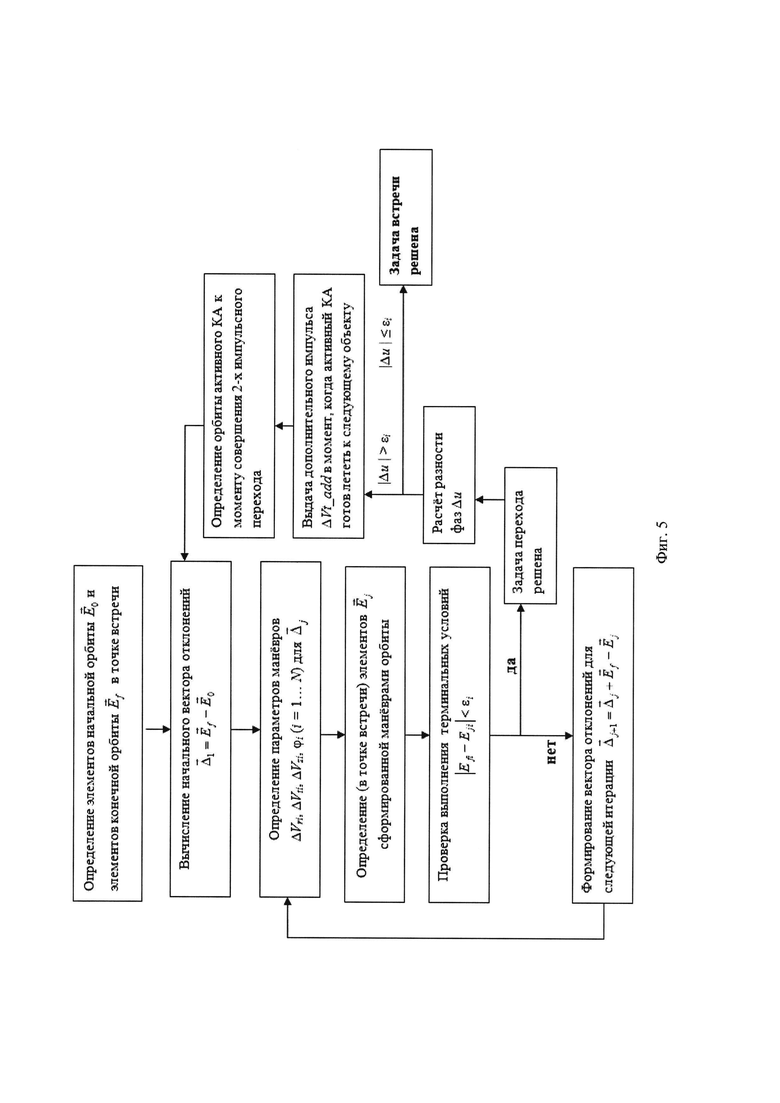
На фиг. 5 представлена итерационная процедура, позволяющая уточнить параметры маневров перелета между двумя ОКМ, маневры перевода ОКМ на орбиту захоронения и маневры возвращения за новым объектом.
Осуществление изобретения
Объекты, находящиеся на ГСО, испытывают заметное влияние возмущений от нецентральности гравитационного поля Земли, гравитационных возмущений со стороны Луны и Солнца, приливных сил, а также от сил светового давления. В связи с этим после потери управления над объектом его орбита перестает быть экваториальной и геосинхронной. Большая полуось и эксцентриситет орбит ОКМ из окрестности ГСО меняются примерно по синусоидальному закону с незначительной амплитудой и довольно большим периодом. Наклонение орбит дрейфует между значениями от 0° до 15°-17° с периодом одного полного колебания примерно равным 51 году. Совокупность графиков, описывающих изменение наклонения орбит исследуемой группы объектов во времени будем называть портретом эволюции наклонений (Фиг. 1).
В соответствии со стандартом ISO 24113:2019(E) область между радиусами 42164±200 км и с широтным диапазоном ±15° относительно плоскости экватора является защищаемой зоной ГСО, а все современные КА в конце срока активного существования должны уводиться на орбиту захоронения (ОЗ), лежащую выше ГСО. При уводе объектов требуется или перелетать между ними напрямую (I вариант), закрепляя на них отделяемые двигательные модули для последующего увода на орбиту захоронения, или буксировать очередной объект на ОЗ и оттуда перелетать к следующему объекту (II вариант).
Рассмотрим некоторые особенности II варианта. Высота орбиты захоронения превышает высоту идеальной ГСО примерно на 250 км. С учетом большой удаленности от притягивающего центра эволюция некоторой орбиты в окрестности ГСО и эволюция соответствующей ей ОЗ с тем же наклонением практически не отличаются друг от друга на временном интервале в несколько дней. Следовательно, схемы перелета между объектами, разработанные в рамках I варианта увода, могут быть использованы и для II варианта. После захвата очередного объекта КА-сборщик, оснащенный химической двигательной установкой, продолжает вместе с ним полет до тех пор, пока до исполнения маневров перелета к следующему объекту не останется несколько дней. Затем активный КА буксирует объект на ОЗ и через непродолжительное время осуществляет возвращение за следующим объектом. При такой схеме облета эволюция орбит в обоих вариантах практически совпадает. К требуемым затратам СХС I варианта увода добавляются затраты на увод на ОЗ, которые в среднем составят около 10 м/с на один ОКМ. Орбита следующего объекта может оказаться как ниже, так и выше ГСО, поэтому для возвращения обратно в очищаемую окрестность ГСО тоже требуется в среднем 10 м/с. Однако между перелетом вверх на ОЗ и возвращением с нее есть большая разница: при уводе на ОЗ исполняются только трансверсальные маневры в плоскости орбиты уводимого объекта, а при возвращении обратно - и трансверсальные, и бинормальные, причем последние, как правило, заметно больше. Эти 10 м/с в виде трансверсального импульса скорости складываются векторно с заметно большим необходимым бинормальным импульсом, что в итоге приводит к незначительному увеличению гипотенузы векторного треугольника, которая соответствует затратам СХС на маневр. Следовательно, затраты СХС на возвращение за новыми объектами с ОЗ в рамках II варианта увода будут практически эквивалентны затратам на перелеты между объектами по I варианту увода. Таким образом, вне зависимости от выбранного варианта увода объекта на ОЗ в случае с ГСО необходимо, в первую очередь, найти рациональную схему перелета между объектами.
Вопрос выбора схемы облета ОКМ имеет первостепенное значение для повышения эффективности миссии. Оптимальный выбор последовательности облета позволяет при тех же ресурсах КА-сборщика облететь больше ОКМ и перевести их на орбиты захоронения. В первую очередь речь идет о минимизации затрат СХС на облет. Для выбора схемы облета предлагается использовать портрет эволюции наклонений (Фиг. 1). Необходимо перелетать между орбитами, плоскости которых практически совпадают, чтобы свести к минимуму затратные боковые маневры. Угол Δγ между плоскостями орбит (Фиг. 2) можно определить по формуле из сферической тригонометрии:
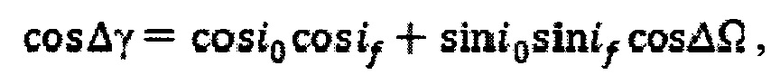
где i0 и iƒ - наклонения начальной и конечной орбит соответственно, ΔΩ=Ωf-Ω0 - различие в ДВУ конечной и начальной орбит. При стремлении наклонения обеих орбит к нулю понятие ДВУ вырождается, при этом угол между плоскостями орбит Δγ также стремится к нулю вне зависимости от величины ΔΩ. На портрете эволюции наклонений для различных временных интервалов можно выделить два диапазона наклонений, которые характеризуются высокой интенсивностью пересечения кривых. Первому диапазону соответствуют величины наклонения 12-15 градусов, второму диапазону - наклонения, близкие к нулю. Для некоторой группы ОКМ из окрестности ГСО можно предложить три схемы облета: №0, А и В.
Схема облета №0. Маневрировать между орбитами с наклонениями 12-15 градусов выгодно только в том случае, когда наклонения начальной и конечной орбит равны, а их отличия в ДВУ близки к нулю. Схема №0 предполагает, что перелеты осуществляются в момент равенства наклонений вблизи значений 12-15 градусов, а последовательность облета определяется положениями точек пересечения кривых в верхней части портрета эволюции наклонений (Фиг. 1). Такая схема крайне чувствительна к точности прогноза движения ОКМ. Кроме того, распределение ДВУ у орбит носит случайный характер, поэтому маловероятно, чтобы у исследуемой группы ОКМ отличия большинства орбит в ДВУ были малыми, поэтому их коррекция потребует больших затрат СХС. В связи с этим, применять такую схему облета не рекомендуется.
Схема облета А. Рассмотрим качественно нижнюю часть портрета эволюции наклонений (Фиг. 3). Наклонения плоскостей орбит ОКМ могут принимать равные значения, чему соответствуют пересечения кривых. Схема облета А предполагает, что в момент совпадения наклонений у орбиты текущего объекта и орбиты следующего объекта активный КА должен повернуть орбитальную плоскость на угол Δγ. Так как в момент исполнения маневра наклонения равны и близки к нулю, то и угол Δγ остается малым даже при больших различиях в ДВУ. На Фиг. 3 кривая №1, описывающая эволюцию наклонения текущей орбиты, пересекается с несколькими другими кривыми, но в качестве следующей необходимо выбрать кривую №2, так как ордината точки пересечения кривых №1 и №2 минимальна. Описанная схема имеет один потенциальный недостаток. Величины минимумов наклонений у орбит объектов хотя и близки к нулю, но разные. Поэтому возможны ситуации, когда минимумы некоторых кривых на Фиг. 3 (например, кривая №5) окажутся выше того уровня значений i, на котором лежит получившаяся последовательность перелета. Это приведет к тому, что решением будут охвачены не все ОКМ исследуемой группы.
Схема облета В. Рассмотрим качественно нижнюю часть портрета эволюции наклонений (Фиг. 4). Схема В предполагает, что перелеты осуществляются с текущей орбиты к следующей в тот момент, когда наклонение орбиты следующего объекта достигает минимума. Это должно облегчить формирование необходимой ДВУ, так как этот элемент орбиты вырождается при i→0°. Так как начальное наклонение и конечное наклонение по-прежнему близки к нулю (наклонение текущей орбиты еще не успело заметно увеличиться, а наклонение следующей орбиты минимально), угол Δγ остается малым. Описанная схема не создает ситуации, при которой ОКМ исследуемой группы остаются не охваченными найденным решением. При Схеме В перелет, как правило, выполняется с орбиты с большим наклонением на орбиту с меньшим наклонением.
Так как в основе схем облета А и В лежит один и тот же физический принцип, рекомендуется для конкретной исследуемой группы ОКМ выполнять расчеты в соответствии с обеими схемами, а затем сравнивать получившиеся результаты по различным критериям.
Задача перелета от одного ОКМ к другому является задачей «встречи». Однако объект пребывает в районе равенства наклонений или минимального значения наклонения своей орбиты некоторое количество дней, за которые разность фаз в момент прилета КА-сборщика в точку встречи может меняться. Кроме того, после достижения очередного ОКМ (или ОЗ очередного ОКМ) активный КА может реализовать небольшой трансверсальный импульс скорости. Он не приведет к заметному изменению большой полуоси или эксцентриситета текущей орбиты, однако за счет длительного ожидания следующего перелета позволит и в момент равенства наклонений, и в момент минимального наклонения орбиты цели получить необходимое фазовое отличие, при котором СХС оптимального решения задачи перехода активного КА с орбиты на орбиту будет равна СХС оптимального решения задачи встречи со следующим ОКМ. Таким образом, для оценки затрат СХС можно рассматривать не решение задачи «встречи», а решение задачи «перехода». При этом сама задача перелета между объектами является заметно некомпланарной.
Непосредственный перелет от одного ОКМ к другому выполняется при помощи близкого к оптимальному двухимпульсного маневра, у которого оба импульса скорости  и
и 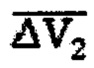 имеют только трансверсальные (ΔVt1 и ΔVt2) и бинормальные (ΔVz1 и ΔVz2) составляющие в безразмерной форме:
имеют только трансверсальные (ΔVt1 и ΔVt2) и бинормальные (ΔVz1 и ΔVz2) составляющие в безразмерной форме:
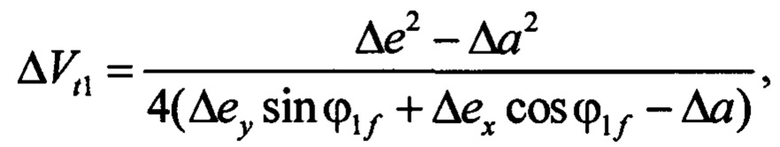

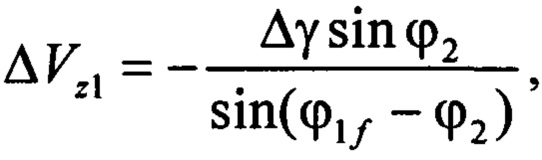
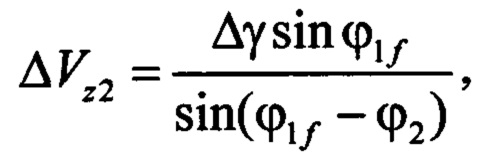
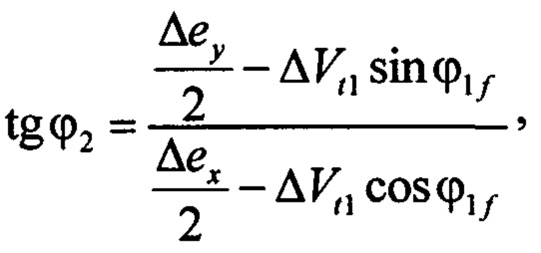
где
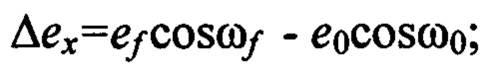
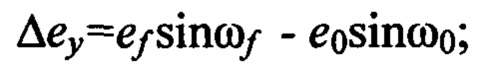
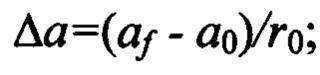
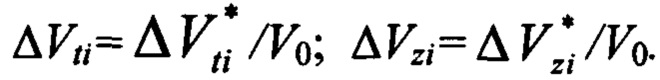
Здесь: «ƒ», «0» - индексы, соответствующие конечной и начальной орбитам; еƒ и е0 - эксцентриситеты орбит; aƒ и а0 - большие полуоси орбит; ωƒ и ω0 - аргументы перицентров орбит; V0 - орбитальная скорость движения по опорной круговой орбите (геостационарной) радиуса r0; ϕi - аргумент широты, на котором прикладывается i-ый импульс скорости; 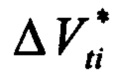
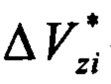 - трансверсальная и боковая составляющие i-го импульса скорости соответственно.
- трансверсальная и боковая составляющие i-го импульса скорости соответственно.
Приведенные выше формулы являются функцией от угла приложения первого импульса скорости ϕ1. Путем перебора этого угла на интервале [0°; 180°] необходимо найти значение ϕ1ƒ, при котором достигает минимума функционал СХС маневра:
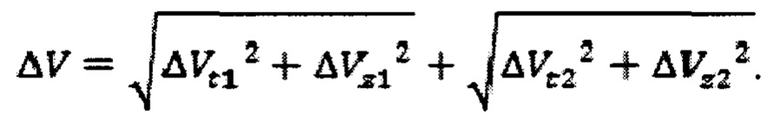
Маневры перелета от одного объекта к другому вычисляются в два этапа. После определения параметров двухимпульсного маневра, обеспечивающего переход между начальной и конечной орбитами, полученные импульсы скорости с учетом углов их приложения подставляются в полную силовую модель движения активного КА и ОКМ. Она учитывает нецентральность земного гравитационного поля, а также различного рода возмущения от Луны и Солнца. Вычисляется оставшееся отличие по фазе. Если оно мало, то остается уточнить параметры маневра перехода между орбитами при помощи итерационной процедуры (Фиг. 5, описание см. ниже). Если разность фаз требует коррекции, то вводится небольшой трансверсальный импульс скорости, который исполняется не в момент совершения перелета к следующему объекту, а как только активный КА готов перелетать к следующему объекту после достижения очередного ОКМ (или ОЗ очередного ОКМ). Как правило, между двумя этими событиями проходит от нескольких дней до многих месяцев. Этот импульс скорости моделируется, а затем для момента перелета к ОКМ уточняются параметры двухимпульсного перехода между орбитами. Величину этого дополнительного трансверсального импульса скорости можно определить по формуле:
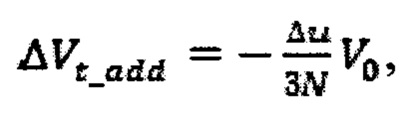
где Δu - разность фаз между ОКМ и активным КА (выраженная в долях витка), получающаяся при перелете между их орбитами только при решении задачи «перехода»; N - количество витков ОКМ между моментом времени, когда активный КА готов выполнить перелет к нему и когда он должен это сделать в соответствии с принятой схемой облета.
Завершающим шагом является применение специальной итерационной процедуры (Фиг. 5). Она представляет собой алгоритм, уточняющий параметры маневров по невязкам, получающимся в результате сравнения желаемой целевой орбиты с реально получающейся после точного численного интегрирования в полной силовой модели движения активного КА и ОКМ. На первом шаге (j=1) по Кеплеровым элементам, задающим начальную Е0 и конечную Еƒ орбиты, формируется вектор корректируемых отклонений Δj и вычисляются по приведенным выше формулам примерные величины импульсов скорости и углы их приложения. Эти данные подставляются в полную силовую модель движения, в которой путем численного интегрирования начальной орбиты с аккуратным моделированием работы двигателя получают на j=1 шаге некоторую сформированную орбиту Ej. Проверяется условие малости вектора невязок |Еƒ - Ej| < ε. Если оно выполнено, задача перехода между орбитами считается решенной. Если нет, то перед следующей j+1 итерацией алгоритма вектор Δj увеличивается на величину (Еƒ - Ej) с учетом знака этой величины. Если задача перехода между орбитами решена, проверяется величина фазовой разницы, которая будет сформирована исполняемыми маневрами «перехода». Если она меньше допустимой, задача встречи с ОКМ считается полностью решенной. Если нет, то задолго до исполнения маневров, обеспечивающих перелет к новому ОКМ, активный КА исполняет небольшой трансверсальный импульс скорости. Определяются параметры его орбиты на момент совершения непосредственного перелета к ОКМ и цикл расчета маневров перехода между орбитами повторяется заново.
Пример реализации.
Первый шаг решения задачи состоит в анализе спутникового каталога и выборе реальных крупных объектов космического мусора (ОКМ), которые необходимо увести на орбиты захоронения из защищаемой зоны геостационарной орбиты (ГСО). По начальным условиям движения отобранных объектов для них строится портрет эволюции наклонений на интервале времени не менее 50 лет, что соответствует примерному периоду долгопериодического изменения наклонения орбиты пассивного объекта в окрестности ГСО. Рекомендуется исследовать две схемы облета: перелет в приэкваториальной плоскости в момент равенства наклонений и перелет в приэкваториальной плоскости в момент, когда наклонение орбиты следующего объекта достигает своего минимума. Параметры орбиты захоронения задаются стандартом ISO 24113:2019(Е) "Space systems - Space debris mitigation requirements", а текущие значения Кеплеровых элементов орбит ОКМ в момент исполнения маневров определяются на основе расчета траекторий в полной силовой модели движения активного КА и ОКМ, учитывающей нецентральность земного гравитационного поля, а также различного рода возмущения от Луны и Солнца. Параметры маневров, которые обеспечивают перелет между объектами и/или их увод на орбиты захоронения с возвращением за новым объектом, рассчитываются на основе формул, определяющих параметры маневров перехода между околокруговыми орбитами. Это двухимпульсные некомпланарные маневры без радиальных составляющих импульсов скорости, в которых учитывается и направление оптимальной коррекции вектора эксцентриситета, и направление оптимальной коррекции ориентации орбитальной плоскости. После получения оценок параметров маневров по приближенным формулам, они уточняются с использованием итерационной процедуры, которая учитывает полную силовую модель движения активного КА и ОКМ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения последовательности перелётов между объектами космического мусора при значительном отличии в долготе восходящего узла их орбит | 2018 |
|
RU2688120C1 |
| СПОСОБ ПЕРЕФАЗИРОВАНИЯ КОСМИЧЕСКИХ АППАРАТОВ НА ОКОЛОЗЕМНОЙ ОРБИТЕ | 2023 |
|
RU2806928C1 |
| Способ ограничения засорения эксплуатируемых областей околоземного космического пространства | 2017 |
|
RU2665156C1 |
| Космический комплекс для утилизации группы объектов крупногабаритного космического мусора | 2018 |
|
RU2695155C1 |
| СПОСОБ КОЛЛОКАЦИИ ПРИ ПЕРЕВОДЕ ГЕОСТАЦИОНАРНОГО КОСМИЧЕСКОГО АППАРАТА НА ДРУГУЮ ДОЛГОТУ СТОЯНИЯ И УВОДЕ ЕГО НА ОРБИТУ ЗАХОРОНЕНИЯ | 2022 |
|
RU2786680C1 |
| СПОСОБ УДАЛЕНИЯ С ГЕОСТАЦИОНАРНОЙ ОРБИТЫ НЕФУНКЦИОНИРУЮЩЕГО КОСМИЧЕСКОГО АППАРАТА | 2014 |
|
RU2559392C1 |
| СПОСОБ ВЫВЕДЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ НА ОРБИТУ | 2023 |
|
RU2794486C1 |
| СПОСОБ УВОДА ПРЕКРАТИВШИХ АКТИВНОЕ СУЩЕСТВОВАНИЕ КОСМИЧЕСКИХ АППАРАТОВ С РАБОЧИХ НАКЛОННЫХ И ЭКВАТОРИАЛЬНЫХ ОРБИТ В ПЛОТНЫЕ СЛОИ АТМОСФЕРЫ | 2018 |
|
RU2708406C1 |
| СПОСОБ УВОДА КОСМИЧЕСКОГО АППАРАТА, ЗАВЕРШИВШЕГО АКТИВНОЕ ФУНКЦИОНИРОВАНИЕ С ГЕОСТАЦИОНАРНОЙ ОРБИТЫ | 2023 |
|
RU2824862C1 |
| СПОСОБ ВЫВЕДЕНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ С ИСПОЛЬЗОВАНИЕМ ДВИГАТЕЛЕЙ МАЛОЙ ТЯГИ | 2014 |
|
RU2586945C2 |
Изобретение относится к области управления движением космических аппаратов с помощью реактивной силы, создаваемой двигательной установкой большой тяги, и с использованием возмущений от Луны, Солнца, нецентральности земного гравитационного поля, светового давления, приводящих к долгопериодическим колебаниям наклонения орбит пассивных объектов из окрестности геостационарной орбиты. Задачей является построение наиболее выгодных схем облета группы объектов космического мусора (ОКМ) при точном расчете маневров активного космического аппарата (КА) и, таким образом, уменьшение затрат суммарной характеристической скорости (СХС) при осуществлении перелетов между каждой парой и всеми ОКМ. Это позволяет при заданных возможностях конкретного КА облететь наибольшее число ОКМ. Для решения задачи предлагается способ определения последовательности перелетов между объектами космического мусора в окрестности геостационарной орбиты. При этом последовательность перелетов и схема облета выбираются на основе вида портрета эволюции наклонений орбит ОКМ. Он представляет собой совокупность линий, описывающих изменение наклонений плоскостей орбит объектов в примерном диапазоне [0°; 17°] относительно экваториальной плоскости Земли. Наибольшие затраты СХС имеют место при изменении плоскости движения КА, в связи с чем рассмотрены три схемы облета. В первом случае перелеты осуществляются в момент равенства наклонений двух орбит при произвольном его значении, при этом рассогласование в долготе восходящего узла (ДВУ) может быть любым по величине и подлежит коррекции при помощи двигательной установки. Такая схема №0 требует заметных затрат СХС и весьма чувствительна к аккуратности расчета движения ОКМ. Во втором случае перелеты выполняются в момент равенства наклонений в приэкваториальной области (наклонения менее 1°), где угол между плоскостями остается малым даже при больших отличиях в ДВУ. Эта схема А выгодна по затратам СХС, но может не позволить охватить все объекты. В третьем случае перелеты также осуществляются в приэкваториальной области, однако в тот момент, когда наклонение орбиты следующего объекта достигает минимального значения. По затратам СХС эта схема перелета В близка к предыдущей, при этом охваченными являются все исследуемые объекты. Поэтому именно она рекомендуется в качестве основной схемы облета группы ОКМ из окрестности геостационарной орбиты. Параметры маневров, которые обеспечивают перелет между объектами, рассчитываются на основе формул для универсального некомпланарного перехода между двумя околокруговыми орбитами. 5 ил.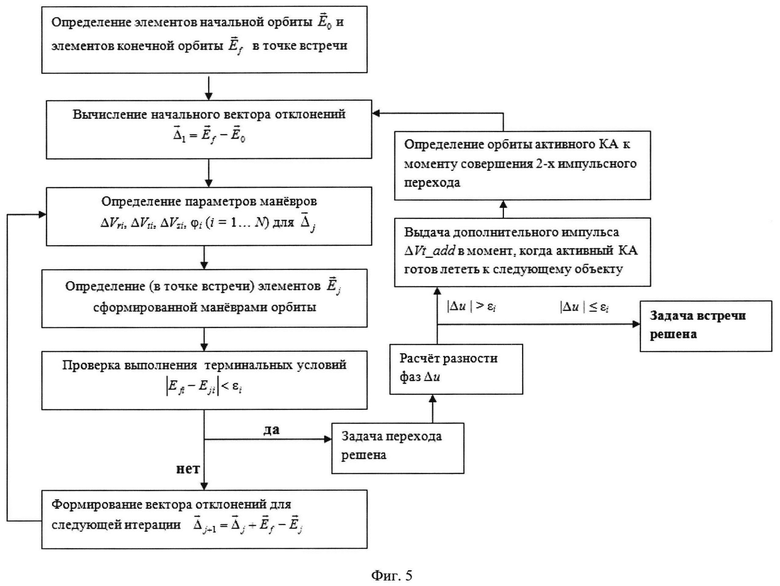
Способ определения последовательности перелетов активного космического аппарата (КА) между объектами космического мусора (ОКМ) в окрестности геостационарной орбиты (ГСО), характеризующийся тем, что первоначально из каталога космических объектов выделяют группу ОКМ, околокруговые орбиты которых полностью лежат в защищаемой зоне ГСО или пересекают ее; для этой группы ОКМ из окрестности ГСО строят портрет эволюции наклонений на интервале времени не менее 50 лет, что соответствует примерному периоду долгопериодического изменения наклонения орбиты пассивного объекта в окрестности ГСО; далее составляют две схемы облета объектов активным КА при движении вдоль нижней приэкваториальной части этого портрета: в первой схеме активный КА выполняет перелет к новому объекту в момент равенства наклонений, при этом наклонения орбит близки к нулю; во второй схеме перелет активного КА с текущей орбиты к новому объекту происходит, когда наклонение орбиты этого следующего объекта достигает минимума, также близкого к нулю; при расчете маневров, обеспечивающих перелет к очередному объекту, Кеплеровы элементы начальной и конечной орбит берут с учетом долговременного прогноза движения активного КА и ОКМ, выполненного в наиболее полной силовой модели, учитывающей нецентральность земного гравитационного поля, а также различного рода возмущения от Луны и Солнца; с учетом длительности интервала прогноза движения и медленного изменения наклонения для оценки параметров маневров используют начальное допущение об оптимальной фазе для решения задачи перехода активного КА с орбиты на орбиту; в случае неоптимальной фазы, сформированной в результате решения задачи «перехода», эту фазу корректируют небольшим вспомогательным трансверсальным импульсом скорости, который активный КА исполняет задолго до перелета между объектами; параметры некомпланарных маневров для каждого перелета активного КА оценивают, используя положения теории маневрирования на околокруговых орбитах; полученные параметры некомпланарных маневров итерационно уточняют, подставляя их в полную силовую модель движения активного КА и ОКМ, при этом изменение скорости может иметь как импульсный, так и непрерывный характер; выбор схемы облета активным КА группы ОКМ из окрестности ГСО осуществляют путем сравнения результатов применения вышеуказанных первой и второй схем по следующим критериям: общие затраты суммарной характеристической скорости на облет группы ОКМ, и/или общая продолжительность миссии облета, и/или количество объектов из рассматриваемой группы ОКМ, уведенных на орбиты захоронения.
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ АКТИВНОГО КОСМИЧЕСКОГО ОБЪЕКТА, СТЫКУЕМОГО С ПАССИВНЫМ КОСМИЧЕСКИМ ОБЪЕКТОМ | 2014 |
|
RU2562908C2 |
| Способ управления сервисным космическим аппаратом при бесконтактном удалении фрагментов космического мусора | 2019 |
|
RU2720606C1 |
| Способ определения последовательности перелётов между объектами космического мусора при значительном отличии в долготе восходящего узла их орбит | 2018 |
|
RU2688120C1 |
| US 7725259 B2, 25.05.2010. | |||
Авторы
Даты
2021-11-08—Публикация
2020-07-16—Подача