Изобретение относится к области управления движением космических аппаратов с помощью реактивной силы, создаваемой двигательной установкой большой тяги, и с использованием несферичности потенциала гравитационного поля, вызывающей прецессию долготы восходящего узла орбиты.
Уровень техники
Известен аналог - патент RU 2531679 С2 (Опубликовано: 27.10.2014 Бюл. №30). Изобретение относится к ракетно-космической технике и может быть использовано для увода с рабочих орбит объектов космического мусора (ОКМ) на орбиты захоронения. Способ включает выведение космического аппарата-буксира (КАБ) и автономного стыковочного модуля (АСМ) в области орбит, предназначенных для очистки от ОКМ. Компенсацию накопленных ошибок параметров движения КАБ при предыдущих маневрах, а также системы целеуказания, распределяют между корректирующими импульсами КАБ на этапе дальнего наведения и АСМ на участке самонаведения.
Недостатком является то, что выбор последовательности увода ОКМ осуществляют путем сравнения вероятности столкновения ОКМ с другими космическими объектами. При этом никак не учитывается геометрическая конфигурация орбитальных плоскостей ОКМ, которая определяет величину импульсов скорости, необходимых для перелета между орбитами. На длительном временном интервале, требуемом для перелета к очередному ОКМ, точно определить вероятность столкновения невозможно.
Известен аналог - патент RU 2562908 С2 (Опубликовано: 10.09.2015 Бюл. №25). Изобретение относится к космической технике и может быть использовано при сближении и последующей стыковке двух космических объектов. Способ включает определение величины и места приложения отлетного импульса перед переводом активного космического объекта (АКО) на траекторию полета к другому небесному телу, исходя из условия пересечения АКО орбиты пассивного космического аппарата (ПКО). Затем АКО переводят на орбиту другого небесного тела путем одновременного приложения к нему тормозного импульса (для обеспечения заданных параметров по высоте орбиты) и бокового импульса (для совмещения плоскостей орбит стыкующихся объектов). На фоне большого тормозного импульса незначительный боковой импульс практически не приведет к увеличению затрат топлива АКО, но существенно сократит время полета АКО до стыковки с ПКО.
Недостатком является то, что орбиты активного и пассивного объектов должны обязательно пересекаться. В задаче облета объектов крупногабаритного космического мусора орбиты в общем случае не пересекаются. Кроме того, в случае предлагаемого способа величина корректируемого угла между плоскостями АКО и ПКО варьируется от долей градуса до нескольких десятков градусов, следовательно, прямая коррекция этого угла потребует приложения больших (порядка 1 км/с) боковых импульсов скорости.
Известен аналог - патент US 7720604 (В1) (Опубликовано 2010-05-18). Предусмотрена спутниковая система, в которой каждый из спутников движется по эллиптической орбите. Каждый спутник имеет запас топлива, необходимый для поддержания скорости дрейфа долготы восходящего узла (ДВУ), большой полуоси, эксцентриситета, аргумента перигея и наклонения орбиты. Начальное значение ДВУ и скорость дрейфа ДВУ для каждой орбиты соответствуют минимальному значению расхода топлива для спутника, имеющего наибольшее значение расхода топлива. Исходное значение ДВУ и скорость дрейфа ДВУ могут быть определены путем вычисления расхода топлива для каждого спутника в системе для всех возможных комбинаций начального значения ДВУ для каждой орбиты и скорости дрейфа ДВУ всей системы.
Недостатком является то, что фактически указанный способ позволяет осуществлять гибкое поддержание спутниковой системы, а не ее создание или восполнение с использованием прецессии (дрейфа) ДВУ. При поддержании системы корректируются только незначительные отклонения ДВУ.
Известен аналог - статья Cerf М. Multiple space debris collecting mission: debris selection and trajectory optimization // Journal of Optimization Theory and Applications, Vol.156, Issue 3, 2013, pp.761-796. В статье для определения оптимальной последовательности перелетов между пассивными ОКМ предпринята попытка построения математической модели, которая включает в себя методы комбинаторики и методы расчета траекторий КА с учетом свойства прецессии ДВУ. Рассмотрен увод ОКМ с солнечно-синхронных орбит.
Недостатком является то, что для выбора последовательности облета 5 объектов из 11 полученная M.Cerf модель содержит 154 двоичные переменные, 341 вещественные переменные и 1070 ограничений. В случае увеличения количества исследуемых объектов сложность реализации предложенного решения неограниченно возрастает. Кроме того, алгоритм поиска решений не нагляден и не позволяет объяснить, почему то или иное решение является оптимальным.
Известен более близкий аналог - автореферат диссертации Д.А. Гришко "Исследование схем облета объектов крупногабаритного космического мусора на низких орбитах" (работа выполнена в МГТУ им. Н.Э. Баумана, автореферат диссертации на соискание ученой степени кандидата физико-математических наук: специальность 01.02.01, Опубликовано: Москва, 2018, 23 с). В диссертации рассмотрены схемы облета крупных ОКМ с использованием свойства прецессии ДВУ. Выделены 5 групп крупногабаритного космического мусора на низких орбитах и выполнена оценка суммарной характеристической скорости маневров КА-сборщика, осуществляющего перелеты между объектами каждой из групп.
Недостатком является то, что расчет маневров активного КА носит оценочный характер: не учитывается необходимость коррекции вектора эксцентриситета и параметры маневров не уточняются в точной модели движения. Кроме того, в качестве крупных ОКМ рассмотрены только последние ступени ракет-носителей и разгонные блоки, в то время как заявляемый способ можно применить к группе любых пассивных космических объектов.
Известен еще один более близкий аналог - статья Баранов А.А., Баранов А.А. (мл.) "Алгоритм расчета параметров маневров формирования спутниковых систем" // Космические исследования, 2009, т.47, №3, с. 256-262. Приводится имеющий геометрическую интерпретацию алгоритм определения параметров маневров, обеспечивающих перелет КА за фиксированное время в заданную точку конечной орбиты. С помощью итерационных процедур определяются параметры четырех импульсов скорости и разница в числе витков полета КА и точки цели. Высокое быстродействие алгоритма позволяет построить зависимость суммарной характеристической скорости маневров от продолжительности перелета на интервале от нескольких десятков витков до нескольких тысяч витков.
Недостатком является то, что в статье решена задача перелета между двумя объектами, а не между совокупностью объектов. Нет облета группы и нет алгоритма по поиску продолжительности перелета между двумя объектами (является входным параметром рассмотренной задачи).
Раскрытие изобретения Задачей предлагаемого способа является устранение недостатков аналогов, а именно:
- распространение способа определения последовательности перелета на все типы ОКМ на низких орбитах;
- возможность построения близкой к оптимальной схемы облета группы космических объектов;
- определение компромиссной продолжительности перелета между двумя объектами;
- построение единой методики определения схем облета ОКМ на низких орбитах;
- обеспечение точного расчета маневров активного КА при длительном перелете между орбитами, имеющими большие расхождения по ДВУ.
Задачей является построение наиболее выгодных схем облета группы объектов космического мусора (ОКМ) при точном расчете маневров активного космического аппарата (КА) и, таким образом, уменьшение затрат суммарной характеристической скорости (СХС) при осуществлении перелетов между каждой парой и всеми ОКМ. Это позволяет при заданных возможностях конкретного КА облететь наибольшее число ОКМ.
Для решения задачи предлагается способ определения последовательности перелетов между объектами космического мусора при значительном отличии в долготе восходящего узла (ДВУ) их орбит.При этом последовательность перелетов и схема облета выбираются на основе вида портрета эволюции отклонений долгот восходящих узлов орбит ОКМ. Он представляет собой совокупность линий, описывающих относительное движение плоскостей орбит объектов. В случае квазипараллельного расположения этих линий выгоднее применять последовательную схему, при которой для достижения следующего объекта активный КА необходимо перевести на орбиту ожидания с измененной скоростью прецессии. В случае многократного пересечения линий рекомендуется сначала применить диагональную схему, при которой орбита уводимого объекта одновременно служит орбитой ожидания для достижения следующего объекта. После выбора схемы облета определяют параметры маневров, которые обеспечивают перелет между объектами, уточнение параметров маневров осуществляют с использованием трех вложенных друг в друга итерационных процедур.
Для решения задачи предлагается способ определения последовательности перелетов между объектами космического мусора при значительном отличии в долготе восходящего узла (ДВУ) их орбит.В основе способа лежит выбор орбиты ожидания, на которую переводится активный КА. Эта орбита ожидания имеет скорость прецессии орбитальной плоскости, отличающуюся от таковой для орбит активного КА и цели. Для определения последовательности перелетов между объектами строится портрет эволюции отклонений ДВУ. Он представляет собой отображение динамики относительного дрейфа орбитальных плоскостей ОКМ во времени.
В том случае, когда увод ОКМ на орбиту захоронения осуществляется при помощи специальных модулей, первоначально расположенных на борту активного КА, для перелета к следующему ОКМ активный КА переводится на орбиту ожидания с измененной скоростью прецессии ДВУ. Параметры этой орбиты выбираются таким образом, чтобы за N витков полета цели активный КА компенсировал расхождение по ДВУ и по аргументу широты по отношению к цели. Остаточное отклонение по ДВУ, имеющее место после окончания фазирования, корректируется при помощи бинормальных составляющих импульсов скорости. Величины бинормальных составляющих импульсов скорости распределяются так, чтобы за счет коррекции, имеющегося первоначально отклонения наклонения способствовать требующемуся изменению скорости прецессии плоскости орбиты ожидания. Полученные аналитическими методами параметры маневров уточняются при помощи 3-х вложенных итерационных процедур. При описанной "последовательной" схеме облета перелеты, как правило, осуществляются в сторону прецессии орбитальной плоскости. Альтернативой перевода активного КА на орбиту ожидания может служить продолжение полета по орбите ОКМ, если параметры этой орбиты обеспечивают относительно быстрое совмещение ее плоскости с плоскостью орбиты следующего ОКМ. Такая "диагональная" схема облета тем более выгодна, чем большее количество объектов можно облететь с ее помощью. Частный случай имеет место, когда увод ОКМ на орбиту захоронения осуществляется самим активным КА. В этом варианте ему необходимо оставаться на орбите захоронения до тех пор, пока ее плоскость не совпадет с плоскостью уводимого объекта.
Перечень фигур
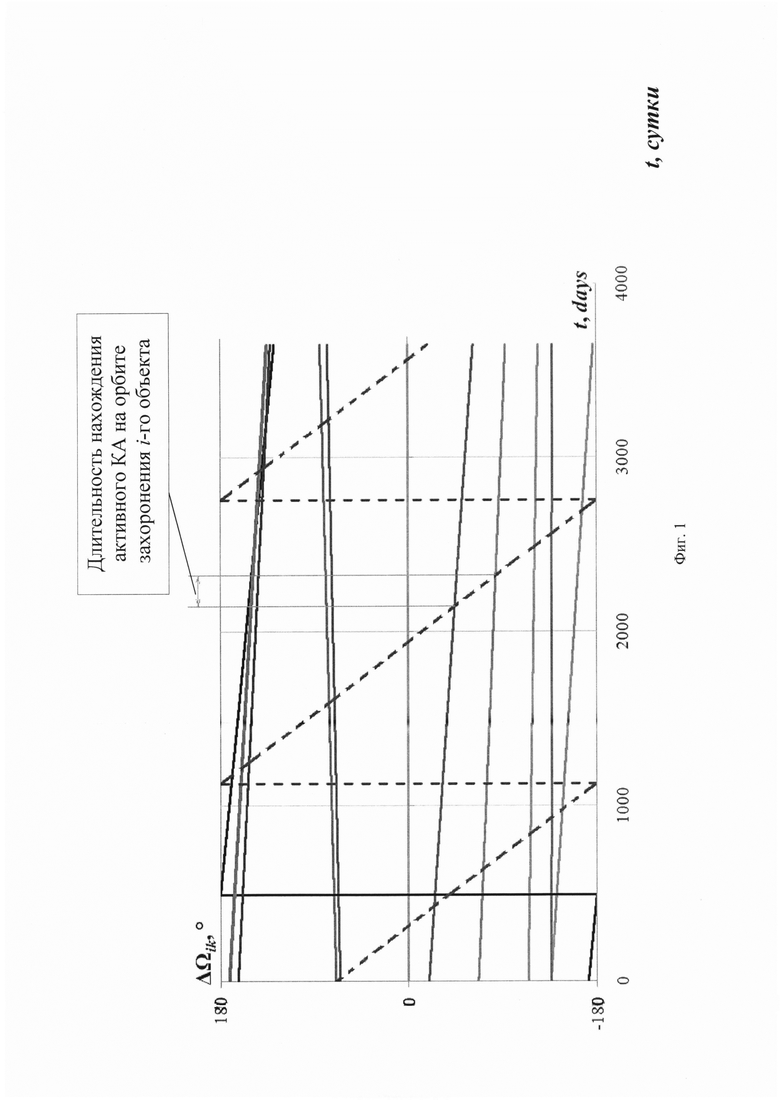
На фиг. 1 представлен портрет эволюции отклонений ДВУ, характерный для группы крупных ОКМ с квазипараллельным расположением линий, описывающих относительную эволюцию орбитальных плоскостей. Пунктирной линией показана эволюция плоскости круговой орбиты захоронения. Предпочтительна последовательная схема облета в направлении естественной прецессии ДВУ.
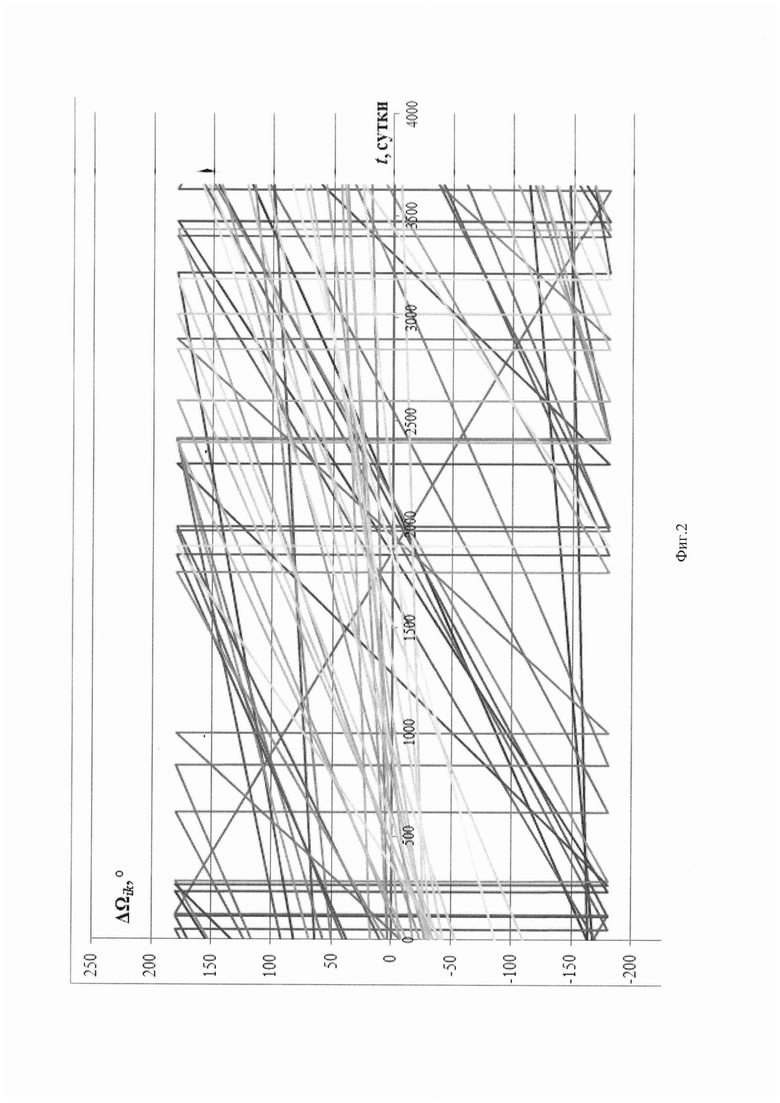
На фиг. 2 представлен портрет эволюции отклонений ДВУ, характерный для группы крупных ОКМ с многократными пересечениями линий, описывающих относительную эволюцию орбитальных плоскостей. Предпочтительная диагональная схема облета
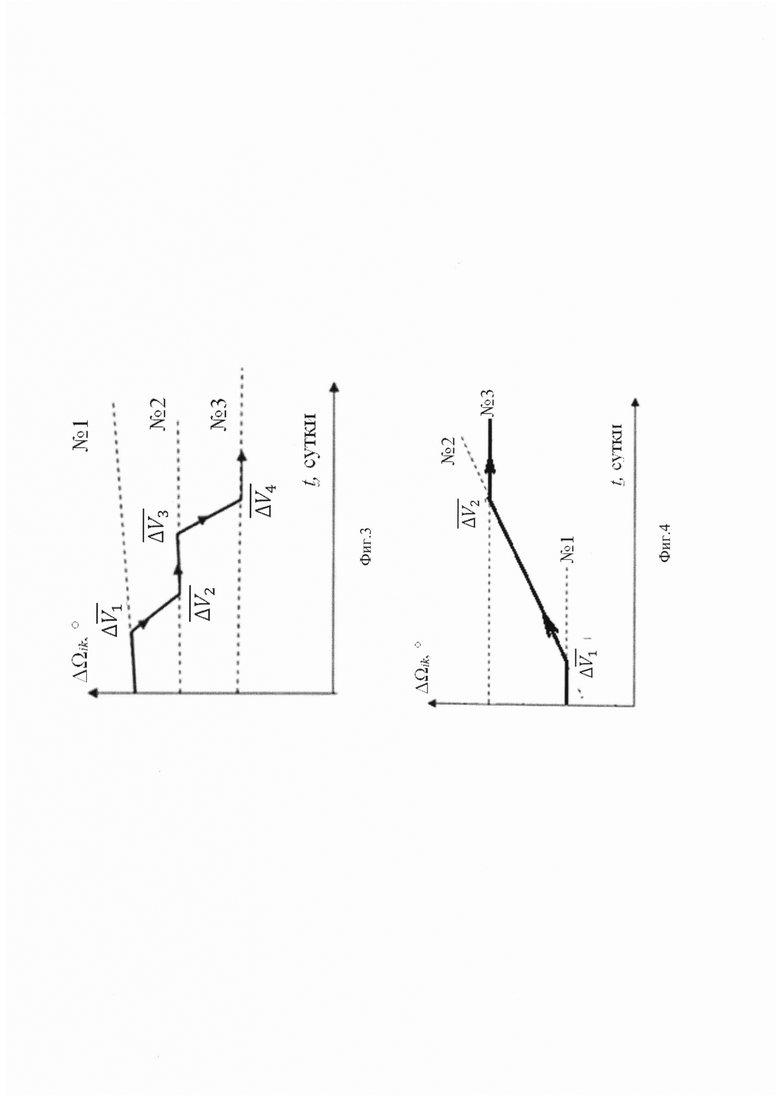
На фиг. 3 на портрете эволюции отклонений ДВУ схематически отображен перевод активного КА на орбиту ожидания и перелет к следующему ОКМ при использовании последовательной схемы облета.
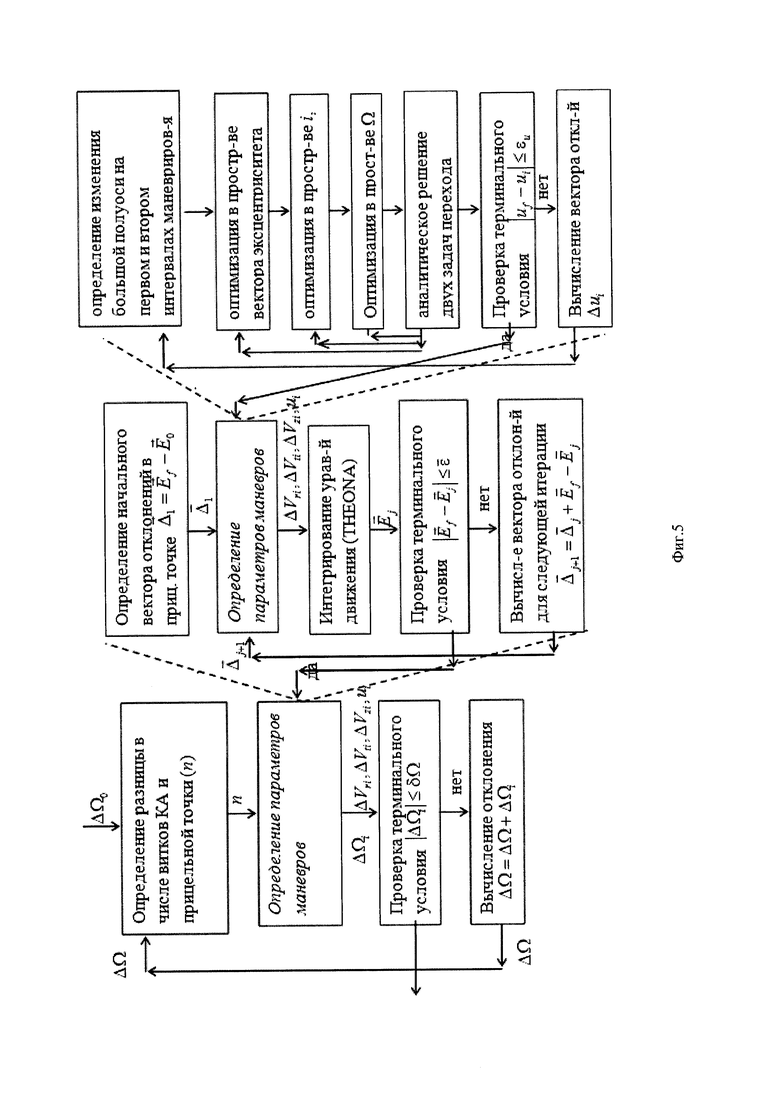
На фиг. 4 на портрете эволюции отклонений ДВУ схематически отображен перелет к следующему ОКМ при использовании диагональной схемы облета.
На фиг. 5 приведены три взаимно вложенные итерационные процедуры, которые позволяют получить точное решение некомпланарной задачи встречи большой продолжительности с использованием прецессии плоскости орбиты.
Осуществление изобретения
Объекты крупногабаритного космического мусора (ККМ) образуют группу, элементы которой не синхронизированы по своему относительному движению. Их орбиты незначительно, но отличаются по большой полуоси (а), эксцентриситету (е) и наклонению (i), расхождение по ДВУ (Ω) может быть любым по величине. Разные скорости прецессии орбитальных плоскостей приводят к изменению относительного расположения плоскостей орбит на длительном интервале времени. В качестве параметра, характеризующего это расположение, целесообразно использовать ΔΩik Е (-π;+π] - отклонение ДВУ орбит всех i-x объектов группы от ДВУ орбиты одного специально выбранного объекта с номером 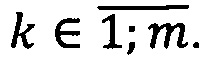 При таком подходе прямые ДЛ,*(0 могут представлять собой как совокупность квазипараллельных линий (Фиг. 1), так и совокупность многократно пересекающихся линий (Фиг. 2).
При таком подходе прямые ДЛ,*(0 могут представлять собой как совокупность квазипараллельных линий (Фиг. 1), так и совокупность многократно пересекающихся линий (Фиг. 2).
Для случая с квазипараллельным распределением линий ΔΩik предлагается применять последовательную (по значениям ДВУ) схему облета. Для перелета между тремя объектами ККМ необходимо выполнить следующую последовательность действий (Фиг. 3). После доставки отделяемого модуля в окрестность объекта №1, маневрирующий КА осуществляет перелет к объекту №2 (ближайшему по ДВУ). Для этого маневром 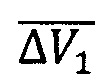 обеспечивается перевод активного КА с орбиты объекта №1 на орбиту ожидания (под маневром здесь подразумеваются, как правило, два включения двигательной установки, локализованные на одном витке). По достижении нужной ориентации плоскости орбиты ожидания и требуемой фазовой разницы при помощи маневра
обеспечивается перевод активного КА с орбиты объекта №1 на орбиту ожидания (под маневром здесь подразумеваются, как правило, два включения двигательной установки, локализованные на одном витке). По достижении нужной ориентации плоскости орбиты ожидания и требуемой фазовой разницы при помощи маневра 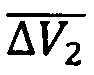 осуществляется перевод активного КА на орбиту объекта №2, для обеспечения возможности фиксации отделяемого модуля на объекте №2. Далее описанные действия повторяются в виде маневров
осуществляется перевод активного КА на орбиту объекта №2, для обеспечения возможности фиксации отделяемого модуля на объекте №2. Далее описанные действия повторяются в виде маневров 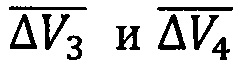 для достижения объекта №3 и т.д. Таким образом, имеет место такой последовательный облет объектов ККМ, при котором перелет всегда осуществляется к ближайшему по ДВУ объекту в сторону естественной прецессии ДВУ орбит рассматриваемой группы.
для достижения объекта №3 и т.д. Таким образом, имеет место такой последовательный облет объектов ККМ, при котором перелет всегда осуществляется к ближайшему по ДВУ объекту в сторону естественной прецессии ДВУ орбит рассматриваемой группы.
При оценке затрат суммарной характеристической скорости на перевод КА в заданную окрестность ОКМ предполагается, что разница эксцентриситетов их орбит мала и существенно не влияет на характер решения, поэтому ей можно пренебречь. Импульсы скорости, имеющие трансверсальные и бинормальные составляющие, прикладываются на экваторе на двух интервалах маневрирования, расположенных соответственно на первом и на последнем витках перелета. За счет трансверсальных составляющих импульсов первого интервала большая полуось орбиты изменяется таким образом, чтобы, двигаясь по новой (фазирующей) орбите, КА компенсировал имеющееся в начальный момент отклонение по аргументу широты Δи и возникающую разницу в числе витков перелета. При этом за счет целенаправленного изменения скорости прецессии орбиты и разного числа витков перелета корректируется также значительное первоначальное угловое рассогласование по ДВУ ΔΩ (Фиг. 3). Бинормальные составляющие импульсов скорости обеспечивают необходимое суммарное изменение наклонения, но так распределены между I и II интервалами маневрирования, чтобы дополнительно нужным образом повлиять на скорость прецессии фазирующей орбиты.
Значения суммы трансверсальных и бинормальных составляющих импульсов скорости первого ΔVtI, ΔVzI и второго ΔVtII, ΔVzII интервалов маневрирования могут быть определены по формулам:
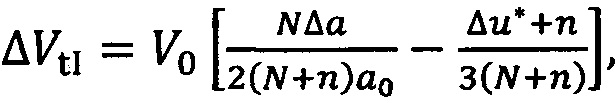
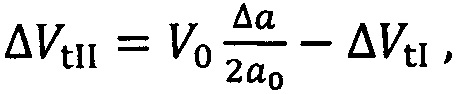
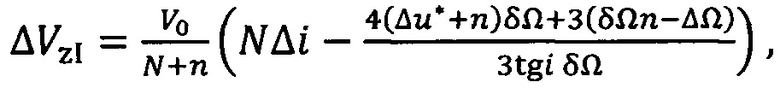
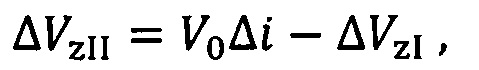
здесь: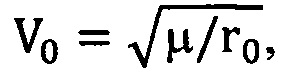 r0=α0 - радиус опорной круговой орбиты, V0 - местная круговая скорость, μ=γМ=398600.44 км3/с2 (у - гравитационная постоянная, М - масса планеты); Δа, ΔΩ, Δi, Δи - отклонения между орбитой цели и активного КА по большой полуоси, долготе восходящего узла, наклонению и аргументу широты соответственно. Угол Δи измеряется в долях витка, его максимальное значение по модулю не может быть больше 1; 7V - количество витков полета цели, за которое осуществляется перевод активного КА в точку встречи; п - целочисленная разница в числе витков полета активного КА и целевой точки, которая накопится за N витков полета цели; δQ=- (2 πε/μр2) ■ cosi - изменение ДВУ за один виток, вследствие влияния второго члена разложения потенциала гравитационного поля в ряд по сферическим функциям геоцентрической широты; / - наклонение орбиты, р -фокальный параметр,
r0=α0 - радиус опорной круговой орбиты, V0 - местная круговая скорость, μ=γМ=398600.44 км3/с2 (у - гравитационная постоянная, М - масса планеты); Δа, ΔΩ, Δi, Δи - отклонения между орбитой цели и активного КА по большой полуоси, долготе восходящего узла, наклонению и аргументу широты соответственно. Угол Δи измеряется в долях витка, его максимальное значение по модулю не может быть больше 1; 7V - количество витков полета цели, за которое осуществляется перевод активного КА в точку встречи; п - целочисленная разница в числе витков полета активного КА и целевой точки, которая накопится за N витков полета цели; δQ=- (2 πε/μр2) ■ cosi - изменение ДВУ за один виток, вследствие влияния второго члена разложения потенциала гравитационного поля в ряд по сферическим функциям геоцентрической широты; / - наклонение орбиты, р -фокальный параметр, 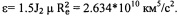
Разницу в количестве витков полета активного КА и цели в первом приближении
можно определить как 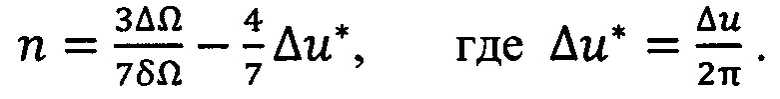
Оптимальным будет значение п, доставляющее минимум функционалу:
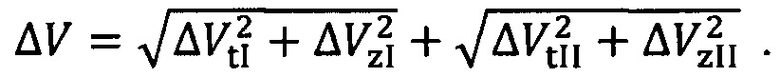
Для случая с многократным пересечением линий ΔΩik(t) предлагается применять диагональную схему облета. В этом случае, находясь на орбите объекта №1 (Фиг. 4), достаточно исполнить один маневр 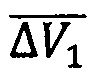 (два включения двигательной установки на витке) в момент совпадения ДВУ, чтобы сблизиться с объектом №2, и также двухимпульсный маневр
(два включения двигательной установки на витке) в момент совпадения ДВУ, чтобы сблизиться с объектом №2, и также двухимпульсный маневр 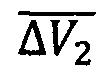 для последующего сближения с объектом №3. Таким образом, количество включений двигательной установки на участке движения от объекта №1 к объекту №3 может быть уменьшено вдвое. Существенно уменьшаются и затраты суммарной характеристической скорости (СХС), так как пропадает наиболее затратная по требуемой СХС коррекция ДВУ: в момент пересечения прямых ΔΩik(t) и ΔΩjk(t) на портрете эволюции отклонений ДВУ орбиты i-го и j-го объектов ККМ имеют равные значения ДВУ. Линию ΔΩik(t), соответствующую одной из орбит ОКМ и пересекающую две линии, соответствующие другим орбитам ОКМ, назовем «диагональю». Имеется возможность найти несколько веток, состоящих из последовательности прямых и диагоналей, позволяющих облететь почти все объекты ККМ, входящие в группу. Представим портрет эволюции отклонений ДВУ как граф и, зная законы изменения ΔΩik(t) в двумерном пространстве t, AQ, определим все узлы графа. Для описания узлов можно использовать квадратную матрицу координат узлов Т размерности n×n с элементами
для последующего сближения с объектом №3. Таким образом, количество включений двигательной установки на участке движения от объекта №1 к объекту №3 может быть уменьшено вдвое. Существенно уменьшаются и затраты суммарной характеристической скорости (СХС), так как пропадает наиболее затратная по требуемой СХС коррекция ДВУ: в момент пересечения прямых ΔΩik(t) и ΔΩjk(t) на портрете эволюции отклонений ДВУ орбиты i-го и j-го объектов ККМ имеют равные значения ДВУ. Линию ΔΩik(t), соответствующую одной из орбит ОКМ и пересекающую две линии, соответствующие другим орбитам ОКМ, назовем «диагональю». Имеется возможность найти несколько веток, состоящих из последовательности прямых и диагоналей, позволяющих облететь почти все объекты ККМ, входящие в группу. Представим портрет эволюции отклонений ДВУ как граф и, зная законы изменения ΔΩik(t) в двумерном пространстве t, AQ, определим все узлы графа. Для описания узлов можно использовать квадратную матрицу координат узлов Т размерности n×n с элементами 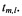

Матрица Т является симметрической, а ее диагональ составляют символы «&», описывающие совпадение прямых ΔΩik(t). Если точка пересечения прямых ΔΩik(t) существует, то в полях элемента tm,l указывается ее координата / (время пересечения прямых ΔΩik(t) и ΔΩjk(t), а если точек пересечения нет, или пересечение имеет место при t → ∞, то вместо элемента матрицы стоят прочерки. Зная последовательность перелетов и параметры орбит объектов, далее можно оценить по известным формулам параметры маневров перелета между ними. Разумно предполагать, что перелеты выполняются при оптимальном фазовом угле, то есть энергетика решения задачи перехода совпадает с энергетикой решения задачи встречи. Добиться оптимальной фазы можно путем небольших корректирующих маневров, прикладываемых задолго до встречи с объектом, при этом необходимо учитывать влияние корректирующих маневров на скорость эволюции орбитальной плоскости активного КА.
При использовании диагональной схемы облета продолжительность перелета между объектами определена матрицей координат узлов графа, однако в последовательной схеме заданная продолжительность нахождения на орбите ожидания определяет параметры этой орбиты, а тем самым - затраты СХС на перелет к очередному объекту. Выбор одинаковой продолжительности перелета между объектами ККМ является заведомо неоптимальным. Требуется искать значения продолжительности перелета, которые находятся в той компромиссной области графика функции ΔV(N), где затраты ΔV перестают резко уменьшаться с ростом N. Для поиска компромиссных продолжительностей перелета можно предложить два подхода, каждый из которых позволяет получить продолжительность перелета как функцию от корректируемой разницы по ДВУ. Первый подход является довольно простым и основан на анализе графиков гиперболически убывающих функций ΔV(N), построенных для различных ΔQ. На координатной плоскости ΔV, N можно провести некоторое количество медленно возрастающих выпуклых кривых, которые будут пересекать графики ΔV(N) в компромиссной области. По точкам пересечения одной такой выбранной кривой с линиями ΔV(N) можно построить зависимость N(ΔΩ). Второй подход предполагает использование функционала, включающего затраты СХС, уменьшающиеся при увеличении продолжительности перелета N, и штраф за увеличение его продолжительности. Функция штрафа возрастает с увеличением N. Проведенные исследования показали, что в качестве нее целесообразно использовать зависимость вида 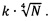
Последним шагом является уточнение величин параметров маневров. Решение состоит из трех вложенных итерационных процедур (Фиг. 5). «Внешняя» используется для определения оптимального отличия в числе витков полета n. «Внутренняя» - для формирования с заданной точностью конечной орбиты (для каждого фиксированного значения n). Третья процедура служит для обеспечения с необходимой точностью времени выхода на заданную орбиту при приближенном определении параметров маневров. При уточнении значения n, определяются углы приложения и составляющие импульсов скорости, формирующие все элементы заданной орбиты за исключением ДВУ. Когда оптимальное значение n найдено, для него во «внутренней» и третьей процедурах корректируются все элементы орбиты, включая ДВУ.
На вход внешней процедуры (левая колонка алгоритмических блоков на Фиг. 5) подаются параметры начальной и целевой орбиты, в том числе определяется величина ΔΩ0, которую необходимо скорректировать. По приведенной выше формуле определяется приближенное значение n, которое вместе с другими начальными условиями поступает в блок "Определение параметров маневров", который представляет собой внутреннюю процедуру. Если в результате приложения рассчитанных маневров отличие в ДВУ ΔΩf между достигнутой орбитой и целевой не превысит величины векового ухода ДВУ за виток δΩ, то задача выполнена; если это терминальное условие не выполнено, то входную величину ΔΩ0 необходимо скорректировать на ΔΩ и повторить расчет.
На вход внутренней процедуры (центральная колонка блоков на Фиг. 5), представляющей собой блок "Определение параметров маневров", приходят параметры начальной и конечной орбиты, а также приближенное значение п. Определяется начальный вектор отклонений Δ1 в прицельной точке. По приближенным формулам из блока "определение параметров маневров" внутренней процедуры (центральная колонка на фиг. 5) определяются параметры маневров, обеспечивающие коррекцию отклонений в соответствии с вектором Δ1 Полученные приближенные параметры маневров (величины радиальных, трансверсальных и бинормальных составляющих импульсов скорости и углы их приложения) проверяются интегрированием движения при помощи формул численно-аналитической теории движения космических аппаратов THEONA (разработана в ИПМ им. М.В. Келдыша РАН). Если параметры достигнутой орбиты Ej, отличаются от требуемых Еƒ в пределах допуска е, то внутренняя процедура завершена, а если терминальное условие не выполнено, то вектор отклонений А\ необходимо скорректировать на разницу Еƒ-Ej.
Третья процедура (правая колонка блоков на фиг. 5) представляет собой раскрытие блока "вычисление параметров маневров из внутренней процедуры". Сначала определяется изменение большой полуоси на первом и втором интервалах маневрирования. Затем последовательно выполняется оптимизация в пространстве ДВУ, наклонения и вектора эксцентриситета, что приводит к аналитическому решению двух задач пространственного перехода (см. статья Баранов А.А., Баранов А.А. (мл.) "Алгоритм расчета параметров маневров формирования спутниковых систем" // Космические исследования, 2009, т. 47, №3, с. 256-262.). Далее вычисляется фактически достигнутое положение КА на орбите после завершения маневров иi, которое сравнивается с положением прицельной точки иƒ. Если задача встречи решена с требуемой точностью, то третья процедура выполнена и происходит возвращение во внутреннюю процедуру, а если терминальное условие по аргументу широты не выполнено, то начальная величина фазы и корректируется на Δи, заново переопределяется изменение большой полуоси и расчет повторяется.
Пример реализации.
Первый шаг решения задачи состоит в анализе спутникового каталога и выборе реальных объектов ККМ, которые необходимо увести на орбиты захоронения. Объекты рекомендуется классифицировать по группам так, чтобы внутри группы орбиты ОКМ имели близкие наклонения. По начальным условия движениям отобранных объектов для конкретной группы строится портрет эволюции отклонений долгот восходящих узлов. При квазипараллельном расположении на нем линий выбирается последовательная схема облета: порядок облета - в направлении прецессии. Облет начинается с ОКМ с таким порядковым номером, чтобы исключить перелет между соседними двумя самыми удаленными друг от друга по ДВУ объектами. Далее определяется продолжительность перелета между объектами и оцениваются параметры маневров, которые обеспечивают формирование орбиты ожидания и решение задачи встречи большой продолжительности. При наличии многократных пересечений выбирается диагональная схема облета: вычисляется матрица координат узлов графа, построенного на основе портрета эволюции отклонений долгот восходящих узлов; далее ищутся наиболее длинные цепочки решений и оцениваются параметры маневров, обеспечивающих решение задачи встречи малой продолжительности. При использовании обеих схем облета далее параметры маневров уточняются с использованием трех вложенных друг в друга итерационных процедур, которые учитывают полную силовую модель движения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения последовательности перелётов между объектами космического мусора в окрестности геостационарной орбиты | 2020 |
|
RU2759026C1 |
| Космический комплекс для утилизации группы объектов крупногабаритного космического мусора | 2018 |
|
RU2695155C1 |
| СПОСОБ ПЕРЕФАЗИРОВАНИЯ КОСМИЧЕСКИХ АППАРАТОВ НА ОКОЛОЗЕМНОЙ ОРБИТЕ | 2023 |
|
RU2806928C1 |
| СПОСОБ ВЫВЕДЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ НА ОРБИТУ | 2023 |
|
RU2794486C1 |
| СПОСОБ ОЧИСТКИ ОРБИТ ОТ КОСМИЧЕСКОГО МУСОРА | 2012 |
|
RU2531679C2 |
| Способ ограничения засорения эксплуатируемых областей околоземного космического пространства | 2017 |
|
RU2665156C1 |
| СПОСОБ ЭЛЕКТРОМАГНИТНОЙ УБОРКИ ЭЛЕКТРОПРОВОДЯЩЕГО КОСМИЧЕСКОГО МУСОРА В ОКОЛОЗЕМНОМ ПРОСТРАНСТВЕ И УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОГО ЗАХВАТА И УДЕРЖАНИЯ ОДНОГО И БОЛЕЕ ЭЛЕКТРОПРОВОДЯЩИХ ОБЪЕКТОВ КОСМИЧЕСКОГО МУСОРА | 2020 |
|
RU2769807C1 |
| Способ перемещения объектов космического мусора с постепенным использованием его вещества космическим аппаратом, оснащенным лазерной двигательной установкой | 2017 |
|
RU2679938C1 |
| Способ обслуживания системы спутников на околокруговых орбитах и космическая обслуживающая система для осуществления способа | 2022 |
|
RU2772498C1 |
| СПОСОБ ВЫВЕДЕНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ С ИСПОЛЬЗОВАНИЕМ ДВИГАТЕЛЕЙ МАЛОЙ ТЯГИ | 2014 |
|
RU2586945C2 |
Изобретение относится к пространственным манёврам космических аппаратов (КА) в нецентральном гравитационном поле Земли при сближении с объектами космического мусора (ОКМ). Схему облёта ОКМ выбирают на основе портрета эволюции отклонений долгот восходящих узлов орбит ОКМ, причём эти отклонения определяют относительно орбиты одного из ОКМ. Если данный портрет имеет вид квазипараллельных линий, то применяют последовательную схему, переводя активный КА на орбиту ожидания с измененной скоростью прецессии линии узлов. При многократном пересечении указанных линий на портрете применяют диагональную схему – когда орбита очередного уводимого ОКМ служит орбитой ожидания КА для достижения следующего ОКМ. После выбора схемы облета ОКМ определяют параметры маневров КА с использованием некоторых трех вложенных друг в друга итерационных процедур. Техническим результатом является уменьшение затрат суммарной характеристической скорости КА для облёта группы ОКМ либо при заданных затратах увеличение числа достижимых ОКМ. 5 ил.
Способ определения последовательности перелетов между объектами космического мусора при значительном отличии в долготе восходящего узла (ДВУ) их орбит, характеризующийся тем, что первоначально для группы объектов космического мусора строят портрет эволюции отклонений долгот восходящих узлов, далее по виду этого портрета определяют схему облета объектов: последовательную или диагональную, причём при последовательной схеме для перелета к новому объекту активный космический аппарат переводят на орбиту ожидания с измененной скоростью эволюции ДВУ, при этом параметры этой орбиты обеспечивают совмещение ее плоскости с плоскостью орбиты цели за компромиссное время, а при диагональной схеме портрет эволюции отклонений ДВУ представляют как граф, для которого вычисляют матрицу координат узлов и далее ищут наиболее длинные цепочки решений, в которых орбита очередного объекта является одновременно орбитой ожидания для достижения следующего объекта, причём используемые при определении схем приближенные параметры маневров уточняют в точной модели движения с использованием трёх вложенных друг в друга итерационных процедур: внешней, которую используют для определения оптимального отличия в числе витков полета n, внутренней - для формирования с заданной точностью конечной орбиты для каждого фиксированного значения n, и третьей процедуры, которая служит для обеспечения с необходимой точностью времени выхода на заданную орбиту при приближенном определении параметров маневров, для чего при уточнении значения n определяют углы приложения и составляющие импульсов скорости, формирующие все элементы заданной орбиты за исключением ДВУ, а когда оптимальное значение n найдено, то для этого значения n во внутренней и третьей процедурах корректируют все элементы орбиты, включая ДВУ.
| Гришко Д.А | |||
| (МГТУ им | |||
| Н.Э | |||
| Баумана) | |||
| Исследование схем облёта объектов крупногабаритного космического мусора на низких орбитах | |||
| Абстракт | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
| Интернет: http://www.iki.rssi.ru/seminar/20180405/abstract.php | |||
| Баранов А.А., Баранов А.А | |||
| (мл.) | |||
| Алгоритм расчета параметров маневров формирования спутниковых систем | |||
| Космические исследования, 2009, т.47, N3, с | |||
| Ножевой прибор к валичной кардочесальной машине | 1923 |
|
SU256A1 |
| СПОСОБ ОЧИСТКИ ОРБИТ ОТ КОСМИЧЕСКОГО МУСОРА | 2012 |
|
RU2531679C2 |
| US 7720604 B1, 18.05.2010 | |||
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ ОЧИСТКИ КОСМОСА ОТ ПАССИВНЫХ КА И ИХ ФРАГМЕНТОВ | 1998 |
|
RU2141436C1 |
| RU 2013107014 A, 10.09.2014. | |||
Авторы
Даты
2019-05-17—Публикация
2018-07-03—Подача