Настоящее изобретение относится к устройству для измерения массового расхода жидкостей и газов, а именно, к кориолисовым расходомерам, в частности, к диагностике и способам поверки кориолисового расходомера и может использоваться в измерительной технике.
Принцип работы устройств для измерения массового расхода жидкостей и газов, таких как кориолисовы расходомеры основан на регистрации движений колеблющегося трубопровода с протекающей по нему рабочей средой. Трубопровод расходомера может включать в себя одну или более измерительных трубок, совершающих вынужденные колебания на резонансной частоте, причем данная частота пропорциональная плотности находящейся в ней среды. Датчики, расположенные на измерительных трубках, измеряют относительные колебания в точках, разнесенных по длине трубки. Когда поток рабочей среды движется по измерительной трубке, то данной измеряемой среде придается составляющая движения вибрирующей трубки в направлении вынуждающей силы. При этом среда, втекающая в трубку, создает сопротивление движению вверх, давя на трубку в противоположном направлении. Поглотив импульс при движении вокруг изгиба трубки, измеряемая среда, вытекающая из трубки, сопротивляется уменьшению составляющей движения трубки в направлении вынуждающей силы, формируя усилие в фазе с вынуждающей силой. Это приводит к закручиванию трубки и фазовому сдвигу в колебаниях между точками, разнесенными по длине трубки. Этот фазовый сдвиг прямо пропорционален массовому расходу:
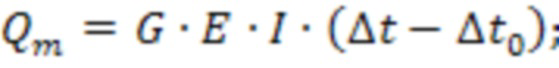
где Qm - массовый расход рабочей среды через расходомер; G - геометрический параметр расходомера; E - модуль Юнга; I - момент инерции; Δt - значение фазового сдвига, возникающее из-за действия сил Кориолиса и получаемое с датчиков, расположенных в точках, разнесенных по длине измерительной трубки; Δt0 - значение фазового сдвига при нулевом значении массового расхода через расходомер.
Группа параметров G, E и I пропорциональна жесткости расходомера. Параметр Δt содержит измеряемое мгновенное значение фазового сдвига. Параметр Δt0 же определяется, как правило, на заводе-изготовителе, при калибровке устройства для измерения массового расхода и не зависит от изменения условий рабочей среды.
Проблема заключается в том, что свойства материала измерительных трубок со временем могут изменяться в процессе эксплуатации, возможен износ, загрязнение продуктами отложений рабочей среды, коррозия, эрозия или другие изменения. Например, от протекающей рабочей среды возможно образование налета на стенках измерительных трубок, плотность которого отлична от плотности рабочей среды, что может негативно сказываться на определении плотности. Другие процессы, например, коррозия или эрозия, приводят к отклонению жесткости трубки от своего изначального значения. В свою очередь, это приводит к увеличению погрешности оценки измеряемых параметров процесса, например, массового расхода, поскольку состояние системы, описанное калибровочными коэффициентами, будет отличаться от реального. Если, к примеру, в случае отклонения параметра Δt0 проблема легко решается обнулением данного значения, и достаточно лишь отслеживать момент изменения нулевого сдвига, то в случае изменения жесткости колебательной системы необходима специальная процедура, которая будет выявлять возможные изменения свойств материала измерительной трубки, параметров ее поперечного сечения и ее жесткость, с последующим указанием неточности определения массового расхода средством измерения.
Известен «Вибрационный расходомер, а также способы и диагностика для поверки измерителя» по патенту RU 2628661. В данном изобретении предлагается преодолевать вышеизложенные проблемы путем возбуждений колебаний расходомера в одномодовом режиме, определения амплитудно-частотных характеристик с помощью тензометрических датчиков с последующим определением жесткости измерителя, после чего предлагается выдавать заключение типа «годен/не годен» по отношению к проблемам, связанным с налетом, эрозией, коррозией и другими повреждениями измерителя.
Недостатком данного способа является повышенное требование к точности определения амплитуды колебаний. Точность определения амплитуды колебаний на резонансной моде равна точности определения коэффициента передачи, который и определяет точность измерения расхода рабочей среды. То есть, если необходимо определять погрешность расходомера на уровне 0.2% от измеряемой величины, то точность измерения амплитуды механических колебаний должна быть не хуже 0.1% от измеряемой величины.
Кроме того, значительный недостаток предлагаемого в вышеназванном патенте способа, заключен в определении амплитудно-частотных характеристик на одной форме колебаний. Из-за того, что измерение проводится на одной форме, а силы Кориолиса, действующие на измерительную трубку при протекании рабочей среды, дают другой вид формы изгиба, то в определенном ряде случаев изменения локальной жесткости измерительной трубки можно не обнаружить возникшую погрешность измерения расходомера.
Известен способ контроля характеристик колебаний в кориолисовом расходомере, который вставляется в трубопровод, (расходомере) включающем колебательную систему, способную совершать механические колебания, колебательная система имеет, по меньшей мере, одну измерительную трубку через которую может течь среда, возбуждение колебательной системы, по меньшей мере, одним возбудителем для выполнения механических колебаний в соответствии с входным сигналом возбуждения, который демонстрирует временные модуляции сигнала, происходящие во временных интервалах, регистрацию датчиком хотя бы одной переменной реакции вызванных механических колебаний колебательной системы, моделирование возбужденной колебательной системы с помощью цифровой модели, которая включает, по меньшей мере, один подбираемый параметр и определение того, превышено ли соответствующее предельное значение, по меньшей мере, одним, интерактивно определенным значением параметра по меньшей мере для одного подбираемого параметра или по меньшей мере одной переменной, полученной из по меньшей мере одного, интерактивно установленного значения параметра; указанное моделирование возбужденной колебательной системы с помощью цифровой модели включает: возбуждение цифровой модели таким же образом, как и колебательной системы; вычисление переменной отклика моделирования имитируемых колебаний согласно цифровой модели, выполняемое по множеству модуляций сигнала, итеративное согласование, по меньшей мере, одного подбираемого параметра таким образом, что переменная отклика моделирования итеративно приближается к переменной отклика (см. US 8950274).
Таким образом, в данном аналоге предлагается воздействовать на цифровую модель устройства сигналом, совпадающим с подаваемым на реальный расходомер, и сравнивать отклик модели и реального расходомера. Данный метод выбран в качестве ближайшего аналога.
Данный способ, как и предыдущий, основывается на измерении передаточных функций между входами и выходами расходомера, следовательно, как и предыдущий способ, требует высокой точности измерения амплитуды сигнала. Также требование данного способа подавать на модель такой же сигнал, как и на расходомер, и необходимость итерационной подгонки модели под расходомер налагает обязательное требование, что специализированное устройство оценки состояния расходомера должно быть подключено к расходомеру на все время оценки или данный способ должен быть реализован непосредственно в расходомере, и невозможно, допустим, сначала измерить параметры расходомера известными в технике стандартными методами и устройствами оценки колебательных систем, а затем, по измеренным параметрам, оценить состояние расходомера. Таким образом, недостатками известного способа являются его некоторая неполнота и не вполне удовлетворительная надежность из-за сложности его осуществления.
Задачей является повышение надежности и обеспечение большей полноты контроля при упрощении осуществления способа оценки состояния.
Поставленная задача решается тем, что в способе оценки состояния датчика кориолисового расходомера для поверки и/или диагностики кориолисового расходомера, включающем возбуждение механических колебаний колебательной системы, измерение механических колебаний при помощи, по меньшей мере, одного датчика колебаний, оценку параметров колебательной системы на основе измеренных колебаний и численной модели колебательной системы, согласно изобретению, при заводской настройке измеряют параметры колебательной системы датчика кориолисового расходомера в виде ее исходных параметров, являющихся функциями ее состояния, составляют по ним численную модель колебательной системы, соответствующую исходному состоянию датчика кориолисового расходомера, принимающую в качестве входных данных измеренные значения собственных форм и частот колебательной системы датчика кориолисового расходомера и выдающую в качестве выходных данных степень соответствия поданных на вход собственных форм и частот исходному состоянию колебательной системы датчика кориолисового расходомера, и сохраняют эту численную модель, во время оценки состояния датчика кориолисового расходомера измеряют собственные формы и частоты колебательной системы и оценивают, насколько собственные формы и частоты колебательной системы соответствуют численной модели колебательной системы датчика кориолисового расходомера в исходном состоянии, и по результату оценки делают вывод о состоянии датчика кориолисового расходомера.
При этом численная модель может включать матрицы, вектора и скалярные величины коэффициентов при второй степени собственной частоты, при первой степени собственной частоты и при нулевой степени собственной частоты, а также собственные формы колебательной системы датчика кориолисового расходомера в исходном состоянии.
Коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
Часть коэффициентов численной модели могут считаться малозначащими и принимаются равными некоторому фиксированному значению.
При этом матрицы и вектора могут иметь одинаковые по величине элементы и сведены к скалярным значениям
А также для оценки того, насколько измеренные собственные формы и частоты колебательной системы датчика кориолисового расходомера соответствуют сохраненной при заводской настройке численной модели, может использоваться набор векторных величин, каждая из которых описывает отклонение соответствующей формы, компоненты каждой векторной величины рассчитываются как сумма произведений степени собственной частоты на соответствующей собственной форме на вектор коэффициентов для этой собственной формы, полученный из результатов калибровки и результатов измерения собственной формы.
При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
А также модель колебательной системы может быть записана в виде
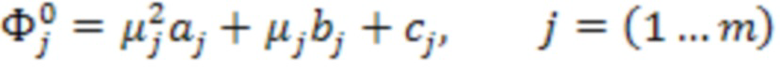
где 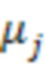 - измеренные собственные частоты колебательной системы,
- измеренные собственные частоты колебательной системы, 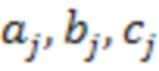 - коэффициенты численной модели колебательной системы, j - номер собственной формы,
- коэффициенты численной модели колебательной системы, j - номер собственной формы, 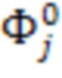 - элемент вектора оценки состояния датчика кориолисового расходомера.
- элемент вектора оценки состояния датчика кориолисового расходомера.
При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
Собственные формы и собственные частоты полностью определяют состояние колебательной системы датчика кориолисового расходомера с точки зрения его метрологических характеристик, а, следовательно, изменения собственных форм и частот свидетельствуют об изменении метрологических характеристик. Поэтому составление и сохранение при заводской настройке численной модели колебательной системы расходомера по параметрам колебательной системы датчика кориолисового расходомера в исходном его состоянии, измерение во время оценки состояния датчика кориолисового расходомера собственных форм и частот, и сопоставление измеренных во время оценки состояния собственных форм и частот с численной моделью колебательной системы в начальном состоянии, с получением степени соответствия, позволяет получить более полную и надежную оценку состояния датчика кориолисового расходомера после начала его эксплуатации. Для оценки текущего состояния кориолисового расходомера используется, таким образом, более полный, по сравнению с аналогами, объем информации о текущем состоянии колебательной системы при сравнении ее параметров с сохраненной численной моделью, что дает возможность повысить надежность оценки. Ввиду того, что способ не требует итеративной подгонки параметров, а также, поскольку некоторые из вариантов осуществления изобретения позволяют пренебрегать изменением собственных форм, это позволяет снизить требования к вычислительной мощности и точности измерения амплитуды и, тем самым упростить реализацию способа.
Технический результат - получение более полной и надежной оценки состояния кориолисового расходомера после начала его эксплуатации и, как следствие, более надежное выявление изменения калибровочного коэффициента расходомера, связанного с массовым расходом и плотностью при более простом осуществлении способа.
Заявляемый способ обладает новизной в сравнении с прототипом, отличаясь от него такими существенными признаками как измерение при заводской настройке параметров колебательной системы датчика кориолисового расходомера в виде ее исходных параметров, являющихся функциями ее состояния, составление по ним численной модели колебательной системы, соответствующей исходному состоянию датчика кориолисового расходомера, принимающей в качестве входных данных измеренные значения собственных форм и частот колебательной системы датчика кориолисового расходомера и выдающей в качестве выходных данных степень соответствия поданных на вход собственных форм и частот исходному состоянию колебательной системы датчика кориолисового расходомера, сохранение этой численной модели, измерение во время оценки состояния датчика кориолисового расходомера собственных форм и частот колебательной системы, оценка, насколько собственные формы и частоты колебательной системы соответствуют численной модели колебательной системы датчика кориолисового расходомера в исходном состоянии, и составление по результату оценки вывода о состоянии датчика кориолисового расходомера, обеспечивающими в совокупности достижение заданного результата.
Заявителю неизвестны технические решения, обладающие указанными выше отличительными признаками, которые обеспечивали бы в совокупности получение заданного результата, поэтому он считает, что заявляемый способ соответствует критерию «изобретательский уровень».
Заявляемый способ оценки состояния датчика кориолисового расходомера для поверки и/или диагностики кориолисового расходомера может найти широкое применение в измерительной технике, а потому соответствует критерию «промышленная применимость».
Заявляемый способ заключается в следующем.
Для оценки состояния датчика кориолисового расходомера при поверке и/или диагностике кориолисового расходомера при заводской настройке измеряют параметры колебательной системы датчика кориолисового расходомера в виде ее исходных параметров, являющихся функциями ее состояния. Составляют по ним численную модель колебательной системы, соответствующую исходному состоянию датчика кориолисового расходомера, принимающую в качестве входных данных измеренные значения собственных форм и частот колебательной системы датчика кориолисового расходомера и выдающую в качестве выходных данных степень соответствия поданных на вход собственных форм и частот исходному состоянию колебательной системы датчика кориолисового расходомера. Сохраняют эту численную модель. Во время оценки состояния датчика кориолисового расходомера измеряют собственные формы и частоты колебательной системы и оценивают, насколько собственные формы и частоты колебательной системы соответствуют численной модели колебательной системы датчика кориолисового расходомера в исходном состоянии. По результату оценки делают вывод о состоянии датчика кориолисового расходомера.
При этом численная модель включает матрицы, вектора и скалярные величины коэффициентов при второй степени собственной частоты, при первой степени собственной частоты и при нулевой степени собственной частоты, а также собственные формы колебательной системы датчика кориолисового расходомера в исходном состоянии. Коэффициенты численной модели являются функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды, причем часть коэффициентов численной модели считаются малозначащими и принимаются равными некоторому фиксированному значению.
При этом численная модель может включать матрицы, вектора и скалярные величины коэффициентов при второй степени собственной частоты, при первой степени собственной частоты и при нулевой степени собственной частоты, а также собственные формы колебательной системы датчика кориолисового расходомера в исходном состоянии. При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды. А также часть коэффициентов численной модели могут считаться малозначащими и приниматься равными некоторому фиксированному значению. При этом матрицы и вектора численной модели могут иметь одинаковые по величине элементы и сведены к скалярным значениям.
А также для оценки того, насколько измеренные собственные формы и частоты колебательной системы датчика кориолисового расходомера соответствуют сохраненной при заводской настройке численной модели, может использоваться набор векторных величин, каждая из которых описывает отклонение соответствующей формы, компоненты каждой векторной величины рассчитываются как сумма произведений степени собственной частоты на соответствующей собственной форме на вектор коэффициентов для этой собственной формы, полученный из результатов калибровки и результатов измерения собственной формы. При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
А также модель колебательной системы может быть записана в вид
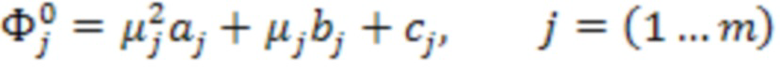
где 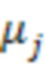 - измеренные собственные частоты колебательной системы,
- измеренные собственные частоты колебательной системы, 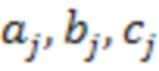 - коэффициенты численной модели колебательной системы, j - номер собственной формы,
- коэффициенты численной модели колебательной системы, j - номер собственной формы, 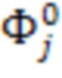 - элемент вектора оценки состояния датчика кориолисового расходомера. При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
- элемент вектора оценки состояния датчика кориолисового расходомера. При этом коэффициенты численной модели могут являться функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
Изобретение иллюстрируется следующими чертежами (фиг. 1-8), где:
Фиг. 1 изображает кориолисовый расходомер в качестве примера согласно изобретению.
Фиг. 2 изображает математическую абстракцию колебательной системы расходомера.
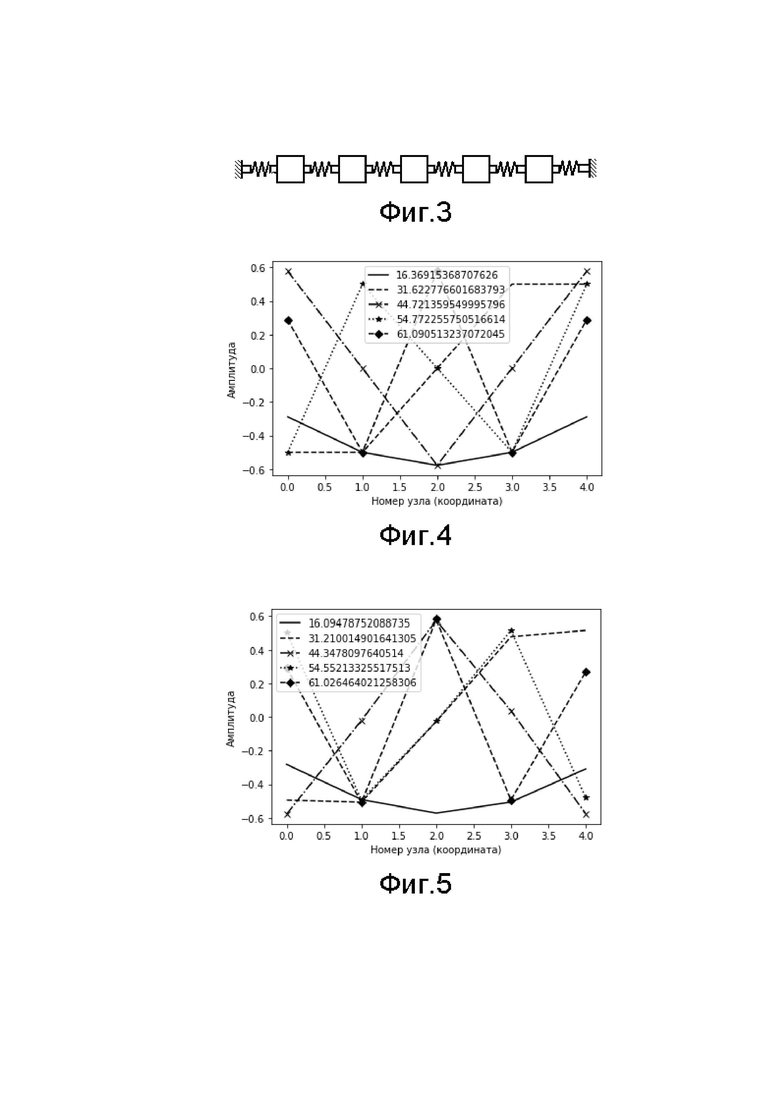
Фиг. 3 изображает простую колебательную систему для иллюстрации применения методики, согласно изобретению.
Фиг. 4 изображает собственные формы и частоты простой колебательной системы, показанной на Фиг. 3, в ее начальном состоянии.
Фиг. 5 изображает собственные формы и частоты простой колебательной системы, показанной на Фиг. 3, в одной из реализаций измененного состояния.
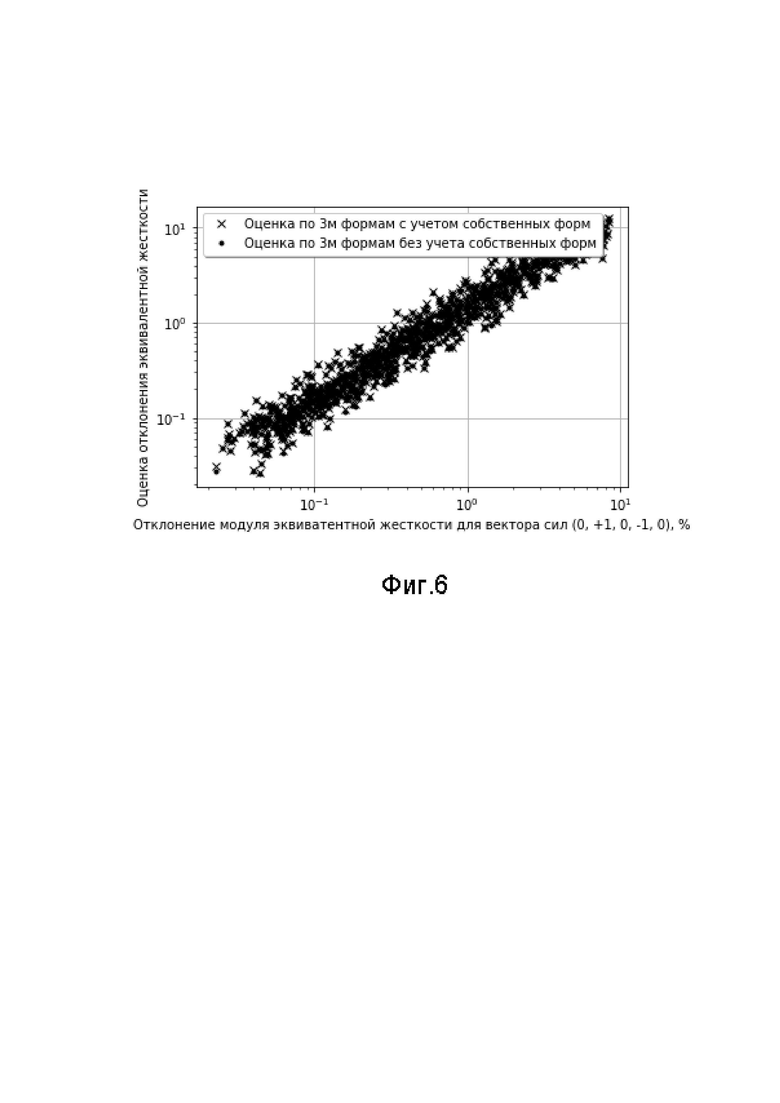
Фиг. 6 изображает пример оценки эквивалентной жесткости для вектора сил формы (0, +1, 0, -1, 0) простой колебательной системы, приведенной на Фиг. 3, по около 1000 различных реализаций отклонений системы от исходного состояния.
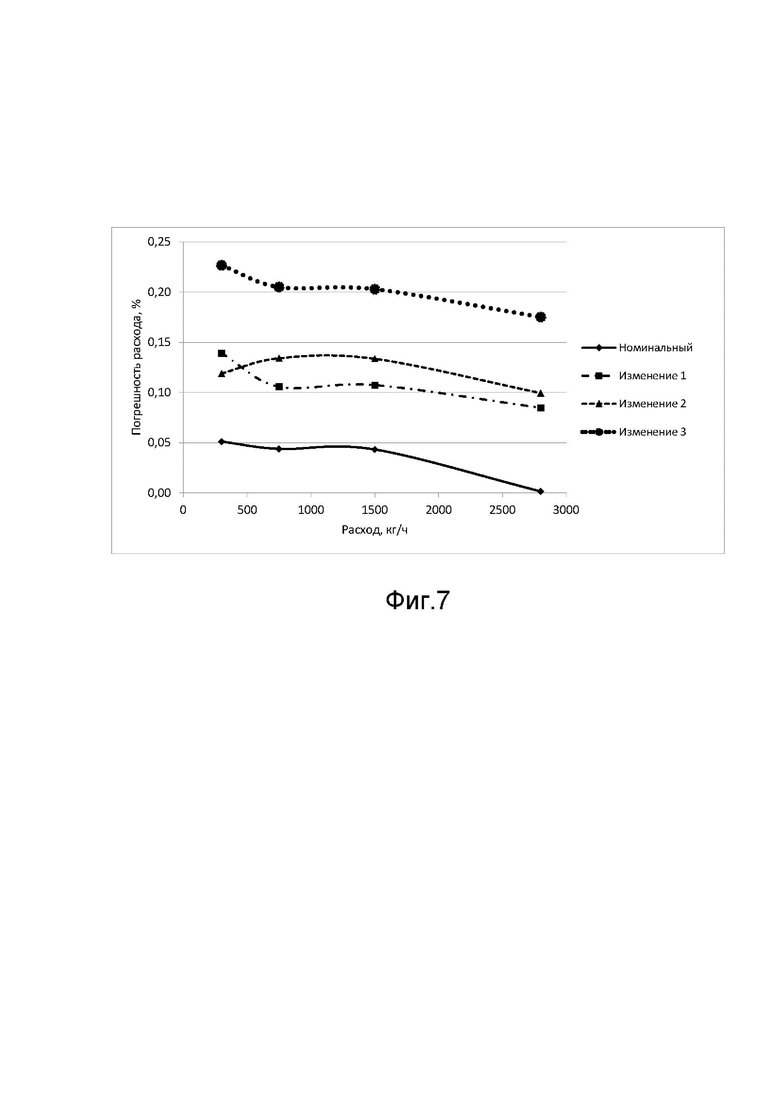
Фиг. 7 изображает графики, демонстрирующие зависимость погрешности от расхода реального расходомера, подвергшегося экспериментальной деградации.
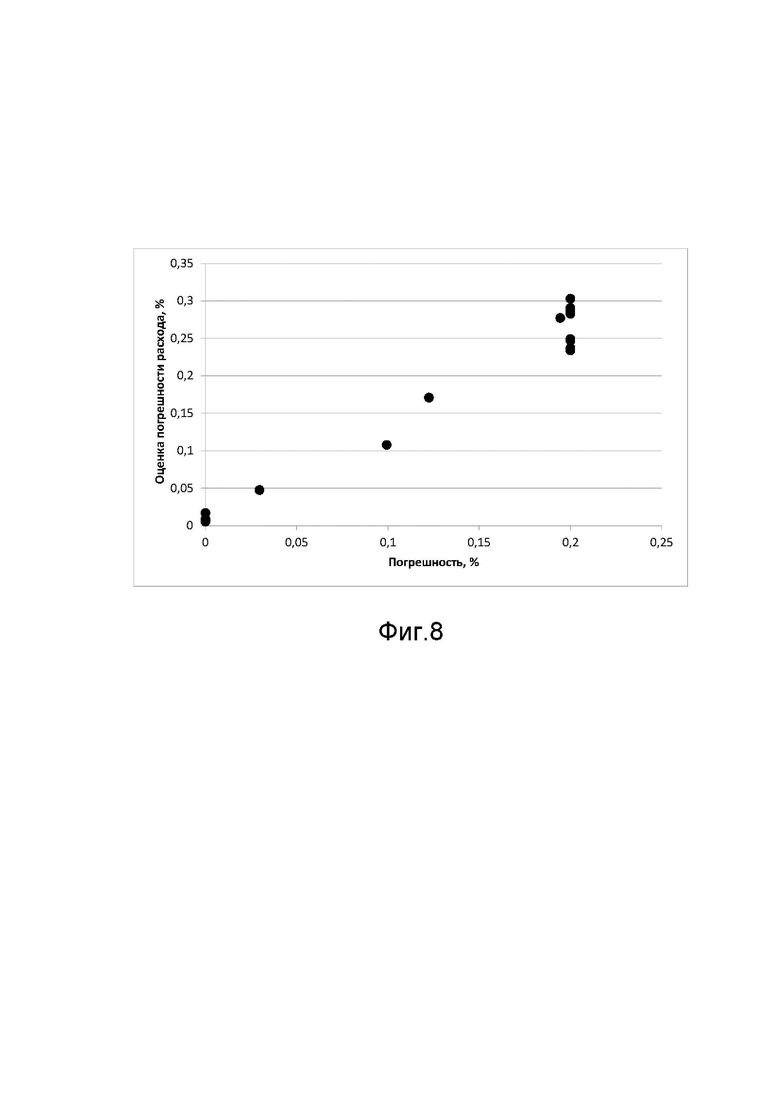
Фиг. 8 изображает пример оценки погрешности по методике, согласно изобретению, реального расходомера, подвергшегося экспериментальной деградации.
Фиг. 1-8 и нижеследующее описание представляют собой примеры, демонстрирующие специалистам в данной области техники то, как осуществить и использовать предпочтительный вариант осуществления изобретения. При раскрытии принципов изобретения некоторые стандартные положения упрощены или исключены. Специалистам в данной области техники будут очевидны вариации этих примеров в рамках объема настоящего изобретения. Специалистам в данной области техники будет видно, что описанные ниже признаки могут объединяться различным образом, образуя множественные варианты изобретения. Таким образом, изобретение не ограничивается описанными ниже специальными примерами, но ограничивается только формулой изобретения и ее эквивалентами.
На фиг. 1 показан расходомер 1, содержащий датчик 2 и электронный блок 3. Датчик 2 реагирует на массовый расход и плотность измеряемого флюида (жидкости или газа). Электронный блок 3 соединен с датчиком 2 посредством линии 4 связи для предоставления информации о параметрах колебательной системы, на основании которых вычисляются массовый расход и плотность измеряемого флюида. Несмотря на то, что описывается конструкция кориолисового расходомера, очевидно, что настоящее изобретение может применяться и для поточного плотномера, без дополнительных измерительных возможностей, предоставляемых кориолисовым расходомером.
Датчик 2 включает в себя основание 5, на котором закреплены по крайней мере два разветвителя 6 и 6', по крайней мере два фланца 7 и 7', по крайней мере пара параллельных измерительных трубок 8 и 8', по крайней мере один привод 9, по крайней мере один датчик 10 температуры и по крайней мере два датчика 11 и 11' колебаний. Измерительные трубки 8 и 8' изгибаются по крайней мере в двух симметрично расположенных местах вдоль их длины и при этом практически параллельны друг другу. По крайней мере две перемычки 12 и 12' между измерительными трубками 8 и 8' служат для определения осей Z и Z', относительно которых колеблется каждая измерительная трубка.
Боковые участки измерительных трубок 8 и 8' жестко связаны с разветвителями 6 и 6', а разветвители 6 и 6', в свою очередь, жестко связаны с основанием 5 и с фланцами 7 и 7'. Это обеспечивает замкнутый непрерывный канал для флюида, протекающего через датчик 2 кориолисового расходомера 1.
Если фланцы 7 и 7', имеющие впускное и выпускное отверстия 13 и 13', подсоединены к трубопроводу (на чертежах не показан), в котором протекает флюид, то флюид проходит через впускное отверстие 13 фланца 7 в разветвитель 6. В пределах разветвителя 6 поток флюида разделяется и направляется через измерительные трубки 8 и 8'. После выхода из измерительных трубок 8 и 8' флюид собирается в общий поток в разветвителе 6' и направляется затем через выпускное отверстие 13' фланца 7' в трубопровод (не показан).
Измерительные трубки 8 и 8' выбираются таким образом и монтируются на разветвителях 6 и 6' так, чтобы иметь практически одинаковое распределение масс и жесткостей относительно осей Z и Z'. Ввиду того, что модуль Юнга измерительных трубок меняется в зависимости от температуры, и это, в свою очередь, сказывается на вычислении массового расхода флюида и его плотности, по крайней мере на одной измерительной трубке 8' установлен по крайней мере один датчик 10 температуры для непрерывного контроля температуры измерительной трубки. Температура измерительной трубки 8', а следовательно, и сигнал с датчика температуры, обусловлены температурой флюида, протекающего через измерительную трубку. Зависящий от температуры сигнал с датчика 10 температуры используется электронным блоком 3 для компенсации изменения модуля упругости измерительных трубок 8 и 8', обусловленных любыми изменениями температуры измерительной трубки.
Измерительные трубки 8 и 8' приводятся в движение по крайней мере одним приводом 9, способным вызывать колебания измерительных трубок на различных формах колебаний. Данный привод 9 может обладать любой из хорошо известных конструкций, например, он может быть выполнен в виде по крайней мере одной установленной на измерительной трубке 8 катушки, через которую для колебаний обеих измерительных трубок пропускается переменный ток, и по крайней мере одного противоположно установленного на измерительной трубке 8' магнита.
Измерительные трубки 8 и 8', привод 9, датчики 11 и 11' колебаний, перемычки 12 и 12' образуют колебательную систему датчика 2 кориолисового расходомера 1.
Электронный блок 3 принимает сигнал с датчика 10 температуры, а также сигналы с датчиков 11 и 11' колебаний по линии 4 связи. Электронный блок 3 генерирует сигнал возбуждения, передаваемый по линии 4 связи приводу 9, приводящему измерительные трубки 8 и 8' в колебательные движения. Электронный блок 3 обрабатывает сигналы с датчиков 11 и 11' колебаний, а также сигнал с датчика 10 температуры для вычисления массового расхода, плотности флюида, проходящего через датчик 2, а также других параметров, необходимых для функционирования расходомера.
Фиг. 2 иллюстрирует математическую абстракцию колебательной системы расходомера. Колебательную систему расходомера, а именно измерительные трубки, математически можно считать балкой, испытывающей в процессе работы прибора преимущественно изгибные колебания. Согласно представлениям математической физики, общая форма дифференциального уравнения собственных колебаний балки имеет вид
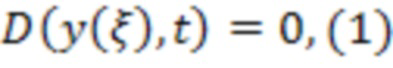
где ξ - обобщенная координата, связанная с длиной трубки;
y - величина прогиба средней линии трубки;
t - время.
Если расписать уравнение (1) для изгибных колебаний трубки без учета диссипативных сил, вызываемых, например, внутренним трением материала, то оно примет следующий вид:
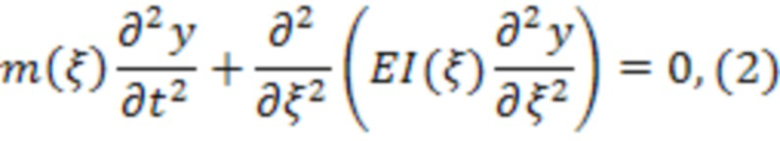
где m(ξ) - погонная масса трубки;
E - модуль упругости первого рода;
I(ξ) - момент инерции сечения.
Поскольку внутри трубки находится флюид, массовый расход которого подвергается измерению в процессе работы кориолисового расходомера, уравнение (2) следует дополнить компонентами, учитывающими массу флюида, при этом считаем, что упругостью флюида и его внутренним трением при изгибных колебаниях можно пренебречь:
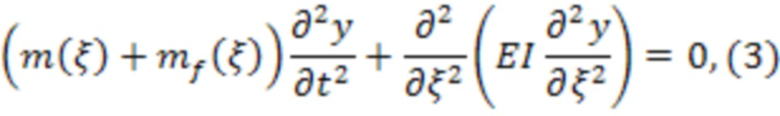
где 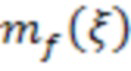 - погонная масса флюида, текущего через трубку;
- погонная масса флюида, текущего через трубку;
m(ξ) - погонная масса трубки;
Уравнение (3) для ограниченного числа n точек на трубке можно переписать в виде системы уравнений, в матричном виде имеющей вид:
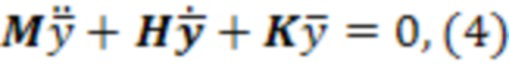
где M, H, K - матрицы мер инерции, демпфирования и жесткости соответственно;
 - вектор прогибов трубки в интересующих нас точках, имеющий размерность n.
- вектор прогибов трубки в интересующих нас точках, имеющий размерность n.
Вектор прогибов трубки в интересующих нас точках можно определить, например, воспользовавшись широко известным методом Галёркина. Метод Галёркина позволяет найти приближенное решение системы (4) и оценить его точность. Для этого запишем вектор прогибов в виде:
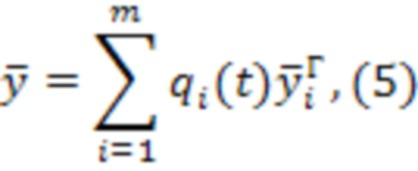
где 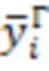 - заданные постоянные векторы смещений, близкие по формам интересующих нас колебаний, имеют размерность n;
- заданные постоянные векторы смещений, близкие по формам интересующих нас колебаний, имеют размерность n;
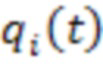 - базисные функции, еще называемые "галеркинские координаты";
- базисные функции, еще называемые "галеркинские координаты";
m - количество рассматриваемых форм колебаний.
Уравнение (5) можно также использовать для описания отличия форм исходной и измененной колебательных систем. Подставив (5) в (4), получим следующее выражение:
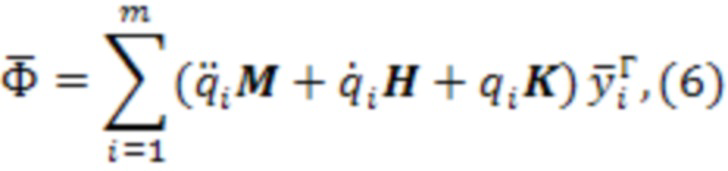
Вектор 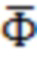 можно толковать как силы реакции связей, наложенных на систему и обеспечивающих движение с заданными формами, определяемыми
можно толковать как силы реакции связей, наложенных на систему и обеспечивающих движение с заданными формами, определяемыми 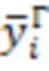 . Если (5) является точным решением (4), то вектор
. Если (5) является точным решением (4), то вектор 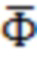 равен нулю. Система для определения
равен нулю. Система для определения 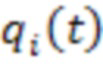 по условию ортогональности вектора невязки к базисным функциям записывается в виде:
по условию ортогональности вектора невязки к базисным функциям записывается в виде:
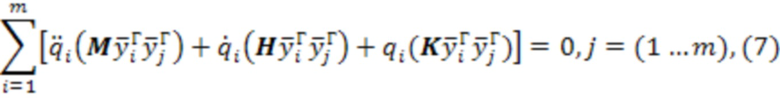
Допустим, что нам известны собственные частоты 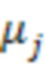 и собственные вектора
и собственные вектора 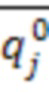 системы (7), которые, в то же время, формируют матрицу связи между собственными формами
системы (7), которые, в то же время, формируют матрицу связи между собственными формами  начальной и
начальной и 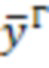 измененной систем. Следовательно, можно найти вектор амплитуд сил реакций связей:
измененной систем. Следовательно, можно найти вектор амплитуд сил реакций связей:
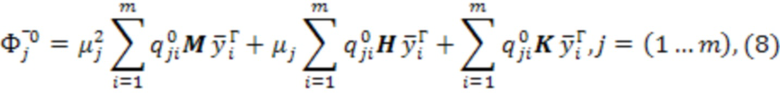
где 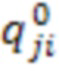 - компонента матрицы связей
- компонента матрицы связей 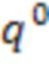 амплитуд смещений из уравнения (5).
амплитуд смещений из уравнения (5).
Упрощенно, формулу (8) можно переписать в виде:
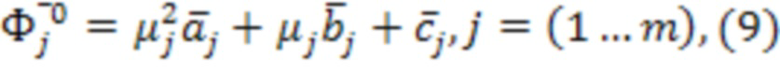
Таким образом, если известны матрицы M, H, K колебательной системы, 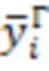 - измеренные фактические вектора амплитуд собственных форм колебательной системы в текущем состоянии,
- измеренные фактические вектора амплитуд собственных форм колебательной системы в текущем состоянии, 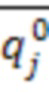 - фактические элементы матрицы изменения форм колебательной системы в текущем состоянии, вычисленные из уравнения (5) или решением системы (7), по измеренным векторам
- фактические элементы матрицы изменения форм колебательной системы в текущем состоянии, вычисленные из уравнения (5) или решением системы (7), по измеренным векторам  собственных форм начальной системы и векторам
собственных форм начальной системы и векторам 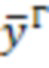 собственных форм системы в текущем состоянии,
собственных форм системы в текущем состоянии, 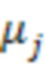 - измеренные фактические собственные частоты колебательной системы в текущем состоянии, то вектор
- измеренные фактические собственные частоты колебательной системы в текущем состоянии, то вектор 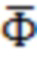 из уравнения (8) будет мерой отличия колебательной системы от начального состояния. И чем больше колебательная система будет отличаться от начального состояния, тем больше будет величина вектора
из уравнения (8) будет мерой отличия колебательной системы от начального состояния. И чем больше колебательная система будет отличаться от начального состояния, тем больше будет величина вектора 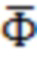 .
.
На практике может быть удобнее использовать оценку не в виде вектора 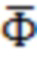 , а в виде некоторой функции над этим вектором, например скалярного произведения
, а в виде некоторой функции над этим вектором, например скалярного произведения 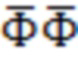 , или функции над компонентами вектора
, или функции над компонентами вектора 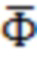 .
.
Матрица H во многих практических случаях может считаться нулевой. Компоненты матрицы M являются функциями плотности среды, температуры, давления, плотности материала трубки, коэффициента теплового расширения трубки и формы трубки. Компоненты матрицы K являются функциями модуля упругости материала трубки, температуры, давления и формы трубки.
Компоненты матриц M, H, K или их эквиваленты могут быть получены по известным в технике методикам, как расчетным путем с последующим уточнением при калибровке, так и прямым измерением на расходомере.
На практике для надежной оценки состояния расходомера может быть достаточно небольшого числа точек на трубке, и соответственно, небольшого числа элементов вектора 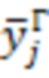 ,
, 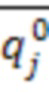 , в большинстве случаев достаточно 2х-3х элементов. При этом в большинстве случаев величина
, в большинстве случаев достаточно 2х-3х элементов. При этом в большинстве случаев величина 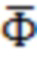 гораздо более чувствительна к изменению квадратов собственных частот
гораздо более чувствительна к изменению квадратов собственных частот 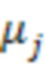 , чем к изменению собственных форм, в связи с чем относительное влияние вектора собственных форм меньше, что позволяет снизить требование к точности измерения амплитуд собственных форм.
, чем к изменению собственных форм, в связи с чем относительное влияние вектора собственных форм меньше, что позволяет снизить требование к точности измерения амплитуд собственных форм.
Так как в любом реальном случае точки создания сил и точки измерения колебаний расположены дискретно по трубке, а формы деформации под воздействием кориолисовых сил не совпадают ни с собственными формами, ни с формами вынужденных деформаций, создаваемых силами в выбранных точках, величина точности оценки состояния системы носит вероятностный характер, в связи со случайным характером величин деградации трубки.
При заводской настройке производится построение численной модели колебательной системы датчика кориолисового расходомера. Например, определяются матрицы M, H, K колебательной системы датчика кориолисового расходомера. При этом принимаем, что эти матрицы являются функциями состояния системы (температура, давление, плотность и т.д.). Для оценки соответствия системы исходному состоянию определяются фактические собственные частоты 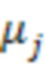 и элементы матрицы связей
и элементы матрицы связей 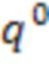 из уравнения (5), по рассчитанным, решением уравнения (4) с известными матрицами M, H, K, собственным формам
из уравнения (5), по рассчитанным, решением уравнения (4) с известными матрицами M, H, K, собственным формам  и измеренным собственным формам системы
и измеренным собственным формам системы 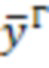 в текущем состоянии, и по уравнению (8) или (9) рассчитываются
в текущем состоянии, и по уравнению (8) или (9) рассчитываются 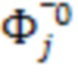 , которые и являются мерой отклонения системы от исходного состояния, учитывая фактические вектора форм. При этом, если мы предположим, что изменением собственных форм можно пренебречь, то есть
, которые и являются мерой отклонения системы от исходного состояния, учитывая фактические вектора форм. При этом, если мы предположим, что изменением собственных форм можно пренебречь, то есть 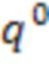 будет представлять собой единичную матрицу, а
будет представлять собой единичную матрицу, а 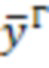 будут равны
будут равны  , то вектора
, то вектора 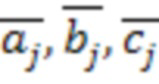 в уравнении (9) получаются зависимыми только от переменных среды и могут быть получены единожды при калибровке расходомера из матриц M, H, K, и векторов
в уравнении (9) получаются зависимыми только от переменных среды и могут быть получены единожды при калибровке расходомера из матриц M, H, K, и векторов  в соответствии с уравнениями (8) и (9). А если учесть, что система симметрична, то допустимо оценивать состояние системы только в одной из симметричных точек. При этом выражение (9) может из векторного превратиться в скалярное.
в соответствии с уравнениями (8) и (9). А если учесть, что система симметрична, то допустимо оценивать состояние системы только в одной из симметричных точек. При этом выражение (9) может из векторного превратиться в скалярное.
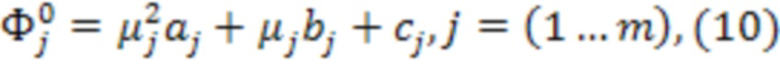
Численную модель колебательной системы датчика кориолисового расходомера в виде (10), в силу ее предельной простоты, можно построить эмпирически при заводской настройке. Очевидно, что модель можно переписать и в других формах, не только в формах (8), (9), (10), но для демонстрации основных аспектов предлагаемого метода этих трех вариантов записи достаточно.
На практике способ осуществляется следующим образом. При заводской настройке производится построение численной модели колебательной системы датчика кориолисового расходомера, при этом форма записи модели определяется компромиссом между техническими требованиями к процедуре оценки состояния датчика кориолисового расходомера, требуемой точностью и надежностью оценки состояния, конструкцией датчика кориолисового расходомера и сложностью процедуры заводской настройки. Для большей точности и надежности может использоваться большее количество узлов модели и, соответственно, большее количество коэффициентов модели, например большая размерность матриц M, H, K, и большее количество участвующих в оценке состояния собственных форм и частот, большее значение m. Для упрощения заводской настройки число узлов модели и число участвующих в оценке состояния собственных форм и частот может минимизироваться. На практике бывает достаточно 2х-3х собственных форм и частот и 1-2 значимых узла (точки) колебательной системы датчика кориолисового расходомера. Численная модель колебательной системы в начальном состоянии запоминается на носителе информации либо в электронном блоке кориолисового расходомера. При оценке состояния датчика кориолисового расходомера измеряют собственные формы и частоты колебательной системы. Измеренные собственные формы и частоты подставляют в численную модель колебательной системы. В результате получают оценку соответствия состояния колебательной системы датчика кориолисового расходомера начальному при заводской настройке, оценка получается в виде числовых значений.
Для демонстрации работы методики используем простой пример - модель одномерной колебательной системы без затухания, состоящей из 5ти последовательно соединенных пружинами масс. Такую систем можно условно изобразить в виде Фиг. 3.
Приведенную систему можно описать уравнением (4). И набором матриц M и K, например такого вида:

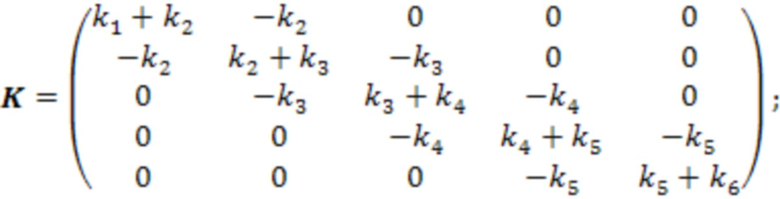
где коэффициенты 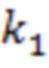 -
- 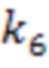 - жесткости шести пружин. Для исходной системы коэффициенты
- жесткости шести пружин. Для исходной системы коэффициенты 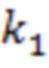 -
- 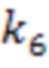 равны 1000.
равны 1000.
Подставив эти матрицы в уравнение (4) и решив его, получим набор собственных форм и частот для исходной колебательной системы, изображенных на Фиг. 4.
Для моделирования измененной системы, будем менять коэффициенты упругости пружин 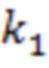 -
- 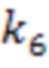 , и получать матрицы измененной колебательной системы
, и получать матрицы измененной колебательной системы 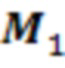 ,
, 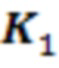 . Решив уравнение измененной системы, будем получать ее собственные формы и частоты. Например, при изменении коэффициента упругости пружины
. Решив уравнение измененной системы, будем получать ее собственные формы и частоты. Например, при изменении коэффициента упругости пружины 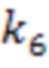 на 10%, собственные формы и частоты примут вид, изображенный на Фиг. 5.
на 10%, собственные формы и частоты примут вид, изображенный на Фиг. 5.
Допустим, нам необходимо оценить, насколько эквивалентная жесткость для вектора сил (0, 1, 0, -1, 0) измененной системы отличается от эквивалентной жесткости исходной системы. Для оценки описанной эквивалентной жесткости, воспользуемся общей оценкой соответствия колебательной системы исходной, для чего применим уравнение (8).
В соответствии с уравнением (5), можно записать уравнение для связи амплитуд собственных форм измененной и исходной системы:
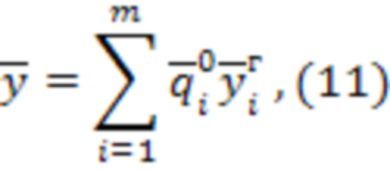
где 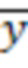 - вектора амплитуд собственных форм исходной системы,
- вектора амплитуд собственных форм исходной системы, 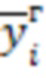 - вектора амплитуд собственных форм измененной системы,
- вектора амплитуд собственных форм измененной системы, 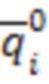 - вектора связи, что есть то же самое, что и вектора собственных форм уравнения (7).
- вектора связи, что есть то же самое, что и вектора собственных форм уравнения (7).
Вектора связи 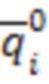 можно найти, решив уравнение (11). Обозначим
можно найти, решив уравнение (11). Обозначим 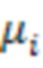 собственные частоты измененной колебательной системы. Вектора
собственные частоты измененной колебательной системы. Вектора 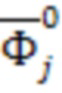 будем вычислять по уравнению (8).
будем вычислять по уравнению (8).
Следовательно, можно вычислить значение векторов 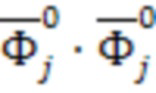 . За меру отклонения колебательной системы от исходного состояния примем линейную функцию от квадратного корня от
. За меру отклонения колебательной системы от исходного состояния примем линейную функцию от квадратного корня от 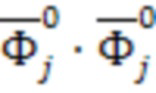 :
:

где 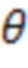 - коэффициент пропорциональности для приведения величины оценки отклонения к удобной форме, например к процентам изменения модуля эквивалентной жесткости, для нашего примера величина
- коэффициент пропорциональности для приведения величины оценки отклонения к удобной форме, например к процентам изменения модуля эквивалентной жесткости, для нашего примера величина 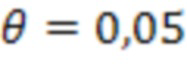 .
.
Рассмотрим оценку эквивалентной жесткости для случая случайного отклонения жесткости каждой пружины с равномерным законом распределения в пределах 90-100% исходной жесткости. Будем вести оценку по сокращенному набору собственных форм - по трем формам с частотами 16.369, 31.623 и 54.772, в соответствии с Фиг. 4. Рассчитаем и построим графики для двух случаев - для случая точной оценки собственных форм измененной системы и для случая игнорирования изменения собственных форм, т.е. когда матрицу векторов 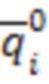 считаем диагональной единичной матрицей. Результаты моделирования приведены на Фиг. 6.
считаем диагональной единичной матрицей. Результаты моделирования приведены на Фиг. 6.
Как видно из графика, оба случая оценки статистически равнозначны, хоть и не всегда дают полностью одинаковый результат. Из графика видно явную корреляцию оценки отклонения эквивалентной жесткости с фактическим отклонением. И, хотя оценка имеет существенный разброс, всегда можно подобрать коэффициент 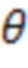 в уравнении (12) таким образом, чтобы обеспечить обнаружение заданного уровня отклонения эквивалентной жесткости колебательной системы с заданной доверительной вероятностью.
в уравнении (12) таким образом, чтобы обеспечить обнаружение заданного уровня отклонения эквивалентной жесткости колебательной системы с заданной доверительной вероятностью.
Экспериментально работа данного изобретения была подтверждена диагностикой ухода параметров расходомера, представленного на Фиг. 1, при изменении жесткости трубок 8 и 8' колебательной системы. Для этого трубки 8 и 8' колебательной системы расходомера 1 подвергались деградации в несколько итераций. После каждой итерации деградации трубок 8 и 8' с расходомера 1 снимались параметры колебательной системы, служащие для выполнения оценки ухода основной относительной погрешности по разработанной методике. Также после каждой итерации деградации проводились испытания определения основной относительной погрешности. Результаты испытаний представлены на Фиг. 7.
Матрицы М и К для исходного закалиброванного состояния измерительных трубок, заполненных воздухом при атмосферном давлении и температуре 20°С, имели следующий вид:

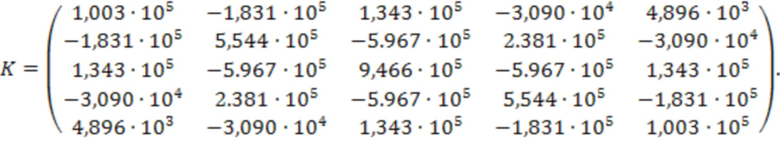
По итогам деградации трубок 8 и 8', представленных на Фиг. 1, и анализа параметров колебательной системы на основе уравнения (8) была проведена оценка отклонения эквивалентной жесткости. На основе вычисленной оценки отклонения эквивалентной жесткости была проведена оценка изменения параметра основной относительной погрешности расходомера. Зависимость оценочного параметра основной относительной погрешности от фактической величины основной относительной погрешности, по результатам эксперимента, приведена на Фиг. 8. Как видно из представленных графиков, наблюдается линейная связь оценки погрешности измерения расхода с фактической погрешностью измерения расхода, определенной при испытаниях.
В сравнении с прототипом заявляемый способ обеспечивает получение более полной и надежной оценки состояния кориолисового расходомера после начала его эксплуатации.
Область использования: изобретение относится к устройству для измерения массового расхода жидкостей и газов, а именно к кориолисовым расходомерам, и относится к диагностике и способам поверки кориолисового расходомера. Технический результат - более надежное выявление изменения калибровочного коэффициента расходомера, связанного с массовым расходом и плотностью и, как следствие, улучшение диагностики состояния измерительной системы расходомера, отсутствие зависимости от метода реализации оценки параметров колебательной системы. Сущность: в способе оценки качества измерения кориолисового расходомера, включающем возбуждение механических колебаний колебательной системы, измерение колебаний механической системы при помощи по меньшей мере одного датчика колебаний и оценку параметров колебательной системы на основе измеренных колебаний и численной модели колебательной системы, согласно изобретению численная модель колебательной системы представляет собой систему уравнений, например дифференциальных уравнений, на основе измеренных собственных форм, частот и известных из результатов калибровки коэффициентов численной модели колебательной системы, вычисляется мера отклонения параметров колебательной системы от исходного состояния для набора собственных форм колебательной системы, на основе меры рассчитывается оценка качества результатов измерения кориолисового расходомера. В качестве коэффициентов численной модели колебательной системы используются полученные в результате калибровки величины собственных форм, частот и матрицы жесткости, массы и демпфирования колебательной системы. Коэффициенты модели являются функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды. В качестве меры отклонения параметров колебательной системы от исходного состояния выступает векторная величина, компоненты которой считаются как произведение степени собственной частоты на соответствующей собственной форме на вектор, полученный из результатов калибровки, или сумма произведений степеней собственной частоты на соответствующей собственной форме на вектора, полученные из результатов калибровки. Для оценки меры отклонения параметров колебательной системы от исходного состояния часть коэффициентов модели считаются малозначащими и принимаются равными нулю. Матрицы и векторы, в силу простоты модели колебательной системы, имеют одинаковые по величине элементы и могут быть сведены к одному скалярному значению. Собственные формы и частоты при калибровке не определяются, а вычисляются по известным из результатов калибровки матрицам мер жесткости, инерции и демпфирования. 8 з.п. ф-лы, 8 ил.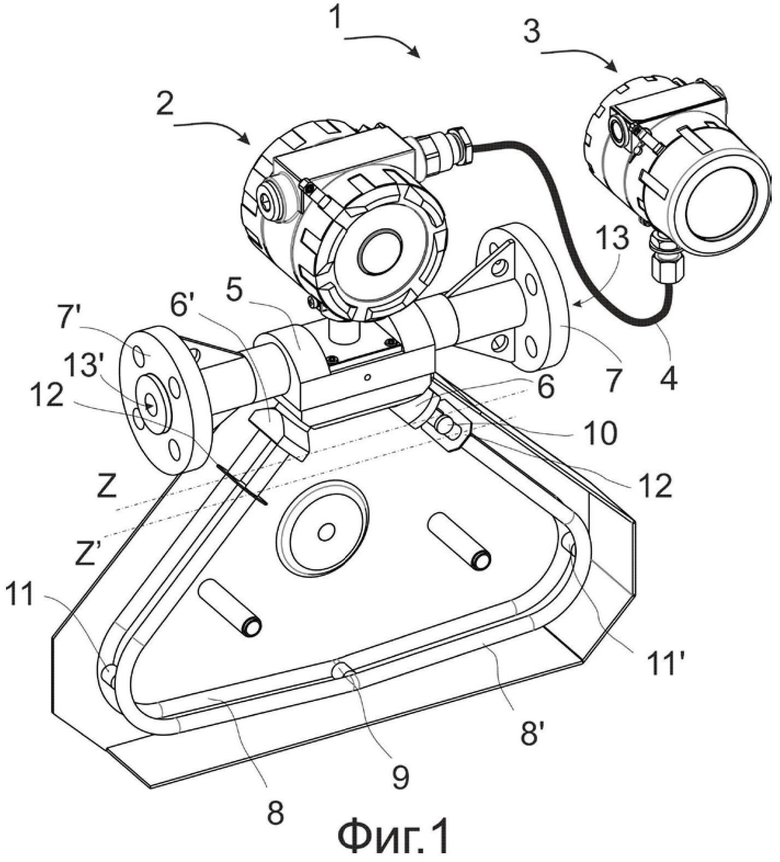
1. Способ оценки состояния датчика кориолисового расходомера для поверки и/или диагностики кориолисового расходомера, включающий возбуждение механических колебаний колебательной системы, измерение механических колебаний при помощи по меньшей мере одного датчика колебаний, оценку параметров колебательной системы на основе измеренных колебаний и численной модели колебательной системы, отличающийся тем, что при заводской настройке измеряют параметры колебательной системы датчика кориолисового расходомера в виде ее исходных параметров, являющихся функциями ее состояния, составляют по ним численную модель колебательной системы, соответствующую исходному состоянию датчика кориолисового расходомера, принимающую в качестве входных данных измеренные значения собственных форм и частот колебательной системы датчика кориолисового расходомера и выдающую в качестве выходных данных степень соответствия поданных на вход собственных форм и частот исходному состоянию колебательной системы датчика кориолисового расходомера, и сохраняют эту численную модель, во время оценки состояния датчика кориолисового расходомера измеряют собственные формы и частоты колебательной системы и оценивают, насколько собственные формы и частоты колебательной системы соответствуют численной модели колебательной системы датчика кориолисового расходомера в исходном состоянии, и по результату оценки делают вывод о состоянии датчика кориолисового расходомера.
2. Способ по п. 1, отличающийся тем, что численная модель включает матрицы, векторы и скалярные величины коэффициентов при второй степени собственной частоты, при первой степени собственной частоты и при нулевой степени собственной частоты, а также собственные формы колебательной системы датчика кориолисового расходомера в исходном состоянии.
3. Способ по п. 2, отличающийся тем, что коэффициенты численной модели являются функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
4. Способ по п. 2, отличающийся тем, что часть коэффициентов численной модели считаются малозначащими и принимаются равными некоторому фиксированному значению.
5. Способ по п. 2, отличающийся тем, что матрицы и векторы имеют одинаковые по величине элементы и сведены к скалярным значениям.
6. Способ по п. 1, отличающийся тем, что для оценки того, насколько измеренные собственные формы и частоты колебательной системы датчика кориолисового расходомера соответствуют сохраненной при заводской настройке численной модели, используют набор векторных величин, каждая из которых описывает отклонение соответствующей формы, компоненты каждой векторной величины рассчитываются как сумма произведений степени собственной частоты на соответствующей собственной форме на вектор коэффициентов для этой собственной формы, полученный из результатов калибровки и результатов измерения собственной формы.
7. Способ по п. 6, отличающийся тем, что коэффициенты численной модели являются функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
8. Способ по п. 1, отличающийся тем, что модель колебательной системы записана в виде
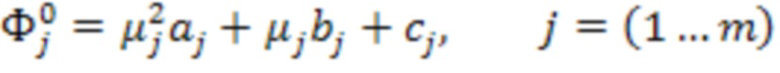 ,
,
где 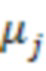 - измеренные собственные частоты колебательной системы,
- измеренные собственные частоты колебательной системы, 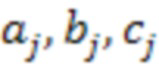 - коэффициенты численной модели колебательной системы, j - номер собственной формы,
- коэффициенты численной модели колебательной системы, j - номер собственной формы, 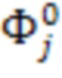 - элемент вектора оценки состояния датчика кориолисового расходомера.
- элемент вектора оценки состояния датчика кориолисового расходомера.
9. Способ по п. 8, отличающийся тем, что коэффициенты численной модели являются функциями температуры, давления, плотности измеряемой среды, температуры окружающей среды.
| US 8950274 B2, 10.02.2015 | |||
| ВИБРАЦИОННЫЙ РАСХОДОМЕР, А ТАКЖЕ СПОСОБЫ И ДИАГНОСТИКА ДЛЯ ПОВЕРКИ ИЗМЕРИТЕЛЯ | 2014 |
|
RU2628661C1 |
| WO 2007040468 A1, 12.04.2007 | |||
| WO 2005050145 A1, 02.06.2005. | |||
Авторы
Даты
2022-06-06—Публикация
2020-12-07—Подача