Изобретение относится к физической геодезии, в частности к способу построения калибровочного гравиметрического полигона с применением геоспутниковых технологий и астрономо-геодезических и гравиметрических измерений (АГГИ).
Основной задачей современной геодезии является изучение физической поверхности и внешнего гравитационного поля Земли (ВГПЗ) в единой системе координат на единую эпоху Т0 [1,2,3].
В результате космических миссий было получено и обработано большое количество измерительной информации, которая позволила существенно повысить точность определения параметров и фигуры Земли и создать новый вид топогеодезической информации - высокостепенные глобальные модели геопотенциала.
Глобальные модели геопотенциала, описывающие ВГПЗ, обеспечивают вычисление таких важных характеристик, как аномалии высот квазигеоида, силы тяжести (ACT), уклонения отвесной линии (УОЛ), а также компонент тензора силы тяжести, кривизны уровенных поверхностей и силовых линий ВГПЗ в любой точке земного шара.
Характеристики, полученные с использованием моделей геопотенциала, используются (могут быть использованы) в качестве исходной информации для эффективного применения современных и перспективных систем и комплексов высокоточного оружия [4].
Таким образом, повышение точности и детальности разработанных (разрабатываемых) математических моделей характеристик ВГПЗ является актуальной задачей и требует разработки соответствующего способов.
В качестве одного из таких решений, предлагается способ построения калибровочного гравиметрического полигона в интересах геодезического и гравиметрического обеспечения Вооруженных Сил Российской Федерации (ВС РФ).
Перспективные требования войск на 2030 год к точности характеристик ВГПЗ указаны в работах [5,6].
Наиболее оперативным и перспективным средством получения исходной информации о характеристиках ВГПЗ являются математические модели геопотенциала. Это стало возможно благодаря внедрению новых методов и способов АГГИ измерений.
Одними из наиболее представительных глобальных моделей ВГПЗ являются такие, как EGM-2008 и EIGEN64C которые характеризуются СКО: определения высот квазигеоида (ВКГ) - 0,05-0,21 м (глобально), ACT - (5-10 мГал), УОЛ (2-3'') [7-10].
Наравне с повышением точности характеристик ВГПЗ, получаемых методами космической геодезии, повысилась точность спутниковых и наземных гравиметрических измерений, которые характеризуются СКО: определения ВКГ - 0,017-0,05 м [11].
Известно что, точность определения характеристик ВГПЗ спутниковыми и наземными гравиметрическими средствами в настоящее время превосходит космические методы, что позволяет применять их в качестве основы для контроля точности создаваемых (созданных) моделей ВГПЗ.
В целях обеспечения контроля по оценке точности характеристик ВГПЗ, систематизации этого процесса и подготовки научно-обоснованного заключения о возможности использования модели ВГПЗ предлагается использовать калибровочный гравиметрический полигон (КГП), построенный по предложенному способу.
В настоящее время, в качестве перспективного метода геодезического обеспечения полигонов, используется комбинация спутниковых измерений, астрономо-геодезической и гравиметрической информации. Теоретические основы совместного уравнивания АГГИ и спутниковых измерений рассмотрены в работах отечественных и зарубежных ученых.
Теоретические основы вышеуказанного метода легли в основу предлагаемого способа создания КГП. При разработке способа используется математическая модель.
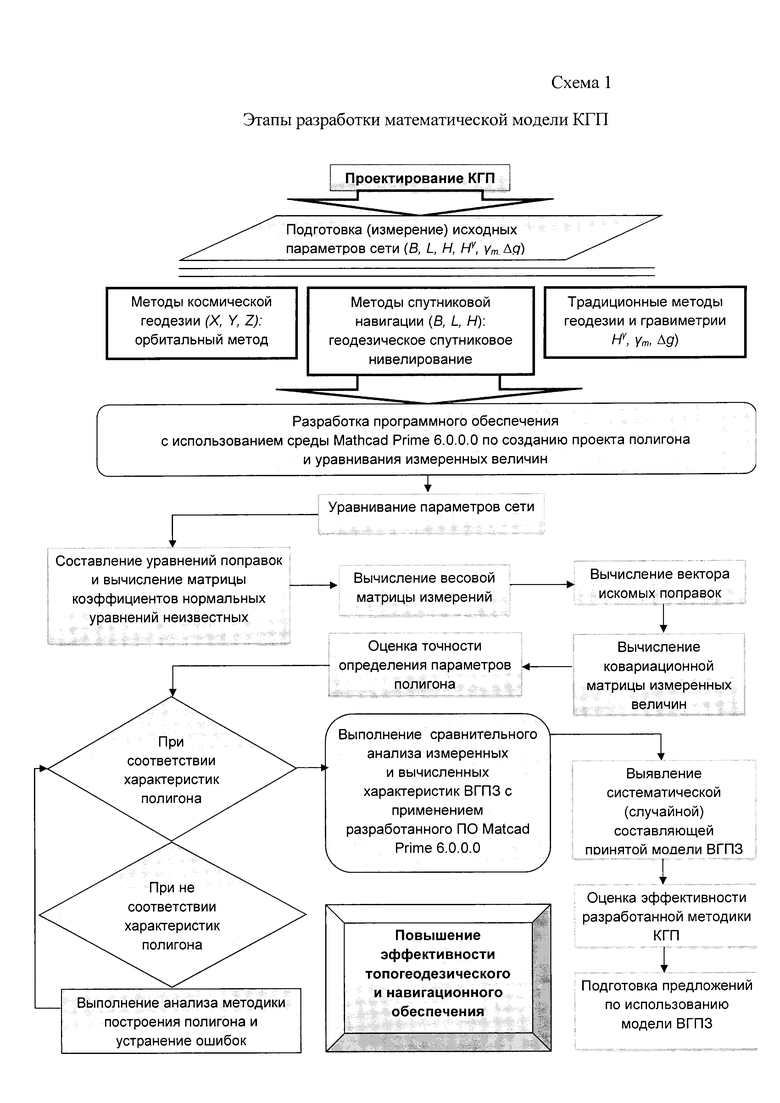
При создании математической модели калибровочного гравиметрического полигона (КГП) необходимо предусмотреть выполнение следующих этапов (схема 1):
1. Разработка программного обеспечения с использованием среды Mathcad Prime 6.0.0.0 по созданию проекта полигона и уравнивания измеренных величин.
2. Разработка проекта построения КГП на основе математического моделирования на Европейскую часть РФ с учетом геометрии пунктов, требований к их точности и количеству, геодинамических и тектонических процессов, в соответствии с требованиями ГОСТа (ГКИНП (ГНТА) - 04-122-03).
3. Подготовка исходных астрономо-геодезических, гравиметрических геофизических, геодинамических и навигационных данных, характеризующих параметры ОЗЭ (ПЗ-90.11), ВГПЗ, ФАГС, ВГС, ГВО на эпоху Т0 на район КГП.
4. Выбор технологий и методов геодезии и спутниковой навигации определения геодезических высот пунктов КГП, с удовлетворяющими перспективные требования войск характеристиками по точности и достоверности.
5. Уравнивание спутниковых и АГГИ на пунктах сети КГП, с использованием усовершенствованных автором теоретических основ и математического аппарата для результатов АГГИ, по методу наименьших квадратов (V'PV=min).
5.1.1. Составление уравнений поправок (V) и вычисление матрицы коэффициентов нормальных уравнений неизвестных (В).
5.1.2. Вычисление весовой матрицы измерений (Р).
5.1.3. Вычисление вектора искомых поправок (δХ) в приращения высот квазигеоида (ζ) пунктов сети КГП.
5.1.4. Вычисление ковариационной матрицы измеренных величин (K).
6. Оценка точности определения параметров сети КГП, характеризуемых среднеквадратическими ошибками (μ).
7. Разработка программного обеспечения с использованием среды Matcad Pro 6.0.0.0 вычисления трансформант возмущающего потенциала (ζ, Δg, ξ, η, Т) с использованием принятых отечественных и зарубежных моделей ВГПЗ и интерполяции параметров сети КГП по узловым точкам сети.
8. Выполнение сравнительного анализа параметров, полученных из результатов обработки и уравнивания выполненных измерений и результатов полученных с использованием моделей ВГПЗ, с целью оценки их точности.
9. Оценка прогнозируемой эффективности построения КГП с учетом критериев: точность, временные и стоимостные затраты.
Рассмотрим более подробно предлагаемый способ построения КГП.
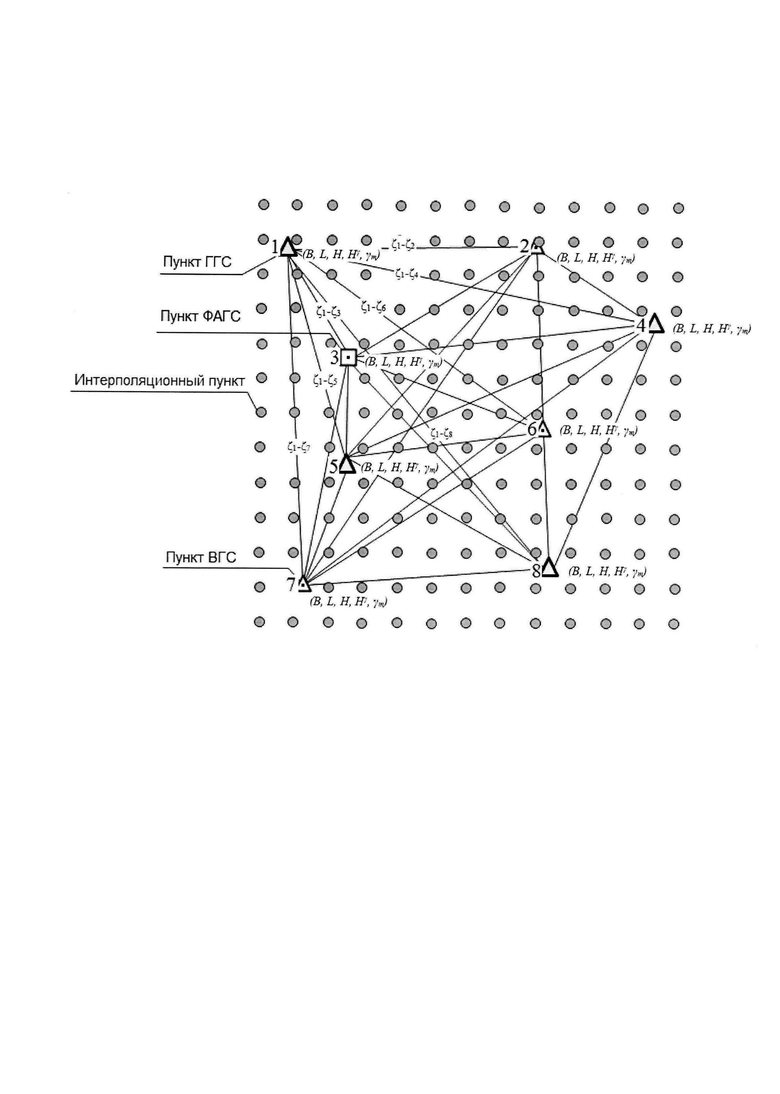
В качестве основной величины, по которой будет оцениваться точность выбранной математической модели геопотенциала, примем высоту квазигеоида. Математической основой полигона является прямоугольная сетка, образованная пунктами, равномерно расположенными по широте и долготе. За исходные пункты полигона принимаются пункты ФАГС, ВГС, ГГС 1, 2-го класса, с измеренной геодезической и нормальной высотой (не ниже геометрического нивелирования II класса). При недостаточной плотности пунктов, производим дополнительные измерения геодезических и нивелирных высот дополнительных пунктов.
С использованием разработанной программы в среде Mathcad Prime 6.0.0.0 выполняем уравнивание измеренных величин. Особенностью уравнивания пунктов полигона является то, что уравниваются не высоты, а приращения высот между пунктами.
Теоретические основы уравнивания параметров сети
В настоящей работе уравнивание комбинации спутниковых и наземных астрономо-геодезических измерений, при определении высот квазигеоида пунктов КГП, будем применять уравнения из работы [12], усовершенствованные автором.
Фундаментальное уравнение связи искомых параметров и измеренных величин 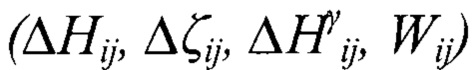 имеет вид:
имеет вид:

где 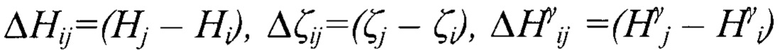 - разности геодезических высот, аномалий высот и нормальных высот точек
- разности геодезических высот, аномалий высот и нормальных высот точек 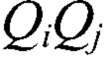 соответственно:
соответственно:
Функциональная связь в неявном виде запишется:
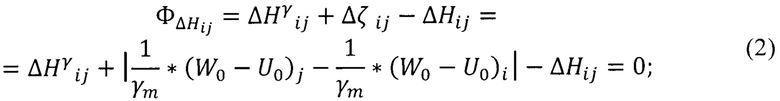
Уравнение приведенное к линейному виду:
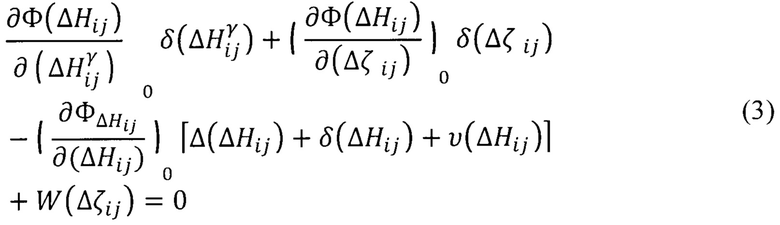
Уравнение поправок (ΔН) будет иметь вид:
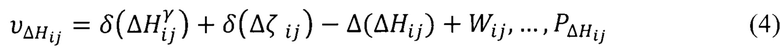
где
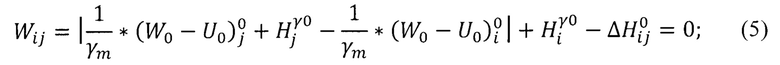
Частные производные для «измеренной разности» (ΔHij) примут значения:
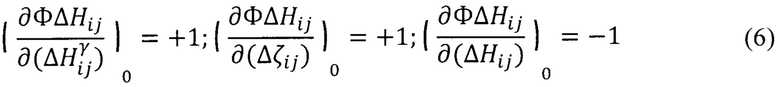
Уравнения поправок (ΔHij) примут вид:
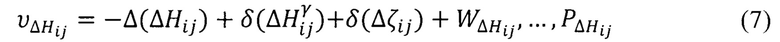
без учета нормальных высот,
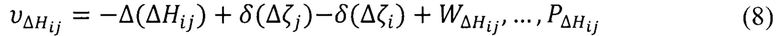
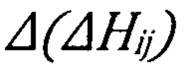 - систематическая погрешность в геодезических высотах;
- систематическая погрешность в геодезических высотах;
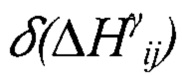 - поправки в разности нормальных высот;
- поправки в разности нормальных высот;
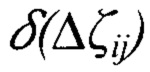 - поправки в разности высот квазигеоида;
- поправки в разности высот квазигеоида;
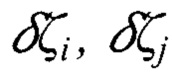 - поправки в высоты квазигеоида точек
- поправки в высоты квазигеоида точек
Рассмотрим алгоритм уравнивания по методу наименьших квадратов. Фундаментальное уравнение связи топоцентрических горизонтных координат (X', Y', Z') и вектора «измеренных» величин ΔHij - W имеет вид:

Уравнение, приведенное к линейному виду, запишется:
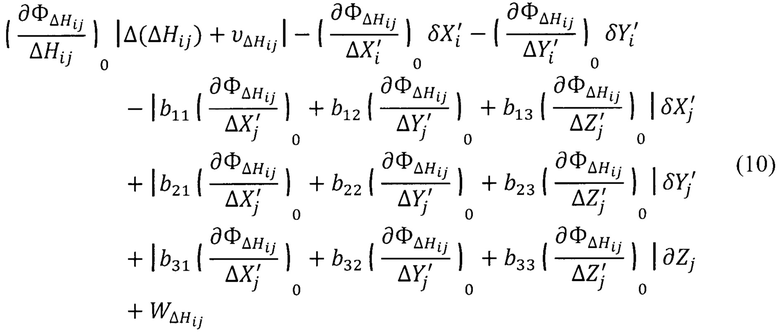
где b11b12…b33 - коэффициенты матрицы преобразования.
Исходя из функциональной связи (ΔHij) и уточняемых высот (ζi, ζj):
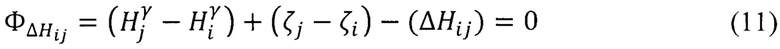
При (Z'=H) частные производные приобретут следующий вид:
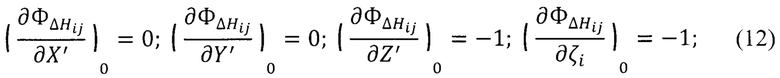
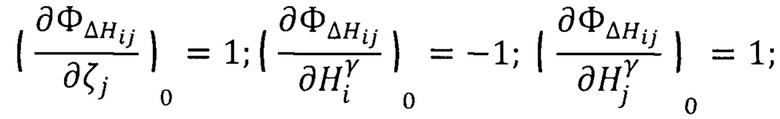
При уточнении геодезических высот пунктов и нормальных высот отдельных точек получим уравнение поправок в общем виде
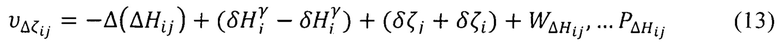
а свободный член запишется
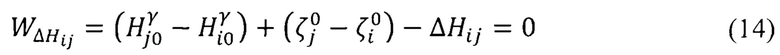
Уравнения поправок для «измерений» в матричной форме имеют вид:

где В - матрица коэффициентов при искомых параметрах; W - вектор свободных членов; Р - матрица весов измерений.
Матрица коэффициентов при искомых параметрах (В) будет иметь вид:
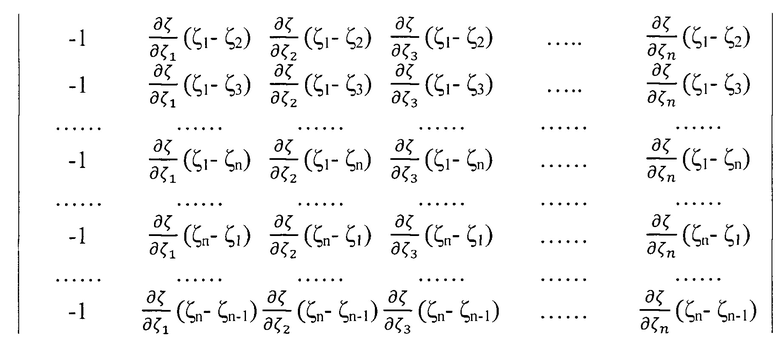
после дифференцирования
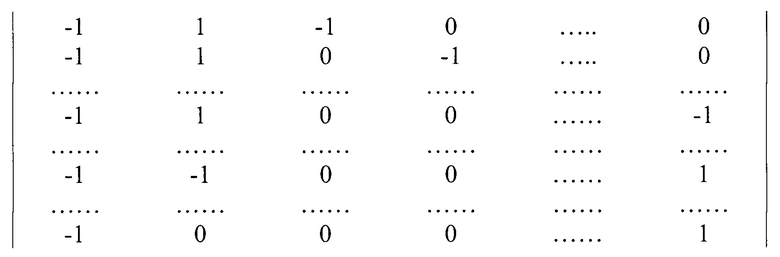
Вектор свободных членов (W):
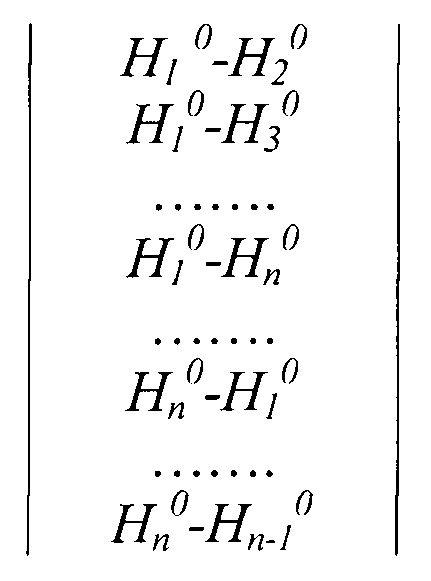
Матрица весов измерений (Р) при отладке программы единичная диагональная:

при проведении эксперимента:

где 1/pn=С2/m2, С - константа, m - средняя квадратическая ошибка измерения, вес которого вычисляется.
Вектор искомых поправок имеет вид:

Вычисляем обратную весовую матрицу результатов измерений (Q):
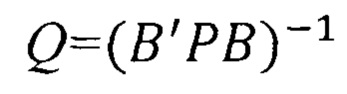
Вычисляем матрицу преобразований (А):
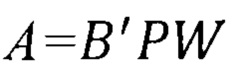
Вычисляем вектор поправок в измеренные величины (V).
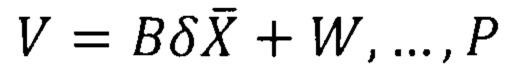
Выполняем оценку точности

Вычисляем ковариационную матрицу искомых поправок

где μ - среднеквадратическая ошибка единицы веса.
Исходя из того что, исходные пункты расположены неравномерно и как правило не находятся в узловых точках прямоугольной сетки (шаг которой может меняться), предлагается выполнить интерполирование высот квазигеоида методом цепных дробей.
Теоретические основы метода интерполирования цепных дробей.
Основы данного метода рассмотрены в работе [13]. Рассмотрим функцию у(х) одной переменной х, заданной n произвольно расположенными узлами yi, (xi), где i=1, 2, …, n. Задача состоит в определении значений функций у(х) в регулярно расположенных узлах путем разложения с помощью цепной дроби
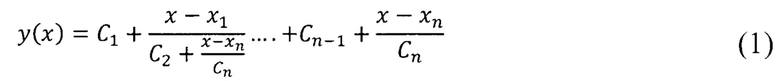
Подставляя значения xi и yi в формулу (15), получим следующие выражения для коэффициента интерполяции:
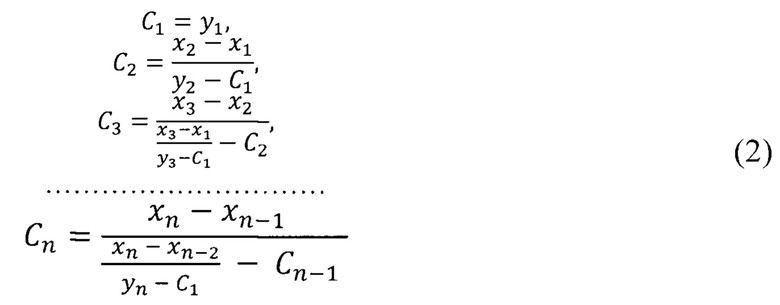
В случае линейной функции очевидно, что С3 → ∞. Это обстоятельство необходимо иметь в виду при аппроксимации некоторых нелинейных функций, ограничивая число узловых точек.
Очевидно, рассмотренный способ интерполяции представляет элементарную задачу и его можно применить для региона ограниченного радиуса при наличии достаточного количества исходных геодезических и гравиметрических пунктов.
С использованием разработанной программы в среде Mathcad Prime 6.0.0.0 вычисляем трансформанты возмущающего потенциала (высота квазигеоида, аномалия силы тяжести, составляющие уклонения отвесной линии) на узловые точки уравненных пунктов полигона.
Выполняем сравнительный анализ «измеренных» и вычисленных высот квазигеоида, выявляем систематическую ошибку.
Далее выполняем оценку эффективности предлагаемого способа и подготовку предложений по использованию выбранной для исследования математической модели геопотенциала в интересах топогеодезического и навигационного обеспечения войск.
Создание такого КГП ВС РФ с применением предложенного способа позволит достичь следующих практических результатов:
существенно повысить эффективность топогеодезического, навигационного и геоинформационного обеспечения - управления войсками и системами оружия ВС РФ, за счет уточнения параметров модели ВГПЗ, с использованием предлагаемого способа построения КГП;
модернизировать государственную систему ГГО территории России;
решить задачу по освоению удаленных, слабо изученных территорий России (суши, акваторий морей и океана).
Основные направления практического применения КГП ВС РФ:
1. обеспечение исходными гравиметрическими данными средств высокоточного оружия и крылатых ракет (РВСН, ВКС, ВМФ).
2. оперативное создание средств топогеодезической информации (карт высот квазигеоида, аномалий силы тяжести, уклонения отвесных линий) в частях топографической службы.
3. применение в учебном процессе в ВВуз МО по военной специальности «Управление топогеодезическим и навигационным обеспечением войск» по программе магистратуры.
4. выполнение исследований по проверке точности и адекватности создаваемых моделей ВГПЗ.
Литература:
1. Машимов М.М. Планетарные теории геодезии. - М.: Недра, 1982, С. 261.
2. Молоденский М.С. Методы изучения внешнего гравитационного поля и фигуры Земли [Текст] / М.С. Молоденский, В.Ф. Еремеев, М.И. Юркина // Тр. ЦНИИГАиК. - Вып. 131. - М.: Геодезиздат, 1960. - 250 с.
3. Бернхард Гофман-Велленгоф, Гельмут Мориц Физическая геодезия: Перевод с английского Ю.М. Неймана, Л.С. Сугаиповой / Под редакцией Ю.М. Неймана. - М.: Изд-во МИИГАиК, 2007, С. 426.
4. Концепция строительства и развития военной организации Российской Федерации на период до 2030 года (утверждена Указом Президента Российской Федерации от 23 сентября 2015 г. №476).
5. НИР «ТГНО - 2035», М.: - НИЦ ТГНО «27 ЦНИИ» МО, 2019.
6. Радионавигационный план РФ (РНП-2018 г.).
7. И.О. Новлянская. Сравнение и оценка точности современных моделей гравитационного потенциала Земли. Казань: Уч. записки Казанского университета, Т. 158, кн. 2, 2016.
8. В.Ф. Канушин, И.Г. Ганагина, Д.Н. Голдобин, Б.А. Харченко. Сравнение и анализ аномалий силы тяжести, полученных по данным глобальной модели EGM2008 и гравиметрических измерений на локальных участках земной поверхности. - Новосибирск: СГГА, 2014.
9. В.Б. Непоклонов Об использовании новых моделей гравитационного поля Земли в автоматизированных технологиях изысканий и проектирования. - М.: ФГУ 29 НИИ МО, 2009.
10. В.Н. Конешов, В.Б. Непоклонов, Р.А. Сермягин, Е.А. Лидовская Современные глобальные модели гравитационного поля Земли и их погрешности. Гироскопия и навигация. - 2013. - №1 (80).
11. Б.А. Харченко. Анализ значений аномалий силы тяжести с использованием данных, полученных из наземных измерений, и современных моделей глобального гравитационного поля Земли. - Новосибирск: СГГА, 2014.
12. К.В. Малец, И.П. Лангеман, Д.Е. Гоманов. Проблема создания Общеземной геодезической системы высот с применением геоспутниковых технологий и астрономо-геодезических и гравиметрических измерений. - М.: ВУНЦ «ОВА ВС РФ», НТС №62, 2012 - С. 18-24.
13. Кирьяк В.Т., Николаев С.П. Аппроксимация геофизических полей с использованием цепных дробей. М: «Геодезия и картография», №11, 1991.
Способ построения калибровочного гравиметрического полигона (КГП) относится к физической геодезии, в частности к способу построения КГП с применением геоспутниковых технологий и астрономо-геодезических и гравиметрических измерений (АГГИ). КГП предназначен для оценки точности характеристик возмущающего потенциала (ζ, Δg, ξ, η, Т), получаемых с использованием глобальных математических моделей геопотенциала, повышения их точности и детальности и дальнейшего использования в целях топогеодезического и навигационного обеспечения войск. За исходные пункты полигона принимаются пункты с измеренной геодезической и нормальной высотой (не ниже геометрического нивелирования II класса). При недостаточной плотности пунктов, производятся измерения геодезических и нивелирных высот дополнительных пунктов. Выполняется уравнивание измеренных приращений высот квазигеоида по методу Гаусса. С целью создания равномерного расположения пунктов выполняется интерполирование высот квазигеоида методом цепных дробей по узловым точкам сети. Вычисляются высоты квазигеоида, выбранной для исследования модели внешнего гравитационного поля Земли (ВГПЗ) на узловые точки уравненных пунктов полигона. Выполняется сравнительный анализ «измеренных» и «вычисленных» высот квазигеоида, вычисляется систематическая ошибка. Дополнительно выполняется анализ качества гармонических коэффициентов модели геопотенциала с использованием тензоров инерции высокого порядка. Технический результат - повышение эффективности топогеодезического, навигационного и геоинформационного обеспечения за счет уточнения параметров модели ВГПЗ, с использованием предлагаемого способа построения КГП. 2 ил.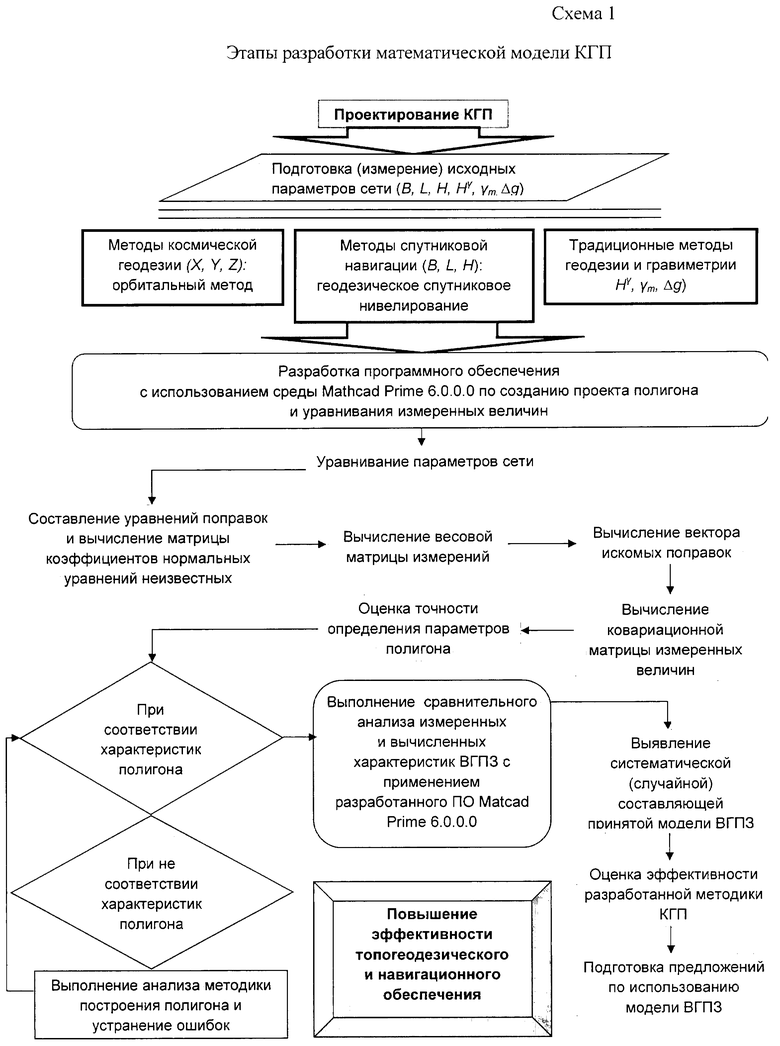
Способ построения калибровочного гравиметрического полигона, включающий в себя высокоточное определение высот квазигеоида на пунктах полигона, расположенных равномерно по широте и долготе в узловых точках образованной меридианами и параллелями прямоугольной сетки, полученных как разность геодезической высоты i-го пункта, определенной абсолютным методом спутниковой навигации, и нивелирной высоты i-го пункта, определенной методом высокоточного геометрического нивелирования, с последующим уравниванием приращений высот квазигеоида между всеми пунктами полигона по методу наименьших квадратов и интерполированием высот квазигеоида методом цепных дробей до необходимой плотности пунктов и с заданной точностью.
| ЛАНГЕМАН И.П., МОТАШЕНКО С.В., "МЕТОДОЛОГИЯ СОЗДАНИЯ УНИВЕРСАЛЬНОЙ ЭЛЕКТРОННОЙ ЦИФРОВОЙ КАРТЫ АСТРОНОМО-ГЕОДЕЗИЧЕСКИХ И ГРАВИМЕТРИЧЕСКИХ ДАННЫХ", РАДИОТЕХНИКА, ЭЛЕКТРОНИКА И СВЯЗЬ | |||
| Сборник докладов Международной научно-технической конференции | |||
| ФГУП "Омский научно-исследовательский институт приборостроения", Омск, 05-08 июля 2011 года, с.370-374 |
Авторы
Даты
2022-06-16—Публикация
2021-06-10—Подача