Изобретение относится к области измерений геодезических координат, измерений траектории движения точки, когда необходимо получить угловые направления на точку в местной топоцентрической горизонтной системе координат, одна из плоскостей которой ориентирована по горизонту в точке размещения угломерного прибора - теодолита (горизонт определяется как плоскость, касательная к Земному эллипсоиду в данной точке). Для правильного проведения измерений плоскость азимутальных углов угломерного прибора должна быть параллельна плоскости горизонта с высокой точностью.
Геодезические приборы, предназначенные для измерений угловых направлений, имеют в своей конструкции элементы, позволяющие установить прибор в горизонт в соответствии с линией отвеса. Точность установки соответствует классу точности прибора. В практике траекторных измерений, когда применяется оптическая или радиолокационная аппаратура, не всегда есть возможность выставки прибора в горизонт с необходимой точностью, результатом чего является получение ошибочных углов визирования на точку цели, что приводит к дополнительным ошибкам (которые могут быть значительными) измерения координат цели.
Уровень техники
Известен способ (патент ЕР 3410063 «Геодезический прибор с коррекцией наклона инструмента», опубл. 31.05.2018) математического горизонтирования геодезического прибора - тахометра, установленного с перекосом к горизонту. Этот способ реализует коррекцию углов визирования на цель посредством введения угловых поправок, которые вычисляются при помощи тригонометрических формул на основании данных от штатного датчика наклона тахометра и от штатного оптико-электронного дальномера. Однако, данный способ не может быть реализован для геодезического прибора типа теодолит, не оборудованного датчиком наклона и оптико-электронным дальномером.
Известны патент РФ №2684733 «Способ определения положения объекта засечкой с двух измерительных пунктов по азимуту, углу места и дальности», опубл. 12.04.2019, патент РФ №2677586 «Способ позиционирования объекта засечкой дальности и угла места с первого измерительного пункта и угла места - со второго», опубл. 17.01.2019 и патент РФ №2667115 «Способ позиционирования объекта засечкой азимута с первого измерительного пункта и угла места с дальностью - со второго», опубл. 14.09.2018. Все три способа дают эффективные решения задачи по измерениям координат точки полигона и применяют углы визирования цели (азимут и угол места (угол возвышения)), полученные угломерными приборами первого и второго пункта в качестве входных данных для вычислений.
Однако, точность определения местоположения объекта в местной горизонтной системе координат полигона существенно зависит от точности горизонтирования координатных систем измерительных пунктов (угломерных приборов). Вопрос горизонтирования в перечисленных способах не рассматривается, т.е. угломерные приборы считаются установленными в плоскость горизонта по определению. Таким образом, предлагаемое изобретение может применяться для повышения точности позиционирования объекта, положение которого в местной горизонтной системе координат определяется согласно способам, изложенным в патентах РФ 2684933, 2677586 С1, 2667115 С1.
Известен патент РФ №2758860 «Способ коррекции углов визирования на точку», опубл. 02.11.2021, реализующий математическое горизонтирование угломерного прибора, установленного с перекосом к горизонту, по двум опорным точкам с известными географическими координатами. Коррекция горизонта прибора осуществляется путем введения угловых поправок в углы визирования цели, которые вычисляются при помощи тригонометрических формул, полученных из сравнения разностей измеренных и вычисленных углов визирования на две опорные точки. Однако, данный способ реализует коррекцию горизонта прибора с ограничением по вертикальным углам: лишь в условиях малых (не более 4-5 градусов) вертикальных углов визирования опорных точек.
При этом математический способ получения углов пространственной ориентации координатной системы угломерного прибора (углов Эйлера-Крылова) не является точным, так как применяет для решения метод последовательных приближений.
Известен способ калибровки тахеометра, установленного с наклоном (патент КНР №113916198 «Способ установки наклона станции для автоматического формирования контрольных точек», опубл. 01.11.2022), в котором значения компенсирующих поправок получены посредством вычисления исходя из преобразования координат трех контрольных точек. Для расчета применяется модель с семью параметрами, относящимися к параметрам преобразования координат (три параметра перемещения, три параметра вращения и один параметр масштабирования). При построении расчетной формулы применяется разложение в ряд Тейлора с удержанием только членов первого порядка, что является следствием исходного предположения о малости угловых отклонений. Вычисления по формуле осуществляются численным способом. Таким образом, применение данного способа калибровки тахеометра ограничено малыми угловыми отклонениями, кроме того, вычисления дают приблизительный результат.
Известен способ определения координат опорных точек, с применением тахеометра и БПЛА (патент США №9772185 «Measuring system and method for determining new points», опубл. 26.09.2017), в котором геодезические координаты опорной точки определяются путем измерения углов визирования на точку и дальности до опорной точки. При этом тахеометр должен быть оснащен лазерным дальномером. Для определения геодезических координат точек, наблюдаемых под большими углами возвышения, предлагается использовать БПЛА, оснащенный отражателем сигнала. Применение данного способа определения геодезических координат опорных точек возможно при наличии измерительных устройств, оборудованных дальномером, а также БПЛА, оборудованных оптическим отражателем сигнала и системой измерения углов визирования на точку.
Раскрытие сущности изобретения
Предлагаемое изобретение направлено на достижение технического результата, заключающегося в повышении точности угловых измерений в горизонтной системе координат угломерного прибора, предназначенного для измерений углов направления на цель, не только оптического (теодолит), но и радиотехнического (радиолокационная станция), включающего в свой состав две угломерные шкалы, которые работают в перпендикулярных плоскостях.
Реализованный в изобретении способ нахождения пространственных углов ориентации координатной системы угломерного прибора свободен от каких-либо ограничений по углам и является точным, так как получен в результате аналитических математических преобразований. Предложенный способ требует проведения геодезической привязки опорных точек, находящихся в зоне видимости угломерного прибора.
Применение изобретения предполагает построение сети опорных точек и математическое сведение множества измерительных угломерных приборов в единую горизонтную систему координат с высокой точностью, что обеспечивает качественные измерения.
Точность горизонтирования угломерного прибора предлагаемым способом ограничивается дискретностью угломерных шкал самого прибора и, по этой причине, может быть весьма высокой, находясь при этом в соответствии с точностными характеристиками того же угломерного прибора.
Для получения указанного технического результата в предлагаемом способе осуществляется следующее:
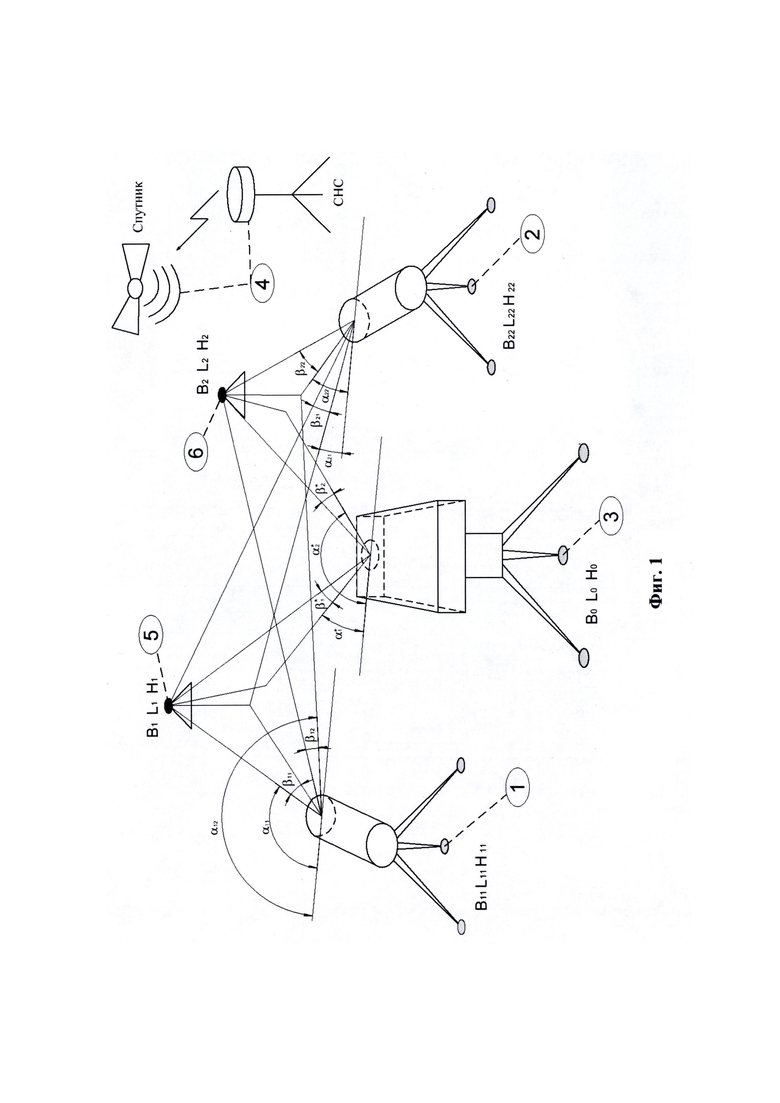
1) размещение в зоне проведения измерений двух оптических теодолитов, измеряющих угол азимута и угол возвышения на опорную точку; измерение геодезических координат местоположения первого теодолита В11, L11, H11 (фиг. 1-1) и второго теодолита B22, L22, H22 (фиг. 1-2); измерение геодезических координат точки размещения угломерного прибора В0, L0, Н0 (фиг. 1-3); измерение геодезических координат двух теодолитов и угломерного прибора осуществляется с применением спутниковой навигационный системы, работающей в дифференциально-фазовом режиме (фиг. 1-4), где В, L, Н - широта, долгота, высота с соответствующими индексами;
2) выбор не менее одной пары опорных точек, наблюдаемых с мест размещения двух теодолитов;
3) измерение углов визирования с первого теодолита на первую опорную точку α11, β11 и на вторую опорную точку α12, β12;
4) измерение углов визирования со второго теодолита на первую опорную точку α21, β21 и на вторую опорную точку α22, β22;
5) определение геодезических координат первой опорной точки B1, L1, H1 (фиг. 1-5) и второй опорной точки В2, L2, Н2 (фиг. 1-6) дистанционно, методом угловой засечки (С.Ф. Еналеев. «Траекторные измерения», часть 2, формула 2.11) с применением геодезических координат первого и второго теодолитов В11, L11, Н11 и B22, L22, H22 и измеренных углов α11, β11, α12, β12, α21, β21, α22, β22;
6) измерение углов визирования угломерного прибора 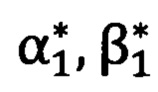 и
и 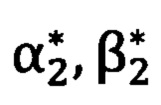 на первую и вторую опорные точки соответственно (фиг. 1), при этом углы
на первую и вторую опорные точки соответственно (фиг. 1), при этом углы 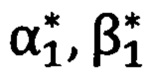 и
и 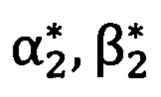 относятся к «перекошенной» системе координат угломерного прибора;
относятся к «перекошенной» системе координат угломерного прибора;
7) определение углов визирования 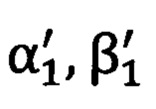 и
и 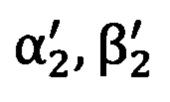 на опорные точки стандартным способом решения обратной геодезической задачи, при этом углы
на опорные точки стандартным способом решения обратной геодезической задачи, при этом углы 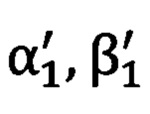 и
и 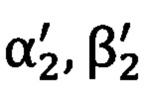 относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где αi - азимутальный угол, βi -угол возвышения на точку с соответствующим индексом.
относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где αi - азимутальный угол, βi -угол возвышения на точку с соответствующим индексом.
Обратная геодезическая задача решается в три этапа.
Первый этап состоит в переводе геодезических координат опорных точек Bi, Li, Hi в геоцентрическую прямоугольную систему координат Xi,Yi; Zi (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 3.2.7, формулы 3.24).
Второй этап заключается в пересчете прямоугольных геоцентрических координат опорных точек Xi, Yi, Zi в прямоугольные декартовы координаты местной (топоцентрической) горизонтной системы координат (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 3.2, формулы 3.1,3.2,3.3).
На третьем этапе из вычисленных в топоцентрической горизонтной системе координат 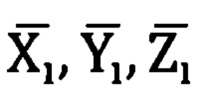 опорных точек находим полярные углы визирования на эти опорные точки (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 3.2.10, формулы 3.48).
опорных точек находим полярные углы визирования на эти опорные точки (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 3.2.10, формулы 3.48).
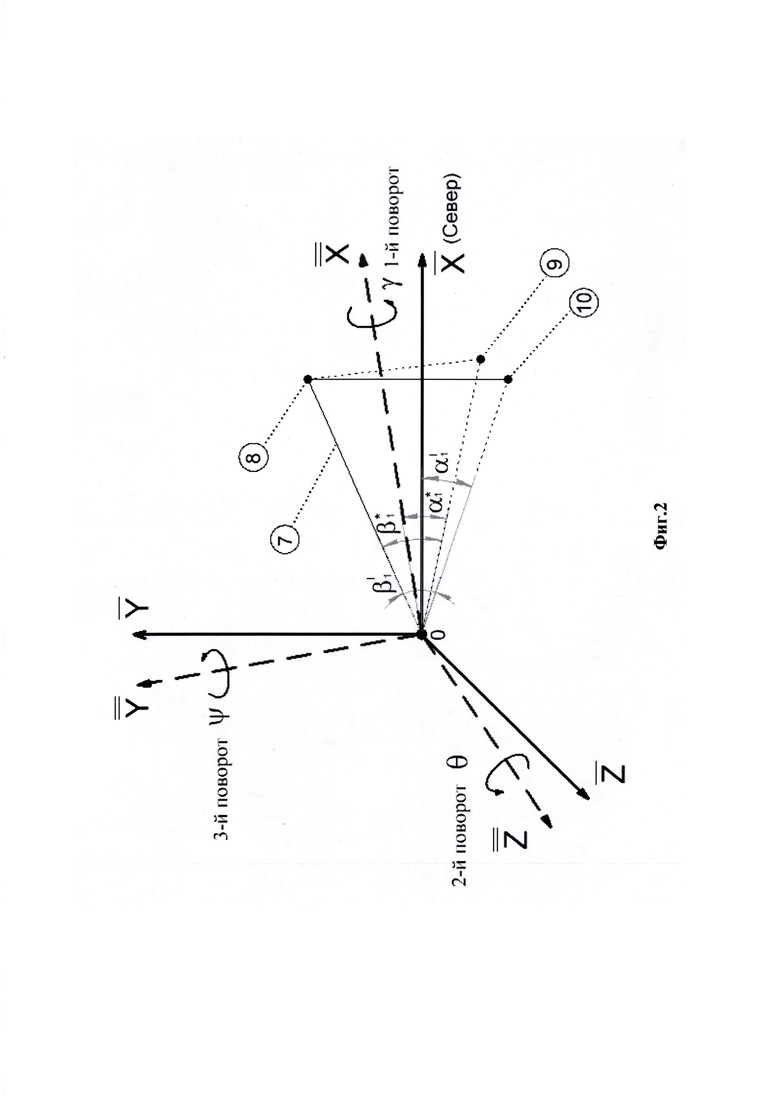
Для получения углов пространственной ориентации «перекошенной» системы координат угломерного прибора (углов Эйлера - Крылова Ψ, θ, ϒ (фиг. 2) применяется решение системы матричных уравнений (1.1), (1.2), где прямоугольные декартовы координаты Xi, Yi, Zi выражаются через углы визирования αi, βi (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 2.3.4, формулы 3.64), построенной на сравнении углов визирования 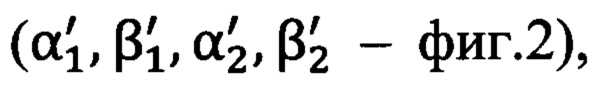 вычисленных по обратной геодезической задаче, и измеренных углов визирования
вычисленных по обратной геодезической задаче, и измеренных углов визирования 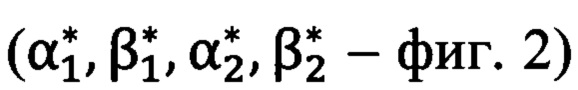 на две опорные точки (на фиг. 2 изображена только одна опорная точка с целью не загромождать рисунок). Система матричных уравнений решается аналитически и точно следующим образом:
на две опорные точки (на фиг. 2 изображена только одна опорная точка с целью не загромождать рисунок). Система матричных уравнений решается аналитически и точно следующим образом:
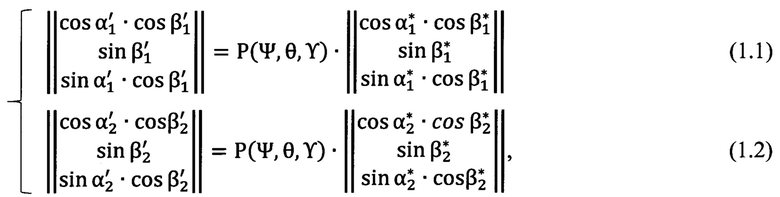
где координата 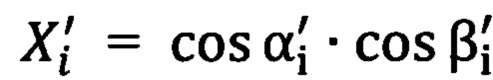 ; координата
; координата 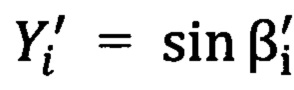 ; координата
; координата 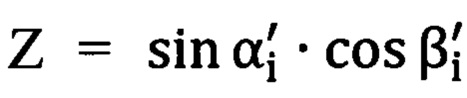 ; координата
; координата 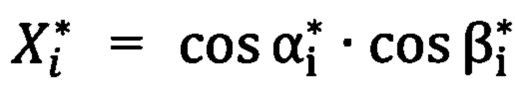 ; координата
; координата 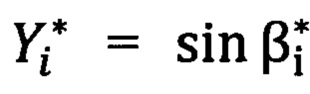 ; координата
; координата 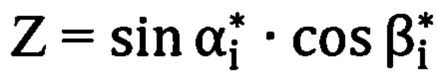 ;
;
P(Ψ, θ, ϒ) - матрица преобразования системы координат (Н.А. Телеганов, Г.Н. Тетерин, «Методы и системы координат в геодезии» - часть 3.2.8, формулы 3.34-3.37)
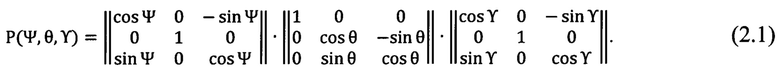
Вычисляют два возможных значения угла θ:

Вычисляют значения углов ϒ1 и ϒ2 согласно правилу:

где

Вычисляют значения углов θ и ϒ
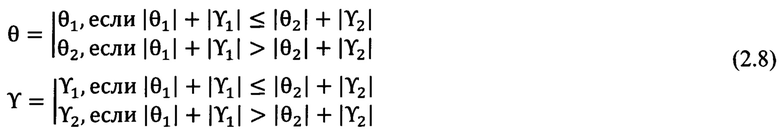 Вычисляют значения угла Ψ
Вычисляют значения угла Ψ
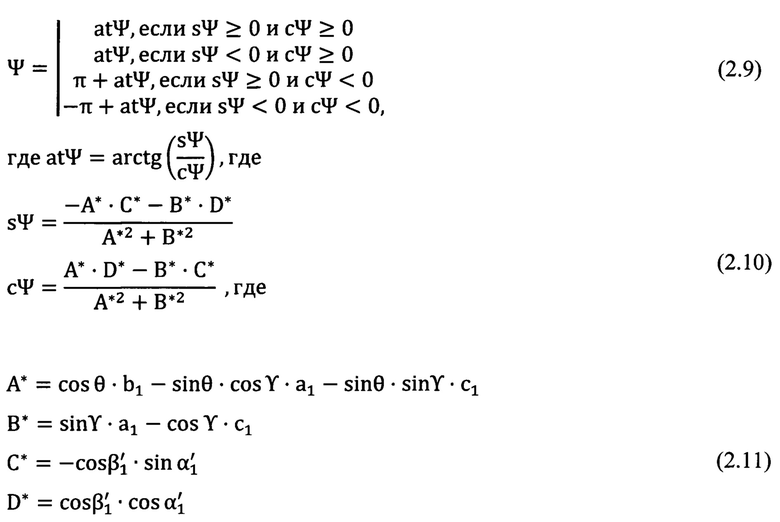
Таким образом, все три угла Эйлера-Крылова Ψ, θ, ϒ) пространственной ориентации «перекошенной» координатной системы угломерного прибора найдены. Формируют стандартную матрицу угловых поправок, т.е. подставляют вычисленные углы Ψ, θ, ϒ в матрицу (2.1), преобразуют углы визирования, полученные угломерным прибором в его «перекошенной» координатной системе, в углы 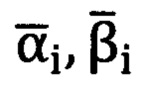 местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (3), (4.1), (4.2), (4.3),
местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (3), (4.1), (4.2), (4.3),
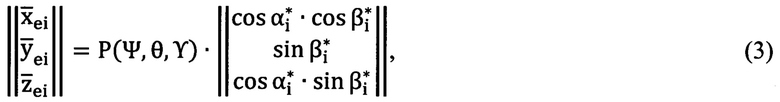
где 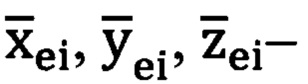 проекции вектора единичной длины на оси
проекции вектора единичной длины на оси 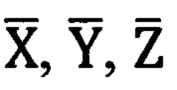 (Фиг. 2) прямоугольной горизонтной системы координат соответственно
(Фиг. 2) прямоугольной горизонтной системы координат соответственно

верное значение угла 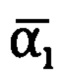 выбирается исходя из условия:
выбирается исходя из условия:

таким образом, «неправильные» угол азимута 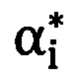 и угол возвышения
и угол возвышения 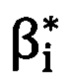 точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат
точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат 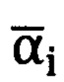 и
и 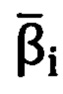 .
.
Результаты эксперимента показывают, что скорректированные значения углов 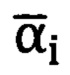 и
и 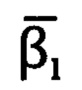 совпадают с эталонными с точностью, соответствующей дискретности угломерных шкал самого угломерного прибора.
совпадают с эталонными с точностью, соответствующей дискретности угломерных шкал самого угломерного прибора.
Краткое описание чертежей
Предлагаемое изобретение иллюстрируется двумя фигурами, на которых изображено:
1) На фиг. 1 представлена схема расположения измерительных приборов, где 1 - первый теодолит; 2 - второй теодолит; 3 - угломерный прибор; 4 - СНС, работающая в дифференциально - фазовом режиме; 5 - первая опорная точка; 6 - вторая опорная точка; В0, L0, Н0 - геодезические координаты угломерного прибора; В1, L1, Н1 - геодезические координаты первой опорной точки; В2, L2, Н2 - геодезические координаты второй опорной точки; В11, L11, Н11 - геодезические координаты первого теодолит; В22, L22, Н22 - геодезические координаты второго теодолита; α11, β11 - углы визирования первого теодолита на первую опорную точку; α12, β12 - углы визирования первого теодолита на вторую опорную точку; α2l, β21 - углы визирования теодолита второго на первую опорную точку; α22, β22 _ углы визирования второго теодолита на первую опорную точку; 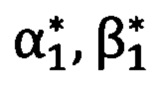 - углы визирования угломерного прибора на первую и вторую опорные точки,
- углы визирования угломерного прибора на первую и вторую опорные точки, 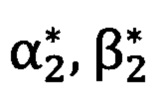 - углы визирования угломерного прибора на вторую опорную точку.
- углы визирования угломерного прибора на вторую опорную точку.
2) На фиг. 2 представлена система координат угломерного прибора, углы Эйлера-Крылова, где 7 - линия визирования угломерного прибора; 8 - первая опорная точка; 9 - точка проекции первой опорной точки на плоскость горизонта угломерного прибора 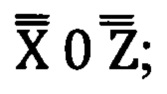 10 - точка проекции первой опорной точки на плоскость горизонта топоцентрической системы координат Земли
10 - точка проекции первой опорной точки на плоскость горизонта топоцентрической системы координат Земли 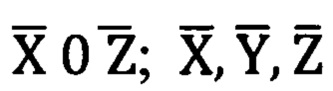 -топоцентрическая горизонтная система координат угломерного прибора;
-топоцентрическая горизонтная система координат угломерного прибора; 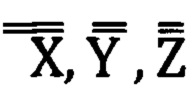 - углы визирования на первую опорную точку; Ψ, θ, ϒ - углы Эйлера-Крылова;
- углы визирования на первую опорную точку; Ψ, θ, ϒ - углы Эйлера-Крылова; 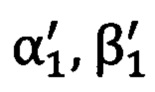 - углы визирования на первую опорную точку с места размещения угломерного прибора, вычисленные по обратной геодезической задаче;
- углы визирования на первую опорную точку с места размещения угломерного прибора, вычисленные по обратной геодезической задаче; 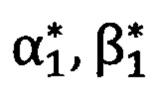 -углы визирования на первую опорную точку, измеренные угломерным прибором.
-углы визирования на первую опорную точку, измеренные угломерным прибором.
Осуществление изобретения
Предлагаемый способ осуществляется в следующей последовательности.
В зоне проведения измерений размещаются два оптических теодолита, измеряющих угол азимута и угол возвышения на точку. Измеряются геодезические координаты первого теодолита B11, L11, Н11 и второго теодолита B22, L22, Н22 (фиг. 1) с применением СНС, работающей в дифференциально-фазовом режиме. Определяется пара опорных точек, хорошо наблюдаемых с точки размещения теодолитов и с точки размещения угломерного прибора. Измеряются углы визирования с первого теодолита на первую опорную точку α11, β11 и на вторую опорную точку α12, β12 (фиг. 1). Измеряются углы визирования со второго теодолита на первую опорную точку α21, β21 и на вторую опорную точку α22, β22 (фиг. 1). Вычисляются дистанционно геодезические координаты первой опорной точки В1, Ll, Н1 и второй опорной точки В2, L2, Н2 методом угловой засечки (фиг. 1). В зоне проведения измерений размещается угломерный прибор. Измеряются геодезические координаты угломерного прибора В0, L0, Н0 (фиг. 1) с применением СНС, работающей в дифференциально-фазовом режиме. Bi - широта, Li - долгота, Hi - высота с соответствующим индексом. Проводятся измерения углов визирования 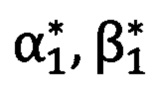 и
и 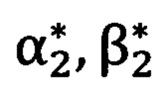 на первую и вторую опорную точку (фиг. 1). Решаются обратные геодезические задачи по вычислению углов визирования
на первую и вторую опорную точку (фиг. 1). Решаются обратные геодезические задачи по вычислению углов визирования 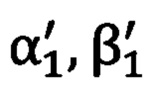 и
и 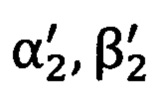 на первую и вторую опорные точки (фиг. 2). Вычисленные (истинные)
на первую и вторую опорные точки (фиг. 2). Вычисленные (истинные) 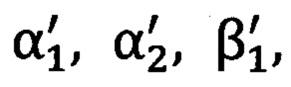
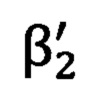 и измеренные
и измеренные 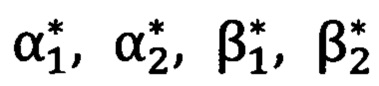 углы сравниваются при помощи уравнений (1.1), (1.2), которые решаются аналитически. В результате решения определяются значения углов Ψ, θ, ϒ ориентации «перекошенной» системы координат угломерного прибора относительно «правильной» топоцентрической горизонтной системы координат. Найденные значения углов Ψ, θ, ϒ (углов Эйлера-Крылова - фиг. 2) подставляются в матрицу угловых поправок (2.1). Полученная матрица угловых поправок (2.1) подставляется в формулу (3), дающую значения проекций единичного вектора на оси горизонтной системы координат
углы сравниваются при помощи уравнений (1.1), (1.2), которые решаются аналитически. В результате решения определяются значения углов Ψ, θ, ϒ ориентации «перекошенной» системы координат угломерного прибора относительно «правильной» топоцентрической горизонтной системы координат. Найденные значения углов Ψ, θ, ϒ (углов Эйлера-Крылова - фиг. 2) подставляются в матрицу угловых поправок (2.1). Полученная матрица угловых поправок (2.1) подставляется в формулу (3), дающую значения проекций единичного вектора на оси горизонтной системы координат 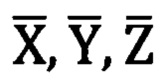 (фиг. 2).
(фиг. 2).
Найденные значения проекций единичного вектора подставляются в формулы (4.1), (4.2), (4.3), которые дают скорректированные значения 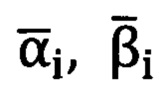 углов визирования на точку цели.
углов визирования на точку цели.
Таким образом «неправильные» углы визирования точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат.
Пример решения задачи
Геодезические координаты первой опорной точки, измеренные с помощью двух теодолитов методом угловой засечки в системе координат WGS-84:
В1=55.58665538° с. ш.
L1=38.13532990° в. д.
Н1=141.05 м.
Геодезические координаты второй опорной точки, измеренные с помощью двух теодолитов методом угловой засечки в системе координат WGS-84:
В2=55.58012837° с. ш.
L2=38.14837129° в. д.
Н2=149.31 м.
Геодезические координаты третьей точки - точки цели, измеренные СНС, работающей в дифференциально-фазовом режиме, в системе координат WGS-84 (измерение необходимо для сравнения истинных значений углов визирования и полученных угломерным прибором):
В3=55.58627382° с. ш.
L3=38.15805406° в. д.
Н3=143.84 м.
Углы визирования на первую опорную точку (измеренные угломерным прибором в «перекошенной» системе координат):
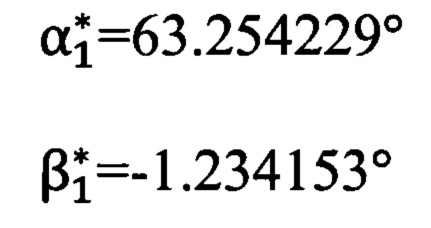
Углы визирования на вторую опорную точку (измеренные угломерным прибором в «перекошенной» системе координат):
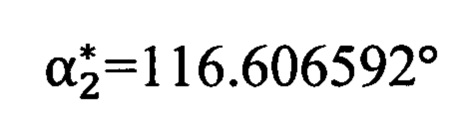
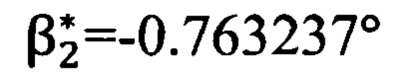
Углы визирования на точку цели (измеренные угломерным прибором в «перекошенной» системе координат):

Углы визирования на первую опорную точку (вычисленные по обратной геодезической задаче в топоцентрической горизонтной системе координат):
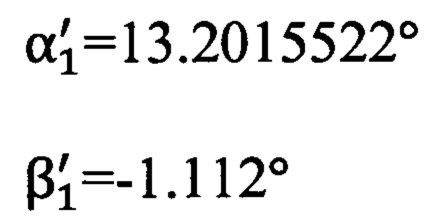
Углы визирования на вторую опорную точку (вычисленные по обратной геодезической задаче в топоцентрической горизонтной системе координат):

Углы визирования на точку цели (вычисленные по обратной геодезической задаче в топоцентрической горизонтной системе координат):

Углы взаимного положения «перекошенной» системы координат измерительного прибора и топоцентрической горизонтной системы координат - углы Эйлера-Крылова, полученные аналитически из решения уравнений (1.1), (1.2) и применения формул (2,2), (2.3), (2.4), (2.5), (2.6), (2.7), (2.8), (2.9), (2.10), (2.11).
Ψ=105.39204619°
θ=0.054293°
ϒ=-0.065336°
Полученные значения углов Эйлера-Крылова подставляются в матрицу угловых поправок (2.1), из которой в совокупности с формулой (3), получаются значения проекций вектора единичной длины на оси 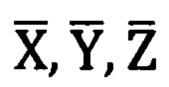 топоцентрической горизонтной системы координат (Фиг. 2).
топоцентрической горизонтной системы координат (Фиг. 2).
Найденные значения проекций единичного вектора подставляются в формулы (4.1), (4.2), (4.3), которые дают скорректированные значения 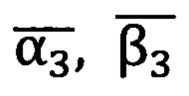 углов визирования на точку цели.
углов визирования на точку цели.

Таким образом, «неправильные» углы визирования точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат.
Погрешности полученных скорректированных значений углов визирования на цель по отношению к точным (вычисленным по обратной геодезической задаче) углам визирования составляют: по азимутальным углам Δα=66.94214648° - 66.93319648°=32.2 угловых секунд, по вертикальным углам (углам места) Δβ=0.2102° - 0.2204°=36.7 угловых секунд. В то время как без математической коррекции горизонта измерительного прибора эти погрешности составляли: по азимутальным углам Δα=66.94214648° - 140.606592°=265192 угловых секунд, по вертикальным углам (углам места) Δβ=0.2102° - 1.512864°=4689 угловых секунд. Что свидетельствует о эффективности заявленного способа математической коррекции горизонта координатной системы угломерного измерительного прибора.
Результаты измерений и коррекции углов визирования на цель даны в таблице 1.
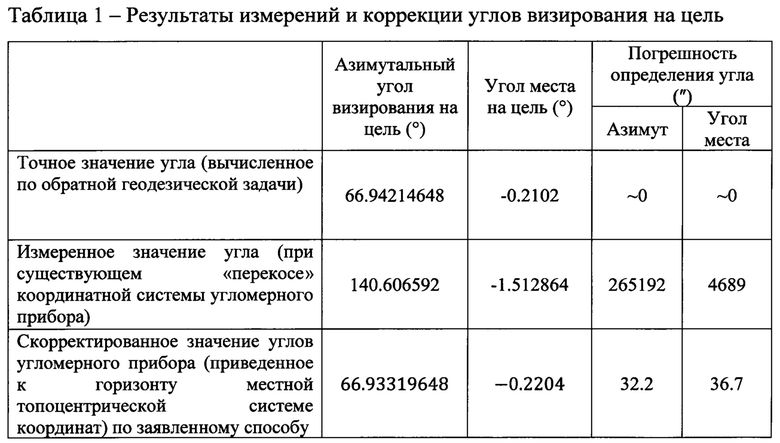
Результат коррекции углов визирования на цель включает инструментальную погрешность применяемого измерительного прибора, которая определена, главным образом, дискретностью угломерных шкал поворотной платформы прибора. Измерения проводились прибором с инструментальной погрешностью, не превышающую 36 угловых секунд, поэтому результат коррекции углов может считаться практически точным.
Таким образом, результаты коррекции углов визирования заявленным способом, представленные в таблице 1, наглядно демонстрируют достижение технического результата, заключающегося в уменьшении погрешности угловых измерений в горизонтной системе координат измерительного прибора, предназначенного для измерений углов направления на цель.
Решая представленную задачу с применением «Способа коррекции углов визирования на точку» (патент РФ №2758860), погрешность угла визирования на цель по азимуту составила 95 угловых секунд, а по углу места 80 угловых секунд.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ коррекции углов визирования на точку | 2020 |
|
RU2758860C1 |
| Способ юстировки зеркальной антенны по сигналам космических радиоизлучающих объектов | 2017 |
|
RU2667337C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ТОЧЕК МЕСТНОСТИ ПО РЕЗУЛЬТАТАМ УГЛОМЕРНЫХ ИЗМЕРЕНИЙ НА КОСМИЧЕСКИХ ИЗОБРАЖЕНИЯХ | 2007 |
|
RU2362973C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ И ЦЕЛЕВОЙ ЗНАК ДЛЯ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ | 2000 |
|
RU2202101C2 |
| СПОСОБ СОГЛАСОВАНИЯ ОСЕЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ С ОСЬЮ НАЗЕМНОГО ТРАНСПОРТНОГО СРЕДСТВА И ИЗМЕРИТЕЛЬНЫЙ КОМПЛЕКС ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2436043C1 |
| СПОСОБ СПУТНИКОВОЙ КОРРЕКЦИИ ГИРОСКОПИЧЕСКИХ НАВИГАЦИОННЫХ СИСТЕМ МОРСКИХ ОБЪЕКТОВ | 2008 |
|
RU2428659C2 |
| Способ построения пространственной геодезической сети в виде цепочки треугольников и угломерный прибор для его осуществления | 1986 |
|
SU1613858A1 |
| СПОСОБ БЕЗОТВЕСНОЙ ГОРИЗОНТАЛЬНОЙ СОЕДИНИТЕЛЬНОЙ СЪЕМКИ ПОДЭТАЖНЫХ ГОРИЗОНТОВ С ПОМОЩЬЮ ЭЛЕКТРОННОГО ТАХЕОМЕТРА | 2020 |
|
RU2736698C1 |
| СПОСОБ ПОСТРОЕНИЯ АСТРОИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2016 |
|
RU2641515C2 |
| Способ определения координат точек объекта | 2020 |
|
RU2740686C1 |
Изобретение относится к способам измерений геодезических координат. Заявленный способ горизонтирования системы координат состоит в следующем: измеряют с применением спутниковой навигационный системы геодезические координаты первого и второго теодолитов, угломерного прибора; выбирают не менее одной пары опорных точек (ОТ); измеряют углы визирования; методом угловых засечек определяют геодезические координаты пары ОТ; измеряют углы визирования на первую и вторую ОТ угломерным прибором; определяют углы визирования на ОТ с применением геодезических координат ОТ и геодезических координат угломерного прибора; применяют решение системы матричных уравнений, где прямоугольные декартовы координаты выражаются через углы визирования; определяют на пару ОТ углы пространственной ориентации нескорректированной системы координат угломерного прибора; осуществляют выбор корректного значения угла. Техническим результатом является повышение точности угловых измерений. 2 ил., 1 табл.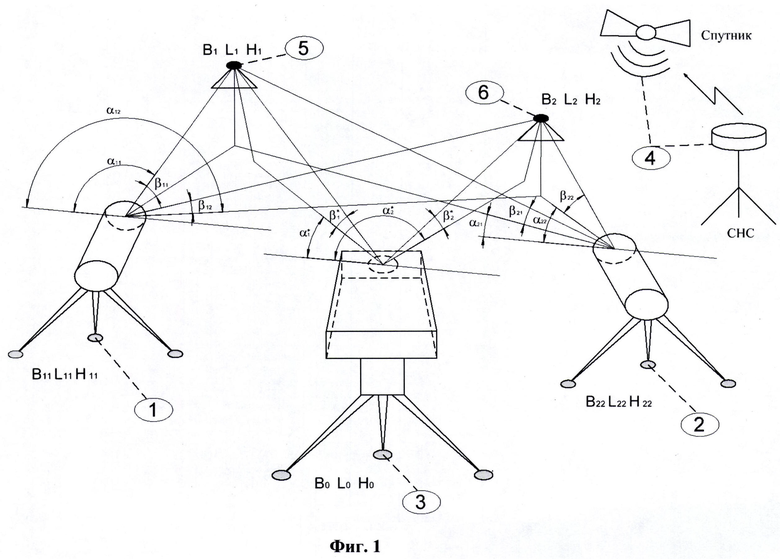
Способ горизонтирования системы координат угломерного прибора по опорным точкам и углам Эйлера-Крылова, предусматривающий: выбор в зоне измерений опорных точек и определение их геодезических координат, отличающийся тем, что
в зоне проведения измерений размещают два оптических теодолита, измеряющих угол азимута и угол возвышения на опорные точки, и угломерный прибор для измерения углов направления на цель;
измеряют с применением спутниковой навигационный системы геодезические координаты первого оптического теодолита В11, L11, H11 и второго оптического теодолита В22, L22, Н22, а также геодезические координаты угломерного прибора В0, L0, Н0, где В, L, Н - широта, долгота, высота с соответствующими индексами;
в зоне измерений выбирают не менее одной пары опорных точек, наблюдаемых как с места размещения угломерного прибора, так и с мест установки двух оптических теодолитов;
измеряют углы визирования с первого оптического теодолита на первую опорную точку α11, β11 и на вторую опорную точку α12, β12, измеряют углы визирования со второго оптического теодолита на первую опорную точку α21, β21 и на вторую опорную точку α22, β22;
дистанционно посредством метода угловых засечек, с применением геодезических координат первого и второго оптических теодолитов B11, L11, Н11 и B22, L22, Н22 и измеренных углов α11, β11, α12, β12, α21, β21, α22, β22 определяют геодезические координаты пары опорных точек (В1, L1, Н1) и (В2, L2, Н2);
измеряют углы визирования 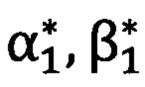 и
и 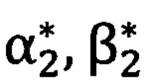 на первую и вторую опорные точки соответственно с применением угломерного прибора, при этом углы
на первую и вторую опорные точки соответственно с применением угломерного прибора, при этом углы 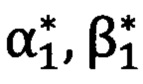 и
и 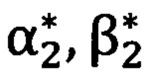 относятся к системе координат угломерного прибора;
относятся к системе координат угломерного прибора;
определяют углы визирования 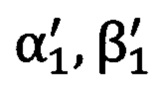 и
и 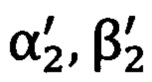 на опорные точки решением обратной геодезической задачи с применением геодезических координат опорных точек (В1, L1, Н1) и (B2, L2, Н2) и геодезических координат угломерного прибора В0, L0, Н0, при этом геодезические координаты опорных точек Bi, Li, Hi переводят в координаты геоцентрической прямоугольной системы координат Xi, Yi, Zi, которые преобразуют в прямоугольные декартовы координаты местной горизонтной системы координат
на опорные точки решением обратной геодезической задачи с применением геодезических координат опорных точек (В1, L1, Н1) и (B2, L2, Н2) и геодезических координат угломерного прибора В0, L0, Н0, при этом геодезические координаты опорных точек Bi, Li, Hi переводят в координаты геоцентрической прямоугольной системы координат Xi, Yi, Zi, которые преобразуют в прямоугольные декартовы координаты местной горизонтной системы координат 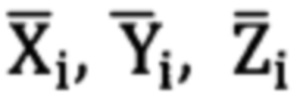 для нахождения полярных углов визирования на опорные точки
для нахождения полярных углов визирования на опорные точки 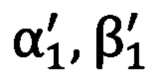 и
и 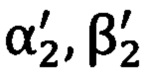 , при этом углы
, при этом углы 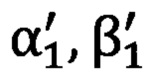 и
и 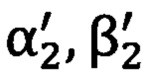 относятся к местной горизонтной системе координат и являются эталонными, где αi - азимутальный угол, βi - угол возвышения на точку с соответствующим индексом;
относятся к местной горизонтной системе координат и являются эталонными, где αi - азимутальный угол, βi - угол возвышения на точку с соответствующим индексом;
применяют решение системы матричных уравнений (1.1), (1.2), где прямоугольные декартовы координаты Xi, Yi, Zi выражаются через углы визирования αi, βi, построенной на сравнении вычисленных углов визирования 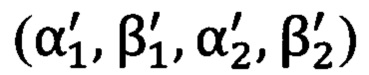 и измеренных углов визирования
и измеренных углов визирования 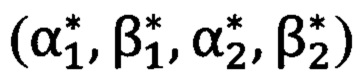 на пару опорных точек, для получения углов пространственной ориентации системы координат угломерного прибора Ψ, θ, ϒ:
на пару опорных точек, для получения углов пространственной ориентации системы координат угломерного прибора Ψ, θ, ϒ:
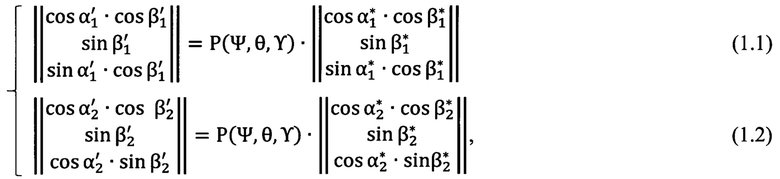
где

вычисляют два значения угла θ:

где

где
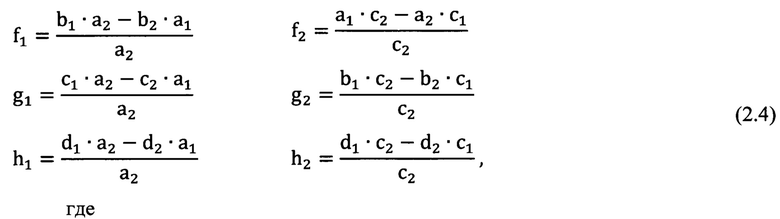
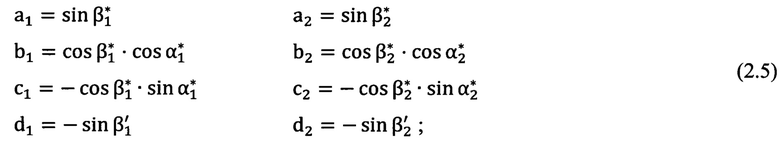
вычисляют значение угла ϒ1 и ϒ2 согласно правилу:
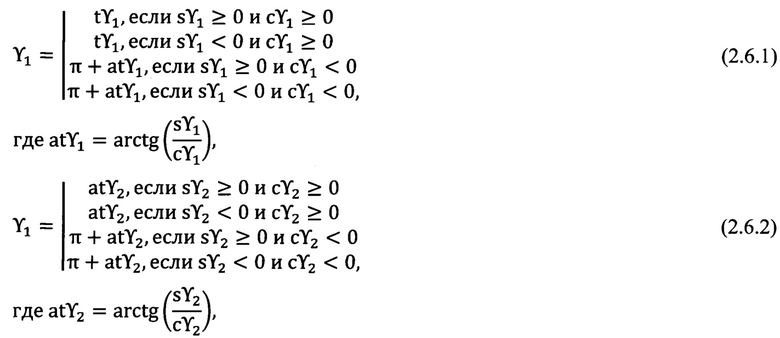
где

вычисляют значения углов θ и ϒ:
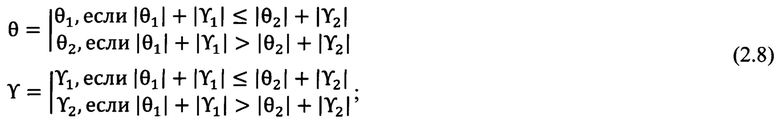
вычисляют значения угла Ψ:
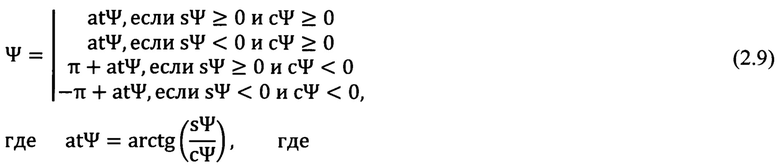
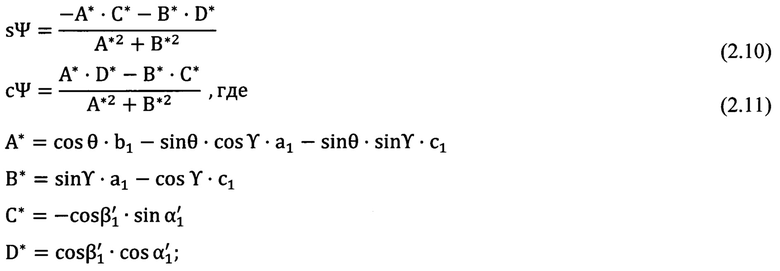
формируют матрицу угловых поправок путем подстановки полученных углов Ψ, θ, ϒ в матрицу (2.1), преобразуют углы визирования 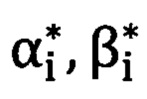 , полученные угломерным прибором в его координатной системе, в углы
, полученные угломерным прибором в его координатной системе, в углы 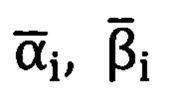 местной горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (3), (4.1), (4.2), (4.3):
местной горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (3), (4.1), (4.2), (4.3):

где 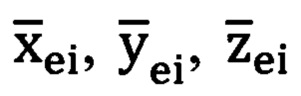 - проекции вектора единичной длины на оси
- проекции вектора единичной длины на оси 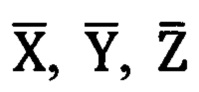 (фиг. 2) прямоугольной горизонтной системы координат соответственно,
(фиг. 2) прямоугольной горизонтной системы координат соответственно,

значение угла 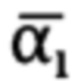 выбирается исходя из условия:
выбирается исходя из условия:

| СПОСОБ ПОЗИЦИОНИРОВАНИЯ ОБЪЕКТА ЗАСЕЧКОЙ ДАЛЬНОСТИ И УГЛА МЕСТА С ПЕРВОГО ИЗМЕРИТЕЛЬНОГО ПУНКТА И УГЛА МЕСТА - СО ВТОРОГО | 2017 |
|
RU2677586C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ОБЪЕКТА ЗАСЕЧКОЙ С ДВУХ ИЗМЕРИТЕЛЬНЫХ ПУНКТОВ ПО АЗИМУТУ, УГЛУ МЕСТА И ДАЛЬНОСТИ | 2017 |
|
RU2684733C2 |
| Способ коррекции углов визирования на точку | 2020 |
|
RU2758860C1 |
| US 9772185 B2, 26.09.2017. | |||
Авторы
Даты
2025-01-09—Публикация
2024-08-26—Подача