Изобретение относится к космической геодезии, в частности к способам построения Мировой космической геодезической сети планетарного масштаба.
Мировая космическая геодезическая сеть - это совокупность надежно (жестко) закрепленных и обозначенных на местности пунктов по всей территории земного шара, плановое положение и высоты которых определены в единой системе координат и высот путем спутниковых (геодезических) измерений на единую эпоху Т0 [2, 3, 4, 18].
Существует проблема наличия в мире множества национальных (континентальных), региональных, отраслевых, специальных, локальных спутниковых геодезических сетей, разделенных по территориальному и национальному признаку, кроме того на отдельных территориях суши и акватории мирового океана элементы спутниковой геодезической сети вовсе отсутствуют. Во многих научных работах [1, 2-4, 11-13, 16, 18] отмечается, что существует нерешенная научно-техническая задача по распространению государственной Общеземной геоцентрической (геодезической) системы координат и Общеземной геодезической системы высот Российской Федерации на весь земной шар в целях успешного решения широкого спектра задач.
Отсутствует глобальная (планетарная) геодезическая сеть, которая позволила бы распространить государственную Общеземную геоцентрическую (геодезическую) систему координат [2, 4, 12, 13, 16, 18, 27, 32] на весь земной шар. Подобную сеть возможно создать методами космической геодезии, объединив результаты наблюдений космических аппаратов спутниковых навигационных систем в единой Мировой космической геодезической сети на эпоху Т0, выполнив построение (развитие) крупной сети первого порядка (имеющую большую протяженность и наивысшую точность), которая принимается за исходную, далее выполняется построение сети последующих порядков (сгущении сети).
Система геодезических параметров «Параметры Земли 1990 года» является основой российской Общеземной геоцентрической (геодезической) системы координат и соответствует всем основным требованиям к системе координат планетарного масштаба [3-5, 11-13, 18, 23-25].
В настоящее время в разных регионах мира действуют сети постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, различающихся по ряду признаков и характеристик (системами геодезических параметров, точностями, условиями наблюдения, национальной принадлежностью и т.д.). Способ позволит выполнить построение единой сети в Общеземной геоцентрической (геодезической) системе координат [3, 5, 18], обеспечив условия для модернизации и развития государственной космической геодезической сети нового формата (поколения), объединив все имеющиеся разнородные спутниковые сети в единой государственной системе координат на единую эпоху времени T0.
Следует учитывать, что Россия принимает непосредственное участие в составе международных геодезических проектов, но своей глобальной сети у нее нет.
В качестве точек Мировой космической геодезической сети в Способе берутся результаты реальных измерений иностранных (международных) и российских постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, координаты фазовых центров антенн (точек) которых получены с высокой точностью методами космической геодезии [10, 11, 17, 18, 22] на основе результатов систематических измерений постоянно действующих (и/или временных) российских и иностранных (международных) измерительных станций наблюдения космических аппаратов глобальных навигационных спутниковых систем, станций радиоинтерферометрии со сверхдлинными базами, станций лазерной локации спутников, станций доплеровских измерений и др., удовлетворяющих требованиям уравниваемой Мировой космической геодезической сети. Опорой для уравниваемой Мировой космической геодезической сети могут быть национальные постоянно действующие астрофизические и астрометрические пункты радиоинтерферометрии со сверхдлинными базами (и/или пункты Космической геодезической сети).
Планетарная Мировая космическая геодезическая сеть после завершения ее построения и развития, будет состоять из станций наблюдения рассредоточенных по всему миру. Данные некоторых международных и национальных постоянно действующих станций (включенных в международную сеть) согласно международным договорам подлежат открытому опубликованию без ограничений точности координат и могут служить дополнительным исходным материалом для аналитического построения Мировой космической геодезической сети.
В Способе пространственное положение пунктов Мировой космической геодезической сети определяется методами космической геодезии в геоцентрической системе координат относительно центра масс Земли, с требуемой точностью, которые основываются на требованиях к национальным сетям такого рода [6, 7, 9, 22-25].
Опорные точки (фазовые центры антенн постоянно действующих станций наблюдения глобальных навигационных спутниковых систем) постоянных или временных станций (пунктов) наблюдения Мировой космической геодезической сети, должны быть жестко (фундаментально) закреплены в пространстве относительно центра масс Земли и отвечать следующим требованиям:
- точка должна располагаться на значительном расстоянии от границ (разломов) тектонических плит;
- измерения (глобальных навигационных спутниковых систем) должны выполняются геодезической спутниковой аппаратурой прецизионной точности;
- наблюдения в точке должны проводиться непрерывно в течение длительного периода или короткого периода, длительность которого удовлетворяет условиям построения и уравнивания сети;
- пункты должны быть обеспечены долговременной стабильностью своего пространственного положения как в плане, так и по высоте;
- пункты должны быть опознаваемы на местности и снимках;
- геометрия расположения пунктов сети должна соответствовать настоящему Способу с соблюдением условий оптимальности и рациональности;
- соблюдение условий спутниковых измерений: полное отсутствие естественных и искусственных препятствий (закрывающих небо более 15-20° над горизонтом) и постоянных источников радиопомех, существенно влияющих на результаты измерений.
Развитие (построение) и модернизация Мировой космической геодезической сети основано на методах спутниковых координатных определений и нацелено обеспечить наиболее рациональное и эффективное практическое применение постоянно действующих станций наблюдения глобальных навигационных спутниковых систем распределенных по всей территории мира. Такая опорная сеть в настоящее время может быть создана при следующих условиях:
- Мировая космическая геодезическая сеть создается с применением результатов наблюдений космических аппаратов спутниковых навигационных систем в виде сплошной сети, в качестве каркаса которой выбран правильный многогранник - икосаэдр, пункты Мировой космической геодезической сети должны равномерно покрывать территорию планеты Земля, с максимальным расстоянием между пунктами до d=2⋅a⋅sin(36°) (м), где а - большая полуось Земли, и со средней квадратической ошибкой взаимного положения пунктов до 10 см (в перспективе точность будет возрастать);
- обязательное совмещение с пунктами существующих международных (глобальных, континентальных) и национальных (территориальных), геодезических сетей с целью их объединения для обеспечения надежной и точной взаимной связи;
- сбор результатов спутниковых измерений с пунктов Мировой космической геодезической сети осуществляется в единую эпоху (для решения координатно-гравитационной задачи в единый момент времени);
- обязательное включение в состав Мировой космической геодезической сети только реально существующих, работающих постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, выполняющих длительные наблюдения или наблюдения в установленный промежуток времени;
- формирование геодезической опоры на основе многогранника (икосаэдра) осуществлять по результатам измерений постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, которые слабо подвержены деформационным геодинамическим процессам;
- создаваемая сеть должна опираться на построения более высокого уровня (например, сети постоянно действующих астрофизических и астрометрических пунктов радиоинтерферометрии со сверхдлинными базами), обеспечивая исключение деформаций регионального и глобального характера;
- основой для построения является единая Общеземная геоцентрическая (геодезическая) система координат на эпоху Т0.
- основа Мировой космической геодезической сети должна состоять из постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, с возможностью ее дополнения периодически определяемыми пунктами, формируя единую сеть на территории Российской Федерации и других заинтересованных государств;
- последующее совместное уравнивание всей сети по методу Гаусса (методу наименьших квадратов) в топоцентрической горизонтной геодезической системе координат [16, 21, 28] (или иному методу уравнивания, превосходящего заявленный).
Мировая космическая геодезическая сеть послужит исходной геодезической основой для дальнейшего повышения точности пунктов более низшего порядка и практической реализацией геоцентрической системы координат в рамках решения задач координатно-временного обеспечения страны, региона, планеты и ближнего космоса.
В отличие от классических методов (триангуляции, трилатерации, полигонометрии и т.д.), опорные геодезические сети, построенные с помощью методов базирующихся на измерении глобальных навигационных спутниковых систем менее чувствительны к геометрии расположения точек опорной сети, но если задачу построения и уравнивания решать в масштабе планеты, то прослеживается прямая зависимость точности сети от количества, взаимного геометрического расположения и пространственного положения точек сети относительно центра масс Земли. В таком случае необходимо стремится к построению опорных сетей с идеальной геометрией на основе правильных пространственных фигур, форма которых исключат нежелательные геометрические искажения (дефекты). Выполнить данное построение возможно на фигуре, которая обладает однородностью всех составляющих ее элементов, так как такое построение подразумевает разумное (рациональное, оптимальное) расположение опорных точек (пунктов) и точек (пунктов) сгущающих сеть, при наличии достаточного числа узловых точек и избыточных измерений. Подход, используемый в Способе, основывается на использовании двадцати треугольных граней икосаэдра, равной площади, равной формы (т.е. равномерно распределенной сети треугольников фиксированного размера).
На поверхности эллипсоида невозможно создать сеть, состоящую из фигур равной площади, одинаковой формы и равномерно распределенных по всей поверхности. Такое построение возможно выполнить на сфере. Если пренебречь искажениями и представить форму Земли близкой к сфере, то для равномерного распределения точек Мировой космической геодезической сети рекомендуется использовать икосаэдр. Исходя из позиции сохранения формы выгоднее всего опираться на симметрию икосаэдра, форма которого выбрана в качестве прототипа каркаса Мировой космической геодезической сети, так как это один из пяти правильных выпуклых многогранников - «Платоновых тел» [19, 20, 21, 28-32], который состоит из одинаковых правильных треугольников. Икосаэдр обладает пространственной симметрией и имеет одинаковых: вершин - 12, ребер - 30, граней (равносторонних треугольников) - 20. Ему присущи некоторые комбинаторные и геометрические свойства, которые наиболее полно подходят к применению его в качестве основы (каркаса) для построения Мировой космической геодезической сети. Среди правильных многогранников икосаэдр представляет собой лучшее приближение к сфере. Икосаэдр имеет наибольшее число граней, наибольший двугранный угол и плотнее всего прижимается к своей вписанной сфере. Использование икосаэдра обеспечит жесткий каркас с однородной строгой зависимостью всех точек пространственной планетарной глобальной сети.
Ожидаемый эффект: построение Мировой космической геодезической сети с применением результатов наблюдений космических аппаратов спутниковых навигационных систем для последующего уравнивания в рамках единой координатно-гравитационной задачи на единую эпоху Т0, аналитически получая высокоточную геодезическую основу на весь земной шар в единой государственной Общеземной (геоцентрической) геодезической системе координат [1, 6, 7, 8, 9, 23-26].
Способ построения Мировой космической геодезической сети вобрал накопленный опыт международных и национальных проектов построения геодезических сетей и обеспечивает перспективную концепцию формирования космической геодезической сети нового уровня.
Общие признаки предлагаемого изобретения: способ построения Мировой космической геодезической сети планетарного масштаба с применением результатов наблюдений космических аппаратов спутниковых навигационных систем.
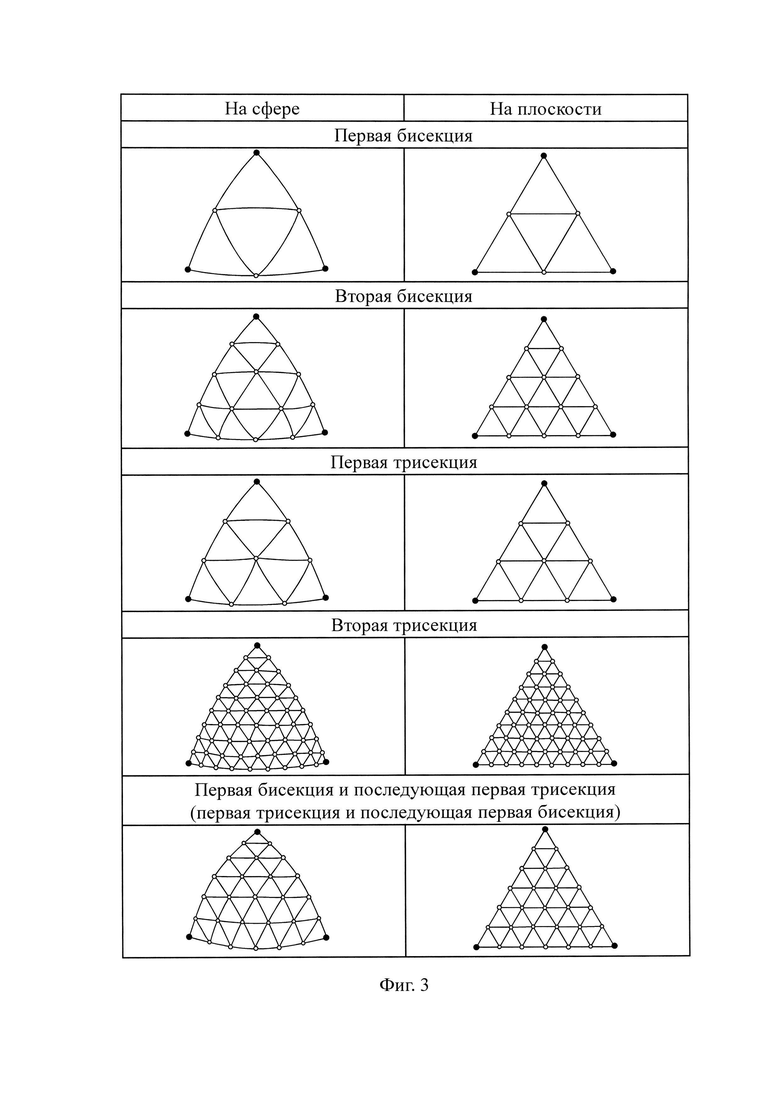
Способ представляет собой аналитическое построение пространственной сети планетарного масштаба для последующего уравнивания. В качестве шаблона проекта модели Мировой космической геодезической сети выбрано идеальное расположение точек на основе вершин (и точек их сгущающих) икосаэдра, перенесенных на сферу (фиг. 2). Сгущение сети с заданной плотностью, производится операциями равномерного дробления граней икосаэдра (фиг. 3), перенесенных на сферу, образовывая вершинами новых треугольников регулярную сеть. Построение Мировой космической геодезической сети выполняется по результатам поиска (по заданному радиусу - rn), сопоставления (математического сравнения) и последовательного отбора ближайших точек (центров реально существующих постоянно действующих станций наблюдения глобальных навигационных спутниковых систем), отображенных на сферической карте мира, и точек шаблона проекта модели Мировой космической геодезической сети, принятых за эталон модели создаваемой сети (фиг. 4).
Распределение точек Мировой космической геодезической сети в Способе рекомендуется выполнять с использованием регулярной сети шаблона проекта модели Мировой космической геодезической сети, узлы которого характеризуют идеальное взаимное равноудаленное распределение всех точек сети по поверхности сферы на основе строгих математических и геометрических зависимостей треугольника (как на плоскости, так и на сфере).
Фиг. 4 - пример набора отобранных точек для проекта модели Мировой космической геодезической сети (фрагмент). (Сгущение сети шаблона проекта модели на основе икосаэдра осуществлено операцией однократной бисекции (фиг. 3), получено 42 узловых (опорных) шаблонных точки). (1) - заданный радиус поиска (rn), (2) - центры (точки) постоянно действующих станций наблюдения глобальных навигационных спутниковых систем участвующих в построении, (3) - опознанные и отобранные постоянно действующие опорные станции наблюдения глобальных навигационных спутниковых систем, (4) - опорные шаблонные точки проекта модели Мировой космической геодезической сети, построенные с заданной плотностью на основе икосаэдра, (5) - линии тектонической границы (разлома) литосферных плит.
Достоинством сети, предлагаемой в изобретении является равномерная (постоянное) плотность (разрешение) всей сети, которую возможно увеличить двоичным или(и) троичным делением (фиг. 3 - бисекцией, трисекцией и их комбинацией). При этом данный Способ не страдает избыточной выборкой около полюсов, в отличие от традиционных прямоугольных квадратных сеток образованных географическим пересечением долготы и широты. Такое построение не приводит к плотным линейным системам спектральных схем как у «Гауссовой сетки». Треугольные ячейки (или треугольные ячейки сгущения) икосаэдра (сферического икосаэдра) минимально искажены относительно друг друга. Напротив, квадратные географические сетки не имеют равной площади и различаются по форме от экватора к полюсам. Икосаэдр имеет наименьший размер грани, и поэтому любые сети, определенные на нем, имеют тенденцию отображать относительно небольшие искажения [19, 20, 29-32].
Так как в описанном сферой икосаэдре точки вершин касаются (совпадают) поверхности сферы (фиг. 1) осуществим перенос граней икосаэдра на сферу (фиг. 2), разбив сферу дугами больших окружностей (лежащих в одной плоскости с вписанным икосаэдром) на замкнутые области (сферические треугольники), получим сферический икосаэдр. Способы разбиения сферы ничем не ограничены, однако регулярные построения обычно основаны на пространственной симметрии. Икосаэдр лучше всего из всех правильных многогранников подходит для триангуляции сферы методом рекурсивного разбиения (алгоритм триангуляции рекурсивно применяется к отдельным частям, а затем производится слияние (объединение, склеивание) полученных отдельных триангуляций). Поскольку он содержит наибольшее среди «Платоновых тел» количество граней, искажение получающихся треугольников по отношению к правильным минимально [19, 20, 29-31]. В качестве единицы сгущения (эталона) в Способе принят равносторонний треугольник (сферический равносторонний треугольник). Количественной мерой близости к эталону может быть, отношение элементов этого треугольника. В соответствии со Способом на поверхности сферы создаются регулярные треугольные сетки, образованные сферическими треугольниками сгущения, близкие по размеру и форме.
Основные определяющие преимущества Мировой космической геодезической сети, проектируемой на базе икосаэдра:
1) основой сети является базовый регулярный многогранник - икосаэдр, с уникальными геометрическими и комбинаторными свойствами применительно к построению Мировой космической геодезической сети;
2) выгодность при иерархическом пространственном построении сети любой плотности за счет равномерного разбиения на максимально похожие (равные или близкие по форме и размеру) фигуры (операциями бисекции, трисекции и их комбинирования);
3) выгодность при переходе из плоской в сферическую (эллипсоидальную) поверхность и обратно;
4) простота отбора точек Мировой космической геодезической сети из массива реальных постоянно действующих станций наблюдения глобальных навигационных спутниковых систем по шаблонной сети;
5) строгая зависимость всех элементов (сети), монолитность и замкнутость всей сети;
6) возможность сгущения сети по заданным критериям (с необходимой плотностью);
7) динамичность и универсальность системы;
8) возможность осуществлять построения с привязкой к реальным точкам наблюдения на единую эпоху Т0.
Решить задачу равномерного построения и сгущения Мировой космической геодезической сети возможно разбиением на равносторонние треугольники (сферические треугольники) в пределах каждой грани икосаэдра, при этом построенная на основе такого треугольника сетка сгущения будет максимально близка к регулярной.
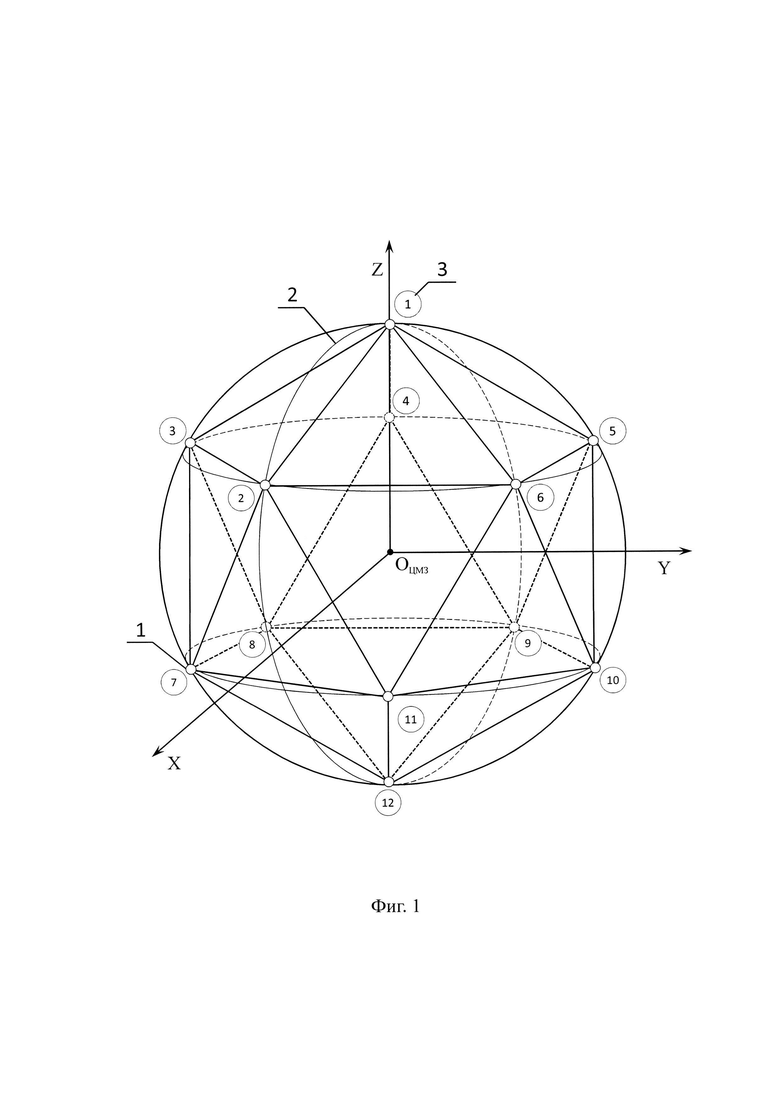
Произведем разбиение сферы на равносторонние (или близкие к равносторонним) сферические треугольники на основе икосаэдра. Введем нумерацию вершин икосаэдра (фиг. 1, 2) и поместим его в прямоугольной декартовой системе координат, таким образом, чтобы центр описанной около него сферы совпал с началом координатных осей (фиг. 1, 2).
Фиг. 1 - начальная ориентация икосаэдра относительно Общеземной геоцентрической (геодезической) системы координат: (1) - опорная (одна из 12-ти) вершина икосаэдра (шаблонная точка сети) принятого за основу шаблона проекта модели Мировой космической геодезической сети, (2) - начальный меридиан, (3) - условная нумерация опорных базовых вершин (с 1 по 12) икосаэдра, принятых в качестве базовых шаблонных точек сети (шаблон проекта модели Мировой космической геодезической сети), обведенные кругом.
Для нахождения связи всех вершин икосаэдра сориентируем оси координатной системы определенным образом (фиг. 1, 2), чтобы две вершины (1-я и 12-я) икосаэдра оказались в полюсах сферической системы координат.
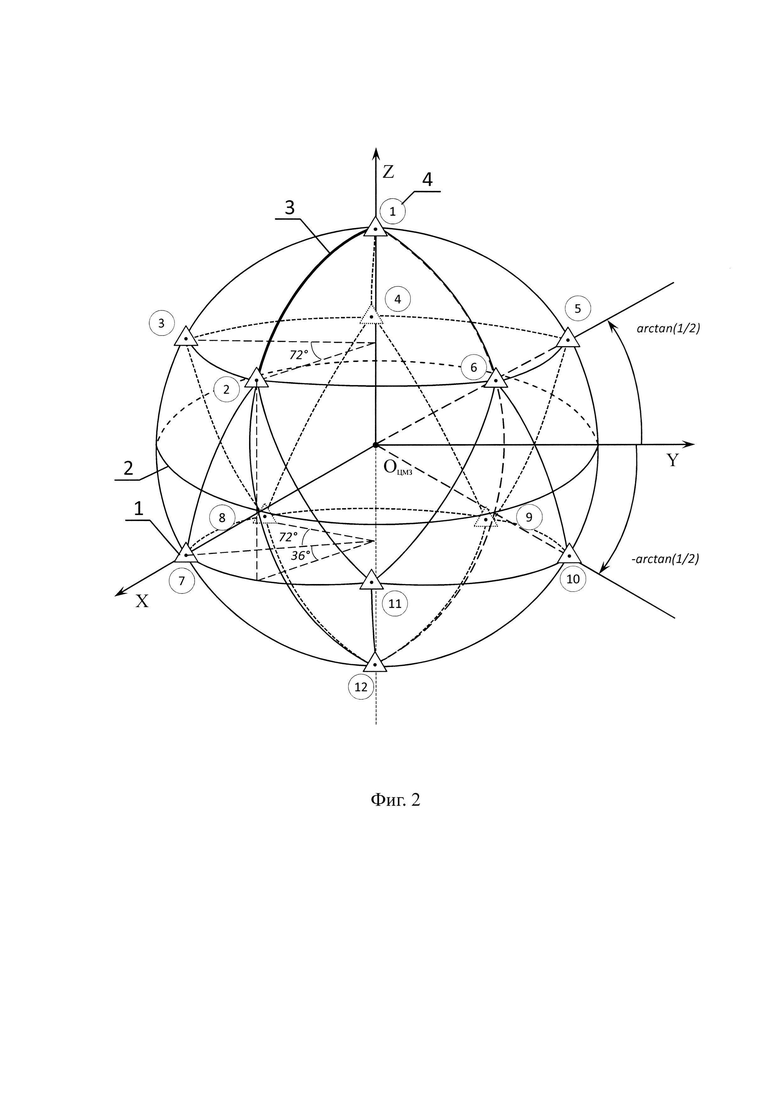
Фиг. 2 - элементы икосаэдра спроецированные на сферу относительно центра Общеземной геоцентрической (геодезической) системы координат: (1) - узловая (опорная) шаблонная точка (одна из 12-ти вершин икосаэдра) проекта модели Мировой космической геодезической сети, построенная на основе икосаэдра, (2) - экватор, (3) - начальный меридиан, (4) - условная нумерация опорных базовых шаблонных точек икосаэдра (шаблона проекта модели Мировой космической геодезической сети) с 1 по 12 точку (вершину), обведенные кругом.
Опишем расположение вершин правильного икосаэдра с помощью сферических координат (широты и долготы). Учитывая, что две вершины находятся на северном и южном полюсах (широта ±90°), то остальные десять вершин находятся на широте ± arctan(1/2) ≈±26.5650511771°. Эти десять вершин находятся на равном расстоянии друг от друга ±36°, чередуя северные и южные широты (по пять в каждой широте, распределены равномерно в одной плоскости под углом 72°).
Представим вершины икосаэдра в декартовых координатах. Если длина ребра правильного икосаэдра равна  то радиус описанной сферы (которая касается икосаэдра во всех вершинах) равен:
то радиус описанной сферы (которая касается икосаэдра во всех вершинах) равен:

тогда прямоугольные пространственные координаты икосаэдра в центральной проекции могут быть вычислены:
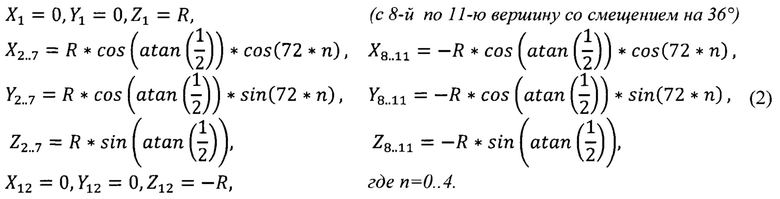
До вращения шаблона проекта модели Мировой космической геодезической сети на основе икосаэдра, начальным положением считается положение номеров вершин (фиг. 1, 2): 1-я вершина совмещается с осью Z, направлена к условному земному северному полюсу (международному условному началу), 2-я ближайшая вершина к 1-й вершине, лежит в плоскости начального меридиана и оси X. При вращении икосаэдра положение всех остальных вершин проекта модели Мировой космической геодезической сети вычисляется на основе зависимостей по формулам (1, 2). Так как проекция является центральной (фиг. 1, 2), то для масштабирования и ориентации положения модели икосаэдра достаточно знать координаты двух точек А и В.
Таким образом, зная закономерность вращения всего шаблона (каркаса) закрепленного координатами вершин икосаэдра вокруг центральной точки (точки начала координат геоцентрической системы, Оцмз - центра масс Земли), возможно выполнить построение проекта модели Мировой космической геодезической сети вращением модели икосаэдра и заполняющих его точек (вершин) сгущения, (которые получены 2- и 3-кратным делением сторон треугольников икосаэдра операциями (фиг. 3): бисекции, трисекции и их комбинированием) с последующим выбором массива точек Мировой космической геодезической сети закрепленных на местности постоянно действующими станциями наблюдения глобальных навигационных спутниковых систем приняв их в состав выстраиваемой сети для дальнейшей обработки (уравнивания).
Преимущество сгущения (дробления) сферы треугольниками, объясняется уникальными геометрическими свойствами равностороннего (правильного) треугольника, который является наиболее компактной единицей для квантования поверхности с наименьшей средней ошибкой относительно других фигур (как на плоскости, так и на сфере), и обладает строгостью геометрических и математических связей построений, которые он образовывает [19, 20, 29-31].
В процедуре деления сторон и последующем построении вновь образованных треугольников, в качестве базы используется каждая спроецированная на сферу грань икосаэдра - сферический треугольник, заданный координатами своих трех вершин.
Операцию деления исходного треугольника на четыре треугольника нового поколения назовем - бисекцией, реализуется делением каждого ребра (стороны) базового треугольника на две равные части. После такого деления середины ребер совпадают с новыми вершинами, которые при соединении новыми ребрами образуют новые треугольники. Следующее поколение треугольников сгущения получается очередной бисекцией (фиг. 3) треугольников, полученных от предыдущего этапа бисекции.
В сферической геодезии задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач [1, 2, 15, 27, 32]. В Способе для простоты математической обработки предлагается бисекцию проводить с использованием векторной алгебры, где концы сторон дуги или прямой заданы векторами а и b, средняя точка q вычисляется как их нормированная сумма (3):

Операцию деления исходного треугольника на девять треугольников нового поколения назовем - трисекцией, реализуется делением каждого ребра (стороны) базовых треугольников на три равные части. После такого деления две точки деления ребра совпадают с новыми вершинами, и при их соединении с новыми ребрами образуются новые треугольники. Следующее поколение треугольников сгущения получается очередной трисекцией (фиг. 3). Таким образом, исходный треугольник делится на девять треугольников нового поколения. В результате трисекции каждая сторона треугольника делится на три равных отрезка, концы которых образуют вершины нового поколения сферических треугольников, образуя шесть новых вершин вдоль сторон (4) и седьмую вершину - в геометрическом центре базового сферического треугольника (5).
Получим координаты точек вершин при трисекции. Зная координаты точек M1(X1, Y1, Z1) и M2(X2, Y2, Z2) и отношение 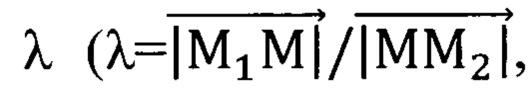 в котором точка М делит направленный отрезок
в котором точка М делит направленный отрезок 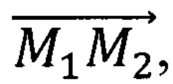 найдем координаты точки М.
найдем координаты точки М.
Пусть Оцмз - начало координат, обозначим 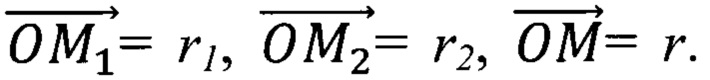 Так как
Так как 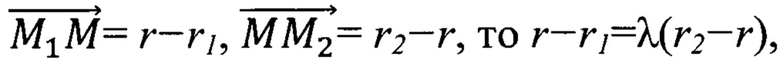 откуда (так как λ≠-1) r=((r1+λr2)/(1+λ).
откуда (так как λ≠-1) r=((r1+λr2)/(1+λ).
Полученная форма дает решение задачи в векторной форме. Переходя к координатам, получим:

Положение центральной точки сферического треугольника g:

где а, b и с - векторы вершин исходного (принятого за базовый) треугольника.
Возможна операция комбинированного квантования с использованием приемов бисекции и трисекции (фиг. 3) поочередно.
Например, выполнив над икосаэдром первую операцию дублирования приемом первой бисекции, получается многогранник с 42 вершинами (узлами) (фиг. 4). Полученный многогранник в диаметральных плоскостях трех направлений образует правильные десятиугольники, что позволяет, используя процедуру дублирования, получать пространственные конфигурации для построения Мировых космических геодезических сетей на сфере [19, 20, 29-31].
Способ включает этапы:
1) подготовка к проектированию шаблона проекта модели Мировой космической геодезической сети: построение икосаэдра (фиг. 1), его предварительное вращение и подготовка к проецированию на поверхность сферы (фиг. 2) в соответствии с заданными требованиями к планируемому построению;
2) подготовка к проектированию сферической карты мира (с использованием макета типа-глобус, специального программного обеспечения трехмерной визуализации или математической модели) с нанесенными на нее точками центров постоянно действующих станций наблюдения глобальных навигационных спутниковых систем, отобранных для использования в построении, далее нанесение дополнительной справочной информации на сферическую карту мира (например, линий тектонической границы (раздела) литосферных плит);
3) выбор пары опорных точек (вершин) А и В для поворота и ориентации шаблона проекта модели Мировой космической геодезической сети на основе икосаэдра;
4) вращение шаблона проекта модели Мировой космической геодезической сети, ориентация его по выбранным опорным точкам А и В относительно карты мира на сфере (сферическую карту мира);
5) построение сферических треугольников по узловым точкам вершин икосаэдра (проецирование их на сферу);
6) выбор приема сгущения шаблона проекта модели Мировой космической геодезической сети операциями: бисекцией, трисекцией или их комбинированием (фиг. 3);
7) сгущение шаблона проекта модели Мировой космической геодезической сети;
8) поиск ближайших реально существующих постоянно действующих станций наблюдения, обозначенных на сферической карте мира точками, относительно точек шаблонного проекта модели Мировой космической геодезической сети (на основе икосаэдра) по установленному радиусу поиска (rn); сопоставление (сравнение) и выбор ближайших точек, удовлетворяющих условиям построения, с последующим включением их в состав проекта модели Мировой космической геодезической сети, при котором отбор точек Мировой космической геодезической сети осуществляется графическим сопоставлением (при котором выбор точек сети осуществляется приемами графического сопоставления точек шаблона (проекта модели Мировой космической геодезической сети) с точками на сферической карте мира в пределах заданного радиуса поиска) и(или) математическим сравнением (при котором выбор точек сети осуществляется приемами математического сравнения численных выражений координат точек шаблона (проекта модели Мировой космической геодезической сети) с точками на сферической карте мира в пределах заданного радиуса поиска);
9) систематизация выбранных точек Мировой космической геодезической сети и подготовка для дальнейшего уравнивания.
В Способе предложен алгоритм построения Мировой космической геодезической сети при высокоточном определении пространственного положения всех точек сети (пунктов наблюдения) методами космической геодезии, относительно друг друга и центра масс Земли, при уравнивании которых обеспечивается жесткая геодезическая основа на весь мир или интересующую территорию.
Основными отличительными признаками и достоинством Способа построения Мировой космической геодезической сети с применением результатов наблюдений космических аппаратов спутниковых навигационных систем является использование новых приемов аналитического построения пространственной планетарной космической геодезической сети, при котором соблюдаются условия построения (пространственного расположения точек сети) максимально приближенные к идеальным, где геометрические и математические искажения и ошибки, влияющие на точность получаемой сети, ничтожно малы. При таком построении (пространственном расположении) точки сети участвуют в последующем уравнивании по методу Гаусса (методу наименьших квадратов) в топоцентрической горизонтной системе координат [2, 3, 11, 14-16, 20-22, 27, 32], при этом достигается максимальная точность, геоцентричность (ошибка положения относительно центра масс Земли, принятого за начало геоцентрической системы координат), строгость (высокоточность, с множественной связью всех элементов сети) и независимость (слабое влияние искажающих факторов) создаваемой Мировой космической геодезической сети планетарного масштаба в единой Общеземной геоцентрической (геодезической) системе координат на эпоху Т0.
Практическое применение Способа подразумевает использование результатов наблюдений космических аппаратов (искусственных спутников Земли) на пунктах постоянно действующих станций наблюдения глобальных навигационных спутниковых систем в определенный промежуток времени (эпоху Т0), расположенных на значительном расстоянии друг от друга, на разных континентах и океанических островах, что позволяет за короткий срок (аналитически) выполнять построение Мировой космической геодезической сети планетарного масштаба в необходимой системе координат и эпоху Т0, распространяя государственную Общеземную геоцентрическую (геодезическую) систему координат на весь земной шар.
Реализация Способа позволит решить ряд научно-технических и стратегических задач, в том числе, позволит обеспечить:
1) модернизацию и развитие Космической геодезической сети, количество точек (пунктов) которой не достаточно для развития системы геодезических параметров «Параметры Земли 1990 года» на весь земной шар и требует нового построения, результатом которого станет Мировая космическая геодезическая сеть;
2) уточнение Внешнего гравитационного поля Земли;
3) отслеживание тектонических движений материков и островов;
4) объединение существующих отечественных и зарубежных (международных) обширных спутниковых геодезических сетей в одной единой Мировой космической геодезической сети России, которая будет обладать рядом преимуществ;
5) использование отечественного и иностранного (международного) опыта построения Мировой космической геодезической сети, при этом закладывая основу постоянного наращивания потенциала отечественной Мировой космической геодезической сети;
6) распространение государственной Общеземной геоцентрической (геодезической) системы координат на весь земной шар;
7) основу для глобального (планетарного) картографирования;
8) основу для глобального (планетарного) позиционирования;
9) вычисление координат всех, включенных пунктов в состав Мировой космической геодезической сети в единой Общеземной геоцентрической (геодезической) государственной системе координат;
10) вычисление (уточнение) параметров связи государственной Общеземной геоцентрической (геодезической) системы координат с другими (отечественными, зарубежными) системами координат на заданную эпоху с учетом региональных особенностей;
11) возможность пересчета нормальных высот пунктов Мировой космической геодезической сети, заданных в иностранных (международных) или национальных системах высот к среднему уровню Мирового океана или в Балтийскую систему высот 1977 г.
Таким образом, Способ построения Мировой космической геодезической сети предусматривает использование существующих и перспективных спутниковых технологий в целях модернизации и развития Мировой космической геодезической сети для решения ряда научно-технических задач геодезии, геодинамики, космической геодезии, фотограмметрии, картографии, геоинформации, навигации и др.
Список использованной литературы
1. Машимов М.М. Планетарные теории геодезии. - М.: Недра, 1982.
2. Машимов М. М. Уравнивание геодезических сетей. - М., Недра, 1979, 367 с.
3. Машимов М.М. Перспективы развития геодезии - М.: Знание №11, 1986 г.
4. Смирнов С.А., Пигулка С.А. Актуальность проблемы топогеодезического, навигационного и геоинформационного обеспечения Вооруженных Сил Российской Федерации на территории иностранных государств, Основные результаты диссертационных исследований докторантов адъюнктов и соискателей академии. Научный сборник - М.: Изд. ВУНЦ СВ «ОВА ВС РФ», 2020, №90, с. 238-246.
5. Специализированный справочник, Параметры Земли 1990 г. (П3-90.11) - М.: ВТУ ГШ ВС РФ, 2020 г.
6. Радионавигационный план Российской Федерации, утвержден приказом Минпромторга России от 4 сентября 2019 г., №3296.
7. Приказ Министерства экономического развития РФ от 29 марта 2017 г. N 138 «Об установлении структуры государственной геодезической сети и требований к созданию государственной геодезической сети, включая требования к геодезическим пунктам».
8. ГОСТ Р 56408-2015 Глобальная навигационная спутниковая система. Сети геодезические спутниковые. Общие требования, Национальный стандарт Российской Федерации.
9. Постановление Правительства Российской Федерации от 24 ноября 2016 г. №1240 «Об установлении государственных систем координат, государственной системы высот и государственной гравиметрической системы».
10. Антонович К.М. Использование спутниковых радионавигационных систем в геодезии, В 2 т. Т. 1. Монография; ГОУ ВПО «Сибирская государственная геодезическая академия». - М.: ФГУП «Картгеоцентр», 2005 - 334 с.
11. Малец К.В. Исследование эффективности методов построения космической геодезической сети. - М.: 29 НИИ, диссертация, инв. №3988, 1975 г., 155 с.
12. Малец К.В. Методы установления ОГСК с применением результатов наблюдений ИСЗ, квазаров и светолокации Луны. - М.: ВИА, диссертация, инв. №1020, 1986 г., 340 с.
13. Малец К.В., Лангеман И.П., Гоманов Д.Е. Проблема создания ОГСВ с применением геоспутниковых технологий. - М.: ВУНЦ СВ «ОВА ВС РФ», НТС №62, 2012 г.
14. Дударев В.И. Уравнивание геодезических сетей по результатам относительных GPS-измерений, Вестник Сибирской государственной геодезической академии. - Новосибирск: СГГА, 2011.
15. Машимов М.М. Методы математической обработки астрономо-геодезических измерений: учебник - М.: Военно-инженерная академия, 1990. - 510 с.
16. Пигулка С.А. Алгоритм методики построения и уравнивания Мировой космической геодезической сети с применением результатов наблюдений космических аппаратов спутниковой навигационной системы ГЛОНАСС/NAVSTAR и астрономо-геодезических и гравиметрических измерений, М.: Общевойсковая академия, Основные результаты диссертационных исследований докторантов, адъюнктов и соискателей академии, Научный сборник №97, 2021 г., 300 с., с. 152-158.
17. Антонович, К.М. Использование спутниковых радионавигационных систем в геодезии, монография на соискание ученой степени доктора технических наук. - Новосибирск, СГГА, 2007.
18. Малец К.В., Рутько И.М., Лангеман И.П., Пигулка С.А. Проблема модернизации и развития Мировой космической геодезической сети Российской Федерации с применением методов и технологий космической геодезии, спутниковой навигации и астрономо-геодезических и гравиметрических измерений, М.: Изд. ВУНЦ СВ «ОВА ВС РФ», Сборник научных трудов академии НИЦ (ОиИТ), часть II, №54.2020 г., с. 538-545.
19. Евтушенко А.И., Самсонова А.Н., Скуратов С.В. Формообразование конструктивных сетей многогранных непологих куполов, Донской государственный технический университет, Ростов-на-Дону, Инженерный вестник Дона, №1, 2017 (ivdon.ru/ru/magazine/archive/n1y2017/4183), Электронный научный журнал «Инженерный вестник Дона».
20. Серапинас Б.Б. Математическая картография: Учебник для вузов / Балис Балио Серапинас - М.: Издательство центр «Академия», 2005. - 336 с. ISBN 5-7695-2131-7.
21. Пигулка С.А. Теоретические основы метода построения и уравнивания Мировой космической геодезической сети с применением результатов наблюдений КА СНС ГЛОНАСС/NAVSTAR и астрономо-геодезических и гравиметрических измерений, М.: Общевойсковая академия, Основные результаты диссертационных исследований докторантов, адъюнктов и соискателей академии, Научный сборник №98, 2021 г., 300 с., с. 160-165.
22. Пигулка С.А. Анализ современного программного обеспечения применительно к методике построения и уравнивания Мировой космической геодезической сети с применением результатов наблюдений космических аппаратов спутниковых навигационных систем ГЛОНАСС, NAVSTAR и астрономо-геодезических и гравиметрических измерений, Тематический сборник: Пути повышения эффективности топогеодезического, навигационного и геоинформационного обеспечения вооруженных сил Российской Федерации, М.: Изд. ВУНЦ СВ «ОВА ВС РФ», №2, 2021 г., 262 с.
23. Постановлением Правительства Российской Федерации от 28 июля 2000 г. №568 геоцентрической системе координат, входящей в систему «Параметры Земли 1990 года» (ПЗ-90).
24. Распоряжение Правительства Российской Федерации от 20 июня 2007 г. №797-р уточненная версия государственной геоцентрической системы координат, входящая в систему «Параметры Земли 1990 года» (ПЗ-90.02).
25. Геометрические и физические числовые геодезические параметры в отношении общеземной геоцентрической системы координат «Параметры Земли 1990 года» (ПЗ-90.11) утверждены приказом Министра обороны Российской Федерации от 15 января 2014 г. №11.
26. Федеральный закон от 30.12.2015 N 431-ФЗ (ред. от 11.06.2021) «О геодезии, картографии и пространственных данных и о внесении изменений в отдельные законодательные акты Российской Федерации».
27. Генике А.А., Побединский Г.Г. Глобальные спутниковые системы определения местоположения и их применение в геодезии. Изд. 2-е, перераб. и доп. - М.: Картгеоцентр, 2004. - 355 с.: ил., ISBN 5-86066-063-4, УДК 528.2:629.78, ББК 26.1.
28. Пигулка С.А., Смирнов С.А. Свидетельство о государственной регистрации программы для ЭВМ № RU 2021615052 «Автоматизация уравнивания Мировой космической геодезической сети в топоцентрической системе координат в среде РТС Mathcad Prime 6», описание к программе, 2021, 1 с.
29. Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени: Пер. с нем. / под ред. А.Н. Тюрина. - М.: Наука. Гл. ред. физ. - мат. лит., 1989, 336 с., ISBN 5-02-014197-6.
30. Венниджер М. Модели многогранников, (перевод с английского В.В. Фирсова), Издательство «Мир», Москва, 1974 г., 242 с.
31. Смирнова И.М., Смирнов В.А. Правильные, полуправильные и звездчатые многогранники. - М.: МЦНМО, 2010, 58 с., УДК. 514.11, ББК 22.151.0 С50, ISBN 978-5-94057-678-5.
32. Глушков В.В., Насрединов К.К., Шаравин А.А. Космическая геодезия: методы и перспективы развития, - М.: Институт политического и военного анализа, 2002, 448 с., ISSN №5-93349-019-9, УДК 629.783+528.3.

Изобретение относится к области космической геодезии, в частности к способам построения Мировой космической геодезической сети планетарного масштаба. Сущность предлагаемого способа заключается в следующем. Шаблоном модели Мировой космической геодезической сети является икосаэдр. Построение Мировой космической геодезической сети выполняется по результатам поиска, сопоставления и последовательного отбора ближайших точек - центров реально существующих и постоянно действующих станций наблюдения глобальных навигационных спутниковых систем - отображенных на сферической карте мира, и эталонных точек шаблона модели Мировой космической геодезической сети. Сгущение сети с заданной плотностью производится операциями бисекции и трисекции граней икосаэдра, перенесенных на сферу, при этом вершины новых треугольников образуют регулярную сеть. Техническим результатом заявленного изобретения является получение высокоточной геодезической основы планетарного масштаба. 5 ил.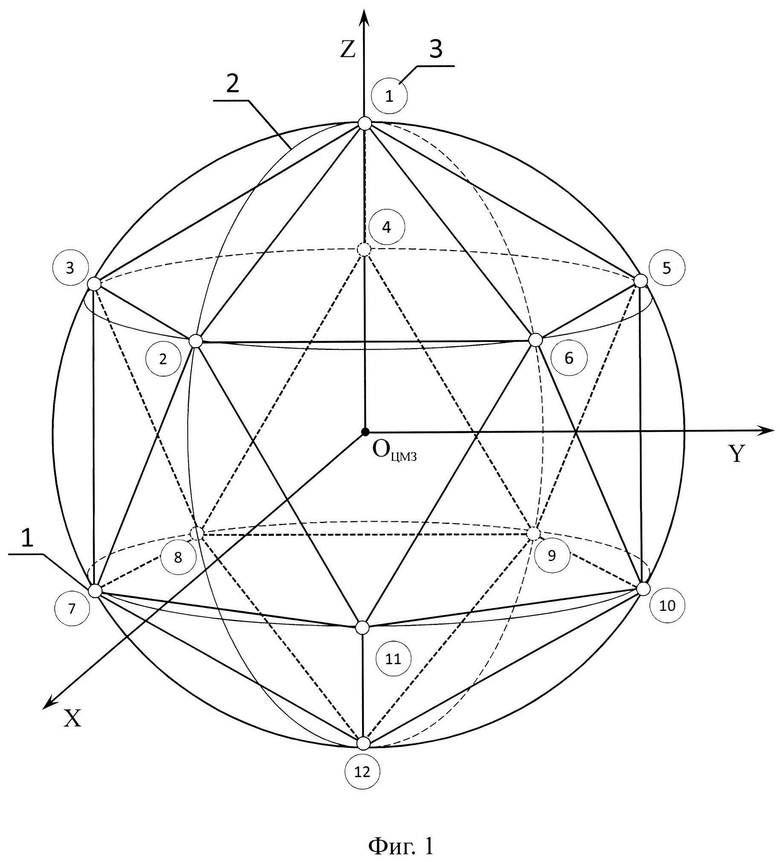
Способ построения Мировой космической геодезической сети с применением результатов наблюдений космических аппаратов спутниковых навигационных систем представляет собой построение космической геодезической сети планетарного масштаба на единую эпоху спутниковых наблюдений T0 в составе единой сети, выполняется посредством отбора постоянно действующих станций (пунктов) наблюдения глобальных навигационных спутниковых систем в состав формируемой Мировой космической геодезической сети по принципу максимальной близости постоянно действующих спутниковых станций наблюдения глобальных навигационных спутниковых систем по заданному радиусу поиска rn к вершинам икосаэдра, который принят за основу Мировой космической геодезической сети, при этом геометрический центр икосаэдра и геометрический центр сферической карты мира, на которой нанесены точки, характеризующие положения пунктов постоянно действующих спутниковых станций наблюдения глобальных навигационных спутниковых систем, совмещаются, а в результате отбора точек, отражающих положение постоянно действующих станций (пунктов) наблюдения глобальных навигационных спутниковых систем на сферической карте мира относительно вершин икосаэдра и точек сгущения, формируется выборка постоянно действующих спутниковых станций наблюдения глобальных навигационных спутниковых систем, максимально соответствующая Мировой космической геодезической сети, а спроецированные вершины икосаэдра на описанную вокруг него сферическую карту мира задают положения вершин сферических треугольников, которые являются базовыми для дальнейшего сгущения Мировой космической геодезической сети путем сечения ребер полученных треугольников операциями бисекции и трисекции с получением нового поколения треугольников, сгущая сеть и формируя регулярный (однородный) сеточный каркас Мировой космической геодезической сети необходимой плотности.
| СПОСОБ СОЗДАНИЯ КОСМИЧЕСКОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ | 1997 |
|
RU2124217C1 |
| Способ построения пространственной геодезической сети в виде цепочки треугольников и угломерный прибор для его осуществления | 1986 |
|
SU1613858A1 |
| CN 105091850 B, 04.05.2018 | |||
| US 7872647 B2, 18.01.2011 | |||
| CN 108205148 A, 26.06.2018. | |||
Авторы
Даты
2022-07-25—Публикация
2021-07-30—Подача