Изобретение относится к космической геодезии в частности к способам спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли.
Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) является средством определения планетарного геоида и обеспечивает получение обширной и полной информации о параметрах внешнего гравитационного поля Земли, профилях геоида 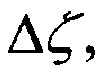 аномалиях силы тяжести Δg, уклонениях отвесной линии (ξ,η).
аномалиях силы тяжести Δg, уклонениях отвесной линии (ξ,η).
Существует зарубежный опыт создания высокоточной модели статического гравитационного поля Земли с высоким разрешением в проекте GOCE (Gravity field and steady-state Ocean Circulation Explorer). Модель представляется через коэффициенты сферических гармоник степени и порядка выше 250, и соответствует коротковолновой его части с пространственным разрешением менее 100 км [18]. Решение данной целевой задачи проекта GOCE основано на совместной обработке измерительной информации следующих сенсорных систем:
- аппаратуры спутниковой навигации (ACH) GPS, осуществляющей наблюдения спутников навигационной системы GPS по линии «спутник-спутник» (hl-SST);
- спутникового гравитационного градиентометра (SGG);
- звездной камеры (Star Tracker).
Эти данные содержат информацию о гравитационном поле Земли почти в глобальном масштабе. Их частотный спектр включает как длинноволновую часть гравитационного поля, определенную по линии «спутник-спутник», так и коротковолновую (высокочастотную) часть, определенную по градиентометрическим измерениям. Исходя из этого, общая матрица нормальных уравнений, составленная для определения параметров гравитационного поля Земли, будет включать в себя матрицу нормальных уравнений, составленную для измерений по линии «спутник-спутник» («высокий-низкий»), и матрицу нормальных уравнений, составленную для градиентометрических измерений.
Но в отличие от предлагаемого способа определения параметров гравитационного поля Земли по наблюдениям в канале «спутник-спутник» в варианте «высокий-низкий» в проекте GOCE использован динамический метод космической геодезии, основанный на точном вычислении орбиты спутника с учетом всех возмущений, действующих на него в полете при использовании аппаратуры спутниковой навигации GPS, спутникового гравитационного градиентометра и звездной камеры.
Существует проблема высокоточного определения параметров модели внешнего гравитационного поля Земли в Общеземной геодезической (геоцентрической) системе координат с применением существующих и перспективных космических геодезических систем при геодезическом и гравиметрическом обеспечении с применением динамического и орбитального метода космической геодезии, которые имеют приоритет в решении задач по определению параметров: модели внешнего гравитационного поля Земли, Общеземной геодезической (геоцентрической) системы координат, положения астрономо-геодезических обсерваторий, установлению Общеземной геодезической системы высот по результатам дальномерных, доплеровских и радиовысотомерных измерений космическими аппаратами до поверхности Мирового океана. Достоинством динамического метода является строгость теории решения указанных задач с учетом корреляционных связей искомых параметров: начальных условий орбитальных дуг, Общеземной геодезической (геоцентрической) системы координат, внешнего гравитационного поля Земли, космической геодезической системы относительно общеземного эллипсоида [2,3,8-14]. Орбитальный метод обладает как достоинством строгости теоретических основ, так и возможностью практической реализации при решении целевых задач с применением существующих и перспективных космических геодезических систем.
Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) предложен для определения параметров глобальных, региональных моделей внешнего гравитационного поля Земли как метод спутникового нивелирования поверхности Земли с применением ГЛОНАСС/GPS-технологий и существующих и перспективных космических геодезических систем работающих в канале «спутник - спутник», вариант «высокий - низкий».
Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ), заключается в определении гармонических коэффициентов - 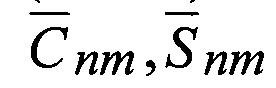 из решения обратной задачи при установлении значения потенциала - W0 на каждую эпоху Т0, основывается на определении положения низкоорбитального космического аппарата (НКА) из состава космической геодезической системы, абсолютным методом спутниковой навигации, посредством измерений прецизионной геодезической аппаратуры потребителя и радиовысотомера (ГАП и РВ), которыми оснащен данный НКА, при этом одновременно с использованием дальномерных и доплеровских измерений между космическими аппаратами ГЛОНАСС и НКА осуществляется: определение координат НКА - xs, ys, zs, относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида, далее с использованием «измеренных величин»: геоцентрического радиуса -
из решения обратной задачи при установлении значения потенциала - W0 на каждую эпоху Т0, основывается на определении положения низкоорбитального космического аппарата (НКА) из состава космической геодезической системы, абсолютным методом спутниковой навигации, посредством измерений прецизионной геодезической аппаратуры потребителя и радиовысотомера (ГАП и РВ), которыми оснащен данный НКА, при этом одновременно с использованием дальномерных и доплеровских измерений между космическими аппаратами ГЛОНАСС и НКА осуществляется: определение координат НКА - xs, ys, zs, относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида, далее с использованием «измеренных величин»: геоцентрического радиуса - 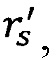 ортометрической высоты -
ортометрической высоты - 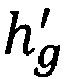 , высоты геоида -
, высоты геоида - 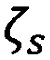 и геодезической высоты - hs, выполняется сравнение полученных значений с вычисленными значениями -
и геодезической высоты - hs, выполняется сравнение полученных значений с вычисленными значениями - 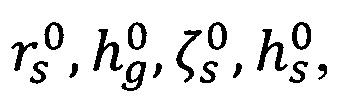 при этом выполняется накопление представительной статистики их разностей и реальных значений потенциала силы тяжести с вычисленными -
при этом выполняется накопление представительной статистики их разностей и реальных значений потенциала силы тяжести с вычисленными - 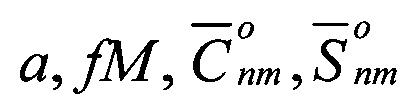 , после чего решается задача определения параметров глобальной модели ВГПЗ по методу наименьших квадратов, где V'PV=min [15, 16, 17]. Данный метод позволит оценить неизвестные величины по результатам накопленных измерений, содержащие случайные ошибки, и найти приближенное представление заданной функции другими (более простыми) функциями при обработке геодезических измерений.
, после чего решается задача определения параметров глобальной модели ВГПЗ по методу наименьших квадратов, где V'PV=min [15, 16, 17]. Данный метод позволит оценить неизвестные величины по результатам накопленных измерений, содержащие случайные ошибки, и найти приближенное представление заданной функции другими (более простыми) функциями при обработке геодезических измерений.
Ожидаемый эффект: использование результатов наблюдений космических аппаратов для применения принципиально новых алгоритмов спутникового нивелирования и получения (уточнения) параметров глобальной модели внешнего гравитационного поля Земли.
Применение Способа спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) позволит определять и уточнять параметры (глобальную модель) ВГПЗ (т.е. гармонические коэффициенты 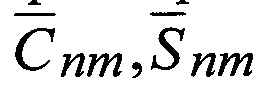 из решения обратной задачи и установить значение потенциала W0 на каждую эпоху Т0).
из решения обратной задачи и установить значение потенциала W0 на каждую эпоху Т0).
Общие признаки предлагаемого изобретения: Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ), представляет собой методику определения параметров ВГПЗ по алгоритмам (1-40), в результате сбора статистической измерительной информации с борта низкоорбитального космического аппарата, с последующей обработкой накопленного массива измеренных и рассчитанных данных с поиском наиболее близкого к истинному значению, решением системы уравнений по методу наименьших квадратов т.е.:
- определяют координаты низкоорбитального КА из состава космической геодезической системы, оснащенного прецизионной геодезической аппаратурой и радиовысотомером, относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида;
- с использованием измеренных величин определяют геоцентрических радиус, ортометрическую высоту, высоту геоида, геодезическую высоту;
- сравнивают определенные значения с вычисленными значениями;
- определяют параметры глобальной модели ВГПЗ по методу наименьших квадратов.
Преимуществом Способа спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) является внедрение нового способа способного решить задачу спутникового нивелирования суши и Мирового океана, а также решать разнообразные геодезические, геофизические и метрологические задачи:
1) повысить точность прогноза положения космических аппаратов (дистанционного зондирования Земли, навигационных спутников, малых спутников, спутников связи, биоспутников, метеорологических спутников, космических станций, космических кораблей, астрономических спутников, разведывательных спутников и др.);
2) повысить эффективность решения целевых задач определения параметров внешнего гравитационного поля Земли, Общеземной геодезической (геоцентрической) системы координат, космической геодезической сети с применением космических геодезических систем (существующих и перспективных);
3) создать глобальную (мировую/планетарную) Общеземную геодезическую систему высот (ОГСВ);
4) повысить эффективность спутникового нивелирования за счет калибровки радиовысотомера на космических аппаратах и, соответственно, повысить точность определения параметров региональной модели внешнего гравитационного поля Земли на территорию Мирового океана;
5) осуществлять мониторинг поверхности Земли, исследования природных ресурсов Земли и т.д.;
6) обеспечить развитие нового метода спутникового геодезического нивелирования с определении глобальной модели ВГПЗ.
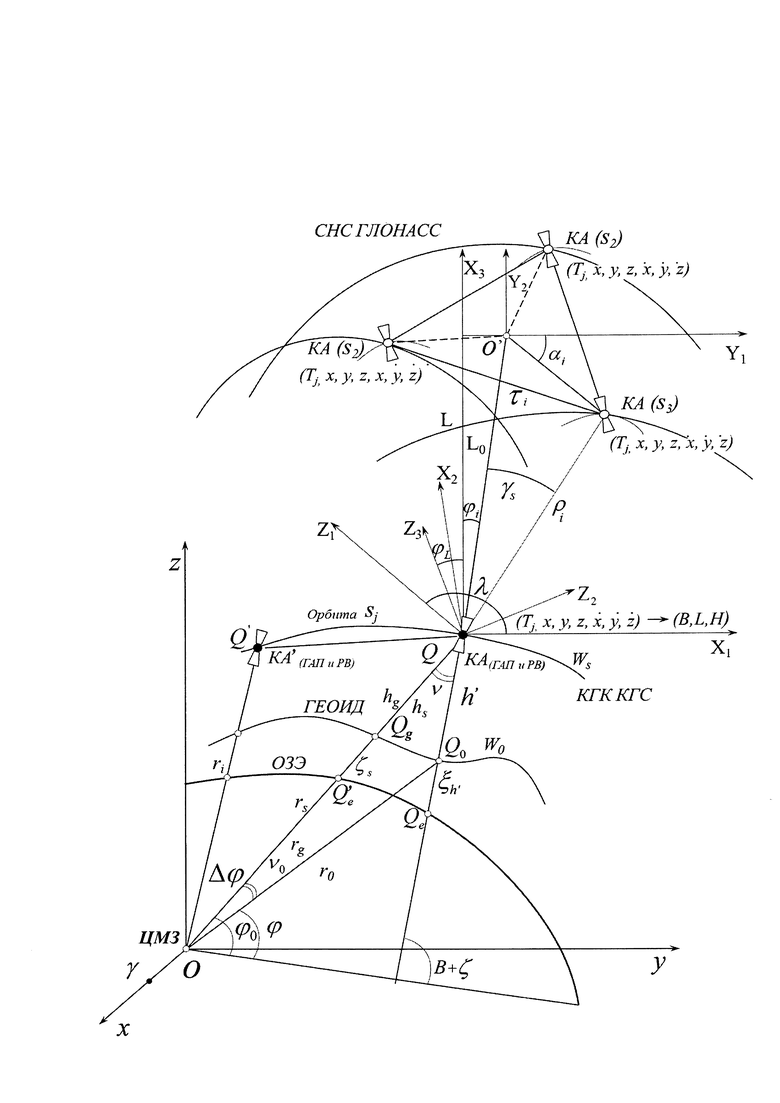
Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) представлена на фиг., где приняты следующие обозначения:
положение 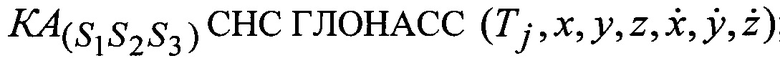 ;
;
точка Q - положения КА, оснащенного прецизионной геодезической аппаратурой потребителя и радиовысотомером, на орбите Sj космической геодезической системы;
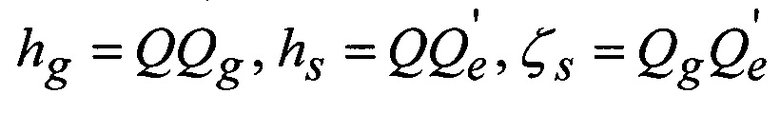 - ортометрическая, геодезическая высоты и высота геоида, соответственно;
- ортометрическая, геодезическая высоты и высота геоида, соответственно;
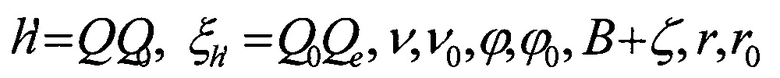 - параметры, характеризующие спутниковое нивелирование поверхности Мирового океана;
- параметры, характеризующие спутниковое нивелирование поверхности Мирового океана;
rs - геоцентрический радиус положения КА (ГАП и РВ) на орбите;
W0, Ws - потенциалы силы тяжести поверхности геоида и орбиты КА;
КА КГС - космический аппарат космической геодезической системы;
ЦМЗ - центр масс Земли;
ОЗЭ - общеземной эллипсоид;
КА (ГАП и РВ) - космический аппарат из состава космической геодезической системы, оснащенный прецизионной геодезической аппаратурой потребителя и радиовысотомером (градиентометром).
В Способе спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) определяются координаты КА (ГАП и РВ) - (xs, ys, zs) относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида с использованием «измеренных величин». Представим теоретические положения по априорной оценке точности определения координат КА (ГАП и РВ) по наблюдениям КА ГЛОНАСС.
Исходя из работы [6] координаты КА в топоцентрической системе:
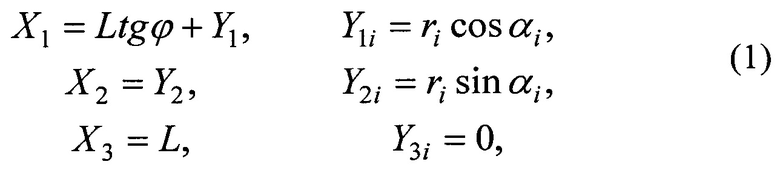
где ri - расстояние от 0 до Si.
Уравнение поправок для измеренного расстояния КА (ГАП и РВ) и КА ГЛОНАСС:
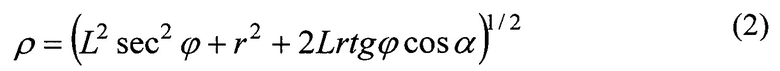
имеет вид
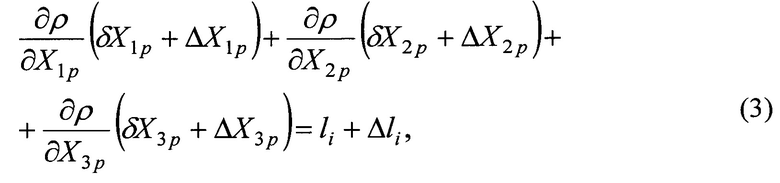
где
δХр, - соответственно случайный и систематический векторы поправок к приближенному вектору положения КА на орбите;
l, Δl - случайная и систематическая части вектора свободных членов.
Ковариационная матрица в координатах систем 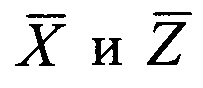 имеет вид
имеет вид
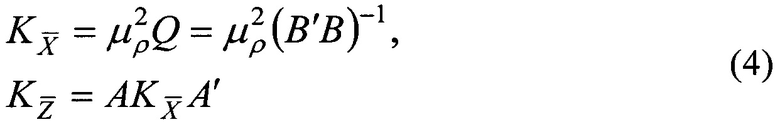
где μр - ср. кв. ошибка единицы веса;
В - матрица коэффициентов уравнений поправок.
Матрица Q=(B'B)-1 и имеет вид:
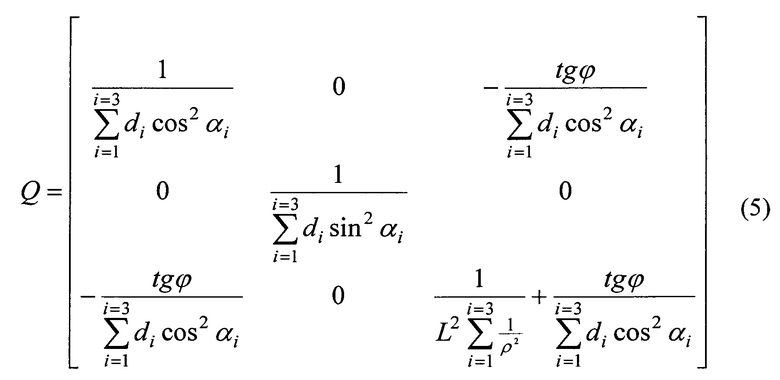
где 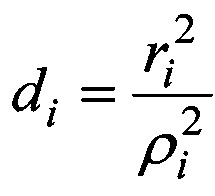 .
.
Матрица преобразования в топоцентрическую СК
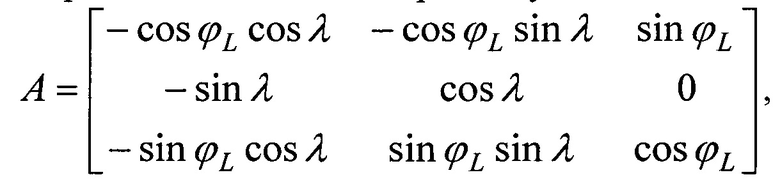
где ϕL, λ - углы между осями координат Z3(H) и X3, Z1 и X1 соответственно.
Среднеквадратические погрешности определения положения по осям системы координат равны соответственно:
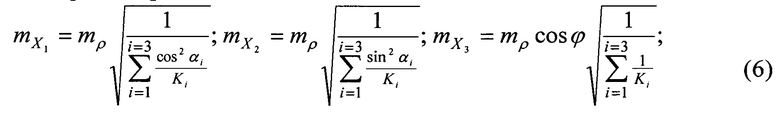
где 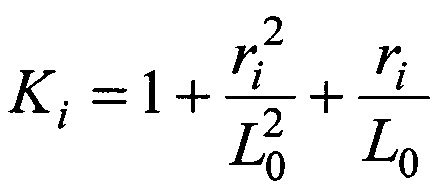 .
.
В топоцентрической горизонтной системе координат (Z1,Z2,Z3=н)
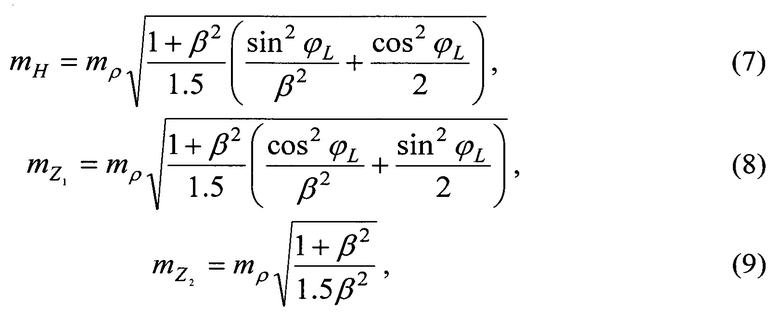
где β=r/L0.
На основании матрицы Q оптимальные геометрические условия для достижения максимальной точности определения положения КА. Его положение определяется с максимальной точностью, если основание пирамиды (треугольник S1S2S3) представляет собой равносторонний треугольник, а угол между ребрами пирамиды равен 90° (угол γs=54,7°).
Таким образом, точность определения положения КА (ГАП и РВ) по наблюдениям КА ГЛОНАСС зависит как от точности самих измерений mp, так и от точности положения КА ГЛОНАСС (mKA).
Оценка точности определения положения КА (ГАП и РВ) на орбите равна
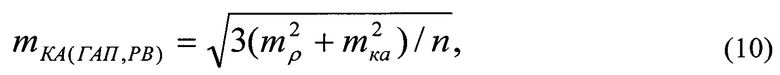
где n - количество оптимальных фигур (S1, S2, S3).
Современная точность определения положения КА ГЛОНАСС, GPS на орбите характеризуется СКП=0.2 м, …, 0.3 м относительно ЦМЗ [14]. При количестве оптимальных созвездий КА (n=9) СКП=0.12, …, 0.06 м, а относительная ошибка «измерения геоцентрического радиуса» (Δrs/rs) составит при: Н=1500 км ≈ 6.6*10-8, 4.4*10-7. НКА=400 км ~ 7.6*10-8, 5.1*10-8 соответственно.
Для снижения влияния ошибок в положении спутников может быть рекомендовано привлечение многоканальных ГАП на КА, наблюдения большого числа спутников ГЛОНАСС, GPS, Beidou и т.п.. Абсолютный метод спутниковой навигации (ГЛОНАСС/GPS) целесообразно широко внедрять при установлении ОСГВ на эпоху Т0 и решении проблемы по решению целевых задач космической геодезической системы.
Представим сущность глобального спутникового геодезического нивелирования с применением результатов определения положения КА (ГАП и РВ) по наблюдениям КА ГЛОНАСС, GPS.
В определении спутникового нивелирования Мирового океана исходим из классического понятия нивелирования с применением радиовысотомера на КА (Q) как определение кратчайшего расстояния QQo между уровенной поверхностью Ws спутникового радиовысотомера Q и уровенной поверхностью Wo геоида, проходящего через нуль-пункт отсчета высот (Qo), фиг.
Уравнения спутникового нивелирования (фиг.) [1,2,3].
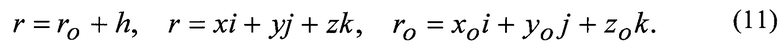
Из уравнений следует, если известен геоцентрический радиус спутникового радиовысотомера и измерен вектор h, то определяется радиус вектор ro подспутниковой точки Q на геоиде, если задан геоид и измерен h, то определяется геоцентрический радиус вектор r радиовысотомера.
При спутниковом геодезическом нивелировании (фиг.) ортометрическая высота hg=QQg - отрезок силовой линии от соответствующего отрезка нормали к ОЗЭ отличается кривизной силовой линии ρ=1,2 млн км, то можно hg отсчитывать по нормали. Аналогично, что отрезок силовой линии HS=QQe, можно заменить геодезической высотой КА относительно ОЗЭ - hs~QQn. Положим, что HS ~ 300 км, В=45°, следовательно, HS-hS=1,8 10-7 м, при HS=1,8 10-7 м. Поэтому не будем делать различия между отрезком силовой линии и от точки Q до поверхности ОЗЭ и геодезической высотой hS.
Уравнения спутникового геодезического нивелирования
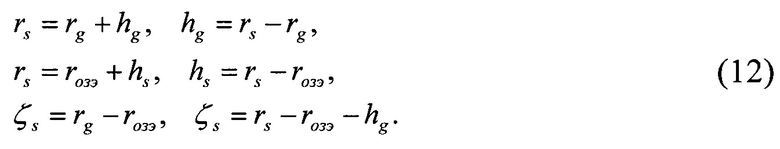
Особый практический интерес при определении глобальной модели ВГПЗ на поверхности Земли представляет вариант при известных «измеренных» геоцентрических радиусах rs(m.Q,Ws) и rg(m.Qg,Wo). В этом варианте можно будет вычислить ортометрические высоты hg и сравнить с «измеренными» его значениями h'g. Набор представительной статистики разностей вычисленных и «измеренных» ортометрических высот КА (ГАП, РВ) можно будет решать разнообразные задачи космической геодезии в космических геодезических системах (существующих и перспективных), осуществлять оценку точности уточнения орбит космических аппаратов различного назначения.
Находим уравнения поправок «измеренных величин»
Пусть функцией измеренной величины, характеризующей спутниковое нивелирование, являются геоцентрический радиус «центр масс Земли-космический аппарат» rs и ортометрическая высота hg, представим в виде

где
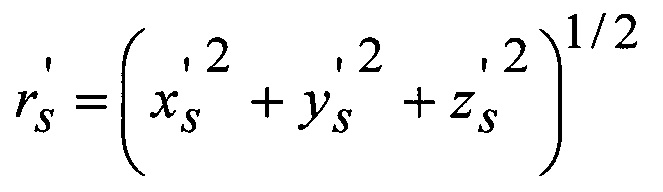 - результат «измерения» геоцентрического радиуса до КА;
- результат «измерения» геоцентрического радиуса до КА;
Δrs,υs - поправки за систематическую и случайную ошибки «измерения» rs;
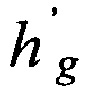 - результат «измерения» ортометрической высоты КА относительно геоида.
- результат «измерения» ортометрической высоты КА относительно геоида.
Счислимые значения:
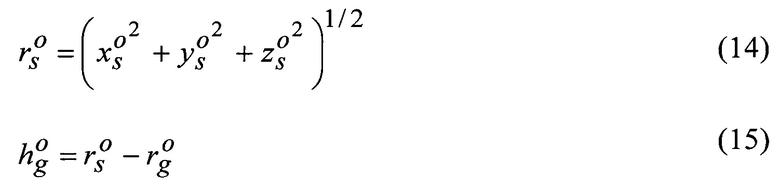
Геоцентрический радиус КА
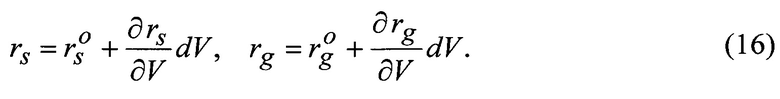
Геоцентрический радиус геоида каждой точки вычисляется по исходным данным 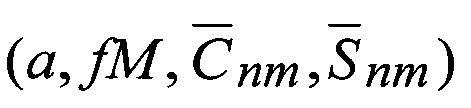 [1].
[1].
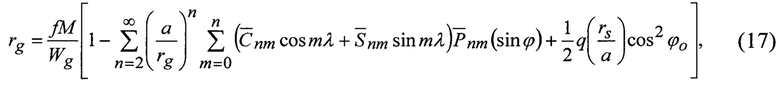
где ϕ,λ - геоцентрическая широта и долгота точки Qg;
q=a3ω2/ƒM, a,ƒM,ω - экваториальный радиус ОЗЭ, геоцентрическая гравитационная постоянная;
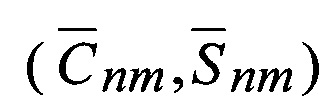 - полностью нормированные коэффициенты степени n и порядка m разложения потенциала силы притяжения [8];
- полностью нормированные коэффициенты степени n и порядка m разложения потенциала силы притяжения [8];
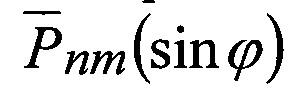 - полностью нормированные полиномы Лежандра.
- полностью нормированные полиномы Лежандра.
С учетом членов первого порядка малости и формул (12,15) для ортометрической высоты дифференциальную формулу представим в виде
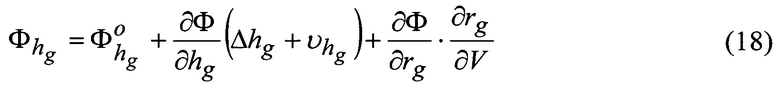
Исходя из формул (13,16,17) и частных производных получим уравнение поправок для «измеренной» ортометрической высоты
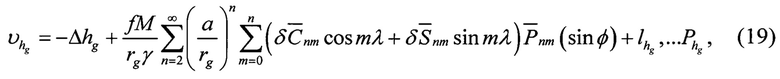
Представленное в явном виде относительно «измерения» h'g,
где 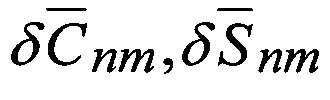 - поправки в нормированные гармонические коэффициенты
- поправки в нормированные гармонические коэффициенты 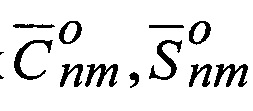 ;
;
γе - ускорение нормальной силы тяжести на экваторе ОЗЭ.
Свободный член равен

где 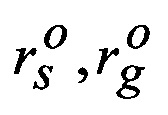 - счислимые значения геоцентрического радиуса КА (ГАП, РВ) и геоцентрического радиуса геоида до точки Qg соответственно; h'g - «измеренная» ортометрическая высота.
- счислимые значения геоцентрического радиуса КА (ГАП, РВ) и геоцентрического радиуса геоида до точки Qg соответственно; h'g - «измеренная» ортометрическая высота.
Уравнение поправок для «измеренной» высоты геоида имеет вид
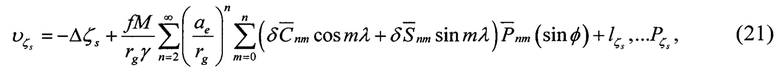
Представленное в явном виде относительно «измеренной» высоты геоида 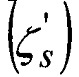 .
.
Свободный член
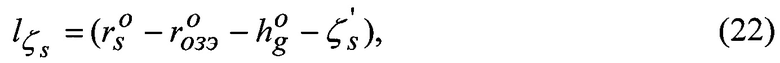
где rS,rОЗЭ - счислимое значение геоцентрического радиуса до КА и ОЗЭ;
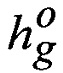 - счислимое значение ортометрической высоты;
- счислимое значение ортометрической высоты;
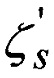 - «измеренная» высота геоида.
- «измеренная» высота геоида.
Уравнение поправок для «измеренного» геоцентрического радиуса 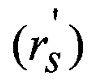 имеет вид
имеет вид
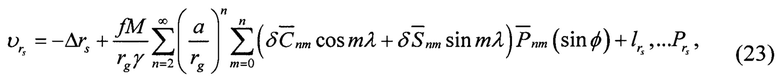
где свободный член
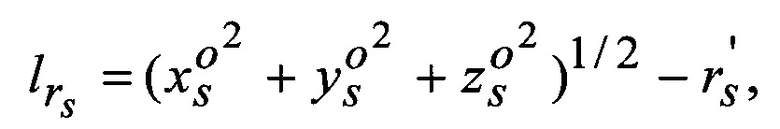
Уравнение поправок для дальномерных измерений ρS между КА ГЛОНАСС и КА из состава космической геодезической системы связывает геоид и геоцентрические радиусы до КА ГЛОНАСС (rг) и до КА (ГАП и РВ) rS
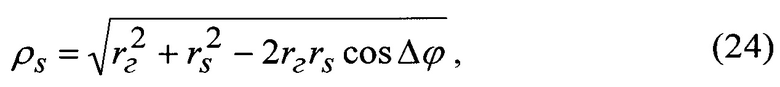
Тогда уравнение спутникового нивелирования имеет вид
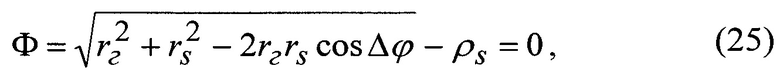
С учетом членов первого порядка малости дифференциальную формулу запишем в виде [3]
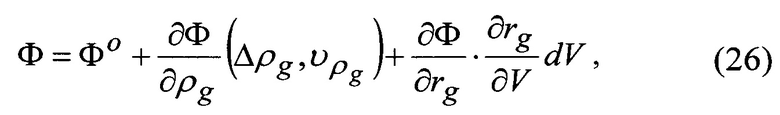
Уравнение поправок для измеренной дальности ρS получим в виде
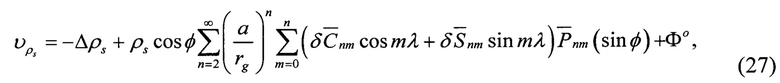
где 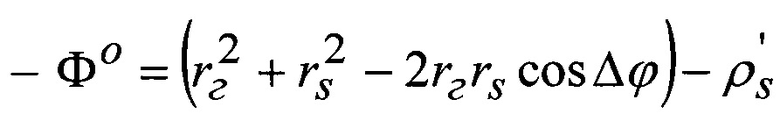 ;
;
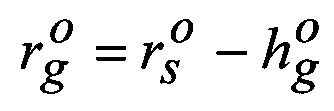 - счислимое значение геоцентрического расстояния до геоида в точке Qg, по исходным данным
- счислимое значение геоцентрического расстояния до геоида в точке Qg, по исходным данным 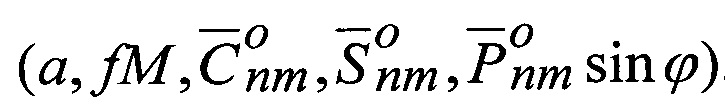 .
.
Для отражения функциональной связи «измеренных величин» и искомых параметров: начальных условий (НУ) орбитальных дуг и параметров модели ВГПЗ, представим уравнение связи «измеренных» геоцентрических радиусов roj с искомыми НУ орбитальной дуги и параметрами ВГПЗ с использованием формулы Брунса в виде
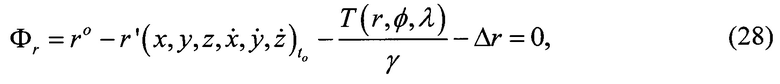
где
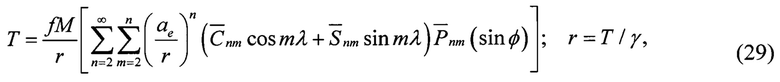
Исходя из работы [9] функциональная зависимость «измеренных величин» L(r1,r2,…,rj) и искомых параметров: к НУ орбитальной дуги (S) в ИГСК - 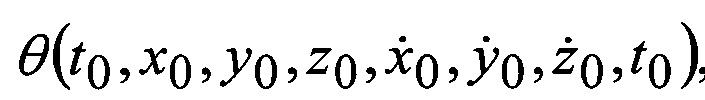 , модели ВГПЗ
, модели ВГПЗ 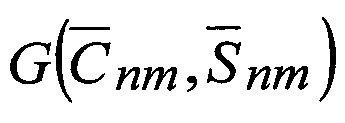 имеет вид
имеет вид

Уравнение поправок для «измеренных» геоцентрических расстояний представим в матричном виде:
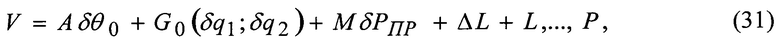
где A, G - матрицы частных производных от «измеренных» rj по искомым поправкам;
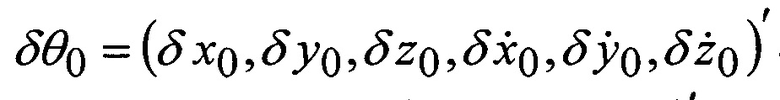 - поправки к НУ орбиты на время t0;
- поправки к НУ орбиты на время t0;
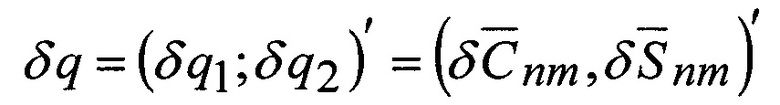
SPПР - вектор поправок в параметры модели приливных явлений
В работах [2] матрица изохронных производных (А) при НУ орбитальных дуг, представлена через кеплеровы элементы орбиты. Приведем НУ орбитальной дуги с учетом результатов «измеренных» геоцентрических радиусов в ИГСК в виде
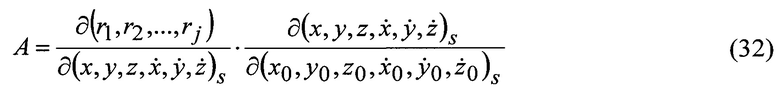
Исходя из работы [9] найдем производные от rj по координатам КА (ГАП и РВ) s
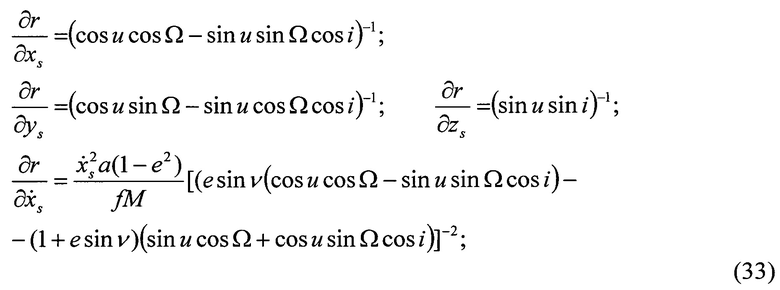
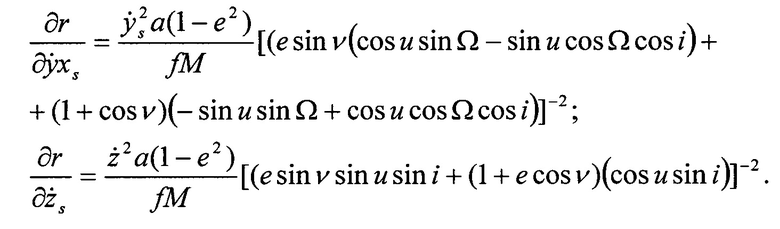
Матрицы частных производных от «измеренных» геоцентрических радиусов положения КА (ГАП и РВ) на орбите (S) по искомым нормированным гармоническим коэффициентам ВГПЗ 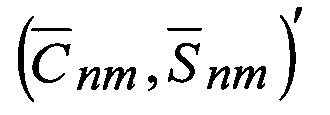 при уточнении возмущающего потенциала силы тяжести имеют вид:
при уточнении возмущающего потенциала силы тяжести имеют вид:

где
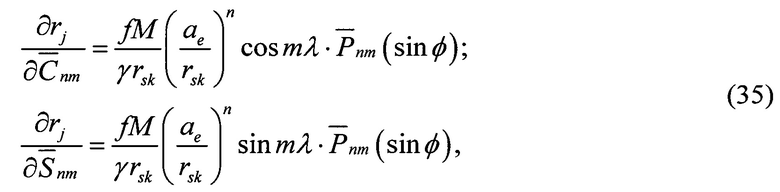
где r,ϕ,λ - геоцентрическое расстояние, широта и долгота положения КА (ГАП и PB)S на орбите;
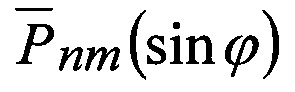 - нормированная функция Лежандра.
- нормированная функция Лежандра.
В соответствии с (ПЗ-90.11) [12] зональные коэффициенты 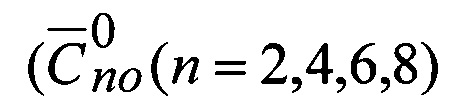 вычисляются с использованием ФГПЗ (ƒM,a,α,ω) и не уточняются, другие коэффициенты уточняются с
вычисляются с использованием ФГПЗ (ƒM,a,α,ω) и не уточняются, другие коэффициенты уточняются с 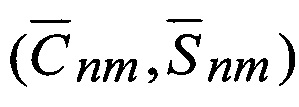 .
.
Уравнение поправок для «измеренного» геоцентрического радиуса КА (rsj) запишем в виде
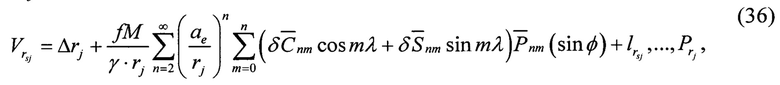
где свободный член
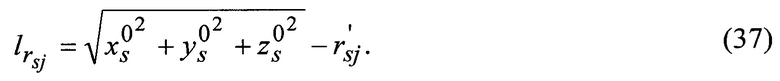
Вместо уравнения поправок для (rsj) в орбитальном методе можно использовать уравнение поправок для «измеренных» ортометрических высот формулы (12,18), высот геоида на ОЗЭ.
Уравнивание «измеренных величин» следует производить с применением многогруппового метода уравнивания по методу наименьших квадратов (методу Гаусса) при (V'PV)=min [15, 16, 17].
Вектор искомых поправок в гармонические коэффициенты 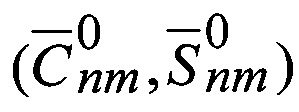 .
.
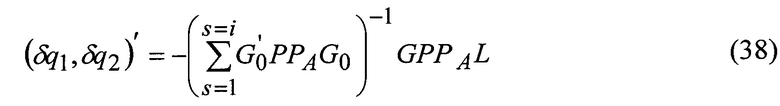
Ковариационная матрица оценки искомых параметров

где
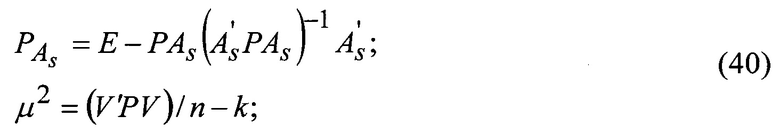
S - количество орбитальных дуг;
(n-k) - количество избыточных измерений.
Техническим результатом применения Способа спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) является определение параметров глобальных, региональных моделей внешнего гравитационного поля Земли, используя данные, полученные спутниковым нивелированием поверхности Земли с применением ГЛОНАСС/GPS-технологий и космических геодезических систем с рядом измерительных приборов на борту, в целях повышения эффективности гравиметрического геодезического обеспечения страны, космических аппаратов в космическом пространстве, развития экономики и наук о Земле.
Список использованных источников
1. Машимов М.М., Планетарные теории геодезии. - М.: Недра, 1982.
2. Машимов М.М., Малец К.В., Смирнов С.А. Динамический метод космической геодезии определения параметров внешнего гравитационного поля Земли по результатам дальномерных, доплеровских и высотомерных измерений. - М.: «Известия ВУЗов», «Геодезия и аэрофотосъемка», №4-5, 1992.
3. Машимов М.М., Методология исследования проблемно-содержательной теории, наилучшим образом воспроизводящей теоретические и практические знания в астрономо-геодезии. - М.: «Известия ВУЗов», «Геодезия и аэрофотосъемка», №2, 2001.
4. Малец К.В., Основные направления развития геодезии в XXI веке. - М.: Геодезисть, №3, (К 150-летию геодезического факультета) 2004.
5. Малец К.В., Лангеман И.П., Гоманов Д.Е. Проблема создания Общеземной геодезической системы высот с применением геоспутниковых технологий и астрономо-геодезических и гравитационных измерений. - М.: ВУНЦ СВ «ОВА ВС РФ», НТС, №62, 2012.
6. Малец К.В., Априорная оценка точности определения пункта по дальномерным наблюдениям ИСЗ. - М.: 29 НИИ, НТС РИО ВТС, №12, 1977.
7. Малец К.В., Смирнов С.А. Основная научная задача геодезии по согласованию фундаментальных постоянных системы геодезических параметров Земли на эпоху Т0. - М.:, ВУНЦ СВ «ОВА ВС РФ», НТС №92, 2017.
8. Малец К.В., Лангеман И.П. Проблема высокоточного определения параметров внешнего гравитационного поля Земли, космической геодезической сети, государственной Общеземной (геоцентрической) системы координат на Единую эпоху Т0 по результатам наблюдений КА КГС. - М.: ВУНЦ СВ «ОВА ВС РФ», ТНС №6, 2018.
9. Малец К.В., Лангеман И.П. Уравнения поправок спутникового нивелирования с применением дальномерных измерений между КА в КГС. - М.: ВУНЦ СВ «ОВА ВС РФ», ТНС №6, 2018.
10. Малец К.В., Лангеман И.П. К проблеме определения региональных моделей внешнего гравитационного поля Земли на территорию Мирового океана орбитальным методом космической геодезии с применением результатов наблюдений КА КГС. - М.: ВУНЦ СВ «ОВА ВС РФ», ТНС №1, 2019.
11. Малец К.В., Смирнов С.А, Рутько И.П., Пигулка С.А. Проблема модернизации и развития Мировой космической геодезической сети Российской Федерации с применением методов и технологий космической геодезии, спутниковой навигации и астрономо-геодезических и гравиметрических измерений. - М.: ВУНЦ СВ «ОВА ВС РФ», СНТА НИЦ (ОиИТ) часть II, 2020.
12. Параметры Земли 1990 года (ПЗ - 90.11). Справочный документ, - М.: ВТУ ГШ, ВС РФ, 2014, с. 52.
13. Пасынков В.В., Применение системы прецизионной навигации для топогеодезического и информационного обеспечения войск. - М.: ОАО НПК «Системы презиционного приборостроения», 2012.
14. Филатов В.Н., Лангеман И.П. Космическая геодезическая система для уточнения геодезических параметров Земли. - М.: ВУНЦ СВ «ОВА ВС РФ», ТНС №1, 2019.
15. Маркузе Ю.И., Клыпин И.А., Учебно-методическое пособие «Уравнивание по методу наименьших квадратов» по курсу «Теория математической обработки геодезических измерений». - М.: МИИГАиК, 2016, с. 50.
16. Коломиец Л.В., Поникарова Н.Ю., Метод наименьших квадратов: метод, указания - Самара: Изд-во Самарского университета, 2017. - 32 с.
17. Куштин И.Ф., Куштин В.И., Инженерная геодезия. Учебник. Ростов-на-Дону: Издательство ФЕНИКС, 2002. - 416 с.
18. GOCE. Mission Requirements Document. GO-RS-ESA-SY-0001. 2000.
Изобретение относится к области спутникового геодезического нивелирования и может быть использовано для определения параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ). Сущность: определяют координаты низкоорбитального космического аппарата относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида. Измеряют геоцентрический радиус, ортометрическую высоту, высоту геоида, геодезическую высоту. Находят разности измеренных значений указанных величин с вычисленными значениями этих величин. Накапливают представительную статистику вычисленных разностей, а также реальных значений потенциала силы тяжести и следующих вычисленных параметров: экваториальный радиус общеземного эллипсоида, геоцентрическая гравитационная постоянная, нормированные гармонические коэффициенты степени n порядка m. Определяют параметры глобальной модели ВГПЗ по методу наименьших квадратов. Технический результат: повышение эффективности определения параметров глобальной модели ВГПЗ. 1 ил.
Способ спутникового геодезического нивелирования с определением параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ), заключается в определении гармонических коэффициентов - 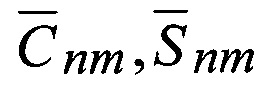 из решения обратной задачи при установлении значения потенциала - W0 на каждую эпоху Т0, основывается на определении положения низкоорбитального космического аппарата (НКА) из состава космической геодезической системы, абсолютным методом спутниковой навигации, посредством измерений прецизионной геодезической аппаратуры потребителя и радиовысотомера (ГАП и РВ), которыми оснащен данный НКА, при этом одновременно с использованием дальномерных и доплеровских измерений между космическими аппаратами ГЛОНАСС и НКА осуществляется: определение координат НКА - xs, ys, zs относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида, далее с использованием «измеренных величин»: геоцентрического радиуса -
из решения обратной задачи при установлении значения потенциала - W0 на каждую эпоху Т0, основывается на определении положения низкоорбитального космического аппарата (НКА) из состава космической геодезической системы, абсолютным методом спутниковой навигации, посредством измерений прецизионной геодезической аппаратуры потребителя и радиовысотомера (ГАП и РВ), которыми оснащен данный НКА, при этом одновременно с использованием дальномерных и доплеровских измерений между космическими аппаратами ГЛОНАСС и НКА осуществляется: определение координат НКА - xs, ys, zs относительно положения центра масс Земли в инерциальной геодезической системе координат и поверхности геоида, далее с использованием «измеренных величин»: геоцентрического радиуса - 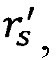 ортометрической высоты -
ортометрической высоты - 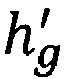 , высоты геоида -
, высоты геоида - 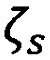 и геодезической высоты - hs выполняется сравнение полученных значений с вычисленными значениями -
и геодезической высоты - hs выполняется сравнение полученных значений с вычисленными значениями - 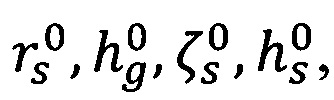 при этом выполняется накопление представительной статистики их разностей и реальных значений потенциала силы тяжести с вычисленными -
при этом выполняется накопление представительной статистики их разностей и реальных значений потенциала силы тяжести с вычисленными - 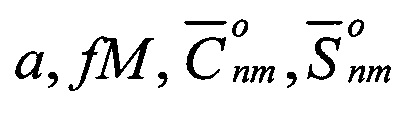 , после чего решается задача определения параметров глобальной модели ВГПЗ по методу наименьших квадратов.
, после чего решается задача определения параметров глобальной модели ВГПЗ по методу наименьших квадратов.
| М.М.Машимов и др | |||
| Динамический метод космической геодезии определения параметров внешнего гравитационного поля Земли по результатам дальномерных, доплеровских и высотомерных измерений / Известия вузов | |||
| Геодезия и аэрофотосъемка, 1992, N4-5, стр.31-39 | |||
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ | 2003 |
|
RU2251127C1 |
| CN 102636818 A, 15.08.2012. | |||
Авторы
Даты
2022-11-15—Публикация
2021-06-10—Подача