Область техники, к которой относится изобретение
Предлагаемое изобретение относится к информационным технологиям и может быть использовано для контроля целостности многомерных массивов данных в системах хранения в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования.
Уровень техники
а) Описание аналогов
Известны способы контроля целостности данных за счет применения криптографических методов: ключевое хэширование, средства электронной подписи (Патент на изобретение RUS №26207030 07.12.2015; Патент на изобретение RUS №2669144 28.11.2017; Патент на изобретение RUS №2680033 22.05.2017; Патент на изобретение RUS №2680350 02.05.2017; Патент на изобретение RUS №2680739 28.11.2017; Патент на изобретение RUS №2686024 25.04.2018; Патент на изобретение RUS №2696425 22.05.2018; Кнут, Д.Э. Искусство программирования для ЭВМ. Том 3 сортировка и поиск [Текст] / Д.Э. Кнут. - М.: «Мир», 1978. - 824 с.; Menezes, A.J. Handbook of Applied Cryptography [Текст] / A.J. Menezes, Paul C. van Oorschot, Scott A. Vanstone. - M.: CRC Press, Inc., 1996. - 816 c.; Biham, E. A framework for iterative hash functions. - HAIFA [Текст] / E.Biham, O.Dunkelman. - M.: HAIFA, ePrint Archive, Report 2007/278. - 20 с.; To же [Электронный ресурс]. - Режим доступа: eprint.iacr.org/2007/278.pdf (July, 2007); Wang, X. How to break MD5 and Other Hash Function [Текст] / X.Wang, H.Yu. - M.: EUROCRYPT 2005, LNCS 3494, Springer-Verlag 2005. - C. 19-35; Bellare, M. New Proofs for NMAC and HMAC: Security without Collision-Resistance [Текст] / M.Bellare. - M.: CRYPTO 2006, ePrint Archive, Report 2006/043. - 31 с.; To же [Электронный ресурс]. - Режим доступа: eprint.iacr.org/2006/043.pdf (2006); Dichenko, S. Two-dimensional control and assurance of data integrity in information systems based on residue number system codes and cryptographic hash functions / S.Dichenko, O.Finko // Integrating Research Agendas and Devising Joint Challenges International Multidisciplinary Symposium ICT Research in Russian Federation and Europe. 2018. P. 139-146; Samoylenko, D. Protection of information from imitation on the basis of crypt-code structures / D. Samoylenko, M. Eremeev, O. Finko, S. Dichenko // Advances in Intelligent Systems and Computing. 2019. №889. P. 317-331; Диченко, С.А. Концептуальная модель обеспечения целостности информации в современных системах хранения данных. Информатика: проблемы, методология, технологии. Сборник материалов XIX международной научно-методической конференции. Под ред. Д.Н. Борисова. Воронеж. - 2019. - С. 697-701; Диченко, С.А. Контроль и обеспечение целостности информации в системах хранения данных. Наукоемкие технологии в космических исследованиях Земли. - 2019. - Т. 11. - №1. - С.49-57; Диченко, С.А. Гибридный крипто-кодовый метод контроля и восстановления целостности данных для защищенных информационно-аналитических систем / С. Диченко, О. Финько // Вопросы кибербезопасности. - 2019. - №6(34). - С. 17-36), для которых типичны две обобщенные схемы вычисления значений хэш-функции: для каждого подблока в блоке данных и для целого блока данных.
Недостатками данных способов являются:
- высокая избыточность при контроле целостности последовательности подблоков блока данных небольшой размерности (при вычислении для каждого подблока блока данных отдельного значения хэш-функции);
- отсутствие возможности обнаружения и локализации искаженных подблоков блока данных (при хэшировании целого блока данных и получении одного общего значения хэш-функции).
б) Описание ближайшего аналога (прототипа)
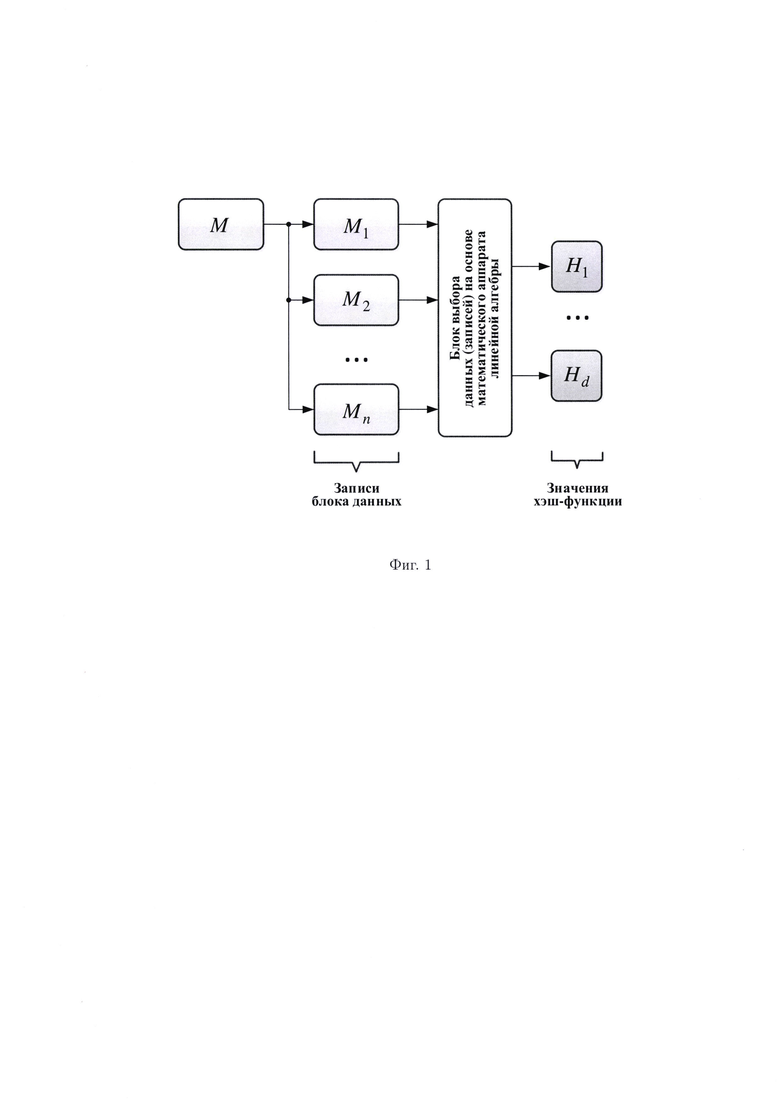
Наиболее близким по технической сущности к заявленному изобретению (прототипом) является способ обеспечения необходимого уровня защищенности (целостности) данных на основе множества хэш-кодов (фиг. 1), полученных с помощью стандартной процедуры реализации хэш-функции от совокупности данных (записей) в порядке, определенном специальной процедурой выбора записи, основанной на математическом аппарате линейной алгебры (линейных систем хэш-кодов) (Финько, О.А. Обеспечение целостности данных в автоматизированных системах на основе линейных систем хэш-кодов / О.А. Финько, С.В. Савин // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. - 2015. - №114. - С. 796-811), где контроль целостности данных (обнаружение ошибки) по аналогии с линейными кодами осуществляется за счет вычисления синдрома, при проверке которого можно сделать вывод о наличии или отсутствии ошибки. Применение линейной системы хэш-кодов позволяет обнаружить и локализовать подблок блока данных с признаками нарушения целостности без необходимости введения высокой избыточности контрольной информации.
Недостатком известного способа является отсутствие возможности обнаружения и локализации двух и более подблоков блока данных с признаками нарушения целостности без вычисления и введения для этого дополнительной контрольной информации.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение
Целью настоящего изобретения является разработка способа контроля целостности данных на основе применения криптографических хэш-функций к защищаемым блокам данных с возможностью обнаружения и локализации двух и более подблоков блока данных с признаками нарушения целостности без вычисления и введения для этого высокой избыточности контрольной информации.
б) Совокупность существенных признаков
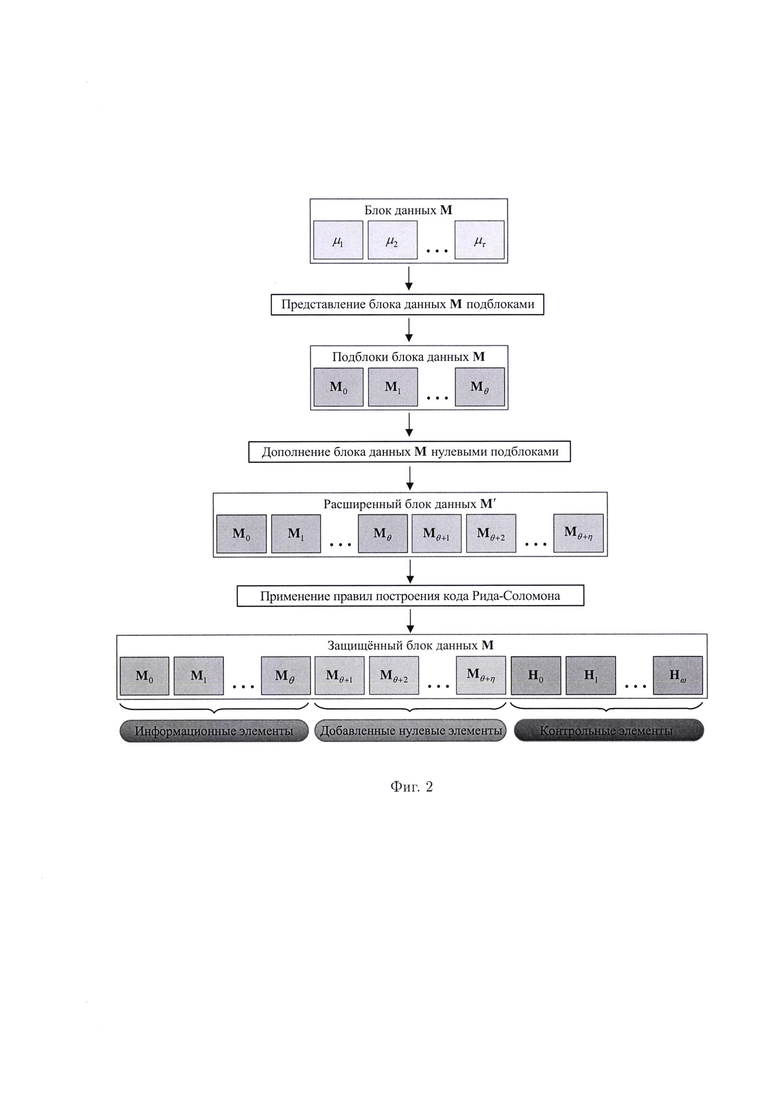
Поставленная цель достигается тем, что в известном способе контроля целостности данных, заключающемся в том, что обнаружение и локализация одного из подблоков M1, М2, …, Mn блока данных М с нарушением целостности обеспечиваются посредством применения линейной системы хэш-кодов, позволяющей за счет вычисления значений H1, …, Hd хэш-функции, где d<n, определять признаки нарушения целостности данных, подлежащих защите, в представленном же способе блок данных М многомерного массива, представленный в виде вектора, для осуществления контроля целостности содержащихся в нем данных фрагментируется на подблоки данных M0, M1, …, Мθ фиксированной длины m, в соответствии с которой выбирается расширенное двоичное поле Галуа GF(2m), каждый ненулевой элемент которого представляется как степень α, при этом бесконечное множество его элементов образуется из начального множества {0, 1, α} путем последовательного умножения элементов на α, после чего задается порождающий полином g(х) соответствующего кода Рида-Соломона, а исходный блок данных М записывается с помощью примитивных элементов, для получения требуемой размерности которого в зависимости от информационной длины k=2m-1-2t выбранного кода Рида-Соломона при необходимости дополняется η=k-θ-1 нулевыми подблоками, где t равно количеству обнаруживаемых и локализуемых подблоков данных с признаками нарушения целостности, полученный при этом расширенный блок данных М' содержит подблоки M0, M1, …, Mθ, Mθ+1, …, Мθ+η, которые представляются элементами GF(2m), в результате кодирования которых образуется кодовый полином с(х), определяется полином ошибки е(х), вычисляются значения Н0, Н1, …, Нω хэш-функции и синдромы Sϖ в точках αϖ, где ϖ=1, 2, …, 2t, проверка которых позволяет определить признаки, характеризующие нарушение целостности подблоков М0, М1, …, Мθ блока данных М многомерного массива, подлежащего защите.
Сопоставительный анализ заявленного решения с прототипом показывает, что предлагаемый способ отличается от известного тем, что поставленная цель достигается за счет представления блока данных М многомерного массива, подлежащего защите, с помощью примитивных элементов, полученный при этом расширенный блок данных М' содержит подблоки данных М0, М1, …, Мθ, Mθ+1,…, Мθ+η, при кодировании которых выбранным кодом Рида-Соломона образуется кодовый полином с(х), вычисляются значения Н0, H1, …, Hω хэш-функции, далее определяется полином ошибки е(х) и вычисляются синдромы Sϖ в точках αϖ, проверка которых позволяет определить признаки, характеризующие нарушение целостности подблоков М0, М1, …, Мθ в блока данных М многомерного массива, подлежащего защите.
Контроль целостности подблоков М0, М1, …, Мθ блока данных М многомерного массива, подлежащего защите, будет осуществляться путем сравнения значений хэш-функции, вычисленных при запросе на использование защищаемых данных, и эталонных значений, что позволит в момент времени ϕ в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования определить подблоки данных с признаками нарушения целостности. Новым является то, что в предлагаемом способе блок данных М многомерного массива фрагментируется на подблоки данных M0, M1, …, Мθ фиксированной длины m, в соответствии с которой выбирается расширенное двоичное поле Галуа GF(2m). Новым является то, что блок данных М многомерного массива записывается с помощью примитивных элементов, для получения требуемой размерности которого в зависимости от информационной длины k=2m-1-2t выбранного кода Рида-Соломона при необходимости дополняется η=k-θ-1 нулевыми подблоками, полученный при этом расширенный блок данных М' содержит подблоки М0, М1, …, Мθ, Mθ+1, …, Мθ+η, которые представляются элементами GF(2m). Новым является то, что в результате кодирования подблоков данных М0, M1, …, Мθ, Мθ+1,…, Mθ+η образуется кодовый полином с(x), определяется полином ошибки е(х), а также вычисляются значения Н0, H1, …, Нω хэш-функции и синдромы Sϖ в точках αϖ, с помощью которых определяются признаки, характеризующие нарушение целостности подблоков M0, M1, …, Мθ блока данных М многомерного массива, подлежащего защите.
в) Причинно-следственная связь между признаками и техническим результатом
Благодаря новой совокупности существенных признаков в способе реализована возможность:
- обнаружения двух и более подблоков блока данных многомерного массива с признаками нарушения целосности без вычисления и введения для этого высокой избыточности контрольной информации в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования;
- локализации обнаруженных подблоков блока данных многомерного массива с признаками нарушения целостности.
Доказательства соответствия заявленного изобретения условиям патентоспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Краткое описание чертежей
Заявленный способ поясняется чертежами, на которых показано: фиг. 1 - схема линейной системы хэш-кодов;
фиг. 2 - схема, иллюстрирующая процедуру контроля целостности многомерных массивов данных на основе правил построения кода Рида-Моломона.
Осуществление изобретения
Блок данных М многомерного массива, подлежащего защите, представленный в виде вектора:
М=[μ1 μ2 … μT]
где  для осуществления контроля целостности содержащихся в нем данных с использованием правил, аналогичных правилам построения кода Рида-Соломона (PC), фрагментируется на подблоки данных фиксированной длины m:
для осуществления контроля целостности содержащихся в нем данных с использованием правил, аналогичных правилам построения кода Рида-Соломона (PC), фрагментируется на подблоки данных фиксированной длины m:
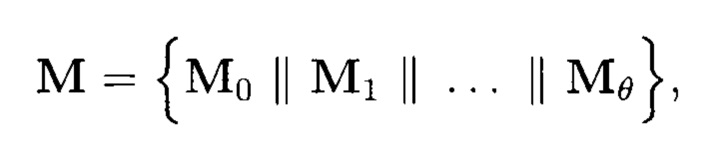
где «⎥⎥» обозначает операцию конкатенации (объединения).
Для построения кода PC используется расширение двоичного поля Галуа GF(2), именуемое полем расширения и обозначаемое как GF(2m).
Каждый ненулевой элемент поля GF(2m) представляется как степень α. При этом бесконечное множество элементов образуется из начального множества {0, 1, α} путем последовательного умножения его элементов на α.
Описание конечного поля осуществляется с помощью примитивного полинома.
Неприводимый полином f(x) порядка ξ будет примитивным, если наименьшим положительным целым числом n, для которого xn-1 делится на f(x), будет n=2m-1. При этом неприводимый полином - это полином который нельзя представить в виде произведения полиномов меньшего порядка.
Посредством примитивного полинома f(x) задается правило понижения степени
f(α)=0
и строится множество элементов поля расширения GF(2m).
Характеристиками кода PC будут являться:
n=2m-1 - кодовая длина (количество подблоков блока данных, подлежащих защите, и подблоков с контрольной информацией);
t - количество исправляемых ошибок (обнаруживаемых и локализуемых подблоков блока данных с признаками нарушения целостности);
k=2m-1-2t - информационная длина (количество подблоков блока данных, подлежащих защите);
r=2t - количество контрольных символов (подблоков с контрольной информацией).
Порождающий полином кода PC g(х) задается формулой:
g(х)=(х-α1)⋅(х-α2) … (х-α2t),
где «⋅» - знак умножения.
Исходный блок данных М многомерного массива, подлежащий защите, записывается с помощью примитивных элементов.
В зависимости от информационной длины:
k=2m-1-2t
выбранного кода PC блок данных М при необходимости дополняется:
η=k-θ-1
нулевыми элементами (подблоками) для получения требуемой размерности и обозначается как:
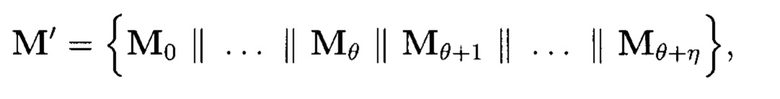
где М' - расширенный блок данных.
Подблоки блока данных М' представляются элементами GF(2m): 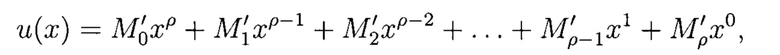
где х - фиктивная переменная, u(х) - информационное слово, ρ=θ+η.
Для возможности осуществления контроля целостности данных выполняется кодирование, при котором вычисляется кодовый полином с(х).
При несистематическом кодировании кодовый полином с(х) вычисляется по формуле:
с(х)=u(х)⋅g(х).
В этом случае кодовое слово не содержит в явном виде информационное слово. Элементы исходного блока данных М, подлежащего защите, записываются с помощью примитивных элементов.
При систематическом кодировании используется типовой алгоритм кодирования для систематических циклических кодов:
- выполняется сдвиг информационного полинома u(х) в крайние старшие разряды кодового слова посредством умножения полинома u(х) на xr;
- полученный полином xr⋅u(х) делится на порождающий полином g(х) для получения остатка от деления р(х);
- искомый кодовый полином с(х) определяется по формуле:
с(х)=xr⋅u(х)+р(х).
В случае систематического кодирования кодовое слово в явном виде содержит информационное слово. Кодовое слово можно записать как:

где Hi - контрольные элементы, i=0, 1, …, ω; ω=r-1.
После кодирования блока данных М, подлежащего защите, данные могут быть отправлены на хранение.
При запросе данных на использование выполняется декодирование.
Пусть полином ошибки равен:

При условии, что произошло ν ошибок, где
0≤ν≤t,
позиции ошибок обозначаются как
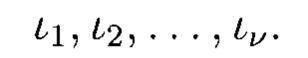
Тогда полином ошибок примет вид:

где  - значение ϕ-й ошибки.
- значение ϕ-й ошибки.
Необходимо найти:
- количество ошибок ν (подблоков блока данных с признаками нарушения целостности);
- позиции ошибок  (подблоков блока данных с признаками нарушения целостности);
(подблоков блока данных с признаками нарушения целостности);
- значения ошибок  (при необходимости восстановления целостности подблоков блока данных).
(при необходимости восстановления целостности подблоков блока данных).
Пусть ν(x)=с(х)+е(х) - полином, полученный при запросе данных, подлежащих защите, на использование.
Вычислим значения синдромов Sϖ в точках αϖ:
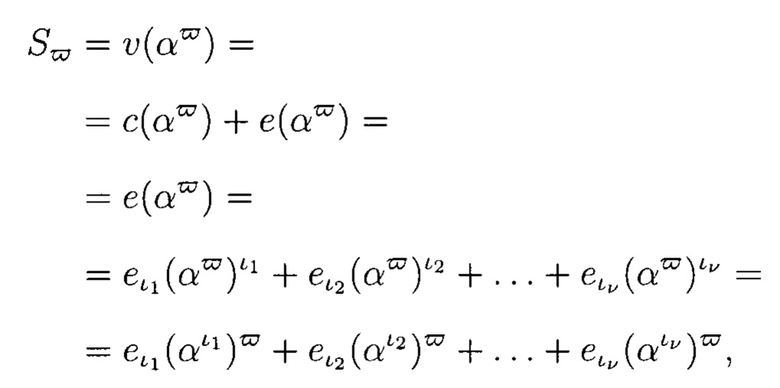
где ϖ=1, 2, …, 2t.
Вводятся обозначения 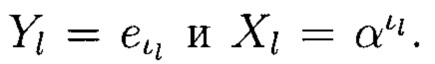 Вычисляются значения
Вычисляются значения 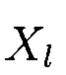 и логарифмируются по основанию α. Определяются все позиции ошибок
и логарифмируются по основанию α. Определяются все позиции ошибок  . Получим систему:
. Получим систему:
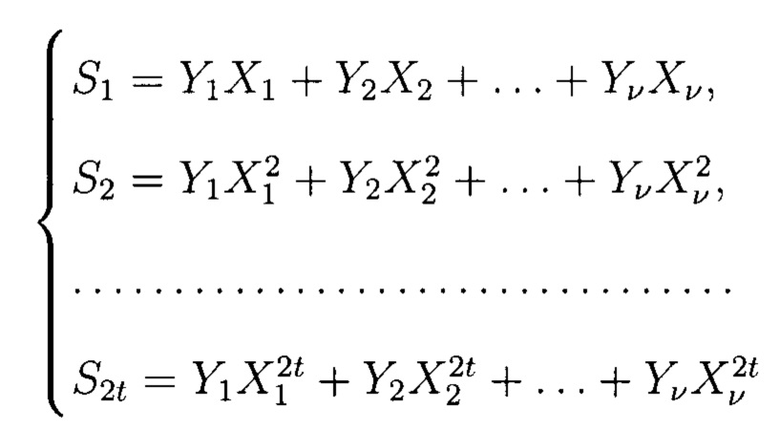
из 2t нелинейных уравнений относительно ν неизвестных локаторов ошибок X1, …, Хν и ν неизвестных значений ошибок Y1, …, Yν. При решении данной системы обнаружим ν ошибок, в случае необходимости исправим их. При этом изначально найдем значения локаторов ошибок, подставим их в систему и получим линейную систему относительно значений ошибок.
Рассмотрим полином:
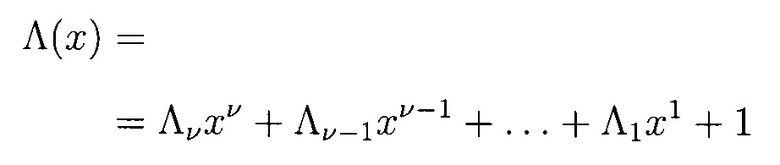
и подберем его коэффициенты так, чтобы его корнями являлись значения 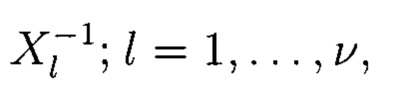 для выполнения равенства:
для выполнения равенства:
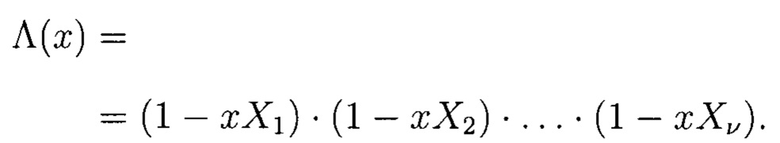
Выразим 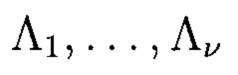 через компоненты синдрома S1, …, S2t и получим систему линейных уравнений:
через компоненты синдрома S1, …, S2t и получим систему линейных уравнений:

где j=1, …, ν. Запишем ее в матричном виде:
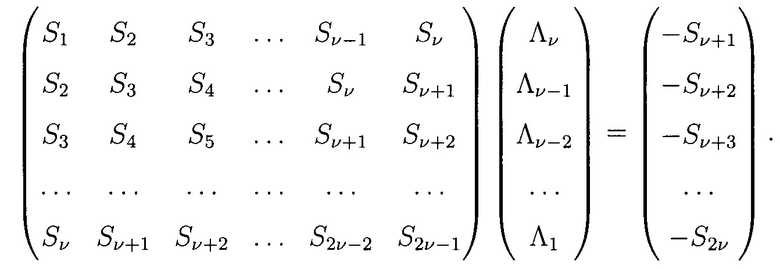
Если произошло ν ошибок, то матрица:
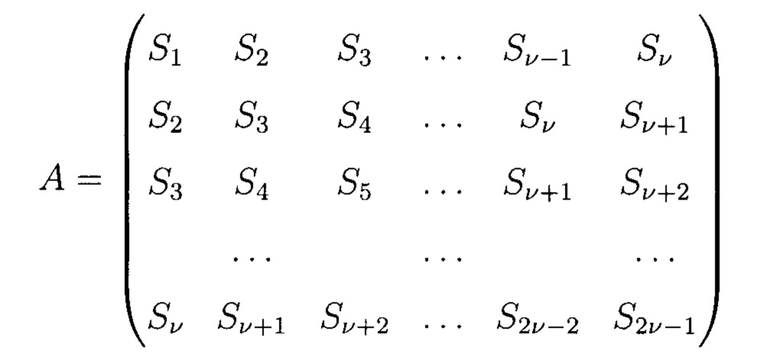
невырождена, следовательно, система разрешима.
Пример.
Дан блок данных М многомерного массива
М=[1 0 1 1 0 1 1 1 1 1 0 0 0 1 0 1].
Фрагментируем блок данных М на подблоки данных фиксированной длины m.При m=4 получим следующий набор подблоков:
М0=[1 0 1 1],
M1=[0 1 1 1],
М2=[1 1 0 0],
М3=[0 1 0 1].
Полученные подблоки данных имеют четырехбитную размерность (m=4), следовательно, для построения кода PC необходимо поле расширения GF(24) двоичного поля Галуа GF(2).
Характеристики кода PC:
n=2m-1=24-1=15 - кодовая длина (количество подблоков блока данных, подлежащих защите, и подблоков с контрольной информацией);
t=2 - количество исправляемых ошибок (обнаруживаемых и локализуемых подблоков блока данных с признаками нарушения целостности);
k=n-2t=15-4=11 - информационная длина (количество подблоков блока данных, подлежащих защите);
r=2t=4 - количество контрольных символов (подблоков с контрольной информацией).
Опишем конечное поле с помощью примитивного полинома:
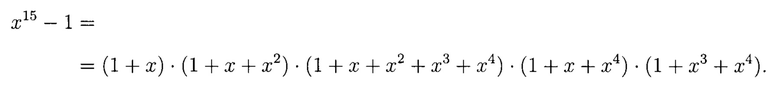
Проверим неприводимый полином  на примитивность, то есть будет ли он делителем
на примитивность, то есть будет ли он делителем
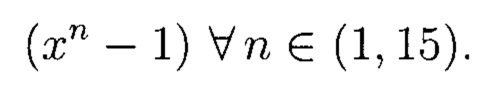
Так как x15-1 делится на 1+х+x4, то повторив вычисления, можно проверить, что ∀n∈(1,15) полином xn-1 не делиться на полином f(x), следовательно, полином 1+х+х4 является примитивным.
Зададим правило понижения степени:
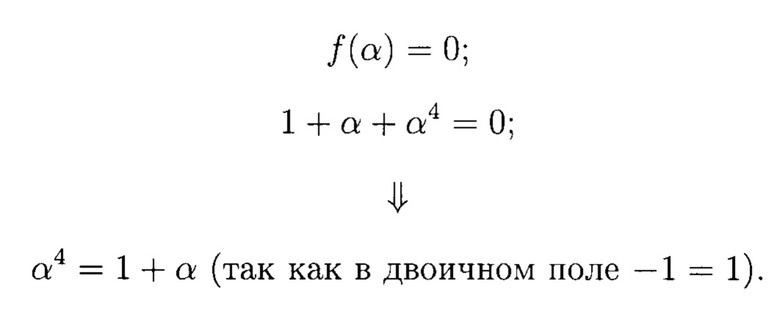
Выразим примитивные элементы поля через базисные элементы α0, α1, α2, α3 и правило понижения степени.
Получим:
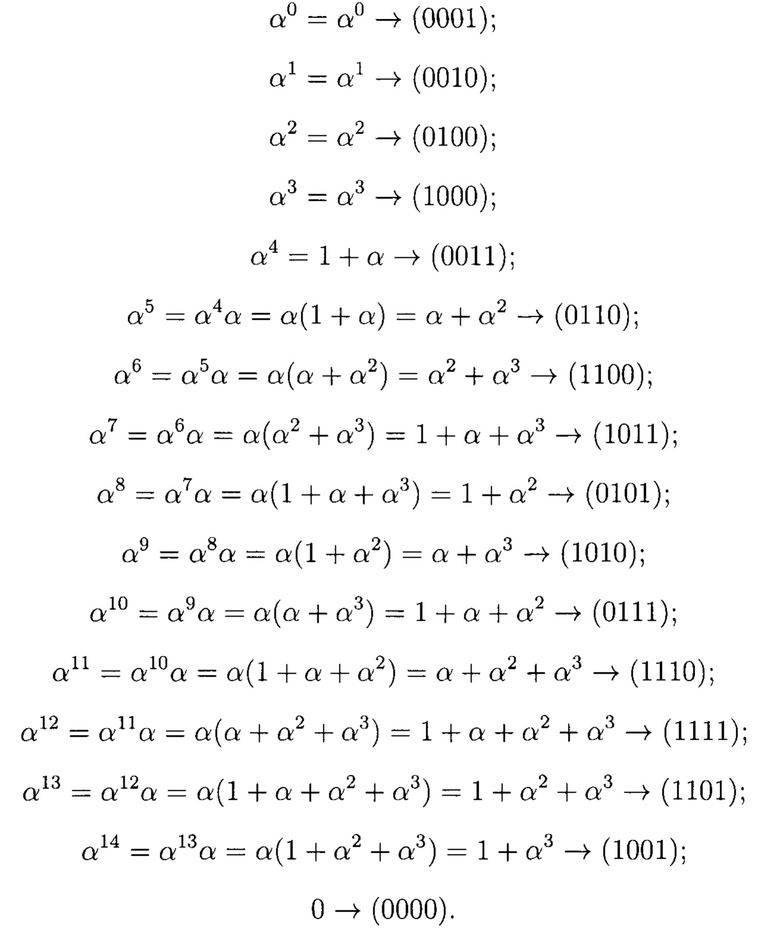
Кодирование.
Порождающий полином равен:
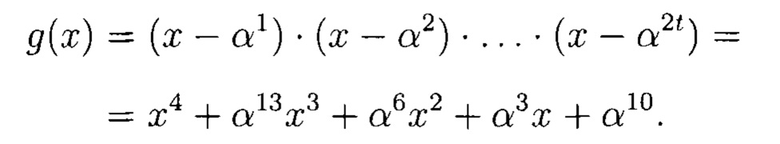
Запишем исходный блок данных М с помощью примитивных элементов:
M{α7 α10 α6 α8}
В рассматриваемом (15,11)-коде PC информационная длина равна k=11.
Так как блок данных М, подлежащий защите, имеет четыре элемента (подблока данных), дополним его
η=11-3-1=7
нулевыми элементами.
Получим:
М'={α7α10α6α80000000}.
Подблоки блока данных М' представим элементами GF(24):
u(х)=α7x10+α10x9+α6х8+α8х7.
Выполним несистематическое кодирование, где полином кодового слова вычисляется по формуле:
v(x)=u(х)⋅g(х)
и равен:
v(x)=α7х14+х13+α2х12+α4х11+α9х10+α8х9+α6х8+α3х7, а соответствующий ему вектор:
v=(α7,1,α2,α4,α9,α8,α6,α3,0,0,0,0,0,0,0).
Исходный блок данных М=[1011011111000101] преобразован посредством применения алгоритма кодирования PC и может быть отправлен на хранение.
При запросе данных для использования выполним декодирование.
Предположим, что была нарушена целостность данных, искажению подверглись следующие элементы кодового слова:
v=(α7,1,α2,α4,α9,α8,α6,α3,0,0,0,0,0,0,0).
Принятая комбинация определена формулой:
r=v+е.
Зададим вектор ошибки:
е=(α4,0,0,0,α9,0,0,0,0,0,0,0,0,0,0),
тогда принятая кодовая комбинация:
r=(α3,1,а2,а4,0,α8,α6,α3,0,0,0,0,0,0,0).
При этом в первом случае произошла подмена элемента, во втором случае его удаление.
Перейдем к полиномиальной записи:
е(х)=α4х14+α9х10;
r(х)=α3х14+х13+α2х12+α4х11+α8х9+α6х8+α3х7.
Вычислим компоненты синдрома Sϖ в точках αϖ, ϖ=1, …, 2t (дополнительно проверим компоненты синдрома Sϖ по полиному ошибок е(αϖ)):

Определим число произошедших ошибок, предположим, что произошло ν=2 ошибки и сформируем матрицу А:
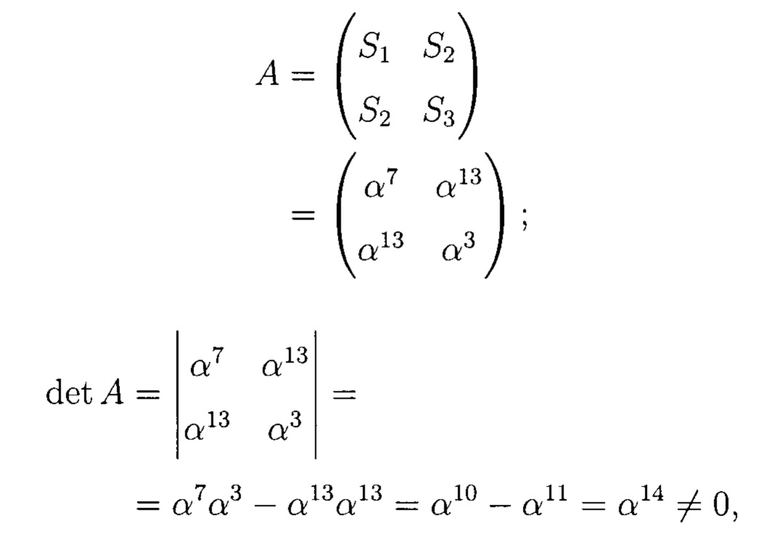
значит, при хранении, действительно, произошло две ошибки.
Локализация ошибки выполняется путем поиска коэффициентов полинома 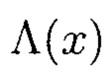 из системы:
из системы:

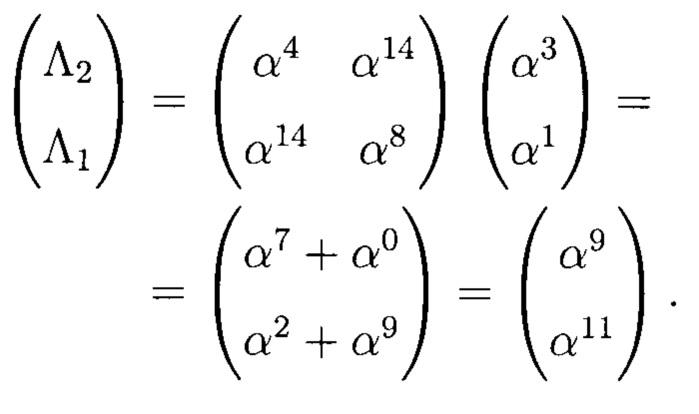
Полином равен:
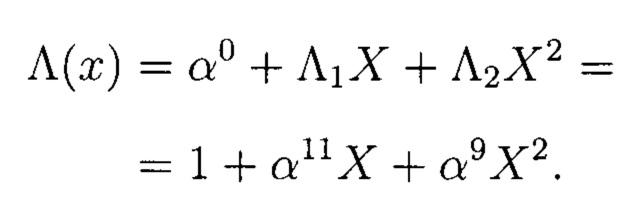
Подставим все степени α и найдем корни многочлена 
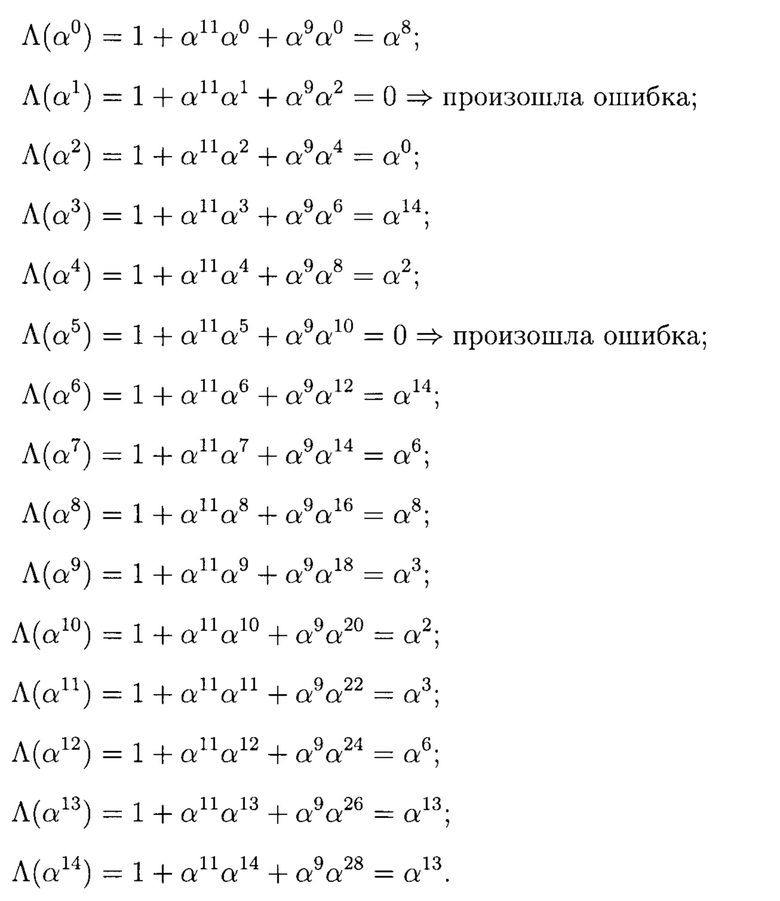
Расположение ошибок является обратной величиной к корням многочлена  то есть корень получаем при
то есть корень получаем при
Х-1=α.
Отсюда
Х1=(α1)-1=α14,
аналогично
Х2=(α5)-1=α10.
Таким образом, были найдены позиции ошибок (подблоки данных с признаками нарушения целостности).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ ДВУМЕРНЫХ КОДОВЫХ КОНСТРУКЦИЙ В КОМПЛЕКСНОЙ ОБЛАСТИ | 2024 |
|
RU2834287C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ НЕРАВНОМЕРНОГО КОДИРОВАНИЯ | 2023 |
|
RU2808759C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2021 |
|
RU2771208C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ПЕРЕХОДА К ПРОСТРАНСТВУ ДАННЫХ С БОЛЬШЕЙ МЕРНОСТЬЮ | 2022 |
|
RU2801082C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ ПРИ ВЫНУЖДЕННОМ СОКРАЩЕНИИ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2801198C1 |
| СПОСОБ ФОРМИРОВАНИЯ КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ В УСЛОВИЯХ СОКРАЩЕНИЯ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2806539C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ДЕГРАДАЦИИ СИСТЕМ ХРАНЕНИЯ | 2022 |
|
RU2801124C1 |
| СПОСОБ ДВУМЕРНОГО КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2018 |
|
RU2696425C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ДАННЫХ С ПОДТВЕРЖДЕННОЙ ЦЕЛОСТНОСТЬЮ | 2021 |
|
RU2771238C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ ПРАВИЛ ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ КОДОВ | 2021 |
|
RU2758194C1 |
Изобретение относится к способу контроля целостности многомерных массивов данных на основе правил построения кода Рида-Соломона. Технический результат заключается в обеспечении контроля целостности данных на основе применения криптографических хэш-функций к защищаемым блокам данных с возможностью обнаружения и локализации двух и более подблоков блока данных с признаками нарушения целостности без вычисления и введения для этого высокой избыточности контрольной информации. В способе блок данных М многомерного массива, представленный в виде вектора, для осуществления контроля целостности содержащихся в нем данных фрагментируется на подблоки данных М0, M1, …, Мθ фиксированной длины m, в соответствии с которой выбирается расширенное двоичное поле Галуа GF(2m), каждый ненулевой элемент которого представляется как степень α, при этом бесконечное множество его элементов образуется из начального множества {0, 1, α} путем последовательного умножения элементов на α, после чего задается порождающий полином g(х) соответствующего кода Рида-Соломона, а исходный блок данных М записывается с помощью примитивных элементов, для получения требуемой размерности которого в зависимости от информационной длины k=2m-1-2t выбранного кода Рида-Соломона при необходимости дополняется η=k-θ-1 нулевыми подблоками, где t равно количеству обнаруживаемых и локализуемых подблоков данных с признаками нарушения целостности, полученный при этом расширенный блок данных М' содержит подблоки M0, M1, …, Mθ, Мθ+1, …, Mθ+η, которые представляются элементами GF(2m), в результате кодирования которых образуется кодовый полином с(х), определяется полином ошибки е(х), вычисляются значения Н0, H1, …, Нω хэш-функции и синдромы Sϖ в точках αϖ, где ϖ=1, 2, …, 2t, проверка которых позволяет определить признаки, характеризующие нарушение целостности подблоков M0, M1, …, Мθ блока данных М многомерного массива, подлежащего защите. 2 ил.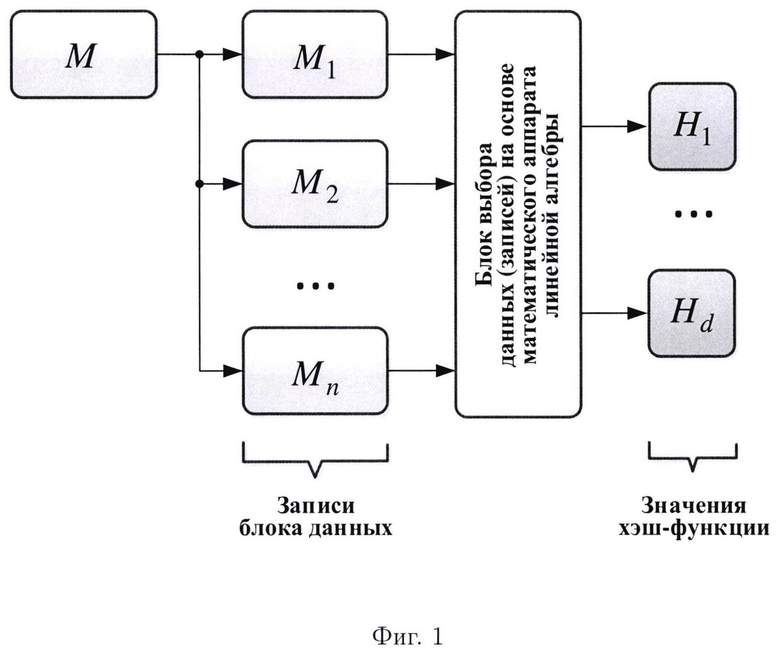
Способ контроля целостности многомерных массивов данных на основе правил построения кода Рида-Соломона, заключающийся в том, что обнаружение и локализация одного из подблоков M1, М2, …, Mn блока данных М с нарушением целостности обеспечиваются посредством применения линейной системы хэш-кодов, позволяющей за счет вычисления значений Н1, …, Hd хэш-функции, где d<n, определять признаки нарушения целостности данных, подлежащих защите, отличающийся тем, что блок данных М многомерного массива, представленный в виде вектора, для осуществления контроля целостности содержащихся в нем данных фрагментируется на подблоки данных М0, M1, …, Мθ фиксированной длины m, в соответствии с которой выбирается расширенное двоичное поле Галуа GF(2m), каждый ненулевой элемент которого представляется как степень α, при этом бесконечное множество его элементов образуется из начального множества {0, 1, α} путем последовательного умножения элементов на α, после чего задается порождающий полином g(х) соответствующего кода Рида-Соломона, а исходный блок данных М записывается с помощью примитивных элементов, для получения требуемой размерности которого в зависимости от информационной длины k=2m-1-2t выбранного кода Рида-Соломона при необходимости дополняется η=k-θ-1 нулевыми подблоками, где t равно количеству обнаруживаемых и локализуемых подблоков данных с признаками нарушения целостности, полученный при этом расширенный блок данных М' содержит подблоки M0, M1, …, Mθ, Мθ+1, …, Mθ+η, которые представляются элементами GF(2m), в результате кодирования которых образуется кодовый полином с(х), определяется полином ошибки е(х), вычисляются значения Н0, H1, …, Нω хэш-функции и синдромы Sϖ в точках αϖ, где ϖ=1, 2, …, 2t, проверка которых позволяет определить признаки, характеризующие нарушение целостности подблоков M0, M1, …, Мθ блока данных М многомерного массива, подлежащего защите.
| СПОСОБ ДВУМЕРНОГО КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2018 |
|
RU2696425C1 |
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2017 |
|
RU2680033C2 |
| СПОСОБ И СИСТЕМА РАСПРЕДЕЛЕННОГО ХРАНЕНИЯ ВОССТАНАВЛИВАЕМЫХ ДАННЫХ С ОБЕСПЕЧЕНИЕМ ЦЕЛОСТНОСТИ И КОНФИДЕНЦИАЛЬНОСТИ ИНФОРМАЦИИ | 2017 |
|
RU2680350C2 |
| СПОСОБ МНОГОУРОВНЕВОГО КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2019 |
|
RU2707940C1 |
| СПОСОБ КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2017 |
|
RU2680739C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ И ПОДЛИННОСТИ ЭЛЕКТРОННЫХ ДОКУМЕНТОВ ТЕКСТОВОГО ФОРМАТА, ПРЕДСТАВЛЕННЫХ НА ТВЕРДЫХ НОСИТЕЛЯХ ИНФОРМАЦИИ | 2015 |
|
RU2591655C1 |
| СПОСОБ КОМПЛЕКСНОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2005 |
|
RU2292122C1 |
| US 10613935 B2, 07.04.2020. | |||
Авторы
Даты
2022-12-14—Публикация
2021-11-17—Подача