Область техники, к которой относится изобретение
Предлагаемое изобретение относится к информационным технологиям и может быть использовано для контроля целостности данных в системах хранения в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования.
Уровень техники
а) Описание аналогов
Известны способы контроля целостности данных за счет применения криптографических методов: ключевое хэширование, средства электронной подписи (Патент на изобретение RUS №2680033,14.02.2019; Патент на изобретение RUS №2680350,19.02.2019; Патент на изобретение RUS №2680739, 26.02.2019; Патент на изобретение RUS №2696425, 02.08.2019; Патент на изобретение RUS №2707940, 02.12.2019; Патент на изобретение RUS №2726930, 16.07.2020; Патент на изобретение RUS №2730365, 21.08.2020; Патент на изобретение RUS №2758194, 26.10.2021; Патент на изобретение RUS №2758943, 03.11.2021; Патент на изобретение RUS №2759240, 11.11.2021; Патент на изобретение RUS №2771146, 27.04.2022; Патент на изобретение RUS №2771208, 28.04.2022; Патент на изобретение RUS №2771209, 28.04.2022; Патент на изобретение RUS №2771236, 28.04.2022; Патент на изобретение RUS №2771238, 28.04.2022; Патент на изобретение RUS №2771273, 29.04.2022; Патент на изобретение RUS №2774099, 15.06.2022; Патент на изобретение RUS №2785484, 08.12.2022; Патент на изобретение RUS №2785800, 13.12.2022; Патент на изобретение RUS №2786617, 22.12.2022; Патент на изобретение RUS №2793782, 06.04.2023; Шеннон, К. Работы по теории информации и кибернетике / К.Шеннон. - М.: Изд-во иностранной литературы, 1963. -829 с.; Шнайер, Б. Секреты и ложь. Безопасность данных в цифровом мире / Б. Шнайер. - СПб.: Питер, 2003. - 367 с.), для которых типичны две обобщенные схемы вычисления значений хэш-функции: для каждого подблока в блоке данных и для целого блока данных.
Недостатками данных способов являются:
- высокая избыточность при контроле целостности последовательности подблоков блока данных небольшой размерности (при вычислении для каждого подблока блока данных отдельного значения хэш-функции);
- отсутствие возможности обнаружения и локализации искаженных подблоков блока данных (при хэшировании целого блока данных и получении одного общего значения хэш-функции);
- необходимость в хранении всей контрольной информации (значений хэш-функции), вычисляемой для обеспечения возможности гарантированного (без учета коллизий) контроля целостности данных.
Известны способы контроля целостности данных за счет применения некриптографических методов: кодов, корректирующих ошибки (Морелос-Сарагоса, Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / Р. Морелос-Сарагоса; перевод с англ. В.Б. Афанасьев. - М.: Техносфера, 2006. - 320 с.; Хемминг, Р.В. Теория кодирования и теория информации / Р.В. Хемминг; перевод с англ. - М.: «Радио и связь», 1983. - 176 с.).
Недостатками данных способов являются:
- контроль целостности данных выполняется с определенной для применяемого кода, корректирующего ошибки, вероятностью;
- необходимость в хранении всей контрольной информации (избыточных блоков), вычисляемой для обеспечения возможности гарантированного контроля целостности данных.
б) Описание ближайшего аналога (прототипа)
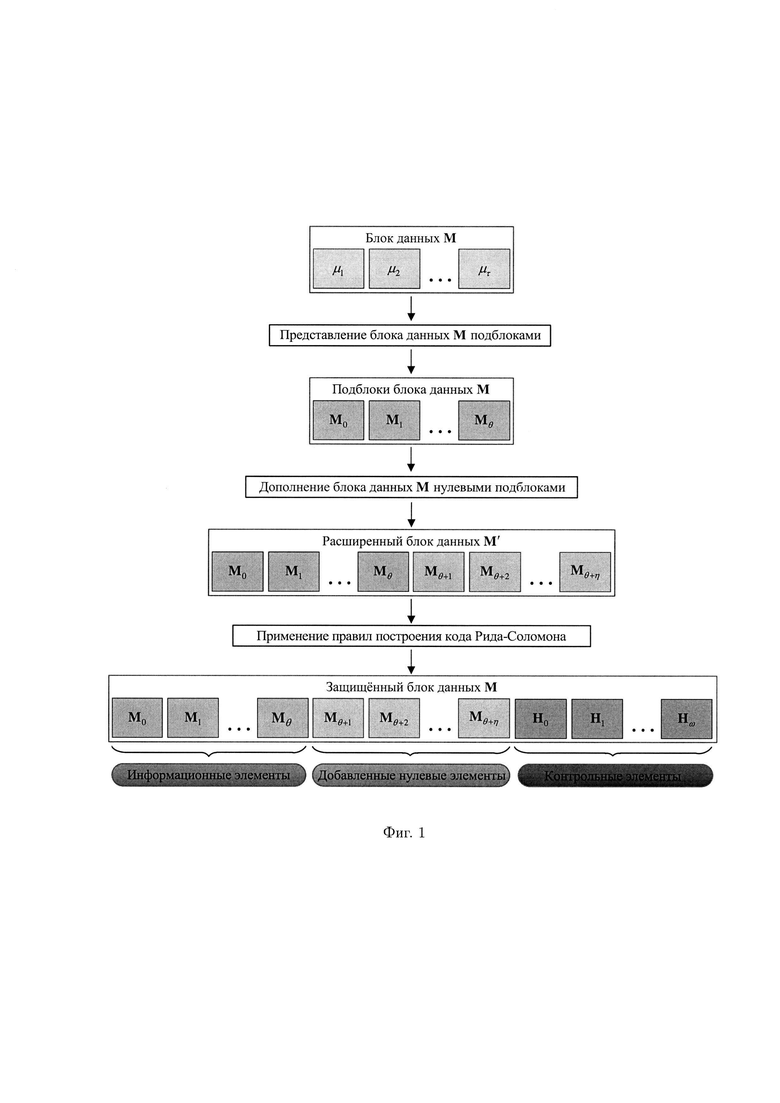
Наиболее близким по технической сущности к заявленному изобретению (прототипом) является способ контроля целостности многомерных массивов данных на основе правил построения кода Рида-Соломона (Патент на изобретение RUS №2785862, 14.12.2022), в котором обеспечивается возможность обнаружения и локализации двух и более подблоков блока данных с признаками нарушения целостности без вычисления и введения для этого высокой избыточности контрольной информации (фиг. 1).
Недостатком известного способа является необходимость в хранении всей контрольной информации, вычисляемой для обеспечения возможности обнаружения и локализации двух и более подблоков блока данных с признаками нарушения целостности.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение Целью настоящего изобретения является разработка способа контроля и восстановления целостности данных, в котором для обеспечения возможности обнаружения и локализации блоков данных с признаками нарушения целостности не требуется хранение всей вычисляемой контрольной информации.
б) Совокупность существенных признаков
Поставленная цель достигается тем, что в известном способе контроля целостности данных, заключающемся в том, что для обеспечения возможности обнаружения и локализации данных с признаками нарушения целостности первоначальный массив разбивается на блоки данных фиксированной длины, с которыми в последующем выполняются преобразования, в представленном же способе с блоками данных Mj, где j=1, 2, …, n, подлежащими защите от изменений, выполняют преобразования, в результате которых получают множество элементов вида 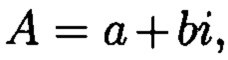 где а и b являются вещественными числами, символ г является мнимой единицей, что позволяет на множестве этих элементов ввести операции сравнения, сложения и умножения, а сами элементы указанного вида с введенными операциями будут являться комплексными числами А, при этом по комплексному модулю
где а и b являются вещественными числами, символ г является мнимой единицей, что позволяет на множестве этих элементов ввести операции сравнения, сложения и умножения, а сами элементы указанного вида с введенными операциями будут являться комплексными числами А, при этом по комплексному модулю 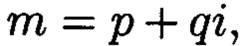 норма которого равна
норма которого равна 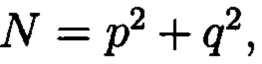 а р и q являются взаимнопростыми числами, каждое целое комплексное число А будет сравнимо с одним и только одним вычетом из ряда 0, 1 …, N-1, при этом каждому комплексному наименьшему вычету
а р и q являются взаимнопростыми числами, каждое целое комплексное число А будет сравнимо с одним и только одним вычетом из ряда 0, 1 …, N-1, при этом каждому комплексному наименьшему вычету 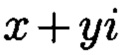 по модулю
по модулю 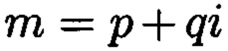 ставят в соответствие вещественный вычет h по модулю
ставят в соответствие вещественный вычет h по модулю 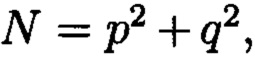 который вычисляется согласно следующему выражению
который вычисляется согласно следующему выражению 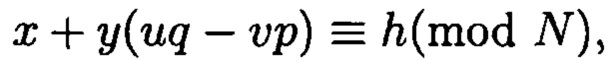 где
где 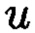 и
и 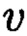 такие, что
такие, что 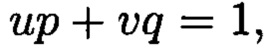 для осуществления контроля целостности данных, обеспечивающего возможность обнаружения и локализации блоков данных с признаками нарушения целостности, посредством фундаментальной теоремы Гаусса устанавливают изоморфизм между множествами вещественных и комплексных чисел, при этом массив М, включающий в себя данные, отправляемые на хранение, и массив G, полученный при запросе на его использование, представляют в виде матриц
для осуществления контроля целостности данных, обеспечивающего возможность обнаружения и локализации блоков данных с признаками нарушения целостности, посредством фундаментальной теоремы Гаусса устанавливают изоморфизм между множествами вещественных и комплексных чисел, при этом массив М, включающий в себя данные, отправляемые на хранение, и массив G, полученный при запросе на его использование, представляют в виде матриц 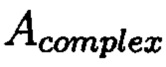 и
и 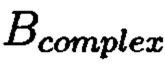 с множеством элементов вида
с множеством элементов вида 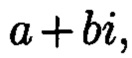 при этом определяют норму, которая должна быть больше максимального элемента в исходном массиве М, формируют избыточные блоки, представленные матрицами S и D, при этом блок S составляет суммы элементов строк матрицы
при этом определяют норму, которая должна быть больше максимального элемента в исходном массиве М, формируют избыточные блоки, представленные матрицами S и D, при этом блок S составляет суммы элементов строк матрицы 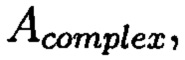 блок D составляет суммы элементов диагоналей матрицы
блок D составляет суммы элементов диагоналей матрицы 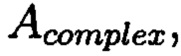 обнаружение и локализация блоков данных с признаками нарушения целостности выполняют за счет вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы
обнаружение и локализация блоков данных с признаками нарушения целостности выполняют за счет вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы 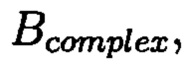 по результатам вычислений принимают решение об отсутствии признаков нарушения целостности данных, либо об обратном, в этом случае блоки данных с признаками нарушения целостности будут находиться на пересечении выявленных строк и диагоналей, для восстановления целостности локализованных блоков данных с признаками ее нарушения к выявленным ошибочным элементам прибавляют результат разности строк избыточного блока, представленного матрицей S, и матрицы
по результатам вычислений принимают решение об отсутствии признаков нарушения целостности данных, либо об обратном, в этом случае блоки данных с признаками нарушения целостности будут находиться на пересечении выявленных строк и диагоналей, для восстановления целостности локализованных блоков данных с признаками ее нарушения к выявленным ошибочным элементам прибавляют результат разности строк избыточного блока, представленного матрицей S, и матрицы 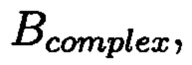 при этом для обеспечения такой возможности требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим.
при этом для обеспечения такой возможности требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим.
Сопоставительный анализ заявленного решения с прототипом показывает, что предлагаемый способ отличается от известного тем, что поставленная цель достигается за счет преобразования данных, подлежащих защите от изменений в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования, в множество элементов вида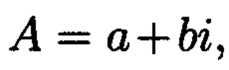 которые являются комплексными числами А, при этом по комплексному модулю
которые являются комплексными числами А, при этом по комплексному модулю 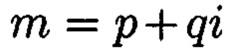 , норма которого равна
, норма которого равна 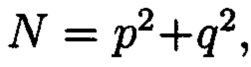 а р и q являются взаимнопростыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0, 1, …, N - 1, при этом каждому комплексному наименьшему вычету
а р и q являются взаимнопростыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0, 1, …, N - 1, при этом каждому комплексному наименьшему вычету 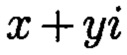 по модулю
по модулю 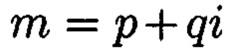 соответствует вещественный вычет h по модулю
соответствует вещественный вычет h по модулю 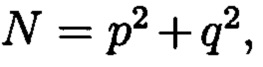 который может быть вычислен согласно следующему выражению
который может быть вычислен согласно следующему выражению 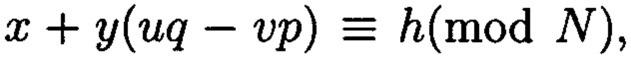 где
где 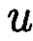 и
и 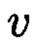 такие, что
такие, что 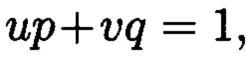 при этом для осуществления контроля целостности данных, а также ее восстановления не требуется хранение всей вычисляемой контрольной информации.
при этом для осуществления контроля целостности данных, а также ее восстановления не требуется хранение всей вычисляемой контрольной информации.
Контроль целостности блоков данных выполняется посредством вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы 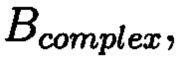 при этом в случае нарушения целостности блоки данных с признаками ее нарушения будут находиться на пересечении строки и диагонали, в которых присутствует ошибка, для восстановления целостности обнаруженного и локализованного блока данных с признаками ее нарушения требуется к ошибочному элементу прибавить результат разности строк избыточного блока, представленного матрицей S, и матрицы
при этом в случае нарушения целостности блоки данных с признаками ее нарушения будут находиться на пересечении строки и диагонали, в которых присутствует ошибка, для восстановления целостности обнаруженного и локализованного блока данных с признаками ее нарушения требуется к ошибочному элементу прибавить результат разности строк избыточного блока, представленного матрицей S, и матрицы 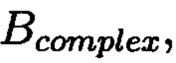 что позволит в момент времени t в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования обеспечить защиту данных от изменений. Новым является то, что в предлагаемом способе блоки данных Mj, где j=1, 2, …, n, подлежащие защите от изменений, преобразовываются в множество элементов вида
что позволит в момент времени t в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования обеспечить защиту данных от изменений. Новым является то, что в предлагаемом способе блоки данных Mj, где j=1, 2, …, n, подлежащие защите от изменений, преобразовываются в множество элементов вида 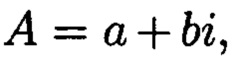 где а и b будут являться вещественными числами, символ г будет являться мнимой единицей, что позволяет на множестве этих элементов ввести операции сравнения, сложения и умножения, а сами элементы указанного вида с введенными операциями будут являться комплексными числами А, при этом по комплексному модулю
где а и b будут являться вещественными числами, символ г будет являться мнимой единицей, что позволяет на множестве этих элементов ввести операции сравнения, сложения и умножения, а сами элементы указанного вида с введенными операциями будут являться комплексными числами А, при этом по комплексному модулю 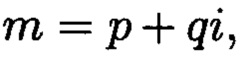 норма которого равна
норма которого равна 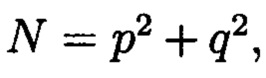 а р и q являются взаимнопростыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0, 1, …, N - 1, при этом каждому комплексному наименьшему вычету
а р и q являются взаимнопростыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0, 1, …, N - 1, при этом каждому комплексному наименьшему вычету 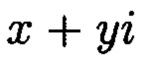 по модулю
по модулю 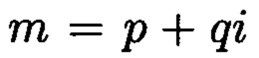 соответствует вещественный вычет h по модулю
соответствует вещественный вычет h по модулю 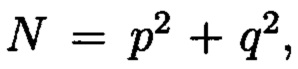 который может быть вычислен согласно следующему выражению
который может быть вычислен согласно следующему выражению 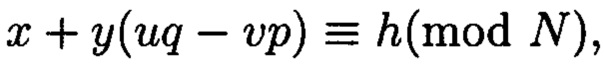 где
где 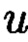 и
и 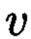 такие, что
такие, что 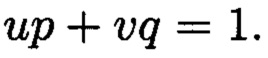 Новым является то, что для обеспечения возможности контроля целостности данных, подлежащих защите, посредством фундаментальной теоремы Гаусса устанавливают изоморфизм между множествами вещественных и комплексных чисел, при этом массив М, включающий в себя данные, отправляемые на хранение, и массив G, полученный при запрсе на его использование, представляют в виде матриц
Новым является то, что для обеспечения возможности контроля целостности данных, подлежащих защите, посредством фундаментальной теоремы Гаусса устанавливают изоморфизм между множествами вещественных и комплексных чисел, при этом массив М, включающий в себя данные, отправляемые на хранение, и массив G, полученный при запрсе на его использование, представляют в виде матриц 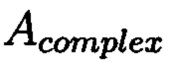 и
и 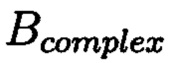 с множеством элементов вида
с множеством элементов вида 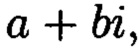 при этом определяют норму, которая должна быть больше максимального элемента в исходном массиве М, формируют избыточные блоки S и D, при этом блок S будет составлять суммы элементов строк матрицы
при этом определяют норму, которая должна быть больше максимального элемента в исходном массиве М, формируют избыточные блоки S и D, при этом блок S будет составлять суммы элементов строк матрицы 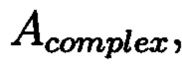 блок D будет составлять суммы элементов диагоналей матрицы
блок D будет составлять суммы элементов диагоналей матрицы 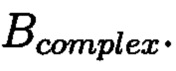 Новым является то, что в предлагаемом способе обнаружение и локализация блоков данных с признаками нарушения целостности выполняется посредством вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы
Новым является то, что в предлагаемом способе обнаружение и локализация блоков данных с признаками нарушения целостности выполняется посредством вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы 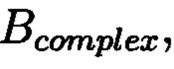 по результатам вычислений принимается решение об отсутствии нарушения целостности блоков данных, либо об обратном, в этом случае блоки данных с признаками нарушения целостности будут находиться на пересечении выявленных строк и диагоналей, для восстановления целостности обнаруженных и локализованных блоков данных с признаками ее нарушения к выявленным ошибочным элементам прибавляют результат разности строк избыточного блока, представленного матрицей S, и матрицы
по результатам вычислений принимается решение об отсутствии нарушения целостности блоков данных, либо об обратном, в этом случае блоки данных с признаками нарушения целостности будут находиться на пересечении выявленных строк и диагоналей, для восстановления целостности обнаруженных и локализованных блоков данных с признаками ее нарушения к выявленным ошибочным элементам прибавляют результат разности строк избыточного блока, представленного матрицей S, и матрицы 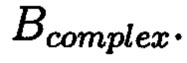 Новым является то, что для обеспечения возможности обнаружения и локализации блоков данных с признаками нарушения целостности требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим. в) Причинно-следственная связь между признаками и техническим результатом Благодаря новой совокупности существенных признаков в способе реализованы возможности:
Новым является то, что для обеспечения возможности обнаружения и локализации блоков данных с признаками нарушения целостности требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим. в) Причинно-следственная связь между признаками и техническим результатом Благодаря новой совокупности существенных признаков в способе реализованы возможности:
- контроля и восстановления целостности данных на основе теоретико-числовых преобразований в комплексной плоскости;
- обнаружения и локализации блоков данных с признаками нарушения целостности, при котором не требуется хранение всей вычисляемой контрольной информации.
Доказательства соответствия заявленного изобретения условиям патентоспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Краткое описание чертежей
Заявленный способ поясняется чертежами, на которых показано:
фиг. 1 - схема, иллюстрирующая способ контроля целостности многомерных массивов данных на основе правил построения кода Рида-Соломона; фиг. 2 - схема, иллюстрирующая разработанный способ контроля и восстановления целостности данных на основе теоретико-числовых преобразований в комплексной плоскости;
фиг. 3 - схема, иллюстрирующая полную систему наименьших комплексных вычетов для нормы N=25 и модуля 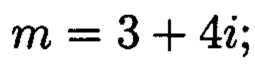
фиг. 4 - схема, иллюстрирующая наименьший и наибольший вычеты в геометрическом представлении;
фиг. 5 - схема, иллюстрирующая порядок следования по оси ординат;
фиг. 6 - схема, иллюстрирующая выбранные вычеты для хранения.
Осуществление изобретения
Данные, подлежащих защите от изменений при их хранении, представленные в виде блоков Mj (j=1, 2, …, n), подлежат преобразованию в множество элементов вида:
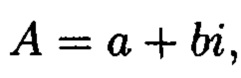
где а и b - вещественные числа, i - символ, называемый мнимой единицей. При этом на множестве этих символов могут быть введены следующие операции:
- сравнение: 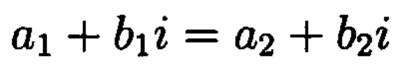 (тогда и только тогда, когда
(тогда и только тогда, когда 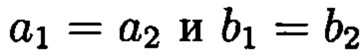 );
);
- сложение: 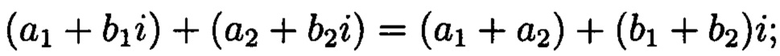
- умножение: 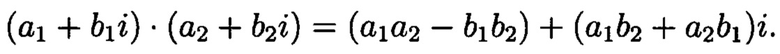
При этом элементы указанного вида с введенными операциями будут являться комплексными числами. Операции сложения и умножения, введенные на множестве комплексных чисел, будут обладать следующими свойствами:
- коммутативность сложения: 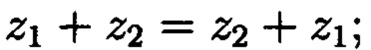
- ассоциативность сложения: 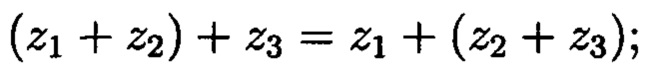
- коммутативность умножения: 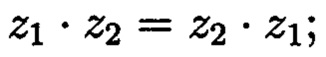
- ассоциативность умножения: 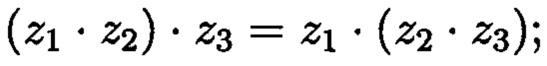
- дистрибутивность сложения и умножения: 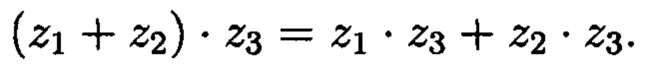
Вещественное число 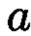 будет являться вещественной частью числа
будет являться вещественной частью числа 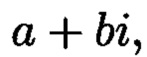 представленного в комплексной плоскости, а число b - его мнимой частью.
представленного в комплексной плоскости, а число b - его мнимой частью.
Если задан ряд положительных целых чисел 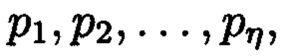 называемых основаниями системы, то под системой в остаточных классах будет пониматься такая система, в которой целое положительное число А представляется в виде набора остатков (вычетов) по выбранным основаниям:
называемых основаниями системы, то под системой в остаточных классах будет пониматься такая система, в которой целое положительное число А представляется в виде набора остатков (вычетов) по выбранным основаниям: 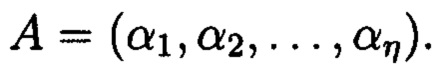
При этом цифра х-го 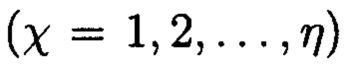 разряда ах числа А есть наименьший положительный остаток от деления А на рх.
разряда ах числа А есть наименьший положительный остаток от деления А на рх.
Основной теоретико-числовой базой системы остаточных классов является теория сравнений, в которой два целых числа а и b сравнимы между собой по модулю р, если их разность 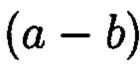 кратна р (делится нацело на р).
кратна р (делится нацело на р).
Для сравнения принято обозначение: 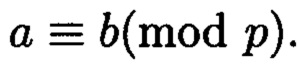
При этом комплексное число 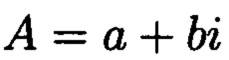 будет кратно комплексному числу
будет кратно комплексному числу 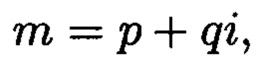 если частное
если частное 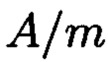 является комплексным числом. В этом случае, частное
является комплексным числом. В этом случае, частное 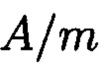 будет целым числом, когда
будет целым числом, когда
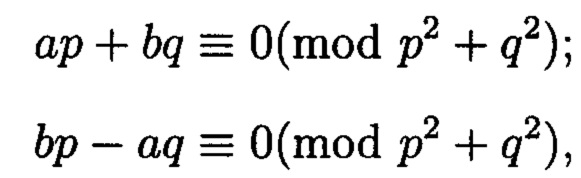
где 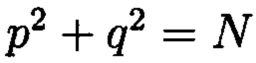 - норма числа m.
- норма числа m.
Наименьшим вычетом числа 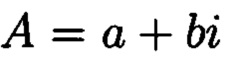 по модулю
по модулю 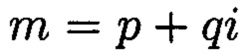 называется такое число
называется такое число 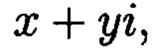 что выполняется следующее соотношение:
что выполняется следующее соотношение:
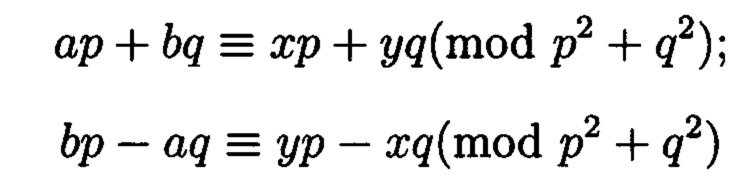
или
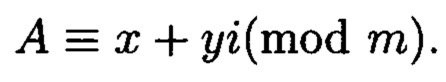
Наименьший вычет любого комплексного числа 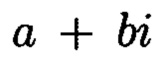 по комплексному модулю
по комплексному модулю 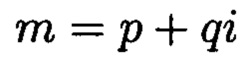 определяется исходя из системы двух вещественных сравнений:
определяется исходя из системы двух вещественных сравнений:
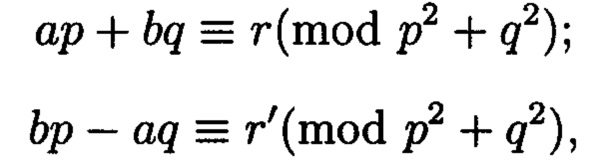
где r и r' - наименьшие положительные вычеты по вещественному модулю N. Определить все возможные пары значений r и r' можно решая сравнение:
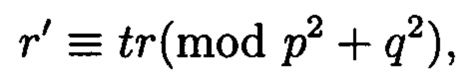
где 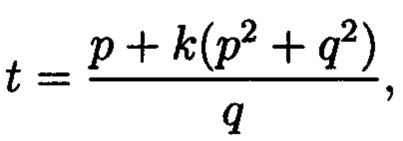 причем к таково, что t - целое, меньшее
причем к таково, что t - целое, меньшее 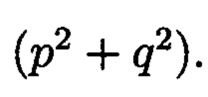
С помощью следующего соотношения:
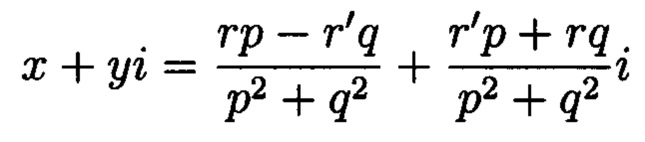
вычисляется наименьший вычет числа А по модулю m.
По заданному комплексному модулю 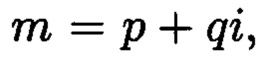 норма которого равна
норма которого равна 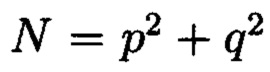 и для которого р и q являются взаимнопростыми числами, каждое целое комплексное число сравнимо с одним и только одним вычетом из ряда: 0, 1, …, N-1.
и для которого р и q являются взаимнопростыми числами, каждое целое комплексное число сравнимо с одним и только одним вычетом из ряда: 0, 1, …, N-1.
Таким образом, каждому комплексному наименьшему вычету 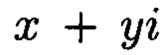 по модулю
по модулю 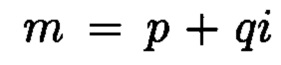 соответствует вещественный вычет h по модулю
соответствует вещественный вычет h по модулю 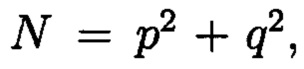 который может быть вычислен согласно следующему выражению:
который может быть вычислен согласно следующему выражению:
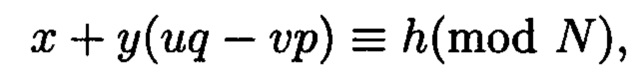
где 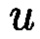 и
и 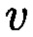 такие, что
такие, что 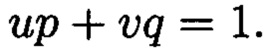
Для обнаружения и локализации блоков данных с признаками нарушения целостности (возникающих ошибок) посредством фундаментальной теоремы Гаусса устанавливается изоморфизм между множествами вещественных и комплексных чисел.
При этом даны два массива данных:
- исходный массив данных М, включающий в себя данные, отправляемые на обработку и хранение в автоматизированную систему, содержащие целевую информацию;
- массив G, включающий в себя данные, полученные после обработки и хранения в автоматизированной системе в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования.
С помощью фундаментальной теоремы Гаусса представим массивы М и G в виде матриц с множеством элементов вида 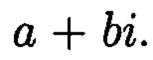 Для этого определим норму, которая должна быть больше максимального элемента в исходном массиве М.
Для этого определим норму, которая должна быть больше максимального элемента в исходном массиве М.
Матрица, соответствующая исходному массиву М примет следующий вид:
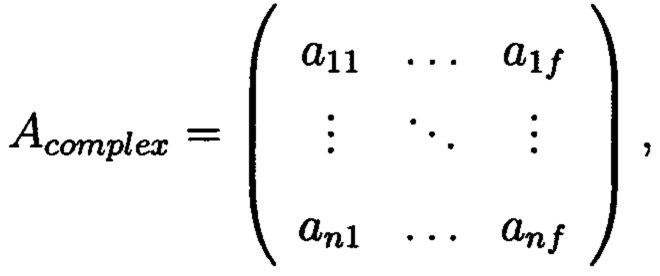
где элемент матрицы - комплексное число, то есть 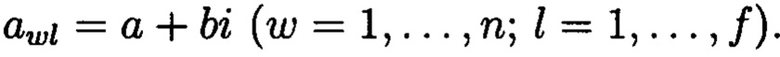
Матрица, соответствующая массиву G, примет следующий вид:
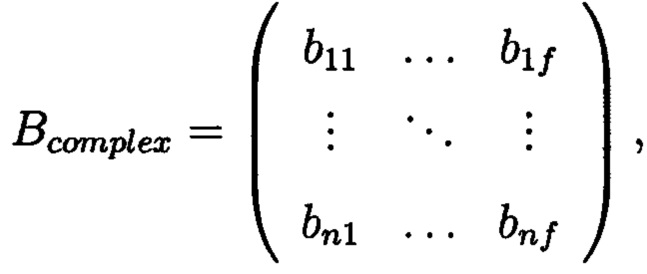
где элемент матрицы - комплексное число, то есть 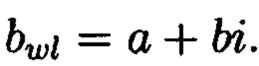
Сформируем избыточные блоки, первый из которых будут составлять суммы элементов строк матрицы 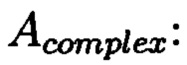
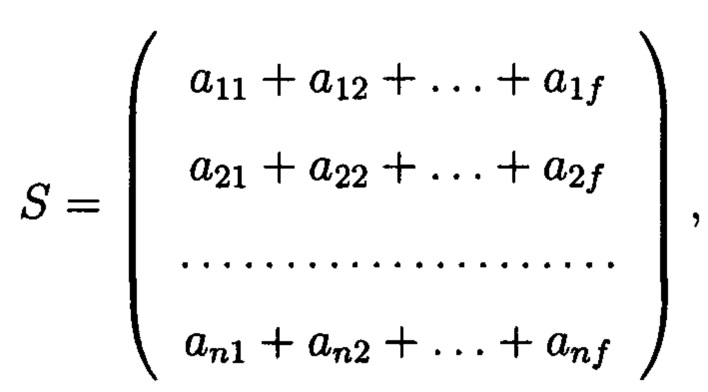
второй блок будут составлять суммы элементов диагоналей матрицы 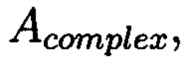 то есть:
то есть:
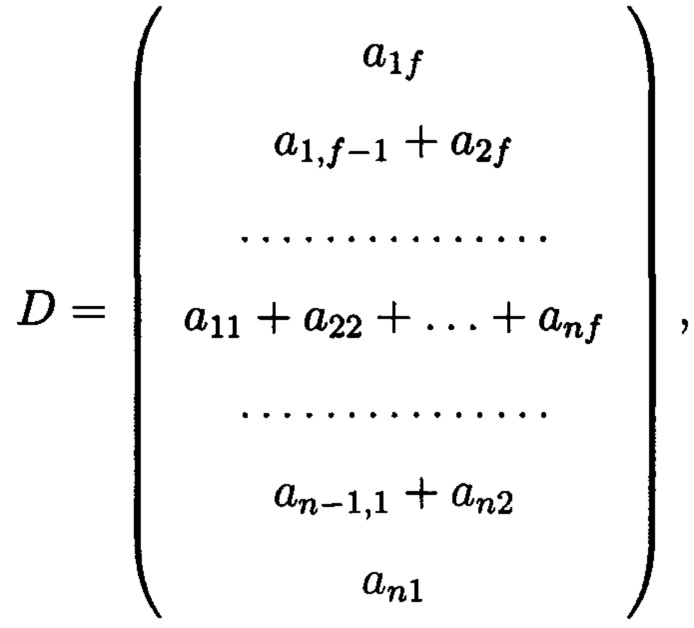
где S - первый избыточный блок, D - второй.
Для обнаружения и локализации блоков данных с признаками нарушения целостности (возникающих ошибок) требуется вычесть из элементов избыточных блоков, представленных матрицами S и D элементы матрицы 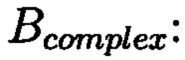
- если в итоге получится «О», то нарушения целостности блоков данных не произошло (ошибка отсутствует);
- в противном случае, подтверждается нарушение целостности блоков данных (возникновение ошибки). При этом элемент (блок данных с признаками нарушения целостности) будет находиться на пересечении строки и диагонали, в которых присутствует ошибка.
Для восстановления целостности обнаруженного и локализованного блока данных с признаками ее нарушения (исправления ошибки) требуется к ошибочному элементу прибавить результат разности строк матриц S и 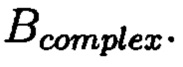
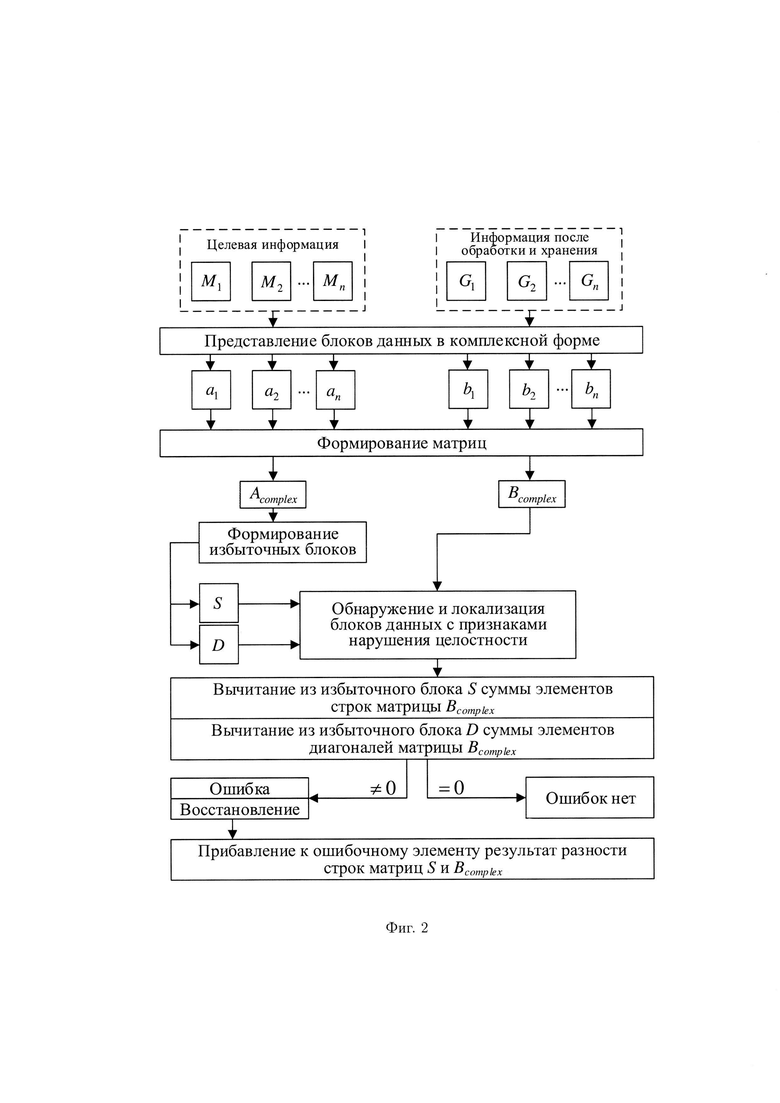
Схема, иллюстрирующая разработанный способ защиты данных от изменений в автоматизированной системе при их обработке и хранении, представлена на фигуре 2.
Пример 1. Допустим, что на обработку и хранение в автоматизированную систему отправлено изображение с соответствующим ему цифровым кодом (массив данных М):
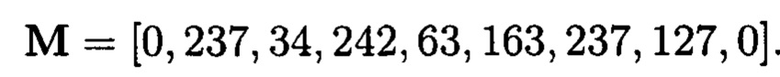
При этом при запросе на его использование после обработки и хранения в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования на выходе получен следующий цифровой код (массив G):
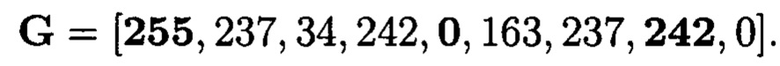
В результате деструктивных воздействий злоумышленника и возмущений среды функционирования произошло искажение информации, то есть нарушение целостности блоков данных, подлежащих защите (возникновение ошибки).
Для обнаружения и локализации блока данных с признаками нарушения целостности (возникшей ошибки) на основе фундаментальной теоремы Гаусса запишем массивы М и G в матричной форме и приведем их элементы к комплексному виду.
Выберем норму N=256 и соответствующий ей модуль 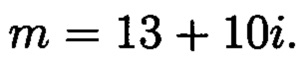
Получим матрицу:
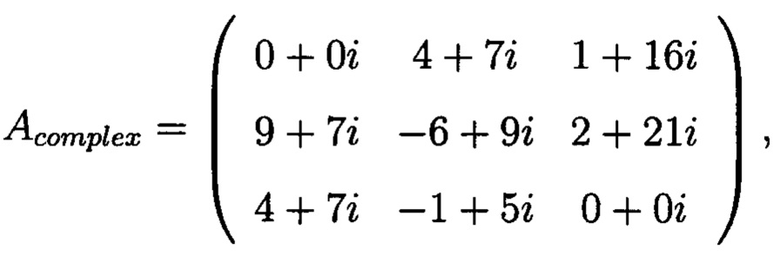
соответствующую массиву М и матрицу, соответствующую массиву G:
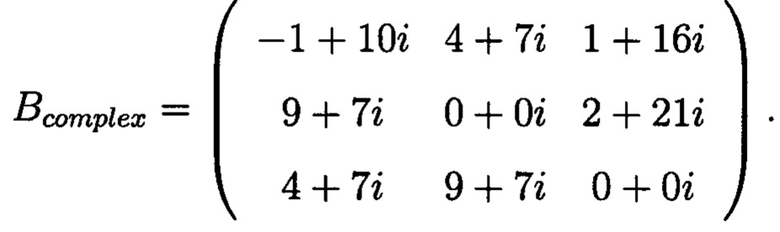
Сформируем избыточные блоки:
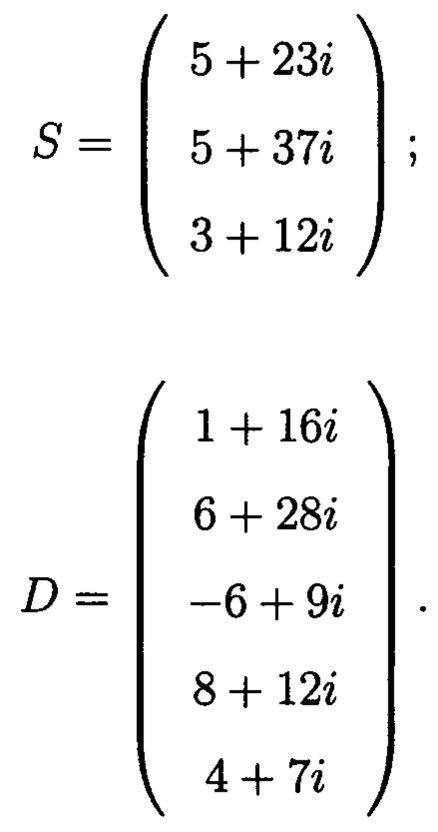
Для обнаружения, локализации и восстановления целостности блоков данных с признаками ее нарушения (обнаружения, локализации и исправления возникшей ошибки) выполним проверку по строкам:
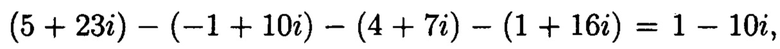 следовательно, присутствует ошибка в первой строке;
следовательно, присутствует ошибка в первой строке;
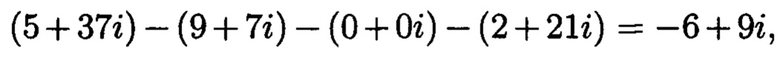 следовательно, присутствует ошибка во второй строке;
следовательно, присутствует ошибка во второй строке;
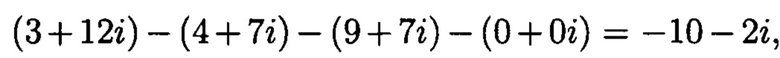 следовательно, присутствует ошибка в третьей строке,
следовательно, присутствует ошибка в третьей строке,
и по диагоналям:
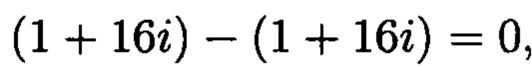 следовательно, ошибки нет;
следовательно, ошибки нет;
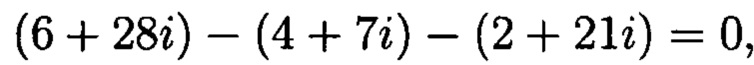 следовательно, ошибки нет;
следовательно, ошибки нет;
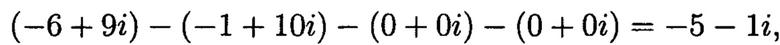 следовательно, ошибка есть;
следовательно, ошибка есть;
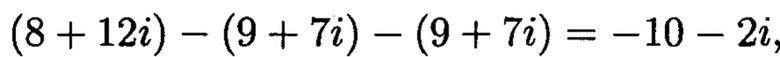 следовательно, ошибка есть;
следовательно, ошибка есть;
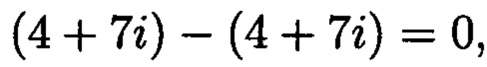 следовательно, ошибки нет.
следовательно, ошибки нет.
Таким образом, ошибочный элемент находится на пересечении строки и диагонали, то есть при обработке и хранении в автоматизированной системе изображения ошибка возникла в элементах 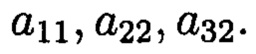
Для исправления ошибки, возникшей при обработке и хранении изображения, требуется к ошибочному элементу прибавить результат разности строк:
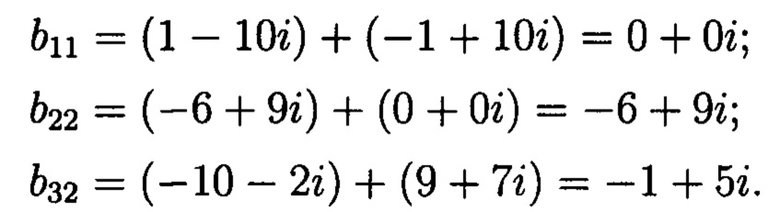
Получим
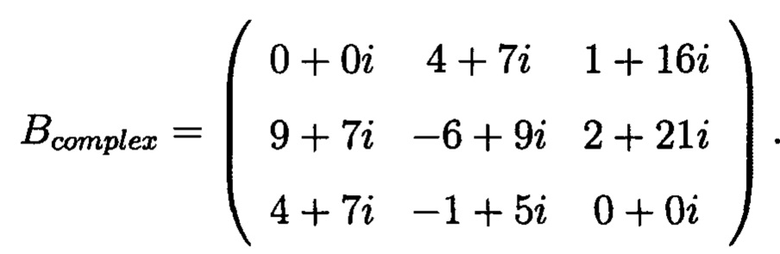
Переведем в вещественную форму:
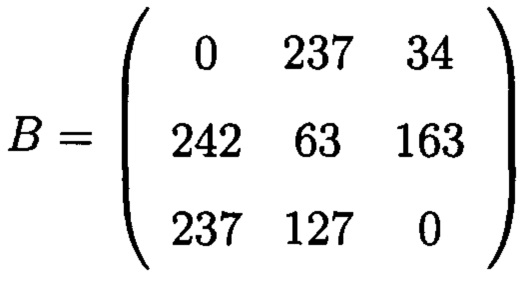
и в результате получим цифровой код (исходный массив), соответствующий отправленному на хранение (фиг. 2).
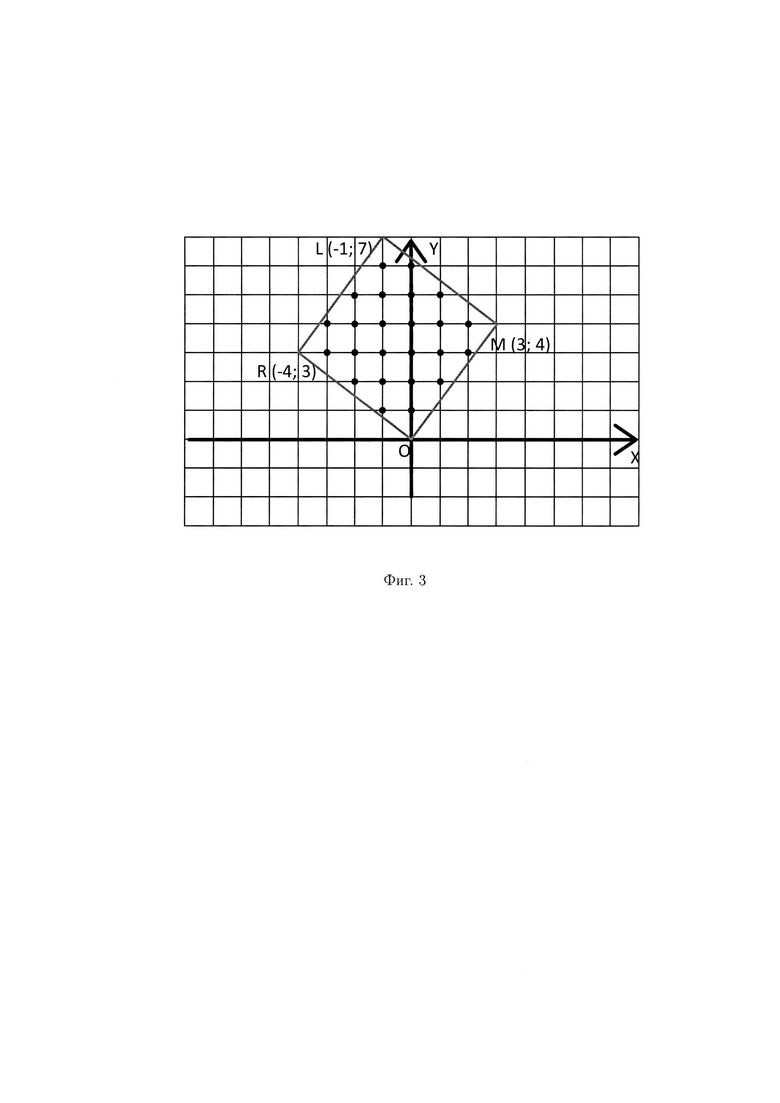
Пример 2. Рассмотрим систему наименьших комплексных вычетов для нормы N=25 и модуля 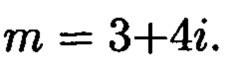 Полную систему наименьших комплексных вычетов найдем с помощью геометрического построения. Отметим на комплексной плоскости точку М с координатами (3; 4), построим квадрат на стороне ОМ и перечислим все целые комплексные числа,
Полную систему наименьших комплексных вычетов найдем с помощью геометрического построения. Отметим на комплексной плоскости точку М с координатами (3; 4), построим квадрат на стороне ОМ и перечислим все целые комплексные числа,
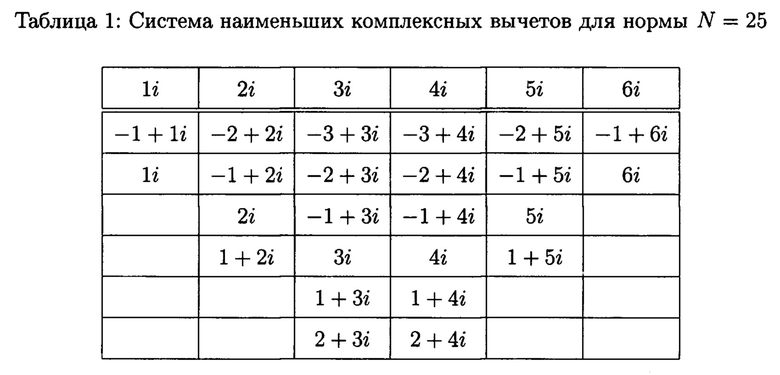
находящихся внутри этого квадрата (фиг. 3). Таким образом, получаем полную систему комплексных вычетов, представленную в таблице 1.
Переведем информацию, содержащуюся в подблоках данных М, в комплексную форму из вещественной.
Вычислим вещественный вычет, который соответствует комплексному вычету по формуле Гаусса:
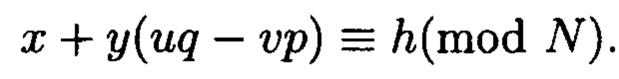
Найдем 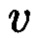 и
и 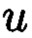 из выражения
из выражения 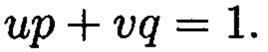
Получается
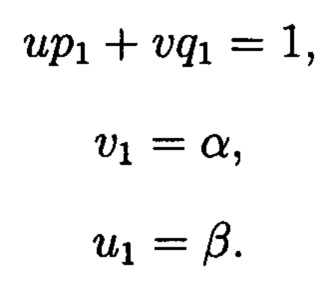
Откуда комплексному вычету 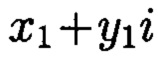 согласно формуле Гаусса для нормы N1 с модулем
согласно формуле Гаусса для нормы N1 с модулем 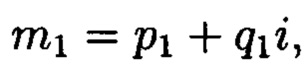 будет соответствовать следующий вещественный вычет:
будет соответствовать следующий вещественный вычет:
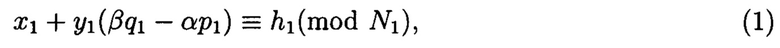
где 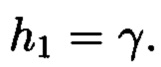
Затем найдем вещественные вычеты, которые соответствуют комплексным вычетам из примера. Норма N=25 и модуль 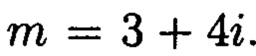 Найдем
Найдем 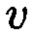 и
и 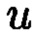 из выражения
из выражения 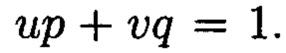
Получаем 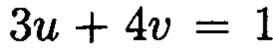 откуда
откуда 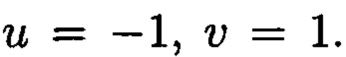 Подставляем
Подставляем 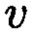 и
и 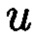 в уравнение Гаусса и получаем:
в уравнение Гаусса и получаем:
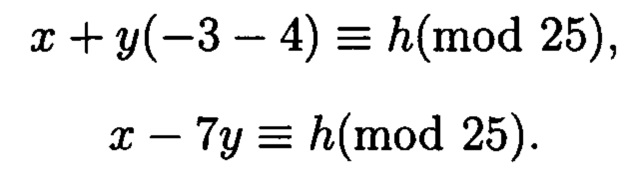
Далее получим вещественные вычеты, подставляя комплексные вычеты в уравнение Гаусса:
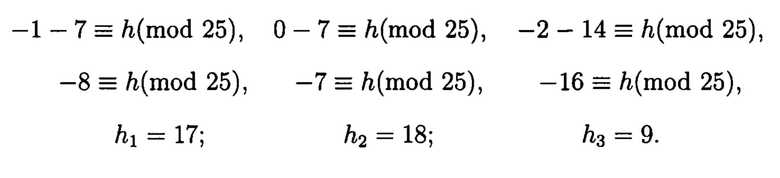
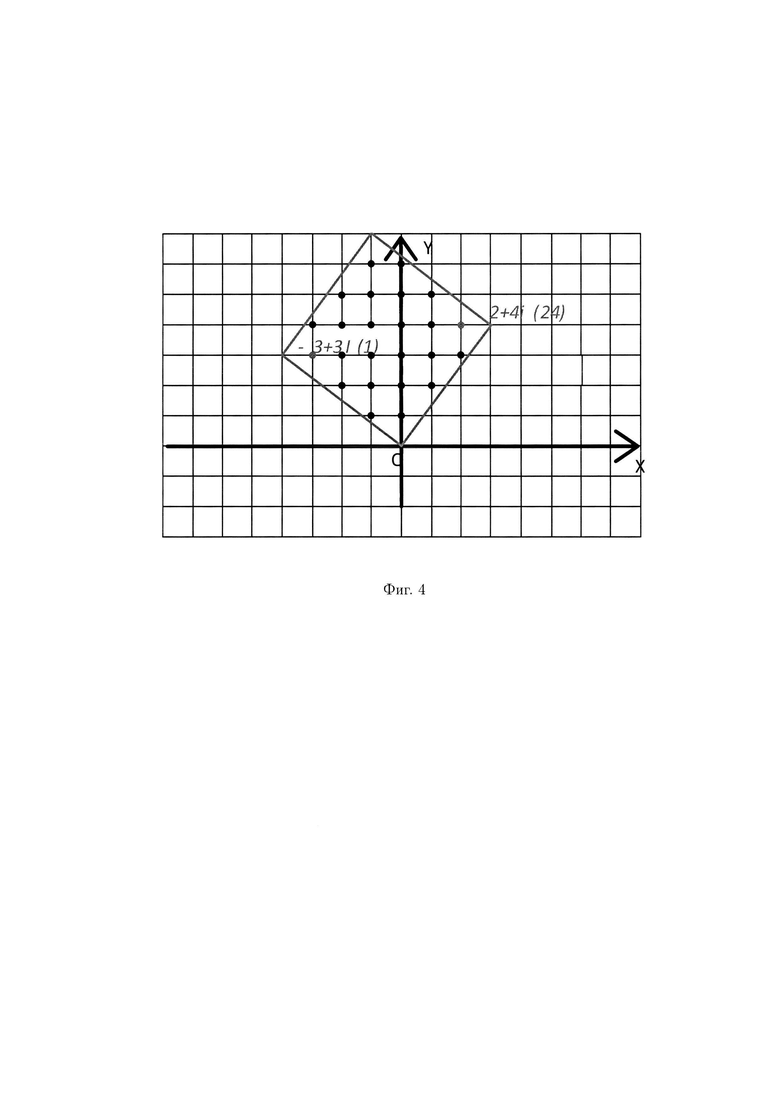
Подобным образом установим соответствие между остальными комплексными и вещественными вычетами (таблица 2).

Из представленной выше таблицы 2 видно, что есть закономерность в том, что вещественный вычет увеличивается на единицу слева направо, начиная от «-3+3i» (вещественный вычет равен 1), заканчивая «2+4i» (вещественный вычет равен 24) (фиг. 4).
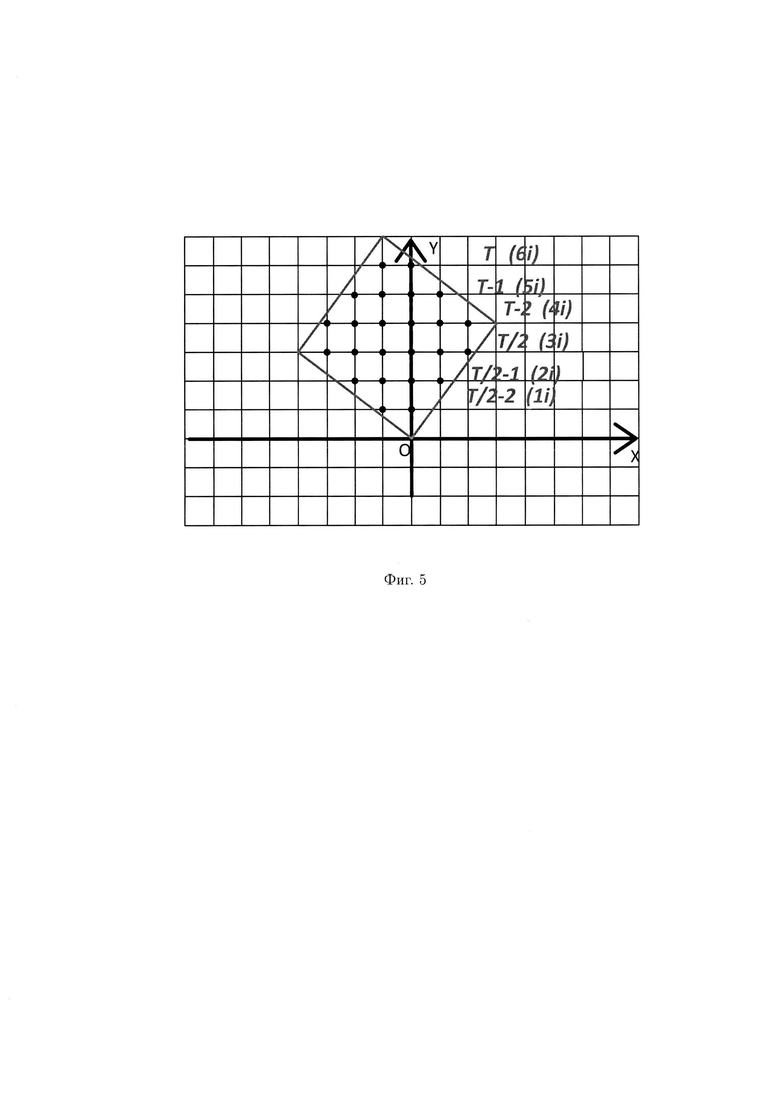
Очередность следования по оси ординат формируется следующим образом: 1) T/2, где T - это количество наименьших вычетов по оси ординат от 0 до границы квадрата; 2) T; 3) T/2 - 1; 4) T - 1; 5) T/2 - 2; 6) T - 2.
В рассматриваемом примере порядок следования по оси ординат следующий: 3i, 6i, 2i, 5i, 1i, 4i (фиг. 5). Такое свойство геометрического представления позволяет без вычислений, согласно выражения (1), определить вещественный вычет и соответствующий ему комплексный вычет.
Таким образом, преобразования вида 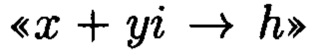 позволяют представлять данные массива М, как вещественные вычеты h по выбранному модулю m и, соответственно изоморфные им комплексные вычеты.
позволяют представлять данные массива М, как вещественные вычеты h по выбранному модулю m и, соответственно изоморфные им комплексные вычеты.
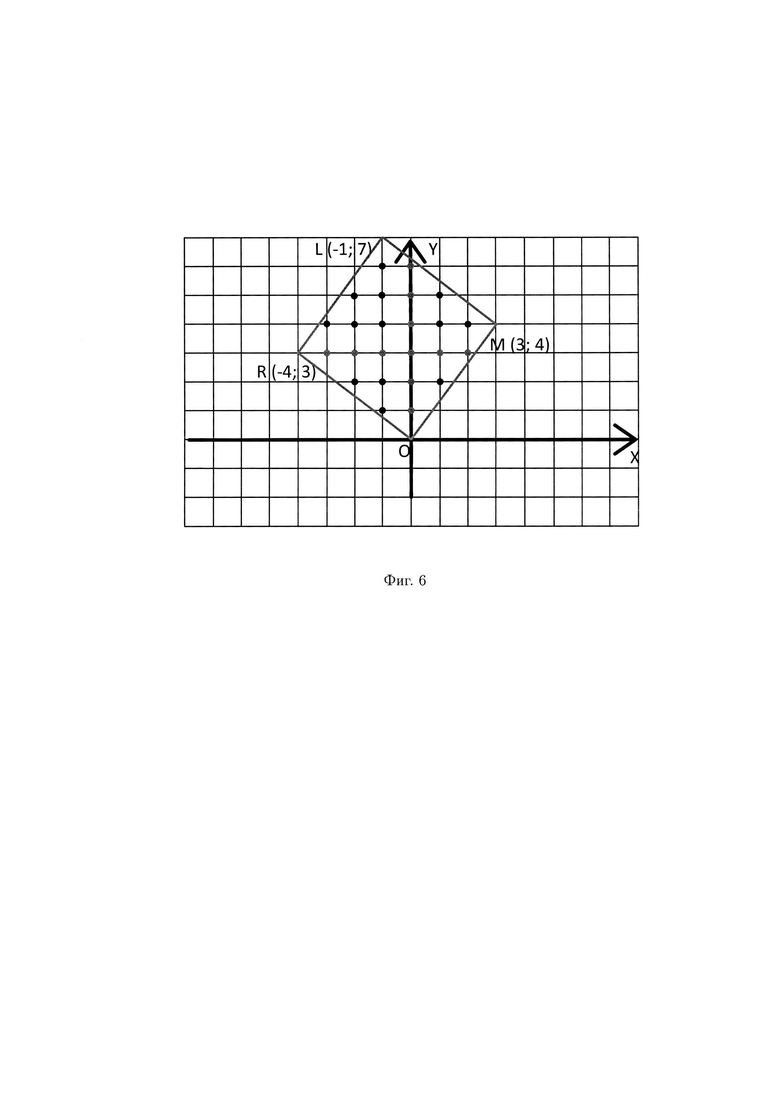
Предположим, что мы имеем массив данных, который в своей геометрической интерпретации представляет квадрат, количество наименьших вычетов которого равно N-1, при N=1000. Это приведет к затрате большого объема памяти, и, как следствие, большого количества времени для контроля целостности данных. В свою очередь, разработанный способ позволяет хранить только те комплексные вычеты (они же вещественные вычеты), диапазон действительной и мнимой частей которых наибольший. В данном случае (см. пример 2) это будут действительные составляющие (-3, -2, -1, 0, 1, 2) и мнимые части 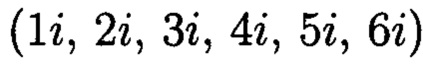 (фиг. 6).
(фиг. 6).
Таким образом, можно тратить меньшее количество ячеек памяти. Допустим, в представленном случае заняты 24 ячейки памяти (24 вычета), но поскольку хранится лишь часть вычетов, то всего ячеек будет 11. Соответственно, при больших размерах геометрического представления наименьших вычетов количество незарезервированных под хранение данных будет намного меньше. Из всего вышеизложенного следует, что в разработанном способе контроля целостности данных для обеспечения возможности обнаружения и локализации блоков данных с признаками нарушения целостности не требуется хранение всей вычисляемой контрольной информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ ДВУМЕРНЫХ КОДОВЫХ КОНСТРУКЦИЙ В КОМПЛЕКСНОЙ ОБЛАСТИ | 2024 |
|
RU2834287C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ДЕГРАДАЦИИ СИСТЕМ ХРАНЕНИЯ | 2022 |
|
RU2801124C1 |
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ ПРИ ДЕГРАДАЦИИ МНОГОМЕРНЫХ СИСТЕМ ХРАНЕНИЯ | 2023 |
|
RU2833352C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2021 |
|
RU2771208C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ ПРИ ВЫНУЖДЕННОМ СОКРАЩЕНИИ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2801198C1 |
| СПОСОБ ФОРМИРОВАНИЯ КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ В УСЛОВИЯХ СОКРАЩЕНИЯ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2806539C1 |
| СПОСОБ И УСТРОЙСТВО ФОРМИРОВАНИЯ МНОГОЗНАЧНЫХ КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ ЗАЩИЩЕННОЙ ПЕРЕДАЧИ ДАННЫХ ПО КАНАЛАМ СВЯЗИ | 2023 |
|
RU2815193C1 |
| СПОСОБ ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ СТРУКТУР ДЛЯ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2023 |
|
RU2808758C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ПЕРЕХОДА К ПРОСТРАНСТВУ ДАННЫХ С БОЛЬШЕЙ МЕРНОСТЬЮ | 2022 |
|
RU2801082C1 |
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ КРИТИЧЕСКОЙ ДЕГРАДАЦИИ СИСТЕМ ИХ ХРАНЕНИЯ | 2023 |
|
RU2828227C1 |
Изобретение относится к способам контроля и восстановления целостности данных в системах хранения. Технический результат заключается в сокращении объема памяти, необходимого для контроля и восстановления целостности данных. Технический результат достигается за счет преобразования данных, подлежащих защите от изменений в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования, в множество элементов вида 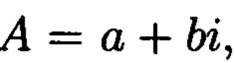 которые будут являться комплексными числами А, при этом по комплексному модулю
которые будут являться комплексными числами А, при этом по комплексному модулю 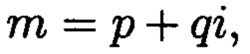 норма которого равна
норма которого равна 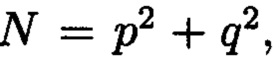 а р и q являются взаимно простыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0,1, …, N-1, при этом каждому комплексному наименьшему вычету
а р и q являются взаимно простыми числами, каждое целое комплексное число А сравнимо с одним и только одним вычетом из ряда 0,1, …, N-1, при этом каждому комплексному наименьшему вычету 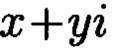 по модулю
по модулю 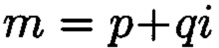 соответствует вещественный вычет h по модулю
соответствует вещественный вычет h по модулю 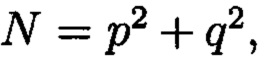 который может быть вычислен согласно следующему выражению:
который может быть вычислен согласно следующему выражению: 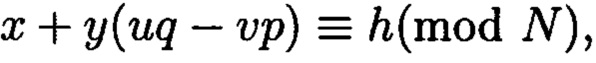 где
где 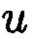 и
и 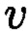 такие, что
такие, что 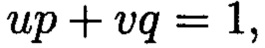 при этом для осуществления контроля целостности данных, а также ее восстановления, требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим. 2 табл., 6 ил.
при этом для осуществления контроля целостности данных, а также ее восстановления, требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим. 2 табл., 6 ил.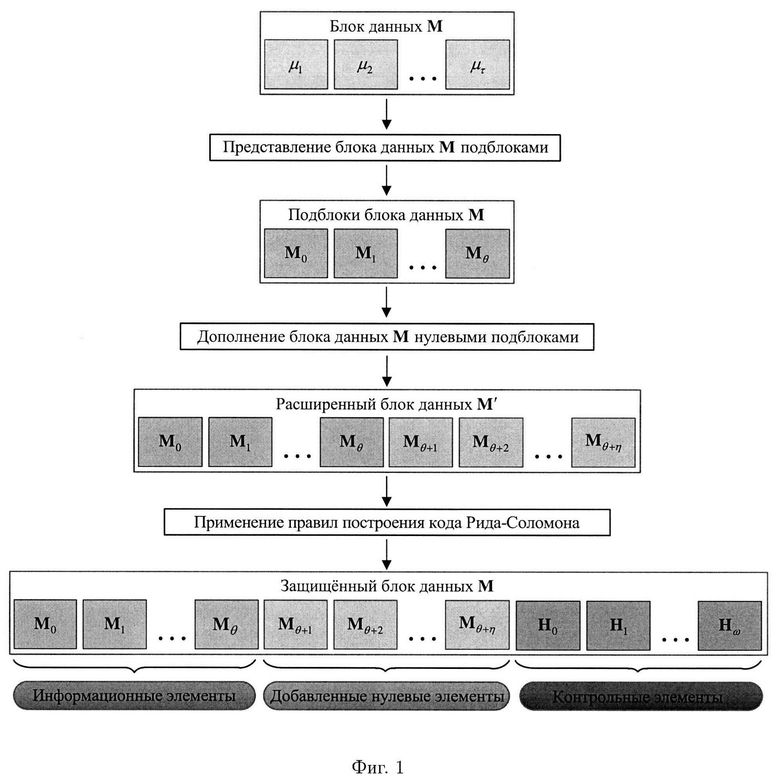
Способ контроля и восстановления целостности данных на основе теоретико-числовых преобразований в комплексной плоскости, заключающийся в том, что для обеспечения возможности обнаружения и локализации данных с признаками нарушения целостности первоначальный массив разбивается на блоки данных фиксированной длины, с которыми в последующем выполняются преобразования, отличающийся тем, что с блоками данных Mj, где j=1, 2, …, n, подлежащими защите от изменений, выполняют преобразования, в результате которых получают множество элементов вида A=a+bi, где а и b являются вещественными числами, символ i является мнимой единицей, что позволяет на множестве этих элементов ввести операции сравнения, сложения и умножения, а сами элементы указанного вида с введенными операциями будут являться комплексными числами А, при этом по комплексному модулю m=p+qi, норма которого равна N = p2 + q2, а р и q являются взаимно простыми числами, каждое целое комплексное число А будет сравнимо с одним и только одним вычетом из ряда 0, 1, …, N-1, при этом каждому комплексному наименьшему вычету x+yi по модулю m=p+qi ставят в соответствие вещественный вычет h по модулю N=p2+q2, который вычисляется согласно следующему выражению x+y(uq-vp)≡h(modN), где u и v такие, что up+vq=1, для осуществления контроля целостности данных, обеспечивающего возможность обнаружения и локализации блоков данных с признаками нарушения целостности, посредством фундаментальной теоремы Гаусса устанавливают изоморфизм между множествами вещественных и комплексных чисел, при этом массив М, включающий в себя данные, отправляемые на хранение, и массив G, полученный при запросе на его использование, представляют в виде матриц Acomplex и Bcomplex с множеством элементов вида a+bi, при этом определяют норму, которая должна быть больше максимального элемента в исходном массиве М, формируют избыточные блоки, представленные матрицами S и D, при этом блок S составляет суммы элементов строк матрицы Acomplex, блок D составляет суммы элементов диагоналей матрицы Acomplex, обнаружение и локализацию блоков данных с признаками нарушения целостности выполняют за счет вычитания из элементов избыточных блоков, представленных матрицами S и D, элементов матрицы Bcomplex, по результатам вычислений принимают решение об отсутствии признаков нарушения целостности данных, либо об обратном, в этом случае блоки данных с признаками нарушения целостности будут находиться на пересечении выявленных строк и диагоналей, для восстановления целостности локализованных блоков данных с признаками ее нарушения, к выявленным ошибочным элементам прибавляют результат разности строк избыточного блока, представленного матрицей S, и матрицы Bcomplex, при этом для обеспечения такой возможности требуется хранить только те комплексные вычеты, диапазон действительной и мнимой частей которых является наибольшим.
| СПОСОБ ДВУМЕРНОГО КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2018 |
|
RU2696425C1 |
| US 8209551 B2, 26.06.2012 | |||
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ ОДНОМЕРНЫХ МАССИВОВ ДАННЫХ НА ОСНОВЕ КОМПЛЕКСИРОВАНИЯ КРИПТОГРАФИЧЕСКИХ МЕТОДОВ И МЕТОДОВ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2022 |
|
RU2786617C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ КРИПТОГРАФИЧЕСКОГО ТРЕУГОЛЬНИКА ПАСКАЛЯ | 2019 |
|
RU2730365C1 |
Авторы
Даты
2023-12-04—Публикация
2023-08-07—Подача