Изобретение относится к навигации и может быть использовано при калибровке прецизионных датчиков угловой скорости на этапе начальной подготовки инерциальной навигационной системы с учетом годичной угловой орбитальной скорости вращения Земли в плоскости эклиптики.
Известны способы калибровки датчиков угловой скорости.
В частности, известен способ [RU 1233653, A1, G01P 21/00, 10.05.2005], заключающийся в задании вращения датчика угловой скорости вокруг его оси чувствительности, измерении тока в цепи датчика момента и определении зависимости его выходного сигнала от входной угловой скорости, гироскопический датчик вращают с постоянной угловой скоростью, равной предельному значению заданного диапазона угловых скоростей, при этом, изменяют скорость вращения ротора гиромотора датчика угловой скорости путем изменения частоты напряжения питания гиромотора от номинального значения с дискретностью l/n, где n - заданное количество калибруемых точек, а ток в цепи датчика момента измеряют на каждой частоте напряжения питания гиромотора.
Недостатком способа являются его относительно низкая точность, поскольку не учитывается годовая орбитальная скорость вращения Земли в плоскости эклиптики.
Кроме этого, известен способ [RU 2727344, C1, G01C 21/00, 21.07.2020], который включает начальную выставку платформы, статический эксперимент при неподвижном положении платформы, последовательное вращение с помощью стендового оборудования, как минимум, по двум непараллельным осям в базисе калибруемого ИБД, запись показания ИБД по каналу датчиков линейного ускорения (ДЛУ) и показания датчиков угловой скорости (ДУС), при этом, идентифицируя предложенную нелинейную математическую модель ДУС, определяют нулевые сигналы ДУС, матрицу, описывающую масштабные коэффициенты, перекрестные связи, нелинейные коэффициенты, для чего разрабатывают программу автоматизации процесса калибровки, которая включает выполнение последовательности вращений и углов наклона платформы в соответствии с 6-ю указанными экспериментами при длительности интервала времени вращений и наклонов платформы порядка 3-4 минут, обработку полученных данных, включая выбор интервала времени длительностью порядка 2-3 минут с установившейся угловой скоростью и углами наклона, вычисление средних значений кодов АЦП ДУС, дифференцирование показаний угломеров и вычисление средних значений угловых скоростей платформы стола и вычисление средних значений показаний датчиков температуры, после чего используя определенные алгоритмы, определяют калибровочные коэффициенты.
Недостатком способа являются его относительно низкая точность, поскольку не учитывается годовая орбитальная скорость вращения Земли в плоскости эклиптики.
Наиболее близким по технической сущности к предложенному является способ [RU 2447404, С2, G01C 21/00, 10.04.2012], согласно которому бесплатформенный инерциальный измерительный модуль (БИИМ) устанавливается на стендовое оборудование, обеспечивающее приблизительно горизонтальное задание вектора угловой скорости с фиксированным направлением в пространстве, вращают БИИМ последовательно, как минимум, по двум непараллельным осям в базисе калибруемого БИИМ, во время вращения записывают показания БИИМ по каналу датчиков линейного ускорения (ДЛУ) и показания датчиков угловой скорости (ДУС), по сигналам ДЛУ определяют угловую скорость БИИМ в базисе ДЛУ, идентифицируя математическую модель ДУС, определяют нулевые сигналы ДУС, матрицу, описывающую масштабные коэффициенты, перекрестные связи, ориентацию осей чувствительности ДУС в БИИМ.
Недостатком наиболее близкого технического решения являются его относительно низкая точность, поскольку при определении нулевых сигналов ДУС и дрейфе нуля не учитывается годовая орбитальная скорость вращения Земли в плоскости эклиптики.
Задачей изобретения является создание способа, который относительно обеспечивает более высокую точность нулевых сигналов ДУС и дрейф нуля за счет учета годовой орбитальной скорости вращения Земли в плоскости эклиптики.
Требуемый технический результат заключается в повышении точности калибровки.
Поставленная задача решается, а требуемый технический результат достигается тем, что в способе, основанном на определении нуля дрейфа датчика угловой скорости (ДУС) из проекций вектора угловой скорости Земли на измерительные оси ДУС, вычитают расчетные проекции вектора вращения Земли вокруг собственной оси на соответствующие измерительные оси, согласно изобретению, из проекций вектора угловой скорости Земли на измерительные оси ДУС дополнительно вычитают расчетные проекции вектора годичной угловой орбитальной скорости вращения Земли в плоскости эклиптики на дату и время проведения калибровки с учетом високосности года, широты и долготы места проведения калибровки, угла между плоскостью эклиптической орбиты и экваториальной плоскостью Земли, а также собственной и переносной по эклиптической орбите угловых скоростей вращения Земли.
На чертеже представлены:
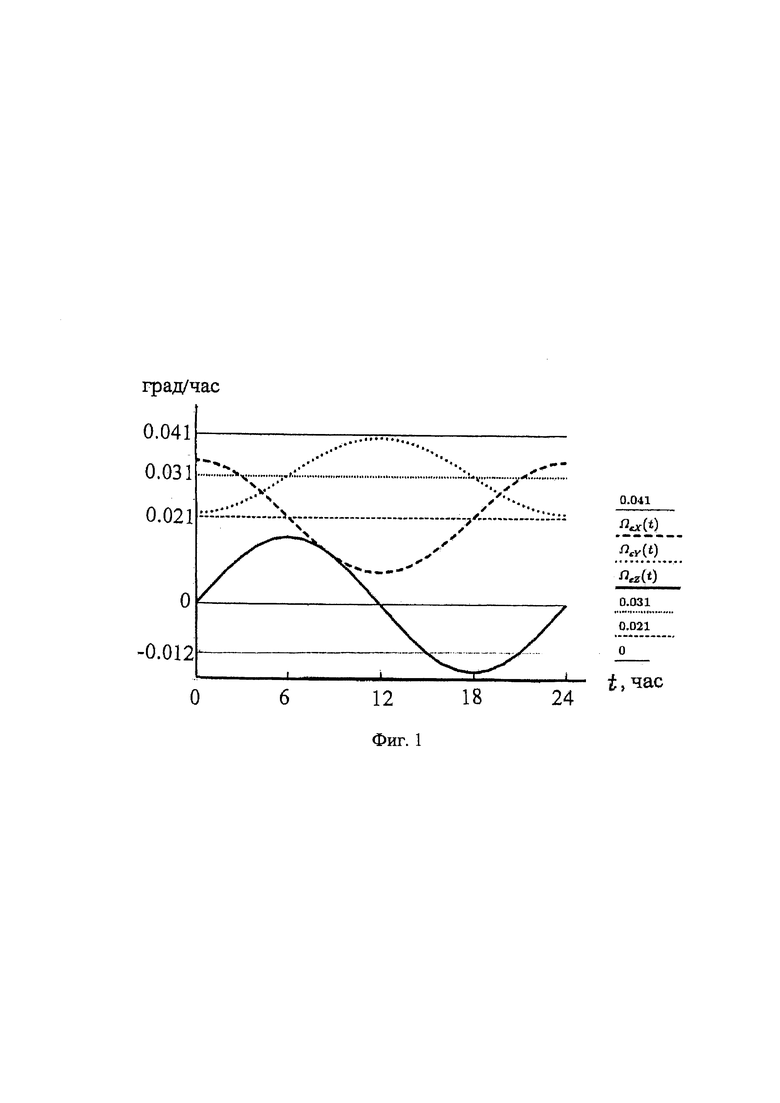
на фиг. 1 - графики проекций годичного вращения Земли на оси географической системы координат на 21 декабря 2022 года;
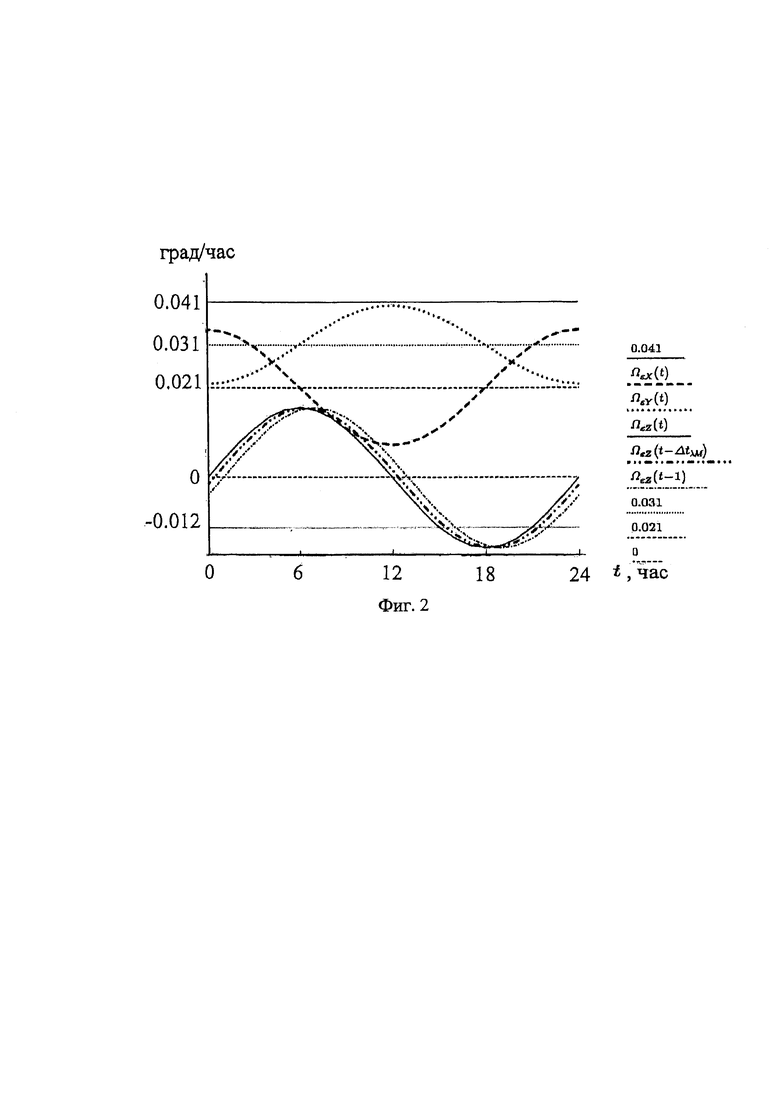
на фиг. 2 - графики проекций годичного вращения Земли на оси географической системы координат на 21 декабря 2022 года, где для оси Z приведены две граничные линии, соответствующие границам часового пояса в пределах восточных долгот 30 и 45 градусов, и одна промежуточная для долготы 39 градусов, соответствующая запаздыванию на 0,4 часа;
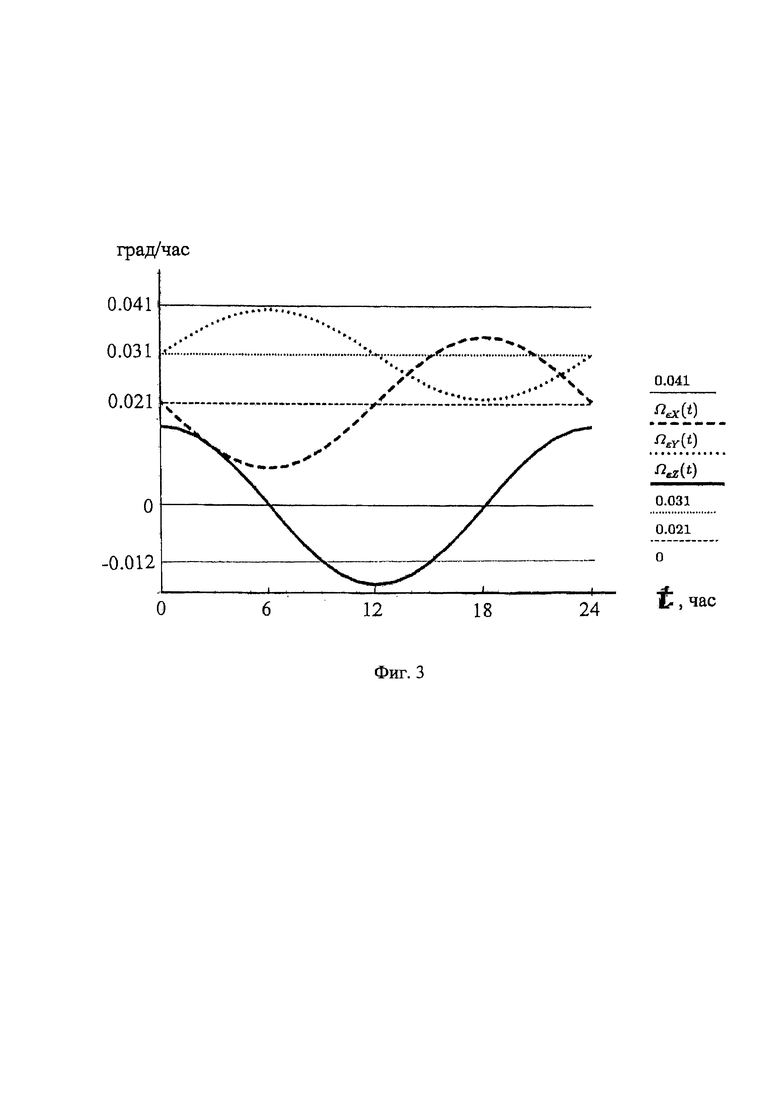
на фиг. 3 - графики проекций годичного вращения Земли на оси географической системы координат на 21 марта 2023 г.;
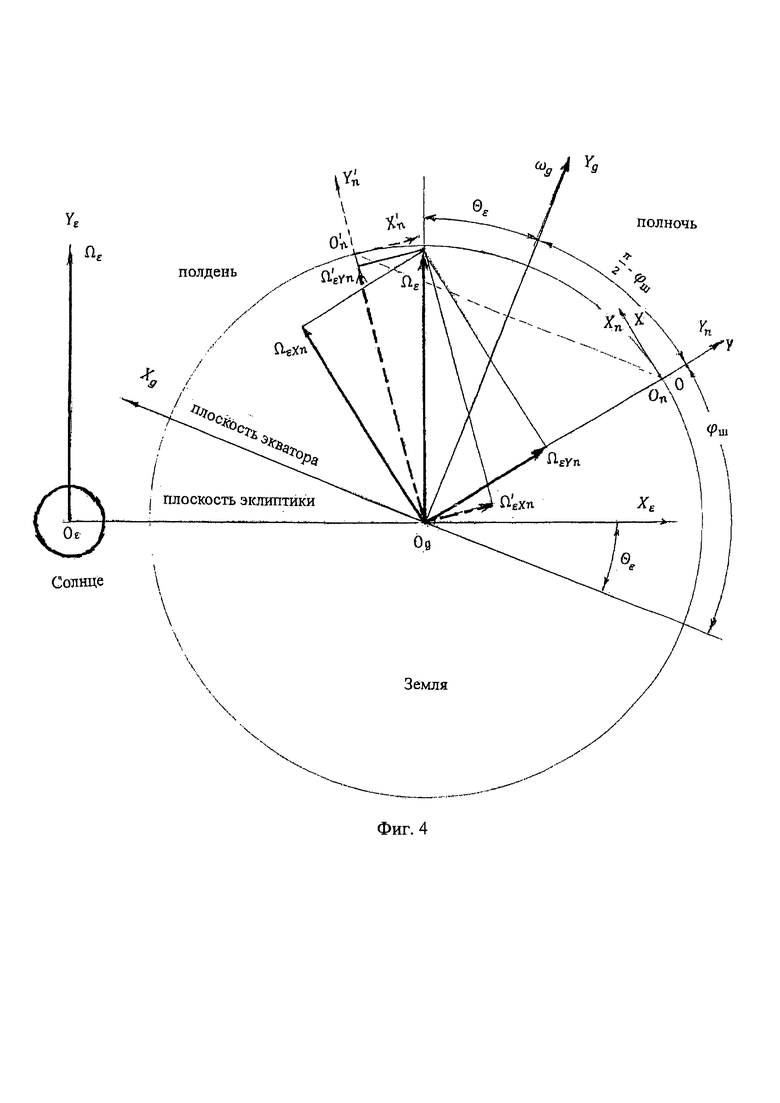
на фиг. 4 - изображена схема, поясняющая механизм изменения во времени проекций годичной (переносной) угловой скорости Земли на измерительные оси ДУС, неподвижного относительно Земли, в инерциальной геоцентрической системе координат.
На схеме изображено положение измерительных осей ДУС OnXnYn на широте ϕш в плоскости меридиана в полночь, т.е. на момент солнечных суток Земли, когда плоскости OεXεYε гелиоцентрической, OgXgYg геоцентрической, OXY географической и OnXnYn приборной систем координат совпадают. Проекции вектора угловой скорости Ωε на измерительные оси приборной системы координат OnXnYn будут ΩεXn и ΩεYn.
Через 12 часов, в полдень, в результате собственного вращения Земли ωg вокруг оси OgYg, приборная система координат займет положение, обозначенное как 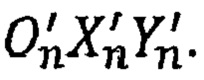 При этом проекции вектора Ωε на приборные оси будут
При этом проекции вектора Ωε на приборные оси будут 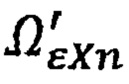 и
и 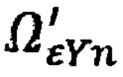 (пунктирные линии).
(пунктирные линии).
Сравнение результатов измерений проекций Ωε на измерительные оси ДУС, неподвижного относительно Земли, проводимых в разное время суток (полночь и полдень), показывает, что проекции Ωε на измерительные оси ДУС меняются в течение суточного времени Земли.
Предложенный способ калибровки реализуется следующим образом.
Предварительно проведем теоретическое обоснование предложенного способа.
Известна модель вращения Земли в инерциальной геоцентрической системе координат [Основы построения бесплатформенных инерциальных навигационных систем / В.В.Матвеев, В.Я. Распопов / Под общ. ред. д.т.н. В.Я. Распопова. - СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009, - 280 с. ISBN 978-5-900780-73-3], в которой на географическую систему координат проектируется вектор собственной угловой скорости вращения Земли (ω=15 угловых градусов в час), рассчитываемого из соотношений:
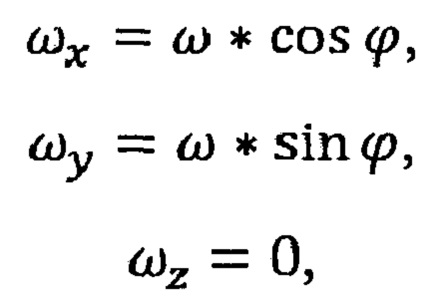
где ωx,ωy,ωz - проекции угловой скорости вращения Земли на оси географической системы координат, ϕ - географическая широта.
Возможно применить модель вращения Земли в инерциальной геоцентрической системе координат, при которой к вектору собственной угловой скорости вращения Земли со добавляется составляющая, обусловленная переносным годичным вращением Земли относительно Солнца по эклиптической орбите, рассчитываемая по формулам:
ωх=(ω+Ω) * cos ϕ,
ωу=(ω+Ω) * sin ϕ,
ωz=0,
где Ω=0,041 угловых градусов в час.
Обе модели не учитывают переменные составляющие проекций суммарного вектора угловой скорости вращения Земли на оси географической системы координат, обусловленные углом наклона плоскости экватора Земли к плоскости эклиптической орбиты θε, который составляет 23°27/ (23 угловых градусов и 27 угловых минут) [Теория инерциальных систем навигации. Бромберг П.В. - М.: Наука. Главная редакция физико-математической литературы. 1979. - 296 с.].
Этого недостатка лишена модель, построенная на следующей концепции.
Угловое движение Земли в плоскости эклиптики осуществляется за счет двух составляющих - вращения вокруг собственной оси и переносного годичного вращения.
Собственную угловую скорость вращения Земли определяем по формуле

где Ts - продолжительность средних солнечных суток, принимается равной 24 часа.
Таким образом, получаем ω=0,262 1/час (15 угловых градусов в час).
Переносную угловую скорость Земли определяем по формуле

где Ns=365.24 - среднее число суток за один год.
В результате вычислений получаем Ω=7.168 * 10-4 1/час (0.041 угловых градусов в час).
Определим суперпозиционную угловую скорость вращения Земли. Угловые скорости переносного и собственного вращений Земли являются векторами, угол между которыми равен углу между плоскостью эклиптической орбиты и экваториальной плоскостью Земли θε.
Суммарный вектор вращения Земли определяем из соотношения:
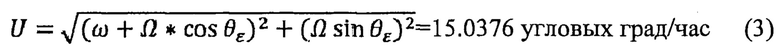
Полученная величина суммарного вектора вращения Земли с высокой точностью соответствует величине 7.29*10-5 1/с для средней солнечной секунды 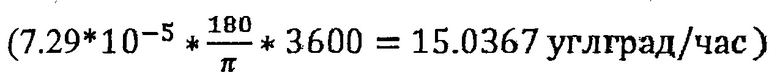 [см. Теория инерциальных систем навигации. Бромберг П.В. -М.: Наука. 1979, стр. 77].
[см. Теория инерциальных систем навигации. Бромберг П.В. -М.: Наука. 1979, стр. 77].
Предлагаемая модель формирования проекций эклиптической и векторно-суммарной угловой скорости Земли на оси географической системы координат лишена недостатков представленных выше моделей и является более точной.
В соответствии с этой моделью суточных проекций суммарного вектора угловой скорости Земли на оси географической системы координат предлагается в виде:
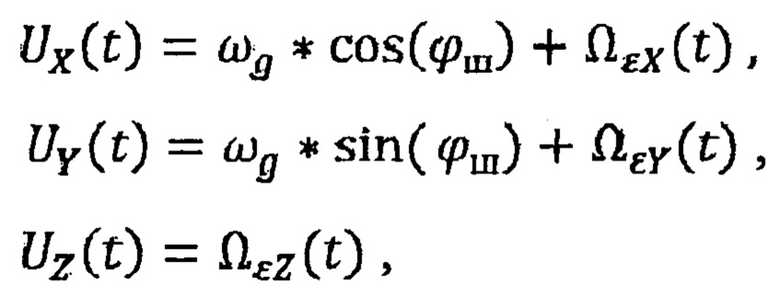
где суточные проекции эклиптической переносной угловой скорости Земли на оси географической системы координат представляются из соотношений:
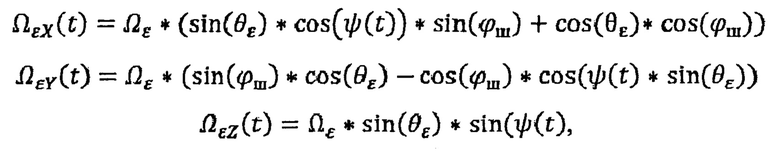
а кинематическое позиционирование Земли на эклиптической орбите вычисляется из следующих исходных данных:
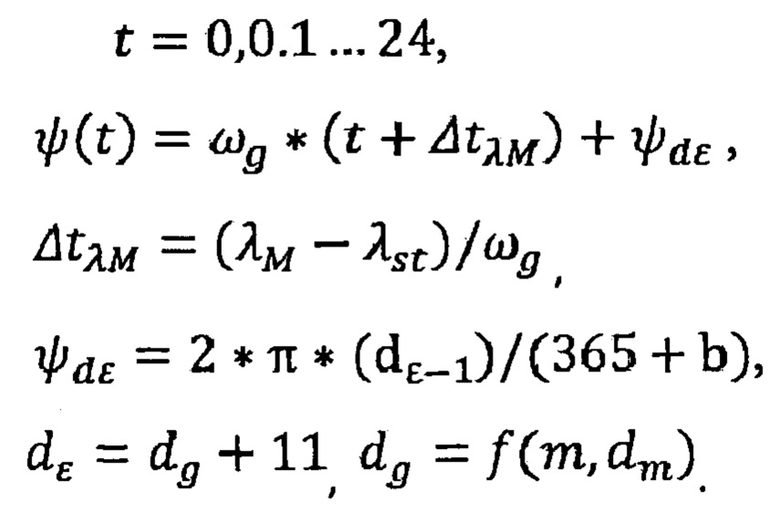
Контрольные параметры формируемых данных для предложенной модели определяются по формулам:
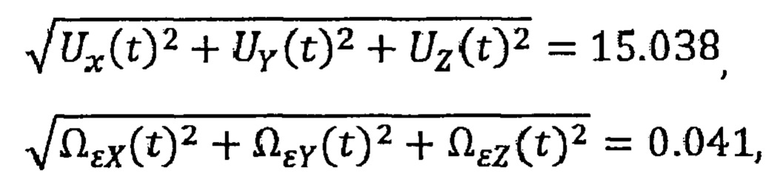
где приняты следующие обозначения:
t - часовое поясное время в течение суток, например, московское;
ψdε - угловое положение на эклиптике плоскости меридиана часового пояса Земли в начале солнечных суток на дату dε относительно положения в день зимнего солнцестояния (dε=1);
dg - порядковый день земного года, определяется датой (число, месяц) по земному календарю;
m - порядковый номер месяца по земному календарю;
dm - номер дня, индексируемый номером соответствующего месяца земного календаря;
dε - порядковый день года по эклиптическому календарю, отсчет от дня зимнего солнцестояния;
λМ - географическая долгота, определяется часовым поясом места проведения испытаний;
λst - географическая долгота места проведения испытаний, располагается в пределах часового пояса;
ΔtxM - временная поправка, обусловленная разностью между географическими долготами λМ и λst;
ϕш - географическая широта места проведения испытаний;
θε - угол между плоскостью эклиптической орбиты и экваториальной плоскостью Земли;
ωg - угловая скорость собственного вращения Земли;
Ωε - переносная угловая скорость годичного вращения Земли;
b - високосность года: b=1 - високосный год, иначе b=0.
Приведенные контрольные параметры свидетельствуют, что в течение суток сумма квадратов проекций переносной угловой скорости Земли соответствует ее значению 0,041 угловой град/час, а суперпозиционный вектор округленному значению величины 15,0376 угловых град/час.
Результаты моделирования (время московское, северная широта 55,76 градусов, восточная долгота в пределах 30-45 градусов, даты 21 декабря 2022 года и 21 марта 2023 года).
На фиг. 1 приведены графики проекций годичного вращения Земли на оси географической системы координат на 21 декабря 2022 г.
Ниже приводятся проекции суточного переносного вращения Земли на оси географической системы координат на время 0, 6, 12 и 18 часов по московскому времени:
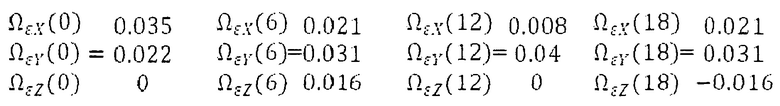
На фиг. 2 приведены графики проекций годичного вращения Земли на оси географической системы координат на 21 декабря 2022 г. в пределах часового пояса. При этом, для оси Z приведены две граничные линии, соответствующие границам часового пояса в пределах восточных долгот 30 и 45 градусов, и одна промежуточная соответствует для долготы 39 градусов, соответствующая запаздыванию на 0,4 часа и 1 час.
Ниже приводятся проекции суточного переносного вращения Земли на ось Z географической системы координат на время 0, 3 и 6 часов по промежуточная соответствует для долготы 39 градусов, соответствующая запаздыванию на 0,4 часа и 1 час.
Ниже приводятся проекции суточного переносного вращения Земли на ось Z географической системы координат на время 0, 3 и 6 часов по московскому времени, что соответствует запаздыванию по времени на 0,4 и 1 час.
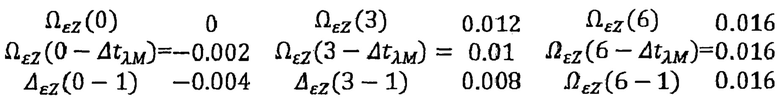
На фиг. 3 приведены графики проекций годичного вращения Земли на оси географической системы координат на 21 марта 2022 г. Эти графики в сравнении с фиг. 2 демонстрирует изменения проекций вектора переносного (годичного) вращения Земли в зависимости от даты.
При моделировании были использованы следующие параметры:
ωg=15, Ωε=0,041, θε=23.45, ϕш=55.76, ΔλМ=0.4.
Таким образом, благодаря введенным усовершенствованиям в предложенном техническом решении достигается требуемый технический результат, который заключается в повышении точности калибровки, поскольку при его реализации дополнительно учитываю расчетные проекции вектора годичной угловой орбитальной скорости вращения Земли в плоскости эклиптики на дату и время проведения калибровки.
Изобретение относится к навигации и может быть использовано при калибровке прецизионных датчиков угловой скорости на этапе начальной подготовки инерциальной навигационной системы. Способ калибровки прецизионных датчиков угловой скорости (ДУС) основан на определении нуля дрейфа ДУС из проекций вектора угловой скорости Земли на измерительные оси ДУС, и согласно которому вычитают расчетные проекции вектора вращения Земли вокруг собственной оси на соответствующие измерительные оси, при котором из проекций вектора угловой скорости Земли на измерительные оси ДУС дополнительно вычитают расчетные проекции вектора годичной угловой орбитальной скорости вращения Земли в плоскости эклиптики на дату и время проведения калибровки с учетом високосности года, широты и долготы места проведения калибровки, угла между плоскостью эклиптической орбиты и экваториальной плоскостью Земли, а также собственной и переносной по эклиптической орбите угловых скоростей вращения Земли. Технический результат – повышение точности калибровки. 4 ил.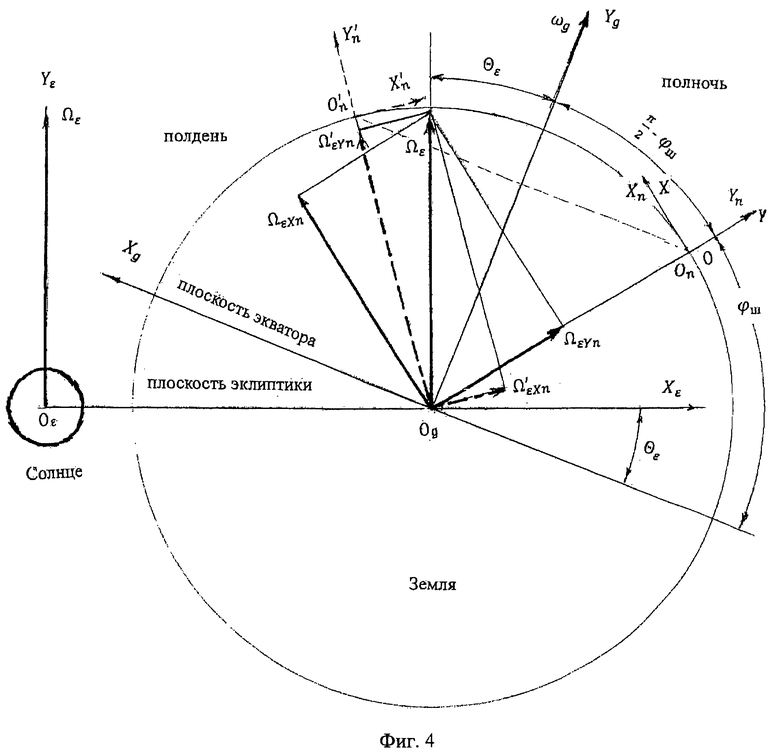
Способ калибровки прецизионных датчиков угловой скорости с учетом годичной угловой орбитальной скорости вращения Земли, основанный на определении нуля дрейфа датчика угловой скорости (ДУС) из проекций вектора угловой скорости Земли на измерительные оси ДУС, неподвижного относительно Земли, согласно которому вычитают расчетные проекции вектора вращения Земли вокруг собственной оси на соответствующие измерительные оси, отличающийся тем, что из проекций вектора угловой скорости Земли на измерительные оси ДУС дополнительно вычитают расчетные проекции вектора годичной угловой орбитальной скорости вращения Земли в плоскости эклиптики на дату и время проведения калибровки с учетом високосности года, широты и долготы места проведения калибровки, угла между плоскостью эклиптической орбиты и экваториальной плоскостью Земли, а также собственной и переносной по эклиптической орбите угловых скоростей вращения Земли.
| СПОСОБ КАЛИБРОВКИ ДАТЧИКОВ УГЛОВОЙ СКОРОСТИ БЕСПЛАТФОРМЕННОГО ИНЕРЦИАЛЬНОГО ИЗМЕРИТЕЛЬНОГО МОДУЛЯ | 2010 |
|
RU2447404C2 |
| СПОСОБ И УСТРОЙСТВО КАЛИБРОВКИ ИНЕРЦИАЛЬНЫХ ИЗМЕРИТЕЛЬНЫХ МОДУЛЕЙ | 2017 |
|
RU2669263C1 |
| СПОСОБ КАЛИБРОВКИ УГЛОВ РАССОГЛАСОВАНИЯ ОСИ ДАТЧИКА УГЛА НЕУПРАВЛЯЕМОГО ГИРОСКОПА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ ЕГО КОРПУСА | 2005 |
|
RU2308683C1 |
| СПОСОБ И УСТРОЙСТВО КАЛИБРОВКИ ИНЕРЦИАЛЬНЫХ ИЗМЕРИТЕЛЬНЫХ МОДУЛЕЙ | 2015 |
|
RU2602736C1 |
| CN 106525073 B, 12.07.2019. | |||
Авторы
Даты
2023-12-29—Публикация
2023-10-03—Подача