Изобретение относится к области вычислительной техники и может быть использовано для обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов (ПСКВ) при выполнении вычислений и преобразований, реализованных в поле Галуа GF(28), а также при передаче информации по каналам связи.
Известно устройство для коррекции ошибок в полиномиальной системе классов вычетов (пат. RU 2453902, опубл. 20.06.2012) содержащее регистр, модуль вычисления синдрома ошибки, блок памяти, сумматор, при этом модуль вычисления синдрома ошибки содержит два блока вычисления синдрома ошибки, каждый из которых содержит четыре многовходовых сумматора по модулю.
Недостатком данного устройства являются значительные аппаратурные затраты.
Основной задачей данного изобретения является снижение объема оборудования, которое выражается в уменьшение объема блок памяти, в котором хранятся вектора ошибки.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является снижение объема оборудования.
Указанный технический результат достигается за счет введения блока сравнения синдромов ошибки и изменения структуры модуля вычисления синдрома ошибки. В результате этого при использовании кода ПСКВ, содержащего два информационных и два контрольных остатка, объем блока памяти сокращается на 25% по сравнению с прототипом.
Технический результат достигается тем, что в устройство для коррекции ошибок в полиномиальной системе классов вычетов, содержащее регистр, вход которого является входом устройства, модуль вычисления синдрома ошибки, который включает в себя первый и второй блоки вычисления синдрома ошибки, входы модуля вычисления синдрома ошибки подключены в первому, второму и третьему выходам регистра, выход блок памяти подключен к четвертому входу выходного сумматора, первый, второй и третий входы которого соединены соответственно с первым, вторым и третьим выходами регистра согласно прототипу, введен блок сравнения синдромов ошибки, входы которого подключены к выходам модуля вычисления синдрома ошибки, при этом первый и второй выходы блока сравнения синдромов ошибки подключены к первому и второму входам блока памяти соответственно, а третий выход подключен к пятому входу сумматора. При этом модуль вычисления синдрома ошибки содержит 16 входов, первый и второй блок вычисления синдрома ошибки, причем каждый из них содержит по четыре многовходовых сумматоров по модулю два, причем входы первого многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к входам 9, 13, 17 модуля вычисления синдрома ошибки модуля, входы второго многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к входам 10, 14, 18 модуля вычисления синдрома ошибки, входы третьего многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к входам 11, 15, 19 модуля вычисления синдрома ошибки, входы четвертого многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к входам 12, 16, 20 модуля вычисления синдрома ошибки модуля, выходы данных сумматоров являются первым выходом модуля вычисления синдрома ошибки, входы первого многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключен к 1, 5, 6, 13 входам 9, 13, 14, 21 модуля вычисления синдрома ошибки модуля, входы второго многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключены к входам модуля 10, 13, 15, 22 вычисления синдрома ошибки, входы третьего многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключен к входам 11, 13, 16, 23 модуля вычисления синдрома ошибки, входы четвертого многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключен к входам 12, 13, 24, при этом выходы данных многовходовых сумматоров являются вторым выходом модуля вычисления синдрома ошибки.
Рассмотрим принципы построения кодов полиномиальной системы классов вычетов. Для их создания выбирают основания, в качестве которых выступают неприводимые полиномы 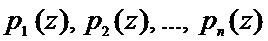 , для которых справедливо
, для которых справедливо
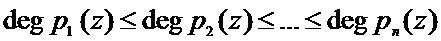 , (1)
, (1)
где 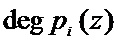 – степень полинома
– степень полинома  ;
; 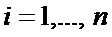 .
.
Произведение выбранных оснований определяют рабочий диапазон кода ПСКВ
 . (2)
. (2)
Чтобы получить кодовую комбинацию ПСКВ, надо выбрать целое двоичное число К, затем представить его в полиномиальной форме К(z). Если выполняется условие
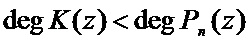 , (3)
, (3)
то получаем кортеж остатков
 , (4)
, (4)
где  ;
; 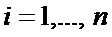 .
.
Так как коды ПСКВ являются арифметическими, то с помощью их можно эффективно выполнять модульные операции. В этом случае для двух полиномов К(z) и Y(z) справедливо
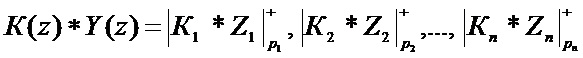 , (5)
, (5)
где * – операции сложения, вычитания и умножения;  ;
; 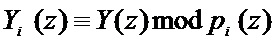 ;
;  .
.
Выражение (5) наглядно показывают достоинства ПСКВ. Во-первых, данные операции выполняются параллельно. Во-вторых, между основаниями модулярных кодов классов вычетов (МККВ) при вычислениях отсутствуют переносы. В-третьих, операнды 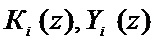 , где
, где  , имеют меньшую разрядность, чем полиномы К(z) и Y(z). Обобщая, можно сделать вывод о том, что коды ПСКВ поддерживают параллельные вычисления, что позволяет повысить скорость вычислений.
, имеют меньшую разрядность, чем полиномы К(z) и Y(z). Обобщая, можно сделать вывод о том, что коды ПСКВ поддерживают параллельные вычисления, что позволяет повысить скорость вычислений.
При этом, благодаря параллельным вычислениям по основаниям 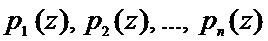 , коды ПСКВ способны обнаруживать и корректировать ошибки, которые возникают в остатках кодовой комбинации.
, коды ПСКВ способны обнаруживать и корректировать ошибки, которые возникают в остатках кодовой комбинации.
Известно, что для исправления однократной ошибки, под которой подразумевается искажение одного остатка в кодовой комбинации ПСКВ, необходимо ввести два контрольных остатка  . В этом случае получаем избыточную комбинацию
. В этом случае получаем избыточную комбинацию
 . (6)
. (6)
В прототипе показан алгоритм обнаружения и коррекции в ПСКВ, в котором для вычисления двух контрольных остатков  используется одно контрольное основание
используется одно контрольное основание 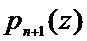 . При этом для данного основания выполняется условие
. При этом для данного основания выполняется условие
 . (7)
. (7)
Контрольные остатки вычисляются согласно
 (8)
(8)
где - Σ суммирование по модулю два; i(z) - полиномиальная форма i-го порядкового номера основания;  .
.
Для обнаружения и коррекции ошибок в коде ПСКВ берутся информационные остатки  , и с помощью них вычисляются контрольные остатки согласно
, и с помощью них вычисляются контрольные остатки согласно
 (9)
(9)
Если в процессе вычислений и передачи по каналу связи в избыточной кодовой комбинации 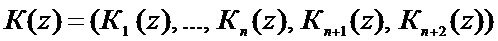 не возникла ошибка, то синдром ошибки, вычисляемый по формуле
не возникла ошибка, то синдром ошибки, вычисляемый по формуле
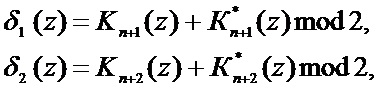 (10)
(10)
будет равен нулю.
Пусть в j-ом остатке произошла ошибка. Тогда ошибочный остаток примет вид
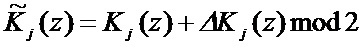 , (11)
, (11)
где  - глубина ошибки;
- глубина ошибки; 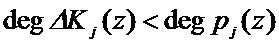 .
.
Тогда ошибочная комбинация кода ПСКВ будет иметь вид
 . (12)
. (12)
В этом случае синдром ошибки будет отличен от нуля. Причем по величине синдрома ошибки можно однозначно определить j-ый ошибочный остаток, а также вектор ошибки, который имеет вид
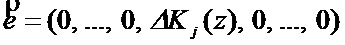 , (14)
, (14)
Тогда процесс исправления имеет вид
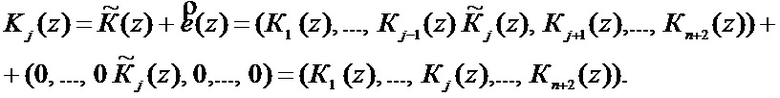 (15)
(15)
Анализ выражения (10) показывает, что если значения синдрома будут равны, то есть  , то это означает, что ошибка произошла по первому основанию кода ПСКВ, а ее глубина равна
, то это означает, что ошибка произошла по первому основанию кода ПСКВ, а ее глубина равна
 . (16)
. (16)
Тогда в блоке памяти можно не хранить векторы ошибок, которым соответствуют синдромы  , а сразу после сравнения
, а сразу после сравнения  , прибавить их к первому ошибочному остатку
, прибавить их к первому ошибочному остатку
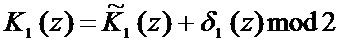 , (17)
, (17)
где  - ошибочный первый остаток.
- ошибочный первый остаток.
Если степень первого основания кода ПСКВ равна  , то объем блока памяти можно уменьшить на
, то объем блока памяти можно уменьшить на  векторов ошибок. Таким образом, будут сокращены аппаратурные затраты на реализацию устройства коррекции ошибок в полиномиальной системе классов вычетов.
векторов ошибок. Таким образом, будут сокращены аппаратурные затраты на реализацию устройства коррекции ошибок в полиномиальной системе классов вычетов.
В настоящее время многие вычисления производится в поле GF(28). Данное поле Галуа было выбрано благодаря простоте реализации вычислительных устройств, в которых входные данные и результаты представляются в виде байтов. Представление этих данных в виде кода ПСКВ позволит обнаруживать и корректировать ошибки, которые могут возникнуть в кодовых комбинациях при вычислениях и передаче по каналу связи.
Пусть в качестве информационных оснований кода ПСКВ выбраны неприводимые полиномы  и
и 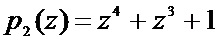 . Тогда рабочий диапазон данного кода равен
. Тогда рабочий диапазон данного кода равен  . Значит любой элемент поля GF(28) можно однозначно представить в данном коде ПСКВ. Пусть задан байт К = 1001010. В полиномиальной форме байт имеет вид
. Значит любой элемент поля GF(28) можно однозначно представить в данном коде ПСКВ. Пусть задан байт К = 1001010. В полиномиальной форме байт имеет вид 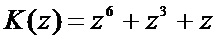 . Представим данный полином в ПСКВ
. Представим данный полином в ПСКВ
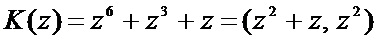 ,
,
где  ;
;  .
.
В качестве контрольного основания выберем  .
.
Согласно (8) вычислим контрольные основания кодовой комбинации

Тогда избыточная комбинация имеет вид
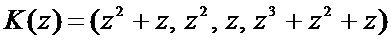 .
.
Пусть в данной кодовой комбинации ошибка отсутствует. Вычислим проверочные остатки, используя (9)

Тогда синдром ошибки равен

Так как синдром ошибки равен нулю, то комбинация не содержит ошибки.
Пусть в процессе вычислений ошибка произошла по первому основанию, а ее глубина равна  . Тогда ошибочный остаток имеет вид
. Тогда ошибочный остаток имеет вид 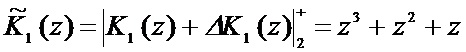 . Тогда комбинация имеет вид
. Тогда комбинация имеет вид
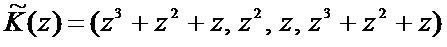 .
.
Вычислим проверочные остатки, используя (9)
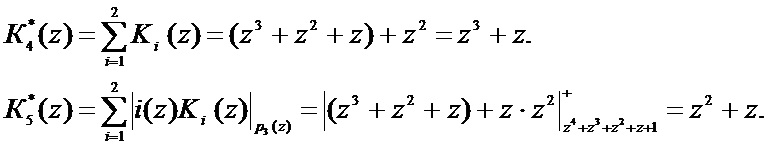
Тогда синдром ошибки равен
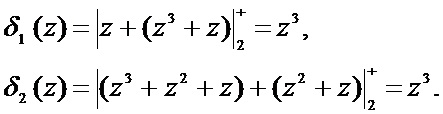
В таблице 1 приведены ошибочные остатки, глубина, синдромы и вектора ошибки для данного кода ПСКВ.
Таблица 1
Получили синдром, для которого справедливо 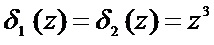 . Данный результат зафиксирован в блоке сравнения синдромов ошибки. Как показано в таблице 1 данному синдрому ошибки соответствует вектор ошибки
. Данный результат зафиксирован в блоке сравнения синдромов ошибки. Как показано в таблице 1 данному синдрому ошибки соответствует вектор ошибки 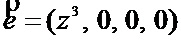 . Значит, этот вектор ошибки можно в блоке памяти не хранить, а полученный синдром
. Значит, этот вектор ошибки можно в блоке памяти не хранить, а полученный синдром 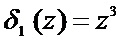 сразу прибавить по модулю два к первому ошибочному остатку. Получаем
сразу прибавить по модулю два к первому ошибочному остатку. Получаем
 .
.
Искаженный остаток исправлен без использования вектора ошибок.
Пусть в процессе вычислений ошибка произошла по второму основанию, а ее глубина равна  . Тогда ошибочный остаток имеет вид
. Тогда ошибочный остаток имеет вид 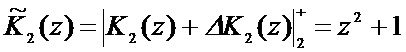 . Тогда комбинация имеет вид
. Тогда комбинация имеет вид
 .
.
Вычислим проверочные остатки, используя (9)
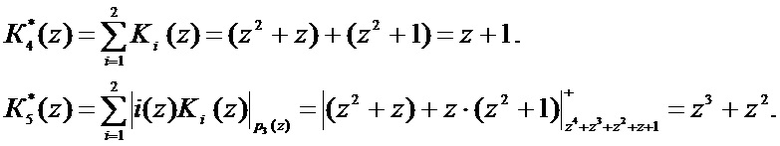
Тогда синдром ошибки равен
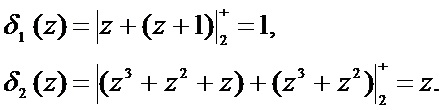
Получили синдром, для которого справедливо  . Данный результат зафиксирован в блоке сравнения синдромов ошибки. Значит, полученный синдром ошибки необходимо передать в блок памяти, где хранятся вектора ошибок.
. Данный результат зафиксирован в блоке сравнения синдромов ошибки. Значит, полученный синдром ошибки необходимо передать в блок памяти, где хранятся вектора ошибок.
Для данного синдрома вектор ошибки имеет вид
 .
.
Исправим ошибочную комбинацию
 .
.
В рассмотренном примере, когда комбинация ПСКВ имеет два информационных и два контрольных остатка, использование блока сравнения синдромов ошибки позволило уменьшить объем блока памяти на 25% от общего объема блока памяти в прототипе.
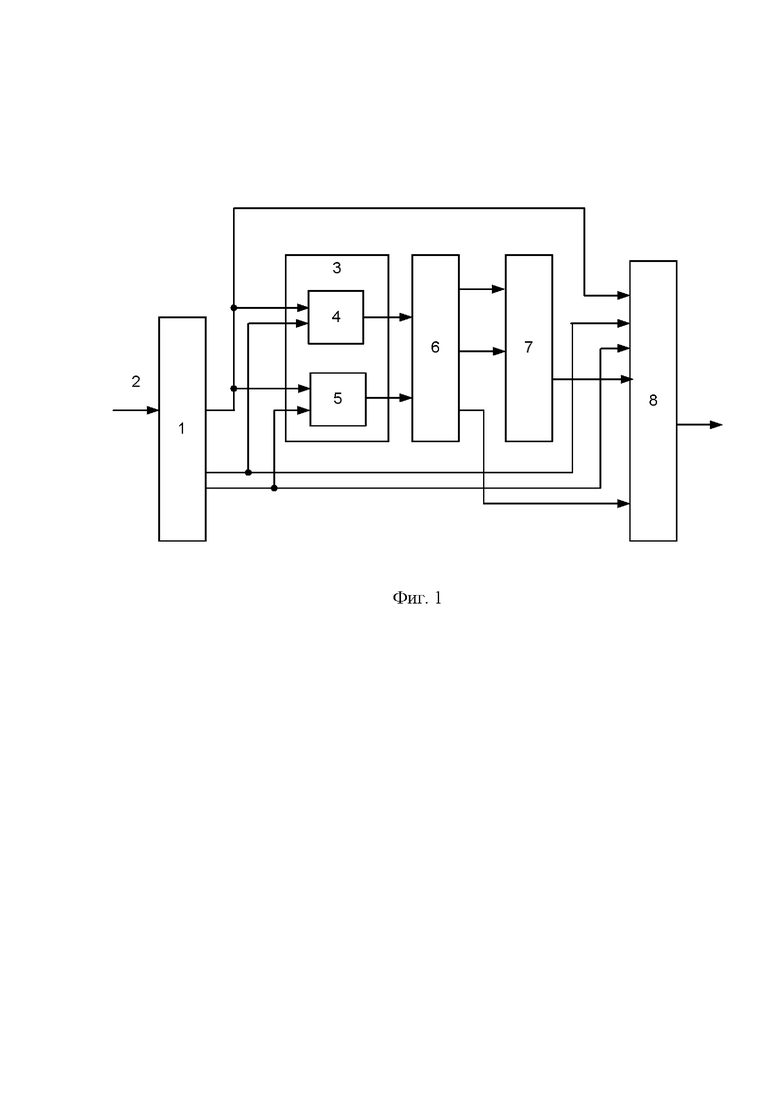
На фиг. 1 представлена функциональная схема устройства. Она включает: регистр 1, вход устройства 2, модуль вычисления синдрома ошибки 3, содержащий первый блок вычисления синдрома ошибки 4, второй блок вычисления синдрома ошибки 5, блок сравнения синдромов ошибки 6, блок памяти 7, сумматор 8.
При этом вход регистра 1 подключен к входу 2 устройства. Первый выход регистра 1 подсоединен к первому входу сумматора 8, а также к первым входам первого 4 и второго 5 блоков вычисления синдрома ошибки, входящих в состав модуля вычисления синдрома ошибки 3. Второй выход регистра 1 подключен ко второму входу сумматора 8, а также ко второму входу первого блока вычисления синдрома ошибки 4. Третий выход регистра 1 подключается к третьему входу сумматора 8, а также ко второму входу второго блока вычисления синдрома ошибки 5. Выходы блоков вычисления синдрома ошибки 4 и 5 подсоединены к первому и второму входам блока сравнения синдромов ошибки 6 соответственно. Первый и второй выходы блока сравнения синдромов ошибки 6 подключены к первому и второму входам блока памяти 7, выход которого подключен к четвертому входу сумматора 8, а к пятому входу сумматора 8 подключен третий выход блока сравнения синдромов ошибки 6. Выход сумматора 8 является выходом устройства.
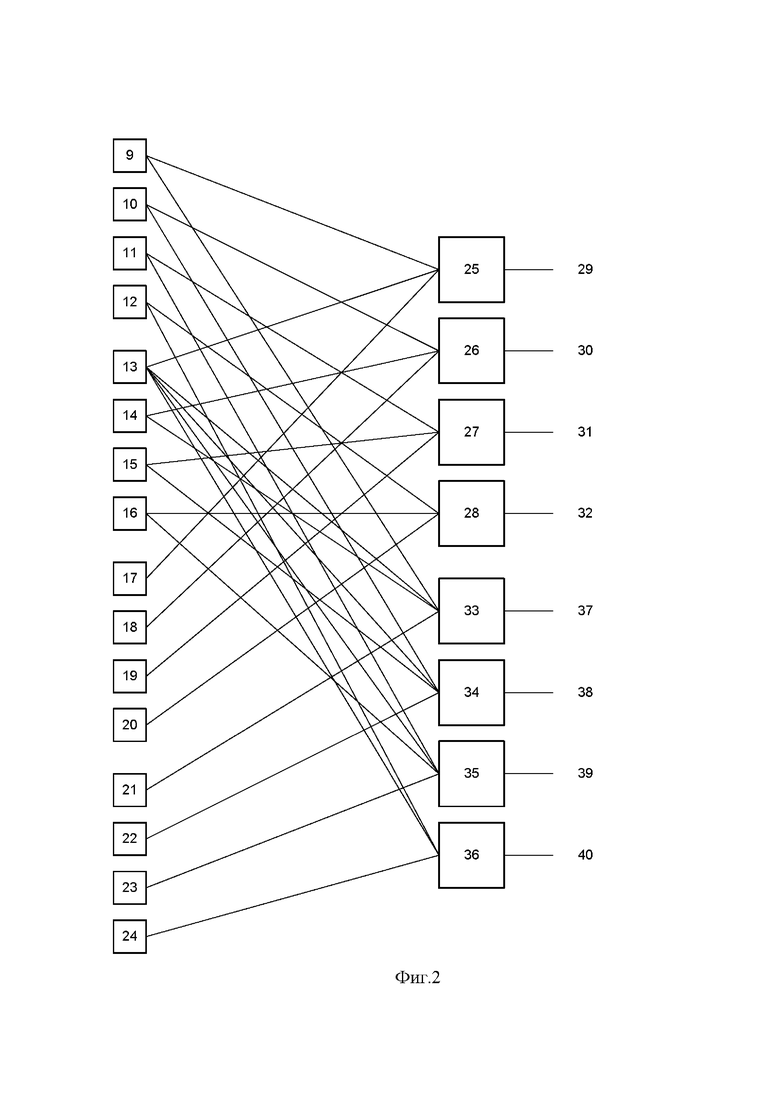
Структура модуля вычисления синдрома ошибки 3 представлена на фиг. 2. Модуль содержит входы 9-24, подключенные к выходам регистра 1, первый и второй блоки вычисления синдрома ошибки. Первый блок вычисления синдрома ошибки содержит многовходовые сумматоры по модулю два 25-28, имеющие соответствующие выходы 29-32. Второй блок вычисления синдрома ошибки содержит четыре многовходовых сумматора по модулю два 33-36, имеющих выходы 37-40 соответственно. Данный модуль предназначен для работы с кодовой комбинацией ПСКВ, содержащей четыре остатка 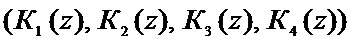 . Первые два остатка являются информационными и получены по основаниям
. Первые два остатка являются информационными и получены по основаниям  и
и 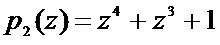 . Они в двоичном параллельном коде поступают на входы 9-12 и 13-16 соответственно. Третий и четвертый остатки являются контрольными, вычисленными с помощью выражения (8). В качестве контрольного основания использовался
. Они в двоичном параллельном коде поступают на входы 9-12 и 13-16 соответственно. Третий и четвертый остатки являются контрольными, вычисленными с помощью выражения (8). В качестве контрольного основания использовался  . Они в двоичном параллельном коде поступают на входы 17-20 и 21-24 соответственно. Старшие разряды остатков
. Они в двоичном параллельном коде поступают на входы 17-20 и 21-24 соответственно. Старшие разряды остатков 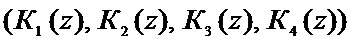 подаются на 9, 13, 17, 21 входы соответственно.
подаются на 9, 13, 17, 21 входы соответственно.
Первый блок вычисления синдрома ошибки содержит многовходовые сумматоры по модулю два 25-28, имеющие соответствующие выходы 29-32. Входы первого сумматора 25 по модулю два подключены к входам 9, 13, 17. Входы второго сумматора 26 по модулю два подключены к входам 10, 14, 18. Входы третьего сумматора 27 по модулю два подключены к входам 11, 15, 19. Входы четвертого сумматора 28 по модулю два подключены к входам 12, 16, 20. С выходов этих сумматоров по модулю два снимается параллельный двоичный код первого синдрома ошибки δ1(z). Старший разряд δ1(z) снимается с выхода 29, а младший - с выхода 32 соответственно.
Второй блок вычисления синдрома ошибки содержит многовходовые сумматоры по модулю два 33-36, имеющие соответствующие выходы 37-40. Входы первого сумматора 33 по модулю два подключены к входам 9, 13, 14, 21. Входы второго сумматора 34 по модулю два подключены к входам 10, 13, 15, 22. Входы третьего сумматора 35 по модулю два подключены к входам 11, 13, 16, 23. Входы четвертого сумматора 36 по модулю два подключены к входам 12, 13, 24. С выходов этих сумматоров по модулю два снимается параллельный двоичный код первого синдрома ошибки δ2(z). Старший разряд δ2(z) снимается с выхода 27, а младший - с выхода 40 соответственно.
Рассмотрим работу устройства при отсутствии ошибок. Пусть на вход 2 устройства поступила комбинация  , которая в двоичном коде имеет вид
, которая в двоичном коде имеет вид  . Она заносится в регистр 1. Первые два остатка через первый выход регистра 1 подаются на первые входы первого 4 и второго 5 блоков вычисления синдрома ошибки, входящих в состав модуля вычисления синдрома ошибки 3, а также на первый вход сумматора 8. Третий остаток в виде двоичного кода через второй выход регистра 1 подается на второй вход первого блока вычисления синдрома ошибки 4 и второй вход сумматора 8. Четвертый остаток в виде двоичного кода через третий выход регистра 1 подается на второй вход второго блока вычисления синдрома ошибки 5 и третий вход сумматора 8.
. Она заносится в регистр 1. Первые два остатка через первый выход регистра 1 подаются на первые входы первого 4 и второго 5 блоков вычисления синдрома ошибки, входящих в состав модуля вычисления синдрома ошибки 3, а также на первый вход сумматора 8. Третий остаток в виде двоичного кода через второй выход регистра 1 подается на второй вход первого блока вычисления синдрома ошибки 4 и второй вход сумматора 8. Четвертый остаток в виде двоичного кода через третий выход регистра 1 подается на второй вход второго блока вычисления синдрома ошибки 5 и третий вход сумматора 8.
Рассмотрим работу первого 4 и второго 5 блоков вычисления синдрома ошибки, входящих в состав модуля вычисления синдрома ошибки 3. Входная кодовая комбинация, представленная в двоичном коде, будет подана на соответствующие входы модуля вычисления синдрома ошибки 3. Распределение двоичных битов комбинации  показано в таблице 2.
показано в таблице 2.
Таблица 2
Втаблице 3 показана работа первого 4 блока вычисления синдрома ошибки. В каждой строке таблицы 3 показан двоичный код, который поступает на входы многовходовых сумматоров по модулю два 25-28. Сигнал на выходах 29-32 представлен в последнем столбце таблицы 3. Он получается путем суммирования по модулю два битов строки.
Таблица 3
В таблице 4 показана работа второго 5 блока вычисления синдрома ошибки.
Таблица 4
Таким образом, с выходов модуля вычисления синдрома ошибки 3 снимается нулевой синдром ошибки. Данный синдром поступает на входы блока сравнения синдромов ошибки 6, а затем через первый и второй выходы подается на входы блока памяти 7. С выхода блока памяти 7 снимается вектор ошибки  . Данный вектор поступает на четвертый вход сумматора 8, который выполняет суммирование
. Данный вектор поступает на четвертый вход сумматора 8, который выполняет суммирование

Пусть ошибка произошла по первому основанию, а ее глубина равна 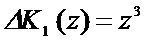 . Тогда ошибочная комбинация в двоичном коде имеет вид
. Тогда ошибочная комбинация в двоичном коде имеет вид
 .
.
В таблице 5 показана работа первого 4 блока вычисления синдрома ошибки для данного случая.
Таблица 5
В таблице 6 показана работа второго 5 блока вычисления синдрома ошибки для данной комбинации.
Таблица 6
Вычисленный синдром  подается с выходов модуля вычисления синдрома ошибки 3 на входы блока сравнения синдромов ошибки 6. Так как выполняется условие
подается с выходов модуля вычисления синдрома ошибки 3 на входы блока сравнения синдромов ошибки 6. Так как выполняется условие  , то с третьего выхода блока сравнения синдромов ошибки 6 на пятый вход сумматора 8 поступает
, то с третьего выхода блока сравнения синдромов ошибки 6 на пятый вход сумматора 8 поступает  . Сумматор 8 корректирует ошибку в первом остатке
. Сумматор 8 корректирует ошибку в первом остатке
 .
.
В результате получаем разрешенную комбинацию

Пусть ошибка произошла по второму основанию, а ее глубина равна  . Тогда ошибочная комбинация в двоичном коде имеет вид
. Тогда ошибочная комбинация в двоичном коде имеет вид
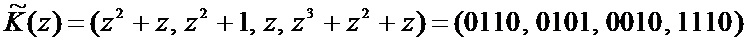 .
.
В таблице 7 показана работа первого 4 блока вычисления синдрома ошибки для данного случая.
Таблица 7
В таблице 8 показана работа второго 5 блока вычисления синдрома ошибки.
Таблица 8
Вычисленный синдром  подается с выходов модуля вычисления синдрома ошибки 3 на входы блока сравнения синдромов ошибки 6. Так как условие
подается с выходов модуля вычисления синдрома ошибки 3 на входы блока сравнения синдромов ошибки 6. Так как условие  не выполняется, то с первого и второго выходов блока сравнения синдромов ошибки 6 синдром ошибки
не выполняется, то с первого и второго выходов блока сравнения синдромов ошибки 6 синдром ошибки  подается на входы блока памяти 7. С выхода блока памяти 7 снимается вектор ошибки
подается на входы блока памяти 7. С выхода блока памяти 7 снимается вектор ошибки 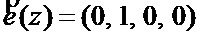 . Данный вектор поступает на четвертый вход сумматора 8, который выполняет суммирование
. Данный вектор поступает на четвертый вход сумматора 8, который выполняет суммирование

В результате ошибка исправлена.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2010 |
|
RU2453902C2 |
| Устройство для коррекции ошибок в полиномиальной системе классов вычетов | 2024 |
|
RU2835075C1 |
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2008 |
|
RU2393529C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ | 2014 |
|
RU2560823C1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЛА ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С КОРРЕКЦИЕЙ ОШИБКИ | 2006 |
|
RU2309535C1 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
Настоящее техническое решение относится к области вычислительной техники. Технический результат заключается в снижении объема оборудования. Технический результат достигается за счёт того, что устройство содержит регистр, модуль вычисления синдрома ошибки, блок сравнения синдромов ошибки, блок памяти, сумматор, при этом модуль вычисления синдрома ошибки содержит два блока вычисления синдрома ошибки, каждый из которых содержит четыре многовходовых сумматора по модулю два. 8 табл., 2 ил.
Устройство для коррекции ошибок в полиномиальной системе классов вычетов, содержащее регистр, вход которого является входом устройства, модуль вычисления синдрома ошибки, который включает в себя первый и второй блоки вычисления синдрома ошибки, входы модуля вычисления синдрома ошибки подключены в первому, второму и третьему выходам регистра, выход блок памяти, выход которого подключен к четвертому входу выходного сумматора, первый, второй и третий входы которого соединены соответственно с первым, вторым и третьим выходами регистра, отличающееся тем, что в него введен блок сравнения синдромов ошибки, входы которого подключены к выходам модуля вычисления синдрома ошибки, при этом первый и второй выходы блока сравнения синдромов ошибки подключены к первому и второму входам блока памяти соответственно, а третий выход подключен к пятому входу сумматора, при этом модуль вычисления синдрома ошибки содержит 16 входов, первый и второй блок вычисления синдрома ошибки, причем каждый из них содержит по четыре многовходовых сумматоров по модулю два, причем входы первого многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к первому, пятому, девятому входам модуля вычисления синдрома ошибки модуля, входы второго многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены ко второму, шестому, десятому входам модуля вычисления синдрома ошибки, входы третьего многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к третьему, седьмому, одиннадцатому входам модуля вычисления синдрома ошибки, входы четвертого многовходового сумматора по модулю два первого блока вычисления синдрома ошибки подключены к четвертому, восьмому, двенадцатому входам модуля вычисления синдрома ошибки модуля, выходы данных сумматоров являются первым выходом модуля вычисления синдрома ошибки, входы первого многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключены к первому, пятому, шестому, тринадцатому входам модуля вычисления синдрома ошибки модуля, входы второго многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключены ко второму, пятому, седьмому, четырнадцатому входам модуля вычисления синдрома ошибки, входы третьего многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключены к третьему, пятому, восьмому, пятнадцатому входам модуля вычисления синдрома ошибки, входы четвертого многовходового сумматора по модулю два второго блока вычисления синдрома ошибки подключены к четвертому, пятому, шестнадцатому входам, при этом выходы данных многовходовых сумматоров являются вторым выходом модуля вычисления синдрома ошибки.
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2010 |
|
RU2453902C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ | 2014 |
|
RU2560823C1 |
| CN 107800439 B, 13.01.2023 | |||
| US 6049903 А, 11.04.2000 | |||
| US 9191029 B2, 17.11.2015. | |||
Авторы
Даты
2024-04-23—Публикация
2023-12-13—Подача