Изобретение относится к автоматике и вычислительной технике и может быть использовано при обработке результатов наблюдений и измерений различных характеристик для текущего анализа принадлежности поступающих случайных сигналов заданной генеральной совокупности.
Известно устройство для идентификации выборки (RU 65664U1), позволяющее определять принадлежность выборки фиксированного объема генеральной совокупности с нормальным законом распределения.
Известно устройство для определения моментов изменения свойств случайного процесса (SU 1282159A1), в котором реализован способ обнаружения разладок, обусловленных изменением среднего значения, дисперсии и корреляционной функции. Однако использование только числовых характеристик распределений снижает точность определения моментов разладок.
Наиболее близким, принятым за прототип, является устройство (SU 1126930А), в котором реализован алгоритм последовательного анализа Вальда, для которого кроме типичных ошибок α и β должны быть заданы наибольшее значение P1 доли случаев брака, при которой контролируемая партия объектов принимается, и наименьшее значение P2 доли случаев брака, при которой контролируемая партия объектов бракуется. При этом распределение генеральной совокупности не задается.
Целью изобретения является увеличение достоверности анализа за счет введения закона распределения генеральной совокупности, гипотеза о принадлежности текущих наблюдений (поступающих случайных сигналов), которому тождественна гипотезе о равномерном распределении преобразованных случайных величин и проверяется по мере их поступления. Технический результат состоит в реализации быстродействующего и эффективного устройства последовательного анализа нефиксированного числа поступающих на вход устройства случайных значений сигналов с целью обнаружения разладок в их принадлежности генеральной совокупности с заданным законом распределения.
Указанный технический результат достигается тем, что согласно предлагаемому изобретению способ последовательного анализа случайных сигналов, включающий преобразование последовательно поступающих на вход устройства нефиксированного числа случайных сигналов в случайные величины, равномерно распределенные в интервале [0;1], последовательный анализ принадлежности преобразованных случайных сигналов заданной генеральной совокупности и формирование сигнала «Разладка» на выходе устройства при снижении достоверности анализа ниже заданного уровня осуществляется при помощи устройства последовательного анализа, содержащего блок ввода параметров закона распределения случайных величин, блок преобразования сигналов, поступающих на вход устройства, три блока сравнения и два блока деления, причём вход устройства является первым входом блока преобразования сигналов, поступающих на вход устройства, второй вход которого соединен с выходом блока ввода параметров закона распределения случайных величин, выход блока преобразования сигналов, поступающих на вход устройства, соединён с входом первого блока сравнения, выход «Да» которого соединен с первым входом второго блока сравнения, выход «Нет» первого блока сравнения соединён со вторым входом второго блока сравнения, выход «Да» которого соединен с входом первого блока деления, а выход «Нет» которого соединен с входом второго блока деления, выход первого блока деления соединен с первым входом третьего блока сравнения, второй вход которого соединен с выходом второго блока деления, выход «Нет» третьего блока сравнения соединен с первым входом второго блока сравнения, выход «Да» третьего блока сравнения является выходом «Разладка» устройства.
Работу устройства с заданными функцией распределения 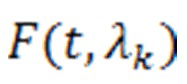 , параметрами
, параметрами 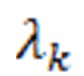 и ошибкой первого рода α рассмотрим на примере последовательного поступления на вход случайных величин ti. Наблюдения продолжаются до тех пор, когда критерий υ примет установленное значение. В статистике такая задача является задачей обнаружения моментов изменения стохастических свойств наблюдаемых случайных последовательностей (разладки), при реализации которых решение о наличии разладки принимается после каждого наблюдения.
и ошибкой первого рода α рассмотрим на примере последовательного поступления на вход случайных величин ti. Наблюдения продолжаются до тех пор, когда критерий υ примет установленное значение. В статистике такая задача является задачей обнаружения моментов изменения стохастических свойств наблюдаемых случайных последовательностей (разладки), при реализации которых решение о наличии разладки принимается после каждого наблюдения.
Пусть поступающие на вход случайные величины ti подчинены закону с функцией распределения 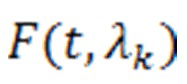 , где
, где 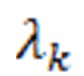 - параметры распределения.
- параметры распределения.
По определению функция распределения является неубывающей функцией на интервале [0;1]. Тогда, используя вероятностное интегральное преобразование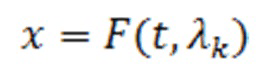 , случайную величину
, случайную величину 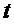 можно преобразовать в случайную величину
можно преобразовать в случайную величину 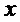 , равномерно распределенную в интервале [0;1]. Преобразование обусловлено наибольшей энтропией у равномерного закона распределения. Кроме того, критерий в виде отношения двух независимых равномерно распределенных в интервале [0;1] случайных величин доминирует по энтропии над критерием в виде их суммы. Поэтому для первых двух случайных величин
, равномерно распределенную в интервале [0;1]. Преобразование обусловлено наибольшей энтропией у равномерного закона распределения. Кроме того, критерий в виде отношения двух независимых равномерно распределенных в интервале [0;1] случайных величин доминирует по энтропии над критерием в виде их суммы. Поэтому для первых двух случайных величин 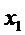 и
и 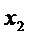 вводится в рассмотрение статистика
вводится в рассмотрение статистика
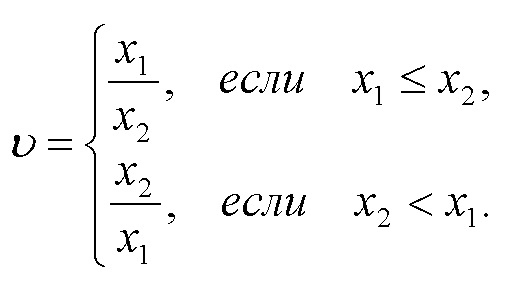
распределение которой является результатом следующей теоремы.
Теорема
Отношение меньшей из двух независимых случайных величин, равномерно распределенных в интервале [0;1], к большей есть случайная величина, равномерно распределенная в интервале [0;1].
Доказательство
Из наблюдений 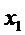 и
и 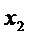 составлен вариационный ряд
составлен вариационный ряд 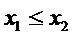 (для упрощения записи здесь и далее члены вариационного ряда не отмечаются штрихом). Плотность вероятности совместного распределения упорядоченных случайных величин
(для упрощения записи здесь и далее члены вариационного ряда не отмечаются штрихом). Плотность вероятности совместного распределения упорядоченных случайных величин 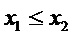 запишется следующим образом
запишется следующим образом
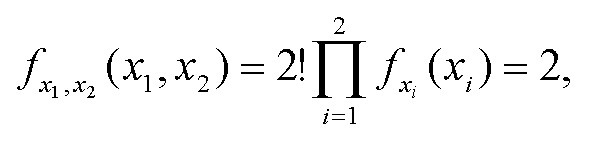
где 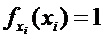 – плотность распределения
– плотность распределения 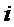 – го наблюдения в исходной выборке.
– го наблюдения в исходной выборке.
Введем в рассмотрение две статистики (по числу членов вариационного ряда)
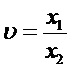 и
и 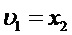 .
.
Так как обратные преобразования 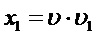 и
и 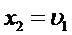 взаимно однозначны, то плотность совместного распределения
взаимно однозначны, то плотность совместного распределения
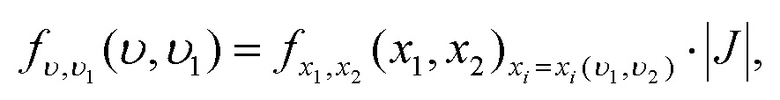
где 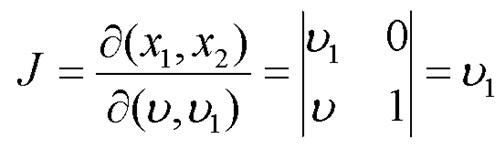 – якобиан преобразования.
– якобиан преобразования.
Тогда плотность совместного распределения статистик 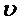 и
и 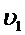 запишется следующим образом
запишется следующим образом
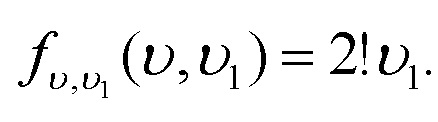
Исключая вспомогательную переменную 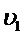 путем интегрирования плотности
путем интегрирования плотности 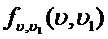 по области значений
по области значений 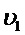 , получим плотность переменной
, получим плотность переменной 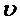
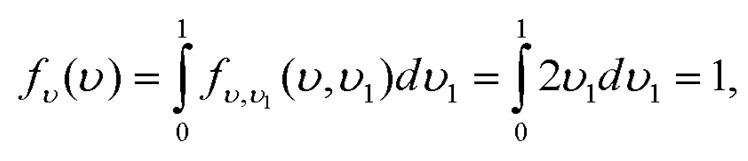
которая является плотностью равномерного распределения переменной 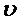 . Теорема доказана.
. Теорема доказана.
Для равномерного в интервале [0;1] распределения вероятность 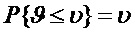 . Поэтому значение статистики
. Поэтому значение статистики 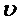 сравнивается с вероятностью
сравнивается с вероятностью 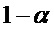 и, если
и, если 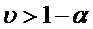 , то анализ заканчивается с выдачей сигнала "Разладка". В противном случае анализ продолжается со статистикой
, то анализ заканчивается с выдачей сигнала "Разладка". В противном случае анализ продолжается со статистикой 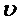 и следующей поступившей и преобразованной случайной величиной
и следующей поступившей и преобразованной случайной величиной 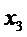 . И так далее.
. И так далее.
Таким образом, предлагаемый способ позволяет с заданной ошибкой первого рода 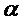 своевременно выявлять изменение (разладку) анализируемого распределения значений случайных величин в реальном масштабе времени.
своевременно выявлять изменение (разладку) анализируемого распределения значений случайных величин в реальном масштабе времени.
Выбор величины α производится, исходя из рекомендаций ГОСТ Р 51901.12-2007 при анализе видов и последствий отказов с помощью матрицы критичности.
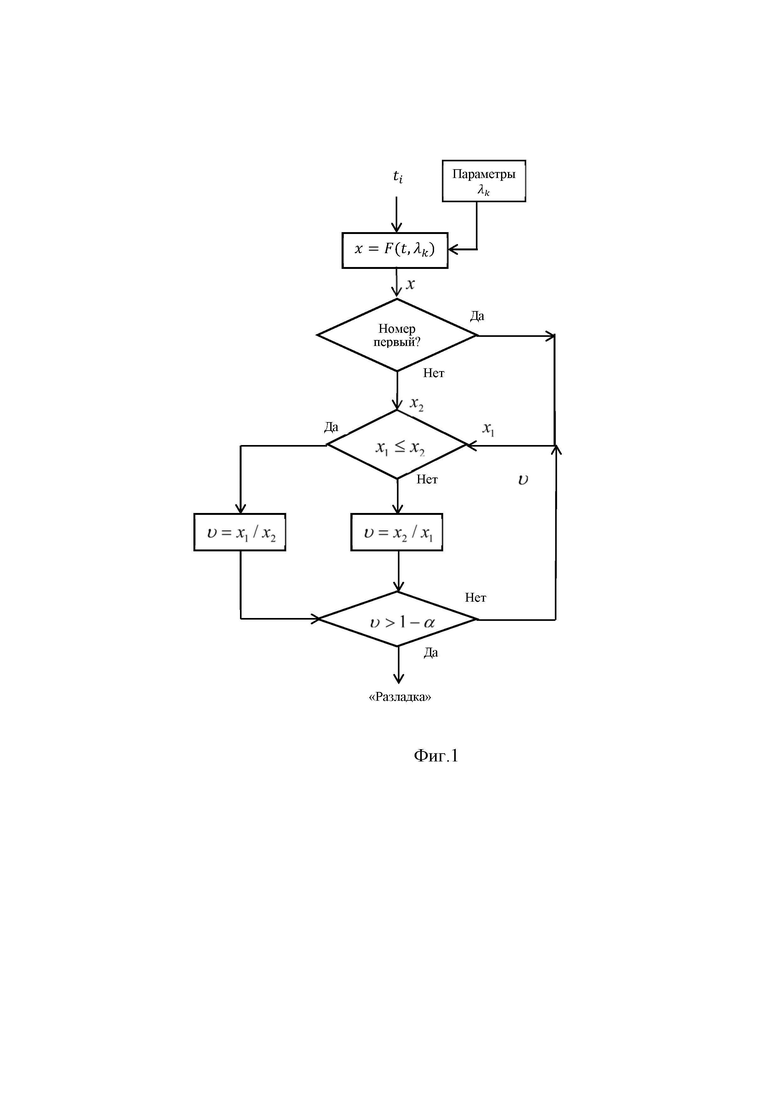
Функциональная схема устройства последовательного анализа, реализующая алгоритм его работы представлена на фиг. 1.
Входными данными служат параметры 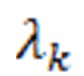 закона распределения, поступающие на вход устройства случайные значения сигналов ti и уровень значимости (ошибка первого рода) α.
закона распределения, поступающие на вход устройства случайные значения сигналов ti и уровень значимости (ошибка первого рода) α.
Входное случайное значение ti поступает на вход блока преобразования для вычисления задаваемой функции распределения 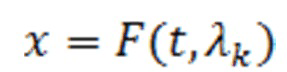 . С выхода блока преобразования значение
. С выхода блока преобразования значение 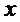 поступает в блок принятия решения, из которого, если случайное значение первое, то
поступает в блок принятия решения, из которого, если случайное значение первое, то 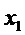 поступает в блок сравнения. Если случайное значение не первое, то
поступает в блок сравнения. Если случайное значение не первое, то 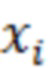 поступает в блок сравнения под наименованием
поступает в блок сравнения под наименованием 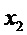 .
.
С выходов блока сравнения 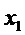 и
и 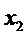 поступают на один из блоков вычисления критерия
поступают на один из блоков вычисления критерия 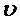 в зависимости от их соотношения и далее в блок принятия решения для сравнения с вероятностью
в зависимости от их соотношения и далее в блок принятия решения для сравнения с вероятностью 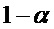 . Если
. Если 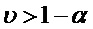 , то формируется выходной сигнал "Разладка". В противном случае значение критерия
, то формируется выходной сигнал "Разладка". В противном случае значение критерия 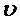 поступает на вход блока сравнения вместо значения
поступает на вход блока сравнения вместо значения 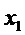 для продолжения анализа.
для продолжения анализа.
Адекватность способа и работоспособность предлагаемой функциональной схемы устройства проверены с помощью имитационной модели при экспоненциальном законе распределения случайной величины t путем проведения вычислительного эксперимента с числом реализаций N=105. Результаты приведены в таблице.

Относительная погрешность данного способа при наиболее используемом значении α=0,1 составляет
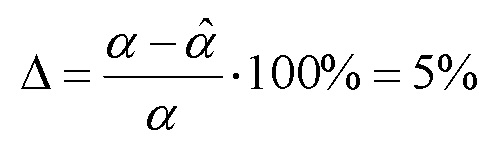 , чем подтверждается адекватность предлагаемого способа.
, чем подтверждается адекватность предлагаемого способа.
Кроме того, исследование показало, что интенсивность выдачи сигнала «Разладка» определяется (почти равна) задаваемой вероятности ошибки первого рода α.
В отличие от прототипа на выявление разладки требуется меньшее число наблюдений, что повышает быстродействие и эффективность устройства.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СИГНАЛИЗАЦИИ НАЛИЧИЯ СТРУЖКИ В МАСЛЕ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2022 |
|
RU2791174C1 |
| Устройство для идентификации малой выборки | 1990 |
|
SU1774350A1 |
| Устройство для определения моментов изменения свойств случайного процесса | 1985 |
|
SU1282159A1 |
| Устройство для идентификации малой выборки | 1990 |
|
SU1774351A1 |
| СПОСОБ СИГНАЛИЗАЦИИ НАЛИЧИЯ СТРУЖКИ В МАСЛЕ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2021 |
|
RU2765325C1 |
| Устройство для определения момента изменения свойств случайного процесса | 1983 |
|
SU1166149A1 |
| СПОСОБ И СИСТЕМА УДАЛЁННОЙ ИДЕНТИФИКАЦИИ И ПРОГНОЗИРОВАНИЯ РАЗВИТИЯ ЗАРОЖДАЮЩИХСЯ ДЕФЕКТОВ ОБЪЕКТОВ | 2018 |
|
RU2686257C1 |
| Анализатор случайных процессов | 1978 |
|
SU813472A1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ | 2014 |
|
RU2586025C2 |
| СПОСОБ ВЫЯВЛЕНИЯ МОШЕННИЧЕСТВА ПРИ ИНСЦЕНИРОВКЕ ДТП И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2460056C1 |
Изобретение относится к автоматике и вычислительной технике и может быть использовано при обработке результатов наблюдений и измерений различных характеристик для текущего анализа принадлежности поступающих случайных сигналов заданной генеральной совокупности. Технический результат заключается в обеспечении быстродействующего и эффективного последовательного анализа нефиксированного числа случайных сигналов с целью обнаружения разладок в их принадлежности генеральной совокупности с заданным законом распределения. Указанный технический результат достигается тем, что согласно предлагаемому изобретению способ последовательного анализа случайных сигналов включает преобразование последовательно поступающих на вход устройства нефиксированного числа случайных сигналов в случайные величины, равномерно распределенные в интервале [0;1], последовательный анализ принадлежности преобразованных случайных сигналов заданной генеральной совокупности и формирование сигнала «Разладка» на выходе устройства при снижении достоверности анализа ниже заданного уровня. 2 н.п. ф-лы, 1 ил.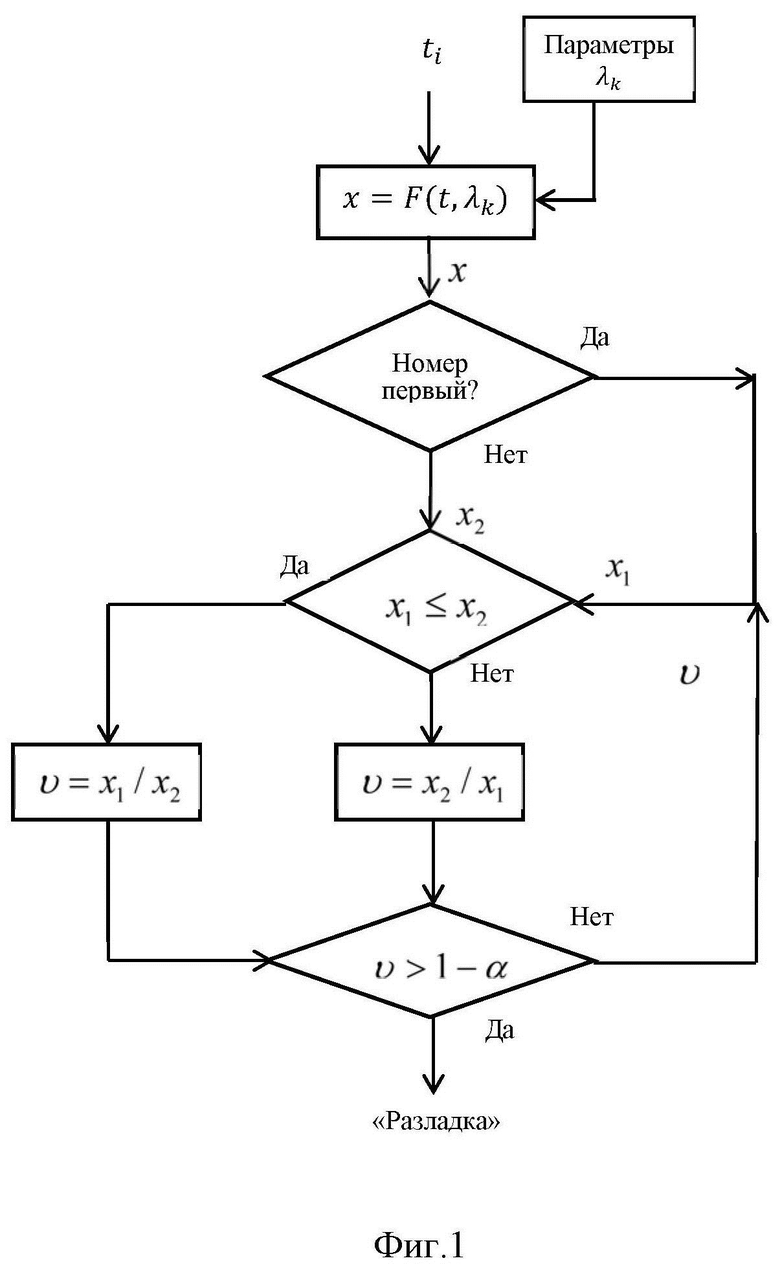
1. Устройство последовательного анализа случайных сигналов, содержащее блок ввода параметров закона распределения случайных величин, блок преобразования сигналов, поступающих на вход устройства, три блока сравнения и два блока деления, причём вход устройства является первым входом блока преобразования сигналов, поступающих на вход устройства, второй вход которого соединен с выходом блока ввода параметров закона распределения случайных величин, выход блока преобразования сигналов, поступающих на вход устройства, соединён с входом первого блока сравнения, выход «Да» которого соединен с первым входом второго блока сравнения, выход «Нет» первого блока сравнения соединён со вторым входом второго блока сравнения, выход «Да» которого соединен с входом первого блока деления, а выход «Нет» которого соединен с входом второго блока деления, выход первого блока деления соединен с первым входом третьего блока сравнения, второй вход которого соединен с выходом второго блока деления, выход «Нет» третьего блока сравнения соединен с первым входом второго блока сравнения, выход «Да» третьего блока сравнения является выходом «Разладка» устройства.
2. Способ последовательного анализа принадлежности поступающих случайных сигналов заданной генеральной совокупности при помощи устройства по п.1, включающий преобразование последовательно поступающих на вход устройства нефиксированного числа случайных сигналов в случайные величины, равномерно распределенные в интервале [0;1], последовательный анализ преобразованных случайных сигналов и формирование сигнала «Разладка» на выходе устройства при снижении достоверности анализа ниже заданного уровня.
| Устройство для определения момента разладки случайных процессов | 1985 |
|
SU1260973A1 |
| Устройство для последовательного анализа | 1983 |
|
SU1126930A1 |
| Искатель металлических предметов в теле человека | 1942 |
|
SU65664A1 |
| СИСТЕМА МОНИТОРИНГА КАЧЕСТВА И ПРОЦЕССОВ НА БАЗЕ МАШИННОГО ОБУЧЕНИЯ | 2019 |
|
RU2716029C1 |
| US 20110243263 A1, 06.10.2011 | |||
| US 10601630 B1, 24.03.2020. | |||
Авторы
Даты
2024-04-23—Публикация
2024-02-20—Подача