Изобретение относится к области радиоэлектроники и может быть использовано при обнаружении полезных сигналов с неизвестной фазовой или временной задержкой в условиях действия аддитивных широкополосных негауссовых помех при любом соотношении мощностей полезного сигнала и помехи, когда распределения мгновенных значений помехи неизвестны или меняются во времени, а вероятность ложной тревоги должна поддерживаться на заданном уровне. При этом спектр помехи шире спектра сигнала настолько, что отсчёты помехи можно считать независимыми.
В качестве прототипа выбран способ обнаружения полезных сигналов при действии аддитивных негауссовских помех [1, Левин Б.Р. Теоретические основы статистической радиотехники. В трёх книгах. Книга третья. М., «Сов.радио», 1976, 288с. Стр.148, формула (3.156)], включающий дискретизацию процесса изменения тока или напряжения 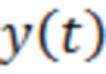 во времени на выходе приёмного тракта в соответствии с теоремой Котельникова и получение последовательности дискретных отсчётов
во времени на выходе приёмного тракта в соответствии с теоремой Котельникова и получение последовательности дискретных отсчётов 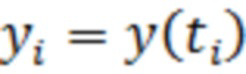 в моменты времени
в моменты времени 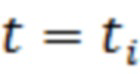 , где
, где 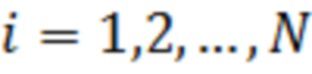 - номер отсчёта, сохранение этих отсчётов в памяти вычислительного устройства, сортировку сохранённых отсчётов по порядку возрастания и получение вариационного ряда, определение для каждого отсчёта
- номер отсчёта, сохранение этих отсчётов в памяти вычислительного устройства, сортировку сохранённых отсчётов по порядку возрастания и получение вариационного ряда, определение для каждого отсчёта 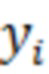 его номера
его номера 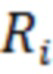 в вариационном ряду, которые нелинейно преобразуют в последовательность отсчётов
в вариационном ряду, которые нелинейно преобразуют в последовательность отсчётов 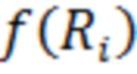 , вычисляют максимальное по модулю значение функции корреляции между последовательностью
, вычисляют максимальное по модулю значение функции корреляции между последовательностью 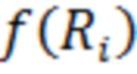 и заданной последовательностью отсчётов полезного сигнала
и заданной последовательностью отсчётов полезного сигнала 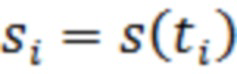 , которое далее сравнивают с заданным порогом обнаружения и в зависимости от результата сравнения принимают решение о наличии или отсутствии полезного сигнала на выходе приёмного тракта.
, которое далее сравнивают с заданным порогом обнаружения и в зависимости от результата сравнения принимают решение о наличии или отсутствии полезного сигнала на выходе приёмного тракта.
При этом решение принимают, сравнивая с порогом статистику обнаружения вида
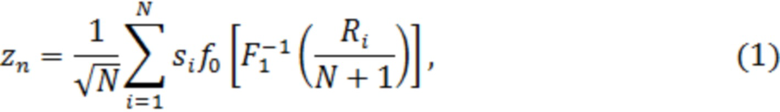
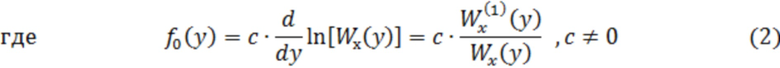
- амплитудная характеристика (АХ) нелинейного преобразования (НП); 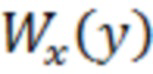 - плотность вероятности (ПВ) значений помехи;
- плотность вероятности (ПВ) значений помехи; 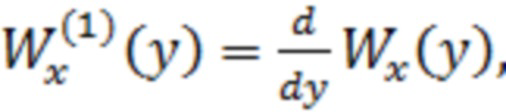 - первая производная от функции
- первая производная от функции 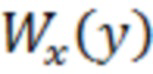 ;
; 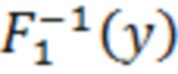 - функция обратная функции распределения значений помехи
- функция обратная функции распределения значений помехи
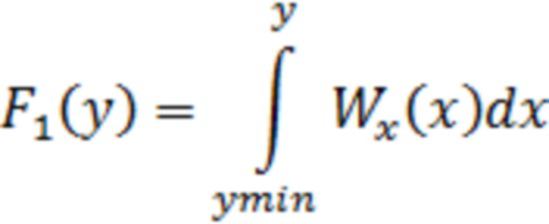
Статистика (1) применима только для детерминированного сигнала. В ситуации, когда время появления полезного сигнала или фаза в момент появления неизвестны вместо статистики обнаружения (1) используют отклик согласованного с полезным сигналом фильтра
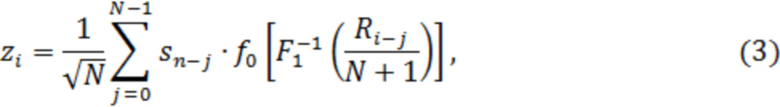
Рассмотренный известный способ является оптимальным с точки зрения максимума отношения правдоподобия при условии, что мощность полезного сигнала 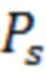 много меньше мощности помехи по
много меньше мощности помехи по 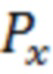 , т.е. отношение сигнал-помеха
, т.е. отношение сигнал-помеха
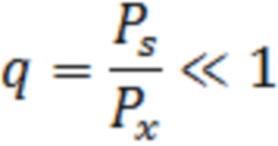
В реальной ситуации распределение значений помехи или её плотность вероятности неизвестны, а помеха может вообще отсутствовать на входе. Заметим, также, что при наличии на входе смеси помехи и сигнала определить характеристики помехи не представляется возможным из-за наличия полезного сигнала.
Рассмотренный известный способ не учитывает реальные условия приёма сигнала и, как показывают эксперименты и моделирование, может существенно проигрывать в эффективности обнаружения по сравнению с обычной линейной корреляционной обработкой или согласованной фильтрацией.
Техническая проблема заключается в необходимости разработки универсального способа, позволяющего в режиме реального времени или с заданной не существенной задержкой максимально эффективно обнаруживать полезный сигнал в реальных условиях приёма, когда вероятностные характеристики помехи неизвестны или меняются во времени, при этом отношение сигнал-помеха может быть произвольным, в том числе и близким к нулю.
Техническим результатом изобретения является возможность поддерживать в реальных условиях приёма сигналов максимально возможными вероятности правильного принятия решений о наличии или отсутствии полезного сигнала в наблюдаемом процессе на входе приёмного тракта.
Для описания предлагаемого способа обнаружения представим амплитудную характеристику нелинейного преобразования полиномом

где 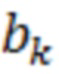 - параметры настройки АХ;
- параметры настройки АХ; 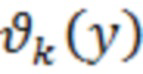 - система из
- система из 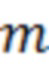 взаимно-ортогональных функций, отвечающих условиям:
взаимно-ортогональных функций, отвечающих условиям:

- для непрерывного множества случайных значений 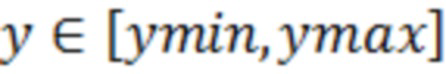 или
или
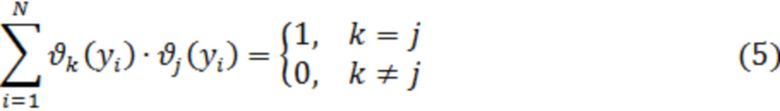
- для дискретного по времени 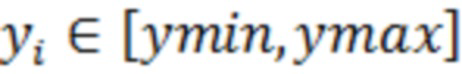 . Здесь
. Здесь 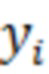 - отсчёт входного процесса;
- отсчёт входного процесса; 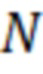 - число отсчётов процесса на интервале наблюдения.
- число отсчётов процесса на интервале наблюдения.
Эти два условия эквивалентны, если на этом интервале наблюдения процесс можно считать стационарным и эргодическим.
Найдём такие коэффициенты  , при которых процесс на выходе
, при которых процесс на выходе 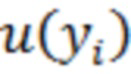 менее всего в среднеквадратичном смысле отличается от эталонного сигнала
менее всего в среднеквадратичном смысле отличается от эталонного сигнала 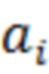
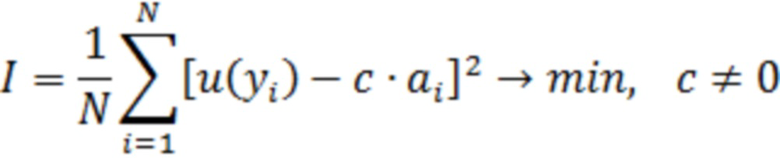
или
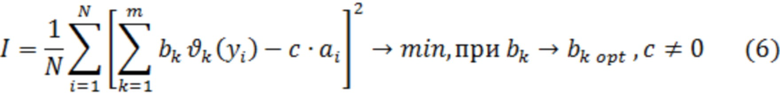
Для поиска минимума 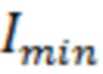 найдём частные производные
найдём частные производные 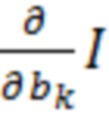 и приравняем их к нулю. Решая полученную систему линейных уравнений, с учётом ортогональности функций
и приравняем их к нулю. Решая полученную систему линейных уравнений, с учётом ортогональности функций 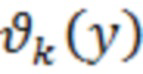 получим выражение для оптимальных значений коэффициентов настройки НП
получим выражение для оптимальных значений коэффициентов настройки НП
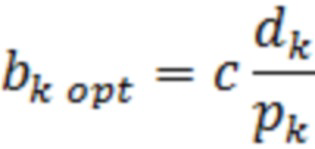
Здесь
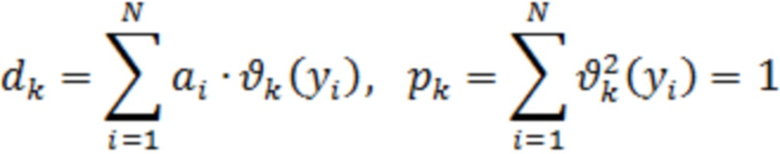
Отсюда следует, что
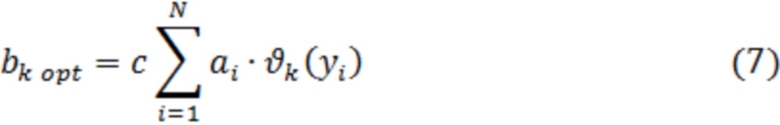
Определим функции следующим образом

Здесь 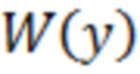 - одномерная плотность вероятности значений отсчётов
- одномерная плотность вероятности значений отсчётов 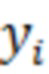 ;
;
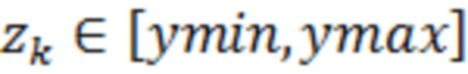 - пороги квантования, причём
- пороги квантования, причём 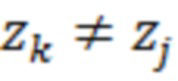 для не равных
для не равных 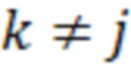 ;
; 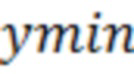 и
и 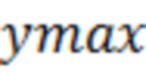 - обозначают соответственно минимальное и максимальное значения последовательности входных отсчётов
- обозначают соответственно минимальное и максимальное значения последовательности входных отсчётов 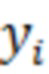 ;
; 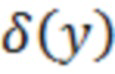 - дельта-функция, т.е.
- дельта-функция, т.е.
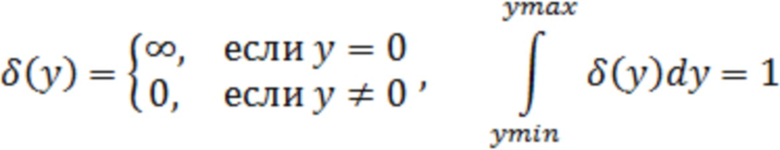
Очевидно, что функции (5) для 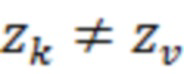 являются взаимно-ортогональными
являются взаимно-ортогональными
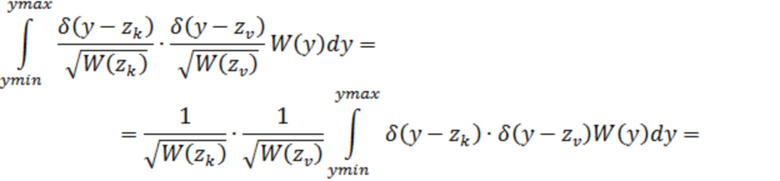

Для дискретных по времени отсчётов 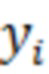 справедливо равенство
справедливо равенство
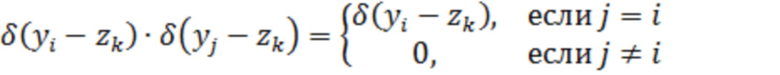
Далее считаем квантование осуществляется с шагом 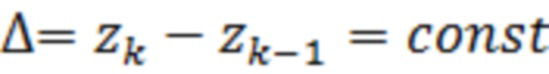 .
.
С учётом (8), выражение (7) для оптимального параметра НП принимает вид
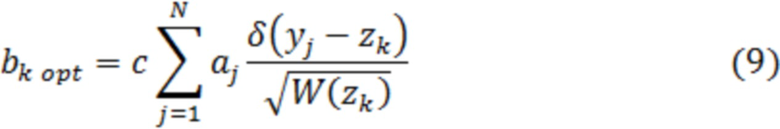
Тогда отсчёт 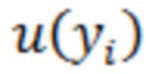 после оптимального НП
после оптимального НП
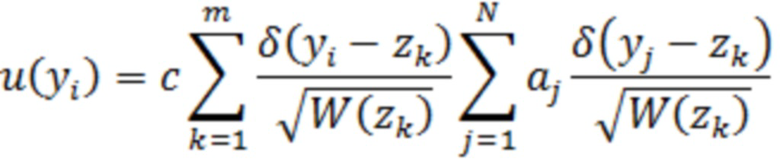
или
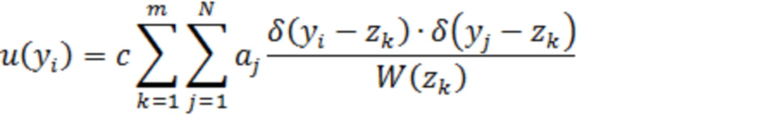
Здесь произведение 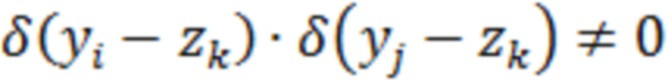 , только если
, только если 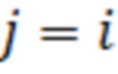 , а
, а 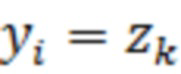 . С учётом этого, отсчёт
. С учётом этого, отсчёт 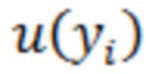 после оптимального НП
после оптимального НП
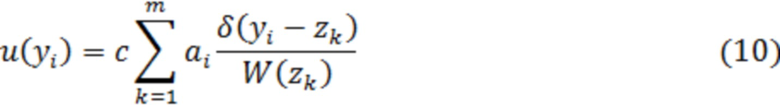
Увеличим количество порогов 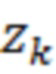 при одновременном уменьшении расстояния между ними:
при одновременном уменьшении расстояния между ними: 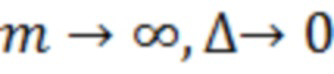 . В пределе получим непрерывное множество значений
. В пределе получим непрерывное множество значений 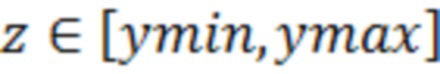 . Тогда сумму в (7) можно заменить интегралом:
. Тогда сумму в (7) можно заменить интегралом:
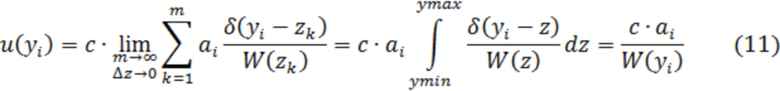
Очевидно, что при замене в (11) функции 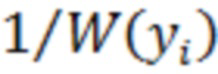 её оценкой, предлагаемый способ становится адаптивным и оптимальным по критерию минимума СКО (6) при любой ПВ
её оценкой, предлагаемый способ становится адаптивным и оптимальным по критерию минимума СКО (6) при любой ПВ 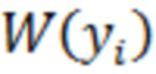 входного сигнала
входного сигнала 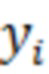 .
.
Предлагаемый способ для слабых сигналов должен быть также эффективен, что и прототип. Для этого разложим в (11) нелинейное преобразование 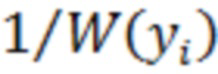 аддитивной смеси
аддитивной смеси 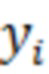 полезного сигнала
полезного сигнала 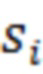 и помехи
и помехи 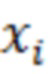 в ряд Тейлора по степеням сигнала
в ряд Тейлора по степеням сигнала 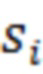 и ограничимся двумя первыми членами ряда ввиду малости
и ограничимся двумя первыми членами ряда ввиду малости 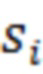
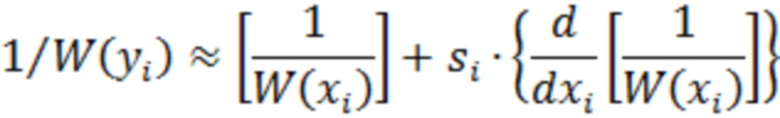
Тогда после НП, с учётом (10), получим
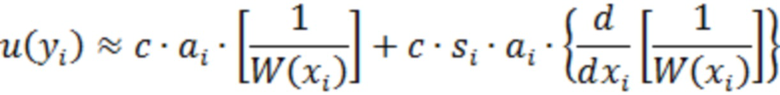
Здесь только второе слагаемое содержит полезный сигнал 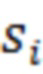 и множитель
и множитель 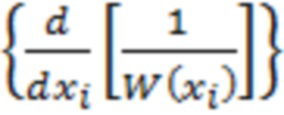 , который приводит к модуляции полезного сигнала
, который приводит к модуляции полезного сигнала 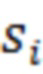 помехой
помехой 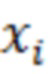 по амплитуде и случайной смене полярности, которая может разрушить когерентность последующего накопления сигнала
по амплитуде и случайной смене полярности, которая может разрушить когерентность последующего накопления сигнала 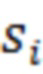 и привести к ухудшению характеристик его обнаружения.
и привести к ухудшению характеристик его обнаружения.
Чтобы не допустить этого достаточно определить опорный сигнал 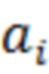 как
как
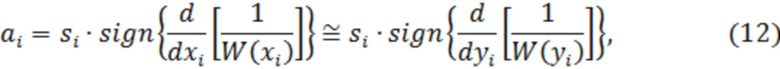
где нелинейное преобразование
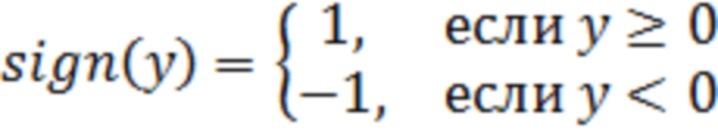
- используется для смены полярности ожидаемого сигнала.
Использование в (12) плотности вероятности значений отсчётов входного процесса 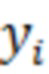 , а не помехи
, а не помехи 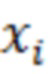 обусловлено их приближённым равенством для слабого сигнала
обусловлено их приближённым равенством для слабого сигнала 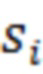 .
.
Таким образом, отсчёты процесса после адаптивного НП
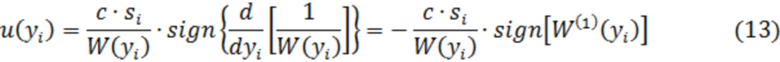
Результат линейной корреляционной обработки, согласованной с сигналом 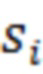 , можно получить простым накоплением отклика
, можно получить простым накоплением отклика 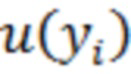
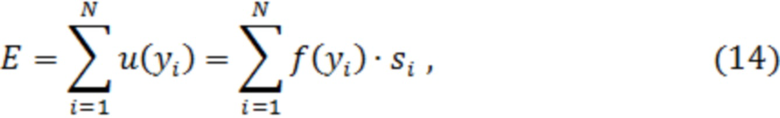
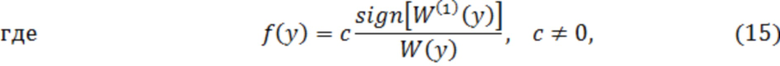
- амплитудная характеристика НП.
Когда полезный сигнал имеет неизвестную начальную фазу и время прихода в качестве линейной согласованной обработки, как правило, используют не корреляционную обработку (14), а согласованную фильтрацию (СФ):

Здесь 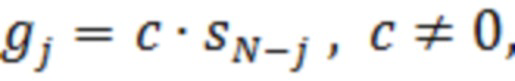 - отсчёты импульсной реакции СФ, а
- отсчёты импульсной реакции СФ, а 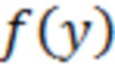 задаётся выражением (15).
задаётся выражением (15).
Для оценивания функции 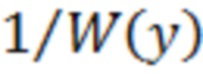 и её первой производной можно использовать как параметрические методы оценивания ПВ
и её первой производной можно использовать как параметрические методы оценивания ПВ 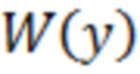 с последующей операцией деления, так и непараметрические.
с последующей операцией деления, так и непараметрические.
Пример непараметрического оценивания (восстановления) ПВ - это использование метода Парзена - Надарая [2, Восстановление зависимостей по эмпирическим данным. Вапник В. Н. Главная редакция физико-математической литературы издательства «Наука», М., 1979, - 448 с. на стр. 323-324], когда её представляют суммой
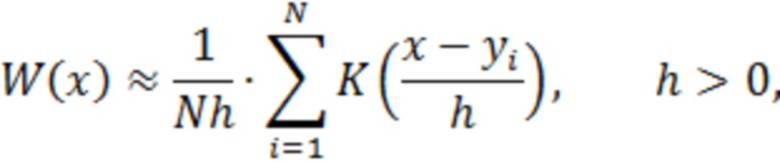
где 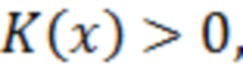 - потенциальная (ядерная) дифференцируемая функция аргумента
- потенциальная (ядерная) дифференцируемая функция аргумента 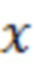 .
.
Параметрическое оценивание ПВ сводится к выбору известной функциональной зависимости от отсчёта 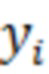 с неизвестными в начале оценивания параметрами, которые оценивают при адаптации и затем используют для управления этой зависимостью. Заметим также, что можно оценивать не саму ПВ, а её функцию.
с неизвестными в начале оценивания параметрами, которые оценивают при адаптации и затем используют для управления этой зависимостью. Заметим также, что можно оценивать не саму ПВ, а её функцию.
Для оценки функции 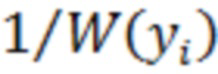 , а также её первой производной, выразим её через функцию распределения вероятностей
, а также её первой производной, выразим её через функцию распределения вероятностей 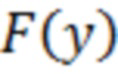 в виде
в виде
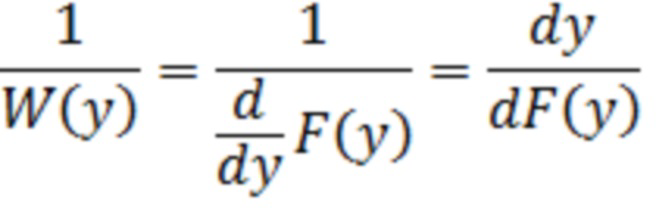
Обозначим 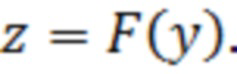 Тогда
Тогда 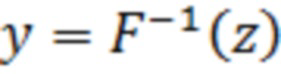 , где
, где 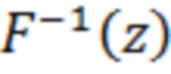 - обратная функции распределения.
- обратная функции распределения.
Причём 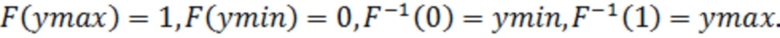
В итоге получим, что

Заметим, что случайная величина 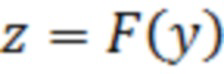 имеет равновероятное распределение, причём
имеет равновероятное распределение, причём 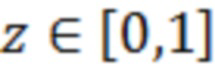 . Значения же функции
. Значения же функции 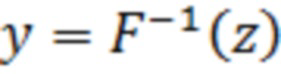 могут быть представлены её дискретным аналогом - вариационным рядом
могут быть представлены её дискретным аналогом - вариационным рядом 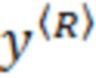 , составленным из
, составленным из 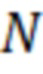 входных отсчётов
входных отсчётов 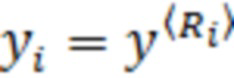 , расположенных в порядке возрастания. Здесь
, расположенных в порядке возрастания. Здесь 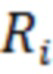 - порядковый номер отсчёта
- порядковый номер отсчёта 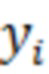 в вариационном ряду или ранг. Значения рангов
в вариационном ряду или ранг. Значения рангов 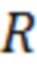 равновероятны на интервале от 1 до
равновероятны на интервале от 1 до 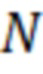 .
.
Для оценивания функции 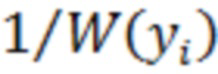 , а также её первой производной, мы аппроксимируем вариационный ряд входных отсчётов
, а также её первой производной, мы аппроксимируем вариационный ряд входных отсчётов 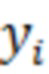 разложением в ряд по дважды дифференцируемым ортогональным функциям.
разложением в ряд по дважды дифференцируемым ортогональным функциям.
Выберем в качестве ортогонального базиса многочлены Лежандра [3], которые ортогональны на интервале 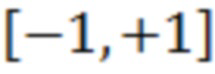 .
.
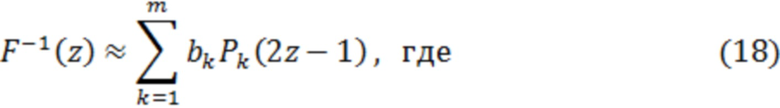
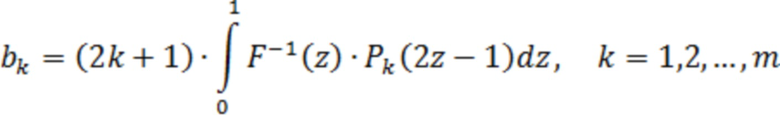
Тогда
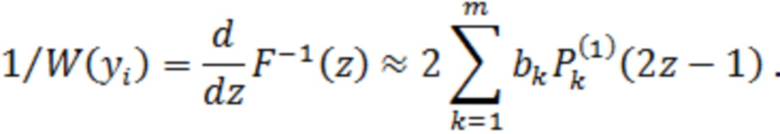
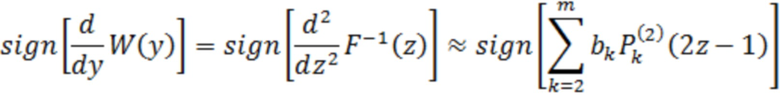
Здесь 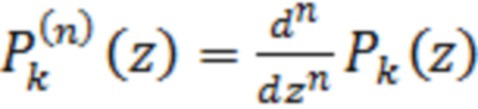 ,
, 
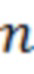 -ая производная многочлена
-ая производная многочлена 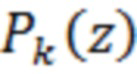 по
по  .
.
Так как количество наблюдаемых данных 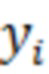 равно
равно 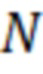 , то на практике лучше использовать заранее вычисленные таблицы значений многочленов Лежандра, а также их первых двух производных, в
, то на практике лучше использовать заранее вычисленные таблицы значений многочленов Лежандра, а также их первых двух производных, в 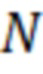 равномерно отстоящих точках от -1 до +1, которые для отсчёта
равномерно отстоящих точках от -1 до +1, которые для отсчёта 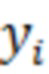 выбираются рангом
выбираются рангом 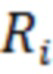 , то есть в выражениях (18) подставляют
, то есть в выражениях (18) подставляют 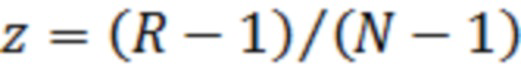 , а интеграл меняют на сумму.
, а интеграл меняют на сумму.
С учётом этого, результат нелинейного преобразования
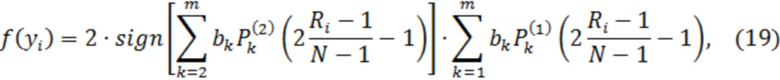
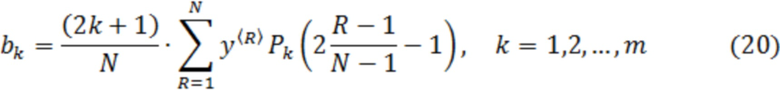
или
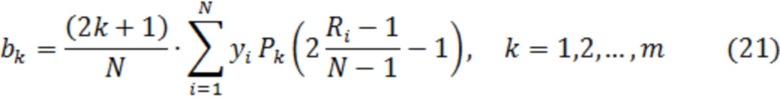
Предлагаемый способ легко может быть реализован с помощью современных сигнальных процессоров с внешним или внутренним аналого-цифровым преобразованием входного процесса 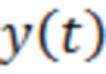 в последовательность дискретных отсчётов
в последовательность дискретных отсчётов 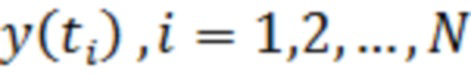 . Это может быть, например, MultiClet R1 (см. руководство по эксплуатации) или TMS320F28335 (см. руководство по эксплуатации).
. Это может быть, например, MultiClet R1 (см. руководство по эксплуатации) или TMS320F28335 (см. руководство по эксплуатации).
Для подтверждения работоспособности и эффективности предлагаемого способа было проведено математическое моделирование обнаружителя одиночного радиоимпульса с частотой заполнения равной 10% от частоты дискретизации в условиях действия помехи импульсного характера с полигауссовской ПВ мгновенных значений
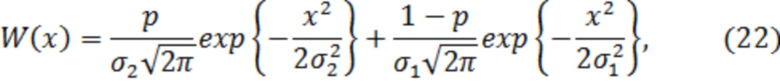
с параметрами 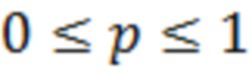 ,
, 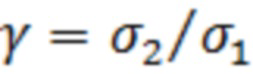 .
.
Для оценки эффективности предлагаемого способа, полученные характеристики обнаружения сравнивались с аналогичными для линейного согласованного фильтра. Длительность импульсной реакции СФ составляла 500 отсчётов. Количество ортогональных функций 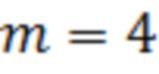 . Оценка характеристик обнаружения проводилась по 1000 реализациям. При этом, порог обнаружения устанавливался соответствующим вероятности ложной тревоги 0,01. Затем, определялся уровень порогового отношения сигнал/(помеха+шум)
. Оценка характеристик обнаружения проводилась по 1000 реализациям. При этом, порог обнаружения устанавливался соответствующим вероятности ложной тревоги 0,01. Затем, определялся уровень порогового отношения сигнал/(помеха+шум) 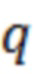 , соответствующий вероятности правильного обнаружения 0,9.
, соответствующий вероятности правильного обнаружения 0,9.
Выигрыш от применения предлагаемого способа по сравнению с линейной согласованной обработкой оценивался показателем
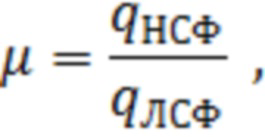
где 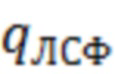 - пороговое отношение
- пороговое отношение 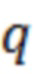 для линейной согласованной с сигналом обработки, а
для линейной согласованной с сигналом обработки, а 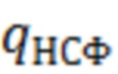 - пороговое отношение
- пороговое отношение 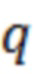 для предлагаемого способа.
для предлагаемого способа.
Ниже результаты моделирования выигрыша 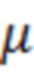 при различных значениях параметров полигауссовской помехи
при различных значениях параметров полигауссовской помехи 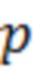 и
и 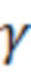 :
:
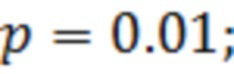
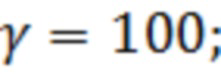
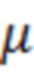 = 20,52 дБ
= 20,52 дБ
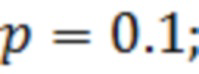
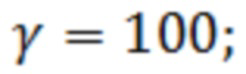
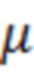 = 26.65 дБ
= 26.65 дБ
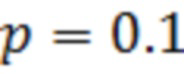 ;
; 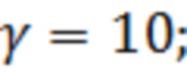
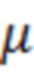 = 7.95 дБ
= 7.95 дБ
Известна методика расчёта выигрыша 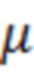 от применения асимптотически оптимальной (для слабого сигнала) нелинейной обработки с амплитудной характеристикой
от применения асимптотически оптимальной (для слабого сигнала) нелинейной обработки с амплитудной характеристикой 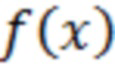 [4, Теория обнаружения сигналов /П.С. Акимов, П.А. Бакут, В.А. Богданович и др.; Под ред. П.А. Бакута. - М.: Радио и связь, 1984.- 440 с. Формула 5.124 на стр.302]
[4, Теория обнаружения сигналов /П.С. Акимов, П.А. Бакут, В.А. Богданович и др.; Под ред. П.А. Бакута. - М.: Радио и связь, 1984.- 440 с. Формула 5.124 на стр.302]

где 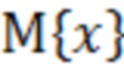 - означает операцию математического ожидания случайной величины
- означает операцию математического ожидания случайной величины 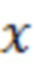 .
.
Максимальный выигрыш 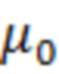 достигается для оптимальной амплитудной характеристики НП, которая согласуется с ПВ помехи в соответствии с выражением (2) и равен [4]
достигается для оптимальной амплитудной характеристики НП, которая согласуется с ПВ помехи в соответствии с выражением (2) и равен [4]
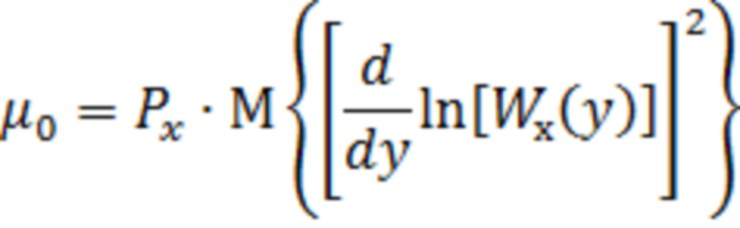
Ниже представлены результаты расчёта показателя эффективности 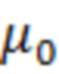 для полигауссовской помехи с ПВ (22) при различных значениях
для полигауссовской помехи с ПВ (22) при различных значениях 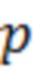 и
и 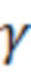 :
:
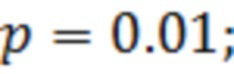
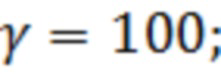
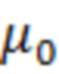 = 19,99 дБ
= 19,99 дБ
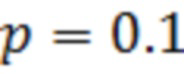 ;
; 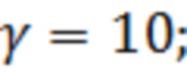
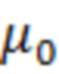 = 9.547 дБ
= 9.547 дБ
Сравнение результатов расчёта с результатами моделирования доказывает высокую эффективность предлагаемого способа обнаружения для слабых сигналов, уступающей асимптотически оптимальному всего 1,5 дБ.
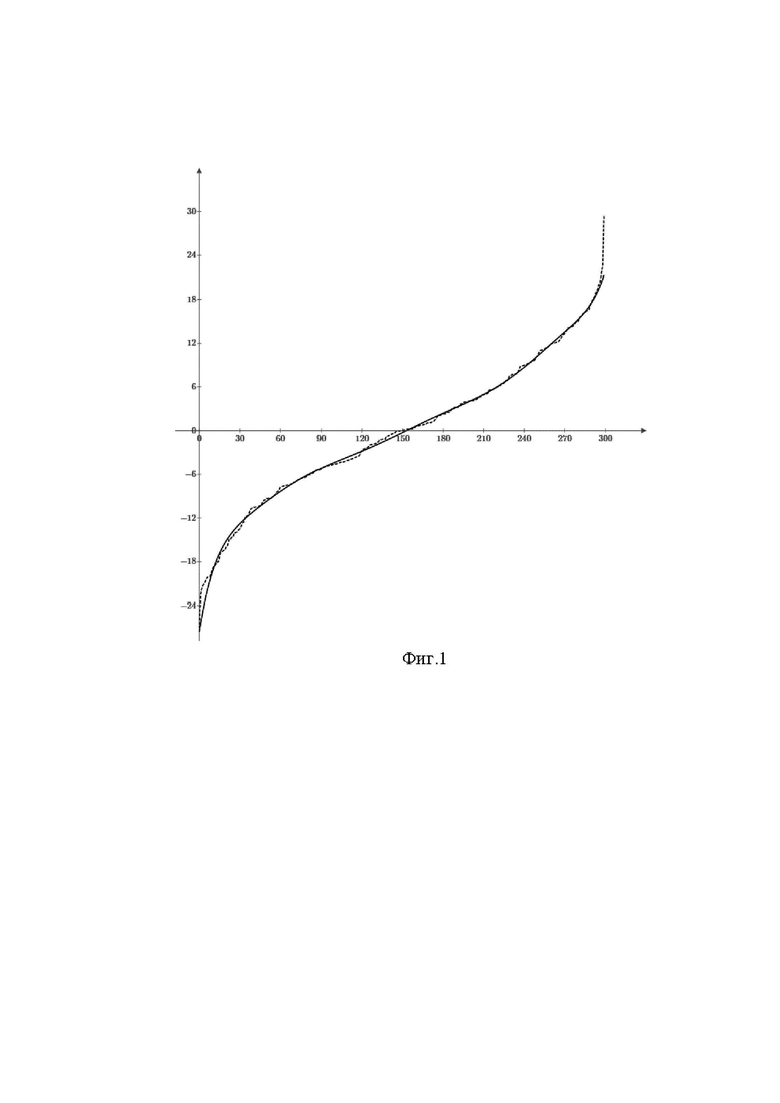
На Фиг.1 представлены 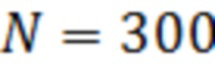 отсчётов вариационного ряда (пунктирной линией) и результат его аппроксимации полиномами Лежандра
отсчётов вариационного ряда (пунктирной линией) и результат его аппроксимации полиномами Лежандра 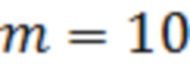 (сплошной линией) для полигаусовской помехи с параметрами
(сплошной линией) для полигаусовской помехи с параметрами 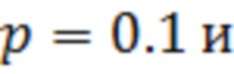
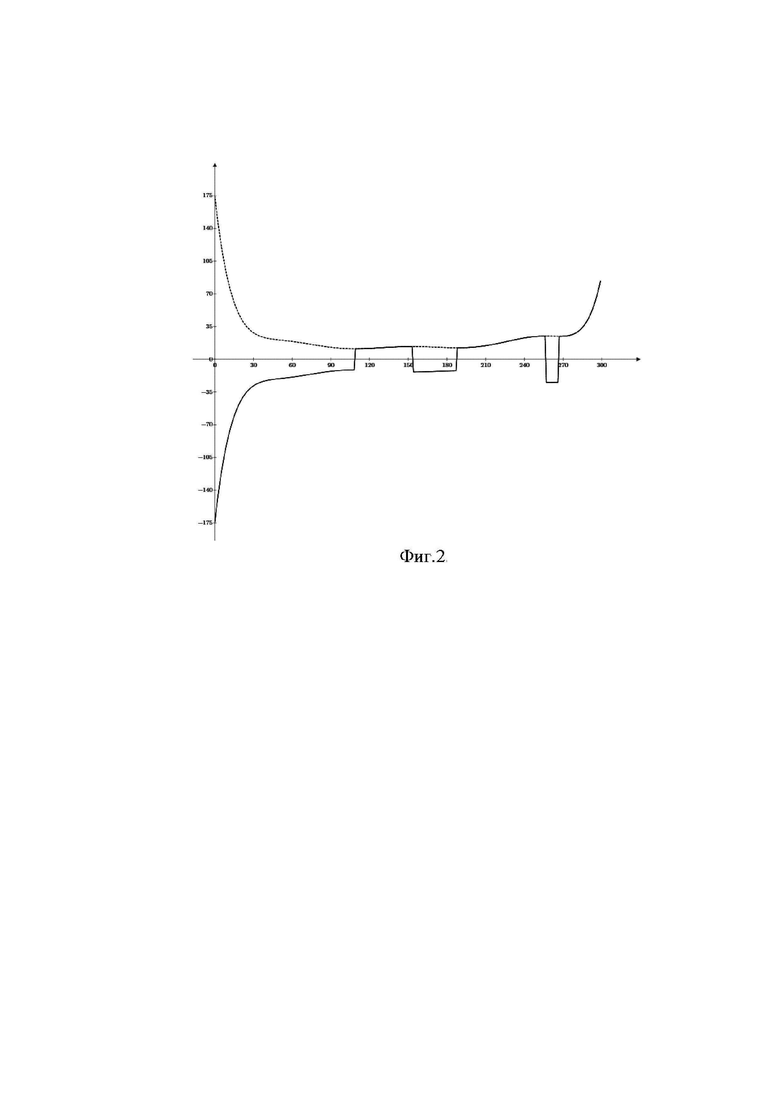
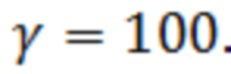 Графики показывают, что вариационный ряд имеет вид возрастающей случайной кривой, в то время как его аппроксимация имеет вид гладкой монотонно возрастающей функции и является по сути сглаженным аналогом вариационного ряда. Для этой же помехи на Фиг.2 представлены графики результата оценивания первой производной сглаженного вариационного ряда равного функции от ПВ
Графики показывают, что вариационный ряд имеет вид возрастающей случайной кривой, в то время как его аппроксимация имеет вид гладкой монотонно возрастающей функции и является по сути сглаженным аналогом вариационного ряда. Для этой же помехи на Фиг.2 представлены графики результата оценивания первой производной сглаженного вариационного ряда равного функции от ПВ 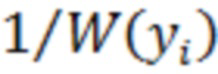 (пунктирной линией) и итоговый результат нелинейного преобразования
(пунктирной линией) и итоговый результат нелинейного преобразования 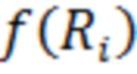 , в котором уже учтена полярность второй производной сглаженного вариационного ряда (сплошной линией).
, в котором уже учтена полярность второй производной сглаженного вариационного ряда (сплошной линией).
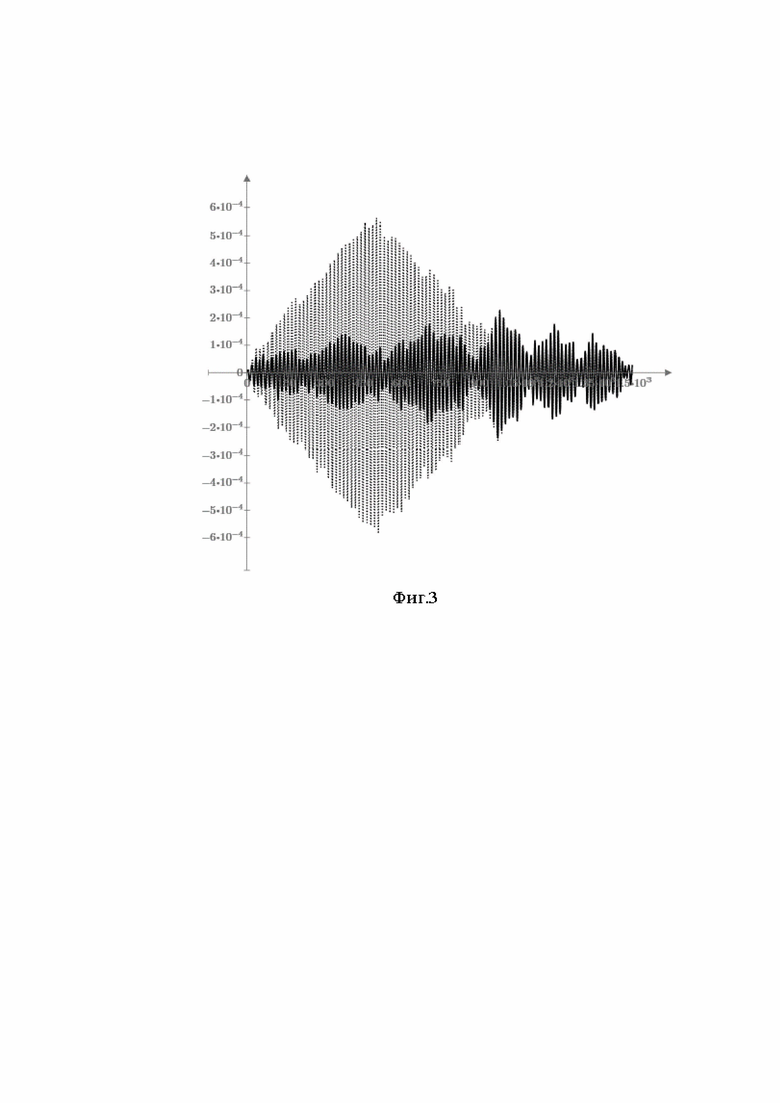
На Фиг.3 представлен отсчёты после нелинейного преобразования 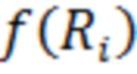 предлагаемого способа при отсутствии полезного сигнала на входе (сплошная линия) и при его наличии (пунктир), когда сигнал - «слабый», то есть отношение сигнал/(помеха+шум) на входе равно -39 дБ при вероятности правильного обнаружения 0,9.
предлагаемого способа при отсутствии полезного сигнала на входе (сплошная линия) и при его наличии (пунктир), когда сигнал - «слабый», то есть отношение сигнал/(помеха+шум) на входе равно -39 дБ при вероятности правильного обнаружения 0,9.
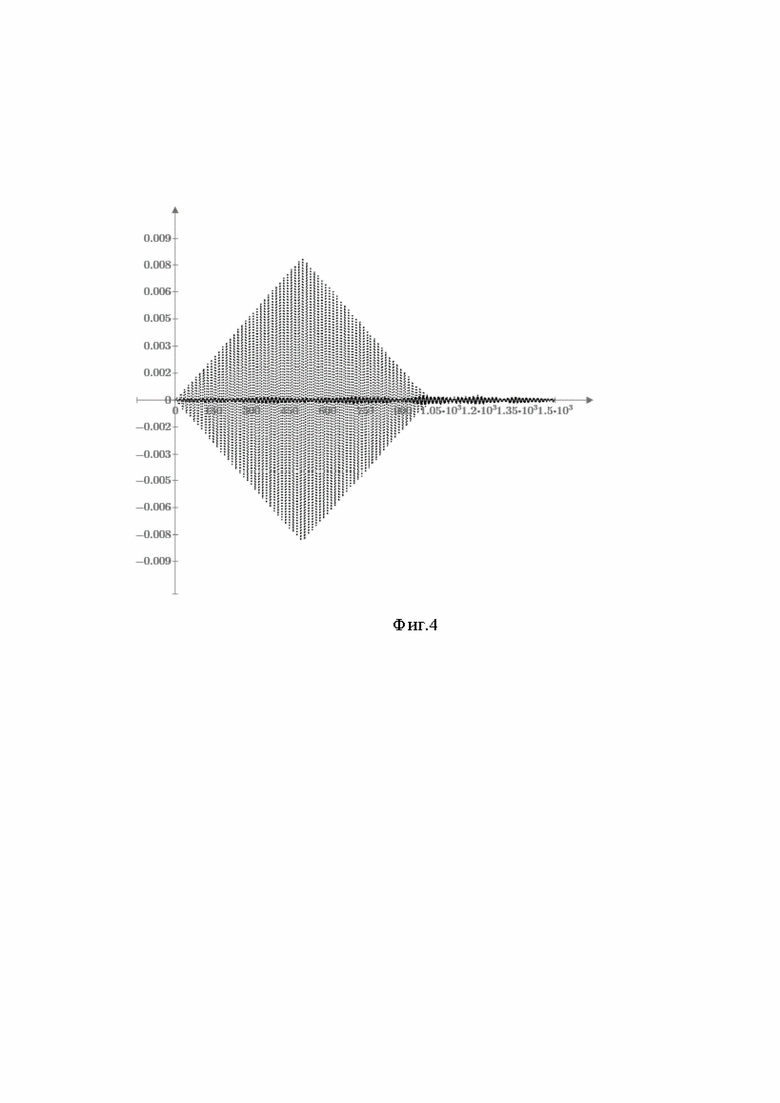
На Фиг.4 представлен отсчёты после нелинейного преобразования 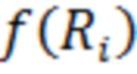 предлагаемого способа без сигнала на входе (сплошная линия) и при его наличии (пунктирная линия), когда сигнал - «сильный», то есть отношение сигнал/(помеха+шум) на входе равно +10 дБ.
предлагаемого способа без сигнала на входе (сплошная линия) и при его наличии (пунктирная линия), когда сигнал - «сильный», то есть отношение сигнал/(помеха+шум) на входе равно +10 дБ.
Форма отклика СФ при наличии сигнала и для слабого сигнал и для сильного полностью соответствует форме автокорреляционной функции (АКФ) одиночного радиоимпульса [5, смотри вид АКФ на Рис.1.10 на стр.36 в книге Тисленко В.И. Статистическая теория радиотехнических систем: Учеб. пособие. -Томск: Том. гос. ун-т систем управления и радиоэлектроники, 2003. - 153 с.].
ЛИТЕРАТУРА.
1. Левин Б.Р. Теоретические основы статистической радиотехники. В трёх книгах. Книга третья. М., «Сов.радио», 1976, 288с.
2. Восстановление зависимостей по эмпирическим данным. Вапник В. Н. Главная редакция физико-математической литературы издательства «Наука», М., 1979, - 448 с.
3. Г.Корн, Т.Корн. Справочник по математике (для научных работников иинженеров). Издательство «Наука». Главная редакция физико-математической литературы, М., 1973. 832 с.
4. Теория обнаружения сигналов /П.С. Акимов, П.А. Бакут, В.А. Богданович и др.; Под ред. П.А. Бакута. - М.: Радио и связь, 1984.- 440 с.
5. Тисленко В.И. Статистическая теория радиотехнических систем: Учеб. пособие. -Томск: Том. гос. ун-т систем управления и радиоэлектроники, 2003. - 153 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ ПОЛЕЗНОГО СИГНАЛА В УЗКОПОЛОСНОЙ СМЕСИ С ПОМЕХОЙ | 2023 |
|
RU2827140C1 |
| СПОСОБ СЛОЖНОСОСТАВНОЙ ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ ДЛЯ ОБНАРУЖЕНИЯ СЛАБЫХ СИГНАЛОВ | 2012 |
|
RU2518443C2 |
| Способ согласованной нелинейной корреляционно-вероятностной фильтрации сигналов и устройство для его реализации | 2018 |
|
RU2723441C2 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
| Способ классификации подвижных объектов наземной техники | 2023 |
|
RU2811811C1 |
| Способ спектрально-корреляционного обнаружения летательных аппаратов по квазинепрерывным импульсным сигналам бортовых радиоэлектронных систем | 2021 |
|
RU2768370C1 |
| УСТРОЙСТВО АДАПТИВНОГО ОЦЕНИВАНИЯ СОСРЕДОТОЧЕННОЙ ПОМЕХИ | 2008 |
|
RU2381620C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ | 2022 |
|
RU2801897C1 |
| Способ повышения эффективности обработки сверхширокополосных короткоимпульсных сигналов на приёмной стороне | 2019 |
|
RU2731207C1 |
| Способ обнаружения подвижных объектов наземной техники | 2023 |
|
RU2816287C1 |
Изобретение относится к области радиоэлектроники и может быть использовано при обнаружении полезных сигналов с неизвестной фазовой или временной задержкой в условиях действия аддитивных широкополосных негауссовых помех при любом соотношении мощностей полезного сигнала и помехи, когда распределения мгновенных значений помехи неизвестны или меняются во времени, а вероятность ложной тревоги должна поддерживаться на заданном уровне. Техническим результатом изобретения является возможность поддерживать в реальных условиях приёма сигналов максимально возможными вероятности правильного принятия решений о наличии или отсутствии полезного сигнала в наблюдаемом процессе на входе приёмного тракта. Способ обнаружения полезного сигнала s(t) на фоне аддитивной помехи заключается в запоминании в памяти вычислительного устройства последовательности дискретных отсчётов, полученной в результате дискретизации процесса изменения тока или напряжения согласно теореме отсчётов, сортировке сохранённых отсчётов в порядке возрастания для получения вариационного ряда, определении для каждого отсчёта 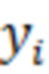 его номера
его номера 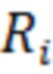 в вариационном ряду, нелинейном преобразовании номера
в вариационном ряду, нелинейном преобразовании номера 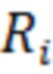 в последовательность отсчётов
в последовательность отсчётов 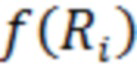 путём аппроксимации вариационного ряда и вычисления для каждого отсчёта
путём аппроксимации вариационного ряда и вычисления для каждого отсчёта 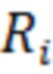 результата аппроксимации в виде отсчёта
результата аппроксимации в виде отсчёта 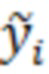 , оценивании плотности вероятности отсчётов
, оценивании плотности вероятности отсчётов 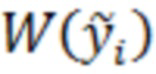 и использовании найденной в результате оценивания зависимости от
и использовании найденной в результате оценивания зависимости от 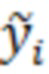 для вычисления отсчётов
для вычисления отсчётов 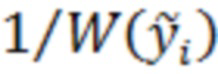 , оценивании для каждого отсчёта
, оценивании для каждого отсчёта 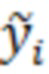 характера наклона найденной зависимости, выдаче как результата нелинейного преобразования
характера наклона найденной зависимости, выдаче как результата нелинейного преобразования 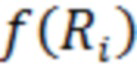 отсчётов
отсчётов 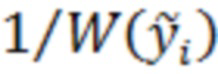 или
или 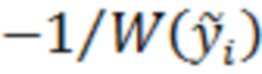 , соответствующих положительному и отрицательному наклону найденной зависимости, вычислении максимального по модулю значения функции корреляции между последовательностью
, соответствующих положительному и отрицательному наклону найденной зависимости, вычислении максимального по модулю значения функции корреляции между последовательностью 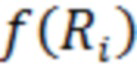 и заданной последовательностью отсчётов полезного сигнала
и заданной последовательностью отсчётов полезного сигнала 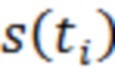 , сравнении с заданным порогом обнаружения и принятии решения о наличии или отсутствии полезного сигнала на выходе приёмного тракта в зависимости от результата сравнения. 4 ил.
, сравнении с заданным порогом обнаружения и принятии решения о наличии или отсутствии полезного сигнала на выходе приёмного тракта в зависимости от результата сравнения. 4 ил.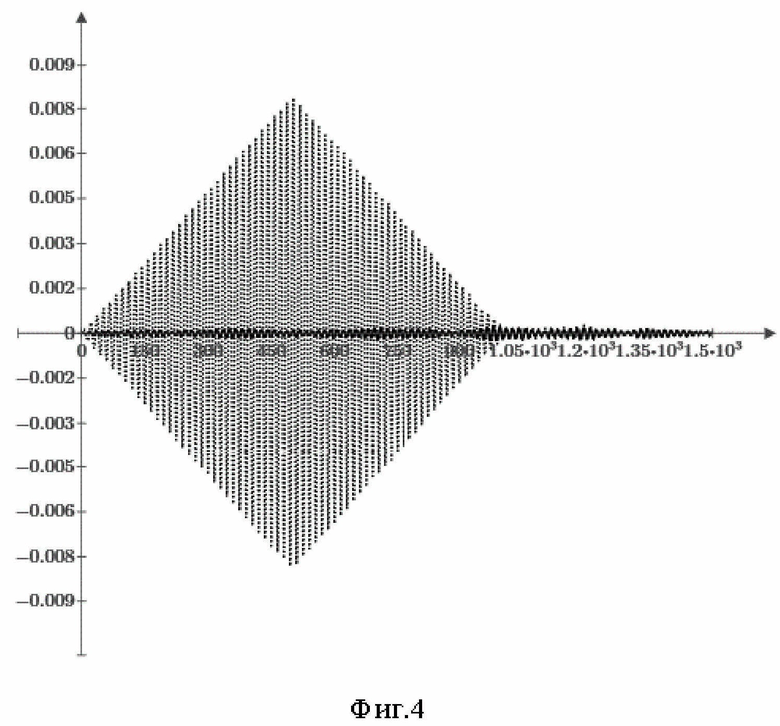
Способ обнаружения полезного сигнала 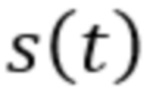 на фоне аддитивной помехи, включающий дискретизацию процесса изменения тока или напряжения
на фоне аддитивной помехи, включающий дискретизацию процесса изменения тока или напряжения 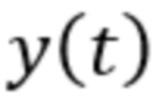 во времени на выходе приёмного тракта в соответствии с теоремой Котельникова и получение последовательности дискретных отсчётов
во времени на выходе приёмного тракта в соответствии с теоремой Котельникова и получение последовательности дискретных отсчётов 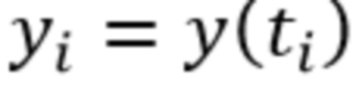 в моменты времени
в моменты времени 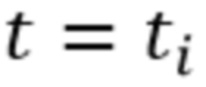 , где
, где 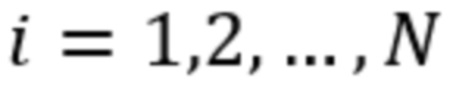 – номер отсчёта, сохранение этих отсчётов в памяти вычислительного устройства, сортировку сохранённых отсчётов по порядку возрастания и получение вариационного ряда, определение для каждого отсчёта
– номер отсчёта, сохранение этих отсчётов в памяти вычислительного устройства, сортировку сохранённых отсчётов по порядку возрастания и получение вариационного ряда, определение для каждого отсчёта 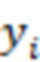 его номера
его номера 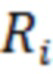 в вариационном ряду, которые нелинейно преобразуют в последовательность отсчётов
в вариационном ряду, которые нелинейно преобразуют в последовательность отсчётов 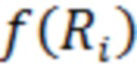 , вычисляют максимальное по модулю значение функции корреляции между последовательностью
, вычисляют максимальное по модулю значение функции корреляции между последовательностью 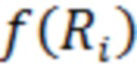 и заданной последовательностью отсчётов полезного сигнала
и заданной последовательностью отсчётов полезного сигнала 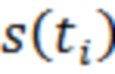 , которое далее сравнивают с заданным порогом обнаружения, и в зависимости от результата сравнения принимают решение о наличии или отсутствии полезного сигнала на выходе приёмного тракта, отличающийся тем, что действие помехи ослабляют путём адаптивной настройки при нелинейном преобразовании на ожидаемый сигнал, что приводит к повышению вероятностей правильного принятия решений о наличии или отсутствии полезного сигнала, для этого адаптацию осуществляют аппроксимацией вариационного ряда и вычислением для каждого отсчёта
, которое далее сравнивают с заданным порогом обнаружения, и в зависимости от результата сравнения принимают решение о наличии или отсутствии полезного сигнала на выходе приёмного тракта, отличающийся тем, что действие помехи ослабляют путём адаптивной настройки при нелинейном преобразовании на ожидаемый сигнал, что приводит к повышению вероятностей правильного принятия решений о наличии или отсутствии полезного сигнала, для этого адаптацию осуществляют аппроксимацией вариационного ряда и вычислением для каждого отсчёта 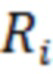 результата аппроксимации в виде отсчёта
результата аппроксимации в виде отсчёта 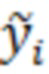 , далее оценивают плотность вероятности отсчётов
, далее оценивают плотность вероятности отсчётов 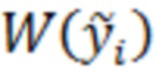 и, используя найденную в результате оценки зависимость от
и, используя найденную в результате оценки зависимость от 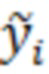 , вычисляют отсчёты
, вычисляют отсчёты 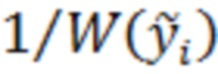 , далее для каждого отсчёта
, далее для каждого отсчёта 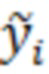 оценивают характер наклона найденной зависимости: положительный или отрицательный, - и выдают как результат нелинейного преобразования
оценивают характер наклона найденной зависимости: положительный или отрицательный, - и выдают как результат нелинейного преобразования 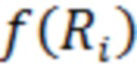 отсчёты
отсчёты 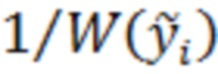 или
или 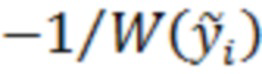 соответственно.
соответственно.
| ЛЕВИН Б.Р | |||
| Теоретические основы статистической радиотехники | |||
| В трёх книгах | |||
| Книга третья | |||
| М., "Сов.радио", 1976, 288с | |||
| Раздвижной паровозный золотник с подвижными по его скалке поршнями между упорными шайбами | 1922 |
|
SU148A1 |
| ПАЛАГИН В.В | |||
| Алгоритмы обнаружения сигналов на фоне негауссовских помех // Радиоэлектроника и информатика | |||
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Способ образования коричневых окрасок на волокне из кашу кубической и подобных производных кашевого ряда | 1922 |
|
SU32A1 |
| WO 9847243 A2, 22.10.1998 | |||
| US 10084495 B2, 25.09.2018 | |||
| Устройство обнаружения радиосигналов | 1980 |
|
SU907488A1 |
Авторы
Даты
2024-05-24—Публикация
2023-08-07—Подача