Область техники, к которой относится изобретение
Способ управления мостовым краном на основе скоростного ПД-регулятора относится к области автоматического управления грузовыми кранами с целью повышения производительности, безопасности при их эксплуатации, снижения эксплуатационных затрат. Рассматривается класс крановых установок, конструкция которых предполагает подвесное крепление груза, в частности - мостовые краны.
Уровень техники
В настоящее время мостовые краны широко используются в различных отраслях промышленности для перемещения грузов. Использование этих кранов сопряжено с маятниковыми колебаниями груза. Они возникают, в основном, во время ускорения или торможения крана, или от воздействий каких-либо внешних возмущений (ветер, неровности пути перемещения крана, перебои в электропитании электропривода и т.д.). Также из-за маятниковых колебаний груза возникают дополнительные нагрузки на механизмы и металлические конструкции крана, снижается безопасность из-за непредвиденного перемещения груза. Кроме того, современные крановые установки характеризуются большим разнообразием переносимых грузов и режимов работы, а также вероятностью возникновения неконтролируемых внешних возмущений, например, из-за воздействия ветра.
Отсюда одним из направлений в совершенствовании мостовых кранов является разработка систем автоматического управления ими с гашением маятниковых колебаний и парированием внешних возмущений. При этом в силу указанных причин, такие системы должны обеспечивать заданные характеристики системы управления при большом многообразии параметров переносимого груза, режимов работы и действии внешних возмущений, обладать простотой построения, не иметь затратных методов эксплуатации и др.
Одним из привлекательных подходов в этом отношении являются системы управления на основе ПИД-, ПИ-, ПД-, П-регуляторов в силу их изученности, простоты построения, достигаемого качества управления, массовости использования в современной автоматизации. Обязательным условием является обеспечение робастных свойств системы управления, достаточных для условий практики, при фиксированной настройке параметров этих регуляторов.
Известен способ управления мостовым краном, задачей которого является повышение точности и скорости перемещения груза по требуемой траектории и компенсации колебаний груза, [1]. Данный способ обеспечивает перемещение груза по требуемой траектории, которая задаётся в виде временных зависимостей декартовых координат. Однако этот метод имеет ряд недостатков. К ним относится то, что в законе управления используется П-регулятор, который настраивается под узкий диапазон параметров крана. Также в этом методе не учитываются возможные внешние возмущения на кран, например, воздействия ветра на транспортируемый груз, неровности подкранового пути, износ приводов крана, следовательно, система управления не способна их парировать. Подобными свойствами обладает метод управления мостовым краном по [2] на основе П- или ПИ-регулятора по отслеживанию заданного углового положения подвеса с расположением датчиков информации на канате подвеса груза.
В работе [3] рассматривается использование двух (трех) ПИД-регуляторов, функционирующих по ошибке линейного перемещения тележки крана, по углу отклонения крюка (груза) от вертикальной оси. Настройку параметров этих регуляторов предлагается строить на основе метода оптимизации роя частиц. В работе [4] рассматривается ПИД-регулятор по ошибке положения тележки и ПД-регулятор по угловому отклонению груза от вертикали. Алгоритм настройки регуляторов - на основе вариации метода стохастического поиска. Похожий алгоритм настройки ПИД-регулятора также описан в [5]. Одним из недостатков этих подходов также является необходимость предварительной настройки коэффициентов регуляторов для достаточно узкой области крана и груза.
В работе [6] рассматривается двухконтурная система перемещения тележки мостового крана. Во внутреннем контуре решается задача гашения угловых колебаний груза, во втором внешнем - задача по перемещению тележки в заданное положение. Оба контура используют ПИД регуляторы. Параметры регуляторов выбираются на основе метода разделения движений на быстрые и медленные в каждом контуре и с учетом априорной информации о параметрах системы управления и груза. Последнее является недостатком, поскольку на практике не все они известны в текущем времени.
В работе [7] рассматривается система управления, состоящая из двух аддитивных составляющих: первая - это ПД-регулятор с входной переменной в виде ошибки перемещения тележки, вторая - регулятор, построенный по методу локализации. Параметры ПД-регулятора подбираются. Метод локализации требует измерения или вычисления старшей производной и использования большого пропорционального коэффициента регулятора. На практике такой подход трудно реализовать из-за сложности достаточно точного определения старшей производной, а также в условиях задержек управления, наличия недомоделированной высокочастотной динамики объекта и пр.
В работе [8] используется нелинейный ПД-регулятор, у которого входной переменной является ошибка линейного перемещения тележки, причем коэффициент в дифференциальной части регулятора нелинейно зависит от угла отклонения груза от вертикали и его скорости. Недостатком решения является отсутствие конкретных рекомендаций по назначению коэффициентов этого регулятора.
Общей особенностью указанных решений является то, что они рассматривают системы управления, формирующие силу воздействия на тележку (балку) крана. Заявленные робастные свойства систем не полностью удовлетворяют требованиям практики. В работах приводятся результаты модельных исследований, где, например, вариация веса груза предполагается максимум в 2 раза. Известно, что на производственных участках вес груза может меняться в десятки и даже сотни раз.
Наиболее близким к предлагаемому изобретению (прототипом) является метод управления мостовым краном, изложенной в [9]. Здесь для гашения угловых колебаний предлагается использовать П-регулятор в замкнутом контуре следящей системы по скорости перемещения тележки крана с входным сигналом в виде угла отклонения груза от вертикали. Коэффициент регулятора рассчитывается на основе длины подвеса, которая определяется автоматически по периоду колебаний. Недостатком подхода является отсутсвие решения по позиционированию груза в назначенной точке.
Задачей предлагаемого изобретения является повышение робастных свойств системы управления краном, предназначенной для точного перемещения груза в целевую точку с гашением маятниковых колебаний, в условиях очень высокой вариации параметров грузов, длины подвеса груза и при действии неконтролируемых внешних воздействий. А также - формирование рекомендаций для настройки параметров регулятора на основе паспортных данных мостового крана и координат целевой точки.
Отличием в предлагаемом изобретении является использование ПД-регулятора, формирующего заданную скорость тележки (балки) мостового крана, оборудованного сервоприводами тележки (балки) крана (в частности, асинхронными сервоприводами). Пропорциональная часть регулятора формирует заданную скорость, прямо пропорциональную ошибке в позиционировании груза, а дифференциальная часть формирует дополнительную заданную скорость, прямо пропорциональную угловой скорости подвеса груза, фильтрованной на низкочастотном фильтре. Параметры регулятора задаются на основании паспортных данных мостового крана: максимальной длины подвеса и максимальной скорости сервоприводов, а также расстояния до целевой точки доставки груза и ее высоты.
Краткое описание чертежей
На фиг.1 представлена схема перемещения мостового крана с грузом по одной горизонтальной оси, соответствующей перемещению тележки крана.
На фиг.2 представлены кривые реализуемых значений относительного коэффициента затухания.
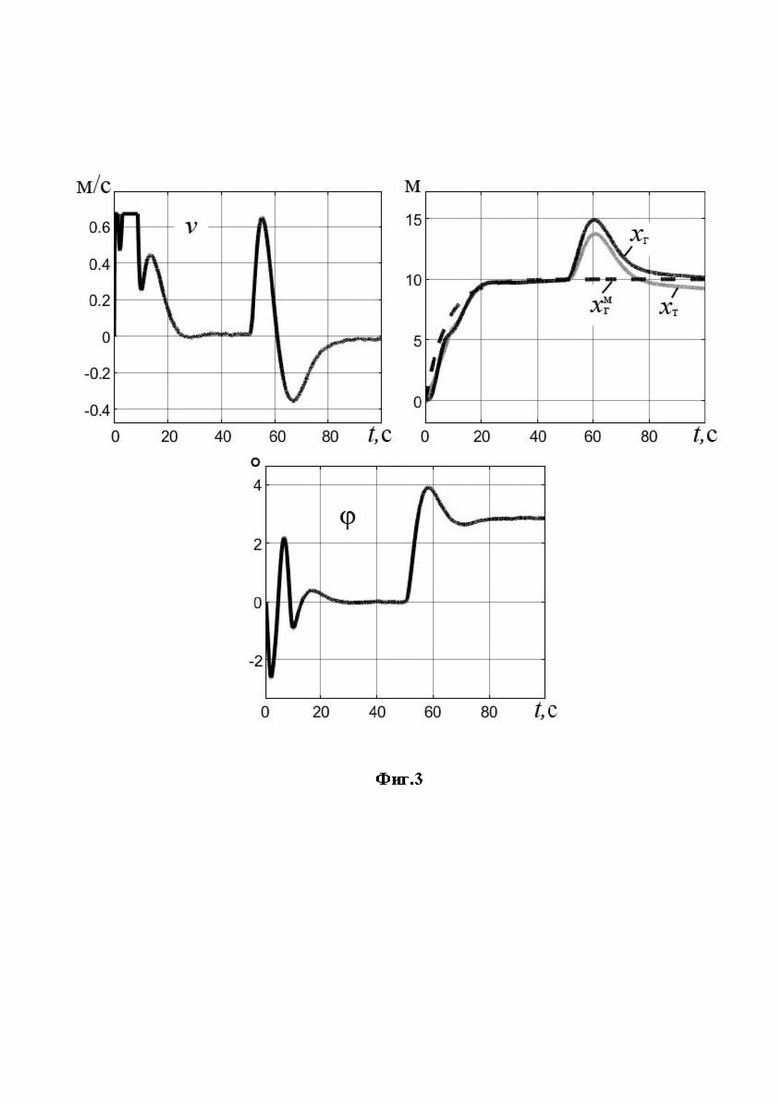
На фиг. 3 представлены результаты модельных исследований замкнутой системы управления для среднего мостового крана при максимальной длине подвеса груза (18 м).
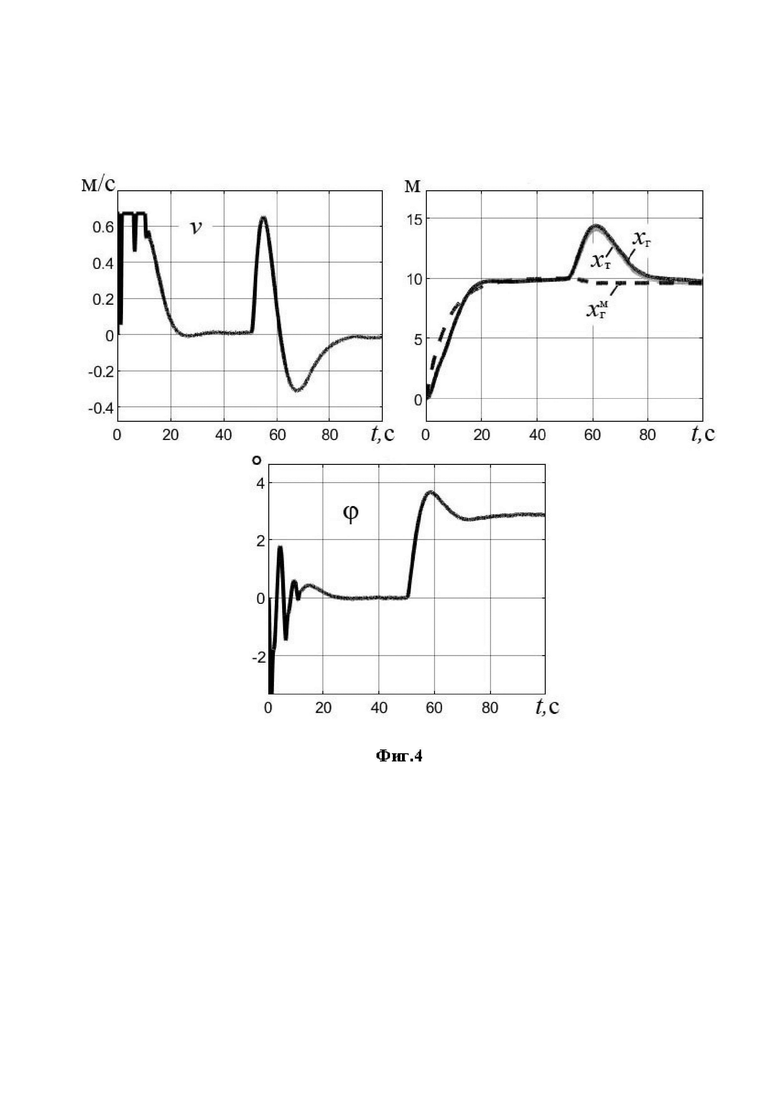
На фиг. 4 представлены результаты модельных исследований замкнутой системы управления для среднего мостового крана при минимальной длине подвеса груза (5 м).
Осуществление изобретения
Ниже будем рассматривать движение крана и груза только по одной оси горизонтального перемещения груза, соответствующем передвижению тележки крана (по другой оси, соответствующей перемещению балки крана - рассуждения аналогичные).
На фиг.1 и в дальнейших рассуждениях используются следующие обозначения:
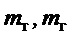 - масса тележки крана, с учетом инерционности вращающихся масс, и масса переносимого груза соответственно (в качестве груза подразумевается непосредственно переносимый груз и захватное устройство - крюк);
- масса тележки крана, с учетом инерционности вращающихся масс, и масса переносимого груза соответственно (в качестве груза подразумевается непосредственно переносимый груз и захватное устройство - крюк);
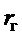 - радиус инерции груза;
- радиус инерции груза;
 - длина подвеса груза, или расстояние от точки крепления подвеса на тележке до центра груза; примем, что
- длина подвеса груза, или расстояние от точки крепления подвеса на тележке до центра груза; примем, что 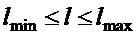 ,
, 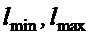 - минимальная и максимальная длина подвеса соответственно;
- минимальная и максимальная длина подвеса соответственно;
 - перемещение тележки вдоль горизонтальной оси
- перемещение тележки вдоль горизонтальной оси 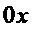 ;
;
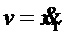 - скорость перемещения тележки c ограничением
- скорость перемещения тележки c ограничением 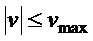 , а
, а 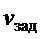 - заданное значение этой скорости;
- заданное значение этой скорости;
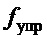 - управляющая сила, формируемая сервоприводом тележки по сигналу
- управляющая сила, формируемая сервоприводом тележки по сигналу 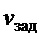 ;
;
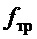 - сила трения, противодействующая перемещению тележки;
- сила трения, противодействующая перемещению тележки;
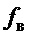 - сила ветрового воздействия, приложенная в центре масс груза;
- сила ветрового воздействия, приложенная в центре масс груза;
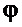 - угол отклонения подвеса груза от вертикальной оси;
- угол отклонения подвеса груза от вертикальной оси;
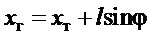 - горизонтальное перемещение груза;
- горизонтальное перемещение груза;
Д - точка расположения совмещенного датчика на канате подвеса;
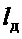 - длина подвеса до совмещенного датчика (расстояние от точки крепления подвеса на тележке до точки Д),
- длина подвеса до совмещенного датчика (расстояние от точки крепления подвеса на тележке до точки Д),  ;
;
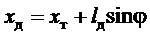 - горизонтальное перемещение совмещенного датчика;
- горизонтальное перемещение совмещенного датчика;
ЦТ - целевая точка доставки груза с координатами 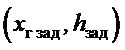 ;
;
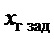 - координата целевой точки по горизонтальной оси
- координата целевой точки по горизонтальной оси 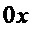 ;
;
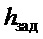 - координата целевой точки по вертикальной оси
- координата целевой точки по вертикальной оси 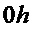 (высота погрузки);
(высота погрузки);
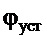 - предполагаемое установившееся постоянное значение угла
- предполагаемое установившееся постоянное значение угла 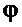 по окончании регулирования;
по окончании регулирования;
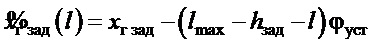 - заданное положение груза по горизонтальной оси на текущей длине подвеса, или расстояние от нулевой точки до линии «А - ЦТ» по оси
- заданное положение груза по горизонтальной оси на текущей длине подвеса, или расстояние от нулевой точки до линии «А - ЦТ» по оси  .
.
Будем считать, что внешнее возмущение движению тележки с грузом, представляющее изменение силы трения и ветрового воздействия, имеет ступенчатый характер с произвольным моментом времени с ограниченной интенсивностью, что является типовым подходом при определении свойств любой автоматической системы управления по парированию внешних возмущений [10].
На основе математической модели поступательного и вращательного движения системы «тележка-груз» (без учёта массы каната и трения углового движения, в силу их малости, а также начальных значений переменных по положению и скорости), описанной в [11], с применением теоремы Пуансо, динамику движения механической системы, изображенной на фиг.1, можно описать следующей системой дифференциальных уравнений (указанные производные переменных взяты по времени 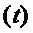 ):
):
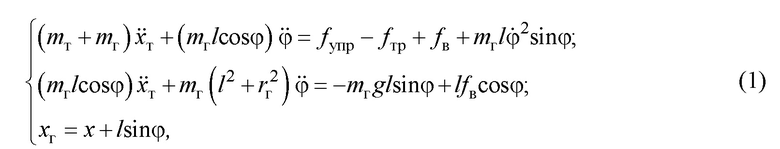
где 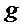 - ускорение свободного падения.
- ускорение свободного падения.
Поскольку угол отклонения груза небольшой (не практике не более 10-20°), угловая скорость также невысокая, с учетом кинематики движения можно принять: 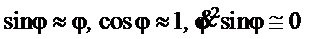 . Поэтому систему (1) можно описать в линеаризованном виде как:
. Поэтому систему (1) можно описать в линеаризованном виде как:
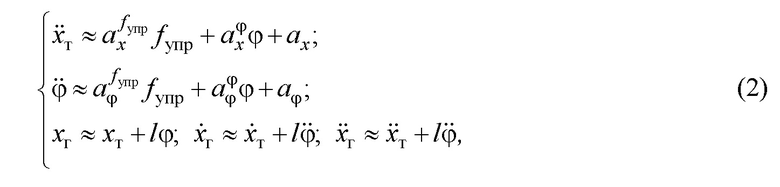
где  ;
;
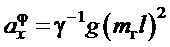 ;
;
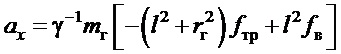 ;
;
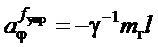 ;
;
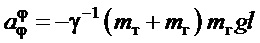 ;
;
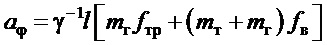 ;
;
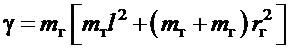 .
.
Подставляя первое и второе уравнения системы (2) в третье уравнение третьей строки системы (2), выражая сигнал 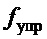 из первого равенства (2) и подставляя его в полученный результат, определим, что движение груза можно описать через скорость тележки следующим приблизительным равенством:
из первого равенства (2) и подставляя его в полученный результат, определим, что движение груза можно описать через скорость тележки следующим приблизительным равенством:

где 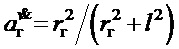 ;
;
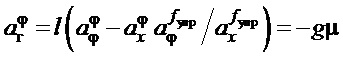 ;
;
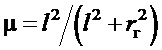 - безразмерный коэффициент влияния радиуса инерции груза;
- безразмерный коэффициент влияния радиуса инерции груза;
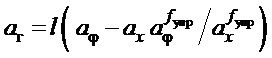 - параметр, равный ускорению, образованному внешними возмущениями.
- параметр, равный ускорению, образованному внешними возмущениями.
С использованием (2), уравнение (3) запишем в следующем виде

Для определения свойств собственного углового движения при отсутствии возмущений и 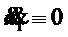 это равенство перепишется как [12]
это равенство перепишется как [12]

где 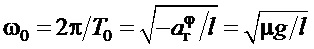 - собственная частота углового движения подвеса груза, равная собственной частоте физического маятника при отсутствии ускорения тележки;
- собственная частота углового движения подвеса груза, равная собственной частоте физического маятника при отсутствии ускорения тележки;
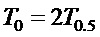 - период собственных колебаний, а
- период собственных колебаний, а 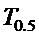 - полупериод собственных колебаний.
- полупериод собственных колебаний.
Для дальнейших рассуждений примем следующее допущение, соответствующее подавляющему большинству практических случаев:

Сформулируем следующую цель, основанную на свойствах апериодического и колебательного движений [10]: построить закон формирования заданной скорости тележки (vзад), который бы при фиксированном наборе своих параметров и условии 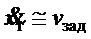 (последнее в силу достаточно высокого быстродействия современных сервоприводов, см., например, [13]) обеспечил для широкой области параметров крана и груза, действия внешнего возмущения следующие свойства переходных процессов:
(последнее в силу достаточно высокого быстродействия современных сервоприводов, см., например, [13]) обеспечил для широкой области параметров крана и груза, действия внешнего возмущения следующие свойства переходных процессов:

где 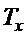 - заданная постоянная времени линейного перемещения груза по апериодической динамике;
- заданная постоянная времени линейного перемещения груза по апериодической динамике;
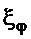 - заданный коэффициент демпфирования углового движения, для дальнейших рассуждений, в качестве примера, примем его следующим:
- заданный коэффициент демпфирования углового движения, для дальнейших рассуждений, в качестве примера, примем его следующим: 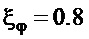 ;
;
знак «≈» в (7) имеет смысл приблизительного обеспечения указанных качественных характеристик замкнутой системы управления.
Переменные 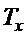 и
и 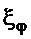 указывают на требование того, чтобы груз перемещался динамикой, близкой динамике апериодического движения с постоянной времени
указывают на требование того, чтобы груз перемещался динамикой, близкой динамике апериодического движения с постоянной времени 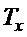 , а угловое движение было близко колебательному движению с коэффициентом демпфирования
, а угловое движение было близко колебательному движению с коэффициентом демпфирования 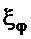 . Также заметим, что первое требование (7), если
. Также заметим, что первое требование (7), если 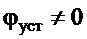 , требует позиционирование груза не над целевой точкой доставки груза, а так, чтобы по окончании регулирования без дополнительных перемещений тележки при опускании груза обеспечить его доставку в целевую точку (движение груза по линии «А - ЦТ»).
, требует позиционирование груза не над целевой точкой доставки груза, а так, чтобы по окончании регулирования без дополнительных перемещений тележки при опускании груза обеспечить его доставку в целевую точку (движение груза по линии «А - ЦТ»).
В качестве датчиков информации предлагается использовать измерители положения тележки (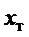 ) и совмещенный датчик, измеряющий угловую скорость подвеса (
) и совмещенный датчик, измеряющий угловую скорость подвеса (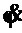 ) и линейное ускорение (
) и линейное ускорение (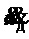 ) в точке размещения датчика на канате подвеса.
) в точке размещения датчика на канате подвеса.
Для достижения поставленной цели рассмотрим четыре варианта законов управления тележки крана по скорости, последовательно вытекающие один из другого.
Первый вариант. Заданную скорость тележки сформируем в виде:

где 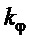 - задаваемый положительный коэффициент.
- задаваемый положительный коэффициент.
Тогда при отсутствии возмущений с учетом (5) и описания колебательного процесса по теории автоматического управления, равенство (4) можно записать как

где 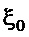 - относительный коэффициент затухания, который можно определить по одному из равенств (в зависимости от располагаемой априорной информации:
- относительный коэффициент затухания, который можно определить по одному из равенств (в зависимости от располагаемой априорной информации: 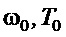 или
или 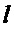 и
и 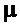 ):
):
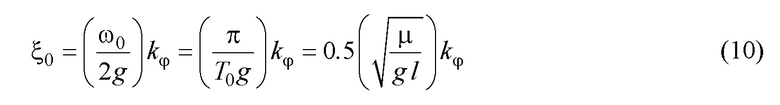
Отсюда несложно определить коэффициент  по заданному значению относительного коэффициента затухания (
по заданному значению относительного коэффициента затухания (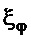 ):
):
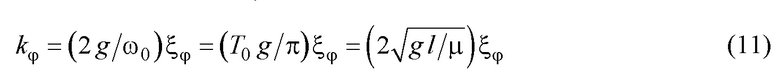
При выборе 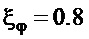 , закон управления (8) обеспечит устойчивость колебательного движения замкнутой системы управления, быстрое и эффективное гашение колебаний при отсутствии внешних возмущений.
, закон управления (8) обеспечит устойчивость колебательного движения замкнутой системы управления, быстрое и эффективное гашение колебаний при отсутствии внешних возмущений.
На основе полученного, можно предложить целесообразный для практики вариант назначения коэффициента 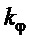 в (8), требующий знание лишь длины подвеса (без учета значения
в (8), требующий знание лишь длины подвеса (без учета значения 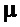 , в силу (6)) или периода собственных колебаний:
, в силу (6)) или периода собственных колебаний:

где единицы измерения соответствуют системе измерений СИ.
Для дальнейших рассуждений далее будем использовать первую зависимость в (12). Не сложно определить, что при назначении 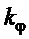 по ней в замкнутой системе управления при всех вариациях радиуса инерции груза в указанном ограничении относительный коэффициент затухания будет находится в диапазоне:
по ней в замкнутой системе управления при всех вариациях радиуса инерции груза в указанном ограничении относительный коэффициент затухания будет находится в диапазоне:
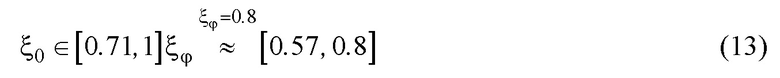
Последнее показано графически на фиг.2 на примере изменения длины подвеса в диапазоне 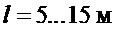 , и изменения радиуса инерции груза в диапазоне
, и изменения радиуса инерции груза в диапазоне 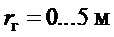 . Это указывает на хорошие характеристики колебательного процесса [10].
. Это указывает на хорошие характеристики колебательного процесса [10].
Из теории автоматического управления следует, что если левая часть равенства (9) является устойчивой, то в силу принятого характера внешнего возмущения угол 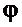 стремится к своему установившемуся значению:
стремится к своему установившемуся значению:

Можно утверждать, что закон управления (8) обеспечивает выполнение второй части целевой задачи (7) по демпфированию угловых колебаний, но не дает решения по перемещению груза в целевую точку.
Второй вариант. Для устранения указанного недостатка первого варианта примем закон управления вместо (8) в виде:
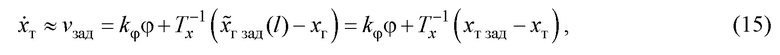
где
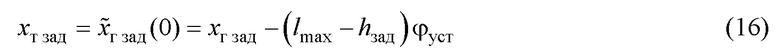
- положение тележки, необходимое для достижения первого условия целевой установки (7);
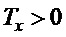 - задаваемая постоянная времени линейного движения, требование к которой указано ниже.
- задаваемая постоянная времени линейного движения, требование к которой указано ниже.
Поскольку по (15) при условии 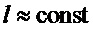 :
:  , подстановка этой зависимости в (4) порождает:
, подстановка этой зависимости в (4) порождает:
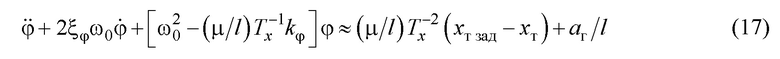
Правая часть этого уравнения практически не зависит от левой его части. Только один ее член зависит от текущего значения 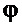 на переходном процессе:
на переходном процессе: 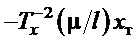 . Но в силу малости первого его коэффициента, на что будет указано ниже, таким влиянием можно пренебречь. Тогда для устойчивости уравнения (17) требуется обеспечить устойчивость левой его части, что, в свою очередь, требует условия
. Но в силу малости первого его коэффициента, на что будет указано ниже, таким влиянием можно пренебречь. Тогда для устойчивости уравнения (17) требуется обеспечить устойчивость левой его части, что, в свою очередь, требует условия 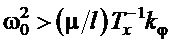 . Подставляя сюда значение
. Подставляя сюда значение 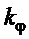 по (11), находим требование к постоянной времени
по (11), находим требование к постоянной времени 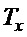 :
:
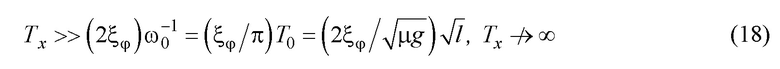
Первое из требований (18) с увеличением 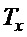 обеспечивает приближение уравнения (17) к уравнению (9), т.е. к переходному процессу по угловому движению при законе управления (8). Нарушение второго требования (18) приводит к затянутости переходного процесса по
обеспечивает приближение уравнения (17) к уравнению (9), т.е. к переходному процессу по угловому движению при законе управления (8). Нарушение второго требования (18) приводит к затянутости переходного процесса по 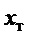 . Это следует непосредственно из закона управления (15):
. Это следует непосредственно из закона управления (15):

Отсюда также ясно, что динамика движения тележки близка к апериодическому процессу с постоянной времени 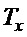 с возмущением от изменения
с возмущением от изменения 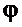 . В силу (17), (18) можно отнести апериодическое (собственное) движение тележки, описываемое левой частью (19), к низкочастотному движению, а угловое движение, или возмущение для апериодического движения - уравнение (17) и правую часть (19) - к высокочастотному. Это объясняет смысловое содержание параметра
. В силу (17), (18) можно отнести апериодическое (собственное) движение тележки, описываемое левой частью (19), к низкочастотному движению, а угловое движение, или возмущение для апериодического движения - уравнение (17) и правую часть (19) - к высокочастотному. Это объясняет смысловое содержание параметра 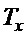 и второе условие (18).
и второе условие (18).
При выборе параметра 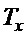 закона управления (15) также нужно учесть максимальную скорость тележки (
закона управления (15) также нужно учесть максимальную скорость тележки (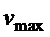 ). Для учета этого будем рассматривать только второе слагаемое в правой части (15). Тогда из динамики собственного апериодического движения (19) следует, что для этого требуется условие:
). Для учета этого будем рассматривать только второе слагаемое в правой части (15). Тогда из динамики собственного апериодического движения (19) следует, что для этого требуется условие: 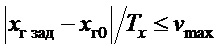 , где
, где 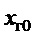 - начальное положение груза [10]. Отсюда, с учетом того, что движение тележки (груза) не чисто апериодическое, можно записать дополнительное требование к назначению параметра
- начальное положение груза [10]. Отсюда, с учетом того, что движение тележки (груза) не чисто апериодическое, можно записать дополнительное требование к назначению параметра 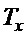 :
:

где 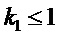 - назначаемый коэффициент для ускорения переходного процесса (с сопутствующим этому отставанием от желаемого движения на некоторых этапах переходного процесса - см. модельные исследования);
- назначаемый коэффициент для ускорения переходного процесса (с сопутствующим этому отставанием от желаемого движения на некоторых этапах переходного процесса - см. модельные исследования);
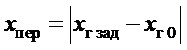 - дальность переноса груза;
- дальность переноса груза;
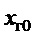 - начальное положение груза.
- начальное положение груза.
Из указанных соотношений (18) - (20) можно сформировать два варианта зависимостей по выбору параметра 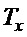 , при
, при 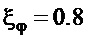 (в приведенных ниже зависимостях - единицы измерения в системе СИ):
(в приведенных ниже зависимостях - единицы измерения в системе СИ):
- если имеется требование обеспечить заданное время переходного процесса (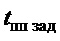 ) с очевидным ограничением
) с очевидным ограничением 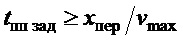 :
:

- если требуется обеспечить максимальное быстродействие крановых работ:
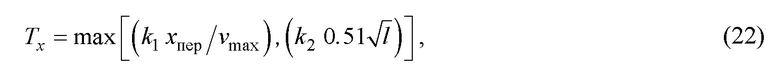
где 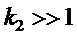 - назначаемый безразмерный коэффициент, по опыту исследований достаточной его величиной является, например, число 3.
- назначаемый безразмерный коэффициент, по опыту исследований достаточной его величиной является, например, число 3.
Кроме указанного при рассмотрении второго варианта закона управления, из (17) при соблюдении (18), зависимости (19) и из ранее изложенного также следует, что при отсутствии внешних возмущений (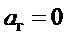 ) в замкнутой системе управления с законом (15) и
) в замкнутой системе управления с законом (15) и 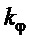 по (11) или (12):
по (11) или (12): 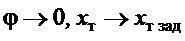 , а значит по (15) и
, а значит по (15) и 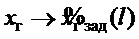 , т.е., с учетом изложенного выше, достигается цель управления (7).
, т.е., с учетом изложенного выше, достигается цель управления (7).
При наличии внешнего возмущения 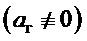 :
: 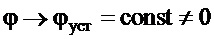 ,
, 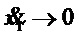 ,
, 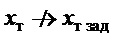 ,
, 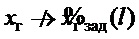 , т.е. цель управления (7) не достигается.
, т.е. цель управления (7) не достигается.
Здесь также рассмотрим вопрос определения величины 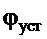 , необходимой для формирования закона управления (15). По своему определению и малости угла отклонения подвеса, она может быть определена по очевидной зависимости:
, необходимой для формирования закона управления (15). По своему определению и малости угла отклонения подвеса, она может быть определена по очевидной зависимости:

где 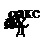 - показания акселерометра, установленного в точке Д подвеса с осью чувствительности, ортогональной канату подвеса (по физике явления при любом движении и отсутствии ветра:
- показания акселерометра, установленного в точке Д подвеса с осью чувствительности, ортогональной канату подвеса (по физике явления при любом движении и отсутствии ветра: 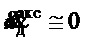 );
);
нижний индекс «нч» обозначает низкочастотную фильтрацию, выполняемую для подавления высокочастотных шумов датчика и выделения низкочастотных составляющих ветровых воздействий.
Третий вариант. Он предназначен для устранения указанного недостатка. Здесь вместо закона управления (15) примем:
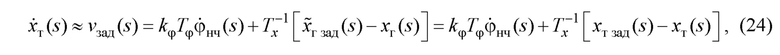
где 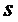 - переменная преобразования Лапласа;
- переменная преобразования Лапласа;
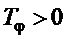 - задаваемая постоянная времени углового движения, требования к которой сформированы ниже;
- задаваемая постоянная времени углового движения, требования к которой сформированы ниже;
 - низкочастотная составляющая скорости углового движения;
- низкочастотная составляющая скорости углового движения;
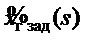 - изображение по Лапласу переменной
- изображение по Лапласу переменной 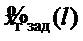 .
.
Исходя из частотных характеристик первого слагаемого рассматриваемого закона управления (см., например, [10]), уравнение (24) с учетом (15) можно записать как:
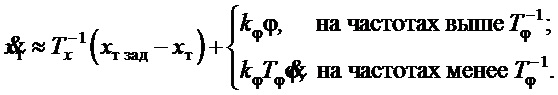
Отсюда и из ранее рассмотренного следует, что на частотах выше 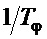 , если в эту область попадает собственная частота угловых движений:
, если в эту область попадает собственная частота угловых движений: 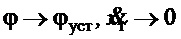 , т.е. обеспечивается устойчивость системы управления. По низким частотам (область частот ниже
, т.е. обеспечивается устойчивость системы управления. По низким частотам (область частот ниже 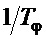 ), в частности, во время приближении переходного процесса к установившемуся состоянию, получаем вместо (19):
), в частности, во время приближении переходного процесса к установившемуся состоянию, получаем вместо (19): 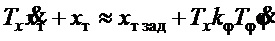 , т.е.
, т.е. 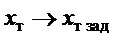 , а значит
, а значит 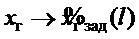 , чем достигается цель управления (7). При этом, если справедливо частотное соотношение:
, чем достигается цель управления (7). При этом, если справедливо частотное соотношение: 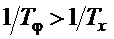 , то это происходит с динамикой не хуже представленной в (7). Обобщая указанное, можно записать требование к параметру
, то это происходит с динамикой не хуже представленной в (7). Обобщая указанное, можно записать требование к параметру  :
:
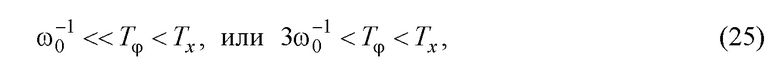
где второе соотношение основано на модельных исследованиях; при этом желательно, чтобы параметр 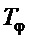 был ближе к середине указанного диапазона.
был ближе к середине указанного диапазона.
На основании (5) и (6), вместо (25) можно записать достаточное условие для его выполнения:

Таким образом, закон управления (24) является ПД-регулятором с пропорциональной частью по ошибке линейного перемещения груза и дифференциальной частью по углу отклонения подвеса груза от вертикали с низкочастотной фильтрацией. Он обеспечивает достижение цели (7), но его недостатком является то, что его параметры 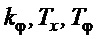 должны перестраиваться в зависимости от длины подвеса. Заметим, что закон управления требует измерения переменных
должны перестраиваться в зависимости от длины подвеса. Заметим, что закон управления требует измерения переменных 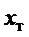 ,
, 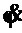 и
и 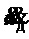 . Первая переменная определяется датчиком положения тележки - энкодером (сервопривод по принципу своей работы имеет такой датчик). Вариантом получения приближенного сигнала к
. Первая переменная определяется датчиком положения тележки - энкодером (сервопривод по принципу своей работы имеет такой датчик). Вариантом получения приближенного сигнала к 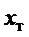 является переменная в виде интеграла от
является переменная в виде интеграла от 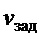 (в силу быстродействия сервопривода). Для измерения
(в силу быстродействия сервопривода). Для измерения 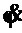 и
и 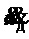 удобно использовать микромеханический датчик типа MPU6050, расположенный на тросе подвеса (см. фиг.1).
удобно использовать микромеханический датчик типа MPU6050, расположенный на тросе подвеса (см. фиг.1).
Из изложенного выше следует, что закон управления (24) требует точных значений сигналов 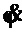 и
и 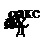 . Известно, что датчик угловой скорости обладает дрейфом, а акселерометр - смещением нуля. Если их считать постоянными, то по (24), (16), (23) их наличие породит неточность позиционирования груза (обозначим как
. Известно, что датчик угловой скорости обладает дрейфом, а акселерометр - смещением нуля. Если их считать постоянными, то по (24), (16), (23) их наличие породит неточность позиционирования груза (обозначим как 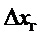 ) величиной:
) величиной:
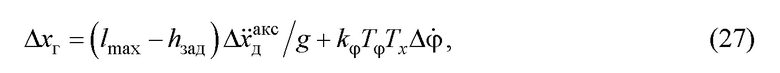
где 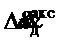 - постоянная погрешность показаний акселерометра из-за неточности его выставки (смещение нуля);
- постоянная погрешность показаний акселерометра из-за неточности его выставки (смещение нуля);
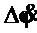 - дрейф датчика угловой скорости.
- дрейф датчика угловой скорости.
Четвертый вариант - результирующий. Он устраняет необходимость настройки по длине подвеса рассмотренный выше ПД-регулятор, или закона управления (24). Здесь предлагается, что все указанные параметры настраиваются по максимальной длине подвеса крана (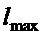 ). То есть в зависимостях: (11), или (12) для расчета
). То есть в зависимостях: (11), или (12) для расчета 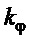 , (21) или (22) для расчета
, (21) или (22) для расчета 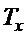 , (26) для назначения
, (26) для назначения 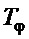 , - вместо
, - вместо 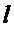 подставляется
подставляется 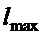 . Обозначим настроенные таким образом параметры как:
. Обозначим настроенные таким образом параметры как: 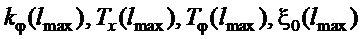 , а параметры по прежней настройке как:
, а параметры по прежней настройке как:  .
.
Из изложенного выше следует, что такая настройка закона управления обеспечит выполнение цели управления (7) при 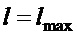 . Возникает естественный вопрос: что будет, если
. Возникает естественный вопрос: что будет, если 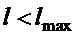 , как будут соблюдаться требования к параметрам закона управления и как будет вести себя замкнутая система управления? Попробуем на него ответить.
, как будут соблюдаться требования к параметрам закона управления и как будет вести себя замкнутая система управления? Попробуем на него ответить.
Из первого неравенства (21) и зависимости (26) следует, что 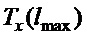 и
и 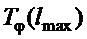 также будут удовлетворять уменьшенным значениям длины подвеса, если вместо
также будут удовлетворять уменьшенным значениям длины подвеса, если вместо 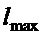 в них подставить
в них подставить 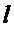 . Из (10) - (12) следует, что
. Из (10) - (12) следует, что 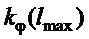 порождает:
порождает:
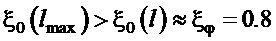 .
.
То есть колебательное движение подвеса будет иметь завышенное значение относительного коэффициента затухания в сравнении с заданной его величиной.
Из теории автоматического управления следует, что увеличение относительного коэффициента затухания приводит к увеличению времени переходного процесса. Будем условно считать, что этот коэффициент может иметь значение: 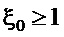 . В этом случае колебательный процесс распадается на апериодический второго порядка с двумя постоянными времени, максимальная из которых (
. В этом случае колебательный процесс распадается на апериодический второго порядка с двумя постоянными времени, максимальная из которых (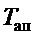 ) определяется как:
) определяется как:
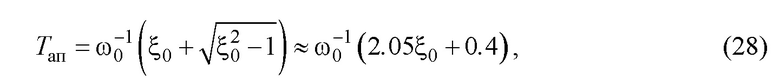
где приблизительная зависимость получена линейной аппроксимацией для 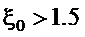 ; при меньших значениях
; при меньших значениях 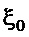 реальная функция меньше аппроксимационной, т.е.
реальная функция меньше аппроксимационной, т.е. 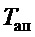 меньше.
меньше.
Как было установлено ранее в (19), движение по  с собственной частотой
с собственной частотой 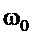 является более высокочастотным, чем собственное апериодическое движение тележки. Если потребовать, чтобы при повышенном относительной коэффициенте затухания выполнялось условие
является более высокочастотным, чем собственное апериодическое движение тележки. Если потребовать, чтобы при повышенном относительной коэффициенте затухания выполнялось условие 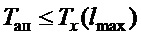 , то, очевидно, на результирующее качество перемещения груза в замкнутой системе управления это не окажет существенного влияния (это далее подтверждено модельными исследованиями). Следовательно, из (28) и последнего соотношения вытекает условие справедливости указанного (в приблизительном смысле):
, то, очевидно, на результирующее качество перемещения груза в замкнутой системе управления это не окажет существенного влияния (это далее подтверждено модельными исследованиями). Следовательно, из (28) и последнего соотношения вытекает условие справедливости указанного (в приблизительном смысле):
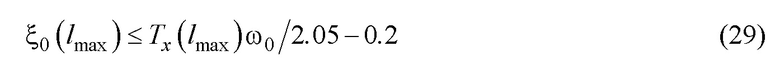
Определим минимальное значение в правой части (29). Оно получится, если подставить сюда минимальное значение 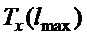 из возможных по (21), (22), т.е. по второму выражению в правой части (22), в плане достаточности, и
из возможных по (21), (22), т.е. по второму выражению в правой части (22), в плане достаточности, и 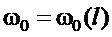 по (5) с минимальным значением
по (5) с минимальным значением 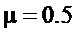 по (6). Отсюда найдем достаточное условие выполнения (29):
по (6). Отсюда найдем достаточное условие выполнения (29):

Из зависимостей (12) и (10) следует, что 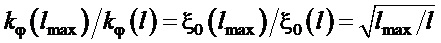 , а также
, а также 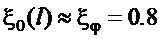 . Это значит, что при настройке с использованием
. Это значит, что при настройке с использованием 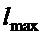 , но при текущем значении длины подвеса
, но при текущем значении длины подвеса  относительный коэффициент затухания увеличится в
относительный коэффициент затухания увеличится в 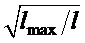 раз. А по зависимости (30), поделенной на
раз. А по зависимости (30), поделенной на 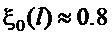 , его можно увеличивать приблизительно в 2 раза больше указанной величины. То есть постоянная
, его можно увеличивать приблизительно в 2 раза больше указанной величины. То есть постоянная 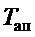 удовлетворяет поставленному условию, а значит предлагаемая форма настройки параметров ПД-регулятора обеспечивает достижение цели управления (7) независимо от реальной длины подвеса.
удовлетворяет поставленному условию, а значит предлагаемая форма настройки параметров ПД-регулятора обеспечивает достижение цели управления (7) независимо от реальной длины подвеса.
Следовательно, закон управления (24) с настройкой своих параметров: 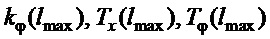 обеспечивает достижение цели (7) без подстроек по длине подвеса. Из зависимостей (11), (12), (21), (22) и (26) следует, что эти параметры не зависят от параметров груза - его массы и момента инерции, и слабо зависят от длины подвеса, а значит система управления практически инвариантна к их вариациям. То есть замкнутая система управления обладает робастными свойствами в очень широкой области вариации параметров крана и груза.
обеспечивает достижение цели (7) без подстроек по длине подвеса. Из зависимостей (11), (12), (21), (22) и (26) следует, что эти параметры не зависят от параметров груза - его массы и момента инерции, и слабо зависят от длины подвеса, а значит система управления практически инвариантна к их вариациям. То есть замкнутая система управления обладает робастными свойствами в очень широкой области вариации параметров крана и груза.
Справедливость указанных выше теоретических выводов была проверена на модельном примере. В его качестве рассматривалось управление тележкой типового среднего крана с параметрами: 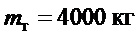 ,
, 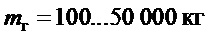 ,
, 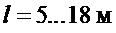 ,
, 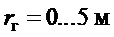 ,
, 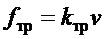 ,
, 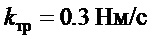 ,
, 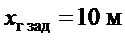 ,
, 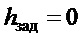 . Сервопривод, формирующий скорость перемещения тележки крана (
. Сервопривод, формирующий скорость перемещения тележки крана (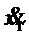 ) по заданной скорости (
) по заданной скорости (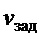 ), моделировался апериодическим звеном с единичным коэффициентом усиления и с постоянной времени 0.04 с. Система управления также имела следующие нелинейности: временную задержку 0.1 c и ограничения по выходному сигналу:
), моделировался апериодическим звеном с единичным коэффициентом усиления и с постоянной времени 0.04 с. Система управления также имела следующие нелинейности: временную задержку 0.1 c и ограничения по выходному сигналу: 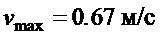 ,
, 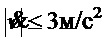 . Большинство из указанных параметров соответствуют стандарту [14] и многообразию типовых переносимых грузов.
. Большинство из указанных параметров соответствуют стандарту [14] и многообразию типовых переносимых грузов.
Предполагалось, что на переносимый груз в момент времени 50 с действует ступенчатое ветровое возмущение интенсивностью 5% от веса груза («ступенька» сглажена апериодическим звеном с постоянной времени 1 с).
Модель с такими параметрами была реализована в компьютерной среде Matlab/Simulink/SimMechanics на основе соотношений (1), описывающих динамику движения крана, закон управления (ПД-регулятор) - по (24), (16), (23) с настройкой его параметров по (12), (22) и (26) для максимальной длины подвеса (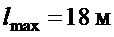 ). Поэтому эти параметры имеют значения (
). Поэтому эти параметры имеют значения (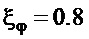 ,
, 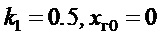 ):
):
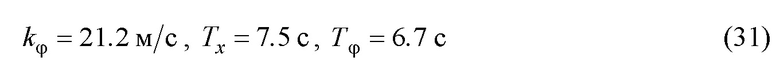
Дифференциальные уравнения решались методом Рунге-Кутты четвертого и пятого порядка с шагом 0.01 с.
Предполагалось измерение сигналов 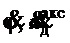 , которые моделировались без постоянных ошибок (
, которые моделировались без постоянных ошибок (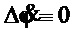 ,
, 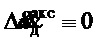 ) с аддитивными шумами, представляющими собой центрированный гауссовский случайный процесс со среднеквадратическим отклонением 0.01 м и 0.1 град/c соответственно [15]. Вместо сигнала
) с аддитивными шумами, представляющими собой центрированный гауссовский случайный процесс со среднеквадратическим отклонением 0.01 м и 0.1 град/c соответственно [15]. Вместо сигнала 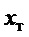 использовался сигнал интеграла от
использовался сигнал интеграла от 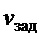 . Для снижения влияния шумов перед их подачей на формирование закона управления они сглаживались на фильтрах низких частот в виде апериодических звеньев с постоянными времени, выбранными по принципу практического отсутствия влияния на основные процессы: по линейному перемещению
. Для снижения влияния шумов перед их подачей на формирование закона управления они сглаживались на фильтрах низких частот в виде апериодических звеньев с постоянными времени, выбранными по принципу практического отсутствия влияния на основные процессы: по линейному перемещению 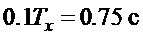 , по угловому движению
, по угловому движению 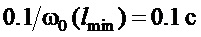 .
.
Для низкочастотной фильтрации по (23) использовалось апериодическое звено с единичным коэффициентом усиления и постоянной времени 2 с.
Поведение замкнутой системы управления по переменной 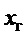 сравнивалось с переменной
сравнивалось с переменной 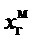 , которая является выходом эталона, соответствующего уравнению (15) без углового движения:
, которая является выходом эталона, соответствующего уравнению (15) без углового движения: 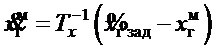 с указанным выше значением параметра
с указанным выше значением параметра 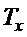 , также оценивалась устойчивость поведения
, также оценивалась устойчивость поведения 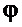 .
.
Исследование проводилось в полном диапазоне указанных характеристик крана и груза при одной настройке ПД-регулятора (31). Результаты представлены на фиг.3, 4.
На фиг.3 приведены графики поведения крана при 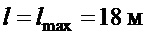 ,
, 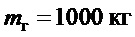 ,
, 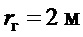 . Представленные графики практически не отличаются от тех, которые получаются при варьировании параметров
. Представленные графики практически не отличаются от тех, которые получаются при варьировании параметров 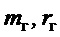 в полных диапазонах их изменения, указанных выше. На фиг. 4 такие же характеристики при
в полных диапазонах их изменения, указанных выше. На фиг. 4 такие же характеристики при  с теми же самыми свойствами. Промежуточные варианты длины подвеса дают промежуточное качество регулирования.
с теми же самыми свойствами. Промежуточные варианты длины подвеса дают промежуточное качество регулирования.
Как видим, линейное движение груза близко к эталонному, угловое движение устойчиво, действие ветрового воздействия парируется. При уменьшении длины подвеса изменение в поведении объекта «тележка - груз» касается только более высокочастотных переходных процессов. Подобные результаты были получены при других значениях 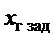 .
.
Таким образом, полученный закон управления тележкой мостового крана (24), (16), (23) представляет собой ПД-регулятор, формирующий заданную скорость перемещения тележки, с пропорциональной частью по ошибке линейного перемещения тележки крана и с дифференциальной частью по углу отклонения подвеса от вертикали с низкочастотной фильтрацией. Настройка его параметров осуществляется по зависимостям (11), или (12) для расчета 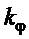 , (21) или (22) для расчета
, (21) или (22) для расчета 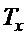 , (26) для назначения
, (26) для назначения 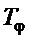 , где вместо
, где вместо 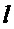 подставляется
подставляется 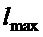 . Этот закон управления обеспечивает достижение цели (7) в полном диапазоне вариаций параметров груза и крана без дополнительных подстроек. Также происходит парирование ветровых возмущений.
. Этот закон управления обеспечивает достижение цели (7) в полном диапазоне вариаций параметров груза и крана без дополнительных подстроек. Также происходит парирование ветровых возмущений.
Особенностью выбора указанных параметров является то, что все они рассчитываются на основе паспортных данных крана и привода, заданных качественных показателей переходного процесса (коэффициента относительного затухания, времени переходного процесса), а также на расстоянии перемещения груза и координат целевой точки. Настройки закона управления не зависят от параметров груза - его массы и момента инерции, и слабо зависят от длины подвеса, а значит система управления практически инвариантна к их вариациям. То есть замкнутая система управления обладает робастными свойствами в очень широкой области вариации параметров крана и груза, покрывающую возможные режимы использования крана на практике. Это было показано на основе теоретических выкладок и модельного примера с основными характеристиками современного оборудования. Поскольку закон управления не требует своей перестройки параметров по режимам работы (исключение составляют расстояние перемещения груза и координаты целевой точки доставки груза), следовательно, снижаются эксплуатационные затраты на использование такой системы управления.
Особенностью рассмотренного способа управления мостовым краном является необходимость начальной выставки датчиков: достаточно точного определения с последующей компенсацией нуля акселерометра и дрейфа датчика угловой скорости. Особенно это касается второго фактора: в соответствии с параметрами закона управления (31), например, для достижения точности позиционирования в 0.1 м по (27) требуется определение дрейфа датчика угловой скорости с точностью до 0.005 град/c. Это говорит о том, что если требуется создать автоматическую систему управления краном, то для этого необходимо использовать датчик угловой скорости высокого класса с очень стабильными характеристиками. Если система управления краном автоматизированная, предполагающая наличие оператора крана в замкнутом контуре системы управления, то требования к характеристикам датчика снижаются. Оператор управляет положением тележки по скорости, поэтому для него не важна постоянная ошибка позиционирования.
Литература
1. Патент RU 2564560 C1, B66C 13/18. Способ повышения точности и скорости перемещения груза по требуемой траектории грузоподъемным краном мостового типа / Щербаков В.С., Корытов М.С., Вольф Е.О; заявитель и патентообладатель Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Сибирская государственная автомобильно-дорожная академия (СибАДИ)" (RU) - 2014118376/11, заявл. 06.05.2014, опубл. 10.10.2015, Бюл. 28.
2. Патент RU 2676210 C1, МПК B66C 13/06. Устройство и способ управления раскачиванием груза, подвешенного на подъёмном устройстве / Саварези С.М., Винати Ф., Винати С., Винати М., Винати М., Винати Д.; заявитель и патентообладатель ВИНАТИ С.Р.Л. - 2016125496; заявл. 06.11.14; опубл. 26.12.18, Бюл. 36.
3. Jaafar H.I., Mohamed Z., Mohd Subha N.A., Husain A.R., Ismail F.S., Ramli L., Shamsudin M.A. Efficient control of a nonlinear double-pendulum overhead crane with sensorless payload motion using an improved PSO-tuned PID controller // Journal of Vibration and Control. - 2018. - No 25(4). - P. 907-921.
4. Mohamed K.T., Abdel-Razak M.H., Haraz E.H., Ata A.A. Fine tuning of a PID controller with inlet derivative filter using Pareto solution for gantry crane systems // AEJ - Alexan-dria Engineering Journal. - 2021. - Vol. 61, No. 9. - P. 6659-6673.
5. Fadlalla A. A. M., Hassan M. Dynamic Modeling and Feedback Linearization Control of a 3-D Overhead Gantry Crane System // 2021 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Toronto, ON, Canada. - 2021. - P. 1-6.
6. Рогова Н.С., Юркевич В.Д. Разработка алгоритмов управления для перемещения груза портальным краном // Сборник научных трудов НГТУ. - 2017. - №2 (88). - С. 7-18.
7. Саблина Г.В., Ходакова Д.И. Разработка алгоритма стабилизации системы «подвешенный груз» // Сборник научных трудов НГТУ. - 2009. - №3 (57). - С. 33-40.
8. Papadopoulos A.-A.D., Rompokos A.A., Alexandridis A.T. Nonlinear and observer-based PD position and sway control of convey-crane systems // 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece. - 2016. - P. 696-700.
9. Enin S. Omelchenko E., Maksimov I. Crane Anti-Sway Control System Algorithm //2019 IEEE Russian Workshop on Power Engineering and Automation of Metallurgy Industry: Research & Practice (PEAMI), Magnitogorsk, Russia. - 2019. - P. 54-58.
10. Первозванский А.А. Курс теории автоматического управления. Учеб. пособие для вузов. Лань, Санкт-Петербург, 2015. 624 с.
11. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.
12. Сивухин Д.В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. - М.: Физматлит, Изд-во МФТИ. - 2005. - 560 с.
13. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем в MATLAB 6.0: Учебное пособие. - СПб.: КОРОНА принт, 2010. - 320 с.
14. ГОСТ 3332-54. Краны мостовые электрические общего назначения грузоподъёмностью от 5 до 50 т среднего и тяжелого режимов работы. Основные параметры и размеры. - М: Издательство стандартов. - 1974.
15. Жмудь В.А., Кузнецов К.А., Кондратьев Н.О. и др. Акселерометр и гироскоп MPU6050: первое включение на STM32 и исследование показаний в статике // Автоматика и программная инженерия. - 2018. - №3(25). - С. 9-22.
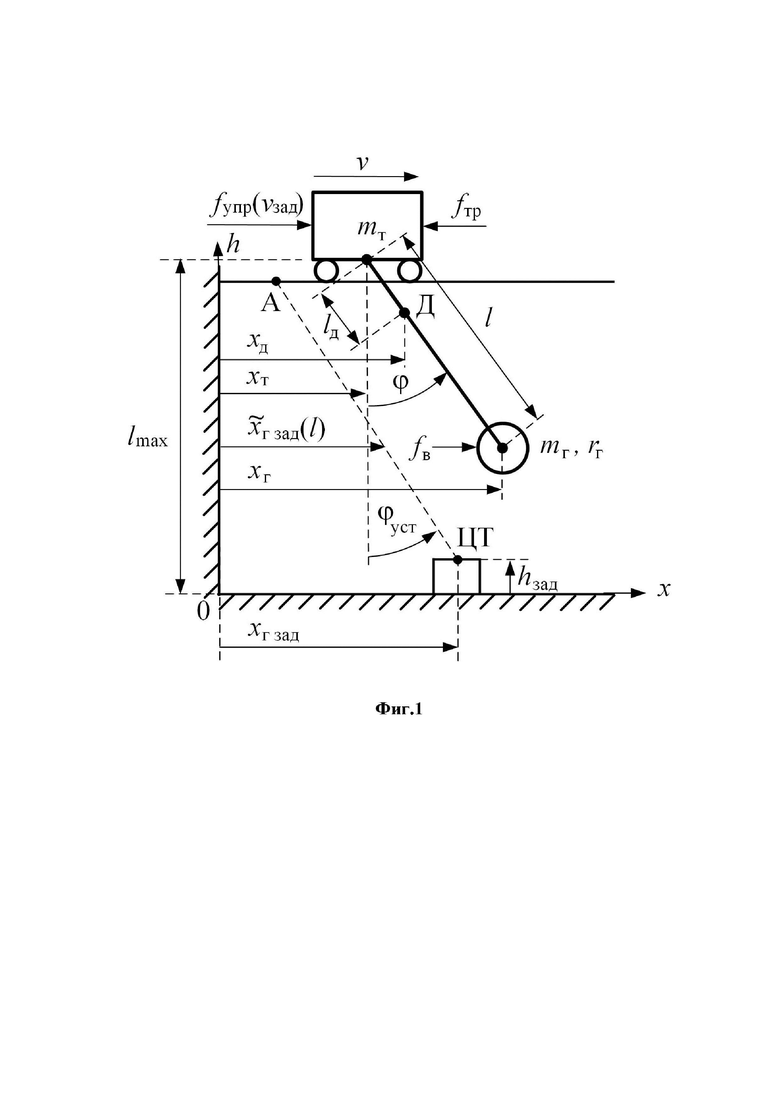

Предлагаемое изобретение относится к области управления крановыми установками с подвешенным расположением груза, в частности - мостовыми кранами. При управлении мостовым краном пропорциональная часть ПД-регулятора формирует заданную скорость, прямо пропорциональную ошибке в позиционировании груза, а дифференциальная часть формирует дополнительную заданную скорость, прямо пропорциональную угловой скорости подвеса груза, фильтрованной на низкочастотном фильтре. Параметры регулятора задают на основании паспортных данных мостового крана: максимальной длины подвеса и максимальной скорости сервоприводов, а также расстояния до целевой точки доставки груза и ее высоты. В качестве датчиков информации используют совмещенный датчик в виде акселерометра и датчика угловой скорости, размещенный на канате подвеса рядом с тележкой крана, а также энкодеры, определяющие положение тележки и балки крана. Для акселерометра и датчика угловой скорости требуется обязательная начальная процедура определения смещения нуля для первого и дрейфа для второго с последующей их компенсацией. Достигается повышение свойств системы управления краном, основанной на ПД-регуляторе, определяющем заданную скорость сервоприводов тележки (балки), а также выработка рекомендаций для настройки параметров регулятора на основе паспортных данных мостового крана и координат целевой точки. 4 ил.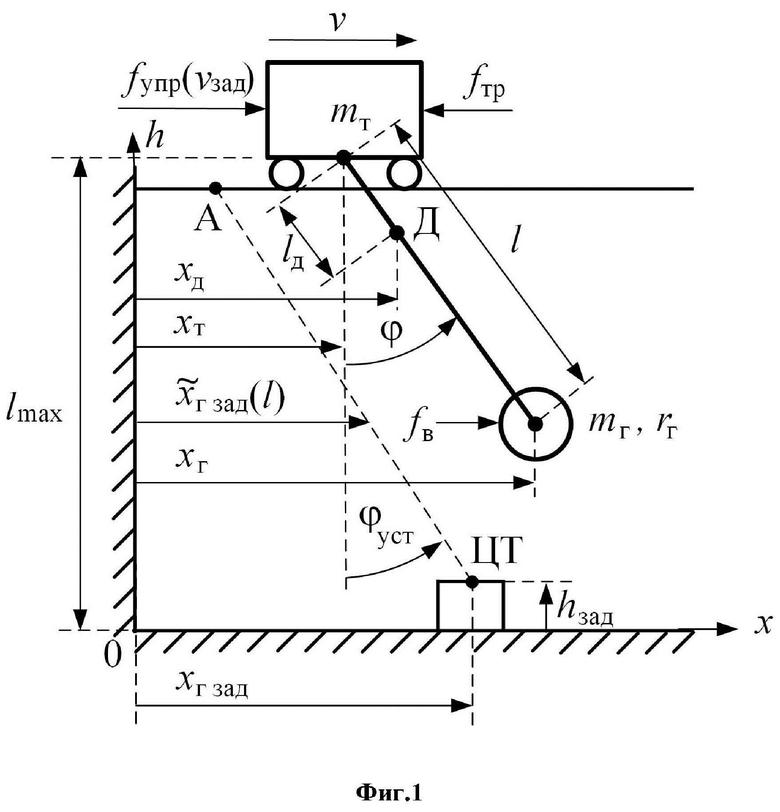
Способ управления мостовым краном на основе скоростного ПД-регулятора, заключающийся в том, что для управления тележкой и балкой крана используют сервоприводы, отрабатывающие заданную скорость тележки и балки крана, отличающийся тем, что в пропорциональной части регулятора формируют заданную скорость, прямо пропорциональную ошибке в позиционировании груза, а в дифференциальной части формируют дополнительную заданную скорость, прямо пропорциональную угловой скорости подвеса груза, фильтрованной на низкочастотном фильтре, по зависимости:
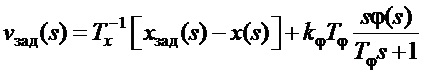 ,
,
где: 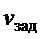 − заданная скорость тележки (балки) крана;
− заданная скорость тележки (балки) крана;
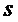 − переменная преобразования Лапласа;
− переменная преобразования Лапласа;
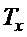 − первый назначаемый параметр ПД-регулятора, определяющий постоянную времени линейного перемещения груза, если последний аппроксимировать апериодическим процессом;
− первый назначаемый параметр ПД-регулятора, определяющий постоянную времени линейного перемещения груза, если последний аппроксимировать апериодическим процессом;
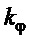 − второй назначаемый параметр ПД-регулятора, определяющий степень демпфирования угловых колебаний;
− второй назначаемый параметр ПД-регулятора, определяющий степень демпфирования угловых колебаний;
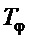 − третий назначаемый параметр ПД-регулятора, определяющий качество парирования внешних возмущений;
− третий назначаемый параметр ПД-регулятора, определяющий качество парирования внешних возмущений;
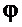 − угол отклонения подвеса груза от вертикали в плоскости движения тележки (балки) крана, а
− угол отклонения подвеса груза от вертикали в плоскости движения тележки (балки) крана, а 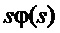 − его скорость в изображении по Лапласу;
− его скорость в изображении по Лапласу;
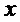 − пройденное расстояние тележкой (балкой) крана;
− пройденное расстояние тележкой (балкой) крана;
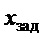 − заданное положение тележки (балки) крана, определяемое зависимостью:
− заданное положение тележки (балки) крана, определяемое зависимостью:
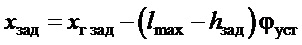 ,
,
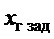 − координата целевой точки доставки груза по оси движения тележки (балки) крана;
− координата целевой точки доставки груза по оси движения тележки (балки) крана;
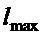 − максимальная длина подвеса груза;
− максимальная длина подвеса груза;
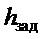 − высота целевой точки доставки груза по вертикальной оси;
− высота целевой точки доставки груза по вертикальной оси;
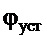 − установившееся постоянное значение угла
− установившееся постоянное значение угла 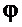 из-за воздействия ветра, определяется по зависимости:
из-за воздействия ветра, определяется по зависимости:
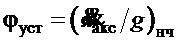 ,
,
где 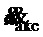 − показания акселерометра, установленного на канате подвеса с соответствующей осью чувствительности;
− показания акселерометра, установленного на канате подвеса с соответствующей осью чувствительности;
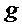 − ускорение свободного падения;
− ускорение свободного падения;
нижний индекс «нч» обозначает низкочастотную фильтрацию, выполняемую для подавления высокочастотных шумов датчика и выделения низкочастотных составляющих ветровых воздействий;
параметры регулятора задаются на основании паспортных данных мостового крана: максимальной длины подвеса и максимальной скорости сервоприводов, а также расстояния до целевой точки доставки груза и ее высоты по зависимостям:
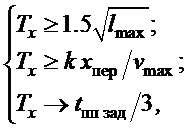
где 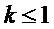 − назначаемый коэффициент для ускорения переходного процесса доставки груза, чем меньше
− назначаемый коэффициент для ускорения переходного процесса доставки груза, чем меньше 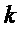 , тем перемещение груза сильнее отличается от апериодического процесса;
, тем перемещение груза сильнее отличается от апериодического процесса;
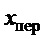 − дальность переноса груза по соответствующей оси движения;
− дальность переноса груза по соответствующей оси движения;
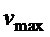 − максимальная скорость привода;
− максимальная скорость привода;
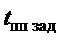 − требуемое время переходного процесса переноса груза в горизонтальной плоскости;
− требуемое время переходного процесса переноса груза в горизонтальной плоскости;
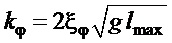 ,
,
где 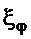 − желаемое значение относительного коэффициента затухания углового колебательного движения;
− желаемое значение относительного коэффициента затухания углового колебательного движения;
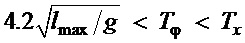 ;
;
в качестве датчиков информации 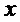 используют датчики пройденного пути тележкой и балкой крана; для измерения
используют датчики пройденного пути тележкой и балкой крана; для измерения 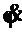 и
и 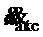 используют совмещенный датчик, содержащий датчик угловой скорости и акселерометр, который крепят на канате подвеса груза рядом с тележкой крана, а также проводят начальную их выставку путем определения дрейфа датчика угловой скорости и смещения нуля акселерометра с дальнейшей их компенсацией.
используют совмещенный датчик, содержащий датчик угловой скорости и акселерометр, который крепят на канате подвеса груза рядом с тележкой крана, а также проводят начальную их выставку путем определения дрейфа датчика угловой скорости и смещения нуля акселерометра с дальнейшей их компенсацией.
| US 20200361751 A1, 19.11.2020 | |||
| Способ адаптивного управления мостовым краном | 2020 |
|
RU2744647C1 |
| EP 3074337 B1, 25.09.2019 | |||
| US 20240101399 A1, 28.03.2024. | |||
Авторы
Даты
2024-11-05—Публикация
2024-04-26—Подача