Область техники, к которой относится изобретение
Предлагаемое изобретение относится к области автоматического управления грузовыми кранами с целью повышения производительности, безопасности при их эксплуатации, снижения эксплуатационных затрат. Рассматривается класс крановых установок, конструкция которых предполагает подвесное крепление груза, в частности мостовых кранов.
В современном мире грузоподъемные краны широко используются в различных отраслях промышленности для перемещения грузов. Наиболее распространенные из них используют подвесное крепление груза, например, мостовые, козловые, стреловые и поворотные (башенные) краны. Использование подобных кранов сопряжено с маятниковыми колебаниями груза. Они возникают, в основном, во время ускорения или торможения крана, или от воздействий каких-либо внешних возмущений (ветер, неровности пути перемещения крана, перебои в электропитании электропривода и т.д.). Крановое оборудование тратит до 20% рабочего времени на фиксацию транспортируемого груза в назначенном месте при погрузочно-разгрузочных работах [1]. Также из-за маятниковых колебаний груза возникают дополнительные нагрузки на механизмы и металлические конструкции крана, снижается безопасность из-за непредвиденного перемещения груза.
Отсюда одним из перспективных направлений в крановой промышленности является разработка автоматического управления с гашением маятниковых колебаний. Как и транспортировка груза, гашение маятниковых колебаний осуществляется только за счет перемещения тележки с заданным направлением и ускорением.
Уровень техники
Известен способ управления мостовым краном, задачей которого является повышение точности и скорости перемещения груза по требуемой траектории и компенсации колебаний груза, [2]. Данный способ обеспечивает перемещение груза по требуемой траектории, которая задается в виде временных зависимостей декартовых координат. Однако этот метод имеет ряд недостатков. К ним относится то, что в законе управления используется П-регулятор, который настраивается под узкий диапазон параметров крана. Также в этом методе не учитываются возможные внешние возмущения на кран, например, воздействия ветра на транспортируемый груз, неровности подкранового пути, износ приводов крана, следовательно, система управления не способна их парировать.
В [3] предложен метод управления мостовым краном на основе П- или ПИ-регулятора по отслеживанию заданного углового положения подвеса с расположением датчиков информации на канате подвеса груза. Недостатком этого подхода является необходимость настройки параметров регулятора для разных грузов и режимов работы крана.
Известен способ управления мостовым краном за счет использования скользящих режимов [4]. Однако основным недостатком этого метода является появление высокочастотных составляющих в управлении приводом, что отрицательно сказывается на эксплуатационных свойствах системы управления.
Известен метод управления мостовым краном на основе нейросетевого контроллера [5]. Его недостатком является большое время обучения нейросети.
Известен способ адаптивного управления тележкой мостового крана, построенный на основе использования функции Ляпунова с настройкой параметров регулятора на основе градиентного алгоритма идентификации [6, 7]. Основным недостатком данного метода является проблема выбора параметров дискретного алгоритма идентификации для конкретного случая с обеспечением устойчивости замкнутой системы управления.
Наиболее близкое решение описывается в работе [8] (прототип). Здесь предлагается подход автоматического управления мостовым краном, нацеленный на непосредственное отслеживание горизонтального перемещения груза на заданной высоте в назначенную точку в условиях текущей априорной неопределенности параметров груза и внешних возмущений. Способ управления основан на схеме адаптивного управления с идентификатором и неявной эталонной моделью с использованием «упрощенных» условий адаптируемости. Эталонная модель назначается в виде колебательного звена с собственной частотой, не превышающей таковую для объекта управления с неподвижным основанием. Собственная частота эталонной модели назначается на основе определении длины подвеса груза по отсчету времени подъема и опускания груза и известной средней скорости этих операций. В качестве источников информации используются датчики, определяющие положение и скорость тележки и балки крана, а также датчики измерения линейного ускорения и угловой скорости, расположенные на захватном устройстве подвеса (крюке). Для текущей параметрической идентификации предлагается использовать рекуррентный метод наименьших квадратов с фактором забывания. Для конкретного крана экспериментально определяется параметр эффективности управления краном. Данный способ управления краном позволяет повысить производительность погрузочно-разгрузочных работ мостовым краном в условиях текущей априорной неопределенности параметров крана и внешних возмущений за счет адаптивной автоматизации управления краном.
Задачей предлагаемого изобретения является упрощение построения системы управления и снижения эксплуатационных затрат на основе модернизации описанного способа.
Отличием в предлагаемом изобретении является использование в качестве управляющего сигнала скорость перемещения тележки и балки крана, отрабатываемой сервоприводами тележки и балки крана. Такое решение оправдано для реальных кранов, где в качестве привода используется сервопривод, в т.ч. на основе асинхронного электродвигателя, или шаговый двигатель. Собственная частота эталонной модели, или постоянная времени регулирования в законе формирования заданной скорости, выбирается исходя из паспортных данных крана: максимальной длины подвеса и максимальной скорости сервопривода, что не требует определения текущей длины подвеса. Акселерометр и датчик угловой скорости предполагается размещать на канате подвеса вблизи от тележки крана на фиксированном расстоянии, что дает ряд преимуществ: есть возможность организовать проводную передачу информации и электропитания датчиков, что надежнее и проще, снижает эксплуатационные затраты; датчики находятся в безопасном месте, не подвергающимся внешним механическим воздействиям; легко организовать фиксацию осей чувствительности датчика (крюк подвеса часто вращается вокруг вертикальной оси); на датчики в меньшей степени передаются неосновные высокочастотные дополнительные (в т.ч. недомоделированные) движения груза. Алгоритм текущей идентификации использует гарантированно линейно-независимые по времени факторные переменные, что обеспечивает устойчивость доставляемых оценок и, в целом, устойчивость алгоритма идентификации типа рекуррентного метода наименьших квадратов. Также предлагаемый подход не требует настройки системы управления пред каждым началом работы, в частности, определения дрейфа датчика угловой скорости. Предполагается только настройка системы управления на этапе ее монтажа на крановую установку.
Предлагается способ адаптивного управления мостовым краном, заключающийся в что до начала перемещения груза задают требуемую траекторию его перемещения в виде неявных эталонных моделей по горизонтальным осям движения груза с заданным конечным его положением, во время перемещения груза на основе обработки данных с датчиков информации, включая текущую параметрическую идентификацию математической модели движения груза, формируют управляющие воздействия приводов мостового крана с использованием «упрощенных» условий адаптируемости, отличающийся тем, что в качестве приводов тележки и балки крана используют сервоприводы, в качестве задающих сигналов которых используют заданные скорости перемещения тележки и балки, сервоприводы отрабатывают заданную скорость, в качестве датчиков информации используют совмещенный датчик, содержащий акселерометр и датчик угловой скорости с несколькими осями чувствительности обоих датчиков, совмещенный датчик крепится на канате подвеса груза рядом тележкой крана на фиксированном расстоянии, а также используют датчики пройденного пути тележкой и балкой крана. Как вариант, вместо последних используют интегрирование заданных скоростей тележки и балки крана.
Краткое описание чертежей
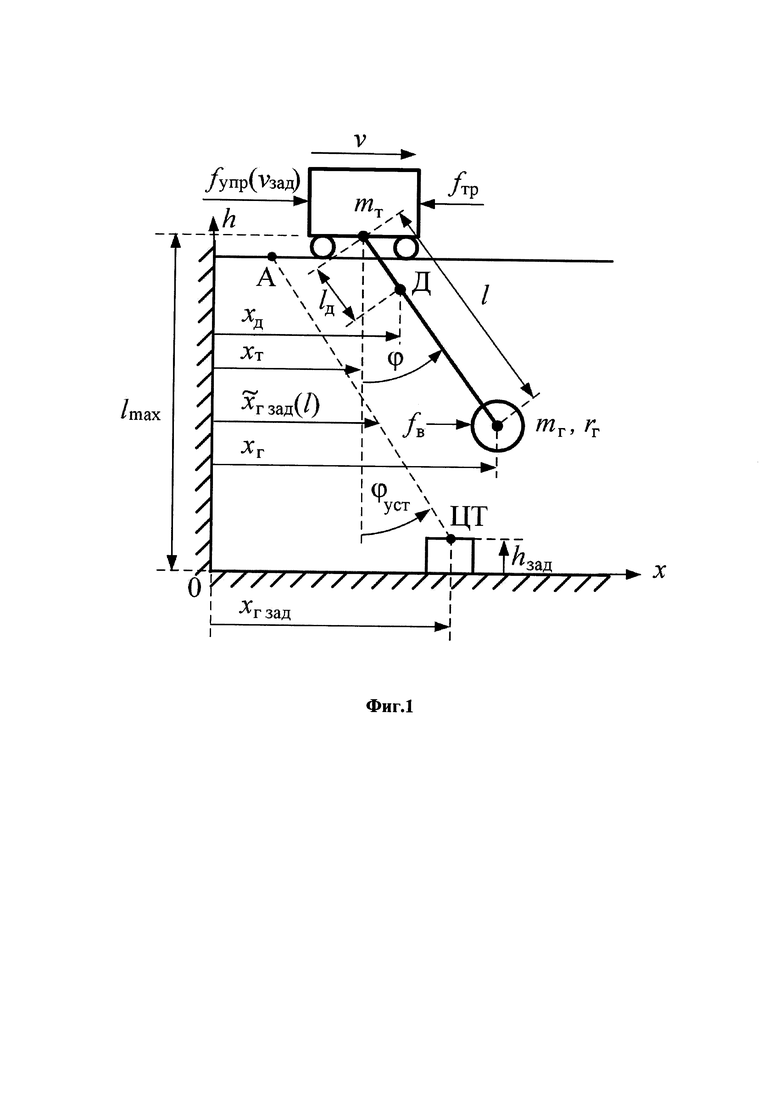
На фиг.1 представлена схема перемещения мостового крана с грузом по одной горизонтальной оси, соответствующей перемещению тележки крана.
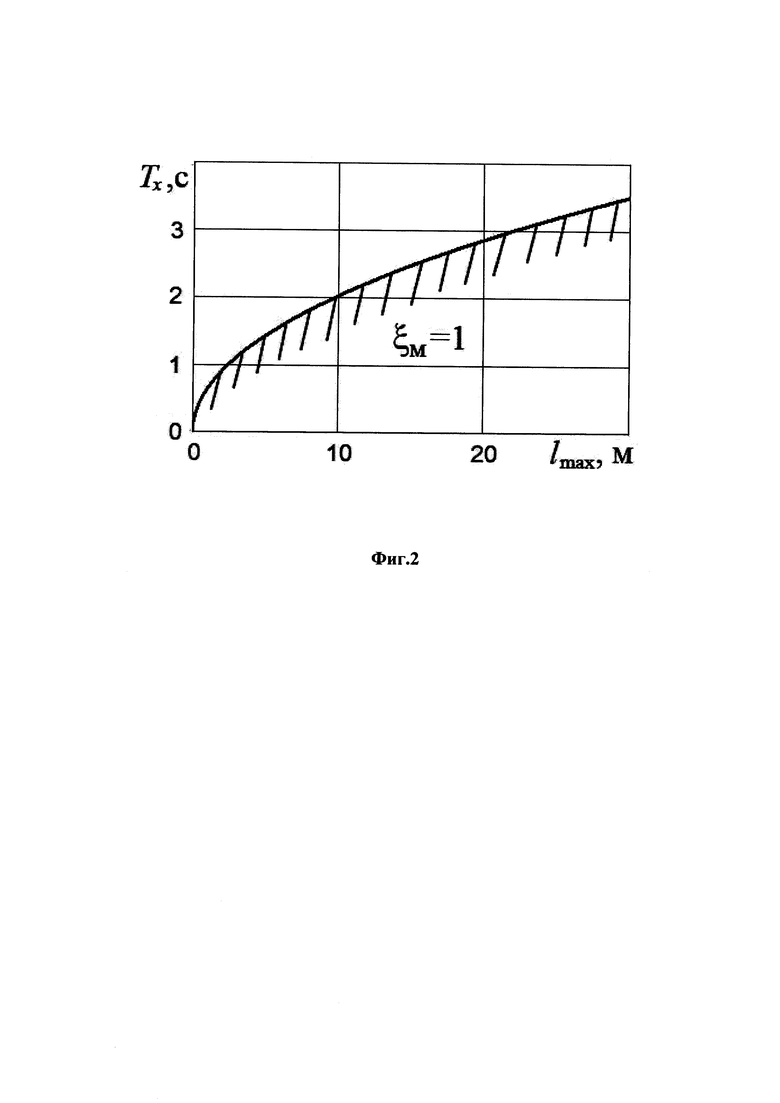
На фиг.2 представлена область допустимых значений параметра Тх закона формирования заданной скорости в зависимости от максимальной длины подвеса крана при единичном значении относительного коэффициента затухания эталонной модели (незаштрихованная область).
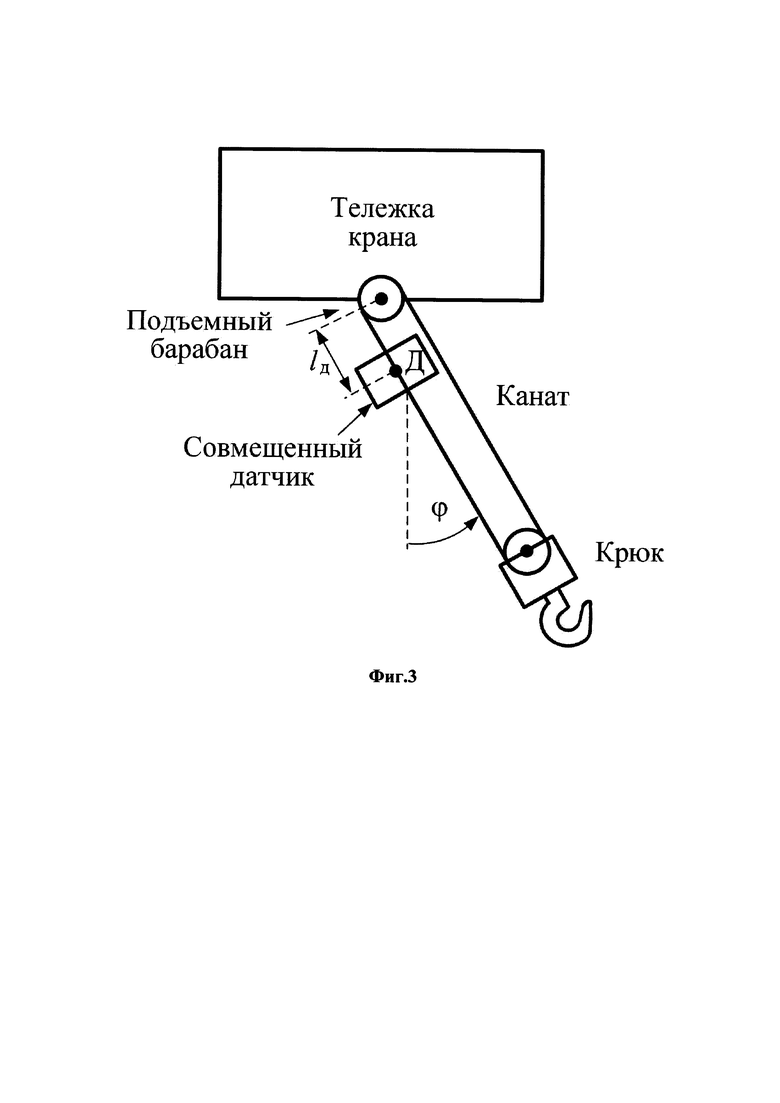
На фиг.3 представлена схема размещения совмещенного датчика на канате подвеса.
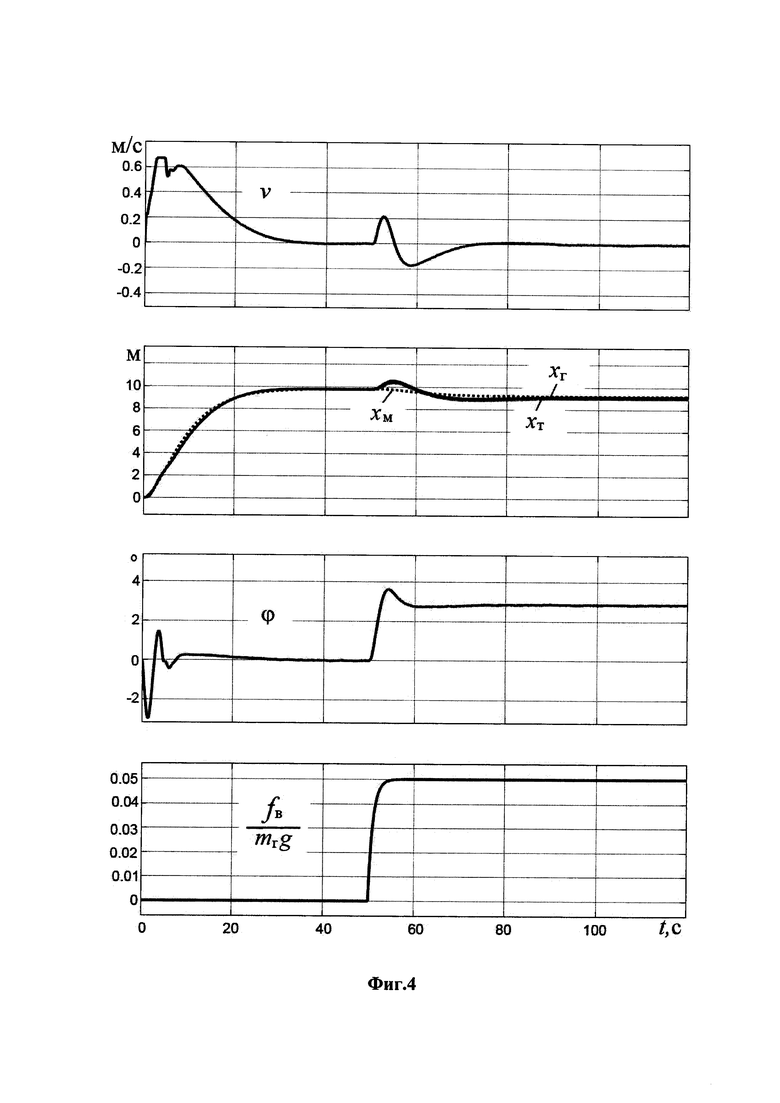
На фиг.4 представлены результаты модельных исследований адаптивной системы управления для среднего мостового крана при минимальной длине подвеса груза (3 м).
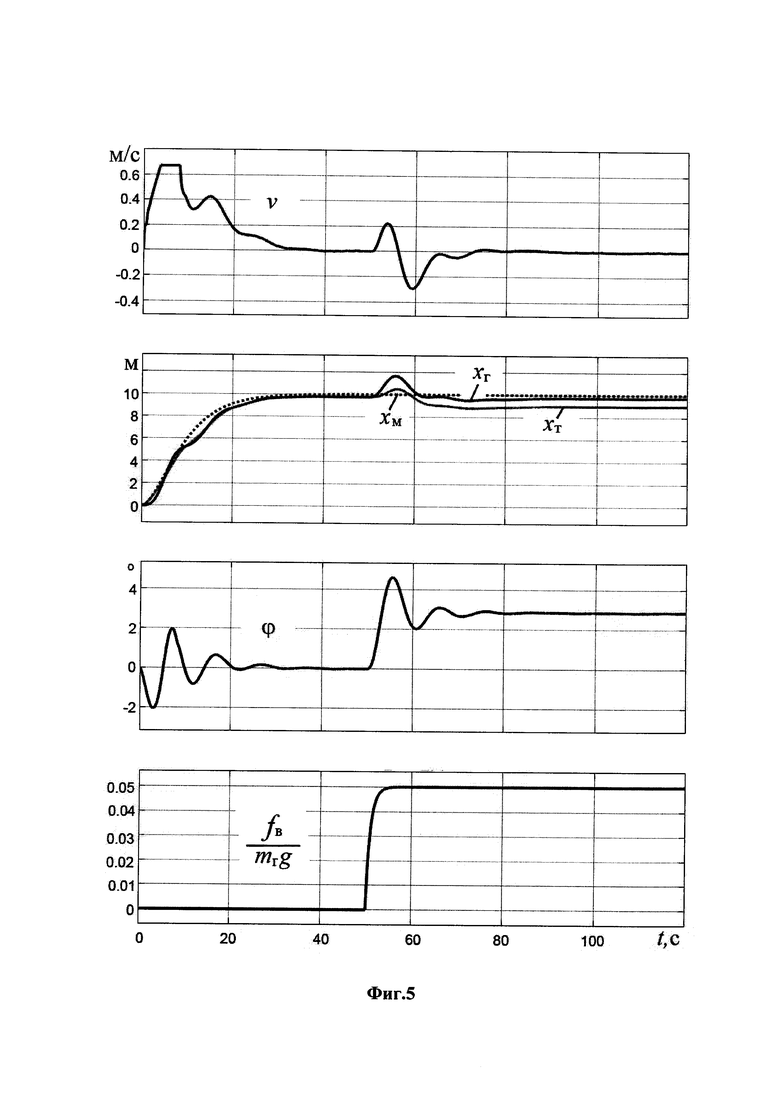
На фиг.5 представлены результаты модельных исследований адаптивной системы управления для среднего мостового крана при максимальной длине подвеса груза (15 м).
Осуществление изобретения
Ниже будем рассматривать движение крана и груза только по одной оси горизонтального перемещения груза, соответствующем передвижению тележки крана (по другой оси, соответствующей перемещению балки крана - рассуждения аналогичные). На фиг.1 и в дальнейших рассуждениях используются следующие обозначения:
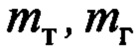 - масса тележки крана, с учетом инерционности вращающихся масс, и масса переносимого груза соответственно (в качестве груза подразумевается непосредственно переносимый груз и захватное устройство - крюк);
- масса тележки крана, с учетом инерционности вращающихся масс, и масса переносимого груза соответственно (в качестве груза подразумевается непосредственно переносимый груз и захватное устройство - крюк);
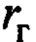 - радиус инерции груза;
- радиус инерции груза;
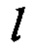 - длина подвеса груза, или расстояние от точки крепления подвеса на тележке до центра груза; примем, что
- длина подвеса груза, или расстояние от точки крепления подвеса на тележке до центра груза; примем, что 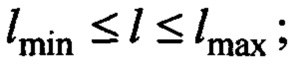
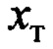 - перемещение тележки вдоль горизонтальной оси
- перемещение тележки вдоль горизонтальной оси 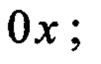
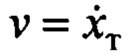 - скорость перемещения тележки с ограничением
- скорость перемещения тележки с ограничением 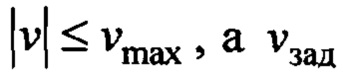 - заданное значение этой скорости;
- заданное значение этой скорости;
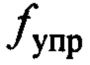 - управляющая сила, формируемая сервоприводом тележки по сигналу
- управляющая сила, формируемая сервоприводом тележки по сигналу 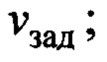
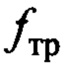 - сила трения, противодействующая перемещению тележки;
- сила трения, противодействующая перемещению тележки;
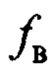 - сила ветрового воздействия, приложенная в центре масс груза;
- сила ветрового воздействия, приложенная в центре масс груза;
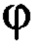 - угол отклонения подвеса груза от вертикальной оси;
- угол отклонения подвеса груза от вертикальной оси;
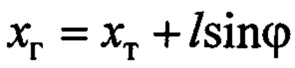 - горизонтальное перемещение груза;
- горизонтальное перемещение груза;
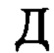 - точка расположения совмещенного датчика на канате подвеса;
- точка расположения совмещенного датчика на канате подвеса;
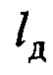 - длина подвеса до совмещенного датчика (расстояние от точки крепления подвеса на тележке до точки Д),
- длина подвеса до совмещенного датчика (расстояние от точки крепления подвеса на тележке до точки Д), 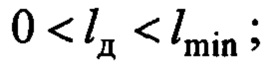
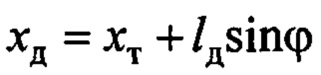 - горизонтальное перемещение совмещенного датчика;
- горизонтальное перемещение совмещенного датчика;
 - целевая точка доставки груза с координатами
- целевая точка доставки груза с координатами 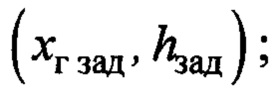
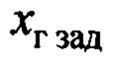 - координата целевой точки по горизонтальной оси
- координата целевой точки по горизонтальной оси 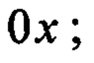
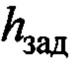 - координата целевой точки по вертикальной оси 0h (высота погрузки);
- координата целевой точки по вертикальной оси 0h (высота погрузки);
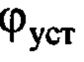 - предполагаемое установившееся постоянное значение угла ϕ по окончании регулирования;
- предполагаемое установившееся постоянное значение угла ϕ по окончании регулирования;
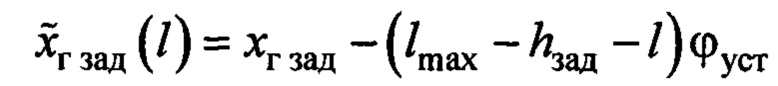 - заданное положение груза по горизонтальной оси на текущей длине подвеса, или расстояние от нулевой точки до линии «А - ЦТ» по оси 0x.
- заданное положение груза по горизонтальной оси на текущей длине подвеса, или расстояние от нулевой точки до линии «А - ЦТ» по оси 0x.
Будем считать, что внешнее возмущение движению тележки с грузом, представляющее изменение силы трения и ветрового воздействия, имеет ступенчатый характер с произвольным моментом времени с ограниченной интенсивностью, что является типовым подходом при определении свойств любой автоматической системы управления по парированию внешних возмущений [9].
На основе математической модели поступательного и вращательного движения системы «тележка-груз» (без учета массы каната и трения углового движения, в силу их малости, а также начальных значений переменных по положению и скорости), описанной в [10], с применением теоремы Пуансо, динамику движения механической системы, изображенной на фиг.1, можно описать следующей системой дифференциальных уравнений (указанные производные переменных взяты по времени (t)):
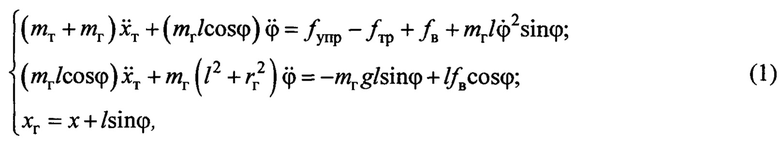
где g - ускорение свободного падения.
Поскольку угол отклонения груза небольшой (не практике не более 10-20°), угловая скорость также невысокая, с учетом кинематики движения можно принять:
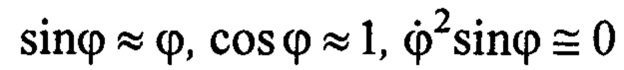 . Поэтому систему (1) можно описать в линеаризованном виде как:
. Поэтому систему (1) можно описать в линеаризованном виде как:

где 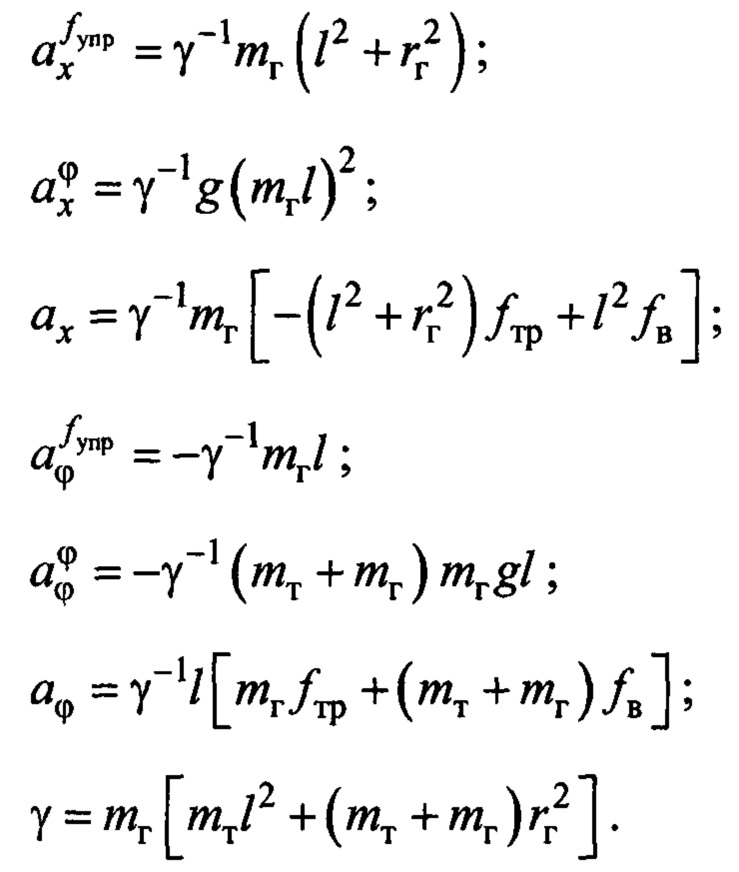
Подставляя первое и второе уравнения системы (2) в третье уравнение третьей строки системы (2), выражая сигнал 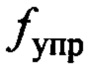 из первого равенства (2) и подставляя его в полученный результат, определим, что движение груза можно описать через скорость тележки следующим приблизительным равенством:
из первого равенства (2) и подставляя его в полученный результат, определим, что движение груза можно описать через скорость тележки следующим приблизительным равенством:

где 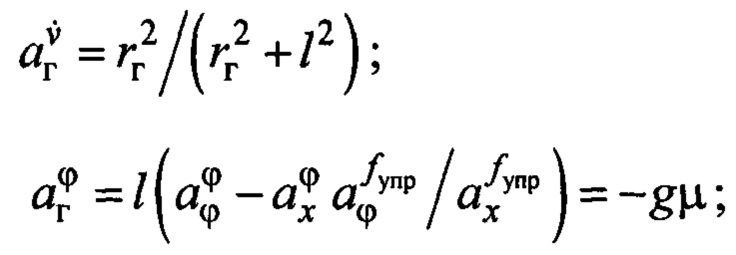
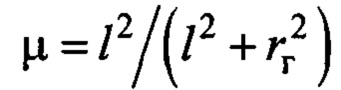 - безразмерный коэффициент влияния радиуса инерции груза;
- безразмерный коэффициент влияния радиуса инерции груза;
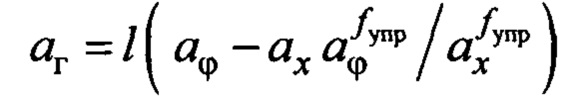 - параметр, равный ускорению, образованному внешними возмущениями.
- параметр, равный ускорению, образованному внешними возмущениями.
Для дальнейших рассуждений вначале примем утверждение, что 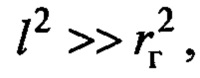 что соответствует большинству случаев практики. Тогда параметр
что соответствует большинству случаев практики. Тогда параметр 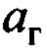 зависит только от ветра и
зависит только от ветра и 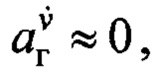 последнее позволяет переписать уравнение (3) в виде
последнее позволяет переписать уравнение (3) в виде

здесь параметр 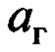 представляет собой ускорение, сформированное силой ветра.
представляет собой ускорение, сформированное силой ветра.
Далее это уравнение будем использовать в качестве объекта управления. Заметим, что столь значительное упрощение модели динамики линейного перемещения груза объясняется не только приведенными доводами, но и тем, что модель (4) далее используется лишь для аппроксимации названного движения.
Из (4) можно определить собственную частоту угловых колебаний груза 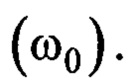
Известно, что собственные колебания описываются уравнением 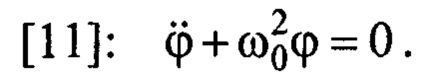 Равенство (4) можно записать как:
Равенство (4) можно записать как: 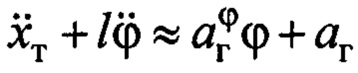 . Частота
. Частота 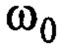 находится при
находится при 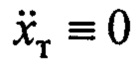 и отсутствии ветра, т.е.
и отсутствии ветра, т.е. 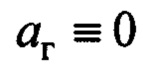 . Следовательно, с учетом (3) и принятого утверждения:
. Следовательно, с учетом (3) и принятого утверждения:
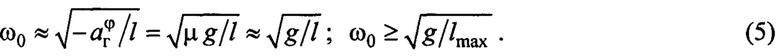
Ставится задача: в условиях текущей неопределенности параметров крана (за исключением паспортных данных крана 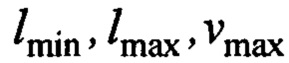 ) , груза и указанных возмущений,
) , груза и указанных возмущений,
сформировать закон управления горизонтальным перемещением груза в виде заданной скорости тележки крана, отработка которой сервоприводом тележки обеспечит условие на заданной высоте погрузки 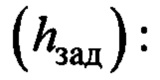

Заметим, что второе требование (6), если 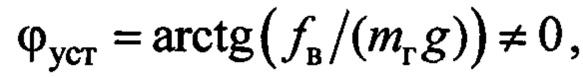 требует позиционирование груза не над целевой точкой доставки груза, а так, чтобы по окончании регулирования без дополнительных перемещений тележки при опускании груза обеспечить его доставку в целевую точку (движение груза по линии «А - ЦТ»). При этом требуется достижения условий (6) с динамикой движений, близкой к требуемой, определяемой с учетом скоростных характеристик сервопривода. При этом, в силу достаточно высокого быстродействия современных асинхронных сервоприводов (задержка в отработке сигнала на уровне сотых и десятых долей секунды) будем считать, что
требует позиционирование груза не над целевой точкой доставки груза, а так, чтобы по окончании регулирования без дополнительных перемещений тележки при опускании груза обеспечить его доставку в целевую точку (движение груза по линии «А - ЦТ»). При этом требуется достижения условий (6) с динамикой движений, близкой к требуемой, определяемой с учетом скоростных характеристик сервопривода. При этом, в силу достаточно высокого быстродействия современных асинхронных сервоприводов (задержка в отработке сигнала на уровне сотых и десятых долей секунды) будем считать, что 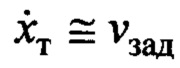 [12].
[12].
Для формирования заданной скорости тележки крана для достижения условий (6) используется подход, основанный на схеме адаптивного управления с неявной эталонной моделью, с алгоритмом текущей параметрической идентификации и использовании «упрощенных» условий адаптируемости [13].
Поскольку динамика движения груза соответствует колебательному процессу, то в качестве эталонной модели, задающей требуемые характеристики перемещения груза, примем неявную эталонную модель (существующую только в виде назначенных ее параметров) в форме колебательного звена со значениями переменных в начальный момент времени 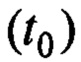 , равными соответствующим для исходного объекта:
, равными соответствующим для исходного объекта:
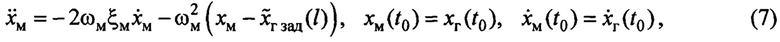
где 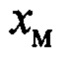 - переменная, описывающая эталонную динамику движения груза, соответствует переменной
- переменная, описывающая эталонную динамику движения груза, соответствует переменной 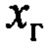 ;
;
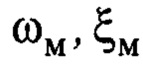 - эталонные значения собственной частоты и относительного коэффициента затухания соответственно - выбираемые параметры эталонной модели [9].
- эталонные значения собственной частоты и относительного коэффициента затухания соответственно - выбираемые параметры эталонной модели [9].
Приравнивая правые части уравнения (4) и первого равенства (7), заменяя 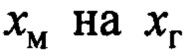 , а
, а 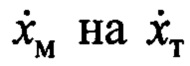 , найдем закон формирования заданной скорости тележки крана
, найдем закон формирования заданной скорости тележки крана 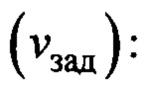
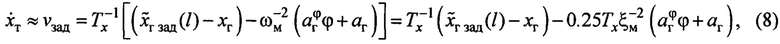
где 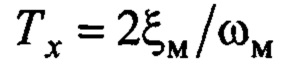 - задаваемая по эталону постоянная времени линейного перемещения тележки и груза, или постоянная времени регулирования.
- задаваемая по эталону постоянная времени линейного перемещения тележки и груза, или постоянная времени регулирования.
Действительно, если в (8) вместо члена 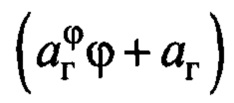 на основании (4) подставить
на основании (4) подставить 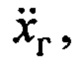 то с учетом введенных обозначений в (7) получим равенство, описывающее поведение груза в замкнутой системе управления с законом (8):
то с учетом введенных обозначений в (7) получим равенство, описывающее поведение груза в замкнутой системе управления с законом (8):
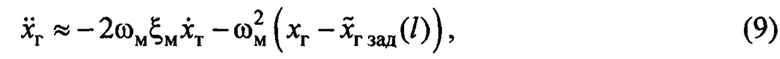
которое соответствует назначенному эталону (7), за исключением того, что вместо 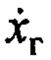 подставлена переменная
подставлена переменная 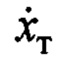 - это сделано специально для устранения внутренней неустойчивости в замкнутой системе управления.
- это сделано специально для устранения внутренней неустойчивости в замкнутой системе управления.
На основании фиг.1, ошибку слежения за положением груза можно переписать в следующем виде

где 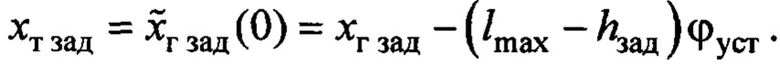
В связи с этим уравнение (8) можно записать в виде зависимости, описывающей динамику замкнутой системы управления
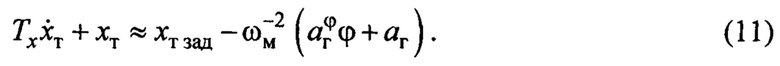
Если бы не было углового движения 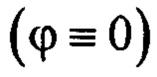 и не было возмущений
и не было возмущений 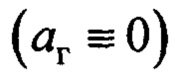 , отсюда следует, что
, отсюда следует, что 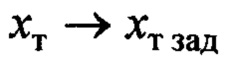 и, соответственно,
и, соответственно, 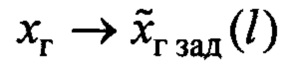 по апериодическому закону с постоянной времени
по апериодическому закону с постоянной времени 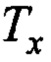 (отсюда название этого параметра). В общем случае это апериодическое движение возмущается угловым движением подвеса крана и внешним возмущением.
(отсюда название этого параметра). В общем случае это апериодическое движение возмущается угловым движением подвеса крана и внешним возмущением.
Из (4) и (11) также следует, что если в замкнутой системе управления достигается установившееся состояние: 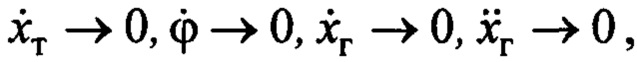 то это может быть только в случае, когда
то это может быть только в случае, когда 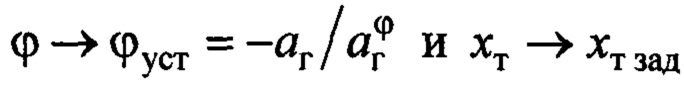 , а значит по (10)
, а значит по (10) 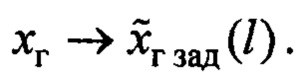
Утверждение. При 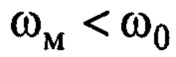 для замкнутой системы управления (2), (4), (8) при
для замкнутой системы управления (2), (4), (8) при 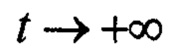 справедливо:
справедливо: 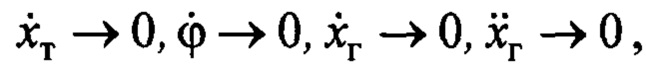 а значит достигается заданная цель управления (6).
а значит достигается заданная цель управления (6).
Доказательство. Для простоты рассуждений, примем, что 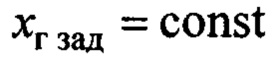 (из последующих выводов следует, что также можно принять
(из последующих выводов следует, что также можно принять 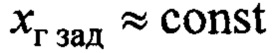 ). Назначим функцию Ляпунова
). Назначим функцию Ляпунова
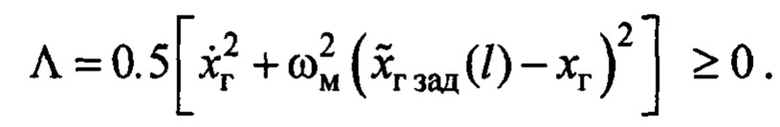
Заметим, что 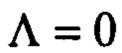 только при
только при 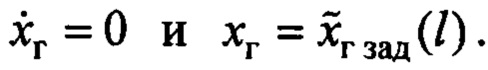 Выразим производную по времени функции Ляпунова, на основании (9), она равна:
Выразим производную по времени функции Ляпунова, на основании (9), она равна: 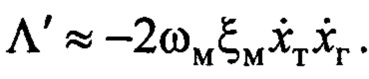 Отсюда следует, что для уменьшения во времени функции Ляпунова, достаточно на подавляющей части периода колебаний выполнения условия:
Отсюда следует, что для уменьшения во времени функции Ляпунова, достаточно на подавляющей части периода колебаний выполнения условия: 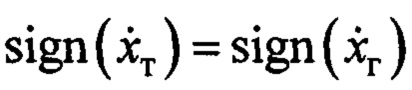 . Определим, когда оно может быть достигнуто.
. Определим, когда оно может быть достигнуто.
С учетом третьей строки системы уравнений (2), равенство (9) можно переписать в виде
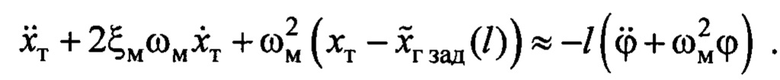
Прибавляя к правой части этого равенства нуль: 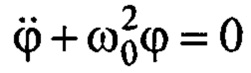 , умноженный на
, умноженный на 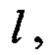 получим
получим
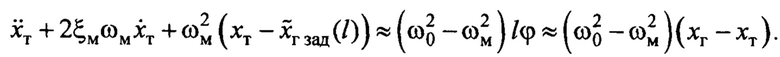
Дифференцируя это приблизительное равенство (это здесь выполнить возможно, в силу того, что приближенность равенства основана на линеаризации с сохранением производных) и выполняя дальнейшие преобразования, можно записать
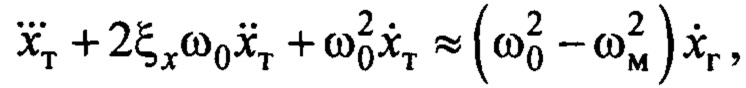
где 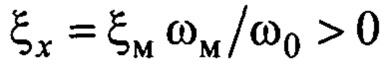 - относительный коэффициент затухания движения переменной
- относительный коэффициент затухания движения переменной 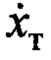 относительно
относительно 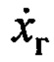 на частоте
на частоте 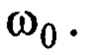
По теории автоматического управления полученное уравнение означает, что динамика движения тележки по переменной 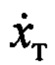 соответствует колебательному звену с собственной частотой выходного сигнала
соответствует колебательному звену с собственной частотой выходного сигнала 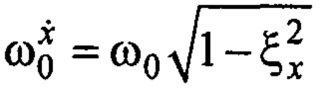 и со стремлением по времени:
и со стремлением по времени:
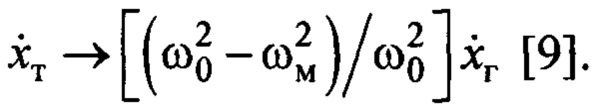
Потребуем выполнения условия: 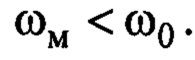 Тогда соотношение собственных частот выходного сигнала замкнутой системы управления
Тогда соотношение собственных частот выходного сигнала замкнутой системы управления 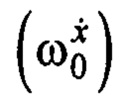 и назначенного эталонного движения по (7):
и назначенного эталонного движения по (7): 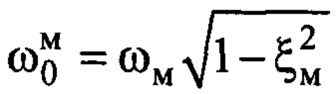 будет следующим:
будет следующим:
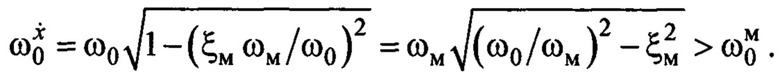
Поскольку закон (8) нацелен на следование переменной 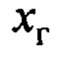 по эталону (7), то преобладающей частотой движений по
по эталону (7), то преобладающей частотой движений по 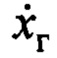 будет собственная частота выходного сигнала эталона
будет собственная частота выходного сигнала эталона 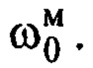 То есть в замкнутой системе управления на переходных процессах движение по
То есть в замкнутой системе управления на переходных процессах движение по 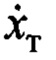 более быстродействующее, чем движение по
более быстродействующее, чем движение по 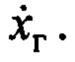 Отсюда и на основании изложенного следует, что
Отсюда и на основании изложенного следует, что 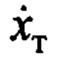 имеет на подавляющей части периода колебательных движений тот же знак, т.е.
имеет на подавляющей части периода колебательных движений тот же знак, т.е. 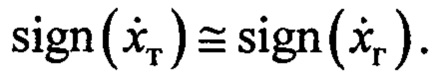
Таким образом, если 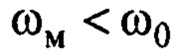 , то функция Ляпунова будет уменьшаться во времени.
, то функция Ляпунова будет уменьшаться во времени.
А по указанным ее свойствам получим: 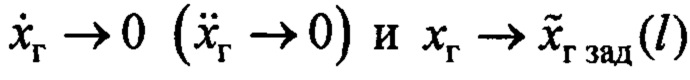 . Тогда из (8) и (4) следует, что
. Тогда из (8) и (4) следует, что 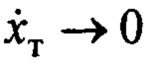 . Из зависимости
. Из зависимости 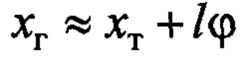 также следует, что
также следует, что 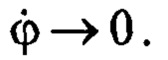
Доказательство завершено.
При ведении крановых работ очевидным желаемым движением груза к целевой точке является процесс, с минимальным перерегулированием с минимально возможным временем регулирования. Известно, что для колебательного звена этому требованию соответствуют значения относительного коэффициента затухания не менее 0.71 [9]. Также нужно учесть, что выбор параметров 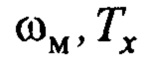 необходимо увязывать с максимальной скоростью привода и необходимым перемещением груза. С учетом этих положений, (8), равенства (11) без последнего слагаемого - рассматривается только апериодический процесс и максимальная его скорость [9], можно записать требования к этим параметрам в следующем виде:
необходимо увязывать с максимальной скоростью привода и необходимым перемещением груза. С учетом этих положений, (8), равенства (11) без последнего слагаемого - рассматривается только апериодический процесс и максимальная его скорость [9], можно записать требования к этим параметрам в следующем виде:
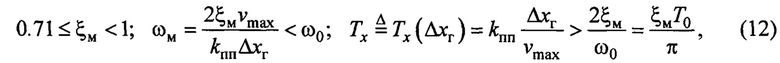
где 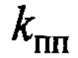 - положительный коэффициент изменения времени переходного процесса, выбираемый с учетом соблюдения неравенств (12);
- положительный коэффициент изменения времени переходного процесса, выбираемый с учетом соблюдения неравенств (12);
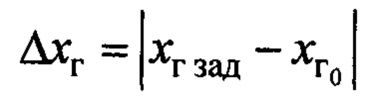 - расстояние переноса груза;
- расстояние переноса груза;
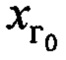 - начальное положение груза;
- начальное положение груза;
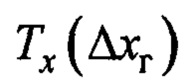 - зависимость параметра
- зависимость параметра 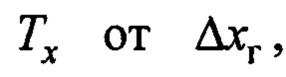 при фиксированной величине указанного аргумента далее также будет использоваться обозначение
при фиксированной величине указанного аргумента далее также будет использоваться обозначение 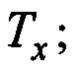
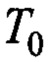 - период собственных маятниковых колебаний подвеса груза; Поясним выбор коэффициента
- период собственных маятниковых колебаний подвеса груза; Поясним выбор коэффициента 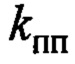 .
. 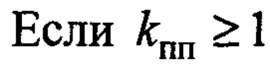 в переходном процессе соблюдается
в переходном процессе соблюдается 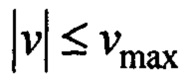 , чем больше коэффициент, тем больше время регулирования. При
, чем больше коэффициент, тем больше время регулирования. При 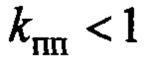 время переходного процесса будет уменьшаться, но при этом скорость тележки может выходить на свое ограничение, соответственно в эти моменты времени управления по гашению колебаний нет, что, конечно же, снижает качество управления;
время переходного процесса будет уменьшаться, но при этом скорость тележки может выходить на свое ограничение, соответственно в эти моменты времени управления по гашению колебаний нет, что, конечно же, снижает качество управления;
В силу (5), третье неравенство в (12) гарантированно будет выполнятся, если
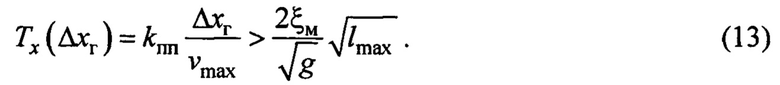
На фиг.2 представлена область допустимых значений параметра 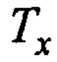 в соответствии его зависимостью от
в соответствии его зависимостью от 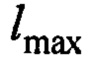 по (13)
по (13) 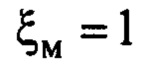 (незаштрихованная область фигуры).
(незаштрихованная область фигуры).
Обозначенная граница представляет минимальное значение 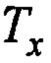 .
.
Отсюда следует, что на основе выражения (13) можно определить параметр 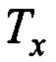 для закона (8) по паспортным данным крановой установки
для закона (8) по паспортным данным крановой установки 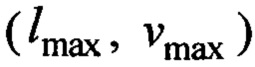 и расстояния переноса груза
и расстояния переноса груза 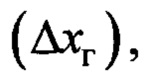 которые заранее известны. Также можно уточнить этот параметр по информации о периоде свободных колебаний подвеса в соответствии с (12).
которые заранее известны. Также можно уточнить этот параметр по информации о периоде свободных колебаний подвеса в соответствии с (12).
Рассмотрим пример выбора параметра 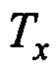 по указанным соотношениям. Пусть
по указанным соотношениям. Пусть 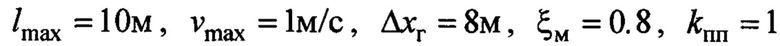 . Тогда по (13)
. Тогда по (13) 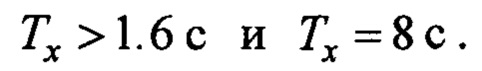
Такое решение на основании (11) (будем считать, что к концу переходного процесса маятниковые колебания будут демпфированы) обеспечивает время регулирования 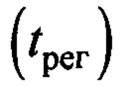 по переносу груза в заданную точку:
по переносу груза в заданную точку: 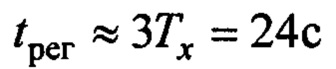 [9]. При уменьшении расстояния переноса груза, получаем уменьшение этих параметров со значениями:
[9]. При уменьшении расстояния переноса груза, получаем уменьшение этих параметров со значениями: 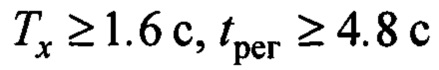 . Эти показатели соответствуют требованиям норм времени по [14], например, для средних кранов с грузоподъемностью до 50 т, которые рассматривается далее в модельном примере.
. Эти показатели соответствуют требованиям норм времени по [14], например, для средних кранов с грузоподъемностью до 50 т, которые рассматривается далее в модельном примере.
Закон формирования заданной скорости (8) построен на точном значении переменной 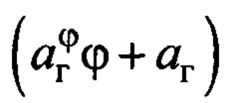 параметров рассматриваемого объекта управления (4):
параметров рассматриваемого объекта управления (4): 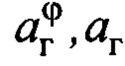 . Но на практике при многообразии типов переносимых грузов, длин подвеса, внешних возмущениях в текущий момент времени параметры
. Но на практике при многообразии типов переносимых грузов, длин подвеса, внешних возмущениях в текущий момент времени параметры 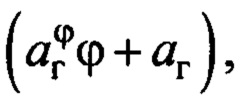 как правило, неизвестны.
как правило, неизвестны.
Проблемой является и точное определение угла ср. Если бы было возможным точно измерять переменную 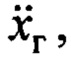 то на основании (4) можно было в законе (8) вместо скобки
то на основании (4) можно было в законе (8) вместо скобки 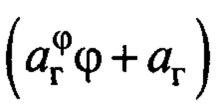 использовать эту переменную. Однако измерение ускорений связано со значительными высокочастотными шумами, поэтому измеренное значение линейного ускорения груза напрямую нельзя подставлять в закон (8) - будут значительными высокочастотные составляющие в управлении. Использование обычного низкочастотного фильтра вносит фазовую задержку, что также отрицательно сказывается на качестве управления.
использовать эту переменную. Однако измерение ускорений связано со значительными высокочастотными шумами, поэтому измеренное значение линейного ускорения груза напрямую нельзя подставлять в закон (8) - будут значительными высокочастотные составляющие в управлении. Использование обычного низкочастотного фильтра вносит фазовую задержку, что также отрицательно сказывается на качестве управления.
Как решение указанных проблем, можно использовать аппроксимацию величины хг на основе текущей параметрической идентификации, дающей низкочастотную фильтрацию без сдвига по фазе, как это использовалось в [8, 15]. Это является частью подхода, названного «упрощенными» условиями адаптируемости [13]. Однако для такого подхода требуется точное значение длины подвеса 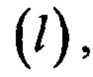 что требует дополнительных аппаратных и алгоритмических решений. Последнее утверждение основано на том, что акселерометр измеряет сумму ускорений - кажущегося ускорения (являющегося порождением реакции опоры из-за силы тяжести) и непосредственно искомого ускорения.
что требует дополнительных аппаратных и алгоритмических решений. Последнее утверждение основано на том, что акселерометр измеряет сумму ускорений - кажущегося ускорения (являющегося порождением реакции опоры из-за силы тяжести) и непосредственно искомого ускорения.
Для того, чтобы упростить систему управления краном, предлагается вместо линейного ускорения груза в законе (8) использовать линейное ускорение совмещенного датчика 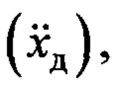 расположенного на фиксированном расстоянии
расположенного на фиксированном расстоянии 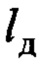 от тележки
от тележки 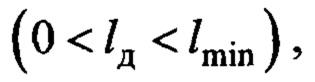 точка Д (см. фиг.1). Линейное ускорение груза с учетом принятых допущений в силу (2) и (4):
точка Д (см. фиг.1). Линейное ускорение груза с учетом принятых допущений в силу (2) и (4): 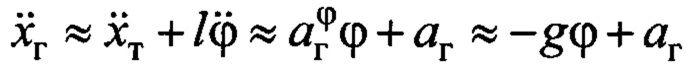 . Очевидно, что такое же ускорение для совмещенного датчика равно:
. Очевидно, что такое же ускорение для совмещенного датчика равно: 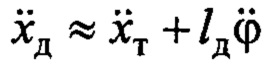 . Сравнивая эти зависимости, несложно найти
. Сравнивая эти зависимости, несложно найти
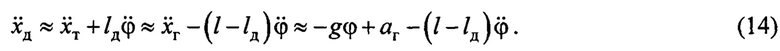
Тогда с учетом (10) вместо закона (8) будет 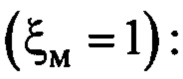
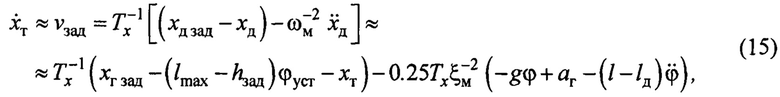
где 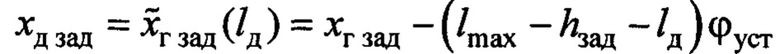 .
.
Из первой части (15) непосредственно следует уравнение, описывающее горизонтальное перемещение совмещенного датчика, аналогичное (9), где вместо переменной 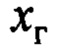 нужно подставить
нужно подставить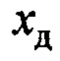 . Если в рассмотренном выше доказательстве сделать такую же замену, получим те же самые выводы, только для линейного перемещения совмещенного датчика. А поскольку последний находится на одной линии между точкой крепления подвеса к тележке и центром тяжести груза, а также на основе (10), отсюда следует, что закон (15) аналогичен (8).
. Если в рассмотренном выше доказательстве сделать такую же замену, получим те же самые выводы, только для линейного перемещения совмещенного датчика. А поскольку последний находится на одной линии между точкой крепления подвеса к тележке и центром тяжести груза, а также на основе (10), отсюда следует, что закон (15) аналогичен (8).
Для реализации закона формирования заданной скорости (15) нужно определять в текущем времени переменные: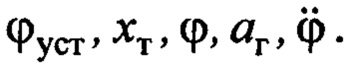
Значение 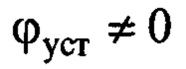 может быть только из-за действия ветра. Если в точке Д подвеса находится акселерометр, измеряющий сумму ускорения реакции опоры от силы тяжести и
может быть только из-за действия ветра. Если в точке Д подвеса находится акселерометр, измеряющий сумму ускорения реакции опоры от силы тяжести и 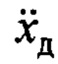 , его значение определится с учетом (14) как
, его значение определится с учетом (14) как 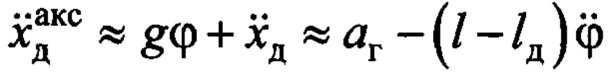 . Как указано выше, на установившемся процессе в замкнутой системе управления
. Как указано выше, на установившемся процессе в замкнутой системе управления 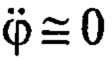 . Поэтому отсюда можно определить искомый параметр:
. Поэтому отсюда можно определить искомый параметр:

где верхний символ 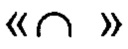 означает оценку;
означает оценку;
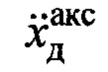 - показания акселерометра, установленного в точке Д подвеса с осью чувствительности, ортогональной канату подвеса;
- показания акселерометра, установленного в точке Д подвеса с осью чувствительности, ортогональной канату подвеса;
нижний индекс «нч» обозначает низкочастотную фильтрацию для устранения составляющих переходного процесса по 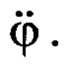
Величина 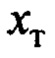 может определяться с помощью встроенного в привод тележки энкодера, либо, в силу быстродействия сервопривода, интегрированием сигнала
может определяться с помощью встроенного в привод тележки энкодера, либо, в силу быстродействия сервопривода, интегрированием сигнала 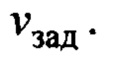
Сигналы 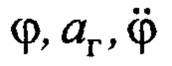 необходимы для построения на них оценки
необходимы для построения на них оценки 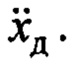 Для определения угла
Для определения угла 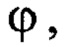 используем датчик угловой скорости, расположенный также в точке Д подвеса. Но в силу известного дрейфа этого датчика такая процедура требует предварительной и текущей оценки величины этого дрейфа для его компенсации, что представляют определенную сложность в реализации. Если использовать интегрирование «сырых» данных с этого датчика, то получим:
используем датчик угловой скорости, расположенный также в точке Д подвеса. Но в силу известного дрейфа этого датчика такая процедура требует предварительной и текущей оценки величины этого дрейфа для его компенсации, что представляют определенную сложность в реализации. Если использовать интегрирование «сырых» данных с этого датчика, то получим:
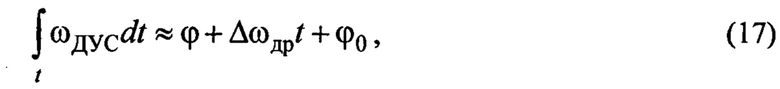
где 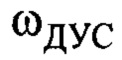 - «сырые» данные с датчика угловой скорости с осью чувствительности, параллельной оси вращения подвеса;
- «сырые» данные с датчика угловой скорости с осью чувствительности, параллельной оси вращения подвеса;
 - дрейф датчика;
- дрейф датчика;
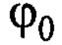 - начальное значение угла
- начальное значение угла 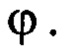
Алгоритм текущей параметрической идентификации предлагается строить на основе уравнений (14) и (17), порождающих равенство:
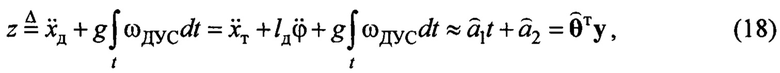
где 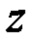 - отклик объекта идентификации;
- отклик объекта идентификации;
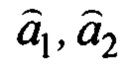 - оценки параметров
- оценки параметров 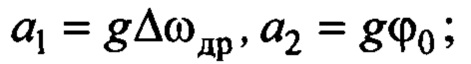
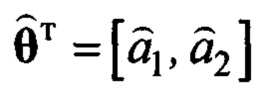 - вектор оцениваемых параметров;
- вектор оцениваемых параметров;
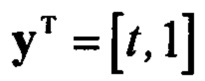 - вектор факторных переменных; индекс «т» обозначает транспонирование.
- вектор факторных переменных; индекс «т» обозначает транспонирование.
В этом выражении не учтено слагаемое 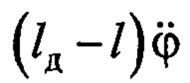 исходного равенства (14). Это соответствует опыту исследований замкнутой системы управления с законом формирования заданной скорости (20) при разных параметрах: в силу быстрой сходимости к нулю процесса
исходного равенства (14). Это соответствует опыту исследований замкнутой системы управления с законом формирования заданной скорости (20) при разных параметрах: в силу быстрой сходимости к нулю процесса 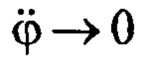 и свойствам самонастройки системы управления,
и свойствам самонастройки системы управления,
оценка этого слагаемого слабо влияет на результирующую динамику движения.
В качестве алгоритма текущей идентификации, предлагается использовать рекуррентный метод наименьших квадратов с фактором забывания (процедура оценивания по методу наименьших квадратов обладает лучшими аппроксимационными свойствами, что общепризнанно) [16]:
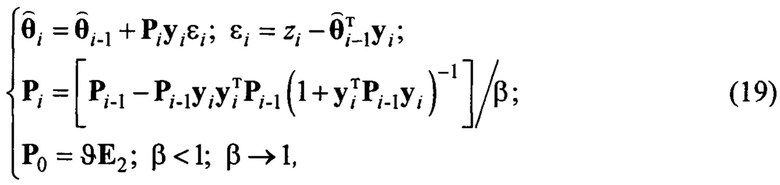
где индекс 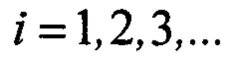 - означает z-ый момент времени с временным шагом Δt; ε - невязка идентификации; Pi - матричный коэффициент усиления алгоритма (2×2); β - назначаемый фактор забывания прошедших измерений для слежения за изменяющимся во времени искомыми параметрами;
- означает z-ый момент времени с временным шагом Δt; ε - невязка идентификации; Pi - матричный коэффициент усиления алгоритма (2×2); β - назначаемый фактор забывания прошедших измерений для слежения за изменяющимся во времени искомыми параметрами; 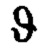 - большое положительное число, определяющее начальную скорость изменения оценок параметров; Е2 - единичная (2×2) матрица.
- большое положительное число, определяющее начальную скорость изменения оценок параметров; Е2 - единичная (2×2) матрица.
Заметим, что алгоритм идентификации (18), (19) использует гарантированно линейно-независимые факторные переменные на любом интервале времени. Это гарантирует устойчивость получаемых оценок и, в целом, устойчивость используемого алгоритма идентификации [13].
Вместо закона (15) запишем закон формирования заданной скорости на текущих оценках 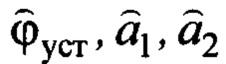 по (16), (18), (19):
по (16), (18), (19):
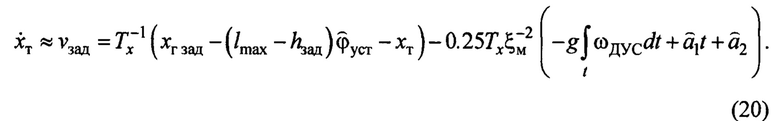
Также в соответствии с рекомендациями [13] желательно фильтровать закон (20) на низкочастотном фильтре для устранения в замкнутой системе высокочастотных составляющих с сохранением точности управления.
Известно, что невязка идентификации алгоритма (19) при линейной независимости элементов вектор-функции 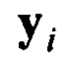 на скользящем временном интервале (а это, как указывалось, гарантированно) и на достаточно малом шаге
на скользящем временном интервале (а это, как указывалось, гарантированно) и на достаточно малом шаге 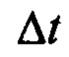 очень быстро сходится в область нуля (буквально с первых шагов работы алгоритма) и остается там, при этом сами оценки параметров могут быть далекими от истинных значений [13]. То есть алгоритм (18), (19) обеспечивает условие:
очень быстро сходится в область нуля (буквально с первых шагов работы алгоритма) и остается там, при этом сами оценки параметров могут быть далекими от истинных значений [13]. То есть алгоритм (18), (19) обеспечивает условие:
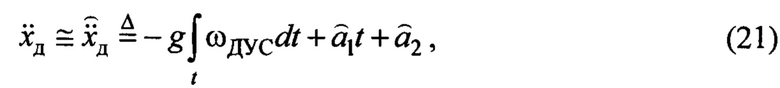
т.е. аппроксимацию переменной 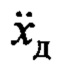 даже при неточных значениях оценок параметров.
даже при неточных значениях оценок параметров.
А это значит, что с самого начала работы алгоритма идентификации оценки можно подставлять в закон (20). Отсюда также следует справедливость приведенного доказательства по достижению цели управления для текущих оценок параметров и 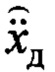 (в приблизительном плане).
(в приблизительном плане).
Исходя из предложенного алгоритмического обеспечения адаптивной системы управления тележкой крана предлагается в качестве датчиков информации и дополнительных алгоритмических построений использовать следующие:
- энкодер на тележке крана, либо, как вариант интегрирование переменной 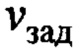 , что является источниками информации о пройденном пути тележки
, что является источниками информации о пройденном пути тележки 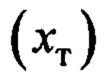 ;
;
- совмещенный датчик в виде акселерометра и датчика угловой скорости, закрепленной на канате подвеса в месте, близком к тележке крана на фиксированном расстоянии 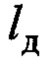 (см. фиг.3) аналогично [3], в точке Д подвеса; акселерометр используется
(см. фиг.3) аналогично [3], в точке Д подвеса; акселерометр используется
для формирования сигнала 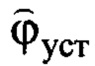 по (16), датчик угловой скорости дает сигнал
по (16), датчик угловой скорости дает сигнал 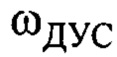 ;
;
- для формирования сигнала 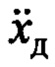 , как вариант, предлагается использовать фильтрацию на реальном дифференцирующем звене сигнала
, как вариант, предлагается использовать фильтрацию на реальном дифференцирующем звене сигнала 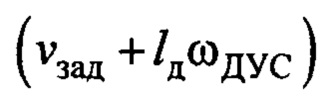 , что дает приближенное получение искомого сигнала без влияния дрейфа датчика угловой скорости [9].
, что дает приближенное получение искомого сигнала без влияния дрейфа датчика угловой скорости [9].
Использование совмещенного датчика на канате по фиг.3 выгодно отличается от предложения работы [15] по расположению его на крюке с дистанционной формой передачи информации:
- есть возможность организовать проводную передачу информации и электропитания, что намного надежнее и проще, снижает эксплуатационные затраты;
- датчик находится в безопасном месте, не подвергающимся внешним механическим воздействиям;
- легко организовать фиксацию осей чувствительности датчика (крюк подвеса часто вращается вокруг вертикальной оси);
- на датчик в меньшей степени передаются неосновные высокочастотные дополнительные (в т.ч. недомоделированные) движения груза.
В заключение теоретической части следует отметить, что все приведенные выше выводы получены при условии, что 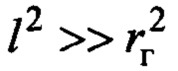 и справедливости (4). Модельные исследования показывают, что в случае нарушения этого, например,
и справедливости (4). Модельные исследования показывают, что в случае нарушения этого, например, 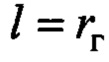 , система управления с законом (20) и алгоритмом идентификации (18), (19) обеспечивает также высокое качество управления. Это объясняется, в частности, хорошими аппроксимационными свойствами алгоритма идентификации (18), (19), доставляющего свойство (21) даже при умеренной некорректности модели (4).
, система управления с законом (20) и алгоритмом идентификации (18), (19) обеспечивает также высокое качество управления. Это объясняется, в частности, хорошими аппроксимационными свойствами алгоритма идентификации (18), (19), доставляющего свойство (21) даже при умеренной некорректности модели (4).
Модельный пример по анализу свойств замкнутой системы управления строился на основании зависимостей (1), (18-20) с использованием (5-7), (12-13), (16). Моделирование проводилось в компьютерной среде Matlab/Simulink/SimMechanics. Дифференциальные уравнения решались методом Рунге-Кутты четвертого и пятого порядка с шагом 0.01 с.
Рассматривалось управление тележкой типового среднего крана с параметрами: 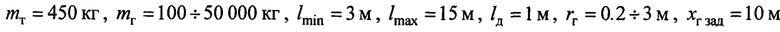
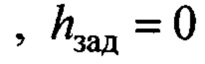 . Сила трения моделировалась в виде вязкого трения:
. Сила трения моделировалась в виде вязкого трения: 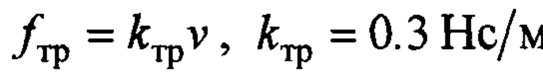 .
.
Сервопривод, формирующий скорость перемещения тележки крана 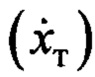 по заданной скорости
по заданной скорости 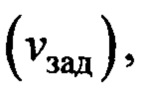 моделировался апериодическим звеном с единичным коэффициентом усиления и с постоянной времени 0.1 с, а также имел дополнительные нелинейности: временную задержку 0.03 с и ограничения по выходному сигналу:
моделировался апериодическим звеном с единичным коэффициентом усиления и с постоянной времени 0.1 с, а также имел дополнительные нелинейности: временную задержку 0.03 с и ограничения по выходному сигналу: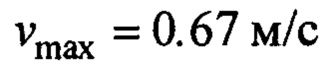 ,
, 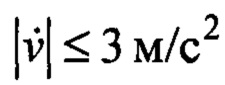 . Многие из указанных параметров соответствуют [17] и многообразию типовых переносимых грузов. Закон формирования заданной скорости (20) фильтровался на апериодическом звене с единичным коэффициентом усиления и постоянной времени 1 с.
. Многие из указанных параметров соответствуют [17] и многообразию типовых переносимых грузов. Закон формирования заданной скорости (20) фильтровался на апериодическом звене с единичным коэффициентом усиления и постоянной времени 1 с.
Предполагалось, что на переносимый груз в момент времени 50 с действует ступенчатое ветровое возмущение интенсивностью 5% от веса груза, соответствующее 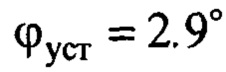 («ступенька» сглажена апериодическим звеном с постоянной времени 1 с).
(«ступенька» сглажена апериодическим звеном с постоянной времени 1 с).
Считалось, что угловая скорость и линейное ускорение измеряются с помощью микромеханического датчика типа MPU-6050. Эти данные зашумлены центрированными гауссовскими шумами со среднеквадратическими ошибками по угловой скорости 0.1 град/с, а по ускорению 0.1 м/с2, 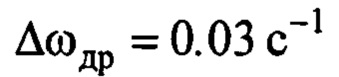 [18]. У акселерометра также предполагалось постоянное смещение показаний («нуль» акселерометра) величиной 0.17 м/с - соответствует неточности угловой выставки акселерометра величиной около 1°. Линейное перемещения тележки
[18]. У акселерометра также предполагалось постоянное смещение показаний («нуль» акселерометра) величиной 0.17 м/с - соответствует неточности угловой выставки акселерометра величиной около 1°. Линейное перемещения тележки 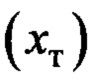 определялось энкодером с аналогичным шумом со среднеквадратической ошибкой 0.01 м.
определялось энкодером с аналогичным шумом со среднеквадратической ошибкой 0.01 м.
Для алгоритма идентификации (18), (19) приняты следующие параметры: Δt=0.01 с, с таким же временным шагом реализуется закон (20); параметры ϑ=10, β=0.996. В алгоритме идентификации вместо переменной 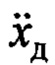 использовалась ее оценка, полученная по зависимости:
использовалась ее оценка, полученная по зависимости: 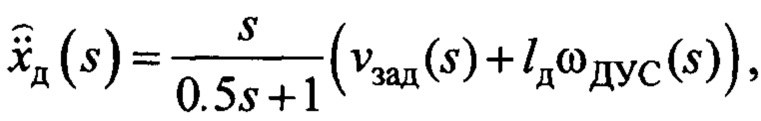 где s - переменная преобразования Лапласа.
где s - переменная преобразования Лапласа.
В представленных вариантах работы крана собственная его частота в соответствии с (5) изменяется в диапазоне 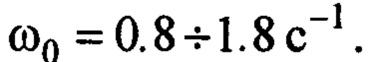 Поэтому параметры закона (20) с учетом (12), (13) приняты:
Поэтому параметры закона (20) с учетом (12), (13) приняты: 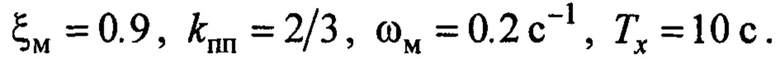 Зависимость (17) реализована в виде:
Зависимость (17) реализована в виде: 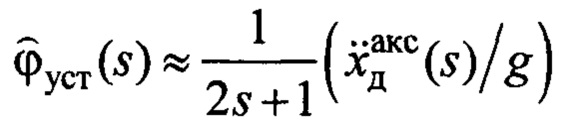
Поведение замкнутой системы управления по переменным 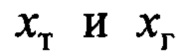 сравнивалось с переменной
сравнивалось с переменной 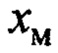 , которая является выходом эталона, соответствующего эталонному движению (7):
, которая является выходом эталона, соответствующего эталонному движению (7): 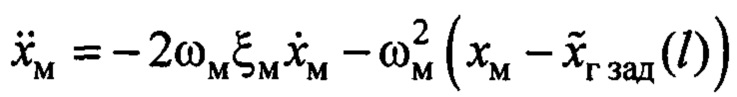 с указанными выше параметрами.
с указанными выше параметрами.
На фиг.4 представлены результаты исследования при средних параметрах работы крана при минимальной длине подвеса 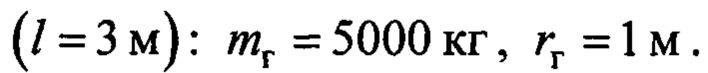 Другие значения двух последних параметров из указанного выше их диапазона дают практически такие же кривые (расхождение - единицы процента).
Другие значения двух последних параметров из указанного выше их диапазона дают практически такие же кривые (расхождение - единицы процента).
На фиг.5 представлены результаты исследования при средних параметрах работы крана при максимальной длине подвеса 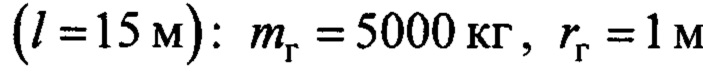 . Так же, как и в предыдущем случае, другие значения двух последних параметров из указанного выше их диапазона дают практически такие же кривые. Постоянная ошибка позиционирования груза в целевой точке составляет около 0.28 м. Если ошибки в угловой выставке акселерометра в совмещенном датчике не будет, то и указанной ошибки позиционирования также не будет.
. Так же, как и в предыдущем случае, другие значения двух последних параметров из указанного выше их диапазона дают практически такие же кривые. Постоянная ошибка позиционирования груза в целевой точке составляет около 0.28 м. Если ошибки в угловой выставке акселерометра в совмещенном датчике не будет, то и указанной ошибки позиционирования также не будет.
На других длинах подвески результаты имеют промежуточный характер. Можно утверждать, что результаты модельных исследований подтверждают изложенные выше теоретические выкладки. Они показывают, что при большом разнообразии параметров груза, его перемещение близко к поведению назначенного эталона с достижением целевой точки на высоте погрузки с небольшой ошибкой, пропорциональной неточности угловой выставки акселерометра в совмещенном датчике (наличии нескомпенсированного «нуля» акселерометра). При возникновении ступенчатого ветрового воздействия оно парируется. Все это при текущей неопределенности указанных параметров. Линейное перемещение груза близко к «эталонному». Время переходного процесса при переносе груза на 10 м составляет около 25 с. Угловое отклонение подвеса груза не более 2 град. Подобные свойства без изменения алгоритма управления были получены и при других параметрах крана.
Указанная постоянная ошибка позиционирования груза также будет возникать, если вместо энкодера для определения сигнала хг использовать интегрирование 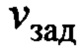 . Но, в целом, эта ошибка совершенно не важна, если описанная система управления краном подразумевает наличие в своем контуре оператора крана, т.е. представляет собой автоматизированную систему. Оператор, наблюдая за положением груза, формирует через органы управления дополнительный сигнал заданной скорости по отношению к формируемому в соответствии с законом (20), компенсируя эту постоянную ошибку. Причем в этом случае сигнал
. Но, в целом, эта ошибка совершенно не важна, если описанная система управления краном подразумевает наличие в своем контуре оператора крана, т.е. представляет собой автоматизированную систему. Оператор, наблюдая за положением груза, формирует через органы управления дополнительный сигнал заданной скорости по отношению к формируемому в соответствии с законом (20), компенсируя эту постоянную ошибку. Причем в этом случае сигнал 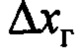 в (12), (13) определяется управляющим воздействием оператора.
в (12), (13) определяется управляющим воздействием оператора.
Отсюда и из вышеизложенного следует, что предлагаемый способ адаптивного управления мостовым краном не требует постоянной настройки системы управления при большом многообразии переносимых грузов и режимов работы. Нужна лишь разовая настройка системы управления при установке ее на кран (возможно также периодическая уточняющая настройка на регламентных работах):
- определение «нуля» акселерометра с целью его вычитания из текущих показаний для устранения постоянной ошибки позиционирования груза, если система управления краном работает в полностью автоматическом режиме (оператора с текущими поправками к работе автоматики нет);
- выбор параметра 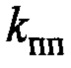 и определение зависимости
и определение зависимости 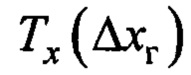 по (12), (13) и паспортным данным крановой установки для закона формирования заданной скорости (20);
по (12), (13) и паспортным данным крановой установки для закона формирования заданной скорости (20);
- выбор и опробование параметров алгоритма текущей идентификации;
- установка параметров указанных выше низкочастотных фильтров.
Литература
1. Щедринов А.В., Сериков С.А., Колмыков В.В. Автоматическая система успокоения колебаний груза для мостового крана. Приборы и системы. Управление, контроль, диагностика. - 2007. - №8. С. 13-17.
2. Патент RU 2564560 C1, В66С 13/18. Способ повышения точности и скорости перемещения груза по требуемой траектории грузоподъемным краном мостового типа / Щербаков B.C., Корытов М.С., Вольф Е.О; заявитель и патентообладатель Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Сибирская государственная автомобильно-дорожная академия (СибАДИ)" (RU) - 2014118376/11, заявл. 06.05.2014, опубл. 10.10.2015, Бюл. 28.
3. Патент RU 2676210 С1, МПК В66С 13/06. Устройство и способ управления раскачиванием груза, подвешенного на подъемном устройстве / Саварези СМ., Винати Ф., Винати С, Винати М., Винати М., Винати Д.; заявитель и патентообладатель ВИНАТИ СР.Л. - 2016125496; заявл. 06.11.14; опубл. 26.12.18, Бюл. 36.
4. Patent CN 108875253 В, G06F30/20. Terminal sliding mode anti-swing control method and system of under-actuated crane system based on disturbance observer /
 Current Assignee Qufu Normal University. Publication 24.06.2022.
Current Assignee Qufu Normal University. Publication 24.06.2022.
URL: https://patents.google.com/patent/CN108875253B/en?oq=CN108875253B
5. Patent CN 108549229 A, G05B13/042. A kind of overhead crane neural network adaptive controller and its design method / Current Assignee Qufu Normal University, Application filed of 20.04.2018, Publication of 18.09.2018.
Current Assignee Qufu Normal University, Application filed of 20.04.2018, Publication of 18.09.2018.
URL: https://patents.google.com/patent/CNl 08549229A/en?oq=CN108549229A
6. Patent CN 104444817 A, B66C 13/063. Self-adaption anti-swing positioning control method of under-actuated crane / Current Assignee Nankai University, Application filed of 14.11.2021, Publication of 25.03.2015.
Current Assignee Nankai University, Application filed of 14.11.2021, Publication of 25.03.2015.
URL: https://patents.google.com/patent/CNl 04444817A/en?oq=CN 104444817 A.
7. Patent CN 110673471 B, G05B13/042. Design method of adaptive controller for crane system, controller and system / Current Assignee University of Jinan, Application filed of 05.09.2019, Publication of 12.04.2022.
Current Assignee University of Jinan, Application filed of 05.09.2019, Publication of 12.04.2022.
URL: https://patents.google.com/patent/CN110673471B/en?oq=CN110673471B.
8. Патент на изобретение RU 2744647 С1. Способ адаптивного управления мостовым краном / Круглов С.П., Ковыршин С.В., Аксаментов Д.Н., заявитель и патентообладатель Федеральное государственное бюджетное образовательное учреждение высшего образование Иркутский государственный университет путей сообщения (ФГБОУ ВО ИрГУПС) (RU) - 2020124779 заявл. 16.07.2020, опубл. 12.03.2021, Бюл.8. (прототип).
9. Первозванский А.А. Курс теории автоматического управления. Учеб. пособие для вузов. Лань, Санкт-Петербург, 2015. 624 с.
10. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.
11. Сивухин Д.В. Общий курс физики. В 5 т.Том I. Механика. 4-е изд. - М.: Физматлит, Изд-во МФТИ. - 2005. - 560 с.
12. Герман-Галкин СГ. Компьютерное моделирование полупроводниковых систем в MATLAB 6.0: Учебное пособие. - СПб.: КОРОНА принт, 2010. - 320 с.
13. Адаптивное управление техническими объектами при текущей параметрической неопределенности на основ?, идентификационного алгоритма и «упрощенных» условий адаптируемости с прикладными задачами. Этап 1: отчет о НИР / ФГБОУ ВО ИрГУПС; рук. СП. Круглов; исполн.: С.В. Ковыршин, Д.В. Буторин, П.Ю. Иванов. Иркутск, 2023. 141 с. №гос.регистрации 123063000060-7.
14. Нормативы времени на погрузочно-разгрузочные работы, выполняемые на железнодорожном, водном и автомобильном транспорте, URL: https://meganorm.ru/data2/1/4293832/4293832120.htm#i18231.
15. Круглов С.П., Ковыршин С.В. Идентификационное скоростное управление мостовым краном с сокращейной моделью переноса груза. Проблемы управления. -2023.-№4. С.28-37.
16. Льюнг Л. Идентификация систем. Теория для пользователя: Пер. с англ. / Под ред. Я.З. Цыпкина. - М.: Наука, гл. ред. физ.-мат.лит.- 1991. - 432 с.
17. ГОСТ 3332-54. Краны мостовые электрические общего назначения грузоподъемностью от 5 до 50 т среднего и тяжелого режимов работы. Основные параметры и размеры. - М: Издательство стандартов. - 1974.
18. Жмудь В.А., Кузнецов К.А., Кондратьев Н.О. и др. Акселерометр и гироскоп MPU6050: первое включение на STM32 и исследование показаний в статике // Автоматика и программная инженерия. - 2018. - №3(25). - С. 9-22.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ управления мостовым краном на основе скоростного ПД-регулятора | 2024 |
|
RU2829659C1 |
| Способ адаптивного управления мостовым краном | 2020 |
|
RU2744647C1 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ И СКОРОСТИ ПЕРЕМЕЩЕНИЯ ГРУЗА ПО ТРЕБУЕМОЙ ТРАЕКТОРИИ ГРУЗОПОДЪЕМНЫМ КРАНОМ МОСТОВОГО ТИПА | 2014 |
|
RU2564560C1 |
| Способ экспериментального определения жесткости канатного подвеса для кранов мостового типа | 2022 |
|
RU2803775C1 |
| СПОСОБ ПРЕДОТВРАЩЕНИЯ РАСКАЧИВАНИЯ ГРУЗА НА ГИБКОМ ПОДВЕСЕ (ВАРИАНТЫ) | 2009 |
|
RU2406679C2 |
| УСТРОЙСТВО И СПОСОБ УПРАВЛЕНИЯ РАСКАЧИВАНИЕМ ГРУЗА, ПОДВЕШЕННОГО НА ПОДЪЕМНОМ УСТРОЙСТВЕ | 2014 |
|
RU2676210C1 |
| СИСТЕМА ИМИТАЦИИ НЕВЕСОМОСТИ | 2014 |
|
RU2565807C2 |
| КРАН ДЛЯ ОБРАЩЕНИЯ С ОТРАБОТАВШИМ ЯДЕРНЫМ ТОПЛИВОМ В ЗАЩИТНОЙ КАМЕРЕ | 2007 |
|
RU2352516C1 |
| СИСТЕМА, УСТРОЙСТВО И СПОСОБ ТЕКУЩЕГО КОНТРОЛЯ ПОЛОЖЕНИЯ И ОРИЕНТАЦИИ ТРАНСПОРТНОГО СРЕДСТВА, ПОГРУЗОЧНОГО УСТРОЙСТВА И ГРУЗА ПРИ РАБОТЕ ПОГРУЗОЧНОГО УСТРОЙСТВА | 2012 |
|
RU2623295C2 |
| Способ адаптивного управления автоматической подачей песка под колеса локомотива | 2022 |
|
RU2780751C1 |
Изобретение относится к области управления крановыми установками с подвешенным расположением груза, в частности мостовыми кранами. При адаптивном управлении краном с идентификатором и неявной эталонной моделью с использованием «упрощенных» условий адаптируемости, в эталонной модели задают собственную частоту и относительный коэффициент затухания. В качестве управляющего воздействия используют заданную скорость перемещения тележки и балки крана, которая отрабатывается сервоприводами. Собственную частоту эталонной модели или постоянную времени регулирования в законе формирования заданной скорости выбирают исходя из паспортных данных крана: максимальной длины подвеса и максимальной скорости сервопривода, а также с учетом расстояния переноса груза, что не требует определения текущей длины подвеса. В качестве датчиков информации используют совмещенный датчик в виде акселерометра и датчик угловой скорости с несколькими осями чувствительности каждый, размещенные на канате подвеса рядом с тележкой крана, а также энкодеры, определяющие положение тележки и балки крана. Достигается упрощение построения системы управления и снижение эксплуатационных затрат на основе модернизации. 1 з.п. ф-лы, 5 ил.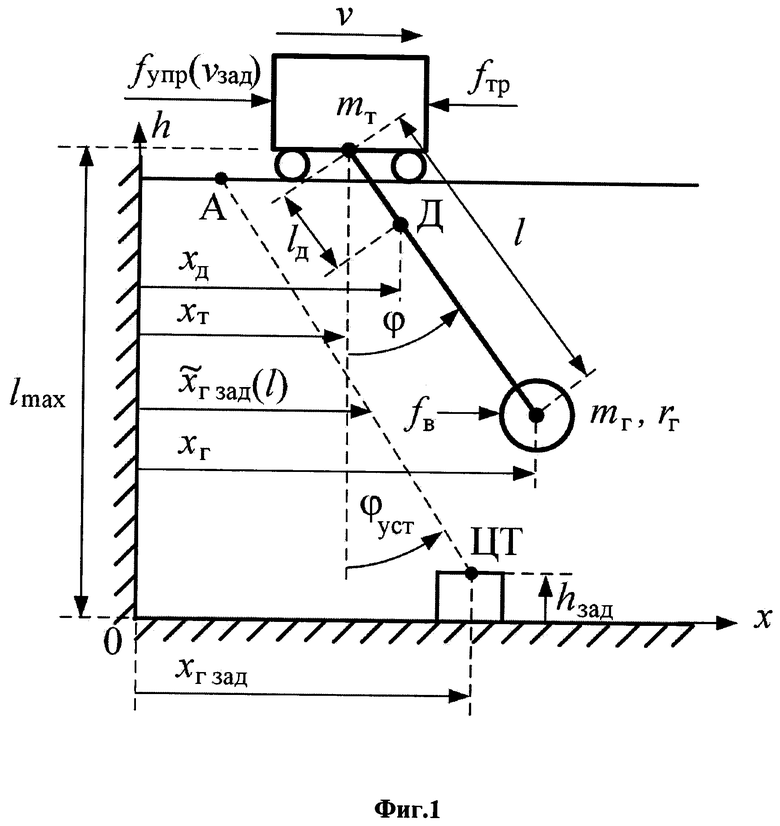
1. Способ адаптивного управления мостовым краном, заключающийся в том, что до начала перемещения груза задают требуемую траекторию его перемещения в виде неявных эталонных моделей по горизонтальным осям движения груза с заданным конечным его положением, во время перемещения груза на основе обработки данных с датчиков информации, включая текущую параметрическую идентификацию математической модели движения груза, формируют управляющие воздействия приводов мостового крана с использованием «упрощенных» условий адаптируемости, отличающийся тем, что в качестве приводов тележки и балки крана используют сервоприводы, в качестве задающих сигналов которых используют заданные скорости перемещения тележки и балки, описываемые зависимостью по формуле
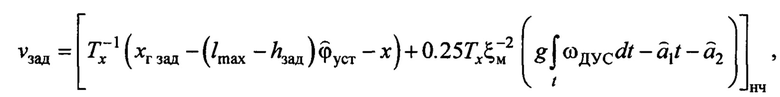
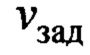 - заданная скорость перемещения тележки или балки крана;
- заданная скорость перемещения тележки или балки крана;
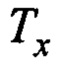 - выбираемый параметр, который может иметь разные значения для управления тележкой и балкой крана;
- выбираемый параметр, который может иметь разные значения для управления тележкой и балкой крана;
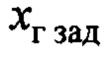 - заданное положение груза по рассматриваемой горизонтальной оси в конце регулирования;
- заданное положение груза по рассматриваемой горизонтальной оси в конце регулирования;
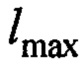 - максимальная длина подвеса крана;
- максимальная длина подвеса крана;
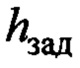 - высота погрузки переносимого груза;
- высота погрузки переносимого груза;
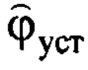 - оценка установившегося значения угла отклонения подвеса от вертикальной оси в конце регулирования из-за постоянного ветра;
- оценка установившегося значения угла отклонения подвеса от вертикальной оси в конце регулирования из-за постоянного ветра;
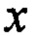 - текущее положение тележки или балки крана;
- текущее положение тележки или балки крана;
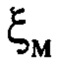 - желаемый относительный коэффициент затухания колебательного процесса или одноименный параметр назначаемой эталонной модели;
- желаемый относительный коэффициент затухания колебательного процесса или одноименный параметр назначаемой эталонной модели;
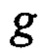 - ускорение свободного падения;
- ускорение свободного падения;
ωДУС - выходной сигнал датчика угловой скорости совмещенного датчика на канате подвеса с осью чувствительности, ортогональной канату и соответствующей угловому движению подвеса при перемещении тележки или балки;
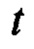 - текущее время;
- текущее время;
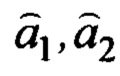 - оценки параметров, доставляемые алгоритмом текущей идентификации; нижний индекс «нч» - означает низкочастотную фильтрацию; выбираемый параметр
- оценки параметров, доставляемые алгоритмом текущей идентификации; нижний индекс «нч» - означает низкочастотную фильтрацию; выбираемый параметр 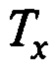 должен удовлетворять соотношениям:
должен удовлетворять соотношениям:
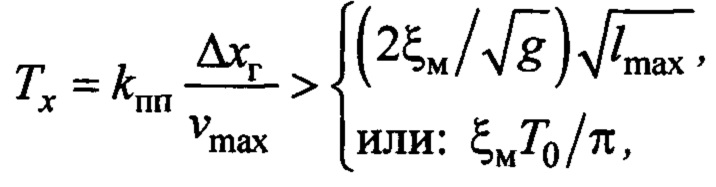
где 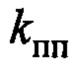 - положительный коэффициент изменения времени переходного процесса, выбираемый с учетом соблюдения этого неравенства и требуемого качества управления;
- положительный коэффициент изменения времени переходного процесса, выбираемый с учетом соблюдения этого неравенства и требуемого качества управления;
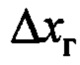 - расстояние переноса груза по горизонтальной оси от начального положения до
- расстояние переноса груза по горизонтальной оси от начального положения до 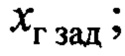 если в контуре системы управления краном непосредственно находится оператор, то этот сигнал увязывается с задающим сигналом оператора;
если в контуре системы управления краном непосредственно находится оператор, то этот сигнал увязывается с задающим сигналом оператора;
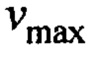 - максимальная скорость тележки или балки;
- максимальная скорость тележки или балки;
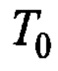 - период собственных маятниковых колебаний подвеса груза;
- период собственных маятниковых колебаний подвеса груза;
оценка установившегося значения угла отклонения подвеса от вертикальной оси в конце регулирования определяется по зависимости
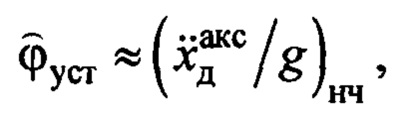
где 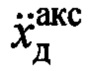 - показания акселерометра совмещенного датчика на канате подвеса по оси чувствительности, ортогональной канату и соответствующей перемещению тележки или балки;
- показания акселерометра совмещенного датчика на канате подвеса по оси чувствительности, ортогональной канату и соответствующей перемещению тележки или балки;
алгоритм текущей идентификации оценивает параметры следующего равенства:
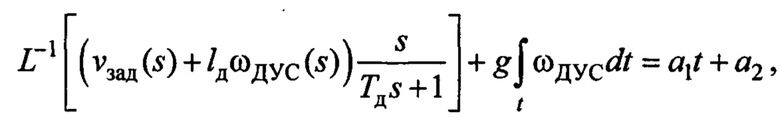
где 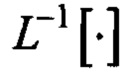 - обратное преобразование Лапласа;
- обратное преобразование Лапласа;
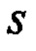 - переменная преобразования Лапласа;
- переменная преобразования Лапласа;
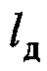 - расстояние от тележки до совмещенного датчика, расположенного на канате подвеса;
- расстояние от тележки до совмещенного датчика, расположенного на канате подвеса;
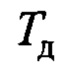 - постоянная времени реального дифференцирующего звена;
- постоянная времени реального дифференцирующего звена;
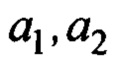 - оцениваемые алгоритмом параметры;
- оцениваемые алгоритмом параметры;
сервоприводы отрабатывают заданную скорость, в качестве датчиков информации используют совмещенный датчик, содержащий акселерометр и датчик угловой скорости с несколькими осями чувствительности обоих датчиков, совмещенный датчик крепится на канате подвеса груза рядом с тележкой крана на выбранном расстоянии, а также используют датчики пройденного пути тележкой и балкой крана.
2. Способ по п. 1, отличающийся тем, что вместо выходных сигналов датчиков пройденного пути тележкой и балкой крана используют интегрирование заданных скоростей тележки и балки крана.
| US 20240101399 A1, 28.03.2024 | |||
| СПОСОБ ДЛЯ СОПОСТАВЛЕНИЯ ПОКАЗАТЕЛЕЙ ИЗМЕРЕНИЙ ПОЗИЦИИ И ПРОФИЛЯ ДЛЯ ГРУЗОПОДЪЕМНОГО УСТРОЙСТВА | 2021 |
|
RU2795358C2 |
| CN 112141888 A, 29.12.2020 | |||
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ И СКОРОСТИ ПЕРЕМЕЩЕНИЯ ГРУЗА ПО ТРЕБУЕМОЙ ТРАЕКТОРИИ ГРУЗОПОДЪЕМНЫМ КРАНОМ МОСТОВОГО ТИПА | 2014 |
|
RU2564560C1 |
Авторы
Даты
2024-11-26—Публикация
2024-04-11—Подача