ОБЛАСТЬ ТЕХНИКИ
[1] Заявленное решение относится к области параллельных компьютерных вычислений, в частности к тензорным вычислениям и реализующим их устройствам.
УРОВЕНЬ ТЕХНИКИ
[2] Операция свертки (также известная как «конволюция», от англ. convolution [1]), а также операция перемножения матриц (как частный случай операции свертки) являются ключевыми инструментами в работе современных нейронных сетей. Данные операции являются функциями от двух аргументов: «фичи» (от англ. feature) - входные данные от пользователя или от других операций; «веса» - матрица коэффициентов перемножения, полученная на этапе обучения нейронной сети.
[3] Устройства на основе систолических массивов спроектированы таким образом, чтобы исполнять данный вид операций на несколько порядков быстрее современных процессоров общего назначения (CPU). В современных задачах исполнения больших языковых моделей (LLM) и задачах по распознаванию и генерации изображений размерности входных данных многократно превышают объем внутренней памяти (кэша) исполняющих устройств.
[4] Из уровня техники известно применение тайлинга в систолических массивах для оптимизации вычислений в таких задачах, как обработка изображений и видео, где объем обрабатываемых данных часто превышает объем памяти, а также влияние тайлинга на обеспечение максимальной производительности систолических массивов [2].
[5] Недостатком известного уровня техники является недостаточная эффективность оптимизации памяти для вычисления сверток большого размера.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[6] Заявленное решение позволяет решить техническую проблему в части оптимизации памяти для вычисления сверток большого размера за счет обеспечения бесперебойной работы систолических массивов, позволяющей одновременно подгружать данные для следующего тайла в память матричного умножителя и учёта конкретных особенностей памятей в устройстве векторных вычислений.
[7] Техническим результатом является повышение производительности процесса разделения (тайлинга) операции свертки, выполняемого на по меньшей мере одном вычислительном устройстве с матричными умножителями на основе систолических массивов.
[8] Заявленный технический результат достигается за счет выполнения способа разделения операции свертки, выполняемого на по меньшей мере одном вычислительном устройстве с матричными умножителями на основе систолических массивов, и содержащего этапы, на которых:
• получают тензоры входных данных и входных весов, являющихся аргументами функций для операции свертки, из высокопропускной памяти,
• разделяют тензоры входных данных и весов на несколько частей с учетом объема векторной и матричной памятей, соответственно,
• резервируют необходимый объем матричной памяти для последующей загрузки частей весов,
• поочередно загружают части входных данных из высокопропускной памяти в векторную память,
• осуществляют дополнительное разделение частей входных данных на несколько подчастей с учётом зарезервированного для весов объема матричной памяти и поочередно загружают указанные подчасти входных данных в матричную память,
• поочередно загружают части весов в матричную память, при этом загрузка частей весов в матричную память осуществляется параллельно c загрузкой подчастей входных данных в матричную память,
• осуществляют обработку подчастей входных данных и частей весов, считанных из матричной памяти, по меньшей мере одним матричным умножителем на основе систолических массивов, в результате которой получают подчасти результирующего тензора,
• загружают части результирующего тензора в высокопропускную память параллельно с обработкой следующих подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов.
[9] В одном из частных примеров реализации на этапе получения тензоров входных весов преобразуют веса по меньшей мере одной операции свертки в необходимый формат для матричной памяти.
[10] В другом частном примере реализации во время обработки подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов параллельно загружают следующую часть входных данных из высокопропускной памяти в векторную память, а также следующую часть весов из высокопропускной памяти в матричную память.
[11] В другом частном примере реализации получение подчасти результирующего тензора дополнительно содержит:
• получение результатов матричного умножителя на основе систолических массивов и их последовательное суммирование первым модулем скалярных операций с последующей загрузкой в память по меньшей мере одного модуля скалярных операций,
• сохранение результата суммирования, как подчасти результирующего тензора, в векторную память.
[12] В другом частном примере реализации суммирование результатов матричного умножителя на основе систолических массивов дополнительно содержит сложение первого результата матричного умножителя на основе систолических массивов с постоянным смещением при помощи первого модуля скалярных операций.
[13] В другом частном примере реализации во время суммирования последнего результата матричного умножителя на основе систолических массивов исполняют функцию активации и сложение с избыточной связью к подчасти результирующего тензора при помощи второго модуля скалярных операций.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
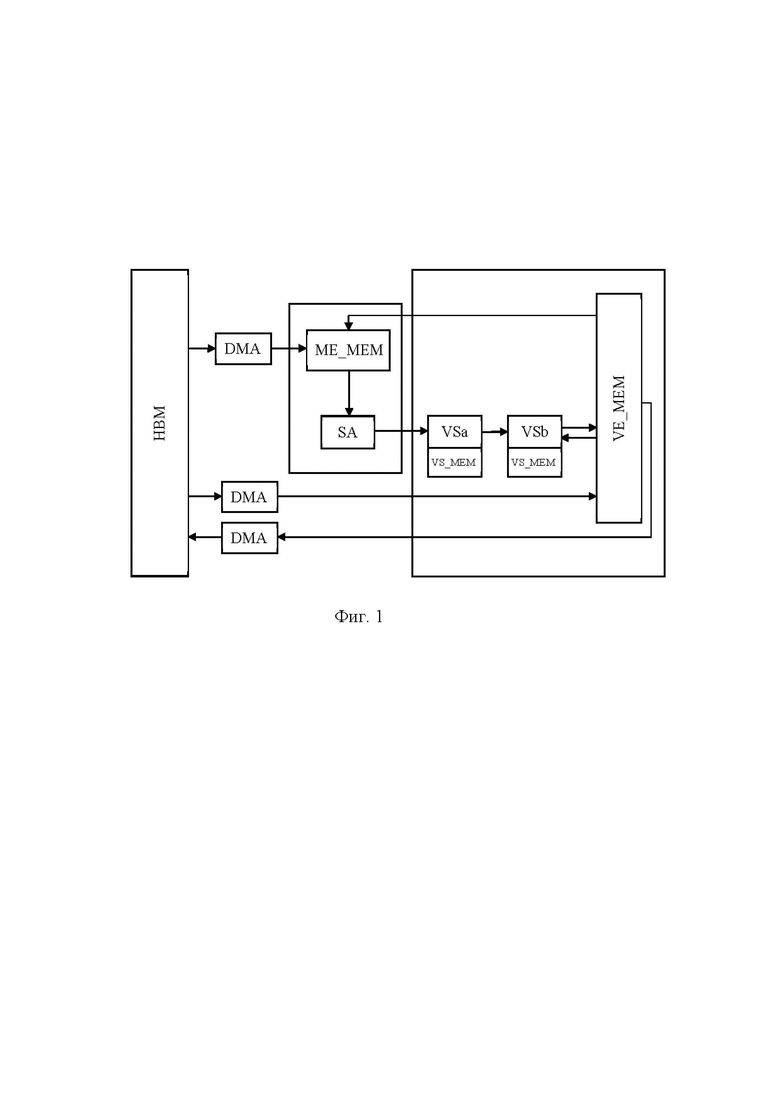
[14] На фиг. 1 представлена общая схема векторного вычислительного устройства.
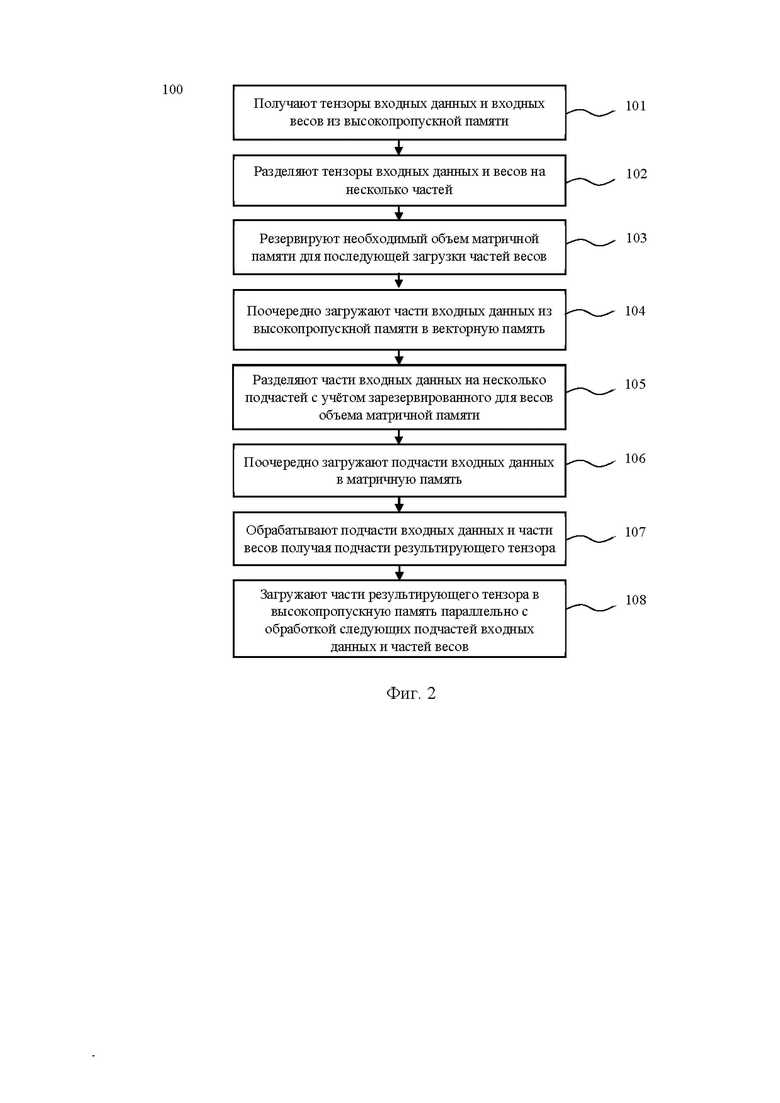
[15] На фиг. 2 представлена блок-схема способа разделения операции свертки, выполняемого на по меньшей мере одном вычислительном устройстве с матричными умножителями на основе систолических массивов.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
[16] Ниже будут описаны понятия и термины, необходимые для понимания настоящего изобретения.
[17] Тайлинг (от англ. tiling) – это разделение входных данных операции на части, и выполнение операций эквивалентных исходной над частями с целью упрощения. Тайлинг необходим в условиях ограниченной памяти, а также применим для увеличения производительности путем конвейеризации тайлов.
[18] Тайл (от англ. tilе) – это часть входных данных операции, которая получается в процессе разделения (тайлинга).
[19] Операция свертки (или свёртка) – это операция, применяемая к входному тензору (изображению) и возвращающая тензор, каждое значение которого для определенной координаты представляет собой взвешенную сумму значений входного тензора в окрестности данной координаты. Веса для расчета взвешенной суммы вычисляются на этапе обучения нейронной сети.
[20] Систолический массив (от англ. systolic array) – это однородная сеть тесно связанных блоков обработки данных (DPU), называемых ячейками или узлами. Каждый узел независимо и параллельно вычисляет частичный результат как функцию данных, полученных от его вышестоящих соседей, сохраняет результат внутри себя и передает его нижестоящим узлам [3].
[21] Тензор – это многомерная структура данных.
[22] Векторный процессор – это процессор, в котором операндами некоторых команд могут выступать упорядоченные массивы данных — векторы [4].
[23] Высокопропускная память (от англ. High Bandwidth Memory, HBM) – это высокопроизводительный интерфейс ОЗУ для DRAM с многослойной компоновкой кристаллов в микросборке [5].
[24] Генератор адресов (Address Pattern Generator, APG) – это механизм адресации, позволяющий за одну инструкцию/команду получить доступ на чтение и запись циклически по заданным значениям шага и количеству шагов.
[25] На фиг. 1 представлен общий вид вычислительного устройства с матричными умножителями на основе систолических массивов с помощью которого реализуется способ разделения операции свертки.
[26] В общем случае вычислительное устройство является векторным, то есть поддерживает одновременные вычисления массива (вектора) данных. Размер вектора (Vector Length, далее VL) обычно равен степени 2 (16, 32, 64, 128), то есть устройство может исполнять за один машинный такт VL операций с плавающей точкой. Векторное вычислительное устройство содержит по меньшей мере два матричных умножителя на основе систолических массивов (Systolic Array, далее SA), каждый из которых способен обсчитывать VL векторов данных одновременно для матричного умножения, и на SA за один машинный такт может вычисляться VL*VL (например, для VL=128: 128*128=16384) операций умножения и сложения с плавающей точкой.
[27] Векторное вычислительное устройство состоит из по меньшей мере следующих модулей (фиг. 1):
[28] - Векторная память (Vector Memory, VE_MEM) – это общая SRAM память между вычислительными модулями (VSa, VSb), размер памяти обычно несколько десятков мегабайт. Поддерживается векторная адресация через APG (Address Pattern Generator), позволяющая разным портам одновременно читать и записывать данные в разные участки памяти (скорость до 1 такта на 1 вектор памяти).
[29] - Матричная память (Matrix Engine Memory, ME_MEM) – это SRAM память для данных в SA, обычно меньшего объема по сравнению с VE_MEM, предназначена для более быстрого доступа SA к необходимым данным. Для каждого SA есть отдельная память ME_MEM. Скорость доступа составляет 1 вектор данных за 1 машинный такт. Матричная память имеет возможность записи из HBM и из VE_MEM.
[30] - Матричный умножитель на основе систолических массивов (Systolic Array, SA), который исполняет матричное умножение входных данных и весов. Входных данных и веса читаются из матричной памяти (ME_MEM). В общем случае, для инициализации весов (загрузки), необходимо минимум VL машинных тактов. Также веса могут обновляться во время досчитывания результатов на предыдущих весах, тем самым сокращая простои в VL тактов между инструкциями. Для расчета матричного умножения и операций свертки на SA необходимо, чтобы входные каналы (последняя размерность входных данных) и выходные каналы (последняя размерность результата) были кратны VL (то есть равны 1VL, 2VL, 3VL и т.д.).
[31] - Высокопропускная память (High Bandwidth Memory, HBM) – это высокоскоростная внешняя память, объемом в несколько гигабайт с последовательной адресацией. Контроллер памяти позволяет также адресовать 1 вектор данных за 1 машинный такт (к примеру, для VL=128 и данных в формате FP24 [6] необходимая скорость HBM памяти для устройства частотой 1ГГц: VL * 3 байта * 10^9 = 384 ГБ/с). В векторном вычислительном устройстве реализована поддержка чтения из высокопропускной памяти (HBM) в векторную (VE_MEM) и матричную (ME_MEM) памяти, при этом запись в HBM поддерживается только из векторной памяти (VE_MEM). В отличие от векторной и/или матричной памятей, не поддерживается одновременная запись и чтение HBM <=> VE_MEM. Чтение и запись из/в HBM производятся DMA (Direct Memory Access) контроллером.
[32] - Модуль скалярных операций (Vector Subunit, VS). В векторном вычислительном устройстве, после исполнения матричного умножения SA, реализована возможность в режиме конвейеризации отправить данные на по меньшей мере два последовательных модуля скалярных операций (VSa, VSb). Первый модуль скалярных операций (VSa) используется для сложения результата операции свертки с постоянным смещением (bias), а также для суммирования результатов с SA, чтобы получить финальный результат свертки. Второй модуль скалярных операций (VSb) чаще всего используется для вычисления активации (RELU, Sigmoid и пр), и сложения с «избыточной связью», при этом данные для «избыточной связи» подаются из векторной памяти (VE_MEM) во второй модуль скалярных операций (VSb) во время исполнения.
[33] - Память VS_MEM – это SRAM память для каждого модуля скалярных операций, которая позволяет хранить промежуточные результаты вычислений SA, и обеспечивает быстрый и практически бесконфликтный доступ к данным. Также в этой памяти эффективно хранить “bias” значение для возможности эффективного сложения. Размер VS_MEM памяти сопоставим с размером векторной памяти (VE_MEM), при этом размер VS_MEM памяти можно взять меньше в 2 раза, поскольку размер выходных данных приблизительно того же порядка, что и размер входных данных, но не нужна конвейеризация внутри VS_MEM памяти. Память VS_MEM встроена внутри каждого модуля скалярных операций (VSa, VSb).
[34] Каждый из указанных модулей векторного вычислительного устройства имеет аппаратное воплощение, например, в виде системы на кристалле (System-on-a-Chip, SoC).
[35] При описании работы способа разделения операции свертки используются следующие условные обозначения:
[36] NHWC – характеризует размерность тензора входных данных операции свертки. Например, для набора изображений NHWC={2, 480, 640, 3}, N=2 означает количество изображений (для рассматриваемого примера - 2 изображения), H=480 характеризует высоту изображения, W=640 означает ширину изображения, C=3 характеризует количество каналов (для рассматриваемого примера - 3 канала).
[37] Для текстовых данных применяют трехмерные тензора NHC, где N – батч (batch), H – номер слова/токена в тексте, С – характеристика токена. Без ограничений общности, можно считать трехмерные тензора NHC четырехмерными NHWC, где W=1.
[38] KRSC – характеризует размерность тензора входных весов, например, KRSC={64,7,7,3}. K означает выходные каналы, R характеризует размер ядра свертки по высоте, S – размер ядра свертки по ширине, последняя размерность совпадает с «C» у тензора входных данных NHWC и означает количество каналов.
[39] NPQK – характеризует размер результирующего тензора, где P – высота результата, Q – ширина результата, K характеризует выходные каналы, N характеризует батч (batch) (для задач компьютерного зрения N – это количество изображений, для задач обработки текста N – это количество фрагментов текста).
[40] Операция свертки также характеризуется дополнительными параметрами:
• Шаг свертки (stride) по осям H/W: sH, sW.
• Дилатации (dilation): шаг внутри ядра свертки: dH, dW.
• Отступы (paddings): pad_begin (pbH/pbW – отступы сверху и слева), pad_end (peH/peW – отступы справа и снизу).
[41] Для удобства расчета в векторах, поскольку вычислительное устройство с матричными умножителями на основе систолических массивов работает исключительно с векторами данных (в предпочтительном варианте воплощения, по VL=128 чисел в каждом), вводятся дополнительные обозначения: Kv и Cv – это размеры K и C в векторах соответственно. Например, для входного тензора NHWC (1x112x112x256) считаем Cv=256/128=2. Аналогично для K: веса KRSC=512x3x3x256 считаем, что Kv=512/128=4.
[42] В контексте вышеизложенного, необходимо отметить, что использование генератора адресов (APG) позволяет адресовать под-тензор для буфера данных, расположенного по последовательным адресам. Под буфером данных (весов, входных данных, результата) понимается область памяти (VE_MEM/ME_MEM), характеризующаяся начальным адресом буфера в памяти и размером буфера. Например, если текущий буфер входных данных {10, 20, 30}, чтобы из него адресовать под-тензор {5, 10, 15}, нужно задать APG вида (5, 60)(10, 30)(15, 1), где 5,10,15 – размеры нового тензора, 60 – шаг для первой (главной/внешней) значащей оси (=20*30), 30 – шаг по второй значащей оси, 1 – шаг по последней (самой внутренней) оси.
[43] В рамках данной заявки APG эффективно использовать для:
• адресации части входных данных NHWCv при копировании из векторной (VE_MEM) в матричную (ME_MEM) память «NHWcv», где сv – это часть входных каналов Сv (к примеру Cv= 4, cv=2);
• при адресации частей результата NPQkv для записи в высокопропускную память (HBM) в виде NPQKv за одну инструкцию.
[44] Для существующих современных операций свертки (например, с входным размером 1x2048x2048x128) необходимо разработать механизм разрезания/разделения (тайлинга) на несколько операций свертки с учетом размеров памятей VE_MEM, VS_MEM, ME_MEM. Также необходимо учитывать, что в операциях свертки веса получены на этапе тренировки нейронной сети и в дальнейшем при использовании не меняются в зависимости от входных данных (т.е. являются константными).
[45] Необходимо отметить, что для случая, когда все тензора помещаются во внутреннюю память (VE_MEM, VS_MEM, ME_MEM) способ разделения (тайлинг) операции свертки не требуется. Однако, в случае очень больших тензоров, которые не помещаются не только в ME_MEM, но и в VE_MEM, конвейерный механизм расчета операции свертки усложняется.
[46] На фиг. 2 представлен способ разделения (тайлинга) операции свертки, выполняемый на по меньшей мере одном вычислительном устройстве с матричными умножителями на основе систолических массивов. В качестве вычислительного устройство с матричными умножителями на основе систолических массивов может выступать, но не ограничиваться указанным примером, векторное вычислительное устройство, раскрытое выше со ссылкой на фиг. 1.
[47] На первом этапе (101) получают тензоры входных данных (фич) и входных весов, являющихся аргументами функций для операции свертки, из высокопропускной памяти (HBM).
[48] В частном примере реализации на этапе получения тензоров входных весов преобразуют веса по меньшей мере одной операции свертки в необходимый формат для матричной памяти (ME_MEM). В предпочтительном варианте исполнения в качестве необходимого формата выступает, но не ограничивается им, формат BF16 (bfloat16) [7].
[49] Поскольку веса не меняются в зависимости от входных данных, то их можно предварительно единоразово преобразовать в необходимый формат для более эффективного последующего доступа. Предобработка весов операции свертки в необходимый формат для внутренней памяти позволяет сократить загрузку весов в матричную память (ME_MEM) примерно в 2 раза, что позволяет дополнительно повысить производительность процесса разделения (тайлинга) операции свертки.
[50] На этапе (102) разделяют тензоры входных данных и весов на несколько частей с учетом объема векторной (VE_MEM) и матричной (ME_MEM) памятей, соответственно, таким образом, чтобы запись одних частей (тайлов) была возможна одновременно с чтением других частей (тайлов) без конфликтов по памяти.
[51] Поскольку поддерживается только последовательный доступ к HBM, имеется возможность только читать части по {1, 1, 1, c_step}, либо по {1, 1, w_step, C}, либо по {1, h_step, W, C}, либо {n_step, H, W, C}. Иначе говоря, невозможно одной инструкцией в HBM из тензора 2x2x256 прочитать под-тензор 2x2x128, поскольку он расположен в памяти непоследовательным буфером.
[52] На этапе (103) резервируют необходимый объем матричной памяти (ME_MEM) для последующей загрузки частей весов. Поскольку загрузка частей весов и подчастей входных данных в матричную память (ME_MEM) осуществляется параллельно, необходим этап резервирования необходимого объема матричной памяти (ME_MEM) для частей весов, чтобы избежать конфликтов по загрузке памяти матричной памяти (ME_MEM).
[53] На этапе (104) поочередно загружают части входных данных из высокопропускной памяти (HBM) в векторную память (VE_MEM). В частном примере реализации сохранение частей входных данных в векторной памяти (VE_MEM) осуществляется в формат FP24 [6].
[54] На этапе (105) осуществляют дополнительное разделение частей входных данных на несколько подчастей с учётом зарезервированного для весов объема матричной памяти (ME_MEM) и поочередно загружают указанные подчасти входных данных в матричную память (ME_MEM).
[55] Дополнительно разделение на подчасти входных данных связано с тем, что в высокопропускной памяти (HBM) не поддерживается APG адресация, т.е. из HBM нельзя одной инструкцией cчитать подчасть входных данных (NHWC_0_0), можно считать только часть входных данных (NHWC_0).
[56] Таким образом, разделение (разрезание) тензоров весов и входных данных осуществляется по всем поддерживаемым размерностям с учетом размеров внутренних памятей (например, путём резервирования необходимого объема матричной памяти) и конкретных особенностей памятей (например, отсутствие поддержки APG в HBM), что способствует оптимизации работы способа разделения (тайлинга) операции свертки и, как следствие, повышению его производительности.
[57] На этапе (106) поочередно загружают части весов в матричную память (ME_MEM), при этом загрузка частей весов в матричную память (ME_MEM) осуществляется параллельно c загрузкой подчастей входных данных в матричную память (ME_MEM). Параллельное осуществление загрузки частей весов и подчастей входных данных в матричную память (ME_MEM) способствует повышению производительности способа разделения (тайлинга) операции свертки за счёт оптимизации загрузки (заполнения) матричной памяти (т.е. обеспечение ситуации, когда подчасть входных данных и часть весов суммарно не превышают объём ME_MEM). Указанное преимущество реализуется путём резервирования необходимого объема матричной памяти для частей весов и учёта этого резервирования при дополнительном разделении частей входных данных на подчасти.
[58] На этапе (107) осуществляют обработку подчастей входных данных и частей весов, считанных из матричной памяти (ME_MEM), по меньшей мере одним матричным умножителем на основе систолических массивов (SA), в результате которой получают подчасти результирующего тензора (NPQK). В предпочтительном варианте воплощения заявленного решения обработка на этапе (107) осуществляется двумя матричными умножителями на основе систолических массивов (SA).
[59] В одном из частных примеров реализации во время обработки подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов (SA) параллельно загружают следующую часть входных данных из высокопропускной памяти (HBM) в векторную память (VE_MEM), а также следующую часть весов из высокопропускной памяти (HBM) в матричную память (ME_MEM). Осуществление загрузки следующей части входных данных из HBM в VE_MEM и следующей части весов из HBM в ME_MEM параллельно с обработкой на этапе (107) позволяет добиться сокращения простоев работы по меньшей мере одного матричного умножителя на основе систолических массивов (SA) за счёт непрерывного поступления данных для обработки, что дополнительно способствует повышению производительности процесса разделения (тайлинга) операции свертки.
[60] В частном варианте воплощения получение подчасти результирующего тензора (NPQK) дополнительно содержит:
• получение результатов матричного умножителя на основе систолических массивов (SA) и их последовательное суммирование первым модулем скалярных операций (VSa) с последующей загрузкой в память (VS_MEM) по меньшей мере одного модуля скалярных операций (VS),
• сохранение результата суммирования, как подчасти результирующего тензора (NPQK), в векторную память (VE_MEM).
[61] Необходимо отметить, что в VS_MEM хранится не все результаты матричного умножителя (например, a, b, c, d, e), а только сумма всех результатов матричного умножителя (сначала a, потом a+b, потом a+b+c и т.д.). Таким образом, память в VS_MEM нужна только для хранения одного результата матричного умножителя.
[62] В одном из частных примеров реализации суммирование результатов матричного умножителя на основе систолических массивов (SA) дополнительно содержит сложение первого результата матричного умножителя на основе систолических массивов (SA) с постоянным смещением (bias) при помощи первого модуля скалярных операций (VSa).
[63] В другом частном примере реализации во время суммирования последнего результата матричного умножителя на основе систолических массивов (SA) исполняют функцию активации и сложение с избыточной связью (residual connection [8]) к подчасти результирующего тензора (NPQK) при помощи второго модуля скалярных операций (VSb).
[64] На этапе (108) загружают части результирующего тензора (NPQK) в высокопропускную память (HBM) параллельно с обработкой следующих подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов (SA).
[65] Обеспечение непрерывности процесса разделения (тайлинга) операции свертки за счёт реализации загрузки части результирующего тензора (NPQK) в HBM параллельно с обработкой следующих подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на SA способствует повышению производительности процесса разделения (тайлинга) операции свертки.
[66] Способ разделения операции свертки продолжается, пока из высокопропускной памяти (HBM) продолжается поступление тензоров входных данных и входных весов. Этапы (106)-(108) повторяются для новых частей входных данных.
[67] Для оценки эффективности заявленного способа разделения операции свертки используют следующие критерии.
[68] Для входных данных NHWC, весов KRSC и результата NPQK количество машинных тактов, необходимых для расчета операции свертки на одном SA без простоев, вычисляется по формуле:
CyclesSA = N * P * Q * Kv * R * S * Cv
[69] Или для простоты для матричного умножения (H=W=P=Q=R=S=1), N >128 (иначе возникнут простои при переключении весов):
CyclesSA = N * Kv * Cv
[70] В случае двух SA кол-во тактов уменьшается в 2 раза.
[71] При разделении входных данных на kF частей, а весов на kW частей, нагрузка на разные памяти составит:
Веса (HBM->ME_MEM, перезагружаются kF раз): CyclesW_HBM = Kv * Cv * kF * VL
Входные данные (HBM->VE_MEM + VE_MEM->HBM): CyclesF_HBM = N * Cv + N * Kv
VE_MEM->ME_MEM: CyclesF_MEMEM = N * Cv – всегда меньше CyclesF_HBM
[72] Из формул видно, что скомпенсировать нагрузку на память во время полезных вычислений можно только в случае, если Kv > 1 и Cv > 1, иначе не удастся скомпенсировать нагрузку на HBM для входных данных. Также необходимо, чтобы kF * VL < N, иначе не удастся скомпенсировать нагрузку на HBM для весов.
[73] В случае операции свертки, формулы расчета тактов аналогичные (для не единичных ядер в большинстве случаев можно без существенных потерь точности пренебречь перекрытиями по H и W):
CyclesW_HBM = Kv * R * S * Cv * kF * VL
CyclesF_HBM = N * H * W * Cv + N * P * Q * Kv
[74] В этом случае требование Cv > 1 ослабляется до Cv * R * S > 1, и kF*VL < N*P*Q. Для больших шагов свертки, sH > 1 или sW > 1 приведет к тому, что H*W > P*Q и необходимо соблюдать требование H * W < P * Q * Kv * R * S, что не всегда возможно обеспечить.
[75] Результаты экспериментов
[76] Для типовой операции свертки в сети ResNet50 с параметрами VL=128, NHWC={N, 56, 56, 128}, KRSC={128, 3, 3, 128}, NPQK={1,56,56,128}, sH=sW=dH=dW=pbH=beH=pbW=peW=1
нагрузка на HBM составит CyclesF_HBM = N * 56 * 56 * 1 + N * 56 * 56 * 1 = 6272*N,
нагрузка на веса (kF*VL=N) составит CyclesW_HBM = 128*3*3*N = 1152*N,
CyclesSA = N * 56 * 56 * 1 * 3 * 3 * 1 = 28224*N, или 14112 * N для двух SA.
[77] Из вышеуказанных экспериментальных данных следует, что для этой операции свертки можно с большим запасом скомпенсировать нагрузку на HBM.
[78] Эксперименты на потактовой модели устройства (с использованием специализированной программы – потактового симулятора) с учетом простоев при переключении весов, конфликтов по памяти, показали эффективность для данного примера в 96% при N = 64: CyclesSA = 903168, общее количество тактов на потактовом симуляторе с учетом загрузки смещения, первой части весов и выгрузки последней части результатов = 950970 тактов.
[79] Без реализации данного способа, при вычислении каждой порции входных данных (фич) отдельно (с учетом распараллеливания вычислений на два SA), общее количество тактов на потактовом симуляторе получалось примерно 1.86 млн тактов, т.е. заявленный способ разделения (тайлинга) операции свертки с достижением максимальной загрузки приблизительно в 1860/950.97 = 1.9 раз эффективнее.
[80] Далее представлено пошаговое описание используемых алгоритмов.
[81] 1. Алгоритм выбора коэффициентов нарезки тензоров NPQK/KRSC по осям. Коэффициенты {dst_n, dst_p, dst_q, dst_k} – нарезка выходного тензора (dst – destination), {w_k, w_r, w_s, w_c} – нарезка по весам (w-weights).
[82] Нужно обратить внимание, что нарезается не входной тензор NHWC, а выходной NPQK. Так алгоритм нарезки существенно упрощается, поскольку не нужно следить за тем, что в каждом тайле помещается целое количество выходных данных. После этого вычисляется, какую часть входных данных NHWC нужно вырезать для получения требуемого результата NPQK.
[83] Например, для входных данных (фич) 0,1,2,3,4,5,6,7,8,9,10 и свертки ядром r=5 и страйдом stride=3, pad_begin=2, pad_end=0 для выходных данных нужно загружать в ME_MEM
вых0: _,_,0,1,2
вых1: 1,2,3,4,5
вых2: 4,5,6,7,8
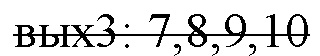 – уже не набирается 5 элементов.
– уже не набирается 5 элементов.
[84] Т.е. выходные данные вых1 и вых2 частично используют одни и те же входные данные (4 и 5) и, если делать цикл по входным данным, то нужно учитывать такого рода перекрытия. А также придется учитывать, что в конце цикла набранных элементов может не хватить и останавливаться раньше. С учетом того, что “r=5” может тоже разделяться на “3+2”, то разрезание в цикле по входным данным (фичам) становится намного более громоздким. Поэтому выбран тайлинг именно по выходным размерностям.
[85] 1.1. Базовые функции
[86] Dst_to_f – функция расчета количества входных данных (фич) по H/W, необходимых для получения определенного количества выходных данных по P/Q.
[87] Dst_min_p – функция оценки минимального значения P у тайла с учетом паддинга в сети. Если паддинг достаточно большой, то первые результаты получаются без участия входных данных (фичей), что приведет к чтению нулевых тензоров. Вычисляем минимальный P/Q, чтобы какая-то минимальная часть входных данных (фичей) все же участвовала в вычислениях, поскольку в инструкции SA невозможно передать пустые входные данных (фичи).
[88] Dst_min_q – аналогично dst_min_p, но для значения Q у тайла.
[89] Is_dst_effective – функция оценки эффективности тайла. Нарезка эффективна, если N*P*Q > VL, иначе могут быть дополнительные простои внутри SA при переключении тайлов весов.
[90] 1.2. Нарезка весов {w_k, w_r, w_s, w_c}
[91] Задача: Для тензора весов W {K, R, S, C} подбираются размеры тайлов (нарезки) w_k, w_r, w_s, w_c, чтобы тензор {w_k, w_r, w_s, w_c} эффективно помещался в ME_MEM.
[92] Алгоритм:
• Первоначально выставляется w_k=VL, w_r=1, w_s=1, w_c = VL;
• Вычисляется максимальный размер по C (w_c), чтобы помещалось 2 тайла, а также как минимум осталось место под эффективный размер входных данных (также 2 тайла), но не меньше dst_min_p/q. После вычисления w_c, считаем, что тайл входных данных также будет w_c. Подбор производится методом перебора от C до VL так, чтобы w_c был делителем C;
• - Если w_c ==C, то аналогично продолжаем поиск нарезки для w_s, после поиска w_s, минимальный размер входных данных также должен быть w_s;
• Если w_s == S, то подбираем w_r;
• w_k всегда можно оставить равным VL, т.к. нет влияния на производительность и поэтому можно взять минимальный тайл.
[93] 1.3 Нарезка входных данных (фич) {dst_n, dst_p, dst_q, dst_k}
[94] Задача: Для тензора входных данных F {N, H, W, C} подбираются размеры тайлов (нарезки), чтобы одна часть эффективно помещалась в ME_MEM. Поскольку нарезка производится по выходному тензору NPQK, т.е. вычисляются размеры выходного тайла {dst_n, dst_p, dst_q, dst_k} таким образом, чтобы соответствующие размеры входных данных эффективно помещались в ME_MEM.
[95] Выбор коэффициентов нарезки входных данных производится методом «двоичного поиска». В отличие от выбора тайла весов – уже не учитывается возможная (или невозможная) будущая эффективность нарезки – стараемся занять максимальное оставшееся место в ME_MEM.
[96] Алгоритм также подбирает тайлы, начиная с самой внутренней размерности:
• dst_k=VL (равен w_k);
• подбирается dst_q, по ней нарезку на W (feat_W, с помощью dst_to_f), бинарным поиском подбираем, чтобы 2 тайла помещались в ME_MEM вместе с двумя тайлами весов;
• если dst_q < Q – то поиск прекращается, для остальных размерностей оставляем минимальные значения, иначе продолжаем поиск по P (dst_p и feat_H);
• если dst_P < P, то считаем dst_n минимальным (dst_n=1), иначе продолжаем поиск dst_n.
[97] В результате работы алгоритма возвращается наиболее эффективная нарезка по выходном тензору и по весам.
[98] 2. Алгоритм разделения (тайлинга)

[99] Важным моментом для достижения производительности является дальнейшее перемешивание инструкций таким образом, чтобы инструкции, которые могут исполняться параллельно, находились друг за другом, т.е. инструкции И3 и И4 загрузки части веса/входных данных должны находится рядом с инструкцией И5 (на SA), вычисляющей матричное умножение предыдущей части уже загруженных весов/входных данных, что позволяет устранить простой в процессе работы SA.
[100] Представленные материалы заявки раскрывают предпочтительные примеры реализации технического решения и не должны трактоваться как ограничивающие иные, частные примеры его воплощения, не выходящие за пределы испрашиваемой правовой охраны, которые являются очевидными для специалистов соответствующей области техники.
[101] Источники информации
[1] Свёрточная нейронная сеть - Википедия. https://ru.wikipedia.org/wiki/Свёрточная_
нейронная_сеть#Слой_свёртки
[2] Udit Kumar Agarwal "Resilience Assessment of Machine Learning Applications under Hardware Faults" (August 2023), раздел «2.3.2 Operation Tiling in Systolic Arrays». https://open.library.ubc.ca/media/stream/pdf/24/1.0435699/4
[3] Систолический массив - Википедия. https://ru.wikipedia.org/wiki/Систолический_массив
[4] Векторный процессор – Википедия. https://ru.wikipedia.org/wiki/Векторный_процессор
[5] Высокопропускная память - Википедия. https://ru.wikipedia.org/wiki/
Высокопропускная_память
[6] Minifloat – Wikipedia. https://en.wikipedia.org/wiki/Minifloat
[7] bfloat16 floating-point format – Wikipedia. https://en.wikipedia.org/wiki/Bfloat16_floating-point_format
[8] Notes on residual connections. https://www.kaggle.com/code/residentmario/notes-on-residual-connections
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОМПИЛЯЦИИ НЕЙРОННЫХ СЕТЕЙ | 2024 |
|
RU2835757C1 |
| УСТРОЙСТВО МАТРИЧНЫХ ВЫЧИСЛЕНИЙ | 2025 |
|
RU2838831C1 |
| Метод построения процессоров для вывода в сверточных нейронных сетях, основанный на потоковых вычислениях | 2020 |
|
RU2732201C1 |
| МАТРИЧНО-ВЕКТОРНЫЙ УМНОЖИТЕЛЬ С НАБОРОМ РЕГИСТРОВ ДЛЯ ХРАНЕНИЯ ВЕКТОРОВ, СОДЕРЖАЩИМ МНОГОПОРТОВУЮ ПАМЯТЬ | 2019 |
|
RU2795887C2 |
| СПОСОБ ОБРАБОТКИ ДАННЫХ ПОСРЕДСТВОМ НЕЙРОННОЙ СЕТИ, ПОДВЕРГНУТОЙ ДЕКОМПОЗИЦИИ С УЧЕТОМ ОБЪЕМА ПАМЯТИ ВЫЧИСЛИТЕЛЬНОГО УСТРОЙСТВА (ВАРИАНТЫ), И КОМПЬЮТЕРНО-ЧИТАЕМЫЙ НОСИТЕЛЬ | 2023 |
|
RU2820172C1 |
| ВЕКТОРНОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2024 |
|
RU2830044C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ГЕНЕРАЛИЗАЦИИ КАРТЫ | 2022 |
|
RU2803880C1 |
| Специализированная вычислительная система, предназначенная для вывода в глубоких нейронных сетях, основанная на потоковых процессорах | 2022 |
|
RU2793084C1 |
| Способ определения результатов векторно-матричных преобразований в параллельных акустооптических процессорах | 1989 |
|
SU1735836A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 2005 |
|
RU2370886C2 |
Изобретение относится к способам организации параллельных компьютерных вычислений. Технический результат заключается в повышении производительности процесса тайлинга операции свертки. Технический результат достигается за счет выполнения способа, содержащего этапы, на которых: получают тензоры входных данных и входных весов из высокопропускной памяти; разделяют тензоры входных данных и весов на несколько частей; резервируют необходимый объем матричной памяти; поочередно загружают части входных данных из высокопропускной памяти в векторную память; осуществляют разделение частей входных данных на несколько подчастей с учётом зарезервированного объема памяти и загружают подчасти в память; поочередно загружают части весов в память, при этом загрузка частей весов в память осуществляется параллельно c загрузкой подчастей входных данных; осуществляют обработку входных данных и весов, считанных из матричной памяти, в результате которой получают подчасти результирующего тензора; загружают части результирующего тензора в высокопропускную память параллельно с обработкой следующих подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов. 5 з.п. ф-лы, 2 ил.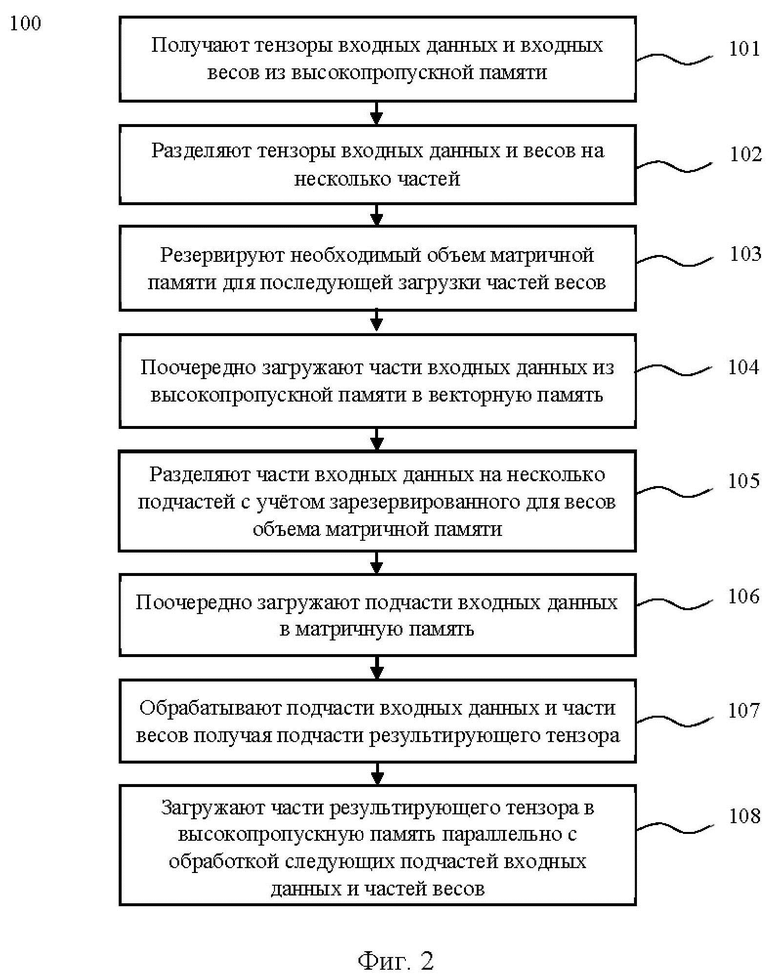
1. Способ разделения операции свертки, выполняемый на по меньшей мере одном вычислительном устройстве с матричными умножителями на основе систолических массивов, содержащий этапы, на которых:
получают тензоры входных данных и входных весов, являющихся аргументами функций для операции свертки, из высокопропускной памяти,
разделяют тензоры входных данных и весов на несколько частей с учетом объема векторной и матричной памятей, соответственно,
резервируют необходимый объем матричной памяти для последующей загрузки частей весов,
поочередно загружают части входных данных из высокопропускной памяти в векторную память,
осуществляют дополнительное разделение частей входных данных на несколько подчастей с учётом зарезервированного для весов объема матричной памяти и поочередно загружают указанные подчасти входных данных в матричную память,
поочередно загружают части весов в матричную память, при этом загрузка частей весов в матричную память осуществляется параллельно c загрузкой подчастей входных данных в матричную память,
осуществляют обработку подчастей входных данных и частей весов, считанных из матричной памяти, по меньшей мере одним матричным умножителем на основе систолических массивов, в результате которой получают подчасти результирующего тензора,
загружают части результирующего тензора в высокопропускную память параллельно с обработкой следующих подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов.
2. Способ по п. 1, характеризующийся тем, что на этапе получения тензоров входных весов преобразуют веса по меньшей мере одной операции свертки в необходимый формат для матричной памяти.
3. Способ по п. 1, характеризующийся тем, что во время обработки подчастей входных данных и частей весов по меньшей мере одним матричным умножителем на основе систолических массивов параллельно загружают следующую часть входных данных из высокопропускной памяти в векторную память, а также следующую часть весов из высокопропускной памяти в матричную память.
4. Способ по п. 1, характеризующийся тем, что получение подчасти результирующего тензора дополнительно содержит:
получение результатов матричного умножителя на основе систолических массивов и их последовательное суммирование первым модулем скалярных операций с последующей загрузкой в память по меньшей мере одного модуля скалярных операций,
сохранение результата суммирования как подчасти результирующего тензора в векторную память.
5. Способ по п. 4, характеризующийся тем, что суммирование результатов матричного умножителя на основе систолических массивов дополнительно содержит сложение первого результата матричного умножителя на основе систолических массивов с постоянным смещением при помощи первого модуля скалярных операций.
6. Способ по любому из пп. 4, 5, характеризующийся тем, что во время суммирования последнего результата матричного умножителя на основе систолических массивов исполняют функцию активации и сложение с избыточной связью к подчасти результирующего тензора при помощи второго модуля скалярных операций.
| CN 111915001 B, 12.04.2024 | |||
| Способ получения продуктов конденсации фенолов с формальдегидом | 1924 |
|
SU2022A1 |
| Электромагнитный прерыватель | 1924 |
|
SU2023A1 |
| Способ получения продуктов конденсации фенолов с формальдегидом | 1924 |
|
SU2022A1 |
| JP 2024036383 A, 15.03.2024 | |||
| Специализированная вычислительная система, предназначенная для вывода в глубоких нейронных сетях, основанная на потоковых процессорах | 2022 |
|
RU2793084C1 |
Авторы
Даты
2024-11-11—Публикация
2024-07-15—Подача